Normalized Compression Distance of Multisets with Applications

Abstract

Pairwise normalized compression distance (NCD) is a parameter-free, feature-free, alignment-free, similarity metric based on compression. We propose an NCD of multisets that is also metric. Previously, attempts to obtain such an NCD failed. For classification purposes it is superior to the pairwise NCD in accuracy and implementation complexity. We cover the entire trajectory from theoretical underpinning to feasible practice. It is applied to biological (stem cell, organelle transport) and OCR classification questions that were earlier treated with the pairwise NCD. With the new method we achieved significantly better results. The theoretic foundation is Kolmogorov complexity.

I. Introduction

The way in which objects are alike is commonly called similarity. This similarity is expressed on a scale of 0 to 1 where 0 means identical and 1 means completely different. A multiset of objects has the property that each object in the multiset is similar to each other object below a certain maximal threshold. This maximum is the subject of the present investigation. We use the information in an individual object and concentrate on classification questions.

To define the information in a single finite object one uses the Kolmogorov complexity [15] of that object (finiteness is taken as understood in the sequel). Information distance [2] is the information required to transform one in the other, or vice versa, among a pair of objects. For research in the theoretical direction see among others [24]. Here we are more concerned with normalizing it to obtain the so-called similarity metric and subsequently approximating the Kolmogorov complexity through real-world compressors [19]. This leads to the normalized compression distance (NCD) which is theoretically analyzed and applied to general hierarchical clustering in [4]. The NCD is parameter-free, feature-free, and alignment-free, and has found many applications in pattern recognition, phylogeny, clustering, and classification, for example [1], [13], [14], [25], [26], [6], [7], [31] and the many references in Google Scholar to [19], [4]. The question arises of the shared information between many objects instead of just a pair of objects.

A. Related Work

In [20] the notion is introduced of the information required to go from any object in a multiset of objects to any other object in the multiset. This is applied to extracting the essence from, for example, a finite nonempty multiset of internet news items, reviews of electronic cameras, tv’s, and so on, in a way that works better than other methods. Let X denote a finite nonempty multiset of n finite binary strings defined by (abusing the set notation) X = {x₁, …, x_n}, the constituting elements (not necessarily all different) ordered length-increasing lexicographic. We use multisets and not sets, since if X is a set then all of its members are different while we are interested in the situation were some or all of the objects are equal. Let U be the reference universal Turing machine, for convenience the prefix one as in Section VI-C. We define the information distance in X by E_max(X) = min{|p| : U(x_i, p, j) = x_j for all x_i, x_j ∈ X}. It is shown in [20], Theorem 2, that

$$E_{max}(X)=\underset{x:x\in X}{max}K(X\mid x),$$ (I.1)

up to an additive term of O(log n). Here the function K is the prefix Kolmogorov complexity as in Section VI-C. The information distance in [2] between strings x₁ and x₂ is denoted by E₁(x₁, x₂) = max{K(x₁|x₂), K(x₂|x₁)}. Here we use the notation max_x:x∈X K(X|x). The two coincide for |X| = 2 since K(x, y|x) = K(y|x) up to an additive constant term. In [27] this notation was introduced and the many results were obtained for finite nonempty multisets. A review of some of the above is [21].

B. Results

For classifying an object into one or another of disjoint classes we aim for the class of which the NCD for multisets grows the least. To compute the NCDs for these classes directly is more straightforward than using the pairwise NCD and gives significantly better results (Section IV). To obtain the NCD for multisets we proceed as follows. First we treat the theory (Section II). The normalization of the information distance for multisets retaining the metricity did not succeed in [27]. Here it is analyzed and performed in Subsection II-A. We require metricity since otherwise the results may be inconsistent across comparisons. This section is the theoretic underpinning of the method in terms of the ideal mathematics notion of Kolmogorov complexity. Subsequently we approach the Kolmogorov complexities of the strings involved by practically feasible lengths of the compressed versions of the strings. We prove first that the transition from information distance to compression distance is a metric as well, Subsection II-B. Next, the compression distance is normalized and proved to retain the metricity, Subsection II-C. We go into the question of how to compute this, and how to apply this to classification in Section III. Then we treat applications in Section IV. We apply the NCD for multisets to retinal progenitor cell classification questions, Section IV-A, and to synthetically generated data, Section IV-B. These were earlier treated with the pairwise NCD. Here we obtain significantly better results. This was also the case for questions about axonal organelle transport, Section IV-C. We apply the NCD for multisets to classification of handwritten digits, Section IV-D. Although the NCD for multisets does not improve on the accuracy of the pairwise NCD for this application, classification accuracy is much improved over either method individually by combining the pairwise and multiset NCD with a partitioning algorithm to divide the data into more similar subsets. This improved combined approach was too computationally intensive to be run on the full MNIST dataset, only a subset was considered. We applied a less computationally demanding approach, using the faster but less accurate JPEG2000 compression with no partitioning. This enabled us to process the full MNIST dataset, still yielding good results. We treat the data, software, and machines used for the applications in Section IV-E. We finish with conclusions in Section V. In Section VI-A we define strings; in Section VI-B computability notions; in Section VI-C Kolomogorov complexity (K); in Section VI-D multisets; in Section VI-E information distance, and in Section VI-F metric. The proofs are deferred to Section VI-G.

II. The Theory

Let 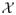be the set of length-increasing lexicographic ordered finite nonempty multisets of finite nonempty strings (Sectiones VI-A, VI-D). The quantitative difference in a certain feature between the strings in a multiset is an admissible multiset distance if it is a mapping D : 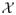→ 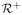with 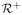is the set of nonnegative real numbers, it is upper semicomputable (Section VI-B), and the following density condition for every string x holds

$$\sum _{x:x\in X\&D(X)>0}{2}^{-D(X)}\le 1,$$ (II.1)

where the X’s run over 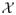. This requirement exclude trivial distances such as D(X) = 1/2 for every X.

A. Normalized Information Distance for Multisets

By (I.1) we have E_max = max_x∈X{K(X|x)} + O(log |X|). Theorem 5.2 in [27] shows that E_max (the proof shows this actually for max_x∈X{K(X|x)}) is universal in that among all admissible multiset distances it is always least up to an additive constant. That is, it accounts for the all computable features (properties) which all the elements of the multiset share.

Admissible multiset distances as defined above are absolute, but if we want to express similarity, then we are more interested in relative ones. For example, if a multiset X of strings of each about 1,000,000 bits has information distance max_x∈X{K(X|x)} = 1,000 bits, then we are inclined to think that those strings are similar. But if a multiset Y consists of strings of each about 1,100 bits and max_y∈Y {K(Y|y)} = 1,000 bits, then we think the strings in Y are different.

To express similarity we therefore need to normalize the information distance in a multiset. It should give a similarity with distance 0 when the objects in a multiset are maximally similar (that is, they are equal), and distance 1 when they are maximally dissimilar. We desire the normalized version of the universal multiset information distance to be also a metric.

For pairs of objects x, y the normalized version e of E_max is defined in [19], [4] by

$$e(x,y)=\frac{max\{K(x,y\mid x),K(x,y\mid y)\}}{max\{K(x),K(y)\}}.$$ (II.2)

It takes values in [0, 1] up to an additive term of O(1/K(x, y)). It is a metric up to additive terms O((logK)/K), where K denotes the maximum of the Kolmogorov complexities involved in each of the metric (in)equalities, respectively. A normalization formula for multisets of more than two elements ought to reduce to that of (II.2) for the case of multisets of two elements. The most natural definition of a normalized information distance for multisets is a generalization of (II.2):

$$e_1(X)=\frac{{max}_{x\in X}\{K(X\mid x)\}}{{max}_{x\in X}\{K(X\backslash \{x\})\}}.$$ (II.3)

However e₁ is not a metric. For example A = {x}, B = {y, y}, C = {y}, K(x) = n, K(x|y) = n, K(y) = 0.9n and by using (VI.1) we have K(x, y) = 1.9n, K(y|x) = 0.9n. But e₁(AB) = K(x|y)/K(x, y) = n/1.9n ≈ 1/2, and e₁(AC) = K(x|y)/K(x) = n/n = 1, e₁(CB) = K(y|y)/K(y) = 0/0.9n = 0. This shows that the triangle inequality is violated for e₁. The reason is the following:

Lemma II.1

Let X, Y ∈ 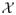and d : 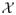→ 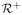be a distance that satisfies the triangle inequality of a metric. If Y ⊆ X then d(Y) ≤ d(X).

The next attempt is nondecreasing over supersets.

Definition II.2

Let X ∈ 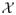. The normalized information distance (NID) for multisets with |X| ≥ 2 is

$$e(X)=max\left\{\frac{{max}_{x\in X}\{K(X\mid x)\}}{{max}_{x\in X}\{K(X\backslash \{x\})\}},\underset{Y\subset X}{max}\{e(Y)\}\right\}.$$ (II.4)

For |X| = 1 we set e(X) = 0.

For |X| = 2 the value of e(X) reduces to that of (II.2). Instead of “distance” for multisets one can also use the term “diameter.” This does not change the acronym NID. The information diameter of a pair of objects is the familiar NID distance between these objects.

Theorem II.3

For every X ∈ 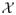we have 0 ≤ e(X) ≤ 1.

Remark II.4

The least value of e(X) is reached if all occurrences of elements of X are equal, say x. In that case 0 ≤ e(X) ≤ O(K(|X|)/K(X \ {x})). The greatest value e(X) = 1 − O(1/K(X \ {x})) is reached if max_x∈X{K(X|x)} = max_x∈X{K(X \ {x}) + O(1). This is shown as follows: (≤) trivially there is an O(1)-bit program computing max_x∈X{K(X|x)} from max_x∈X{K(X \ {x}); and (≥) if X = {x, y}, K(y|x) + O(1) = K(y), and K(x) > K(y), then K(X|x) = K(y) ± O(1).

Another matter is the consequences of (II.4). Rewrite both the numerator and the denominator of (II.3) (that is, the left-hand term inside the maximalization of (II.4)) by the symmetry of information law (VI.1).

Then we obtain with equality up to additive logarithmic terms in the numerator and denominator

$$\begin{array}{l}{e}_1(X)=\frac{{max}_{x\in X}\{K(X\mid x)\}}{{max}_{x\in X}\{K(X\backslash \{x\})\}}=\frac{K(X)-{min}_{x\in X}\{K(x)\}}{K(X)-{min}_{x\in X}\{K(x\mid X\backslash \{x\})\}}\\ =1-\frac{{min}_{x\in X}\{K(x)\}-{min}_{x\in X}\{K(x\mid X\backslash \{X\})\}}{K(X)-{min}_{x\in X}\{K(x\mid X\backslash \{x\})\}}.\end{array}$$ (II.5)

That is, e₁(X) → 1 (and hence e(X) → 1 while e₁(X) = e(X) for infinitely many X), if both

$$K(X)\to \infty \text{and}\frac{{min}_{x\in X}\{K(x)\}}{K(X)}\to 0.$$

This happens, for instance, if |X| = n, min_x∈X = 0, K(X) > n, and n → ∞. Also in the case that X = {x, x, …, x} (n copies of a fixed x) and n → ∞. Then K(X) → ∞ and min_x∈X{K(x)}/K(X) → 0 with |X| → ∞. To consider another case, we have K(X) → ∞ and min_x∈X{K(x)}/K(X) → 0 if min_x∈X{K(x)} = o(K(X)) and max_x∈X{K(x)} − min_x∈X{K(x)} → ∞, that is, if X consists of at least two elements, the element of minimum Kolmogorov complexity is always the same, and gap between the minimum Kolmogorov complexity and the maximum Kolmogorov complexity of the elements grows to infinity when K(X) → ∞.

Remark II.5

When is Y ⊂ X and e(X) = e(Y) while e₁(X) < e₁(Y)? This happens if

$$\frac{K(Y)-{min}_{x\in Y}\{K(x)\}}{{max}_{x\in Y}\{K(Y\backslash \{x\})\}}>\frac{K(X)-{min}_{x\in X}\{K(x)\}}{{max}_{x\in X}\{K(X\backslash \{x\})\}},$$ (II.6)

ignoring logarithmic additive terms. An example is X = {x, y, y} and Y = {x, y}. Then Y ⊂ X. The left-hand side of (II.6) equals 1 and the right-hand side equals ≈ 1/2. Therefore, e₁(Y) > e₁(X) and by (II.4) we have e(X) = e(Y).

Theorem II.6

The function e as in (II.4) is a metric up to an additive O((logK)/K) term in the respective metric (in)equalities, where K is the largest Kolmogorov complexity involved the (in)equality.

B. Compression Distance for Multisets

If G is a real-world compressor. then K(x) ≤ G(x) for all strings x. We assume that the notion of the real-world compressor G used in the sequel is “normal” in the sense of [4]. Let X ∈ 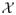and X = {x₁, …, x_n}. The information distance E_max(X) can be rewritten as

$$max\{K(X)-K(x_1),\dots ,K(X)-K(x_n)\},$$ (II.7)

up to an additive term of O(logK(X)), by (VI.1). The term K(X) represents the length of the shortest program for X.

Definition II.7

By G(x) we mean the length of string x when compressed by G. Consider X ∈ 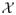as a string consisting of the concatenated strings of its members ordered length-increasing lexicographic with a means to tell the constituent elements apart.

$$E_{G,max}(X)=max\{G(X)-G(x_1),\dots ,G(X)-G(x_n)\}=G(X)-\underset{x\in X}{min}\{G(x)\}.$$ (II.8)

Approximation of E_max(X) by a compressor G is straightforward. We need to show E_max(X) is an admissible distance and a metric.

Lemma II.8

If G is a normal compressor, then E_G,max(X) is an admissible distance.

Lemma II.9

If G is a normal compressor, then E_G,max(X)) is a metric with the metric (in)equalities satisfied up to logarithmic additive precision.

C. Normalized Compression Distance for Multisets

The transformation of e(X) as in (II.4) by using the compressor G based approximation of the Kolmogorov complexity K, is called the normalized compression distance (NCD) for multisets:

$$\mathit{NCD}(X)=max\left\{\frac{G(X)-{min}_{x\in X}\{G(x)\}}{{max}_{x\in X}\{G(X\backslash \{x\}\}},\underset{Y\subset X}{max}\{\mathit{NCD}(Y)\}\right\},$$ (II.9)

for |X| ≥ 2 and NCD(X) = 0 for |X| = 1.

From (II.9) it follows that the NCD is in the real interval [0, 1]. Its value indicates how different the files are. Smaller numbers represent more similar files, larger numbers more dissimilar files. In practice the upper bound may be 1 + ε. This ε is due to imperfections in our compression techniques, but for most standard compression algorithms one is unlikely to see an ε above 0.1 (in our experiments gzip and bzip2 achieved such NCD’s above 1, but PPMZ always had NCD at most 1. If G(X) − min_x∈X{G(x)} > 1.1(max_x∈X{G(X\{x}}), then the total length of compressed separate files is much less than the length of the compressed combination of those files. This contradicts the notion of compression. If the compressor G is that bad then one should switch to a better one.

Theorem II.10

If the compressor is normal, then the NCD for multisets is a normalized admissible distance and satisfies the metric (in)equalities up to an ignorable additive term, that is, it is a similarity metric.

III. Computing the NCD and Its Application

Define

$${\mathit{NCD}}_1(X)=\frac{G(X)-{min}_{x\in X}\{G(x)\}}{{max}_{x\in X}\{G(X\backslash \{x\}\}},$$ (III.1)

the first term of (II.9) inside the maximalization. Assume we want to compute NCD(X) and |X| = n ≥ 2. In practice it seems that one can do no better than the following (initialized with M_i = 0 for i ≥ 1):

for i = 2, …, n
do Mi := max{maxY{NCD1(Y) : Y ⊂ X, |Y| = i}, Mi−1} od
NCD(X) := Mn

However, this process involves evaluating the NCD’s of the entire powerset of X requiring at least order 2ⁿ time.

Theorem III.1

Let X be a multiset and n = |X|. There is a heuristic algorithm to approximate NCD(X) from below in O(n²) computations of G(Y) with Y ⊆ X. (Assuming every x ∈ Y to be a binary string of length at most m and that G compresses in linear time, then G(Y) is computed in O(nm) time.)

This is about computing or approximating the NCD. However, the applications in Section IV concern classifications. Given a finite set of classes we consider the changes in normalized compression distances of each class under addition of the element to be classified. To compare these changes we require as much discriminatory power as possible. Since the NCD of (II.9) is a smoothed version of the NCD₁ of (III.1), we use the latter. Let us illustrate the reasons in detail.

Theoretic Reason for Using NCD₁ Instead of NCD

Suppose we want to classify x as belonging to one of the classes represented by multisets A, B, …, Z. Our method is to consider NCD(A∪{x}) − NCD(A), and similar for classes represented by B, …, Z, and then to select the least difference. However, this difference is always greater or equal to 0 by Lemma II.1. If we look at NCD₁(A∪{x}) − NCD₁(A) then the difference may be negative, zero, or positive and possibly greater in absolute value. This gives larger discriminatory power in the classes selection.

Reason from Practice for Using NCD₁ Instead of NCD

This is best illustrated with details from the proof of Theorem III.1, and we defer this discussion to Remark VI.5 the end of that proof in Section VI-G.

Kolmogorov Complexity of Natural Data

The Kolmogorov complexity of a file is a lower bound on the length of the ultimate compressed version of that file. Above we approximate the Kolmogorov complexities involved from above by a real-world compressor G. Since the Kolmogorov complexity is incomputable, in the approximation we never know how close we are to it. However, we assume that the natural data we are dealing with contain no complicated mathematical constructs like π = 3.1415 … or Universal Turing machines. In fact, we assume that the natural data we are dealing with contains mostly effective regularities that a good compressor like G finds. Under those assumptions the Kolmogorov complexity K(x) of object x is not much smaller than the length of the compressed version G(x) of the object.

Partition Algorithm

Section IV-D describes an algorithm that we developed to partition data for classification in cases where the classes are not well separated according to (IV.2) in that section. This results in that there are no subsets of a class with separation larger than that of the smallest inter-class separation. This heuristic works well in practice, although it is computationally demanding for large sets.

IV. Applications

We detail preliminary results using the NCD for multisets. (In the classification examples below we use the non-smooth version NCD₁ to which all remarks below also apply.) For classification of multisets with more than two elements we use the NCD₁ for the reasons as given in Section III.

The NCD for pairs as originally defined [4] has been applied in a wide range of application domains—without domain-specific knowledge. In [12] a close relative was compared to every time series distance measure published in the decade preceding 2004 from all of the major data analysis conferences and found to outperform all other distances aside from the Euclidean distance with which it was competitive. The NCD for pairs has also been applied in biological applications to analyze the results of segmentation and tracking of proliferating cells and organelles [6], [7], [29].

The NCD is unique in allowing multidimensional time sequence data to be compared directly, with no need for alignment or averaging. The NCD is also parameter-free. Specifically, this means that normalized distance between pairs or multisets of digital objects can be computed with no additional inputs or domain knowledge required. It is important to note that many, if not all, of the analytical steps such as segmentation and feature extraction that are prerequisite to the application of the NCD may still require application-specific parameters. For example, parameters dealing with necessarily application-specific factors such as imaging characteristics and object appearances and behaviors are required by most (if not all) current algorithms for segmenting and tracking objects over time. Still, by isolating these application specific values in a modular way it enables the computation of distances and subsequent classification steps to avoid the need for empirical or other approaches to determining additional parameters specific to the similarity measurement.

Here, we compare the performance of the proposed NCD for multisets (always in the form of the NCD₁) to that of a previous application of the NCD for pairs for predicting retinal progenitor cell (RPC) fate outcomes from the segmentation and tracking results from live cell imaging [7]. We also apply the proposed NCD to a synthetic data set previously analyzed with the pairwise NCD [6]. Finally, we apply the proposed NCD for multisets to the classification of handwritten digits, an application that was previously evaluated using the pairwise NCD in [4].

A. Retinal Progenitor Cell Fate Prediction

In [7], long-term time-lapse image sequences showing rat RPCs were analyzed using automated segmentation and tracking algorithms. Images were captured every five minutes of the RPCs for a period of 9–13 days. Up to 100 image sequences may be captured simultaneously in this manner using a microscope with a mechanized stage. For an example see Figure 1. At the conclusion of the experiment, the “fate” of the offspring produced by each RPC was determined using a combination of cell morphology and specific cell-type fluorescent markers for the four different retinal cell types produced from embryonic day 20 rat RPCs [3]. At the conclusion of the imaging, automated segmentation and tracking algorithms [28] were applied to extract the time course of features for each cell. These automated segmentation and tracking algorithms extract a time course of feature data for each stem cell at a five-minute temporal resolution, showing the patterns of cellular motion and morphology over the lifetime of the cell. Specifically, the segmentation and tracking results consisted of a 6-dimensional time sequence feature vector incorporating two-dimensional motion (Δx, Δy), as well as the direction of motion, total distance travelled, cellular size or area (in pixels) and a measure of eccentricity on [0, 1] (0 being linear, 1 being circular shape). The time sequence feature vectors for each of the cells are of different length and are not aligned. The results from the segmentation and tracking algorithms were then analyzed as follows.

Fig. 1.

Example frames from two retinal progenitor cell (RPC) image sequences showing segmentation (blue lines) and tracking (red lines) results. The type of cells the RPCs will eventually produce can be predicted by analyzing the multidimensional time sequence data obtained from the segmentation and tracking results. The NCD for multisets significantly improves the accuracy of the predictions.

The original analysis of the RPC segmentation and tracking results used a multiresolution semi-supervised spectral analysis based on the originally formulated pairwise NCD. An ensemble of distance matrices consisting of pairwise NCDs between quantized time sequence feature vectors of individual cells is generated for different feature subsets f and different numbers of quantization symbols n for the numerical time sequence data. The fully automatic quantization of the numeric time sequence data is described in [6]. All subsets of the 6-dimensional feature vector were included, although it is possible to use non-exhaustive feature subset selection methods such as forward floating search, as described in [6]. Each distance matrix is then normalized as described in [7], and the eigenvectors and eigenvalues of the normalized matrix are computed. These eigenvectors are stacked and ordered by the magnitude of the corresponding eigenvalues to form the columns of a new “spectral” matrix. The spectral matrix is a square matrix, of the same dimension N as the number of stem cells being analyzed. The spectral matrix has the important property that the ith row of the matrix is a point in ℝ^N (ℝ is the set of real numbers) that corresponds to the quantized feature vectors for the ith stem cell. If we consider only the first k columns, giving a spectral matrix of dimension N × k, and run a K-Means clustering algorithm, this yields the well-known spectral K-Means algorithm [11]. If we have known outcomes for any of the objects that were compared using the pairwise NCD, then we can formulate a semi-supervised spectral learning algorithm by running for example nearest neighbors or decision tree classifiers on the rows of the spectral matrix. This was the approach adopted in [7].

In the original analysis, three different sets of known outcomes were considered. First, a group of 72 cells were analyzed to identify cells that would self-renew (19 cells), producing additional progenitors and cells that would terminally differentiate (53 cells), producing two retinal neurons. Next, a group of 86 cells were considered on the question of whether they would produce two photoreceptor neurons after division (52 cells), or whether they would produce some other combination of retinal neurons (34 cells). Finally, 78 cells were analyzed to determine the specific combination of retinal neurons they would produce, including 52 cells that produce two photoreceptor neurons, 10 cells that produce a photoreceptor and bipolar neuron, and 16 cells that produced a photoreceptor neuron and an amacrine cell. Confidence intervals are computed for the classification results by treating the classification accuracy as a normally distributed random variable, and using the sample size of the classifier together with the normal cumulative distribution function (CDF) to estimate the region corresponding to a fixed percentage of the distribution [30, pp. 147–149]. For the terminal versus self-renewing question, 99% accuracy was achieved in prediction using a spectral nearest neighbor classifier, with a 95% confidence interval of [0.93, 1.0]. In the sequel, we will list the 95% confidence interval in square brackets following each reported classification accuracy. For the two photoreceptor versus other combination question, 87% accuracy [0.78, 0.93] was achieved using a spectral decision tree classifier. Finally, for the specific combination of retinal neurons 83% accuracy [0.73, 0.9] was achieved also using a spectral decision tree classifier.

Classification using the newly proposed NCD (II.4) is much more straightforward and leads to significantly better results. Given multisets A and B, each consisting of cells having a given fate, and a cell x with unknown fate, we proceed as follows. We assign x to whichever multiset has its distance (more picturesque “diameter”) increased the least with the addition of x. In other words, if

$${\mathit{NCD}}_1(Ax)-{\mathit{NCD}}_1(A)<{\mathit{NCD}}_1(Bx)-{\mathit{NCD}}_1(B),$$ (IV.1)

we assign x to multiset A, else we assign x to multiset B. (The notation Xx is shorthand for the multiset X with one occurrence of x added.) Note that for classification purposes we consider the impact of element x on the NCD₁ (III.1) only and do not evaluate the full NCD for classification. We use the NCD₁ in (IV.1) rather than the NCD because the NCD₁ has the ability to decrease when element x contains redundant information with respect to multiset A. See also the reasons in Section III.

The classification accuracy improved considerably using the newly proposed NCD for multisets. For the terminal versus self-renewing question, we achieved 100% accuracy in prediction [0.95,1.0] compared to 99% accuracy [0.93,1.0] for the multiresolution spectral pairwise NCD. For the two photoreceptor versus other combination question, we also achieved 100% accuracy [0.95,1.0] compared to 87% [0.78,0.93]. Finally, for the specific combination of retinal neurons we achieved 92% accuracy [0.84,0.96] compared to 83% [0.73,0.9] with the previous method.

B. Synthetic Data

In [6], an approach was developed that used the pairwise NCD to compute a concise and meaningful summarization of the results of automated segmentation and tracking algorithms applied to biological image sequence data obtained from live cell and tissue microscopy. A synthetic or simulated data set was analyzed using a method that incorporated the pairwise NCD. allowing precise control over differences between objects within and across image sequences. The features for the synthetic data set consisted of a 23-dimensional feature vector. The seven features relating to 3-D cell motion and growth were modeled as described below, the remaining 16 features were set to random values. Cell motility was based on a so-called “run-and-tumble” model similar to the motion of bacteria. This consists of periods of rapid directed movement followed by a period of random undirected motion. Cell lifespan was modeled as a gamma distributed random variable with shape parameter 50 and scale parameter 10. Once a cell reaches its lifespan it undergoes cell division, producing two new cells, or, if a predetermined population limit has been reached, the cell undergoes apoptosis, or dies. The final aspect of the model was cell size. The initial cell radius, denoted r₀, is a gamma-distributed random variable with shape parameter 200 and scale parameter 0.05. The cells growth rate is labeled υ. At the end of its lifespan, the cell doubles its radius. The radius at time t is given by

$$r(t)=r_0+r_0·{\left(\frac{t-t_0}{\mathit{lifespan}}\right)}^v$$

In the original analysis, two different populations were simulated, one population having an υ value of 3, the second having an υ value of 0.9.

The data was originally analyzed using a multiresolution representation of the time sequence data along with feature subset selection. Here we repeat the analysis for a population of 656 simulated cells, with between 228 and 280 time values for each 23 dimensional feature vector. This data was analyzed using a minimum distance supervised classifier with both the original pairwise and the proposed NCD for multisets. Omitting the feature subset selection step and incorporating the entire 23 dimensional feature vector, the pairwise NCD was 57% correct [0.53,0.61] at classifying the data, measured by leave-one-out cross validation. Using NCD for multisets, we achieved 91% correct [0.89,.93] classification, a significant improvement. When a feature subset selection step was included, both approaches achieved 100% correct classification.

C. Axonal Organelle Transport

Deficiencies in the transport of organelles along the neuronal axon have been shown to play an early and possibly causative role in neurodegenerative diseases including Huntington’s disease [9]. In [29], we analyzed time lapse image sequences showing the transport of fluorescently labeled Brain Derived Neurotrophic Factor (BDNF) organelles in a wild-type (healthy) population of mice as well as in a mutant huntingtin protein population. The goal of this study was to examine the relationship between BDNF transport and Huntington’s disease. The transport of the fluorescently labeled BDNF organelles was analyzed using a newly developed multi-target tracking approach we termed ”Multitemporal Association Tracking” (MAT). In each image sequence, organelles were segmented and then tracked using MAT and instantaneous velocities were calculated for all tracks.

Image data was collected over eight time-lapse experiments, with each experiment containing two sets of simultaneously captured image sequences, one for the diseased population and one for the wild type population. There were a total of 88 movies from eight data sets. Although the pairwise NCD was not able to accurately differentiate these populations for individual image sequences, by aggregating the image sequences so that all velocity data from a single experiment and population were considered together, we were able to correctly classify six of the eight experiments as wild type versus diseased for 75% correct classification accuracy. Analyzing the velocity data from the individual image sequences using pairwise NCD with a minimum distance classifier, we were able to classify 57% [0.47,0.67] of the image sequences correctly into wild type versus diseased populations. Using the NCD for multisets formulation described in (IV.1) with the same minimum distance approach, as described in the previous sections, we achieved a classification accuracy of 97% [0.91,0.99].

D. NIST handwritten digits

In addition to the previous applications, we applied the new NCD for multisets to analyzing handwritten digits from the MNIST handwritten digits database [17], a free and publicly available version of the NIST handwritten digits database 19 that was classified in [4]. The NIST data consists of 128×128 binary images while the MNIST data has been normalized to a 28×28 grayscale (0,..,255) images. The MNIST database contains a total of 70,000 handwritten digits consisting of 60,000 training examples and 10,000 test examles. Here we consider only the first 1000 digits of the training set as a proof of principle due to the time requirements of the partitioning algorithm described below. We also considered the entire data base using a much faster method based on JPEG2000 compression but at the price of poorer accuracy. The images are first scaled by a factor of four and then adaptive thresholded using an Otsu transform to form a binary image. The images are next converted to one-dimensional streams of binary digits and used to form a pairwise distance matrix between each of the 1000 digits. Originally the input looks as Figure 2.

Fig. 2.

Example MNIST digits. Classification accuracy for this application was improved by combining the proposed NCD for multisets with the pairwise NCD.

Following the same approach as described for the retinal progenitor cells above, we form a spectral matrix from this pairwise distance matrix. In [4], a novel approach was developed for using the distances as input to a support vector machine also for a subset of the NIST handwritten digits dataset. Random data examples along with unlabeled images of the same size were selected and used as training data, achieving a classification accuracy of 85% on a subset of the unscaled NIST database 19 digits. We follow the same approach of incorporating the distances into a supervised learning framework, using our spectral matrix as input to an ensemble of discriminant (Gaussian mixture model) classifiers [10]. Using leave-one-out cross validation, this approach using the pairwise NCD achieved 82% correct classification [0.79,0.84] for the 1000 scaled and resized MNIST digits.

In applying the multisets NCD to this data, we measured the separation between classes or the margin. Given multisets A and B, each corresponding to a class in the testing data, we measure the separation between the two classes as

$${\mathit{NCD}}_1(AB)-{\mathit{NCD}}_1(A)-{\mathit{NCD}}_1(B).$$ (IV.2)

This follows directly from the relevant Venn diagram. Our goal is to partition the input classes such that the separation between classes is larger than any separation between subsets of the same class, subject to a minimum class size. We have found that this approach works well in practice. We have developed an expectation maximization algorithm to partition the classes such that there exist no subsets of a class separated by a margin larger than the minimum separation between classes.

Our expectation maximization algorithm attempts to partition the classes into maximally separated subsets as measured by (IV.2). This algorithm, that we have termed K-Lists, is modeled after the K-means algorithm. Although it is suitable for general clustering, here we use it to partition the data into two maximally separated subsets. The algorithm is detailed in Table I. There is one important difference between proposed K-Lists algorithm and the K-Means algorithm. Because we are not using the centroid of a cluster as a representative value as in K-Means, but rather the subset itself via the NCD for multisets, we only allow a single element to change subsets at every iteration. This prevents thrashing where groups of elements chase each other back and forth between the two subsets. the algorithm is run until it either can not find any partitions in the data that are separated by more than the maximal inter-class separation, or until it encounters a specified minimum cluster size.

TABLE I.

Partitioning algorithm for identifying maximally separated subsets For each class (multiset) X, partition X into two subsets A and B such that NCD₁(AB) − NCD₁(A) − NCD₁(B) is a maximum.

(Initialize) Pick two elements (seeds) of X at random, assigning one element to each A and B. For each remaining element x, assign x to the closer one of A or B using pairwise NCD to the random seeds For each element x, compute the distance from x to class A and B using (IV.1) and assign to whichever class achieves the smaller distance. Choose the single element that wants to change subsets, e.g. from A to B or vice versa and whose change maximizes NCD1(AB) − NCD1(A) − NCD1(B) and swap that element from A to B or vice versa. Repeat steps 2 and 3 until no more elements want to change subsets or until we exceed e.g. 100 iterations.

Repeat the whole process some fixed number of times (here we use 5) for each X and choose the subsets that achieve the maximum of NCD1(AB) − NCD1(A) − NCD1(B). If that value exceeds the minimum inter-class separation and the subsets are not smaller than the specified minimum size then divide X into A and B and repeat the process for A and B. If the value does not exceed the minimum inter-class separation of our training data or the subsets exceed the specified minimum size, then accept X as approximately monotonic and go on to the next class.

For the retinal progenitor cell data and synthetic data sets described in the previous sections, the K-Lists partitioning algorithm was not able to find any subsets that had a larger separation as measured by (IV.2) compared to the separation between the classes. For the MNIST handwritten digits data, the partitioning algorithm was consistently able to find subsets with separation larger than the between class separation. The partitioning was run for a range of different minimum cluster sizes (10%, 20% and 30% of the original class size). This results in multiple distances to each original digit class. Here we included the two minimum distances to each class as input to the ensemble of discriminant classifiers. This resulted in a classification accuracy of 85% [0.83,0.87] for the 30 element partition size. The other two partition sizes had marginally lower classification accuracy. Finally, we combined the two minimal class distances from the partitioned multisets data along with the pairwise spectral distances described above as input to the classification algorithm, resulting in a combined leave-one-out cross validation accuracy of 99.1% correct [0.983,0.995], a significant improvement over the accuracy achieved using either the pairwise or multisets NCD alone. This is without any essential domain-specific knowledge.

The partitioning algorithm is based on an expectation-maximization approach that generates an approximate solution to NP-hard problem of finding combinations of elements (partitions) from the training set that are more similar to each other and less similar other partitions. Given a data set of size N, the number of iterations required by the K-Lists algorithm is at least O(log N) for the case where each iteration partitions the data in two equal size sets, and at most O(N) corresponding to the case where each iteration partitions the data into sets of size N − 1 and 1. At each iteration, N computations of the NCD must be computed, with each distance taking O(N) compression operations. The complexity of the K-Lists algorithm is therefore O(N² log N) in the best case, and O(N³) worst case. As described in the Section IV-E below, the time constraints imposed by the partitioning algorithm precluded our applying this approach to the full MNIST dataset, but we still believe these results an encouraging step. At this time of writing the record using any method and computing power, is held by a classifier for the MNIST data which achieves an accuracy of 99.77% correct [5] (according to the MNIST website http://yann.lecun.com/exdb/mnist/). Using a medium sized network trained using the approach of Ciresan et al.. [5], classification errors were evenly distributed across the test set, with approximately 10% of the errors occuring in the 1000 digit subset that was analyzed here. Their approach also required less than one day to fully process and classify the 70,000 elements of the training and test sets.

A significant drawback of the multiset NCD with partitioning-based classification approach for the MNIST digits is that the underlying bzip2 compression is extremely computationally demanding. Running on a 94 core Xeon and i7 cluster, partitioning and classifying 1,000 MNIST digits required nearly five days of compute time. Extending this naively to partition the full 60,000 element MNIST training set would increase this time requirement by at least on the order of 60² log 60, clearly intractable. The major component of the time requirement is the bzip2 compression step. In other ongoing experiments using the NCD multiples approach for biological image classification applications in mitosis detection and stem cell viability categorization we have found that using the JPEG2000 image compression algorithm achieves good results with the NCD multiples, results that will be submitted to a biological journal. The compression ratio achieved using bzip2 is far better, nearly four times as much compression compared to JPEG2000 but JPEG2000 runs nearly 25 times faster compared to bzip2 for compressing a single digit from the MNIST dataset. This makes it feasible to process the full 70,000 element dataset using JPEG2000 compression. Following the approach from [4], we picked 500 five element sets randomly for each digit from the training data. We computed the NCD multiples distances from each remaining training element to these sets using JPEG2000 as the compressor. The distances from the remaining training data to each of the training sets were then used to train a supervised classifier. Finally, we compute the distance from each test element to the training sets and use the resulting distances as input to the supervised classifier. Using the same 94 core cluster the entire process required approximately 50 hours to process and classify the full MNIST dataset. We achieved classification accuracy of 81% [0.802,0.818] correct. For the supervised classifier, we used the same ensemble of discriminant classifiers used in the partitioning above. We also obtained the same result in signicantly less training time using a feed-forward neural network for the supervised classier. By many standards, the MNIST dataset is not considered extremely large, but processing this fully with the NCD can still be prohibitively time intensive. Finding more time efficient approaches to process very large datasets will be a challenge going forward for approaches based on the NCD.

E. Data, Software, Machines

All of the software and the time sequence data for the RPC fate outcome problem can be downloaded from http://bioimage.coe.drexel.edu. The software is implemented in C and uses MPI for parallelization. All data compression was done with bzip2 using the default settings, except that JPEG2000 used to analyze the full MNIST dataset. Data import is handled by a MATLAB script that is also provided. The same software implementation was used for the retinal progenitors, the axonal organelle transport and the synthetic dataset. For the analysis of the full MNIST dataset using JPEG2000, all of the software was implemented in MATLAB, and the MATLAB JPEG2000 implementation with default settings was used. The software has been run on a small cluster, consisting of 94 (hyperthreaded for 188 parallel threads of execution) Xeon and i7 cores running at 2.9 Ghz. The RPC and synthetic classification runs in approximately 20 minutes for each question. For the MNIST handwritten digits, the classification was applied to a 1,000 digit subset of the full data due to the time requirements of the partitioning algorithm. Execution time for the partitioning algorithm vary due to the random initialization of the algorithm, but ranged between 24–36 hours for each of the three minimum partition sizes that were combined for classification. The subsequent distance calculations for cross-validation required from 1–6 hours for each partition size. The total time required to partition and classify the 1000 element subset of the MNIST test data was nearly five days. Using JPEG2000 compression significantly reduces the time requirements for the MNIST data. JPEG2000 was nearly 25 times faster compared to bzip2, but bzip2 achieved four times the compression ratio. The JPEG2000-based analysis of the MNIST dataset required approximately 50 hours to process and classify the full MNIST dataset.

V. Conclusion

An object capable of being manipulated in a computer is a string. The information distance of a multiset of strings (each string can occur more than once) is expressed as the length of the shortest binary program that can transform any string of the multiset into any other string of the multiset. If the multiset consists of identical strings then this length is small, and if it consists of very different strings then this length is large. By dividing the realized distance by the maximally possible distance we obtain a value between 0 and 1. This value is a formalization of the similarity of the strings in the multiset. We present necessary conditions for such a formal notion to be a metric. The proposed similarity is called the normalized information distance for multisets, and reduces to the formulation in [19], [4] for pairs. The similarity is expressed in terms of the incomputable Kolmogorov complexity and shown to possess all relevant computable properties, it is in normalized form, a metric, and it ranges from 0 to 1. Subsequently the Kolmogorov complexities involved are approximated from above by compression programs leading to the normalized compression distance (NCD) for multisets.

In classification problems the multiset version is conceptually simpler than the pairwise version. Additionally we showed that it is also performs better. One challenge to the NCD in general, and particularly to the more computationally demanding multiples formulation of the NCD is the time requirement. As in the MNIST dataset, using different compression algorithms such as JPEG2000 can reduce the time needed to process the data, but with a potential to decrease classification accuracy. There is also the question, as datasets become very large, of how to best present data to the compressor. Partitioning is one approach to divide large datasets into more manageable subsets for analysis with the NCD. Still, there will be a need moving forward to find new ways to best leverage the capabilities of the multiset NCD and of the underlying compression algorithms for detecting similarities in complex data.

The NCD for multisets is applied to previous applications where the pairwise NCD was used in order that comparison is possible. In some applications, including retinal progenitor cell fate prediction, axonal organelle transport in neurodegenerative disease and the analysis of simulated populations of proliferating cells, the new NCD for multisets obtained major improvements over the pairwise NCD. For these applications, the use of the NCD allowed a single software tool to analyze the data, with no application specific settings for the analysis. The ability of the NCD to compare multidimensional time sequence data directly, with no parameters or alignment is especially useful for diverse biological time sequence data. The NCD needs no application specific knowledge, making it especially well suited for exploratory investigation of data with unknown chacteristics. In other applications such as the MNIST handwritten digits, the NCD for multisets alone did not significantly improve upon the result from the pairwise NCD, but a significant overall improvement in accuracy resulted by combining both distance measures. For the MNIST dataset, we did modify the way we presented the input data to the NCD software, partitioning the large amount of data into smaller sets more effectively classified by the compressor. We also modified our approach to use a different compression algorithm, trading classification accuracy for reduced computational time. In all cases, we applied the same parameter-free formulation of both the multiple version and the pairwise version of the NCD. That is, no features of the problems were used at all.

VI. Theory Requirements and Proofs

A. Strings

We write string to mean a finite binary string, and ε denotes the empty string. The length of a string x (the number of bits in it) is denoted by |x|. Thus, |ε| = 0. We identify strings with natural numbers by associating each string with its index in the length-increasing lexicographic ordering according to the scheme (ε, 0), (0, 1), (1, 2), (00, 3), (01, 4), (10, 5), (11, 6), …. In this way the Kolmogorov complexity in Section VI-C can be about finite binary strings or natural numbers.

B. Computability Notions

A pair of integers, such as (p, q) can be interpreted as the rational p/q. We assume the notion of a function with rational arguments and values. A function f(x) with x rational is upper semicomputable if it is defined by a rational-valued total computable function ϕ(x, k) with x a rational number and k a nonnegative integer such that ϕ(x, k + 1) ≤ ϕ(x, k) for every k and lim_k→∞ ϕ(x, k) = f(x). This means that f (with possibly real values) can be computed in the limit from above (see [22], p. 35). A function f is lower semicomputable if −f is semicomputable from above. If a function is both upper semicomputable and lower semicomputable then it is computable.

C. Kolmogorov Complexity

The Kolmogorov complexity is the information in a single finite object [15]. Informally, the Kolmogorov complexity of a string is the length of the shortest string from which the original can be lossless reconstructed by a general-purpose computer. Hence the Kolmogorov complexity of a string constitutes a lower bound on how far a lossless compression program can compress. For definiteness the computers considered here are prefix Turing machines (see for example [22]) with a separate read-only input tape on which the program is placed and that is scanned from left to right without backing up, a separate work tape on which the computation takes place, a tape on which an auxiliary string is placed, and a separate output tape. The programs for such a machine are by construction a prefx code: no program is a proper prefix of another program. These machines can be computably enumerated as T₁, T₂, …. There are machines in this list, say T_u, such that T_u(i, p, y) = T_i(p, y) for all indexes i, programs p, and auxiliary strings y. One of those is selected as the reference universal prefix Turing machine U.

Formally, the conditional Kolmogorov complexity K(x|y) is the length of the shortest program p such that the reference universal prefix Turing machine U on input q (replacing the above pair (i, p) by a possibly shorter single string q) with auxiliary information y outputs x. The unconditional Kolmogorov complexity K(x) is defined by K(x|ε) where ε is the empty string. In these definitions both x and y can consist of strings into which finite multisets of finite binary strings are encoded. The Kolmogorov complexity function K is incomputable.

Theory and applications are given in the textbook [22]. A deep, and very useful, result due to L.A. Levin and A.N. Kolmogorov [33] called symmetry of information states that(in the prefix Kolmogorov complexity variant of [8])

$$K(x,y)=K(x)+K(y\mid x,K(x))=K(y)+K(x\mid y,K(y)),$$ (VI.1)

with the equalities holding up to a O(1) additive term. Here K(y|x, K(x)) = K(y|x) + O(log K(x))).

D. Multiset

A multiset is also known as bag, list, or multiple. A multiset is a generalization of the notion of set. The members are allowed to appear more than once. For example, if x ≠ y then {x, y} is a set, but {x, x, y} and {x, x, x, y, y} are multisets, with abuse of the set notation. For us, a multiset is finite such as {x₁, …, x_n} with 0 ≤ n < ∞ and the members are finite binary strings in length-increasing lexicographic order. If X is a multiset, then some or all of its elements may be equal. The notation x_i ∈ X means that “x_i is an element of multiset X.” Thus, x ∈ {x, x, y} and z ∉ {x, x, y} for z ≠ x, y. If X, Y are multisets X = {x₁, …, x_n} and Y = {y₁, …, y_m} we denote XY = {x₁, …, x_n, y₁, …, y_m} (with the elements ordered length-increasing lexicographic). If X ⊆ Y then the elements of X occur (not necessary consecutive) in Y. If X, Y, Z are multisets such that X = Y Z with Z ≠ Ø, then we write Y ⊂ X. With {x₁, …, x_n} \ {x} we mean the multiset {x₁, …, x_n} with one occurrence of x removed.

The finite binary strings, finiteness and length-increasing lexicographic order allows us to assign a unique Kolmogorov complexity to a multiset. The conditional prefix Kolmogorov complexity K(X|x) of a multiset X given an element x is the length of a shortest program p for the reference universal Turing machine that with input x outputs the multiset X. The prefix Kolmogorov complexity K(X) of a multiset X is defined by K(X|ε). One can also put multisets in the conditional such as K(x|X) or K(X|Y). We will use the straightforward laws K(·|X, x) = K(·|X) and K(X|x) = K(X′|x) up to an additive constant term, for x ∈ X and X′ equals the multiset X with one occurrence of the element x deleted.

E. Information Distance

The information distance in a multiset X (|X| ≥ 2) is given by (I.1). To obtain the pairwise information distance in [2] we take X = {x, y} in (I.1). The resulting formula is equivalent to E_max(x, y) = max{K(x|y), K(y|x)} up to a logarithmic additive term.

F. Metricity

A distance function d on 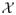is defined by d : 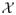→ 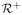where 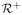is the set of nonnegative real numbers. If X, Y, Z ∈ 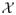, then Z = XY if Z is the multiset consisting of the elements of the multisets X and Y ordered length-increasing lexicographic. A distance function d is a metric if

1. Positive definiteness: d(X) = 0 if all elements of X are equal and d(X) > 0 otherwise.

2. Symmetry: d(X) is invariant under all permutations of X.

3. Triangle inequality: d(XY) ≤ d(XZ) + d(ZY).

We recall Theorem 4.1 and Claim 4.2 from [27].

Theorem VI.1

The information distance for multisets E_max is a metric where the (in)equalities hold up to a O(log K) additive term, where K is the largest quantity involved in each metric (in)equality 1 to 3, respectively.

Claim VI.2

Let X, Y, Z ∈ 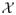and K = K(XYZ). Then, E_max(XY) ≤ E_max(XZ) + E_max(ZY) up to an O(log K) additive term.

G. Proofs

Proof of Lemma II.1

Let A, B, C ∈ 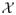, AB ⊆ C, and d a distance that satisfies the triangle inequality. Assume that the lemma is false and d(C) < d(AB). Let D = C\A. It follows from the triangle inequality that

$$d(AB)\le d(AD)+d(DB).$$

Since AD = C this implies d(AB) ≤ d(C) + d(DB), and therefore d(C) ≥ d(AB). But this contradicts the assumption.

Proof of Theorem II.3

By induction on n = |X|.

Base case

The theorem is vacuously true for n = 1.

Induction: n > 1

Assume that the lemma is true for the cases 1, …, n − 1. Let |X| = n. If e(X) = max_Y⊂X {e(Y)} then the lemma holds by the inductive assumption since |Y| < n. Hence assume that

$$e(X)=\frac{{max}_{x\in X}\{K(X\mid x)\}}{{max}_{x\in X}\{K(X\backslash \{x\})\}}.$$

For every x ∈ X we have K(X|x) ≤ K(X\{x}|x) + O(1) ≤ K(X\{x}). Therefore, the numerator is at most the denominator minus an O(1) additive term. The lemma is proven. For n = 2 the definition of e(X) is (II.2). The proof in [19] is more complex than for the general case above.

Proof of Theorem II.6

The quantity e(X) satisfies positive definiteness and symmetry up to an O((log K(X))/K(X)) additive term, as follows directly from the definition of e(X) in (II.4). It remains to prove the triangle inequality:

Let X, Y, Z ∈ 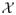. Then, e(XY) ≤ e(XZ) + e(ZY) within an additive term of O((log K)/K) where K = max{K(X), K(Y), K(Z)}. The proof proceeds by induction on n = |XY|.

Base Case: n = 1

This case is vacuously true.

Induction n > 1

Assume that the lemma is true for the cases 1, …, n − 1. Let |XY| = n. If e(XY) = max_Z⊂XY {e(Z)} then the lemma holds by the inductive assumption since |Z| < n. Therefore assume that

$$e(XY)=e_1(XY)=\frac{K(XY\mid x_{XY})}{K(XY\backslash \{x_{xy}\})},$$

where x_V is such that K(V|x_V) = max_x∈V {K(V|x)}, and x_u is such that K(U\{x_u}) = max_x∈U {K(U\{x})}.

Claim VI.3

Let X, Y, Z ∈ 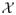. Then, K(XYZ|x_XYZ) ≤ K(XZ|x_XZ) + K(ZY|x_ZY) up to an additive O(log K) term, where K = K(XYZ).

Proof

(If one or more of X, Y, Z equal Ø the claim holds trivially.) By Theorem VI.1 we have that E_max and hence K(XY|x_XY) is a metric up to an O(log K) additive term. In particular, the triangle inequality is satisfied by Claim VI.2: K(XY|x_XY) ≤ K(XZ|x_XZ) + K(ZY|x_ZY) up to an additive term of O(log K). Thus with X′ = XZ and Y′ = ZY we have K(X′Y′|x_X′Y′) ≤ K(X′Z|x_X′Z) +K(ZY′|x_ZY′) up to the logarithmic additive term. Writing this out K(XZZY|x_XZZY) ≤ K(XZZ|x_XZZ) + K(ZYZ|x_ZYZ) or K(XYZ|x_XYZ) ≤ K(XZ|x_XZ) + K(ZY|x_ZY) up to an additive term of O(log K).

Now consider the following inequalities:

$$\begin{array}{l}{e}_1(\mathit{XYZ})=\frac{K(\mathit{XYZ}\mid x_{\mathit{XYZ}})}{K(\mathit{XYZ}\backslash \{x_{\mathit{xyz}}\})}\\ \le \frac{K(XZ\mid x_{XZ})}{K(\mathit{XYZ}\backslash \{x_{\mathit{xyz}}\})}+\frac{K(ZY\mid x_{ZY})}{K(\mathit{XYZ}\backslash \{x_{\mathit{xyz}}\})}\\ \le \frac{K(XZ\mid x_{XZ})}{K(XZ\backslash \{x_{xz}\})}+\frac{K(ZY\mid x_{ZY})}{K(ZY\backslash \{x_{zy}\})}\\ =e_1(XZ)+e_1(ZY),\end{array}$$ (VI.2)

up to a O((log K)/K) additive term. The first inequality is Claim VI.3 (each term with the same denominator). The second inequality follows from K(XYZ \ {x_xyz}) ≥ K(XZ \ {x_xz}) and K(XYZ \ {x_xyz}) ≥ K(ZY \ {x_zy}) using the principle that K(u, v) ≥ K(u) + O(1) since K(u, v) = K(u) + K(v|u, K(u)) + O(1) by the symmetry of information (VI.1), reducing both denominators and increasing the sum of the quotients (by this inequality the numerators are unchanged). The last equality follows by (II.3).

By (II.4) and (II.3) a multiset XYZ has e(XYZ) = e₁(XYZ) or it contains a proper submultiset U such that e(U) = e₁(U) = e(XYZ). This U ⊂ XYZ is the multiset (if it exists) that achieves the maximum in the left-hand term of the outer maximalization of e(XYZ) in (II.4).

Assume U exists. Denote X′ = X∩U, Y′ = Y∩U, and Z′ = Z∩U. Then (VI.2) holds with X′ substituted for X, Y ′ substituted for Y, and Z′ substituted for Z. Since e(U) = e₁(U) and e(XY) ≤ e(XYZ) = e(U) we have e(XY) ≤ e₁(X′Z′) + e₁(Z′Y′) up to a O((log K)/K) additive term.

Assume U does not exist. Then e(XY) ≤ e(XYZ) = e₁(XYZ). By (VI.2) we have e(XY) ≤ e₁(XZ) + e₁(ZY) up to a O((log K)/K) additive term.

By the monotonicity property of (II.4) and since X′Z′ ⊆ XZ and Z′Y′ ⊆ ZY we have e(XZ) ≥ e₁(X′Z′), e₁(XZ) and e(ZY) ≥ e₁(Z′Y′), e₁(ZY). Therefore, e(XY) ≤ e(XZ) + e(ZY) up to an O((log K)/K) additive term. This finishes the proof. (The definition of e(XY) with |XY| = 2 is (II.2). The proof of the Theorem for this case is in [19], but it is more complex than the proof above.)

Proof of Lemma II.8

Let X ∈ 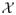and G a normal compressor as in [4]. For E_G,max(X) to be an admissible distance it must satisfy the density requirement (II.1) and be upper semicomputable (Section VI-B). Since the length G(x) is computable it is a fortiori upper semicomputable. The density requirement (II.1) is equivalent to the Kraft inequality [16] which states if a set of strings has lengths l₁, l₂ … satisfying Σ_i 2^−l_i ≤ 1, then this set is a prefix code: no code word is a proper prefix of another code word, and if the set of strings is a prefix code then it satisfies the inequality. Hence, for every string x, the set of E_G,max(X) is a prefix-free code for the set of X’s containing x, provided |X| ≥ 2 and X contains nonequal elements. According to (II.8) we have for every x ∈ X that E_G,max(X) ≥ G(X)−G(x) and clearly G(X) − G(x) ≥ G(X \ {x}). Thus, 2^{−E_G,max(X)} ≤ 2^−G(X\{x}) and therefore

$$\sum _{x:x\in X}{2}^{-E_{G,max}(X)}\le \sum _{x:x\in X}{2}^{-G(X\backslash \{x\})}.$$

A compressor G compresses strings into a uniquely decodable code (it must satisfy the unique decompression property) and therefore the lengths set of the compressed strings must satisfy the Kraft inequality [23]. Thus, for every x the compressed codes for the multisets X \ {x} with x ∈ X must satisfy this inequality. Hence the right-hand side of above displayed inequality is at most 1.

Proof of Lemma II.9

Let X, Y, Z ∈ 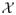and G a normal compressor as in [4]. The positive definiteness and the symmetry property of X hold clearly up to an O(log G(X))) additive term. Only the triangular inequality is nonobvious. For every compressor G we have G(XY) ≤ G(X) + G(Y) up to an additive O(log G(XY)) term, otherwise we obtain a better compression by dividing the string to be compressed. (This also follows from the distributivity property of normal compressors.) By the monotonicity property G(X) ≤ G(XZ) and G(Y) ≤ G(YZ) up to an O(log G(XY)) or O(log G(YZ)) additive term, respectively. Therefore, G(XY) ≤ G(XZ) + G(ZY) up to an O(log G(XYZ)) additive term.

Proof of Theorem II.10

Let X, Y, Z ∈ 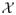and G a normal compressor as in [4]. The NCD (II.9) is a normalized admissible distance by Lemma II.8. It is normalized to [0, 1] up to an additive term of O((log G)/G) with G = G(XYZ) as we can see from the formula (II.9) and Theorem II.3 with G substituted for K throughout. We next show it is a metric.

Let X consist of equal elements. We must have that NCD(X) = 0 up to negligible error. The idempotency property of a normal compressor is up to an additive term of O(log G(X)). Hence the numerator of both terms in the maximalization of (II.4) are 0 up to an additive term of O((log G(X))/G(X)). If X does not consist of equal elements then the numerator of NCD(X) is greater than 0 up to an additive term of O((log G(X))/G(X)). Hence the positive definiteness of NCD(X) is satisfied up to this additive term of O((log G(X))/G(X)). The order of the members of X is assumed to be length-increasing lexicographic. Therefore it is symmetric. It remains to show the triangle inequality NCD(XY) ≤ NCD(XZ)+NCD(ZY) up to an additive term of O((log G)/G) where G = G(XYZ). We do this by induction on n = |XY|.

Base case: n = 1

The triangle property is vacuously satisfied.

Induction: n > 1

Assume the triangle property is satisfied for the cases 1, …, n − 1. We prove it for |XY| = n. If NCD(XY) = NCD(U) for some U ⊂ XY then the case follows from the inductive argument. Therefore, NCD(XY) is the first term in the outer maximization of (II.9). Write G(XY|x_XY) = G(XY) −min_x∈XY {G(x)} and G(XY \{x_xy}) = max_x∈XY {G(XY)\{x}} and similar for XZ, Y Z, XYZ. Following the induction case of the triangle inequality in the proof of Theorem II.6, using Lemma II.9 for the metricity of E_G,max wherever Theorem VI.1 is used to assert the metricity of E_max, and substitute G for K in the remainder. This completes the proof. That is, for every Z we have

$$\mathit{NCD}(XY)\le \mathit{NCD}(XZ)+\mathit{NCD}(ZY),$$

up to an additive term of O((log G)/G). This finishes the proof. For |XY| = 2 the triangle property is also proved in [4]. This proof of the general case is both simpler and more elementary.

Proof of Theorem III.1

We use the analysis in Remark II.5 and in particular the inequality (II.6). We ignore logarithmic additive terms. We approximate NCD(X) from below by max_Y⊆X {NCD₁(Y)} for a sequence of n − 1 properly nested Y’s of decreasing cardinality. That is, in the computation we set the value of NCD(X) to NCD₁(X) unless the Y with maximal NCD₁ in the sequence of Y’s has NCD₁(X) < NCD₁(Y). In that case we set the value of NCD(X) to NCD₁(Y). (In the form of e₁(Y) > e₁(X) this occurs in the example of Remark II.5.) How do we choose this sequence of Y’s?

Claim VI.4

Let Y ⊂ X and G(X) − min_x∈X {G(x)} − max_x∈X {G(X \ {x})} < G(Y) − min_x∈Y {G(x)} − max_x∈Y {G(Y \ {x})}. Then, NCD₁(X) < NCD₁(Y).

Proof

We first show that max_x∈Y {G(Y \ {x})} ≤ max_x∈X {G(X \ {x})}. Let G(Y \ {y}) = max_x∈Y {G(Y \ {x})}. Since Y ⊂ X we have G(Y \ {y}) ≤ G(X \ {y}) ≤ max_x∈X {G(X \ {x})}.

We next show that if a − b < c − d and d ≤ b then a/b < c/d. Namely, dividing the first inequality by b we obtain a/b − b/b < (c − d)/b ≤ (c − d)/d. Hence, a/b < c/d.

Setting a = G(X) − min_x∈X {G(x)}, b = max_x∈X {G(X \ {x})}, c = G(Y) − min_x∈Y {G(x)}, and d = max_x∈Y {G(Y \ {x})}, the above shows that the claim holds.

Claim VI.4 states that the only candidates Y (Y ⊂ X) for NCD₁(Y) > NCD₁(X) are the Y such that G(X) − min_x∈X {G(x)} − max_x∈X {G(X \{x})} < G(Y) − min_x∈Y {G(x)} − max_x∈Y {G(Y \{x})}.

For example, let X = {x₁, x₂, …, x_n}, |Y| = 2, G(X) = max_x∈X {G(X \ {x})} (for instance x₁ = x₂), and min_x∈X {G(x)} > 0. Clearly, G(Y) − max_x∈Y {G(Y \ {x})} = G(Y) − max_x∈Y {G(x)} = min_x∈Y {G(x)}. Then, 0 = G(X) − max_x∈X {G(X \{x})} < G(Y) − max_x∈Y {G(Y \ {x})} + min_x∈X {G(x)} − min_x∈Y {G(x)} = min_x∈Y {G(x)} + min_x∈X {G(x)} − min_x∈Y {G(x)} = min_x∈X {G(x)}.

Hence for Y ⊂ X, if G(X) − max_x∈X {G(X \ {x})} is smaller than G(Y) − max_x∈Y {G(Y \ {x})} + min_x∈X {G(x)} − min_x∈Y {G(x)} then NCD₁(Y) > NCD₁(X). Note that if the x that maximizes max_x∈X {G(X \ {x})} is not the x that minimizes min_x∈X {G(x)} then min_x∈X {G(x)} − min_x∈Y {G(x)} = 0, otherwise min_x∈X {G(x)} − min_x∈Y {G(x)} < 0.

Removing the element that minimizes G(X) − max_x∈X {G(X \ {x})} may make the elements of Y more dissimilar and therefore increase G(Y) − G(max_x∈Y {G(Y \ {x})}. Iterating this process may make the elements of the resulting sets ever more dissimilar, until the associated NCD₁ declines due to decreasing cardinality.

Therefore, we come to the following heuristic. Let X = {x₁, …, x_n} and m = max{|x| : x ∈ X}. Compute

$$G(X)-\underset{x\in X}{max}\{G(X\backslash \{x\})\}.$$

Let I be the index i for which the maximum in the second term is reached. Set Y₁ = X \ {x_I}. Repeat this process with Y₁ instead of X to obtain Y₂, and so on. The result is Y₀ ⊃ Y₁ ⊃ ··· ⊃ Y_n−2 with Y₀ = X and |Y_n−2| = 2. Set NCD(X) = max_{0≤i≤n−2}{NCD₁(Y_i)}. The whole process to compute this heuristic to approximate NCD(X) from below takes O(n²) steps where a step involves compressing a subset of X in O(nm) time.

Remark VI.5

Reason from Practice for Using NCD₁ Instead of NCD

Let Y₀ = A∪{x} be as in the proof of Theorem III.1. For the handwritten digit recognition application in Section IV-D we computed NCD₁(Y₀) for digits 1, 2, …, 9, 0. The values were 0.9845, 0.9681, 0.9911, 0.9863, 0.9814, 0.9939, 0.9942, 0.9951, 0.992, 0.9796. Let us consider the class of digit 1. This class without the handwritten digit x to be classified is A and Y₀ = A∪{x}. For this class max_{0≤i≤n−2}{NCD₁(Y_i)} = 0.9953 where the maximum is reached for index i = 21. Thus NCD(A∪{x}) − NCD₁(A∪{x}) = 0.0108 computing the NCD as max_{0≤i≤n−2}{NCD₁(Y_i)} according to Theorem III.1. By Lemma II.1 we have NCD(A) ≤ NCD(A∪{x}) because A ⊂ A∪{x}. Now comes the problem. Computing NCD(A) also according to Theorem III.1 may yield the same multiset Y_j for A∪{x} as the multiset Y_j−1 for A for some 1 ≤ j ≤ 21. In this case NCD(A) = NCD(A∪{x}). This has nothing to do with the element x we try to classify. The same may happen in the case of class B, that is, NCD(B∪{x}) = NCD(B), and so on. Then, the classification of x using the NCD is worthless. This scenario is impossible using NCD₁.

Biographies

Andrew R. Cohen received his Ph.D. from the Rensselaer Polytechnic Institute in May 2008. He is currently an associate professor in the department of Electrical & Computer Engineering at Drexel University. Prior to joining Drexel, he was an assistant professor in the department of Electrical Engineering and Computer Science at the University of Wisconsin, Milwaukee. He has worked as a software design engineer at Microsoft Corp. on the Windows and DirectX teams and as a CPU Product Engineer at Intel Corp. His research interests include 5-D image sequence analysis for applications in biological microscopy, algorithmic information theory, spectral methods, data visualization, and supercomputer applications. He is a senior member of the IEEE.

Paul M.B. Vitányi received his Ph.D. from the Free University of Amsterdam (1978). He is a CWI Fellow at the national research institute for mathematics and computer science in the Netherlands, CWI, and Professor of Computer Science at the University of Amsterdam. He served on the editorial boards of Distributed Computing, Information Processing Letters, Theory of Computing Systems, Parallel Processing Letters, International journal of Foundations of Computer Science, Entropy, Information, Journal of Computer and Systems Sciences (guest editor), and elsewhere. He has worked on cellular automata, computational complexity, distributed and parallel computing, machine learning and prediction, physics of computation, Kolmogorov complexity, information theory, quantum computing, publishing more than 200 research papers and some books. He received a Knighthood (Ridder in de Orde van de Nederlandse Leeuw) and is member of the Academia Europaea. Together with Ming Li they pioneered applications of Kolmogorov complexity and co-authored “An Introduction to Kolmogorov Complexity and its Applications,” Springer-Verlag, New York, 1993 (3rd Edition 2008), parts of which have been translated into Chinese, Russian and Japanese.