Computational modeling of chemo-electro-mechanical coupling: A novel implicit monolithic finite element approach

Summary

Computational modeling of the human heart allows us to predict how chemical, electrical, and mechanical fields interact throughout a cardiac cycle. Pharmacological treatment of cardiac disease has advanced significantly over the past decades, yet it remains unclear how the local biochemistry of an individual heart cell translates into global cardiac function. Here we propose a novel, unified strategy to simulate excitable biological systems across three biological scales. To discretize the governing chemical, electrical, and mechanical equations in space, we propose a monolithic finite element scheme. We apply a highly efficient and inherently modular global-local split, in which the deformation and the transmembrane potential are introduced globally as nodal degrees of freedom, while the chemical state variables are treated locally as internal variables. To ensure unconditional algorithmic stability, we apply an implicit backward Euler finite difference scheme to discretize the resulting system in time. To increase algorithmic robustness and guarantee optimal quadratic convergence, we suggest an incremental iterative Newton-Raphson scheme. The proposed algorithm allows us to simulate the interaction of chemical, electrical, and mechanical fields during a representative cardiac cycle on a patient-specific geometry, robust and stable, with calculation times on the order of four days on a standard desktop computer.

1. Motivation

Pharmacological treatment has opened new avenues for managing various types of cardiac disease. On a daily basis, cardiologists now prescribe antiarrhythmic agents to control heart rhythm disorders such as atrial fibrillation, atrial flutter, ventricular tachycardia, and ventricular fibrillation [11]. While the pharmacological control of the electrical activity of the heart is reasonably well understood, the pharmacological manipulation of the mechanical activity of the heart remains severely understudied. This is an important problem in heart failure [2], a disease associated with an annual health care cost of more than $30 billion in the United States alone [33]. To understand how a new drug affects the interaction between chemical, electrical, and mechanical fields, systematic drug testing is of incredible clinical importance [53]. Not surprisingly, it covers a huge market ranging from single cell testing using patch clamp electrophysiology [1, 29], via cell culture testing using microelectroarray recordings [13, 70], to large animal experiments [36, 71]. While the pharmacological manipulation of chemo-electro-mechanical coupling is relatively well understood on the single cell level [6, 7], little is known whether or not this knowledge translates into clinically relevant function on the organ level [54]. This knowledge gap presents a tremendous opportunity for quantitative, predictive computational modeling [20]. Most importantly, the nature of coupling between the underlying chemical, electrical, and mechanical fields is ideally tailored for finite element simulations, a circumstance that has been largely overlooked until today.

The first model to quantitatively characterize the electrical activity of excitable cells was the Nobel-price winning Hodgkin-Huxley model introduced more than half a century ago [31]. Initially designed for nerve cells [21, 47], the model was soon adopted for other cell types, such as pacemaker cells [51], Purkinje fiber cells [45], atrial cells [16], and ventricular cells [5, 43, 72] of the heart. Originally proposed for single cells, these approaches were generalized to multiple cells, tissues, and organs by adding a phenomenological flux term to characterize the propagation of the excitation wave. Traditionally, simulations of propagating electrical signals were dominated by biophysicists and electrical engineers [3, 37]. Their models were based on simple straightforward algorithms, discretized in space using finite differences, discretized in time using explicit time stepping schemes [14]. To compensate for the lack of sophistication in algorithmic design, these initial models generally use a high spatial and temporal resolution, small grids and small time steps. Not surprisingly, these initial methods are extremely expensive from a computational point of view [41].

Within the past decade, physiological function has become a key focus in cardiac simulations [62], paving the way for mechanical models and finite element methods [9, 57]. However, progress was dampened by the finite difference nature of existing algorithms, making it virtually impossible to integrate mechanical deformation, in particular in the context of finite strains. The first generation of electro-mechanical heart models combined previously established finite difference based electrical algorithms with finite element based mechanical algorithms [38]. Most versions of these models are coupled unidirectionally, i.e., the algorithm first calculates the electrical field and then uses it as an input to calculate the mechanical field. The advantage of this approach is that it allows us to combine different spatial and temporal resolutions for both fields [42, 52]. For loosely coupled problems, these algorithms typically perform sufficiently well [69], although we can not really quantify the loss of information and the possible energy blow-up associated with the explicit discretization of the coupling terms. For strongly coupled problems, these algorithms require an extremely fine spatial and temporal resolution, especially during the rapid upstroke phase when all fields undergo rapid changes. To eliminate potential algorithmic instabilities, revised versions of these models are coupled bidirectionally, i.e., they iterate between electrical and mechanical fields. It is not surprising that those algorithms, which integrate more information about the nature of coupling upfront have enhanced stability and performance properties [49].

Here we challenge existing excitation-contraction algorithms and propose a second generation of chemo-electro-mechanical heart models, algorithmically redesigned from scratch. We propose a novel unified algorithm, which is entirely finite element based, fully coupled, monolithic, implicitly time-integrated, and consistently linearized [66]. This allows us to use existing finite element infrastructures, such as simple, ad hoc adaptive time stepping schemes [68]. In designing our new algorithm, we take advantage of the multiscale nature of the underlying problem illustrated in Figure 1, and discretize all chemical unknowns locally on the integration point level and all electrical and mechanical unknowns globally on the node point level [22, 60, 76]. In Section 2, we summarize the underlying kinematic, balance, and constitutive equations for chemo-electro-mechanical problems. In Section 3, we then illustrate their temporal and spatial discretizations. We introduce the global system of equations, which we solve using an incremental iterative Newton Raphson strategy. In Section 4, we specify the constitutive equations for the electrical and mechanical source and flux terms, which naturally introduce the coupling between the underlying chemical, electrical, and mechanical fields. In Section 5, we illustrate the features of the proposed model, first locally at the single cell level, then globally for the model problem of a flat square panel, and then globally at the whole heart level. We conclude with a discussion and a brief outlook in Section 6.

Figure 1.

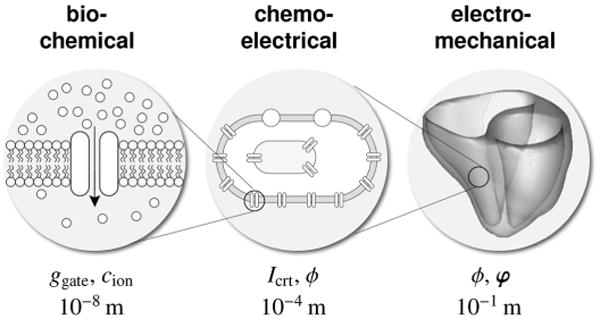
Multiscale model of the human heart. At the molecular level, gating variables g_gate and ion concentrations c_ion characterize the bio-chemical response. At the cellular level, ionic currents I_crt and the transmembrane potential ϕ characterize the chemo-electrical response. At the organ level, the propagation of the electrical potential ϕ and the deformation φ characterize the electro-mechanical response.

2. Continuous Problem of Chemo-Electro-Mechanics

In this section, we summarize the generic continuous equations of chemo-electro-mechanical coupling characterized through a set of partial differential equations for the electrical and mechanical problems and through a system of ordinary differential equations for the chemical problem. The primary unknowns of the electrical and mechanical problems are the transmembrane potential ϕ and the deformation φ. The unknowns of the chemical problem are the local state variables which we collectively summarize in the vector q. For simple two-parameter models, q would only contain a single variable, the phenomenological recovery variable r. For more sophisticated ionic models, q contains a set of gating variables g_gate and a set of ion concentrations c_ion, which, at any point in time, characterize the local ionic currents I_crt.

2.1. Kinematic equations

To characterize the kinematic state of the body under consideration, we introduce the nonlinear deformation φ that maps particles from the undeformed reference configuration ℬ₀ at time t₀ to the deformed current configuration ℬ_t at time t ∈ ℝ,

$$\mathit{x}=\mathit{\phi }(\mathit{X},t):{\mathcal{B}}_0\times \mathbb{R}\to {\mathcal{B}}_t.$$ (1)

In what follows, {○̇} = d_t{○}|_X and ∇{○} =d_X{○}|_t denote the material time derivative and the material gradient of a quantity {○}. Accordingly, Div{○} = ∇{○} : I denotes the material divergence, where I is the second-order identity tensor. With these definitions, we can introduce the deformation gradient F as the linear tangent map from the material tangent space Tℬ₀ to the spatial tangent space Tℬ_t,

$$\mathit{F}=\nabla \mathit{\phi }(\mathit{X},t):T{\mathcal{B}}_0\to T{\mathcal{B}}_t.$$ (2)

We will utilize the right Cauchy-Green deformation tensor and its inverse

$$\mathit{C}={\mathit{F}}^{\mathrm{t}}·\mathit{F}\text{and}{\mathit{C}}^{-1}={\mathit{F}}^{-1}·{\mathit{F}}^{-\mathrm{t}}$$ (3)

to define relevant strain measures. In particular, we introduce the Jacobian J and the trace I₁ as characteristic isotropic invariants,

$$\begin{array}{cc}J=det(\mathit{F})& I_1=\mathit{C}:\mathit{I}\end{array}$$ (4)

and I_ff, I_ss, and I_fs as characteristic anisotropic invariants,

$$\begin{array}{ccc}{I}_{\text{ff}}=\mathit{C}:[{\mathit{f}}_0\otimes {\mathit{f}}_0]& I_{\text{ss}}=\mathit{C}:[{\mathit{s}}_0\otimes {\mathit{s}}_0]& I_{\text{fs}}=\mathit{C}:{[{\mathit{f}}_0\otimes {\mathit{s}}_0]}^{\text{sym}},\end{array}$$ (5)

where ${[◯]}^{\text{sym}}=\frac{1}{2}[◯]+\frac{1}{2}{[◯]}^{\mathrm{t}}$ extracts the symmetric part of a second order tensor [○]. Here, I_ff and I_ss are the stretches squared along the myocardial fiber and sheet directions, which we denote by f₀ and s₀ in the reference configuration ℬ₀ and by f = F · f₀ and s = F · s₀ in the current configuration ℬ_t.

2.2. Balance equations

The balance equation of the electrical problem balances the rate of change of the transmembrane potential ϕ with the divergence of the electrical flux, Div Q, and the electrical source, F^ϕ,

$$\dot{\varphi }=\text{Div}\mathit{Q}+F^{\varphi }.$$ (6)

The balance equation of the mechanical problem balances the rate of change of the linear momentum with the divergence of the momentum flux, Div P, where P is the first Piola Kirchhoff stress tensor, and the momentum source, F^φ,

$$\mathbf{0}=\text{Div}\mathit{P}+F^{\phi }.$$ (7)

Here, the divergences Div Q and Div P of the electrical and mechanical fluxes refer to the undeformed reference configuration. For the sake of simplicity, we model the electrical problem (6) using the classical monodomain equation and model the mechanical problem (7) as quasi-static, such that the rate of change of the linear momentum vanishes identically. The balance of angular momentum is identically satisfied through the symmetry of the Cauchy stress σ =1/J P · F^t = σ^t.

2.3. Constitutive equations

The electrical and mechanical problems (6) and (7) are coupled constitutively through the corresponding flux and source terms. The electrical flux Q is typically introduced phenomenologically and characterizes the propagation speed of the electrical signal. It is usually proportional to the potential gradient ∇ϕ and can potentially be coupled to the mechanical problem through the deformation gradient ∇φ to account for stretch-induced changes in the propagation speed,

$$\mathit{Q}=\mathit{Q}(\nabla \varphi ,\nabla \phi ).$$ (8)

The electrical source F^ϕ characterizes the electrophysiology of the individuals cells on the local level. Through voltage-gated ion channels, F^ϕ depends on the electrical potential ϕ. Through possible stretch-activated ion-channels, F^ϕ may depend on the deformation gradient ∇φ. Through the cell's biochemistry, F^ϕ also depends on the set of internal variables collectively summarized in the vector q, which, in our case, contains a set of gating variables g_gate and a set of ion concentrations c_ion [76],

$$F^{\varphi }=F^{\varphi }(\varphi ,\nabla \phi ,\mathit{q}).$$ (9)

The momentum flux P is simply the Piola stress, which we can additively decompose into a passive and an active part according to Hill's classical muscle model [30]. The passive stress P^pas depends on the deformation gradient ∇φ and characterizes the passive myocardium. The active stress P^act either depends on the electrical potential ϕ [23] or on the set of internal variables q [69], as proposed here, and introduces coupling to the electro-chemical problem. The two-field nature of the Piola stress introduces an additional dependance on the deformation gradient ∇φ,

$$\mathit{P}={\mathit{P}}^{\text{pas}}(\nabla \phi )+{\mathit{P}}^{\text{act}}(\nabla \phi ,\mathit{q}).$$ (10)

The momentum source F^φ characterizes volume forces such as gravity, which we assume to be negligibly small in the subsequent analyses,

$${\mathit{F}}^{\phi }=\mathbf{0}.$$ (11)

We will now illustrate the computational solution of the coupled chemo-electro-mechanical problem using a weighted-residual based finite element approach.

3. Discrete Problem of Chemo-Electro-Mechanics

To discretize the continuous chemo-electro-mechanical problem, we rephrase the electrical and mechanical balance equations (6) and (7) in their residual formats,

$$\begin{array}{c}{\mathrm{R}}^{\varphi }=\dot{\varphi }-\text{Div}\mathit{Q}-F^{\varphi }\dot{=}0\text{in}{\mathcal{B}}_0\\ {\mathbf{R}}^{\phi }=-\text{Div}\mathit{P}-{\mathit{F}}^{\phi }\dot{=}\mathbf{0}\text{in}{\mathcal{B}}_0,\end{array}$$ (12)

where both are valid in the entire domain ℬ₀. We then partition the boundary ∂ℬ₀ into disjoint parts $\partial {\mathcal{B}}_0^{\varphi }$ and $\partial {\mathcal{B}}_0^Q$ for the electrical problem and equivalently into $\partial {\mathcal{B}}_0^{\phi }$ and $\partial {\mathcal{B}}_0^P$ for the mechanical problem and prescribe the corresponding Dirichlet and Neumann boundary conditions,

$$\begin{array}{cc}\varphi =\overline{\varphi }\text{on}\partial {\mathcal{B}}_0^{\varphi }& \mathit{Q}·\mathit{N}={\overline{T}}^Q\text{on}\partial {\mathcal{B}}_0^Q\\ \phi =\overline{\phi }\text{on}\partial {\mathcal{B}}_0^{\phi }& \mathit{P}·\mathit{N}={\overline{\mathit{T}}}^P\text{on}\partial {\mathcal{B}}_0^P,\end{array}$$ (13)

where N denotes the outward normal to ∂ℬ₀. To derive the weak forms of the electrical and mechanical problems G^ϕ and G^φ, we integrate the the residual statements (12) over the domain ℬ₀, multiply both with the scalar- and vector-valued test functions δϕ in $H_1^0({\mathcal{B}}_0)$ and δφ in $H_1^0({\mathcal{B}}_0)$, integrate them by parts, and apply the corresponding Neumann boundary conditions (13.2) and (13.4),

$$\begin{array}{c}{\mathrm{G}}^{\rho }={\int }_{{\mathcal{B}}_0}\delta \varphi \dot{\varphi }\mathrm{d}V+{\int }_{{\mathcal{B}}_0}\nabla \delta \varphi ·\mathit{Q}\mathrm{d}V-{\int }_{\partial {\mathcal{B}}_0^Q}\delta \varphi {\overline{T}}^Q\mathrm{d}A-{\int }_{{\mathcal{B}}_0}\delta \varphi F^{\varphi }\mathrm{d}V=0\forall \delta \varphi \\ {\mathrm{G}}^{\phi }={\int }_{{\mathcal{B}}_0}\nabla \delta \phi :\mathit{P}\mathrm{d}V-{\int }_{\partial {\mathcal{B}}_0^P}\delta \phi ·{\overline{\mathit{T}}}^P\mathrm{d}A-{\int }_{{\mathcal{B}}_0}\delta \phi ·{\mathit{F}}^{\phi }\mathrm{d}V=0\forall \delta \phi .\end{array}$$ (14)

3.1. Temporal discretization

For the temporal discretiation, we partition the time interval of interest into n_step subintervals [t_n, t] as $\mathcal{T}={\cup }_{\mathrm{n}=0}^{n_{\text{step}}-1}[t_{\mathrm{n}},t]$ and focus on a typical time slab [t_n, t]. Here and from now on we omit the index n+1 associated with the current time step. We assume, that the primary unknowns ϕ_n and φ_n and all derivable flux terms, source terms, and state variables are known at the beginning of the current interval. To approximate the material time derivative of the transmembrane potential ϕ, we apply a first order finite difference scheme,

$$\dot{\varphi }=[\varphi -{\varphi }_{\mathrm{n}}]/\mathrm{\Delta }t,$$ (15)

where Δt := t – t_n > 0 denotes the current time increment. To solve for the unknowns ϕ and φ, we then apply a classical backward Euler time integration scheme and evaluate the discrete set of governing equations (14) at the current time point t.

3.2. Spatial discretization

For the spatial discretization, we apply a ⁰-continuous interpolation of the transmembrane potential ϕ and of the deformation φ and introduce both ϕ and φ as global degrees of freedom at the node point level. We partition the domain of interest ℬ₀ into n_el elements ${\mathcal{B}}_0^{\mathrm{e}}$ as ${\mathcal{B}}_0={\cup }_{\mathrm{e}=1}^{n_{\text{el}}}{\mathcal{B}}_0^{\mathrm{e}}$. Using the isoparametric concept, we interpolate the trial functions ϕ^h, φ^h ∈ H₁ (ℬ₀) on the element level with the same basis function N^ϕ and N^φ as the element geometry. Using the Bubnov-Galerkin approach, we interpolate the test functions δϕ^h, $\delta {\phi }^h\in H_1^0({\mathcal{B}}_0)$ on the element level with the same basis function N^ϕ and N^φ as the trial functions,

$$\begin{array}{cc}\delta {\varphi }^h{|}_{{\mathcal{B}}_0^{\mathrm{e}}}={\sum }_{i=1}^{n_{\mathrm{e}\varphi }}{N}_i^{\varphi }\delta {\varphi }_i& {\varphi }^h{|}_{{\mathcal{B}}_0^{\mathrm{e}}}={\sum }_{k=1}^{n_{\mathrm{e}\rho }}{N}_k^{\varphi }{\varphi }_k\\ \delta {\phi }^h{|}_{{\mathcal{B}}_0^{\mathrm{e}}}={\sum }_{j=1}^{n_{\mathrm{e}\phi }}{N}_j^{\phi }\delta {\phi }_j& {\phi }^h{|}_{{\mathcal{B}}_0^{\mathrm{e}}}={\sum }_{l=1}^{n_{\mathrm{e}\phi }}{N}_l^{\phi }{\phi }_l.\end{array}$$ (16)

We then rephrase the residuals of the electrical and the mechanical problem (12) in their discrete forms,

$$\begin{array}{c}{\mathrm{R}}_I^{\varphi }=\underset{\mathrm{e}=1}{\overset{n_{\text{el}}}{\mathbf{A}}}{\int }_{{\mathcal{B}}_0^{\mathrm{e}}}{N}_i^{\varphi }\frac{1}{\mathrm{\Delta }t}[\varphi -{\varphi }_{\mathrm{n}}]+\nabla N_i^{\varphi }·\mathit{Q}-N_i^{\varphi }{F}^{\varphi }\mathrm{d}{V}_{\mathrm{e}}-{\int }_{\partial {\mathcal{B}}_0^Q}{N}_i^{\varphi }{\overline{T}}^Q\mathrm{d}{A}_{\mathrm{e}}=0\\ {\mathbf{R}}_J^{\phi }=\underset{\mathrm{e}=1}{\overset{n_{\text{el}}}{\mathbf{A}}}{\int }_{{\mathcal{B}}_0^{\mathrm{e}}}\nabla N_j^{\phi }·\mathit{P}-N_j^{\phi }{\mathit{F}}^{\phi }\mathrm{d}{V}_{\mathrm{e}}-{\int }_{\partial {\mathcal{B}}_0^P}{N}_j^{\phi }{\overline{\mathit{T}}}^P\mathrm{d}{A}_{\mathrm{e}}=\mathbf{0}.\end{array}$$ (17)

Here the operator A symbolizes the assembly of all element contributions at the local electrical and mechanical element nodes i = 1, …, n_eϕ and j = 1, …, n_eφ to the overall residuals at the global electrical and mechanical nodes I = 1, …, n_nϕ and J = 1,…, n_nφ.

3.3. Linearization

To solve the resulting coupled nonlinear system of equations (17), we propose a monolithic incremental iterative Newton-Raphson solution strategy based on consistent linearization of the governing equations [66],

$$\begin{array}{c}{\mathrm{R}}_{I\mathrm{k}+1}^{\varphi }={\mathrm{R}}_{I\mathrm{k}}^{\varphi }+{\sum }_K{\mathrm{K}}_{IK}^{\varphi \varphi }\mathrm{d}{\varphi }_K+{\sum }_L{\mathbf{K}}_{IL}^{\varphi \phi }·\mathrm{d}{\phi }_L\dot{=}0\\ {\mathbf{R}}_{J\mathrm{k}+1}^{\phi }={\mathbf{R}}_{J\mathrm{k}}^{\phi }+{\sum }_K{\mathbf{K}}_{JK}^{\phi \varphi }\mathrm{d}{\varphi }_K+{\sum }_L{\mathbf{K}}_{JL}^{\phi \phi }·\mathrm{d}{\phi }_L\dot{=}\mathbf{0}.\end{array}$$ (18)

in terms of the following iteration matrices,

$$\begin{array}{c}{\mathrm{K}}_{IK}^{\varphi \varphi }=\frac{\mathrm{d}{\mathrm{R}}_I^{\varphi }}{\mathrm{d}{\varphi }_K}=\underset{\mathrm{e}=1}{\overset{n_{\text{el}}}{\mathbf{A}}}{\int }_{{\mathcal{B}}_0^e}{N}_i^{\varphi }\frac{1}{\mathrm{\Delta }t}{N}_k^{\varphi }-N_i^{\varphi }{\mathrm{d}}_{\varphi }{F}^{\varphi }{N}_k^{\varphi }\mathrm{d}{V}_{\mathrm{e}}+\underset{\mathrm{e}=1}{\overset{n_{\text{el}}}{\mathbf{A}}}{\int }_{{\mathcal{B}}_0^e}\nabla N_i^{\varphi }·{\mathrm{d}}_{\nabla \varphi }\mathit{Q}·\nabla N_k^{\varphi }\mathrm{d}{V}_{\mathrm{e}}\\ {\mathbf{K}}_{IL}^{\varphi \phi }=\frac{\mathrm{d}{\mathrm{R}}_I^{\varphi }}{\mathrm{d}{\phi }_L}=\underset{\mathrm{e}=1}{\overset{n_{\text{el}}}{\mathbf{A}}}{\int }_{{\mathcal{B}}_0^e}{N}_i^{\varphi }·{\mathrm{d}}_{\mathit{F}}{F}^{\varphi }·\nabla N_i^{\phi }\mathrm{d}{V}_{\mathrm{e}}+\underset{\mathrm{e}=1}{\overset{n_{\text{el}}}{\mathbf{A}}}{\int }_{{\mathcal{B}}_0^e}\nabla N_i^{\varphi }·{\mathrm{d}}_{\mathit{F}}\mathit{Q}·\nabla N_l^{\phi }\mathrm{d}{V}_{\mathrm{e}}\\ {\mathbf{K}}_{JK}^{\phi \varphi }=\frac{\mathrm{d}{\mathbf{R}}_J^{\phi }}{\mathrm{d}{\varphi }_K}=\underset{\mathrm{e}=1}{\overset{n_{\text{el}}}{\mathbf{A}}}{\int }_{{\mathcal{B}}_0^e}\nabla N_j^{\phi }·{\mathrm{d}}_{\varphi }\mathit{P}{N}_k^{\varphi }\mathrm{d}{V}_{\mathrm{e}}\\ {\mathbf{K}}_{JL}^{\phi \phi }=\frac{\mathrm{d}{\mathbf{R}}_J^{\phi }}{\mathrm{d}{\phi }_L}=\underset{\mathrm{e}=1}{\overset{n_{\text{el}}}{\mathbf{A}}}{\int }_{{\mathcal{B}}_0^e}\nabla N_j^{\phi }·{\mathrm{d}}_{\mathit{F}}\mathit{P}·\nabla N_l^{\phi }\mathrm{d}{V}_{\mathrm{e}}.\end{array}$$ (19)

The solution of the system of equations (18) renders the iterative update for the increments of the global unknowns ϕ_I ← ϕ_I + dϕ_I and φ_J ← φ_J + dφ_J.

4. Model Problem of Chemo-Electro-Mechanics

In this section, we briefly summarize the constitutive equations of the electrical flux, the electrical source, and the mechanical flux. In the discrete setting, we evaluate these equations on the integration point level, where we store the set of internal variables q once the global Newton-Raphson iteration (18) has converged [23].

4.1. Electrical flux

The electrical flux Q in equation (17.1) is typically assumed to depend on both the potential gradient ∇ϕ and the deformation gradient ∇φ. We now specify this dependency to be multiplicative. In analogy to Fick's law of diffusion and Fourier's law of heat conduction, we apply Ohm's law and assume that the electrical flux Q is proportional to the gradient of the electrical potential ∇ϕ,

$$\mathit{Q}=\mathit{D}·\nabla \varphi \text{with}\mathit{D}=d^{\text{iso}}{\mathit{C}}^{-1}+d^{\text{ani}}{\mathit{f}}_0\otimes {\mathit{f}}_0.$$ (20)

The second order conductivity tensor D can account for both isotropic propagation d^iso and anisotropic propagation d^ani along preferred directions f₀. Stretch-induced changes in the propagation speed are incorporated indirectly through the inverse left Cauchy-Green tensor C⁻¹ = F⁻¹ · F^−t motivated by the assumption of a spatial rather than material isotropy [23], for which the isotropic term would simply scale with the second order identity tensor I. To evaluate the iteration matrices (19.1) and (19.2), we perform the consistent linearization of the electrical flux Q with respect to the electrical gradient d_∇ϕQ and with respect to the deformation gradient d_FQ, where the former is nothing but the conductivity tensor D and the latter reflects the above-discussed stretch-induced change in the propagation speed, see [23] for details.

4.2. Electrical source

The electrical source F^ϕ in equation (17.1) is a result of the local electrophysiology on the cellular level. As such, it is a function of the electrical potential ϕ, the deformation gradient ∇φ, and a set of internal variables q, which characterize the electrochemical behavior of the cell. For the simplest possible models, q only contains a single variable, the phenomenological recovery variable r [18, 22]. For the particular ventricular cardiomyocytes we consider here [43, 44, 72], q contains a total of 17 variables, i.e., n_gate = 13 gating variables g_gate = [g_m, g_h, g_j, g_xr1, g_xr2, g_xs, g_r, g_s, g_d, g_f, g_xK1∞, g_fCa, g_g] and n_ion = 4 ion concentrations $c_{\text{ion}}=[c_{\text{Na}},c_{\mathrm{K}},c_{\text{Ca}},c_{\text{Ca}}^{\text{sr}}]$. These state variables define n_crt = 15 ionic currents I_crt = [I_Na, I_bNa, I_NaK, I_NaCa, I_K1, I_Kr, I_Ks, I_pK, I_t0, I_CaL, I_bCa, I_pCa, I_leak, I_up, I_rel], as illustrated in Figure 2. The electrical source F^ϕ is directly related to the negative sum of all these currents I_crt across the cell membrane due to the outward positive convention established in experiments,

Figure 2.

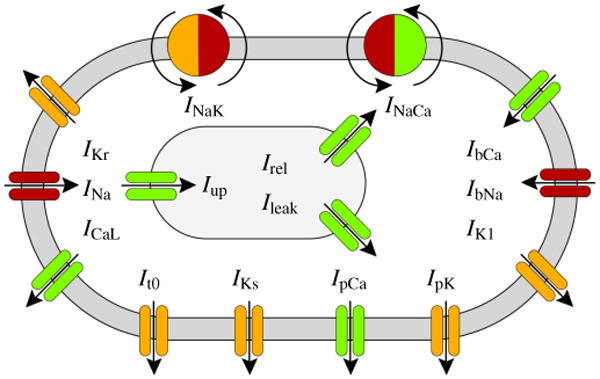
Human ventricular cardiomyocyte model with 15 ionic currents resulting from ten transmembrane channels, one exchanger, and one pump. Three additional currents characterize ionic changes inside the sarcoplasmic reticulum, shown in grey. Sodium currents are indicated in red, potassium currents in orange, and calcium currents in green.

$$F^{\varphi }=-[I_{\text{Na}}+I_{\text{bNa}}+I_{\text{NaK}}+I_{\text{NaCa}}+I_{\mathrm{K}1}+I_{\text{Kr}}+I_{\text{Ks}}+I_{\text{pK}}+I_{\mathrm{t}0}+I_{\text{CaL}}+I_{\text{bCa}}+I_{\text{pCa}}].$$ (21)

Here, I_Na is the fast sodium current, I_bNa is the background sodium current, I_NaK is the sodium potassium pump current, I_NaCa is the sodium calcium exchanger current, I_K1 is the inward rectifier current, I_Kr and I_Ks are the rapid and slow delayed rectifier currents, I_pK is the plateau potassium current, I_CaL is the long-lasting L-type calcium current, I_bCa is the background calcium current, and I_pCa is the plateau calcium current. In addition, we also have three intracellular currents, I_leak is the leakage current, I_up is the sarcoplasmic reticulum uptake current, and I_rel is the sarcoplasmic reticulum release current. For our particular cell model, none of the channels are mechanically gated, i.e., all currents are independent of the deformation gradient ∇φ. Instead, all channels are voltage gated and their currents depend on the electrical potential ϕ. In addition, the currents depend on the set of internal variables q consisting of the chemical state variables, i.e., the gating variables g_gate and the ion concentrations c_ion. We can characterize all ionic currents through generic equations of the following generic form,

$$I_{\text{crt}}=I_{\text{crt}}(\varphi ,g_{\text{gate}},c_{\text{ion}}),$$ (22)

which we specify in detail in the Appendix. From a mathematical point of view, the chemical problem is defined in terms of two sets of state variables, the n_gate gating variables g_gate and the n_ion ion concentrations c_ion. Both are governed through ordinary differential equations depending on the transmembrane potential ϕ, on the gating variables g_gate, and on the ion concentrations c_ion,

$$\begin{array}{c}{\dot{g}}_{\text{gate}}=f_{\text{gate}}(\varphi ,g_{\text{gate}},c_{\text{ion}})\\ {\dot{c}}_{\text{ion}}=f_{\text{ion}}(\varphi ,g_{\text{gate}},c_{\text{ion}}).\end{array}$$ (23)

The gating variables g_gate characterize the states of the individual ion channels, either open or closed. They are defined through a set of ordinary differential equations of Hodgkin-Huxley type,

$${\dot{g}}_{\text{gate}}=[g_{\text{gate}}^{\infty }(\varphi ,c_{\text{ion}})-g_{\text{gate}}]/{\tau }_{\text{gate}}(\varphi ),$$ (24)

which we specify in detail in the Appendix. Here, $g_{\text{gate}}^{\infty }$ is a steady-state value and τ_gate is the time constant for reaching this steady state. Both are usually exponential functions of the membrane potential ϕ. The ion concentrations inside the cell c_ion change in response to the transmembrane currents I_crt. For our particular cardiomyocyte model, the relevant ion concentrations are the sodium concentration c_Na, the potassium concentration c_K, the calcium concentration c_Ca, and the calcium concentration in the sarcoplasmic reticulum $c_{\text{Ca}}^{\text{sr}}$. Collectively, these ion concentrations c_ion are defined through a set of ordinary differential equations,

$$\begin{array}{c}{\dot{c}}_{\text{Na}}=-\frac{C}{VF}[I_{\text{Na}}+I_{\text{bNa}}+3I_{\text{NaK}}+3I_{\text{NaCa}}]\\ {\dot{c}}_{\mathrm{K}}=-\frac{C}{VF}[I_{\mathrm{K}1}+I_{\text{Kr}}+I_{\text{Ks}}-2I_{\text{NaK}}+I_{\text{pK}}+I_{\mathrm{t}0}+I_{\text{stim}}]\\ {\dot{c}}_{\text{Ca}}=-\frac{C}{2VF}[I_{\text{CaL}}+I_{\text{bCa}}+I_{\text{pCa}}-2I_{\text{NaCa}}]{\gamma }_{\text{Ca}}+[I_{\text{leak}}-I_{\text{up}}+I_{\text{rel}}]{\gamma }_{\text{Ca}}\\ {\dot{c}}_{\text{Ca}}^{\text{sr}}=+\frac{V}{V^{\text{sr}}}[I_{\text{up}}-I_{\text{leak}}-I_{\text{rel}}]{\gamma }_{\text{Ca}}^{\text{sr}}.\end{array}$$ (25)

Here C is the membrane capacitance per unit surface area, V is the cytoplasmic volume, V^sr is the volume of the sarcoplasmic reticulum, F is the Faraday constant, and γ_Ca and ${\gamma }_{\text{Ca}}^{\text{sr}}$ are scaling coefficients. While the electrical and mechanical problems are global in nature, the chemical problem remains strictly local. When using a finite element discretization, this allows us to store the chemical state variables g_gate and c_ion locally as internal variables on the integration point level. It is obvious that their complex, nonlinear coupled system of ordinary differential equations (24) and (25) cannot be solved analytically. Here, we apply a numerical solution using an implicit Euler backward time stepping scheme embedded in a local Newton iteration. To evaluate the iteration matrices (19.1) and (19.2), we perform the consistent linearization of the electrical source F^ϕ with respect to the transmembrane potential d_ϕF^ϕ related to voltage-gated ion channels and with respect to the deformation gradient d_FF^ϕ related to stretch-activated ion channels [76]. For our particular cell model, in the absence of stretch-activated ion channels, the second term vanishes identically.

4.3. Mechanical flux

The momentum flux P in equation (17.2) depends on both the electrical potential ϕ and the deformation gradient φ. We adopt the common assumption to decompose the overall stress additively into a passive mechanically-induced part P^pas and an active electrically-induced part P^act, such that P = P^pas + P^act. For the passive Piola stress, we select a compressible orthotropic model [25, 32],

$${\mathit{P}}^{\text{pas}}=\kappa [J-1]{\mathit{F}}^{-\mathrm{t}}+aexp(b[I_1-3])\mathit{F}+2a_{\text{ff}}[I_{\text{ff}}-1]exp(b_{\text{ff}}{[I_{\text{ff}}-1]}^2)\mathit{f}\otimes {\mathit{f}}_0+2a_{\text{ss}}[I_{\text{ss}}-1]exp(b_{\text{ss}}{[I_{\text{ss}}-1]}^2)\mathit{s}\otimes {\mathit{s}}_0+a_{\text{fs}}{I}_{\text{fs}}exp(b_{\text{fs}}{I}_{\text{fs}}^2)\mathit{f}\otimes {\mathit{s}}_0+a_{\text{fs}}{I}_{\text{fs}}exp(b_{\text{fs}}{I}_{\text{fs}}^2)\mathit{s}\otimes {\mathit{f}}_0,$$ (26)

parameterized in terms of the isotropic invariants J and I₁, and the anisotropic invariants I_ff, I_ss, and I_fs, weighted by the bulk modulus κ and the four sets of parameters a and b [63, 75]. Here, rather than using the original quasi-incompressible formulation proposed in the literature [32], for conceptual simplicity, we assume that the myocardial tissue is decently compressible due to its vascular network [79]. More recent cardiac models additionally even account for tissue porosity and model the myocardium as porous medium [15], an approach that we do not pursue here. For the active Piola stress P^act, we assume that an increase in the intracellular calcium concentration c_Ca above a critical level $c_{\text{Ca}}^{\text{crit}}$ induces an active cardiomyocyte contraction F^act [28,61], which is acting along the fiber direction f₀ [12,23]. The contractile force F^act displays a twitch-type behavior [48], with a smooth off-on transition characterized through the twitch-function ε.

$$\begin{array}{c}{\mathit{P}}^{\text{act}}=F^{\text{act}}\mathit{f}\otimes {\mathit{f}}_0\\ {\dot{F}}^{\text{act}}=\epsilon [\eta [c_{\text{Ca}}-c_{\text{Ca}}^{\text{rest}}]-F^{\text{act}}\\ \epsilon ={\epsilon }_0+[{\epsilon }_{\infty }-{\epsilon }_0]exp(-exp(-\xi [c_{\text{Ca}}-c_{\text{Ca}}^{\text{crit}}]))\end{array}$$ (27)

Here, η controls the saturation of the active contractile force F^act, $c_{\text{Ca}}^{\text{rest}}$ is the resting concentration, ε₀ and ε_∞ are the minimum and maximum values of ε, $c_{\text{Ca}}^{\text{crit}}$ is the limit value above which contraction is initiated, and ξ is the transition rate from ε₀ to ε_∞ at $c_{\text{Ca}}^{\text{crit}}$ [23]. More sophisticated constitutive models for active stress generation additionally include a velocity dependence [34, 49] and fully three-dimensional effects [71]. Alternatively, recent approaches suggest to model active contraction kinematically through the multiplicative decomposition of the deformation gradient [4, 26]. To evaluate the iteration matrices (19.3) and (19.4), we perform the consistent linearization of the Piola stress P with respect to the transmembrane potential d_ϕP related to the active stress and with respect to the deformation gradient d_F P related mainly to the passive stress [25].

5. Examples

5.1. Chemo-electro-mechanical coupling in a single cell

To illustrate the local features of our chemo-electrical-mechanical model, we simulate the electrophysiology of an epicardial human ventricular cardiomyocyte throughout a representative excitation cycle. For the chemical parameters, we use the values summarized in Table I. For the electro-mechanical coupling parameters, we choose the saturation of cardiomyocyte contraction to η = 12.5kPa/μM, the resting concentration of calcium to $c_{\text{Ca}}^{\text{rest}}=0.05\mu \mathrm{M}$, the minimum and maximum values scaling fiber contraction to ε₀ = 0.1/ms and ε_∞ = 1.0/ms, the critical calcium concentration above which contraction is initiated to $c_{\text{Ca}}^{\text{crit}}=0.8\mu \mathrm{M}$, and the transition rate to ξ = 4.0/μM. We initialize the global membrane potential with ϕ = − 86 mV, and the local ion concentrations with c_Na = 11.6mM, c_K = 138.3mM, and c_Ca = 0.08μM, mimicking the resting state. For the gating variables, we choose the following initial conditions g_m = 0, g_h = 0.75, g_j = 0.75, g_d = 0, g_f = 1, g_fCa = 1, g_r = 0, g_s = 1, g_xs = 0, g_xr1 = 0, g_xr2 = 0, g_xK1∞ = 0.05, and g_g = 1. To initiate a characteristic action potential, we apply an initial electrical stimulus slightly above the critical stimulation threshold [76].

Table I.

Chemo-electrical material parameters of human ventricular cardiomyocyte.

	sodium related	potassium related	calcium related	calciumsr related
concentrations	cNa0 = 140 mM	cK0 = 5.4 mM	cCa0 = 2 mM	-
maximum currents	$I_{\text{NaCa}}^{max}=1000\text{pA}/\text{pF}$		$I_{\text{NaCa}}^{max}=1000\text{pA}/\text{pF}$
	$I_{\text{NaK}}^{max}=1.362\text{pA}/\text{pF}$	$I_{\text{NaK}}^{max}=1.362\text{pA}/\text{pF}$	$I_{\text{leak}}^{max}=0.08{\mathrm{s}}^{-1}$	$I_{\text{leak}}^{max}=0.08{\mathrm{s}}^{-1}$
			$I_{\text{up}}^{max}=0.425\text{mM}/\mathrm{s}$	$I_{\text{up}}^{max}=0.425\text{mM}/\mathrm{s}$
			$I_{\text{rel}}^{max}=8.232\text{mM}/\mathrm{s}$	$I_{\text{rel}}^{max}=8.232\text{mM}/\mathrm{s}$
maximum conductances	$C_{\text{Na}}^{max}=14.838\text{nS}/\text{pF}$	$C_{\mathrm{K}1}^{max}=5.405\text{nS}/\text{pF}$	$C_{\text{CaL}}^{max}=0.175{\text{mm}}^3/[\mu \text{Fs}]$
	$C_{\text{bNa}}^{max}=0.00029\text{nS}/\text{pF}$	$C_{\text{Kr}}^{max}=0.0096\text{nS}/\text{pF}$	$C_{\text{bCa}}^{max}=0.000592\text{nS}/\text{pF}$
		$C_{\text{Ks},\text{epi}}^{max}=0.245\text{nS}/\text{pF}$	$C_{\text{pCa}}^{max}=0.825\text{nS}/\text{pF}$
		$C_{\text{Ks},\text{endo}}^{max}=0.245\text{nS}/\text{pF}$
		$C_{\text{Ks},\mathrm{M}}^{max}=0.062\text{nS}/\text{pF}$
		$C_{\text{pK}}^{max}=0.0146\text{nS}/\text{pF}$
		$C_{\mathrm{t}0,\text{epi}}^{max}=0.294\text{nS}/\text{pF}$
		$C_{\mathrm{t}0,\text{endo}}^{max}=0.073\text{nS}/\text{pF}$
		$C_{\mathrm{t}0,\mathrm{M}}^{max}=0.294\text{nS}/\text{pF}$
half saturation constants	cCaNa = 1.38 mM		cCaNa= 1.38 mM
	cCNa = 87.50 mM		cNaCa = 87.50 mM
	cKNa = 1.00 mM	cKNa = 1.00 mM	cpCa = 0.0005 mM
	cNaK = 40.00 mM	cNaK == 410.0.000mM	cup = 0.00025 mM	cup = 0.00025 mM
			crel = 0.25 mM	crel =0.25 mM
			cbuf = 0.001 mM	$c_{\text{buf}}^{sr}=0.3\text{mM}$
other parameters	$k_{\text{NaCa}}^{\text{sat}}=0.10$	pKNa = 0.03	γrel = 2	γrel = 2
	γNaCa= 2.50		γtot = 0.15 mM	$c_{\text{tot}}^{\text{sr}}=10\text{mM}$
	γ = 0.35
gas constant R =8.3143 J K−1 mol−1		temperature T =310 K	cytoplasmic volume V =16404μm3
Faraday constant F =96.4867 C/mmol		membrane capacitance C =185 pF	sarcoplasmic reticulum volume Vsr= 1094μm3

Figure 3, top left, illustrates the evolution of the transmembrane potential ϕ. In cardiac cells at rest, the transmembrane potential is -86 mV, which implies that the intracellular domain is negatively charged in comparison to the extracellular domain. The application of an external stimulus generates an initial depolarization across the cell membrane. Once the stimulus exceeds the critical threshold, the transmembrane potential increases rapidly from its resting state of -86 mV via an overshoot of +38 mV to its excited state of +20 mV. After a brief period of partial initial repolarization, the transmembrane potential experiences a characteristic plateau of 0.2 ms, before the cell gradually repolarizes to return to its initial resting state.

Figure 3.

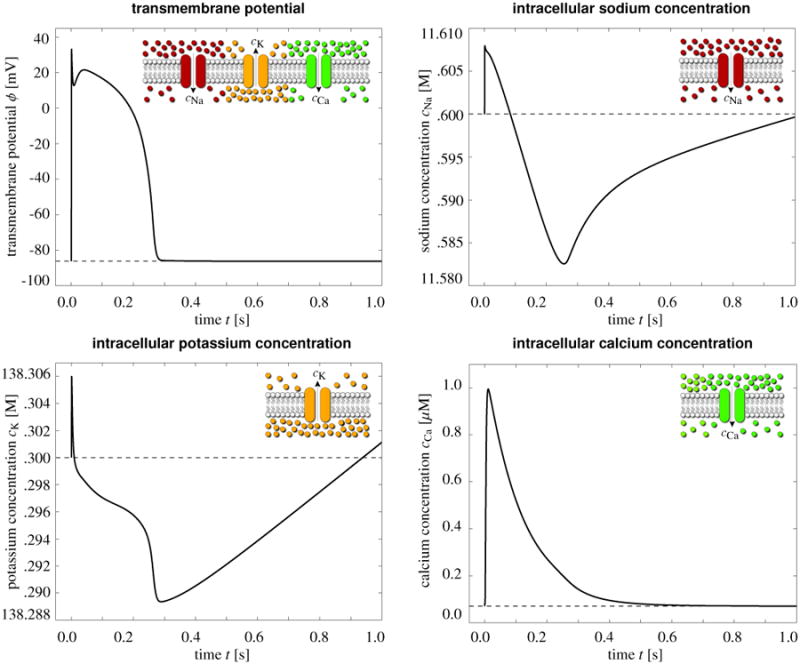
Electrochemistry in a human ventricular cardiomyocyte. Temporal evolution of the transmembrane potential ϕ and of the intracellular sodium potassium and calcium concentrations c_Ca, c_K, and c_Ca. The influx of positively charged sodium ions generates a rapid upstroke in the transmembrane potential. At peak, the efflux of positively charged potassium ions initiates an early, partial repolarization. During the plateau, the influx of positively charged calcium ions balances the efflux of positively charged potassium ions. Final repolarization begins when the efflux of potassium ions exceeds the influx of calcium ions. Throughout the interval between the end of repolarization and the beginning of the next cycle, the cell is at rest.

Figure 3, top right, illustrates the evolution of the intracellular sodium concentration c_Na, which rises sharply at the beginning of the cycle to create the rapid upstroke of the transmembrane potential. The sodium concentration then decays slowly towards the end of the repolarization phase and increases gradually during the resting phase to return to its initial value. Figure 3, bottom left, illustrates the evolution of the intracellular potassium concentration c_K. After a rapid increase, c_K decreases in a stepwise fashion, regulated by the sequential activation of the individual potassium channels. At the end of the repolarization phase, c_K increases gradually to smoothly return to its initial value. Figure 3, bottom right, illustrates the evolution of the intracellular calcium concentration c_Ca. Slightly after the upstroke of the transmembrane potential, the calcium concentration increases to its peak value and then decays smoothly to its original value throughout the remaining phases of the cycle. In the following section, we will demonstrate how an increase in the intracellular calcium concentration can initiate mechanical contraction. In summary, the model reproduces all characteristic features of human ventricular cardiomyocytes [72, 73, 76]: an initial increase in sodium to create a rapid upstroke in the transmembrane potential, a combined decrease in potassium and increase in calcium to generate the characteristic plateau, and an increase in potassium during the recovery phase to bring the cell back to its resting state. Despite drastic changes in the membrane potential from -86 mV to +20 mV, changes in the individual ion concentrations remain remarkably small, typically in the order of less than one percent.

Figure 4 illustrates the evolution of the active contractile force F^act throughout an excitation cycle. The rapid increase in the intracellular calcium concentration c_Ca initiates a rapid increase in the active force. After reaching its peak value, the force gradually returns to zero.

Figure 4.

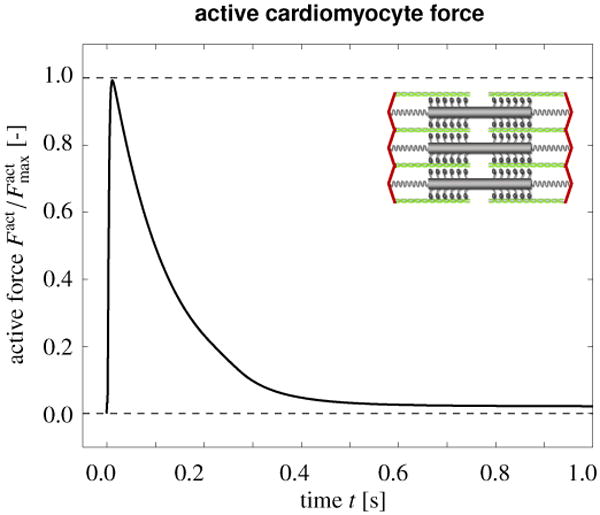
Mechanical contraction in a human ventricular cardiomyocyte. Temporal evolution of the active force F^act throughout an excitation cycle. The rapid increase in the intracellular calcium concentration c_Ca initiates a rapid increase in the active force. After reaching its peak value, the force gradually returns to zero.

5.2. Chemo-electro-mechanical coupling in a square panel

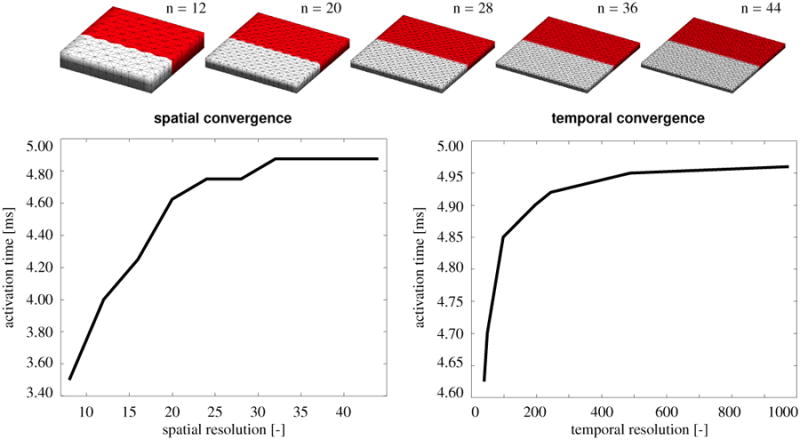
To demonstrate the convergence of our chemo-electrical-mechanical model, we simulate the wave propagation in a square flat panel, and compare the activation times for different spatial and temporal discretizations. In particular, we discretize the 8 mm×8 mm panel with epicardial human ventricular cardiomyocytes using the material parameters summarized in Tables I and II. We initialize the panel with homogeneous initial conditions for the local ion concentrations and the local gating variables using the same parameter values as described in Section 5.1 to mimic the initial resting state. We initialize the global membrane potential with a resting value of ϕ = −86 mV, and perturb its value at the upper edge of the panel with a value of ϕ = +40 mV to initiate a downward traveling wave. For the spatial convergence study, we discretize the panel in space with n×n×12 linear tetrahedral elements, (n+1)×(n+1)×3 nodes, and (n+1)×(n+1)× 12 degrees of freedom, where we systematically increase n from 8 to 44 in steps of four. Accordingly, our finest mesh thus consists of 23,232 elements, 6,075 nodes, and 24,300 degrees of freedom. For this study, we fix the temporal discretization at a constant time step size of Δt = 0.125 ms. For the temporal convergence study, we discretize the travel time with 40 to 975 equidistant finite difference steps and fix the spatial discretization at a constant mesh size parameterized with n=12.

Table II.

Electro-mechanical material parameters of human cardiac tissue.

	electrical parameters
isotropic conduction septum	diso = 5 mm2/ms [23]
anisotropic conduction septum	dani = 10mm2/ms [23]
isotropic conduction	diso = 0.1mm2/ms [23]
anisotropic conduction	dani = 0.2mm2/ms [23]
	mechanical parameters
isotropic bulk	κ = 100 kPa
isotropic myocardium	a = 0.496 kPa, b = 7.209 [25]
anisotropic myocardium	aff = 15.193 kPa, bff = 20.417 [25]
	ass = 3.283 kPa, bss = 11.176 [25]
	afs = 0.662 kPa, bfs = 9.466 [25]
	electro-mechanical parameters
saturation of contraction	η = 12.5 kPa/μM [23]
resting calcium concentration	$c_{\text{Ca}}^{\text{rest}}=0.05\mu \mathrm{M}$ [76]
critical calcium concentration	$c_{\text{Ca}}^{\text{crit}}=0.8\mu \mathrm{M}$
minimum activation	ε0 = 0.1/ms [23]
maximum activation	ε∞ = 1.0/ms [23]
transition rate	ξ = 4.00/μM [23]

Figure 5, top, illustrates five representative spatial discretizations parameterized with n=12, 20, 28, 36, and 44. Red colors indicate tissue regions that are already excited, grey regions indicate tissue still at the resting state. All five snap shots correspond to t = 2.00 ms, the time at which the wave front has reached the centerline of the panel for the finest discretization, shown on the right. For the coarsest discretization, shown on the left, the wave has already passed the centerline, indicating that the wave speed is slightly higher for coarser meshes.

Figure 5.

Algorithmic convergence upon spatial and temporal refinement. The panel is discretized in space with n×n×12 tetrahedral elements, (n+1)×(n+1)×3 nodes, and (n+1)×(n+1)×12 degrees of freedom, where n is increased from 8 to 44. The activation sequence is discretized in time with 40 to 975 equidistant finite difference steps. Both spatial and temporal discretization converge smoothly towards a finite activation time.

Figure 5, bottom, illustrates the algorithmic convergence upon spatial refinement, left, and temporal refinement, right. As a global metric for the traveling wave, we plot the activation time of the lower panel edge for different spatial and temporal discretizations. In agreement with the color-coded panels in the top row, both activation graphs reveal that the wave travels slightly faster for coarser spatial and temporal discretizations. However, upon spatial and temporal refinement, both solutions converge smoothly towards a finite activation time.

5.3. Chemo-electro-mechanical coupling in the human heart

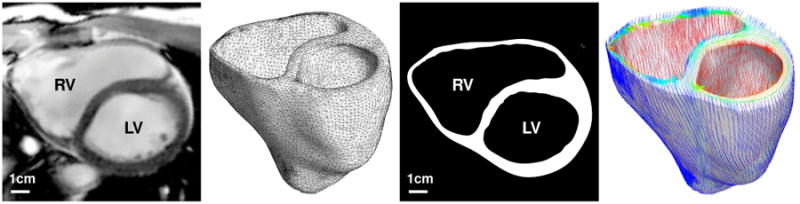
To illustrate the global features of our chemo-electrical-mechanical model, we simulate excitation-contraction coupling in a human heart throughout a representative cardiac cycle. We reconstruct a patient-specific human heart model from magnetic resonance images [39], see Figure 6. Figure 6, middle, illustrates the finite element discretization consisting of 46,896 linear tetrahedral elements, 13,831 nodes, and 55,324 degrees of freedom. To account for the characteristic microstructure of the heart, we assign locally varying fiber vectors f₀ and sheet vectors s₀ created from a feature-based Poisson interpolation [78]. Specifically, we enforce the Poisson interpolation in the weak sense using a standard linear finite element algorithm for scalar-valued second-order boundary value problems. We introduce fiber and sheet angles as a global unknowns and enforce their epicardial and endocaridal values in the strong sense as Dirichlet boundary conditions. We have previously demonstrated that this concept is capable of generating smoothly varying fibre orientations, quickly, efficiently and robustly, both in a generic bi-ventricular model and in a patient-specific human heart [78]. Figure 6, right, illustrates the resulting fiber distribution across the left and right ventricles. Fiber directions vary gradually from -70° in the epicardium, the outer wall shown in blue, to +80° in the endocardium, the inner wall shown in red. Sheet directions are outward-pointing with respect to the epicardial surface.

Figure 6.

Human heart model created from magnetic resonance images, left. The mesh consists of 46,896 linear tetrahedral elements, 13,831 nodes, and 55,324 degrees of freedom, middle. The fiber orientation created from a feature-based Poisson interpolation varies gradually from -70° in the epicardium, the outer wall shown in blue, to +80° in the endocardium, the inner wall shown in red, right.

Similar to the single cell example in Section 5.1, we apply initial conditions which mimic the resting state, with a global membrane potential of ϕ = −86 mV, and the local ion concentrations of c_Na = 11.6mM, c_K = 138.3 mM, c_Ca = 0.08 μM, and $c_{\text{Ca}}^{\text{sr}}=0.56\text{mM}$, and gating variables of g_m = 0, g_h = 0.75, g_j = 0.75, g_d = 0, g_f = 1, g_fCa = 1, g_r = 0, g_s = 1, g_xs = 0, g_xr1 = 0, g_xr2 = 0, g_xK1∞ = 0.05, and g_g = 1. Tables I summarizes the chemo-electrical parameters which are similar to single cell example in Section 5.1. To account for regionally varying action potential durations, we divide the heart in five regions, basal septum, apical septum, apex, mid-ventricular wall, and lateral ventricular wall [35]. We systematically increase the bulk ion channel conductances $C_{\text{Kr}}^{max}$, $C_{\text{Ks}}^{max}$, and $C_{\text{CaL}}^{max}$ from upper septum to lateral wall by ±30%. The electro-mechanical coupling parameters are the saturation of cardiomyocyte contraction η = 12.5kPa/μM, the resting concentration of calcium $c_{\text{Ca}}^{\text{rest}}=0.05\mu \mathrm{M}$, the minimum and maximum values scaling fiber contraction ε₀ = 0.1/ms and ε_∞ = 1.0/ms, the critical calcium concentration above which contraction is initiated $c_{\text{Ca}}^{\text{crit}}=0.8\mu \mathrm{M}$, and the transition rate ξ = 4.0/μM. These are the same values as in the single cell example in Section 5.1, which have been calibrated such that the maximum fiber contraction λ_ff is approximately 15% [71]. The electrical parameters are the isotropic and anisotropic conduction d^iso = 5mm²/ms and d^ani = 10mm²/ms in the Purkinje fiber rich septal region, and d^iso = 0.1mm²/ms and d^ani = 0.2mm²/ms in the lateral ventricular walls. We would like to point out though that the degree of anisotropy chosen here is relatively low as compared to physiological anisotropy ratios of 1:5 or even 1:10 [18]. Moreover, in reality, the Purkinje fibers are isolated from the septum and activate the heart from the endocardium of the left and right ventricular walls from the apex, to about three fourth of the total ventricular length. A discrete representation of the Purkinje fiber network [39] would therefore provide a more accurate reflection of the excitation pattern with a more realistic representation of transmural activation gradients [71]. The mechanical parameters are the isotropic elastic bulk modulus κ = 100.0 kPa, the isotropic elastic tissue parameters a = 0.496 kPa and b = 7.209, the anisotropic elastic parameters, a_ff = 15.193 kPa and b_ff = 20.417, a_ss = 3.283 kPa and b_ss = 11.176, and a_fs = 0.662 kPa and b_fs = 9.466, which we have identified [25] using simple shear experiments from the literature [19, 32]. Table II summarizes the electro-mechanical parameters.

For the electrical problem, we apply the common assumption of homogeneous Neumann boundary conditions. For the mechanical problem, we apply homogeneous Dirichlet boundary conditions throughout the basal plane [24]. We excite the heart through an external stimulus in the region of the atrioventricular node located in the center of the basal septum. We apply an adaptive time stepping scheme, for which we select the convergence tolerance to 1.0E-09 and the optimal number of iterations to four [76]. For a larger number of iterations, the adaptive scheme automatically decreases the time step size; for a smaller number of iterations, the adaptive scheme increases the time step size [68].

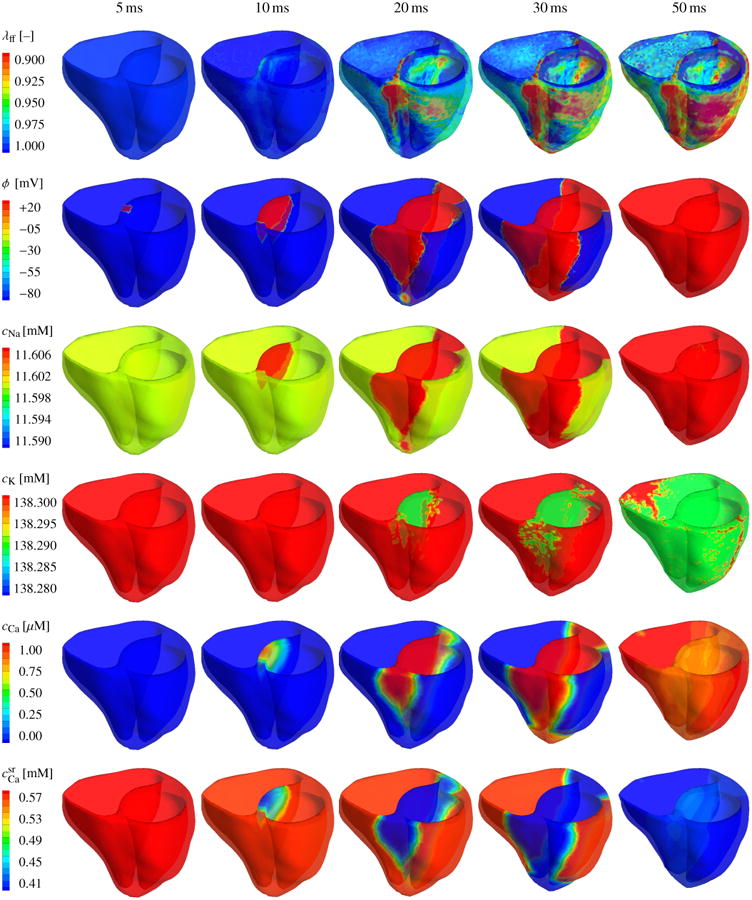
Figures 7 and 8 illustrate the evolution of the fiber contraction λ_ff, of the transmembrane potential ϕ, and of the individual ion concentrations c_Na, c_K, c_Ca, and $c_{\text{Ca}}^{\text{sr}}$ during the depolarization and repolarization phases, respectively. Figure 7 shows how depolarization is initiated through changes in the intracellular sodium concentration c_Ca, which increases rapidly within the first milliseconds of the cardiac cycle, third row. This increase is associated with a rapid increase in the membrane potential ϕ, second row, which, in turn, affects the voltage-gated calcium and potassium channels within the cell membrane. The intracellular calcium concentration c_Ca increases, fifth row. The intracellular potassium concentration c_K follows with a slight time delay of 15 ms, fourth row. The intracellular calcium concentration c_Ca increases further as calcium is released from the sarcoplasmic reticulum $c_{\text{Ca}}^{\text{sr}}$, sixth row. The increase in the intracellular calcium concentration directly initiates cardiomyocyte contraction λ_ff, first row. The contraction varies regionally and transmurally with maximum values of 10% and more, corresponding to λ_ff = 0.90 and less. As the heart contracts, the apex moves markedly upward towards the fixed base, columns four and five. After 50 ms, the heart is entirely depolarized. The transmembrane potential ϕ has reached its peak value of 20 mV throughout both ventricles, and the heart is maximally contracted.

Figure 7.

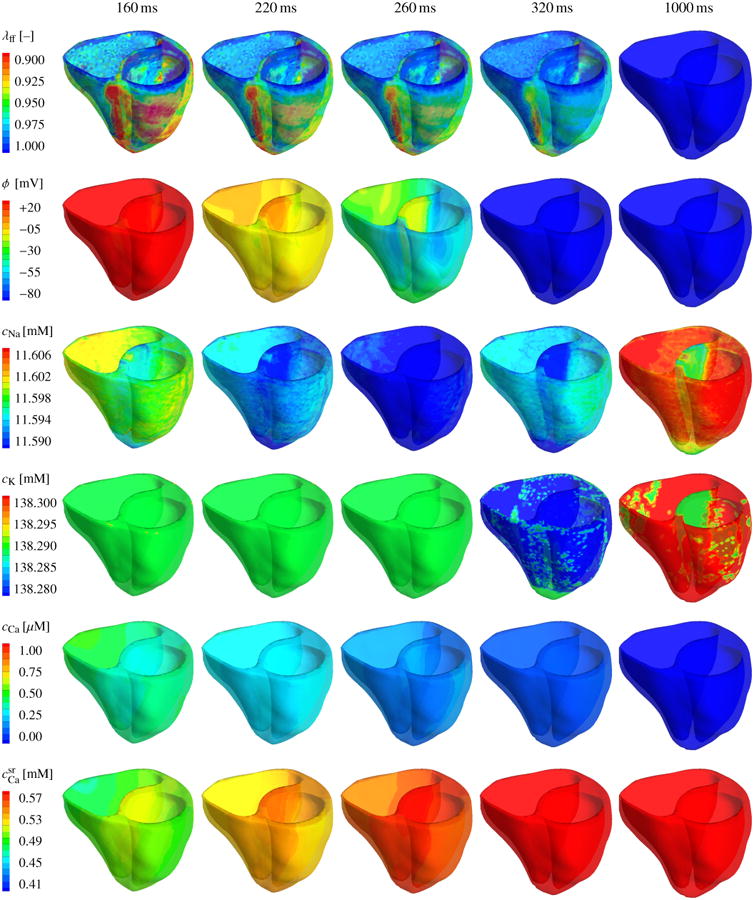
Chemo-electro-mechanical coupling in the human heart. Spatio-temporal evolution of the fiber contraction λ_ff, the transmembrane potential ϕ, the intracellular sodium, potassium, and calcium concentrations c_Na, c_K, and c_Ca, and the calcium concentration in the sarcoplasmic reticulum $c_{\text{Ca}}^{\text{sr}}$ during the rapid depolarization phase of the cardiac cycle. Changes in the individual ion concentrations initiate an increase in the transmembrane potential ϕ from -86 mV to +20 mV. Changes in the intracellular calcium concentration c_Ca initiate a mechanical contraction λ_ff of up to 10-15%. During the contraction phase, the apex moves rapidly towards the base and the heart undergoes a clockwise rotation around its long axis.

Figure 8.

Chemo-electro-mechanical coupling in the human heart. Spatio-temporal evolution of the fiber contraction λ_ff, the transmembrane potential ϕ, the intracellular sodium, potassium, and calcium concentrations c_Na, c_K, and c_Ca, and the calcium concentration in the sarcoplasmic reticulum $c_{\text{Ca}}^{\text{sr}}$ during the gradual repolarization phase of the cardiac cycle. Changes in the individual ion concentrations initiate a slow decrease in the transmembrane potential ϕ from +20 mV to -86 mV. A decrease in the intracellular calcium concentration c_Ca initiates mechanical relaxation with λ_ff returning gradually to 0%. During the filling phase, the apex moves away from the base and the heart undergoes a counterclockwise rotation back to its original position.

Figure 8 displays the repolarization phase characterized through a smooth decrease of the transmembrane potential ϕ and the mechanical contraction λ_ff back to their resting values, first and second row. Decrease in mechanical contraction is caused by a gradual decrease of the intracellular calcium c_Ca concentration back to its resting value, fifth row. The sarcoplasmic reticulum takes up the intracellular calcium, and $c_{\text{Ca}}^{\text{sr}}$ returns back to its resting value, sixth row. At the same time, the intracellular sodium concentration c_Na, which has initially increased, now dips even below its initial value and reaches a minimum after 260 ms, third row. The intracellular potassium concentration c_K reaches its minimum approximately at the same time, fourth row. In the course of time, both sodium and potassium then slowly return to their resting values as their concentrations increase gradually. The temporal evolution of the mechanical, electrical, and chemical fields is in excellent qualitatively and quantitatively agreement with the single cardiomyocyte transients documented in Figures 3 and 4. However, because of the heterogeneous character of the whole heart simulation, the intracellular sodium and potassium concentrations c_Na and c_K still display small local deviations from the complete resting state 1000 ms after the onset of excitation, see Figures 8, third and fourth row, last column.

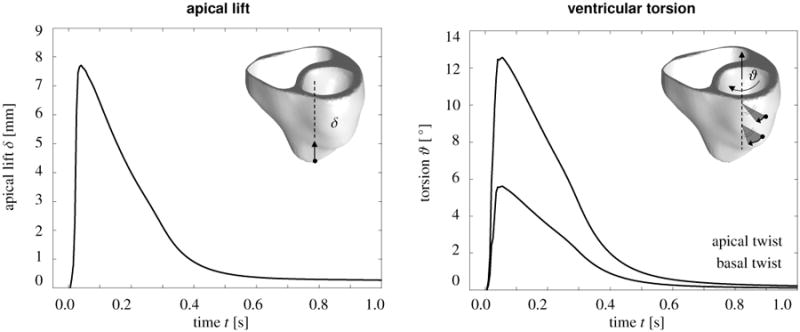
Figure 9 illustrates the global performance of the heart in dry pumping in terms of two characteristic clinical metrics of cardiac function, apical lift δ and of ventricular torsion ϑ. Figure 9, left, shows the apical lift, i.e., the vertical movement of the apex along the heart's long axis towards the fixed base. Shortly after the onset of excitation, the apex lifts rapidly towards the base moving upward by approximately 8mm. Figure 9, right, shows the ventricular torsion, i.e., the rotation of two marked locations in the lateral left ventricular wall, at approximately 1/3 and 2/3 height, around the heart's long axis. Shortly after the onset of excitation, the heart undergoes a rapid twist, rotating clockwise by approximately 6° and 13°, with the amount of torsion increasing from the fixed base to the free apex. Both apical lift and ventricular torsion then decrease gradually to zero as the heart returns to its original position. These characteristics of apical lift and ventricular torsion are in excellent qualitative agreement with clinical observations [46].

Figure 9.

Mechanical contraction in the human heart. Temporal evolution of apical lift δ characterizing the vertical movement of the apex along the heart's long axis towards the fixed base, left. Temporal evolution of ventricular torsion ϑ characterizing the rotation of two locations in the lateral left ventricular wall around the heart's long axis, right. Shortly after the onset of excitation, the apex lifts rapidly towards the base moving upward by approximately 8mm. Simultaneously, the heart twists rapidly about its long axis rotating clockwise by approximately 6° and 13°, with the amount of torsion increasing from the fixed base to the free apex. Both apical lift and ventricular torsion then decrease gradually as the heart returns smoothly to its resting state.

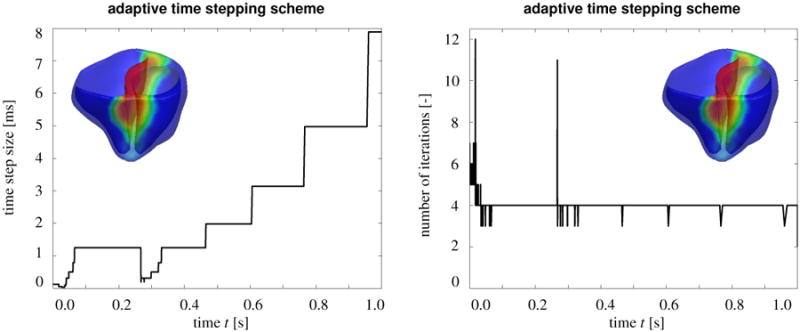
Figure 10 demonstrates the performance of our fully implicit monolithic finite-element based algorithm. Figure 10, left, shows the variation of the time step size and Figure 10, right, shows the corresponding number of Newton iterations within the adaptive time stepping scheme. The algorithm typically converges within four Newton-Raphson iterations. For more required iterations, the adaptive algorithm automatically decreases the time step size, for example, during the rapid upstroke phase before t = 0.05 s where the time step size becomes as small as Δt = 0.03 ms and during the repolarization phase between t = 0.25 s and t = 0.32 s where the time step size becomes as small as Δt = 0.31 ms. For less required iterations, the adaptive algorithm automatically increases the time step size, for example during the plateau phase, between t = 0.05 s and t = 0.25 s where the time step size becomes as large as Δt = 1.25 ms and during the resting phase after t = 0.32 s where the time step size becomes as large as Δt = 7.89 ms.

Figure 10.

Algorithmic performance. Time step size and number of iterations for adaptive time stepping scheme. The algorithm typically convergences within four Newton Raphson iterations. For more iterations, the adaptive algorithm automatically decreases the time step size, for example, during the rapid upstroke phase before t =0.05 s and during the repolarization phase between t =0.25s and t =0.32s. For less iterations, the adaptive algorithm automatically increases the time step size, for example during the plateau phase, between t =0.05s and t =0.25 s and during the resting phase after t =0.32 s. The total number of time increments is 1,288, and the overall run time is 51.97 hours, calculated on a single core of an i7-950 3.06 GHz desktop with 12GB of memory.

Table III confirms these observations. During the rapid upstroke phase, at t = 0.0125 s, the algorithm requires six Newton iterations to fully converge with the given convergence tolerance of 1.0E-09. During the early repolarization phase, at t = 0.050 s, during the plateau phase, at t = 0.125 s, and during the resting phase, at t = 0.750 s, the algorithm requires only three Newton iterations. During the final repolarization phase, at t = 0.250 s, the algorithm requires four Newton iterations. Overall, Table III confirms the consistent linearization of our algorithm through the quadratic convergence of the global Newton iteration during all five phases of the cardiac cycle.

Table III.

Algorithmic performance. Characteristic quadratic convergence of global Newton Raphson iteration, illustrated in terms of the representative residuals of the relative error during five different phases of the cardiac cycle.

	phase 0 upstroke [0.0125 s]	phase 1 early repolarization [0.050 ms]	phase 2 plateau [0.125 s]	phase 3 final repolarization [0.250 s]	phase 4 resting state [0.750 s]
iteration 1	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E+00	1.0000E–01
iteration 2	2.8851E–01	9.2488E–06	1.9453E–04	1.3929E–04	9.1883E–06
iteration 3	1.5778E–02	5.1421E–11	4.8334E–10	1.6442E–09	2.8551E–10
iteration 4	1.0136E–04	–	–	4.5720E–14	–
iteration 5	6.8749E–08	–	–	–	–
iteration 6	7.3132E–14	–	–	–	–

We do not observe stability issues, which we attribute to the implicit nature of the underlying time integration scheme. The simulation run of an entire cardiac cycle finishes after a total number of time increments of 1,288. The overall run time is 51.97 hours, calculated on a single core of an i7-950 3.06 GHz desktop with 12GB of memory.

6. Discussion

We have presented a unified, fully coupled finite element formulation for chemo-electro-mechanical phenomena in living biological systems and demonstrated its potential to simulate excitation-contraction coupling in a patient-specific human heart. The novel aspect of this work is that all chemical, electrical, and mechanical fields are solved monolithically using an implicit time integration scheme, consistently linearized, embedded in a Newton-Raphson solution strategy. In contrast to most existing algorithms, the proposed discretization scheme is unconditionally stable, computationally efficient, highly modular, geometrically flexible, and easily expandable.

Unconditional stability is guaranteed by a using a fully coupled, implicitly integrated, consistently linearized finite element approach. Existing algorithms are typically based on sequential, staggered solution techniques [69] and utilize explicit time marching schemes [38, 41]. They are inherently unstable and limited in time step size [55], which might make them less robust and less efficient. Especially during the rapid upstroke phase, steep spatial and temporal gradients in the unknown fields might initiate spurious instabilities when using explicit time stepping schemes [49]. To avoid these potential limitations, we have applied an implicit backward Euler time integration scheme [23, 76]. We have shown that this scheme is capable of handling sharp chemical, electrical, and mechanical profiles associated with rapid changes in the local and global unknowns. Since our algorithm follows the classical layout of nonlinear finite element schemes, we can utilize readily available adaptive time stepping schemes at no extra cost or effort [68]. We have demonstrated that a simple, ad-hoc, iteration-counter based time adaptive scheme automatically decreases the time step size during phases with steep temporal gradients and, conversely, increases the time size when all unknowns evolve smoothly.

Efficiency is not only increased by using time adaptive schemes, but also by using a classical finite-element specific global-local split [22, 60]. While most existing algorithms discretize all unknowns globally, we only introduce four global degrees of freedom at the node point level, i.e., the vector-valued mechanical deformation and the scalar-valued electrical potential. We introduce, update, and store all other state variables locally on the integration point level [24, 57, 65], i.e., the thirteen chemical gating variables and the four ion concentrations for our particular cardiomyocyte model. Accordingly, our global system matrix remains small and efficiently to invert during the solution procedure.

Modularity originates from the nature of the underlying finite element discretization, which introduces all cell-specific unknowns as local internal variables on the integration point level. This allows us to modularly integrate the proposed algorithm into any commercial finite element package that can handle a coupled nonlinear system of vector- and scalar-valued governing equations [68]. The simplest strategy would be to use an existing thermo-mechanical element formulation and re-interpret the temperature field as the transmembrane potential. Algorithmic modifications are then restricted exclusively to the constitutive subroutine, in which we would solve the chemical problem and store the ion concentrations and gating variables as internal variables at each integration point [76]. Another natural benefit of using finite element schemes is that the modular treatment of the constitutive equations allows us to combine arbitrary cell types, e.g., epicardial and endocardial ventricular cells [43, 72], Purkinje fiber cells [45], atrial cells [16], and pacemaker cells [51], to effortlessly account for microstructural inhomogeneities. We have successfully combined excitable and non-excitable cells [13], self-excitable pacemaker cells and stable ventricular cells [22], ventricular cells and Purkinje fiber cells with different conductivities [39], and ventricular cells with different action potential durations [35] to seamlessly incorporate the structural inhomogeneities of cardiac tissue.

Geometrical flexibility is probably the most advantageous feature of finite element techniques when compared to finite difference schemes or finite volume methods. Unlike existing schemes which are most powerful on regular grids, the proposed algorithm can be applied to arbitrary geometries with arbitrary initial and boundary conditions [64]. Finite element algorithms can easily handle medical-image based patient-specific geometries [8, 39, 67]. In a simple pre-processing step, we could even utilize finite element algorithms to create fiber orientations on arbitrary patient-specific meshes using Lagrangian feature-based interpolation as illustrated in Figure 6. The key advantage of finite element algorithms, however, is that they allow us to simulate finite deformations throughout the cardiac cycle in a straightforward and natural way [23]. Finite element models inherently allow for global or local, adaptive mesh refinement to increase the accuracy of the solution [69], e.g., to accurately resolve transmural gradients of the underlying activation and deactivation patterns [71].

Ease of expandability is attributed to the fact that we use a single unified discretization technique. Being finite-element based and transparent in nature, our approach lays the groundwork for a robust and stable whole heart model of excitation-contraction coupling. Through the incorporation of an additional scalar-valued global unknown, e.g., to characterize the extracellular potential field, we could easily expand the proposed monodomain formulation into a more accurate bidomain formulation [17,18,56]. Through the incorporation of additional gating variables as local unknowns, e.g., to characterize the optical manipulation of cardiac cells [1], we could easily expand the proposed formulation into a photo-electro-chemical formulation [77].

In the future, we will further calibrate and validate our model across the different scales. On the cellular level, we will perform local patch clamp electrophysiology [1], on the cell culture level, we will analyze microelectroarray recordings [13], on the tissue level, we will perform heart slice force measurements [9]. On the organ level, we will consult large animal experiments [71] and patient-specific clinical data [39, 40]. A current trend in cardiac electromechanics is to establish valuable libraries of benchmark solutions [50, 58], against which we will compare our model both qualitatively and quantitatively in the near future. We have already validated the electrical module of our model using a patient-specific electrocardiogram extracted from the electrical flux vector Q integrated over the cardiac domain [35, 39]. We have also validated the mechanical module in terms of the maximum fiber contraction λ_ff of approximately 10%, which agrees nicely with an earlier study in an ovine model where the maximum fiber contraction was found to lie within 8% and 10%. We plan to further validate the mechanical module in terms of the apical lift and ventricular torsion extracted from Figure 9, and, ultimately, in terms of pressure-volume loops.

In summary, we believe that there are compelling reasons to consider the use of fully coupled, implicitly integrated, consistently linearized discretization strategies that enjoy the advantages inherent to finite element schemes. Initially, it may seem tedious to transition existing chemical, electrical, and mechanical algorithms into a single unified chemo-electro-mechanical algorithm. However, we are convinced that these efforts will pay off when it comes to truly predicting the impact of pharmacological, interventional, and surgical treatment options to systematically manipulate chemical, electrical, and mechanical fields in the human heart.

Appendix

In this section, we specify the constitutive equations of the chemo-electrical problem for a ventricular cardiomyocyte [76]. The cell model draws on the classical Luo-Rudy model [43, 44], enhanced by several recent modifications [27, 59, 72, 74] and accounts for n_ion = 4 ion concentrations, $c_{\text{ion}}=[c_{\text{Na}},c_{\mathrm{K}},c_{\text{Ca}},c_{\text{Ca}}^{\text{sr}}]$, where c_Na, c_K, and c_Ca are the intracellular sodium, potassium, and calcium concentration, and $c_{\text{Ca}}^{\text{sr}}$ is the calcium concentration in the sarcoplasmic reticulum. The model contains n_crt = 15 ionic currents, I_crt = [I_Na, I_bNa, I_NaK, I_NaCa, I_K1, I_Kr, I_Ks, I_pK, I_t0, I_CaL, I_bCa, I_pCa, I_leak, I_up, I_rel], as illustrated in Figure 2. The states of the channels associated with these currents are gated by n_gate = 13 gating variables, g_gate = [g_m, g_h, g_j, g_xr1, g_xr2, g_xs, g_r, g_s, g_d, g_f, g_xK1∞, g_fCa, g_g]. For each ion, sodium, potassium, and calcium, we evaluate the classical Nernst equation,

$${\varphi }_{\text{ion}}=\frac{RT}{z_{\text{ion}}F}log\left(\frac{c_{\text{ion}0}}{c_{\text{ion}}}\right)\text{with}{\varphi }_{\text{ion}}=[{\varphi }_{\text{Na}},{\varphi }_{\mathrm{K}},{\varphi }_{\text{Ca}}],$$ (28)

to determine the concentration-dependent reversal potential ϕ_ion, i.e., the potential difference across the cell membrane, which would be generated by this particular ion if no other ions were present. In that case, if the membrane were permeable to this specific ion, its transmembrane potential ϕ would approach this ion's equilibrium potential ϕ_ion. Here, R = 8.3143 JK⁻¹mol⁻¹ is the gas constant, T = 310 K is the absolute temperature, and F = 96.4867 C/mmol is the Faraday constant. The constant z_ion is the elementary charge per ion. For singly-charged sodium and potassium ions z_Na=1 and z_K=1, and for doubly-charged calcium ions z_Ca=2. The extracellular sodium, potassium, and calcium concentrations are c_Na0 = 140 mM, c_K0 = 5.4 mM, and c_Ca0 = 2mM. We now specify the individual concentrations, currents, and gating variables for sodium, potassium, and calcium to define the source term F^ϕ for the electrical problem (21). In what follows, we use the units milliseconds for time t, millivolts for voltage ϕ, picoamperes per picofarad for ionic currents across the cell membrane, millimolar per millisecond for ionic currents across the membrane of the sarcoplasmic reticulum, nanosiemens per picofarad for conductances C_crt, and millimoles per liter for intracellular and extracellular ion concentrations c_ion. Table I summarizes all local chemo-electrical parameters of our human ventricular cardiomyocyte model.

6.1. Sodium concentration, currents, and gating variables

Sodium plays a crucial role in generating the fast upstroke in the initial phase of the action potential. At rest, the intracellular sodium concentration is approximately c_Na = 11.6mM. This implies that, according to equation (28), the sodium equilibrium potential is ϕ_Na = +66.5 mV. Accordingly, both electrical forces and chemical gradients draw extracellular sodium ions into the cell. At rest, the influx of sodium ions is low since the membrane is relatively impermeable to sodium. An external stimulus above a critical threshold value causes the fast sodium channel to open and initiates a rapid inflow of sodium ions associated with the rapid depolarization of the cell membrane. The transmembrane potential increases rapidly by more than 100 mV in less than 2ms, see Figure 3. At the end of the upstroke, the cell membrane is positively charged, and the fast sodium channels return to their closed state. In our specific cell model, the sodium concentration

$${\dot{c}}_{\text{Na}}=-\frac{C}{VF}[I_{\text{Na}}+I_{\text{bNa}}+3I_{\text{NaK}}+3I_{\text{NaCa}}]$$ (29)

is evolving in response to the fast sodium current I_Na, the background sodium current I_bNa, the sodium potassium pump current I_NaK, and the sodium calcium exchanger current I_NaCa according to Faraday's law of electrolysis. The membrane capacitance per unit surface area is C = 185 pF, the cytoplasmic volume is V = 16404 μm³, and the Faraday constant is F = 96.4867 C/mmol. Both the sodium potassium pump and the sodium calcium exchanger operate at a three-to-two ratio as indicated by the scaling factor of three. The sodium related currents are functions of the transmembrane potential ϕ, the gating variables g_gate and the ion concentrations c_ion,

$$\begin{array}{c}{I}_{\text{Na}}=C_{\text{Na}}^{max}{g}_{\mathrm{m}}^3{g}_{\mathrm{h}}{g}_{\mathrm{j}}[\varphi -{\varphi }_{\text{Na}}]\\ I_{\text{bNa}}=C_{\text{bNa}}^{max}[\varphi -{\varphi }_{\text{Na}}]\\ I_{\text{NaK}}=I_{\text{NaK}}^{max}[c_{\mathrm{K}0}{c}_{\text{Na}}]{[[c_{\text{Na}}+c_{\text{NaK}}][c_{\mathrm{K}0}+c_{\text{KNa}}][1+0.1245e^{-0.1\varphi F/RT}+0.0353e^{-\varphi F/RT}]]}^{-1}\\ I_{\text{NaCa}}=I_{\text{NaCa}}^{max}[e^{\gamma \varphi F/RT}{c}_{\text{Na}}^3{c}_{\text{Ca}0}-e^{(\gamma -1)\varphi F/RT}{c}_{\text{Na}0}^3{c}_{\text{Ca}}\gamma \text{NaCa}]{[[c_{\text{NaCa}}^3+c_{\text{Na}0}^3][c_{\text{CaNa}}+c_{\text{Ca}0}][1+k_{\text{NaCa}}^{\text{sat}}{e}^{(\gamma -1)\varphi F/RT}]]}^{-1}.\end{array}$$ (30)

Here the scaling factors are the maximum fast sodium conductance $C_{\text{Na}}^{max}=14.838\text{nS}/\text{pF}$, the maximum background sodium conductance $C_{\text{bNa}}^{max}=0.00029\text{nS}/\text{pF}$, the maximum sodium potassium pump current $I_{\text{NaK}}^{max}=1.362\text{pA}/\text{pF}$, and the maximum sodium calcium exchanger current $I_{\text{NaCa}}^{max}=1000\text{pA}/\text{pF}$. The rapid upstroke in the membrane potential is generated by the fast sodium current I_Na, characterized through a three-gate formulation of Beeler-Reuter type [5] in terms of the sodium activation gate g_m, the fast sodium inactivation gate g_h, and the slow sodium inactivation gate g_j. The gating variables follow classical Hodgkin-Huxley type equations (24) of the format ${\dot{g}}_{\text{gate}}=[g_{\text{gate}}^{\infty }-g_{\text{gate}}]/{\tau }_{\text{gate}}$. Here $g_{\text{gate}}^{\infty }$ characterizes the steady state value and τ_gate denotes the time constant associated with reaching the steady state. For the sodium activation gate ${\dot{g}}_{\mathrm{m}}=[g_{\mathrm{m}}^{\infty }-g_{\mathrm{m}}]/{\tau }_{\mathrm{m}}$, which initiates the rapid upstroke, they take the following explicit representations

$$\begin{array}{c}{g}_{\mathrm{m}}^{\infty }={[1+e^{(-56.86-\varphi )/9.03}]}^{-2}\\ {\tau }_{\mathrm{m}}=0.1{[1+e^{(-60-\varphi )/5}]}^{-1}[{[1+e^{(\varphi +35)/5}]}^{-1}+{[1+e^{(\varphi -50)/200}]}^{-1}].\end{array}$$ (31)

For the fast sodium inactivation gate ${\dot{g}}_{\mathrm{h}}=[g_{\mathrm{h}}^{\infty }-g_{\mathrm{h}}]/{\tau }_{\mathrm{h}}$, which initiates a fast inactivation of the sodium channel almost instantaneously after the rapid upstroke, the steady state value and the corresponding time constant take the following forms,

$$\begin{array}{c}{g}_h^{\infty }={[1+e^{(\varphi +71.55)/7.43}]}^{-2}\\ {\tau }_{\mathrm{h}}=\{\begin{array}{cc}0.1688[1+e^{-(\varphi +10.66)/11.1}]& \text{if}\varphi \ge -40\\ {[0.057e^{-(\varphi +80)/6.8}+2.7e^{0.079\varphi }+3.1\cdot {10}^5{e}^{0.3485\varphi }]}^{-1}& \text{if}\varphi <-40.\end{array}\end{array}$$ (32)

For the slow sodium inactivation gate ${\dot{g}}_{\mathrm{j}}=[g_{\mathrm{j}}^{\infty }-g_{\mathrm{j}}]/{\tau }_{\mathrm{j}}$, which gradually inactivates the fast sodium channel over a time span of 100 to 200 ms, the Hudgkin Huxley constants take the following form,

$$\begin{array}{c}{g}_{\mathrm{j}}^{\infty }={[1+e^{(\varphi +71.55)/7.43}]}^{-2}\\ {\tau }_{\mathrm{j}}={[{\alpha }_{\mathrm{j}}+{\beta }_{\mathrm{j}}]}^{-1}\\ {\alpha }_{\mathrm{j}}=\{\begin{array}{cc}0& \text{if}\varphi \ge -40\\ [-2.5428\cdot {10}^4{e}^{0.2444\varphi }-6.948\cdot {10}^{-6}{e}^{-0.04391\varphi }][\varphi +37.78]{[1+e^{0.311(\varphi +79.23)}]}^{-1}& \text{if}\varphi <-40\end{array}\\ {\beta }_{\mathrm{j}}=\{\begin{array}{cc}0.6e^{0.057\varphi }{[1+e^{-0.1(\varphi +32)}]}^{-1}& \text{if}\varphi \ge -40\\ 0.02424e^{-0.01052\varphi }{[1+e^{-0.1378(\varphi +40.14)}]}^{-1}& \text{if}\varphi <-40.\end{array}\end{array}$$ (33)

The sodium ions that enter the cell rapidly during the fast upstroke are removed from the cell by the sodium potassium pump I_NaK, a metabolic pump that continuously expels sodium ions from the cell interior and pumps in potassium ions. The intracellular sodium concentration is further affected by expulsion of intracellular calcium ions through sodium calcium exchange I_NaCa. The additional parameters for the sodium potassium pump current I_NaK and for the sodium calcium exchanger current I_NaCa are the extracellular sodium, potassium, and calcium concentrations c_Na0 = 140 mM, c_K0 = 5.4 mM, and c_Ca0 = 2mM, the half saturation constants c_CaNa = 1.38 mM, c_NaCa = 87.5mM, c_KNa = 1mM, c_NaK = 40mM, the sodium calcium saturation factor $k_{\text{NaCa}}^{\text{sat}}=0.1$, the outward sodium calcium pump current enhancing factor γ_NaCa = 2.5, and the voltage dependent sodium calcium parameter γ = 0.35.

6.2. Potassium concentration, currents, and gating variables

Potassium plays an important role in maintaining the appropriate action potential profile in all four phases after the rapid upstroke. At rest, the intracellular potassium concentration is typically about c_K = 138.3 mM, and the related equilibrium potential is ϕ_K = −86.6mV according to equation (28). This value is very close to, but slightly more negative than, the resting potential of ϕ = −86 mV actually measured in ventricular cardiomyocytes. Unlike for sodium, the electrical force that pulls potassium ions inward is slightly weaker than the chemical force of diffusion pulling potassium ions outward. This implies that potassium tends to leave the resting cell. At the end of the rapid upstroke, before the beginning of the plateau, we observe an early, brief period of limited repolarization governed by the voltage-activated transient outward current I_t0. The following plateau phase is dominated by an influx of calcium ions which is balanced by the efflux of an equal amount of positively charged potassium ions, mainly regulated by the rapid and slow delayed rectifier currents I_Kr and I_Ks. The final repolarization phase can almost exclusive be attributed to potassium ions leaving the cell such that the membrane potential can return to its resting state, see Figure 3. In summary, the evolution of the potassium concentration

$${\dot{c}}_{\mathrm{K}}=-\frac{C}{VF}[I_{\mathrm{K}1}+I_{\text{Kr}}+I_{\text{Ks}}-2I_{\text{NaK}}+I_{\text{pK}}+I_{\mathrm{t}0}+I_{\text{stim}}]$$ (34)

is mainly controlled by four currents, the inward rectifier current I_K1, the rapid delayed rectifier current I_Kr, the slow delayed rectifier current I_Ks, and the transient outward current I_t0. Moreover, it is affected by the sodium potassium pump current I_NaK, and the plateau potassium current I_pK. Currents are scaled by the membrane capacitance per unit surface area C = 185 pF, the cytoplasmic volume V = 16404 μm³, and the Faraday constant F = 96.4867 C/mmol. The individual potassium related currents take the following forms,

$$\begin{array}{c}{I}_{\mathrm{K}1}=C_{\mathrm{K}1}^{max}{g}_{\mathrm{K}1}^{\infty }{[c_{\mathrm{K}0}/5.4]}^{1/2}[\varphi -{\varphi }_{\mathrm{K}}]\\ I_{\text{Kr}}=C_{\text{Kr}}^{max}{g}_{\text{xr}1}{g}_{\text{xr}2}{[c_{\mathrm{K}0}/5.4]}^{1/2}[\varphi -{\varphi }_{\mathrm{K}}]\\ I_{\text{Ks}}=C_{\text{Ks}}^{max}{g}_{\text{xs}}^2[\varphi -{\varphi }_{\text{Ks}}]\\ I_{\text{NaK}}=I_{\text{NaK}}^{max}[c_{\mathrm{K}0}{c}_{\text{Na}}]{[[c_{\text{Na}}+c_{\text{NaK}}][c_{\mathrm{K}0}+c_{\text{KNa}}][1+0.1245e^{-0.1\varphi F/RT}+0.0353e^{-\varphi F/RT}]]}^{-1}\\ I_{\text{pK}}=C_{\text{pK}}^{max}{[1+e^{[25-\varphi ]/5.98}]}^{-1}[\varphi -{\varphi }_{\mathrm{K}}]\\ I_{\mathrm{t}0}=C_{\mathrm{t}0}^{max}{g}_{\mathrm{r}}{g}_{\mathrm{s}}[\varphi -{\varphi }_{\mathrm{K}}],\end{array}$$ (35)

where the individual scaling factors are the maximum inward rectifier conductance $C_{\mathrm{K}1}^{max}=5.405\text{nS}/\text{pF}$, the maximum rapid delayed rectifier conductance $C_{\text{Kr}}^{max}=0.096\text{nS}/\text{pF}$, the maximum slow delayed rectifier conductance for epicardial and endocardial cells $C_{\text{Ks},\text{epi}}^{max}=C_{\text{Ks},\text{endo}}^{max}=0.245\text{nS}/\text{pF}$ and for M cells $C_{\text{Ks},\mathrm{M}}^{max}=0.062\text{nS}/\text{pF}$, the maximum sodium potassium pump current $I_{\text{NaK}}^{max}=1.362\text{pA}/\text{pF}$, the maximum potassium pump conductance $C_{\text{pK}}^{max}=0.0146\text{nS}/\text{pF}$, and the maximum transient outward conductance for epicardial and M cells $C_{\mathrm{t}0,\text{epi}}^{max}=C_{\mathrm{t}0,\mathrm{M}}^{max}=0.294\text{nS}/\text{pF}$ and for endocardial cells $C_{\mathrm{t}0,\text{endo}}^{max}=0.073\text{nS}/\text{pF}$. The maximum inward rectifier current I_K1, which is most active during the later phases of the action potential, depends explicitly on the extracellular potassium concentration c_K0 = 5.4 mM. It further depends on the time-independent inward recrification factor $g_{\mathrm{K}1}^{\infty }$ parameterized in terms of the potential equilibrium potential ϕ_K given in equation (28),

$$\begin{array}{c}{g}_{\mathrm{K}1}^{\infty }={\alpha }_{\mathrm{K}1}{[{\alpha }_{\mathrm{K}1}+{\beta }_{\mathrm{K}1}]}^{-1}\\ {\alpha }_{\mathrm{K}1}=0.1{[1+e^{0.06(\varphi -{\varphi }_{\mathrm{K}}-200)}]}^{-1}\\ {\beta }_{\mathrm{K}1}=[3e^{0.0002(\varphi -{\varphi }_{\mathrm{K}}+100)}+e^{0.1(\varphi -{\varphi }_{\mathrm{K}}-10)}]{[1+e^{-0.5(\varphi -{\varphi }_{\mathrm{K}})}]}^{-1}.\end{array}$$ (36)

The plateau of the transmembrane potential is generated by an influx of charged calcium ions balanced by the efflux of potassium ions. The latter is governed by the rapid and slow delayed rectifier current I_Kr and I_Ks. The channel for the rapid delayed rectifier current I_Kr is gated by an activation gate ${\dot{g}}_{\mathrm{x}1}=[g_{\mathrm{x}1}^{\infty }-g_{\mathrm{x}1}]/{\tau }_{\mathrm{x}1}$ with the steady state value and time constant given as

$$\begin{array}{c}{g}_{\text{xr}1}^{\infty }={[1+e^{(-26-\varphi )/7}]}^{-1}\\ {\tau }_{\text{xr}1}=2700{[1+e^{(-45-\varphi )/10}]}^{-1}{[1+e^{(\varphi +30)/11.5}]}^{-1}\end{array}$$ (37)

and by an inactivation gate ${\dot{g}}_{\mathrm{x}2}=[g_{\mathrm{x}2}^{\infty }-g_{\mathrm{x}2}]/{\tau }_{\mathrm{x}2}$, with the following steady state value and time constant.

$$\begin{array}{c}{g}_{\text{xr}2}^{\infty }={[1+e^{(\varphi +88)/24}]}^{-1}\\ {\tau }_{\text{xr}2}=3.36{[1+e^{(-60-\varphi )/20}]}^{-1}{[1+e^{(\varphi -60)/20}]}^{-1}.\end{array}$$ (38)

The channel for the slow delayed rectifier current I_Ks is a function of the reversal potential ϕ_Ks = RT/F log([c_K0 +p_KNa c_Na0][c_K + p_KNa c_Na]⁻¹) parameterized in terms of its permeability to sodium ions p_KNa = 0.03. It is gated by an activation gate ${\dot{g}}_{\text{xs}}=[g_{\text{xs}}^{\infty }-g_{\text{xs}}]/{\tau }_{\text{xs}}$ in terms of the following parameterization,

$$\begin{array}{c}{g}_{\text{xs}}^{\infty }={[1+e^{(-5-\varphi )/14}]}^{-1}\\ {\tau }_{\text{xs}}=1100{[1+e^{(-10-\varphi )/6}]}^{-1/2}{[1+e^{(\varphi -60)/20}]}^{-1}.\end{array}$$ (39)

The transient potassium outward current I_t0 is responsible for the transition between the rapid upstroke and the plateau phase, where it generates an early short period of limited repolarization. It is gated by a voltage-dependent activation gate g_r with ${\dot{g}}_{\mathrm{r}}=[g_{\mathrm{r}}^{\infty }-g_{\mathrm{r}}]/{\tau }_{\mathrm{r}}$ defined through the following steady state value and time constant,

$$\begin{array}{c}{g}_{\mathrm{r}}^{\infty }={[1+e^{(20-\varphi )/6}]}^{-1}\\ {\tau }_{\mathrm{r}}=9.5e^{-{(\varphi +40)}^2/1800}+0.8,\end{array}$$ (40)

and by the voltage-dependent inactivation gate g_s with ${\dot{g}}_{\mathrm{s}}=[g_{\mathrm{s}}^{\infty }-g_{\mathrm{s}}]/{\tau }_{\mathrm{s}}$ with the steady state value and time constant given as follows,

$$\begin{array}{c}\begin{array}{c}{g}_{\mathrm{s}}^{\infty }=[1+e^{(\varphi +20)/5}]\\ {\tau }_{\mathrm{s}}=85e^{-{(\varphi +45)}^2/320}+5[1+e^{(\varphi -20)/5}]+3\end{array}\}\text{epicardium}\\ \begin{array}{c}{g}_{\mathrm{s}}^{\infty }=[1+e^{(\varphi +28)/5}]\\ {\tau }_{\mathrm{r}}=1000e^{-{(\varphi +67)}^2/1000}+8.\end{array}\}\text{endocardium}\end{array}$$ (41)

This voltage dependent potassium inactivation gate displays a significantly different behavior for epicardial and endocardial cells and is therefore characterized differently for the individual cell types. Similar to the previous subsection, we have introduced the extracellular sodium and potassium concentrations c_Na0 = 140 mM and c_K0 = 5.4 mM, and the half saturation constants c_KNa = 1 mM and c_NaK = 40 mM.

6.3. Calcium concentration, currents, and gating variables

Calcium is the key player to translate electrical excitation into mechanical contraction. With a typical intracellular resting concentrations of c_Ca = 0.08 μM, its equilibrium potential of ϕ_Ca = +135.3 mV is much larger than the resting potential. During the plateau of the action potential, calcium ions enter the cell through calcium channels that typically activate and inactivate much more slowly than the fast sodium channels. The influx of positively charged calcium ions through the L-type calcium channel I_CaL is balanced by an efflux of positively charged potassium ions. The letter L is meant to indicate the long lasting nature of the inward calcium current. Overall, changes in the intracellular calcium concentration

$${\dot{c}}_{\text{Ca}}={\gamma }_{\text{Ca}}[-\frac{C}{2VF}[I_{\text{CaL}}+I_{\text{bCa}}+I_{\text{pCa}}-2I_{\text{NaCa}}]+I_{\text{leak}}-I_{\text{up}}+I_{\text{rel}}]$$ (42)

are affected by the L-type calcium current I_CaL, the background calcium current I_bCa, the plateau calcium current I_pCa, and the sodium calcium pump current I_NaCa, weighted by the membrane capacitance per unit surface area C = 185 pF, the cytoplasmic volume V = 16404 μm³, and the Faraday constant F = 96.4867 C/mmol. In addition, the intracellular calcium concentration is affected by a calcium loss to the sarcoplasmic reticulum characterized through the leakage current I_leak, the sarcoplasmic reticulum uptake current I_up, and the sarcoplasmic reticulum release current I_rel. The individual calcium related currents are defined as follows,

$$\begin{array}{c}{I}_{\text{CaL}}=C_{\text{CaL}}^{max}[g_{\mathrm{d}}{g}_{\mathrm{f}}{g}_{\text{fCa}}[4\varphi F^2]/[\mathit{\text{RT}}]]{[[c_{\text{Ca}}{e}^{2\varphi F/[\mathit{\text{RT}}]}-0.341c_{\text{Ca}0}][e^{2\varphi F/[\mathit{\text{RT}}]}-1]]}^{-1}\\ I_{\text{bCa}}=C_{\text{bCa}}^{max}[\varphi -{\varphi }_{\text{Ca}}]\\ I_{\text{pCa}}=C_{\text{pCa}}^{max}{c}_{\text{Ca}}{[c_{\text{pCa}}+c_{\text{Ca}}]}^{-1}\\ I_{\text{NaCa}}=I_{\text{NaCa}}^{max}[e^{\gamma \varphi F/\mathit{\text{RT}}}{c}_{\text{Na}}^3{c}_{\text{Ca}0}-e^{(\gamma -1)\varphi F/\mathit{\text{RT}}}{c}_{\text{Na}0}^3{c}_{\text{Ca}}\gamma \text{NaCa}]{[[c_{\text{NaCa}}^3+c_{\text{Na}0}^3][c_{\text{CaNa}}+c_{\text{Ca}0}][1+k_{\text{NaCa}}^{\text{sat}}{e}^{(\gamma -1)\varphi F/\mathit{\text{RT}}}]]}^{-1}\\ I_{\text{leak}}=I_{\text{leak}}^{max}[c_{\text{Ca}}^{\text{sr}}+c_{\text{Ca}}]\\ I_{\text{up}}=I_{\text{up}}^{max}{[1+c_{\text{up}}^2/c_{\text{Ca}}^2]}^{-1}\\ I_{\text{rel}}=I_{\text{rel}}^{max}{g}_{\mathrm{d}}{g}_{\mathrm{g}}[1+{\gamma }_{\text{rel}}{c}_{\text{Ca}}^{\text{sr}2}{[c_{\text{rel}}^2+c_{\text{Ca}}^{\text{sr}2}]}^{-1}],\end{array}$$ (43)

where the individual scaling factors are the maximum calcium conductance $C_{\text{CaL}}^{max}=0.175{mm}^3\mu {\mathrm{F}}^{-1}{\mathrm{s}}^{-1}$, the maximum background calcium conductance $C_{\text{bCa}}^{max}=0.000592\text{nS}/\text{pF}$, the maximum plateau calcium conductance $C_{\text{pCa}}^{max}=0.825\text{nS}/\text{pF}$, the maximum sodium calcium pump current $I_{\text{NaCa}}^{max}=1000\text{pA}/\text{pF}$, the maximum leakage current $I_{\text{leak}}^{max}=0.08{\mathrm{s}}^{-1}$, the maximum sarcoplasmic reticulum calcium uptake current $I_{\text{up}}^{max}=0.000425\text{mM}/ms$, and the maximum sarcoplasmic reticulum calcium release current $I_{\text{rel}}^{max}=8.232\text{mM}/\mathrm{s}$. The major calcium channel, the long-lasting L-type calcium channel I_CaL, is controlled by the voltage-dependent activation gate ${\dot{g}}_{\mathrm{d}}=[g_{\mathrm{d}}^{\infty }-g_{\mathrm{d}}]/{\tau }_{\mathrm{g}}$ characterized through the following steady state value and time constant

$$\begin{array}{c}{g}_{\mathrm{d}}^{\infty }={[1+e^{(-5-\varphi )/7.5}]}^{-1}\\ {\tau }_{\mathrm{d}}=[1.4{[1+e^{(-35-\varphi )/13}]}^{-1}+0.25][1.4[1+e^{(\varphi +5)/5}]]+[1+e^{(50-\varphi )/20}],\end{array}$$ (44)

by the voltage-dependent inactivate gate ${\dot{g}}_{\mathrm{f}}=[g_{\mathrm{f}}^{\infty }-g_{\mathrm{f}}]/{\tau }_{\mathrm{f}}$ characterized through

$$\begin{array}{c}{g}_{\mathrm{f}}^{\infty }={[1+e^{(\varphi +20)/7}]}^{-1}\\ {\tau }_{\mathrm{f}}=1125e^{-{(\varphi +27)}^2/240}+165{[1+e^{(25-\varphi )/10}]}^{-1}+80,\end{array}$$ (45)

and by the intracellular calcium dependent inactivation gate ${\dot{g}}_{\text{fCa}}=[g_{\text{fCa}}^{\infty }-g_{\text{fCa}}]/{\tau }_{\text{fCa}}$ characterized through

$$\begin{array}{c}{g}_{\text{fCa}}^{\infty }=0.685[{[1+{(c_{\text{Ca}}/0.000325)}^8]}^{-1}+0.1{[1+e^{(c_{\text{Ca}}-0.0005)/0.0001}]}^{-1}+0.2{[1+e^{(c_{\text{Ca}}-0.00075)/0.0008}]}^{-1}+0.23]\\ {\tau }_{\text{fCa}}=\{\begin{array}{cc}\infty & \text{if}{\mathrm{g}}_{\text{fCa}}^{\infty }>g_{\text{fCa}}\text{and}\varphi \ge -60\text{mV}\\ 2ms& \text{otherwise}.\end{array}\end{array}$$ (46)

Accordingly, the steady state response $g_{\text{fCa}}^{\infty }$ has a switchlike shape when going from no inactivation to considerable but incomplete inactivation, depending mildly on the calcium concentration c_Ca for suprathreshold concentrations. Last, the calcium-induced calcium release current I_rel is characterized through the activation gate g_d, the same gate that is also activating the L-type calcium channel of I_CaL, and through the calcium-dependent inactivation gate ${\dot{g}}_{\mathrm{g}}=[g_{\mathrm{g}}^{\infty }-g_{\mathrm{g}}]/{\tau }_{\mathrm{g}}$ characterized through the following steady state value and time constant,

$$\begin{array}{c}{g}_{\mathrm{g}}^{\infty }=\{\begin{array}{cc}{[1+c_{\text{Ca}}^6/{0.00035}^6]}^{-1}& \text{if}{c}_{\text{Ca}}\le 0.00035\\ {[1+c_{\text{Ca}}^{16}/{0.00035}^{16}]}^{-1}& \text{otherwise}\end{array}\\ {\tau }_{\mathrm{g}}=\{\begin{array}{cc}\infty & \text{if}{\mathrm{g}}_{\mathrm{g}}^{\infty }>g_{\mathrm{g}}\text{and}\varphi \ge -60\text{mV}\\ 2ms& \text{otherwise}.\end{array}\end{array}$$ (47)

The remaining parameters governing the response of the plateau calcium current I_pCa, the calcium uptake current I_up, and the sarcoplasmic reticulum calcium release current I_rel are the half saturation constants for the plateau calcium concentration c_pCa = 0.0005 mM, for the sarcoplasmic reticulum calcium uptake c_up = 0.00025 mM, and for the sarcoplasmic reticulum calcium release c_rel = 0.25 mM, respectively. The parameter γ_NaCa = 2.5 has been introduced to enhance the outward nature of the sodium calcium pump current I_NaCa. The additional parameter γ_rel = 2 weighs the relative influence of the sarcoplasmic reticulum calcium concentration on sarcoplasmic reticulum calcium release I_rel. Finally, we take into account that the total intracellular calcium concentration $c_{\text{Ca}}^{\text{tot}}=c_{\text{Ca}}+c_{\text{Ca}}^{\text{buf}}$ in the cytoplasm is the sum of the free intracellular calcium concentration c_Ca and the buffered calcium concentration $c_{\text{Ca}}^{\text{buf}}=[c_{\text{Ca}}{c}_{\text{Cabuf}}^{\text{tot}}]{[c_{\text{Ca}}-c_{\text{Cabuf}}]}^{-1}$. The definition of the free intracellular calcium concentration in equation (42) is therefore weighted by the parameter γ_Ca = [1 + [c_tot c_buf][c_Ca + c_buf]⁻²]⁻¹, where c_tot = 0.15 mM and c_buf = 0.001 mM are the total and half saturation cytoplasmic calcium buffer concentrations, respectively.

6.4. Sarcoplasmic reticulum calcium concentration, currents, and gating variables

The specification of the sarcoplasmic reticulum calcium concentration

$${\dot{c}}_{\text{Ca}}^{\text{sr}}={\gamma }_{\text{Ca}}^{\text{sr}}\frac{V}{V^{\text{sr}}}[-I_{\text{leak}}+I_{\text{up}}-I_{\text{rel}}]$$ (48)

is now relatively straightforward since it mimics the corresponding loss of intracellular calcium characterized. However, now we scale it by the ratio between the volume of the cytoplasm V = 16404 μm³ and the volume of the sarcoplasmic reticulum V^sr = 1094 μm³ to account for differences in chemical concentrations due to ionic flux. The leakage current I_leak, the sarcoplasmic reticulum uptake current I_up, and the sarcoplasmic reticulum release current I_rel are defined as before,

$$\begin{array}{c}{I}_{\text{leak}}=I_{\text{leak}}^{max}[c_{\text{Ca}}^{\text{sr}}-c_{\text{Ca}}]\\ I_{\text{up}}=I_{\text{up}}^{max}{[1+c_{\text{up}}^2/c_{\text{Ca}}^2]}^{-1}\\ I_{\text{rel}}=I_{\text{rel}}^{max}{g}_{\mathrm{d}}{g}_{\mathrm{g}}{[1+{\gamma }_{\text{rel}}{c}_{\text{Ca}}^{\text{sr}2}[c_{\text{rel}}^2+c_{\text{Ca}}^{\text{sr}2}]}^{-1}].\end{array}$$ (49)

The maximum leakage current $I_{\text{leak}}^{max}=0.08{\mathrm{s}}^{-1}$, the maximum sarcoplasmic reticulum calcium uptake current $I_{\text{up}}^{max}=0.000425\text{mM}/ms$, and the maximum sarcoplasmic reticulum calcium release current $I_{\text{rel}}^{max}=8.232\text{mM}/\mathrm{s}$, the half saturation constants for the calcium uptake c_up = 0.00025 mM, and for the calcium release c_rel = 0.25 mM, and the weighting coefficient γ_rel = 2 have already been introduced in the previous subsection. Similar to the previous subsection, we need to take into account that the total calcium concentration in the sarcoplasmic reticulum $c_{\text{Ca}}^{\text{sr tot}}=c_{\text{Ca}}^{\text{sr}}+c_{\text{Ca}}^{\text{sr buf}}$ is the sum of the free sarcoplasmic reticulum calcium concentration $c_{\text{Ca}}^{\text{sr}}$ and the buffered sarcoplasmic reticulum calcium concentration $c_{\text{Ca}}^{\text{sr buf}}=[c_{\text{Ca}}^{\text{sr}}{c}_{\text{tot}}^{\text{sr}}]{[c_{\text{Ca}}^{\text{sr}}-c_{\text{buf}}^{\text{sr}}]}^{-1}$. The definition of the free sarcoplasmic reticulum calcium concentration in equation (48) is therefore weighted by the parameter ${\gamma }_{\text{Ca}}^{\text{sr}}={[1+[c_{\text{tot}}^{\text{sr}}{c}_{\text{buf}}^{\text{sr}}]{[c_{\text{Ca}}^{\text{sr}}+c_{\text{buf}}^{\text{sr}}]}^{-2}]}^{-1}$, where $c_{\text{tot}}^{\text{sr}}=10\text{mM}$ and $c_{\text{buf}}^{\text{sr}}=0.3\text{mM}$ are the total and half saturation sarcoplasmic reticulum calcium buffer concentrations, respectively.