Abstract
Purpose
To develop new techniques for reducing the effects of microscopic and macroscopic patient motion in diffusion imaging acquired with high-resolution multi-shot EPI.
Theory
The previously reported Multiplexed Sensitivity Encoding (MUSE) algorithm is extended to account for macroscopic pixel misregistrations as well as motion-induced phase errors in a technique called Augmented MUSE (AMUSE). Furthermore, to obtain more accurate quantitative DTI measures in the presence of subject motion, we also account for the altered diffusion encoding among shots arising from macroscopic motion.
Methods
MUSE and AMUSE were evaluated on simulated and in vivo motion-corrupted multi-shot diffusion data. Evaluations were made both on the resulting imaging quality and estimated diffusion tensor metrics.
Results
AMUSE was found to reduce image blurring resulting from macroscopic subject motion compared to MUSE, but yielded inaccurate tensor estimations when neglecting the altered diffusion encoding. Including the altered diffusion encoding in AMUSE produced better estimations of diffusion tensors.
Conclusion
The use of AMUSE allows for improved image quality and diffusion tensor accuracy in the presence of macroscopic subject motion during multi-shot diffusion imaging. These techniques should facilitate future high-resolution diffusion imaging.
Keywords: diffusion-weighted imaging, diffusion-tensor imaging, echo-planar imaging, high-resolution, motion, multiplexed sensitivity encoding
INTRODUCTION
Over the past two decades diffusion-weighted imaging (DWI) has established itself as an important tool in both clinical and research settings to study water diffusion characteristics in health and in disease. One of its greatest clinical utilities is in the detection of acute ischemic stroke in its early stages (1,2). The early diagnosis of acute stroke allows for greater flexibility in treatment options, and can greatly improve the therapeutic outcomes for patients (3,4). DWI is also capable of successfully discriminating among abnormalities such as brain tumors and abscesses (5,6), and is thus an important tool in diagnostic evaluations. Furthermore, diffusion-tensor imaging (DTI) enables detailed mapping of neuronal connectivity in the brain (7–10), which has shown promise in characterizing alterations of neuronal micro-structures in neurodegenerative disorders such as Parkinson’s and Alzheimer’s (9,10).
Despite the wide utility of DWI, a major limitation of the technique is its sensitivity to patient motion. The application of large diffusion gradients makes DWI sensitive not only to water diffusion, but also to subject movement. A common solution in clinical practice is to use a single-shot pulse sequence such as single-shot echo-planar imaging (EPI), because of its fast acquisition time and low sensitivity to patient motion (11). There are however several drawbacks to single-shot EPI acquisitions (12–18). First, single-shot EPI data are affected by significant vulnerability to magnetic field inhomogeneity (12). Moreover, single-shot EPI is inherently limited in its maximum attainable spatial resolution (13). Due to these shortcomings, small anatomical structures of clinical significance may be difficult to identify with single-shot DWI acquisitions.
On the other hand, multi-shot techniques such as interleaved EPI can greatly improve spatial resolution and reduce distortions (4,19–23), thereby enabling the identification of microstructures. At present, however, multi-shot acquisitions in DWI pose challenges when patient motion occurs. Specifically, minuscule patient motion and cerebrospinal fluid pulsations during the application of diffusion gradients causes phase variations among interleaves, leading to ghosting artifacts in the reconstructed image (19,20). Furthermore, in the presence of macroscopic motion (i.e. large changes in head position), multi-shot acquisitions suffer from two additional errors, the first being pixel misregistrations which result in blurred images, and the second being an altered diffusion contrast which can result in inaccurate estimations of diffusion tensors and their related measures. This second error, while relatively straightforward to correct in single-shot EPI, is more difficult to correct in multi-shot acquisitions as individual shots would experience potentially very different diffusion-encoding directions (21,22).
To address some of these errors, navigator-based acquisitions are often used to estimate the phase variations and degree of macroscopic motion between interleaves (18,21,22,24–32). This information can then be used to reduce artifacts through improved image reconstruction. An advantage of using navigators is that they allow flexibility in acquisition trajectories. For example, it has been shown that navigator-based acquisitions combined with readout-segmented EPI instead of interleaved EPI can simplify the correction of motion-induced phase variations in DWI (18). However, navigator approaches in general suffer from two limitations: reduced imaging throughput, and less accurate estimations for cases in which motion occurs in the interval between the interleaf and navigator acquisition. Moreover, very few studies have been presented which address the problem of correcting altered diffusion-encoding due to motion in multi-shot DTI (21).
As an alternative to multi-shot acquisitions with navigation, PROPELLER-based acquisitions have also been applied to DWI (16,17). These methods are effective due to their inherent self-navigation and ability to satisfy the Nyquist criterion, allowing relatively straightforward reconstruction and motion correction. However, PROPELLER-based acquisitions have their limitations. For example, the FSE-based PROPELLER suffers from difficulties in satisfying CPMG conditions (16), and concerns about specific absorption rates (17). On the other hand, PROPELLER EPI suffers from geometric distortions due to off-resonance effects that are not unidirectional, as they are with Cartesian EPI. This causes blurring when combining PROPELLER EPI blades and compromises the final image quality (17,33). Additionally, the levels of geometric distortions in PROPELLER EPI are typically similar to those of single-shot EPI, although this can be alleviated using a short-axis acquisition (33).
Recently, our group presented a technique, termed Multiplexed Sensitivity-Encoding (MUSE), to inherently correct motion-induced phase errors arising from minuscule motion in multi-shot diffusion EPI without the need for navigator echoes (23). A similar method has also been recently presented for the case of multi-shot spiral DTI (34). While these techniques were shown to effectively suppress the ghosting artifacts associated with minuscule motion and reduce geometric distortions compared to single-shot EPI, their implementations lacked the capability to correct for macroscopic patient motion. In light of this, here we present an improved method which inherently estimates and simultaneously corrects 1) motion-induced phase errors, 2) macroscopic blurring, and 3) motion-corrupted diffusion-encoding in multi-shot diffusion EPI, without the need for navigator echoes. The method, termed Augmented MUSE (AMUSE), enables reliable high-resolution diffusion images and accurate diffusion tensor estimation even in the presence of macroscopic subject motion during interleaved EPI scans.
THEORY
Without loss of generality, we will discuss the AMUSE procedure for a 2-shot interleaved EPI sequence with an arbitrary number of diffusion directions, acquired using an arbitrary number of coil channels.
Minuscule Motion
First consider the case in which the only motion is minuscule motion (e.g., < 1 voxel) during the application of diffusion gradients. Such motion typically occurs in the form of brain pulsations and results in a random spatially-varying phase term for each interleaf, which in turn produces aliasing artifacts in the final reconstructed interleaved DWI image. These phase terms can be inherently estimated from the originally acquired data and used to produce artifact-free images in the following manner.
Reconstruction of each interleaf separately results in aliased images which can be described by
| [1] |
| [2] |
where γ is the coil number (γ = 1…Nγ), and δ is the diffusion-gradient direction number (δ = 1…Nδ). Sγ are the sensitivity profiles for each coil γ, and pε,δ is the ideal unaliased full-FOV image from an interleaf ε (ε = 1,2 in this example) and diffusion direction δ. Note that the second terms in Eqs. [1,2] have opposite signs due to the k-space shift between the two interleaf trajectories. The images a1,γ,δ and a2,γ,δ are aliased because each interleaf in multi-shot EPI is undersampled along ky, much like in a parallel-imaging acquisition. Therefore, using the known sensitivity profiles Sγ, the unaliased images pε,δ can be calculated from Eqs. [1,2] using the SENSE reconstruction method (35) commonly employed in parallel-imaging. The resulting images are given by
| [3] |
where Iδ and θδ represent the magnitude and global background phase, respectively, of the diffusion-weighted image signal for each diffusion direction δ. Additionally, φε,δ are the different motion-induced phase terms of each interleaf for each diffusion direction. For convenience, we will combine the motion-induced and background phase terms such that Φε,δ = φε,δ + θδ, giving
| [4] |
In Eqs. [3,4] ηε,δ are the SENSE-produced noise terms associated with each image. Despite this noise, the phase terms Φ1,δ and Φ2,δ can still be reliably estimated from the SENSE images in Eq. [4]. Assuming the phase variations are spatially smooth, which is generally the case, Φε,δ can be estimated as
| [5] |
where TV is the total variation denoising operator (36). Thus we are able to estimate the shot-specific phase errors using SENSE reconstructions of the original data. Note that because the phase is estimated from full field-of-view (FOV) SENSE reconstructions in the image domain as opposed to estimation in k-space, the nonlinearity of motion-induced phase errors is easily captured by this approach.
Now, using these estimates of Φ1,δ and Φ2,δ, Eqs. [1–2] can be re-written as
| [6] |
| [7] |
from which we can directly calculate the artifact-free diffusion-weighted images Iδ. Note that Eqs. [6,7] have two common unknowns, Iδ(x, y) and Iδ(x, y + FOVy/2), and a combined total of 2 x Nγ equations, assuming that shot-to-shot phase variations derived from Eq [5] are accurate. This is an improvement over the conditions in the conventional SENSE procedure (two unknowns and only Nγ equations), and as a result the noise levels in the reconstructed images Iδ from this procedure are comparatively lower than the SENSE images.
Putting the above procedure in matrix form, for a given location (x = xm, y = yn) in the aliased image of diffusion direction δ, the voxels at (xm, yn) and (xm, yn + FOVy/2) in the image Iδ can be calculated via matrix inversion by solving
| [8] |
This can be repeated until Iδ is solved for all (x, y). That is, we can split up the calculation of the final diffusion image into many small matrix inversions.
The above procedure summarizes the initial implementation of MUSE, as presented in (23). Note that while MUSE can effectively correct the effects of minuscule motion as described in this section, it fails to account for macroscopic motion (e.g., > 1 voxel). We would like to point out that the SNR and accuracy of MUSE produced images may be reduced by undesirable noises in the SENSE-estimated phase values (i.e., Φε,δ in Eq. [8]). Therefore, it is important to first denoise the SENSE-estimated phase values (e.g., with Eq. [5]), assuming that shot-to-shot phase variations are spatially smooth.
Macroscopic Motion
Consider the more general case in which macroscopic motion is also present in addition to minuscule motion. Macroscopic motion is characterized as large movements occurring between interleaves of the acquisition, i.e. large-scale head movement. Starting again from Eqs. [1,2], a SENSE reconstruction of each interleaf in this case produces images given by
| [9] |
Ωε,δ represents a spatial transformation of the image for each interleaf ε and diffusion direction δ, and describes the changes in object position among interleaves. In the case of rigid-body motion, it is a combination of both rotation and translation parameters, and transforms an image according to Ωε,δ(x,y)=Rε,δ[x,y]T+[Δxε,δΔyε,δ]T, where Rε,δ is the rotation matrix and [Δxε,δ Δyε,δ]T is the translation vector. In the case of non-rigid body motion, Ωε,δ will represent the affine matrix transformation of the point (x, y). The second exponential term in Eq. [9] represents the change in diffusion-encoding contrast due to rotational motion. D is the diffusion tensor, and B*ε,δ is a modified b-matrix given by
| [10] |
where Bδ is the b-matrix given by the originally applied gradient orientations for the diffusion direction δ. Note that when there is no rotation B*ε,δ equals zero and the exponential term in Eq. [9] equals one, indicating no alterations in the diffusion-encoding contrast as expected.
To correct macroscopic motion and obtain the ideal diffusion images Iδ, estimates of the parameters Rε,δ and [Δxε,δ Δyε,δ]T are needed to calculate Ωε,δ and B*ε,δ. In AMUSE, these motion parameters are estimated by performing a 2D registration among the SENSE-produced images from Eq. [9]. Choosing one of the images as a reference image (e.g. p1,3), all other SENSE-produced images can be registered to this reference image. These registrations will in turn supply estimates of Rε,δ and Ωε,δ for all images. Note that the registered images are not actually used; the registration process is done only to estimate Rε,δ and Ωε,δ which describe the motion among all interleaves. If an affine registration is used to estimate Ωε,δ instead of a rigid-body registration, the affine transformation represented by Ωε,δ should be decomposed to determine Rε,δ, which is needed for the modified b-matrix in Eq. [10].
Using Eq. [5] to estimate the phase terms Φε,δ arising from minuscule motion, we can now re-write Eqs. [1,2] for the case of both minuscule and macroscopic motion:
| [11] |
| [12] |
where
| [13] |
| [14] |
In the majority of cases rotation will be a component of Ωε,δ, and as a result the location given by Ωε,δ(x, y) will typically not fall on the image grid. To address this, one can modify Eqs. [11,12] such that some number, Ninterp, of neighboring grid points around Ωε,δ(x, y) are incorporated with an appropriate weighting.
It is clear from Eqs. [11,12] that when Ω1,δ ≠ Ω2,δ, which is the case for macroscopic motion, there are no common unknowns between the interleaves. Therefore Eqs. [11,12] cannot be solved in the same manner as in Eq. [8], in which Iδ is solved two voxels at a time. Instead, all voxels in Iδ must be solved simultaneously.
We therefore denote a solution vector vδ which contains the values of Iδ for all voxels, i.e. vδ = [Iδ(r1) Iδ(r2) … Iδ(rNx x Ny)]T, where rp (p = 1 … Nx x Ny) is the spatial location in an image of matrix size Nx x Ny. We also denote a vector aδ which contains the values of a1,γ,δ and a2,γ,δ for all voxels within half of FOVy, for all coils: aδ =
Next we define the coefficient matrix Eδ, containing the coil sensitivities, motion-induced phase terms, and altered diffusion contrast τ, which will allow us to solve vδ in the form
| [15] |
The structure of Eδ will be dependent on Ωε,δ. That is, using Eqs. [11,12], the elements of Eδ must be arranged such that Eq. [15] is valid. In this two-interleaf example, Eδ would contain 2 x Ninterp non-zero elements per row, positioned in columns corresponding to the voxel locations given by Eqs. [11,12].
In general, Eδ can be of considerable size, with dimensions (Nγ x Nx x Ny) x (Nx x Ny). As a result, a direct inversion to solve Eq. [15] for vδ is impractical. However Eδ is also sparse, containing only Nε x Ninterp non-zero elements per row. Because of this we can apply the Conjugate Gradient (CG) method (37), which is well suited for solving systems involving large sparse matrices. Using CG to solve Eq. [15] we consequently can obtain vδ, a diffusion-weighted image free of both ghosting artifacts from minuscule motion, and blurring from macroscopic motion.
However, it can be seen from Eqs. [11,12,14] that in order to solve Eq. [15] accurately we must already know τ, which would require a priori knowledge of the diffusion tensors D at all locations in the image. Clearly this is not possible. As τ represents the altered diffusion contrast due to motion, neglecting these terms in Eq. [15] would result in images with incorrect diffusion-weighting, and thereby inaccurate estimates of the diffusion tensors calculated from these images. To address this problem, we hypothesize that it is sufficient to estimate τ by obtaining initial estimates of D from the SENSE produced images. Namely, initial tensor estimates are calculated by using multivariate regression (38) on the registered SENSE images from all shots and diffusion directions, taking into account any b-matrix rotations corresponding to rotations of each shot (39). These estimates are subsequently used to calculate the τ terms for matrix Eδ, after which Eq. [15] can be solved for diffusion images with more accurate contrast. These more accurate images are then used to calculate diffusion tensors with reduced error resulting from macroscopic motion. A flowchart of the AMUSE procedure is provided in Figure 1.
Figure 1.
Flowchart depicting the AMUSE procedure within an acquired diffusion direction for a two interleave example. a1 and a2 are the aliased signals of each interleave, and S are the coil sensitivity profiles. Ω1 and Ω2 are the macroscopic motion parameters calculated for each interleave. Dest are the initial estimates of the diffusion tensors calculated using coregistered SENSE images from all diffusion directions, and D are the final estimates of the diffusion tensors calculated using AMUSE images from all diffusion directions.
For studies in which diffusion tensors are not desired (e.g. clinical DWI), it may be appropriate to neglect the inclusion of τ in the reconstruction method. To clarify the difference when comparing results with or without the inclusion of τ, here we will refer to reconstruction without its inclusion as “AMUSE-DWI”, which corrects ghosting from minuscule motion and blurring from macroscopic motion, but not altered diffusion contrast. When τ is included to correct the altered diffusion (e.g. in studies where diffusion tensors are of interest), we will refer to it as “AMUSE-DTI”, which will be required to produce quantitatively accurate DTI measures while mitigating macroscopic motion effects.
METHODS
All experiments were conducted on a 3T system (GE HD, Waukesha, WI) using healthy volunteers. T2-weighted and diffusion-weighted data were acquired using a 4-shot interleaved EPI sequence. Multiple image reconstruction methods were employed in each experiment to compare the effectiveness of each method. Prior to all reconstructions, Nyquist artifacts were removed from the T2-weighted and diffusion data using a recently developed phase-cycled reconstruction procedure (40). The reconstruction methods used were:
No motion correction: Images were produced only by directly applying the 2-D Fourier transform on the interleaved diffusion data.
Minuscule motion correction with MUSE: Images were reconstructed using the MUSE method, as outlined above and in (23). Coil sensitivity profiles were estimated from the T2-weighted image.
Minuscule and macroscopic motion correction with AMUSE-DWI: Images were reconstructed using the new method described above. To account for macroscopic motion and estimate Ω1–4,1–15, a 2D registration with 5 degrees of freedom (1 rotation, 2 translations, 2 scaling parameters) using FSL-FLIRT (41–43) was performed on the SENSE-produced images. The two scaling parameters were included to account for differing geometric distortions coupled to motion (44). The reference image used for registration was chosen as the one that had the maximum correlation coefficient among all SENSE images. The estimated motion parameters from registration were then used to set up Eq. [15] without τ, which was subsequently solved using the Conjugate Gradient algorithm to produce the final DWI images. Implementation of Conjugate Gradients was done with the built-in MATLAB function “pcg”.
Minuscule and macroscopic motion correction + initial tensor estimation with SENSE: A purely SENSE-based motion correction was performed by phase-correcting and coregistering (using the same registration as method C above) the initial SENSE images of each shot. As described in the theory section, initial estimates of diffusion tensors were then calculated via multivariate regression on the coregistered and b-matrix corrected SENSE images.
Minuscule and macroscopic motion correction + tensor correction with AMUSE-DTI: Reconstruction was performed following the same steps as in method C, however τ was included. τ was calculated from the initial diffusion tensors provided from method D above.
DWI correction
The motivation of this experiment was to determine the effectiveness of macroscopic motion correction using AMUSE-DWI. Four diffusion scans were acquired on the volunteer using an 8-channel GE coil. Scan parameters included: in-plane resolution = 0.75 × 0.75 mm2 (without sinc-interpolation), slice thickness = 4 mm, number of slices = 30, effective echo-spacing (for 4 interleaves) = 250 µs, FOV = 19 cm2, number of partial Fourier overscans (i.e. the number of additionally acquired ky lines beyond half Fourier EPI) = 12, TR = 6 s, TE = 71 ms, number of diffusion gradient directions = 15, and b-value = 800 s/mm2. Partial Fourier reconstruction of the acquired data was performed using the Cuppen method (45). In the first two scans the volunteer was asked to remain stationary during acquisition. Between the two scans, the volunteer was asked to rotate his head by ~ 15°. A hybrid-simulation of macroscopic motion corruption was then simulated by combining data from both scans (i.e., from both head positions). Specifically, the first and third interleaves from the first scan were combined with the second and fourth interleaves from the second scan. In the third diffusion scan the volunteer was asked to rotate his head by small amounts of ~ ±5° every 10–15 seconds during the acquisition (about every 2 TR), resulting in data with actual macroscopic motion corruption. Similarly, in the fourth diffusion scan the volunteer was asked to rotate his head by slightly larger amounts of ~ ±10° every 10–15 seconds during acquisition. Image reconstruction methods A-D were performed on the hybrid-simulated dataset and the in vivo datasets with actual motion corruption. The reconstruction results were compared with the first stationary scan, which was used as a gold-standard image. The gold-standard image was processed using methods A-D. Since the motivation of this experiment was only to characterize motion correction on DWI image quality, diffusion tensors were not calculated in method D. The signal-to-noise ratios (SNR) and contrast-to-noise ratios (CNR) were calculated for both the SENSE-based corrections and the AMUSE-DWI corrections for quantitative comparison. SNRs were calculated on the mean diffusion-weighted images (i.e. the mean of 15 images for AMUSE-DWI, and 60 images for SENSE) within a white-matter (WM) region: , where S is the mean diffusion-weighted image for AMUSE-DWI or SENSE and σB is the standard deviation in a background region of S. Similarly, CNR was calculated between gray matter (GM) and white-matter as: .
Diffusion contrast and tensor correction simulations
The primary purpose of this experiment was to thoroughly characterize tensor correction with AMUSE-DTI for various levels of motion using simulations. A diffusion scan was acquired on the same volunteer. Scan parameters included: in-plane resolution = 0.75 × 0.75 mm2, slice thickness = 4 mm, number of slices = 39, effective echo-spacing = 250 µs, FOV = 19 cm2, number of partial Fourier overscans = 20, TR = 5 s, TE = 73 ms, number of diffusion gradient directions = 15, and b-value = 800 s/mm2. The volunteer was asked to remain stationary during the scan, and the diffusion data was processed using method B to obtain a gold-standard set of diffusion tensors D and a gold standard T2-weighted image. Simulations of macroscopic motion for a 4-shot interleaved EPI sequence with 15 diffusion gradient directions were then performed in the following manner. First, the gold-standard tensors D were replicated 4×15 = 60 times, resulting in a set of diffusion tensors Dε,δ for each interleaf and diffusion gradient direction. Next, each set of tensors were either rotated by a chosen angle αε,δ > 0° or kept unchanged (αε,δ = 0°) with a random probability of 1/2 for either option of α.
Following these rotations, the modified tensor sets were used to create simulated diffusion-weighted images. This was done by creating diffusion-weighting exponential terms from the tensor sets and their corresponding diffusion direction and multiplying these exponential terms to the gold-standard T2-weighted image. This resulted in a total of 60 diffusion weighted images. As the final step in simulating macroscopic motion, each image was rotated by the same angle αε,δ for which its tensors were rotated. MATLAB’s “imrotate” with bicubic interpolation was used for the image rotations. To simulate the effects of minuscule motion, all images were multiplied by a unique linear phase ramp.
Next, a gold-standard T2-weighted image was used to estimate the coil sensitivities for our 8-channel coil. The estimated sensitivities were subsequently fitted to fill the entire FOV, and then applied individually to all diffusion-weighted images, resulting in 4×15×32 = 1920 images. These images were then grouped by their respective diffusion gradient directions and underwent FFTs into k-space. Within each group, the k-space datasets were then separated by interleaf, and 1/4 of the k-space lines from each interleaf were extracted in a fashion resembling 4-shot EPI. Finally, these extracted lines from each interleaf were combined together into one dataset per diffusion direction, thereby creating a synthetic k-space dataset with the effects of motion corruption in 4-shot interleaved EPI.
The simulations were performed with three different choices of αε,δ > 0° : 20° (small motion), 40° (moderate motion), and 60° (large motion). Furthermore, noise was added to the datasets for all simulations in order to assess the reconstruction methods at multiple SNR levels. For each simulation, image reconstruction methods B-E were used. Three quantitative criteria were used to assess the tensors calculated from each reconstruction method B-E for all simulations: 1) the percentage error in fractional anisotropy (FAerr) compared to gold-standard values, 2) the percentage error in mean diffusivity (MDerr) compared to gold-standard values, and 3) the angular deviation of the principal eigenvectors V1 (∡V1) from the gold-standard values. The criteria were calculated within a known white-matter ROI obtained from the gold-standard diffusion images; the threshold used for the white-matter ROI was an FA greater than 0.4.
In Vivo Diffusion Tensor Correction
In vivo sagittal diffusion scans were acquired on the same volunteer using the 8-channel GE coil. Scan parameters were: in-plane resolution = 0.86 × 0.86 mm2, slice thickness = 5 mm, number of slices = 30, effective echo-spacing = 250 µs, FOV = 22 cm2, number of partial Fourier overscans = 24, TR = 4 s, TE = 73 ms, number of diffusion gradient directions = 15, and b-value = 800 s/mm2. Two scans were acquired: one in which the volunteer was asked to remain stationary, and one in which the volunteer was asked to nod his head (in-plane rotations) between 0 degrees and the maximum amount possible within the head coil (~ ±25° degrees) every 8–10 seconds (~ every 2 TR). Image reconstruction methods B-E were applied on these in vivo motion-corrupted datasets. The final diffusion images for each method were then denoised using anisotropic filtering (46,47) before applying multivariate regression to calculate a final set diffusion tensors. These final sets of tensors were compared to the tensors calculated from the stationary dataset using the same metrics as in the simulation experiments (i.e., FAerr, MDerr, and ∡V1).
All processing was performed in MATLAB (The MathWorks, Natick MA) on a Linux machine (2.30 GHz CPU, 16 GB RAM).
RESULTS
DWI Correction
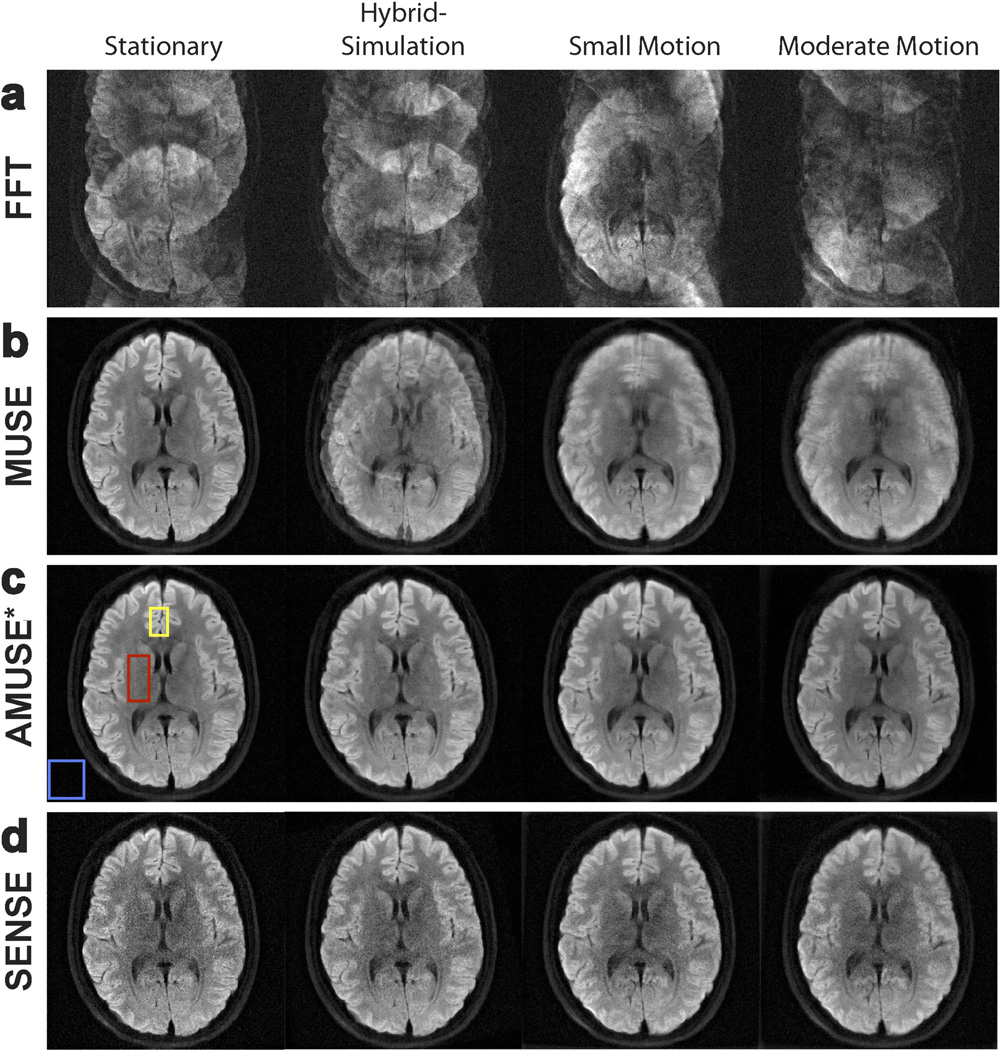
Figure 2 shows the results of our reconstruction procedures (averaged over all diffusion directions) for the hybrid-simulated DWI dataset and the in vivo motion-corrupted DWI datasets. Reconstruction of the gold-standard dataset is shown in the leftmost column of Figure 2 for reference. For all datasets, reconstruction with a direct FFT resulted in severe ghosting artifacts due to the presence of minuscule motion (Figure 2a). A clear improvement in image quality was seen after using MUSE (Figure 2b), in which the phase errors among interleaves were corrected to suppress the ghosting artifacts. However, the datasets with macroscopic motion-corruption still had degradation in image quality even after MUSE, as seen by the blurring effects in the rightmost columns of Figure 2b. Figure 2c shows the results of AMUSE-DWI reconstruction, in which both the ghosting artifacts from minuscule motion and the blurring effects from macroscopic motion were corrected. The resulting AMUSE-DWI images for the motion-corrupted datasets were very similar to the gold-standard image. Note that MUSE and AMUSE-DWI reconstructions produced the same results for the gold-standard dataset because no macroscopic motion was present.
Figure 2.
Reconstruction of diffusion-weighted images with varying levels of motion, using a) direct FFT, b) MUSE, c) “AMUSE*” (AMUSE-DWI), and d) a SENSE-based motion-correction. While MUSE is capable of correcting ghosting artifacts, blurring from macroscopic motion remains. AMUSE-DWI and the SENSE-based correction can correct both ghosting and macroscopic motion effects, however it can be appreciated that AMUSE provides higher SNR.
Figure 2d shows the results of the purely SENSE-based motion correction (times 4 and averaged over all interleaves/diffusion directions). A visual decrease in SNR can be seen in these images compared to those produced by AMUSE*. Table 1 lists the SNRs and CNRs for AMUSE-DWI and the SENSE-based correction for each dataset. The white-matter, gray-matter, and background regions used to calculate the SNR/CNR in all images are indicated by the red, yellow, and blue boxes, respectively, in Figure 2c for the stationary dataset. Table 1 demonstrates that AMUSE-DWI provided an improvement in both SNR and CNR compared to the purely SENSE-based correction.
Table 1.
Signal to noise ratios (SNR) and contrast to noise ratios (CNR) of our AMUSE-DWI motion-correction scheme and a SENSE-based motion-correction scheme. Images reconstructed with AMUSE-DWI had both higher SNR and CNR for all experiments.
| SNRs and CNRs of AMUSE and SENSE-based Motion Correction | ||||
|---|---|---|---|---|
| SNR | CNR | ||||
| Stationary | Hybrid Simulation |
Small Motion |
Large Motion |
|
|
AMUSE-DWI Correction |
20.00 | 15.28 | 23.83 | 17.32 | 23.44 | 18.49 | 23.57 | 17.39 |
| SENSE Correction | 11.89 | 10.07 | 14.78 | 11.53 | 14.34 | 12.84 | 14.27 | 11.86 |
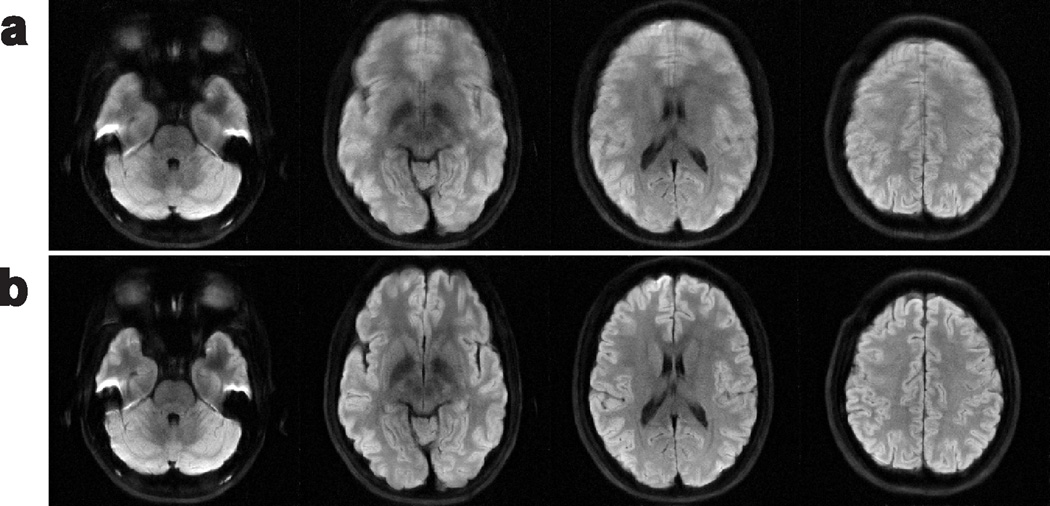
Figure 3 further demonstrates AMUSE-DWI on several other slices of the moderate-motion dataset, with MUSE results also shown to provide context of the macroscopic motion levels.
Figure 3.
Diffusion-weighted images reconstructed from the moderate-motion dataset at several slices using a) MUSE, and b) AMUSE-DWI.
The average computation times of the initial SENSE reconstructions and phase error estimations were 11.8 and 4.0 seconds per diffusion direction, respectively. The average computation time of the 2D registration was 13.4 seconds per diffusion direction. The final image reconstructions for AMUSE had average computation times of 6.67 seconds per diffusion direction.
Diffusion contrast and tensor correction simulations
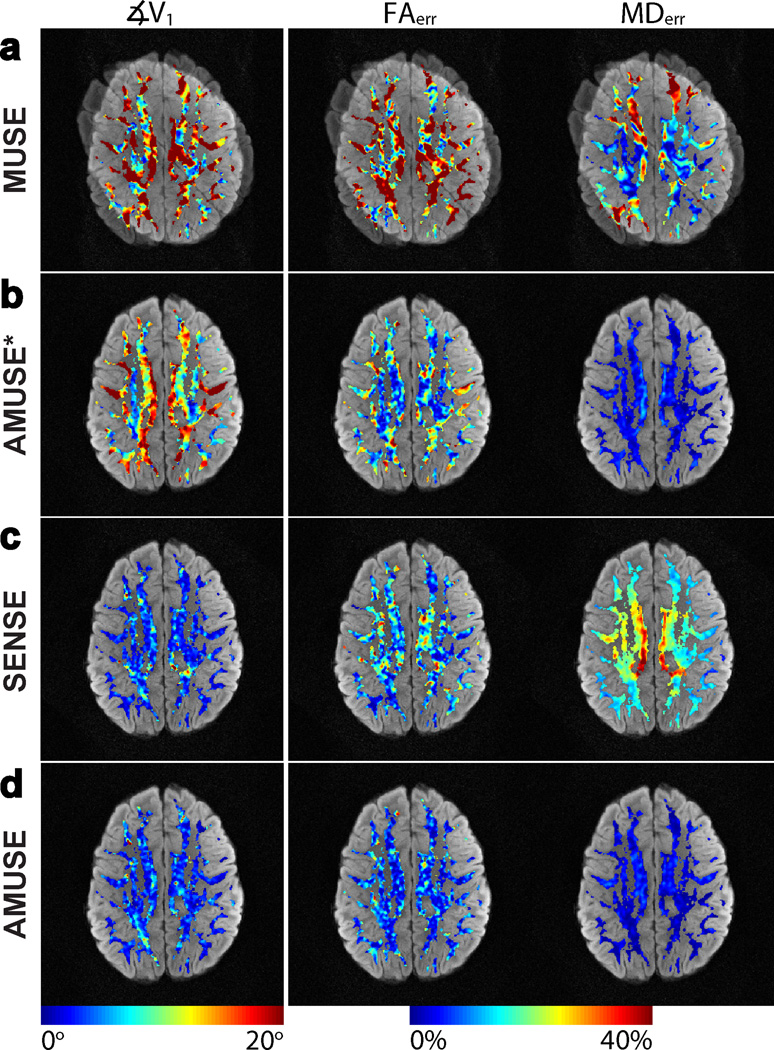
Figure 4 shows the results of our reconstruction methods with αε,δ = 40° at SNR = 5 (SNR was calculated within a SENSE produced image of a single simulated shot, not shown). The leftmost column of Figure 4 shows ∡V1 between tensors calculated from the reconstructed images and the gold-standard image, the middle column shows FAerr, and the final column shows MDerr (note the different scales). The metrics are shown within our white-matter ROI and are overlaid on their corresponding reconstructed image. MUSE reconstructions, shown in Figure 4a, produced images with severe blurring due to the method's inability to correct macroscopic motion. As a result, the principal eigenvectors V1 calculated from these blurred images had very large angular deviations from the gold-standard dataset, and the percentage errors in FA and MD from their respective gold-standard values were also high. Using AMUSE-DWI reconstruction resulted in a correction of these blurring effects from macroscopic motion, and the V1 calculated from these images showed some reduction in angular deviation from the gold-standard dataset. Likewise, the FAerr and MDerr were also reduced compared to MUSE. However, residual errors still existed due to the effects of altered diffusion contrast from macroscopic motion, which was not accounted for in AMUSE-DWI.
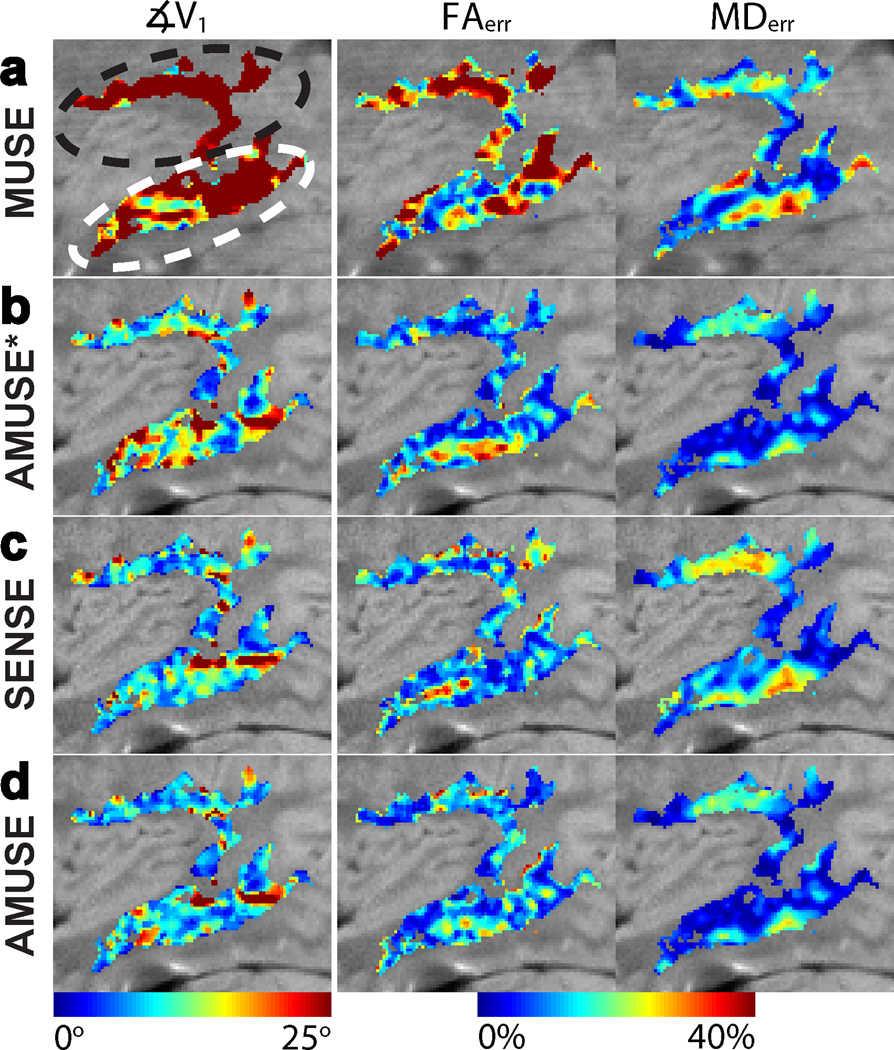
Figure 4.
Colormaps of the tensor error metrics ∡V1, FAerr, and MDerr from images reconstructed with a) MUSE, b) “AMUSE*” (AMUSE-DWI), c) SENSE-based correction, and d) “AMUSE” (AMUSE-DTI) for motion simulations with αε,δ = 40° and SNR = 5. ∡V1was reduced greatly with both AMUSE-DTI and SENSE reconstructions, but AMUSE-DTI moreover reduced FAerr and MDerr in the most significant manner.
With the application of AMUSE-DTI or the SENSE-based correction to include the altered diffusion contrast, a significant reduction in ∡V1 was seen, as shown by Figures. 4c–d. Similarly, the FAerr was reduced for both methods compared to AMUSE-DWI. However, AMUSE showed a larger reduction in FAerr than the SENSE-based correction. Furthermore, MDerr was much higher in the SENSE-based correction than with either AMUSE-DWI or AMUSE-DTI.
The average FAerr, MDerr, and ∡V1 of the reconstruction methods for all motion simulations (αε,δ = 20°, 40°, 60°) at SNR = 5 are listed in Table 2. The AMUSE-DTI and SENSE-based corrections performed similarly in reducing ∡V1, however AMUSE-DTI outperformed the SENSE-based correction in terms of residual FAerr and MDerr.
Table 2.
FAerr, MDerr, and ∡V1 calculated from images of all reconstructions in our motion simulations at SNR = 5. SENSE-based correction and AMUSE-DTI both produced low ∡V1 compared to MUSE and AMUSE-DWI. AMUSE-DTI furthermore produced the lowest residual FAerr and MDerr for all simulations.
| Tensor Correction Simulation Results | |||
|---|---|---|---|
| 20° Motion Simulation | |||
| ∡V1 (degrees) |
FAerr (%) | MDerr (%) | |
| MUSE | 11.59 ± 12.36 | 24.90 ± 15.00 | 10.67 ± 8.34 |
| AMUSE-DWI | 5.09 ± 3.47 | 6.20 ± 4.15 | 2.74 ± 1.61 |
| SENSE | 3.37 ± 2.31 | 9.37 ± 5.43 | 13.60 ± 4.77 |
| AMUSE-DTI | 2.77 ± 1.89 | 5.18 ± 3.62 | 2.51 ± 1.46 |
| 40° Motion Simulation | |||
| ∡V1 (degrees) |
FAerr (%) | MDerr (%) | |
| MUSE | 20.24 ± 14.67 | 27.36 ± 15.22 | 13.50 ± 11.09 |
| AMUSE-DWI | 12.69 ± 5.92 | 10.89 ± 6.80 | 3.11 ± 1.66 |
| SENSE | 3.59 ± 2.77 | 9.55 ± 5.77 | 14.26 ± 5.03 |
| AMUSE-DTI | 3.65 ± 2.48 | 6.06 ± 3.87 | 2.36 ± 1.54 |
| 60° Motion Simulation | |||
| ∡V1 (degrees) |
FAerr (%) | MDerr (%) | |
| MUSE | 20.76 ± 13.82 | 27.41 ± 15.91 | 14.92 ± 16.06 |
| AMUSE-DWI | 18.73 ± 10.00 | 20.18 ± 11.36 | 3.48 ± 1.88 |
| SENSE | 4.01 ± 2.97 | 9.39 ± 5.55 | 15.20 ± 5.37 |
| AMUSE-DTI | 5.26 ± 3.84 | 7.97 ± 5.11 | 2.33 ± 1.46 |
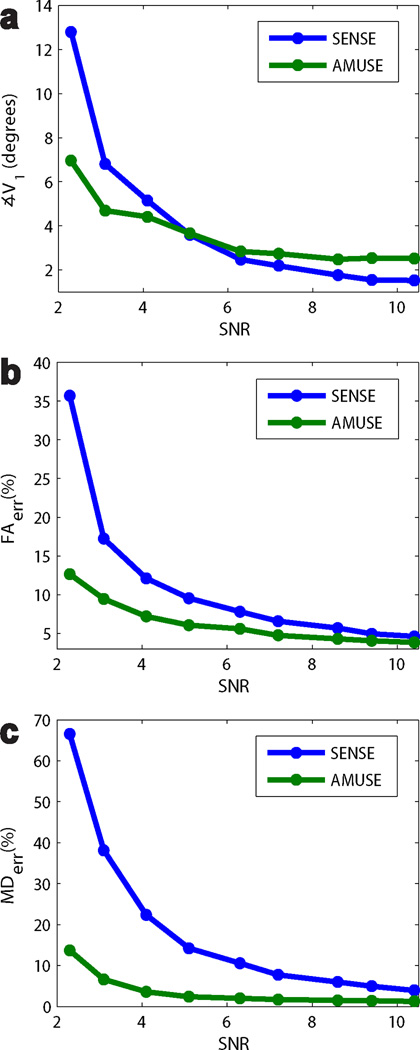
The average ∡V1, FAerr, and MDerr of AMUSE-DTI and SENSE-based corrections at varying SNR and constant αε,δ = 40° are shown in Figure 5. AMUSE-DTI resulted in lower FAerr and MDerr for all SNR levels, with the most marked differences from SENSE at lower SNRs. In terms of ∡V1 both techniques performed similarly however, with only minute differences on the order of a few degrees.
Figure 5.
Plots of ∡V1, FAerr, and MDerr of tensors from SENSE and AMUSE-DTI reconstructions at varying SNR levels in our motion simulations (αε,δ = 40 °). AMUSE-DTI produced the lowest FAerr and MDerr at all SNR levels, with increasing improvement over SENSE at lower SNRs. For ∡V1, AMUSE-DTI and SENSE performed similarly with only slight differences of a few degrees at most SNR levels. However more significant differences in ∡V1 start to become apparent at lower SNRs.
In Vivo Diffusion Tensor Correction
The results of applying MUSE, SENSE-based correction, and AMUSE-DTI on an in-vivo motion-corrupted sagittal slice are shown in Figure 6. Figure 7 shows tensor error metrics (compared to the gold-standard stationary data acquired) for MUSE, AMUSE-DWI, SENSE-based correction, and AMUSE-DTI, in a zoomed-in region from the slice in Figure 6 (blue box in Figure 6c). The zoomed-in region shown in Figure 7 contains the superior longitudinal fasciculus (SLF) and sagittal stratum (SS) white-matter tracts, as pointed out in the leftmost image of Figure 7a. As expected, with MUSE there was severe blurring due to pixel misregistrations among shots, and the resulting tensor metrics in these white-matter regions had large errors (Figure 7a). While the macroscopic blurring was corrected by using AMUSE-DWI, there were still errors in the calculated tensor metrics due to the uncorrected changes in diffusion-encoding among shots. Figures 7c–d show the metrics after correction of the altered diffusion-encoding with SENSE-based correction and AMUSE-DTI. These images show a reduced ∡V1 and FAerr compared to AMUSE-DTI, however the SENSE correction resulted in an increased MDerr.
Figure 6.
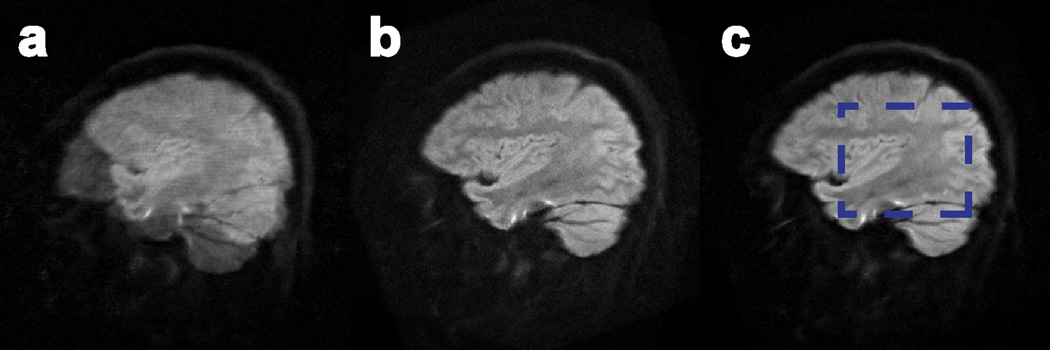
Images reconstructed from a slice of the in-vivo motion-corrupted dataset with a) MUSE, b) SENSE-based correction, and c) AMUSE-DTI. Diffusion tensors were calculated from these images and compared to gold-standard (stationary) tensors within the region given by the blue box in c). The results of these comparisons are shown in Figure 7.
Figure 7.
Colormaps of the tensor error metrics ∡V1, FAerr, and MDerr from images reconstructed with a) MUSE, b) “AMUSE*” (AMUSE-DWI), c) SENSE-based correction, and d) “AMUSE” (AMUSE-DTI) for the in-vivo head nodding experiment from Figure 6. The metrics were calculated within the SLF (black oval) and SS (white oval) white-matter regions. Average values of these errors are given in Table 3; AMUSE-DTI produced the smallest errors considering all metrics overall.
Table 3 lists the average errors in tensor metrics in the SLF and SS for each reconstruction method. In all slices, AMUSE-DTI provided the smallest residual ∡V1 and FAerr.
Table 3.
∡V1, FAerr, and MDerr calculated from images of all reconstruction methods on the in-vivo head nodding motion dataset. Considering all three metrics, AMUSE-DTI either matched or performed better than SENSE-based correction at reducing the tensor errors arising from macroscopic head nodding.
| In Vivo Tensor Correction | ||||||
|---|---|---|---|---|---|---|
| ∡V1 (degrees) | FAerr (%) | MDerr (%) | ||||
| SLF | SS | SLF | SS | SLF | SS | |
| MUSE | 44.08 ± 20.57 | 29.82 ± 19.51 | 32.21 ± 15.69 | 26.66 ± 16.48 | 13.93 ± 7.04 | 32.21 ± 15.69 |
|
AMUSE- DWI |
9.70 ± 6.07 | 13.62 ± 9.81 | 10.58 ± 5.73 | 14.55 ± 9.39 | 9.62 ± 6.26 | 7.12 ± 5.05 |
| SENSE | 10.49 ± 7.57 | 11.10 ± 8.72 | 14.44 ± 7.67 | 13.30 ± 8.30 | 13.79 ± 8.00 | 12.15 ± 7.60 |
| AMUSE-DTI | 8.98 ± 6.41 | 11.11 ± 8.94 | 10.75 ± 6.07 | 13.40 ± 9.07 | 10.32 ± 7.11 | 7.77 ± 5.88 |
DISCUSSION
DWI Correction
The results of the multi-shot DWI motion correction experiment, presented in Figure 2, demonstrate the ability of AMUSE-DWI to correct both minuscule and macroscopic motion corruption effectively without the use of navigator data. By using preliminary SENSE images to inherently estimate the motion parameters and phase errors among shots, blurring and ghosting artifacts can be corrected through a multiplexed reconstruction using the estimated information. It should be noted that a slight decrease in apparent resolution and a loss of detail in the ventricles in the images in Figure 2 are due to the averaging of multiple diffusion directions. As the data were not corrected for eddy current induced distortions, there are slight discrepancies among images for each diffusion direction, which when averaged appears to reduce the resolution. Furthermore, the contrast in the lateral ventricles varies among diffusion directions, which results in a loss of detail in this region when averaged.
Compared to using phase-corrected and registered SENSE images directly (Figure 2e), AMUSE-DWI provides better SNR in the final images due to its multiplexed nature and improved matrix conditioning. As described in the Theory section, 1) the MUSE reconstruction relies on accurate estimation of shot-to-shot phase variations, and 2) the SNR of MUSE reconstructed images may be lower than the theoretically expected value due to the noises in SENSE-produced phase variation maps. A potential difficulty of using the initial SENSE images to estimate macroscopic motion parameters through registration can occur if the SENSE images are significantly noisy. The dominance of noise can cause registration schemes to perform poorly, thereby producing inaccurate estimations of motion among shots. A quick method for resolving this is to apply a low-pass filter to the k-space of the SENSE images to reduce the level of noise, and subsequently use these filtered images for registration. Similarly, one may use regularized SENSE (48) to reduce the noise levels in the reconstructed SENSE images.
When the shot-to-shot phase variations in interleaved DWI scans are accurately measured (either from navigator echoes or a SENSE-based estimation), they can be used to reduce interleaved DWI artifacts with different approaches. The existing ‘direct phase subtraction’ methods remove phase errors directly from each individual segment, and then combine the phase-corrected segments to produce full-FOV images (28). However, because the complicated segment-specific signal overlapping patterns (in reduced FOV) are not taken in consideration in this simple phase subtraction procedure, the residual artifacts are usually noticeable. In contrast, the MUSE and AMUSE methods incorporate the segment-specific phase terms when reconstructing full-FOV images through a matrix inversion that takes segment-specific signal overlapping patterns into consideration, and can more effectively reduce aliasing artifacts in interleaved DWI data. The MUSE and AMUSE methods also incorporate the coil sensitivity profiles, as additional constraints, to stabilize the image reconstruction.
AMUSE is an image-based correction technique, and as such it provides benefits over k-space-based correction methods, including the ability to account for non-rigid motion types (49). The experiments in this work used motion parameters estimated from non-rigid 2D registrations with 5 degrees of freedom (DOF). The two scaling parameters in the 5 DOF registration produce improved alignment between shots in which some level of non-rigid transformation has occurred, such as differences in geometric distortions (44) or slight through-plane motion. Our framework can also incorporate motion parameters estimated from even more complex nonlinear registrations with higher DOF if needed.
The matrix formalism of AMUSE is similar to that used in other multi-shot motion correction techniques, such as those presented by Bammer et al. (31) and Batchelor et al. (49). This formalism is also presented in the works by Atkinson et al. (15), Liu et al. (30), and Truong and Guidon (34), however they are specific to correcting motion-induced phase errors only, and do not address macroscopic motion. The consensus among these works is that the matrix system approach is well suited to multi-shot trajectories that are undersampled (e.g. interleaved EPI), and for which alternative methods like direct phase subtraction to correct motion-induced errors (16–18,20) would be less effective (30).
Furthermore, it should be noted that our approach differs from the works of Bammer et al. (31) and Liu et al. (30), which when combined address both minuscule and macroscopic motion (21), in two aspects. First, our framework is specifically designed for interleaved EPI, and can therefore exploit its properties for a more straightforward implementation. Namely, we exploit the simple image-space aliasing patterns of each undersampled EPI interleave in order to explicitly form a sparse matrix describing the motion effects. We directly relate the desired uncorrupted image to the aliased images of all interleaves using this explicit matrix, and avoid the need for gridding as would be necessary in an image-space/Fourier-space relationship for motion correction. Thus our approach provides benefits in implementation as it is specific to interleaved EPI. However, for alternative multi-shot trajectories other than EPI (e.g. non-Cartesian trajectories) in which the aliasing patterns are more complex, an explicit relation of the desired image to aliased images will be less straightforward, and therefore a framework more similar to those presented in (21,31,49) could be more appropriate.
The second difference is that AMUSE uses initial SENSE images for inherent motion correction instead of navigator data. This inherent correction method was previously demonstrated by Chen et al. (23) and Truong et al. (34) to correct motion-induced phase errors in interleaved EPI and multi-shot spiral, respectively, but these works did not capitalize on the ability to use the initial SENSE images for correcting macroscopic motion as well. The main benefit of this inherent approach compared to navigator-based motion estimation methods is an improved imaging throughput. Additionally, using SENSE images to estimate the motion prevents the possibility of an inaccurate estimation with navigators if motion occurs between the primary data and navigator data acquisition. Furthermore, navigator-produced information usually has a lower spatial-resolution than the actual DWI data, potentially lowering the accuracy of the reconstructed images.
On the other hand, a drawback of our inherent approach compared to navigator-based methods is that it is dependent on the quality of SENSE reconstructions for each interleave. As the number of shots approaches or exceeds the number of coil channels the SENSE images will be prone to stronger g-factor noise, making the estimation of accurate motion information difficult. Therefore, in our current implementation the number of achievable shots is limited by the number of coil channels. This is not an issue in the navigator-based correction techniques (15,21,30,31), which can be applied with any number of shots and are not dependent on the number of coil channels. However, recent works using projection onto convex sets (POCS) combined with MUSE (POCSMUSE) (50), or a self-feeding MUSE technique (51), have demonstrated the ability to perform inherent phase correction at higher numbers of shots less strictly limited by the number of coil channels (50, 51). These recent advances could be combined with the AMUSE technique to partially overcome its current shot limitations, enabling both macroscopic and minuscule motion correction with more interleaves.
Diffusion contrast and tensor correction simulations
Using a set of gold-standard tensors for motion simulations allowed us to quantitatively assess the performance of our tensor correction approach with AMUSE-DTI. As seen by Figure 5b and Table 2, correcting for macroscopic motion between shots without accounting for the altered diffusion encoding produces significant errors in tensor calculations. These errors manifest themselves as incorrect estimations of the principal diffusion direction (as given by V1) and FA. Both of these effects can have serious implications on the analysis of diffusion data. For example, the principal diffusion direction V1 is a very important metric for many fiber tractography algorithms (39,52), and thus errors in V1 can lead to inaccurate estimations of tracts. Furthermore, some pathologies have been shown to be associated with reduced FA in specific regions (52–54). Therefore in order to ensure that interpretations of tractography and FA evaluations are accurate in studies using multi-shot diffusion data, it is necessary to correct the altered diffusion contrast in addition to the pixel misregistrations and phase errors among shots.
The results shown in Figure 5d and Table 2 demonstrate that AMUSE is able to correct this altered diffusion encoding arising from macroscopic motion and produce significantly more accurate calculations of the diffusion tensors, even for large rotations of up to 60 degrees (Table 2). The correction resulted in improved estimations of V1, FA, and MD.
An important finding in our simulations is that AMUSE-DTI provides improved FA and MD metrics compared to only using the coregistered (and b-matrix corrected) SENSE images, as demonstrated by Table 2 and Figures 5–6. This improvement is particularly apparent at lower SNR levels, with the mean diffusivity being most vulnerable to errors from noise (Figure 6). These findings indicate that despite the errors in the initial SENSE-based tensors, AMUSE-DTI can use these tensor estimates to reconstruct more accurate diffusion images, which subsequently can be used to calculate new tensors with reduced error. This has important implications for multi-shot data acquired at very high spatial resolutions and/or using a number of shots approaching the number of coil channels, which generally produce images with reduced SNR. The application of AMUSE-DTI in these types of acquisitions could alleviate the effects of noise in tensor calculations.
In Vivo Diffusion Tensor Correction
AMUSE-DTI was evaluated on data that contained the largest amount of motion our volunteer could perform within our head coil, at intervals of approximately every 2 shots (i.e. 2 TR), thereby creating a difficult case of macroscopic motion with large changes in diffusion-encoding between shots. Even in this difficult scenario AMUSE-DTI performed well in correcting the diffusion images and subsequent tensor calculations, as demonstrated by Figure 7 and Table 3. In agreement with our simulation results, AMUSE-DTI again outperformed SENSE-based correction in this in-vivo scenario. Residual errors in the tensor calculations after AMUSE-DTI can be attributed to several effects.
The primary effects are those caused by through-plane motion; for very large rotations, such as those in this experiment, it is likely that some level of through-plane motion is involved. The first potential effect of through-plane motion is large signal dropout, and in this scenario it is best to simply discard the shot experiencing the dropout from reconstruction. The second potential effect occurs when there is no signal dropout, but instead the brain is imaged at a different location along the slice direction. This is problematic since the assumption that anatomy does not change between shots becomes invalid for through-plane motion. Consequently our 2D correction approach will incorrectly mix anatomy from different brain locations along z, and this results in significant errors in tensor calculations. An additional effect of through-plane motion is the change in diffusion-encoding when rotation occurs along the through-plane axis. A 2D correction approach will be unable to estimate these rotations, and thus will not be able to correct the altered diffusion-encoding. These effects of through-plane motion can potentially be solved in the future by extending the AMUSE framework to 3D.
Another minor effect that can cause residual tensors errors is imperfect registrations to estimate the motion parameters. While we used a registration model with 5 DOF (1 rotation, 2 translations, 2 scaling parameters), this may not perfectly estimate motion in which the object has deformed in a more complex fashion, as can be the case with large rotations (44). Given that the AMUSE framework can be applied with any type of motion parameters, these effects can potentially be corrected by using registrations with higher DOF (e.g. including shear deformations). However, while higher DOF registrations may provide improved alignment visually, one must consider the possible effects of over-warping on the accuracy of tensor calculations.
In comparison to the multi-shot tensor correction method developed by Aksoy et al. (21), which uses a non-linear conjugate gradient (NLCG) approach, our findings produced similar results to those presented in their paper. However the primary advantage of our approach is in its significantly faster computation time. Namely, their work reported computation times on the order of ~ 4 hrs, while the method presented here achieved corrections on the order of minutes. It should be noted that our current implementation is specific to correction for multi-shot EPI, whereas the NLCG approach can be generalized to arbitrary multi-shot trajectories. However, we expect that future implementations of AMUSE should be able to account for non-Cartesian trajectories, such as spiral imaging, in addition to EPI. This can be accomplished by incorporating the macroscopic transformation and altered diffusion properties of AMUSE with the recently developed POCSMUSE, which is applicable to arbitrary k-space trajectories (50,55).
Furthermore, while our findings in this paper were specific to 4 shots, AMUSE can be generalized to a higher number of shots approaching or exceeding the number of coil channels if a method such as POCSMUSE (50), or self-feeding MUSE (51), is incorporated in a future implementation. Given the computational efficiency of the AMUSE, this provides a very high potential for practical motion-immune imaging at even higher spatial resolutions. It is important to note, however, that a higher number of shots necessarily requires a longer scan time for any multi-shot technique. Therefore in order to acquire a set number of diffusion directions within a given scan time it is not always possible to arbitrarily increase the number of shots, and the tradeoff between spatial and angular resolution must be considered.
CONCLUSION
While multi-shot diffusion-weighted imaging offers several advantages over single-shot techniques, its capabilities have been limited by the effects of patient motion. Namely, macroscopic patient motion can introduce phase errors, pixel misregistrations, and altered diffusion-encoding among shots, leading to unusable or inaccurate images. Here we have presented a novel approach to inherently estimate and correct all of the aforementioned effects from patient motion. As a result, diffusion tensor information that would otherwise be inaccurate can be estimated more precisely. We therefore expect that this method will be valuable for clinical and neuroscience investigations in which accurate high-resolution diffusion information is needed, even with the presence of subject motion.
ACKNOWLEDGEMENT
This research was supported by NIH R01-NS074045, NIH R21-EB018419, NIH R01-NS075017, and NIH R01-EB009483.
REFERENCES
- 1.Moseley ME, Kucharczyk J, Mintorovitch J, Cohen Y, Kurhanewicz J, Derugin N, Asgari H, Norman D. Diffusion-weighted MR imaging of acute stroke: correlation with T2-weighted and magnetic susceptibility-enhanced MR imaging in cats. AJNR Am J Neuroradiol. 1990;11(3):423–429. [PMC free article] [PubMed] [Google Scholar]
- 2.Warach S, Chien D, Li W, Ronthal M, Edelman RR. Fast magnetic resonance diffusion-weighted imaging of acute human stroke. Neurology. 1992;42(9):1717–1723. doi: 10.1212/wnl.42.9.1717. [DOI] [PubMed] [Google Scholar]
- 3.Lansberg MG, Norbash AM, Marks MP, Tong DC, Moseley ME, Albers GW. Advantages of adding diffusion-weighted magnetic resonance imaging to conventional magnetic resonance imaging for evaluating acute stroke. Arch Neurol. 2000;57(9):1311–1316. doi: 10.1001/archneur.57.9.1311. [DOI] [PubMed] [Google Scholar]
- 4.Bammer R. Basic principles of diffusion-weighted imaging. Eur J Radiol. 2003;45(3):169–184. doi: 10.1016/s0720-048x(02)00303-0. [DOI] [PubMed] [Google Scholar]
- 5.Ebisu T, Tanaka C, Umeda M, Kitamura M, Naruse S, Higuchi T, Ueda S, Sato H. Discrimination of brain abscess from necrotic or cystic tumors by diffusion-weighted echo planar imaging. Magnetic Reson Imaging. 1996;14(9):1113–1116. doi: 10.1016/s0730-725x(96)00237-8. [DOI] [PubMed] [Google Scholar]
- 6.Lai PH, Ho JT, Chen WL, Hsu SS, Wang JS, Pan HB, Yang CF. Brain abscess and necrotic brain tumor: discrimination with proton MR spectroscopy and diffusion-weighted imaging. AJNR Am J Neuroradiol. 2002;23(8):1369–1377. [PMC free article] [PubMed] [Google Scholar]
- 7.Mori S, Crain BJ, Chacko VP, van Zijl PC. Three-dimensional tracking of axonal projections in the brain by magnetic resonance imaging. Ann Neurol. 1999;45(2):265–269. doi: 10.1002/1531-8249(199902)45:2<265::aid-ana21>3.0.co;2-3. [DOI] [PubMed] [Google Scholar]
- 8.Basser PJ, Pajevic S, Pierpaoli C, Duda J, Aldroubi A. In vivo fiber tractography using DT-MRI data. Magn Reson Med. 2000;44(4):625–632. doi: 10.1002/1522-2594(200010)44:4<625::aid-mrm17>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- 9.Ciccarelli O, Catani M, Johansen-Berg H, Clark C, Thompson A. Diffusion-based tractography in neurological disorders: concepts, applications, and future developments. Lancet Neurol. 2008;7(8):715–727. doi: 10.1016/S1474-4422(08)70163-7. [DOI] [PubMed] [Google Scholar]
- 10.Moritani T, Ekholm S, Westesson PL. Diffusion-weighted MR imaging of the brain. Berlin: Springer-Verlag; 2009. [Google Scholar]
- 11.Turner R, Le Bihan D, Maier J, Vavrek R, Hedges LK, Pekar J. Echo-planar imaging of intravoxel incoherent motion. Radiology. 1990;177(2):407–414. doi: 10.1148/radiology.177.2.2217777. [DOI] [PubMed] [Google Scholar]
- 12.Jezzard P, Balaban RS. Correction for geometric distortion in echo planar images from B0 field variations. Magn Reson Med. 1995;34(1):65–73. doi: 10.1002/mrm.1910340111. [DOI] [PubMed] [Google Scholar]
- 13.Farzaneh F, Riederer SJ, Pelc NJ. Analysis of T2 limitations and off-resonance effects on spatial resolution and artifacts in echo-planar imaging. Magn Reson Med. 1990;14(1):123–139. doi: 10.1002/mrm.1910140112. [DOI] [PubMed] [Google Scholar]
- 14.Atkinson D, Porter DA, Hill DL, Calamante F, Connelly A. Sampling and reconstruction effects due to motion in diffusion-weighted interleaved echo planar imaging. Magn Reson Med. 2000;44(1):101–109. doi: 10.1002/1522-2594(200007)44:1<101::aid-mrm15>3.0.co;2-s. [DOI] [PubMed] [Google Scholar]
- 15.Atkinson D, Counsell S, Hajnal JV, Batchelor PG, Hill DL, Larkman DJ. Nonlinear phase correction of navigated multi-coil diffusion images. Magn Reson Med. 2006;56(5):1135–1139. doi: 10.1002/mrm.21046. [DOI] [PubMed] [Google Scholar]
- 16.Pipe JG, Farthing VG, Forbes KP. Multishot diffusion-weighted FSE using PROPELLER MRI. Magn Reson Med. 2002;47(1):42–52. doi: 10.1002/mrm.10014. [DOI] [PubMed] [Google Scholar]
- 17.Wang FN, Huang TY, Lin FH, Chuang TC, Chen NK, Chung HW, Chen CY, Kwong KK. PROPELLER EPI: an MRI technique suitable for diffusion tensor imaging at high field strength with reduced geometric distortions. Magn Reson Med. 2005;54(5):1232–1240. doi: 10.1002/mrm.20677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Porter DA, Heidemann RM. High resolution diffusion-weighted imaging using readout-segmented echo-planar imaging, parallel imaging and a two-dimensional navigator-based reacquisition. Magn Reson Med. 2009;62(2):468–475. doi: 10.1002/mrm.22024. [DOI] [PubMed] [Google Scholar]
- 19.Anderson AW, Gore JC. Analysis and correction of motion artifacts in diffusion weighted imaging. Magn Reson Med. 1994;32(3):379–387. doi: 10.1002/mrm.1910320313. [DOI] [PubMed] [Google Scholar]
- 20.Miller KL, Pauly JM. Nonlinear phase correction for navigated diffusion imaging. Magn Reson Med. 2003;50(2):343–353. doi: 10.1002/mrm.10531. [DOI] [PubMed] [Google Scholar]
- 21.Aksoy M, Liu C, Moseley ME, Bammer R. Single-step nonlinear diffusion tensor estimation in the presence of microscopic and macroscopic motion. Magn Reson Med. 2008;59(5):1138–1150. doi: 10.1002/mrm.21558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Holdsworth SJ, Aksoy M, Newbould RD, Yeom K, Van AT, Ooi MB, Barnes PD, Bammer R, Skare S. Diffusion tensor imaging (DTI) with retrospective motion correction for large-scale pediatric imaging. J Magn Reson Imaging. 2012;36(4):961–971. doi: 10.1002/jmri.23710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chen NK, Guidon A, Chang HC, Song AW. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE) NeuroImage. 2013;72:41–47. doi: 10.1016/j.neuroimage.2013.01.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Ordidge RJ, Helpern JA, Qing ZX, Knight RA, Nagesh V. Correction of motional artefacts in diffusion-weighted MR images using navigator echoes. J Magn Reson Imaging. 1994;12(3):455–460. doi: 10.1016/0730-725x(94)92539-9. [DOI] [PubMed] [Google Scholar]
- 25.de Crespigny AJ, Marks MP, Enzmann DR, Moseley ME. Navigated diffusion imaging of normal and ischemic human brain. Magn Reson Med. 1995;33(5):720–728. doi: 10.1002/mrm.1910330518. [DOI] [PubMed] [Google Scholar]
- 26.Butts K, de Crespigny A, Pauly JM, Moseley M. Diffusion-weighted interleaved echo-planar imaging with a pair of orthogonal navigator echoes. Magn Reson Med. 1996;35(5):763–770. doi: 10.1002/mrm.1910350518. [DOI] [PubMed] [Google Scholar]
- 27.Butts K, Pauly J, de Crespigny A, Moseley M. Isotropic diffusion-weighted and spiral-navigated interleaved EPI for routine imaging of acute stroke. Magn Reson Med. 1997;38(5):741–749. doi: 10.1002/mrm.1910380510. [DOI] [PubMed] [Google Scholar]
- 28.Liu C, Bammer R, Kim DH, Moseley ME. Self-navigated interleaved spiral (SNAILS): application to high-resolution diffusion tensor imaging. Magn Reson Med. 2004;52(6):1388–1396. doi: 10.1002/mrm.20288. [DOI] [PubMed] [Google Scholar]
- 29.Li TQ, Kim DH, Moseley ME. High-resolution diffusion-weighted imaging with interleaved variable-density spiral acquisitions. J Magn Reson Imaging. 2005;21(4):468–475. doi: 10.1002/jmri.20287. [DOI] [PubMed] [Google Scholar]
- 30.Liu C, Moseley ME, Bammer R. Simultaneous phase correction and SENSE reconstruction for navigated multi-shot DWI with non-cartesian k-space sampling. Magn Reson Med. 2005;54(6):1412–1422. doi: 10.1002/mrm.20706. [DOI] [PubMed] [Google Scholar]
- 31.Bammer R, Aksoy M, Liu C. Augmented generalized SENSE reconstruction to correct for rigid body motion. Magn Reson Med. 2007;57(1):90–102. doi: 10.1002/mrm.21106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Van AT, Karampinos DC, Georgiadis JG, Sutton BP. K-space and image-space combination for motion-induced phase-error correction in self-navigated multicoil multishot DWI. IEEE Trans Med Imaging. 2009;28(11):1770–1780. doi: 10.1109/TMI.2009.2023212. [DOI] [PubMed] [Google Scholar]
- 33.Skare S, Newbould RD, Clayton DB, Bammer R. Propeller EPI in the other direction. Magn Reson Med. 1999;55(6):1298–1307.34. doi: 10.1002/mrm.20890. [DOI] [PubMed] [Google Scholar]; Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42(5):952–962. [PubMed] [Google Scholar]
- 34.Truong TK, Guidon A. High-resolution multishot spiral diffusion tensor imaging with inherent correction of motion-induced phase errors. Magn Reson Med. 2014;71:790–796. doi: 10.1002/mrm.24709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42(5):952–962. [PubMed] [Google Scholar]
- 36.Rudin L, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms. Physica D. 1992;60(1–4):259–268. [Google Scholar]
- 37.Hestenes MR, Stiefel E. Methods of conjugate gradients for solving linear systems. Natl Bur Standards J Res. 1952;49:409–436. [Google Scholar]
- 38.Basser PJ, Mattiello J, LeBihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. J Magn Reson B. 1994;103(3):247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
- 39.Leemans A, Jones DK. The B-matrix must be rotated when correcting for subject motion in DTI data. Magn Reson Med. 2009;61(6):1336–1349. doi: 10.1002/mrm.21890. [DOI] [PubMed] [Google Scholar]
- 40.Chen NK, Avram AV, Song AW. Two-dimensional phase cycled reconstruction for inherent correction of echo-planar imaging Nyquist artifacts. Magn Reson Med. 2011;66(4):1057–1066. doi: 10.1002/mrm.22896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Jenkinson M, Beckmann CF, Behrens TE, Woolrich MW, Smith SM. FSL. NeuroImage. 2012;62(2):782–790. doi: 10.1016/j.neuroimage.2011.09.015. [DOI] [PubMed] [Google Scholar]
- 42.Jenkinson M, Smith SM. A global optimisation method for robust affine registration of brain images. Med Image Anal. 2001;5(2):146–156. doi: 10.1016/s1361-8415(01)00036-6. [DOI] [PubMed] [Google Scholar]
- 43.Jenkinson M, Bannister PR, Brady JM, Smith SM. Improved optimisation for the robust and accurate linear registration and motion correction of brain images. NeuroImage. 2002;17(2):825–841. doi: 10.1016/s1053-8119(02)91132-8. [DOI] [PubMed] [Google Scholar]
- 44.Ooi MB, Krueger S, Muraskin J, Thomas WJ, Brown TR. Echo-planar imaging with prospective slice-by-slice motion correction using active markers. Magn Reson Med. 2011;66(1):73–81. doi: 10.1002/mrm.22780. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Cuppen JJ, van Est A. Reducing MR imaging time by one-sided reconstruction. J Magn Reson Imaging. 1987;5(6):526–527. [Google Scholar]
- 46.Perona P, Malik J. Scale-space and edge detection using anisotropic diffusion. IEEE Trans Pattern Anal Mach Intell. 1990;12:629–639. [Google Scholar]
- 47.Jones DK. Diffusion MRI: theory, methods, and application. New York: Oxford University Press; 2010. [Google Scholar]
- 48.Ying L, Liu B, Steckner MC, Wu G, Wu M, Li SJ. A statistical approach to SENSE regularization with arbitrary k-space trajectories. Magn Reson Med. 2008;60(2):414–421. doi: 10.1002/mrm.21665. [DOI] [PubMed] [Google Scholar]
- 49.Batchelor PG, Atkinson D, Irarrazaval P, Hill DL, Hajinal J, Larkman D. Matrix description of general motion correction applied to multishot images. Magn Reson Med. 2005;54(5):1273–1280. doi: 10.1002/mrm.20656. [DOI] [PubMed] [Google Scholar]
- 50.Chu ML, Chang HC, Chung HW, Truong TK, Bashir MR, Chen NK. POCS-based reconstruction of multiplexed sensitivity encoded MRI (POCSMUSE): A general algorithm for reducing motion-related artifacts. Magn Reson Med. 2014 Nov 13; doi: 10.1002/mrm.25527. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Zhang Z, Huang F, Ma X, Xie S, Guo H. Self-feeding MUSE: A robust method for high resolution diffusion imaging using interleaved EPI. Neuroimage. 2014 Oct 16; doi: 10.1016/j.neuroimage.2014.10.022. pii: S1053-8119(14)00846-5. [Epub ahead of print] [DOI] [PubMed] [Google Scholar]
- 52.Lin F, Yu C, Jiang T, Li K, Chan P. Diffusion tensor tractography-based group mapping of the pyramidal tract in relapsing-remitting multiple sclerosis patients. AJNR Am J Neuroradiol. 2007;28(2):278–282. [PMC free article] [PubMed] [Google Scholar]
- 53.Chan LL, Rumpel H, Yap K, Lee E, Loo HV, Ho GL, Fook-Chong S, Yuen Y, Tan EK. Case control study of diffusion tensor imaging in Parkinson’s disease. J Neurol Neurosurg Psychiatry. 2007;78(12):1383–1386. doi: 10.1136/jnnp.2007.121525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Gattellaro G, Minati L, Grisoli M, Mariani C, Carella F, Osio M, Ciceri E, Albanese A, Bruzzone MG. White matter involvement in idiopathic Parkinson disease: a diffusion tensor imaging study. AJNR Am J Neuroradiol. 2009;30(6):1222–1226. doi: 10.3174/ajnr.A1556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Samsonov AA, Kholmovski EG, Parker DL, Johnson CR. POCSENSE: POCS-based reconstruction for sensitivity encoded magnetic resonance imaging. Magn Reson Med. 2004;52(6):1397–406. doi: 10.1002/mrm.20285. [DOI] [PubMed] [Google Scholar]