Stochastic S-system modeling of gene regulatory network

Abstract

Microarray gene expression data can provide insights into biological processes at a system-wide level and is commonly used for reverse engineering gene regulatory networks (GRN). Due to the amalgamation of noise from different sources, microarray expression profiles become inherently noisy leading to significant impact on the GRN reconstruction process. Microarray replicates (both biological and technical), generated to increase the reliability of data obtained under noisy conditions, have limited influence in enhancing the accuracy of reconstruction . Therefore, instead of the conventional GRN modeling approaches which are deterministic, stochastic techniques are becoming increasingly necessary for inferring GRN from noisy microarray data. In this paper, we propose a new stochastic GRN model by investigating incorporation of various standard noise measurements in the deterministic S-system model. Experimental evaluations performed for varying sizes of synthetic network, representing different stochastic processes, demonstrate the effect of noise on the accuracy of genetic network modeling and the significance of stochastic modeling for GRN reconstruction . The proposed stochastic model is subsequently applied to infer the regulations among genes in two real life networks: (1) the well-studied IRMA network, a real-life in-vivo synthetic network constructed within the Saccharomycescerevisiae yeast, and (2) the SOS DNA repair network in Escherichiacoli.

Introduction

Recent advancements in microarray technology have generated a huge amount of gene expression data allowing analysis of genetic interactions during different cellular processes. Although expression profiles are being applied in various applications, e.g., drug design, its application for reconstruction of gene regulatory network (GRN) is still considered as a critical and challenging problem in systems biology (de Jong 2002). Although GRN modeling considers gene expression and regulation as deterministic, a number of experimental substantiations (Arkin et al. 1998; Bennett 1983; Walters et al. 1995) point out the presence of stochastic fluctuations in these processes in both prokaryotic and eukaroyotic cells. The microarray data shows unpredictable variations, which are often ascribed to causes that are either biological or technical, or both. While the biological variations mainly reflect the changes in mRNA levels, the key reasons for technical variations include sampling, labeling, and hybridization (Tian 2010). According to Rocke and Durbin (2001), the variations can be in the range 20–30 % of the original expression value. Hence, it is imperative to account for this noise for accurate inference of GRNs.

As it is well known, in any biological network, there are two sources of noise, internal and external, which are also commonly known as intrinsic and extrinsic noise, respectively (Climescu-Haulica and Quirk 2007; EI Samad et al. 2005). The internal noise occurs from the biological reactions in the system, which is due to small copy number of a few key molecular species. The noise propagation from biological pathways or environmental fluctuations leads to external noise. Apart from these two sources of noise, measurement errors are also treated as noise (Tu et al. 2002). Signal processing techniques (Walleczek 2000), often applied for analyzing biological systems, are very sensitive to environmental fluctuations and/or the unpredictable intrinsic noise occurring in certain time periods. During the modeling, we have considered three different types of noise (in five different ways) in the proposed Stochastic S-system Modeling. Although, the first and the simplistic noise, namely the additive noise, have no physical meaning with respect to GRNs, it essentially mimics the effect of nature’s random processes. The multiplicative noise, on the other hand, is models the external noise that gets imposed on GRN. Since noise is widely used to test the concentration of a gene product, we have evaluated the performance of Stochastic S-system modeling with multiplicative noise both in genes’ production and degradation. Finally, Langevin noise is used to model the internal noise of a network, where this noise can occur because of small copy number of a few key molecular species. Similar to testing the proposed stochastic model with multiplicative noise, the model is also studied with Langevin noise in both production and degradation mode. After careful observation of the impact of these five types of noises, we propose a new modeling approach having composite noise terms in it, which is capable of dealing both internal and external noise of a GRN.

The GRN models, based on current state-of-the-art deterministic approaches, are unable to cater to the inherent stochasticity present in microarray data, thereby underscoring the need for a suitable stochastic model incorporating the randomness in the process. Such models have additional term(s) of noise or probability distribution along with the regular deterministic term. For GRN modeling, probabilistic Boolean network (Shmulevich et al. 2002) is considered as a common example of a discrete stochastic model. Recently, stochastic modeling of GRN was also carried out using Boolean models (Gillespie 2007; Gillespie and Petzold 2003), Petri nets (Golding et al. 2005; Gonze et al. 2002) or other modeling techniques (Tian and Burrage 2001, 2006; Wahde and Hertz 2000; Wilkinson 2009). Further, probabilistic hybrid approaches (Goldbeter 1995) and multi-scale hybrid models (Goss and Peccoud 1998; Poovathingal and Gunawan 2010), that include both stochastic and deterministic dynamics, have also been proposed. Recent GRN approaches deal with either stability of the network or stochastic delayed regulations or both (He and Cao 2008; Luo et al. 2010; Wang et al. 2009). However, the aforementioned methods, due to using non-differential equation models, fail to completely capture the changing behavior of expression profiles. Hence, ordinary differential equations (ODEs) are essential when continuously varying quantities and their changing characteristics over time must be captured. The ODE models show promise in reconstructing GRNs from continuous time-expression profiles (Chowdhury and Chetty 2011; Chowdhury et al. 2012, 2013a, b; Kikuchi et al. 2003; Savageau 1976). Recently, stochastic differential equations (Tian and Burrage 2001, 2006) have been applied for capturing system dynamics. Tian and Burrage (2001, (2006) developed a stochastic modeling technique based on the following ordinary differential equation describing the dynamics of gene transcript:

$$\begin{array}{c}\hfill \frac{dI}{dT}=a+bf(t)-KI\end{array}$$ 1

The above stochastic modeling emphasizes the regulations only in production and fails to capture regulation in the degradation. Using the non-linear S-system model, we can represent regulations both in the production and degradation phases. However, the traditional S-system model is deterministic and fails to cope with noisy microarray data. This paper proposes new stochastic S-system model and investigates the effect of different types of noise, e.g., additive, multiplicative, Langevin, in a widely used deterministic S-system model. Both synthetic and real life networks are considered.

The reminder of this paper is organized as follows: “Stochastic modeling of gene regulatory network” section highlights the proposed stochastic S-system models along with the modified numerical integration. In “Experimental results and discussions” section, the performance of the proposed model is evaluated using various synthetic and real networks. “Conclusion” section concludes the paper.

Stochastic modeling of gene regulatory network

The model

GRN modeling is considered as a non-linear identification problem with the presence of numerous interacting genes in the network (Cantone et al. 2009; Kim et al. 2007). A promising non-linear model, the S-system model (Savageau 1976) is capable of capturing the dynamics of various complex regulations. While the S-system is able to represent both the production and the degradation phases, it is still a deterministic model and unable to capture the stochasticity of a real GRN. In this paper, we propose a novel stochastic S-system model capable of realistically modeling the noisy variations observed in measured time series data.

Before introducing the stochastic S-system model, we briefly discuss the deterministic S-system model. The S-system approach, proposed by Savageau (1976), is well-known for modeling biochemical networks and has attracted significant attention in the past decade (Kikuchi et al. 2003; Maki et al. 2002; Voit and Radivoyevitch 2000). Considering N as the number of genes in a network, the S-system model can be described by the following equation:

$$\begin{array}{c}\hfill \frac{\text{d}}{\text{dt}}{X}_i={\mathit{\alpha }}_i\prod _{j=1}^N{X}_j^{g_{ij}}-{\mathit{\beta }}_i\prod _{j=1}^N{X}_j^{h_{ij}},i=1\dots N\end{array}$$ 2

where, $X_i$ is the expression level of the ith gene. Two non-negative parameters ${\mathit{\alpha }}_i$, ${\mathit{\beta }}_i$ are called rate constants and real-valued exponents $g_{ij}$, $h_{ij}$ are referred to as kinetic orders. The typical values of rate constants and kinetic order parameters range from 0 to 20 and $-3.00$ to 3.00, respectively. The term ${\mathit{\alpha }}_i\prod X_j^{g_{ij}}$ models the process of RNA production, while the term ${\mathit{\beta }}_i\prod X_j^{h_{ij}}$ models the process of RNA degradation. In production, a positive value of $g_{ij}$ implies the activation from Gene-j to Gene-i, while a negative value of $g_{ij}$ indicates the inhibition from Gene-j to Gene-i. On the other hand, in the degradation phase, suppression and inhibition on Gene-i from Gene-j are indicated with negative and positive values of $h_{ij}$, respectively. If $g_{ij}=0$ ($h_{ij}=0$), it implies that there is no activation (inhibition) from Gene-j to Gene-i. For the canonical S-system model, as shown in Eq. (2), where all N genes are considered at the same time for modeling, the set of parameters that defines the model is given by $\mathit{\theta }$ = $\{\mathit{\alpha }$, $\mathit{\beta }$, g, $h\}$. Thus, to infer a GRN of N genes using the S-system model, 2$\times N(N+1)$ parameters must be estimated. However, Maki et al. (2002) proposed the following de-coupled S-system model by decomposing the canonical system into smaller problems:

$$\begin{array}{c}\hfill \frac{\text{d}}{\text{dt}}{X}_i={\mathit{\alpha }}_i\prod _{j=1}^N{Y}_j^{g_{ij}}-{\mathit{\beta }}_i\prod _{j=1}^N{Y}_j^{h_{ij}},i=1\dots N\end{array}$$ 3

For solving Eq. (3), $Y_{i=j}$ is obtained by numerical integration, whereas $Y_{i!=j}$ is obtained by pre-calculations directly via observed times-series data. Although the accuracy may decrease due to direct estimation rather than numerical calculation, decoupling greatly reduces the computational burden. In the rest of this paper, we denote this model [Eq. (3)] as DSS (deterministic S-system).

We now write the stochastic differential equations with generalized term (Shmulevich and Aitchison 2009) in the following equation:

$$\begin{array}{c}\hfill \frac{\text{d}}{\text{dt}}{X}_i=f_i(X,u,t)+\mathit{\mu }g(X_i){\mathit{\zeta }}_i(t)\end{array}$$ 4

Here, $f_i$ represents the deterministic differential equations to model genetic interactions and $\mathit{\mu }g(X_i){\mathit{\zeta }}_i(t)$ represents its stochastic part. The stochastic part contains three terms: $\mathit{\mu }$ represents noise strength, $g(X_i)$ is the contribution of signal fluctuation, and ${\mathit{\zeta }}_i(t)$ is Gaussian white noise with zero mean and unit variance. Tian (2011) considered $\mathit{\zeta }$ as a Weiner process W(t) with increment $△W(t)$ = $W(t+△)-W(t)\sim N(0,t)$ as a Gaussian random variable. We consider Eq. (2) as the deterministic function for Eq. (4) and form the generalized Stochastic S-system Model as follows:

$$\begin{array}{c}\hfill \frac{\text{d}}{\text{dt}}{X}_i=\left[{\mathit{\alpha }}_i\prod _{j=1}^N{X}_j^{g_{ij}}-{\mathit{\beta }}_i\prod _{j=1}^N{X}_j^{h_{ij}}\right]+\mathit{\mu }g(X_i){\mathit{\zeta }}_i(t),i=1\dots N\end{array}$$ 5

While considering only the additive noise, the stochastic model, denoted by ${\text{SSS}}^{\mathrm{a}}$, is as follows

$$\begin{array}{c}\hfill \frac{\text{d}}{\text{dt}}{X}_i=\left[{\mathit{\alpha }}_i\prod _{j=1}^N{X}_j^{g_{ij}}-{\mathit{\beta }}_i\prod _{j=1}^N{X}_j^{h_{ij}}\right]+\mathit{\mu }{\mathit{\zeta }}_i(t),i=1\dots N\end{array}$$ 6

where, $g(X_i)$ = 1 in Eq. (4). We note that, integral of a white noise is Brownian motion that produces Brownian noise. The key reason of selecting the additive noise (Wiener process) in the new modeling approach is to imitate the effect of nature’s random processes. However, we also evaluated the stochasticity with multiplicative noise and Langevin noise, and later, proposed stochastic S-system model having hybrid noise terms with deterministic S-system equation.

It may be noted that, both the production and degradation processes can contribute towards noise and $g(X_i)$ can be considered as originating from either production or degradation, or both. For ease of understanding, we define $\mathit{\rho }(X_i)$ and $\mathit{\varrho }(X_i)$ as the noise contributions in production and degradation, respectively:

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathit{\rho }(X_i)={\mathit{\alpha }}_i\prod _{j=1}^N{X}_j^{g_{ij}}\\ \hfill \mathit{\varrho }(X_i)={\mathit{\beta }}_i\prod _{j=1}^N{X}_j^{h_{ij}}\end{array}\end{array}$$ 7

The stochastic S-system model with multiplicative noise and Langevin noise in production, denoted as ${\text{SSS}}^{\mathrm{mT}}$ and ${\text{SSS}}^{\mathrm{LT}}$, can be expressed by the following Eqs. (8) and (9), respectively:

$$\begin{array}{cc}& \frac{\text{d}}{\text{dt}}{X}_i=\left[{\mathit{\alpha }}_i\prod _{j=1}^N{X}_j^{g_{ij}}-{\mathit{\beta }}_i\prod _{j=1}^N{X}_j^{h_{ij}}\right]+\mathit{\mu }\mathit{\rho }(X_i){\mathit{\zeta }}_i(t),i=1\dots N\hfill \end{array}$$ 8

$$\begin{array}{cc}& \frac{\text{d}}{\text{dt}}{X}_i=\left[{\mathit{\alpha }}_i\prod _{j=1}^N{X}_j^{g_{ij}}-{\mathit{\beta }}_i\prod _{j=1}^N{X}_j^{h_{ij}}\right]+\mathit{\mu }\sqrt[]{\mathit{\rho }(X_i)}{\mathit{\zeta }}_i(t),i=1\dots N\hfill \end{array}$$ 9

In most of the existing approaches for GRN modeling, stochastic components are usually additive noise or degradation process. Here, we consider the stochastic S-system model with transcription process in terms of multiplicative and Langevin noise:

$$\begin{array}{cc}& \frac{\text{d}}{\text{dt}}{X}_i=\left[{\mathit{\alpha }}_i\prod _{j=1}^N{X}_j^{g_{ij}}-{\mathit{\beta }}_i\prod _{j=1}^N{X}_j^{h_{ij}}\right]+\mathit{\mu }\mathit{\varrho }(X_i){\mathit{\zeta }}_i(t),i=1\dots N\hfill \end{array}$$ 10

$$\begin{array}{cc}& \frac{\text{d}}{\text{dt}}{X}_i=\left[{\mathit{\alpha }}_i\prod _{j=1}^N{X}_j^{g_{ij}}-{\mathit{\beta }}_i\prod _{j=1}^N{X}_j^{h_{ij}}\right]+\mathit{\mu }\sqrt[]{\mathit{\varrho }(X_i)}{\mathit{\zeta }}_i(t),i=1\dots N\hfill \end{array}$$ 11

We denote the above two models as ${\text{SSS}}^{\mathrm{mD}}$ and ${\text{SSS}}^{\mathrm{mT}+\mathrm{LD}}$, respectively. The aforementioned five stochastic S-system equations incorporate the noise either from production or from degradation or none. Similar to Tian (2010), we also consider the stochastic S-system model with multiple (two) noise terms, denoted SSS${}^{mT+LD}$, according to the following equation:

$$\begin{array}{c}\hfill \frac{\text{d}}{\text{dt}}{X}_i=\left[{\mathit{\alpha }}_i\prod _{j=1}^N{X}_j^{g_{ij}}-{\mathit{\beta }}_i\prod _{j=1}^N{X}_j^{h_{ij}}\right]+{\mathit{\mu }}_1\mathit{\varrho }(X_i){\mathit{\zeta }}_i(t)+{\mathit{\mu }}_2\sqrt[]{\mathit{\rho }(X_i)}{\mathit{\zeta }}_i(t),i=1\dots N\end{array}$$ 12

The above equation takes account of noise from both production and degradation. However, the choice of multiplicative noise in production and Langevin noise in degradation is based on the empirical experimental observation that we performed on various GRNs.

Numerical integration with stochastic S-system model

Due to the additional stochastic term in the model equations [Eqs. (6), (8)–(11)], the stochastic S-system (SSS) model defined in the previous section requires additional parameters to be inferred compared to the traditional S-system model due to the additional stochastic term in the model equations. In order to understand the enhancements necessary for numerical integration for the SSS model, let us first consider the generalized equation of the SSS [Eq. (4)]. Although Eq. (4) can be solved by numerical integration using any standard techniques, such as Runge–Kutta fourth order equation (RK4), it requires multiple Gaussian white noise to be generated for single t. To illustrate, let us consider the four component equations of standard RK4 to calculate numerical integration at the tth time:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill k_1& =f(t,X)\hfill \\ \hfill k_2& =f(t+\frac{h}{2},X+\frac{h}{2}{k}_1)\hfill \\ \hfill k_3& =f(t+\frac{h}{2},X+\frac{h}{2}{k}_2)\hfill \\ \hfill k_4& =f(t+h,X+h{k}_3)\hfill \end{array}\end{array}$$ 13

where $h>0$ is the step size. We observe that, evaluation of the function f(t, X) is required at three different internal time-stamps (i.e., t, $(t+\frac{h}{2})$, and $(t+h)$) between two consecutive t values (i.e., $t_n$ and $t_{n+1}$). Since, $t_{n+1}=t_n+h$, we can safely assume two different internal time-stamps, i.e., t and $t+\frac{h}{2}$, other than the final t (i.e., $t_T$). Hence, the numerical integration requires two different noise values for each t. However, since a typical h value is extremely small, our proposed model can safely assume that the noise at t and $t+\frac{h}{2}$ are the same. To keep the simulation simple, we also consider, in a particular time-stamp t, the same noise value will have an effect on the concentrations of all N genes.

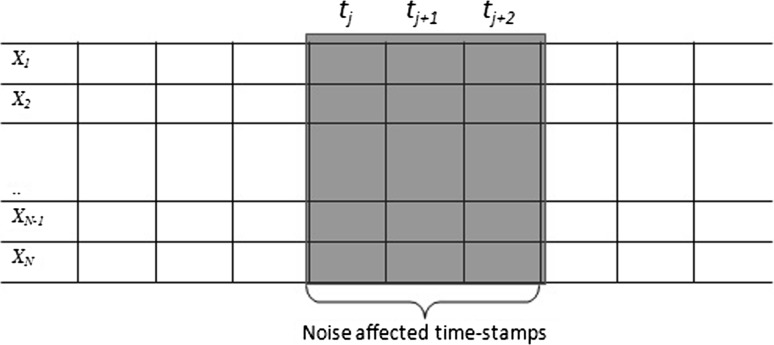
Although noise affects on certain time-samples, the genes’ concentration in the subsequent time-stamps will continue to carry forward the effect of noise affected concentrations. Rather than considering the occurrences of random noise, we assume that the noise appears in a particular window frame of single dimension $[t_s,t_e]$ with $t_0\le t_s\le t_e\le t_T$, where $t_s$ and $t_e$, respectively represent the start and end time-stamp of the noise window, while $t_0$ and $t_T$ represent the start and end time-stamp of the microarray. The situation, for a single time-series data, is shown in Fig. 1. Since, the biological noise can appear only in certain samples, we assume that $(t_e-t_s)\le ma{x}_t$, where $ma{x}_t$ is the maximum size of the window.

Fig. 1.

Noisy microarray

However, any meaningful conclusion about complex dynamics cannot be derived using a single set of time-course data; multiple time-course data set are often considered. Hence, for K different data sets, we consider K different single dimensional window frames for noise to appear. Thus, we define the following noise matrix:

$$NS=\left(\begin{array}{cccc}N{S}_{1,t_s}& N{S}_{1,t_{s+1}}& \cdots & N{S}_{1,t_e}\\ N{S}_{2,t_s}& N{S}_{2,t_{s+1}}& \cdots & N{S}_{2,t_e}\\ ⋮& ⋮& \ddots & ⋮\\ N{S}_{K,t_s}& N{S}_{K,t_{s+1}}& \cdots & N{S}_{K,t_e}\end{array}\right)$$ 14

where $N{S}_{p,q}$ is Gaussian white noise with zero mean and unit variance at the qth time-stamp in the pth data set.

Inference mechanism

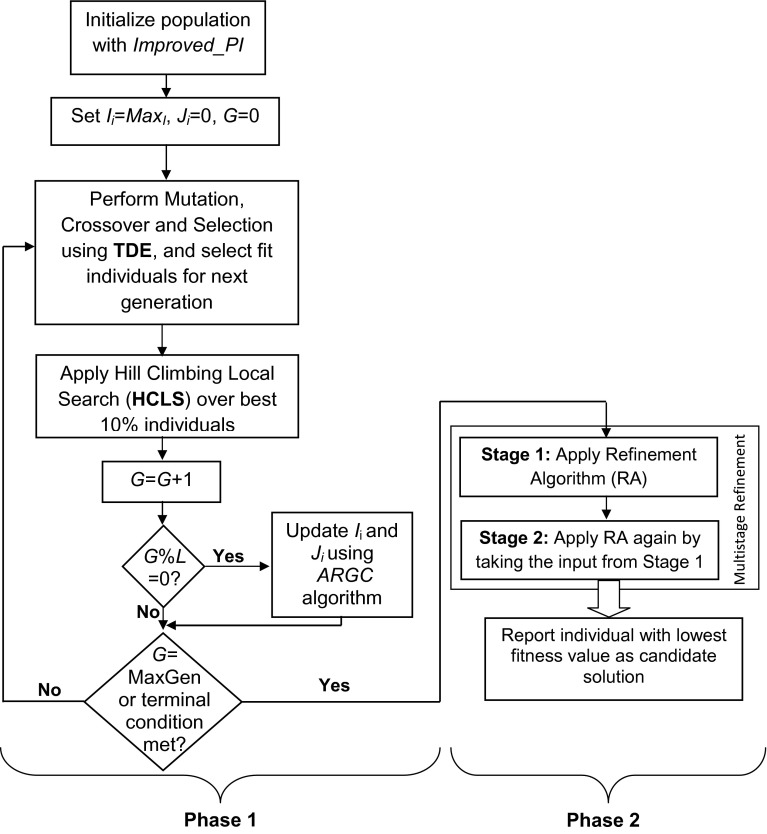
In order to evaluate the performance of the proposed Stochastic S-system model, we have used our previously developed optimization technique REGARD (Reverse Engineering GRN with Adaptive Regulatory-genes-cardinality) (Chowdhury et al. 2012). Both the stochastic and deterministic S-system models are tested with this REGARD algorithm. REGARD was developed in Chowdhury et al. (2012) based on Trigonometric Differential Evolution algorithm incorporating various sub-modules for appropriate inference of the GRNs. It starts with an improved initialization algorithm that includes the knowledge of cardinality in the initial seeds. After that, evolution is performed with trigonometric mutation and cross-over operations. During the evolution, our proposed cardinality-based fitness criteria is invoked along with the Adaptive-regulatory-Genes Cardinality (ARGC) algorithm that adapts the cardinality values based on a probabilistic criteria. We also used a local-search search technique that fine-tunes best 10 % solutions in every iteration. When maximum number of iterations are completed, the candidate solutions go through our proposed multi-stage refinement algorithm that further fine-tunes the candidate solutions and finds single candidate solution. The steps of the REGARD algorithm is shown in Fig. 2.

Fig. 2.

Flow-chart of our previously proposed optimization algorithm ‘Reverse Engineering GRN with Adaptive-regulatory-Genes Cardinality (REGARD)’ (L in the flow-chart denotes the update interval for $I_i/J_i$ with ARGC algorithm)

Experimental results and discussions

The evaluation of various stochastic S-system models proposed has been performed on GRNs of different sizes: both synthetic and real-life networks. For synthetic networks, we have considered two network sizes and for real life networks we again consider two networks: IRMA network in yeast and SOS DNA repair network in E. coli. First, we generate expression profiles using the newly proposed stochastic S-system model for the well-studied 5-gene and 20-gene networks (Kikuchi et al. 2003; Noman 2007). Then, the two synthetic networks and two other real-life GRNs are inferred with the proposed SSS model.

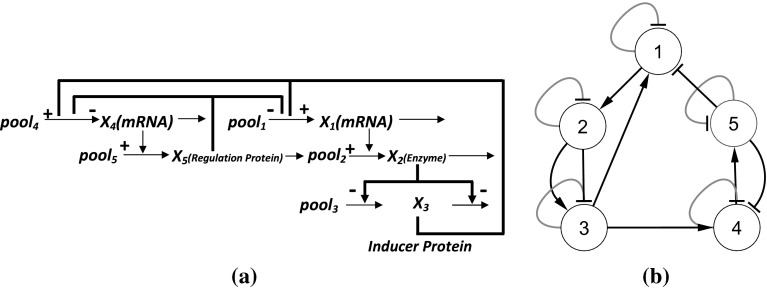
For our experiments, we consider a 5-gene synthetic network, first used by Kikuchi et al. (2003) and commonly employed for many S-system model based reverse engineering of GRNs. The schematic diagram is shown in Fig. 3a. Based on the network Fig. 3a, Kikuchi et al. designed a GRN with 13 regulations, shown in Fig. 3b, with the corresponding S-system parameters of Table 1. According to Kikuchi et al. (2003), this is a typical regulatory system with gene interaction centering on two genes (genes 1 and 4). $X_1$ is the mRNA produced from gene 1, $X_2$ is an enzyme protein gene 2 produces, and $X_3$ is an inducer protein catalyzed by $X_2$. $X_4$ is an mRNA produced from gene 4 and $X_5$ is a regulator protein produced by gene 5. Positive feedback from the inducer protein $X_3$ and negative feedback from the regulator protein $X_5$ are assumed in the mRNA production processes of genes 1 and 4. This model has been developed to analyze the interaction of regulator and effector genes.

Fig. 3.

a A GRN of 5 genes. b Corresponding graphical representation of the GRN (black and grey colored regulations represent interactions in production phase and degradation phase, respectively, arrow and block ended regulations represent activation and supression, respectively)

Table 1.

S-system parameters for 5-gene synthetic network

i	${\mathit{\alpha }}_i$	$g_{i,1}$	$g_{i,2}$	$g_{i,3}$	$g_{i,4}$	$g_{i,5}$	${\mathit{\beta }}_i$	$h_{i,1}$	$h_{i,2}$	$h_{i,3}$	$h_{i,4}$	$h_{i,5}$
1	5.00	0.00	0.00	1.00	0.00	−1.00	10.00	2.00	0.00	0.00	0.00	0.00
2	10.00	2.00	0.00	0.00	0.00	0.00	10.00	0.00	2.00	0.00	0.00	0.00
3	10.00	0.00	−1.00	0.00	0.00	0.00	10.00	0.00	−1.00	2.00	0.00	0.00
4	8.00	0.00	0.00	2.00	0.00	−1.00	10.00	0.00	0.00	0.00	2.00	0.00
5	10.00	0.00	0.00	0.00	2.00	0.00	10.00	0.00	0.00	0.00	0.00	2.00

From the S-system parameters of the network (Table 1), we generated ten datasets from ten random initial conditions using deterministic S-system model [i.e., DSS or Eq. (2)] and proposed Stochastic S-system models (SSS) of various types of noises [Eqs. (6), (8)–(12)]. In addition, we have analyzed the effect of noise terms in the expression profiles for different levels of noise strengths (i.e., $\mathit{\mu }=10,15,20$). The expression profiles for a randomly selected gene (gene-1) of single data set for all three noise strength values are shown in Fig. 4. While analyzing the effect of various noises, we observe that effects of additive noise in the expression profiles are very small for any noise strength. On the other hand, an abrupt effect in expression profiles is observed for multiplicative noise in degradation, while significant regular changes are observed for the Langevin noise in production. The remaining noise types cause irregular changes in the expression profiles. Furthermore, we note that their expression profiles exhibit little or no variation and remain close to the original values for $\mathit{\mu }=10$, whereas massive fluctuations are noted for $\mathit{\mu }=20$. Thus, the parameter for noise strength is set to 15 (i.e., $\mathit{\mu }=15$) in all the experiments.

Fig. 4.

Expression profiles of gene-1 for different noise strenght values a $\mathit{\mu }$ = 10, b $\mathit{\mu }$ = 15 and c $\mathit{\mu }$ = 20

For inferring a network from microarray time-series data, our previously proposed REGARD (Reverse Engineering GRN with Adaptive Regulatory Genes’ Cardinality) method (Chowdhury et al. 2012) is used for learning the parameters of the stochastic model, i.e., SSS. The start and end point of noise window is implemented from 3rd till 6th time-stamp for all experiments. The noise matrix is initialized prior to the inference using zero mean unit variance Gaussian white noise.

5-Gene synthetic network

As mentioned earlier, for the 5-gene network, we used the expression profiles generated using the proposed stochastic S-system model with multiplicative noise in production [Eq. (10)]. However, for validation all the proposed stochastic models are applied separately to the data. The sensitivity-specificity plots are shown in Fig. 5a in terms of ROC plots. Since the data is generated with ${\text{SSS}}^{\mathrm{mT}}$ model, inference with ${\text{SSS}}^{\mathrm{mT}}$ model exhibits the best performance among all models, other than ${\text{SSS}}^{\mathrm{mT}+\mathrm{LD}}$. The proposed stochastic model ${\text{SSS}}^{\mathrm{mT}+\mathrm{LD}}$ is also robust and able to cope with the data generated with a different model (i.e., ${\text{SSS}}^{\mathrm{mT}}$). Further, we observe that the precision and F-score for ${\text{SSS}}^{\mathrm{mT}+\mathrm{LD}}$ and ${\text{SSS}}^{\mathrm{mT}}$ are best among all SSS models. Figure 6 shows the plot of absolute error between two rate constant values (i.e., $\mathit{\alpha }$ and $\mathit{\beta }$) calculated using the equation $|R{c}_{T,i}-R{c}_{I,i}|$, where $R{c}_{T,i}$/ $R{c}_{I,i}$ indicate the ith rate constant in target network and inferred network, respectively. Furthermore, average error is calculated as follows:

$$\begin{array}{c}\hfill AE=\frac{1}{|Params|}\sum _{i=1}^{|Params|}|d_{T,i}-d_{I,i}|\end{array}$$ 15

Here, $d_{T,i}$/ $d_{I,i}$ are the ith parameter values for Target/ Inferred network, |Params| indicates the total number of parameter of a particular category. For example, while calculating the average error for rate constant values, $|Params|=2\times N$, for kinetic orders values $|Params|=2\times N\times N$, and $|Params|=2\times N(N+1)$ while all S-system parameters are considered. A comparison of errors for inferring model parameters between deterministic S-system model and proposed SSS${}^{mT+LD}$, shown in Fig. 6, clearly indicates the superiority of the proposed stochastic modeling over the deterministic models.

Fig. 5.

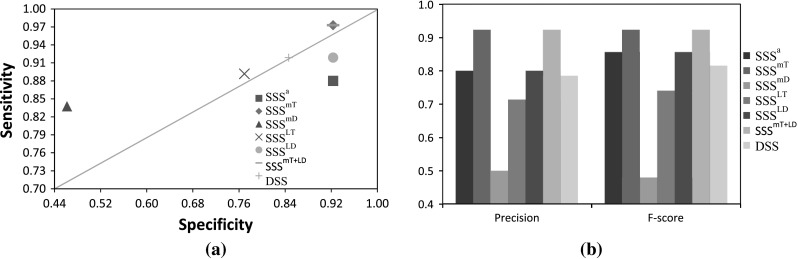
a ROC points. b Precision and F-score for the proposed stochastic models and existing DSS

Fig. 6.

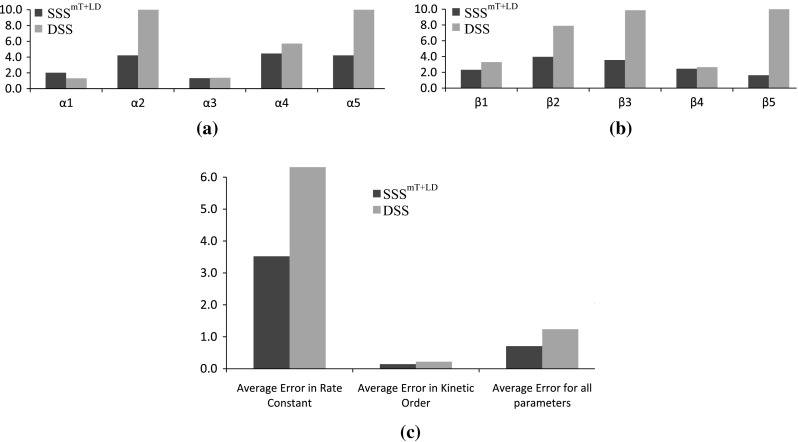
Error for a $\mathit{\alpha }$ values, b $\mathit{\beta }$ values and c average errors calculated for inferred parameters with ${\text{SSS}}^{\mathrm{mT}+\mathrm{LD}}$

Finally, the error between inferred and target expression profile in Fig. 7 shows that the magnitude of the error bars to be very small indicating near-overlap of the two expression profiles. The performance of the proposed ${\text{SSS}}^{\mathrm{mT}+\mathrm{LD}}$ is on a par with the ${\text{SSS}}^{\mathrm{mT}}$ model while inferring the 5-gene network and robust enough to withstand the presence of noise in the expression profiles generated by ${\text{SSS}}^{\mathrm{mT}}$ model.

Fig. 7.

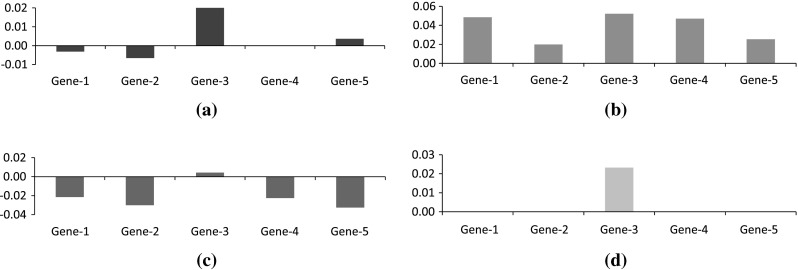
Error at various time-stamps. a Error at t = 3. b Error at t = 5. c Error at t = 8. d Error at t = 10

20-Gene network

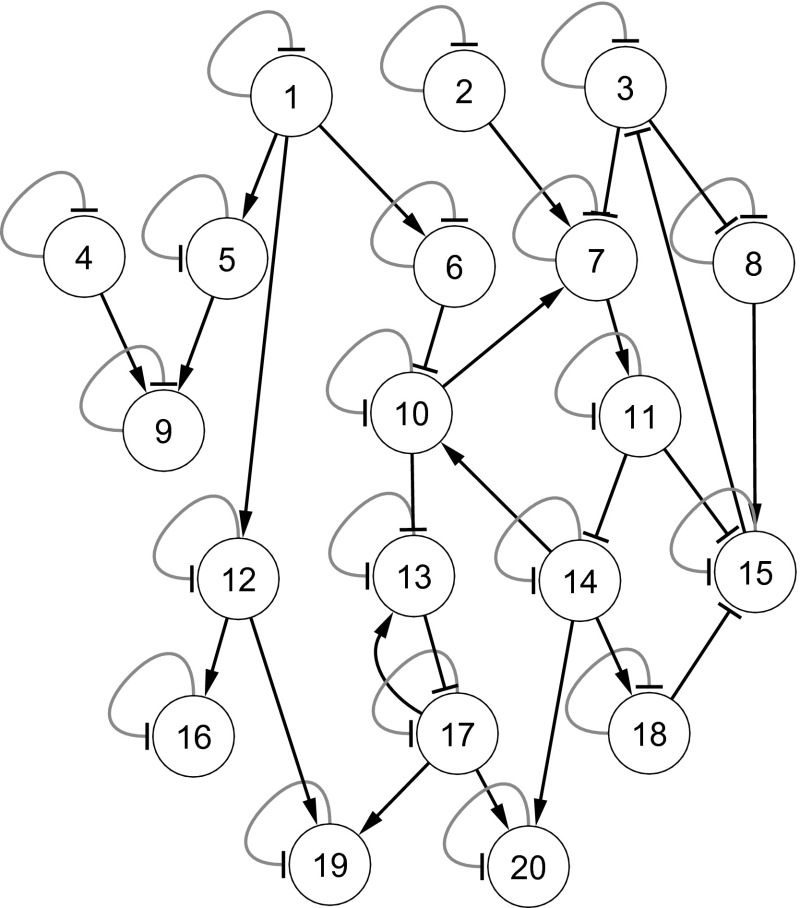
The effectiveness of the proposed stochastic model is further evaluated with a 20-gene synthetic network. This 20-gene network, shown in Fig. 8, is a as medium-scale network and has been frequently used to test model performance (Chowdhury et al. 2012, 2013b; Noman 2007). For this network, we again generate ten data sets from ten different initial conditions using ${\text{SSS}}^{\mathrm{mT}}$ [Eq. (10)]. The evaluation of ${\text{SSS}}^{\mathrm{mT}+\mathrm{LD}}$ for inferring the 20-gene network, using the existing REGARD (Chowdhury et al. 2012), is shown in Table 2, and indicates that the proposed method with ${\text{SSS}}^{\mathrm{mT}+\mathrm{LD}}$ is successful in inferring more regulations and non-regulations than the deterministic S-system model. The absolute errors with target expression profiles for proposed and existing methods are shown in Fig. 9 for three randomly selected genes. We observe that, although the errors for the proposed ${\text{SSS}}^{\mathrm{mT}+\mathrm{LD}}$ are a little higher in the early stages of introducing noise at $t_3$, the errors for the proposed method are much smaller compared with the traditional model in the later time-stamp. This indicates that ${\text{SSS}}^{\mathrm{mT}+\mathrm{LD}}$ has the ability to rapidly adjust with the noise during the optimization process.

Fig. 8.

20-Gene network adapted from Noman (2007). Arrow and block ended arcs represent activation and suppression, respectively. Black and grey colored arcs indicate instantaneous activation/supression in production and degradation phases, respectively

Table 2.

Evaluation of ${\text{SSS}}^{\mathrm{mT}+\mathrm{LD}}$ for inferring 20-gene network

Method	$S_n$	$S_p$	$P_r$	$F\text{-}score$
${\text{SSS}}^{\mathrm{mT}+\mathrm{LD}}$	0.53	0.94	0.39	0.45
DSS	0.29	0.95	0.47	0.36

Fig. 9.

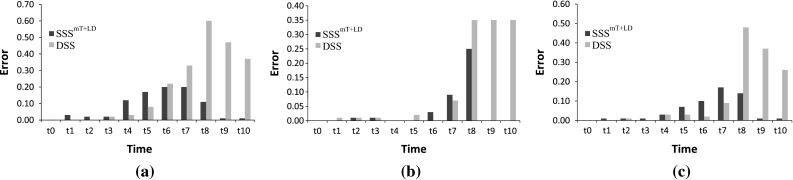
Error at different time-stamps for three randomly selected genes. a Error for gene 5. b Error for gene 16. c Error for gene 19

IRMA network in yeast

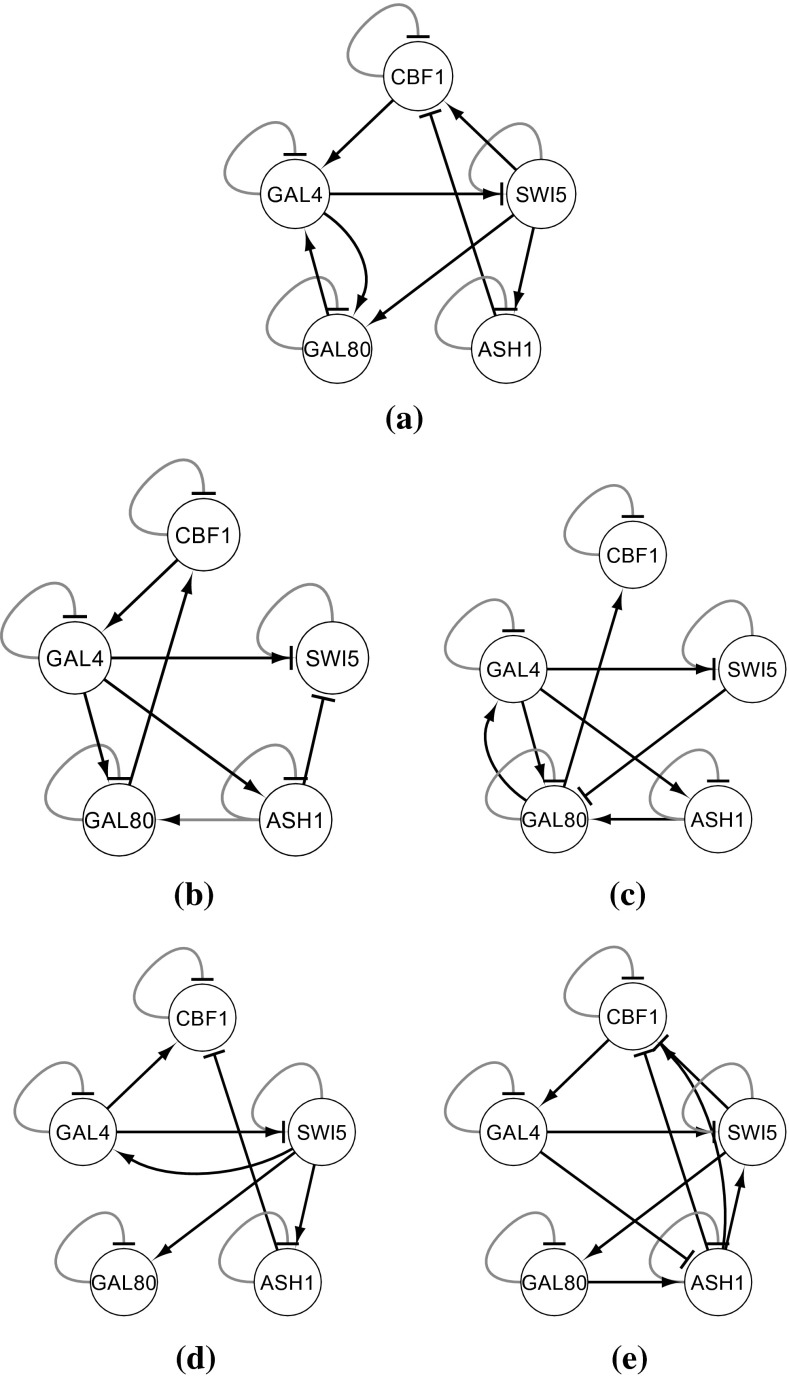
The proposed stochastic S-system model is next applied to a real-life biological data of Saccharomyces cerevisiae (yeast) called IRMA (Cantone et al. 2009). This is a 5-gene network with the genes CBF1, GAL4, SWI5, GAL80, ASH1, regulating each other. Cantone et al. (2009) provided two sets of gene expression profiles, namely Switch ON and Switch OFF data having 16 and 21 time series data points, respectively. The ON dataset corresponds to the shifting of the growth medium from glucose to galactose, while the OFF data set corresponds to shifting from galactose to glucose. In addition to the true 8 regulations, we also consider N (=5) self-regulations as true positives (Chowdhury et al. 2012, 2013a). Figure 10 shows the ratget IRMA network (Cantone et al. 2009) and also the networks inferred by the proposed SSS${}^{\text{mT+LD}}$ and current deterministic S-system model. Although the true network is not inferred by the the proposed method, the number of inferred true regulations and non-regulations are more than the existing model (Chowdhury et al. 2012). Further, the errors for the proposed method are found to be generally lower than the existing methods, as shown in Figs. 11 and 12.

Fig. 10.

IRMA network a Target, b inferred with proposed ${\text{SSS}}^{\mathrm{mT}+\mathrm{LD}}$ from ON data set, c inferred with DSS from ON data set, d inferred with proposed ${\text{SSS}}^{\mathrm{mT}+\mathrm{LD}}$ from OFF data set, e inferred with DSS from OFF data set. Arrow ended black lines and block ended grey lines indicate instantaneous activation and suppression, respectively

Fig. 11.

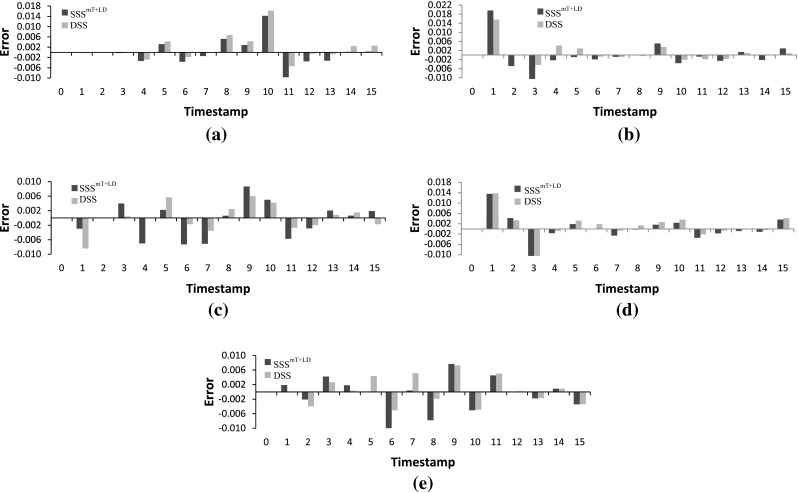
Error at different time-stamps in IRMA ON dataset

Fig. 12.

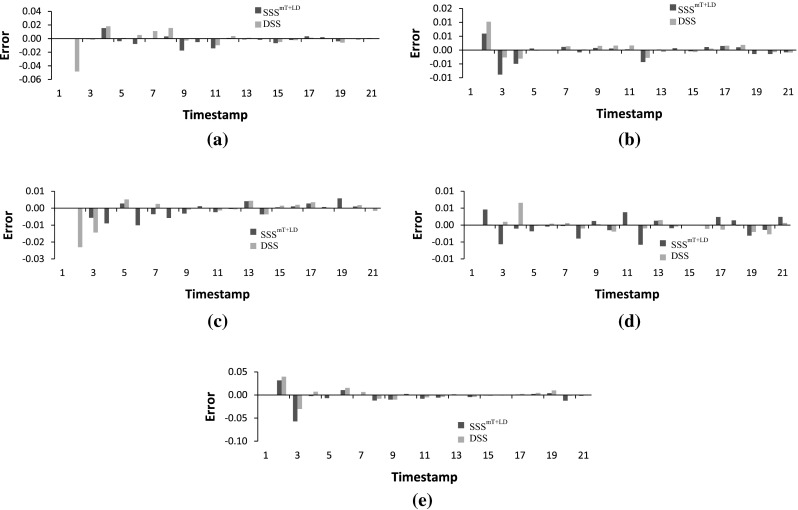
Error at different time-stamps in IRMA OFF dataset

SOS DNA repair network in Escherichia coli

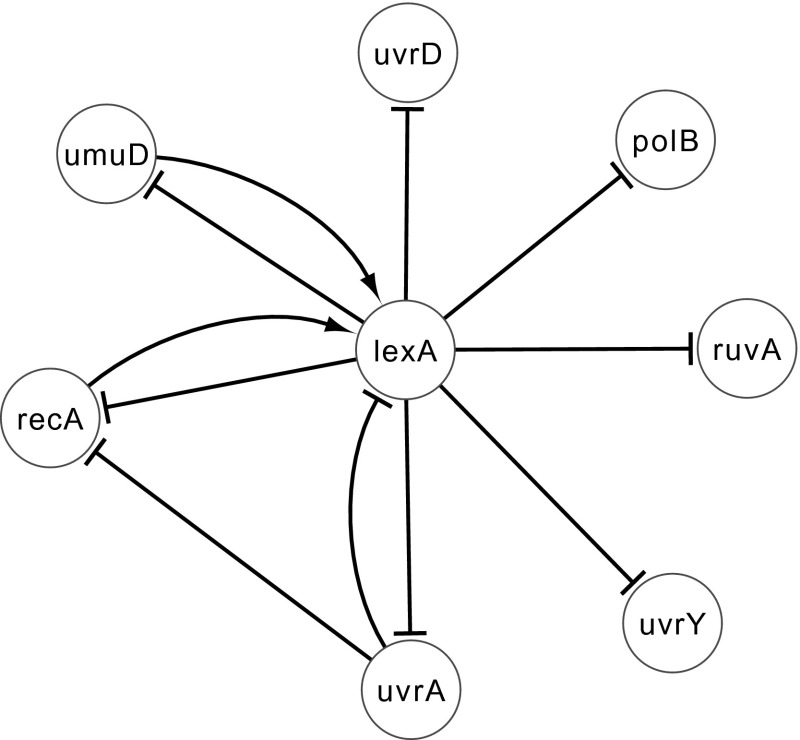
Next, we consider the well-studied SOS DNA repair network within Escherichiacoli (E. coli). While the entire DNA repair system of E. coli involves more than 100 genes (Perrin et al. 2003), only 30 of its genes contribute towards key regulations at the transcription level. We use the expression data set from Ronen et al. (2002), which contains information about eight genes, namely uvrD, lexA, umuD, recA, uvrA, uvrY, ruvA, and polB. The data sets are obtained from four different experiments under various UV light conditions, with the gene expression levels being measured at 50 instants evenly spaced at 6-min interval. Following Noman (2007), we normalize the input data by dividing the expression profile of each gene by its maximum value.

We calculate the four performance metrics, i.e., sensitivity, specificity, precision and F-score, according to (1) the functional description of each gene in the original paper (Ronen et al. 2002) and (2) the novel regulations inferred by Perrin et al. (2003). Based on the two above criteria, we reconstruct the target network for SOS DNA repair network as shown in E. coli in Fig. 13. The evaluation of the proposed ${\text{SSS}}^{\mathrm{mT}+\mathrm{LD}}$ and existing deterministic S-system modeling approach is shown in Table 3. We observe that in all the four performance metrics, the proposed ${\text{SSS}}^{\mathrm{mT}+\mathrm{LD}}$ outperformed the existing method. Since, the expression data contains noise, the experimental result is the successful application of the stochastic modeling approach over the deterministic model.

Fig. 13.

Target SOS network

Table 3.

Evaluation of ${\text{SSS}}^{\mathrm{mT}+\mathrm{LD}}$ for inferring E. coli network

Method	$S_n$	$S_p$	$P_r$	$F\text{-}score$
${\text{SSS}}^{\mathrm{mT}+\mathrm{LD}}$	0.40	0.95	0.62	0.43
DSS	0.25	0.93	0.50	0.33

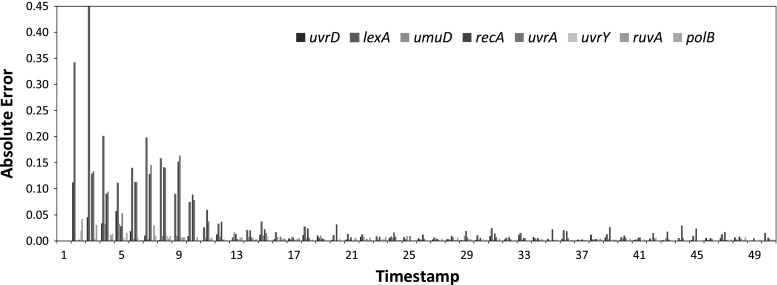
We also show the absolute error in all the time-stamps with all the eight genes for a single data set in Fig. 14. The bar graph indicates that, despite slightly higher errors in the early stages of the expression profiles, the magnitude of errors reduces and are near-zero in the subsequent time-stamps. This error bars shows the ability of the proposed stochastic S-system model to adapt for inferring real-life gene regulatory network.

Fig. 14.

Error at different time-stamps in SOS dataset

Conclusion

Noise is an inherent characteristics of all biological networks. S-system modeling is specially tailored to model biological process. While there have been efforts to incorporate stochastic terms in GRN models, the S-system model in its current form is unable to include stochasticity. In this paper, we have developed a stochastic S-system modeling approach to cope with the inherent noise present in the microarray data. In order to identify the most suitable stochastic model, we have tested the performance of the stochastic S-system (SSS) model with various types of noise including hybrid noise factors. Experimental results show that the proposed SSS is effective in reconstructing the expressions profiles as well as inferring higher number of regulations than deterministic modeling. Currently, studies are being performed to extend and evaluate the technique to large scale real-life GRNs.