Dynamic viscoelastic models of human skin using optical elastography

Abstract

A novel technique for measuring in vivo human skin viscoelastic properties using optical elastography has been developed. The technique uses geometrically focused surface (GFS) waves that allow for wide bandwidth measurements of the wave field. An analytical solution for the case of a radiating annular disk surface source was fit to experimentally measured GFS waves, enabling an estimate of the frequency-dependent surface wavenumber, which can then be related to the dynamic shear modulus. Several viscoelastic models were then fit to the dynamic shear modulus dispersion curve. Viscoelastic models were evaluated based on their overall quality of fit and variability amongst healthy volunteers. An Ecoflex phantom was used to validate the procedure and results by comparison to similar studies using the same type of phantom. For skin results, it was found that the “α” parameters from the fractional models had the least variability, with coefficients of variability of 0.15, and 0.16. The best fitting models were the standard linear solid, and the fractional Voigt, with a mean fit correlation coefficient, R², of 0.93, 0.89, respectively. This study has demonstrated the efficacy of this new method, and with larger studies the viscoelastic skin models could be used to identify various skin diseases and their response to treatment.

1. Introduction

Viscoelastic properties of human skin are affected by disease and injury; measurement of these properties can be used as a diagnostic aid for detection and monitoring of conditions that affect the epidermis and dermis. For example, Raynaud's phenomena and scleroderma have been shown to increase shear elasticity and shear viscosity [1, 2] as well as affect the thickness of skin [3]. However, skin viscoelastic properties are also affected by ambient temperature, humidity, moisture content [4, 5], thickness, age [6–8], sex, and the direction of applied stress [9]. These confounders have limited the utility of viscoelasticity measurements.

Early measurement methods relied mainly on excised strips of skin and tensometer equipment [6]. These tests were accurate and could be performed alongside histological analysis to correlate the stress-strain relationship with changes in molecular structure. However, this was too invasive to be used as a diagnostic tool for skin disorders. Advances in more sensitive measuring equipment led to in vivo measurements of shear strain hysteresis curves [4]. Up to this point, the majority of the studies were based on static methods until [5] studied the dynamic viscoelastic properties of skin, over a frequency range of near zero to 1000 Hz, using propagating surface waves. It was found that the viscoelastic properties were dispersive (and therefore frequency-dependent). A similar study also found comparable results; using surface wave propagation, a direct measurement of the complex Young's modulus of excised rabbit skin was made [10]. Even though it has been determined that skin is viscoelastic, static methods, such as the suction method or indentation method, have proven reliable and practical for clinical use [11–14]; however, they cannot measure the frequency dependence or viscous behavior.

Focusing on the dynamic response of skin, elastography techniques have been developed that use surface waves as the source for elastography imaging. Elastography uses the principle that the wavelength and attenuation of a propagating mechanical wave is dependent on the mechanical properties. Using this principle, several imaging modalities have been used to derive the Young's modulus or shear modulus. Ultrasound shear wave elastography was used in [15], having the advantage of subsurface imaging of the skin, but was only able to acquire a single frequency per scan. Optical shear wave coherence elastography (OCE) has been used to measure skin viscoelasticity [16], and excised animal tissue [17]. OCE has the advantages of micrometer scale resolution, and 3-D imaging capabilities that penetrate the surface; however, only the real part of the complex Young's modulus is measured. Optical surface wave elastography (OE), the technique employed in this paper, uses a LASER Doppler vibrometer (LDV) to measure the surface displacement using the Doppler effect [18, 19]. OE has the advantage of high SNR due to the sensitivity of LASER probes, but it cannot penetrate the surface. Also, current OE methods for skin use outward propagating, point source, surface waves which suffer significantly from attenuation.

All of the previous studies mentioned have been successful in measuring the viscoelastic properties of skin; yet, the standard deviations are large and with the plethora of measured parameters (i.e. wave speed, Young's modulus, shear modulus, distention, relaxation, etc.) it is not straight forward to compare results that often require an estimate of Poisson's ratio, which can lead to erroneous results. There is a clear need for a less variable, repeatable, and comparable viscoelastic model or parameter value of human skin for better diagnostic accuracy.

This study will assess a novel measurement method using optical elastography to image surface wave propagation over a large bandwidth of frequencies. By measuring large bandwidth data, viscoelastic models can be fit to shear modulus dispersion curves for detailed analysis. To accomplish this, an annular mechanical radiator has been developed that creates geometrically focused surface (GFS) waves, similar to [15, 20]. GFS waves are surface waves that converge in a cylindrical manner to a focal point. This has the advantage of decreased attenuation and allows for a larger bandwidth than point or line sources. The major drawback of using OE is the inability to probe below the surface. The amplitude and phase of the surface waves are measured using a scanning LASER Doppler vibrometer (SLDV), which produces a spatial profile curve of the actual surface wave. The wave profile can then be fit to a frequency response function to estimate the complex shear modulus. A wideband frequency spectrum of the complex shear modulus can then be fit to various viscoelastic models for detailed analysis.

2. Theory

The theoretical background used to obtain the solution of an annular radiating surface source will be briefly described followed by a description of the viscoelastic models used. In the following, the skin is assumed to be a homogenous isotropic semi-infinite viscoelastic half-space; as a consequence, the surface waves measured are assumed to represent a weighted average of the material properties of the skin including all of the internal layers. Displacements are small enough, on the order of μm, so that linear system theory is valid. Particle motion of the continuum is governed by Navier's equations in the absence of body forces

$$(\lambda +\mu )\nabla \nabla \cdot \mathbf{u}+\mu {\nabla }^2\mathbf{u}=\rho \frac{{\partial }^2\mathbf{u}}{\partial t^2}.$$ (1)

For a complete derivation of equation (1) refer to [21]. Definitions: u is the displacement vector, ρ is the density of the medium, ∂/∂t denotes a derivative with respect to time, ▽ is the spatial Laplacian operator dependent upon the chosen coordinate system, and λ and μ are the Lame parameters. The Lame parameters are rate dependent and complex, where λ represents volume viscoelastic coefficient and μ is the shear viscoelastic coefficient. There are two wave types in equation (1), compression and shear waves. The waves propagate independently of each other. Taking the divergence of both sides of equation (1) yields

$${\nabla }^2(\nabla \cdot \mathbf{u})=\frac{1}{c_1^2}\frac{{\partial }^2(\nabla \cdot \mathbf{u})}{\partial t^2}\mathit{with}{c}_1=\sqrt{\frac{(\lambda +2\mu )}{\rho }}$$ (2)

where c₁ is the compression wave speed. Similarly, taking the curl of both sides of equation (1) yields

$${\nabla }^2(\nabla \times \mathbf{u})=\frac{1}{c_2^2}\frac{{\partial }^2(\nabla \times \mathbf{u})}{\partial t^2}\mathit{with}{c}_2=\sqrt{\frac{\mu }{\rho }}$$ (3)

where c₂ is the shear wave speed. For this study it is more convenient to express the wave speeds as the wave numbers

$$k_1=\omega \sqrt{\frac{\rho }{\lambda +2\mu }}\mathit{and}{k}_2=\omega \sqrt{\frac{\rho }{\mu }}$$ (4)

where k₁ and k₂ are the complex compression and shear wave numbers respectively. Using the zero stress boundary condition on the free surface, at z = 0 (see Figure 1), the solutions to the equations of motion for a half-space yield the following relation between the surface wave number and shear wave number

$$p^3-8p^2+\left(24-16\left(\frac{1-2\nu }{2(1-\nu )}\right)\right)p-16\left(1-\left(\frac{1-2\nu }{2(1-\nu )}\right)\right),$$ (5)

where p = (k₂/k_su)² (see [21] page 325 for complete derivation). The surface wave number k_su, can be related to k₂ by finding the roots of equation (5). Of the three roots of equation (5), only the real roots and solutions that satisfy the condition k₂/k_su > 1 are valid, leaving only one solution. For this study ν = 0.495 yields k₂/k_su = 0.954.

Figure 1.

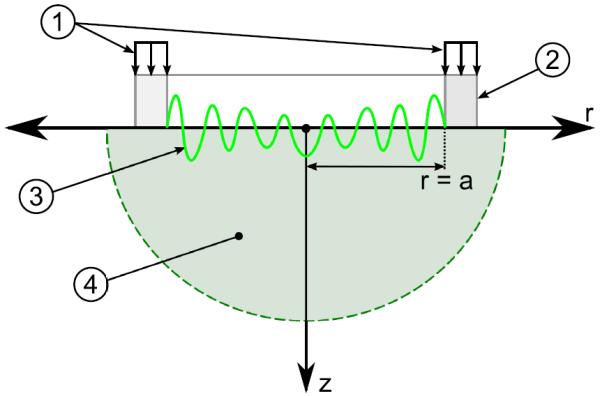
Schematic section view of the annular radiating surface source theoretical problem with coordinate frame; symmetry is about the line r = 0. 1) Applied periodic stress P = P₀exp[jωt]. 2) Annular actuator end piece with radius “a”. 3) Example of a typical GFS wave curve produced from source. 4) Semi-Infinite medium with free surface at z = 0.

The surface source problem in Figure 1 is analogous to a known solution of a finite circular disk of radius “a” oscillating on a half-space first solved by [22]. A more exact solution was found by [23]. However this solution was a bit cumbersome so a more compact form of the solution was found in [24] and is referred to as the frequency response function (FRF) of the surface wave motion at r with respect to the surface wave motion and given by

$$\mathit{FRF}=\frac{u_z\left(r\right)}{u_z\left(a\right)}=\frac{K_0\left(jr{k}_{\mathit{su}}\right)}{K_0\left(ja{k}_{\mathit{su}}\right)}.$$ (6)

Here, K₀ is the modified Bessel function of the second kind, and $j=\sqrt{-1}$. This expression satisfies the governing wave equation and the nonhomogeneous boundary condition imposed by the circular disk of radius “a”. As equation (6) denotes radially outward bound surface waves, radially inward bound surface waves can be defined by replacing the modified Bessel function of the second kind, K₀, which asymptotically approaches zero as the argument increases, with the complementary modified Bessel function of the first kind, I₀, which asymptotically approaches a finite value as the argument approaches zero.

$$\mathit{FRF}=\frac{u_z\left(r\right)}{u_z\left(a\right)}=\frac{I_0\left(jr{k}_{\mathit{su}}\right)}{I_0\left(ja{k}_{\mathit{su}}\right)}$$ (7)

This satisfies the new nonhomogenous boundary condition imposed by the new surface source, the annular ring of inner radius “a”. Equation (7) will be used as the objective function to fit to the experimental data.

Surface waves are known to travel below the surface, as well, with the penetration depth being a function of surface wave wavelength [21]. For this study, it is expected that the surface wave wavelengths will fall in the range of 2 – 30 mm. The low frequency waves will correspond to the larger wavelengths and will penetrate all skin layers, and beyond, even to the subcutaneous fat and muscle, while the high frequency waves will only affect the epidermis layer. Currently, there is no known theory of how each layer will affect the wavelength and attenuation of the surface wave at the surface itself. Since model identification of healthy human skin measured at the surface is the goal of this paper, the interactions between the layers of skin are neglected and only the skin as a whole is modeled.

Several types of viscoelastic models are used to estimate material parameters with up to 3 parameters; see Figure 2. Each of these models, shown in Table 1, represent the dynamic shear modulus μ. The fractional models – spring-pot and fractional Voigt – represent models derived from fractional derivatives and the α parameter represents the fraction of viscosity, 0 being purely elastic and 1 being a viscous fluid.

Figure 2.

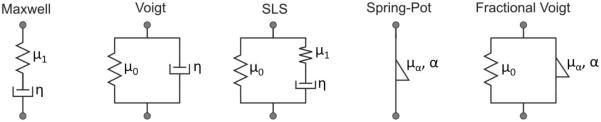
Viscoelastic models shown in their mechanical analogy form using spring, dampers, and spring-pot symbols. SLS (standard linear solid).

Table 1.

Viscoelastic model parameters in the frequency domain representing the dynamic shear modulus separated into real and imaginary parts; also referred to as the storage modulus and the loss modulus, respectively.

Viscoelastic Model	Storage Modulus μR	Loss Modulus μI
Maxwell	$\frac{{\omega }^2{\eta }^2{\mu }_0}{{\mu }_0^2+{\omega }^2{\eta }^2}$	$\frac{\omega \eta {\mu }_0^2}{{\mu }_0^2+{\omega }^2{\eta }^2}$
Voigt	μ 0	ω η
SLS	$\frac{{\mu }_0{\mu }_1^2+{\omega }^2{\eta }^2({\mu }_0+{\mu }_1)}{{\mu }_1^2+{\omega }^2{\eta }^2}$	$\frac{\omega \eta {\mu }_1^2}{{\mu }_1^2+{\omega }^2{\eta }^2}$
Spring-Pot	${\mu }_{\alpha }{\omega }^{\alpha }\cos \left(\frac{\pi }{2}\alpha \right)$	${\mu }_{\alpha }{\omega }^{\alpha }\sin \left(\frac{\pi }{2}\alpha \right)$
Fractional Voigt	${\mu }_0+{\mu }_{\alpha }{\omega }^{\alpha }\cos \left(\frac{\pi }{2}\alpha \right)$	${\mu }_{\alpha }{\omega }^{\alpha }\sin \left(\frac{\pi }{2}\alpha \right)$

3. Methods

3.1. Apparatus

Mechanical wave motion was induced using a custom designed ring (annular disk) actuator shown in Figure 3. Three preloaded piezos (P-840.1, Physik Instrumente GmbH & Co., Karlsruhe Germany) were arrayed in 120° increments around the outside of the ring, allowing for an even distribution of displacement and clear line of sight for the LASER. The largest usable diameter ring is 62 mm and smaller sized rings could be nested concentrically within the larger ring as desired. For this study only 2 ring sizes were used: 62 mm for the Ecoflex sample, and 25.4 mm for the human subjects. The annular actuator sub assembly was then attached to a box frame composed of 6061 Al, which provided the fixed based.

Figure 3.

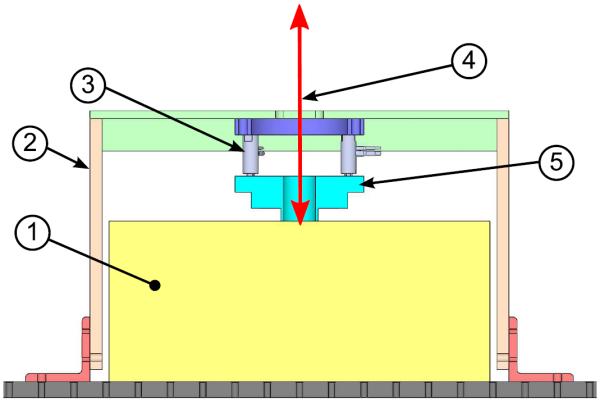
Schematic section view of the experimental setup. 1) Location of where the Ecoflex sample or human forearm is placed, rectangle represents a simple section view of an Ecoflex sample. 2) Al 6061 box frame. 3) Three preloaded piezos. 4) SLDV LASER. 5) Annular mechanical radiator. Not shown is the SLDV head located approximately 300 mm above the sample surface and the third piezo.

Early preliminary tests of the experiment revealed that approximately one wavelength should be visible inside the actuator ring for quality estimates of the shear modulus, otherwise the fitting algorithm, described later, suffers from too many possible solutions. Therefore, separate ring sizes had to be used for the phantom and human experiments to meet the requirement, as the phantom used is stiffer (longer wavelengths at the same frequency) than human skin. The scale of the apparatus in no way affects the wave pattern.

Measurement of vibrations were performed using a scanning LASER Doppler vibrometer (SLDV) (PSV-400, Polytec Inc., Hopkinton, MA) with a visible light heliumneon LASER of 632.8 nm wavelength. The PSV-A-410 close up lens was used together with the #2 diopter which resulted in a maximum field of view of 70 mm × 55 mm and a spot size of 40 μm. The SLDV uses the Doppler principle to determine surface velocity of a point in the Z-direction; see coordinate frame in Figure 1. Software and control hardware was included with the PSV-400 system, which processed the FFT on the recorded time signal. Periodic chirp waveforms with a frequency range of 100-1000 Hz were generated using the internal PSV-400 signal generator. Surface wave displacement ranged from 50–300 nm across the entire frequency spectrum.

3.2. Ecoflex sample

An Ecoflex phantom sample (ECOFLEX-0010, Smooth-On, Inc., Easton, Pennsylvania) was used to validate the method as it can be directly compared to similar studies [20, 24, 25]. A homogenous sample 140 mm in diameter and 20 mm thickness was used. Preparation of the sample comprised multiple steps. Parts A and B were mixed at a 1:1 ratio, then placed in a vacuum chamber to pull all the air bubbles out of the mixture. Removing the air bubbles took approximately 15 min at 51 cmHg. The bubble free mixture was then poured into the mold and allowed to cure for 24 hr. The mold required use of mold release agent (Ease Release 200, Smooth-On, Inc., Easton, Pennsylvania) which was allowed to dry for 20 min before pouring of the mold.

3.3. Procedure

All scans consisted of a single line of points across the diameter of the sample inside of the ring shown in Figure 3. Specifications of each scan can be seen in Table 2. Spatial resolution was chosen so that the smallest estimated wavelength, using test scans and results from [20], would have at least 10 points and thereby ensuring the Nyquist criterion was not violated. The phantom study consisted of 1 sample measured in 6 trials. The sample was positioned under the ring actuator with a slight amount of preload (approximately 1–2 mm indentation) to ensure the sample was fully seated against the actuator surface. Ecoflex scans consisted of 6 trials and human scans of 3 trials, with each trial being separated by removing the sample/subject and then replacing it back into position. This was done to allow the subject time to rest after each scan and assess repeatability. Subjects were scanned in a flat area on the volar forearm.

Table 2.

Applicable specifications used in each experiment. Poisson's ratio was chosen based on [16] and chosen to be slightly less than incompressible (0.495). Ecoflex density was based on [25], and Human density was from [5, 15].

Specification	Ecoflex Sample	Human
Field of View	63 mm	25 mm
Spatial Resolution	0.377 mm	0.239* mm
Frequency Range	200–1000 Hz	100-1000 Hz
Frequency Resolution	25 Hz	12.5 Hz
Trials	6	3
Density	1030 kg/m3	1100 kg/m3
Poisson's Ratio	0.495	0.495
Averages	20	3

^*Resolution was slightly smaller for subjects 1,2 and 3 (0.2065 mm for subjects 1, 2 and 0.2153 mm for subject 3).

All testing of human volunteers was done with approval of the University of Illinois at Chicago Institutional Review Board.

3.4. Data post processing

Post processing of the phantom data and skin data was performed in the following manner. First a spatial butterworth bandpass filter was applied to remove waves larger than the actuator diameter and any high frequency noise; cutoffs were 40 mm on the low end and 2 mm on the high end. After application of the spatial filter all trials were run through the curve fitting algorithm to estimate the surface wave number which is related to the shear wave number by equation (5). Lastly, the estimated shear modulus was fit to various viscoelastic models to evaluate their quality of fit and robustness of parameters.

Experimental data was fit to equation (7) using the “Global Optimization” toolbox provided by MATLAB. The algorithm used the same objective function as in the work by [20], and the objective function is given by

$${\mathit{FRF}}_{\mathit{obj}}=X_1{e}^{i{x}_2}\frac{I_0\left(j{X}_3\right(r-X_4\left)\right)}{I_0\left(ja{X}_3\right)}+X_5.$$ (8)

The principal parameter, X₃, in equation (8) is the surface wave number. The other parameters represent the following: X₁ amplitude (required to correct amplitude), X₂ phase (not all measurements were made at exactly zero start phase), X₄ symmetry shift (out of phase piezos could shift the center focal point of the wave pattern), and X₅ zero offset (compensation for reflected compression waves). The curve fitting algorithm in this study used the nonlinear curve fit function, “lsqcurvefit”, with the “levenbergmarquardt” search algorithm, which minimized the error function,

$$\mathit{Error}=\sum _{i=1}^n{\left({\mathit{FRF}}_{\mathit{obj}}\right(X,r_i)-{\mathrm{FRF}}_i)}^2,$$ (9)

with, i, being each data point, and n, the total number of data points. The advantage of this algorithm was the ability to estimate complex parameters, and unbounded parameters. To further increase the accuracy of the curve fit, the Jacobian of the objective function was also manually derived. With 5 complex parameters to estimate, the curve fit was sensitive to local minima. Therefore, 10 random start positions were chosen, and the best fit was decided using the highest coefficient of determination or R². The number of random start points were chosen based on more exhaustive searches which did not yield an improvement in results.

After estimating the shear modulus, viscoelastic models were fit to each trial and the viscoelastic parameters of each trial were then averaged. The algorithm to fit the viscoelastic models was almost identical to the previous step, the only difference being rejection of outliers. Rejection of outliers was critical in the evaluation of the quality of the viscoelastic models, particularly with respect to the R² parameter, because the outliers would cause a bias that lowered R² even though visually the fit was fine. There is no standard way to remove outliers in nonlinear regression. Outliers were deemed to be data points that were 2 standard deviations from the residual error mean of the curve fit. These outliers were rejected and curve fits were rerun a second time again rejecting any outliers. This type of feedback outlier rejection is similar to the method used in [26]. Outlier rejection had the effect of making a more balanced error distribution of R² with only 1 peak near R² of 0.9; see supplementary data online for plot. As expected, outlier rejection had an effect on the model parameter values as well. However, the majority of changes were below 10%; see supplementary data online for plot.

4. Results

4.1. Ecoflex Phantom

Examples of a typical curve fit to equation (8) at 200, 600, and 1000 Hz are given in Figure 4. From this plot it can be seen that as the frequency increases the coefficient of determination decreases in quality of fit. The 200 and 600 Hz plots show the effect of a static offset in the results as the data does not clearly oscillate about zero. This was accounted for in the curve fit equation as a static complex offset (parameter X₅). For the 1000 Hz plot another phenomena that was not accounted for in the curve fit equation can be seen near the source, particularly evident in the real part. The wave near the source, |r| ≥ 15, does not oscillate about zero yet further away, |r| < 15 mm, the oscillation tends back to oscillating about zero.

Figure 4.

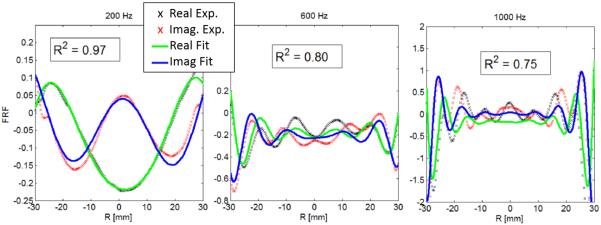
Curve fit of frequency response function to experimental surface wave data. From left to right is 200, 600, and 1000 Hz curve fits from trial 2 Ecoflex data. The coefficient of determination is given inside the box for each plot.

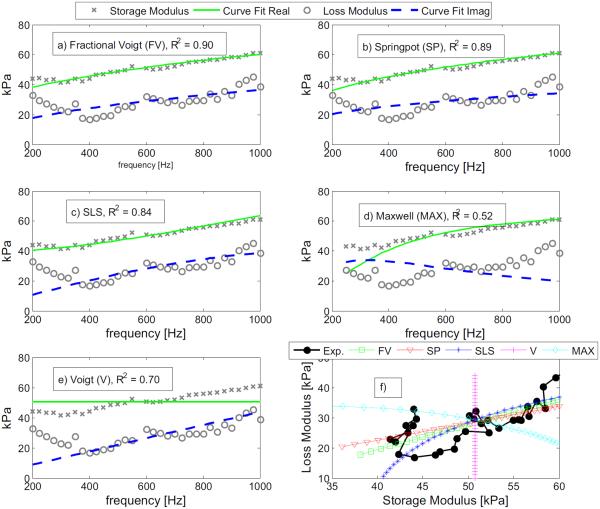
The derived shear modulus was then fit to the five viscoelastic models in Figure 5. From the coefficient of determination and visually, it can be seen that the fractional Voigt model, spring-pot, and SLS models have better fits than the Maxwell and Voigt models. For each model the outlier rejection algorithm rejected different frequencies and can be seen as missing points. However, all models started with the same data points prior to outlier rejection. The shear modulus dispersion curve is close to monotonically increasing starting from 300 Hz for the storage modulus and 400 Hz for the loss modulus. A supplemental plot was added to Figure 5 which shows the relation between the storage and loss modulus. The data, in black solid circles, has a broad linear profile in Figure 5f; this is in contrast to the Voigt and Maxwell models which have constant and curved profiles, respectively.

Figure 5.

Viscoelastic model fits for trial 2 of Ecoflex phantom. Plots a) - e) show the dispersion curve of the real and imaginary components of the estimated complex shear modulus. f) All viscoelastic model curves including the experimental data of the loss modulus vs. the storage modulus.

The mean parameter values ± the standard deviations of the viscoelastic models are given in Table 3. The 2^nd column in Table 3 is the mean R² coefficient used to evaluate mean quality of fit for all 6 trials. The fractional Voigt model and the spring-pot model have identical quality of fits; however, the viscoelastic parameters vary significantly from one another. Indentation testing measured the static shear modulus at 12.5 kPa and is used as a comparison to the accuracy of the μ₀ parameter. Table 4 is used to compare data to literature using the same material type and similar but not identical elastography techniques.

Table 3.

Mean viscoelastic model parameter values for Ecoflex sample. The plus minus error is one standard deviation. Also included is the mean correlation coefficient (R²) for each model. Not all models have the same parameters; spaces are left blank where this occurs.

Viscoelastic Model		Model Parameters
	R 2	μ0 (kPa)	μ1 (kPa)	μα (kPa sα)	η (Pa s)	α
Fractional Voigt	0.93	17.0±5.0		1.33±0.50		0.43±0.04
Spring-Pot	0.93			2.35±1.06		0.26±0.04
SLS	0.90	12.5±6.4	20.0±11.5		3.42±1.65
Maxwell	0.64		22.2±11.0		16.4±7.10
Voigt	0.78	17.8±8.4			2.01±1.08

Table 4.

Comparison of Ecofiex model parameters to literature using models, standard linear solid and fractional Voigt.

	SLS Parameters
Study	μ0 (kPa)	% Error	μ1 (kPa)	% Error	η (Pa s)	% Error
Current	12.5		20		3.42
[20]	13.3*	−6.4	35.3	−76.5	18.1	−429
[24]	13.3*	−6.4	27.5	−37.5	17.8	−420

	Fractional Voigt Parameters
Study	μ0 (kPa)	% Error	μα (kPa sα)	% Error	α	% Error
Current	17.0		1329		0.43
[20]	13.3*	21.8	2038	−53.3	0.33	23.0
[24]	13.3*	21.8	350.8	73.6	0.55	−28.0

^*This parameter was not estimated but experimentally measured using indentation method.

To analyze the variability of each parameter the coefficient of variation was used and is the standard deviation divided by the mean. The two parameter models were compared in Figure 6 left, and three parameter models in Figure 6 right. In both the 3 and 2 parameter models the fractional models (fractional Voigt, spring-pot) had lower coefficients of variations for most parameters then the other models.

Figure 6.

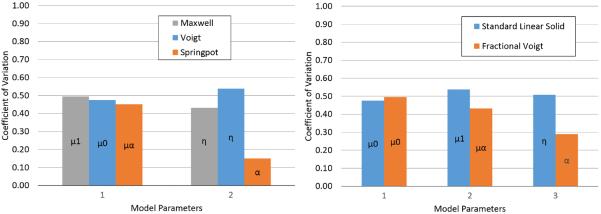
Coefficient of variation of Ecoflex phantom for 2 (left) and 3 (right) parameter viscoelastic models. Parameter name is identified inside the associated bar.

4.2. Human Skin

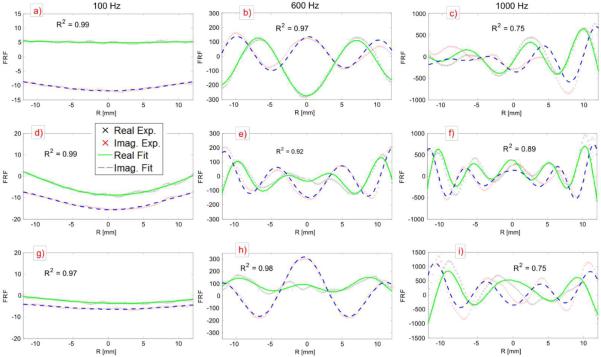
Like in the phantom experiments the human in vivo results first start with the curve fitting of equation (8); typical examples of this complex curve fit can be seen in Figure 7. The uneven oscillation about the zero line is not as evident for the human case as the phantom case. Note that the field of view for the human study is smaller than that of the phantom study; this is due to the large difference in static stiffness of the two materials. Overall, skin is softer than the Ecoflex material, and therefore, needs a smaller field of view to capture multiple wavelengths in a single plot. The softer tissue of skin allowed for a slightly larger bandwidth 100-1000 Hz as compared to 200–1000 Hz for the phantom study. Looking at Figure 7c, it can be seen that there is an error in the symmetry about the R = 0 line of the surface wave. Another item of note from Figure 7 is the R² coefficient decreasing as frequency increases. Comparing the different subjects (along columns Figure 7) it can be visually seen, by wavelength alone, that subjects vary in stiffness at the same frequency.

Figure 7.

Typical curve fits for skin in vivo experiments. The columns represent 3 frequencies of 100, 600, and 1000 Hz respectively and the rows represent subjects. Row 1 subject 1 trial 3 (a–c), row 2 subject 3 trial 3 (d–f), row 3 subject 7 trial 2 (g–i). The y-axis is the FRF amplitude, and the x-axis is the radial coordinate. Inside each plot is the coefficient of determination to assess goodness of fit.

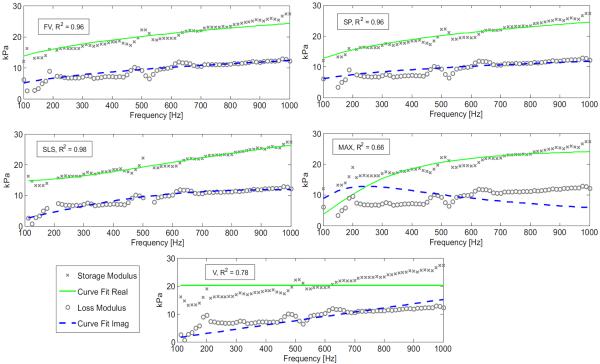
From the typical dispersion curve of the shear modulus in Figure 8, it can be seen that the storage and loss moduli all have a generally monotonically increasing curve. The best fit according to the R² coefficient is the SLS model and the worst fit is the Maxwell model, Table 5. From the Voigt model fit in Figure 8, it can be seen that the assumption of a constant storage modulus does not resemble the dispersion curve shown. Also, for the Maxwell model an estimate of a loss modulus that decreases with frequency does not reflect the measured dispersion curve. The best fit models are then fractional Voigt, spring-pot, and SLS.

Figure 8.

Viscoelastic models fit to complex shear modulus (human skin) of subject 3 trial 3. FV = Fractional Voigt, SP = spring-pot, SLS = Standard Linear Solid, Max = Maxwell, and V = Voigt. The R² coefficient is given in the box next to each models name.

Table 5.

Mean viscoelastic model parameter values for all human volunteers. The plus minus error is one standard deviation. Also included is the mean correlation coefficient (R²) for each model. Not all models have the same parameters, spaces are left blank where this occurs.

Viscoelastic Model		Model Parameters
	R 2	μ0 (kPa)	μ1 (kPa)	μα (kPa sα)	η (Pa s)	α
Fractional Voigt	0.89	6.39±5.76		0.78±0.33		0.38±0.06
Spring-Pot	0.88			2.40±1.22		0.27±0.04
SLS	0.93	12.7±6.8	19.9±10.7		3.54±1.51
Maxwell	0.67		22.6±10.8		16.6±7.84
Voigt	0.71	18.1±8.68			2.02±1.02

For an additional measurement of the variability of models, the coefficient of variation is shown in Figure 9. Only the models with the same number of parameters can be compared to each other. It can be seen from Figure 9 that the fractional Voigt model has parameters that are more stable than the SLS model in 2 out of 3 parameters. For the 2 parameter models, the spring-pot model is more stable in only 1 out of 2 parameters. For both the 2 and 3 parameter models the α parameter has the smallest variation of all.

Figure 9.

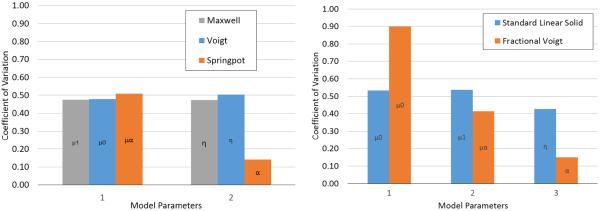
Coefficient of variation of human skin for 2 (left) and 3 (right) parameter viscoelastic models. Parameter name is identified inside the associated bar.

Finally a comparison to the literature is shown in Table 6. Table 6 is not exhaustive; however, it represents the literature using dynamic surface wave excitation and estimation of shear modulus. The only reference that used a model was [18] and it was the Voigt model. All other references examined only a single frequency and can only be compared using the static shear modulus parameter. The ratio range is of the three models listed for the current study. From the ratio range it can be seen that the best comparison is to reference [18]. All the other studies have a much larger estimate of the static shear modulus.

Table 6.

Comparison of only the static parameter or, a single frequency measurement, of the shear modulus of human skin to literature. Only the static parameter could be compared to literature that did not use a model, as μ₀ is the static shear modulus. Reference [16] had a significant number of data points to possibly compare; this particular point was chosen for similarity in measurement site, and comparison to normal skin.

Study	Model Used	Spectrum (Hz)	μ0 (kPa)	Ref : Current*
Current	Fractional Voigt	100-1000	6.39
Current	SLS	100-1000	12.7
Current	Voigt	100-1000	18.1
[15]	None	300	1980	109–310
[16]	None	50	33.8	1.87–5.29
[18]	Voigt	100–400	14.5	0.80–2.27

^*The last column is a comparison of the current study, μ₀, to the listed references for each model used giving a range from least to greatest, comparison is a simple ratio (μ₀ Ref)/(μ₀ Current).

5. Discussion

Diagnosing and monitoring skin diseases using a non-invasive elastography technique, such as the one developed in this paper, requires that a known and consistent model of healthy skin can be found and that the technique itself is repeatable. This study has shown that the proposed method is repeatable and works well enough to warrant further development. A potential repeatable model has been found using the fractional order models. These statements will be addressed by examining the quality of the fits in the phantom and skin results, and then finally looking at the stability of the models as well as comparing them to literature.

It can be seen in the phantom curve fits of Figure 4, that equation (7) can be successfully fit to the experimentally measured GFS wave curve and that the mechanical setup does produce a symmetric GFS wave. However, comparing Figures 4 and 7 it is evident that, overall, human skin was a better fit to the objective function than the Ecoflex phantom. For both the phantom and in vivo experiments as frequency increases quality of fit went down. However, even as the quality of fit decreased, by examining Figures 4 and 7 closely it can be seen that the wavelength is accurately estimated even though attenuation is not. This should not have an affect on the quality of the overall shear modulus estimate; as the storage modulus and the loss modulus are both dependent on the real and imaginary parts of k₂ [27]. There will still be errors associated with the inaccurate measurement of attenuation, but both the storage modulus and the loss modulus will be affected by this.

Many reasons for inaccuracies in the overall quality of fit are from known mechanical issues encountered during the study. Imperfect phase coherence between the 3 piezos led to 2 problems: the loss of symmetry in the wave profile about the r = 0 line, and a slight linear tilt (i.e. Y = rx) of the wave curve. Also, the static indentation of the actuator ring creates a static strain curve not accounted for by the objective function. For this study it was not the intention to measure the impact of these sources of error. However, they can be overcome by improvement to the mechanical setup, such as finding a minimal preload to minimize the static strain curve, and use of a single element ring piezo to remove phase incoherence. Inaccuracies from unknown phenomena could be any or none of the following: wave reflections, compression waves, and layered media. Layered media has been found to affect the Young's modulus in [16]; however, there is to date no predictable relation between penetration depth of surface waves to the wave profile and speed at the surface. Compression waves can be easily accounted for by adding the static component to equation (7) and reflections can be minimized by averages and sample size. All three of the previously stated unknowns would likely have the largest impact on the estimation of the loss modulus from the interference of wave patterns. Finally, other potential unknowns are the possibility of multiple surface waves [28] and complex Poisson's ratio [29, 30].

A viscoelastic model that fit well to the complex shear modulus of skin and has minimal variability between volunteers was a goal of this study. From the results in Figure 8 and Table 5 the model that best meets this goal is the fractional Voigt model or the spring-pot model, both of fractional order. This conclusion is based primarily on the α parameter's, coefficient of variation (0.14 – 0.15) and the model's R² of 0.88 – 0.89. The other parameters (μ₀ and μ_α) in these two models still have a significantly high coefficient of variation 0.48 – 0.90. Reasons for the high variability could be due to changes in hydration levels of the skin [4, 5, 16], or Langer lines as found in [16]. It has also been found by [8] that changes in age can lead to physical changes in the skin.

For validation of these results a comparison to literature would be a preferred method and a small comparison is found in Tables 4 and 6. It is however, particularly difficult to compare a dynamic complex shear modulus as it is dependent on frequency. Also, many studies such as [9, 19, 31] use static methods or time dependence, both of which are not directly comparable to this study. It is then determined in this study that fitting a viscoelastic model to as wide a bandwidth as possible, as in [20, 24], would make comparison between dynamic elastography methods more practical. This is most evident in Table 6 of ref. [18], where comparing even a poor fitting model such as the Voigt model results in a better comparison of viscoelastic properties between studies than just a single frequency. It is then suggested for further studies to make use of large bandwidths and viscoelastic models.

6. Conclusion

Using GFS waves, the complex shear modulus of human skin can be measured over a large bandwidth in a noninvasive manner. It was found that using viscoelastic models provides a reliable and robust method when comparing between different studies. The best viscoelastic model for skin in terms of variability is the fractional Voigt model. However, in terms of best curve fit the model of choice would be the standard linear solid model; but, it is not recommended due to its high variability from subject to subject. Continuation of this technology will include larger studies with more volunteers as well as volunteers with skin disease. Also, to increase model accuracy, investigation into the relationship between surface wavelength and layered material will be conducted.