Geometry and mechanics of two-dimensional defects in amorphous materials

Significance

Modeling defects, or localized strain carriers, are a central challenge in the formulation of elasto-plastic theory of amorphous solids. Whereas in crystalline solids defects are identified as local deviations from the crystal order, it is not clear how, or even if, equivalent intrinsic entities can be defined in amorphous solids. This work presents a new way of defining and describing localized intrinsic geometrical defects in amorphous solids and for computing the stresses within defected bodies. The methods and results that are presented here can be integrated into phenomenological theories of plasticity and can be applied to biomechanical problems that involve strain localization.

Abstract

We study the geometry of defects in amorphous materials and their elastic interactions. Defects are defined and characterized by deviations of the material’s intrinsic metric from a Euclidian metric. This characterization makes possible the identification of localized defects in amorphous materials, the formulation of a corresponding elastic problem, and its solution in various cases of physical interest. We present a multipole expansion that covers a large family of localized 2D defects. The dipole term, which represents a dislocation, is studied analytically and experimentally. Quadrupoles and higher multipoles correspond to fundamental strain-carrying entities. The interactions between those entities, as well as their interaction with external stress fields, are fundamental to the inelastic behavior of solids. We develop analytical tools to study those interactions. The model, methods, and results presented in this work are all relevant to the study of systems that involve a distribution of localized sources of strain. Examples are plasticity in amorphous materials and mechanical interactions between cells on a flexible substrate.

The characterization of defects in amorphous solids is a fundamental problem in material science. In crystalline solids defects are localized structural deviations of matter from its ordered state. The modeling of those defects in the framework of continuum mechanics is via constraints on the configurations of the body (1). When trying to develop plasticity theories for amorphous materials, in which no structural order exists, one faces the problem of how to define defects as intrinsic geometric objects (2–4).

The first attempt to classify defects in a continuum description is due to Volterra (5). In this description, defects are sources of geometric incompatibility that results in elastic stresses. Volterra described elementary states of frustration in elastic materials, using cut–shift–weld protocols. Volterra’s constructions provide a list of pathways that result in geometrically frustrated states. However, these constructions cannot be regarded as definitions of defects, because very different procedures can result in the same material geometry.

The idea to describe distributions of defects using smooth geometric fields began with Kondo (6) and Bilby et al. (7) (more recent works are in refs. 8–10). Inspired by properties of defects in crystalline materials, they suggested to describe defects in continuum by geometric fields such as curvature and torsion tensors. This formalism describes the intrinsic geometry associated with defects, but it was not integrated into the theory of elasticity. Moreover, different types of defects involve different geometric fields, which makes such an approach complicated.

A possibly different approach for the description of defects is motivated by ref. 11 in the context of flexible membranes with a hexagonal crystalline order. Studying the stress state of a disc with a single disclination (a “5” or “7” defect in hexagonal lattice) or dislocation (a “5–7” pair), it was shown that these intrinsic structural defects lead to a source term in the elastic stress equation. Thin discs buckle into 3D configurations, “screening” the stress sources by the Gaussian curvature of the buckled surface. This observation suggests that the perturbation to the crystalline order associated with topological defects affects the mechanical state by generating localized intrinsic Gaussian curvature. It is natural to ask, then, whether similar localized distributions of intrinsic Gaussian curvature can also be found in amorphous materials that undergo irreversible deformations and, if so, what the proper field would be to describe it.

A large volume of work has recently been dedicated to the description of irreversibly deformed amorphous solids, using the framework of incompatible elasticity (12). In this description an elastic body is modeled as a 3D Riemannian manifold, equipped with a reference metric $\overline{\mathfrak{g}}$, which represents local equilibrium distances between material elements. Every configuration of the body induces on that manifold a metric, $\mathfrak{g}$, which we call the actual metric. The elastic strain is the deviation of $\mathfrak{g}$ from $\overline{\mathfrak{g}}$. In cases where the intrinsic geometry of the body is invariant under translations along an axis, the reference metric is determined by its value on a cross section; i.e., it is effectively 2D. Two-dimensional metrics are characterized by a single scalar field—the Gaussian curvature (13). For such intrinsic geometries, incompatibility amounts to a nonzero reference Gaussian curvature $\overline{K}$ (the Gaussian curvature associated with the reference metric).

The elastic model is fully determined by a constitutive relation, which relates the internal stresses to the strain field. In the case of a hyperelastic material, the constitutive relation can be defined by an energy functional, which is an additive measure of a local energetic cost of deviations of the actual metric from the reference metric. In the case of an amorphous solid, we assume that the microscopic structure of the solid is fully encoded by the reference metric $\overline{\mathfrak{g}}$, in which case the elastic energy is of the form

$$E={\displaystyle \int W\left(\mathfrak{g}\left(x\right);\overline{\mathfrak{g}}\left(x\right)\right)\hspace{0.17em}d{\text{Vol}}_{\overline{\mathfrak{g}}}}.$$

Here $d{\text{Vol}}_{\overline{\mathfrak{g}}}$ is the volume element, and W is a nonnegative energy density that vanishes if and only if $\mathfrak{g}\left(x\right)=\overline{\mathfrak{g}}\left(x\right)$. Incompatibility manifests in that $\mathfrak{g}$ cannot equal $\overline{\mathfrak{g}}$ everywhere simultaneously. In this formulation there is a complete separation between the description of the intrinsic geometry of the material (determining $\overline{\mathfrak{g}}$) and the description of the elastic problem (finding the energy minimizing $\mathfrak{g}$). The reference metric is an objective measure that is independent, for example, of the actual configuration or the elastic energy functional.

Incompatible elasticity was recently used in the analysis of thin sheets endowed with an imposed global deformation field, which induces smooth reference Gaussian curvature fields (14–20) (a discontinuous reference metric was considered in refs. 21 and 22). Smooth reference metrics can describe a wide range of geometrically frustrated material; however, they are incapable of describing geometric singularities, such as in localized defects (23). In this work we perform two main steps: First, we identify a set of reference metrics associated with 2D defects in a 3D amorphous material. These defects are expressed by a multipole expansion of the reference Gaussian curvature field. We show that the first three multipoles in the hierarchy correspond to known defects in crystalline materials. We compare our analytical results to experiments with amorphous materials containing an isolated curvature dipole. In the second part of the paper the advantages of the formalism are demonstrated by solving the elastic problem of interacting curvature quadrupoles. We provide analytical expressions for interaction energies of curvature quadrupoles with external stress and with each other. The energy landscape that results from these expressions indicates an increasing tendency to stress localization, depending on the parameters of the system.

Defects generate internal stresses resulting from geometric frustration. It is well known that a crystalline body that contains a defect is residually stressed—it has no stress-free configuration. However, every part of it that does not contain the defect is a perfect crystal. Therefore, once separated from the body, it does have a stress-free configuration. Similarly, we model a defect-free amorphous material by a reference metric that can be embedded in Euclidean space without strain, i.e., isometrically. A body containing a line defect, which in the case of a 2D geometry implies that the defect is concentrated at a point, is therefore modeled by a reference metric that is locally Euclidean everywhere, except at that point (which will be taken as the origin). Local flatness means that every point has a neighborhood that can be embedded in Euclidean space isometrically. Incompatibility manifests in that the entire manifold cannot be isometrically embedded in Euclidean space. The characteristic of such metrics is that the reference Gaussian curvature vanishes everywhere except for the origin, where it is singular.

We are thus looking for 2D metrics that are locally Euclidean. Note that we are focusing our attention on the reference metric of the material. The solution of the resulting elastic problem is addressed further below.

It is known that every 2D metric is locally conformally flat (24), which means that it can be expressed as the product of a Euclidean metric and a positive scalar function. Adopting polar coordinates $\left(r,\theta \right)$, a conformally flat reference metric takes the form

$$\overline{\mathfrak{g}}=e^{2\phi \left(r,\theta \right)}\left(\begin{array}{cc}1& 0\\ 0& r^2\end{array}\right).$$ [1]

The function $e^{2\phi \left(r,\theta \right)}$ can be interpreted as a local expansion factor. Also, we call $\phi \left(r,\theta \right)$ the conformal factor.

Using the Brioschi equation (13), the corresponding reference Gaussian curvature is

$$\overline{K}=-e^{-2\phi \left(r,\theta \right)}\mathrm{\Delta }\phi \left(r,\theta \right),$$ [2]

where $\mathrm{\Delta }$ is the Euclidean Laplacian. It follows that the reference metric is locally Euclidean if φ is harmonic,

$$\mathrm{\Delta }\phi \left(r,\theta \right)=0.$$ [3]

Using a multipole expansion, we obtain a large family of locally Euclidean metrics by setting

$$\phi \left(r,\theta \right)=\beta +\alpha \ln r+{\displaystyle \sum _{n=1}^{\infty }\left(A_n{r}^n+B_n{r}^{-n}\right)\cos n\left(\theta -{\theta }_n\right)},$$ [4]

where $\alpha ,\beta ,A_n,B_n,{\theta }_n$ are parameters. Setting $A_n=0$ amounts to $\left(r,\theta \right)$ being standard polar Euclidean coordinates as $r\to \infty$. The parameter β is a homogeneous scaling factor that globally induces zero reference Gaussian curvature and hence may be set to zero.

When plugged into Eq. 1, the parameters $B_n$ and α determine a large family of reference metrics, each with a different singularity of $\overline{K}$ at the origin. Mechanically, these singularities act as intrinsic localized sources of stress and therefore can be regarded as defects.

We now study the geometric interpretation of each multipole term in this expansion by considering an annular domain, which represents a cross section of a punctured 3D cylinder. The inner radius serves as a cutoff for the curvature singularity. Consider first the case where α is the only nonzero coefficient, which corresponds to a monopole of Gaussian curvature. It can be shown that such a metric models a disclination with an excess angle of $2\pi \alpha$ (SI Text). The same geometry can be obtained via a Volterra construction (5), by removing/inserting a section $2\pi \alpha$ out of/into a dissected annulus. When applied to thin sheets, these constructions lead to cone and anticone configurations (11, 25). In a hexagonal crystalline material $6\alpha$ must be an integer leading, for example, to the well-known 5 or 7 defects (11).

Consider next the case where $B_1$ is the only nonzero coefficient, which corresponds to a dipole of Gaussian curvature; without loss of generality we may take ${\theta }_1=0$, which amounts to setting the x axis parallel to the dipole. The reference metric takes the form

$${\overline{\mathfrak{g}}}_{\text{D}}=e^{b\cos \theta /\pi r}\left(\begin{array}{cc}1& 0\\ 0& r^2\end{array}\right),$$ [5]

where $b=2\pi B_1$. A dipole is a far field approximation of a pair of monopoles of opposite charges. In the present context, a metric of the form [5] is generated by a cone–anticone pair. In crystals, cone–anticone pairs (e.g., 5–7 pairs in hexagonal lattices) are edge dislocations. Thus, the metric [5] represents an edge dislocation in amorphous materials.

Dislocations are classically quantified by a Burgers vector, which in crystalline solids measures a discontinuity in the displacement field, where the latter is expressed in crystallographic units (1). Note that the notion of displacement assumes the existence of a reference configuration; i.e., it is not an intrinsic quantity. In contrast, the geometric description of dislocation in crystalline materials relies on a notion of parallelism. One assumes the existence of a parallel frame field, which represents the crystalline axes (2, 6, 7). The Burgers vector is then associated with an asymmetric parallel transport.

In an amorphous material, the only structure is a metric. Then, the only natural notion of parallelism is induced by the Levi–Civita connection (13), which induces a symmetric parallel transport. It is a priori unclear how to obtain a nontrivial Burgers vector from a parallel transport that is symmetric.

Assume a reference metric of the form [5]. Let ${\mathrm{\Pi }}_q^p$ be the Levi–Civita parallel transport operator from point q to point p, induced by [5] (details in SI Text). This operator is well defined because the total curvature enclosed by any loop is zero, and hence parallel transport is path independent. We then follow the classical definition of the Burgers vector by integrating infinitesimal displacement vectors along a closed loop $\gamma \left(t\right)$; however, unlike the classical approach, this integration takes place in the reference manifold

$$d\left(\gamma ,p\right)={\displaystyle \int {\displaystyle {\prod }_{\gamma \left(t\right)}^p}\left(\dot{\gamma }\left(t\right)\right)\hspace{0.17em}dt},$$ [6]

where p is an arbitrary reference point. $d\left(\gamma ,p\right)$ is a vector at p that depends on the loop γ. It is proportional to the number of times that the loop surrounds the singularity (23). Moreover, the vector $d\left(\gamma ,p\right)$ is independent of the reference point p. Therefore, we define the Burgers vector $\mathbf{b}$ as $d\left(\gamma ,p\right)$ for loops γ that surround the singularity once. This generalizes the notion of a Burgers vector for amorphous materials.

A direct calculation shows that for a reference metric of the form [5] and a reference point $p=\left(r_0,0\right)$, the Burgers vector is given by

$$\mathbf{b}=-b{e}^{-b/2\pi r_0}\hspace{0.17em}\widehat{y},$$ [7]

where $\widehat{y}$ is a unit vector along the y axis. As expected, it is perpendicular to the axis of the metric dipole. Its magnitude is

$$\left|\mathbf{b}\right|=\sqrt{{\langle \mathbf{b},\mathbf{b}\rangle }_{{\overline{\mathfrak{g}}}_{\text{D}}}}=b.$$

Conformally flat metrics, and in particular the metric [5], can be induced on an originally Euclidean manifold, by differential swelling. Using this idea, we imposed a reference metric of the form ${\overline{\mathfrak{g}}}_{\text{D}}$ on annulus-shaped discs of a N-isopropylacrylamide (NIPA) gel, using an experimental technique similar to the one described in refs. 15 and 18. The local swelling factor is set by the cross-linking density of the gel, which is determined by the local exposure of the gel to UV irradiation (SI Text). Note that such a differential swelling generates bodies that contain a single edge dislocation, even though the plastic deformation is smooth everywhere (unlike Volterra’s cut-and-weld procedures).

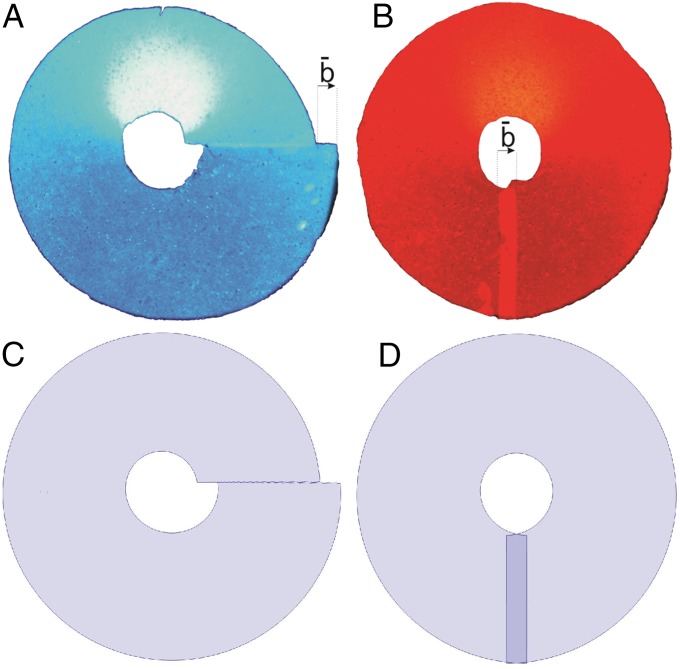
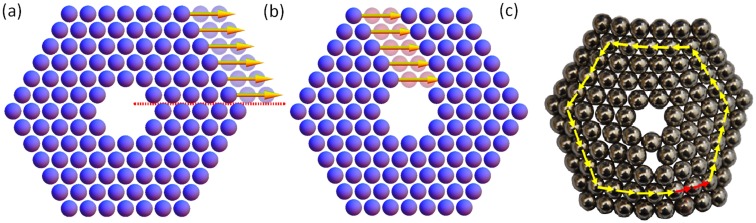
When such annular discs are flattened, mimicking a cross section of a 3D body, they are stressed. The insertion of a radial cut allows the locally flat body to relax into a stress-free flat configuration. Fig. 1 A and B displays two such annuli cut along the $\theta =0$ and $\theta =-\left(\pi /2\right)$ directions. In Fig. 1A the new stress-free configuration exhibits a constant discontinuous shift along the cut. In Fig. 1B the new stress-free configuration exhibits a constant discontinuous shift perpendicular to the cut. The plastic deformations needed to restore the bodies as they were before the cut coincide with Volterra constructions of an edge dislocation. This proves that differential swelling can yield a stress field identical to that of a dislocation. Fig. 1 C and D displays analytical calculations of isometric immersions of cut discs with metrics of the form [5] for $b=5$ mm (details in SI Text). The agreement with experiments is excellent.

Fig. 1.

(A and B) Experiments. NIPA annular gels with a reference metric [5] for $b=5$ mm. Sample A is cut along the $\theta =0$ axis and sample B is cut along the $\theta =-\pi /2$ axis. The slightly lighter band in B is a region of overlap of two surfaces. Radial cuts allow the gels to adopt a flat stress-free configuration. In both cases, relaxation is accompanied with a constant shift of about 4 mm. (C and D) Calculation. Shown is isometric embedding of the same reference metric with branch cuts along the rays $\theta =0$ and $\theta =-\pi /2$.

Similar to disclinations and dislocations in crystals, the curvature monopole and dipole are “topological defects.” They cannot be removed, or even altered, by local deformations or by the removal of a region around the defect. The mathematical description of topological defects in Riemannian manifolds involves the notion of a monodromy. The monodromy associated with curvature monopoles and dipoles is nontrivial. In contrast, the monodromy associated with curvature quadrupoles and higher-order multipoles is trivial, meaning that by removing the defect locus all stresses can be relaxed (23).

The lowest multipole that can be generated by localized plastic deformations is the quadrupole. It can be identified with strain carriers in phenomenological theories of plasticity (26–29) or with Eshelby inclusions (30–32). Such localized sources of stress appear in a biological context as well, when cells that are deposited on a flexible substrate contract uniaxially. The strains/stresses generated by the cells are known to affect their relative motion and generate collective organization patterns (for a review on this subject see ref. 33 and references therein).

A body that contains a single quadrupole is described by the reference metric [1] in which the only nonzero coefficient in the multipole expansion [4] is $B_2$,

$${\phi }_Q\left(r,\theta \right)=\frac{Q\hspace{0.17em}\cos 2\left(\theta -\alpha \right)}{4\pi r^2},$$ [9]

where $Q=4{\pi }^2{B}_2$ and $\alpha ={\theta }_2$.

To understand the geometrical interpretation of defects carrying a quadrupole charge, consider an annulus whose initial reference metric with conformal factor $\phi =0$. Change now its reference metric into one with conformal factor ${\phi }_Q$ given by [9]. Both reference metrics are globally flat, and hence they can be embedded isometrically (i.e., stress-free) in the plane. The comparison between the two stress-free configurations reveals the deformation inducing the curvature quadruple.

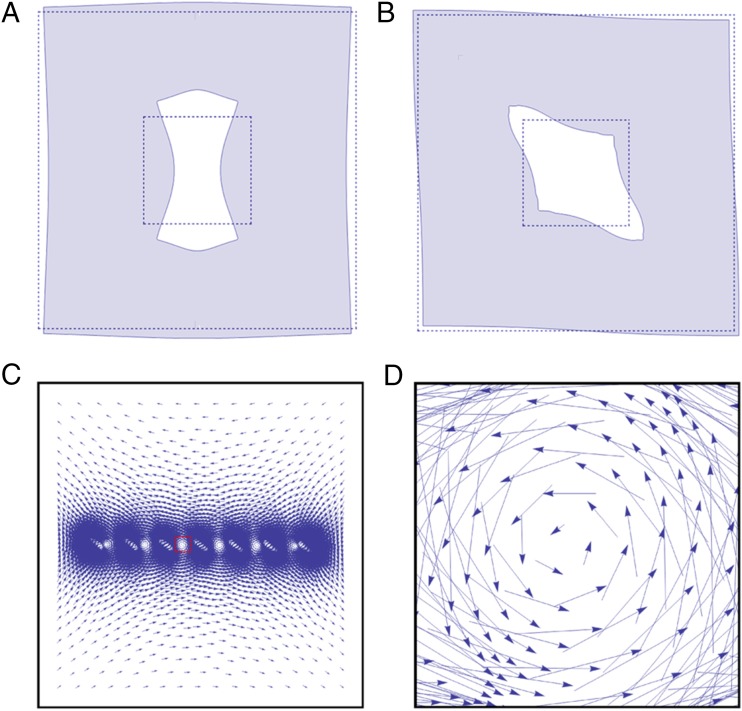
Fig. 2A displays the change in the stress-free configuration for $\alpha =0$. The solid lines represent the stress-free configuration for $\phi =0$, whereas the color-filled shape represents the stress-free configuration for $\phi ={\phi }_Q$. In this case the local deformation that induces the metric is a compression. Fig. 2B displays the change in the stress-free configuration for $\alpha =\pi /4$. In this case the local deformation that induces the metric is a shear (details in SI Text).

Fig. 2.

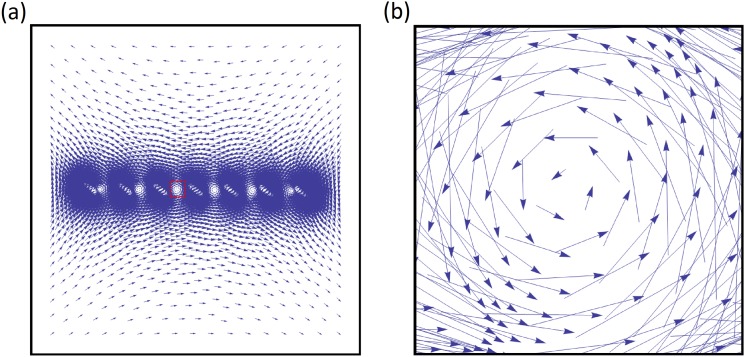
(A and B) An analytical calculation of the planar embedding of annuli endowed with reference metrics with conformal factor [9]. The case (A) $\alpha =0$ represents a compression-like deformation, whereas the case (B) $\alpha =\pi /4$ represents a shear-like deformation. (C) An analytic solution of the displacement field induced by a linear array of seven quadrupoles oriented with $\pi /4$ with respect to the external shear direction. (D) A magnification of the region between two adjacent quadrupoles.

So far we have shown that the reference metric field can describe localized sources of stress in amorphous materials, which share many similarities with defects in crystalline materials. Curvature monopoles and curvature dipoles are equivalent to disclinations and dislocations, respectively. Curvature quadrupoles are equivalent to Stone–Wales defects (34) and can be generated via localized deformations. The description of defects using a reference metric does not depend on the constitutive laws of the underlying material and does not involve any linearization. In addition, because it is defined in the reference manifold, it does not depend on the actual configuration of the body. This property is important when dealing with problems that contain many defects: Such bodies can be described by a reference metric (Eq. 1), with

$$\phi \left(\mathbf{x}\right)={\displaystyle \sum _i{\phi }_i\left(\mathbf{x}-{\mathbf{x}}_i\right)},$$ [10]

where ${\phi }_i\left(\mathbf{x}-{\mathbf{x}}_i\right)$ is the conformal factor of a single defect, located at ${\mathbf{x}}_i$. This superposition property is exact and is crucial for modeling “many body problems” (Fig. 2 C and D). Finally, the resultant (nonlinear) elastic problem can be solved analytically (35). Given a reference metric, one obtains a partial differential equation for an incompatible stress function (ISF). The ISF is a generalization of the classical Airy stress function.

With these tools in hand, we turn to analyze a mechanism related to strain localization in sheared amorphous solids.

It was recently suggested (31, 32) that the formation of shear bands during the failure of amorphous solids is initiated by the appearance of lines of correlated Eshelby-like singularities. These localized plastic deformations are induced by an external load, but their positions and orientations are driven by their mutual interactions as well as by their interaction with the external load. Thus, to elucidate the formation of shear bands it is necessary to understand these interactions, which is a notoriously hard problem. Analytical solutions for the arrangement of multiple localized plastic deformations were obtained in ref. 31 for the case of few, weakly interacting Eshelby inclusions (such an approximation is required due to the nonadditivity of linear elastic theory with respect to Eshelby inclusions).

Motivated by ref. 31, we proceed to study the mechanical state of an externally loaded amorphous solid that contains a given distribution of localized defects. Specifically, we study the mutual interaction of two curvature quadrupoles in an external stress field. The superposition property of our formalism and its nonlinearity allow a formulation without the approximations made in ref. 31. In particular, we can capture the transition from weak to strong coupling between the quadrupoles. The quadrupoles are located at $\left(\mathrm{0,0}\right)$ and $R\left(\cos \mathrm{\Theta },\sin \mathrm{\Theta }\right)$. Their orientations and charges are ${\alpha }_1,Q_1$, and ${\alpha }_2,Q_2$, respectively.

Using the ISF method mentioned above, and assuming that the two quadrupoles are separated by a distance, $r\gg \sqrt{Q_i}$, we obtain the interaction energy of two quadrupoles,

$$U_{QQ}=\frac{Y{Q}_1{Q}_2}{16\pi R^2}\cos \left(2\left({\alpha }_1+{\alpha }_2-2\mathrm{\Theta }\right)\right),$$ [11]

where Y is the Young modulus. Physically, we expect the interaction energy to be large when R is below a core size, $R_c$, and thus we assume $U_{QQ}$ to be given by [11] for $R\ge R_c$ and infinite otherwise.

The interaction of a quadrupole with an external stress field is computed in a similar way. Taking for example an asymptotic shear stress field, ${\sigma }^{xy}\to {\sigma }^{\infty }$ as $\left|y\right|\to \infty$, we obtain

$$U_{\text{ext}}=-\frac{1}{2}Q{\sigma }^{\infty }\sin 2\alpha$$ [12]

(detailed calculations in SI Text).

Consider then a body subjected to an asymptotic shear stress field. Suppose the body contains two quadrupoles of orientations ${\alpha }_1,{\alpha }_2$ and a fixed magnitude Q, located at points $x_1,x_2$, such that $x_2-x_1=R\left(\cos \mathrm{\Theta },\sin \mathrm{\Theta }\right)$. The total interaction energy for $R\ge R_c$ is

$$U_{\text{total}}=\frac{1}{2}Q{\sigma }^{\infty }\left(-\sin 2{\alpha }_1-\sin 2{\alpha }_2+B\frac{R_c^2}{R^2}\cos \left(2{\alpha }_1+2{\alpha }_2-4\mathrm{\Theta }\right)\right),$$

where

$$B=\frac{QY}{8\pi R_c^2{\sigma }^{\infty }}$$

is a dimensionless parameter.

Minimizing this energy over ${\alpha }_1$, ${\alpha }_2$, R and $\mathrm{\Theta }$, the state of minimal energy is

$${\alpha }_1={\alpha }_2=\frac{\pi }{4},\hspace{1em}R=R_c,\hspace{1em}\text{and}\hspace{1em}\mathrm{\Theta }=0.$$

Thus, a state of minimum energy is obtained when the quadrupoles are close to each other, the line that connects them is parallel to the direction of the shear, and their orientations are at an angle of $\pi /4$ relative to the direction of the shear. This prediction is consistent with ref. 31 and extends it as it is valid also for strong quadrupole–quadrupole interactions.

In the above analysis the distance between the quadrupoles is a variable determined by energetic considerations. In other models, however, both the positions and the magnitudes of the localized plastic deformations are predetermined. In these models the distance $R_c$ in the definition of B should be replaced by the actual distance between the quadrupoles.

The fact that the energy minima of the weakly and strongly interacting quadrupoles coincide does not imply that materials behave similarly in these two limits. The difference between the two cases is significant in the presence of noise. Then, the full energy landscape is important and not just the location of the minima. For a strong shear field, i.e., for $B\ll 1$, the total energy is dominated by the interaction with the external field, which implies that ${\alpha }_1,{\alpha }_2$ will not deviate much from their optimal value. For a weak shear field, i.e., for $B\gg 1$, the total energy is dominated by the mutual interaction of the quadrupoles, and hence $\mathrm{\Theta }$ will not deviate much from ${\alpha }_1+{\alpha }_2-\pi /2$. For fixed $\mathrm{\Theta }$, ${\alpha }_1,{\alpha }_2$ may fluctuate as long as their sum remains constant.

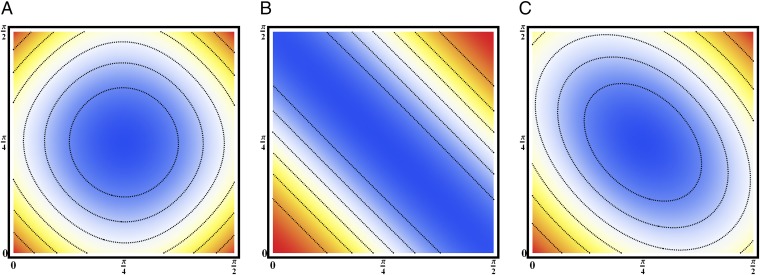
Fig. 3 shows the interaction energy landscape as function of ${\alpha }_1$ and ${\alpha }_2$ for $R=R_c$ and $\mathrm{\Theta }=0$. Fig. 3A corresponds to $B\gg 1$. The energy landscape displays a unique global minimum at ${\alpha }_1={\alpha }_2=\pi /4$. Fig. 3B corresponds to $B\ll 1$. In this case there is a degeneracy with a global minimum along the line ${\alpha }_1=\pi /2-{\alpha }_2$. Fig. 3C corresponds to an intermediate regime. The deviations from the unique global minimum are shallower along the line ${\alpha }_1=\pi /2-{\alpha }_2$, and these are expected to dominate noisy statistics in realistic materials.

Fig. 3.

The interaction energy landscape as function of ${\alpha }_1$ and ${\alpha }_2$ for $R=R_c$ and $\mathrm{\Theta }=0$ (blue represents low energy). (A) $B\gg 1$: The system is dominated by the interaction of quadrupoles with the external field. The energy has a single minimum. (B) $B\ll 1$: The system is dominated by quadrupole–quadrupole interactions. The minimum of the energy is degenerate. (C) Intermediate value of B: There are “soft” modes of deformations along the ${\alpha }_2=\pi /2-{\alpha }_1$ line.

In summary, we presented a geometric approach to 2D defects in 3D amorphous elastic bodies. In this approach, the defective body is described by a single geometric field—the reference metric. The latter is an intrinsic property, independent of the body’s configuration.

We identified a family of defects associated with multipoles of the reference Gaussian curvature and demonstrated the correspondence between the various multipoles and known defects in crystals. The monopole term corresponds to a disclination, and the dipole term corresponds to an edge dislocation. Both terms are associated with a topological property of the reference manifold—the monodromy. It was demonstrated experimentally that a single dipole defect with a given Burgers vector can be generated in an amorphous gel by controlling the reference metric. Curvature quadrupoles are of special interest in the context of inelastic deformations in amorphous solids and in the context of the mechanical interaction between living contracting cells (33). They can be generated via localized deformations and are qualitatively similar to strain carriers in phenomenological theories of plasticity (26–30). Applying the method of incompatible stress function (35), we obtain the interaction energy of multiple quadrupoles in an external stress field. We identify a dimensionless parameter B that governs the energy landscape of the interaction energy. We show that for intermediate values of B the energy landscape exhibits “soft” deformation modes. These modes are expected to be reflected in the statistics of the orientation and location of defects in amorphous solids under external stresses. In the present analysis, the magnitude Q of a quadrupole was taken as a fixed parameter. In addition, the reference metric before the formation of the quadrupoles was assumed Euclidean. In reality, Q is determined by the energetics of a nucleation process, and it is formed on top of an approximately Euclidean, noisy reference metric. Our analysis can be extended to include the nucleation of defects by the addition of a term of nucleation energy. Moreover, the amorphous structure of the material can be described by a random conformal factor with proper statistical measures. We expect the geometric approach to defective amorphous solids to be generally relevant to the description of plasticity, in which quadrupoles, as well as higher multipoles, are the fundamental strain-carrying objects.

Volterra Constructions on a Crystalline Lattice

Parallel Transport and Reference Burgers Vector.

The procedure of parallel transport relies on a more fundamental notion, that is, the affine connection, usually denoted $\nabla$. Roughly speaking, one can say that the affine connection tells us “how a vector changes while moving in a given direction.” Formally

$${\nabla }_{e_i}{e}_j={\mathrm{\Gamma }}_{ij}^k{e}_k,$$

where ${\mathrm{\Gamma }}_{ij}^k$ are known as the connection coefficients or Christoffel symbols. The expression ${\nabla }_{e_i}{e}_j$ describes the change of the unit vector $e_j$ when infinitesimally moving in the $e_i$ direction.

Given a connection, one can define the notion of parallel transport accordingly; a vector field is a parallel field if it “changes” exactly as the connection dictates. Explicitly, the vector field X is said to be parallel when moving along the vector field Y if ${\nabla }_{Y}X=0$. Generally, there is complete freedom in defining the connection. However, when considering physical systems, one wants the connection to preserve two basic properties; the first is that the inner product between two vectors would not be affected by infinitesimal parallel transport. The second is that the outcome of a sequential application of parallel transport in two infinitesimal directions should not depend on the order of transportation. Requiring these two properties leads to only one possible connection: the Levi–Civita connection (13). When using this connection the variation in the vector, which is parallel transported along a closed loop, is determined by the total intrinsic curvature surrounded by the loop. An immediate result is that generally the procedure of parallel transport from point to point directly depends on the chosen path. However, if one deals with a manifold where every loop on it contains zero curvature, the parallel transport operation is path independent. In this case the procedure of parallel transport can be described by an operator ${\displaystyle {\prod }_p^{q}X}$, that is, the parallel transportation of a vector X from p to q.

The case of a locally Euclidean manifold with a dipole of curvature at the origin is exactly this case. Given the metric of a manifold with a dipole of curvature ${\overline{\mathfrak{g}}}_{\text{dipole}}$, one can calculate the Levi–Civita connection (13) and hence calculate the operator ${\displaystyle {\prod }_p^{q}X}$. Detailed calculations of ${\displaystyle {\prod }_p^{q}X}$ and examples are presented in ref. 23.

Our definition of the Burgers vector involves integration of vectors on the reference manifold, which is not globally Euclidean. In general, there is no canonic way of summing vectors on a manifold. Given a vector field, each vector lives in a different tangent space. Therefore, before summing the vectors one should transport them all to the same point, the same tangent space. This procedure is well defined only when the operation of parallel transport is path independent.

In crystals, the Burgers vector is measured according to “counting lattice steps” along a closed loop. Generalizing this idea and adjusting it to the continuum metric description, we replace “steps” with infinitesimal displacement. Given a closed loop $\gamma :\left[\mathrm{0,1}\right]\to M$ (M is the manifold with the reference metric ${\overline{\mathfrak{g}}}_{\text{dipole}}$), the tangent to the loop is given by $\dot{\gamma }$ and the infinitesimal step is $\dot{\gamma }dt$. The expression $\dot{\gamma }dt$ is a vector field along the loop γ. Summing this field should be related to the Burgers vector. Because in the case of the current manifold the parallel transport is path independent, one can transport all $\dot{\gamma }dt$ to some point q and then to sum them all. This is expressed in Eq. 6 in the main text. In ref. 23 we have rigorously constructed this definition of the Burgers vector, based on the notion of monodromy.

Explicit Calculations of Some of the Results

Interpretation of the Monopole Term.

From Eq. 4 in the main text the monopole term is

$$\phi \left(r,\theta \right)=\alpha \ln r;$$

that is, the metric of a monopole is given by

$${\overline{\mathfrak{g}}}_{\text{mono}}=r^{2\alpha }\left(\begin{array}{cc}1& 0\\ 0& r^2\end{array}\right).$$ [S1]

Rescaling the radial coordinate as $R={\left(1+\alpha \right)}^{-1}{r}^{1+\alpha }$ leads to a metric of the form [in the $\left(R,\theta \right)$ coordinates]

$${\overline{\mathfrak{g}}}_{\text{mono}}=\left(\begin{array}{cc}1& 0\\ 0& {\left(1+\alpha \right)}^2{R}^2\end{array}\right).$$ [S2]

On the other hand we can write down the reference metric of a cone. Assume we start with a flat disc and insert (or remove) a wedge with an angle $\mathrm{\Delta }\varphi$. The metric of such body can be written as

$$\mathfrak{g}=\left(\begin{array}{cc}1& 0\\ 0& R^2\end{array}\right),$$ [S3]

where $0<\tilde{\theta }<2\pi +\mathrm{\Delta }\varphi$. We redefine the angular coordinate $\theta =2\pi \tilde{\theta }/\left(2\pi +\mathrm{\Delta }\varphi \right)$. Under this isometric coordinate transformation the metric takes the form

$${\overline{\mathfrak{g}}}_{\text{cone}}=\left(\begin{array}{cc}1& 0\\ 0& {\left(1+\frac{\mathrm{\Delta }\varphi }{2\pi }\right)}^2{R}^2\end{array}\right).$$ [S4]

This form is exactly as the one of a monopole singularity in the Gaussian curvature with

$$\alpha =\frac{\mathrm{\Delta }\varphi }{2\pi };$$

that is, positive (negative) α amounts to insertion (removal) of angle. Thus, the monopole term represents a disclination.

Isometric embedding—analysis, the dipole term.

A manifold with the dipole reference metric

$${\overline{\mathfrak{g}}}_{\text{dipole}}=e^{2b\cos \theta /r}\left(\begin{array}{cc}1& 0\\ 0& r^2\end{array}\right)$$

is locally Euclidean, but cannot be isometrically embedded into a 2D Euclidean plane (23). However, the insertion of radial cuts into the domain makes such isometric embedding possible. There are many different such configurations that correspond to different Volterra constructions. Defining a new coordinate system

$$u=r\cos \left(\theta -\frac{b\sin \left(\theta \right)}{r}\right)\left(\text{sinh}\left(\frac{b\cos \left(\theta \right)}{r}\right)+\text{cosh}\left(\frac{b\cos \left(\theta \right)}{r}\right)\right)-\frac{b}{2}\left(\text{Ei}\left(\frac{b{e}^{-i\theta }}{r}\right)+\text{Ei}\left(\frac{b{e}^{i\theta }}{r}\right)\right)$$

$$v=-r\sin \left(\theta -\frac{b\sin \left(\theta \right)}{r}\right)\left(\text{sinh}\left(\frac{b\cos \left(\theta \right)}{r}\right)+\text{cosh}\left(\frac{b\cos \left(\theta \right)}{r}\right)\right)-\frac{ib}{2}\left(\text{Ei}\left(\frac{b{e}^{-i\theta }}{r}\right)-\text{Ei}\left(\frac{b{e}^{i\theta }}{r}\right)\right),$$

the metric takes the form

$$\overline{\mathfrak{g}}=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right).$$

Because this metric is Euclidean, the isometric embedding configuration is given by

$$\left(X\left(u,v\right),Y\left(u,v\right)\right)=\left(u,v\right).$$

Note that the exponential integral function $\text{Ei}\left(z\right)$ has a branch-cut discontinuity running from $z=0$ to $-\infty$. To recover a specific stress-free configuration one should chose correctly the branch cuts. In the main text we presented two different choices, one with a branch cut along the $\theta =0$ direction and the other one along the $\theta =\pi /2$ direction.

We see that both embeddings correspond to Volterra constructions of inserting a line or creating a shift along a plane.

The quadrupole term.

The metric is of the form

$${\overline{\mathfrak{g}}}_{\text{quad}}=e^{2\left(\left(a\cos 2\theta +b\sin 2\theta \right)/r^2\right)}\left(\begin{array}{cc}1& 0\\ 0& r^2\end{array}\right).$$

Let us define a new coordinate system

$$u=\frac{1}{2}r\left(e^{e^{2i\theta }\overline{\alpha }/r^2-i\theta }+e^{i\theta +\alpha e^{-2i\theta }/r^2}\right)-\frac{\sqrt{\pi }}{2}\left(\sqrt{\alpha }\text{Erfi}\left(\frac{\sqrt{\alpha }{e}^{-i\theta }}{r}\right)+\sqrt{\overline{\alpha }}\text{Erfi}\left(\frac{e^{i\theta }\sqrt{\overline{\alpha }}}{r}\right)\right)$$

$$v=i\frac{1}{2}r\left(e^{i\theta +\alpha e^{-2i\theta }/r^2}-e^{e^{2i\theta }\overline{\alpha }/r^2-i\theta }\right)+i\frac{\sqrt{\pi }}{2}\left(\sqrt{\overline{\alpha }}\text{Erfi}\left(\frac{e^{i\theta }\sqrt{\overline{\alpha }}}{r}\right)-\sqrt{\alpha }\text{Erfi}\left(\frac{\sqrt{\alpha }{e}^{-i\theta }}{r}\right)\right),$$

where $\alpha =a+ib$ and Erfi is the imaginary error function $-i\text{Erf}\left(iz\right)$. Under a change of coordinates from $\left(r,\theta \right)$ to $\left(u,v\right)$ one finds that the metric takes the form

$$\overline{\mathfrak{g}}=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right);$$

hence the stress-free configuration, i.e., isometric embedding of ${\overline{\mathfrak{g}}}_{\text{quad}}$, is given by

$$\left(X\left(u,v\right),Y\left(u,v\right)\right)=\left(u,v\right).$$

Two such embeddings are presented in the main text.

The Interaction Between Quadrupoles.

The reference metric of two quadrupoles located at ${\overrightarrow{p}}_0=\left(\mathrm{0,0}\right)$ and ${\overrightarrow{p}}_1=\left(r\cos \theta ,r\sin \theta \right)$ with charges

$${\mathbf{Q}}_0=\left(\begin{array}{cc}{Q}_0\cos 2{\alpha }_0& Q_0\sin 2{\alpha }_0\\ Q_0\sin 2{\alpha }_0& -Q_0\cos 2{\alpha }_0\end{array}\right)$$

and

$${\mathbf{Q}}_1=\left(\begin{array}{cc}{Q}_1\cos 2{\alpha }_1& Q_1\sin 2{\alpha }_1\\ Q_1\sin 2{\alpha }_1& -Q_1\cos 2{\alpha }_1\end{array}\right)$$

is given by

$$\overline{\mathfrak{g}}=e^{2\varphi }\eta ,$$

where η is the Euclidean metric, and

$$\varphi =\frac{{\widehat{r}}_0^T\cdot {\mathbf{Q}}_0\cdot {\widehat{r}}_0}{r_0^2}+\frac{{\widehat{r}}_1^T\cdot {\mathbf{Q}}_1\cdot {\widehat{r}}_1}{r_1^2},$$

where

$${\overrightarrow{r}}_0=\overrightarrow{r}-{\overrightarrow{p}}_0\hspace{1em}\text{and}\hspace{1em}{\overrightarrow{r}}_1=\overrightarrow{r}-{\overrightarrow{p}}_1.$$

The interaction energy is derived from the total elastic energy stored in the medium due to the presence of the two quadrupoles. Using the method of incompatible stress function, we can solve the elastic problem up to any required accuracy. The method is composed of three stages:

• i)
  The solution for the equilibrium equation for the stress can be exactly represented in terms of a single scalar function

  $${\sigma }^{\mu \nu }=\frac{1}{\sqrt{\left|\mathfrak{g}\right|}}\frac{1}{\sqrt{\left|\overline{\mathfrak{g}}\right|}}{\mathit{ϵ}}^{\mu \alpha }{\mathit{ϵ}}^{\nu \beta }{\nabla }_{\alpha }{\nabla }_{\beta }\psi .$$ [S5]

  This representation of the solution is exact and involves no linearizations.
• ii)
  Choose a specific constitutive relation that relates stress with strain

  $$u=F\left(\sigma \right)$$

  and then express the actual metric in terms of the incompatible stress function ψ,

  $$\mathfrak{g}=\overline{\mathfrak{g}}+2F\left(\sigma \right).$$
• iii)
  Require zero Gaussian curvature for the actual metric and obtain an equation for the incompatible stress function

  $$K\left(\mathfrak{g}\right)=0.$$

Here we solve the problem for the case of Hookean constitutive law up to first order, where the small parameter is $\sqrt{Q}/r$, meaning that the quadrupoles are far apart.

The equation of the ISF up to this order is

$$\mathrm{\Delta }\mathrm{\Delta }\psi =-Y\mathrm{\Delta }\varphi ,$$

which is linear in the source term ϕ. Thus, it is sufficient to find the ISF of a single quadrupole. The solution of the full equation is composed of the solutions for each quadrupole. It can be verified, using Green’s function of the bi-Laplacian operator for example, that the solution of the equation

$$\mathrm{\Delta }\mathrm{\Delta }{\psi }_0=-Y\mathrm{\Delta }{\varphi }_0,$$

where ${\varphi }_0$ is the conformal factor of a single quadrupole at the origin, is given by

$${\psi }_0=\frac{Y{Q}_0}{16\pi }\left(\cos 2\theta \cos 2{\alpha }_0+\sin 2\theta \sin 2{\alpha }_0\right).$$

Writing the solution for the stress function in the presence of the two quadrupoles, one can write the total elastic energy stored in the system,

$$E=\frac{1}{2}{\displaystyle \int \frac{1}{\text{det}{\overline{\mathfrak{g}}}^2}{A}_{\mu \nu \rho \sigma }{\epsilon }^{\mu \alpha }{\epsilon }^{\nu \beta }{\epsilon }^{\rho \gamma }{\epsilon }^{\sigma \delta }\left({\overline{\nabla }}_{\alpha }{\overline{\nabla }}_{\beta }\psi \right)\left({\overline{\nabla }}_{\gamma }{\overline{\nabla }}_{\delta }\psi \right)\sqrt{\overline{\mathfrak{g}}}\hspace{0.17em}dS}.$$

Expanding the integrand according to the representation of the stress function as the sum of two stress functions, we find that terms that involve only ${\psi }_0$ or only ${\psi }_1$ diverge. This divergence represents the self-interaction of each multipole with itself. To avoid this divergence we need to consider only terms that mix ${\psi }_0$ and ${\psi }_1$. That is,

$$U={\displaystyle \int \frac{1}{\text{det}{\overline{\mathfrak{g}}}^2}{A}_{\mu \nu \rho \sigma }{\epsilon }^{\mu \alpha }{\epsilon }^{\nu \beta }{\epsilon }^{\rho \gamma }{\epsilon }^{\sigma \delta }\left({\overline{\nabla }}_{\alpha }{\overline{\nabla }}_{\beta }{\psi }_0\right)\left({\overline{\nabla }}_{\gamma }{\overline{\nabla }}_{\delta }{\psi }_1\right)\sqrt{\overline{\mathfrak{g}}}\hspace{0.17em}dS}.$$

Expanding the integrand to first order in $\sqrt{Q_i}/r$, the integral can be evaluated explicitly and yields

$$U_{\text{QQ}}=\frac{Y{Q}_0{Q}_1}{16\pi r^2}\cos \left(2{\alpha }_0+2{\alpha }_1-4\theta \right).$$

The same procedure can be repeated for the case of a single quadrupole in a system under uniform external load. The stress function for the external load part is

$${\psi }_{\text{BC}}=\frac{1}{2}{x}^i{x}^j{\mathit{ϵ}}_{ik}{\mathit{ϵ}}_{jl}{\sigma }^{kl}.$$

Writing the stress function of the entire system as a sum of ${\psi }_0$ and ${\psi }_{\text{BC}}$, writing the elastic energy of the system, substracting self-interacting terms, and evaluating the integral lead to

$$U_{Q\sigma }=-\frac{1}{2}Q{\sigma }_{xy}^{\infty }\sin 2\alpha +\frac{1}{4}Q\left({\sigma }_{yy}^{\infty }-{\sigma }_{xx}^{\infty }\right)\cos 2\alpha .$$

Simulation and Experimental Settings

Planar Amorphous Simulation.

To find the equilibrium planar configuration, that is, the plane stress solution, of an amorphous elastic disk with a given reference metric we use a 2D finite element simulation, which models the sheet as a 2D disordered triangular mesh. We relate to each triangle elastic properties: Young’s modulus Y and Poisson’s ratio ν. Additionally we relate the triangles with a reference metric $\overline{a}$. Given a configuration of the triangles’ vertices in 2D Euclidean space, we estimate for each triangle its metric according to the conformation of the triangle and its neighbors. The elastic energy density is a measure of the deviation of the actual metric from the reference one. As t is the thickness and $A^{\mu \nu \rho \sigma }$ is the elastic tensor, we have

$${\mathcal{W}}_{st}=\frac{1}{8}t{A}^{\mu \nu \rho \sigma }\left(a_{\mu \nu }-{\overline{a}}_{\mu \nu }\right)\left(a_{\rho \sigma }-{\overline{a}}_{\rho \sigma }\right),$$ [S6]

where

$$A^{\mu \nu \rho \sigma }=\frac{Y}{1+\nu }\left(\frac{\nu }{1-\nu }{\overline{a}}^{\mu \nu }{\overline{a}}^{\rho \sigma }+{\overline{a}}^{\mu \rho }{\overline{a}}^{\nu \sigma }\right).$$ [S7]

The total elastic energy is obtained by summing the energy density over all triangles, where the area element is defined according to the reference metric. Given an initial configuration of the sheet, we minimize the elastic energy with respect to the vertices’ coordinates.

Simulating the stressed state of a curvature dipole.

In the case of the reference metric of a curvature dipole,

$${\overline{\mathfrak{g}}}_{\text{dipole}}=e^{2b\cos \theta /r}\left(\begin{array}{cc}1& 0\\ 0& r^2\end{array}\right),$$

there is a divergence of the metric at the origin. Therefore, instead of simulating a disc-shaped sheet, we simulated an annulus with coordinate radii $r_{\text{in}}$ and $r_{\text{out}}$. The elastic parameters we use are Young’s modulus $Y=1$, Poisson’s ratio $\nu =1/3$, thickness $t=0.1$, and radii $r_{\text{in}}=0.1$, $r_{\text{out}}=50$. The inner radius in this simulation is analog to the lattice unit scale in a crystalline material or alternatively the scale of plastic deformations, and hence it serves as a cutoff to regularize the energy density divergence near the singularity.

An application to local plastic deformations of amorphous materials.

It was shown in refs. 31 and 32 using an MD simulation that an amorphous solid subjected to external shear develops a set of localized plastic shear deformations ordered on a line parallel to the edges. Each plastic “event” induces a displacement field that is of a quadrupolar nature. Such plastic events are commonly modeled as Eshelby circular inclusions.

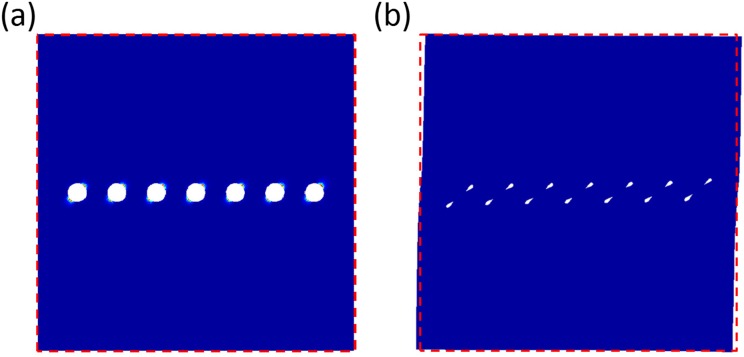
In the geometric framework presented here, such plastic deformations are naturally described by quadrupoles of the reference Gaussian curvature. The conformal function φ corresponds to seven quadrupoles equally spaced on the domain $\left[\mathrm{0,10}\right]\times \left[\mathrm{0,10}\right]$. An example similar to the one presented in ref. 32 is

$$\phi \left(r,\theta \right)=q{\displaystyle \sum _{i=1}^7\frac{2\left(r\cos \theta -i\times 10/8\right)\left(r\sin \theta -5\right)}{{\left({\left(r\cos \theta -i\times 10/8\right)}^2+{\left(r\sin \theta -5\right)}^2\right)}^2}}.$$

Using a numerical simulation, we found that such an array of quadrupoles results in a shear displacement (Fig. S2A) that is reminiscent of the one observed in ref. 32.

Fig. S2.

The deformation due to a linear array of curvature quadrupoles. (A) The dashed line is the shape of a squared domain with no defect in it. (B) After introducing an array of quadrupoles, the minimization process for the elastic energy changes the shape of the domain. The comparison with the dashed line reveals that the deformation induced is almost a pure shear.

Fig. S1.

Realization of an edge dislocation in a hexagonal lattice. (A) The crystal is cut along the dashed red line and particles above the cut are shifted by 2 atomic units. (B) The red particles are removed and the loose edges are welded together. (C) A 5–7 pair resulting from an edge dislocation. A contour of four lattice spacing along each crystallographic direction (yellow arrows) requires two additional lattice units (red arrows) to close up a loop.

In addition, we found that an exact displacement field can be obtained analytically with no approximations. As will be explained, the absence of geometric approximations together with the solution for a single quadrupole is the key for the tractability of the problem.

Earlier we found the isometric embedding of a given reference metric of a single quadrupole. Because both before and after the appearance of the quadrupole the manifold was globally isometric to the Euclidean plane, the quadrupole results only in a “change of shape.” Hence, to describe the effect of the appearance of a quadrupole, one can write the displacement field it induces. We denote $\text{Dis}\left(\overrightarrow{x},\overrightarrow{x_0},\overrightarrow{Q}\right)$ the displacement field in $\overrightarrow{x}$ induced by a quadrupole located at $\overrightarrow{x_0}$ with a quadrupole charge $\overrightarrow{Q}=\left(Q_1,Q_2\right)$.

Note that the displacement field depends in the coordinates of the reference manifold alone. This fact enables us to set up an array of quadrupoles on the reference manifolds while we know exactly what will be the effect of each of them on some point $\overrightarrow{x}$. Because each multipole creates a well-known displacement field on a given point, the total displacement is the sum of the different displacement fields. Explicitly,

$$\text{Dis}\left(\overrightarrow{x}\right)={\displaystyle \sum _{i=1}^7\text{Dis}\left(\overrightarrow{x},\left(\frac{10i}{8},5\right),\left(0,q\right)\right)}.$$

In both the simulation and the analytic solution we took $2q=-0.35$. The analytic result is presented in Fig. S3 A and B. The fact that the displacement field can be deduced so easily shows that the geometric approach we presented is a powerful tool.

Fig. S3.

Analytical calculation of the displacement field induced by a linear array of curvature quadrupoles. (A) An analytical solution for the displacement field of an array of quadrupoles. (B) A zoom-in on a region between two quadrupoles (marked in a red dashed line in A). It is very similar to the displacement field observed in ref. 33.

Fig. S4.

A gray-level mask used to build discs with $\overline{\mathfrak{g}}=e^{2b\cos \theta /r}\left(d{r}^2+r^{2}d{\theta }^2\right)$ with $b={\left(5/2\pi \right)}_{mm}$ as in Fig. 1 in the main text. The metric in the inner circle deviates from $\overline{\mathfrak{g}}$ due to limited variation in shrinkage, and hence this circle is removed (Fig. 2 in the main text).

The Experimental Setting.

Our sheets are constructed from a temperature-responsive N-isopropylacrylamide (NIPA) gel. The gel shrinks at about $34\hspace{0.5em}°\text{C}$ with a shrinkage factor that depends on the cross-linking density. The reference metric is prescribed via spatial variation of the cross-linking ratio across the sheet. The polymerization of the NIPA monomers (8% in water) is made using ammonium persulfate (APS) (0.8%) and tetramethylethylenediamine (TEMED) (0.08 pcm). The resultant polymer solution is left for 1 wk to ensure a completion of the chemical reaction. Next, we mix the NIPA polymer solution with the cross-linker (Laptonite XLS) and the photoinitiator (riboflavin). The solution is degassed and placed between two fused silica plates spaced 0.5 mm apart. The desired target metric is calculated using locally conformal coordinates, and a local conformal factor is obtained. The conformal factor “map” is converted into a grayscale color mask, using a calibration function. The calculated mask and its mirror image are printed on polyethylene sheets, using a laser printer. The masks are then placed on the outer side of two silica plates. The polymer solution is irradiated by a broad spectrum UV source from both sides for 10 min and turns into a nonhomogeneous gel sheet. We cut the gel into the desired shape and it is left in water for the night to wash the reaction products and to let it swell into its hydrated size. To “activate” the target metric, the gel is slowly heated in a water bath to $34.3\hspace{0.5em}°\text{C}$. The planar configuration is then measured using a camera that is installed at the top of the experimental system.