Amplifying the response of soft actuators by harnessing snap-through instabilities

Significance

Although instabilities have traditionally been avoided as they often represent mechanical failure, here we embrace them to amplify the response of fluidic soft actuators. Besides presenting a robust strategy to trigger snap-through instabilities at constant volume in soft fluidic actuators, we also show that the energy released at the onset of the instabilities can be harnessed to trigger instantaneous and significant changes in internal pressure, extension, shape, and exerted force. Therefore, in stark contrast to previously studied soft fluidic actuators, we demonstrate that by harnessing snap-through instabilities it is possible to design and construct systems with highly controllable nonlinear behavior, in which small amounts of fluid suffice to generate large outputs.

Abstract

Soft, inflatable segments are the active elements responsible for the actuation of soft machines and robots. Although current designs of fluidic actuators achieve motion with large amplitudes, they require large amounts of supplied volume, limiting their speed and compactness. To circumvent these limitations, here we embrace instabilities and show that they can be exploited to amplify the response of the system. By combining experimental and numerical tools we design and construct fluidic actuators in which snap-through instabilities are harnessed to generate large motion, high forces, and fast actuation at constant volume. Our study opens avenues for the design of the next generation of soft actuators and robots in which small amounts of volume are sufficient to achieve significant ranges of motion.

The ability of elastomeric materials to undergo large deformation has recently enabled the design of actuators that are inexpensive, easy to fabricate, and only require a single source of pressure for their actuation, and still achieve complex motion (1–5). These unique characteristics have allowed for a variety of innovative applications in areas as diverse as medical devices (6, 7), search and rescue systems (8), and adaptive robots (9–11). However, existing fluidic soft actuators typically show a continuous, quasi-monotonic relation between input and output, so they rely on large amounts of fluid to generate large deformations or exert high forces.

By contrast, it is well known that a variety of elastic instabilities can be triggered in elastomeric films, resulting in sudden and significant geometric changes (12, 13). Such instabilities have traditionally been avoided as they often represent mechanical failure. However, a new trend is emerging in which instabilities are harnessed to enable new functionalities. For example, it has been reported that buckling can be instrumental in the design of stretchable soft electronics (14, 15), and tunable metamaterials (16–18). Moreover, snap-through transitions have been shown to result in instantaneous giant voltage-triggered deformation (19, 20).

Here, we introduce a class of soft actuators comprised of interconnected fluidic segments, and show that snap-through instabilities in these systems can be harnessed to instantaneously trigger large changes in internal pressure, extension, shape, and exerted force. By combining experiments and numerical tools, we developed an approach that enables the design of customizable fluidic actuators for which a small increment in supplied volume (input) is sufficient to trigger large deformations or high forces (output).

Our work is inspired by the well-known two-balloon experiment, in which two identical balloons, inflated to different diameters, are connected to freely exchange air. Instead of the balloons becoming equal in size, for most cases the smaller balloon becomes even smaller and the balloon with the larger diameter further increases in volume (Movie S1). This unexpected behavior originates from the balloons’ nonlinear relation between pressure and volume, characterized by a pronounced pressure peak (21, 22). Interestingly, for certain combinations of interconnected balloons, such nonlinear response can result in snap-through instabilities at constant volume, which lead to significant and sudden changes of the membranes’ diameters (Figs. S1 and S2). It is straightforward to show analytically that these instabilities can be triggered only if the pressure–volume relation of at least one of the membranes is characterized by (i) a pronounced initial peak in pressure, ($ii$) subsequent softening, and ($iii$) a final steep increase in pressure (Analytical Exploration: Response of Interconnected Spherical Membranes Upon Inflation).

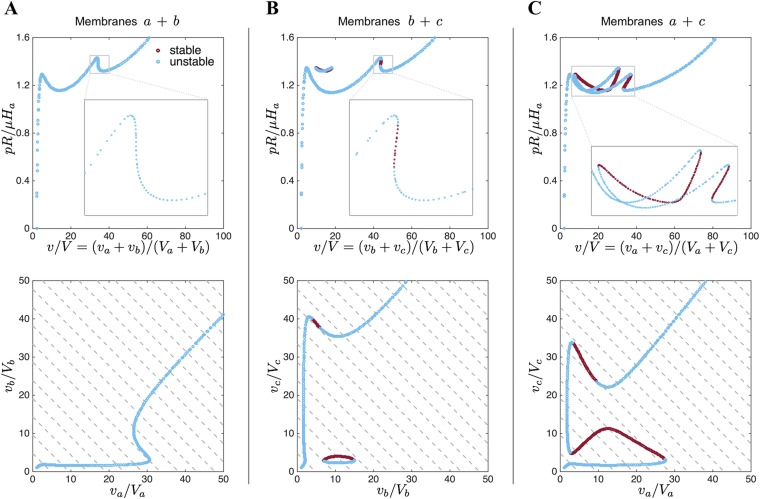
Fig. S1.

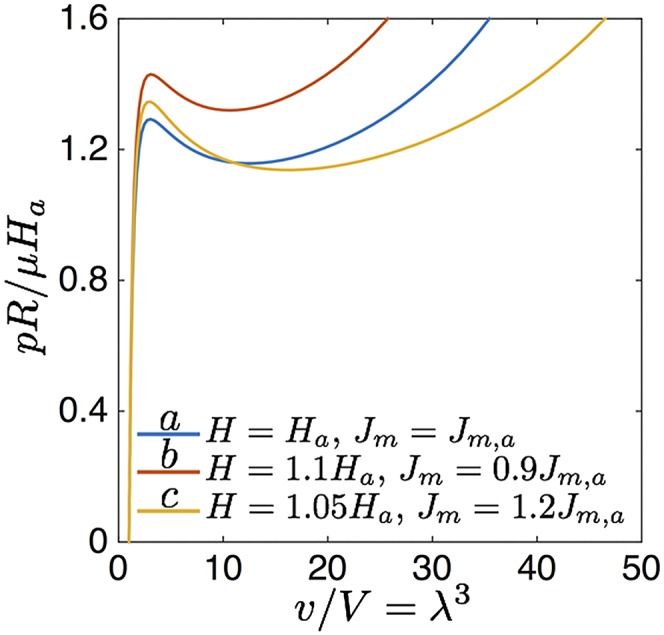
Relation between the pressure and volume for three different hyperelastic spherical membranes upon inflation.

Fig. S2.

Response of two interconnected spherical membranes upon inflation. The response of the individual membranes is shown in Fig. S1. The equilibrium states and their stability have been obtained numerically. The pressure–volume relation and the relation between the volume of the individual membranes are shown for systems comprising (A) membranes a and b, (B) membranes b and c, and (C) membranes a and c.

Highly Nonlinear Fluidic Segments

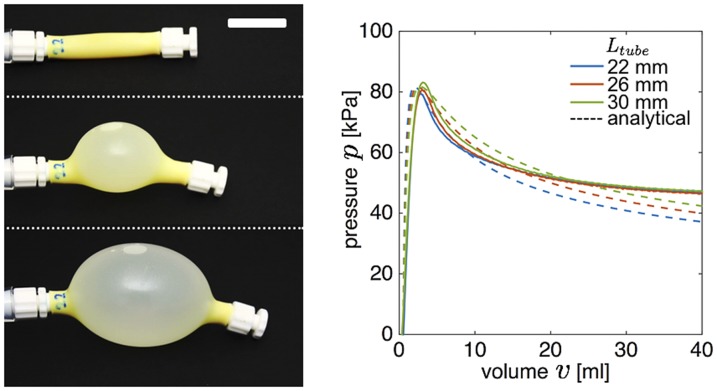
To experimentally realize inflatable segments characterized by such a nonlinear pressure–volume relation, we initially fabricated fluidic segments that consist of a soft latex tube of initial length $L_{tube}$, inner radius $R=6.35$ mm, and thickness $H=0.79$ mm. We measured the pressure–volume relation experimentally for three segments with $L_{tube}=22-30$ mm, and found that their response is not affected by their length (Fig. S3). Moreover, the response does not show a final steep increase in pressure. This is because latex has an almost linear behavior, even at large strains.

Fig. S3.

Evolution of pressure (p) as a function of the supplied volume (v) for three latex tubes characterized by $L_{tube}=$ 22, 26, and 30 mm as measured in experiments (solid lines) and predicted by the analytical model (dashed lines). Snapshots of a tube characterized by $L_{tube}=22$ mm at $v=0,20,40$ mL are shown on the left. (Scale bar: 10 mm.)

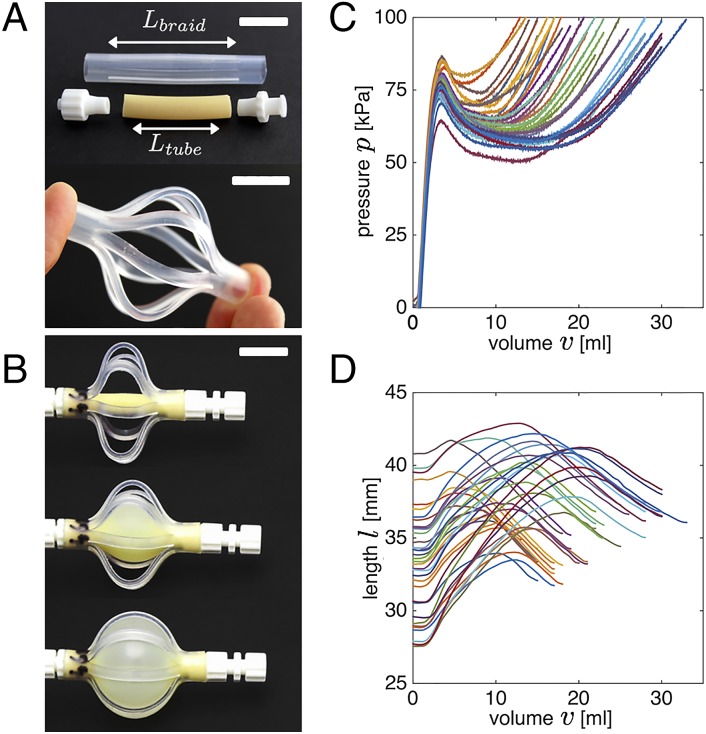
Next, to construct fluidic segments with a final steep increase in pressure and a response that can be easily tuned and controlled, we enclosed the latex tube by longer and stiffer braids of length $L_{braid}$ (Fig. 1A). It is important to note that the effect of the stiff braids is twofold. First, as $L_{braid}>L_{tube}$, the braids are in a buckled state when connected to the latex tube (Fig. 1B), and therefore apply an axial force, F, to the membrane. Second, at a certain point during inflation when the membrane and the braids come into contact, the overall response of the segments stiffens.

Fig. 1.

(A) Outer and stiffer braids are added to the latex tube to create fluidic segments with highly nonlinear response. (B) Snapshots of a segment characterized by $\left(L_{braid},L_{tube}\right)=\left(46,20\right)$ during inflation at $v=0,10,20$ mL. Evolution of (C) pressure (p) and (D) length (l) as a function of the supplied volume (v) for 36 fluidic segments characterized by $L_{braid}=40-50$ mm and $L_{tube}=20-30$ mm. (Scale bars: 10 mm.)

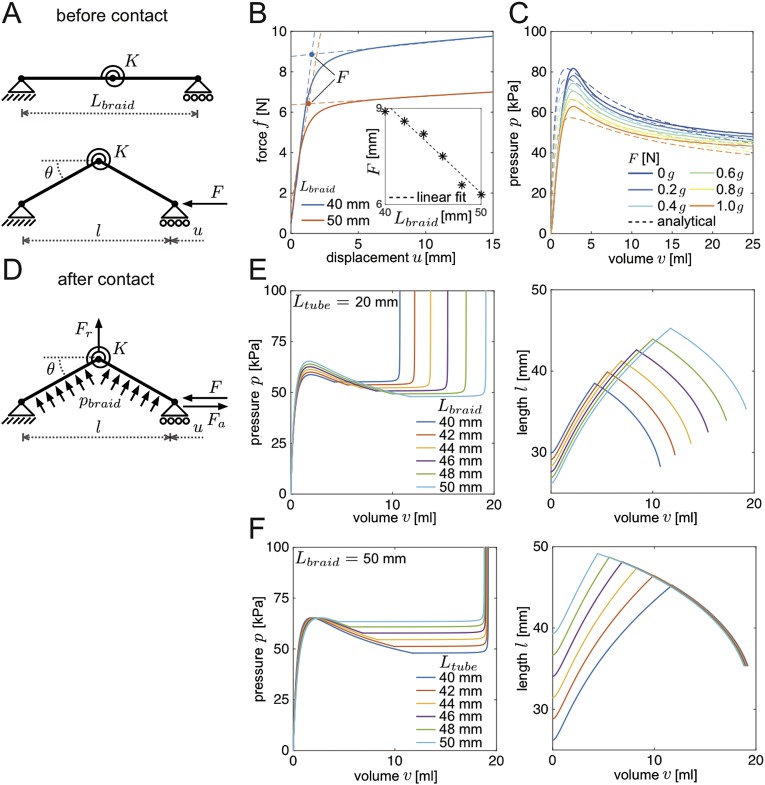
We derived a simple analytical model to predict the effect of $L_{braid}$ and $L_{tube}$ on the nonlinear response of these braided fluidic segments (Simple Analytical Model to Predict the Response of the Fluidic Segments). It is interesting to note that our analysis indicates that for a latex tube of given length, shorter braids lower the peak pressure due to larger axial forces (Fig. S4 C and E). Moreover, it also shows that $L_{braid}$ strongly affects the volume at which stiffening occurs. In fact, the shorter the braids, the earlier contact between the braids and the membrane occurs, reducing the amount of supplied volume required to have a steep increase in pressure. Conversely, if $L_{braid}$ is fixed, and the length of the membrane is varied, both the pressure peak and the volume at which stiffening occurs remain unaltered (Fig. S4F). However, in this case we find that shorter tubes lower the pressure of the softening region. Finally, the analytical model also indicates that the length of the fluidic segments, $l={\lambda }_z{L}_{tube}$, initially increases upon inflation (Fig. S4 E and F). However, when the tube and braids come into contact, further elongation is restrained by the braids and the segments shorten as a function of the supplied volume.

Fig. S4.

Analytical prediction of the response of individual fluidic segments. (A) Diagram of the braids before contact with the membrane (i.e., $v<v_{braid}$). (B) Experimentally obtained force-displacement relation for braids with $L_{braid}=40-50$ under uniaxial compression. The Inset shows the critical force, F, measured from experiments. (C) Evolution of pressure (p) as a function of the supplied volume (v) for a latex tube subjected to an axial force $F=0-1\hspace{0.17em}g$ (g denoting the gravitational acceleration). Continuous and dashed lines correspond to experimental data and analytical predictions, respectively. (D) Diagram of the braids after contact with the membrane. (E) Predicted response for six segments characterized by $L_{tube}=20$ mm and $L_{braid}=40-50$ mm. (F) Predicted response for six segments characterized by $L_{tube}=20-30$ mm and $L_{braid}=50$.

Having demonstrated analytically that fluidic segments with the desired nonlinear response can be constructed by enclosing a latex tube by longer and stiffer braids, and that their response can be controlled by changing $L_{braid}$ and $L_{tube}$, we now proceed to fabricate such actuators. The stiffer braids are made from polyethylene-lined ethyl vinyl acetate tubing, with an inner radius of 7.94 mm and a thickness of 1.59 mm. Eight braids are formed by partly cutting this outer tube along its length guided by a 3D printed socket. Finally, Nylon Luer lock couplings (one socket and one plug) are glued to both ends of the fluidic segments to enable easy connection (Fig. 1A). We then measure their response experimentally by inflating them with water at a rate of 60 mL/min, ensuring quasi-static conditions (Fig. 1B and Movie S2).

We fabricated 36 segments with $L_{braid}=40-50$ mm and $L_{tube}=20-30$ mm. As shown in Fig. 1C, all fluidic segments are characterized by the desired nonlinear pressure—volume relation and follow the trends predicted by the analytical model (Fig. S4 E and F). In particular, we find that for the 36 tested segments the initial peak in pressure ranges between 65 and 85 kPa (Fig. 1C). We also monitored the length of the segments during inflation (Fig. 1D). As predicted by the analytical model, we find that initially the segments elongate, but then shorten when the tube and braids come into contact. It is important to note that no instabilities are triggered upon inflation of the individual segments, because the supplied volume is controlled, not the pressure.

Combined Soft Actuator

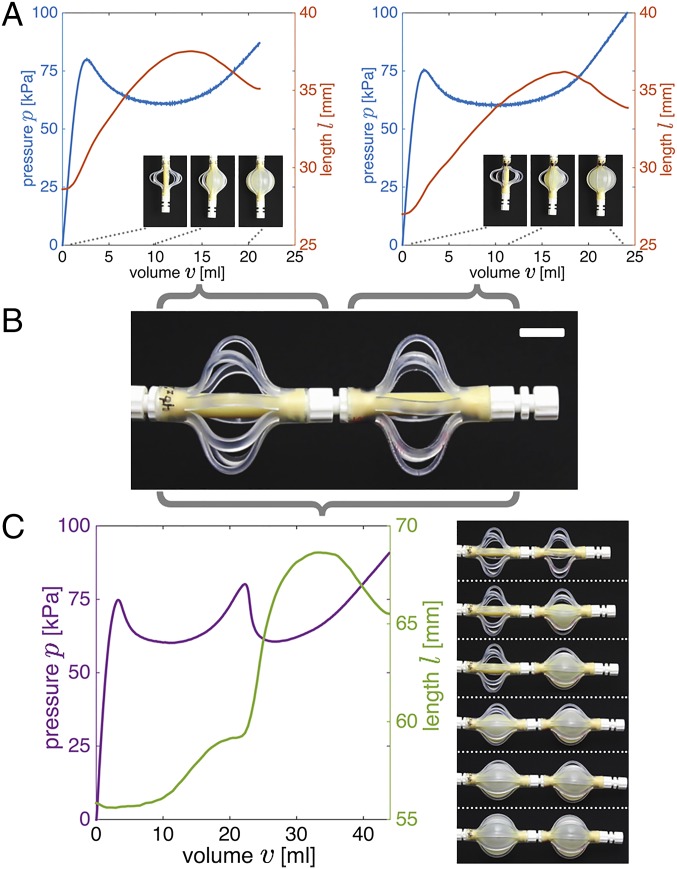
Next, we created a new, combined soft actuator by interconnecting the two segments whose individual response is shown in Fig. 2A. Upon inflation of this combined actuator, very rich behavior emerges (Fig. 2C and Movie S3). In fact, the pressure–volume response of the combined actuator is not only characterized by two peaks, but the second peak is also accompanied by a significant and instantaneous elongation. This suggests that an instability at constant volume has been triggered.

Fig. 2.

(A) Evolution of pressure (p) and length (l) as a function of the supplied volume (v) for two fluidic segments characterized by $\left(L_{braid},L_{tube}\right)=\left(46,20\right)$ and $\left(46,22\right)$ mm. Snapshots of the fluidic segments at $v=0,10,20$ and $v=0,12,24$ mL are shown as Insets, respectively. (B) The two fluidic segments are connected to form a new, combined soft actuator. (C) Evolution of pressure (p) and length (l) as a function of the supplied volume (v) for the combined actuator. Snapshots of the combined actuator at $v=0,9,18,27,36,45$ mL are shown as Insets.

Numerical Algorithm.

To better understand the behavior of such combined actuators, we developed a numerical algorithm that accurately predicts the response of systems containing n segments, based solely on the experimental pressure–volume curves of the individual segments. By using the 36 segments from experiments as building blocks, we can construct $36!/\left[\left(36-n\right)!n!\right]$ combined actuators comprising n segments (i.e., 630 different combined actuators for $n=2$; 7,140 for $n=3$; and 58,905 for $n=4$), where we assume that the order in which we arrange the segments does not matter. It is therefore crucial to implement a robust algorithm to efficiently scan the range of responses that can be achieved.

We start by noting that, upon inflation, the state of the ith segment is defined by its pressure $p_i$ and volume $v_i$, and its stored elastic energy can be calculated as

$$E_i\left(v_i\right)={\displaystyle \underset{V_i}{\overset{v_i}{\int }}{p}_i\left(\tilde{v}\right)\mathrm{d}\tilde{v}},$$ [1]

in which we neglect dynamic effects. Moreover, $V_i$ denotes the volume of the ith segment in the unpressurized state. When the total volume of the system, $v={\displaystyle {\sum }_{i=1}^n{v}_i}$, is controlled (as in all our experiments), the response of the system is characterized by $n-1$ variables $v_1,\dots ,v_{n-1}$ and the constraint

$$v_n=v-{\displaystyle \sum _{i=1}^{n-1}{v}_i}.$$ [2]

To determine the equilibrium configurations, we first define the elastic energy, E, stored in the system, which is given by the sum of the elastic energy of the individual segments

$$E\left(v_1,\dots ,v_n\right)={\displaystyle \sum _{i=1}^n{\displaystyle \underset{V_i}{\overset{v_i}{\int }}{p}_i\left(\tilde{v}\right)\mathrm{d}\tilde{v}}},$$ [3]

and use Eq. 2 to express the energy in terms of $n-1$ variables

$$\tilde{E}\left(v_1,\dots ,v_{n-1}\right)={\displaystyle \sum _{i=1}^{n-1}{\displaystyle \underset{V_i}{\overset{v_i}{\int }}{p}_i\left(\tilde{v}\right)\mathrm{d}\tilde{v}}}+{\displaystyle \underset{V_n}{\overset{v-{\displaystyle {\sum }_{i=1}^{n-1}{v}_i}}{\int }}{p}_n\left(\tilde{v}\right)\mathrm{d}\tilde{v}}.$$ [4]

Next, we implement a numerical algorithm that finds the equilibrium path followed by the actuator upon inflation (i.e., increasing v). Starting from the initial configuration (i.e., $v_i=V_i$), we incrementally increase the total volume of the system (v) and locally minimize the elastic energy ($\tilde{E}$). Because Eq. 4 already takes into account the volume constraint (Eq. 2), we use an unconstrained optimization algorithm such as the Nelder–Mead simplex algorithm implemented in Matlab (23). Note that this algorithm looks only locally for an energy minimum, similar to what happens in the experiments, and therefore it does not identify additional minima at the same volume that may appear during inflation.

Using the aforementioned algorithm, we find that for many actuators the energy can suddenly decrease upon inflation, indicating that a snap-through instability at constant volume has been triggered. To fully unravel the response of the actuators, we also detect all equilibrium configurations and evaluate their stability. The equilibrium states for the system can be found by imposing

$$\frac{\partial \tilde{E}}{\partial v_i}=0,\hspace{1em}\hspace{1em}\forall i\in \left\{1,\dots ,n-1\right\}.$$ [5]

Substitution of Eq. 4 into Eq. 5, yields

$$\begin{array}{c}\frac{\partial \tilde{E}}{\partial v_i}=p_i\left(v_i\right)-p_n\left(v-{\displaystyle \sum _{j=1}^{n-1}{v}_j}\right)=0,\\ \forall i\in \left\{1,\dots ,n-1\right\},\end{array}$$ [6]

which, when substituting Eq. 2, can be rewritten as

$$p_1\left(v_1\right)=p_2\left(v_2\right)=\dots =p_n\left(v_n\right).$$ [7]

As expected, Eq. 7 ensures that the pressure is the same in all n segments connected in series.

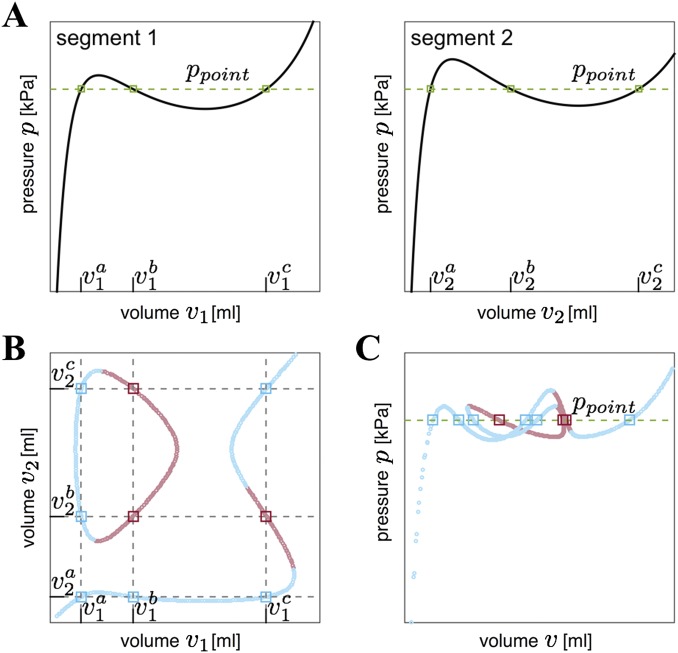
Operationally, to determine all of the equilibrium configurations of a combined soft actuator comprising n fluidic segments, we first define 1,000 equispaced pressure points between 0 and 100 kPa. Then, for each of the n segments we find all volumes that result in those values of pressure (Fig. S5A). Finally, for each value of pressure, we determine the equilibrium states by making all possible combinations of those volumes (Fig. S5B). Note that by using Eq. 2 we can also determine the total volume in the system at each equilibrium state, and then plot the pressure–volume response for the combined actuator (Fig. S5C).

Fig. S5.

Numerical procedure to determine the equilibrium configurations for a combined actuator with $n=2$. (A) We identify the volumes of each segment that correspond to a given value of pressure (in this case $p_{point}$). (B) We find all corresponding equilibrium configurations for the combined actuator by combining all those volumes. (C) Because $v=v_1+v_2$, we can also identify all equilibrium points in the pressure–volume curve for the combined actuator.

Finally, we check the stability of each equilibrium configuration. Because an equilibrium state is stable when it corresponds to a minimum of the elastic energy $\tilde{E}$ defined in Eq. 4, at any stable equilibrium solution the Hessian matrix

$$H\left(\tilde{E}\right)\left(v_1,\dots ,v_{n-1}\right)=\left[\begin{array}{ccc}\frac{{\partial }^2\tilde{E}}{\partial v_1^2}& \dots & \frac{{\partial }^2\tilde{E}}{\partial v_1\partial v_{n-1}}\\ ⋮& \ddots & ⋮\\ \frac{{\partial }^2\tilde{E}}{\partial v_{n-1}\partial v_1}& \dots & \frac{{\partial }^2\tilde{E}}{\partial v_{n-1}^2}\end{array}\right]$$ [8]

is positive definite. Note that the second-order partial derivatives in Eq. 8 can be evaluated as

$$\frac{{\partial }^2\tilde{E}}{\partial v_i\partial v_j}=\{\begin{array}{ll}{p}_i\prime \left(v_i\right)+p_n\prime \left(v-{\displaystyle \sum _{k=1}^{n-1}{v}_k}\right),\hfill & \text{if}\hspace{0.17em}i=j\hfill \\ p_n\prime \left(v-{\displaystyle \sum _{k=1}^{n-1}{v}_k}\right),\hfill & \text{if}\hspace{0.17em}i\ne j,\hfill \end{array}$$ [9]

in which $p_i\prime \left(\tilde{v}\right)=\mathrm{d}{p}_i/\mathrm{d}\tilde{v}$. Taking advantage of the fact that all off-diagonal terms of the Hessian matrix are identical and using Sylvester’s criterion (24), we find that an equilibrium state is stable if

$$\begin{array}{l}{\displaystyle \prod }_{i=1}^k{p}_i\prime \left(v_i\right)+p_n\prime \left(v-{\displaystyle \sum _{k=1}^{n-1}{v}_k}\right){\displaystyle \sum _{i=1}^k{\displaystyle \prod _{j=1,j\ne i}^k{p}_j\prime \left(v_j\right)>0}},\\ \forall k=1,\dots ,n-1.\end{array}$$ [10]

Numerical Results.

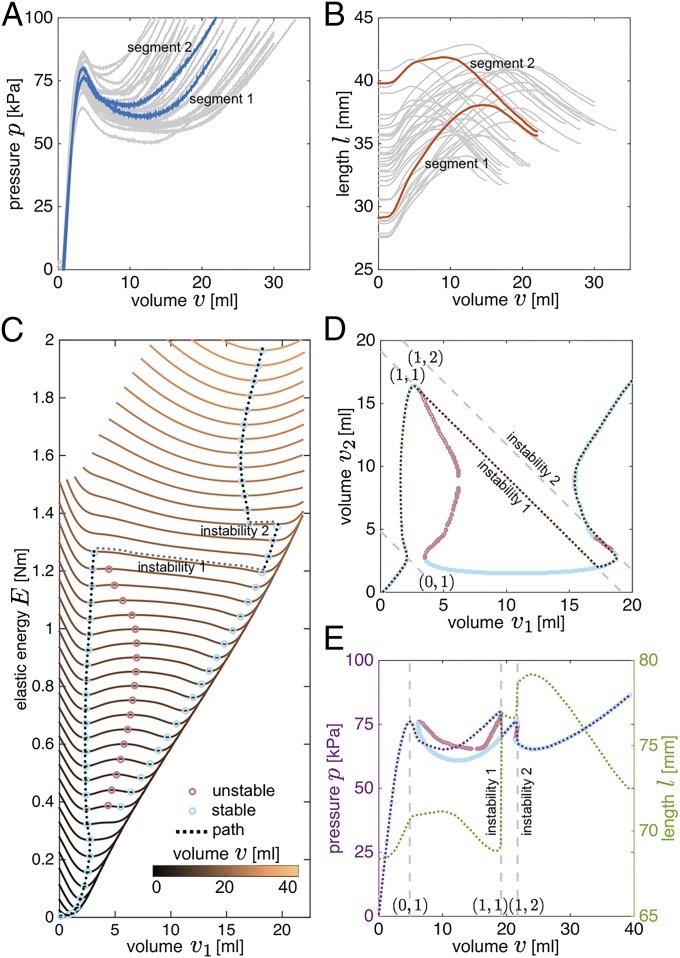
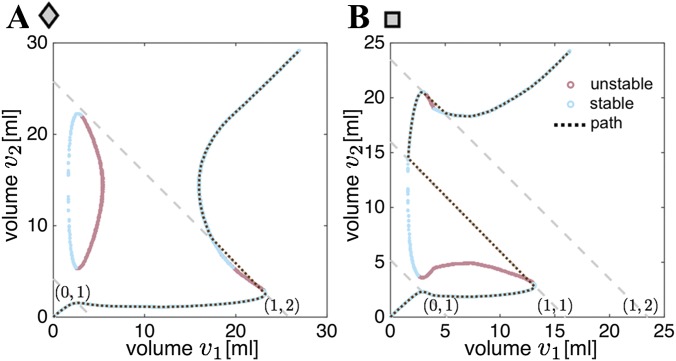
To demonstrate the numerical algorithm, we focus on two segments where the experimentally measured pressure–volume and length–volume responses are highlighted in Fig. 3 A and B. In Fig. 3C we report the evolution of the total elastic energy of the system, E, as a function of the volume of the first segment, $v_1$, for increasing values of the total supplied volume, v, and in Fig. 3D we show all equilibrium configurations in the $v_1$–$v_2$ plane. We find that initially ($0<v<5$ mL) the volume of both segments increases gradually. However, for $5<v<19$ mL, $v_1$ remains almost constant and all additional volume that is added to the system flows into the second segment. Moreover, at $v=6$ mL a second local minimum for E emerges, so that for $6<v<19$ mL the system is characterized by two stable equilibrium configurations. Although for $v>13$ mL this second minimum has the lowest energy, the system remains in the original energy valley until $v=19$ mL. At this point the local minimum of E in which the system is residing disappears, so that its equilibrium configuration becomes unstable, forcing the actuator to snap to the second equilibrium characterized by a lower value of E. Interestingly, this instability triggers a significant internal volume flow from the second to the first segment (Fig. 3D) and a sudden increase in length (Fig. 3E). Further inflating the system to $v=22$ mL triggers a second instability, at which some volume suddenly flows back from the first to the second segment. After this second instability, increasing the system’s volume further inflates both segments simultaneously.

Fig. 3.

(A) Experimentally measured pressure–volume relations for all 36 fabricated fluidic segments. (B) Experimentally measured length–volume relations for all 36 fabricated segments. (C) Numerically determined elastic energy, E, for a combined actuator comprising the two segments whose individual behavior is highlighted in A and B. The energy is shown for increasing values of the supplied volume, v. The stable and unstable equilibrium configurations are highlighted by blue and red circular markers, respectively. (D) Equilibrium configurations for the combined actuators. At $v=19$ mL an unstable (1, 1) transition is found, resulting in a significant internal volume flow. A second instability of type (1, 2) is then triggered at $v=22$ mL. (E) Numerically determined pressure–volume and length–volume relations for the combined soft actuator.

All transitions that take place upon inflation (i.e., at $v=5$, 19, and 22 mL) are highlighted by a peak in the pressure–volume curve (Fig. 3E), and correspond to instances at which one or more of the individual segments cross their own peak in pressure. These state transitions can either be stable or unstable (Fig. 3 C–E). A stable transition always leads to an increase of the elastic energy stored in the system, and an instability results in a new equilibrium configuration with lower energy. Each state transition can therefore be characterized by the elastic energy release, which we define as a normalized scalar $\mathrm{\Delta }\widehat{E}=\left(E_{post}-E_{pre}\right)/E_{pre}$. Here and in the following, the subscripts $pre$ and $post$ indicate the values of the quantity immediately before and after the state transition. Moreover, to better understand the effects of each transition on the system, we define the associated normalized changes in internal volume distribution, length and pressure as $\mathrm{\Delta }\widehat{v}=\underset{i}{\text{max}}\left(v_{i,post}-v_{i,pre}\right)/v_{pre}$, $\mathrm{\Delta }\widehat{l}=\left(l_{post}-l_{pre}\right)/\left(l_{pre}\right)$ and $\mathrm{\Delta }\widehat{p}=(p_{post}-p_{pre})/p_{pre}$.

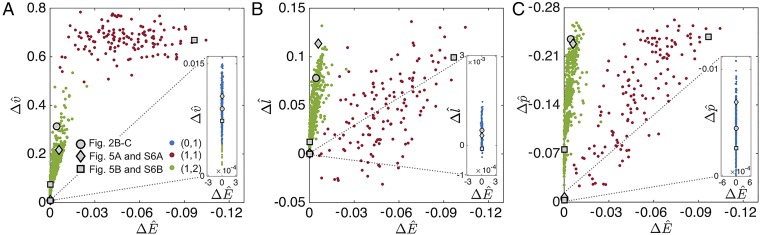
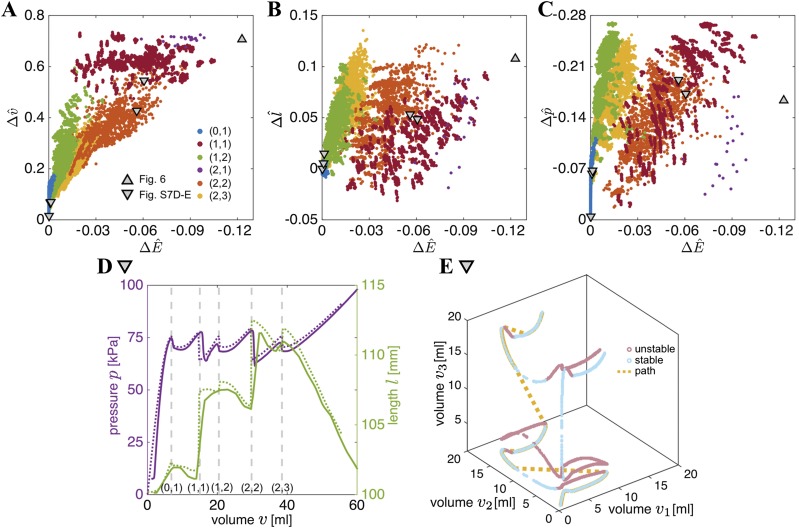
In Fig. 4 we report $\mathrm{\Delta }\widehat{v}$, $\mathrm{\Delta }\widehat{l}$, and $\mathrm{\Delta }\widehat{p}$ versus the normalized change in energy, $\mathrm{\Delta }\widehat{E}$, for all transitions that occur in the 630 combined soft actuators comprising $n=2$ segments. Note that there are more than 630 data points, because all actuators show two or more state transitions. We find that $-0.1\le \mathrm{\Delta }\widehat{E}\le 4\hspace{0.17em}\cdot \hspace{0.17em}{10}^{-5}$, indicating that some of the transitions are stable (i.e., $\mathrm{\Delta }\widehat{E}>0$), and others are unstable ($\mathrm{\Delta }\widehat{E}<0$). We furthermore observe that the energy increase for stable transitions is very small, and is therefore sensitive to the increment size used in the numerical algorithm. By contrast, the elastic energy released during unstable transitions can be as high as 10% of the stored energy.

Fig. 4.

A–C show $\mathrm{\Delta }\widehat{v}$, $\mathrm{\Delta }\widehat{l}$ and $\mathrm{\Delta }\widehat{p}$ versus the normalized change in energy $\mathrm{\Delta }\widehat{E}$ for all state transitions that occur in the 630 combined soft actuators comprising $n=2$ fluidic segments. Blue, red, and green markers correspond to $\left(0,1\right)$, $\left(1,1\right)$, and $\left(1,2\right)$ transitions, respectively; (A) $\mathrm{\Delta }\widehat{v}$ versus $\mathrm{\Delta }\widehat{E}$; (B) $\mathrm{\Delta }\widehat{l}$ versus $\mathrm{\Delta }\widehat{E}$; and (C) $\mathrm{\Delta }\widehat{p}$ versus $\mathrm{\Delta }\widehat{E}$.

We also characterize each state transition according to the changes induced in the individual segments, and use $\left(\alpha ,\beta \right)$ to identify the number of segments to the right of their pressure peak before (α) and after (β) the state transition. For combined soft actuators comprising $n=2$ segments, the numerical results show three possible types of transitions: $\left(0,1\right)$, in which both segments are initially on the left of their peak in pressure and then one of them crosses its pressure peak during the state transition (blue markers in Fig. 4); $\left(1,2\right)$, in which the second segment also crosses its peak in pressure (green markers in Fig. 4); $\left(1,1\right)$, in which both segments cross their pressure peak, but one while inflating and the other while deflating (red markers in Fig. 4). We find that transitions of type $\left(0,1\right)$ occur in all combined actuators and are always stable. Therefore, the associated changes in elastic energy, length, pressure, and the internal volume distribution are approximately zero. By contrast, transitions of type $\left(1,1\right)$ are always unstable and result in both high elastic energy release (up to 10%) and high internal volume flow (up to 80%). Unlike $\left(1,1\right)$, transitions of type $\left(1,2\right)$ can be either stable or unstable. The unstable transitions result in moderate energy release (up to 2.5%), but can lead to significant and instantaneous changes in length (up to $14\text{\%}$). Therefore, our analysis clearly indicates not only that snap-through instabilities at constant volume can be triggered in soft fluidic actuators, but also that the associated released energy can be harnessed to trigger sudden changes in length, drops in pressure, and internal volume flows.

Experimental Results.

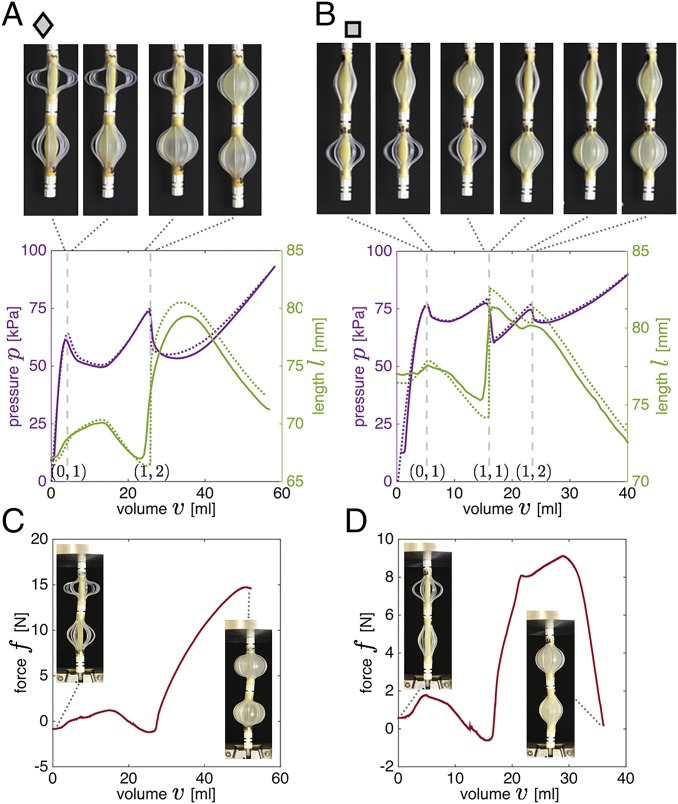
To validate the numerical predictions, we measured experimentally the response of several combined actuators. In Fig. 5A we show the results for the system whose predicted transitions are indicated by the diamond gray markers in Fig. 4. We compare the numerically predicted and experimentally observed mechanical response, finding an excellent agreement. In particular, for this combined actuator we find that the pressure–volume curve is characterized by two peaks, indicating that two transitions take place upon inflation. Although the $\left(0,1\right)$ transition is stable, the $\left(1,2\right)$ transition is unstable and results in an instantaneous and significant increase in length of 11% and a high pressure drop of 23% (Fig. 5A and Movie S4). This unstable transition is also accompanied by a moderate internal volume redistribution of 22%, resulting in the sudden inflation of the top actuator (see snapshots in Fig. 5A and numerical result in Fig. S6A).

Fig. 5.

(A and B) Experimental (solid lines) and numerical (dashed lines) pressure–volume curves for two soft actuators comprising $n=2$ fluidic segments. (A) Results for a combined actuator with $\left(L_{braid},L_{tube}\right)=\left(48,30\right)$ and $\left(50,20\right)$ mm. The transitions for this actuator are highlighted by diamond markers in Fig. 4. Snapshots of the combined actuators 0.5 mL before and after each state transition (at $v=4,26$ mL) are also shown. (B) Results for a combined actuator with $\left(L_{braid},L_{tube}\right)=\left(44,30\right)$ and $\left(48,26\right)$ mm. The transitions for this actuator are highlighted by square markers in Fig. 4. Snapshots of the combined actuators 0.5 mL before and after each state transition (at $v=5,16,24$ mL) are also shown. Experimentally measured exerted force as a function of the supplied volume for a combined actuator with (C) $\left(L_{braid},L_{tube}\right)=\left(48,30\right)$ and $\left(50,20\right)$ mm and (D) $\left(L_{braid},L_{tube}\right)=\left(44,30\right)$ and $\left(48,26\right)$ mm with constrained ends.

Fig. S6.

Numerical results for two combined soft actuators with $n=2$. (A) Relation between the individual volumes of the segments for a soft actuator with $\left(L_{braid},L_{tube}\right)=\left(48,30\right)$ and $\left(50,20\right)$ mm. (B) Relation between the individual volumes of the segments for a soft actuator with $\left(L_{braid},L_{tube}\right)=\left(44,30\right)$ and $\left(48,26\right)$ mm.

In Fig. 5B we present the results for the combined actuator whose response is indicated by the square gray markers in Fig. 4. Our analysis indicates that one stable $\left(0,1\right)$ transition and two unstable transitions are triggered during its inflation. The first snap-through instability is a $\left(1,1\right)$ transition and is accompanied by a significant and sudden volume redistribution (see snapshots in Fig. 5B and numerical result in Fig. S6B) and a large increase in length (Movie S5), and the second instability is a $\left(1,2\right)$ transition and results in smaller values for $\mathrm{\Delta }\widehat{l}$ and $\mathrm{\Delta }\widehat{v}$. Again, we observe an excellent agreement between experimental and numerical results, indicating that our modeling approach is accurate and can be used to effectively design soft actuators that harness instabilities to amplify their response.

Although the results reported in Fig. 5 A and B are for actuators free to expand, these systems can also be used to exert large forces while supplying only small volumes. To this end, in Fig. 5 C and D we show the force measured during inflation when the elongation of the actuators is completely constrained. We find that also in this case an instability is triggered, resulting in a sudden, large increase in the exerted force. Note that the volume at which the instability occurs is slightly different from that found in the case of free inflation. This discrepancy arises from the fact that the pressure–volume relation of each segment is affected by the conditions at its boundaries.

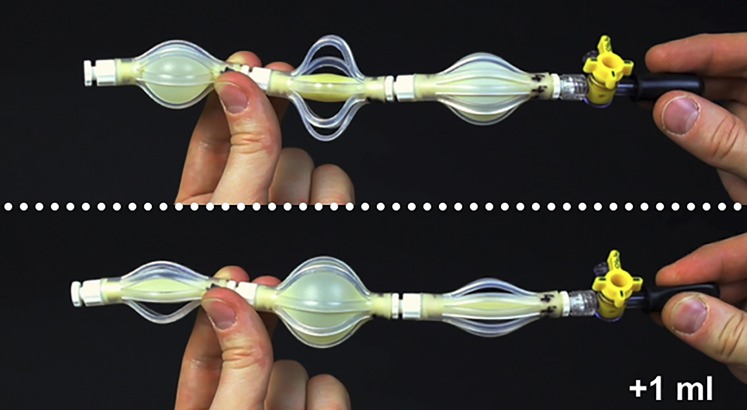
The proposed approach can be easily extended to study more complex combined actuators comprising a larger number of segments. By increasing n, new types of state transitions can be triggered. For example, transitions of type $\left(\mathrm{2,1}\right)$ are also observed for $n=3$ (Fig. S7 A–C), in which two segments deflate into a single one, causing all three segments to cross their peak in pressure. In Fig. 6, we focus on an actuator that undergoes an unstable $\left(\mathrm{2,1}\right)$ transition at $v=29$ mL. We first inflate the actuator to $v=28$ mL, and then decouple it from the syringe pump and connect it to a small reservoir containing only 1 mL of water. Remarkably, by adding only 1 mL of water to the system, we are able to trigger a significant internal volume flow of ∼20 mL that results in the deflation of two segments into one segment (Fig. 6 and Movie S6).These results further highlight that snap-through instability can be harnessed to amplify the effect of small inputs.

Fig. S7.

(A–C) $\mathrm{\Delta }\widehat{v}$, $\mathrm{\Delta }\widehat{l}$ and $\mathrm{\Delta }\widehat{p}$ versus the normalized change in energy $\mathrm{\Delta }\widehat{E}$ for all state transitions that occur in the 7,140 combined soft actuators comprising $n=3$ fluidic segments. Blue, red, green, purple, orange, and yellow markers correspond to $\left(0,1\right)$, $\left(1,1\right)$, $\left(1,2\right)$, $\left(2,1\right)$, $\left(2,2\right)$, and $\left(2,3\right)$ transitions, respectively. (D) Experimental (solid line) and numerical (dashed line) evolution of pressure and length as a function of the supplied volume for a soft actuator with $n=3$, characterized by $\left(L_{braid},L_{tube}\right)=\left(40,28\right)$, $\left(44,22\right)$, and $\left(48,26\right)$ mm. (E) Numerically determined relation between the individual volumes of the three segments.

Fig. 6.

Snapshots of a combined actuator with $\left(L_{braid},L_{tube}\right)=\left(\mathrm{40,28}\right)$, $\left(44,30\right)$, and $\left(50,24\right)$ mm. The numerical analysis predicts a $\left(2,1\right)$ state transition at $v=29$ mL (see gray triangle in Fig. S7 A–C). The combined actuator is inflated to $v=28$ mL, and then decoupled from the syringe pump and connected to a small reservoir containing only 1 mL of water. An additional volume of 1 mL supplied to the system is enough to trigger a significant internal volume flow of ∼20 mL that results in the deflation of two segments into one segment (Movie S6).

Conclusion

In summary, by combining experimental and numerical tools we have shown that snap-through instabilities at constant volume can be triggered when multiple fluidic segments with a highly nonlinear pressure–volume relation are interconnected, and that such unstable transitions can be exploited to amplify the response of the system. In stark contrast to most of the soft fluidic actuators previously studied, we have demonstrated that by harnessing snap-through instabilities it is possible to design and construct systems in which small amounts of fluid suffice to trigger instantaneous and significant changes in pressure, length, shape, and exerted force.

To simplify the analysis, in this study we have used water to actuate the segments (due to its incompressibility). However, it is important to note that the actuation speed of the proposed actuators can be greatly increased by supplying air. In fact, we find that water introduces significant inertia during inflation, limiting the actuation speed. It typically takes more than 1 s for the changes in length, pressure, and internal volume induced by the instability to fully take place (Movie S7). However, by simply using air to actuate the system and by adding a small reservoir to increase the energy stored in the system, the actuation time can be significantly reduced (from $\mathrm{\Delta }t=1.4$ to 0.1 s for the actuator considered in Movie S7), highlighting the potential of these systems for applications where speed is important. Although this actuation time is similar to that of recently reported high-speed soft actuators (3), only a small volume of supplied fluid is required to actuate the system because we exploit snap-through instabilities at constant volume. As a result, small compressors are sufficient to inflate these actuators, making them highly suitable for untethered applications.

Our results indicate that by combining fluidic segments with designed nonlinear responses and by embracing their nonlinearities, we can construct actuators capable of large motion, high forces, and fast actuation at constant volume. Although here we have focused specifically on controlling the nonlinear response of fluidic actuators, we believe that our analysis can also be used to enhance the response of other types of actuators (e.g., thermal, electrical and mechanical) by rationally introducing strong nonlinearities. Our approach therefore enables the design of a class of nonlinear systems that is waiting to be explored.

Materials and Methods

All individual soft fluidic segments and combined actuators investigated in this study are tested using a syringe pump (Standard Infuse/Withdraw PHD Ultra; Harvard Apparatus) equipped with two 50-mL syringes that have an accuracy of $\pm$ 0.1% (1000 series, Hamilton Company). The segments and the combined actuators are inflated at a rate of 60 and 20 mL/min, respectively, ensuring quasi-static conditions. Moreover, during inflation the pressure is measured using a silicon pressure sensor (MPX5100; Freescale Semiconductor) with a range of 0–100 kPa and an accuracy of $\pm$ 2.5%, which is connected to a data acquisition system (NI USB-6009, National Instruments). The elongation of the actuators is monitored by putting two markers on both ends of each actuator, and recording their position every two seconds with a high-resolution camera (D90 SLR, Nikon). The length of the actuator is then calculated from the pictures using a digital image processing code in Matlab. Each experiment is repeated 5 times, and the final response of the actuator as shown in the paper is determined by averaging the results of the last four tests. Finally, we measured the force exerted by the actuators during inflation when their elongation is completely constrained. In this case we use a uniaxial materials testing machine (model 5544A; Instron, Inc.) with a 100-N load cell to measure the reaction force during inflation.

Analytical Exploration: Response of Interconnected Spherical Membranes Upon Inflation

To identify the key components in the design of an inflatable system that undergoes a snap-through instability upon inflation, we analytically explore the equilibrium states of two spherical membranes, connected in series. We start by describing the equations governing the response of a single hyperelastic spherical membrane upon inflation (25, 26), and then discuss the behavior of two interconnected spherical membranes (27–30).

Response of a Hyperelastic Spherical Membrane upon Inflation.

We consider a spherical membrane with initial radius R, and initial thickness H, and assume that the membrane is thin (i.e., $H\ll R$), so that the contribution from bending and shear forces can be neglected. When the membrane is subjected to a uniform pressure p, a biaxial state of stress is achieved and the principal stretches are given by

$${\lambda }_{\theta }={\lambda }_{\varphi }=\frac{r}{R},\hspace{0.17em}{\lambda }_r=\frac{h}{H},$$ [S1]

r and h denoting respectively the radius and thickness of the membrane in the deformed configuration. Moreover, equilibrium requires

$${\sigma }_{\theta }={\sigma }_{\varphi }=\frac{pr}{2h},$$ [S2]

and the assumption of a plane stress condition yields

$${\sigma }_r=0,$$ [S3]

where ${\sigma }_{\theta }$, ${\sigma }_{\varphi }$, and ${\sigma }_r$ are the principal Cauchy stresses.

We consider the membrane to be made of a hyperelastic, incompressible material, the response of which is captured by the strain energy W. Because of incompressibility we have

$${\lambda }_r=\frac{1}{{\lambda }_{\theta }{\lambda }_{\varphi }},$$ [S4]

and therefore the stress in the material is given by

$${\sigma }_{\theta }={\sigma }_{\varphi }={\lambda }_{\theta }\frac{\partial W\left({\lambda }_{\theta },{\lambda }_{\varphi }\right)}{\partial {\lambda }_{\theta }}.$$ [S5]

Here, we model the material response using the incompressible Gent model (31), for which the strain energy is defined by

$$W\left({\lambda }_{\theta },{\lambda }_{\varphi }\right)=-\frac{\mu J_m}{2}\text{log}\left(1-\frac{{\lambda }_{\theta }^2+{\lambda }_{\varphi }^2+{\lambda }_{\theta }^{-2}{\lambda }_{\varphi }^{-2}-3}{J_m}\right),$$ [S6]

where μ is the initial shear modulus and $J_m$ is a constant related to the strain saturation of the material (as the stresses become infinite when $J_m-{\lambda }_{\theta }^2-{\lambda }_{\varphi }^2-{\lambda }_{\theta }^{-2}{\lambda }_{\varphi }^{-2}+3$ approaches zero). Note that the nonlinear pressure–volume response of an inflated spherical membrane depends greatly on the constitutive material model. Although in this study we have focused on a Gent model to achieve a final steep increase in pressure, when using a Varga, neo-Hookean, or three-term Ogden model no strain stiffening is observed upon inflation (32, 33). Although the material parameters entering in the Ogden model can be tuned to account for strain stiffening or to even suppress the pressure peak encounter during inflation, here we preferred to use the Gent model because only μ and $J_m$ need to be changed to control the nonlinear response (26).

Substitution of Eqs. S1, S2, and S6 into Eq. S5 yields

$${\sigma }_{\theta }=\frac{pr}{2h}=\mu J_m\frac{{\lambda }_{\theta }^6-1}{-1+{\lambda }_{\theta }^4\left(3+J_m\right)-2{\lambda }_{\theta }^6},$$ [S7]

which can be rewritten as

$$\frac{pR}{\mu H}=\frac{2J_m}{{\lambda }^3}\frac{{\lambda }^6-1}{-1+{\lambda }^4\left(3+J_m\right)-2{\lambda }^6},$$ [S8]

where we use Eq. S4 to express h as a function of r (i.e., $h=H{R}^2/r^2$), and in which we set $\lambda ={\lambda }_{\theta }$ for convenience. Eq. S8 clearly shows that the initial radius R, initial thickness H, and shear modulus μ only scale the value of the pressure and that the only parameter that changes the shape of the $p-\lambda$ curve is the stretching limit $J_m$. Note that the volume inside the membrane can be easily determined as

$$v=\frac{4\pi }{3}{\left(\lambda R\right)}^3.$$ [S9]

As an example, in Fig. S1 we show the $p-v$ curves for three spherical membranes characterized by the same radius R and shear modulus μ and (a) $H_a$ and $J_{m,a}$, (b) $H_b=1.1H_a$ and $J_{m,b}=0.9J_{m,a}$, and (c) $H_c=1.05H_a$ and $J_{m,c}=1.2J_{m,a}$.

It is important to note that in our analysis we assume that the deformation is homogeneous throughout the membrane, although it has been shown that this assumption can be violated by spherical membranes as they can exhibit asymmetric bifurcation modes (32, 34). However, these asymmetric modes do not affect the main features of the nonlinear pressure–volume relation typical for such membranes, and as such our analysis provides enough detail to qualitatively study the response of systems of interconnected membranes.

Response of Two Interconnected Spherical Membranes upon Inflation.

Having determined the pressure–volume curve for a single spherical membrane, we now determine the equilibrium states for a system of two interconnected membranes. For both membranes, we use the pressure–volume relation defined by Eqs. S8 and S9. Specialization of Eqs. 9 and 14 to a system comprising two spherical membranes, yields

$$v=v_1+v_2,$$ [S10]

and

$$p=p_1=p_2.$$ [S11]

Moreover, Eq. 17 reduces to

$$p_1\prime \left(v_1\right)+p_2\prime \left(v_2\right)>0,$$ [S12]

so that an equilibrium configuration for a system comprising $n=2$ spherical membranes is stable when

$${\displaystyle \sum _{i=1}^2-\hspace{0.17em}\frac{2H_i{\mu }_i{J}_{lm,i}}{R_i}\frac{3}{4\pi R_i}{\left({\lambda }_i{R}_i^3\right)}^{-2/3}\frac{3-7\left(3+J_{lm,i}\right){\lambda }_i^4+21{\lambda }_i^6+\left(3+J_{lm,i}\right){\lambda }_i^{10}-6{\lambda }_i^{12}}{{\lambda }_i^4{\left(1-\left(3+J_{lm,i}\right){\lambda }_i^4+2{\lambda }_i^6\right)}^2}>0},$$ [S13]

where ${\lambda }_i$ indicates the stretch in the ith membrane. Moreover, $H_i$ and $R_i$ denote the initial thickness and radius of the ith membrane and ${\mu }_i$ and $J_{lm,i}$ its shear modulus and strain saturation constant, respectively.

In Fig. S2 we show the response of the systems obtained by interconnecting membranes a and b (Fig. S2A), b and c (Fig. S2B), and a and c (Fig. S2C). Note that the pressure–volume curves for the individual segments are shown in Fig. S1. When connecting membranes a and b (Fig. S2A), upon inflation membrane a inflates first. Then, when this membrane starts to stiffen, membrane b also increases in volume. However, for this combined system all equilibrium points are stable. More interesting behavior is observed when combining membrane b and c (Fig. S2B). Initially, this system behaves similarly to the system shown in Fig. S2, with membrane c inflating first. However, at $v/V_a=42$ a snap-through instability is triggered, resulting in a sudden decrease in pressure and increase in the diameter of membrane b. Therefore, at the instability a significant amount of volume flows from membrane c to membrane b. We also note that this system is characterized by equilibrium configurations that are disconnected from the main curve, so that they will never be reached upon inflation. Finally, even more complex behavior can be achieved by connecting membranes a and c (Fig. S2C). Here, a first instability causes all volume to flow from membrane a to membrane c, and a second instability forces some volume to flow back from membrane c to membrane a.

Simple Analytical Model to Predict the Response of the Fluidic Segments

The analytical predictions reported above reveal that snap-through instabilities at constant volume can be triggered in a system comprising interconnected spherical membranes only if the pressure–volume relation of at least one of the membranes is characterized by (i) a pronounced initial peak in pressure, ($ii$) subsequent softening, and ($iii$) a final steep increase in pressure. As for the case of the Gent model used in the previous analytical exploration, such response can be achieved by using membranes made of elastomeric materials that exhibit stiffening at large strains. However, it is important to note that commercially available latex tubes are characterized by an almost linear behavior, so that their response can be nicely captured using a neo-Hookean model (35), for which the strain energy is defined as

$$W\left({\lambda }_1,{\lambda }_2,{\lambda }_3\right)=\frac{\mu }{2}\left({\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2-3\right),$$ [S14]

where $\mu =0.49$ MPa is the initial shear modulus of the latex material and ${\lambda }_i$ are the principal stretches. Note that the neo-Hookean strain energy in Eq. S14 can be obtained from the Gent energy density in the limit as $J_m\to \mathrm{\infty }$.

In the following, we first derive the pressure–volume relationship for a latex tube, and then we develop a simple analytical model to capture the response of the highly nonlinear braided fluidic segments used in this study.

Response of a Latex Tube Upon Inflation.

We start by investigating analytically the response of a cylindrical latex membrane with initial radius R, initial length $L_{tube}$, and initial thickness H, and assume that the membrane is thin (i.e., $H\ll R$), so that the contribution from bending and shear forces can be neglected. In particular, we determine the response when the membrane is inflated by an internal pressure p. For simplicity, we neglect end effects and local instabilities resulting from bulging (36–38), and assume that the cylindrical membrane deforms uniformly. The principal stretches are then given by

$${\lambda }_{\theta }=\frac{r}{R},\hspace{0.17em}{\lambda }_z=\frac{l}{L_{tube}},\hspace{0.17em}{\lambda }_r=\frac{h}{H},$$ [S15]

r, l, and h denoting the membrane’s radius, length, and thickness in the deformed configuration, respectively. Moreover, as in experiments, we assume that the tube has closed ends, so that it is subjected to an axial force $p\pi r^2$. For such a membrane, equilibrium requires

$${\sigma }_{\theta }=\frac{2prl}{2hl}=\frac{pr}{h},$$ [S16]

$${\sigma }_z=\frac{p\pi r^2}{2\pi rh}=\frac{pr}{2h},$$ [S17]

and the assumption of plane stress conditions yields

$${\sigma }_r=0,$$ [S18]

where ${\sigma }_i$ denote the principal Cauchy stresses.

We consider the membrane to be made of an incompressible neo-Hookean material (Eq. S14) and because of incompressibility we have

$${\lambda }_r{\lambda }_{\theta }{\lambda }_z=1.$$ [S19]

The stress in the material can then be expressed as

$${\sigma }_r={\lambda }_r\frac{\partial W}{\partial {\lambda }_r}-\tilde{p}=\mu {\lambda }_r^2-\tilde{p}=0\hspace{1em}\to \hspace{1em}\tilde{p}=\mu {\lambda }_r^2,$$ [S20]

$${\sigma }_{\theta }={\lambda }_{\theta }\frac{\partial W}{\partial {\lambda }_{\theta }}-\tilde{p}=\mu \left({\lambda }_{\theta }^2-{\lambda }_r^2\right),$$ [S21]

$${\sigma }_z={\lambda }_z\frac{\partial W}{\partial {\lambda }_z}-\tilde{p}=\mu \left({\lambda }_z^2-{\lambda }_r^2\right),$$ [S22]

where $\tilde{p}$ is a Lagrange multiplier. Substitution of Eqs. S15–S17 and S19 into Eqs. S21 and S22 yields

$$\frac{pR}{\mu H}={\lambda }_z^{-1}-{\lambda }_r^4{\lambda }_z,$$ [S23]

$$\frac{pR}{\mu H}=2{\lambda }_r^2{\lambda }_z\left({\lambda }_z^2-{\lambda }_r^2\right).$$ [S24]

Combining Eqs. S19, S23, and S24 results in

$${\lambda }_r^{-2}{\lambda }_z^{-2}=2{\lambda }_z^2-{\lambda }_r^2,$$ [S25]

which can be solved to obtain

$${\lambda }_r=\sqrt{{\lambda }_z^{-2}\sqrt{{\lambda }_z^8-{\lambda }_z^2}+{\lambda }_z^2},$$ [S26]

where we used ${\lambda }_r\ge 1$ and ${\lambda }_z\ge 1$. Finally, substitution of Eq. S26 into Eq. S23 provides the evolution of the pressure as a function of the axial stretch ${\lambda }_z$

$$\frac{pR}{\mu H}={\lambda }_z^{-1}-{\left({\lambda }_z^{-2}\sqrt{{\lambda }_z^8-{\lambda }_z^2}+{\lambda }_z^2\right)}^2{\lambda }_z.$$ [S27]

Note that the pressure–volume relationship for an inflated latex tube can be easily obtained from Eq. S27, because the volume enclosed by the membrane, v, is given by

$$v=l\pi r^2=\pi {\lambda }_z{L}_{tube}{\lambda }_{\theta }^2{R}^2=\frac{\pi \hspace{0.17em}{R}^2{L}_{tube}}{{\lambda }_z^3+\sqrt{{\lambda }_z^6-1}}.$$ [S28]

In Fig. S3 we report the pressure–volume relation measured experimentally, and find excellent agreement with the analytical model (Eq. S27). Furthermore, we immediately see that no stiffening occurs, even for very high volumes. As a result, we do not expect to trigger any instability at constant volume in systems comprising interconnected latex tubes. Moreover, we also note that it is not possible to tune the pressure response of these inflatable tubes by changing their length, as the pressure does not depend on $L_{tube}$.

Response of a Braided Fluidic Segment.

To construct fluidic segments with a final steep increase in pressure and whose response can be easily tuned and controlled, we enclosed the latex tube of initial length $L_{tube}$ by longer and stiffer braids of initial length $L_{braid}$ (Fig. 1A). The effect of the stiff braids is twofold: (i) as $L_{braid}>L_{tube}$, the braids have to be buckled first before attaching them the latex tube, resulting in an axial force, F, applied to the membrane; ($ii$) at a critical point during inflation the braids come into contact with the latex tube, stiffening the response of the segment upon further inflation.

Effect of the axial force.

To determine the effect of the braids on the initial response of the segments, we first estimate the axial force F introduced by n braids that enclose the latex tube. For the sake of simplicity, we model each individual braid as two rigid segments of length $L_{braid}/2$, connected by a torsional spring with stiffness K (Fig. S4A). As the braids are longer than the latex tube, before attaching them together, they are shortened by $u=L_{braid}-l=L_{braid}\sin \theta$ (Fig. S4B), causing them to buckle. Balance of the work done by the axial force F and the elastic energy requires

$$F{L}_{braid}\sin \theta =2nK\theta ,$$ [S29]

from which we obtain

$$F=\frac{2nK\theta }{L_{braid}\sin \theta }.$$ [S30]

For the fluidic segment considered in this study $\theta <40°$ we approximate $\sin \theta \approx \theta$, so that Eq. S30 reduces to

$$F\approx \frac{2nK}{L_{braid}}.$$ [S31]

Note that this approximation yields a constant axial force F, and introduces an error that is within 9%.

Finally, we experimentally estimate the torsional stiffness K by performing uniaxial compression tests on braids of different length and comparing the experimentally measured critical forces to Eq. S31. From the results reported in Fig. S4B we obtain that for the braids used in this study

$$K\approx L_{braid}\frac{-0.281L_{braid}+20.4}{2n}.$$ [S32]

Next, we investigate the effect of the axial force F on the latex tube. To account for the axial force, Eq. S17 modifies as

$${\sigma }_z=\frac{pr}{2h}+\frac{F}{2\pi rh},$$ [S33]

so that Eq. S24 becomes

$$\frac{pR}{\mu H}=2{\lambda }_r^2{\lambda }_z\left({\lambda }_z^2-{\lambda }_r^2\right)-\frac{F{\lambda }_r^2{\lambda }_z^2}{\pi \mu HR},$$ [S34]

and Eqs. S16 and S23 remain unaltered. Note that Eq. S34 can also be used to estimate the axial stretch introduced into the tube by the braids in the unpressurized state (i.e., $p=0$)

$${\lambda }_{z,0}\ge \frac{1}{6}\left(c+\frac{{\tilde{F}}^2}{c}+\tilde{F}\right),\hspace{1em}c=\sqrt[3]{{\tilde{F}}^3+6\sqrt{6}\sqrt{{\tilde{F}}^3+54}+108},$$ [S35]

in which $\tilde{F}=F/\left(\pi \mu HR\right)$.

By combining Eqs. S4, S23, and S34 we obtain

$${\lambda }_r^{-2}{\lambda }_z^{-2}=2{\lambda }_z^2-{\lambda }_r^2-\tilde{F}{\lambda }_z,$$ [S36]

from which the stretch in radial direction can be determined as

$${\lambda }_r=\sqrt{{\lambda }_z^2-\frac{\tilde{F}}{2}{\lambda }_z-\frac{\sqrt{{\left(-2{\lambda }_z^4+\tilde{F}{\lambda }_z^3\right)}^2-4{\lambda }_z^2}}{2{\lambda }_z^2}},$$ [S37]

where we assumed ${\lambda }_r\ge 0$ and ${\lambda }_z\ge {\lambda }_{z,0}$. By substituting Eq. S37 into Eq. S34 the pressure–axial stretch relationship is finally obtained as

$$\frac{pR}{\mu H}={\lambda }_z^{-1}-{\left({\lambda }_z^2-\frac{\tilde{F}}{2}{\lambda }_z-\frac{\sqrt{{\left(-2{\lambda }_z^4+\tilde{F}{\lambda }_z^3\right)}^2-4{\lambda }_z^2}}{2{\lambda }_z^2}\right)}^2{\lambda }_z,$$ [S38]

and the relation between the volume and the axial stretch is given by

$$v=\frac{\pi L_{tube}{R}^2}{{\lambda }_z^3-\frac{\tilde{F}}{2}{\lambda }_z^2-\frac{1}{2}\sqrt{{\lambda }_z^4{\left(\tilde{F}-2{\lambda }_z^2\right)}^2-4}},$$ [S39]

in which we assumed that ${\lambda }_z\ge 0$ and $\tilde{F}\ge 0$.

In Fig. S4C we show the analytically predicted pressure–volume curves for a latex tube of length $L_{tube}=30$ mm subjected to an axial force $0\le F\le g$ N (where g = 9.81 m s⁻¹ is the gravitational acceleration). As previously observed (37), the results show that an increase in the axial force applied to the membrane results in a lower peak pressure, indicating that the axial force resulting from the braids can be used to control the initial response of the fluidic segments. In Fig. S4C the analytical predictions (dashed lines) are also compared with experimental results (continuous lines) obtained inflating a latex tube of length $L_{tube}=30$ mm with a weight attached to one of its ends. The good agreement between analytical and experimental results indicate that, despite the simplifications introduced in the derivation, our analysis captures all of the important features.

Effect of contact.

At a critical point during inflation, the braids and the membrane come into contact, stiffening the overall response of the segments. Here, we assume that contact occurs when $v_{braid}=v$, where $v_{braid}$ is the volume enclosed by the braids, which can be approximated as

$$\begin{array}{c}{v}_{braid}=2\pi {\displaystyle \underset{0}{\overset{l/2}{\int }}{\left(R+x\tan \theta \right)}^{2}dx}\\ =\frac{2\pi }{3\tan \theta }{\left(R+\frac{{\lambda }_z{L}_{tube}\tan \theta }{2}\right)}^3-\frac{2\pi R^3}{3\tan \theta },\end{array}$$ [S40]

in which

$$\theta ={\text{cos}}^{-1}\left({\lambda }_z{L}_{tube}/L_{braid}\right).$$ [S41]

Because the pressure–volume relationship provided by Eqs. S38 and S39 is valid only for $v<v_{braid}$, we now proceed to determine how these modify after contact. We assume that the contact between the tube and the braids results in an uniform pressure, $p_{braid}$, applied to the braids (Fig. S4D). Because the beams are modeled as rigid, this pressure results in two effective forces with radial, $F_r$, and axial, $F_a$, components (Fig. S4D), given by

$$F_r=\frac{p_{braid}{L}_{braid}}{2}\cos \theta ,$$ [S42]

and

$$F_a=\frac{p_{braid}{L}_{braid}}{4}\sin \theta .$$ [S43]

Balancing the external work and the elastic energy yields

$$\left(\frac{F_r}{2}+F-F_a\right)L_{braid}\sin \theta =2nK\theta ,$$ [S44]

where F is defined in Eq. S31. Furthermore, we assume that after contact the response is fully dominated by the braids so that

$$p=p_{braid}+\widehat{p},$$ [S45]

in which $\widehat{p}=p(v_{braid}=v)$ can be calculated from Eqs. S38–S40. Finally, combining Eqs. S42–S45 we obtain

$$p=\frac{8nK\theta -4F{L}_{braid}\sin \theta }{L_{braid}^2\left(\cos \theta \sin \theta -{\sin }^2\theta \right)}+\widehat{p}.$$ [S46]

In Fig. S4E we show the predicted response for six segments characterized by $L_{tube}=20$ mm and $L_{braid}=40-50$ mm. The results indicate that for shorter braids, the peak in pressure is lower, demonstrating that the braids can be used to control the initial response of the fluidic segments. Moreover, the predicted response also clearly shows that $L_{braid}$ strongly affects the volume at which stiffening occurs. In fact, the shorter the braids, the earlier contact between the braid and the membrane occurs, reducing the amount of volume that needs to be supplied to have a steep increase in pressure.

However, if the braid length is kept constant at $L_{braid}=50$ mm and $L_{tube}$ is varied ($L_{tube}=20-30$ mm), both the pressure peak and the volume at which stiffening occurs remain unaltered (Fig. S4F). However, in this case we find that shorter tubes lower the pressure of the softening region. Finally, the analytical model also indicates that the length of the fluidic segments, $l={\lambda }_z{L}_{tube}$, initially increases. However, when the tube and braids come into contact, further elongation is restrained by the braids and the segments shorten as a function of the supplied volume (Fig. S4 E and F).

Therefore, this simple analytical model indicates that, by enclosing inflatable tubes with stiffer and longer braids, fluidic segments with the desired nonlinear response can be realized. Importantly, we have also found that by changing $L_{braid}$ and $L_{tube}$ their pressure–volume response (i.e., height of the initial pressure peak, softening response, and volume at which the final steep increase in pressure occurs) can be tuned and controlled. Therefore, we expect that by rationally interconnecting these braided fluidic segments, we can design systems in which snap-through instabilities at constant volume can be triggered.

Finally, it is important to note that we expect this model to predict only qualitatively and not quantitatively the response of the segments. This is mainly due to the effect of boundary conditions (i.e., the deformation is not uniform throughout the membrane) and inextensibility of the braids. Moreover, it has also been shown that local instabilities resulting in bulges (36–38) are triggered during the inflated of tubes. Although our model aims to provide design guidelines, accounting for all these effects would have lead to a significantly more complicated and less intuitive model, which falls outside the scope of this study.