Characteristics of Plant Essential Genes Allow for within- and between-Species Prediction of Lethal Mutant Phenotypes

Essential genes in Arabidopsis thaliana display distinct characteristics that are used to build machine learning models capable of predicting lethal-phenotype genes within and between species.

Abstract

Essential genes represent critical cellular components whose disruption results in lethality. Characteristics shared among essential genes have been uncovered in fungal and metazoan model systems. However, features associated with plant essential genes are largely unknown and the full set of essential genes remains to be discovered in any plant species. Here, we show that essential genes in Arabidopsis thaliana have distinct features useful for constructing within- and cross-species prediction models. Essential genes in A. thaliana are often single copy or derived from older duplications, highly and broadly expressed, slow evolving, and highly connected within molecular networks compared with genes with nonlethal mutant phenotypes. These gene features allowed the application of machine learning methods that predicted known lethal genes as well as an additional 1970 likely essential genes without documented phenotypes. Prediction models from A. thaliana could also be applied to predict Oryza sativa and Saccharomyces cerevisiae essential genes. Importantly, successful predictions drew upon many features, while any single feature was not sufficient. Our findings show that essential genes can be distinguished from genes with nonlethal phenotypes using features that are similar across kingdoms and indicate the possibility for translational application of our approach to species without extensive functional genomic and phenomic resources.

INTRODUCTION

In the postgenome era, one major challenge in genetic research is in linking genotypes to phenotypes (Abecasis et al., 2010; Dowell et al., 2010). Genome-wide phenotype information, obtained through large-scale loss-of-function studies, is available for several eukaryotic models, including Saccharomyces cerevisiae (Winzeler et al., 1999), Caenorhabditis elegans (Kamath et al., 2003), Drosophila melanogaster (Boutros et al., 2004), and Schizosaccharomyces pombe (Kim et al., 2010). This information allows systematic analysis of genotype-phenotype connections and provides clues on homologous gene functions in species where large-scale loss-of-function analysis cannot be readily applied. By comparison, only a small proportion (∼15%) of genes in the model plant Arabidopsis thaliana are associated with well-curated phenotype information (Lloyd and Meinke, 2012), despite the availability of powerful reverse genetics resources that allow for the potential of near-saturation mutagenesis studies (Kuromori et al., 2009). This is due in large part to the time and resources required for cultivating and phenotyping mutant populations. While S. cerevisiae and C. elegans have generation times measured in hours or days, A. thaliana, a relatively fast-growing plant, requires 5 to 6 weeks to begin seed production (Meyerowitz, 1989). These difficulties are exacerbated by high gene duplication rates in plants, due to both polyploidization (Soltis et al., 2009) and tandem duplications (Rizzon et al., 2006; Hanada et al., 2008), which result in many genes not exhibiting a phenotype under controlled conditions. Thus, the ability to effectively prioritize gene selection by predicting mutant phenotypes would represent an important step toward streamlining intensive and costly phenotypic analysis in plants.

Among genes with apparent phenotypes when lost, “essential” genes (lethal-phenotype genes) have been the target of focused analysis because they perform functions required for organismal viability and are critical in the investigation of potential drug targets in microbes (Golling et al., 2002; Firon et al., 2003; Kobayashi et al., 2003; Glass et al., 2006; Meinke et al., 2008; Silva et al., 2008). In S. cerevisiae, a variety of genomic features are associated with essential genes, including but not limited to singleton status, elevated transcription levels, and strong phylogenetic conservation (Winzeler et al., 1999; Kim et al., 2010). Some of these attributes are shared by lethal-phenotype genes in C. elegans, S. pombe, and Mus musculus (Kamath et al., 2003; Kim et al., 2010; Yuan et al., 2012). Using these features, lethal-phenotype genes have been predicted in S. cerevisiae and M. musculus (Seringhaus et al., 2006; Acencio and Lemke, 2009; Yuan et al., 2012).

In plants, essential genes tend to be single copy (Mutwil et al., 2010; Lloyd and Meinke, 2012) and have distinct functional biases (Tzafrir et al., 2004; Lloyd and Meinke, 2012). It has also been shown that genes with housekeeping functions (that may or may not have lethal phenotypic consequences) tend to be present in single copy across many plant species (De Smet et al., 2013). In addition to single-copy status, essential genes are often highly connected in gene functional networks (Mutwil et al., 2010), and genes with embryo-lethal defects tend to be connected with one another in the AraNet functional network (Lee et al., 2010). With these pioneering studies, an outstanding question is what other characteristics plant essential genes possess. For example, although single-copy genes tend to be essential, there are a number of duplicate genes that are essential. Thus, from the gene duplication perspective, it is possible that the extent, timing, and mechanism of duplication may be important. Similarly, one would expect that cross-species conservation, selective pressure, and expression characteristics will be related to whether a gene is essential or not. Nonetheless, these features have not been evaluated for their relationship with plant essential genes.

Aside from the studies of essential gene features, Mutwil et al. (2010) identified clusters in their gene network with higher proportions of lethal-phenotype genes and predicted six novel essential genes. Although this study established a set of essential gene predictions in plants, the method will miss any essential genes outside of enriched clusters and therefore is not applicable genome wide. One potential solution to this is to predict lethal-phenotype genes based on many gene features beyond simply presence in a coexpression cluster, as this can produce genome-wide and potentially more accurate predictions. A data integration approach that made use of sequence data and expression correlation was successful in predicting functional overlap between A. thaliana duplicates, i.e., the absence of a phenotype due to buffering effects from another gene (Chen et al., 2010). Although the prediction of genetic buffering effects represents the opposite extreme of potential mutant phenotypes, a similar methodological framework could be used to predict essentiality or other detectable phenotypes on a genome scale. However, such a framework is not currently available.

To determine the feasibility of large-scale lethal-phenotype gene prediction in A. thaliana, we collected loss-of-function phenotype data for ∼3500 genes and assessed relationships between phenotype lethality and gene function, copy number, duplication, expression levels and patterns, rate of evolution, cross-species conservation, and network connectivity, many of which were not explored previously in detail. We generated machine learning models to identify additional lethal-phenotype genes on the basis of multiple gene features, including a predictive model based only on sequence-derived features. Finally, as lethal-phenotype genes share many characteristics between species, we tested whether lethal-phenotype predictions would be possible across species boundaries.

RESULTS AND DISCUSSION

Phenotype Classification and Functions of Genes with Lethal Phenotypes

To predict lethal mutant phenotypes in A. thaliana, loss-of-function phenotype descriptions were collected for 3443 genes (Kuromori et al., 2006; Ajjawi et al., 2010; Lloyd and Meinke, 2012; Savage et al., 2013; Supplemental Data Set 1), covering 12.7% of A. thaliana protein-coding genes. A phenotype was considered “lethal” if it resulted in developmental arrest at the gametophytic, embryonic, seedling, or rosette stage prior to bolting or extreme developmental defects that are expected to significantly affect plant growth in laboratory growth conditions. Under this definition, the loss-of-function phenotypes of 705 (20.5%) genes were considered lethal and the remaining (2738; 79.5%) were considered nonlethal (Supplemental Data Set 1). Genes displaying lethal and nonlethal mutant phenotypes are referred to as “lethal genes” (essential genes) and “nonlethal genes,” respectively. Genes not in our phenotype data set are referred to as “undocumented genes.”

An earlier study demonstrated that genes involved in, for example, RNA synthesis and modification, protein synthesis, and protein degradation tend to have higher essential-to-nonessential gene ratios (Lloyd and Meinke, 2012). However, that study classified genes into 11 categories and included only 5% of A. thaliana genes. In addition, despite the differences in ratios, the statistical significance of such differences is unclear. To assess if there is a significant bias in the function of lethal genes and to assess if gene functions may be useful for generating predictions genome-wide, we tested for over- and underrepresentation of lethal genes in Gene Ontology (GO) categories (see Methods). We identified 28 terms in which lethal genes are significantly over- or underrepresented compared with nonlethal genes (Fisher’s exact tests [FETs], adjusted P < 0.05; Supplemental Figure 1). Lethal genes in our data set tend to be enriched in the translation, nucleolus, mitochondrion, and plastid categories and are rarely associated with signaling and regulation-related terms (signal transduction, cell communication, kinase and transcription factor activity, and response to endogenous, biotic, and abiotic stimulus). We also found that several basic developmental processes, such as reproduction, pollination, and the cell cycle, tend to be overrepresented with lethal genes. In total, 27 GO terms that contain over- or underrepresented numbers of lethal genes (not including the embryo development term; see Methods) were used in machine learning predictions of lethal-phenotype genes.

Copy Number of Lethal Genes

In addition to functional bias, the presence or absence of paralogs is correlated with phenotypic severity in fungi (Winzeler et al., 1999; Gu et al., 2003; Kim et al., 2010) as paralogs may compensate for the loss of related genes and buffer the effects of gene loss. It has also been shown that single-copy genes in A. thaliana tend to be lethal genes (Mutwil et al., 2010; Lloyd and Meinke, 2012). Consistent with these studies, lethal genes in our phenotype data set are more commonly present as single-copy genes than nonlethal genes (FET, P < 4e-10; Figure 1A). This result provides additional support for the relationship between lethality and singleton status in plants, with a much larger gene set than in a previous study (Mutwil et al., 2010) and also indicates that gene copy number represents a potentially useful feature for lethal gene prediction. While we expected that lethal genes would be overrepresented in other small paralogous groups, both double- and triple-copy genes have a statistically similar proportion of lethal and nonlethal genes (FET, P = 0.29 and 0.11 for double-copy and triple-copy genes, respectively; Figure 1A). Thus, the presence of even a single paralog provides appreciable functional overlap and therefore reduces the likelihood of lethality following disruption of a gene in laboratory conditions.

Figure 1.

Copy Number of Phenotype Genes in A. thaliana and Rice.

(A) Frequency distribution of the number of paralogs (copy number) in the sets of lethal, nonlethal, and undocumented (i.e., no documented phenotype) genes.

(B) Distributions of orthologous group sizes between A. thaliana and rice. Rows indicate A. thaliana gene copy numbers in the orthologous groups, while columns denote phenotype categories.

As lethal genes are enriched among certain functional categories and tend to be single copy, it is possible that lethal gene duplicates with particular functions were preferentially reduced to single copy. This preferential reduction to single copy appears to be conserved across species. Single-copy A. thaliana lethal genes tend to more often have one rice (Oryza sativa) ortholog compared with nonlethal and undocumented genes (Figure 1B). More lethal A. thaliana genes also have readily identifiable homologs in rice (87%) compared with nonlethal (77%; FET, P < 5e-10) and undocumented (54%; FET, P < 5e-10) genes, which suggests a stronger degree of selective constraint on lethal genes. Considering that there were repeated rounds of whole-genome duplications in both the A. thaliana and the rice lineages (Paterson et al., 2004; Cui et al., 2006), the conserved single-copy status of A. thaliana lethal genes and their rice orthologs suggests that the loss of lethal gene paralogs compared with nonlethal gene paralogs is not completely random. In addition, this conservation of single-copy status suggests that single-copy rice orthologs are likely lethal-phenotype genes as well. Such cross-species conservation is explored in greater depth in a later section.

Duplication Timing of Lethal Genes

Although lethal genes are more likely to be single copy compared with nonlethal and undocumented genes, ∼67% of lethal genes have paralogs, raising the question: Why do some duplicate genes have a lethal phenotype in null mutant backgrounds? For genes with paralogs, a greater period since duplication may allow for a higher degree of functional divergence, which lessens the ability of duplicates to compensate for the loss of one another. An earlier study found that essential genes tend to have greater protein sequence divergence from their paralogs (Lloyd and Meinke, 2012). Accordingly, we asked if lethal genes with paralogs (referred to as “lethal gene duplicates”) would be the product of older duplication events compared with nonlethal genes with paralogs (“nonlethal gene duplicates”). Using synonymous substitution rate (Ks) as a proxy for duplication time, best matching lethal gene duplicate pairs are significantly older with higher Ks values (median = 1.69) than those of best matching nonlethal gene duplicate pairs (median = 1.07; Kolmogorov-Smirnov test [KST], P < 3e-08; Figure 2A). One possible explanation for the lower median Ks among nonlethal gene duplicates is that they tend to be lineage-specific genes that arose after duplication events took place. To assess this, we eliminated a subset of lineage-specific genes by focusing on genes with homologs in rice and again performed the Ks analysis. The results were almost identical to the results based on the full set of lethal and nonlethal genes (median lethal Ks = 1.7, median nonlethal Ks = 1.03; KST, P < 5e-08), indicating that lineage-specific genes may not fully explain the differences in Ks distributions between lethal and nonlethal genes.

Figure 2.

Duplication Timing and Type of A. thaliana Phenotype Genes.

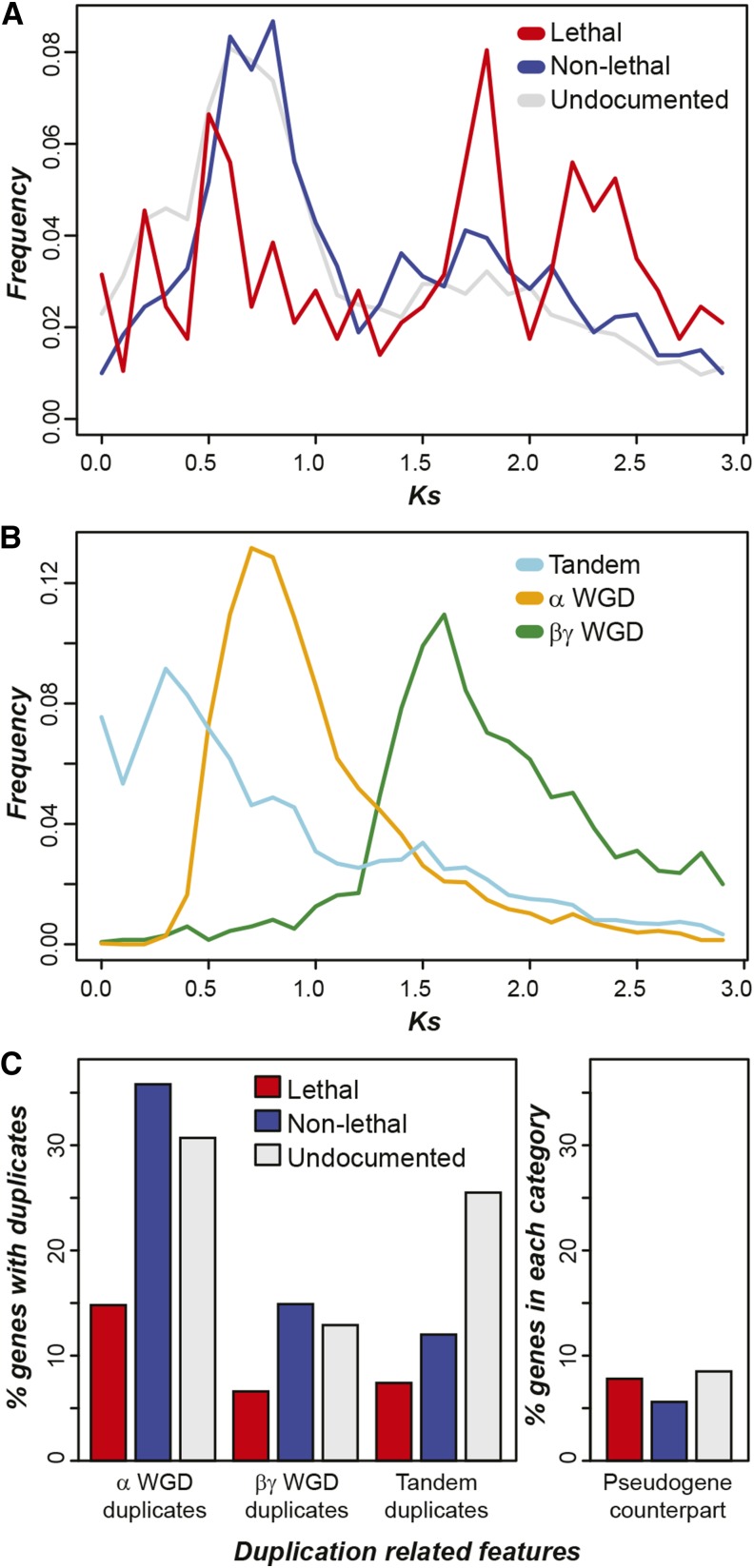
(A) Synonymous substitution rate (Ks) distributions for gene pairs of lethal, nonlethal, and undocumented genes and their most similar paralog. Gene pairs with higher Ks values are expected to be the result of older duplication events. Genes in a pair may not be from the same phenotype category.

(B) Ks distributions of genes duplicated via tandem and the α and βγ WGD. Some genes are derived from both tandem and WGDs.

(C) Percent of duplicated lethal, nonlethal, and undocumented genes that have a paralog derived from α WGD, βγ WGD, and tandem duplications. Percent of all lethal, nonlethal, and undocumented genes with significant sequence similarity (percentage of identity ≥ 40%) to ≥1 pseudogenes is shown in the right-most portion of the panel.

Interestingly, the major Ks peak for nonlethal gene duplicates coincides with that for duplicates derived from the α whole-genome duplication (WGD) event that took place 50 to 65 million years ago (Beilstein et al., 2010; Figure 2B). By contrast, the major Ks distribution peaks for lethal gene duplicates (Figure 2A) coincide with the peak Ks for not only duplicates derived from the α but also the much older βγ WGD (Bowers et al., 2003; Figure 2B), contributing to the significantly higher Ks values among lethal gene duplicates compared with nonlethal ones. This suggests that lethal gene duplicates may be generated from both WGD events, raising the question of how often lethal-phenotype genes retain their duplicates from these events.

Assuming that duplication rates are similar among all genes, significantly higher Ks values among lethal gene duplicates suggest that duplicates of lethal genes are more frequently lost than nonlethal gene duplicates. This is consistent with the finding that lethal genes tend to be single copy (Mutwil et al., 2010; Lloyd and Meinke, 2012; Figure 1). In addition, we found that significantly fewer lethal genes with paralogs are retained following WGD events compared with nonlethal genes (FET, P < 4e-10 and 3e-7 for the α and βγ events, respectively; Figure 2C). This analysis focuses on all possible duplicate pairs and the conclusion remains the same for the α WGD if we examine only the most closely related paralogs (as in Figure 2A; FET, α, P < 3e-10, and, βγ, P = 0.06; Supplemental Figure 2). Thus, some lethal genes retain their duplicates from WGD events, but the retention rate of lethal genes is lower than that of nonlethal genes. In addition, while a major peak in the lethal gene Ks distribution (Figure 2A) coincides with the Ks peak from the βγ WGD events (Figure 2B), the lethal gene pairs underlying the peak in Figure 2A may not necessarily represent duplicates retained from the βγ WGD event. We also found that pseudogenes resembling lethal genes are more often present compared with those resembling nonlethal genes (FET, P = 0.03), although this proportion is not significantly different from that for undocumented genes (P = 0.54; Figure 2C). In addition to WGD, tandem duplication is another major mechanism that contributes to paralogous genes (Rizzon et al., 2006; Hanada et al., 2008). We found that duplicate lethal genes are less likely to be present in tandem clusters compared with nonlethal duplicates (FET, P < 0.01) and undocumented duplicates (FET, P < 4e-10; Figure 2C). Furthermore, the few lethal genes derived from tandem duplications tend to have larger Ks values (median = 1.22) compared with nonlethal (median = 0.64; KST, P = 0.05) and undocumented (median = 0.69; KST, P < 0.02) tandem duplicates. These results indicate that lethal gene duplicates have a significantly higher loss rate after WGD and a significantly lower proportion of tandem genes compared with nonlethal and undocumented gene duplicates. If lethal gene duplicates cannot be attributed to tandem or WGDs, then what mechanisms were responsible for generating these duplicates? One explanation may be that lethal gene duplicates were generated via WGD, but are not in present in recognizable WGD blocks. However, the α WGD blocks cover ∼90% of A. thaliana genes (Bowers et al., 2003); thus, the above explanation can only account for few of the lethal gene duplication events. It is also possible that duplicates of lethal genes may be commonly produced through segmental duplication events similar to those found in human (Bailey et al., 2002), but that remains to be verified. In either case, this represents an intriguing question that calls for further study.

Although lethal genes tend to be present as singletons, when lethal gene paralogs are present, they are derived from relatively ancient duplication events, consistent with the interpretation that deletion of a gene with a lesser degree of functional overlap with its paralog(s) due to longer divergence time will result in more severe phenotypic effects. Our findings also identify a number of features that can be used for lethal-phenotype gene prediction, including singleton status, Ks with top paralog, presence of duplicates from the α or βγ WGD or tandem duplication events, presence of pseudogene counterparts, and absence of orthologs in other species (Table 1).

Table 1. Genomic Features of Essential Genes in A. thaliana.

Category	Feature	Data Type	Sign of Lethal Associationa	P Valueb	Seq. Based Featurec	Riced	Yeastd
Gene duplication	α WGD duplicate retained	Binary	−	3.17E-10	No	No	No
	βγ WGD duplicate retained	Binary	−	3.07E-10	No	No	No
	Pseudogene present	Binary	+	0.035	Yes	Yes	No
	Tandem duplicate	Binary	−	7.93E-06	Yes	Yes	No
	Paralog Ks	Numeric	+	2.17E-08	Yes	Yes	Yes
	Gene family size	Numeric	−	1.20E-24	Yes	Yes	Yes
Expression	Median expression	Numeric	+	1.60E-08	No	Yes	Yes
	Expression variation	Numeric	−	0.002	No	Yes	Yes
	Expression breadth	Numeric	+	5.47E-20	No	Yes	No
	Expression correlation	Numeric	NA	0.072	No	No	No
	Expression correlation (Ks < 2)	Numeric	−	0.004	No	No	No
Evolution and conservation	Core eukaryotic gene	Binary	+	2.44E-08	No	No	Yes
	Homolog not found in rice	Binary	−	4.04E-10	Yes	No	No
	Percentage identity in plants	Numeric	+	2.73E-06	Yes	No	No
	Percentage identity in metazoans	Numeric	NA	0.254	Yes	No	No
	Percentage identity in fungi	Numeric	NA	0.077	Yes	No	No
	A. lyrata homolog Ka/Ks	Numeric	−	0.012	Yes	No	No
	P. trichocarpa homolog Ka/Ks	Numeric	−	0.008	Yes	No	No
	V. vinifera homolog Ka/Ks	Numeric	−	0.003	Yes	No	No
	Rice homolog Ka/Ks	Numeric	−	0.012	Yes	No	No
	P. patens homolog Ka/Ks	Numeric	−	0.038	Yes	No	No
	Nucleotide diversity	Numeric	−	0.001	No	No	No
	Paralog Ka/Ks	Numeric	+	2.51E-14	Yes	Yes	Yes
Networks	Expression module size	Numeric	+	1.94E-34	No	No	Yes
	Gene network connections	Numeric	+	9.84E-11	No	No	Yes
	Protein-protein interactions	Numeric	NA	0.72	No	No	No
Miscellaneous	Gene body methylated	Binary	+	3.46E-10	No	No	No
	Paralog percentage identity	Numeric	−	2.75E-33	Yes	Yes	Yes
	Protein length	Numeric	+	1.22E-06	Yes	Yes	Yes
	Domain number	Numeric	+	0.023	Yes	Yes	Yes

^aFor each binary feature, + and – indicate that the proportion of lethal genes are significantly higher (overrepresentation) or lower (underrepresentation) than nonlethal genes, respectively. For each numeric feature, + and − indicate that lethal genes have significantly higher or lower feature values compared to nonlethal genes, respectively. NA indicates that there is no significant difference between lethal and nonlethal genes.

^bP values from Fisher’s exact tests (used for binary data) or Kolmogorov-Smirnov tests (used for numeric data).

^cSequence-based features, where “Yes” indicates that a feature can be derived from genome sequence data.

^dFeature used (“Yes”) or not used (“No”) in rice or yeast lethal phenotype gene predictions.

Relationship between Lethality and Gene Expression

Overrepresentation of lethal genes among older duplicates compared with nonlethal genes suggests a higher degree of functional divergence among lethal gene duplicates. To explore this further, we compared gene expression levels and patterns between lethal and nonlethal genes. Duplicates with a higher degree of expression divergence are expected to perform their molecular functions in more distinct temporal, spatial, and conditional contexts. Because of this, we expect lethal genes may show higher degrees of expression divergence with their paralogs compared with nonlethal genes. Consistent with this expectation, lethal gene duplicate pairs have significantly lower expression correlation (and thus higher divergence) compared with nonlethal gene duplicates when Ks ≤ 2 (KST; 0 < Ks ≤ 1, P < 4e-4; 1 < Ks ≤ 2, P < 0.01; Figure 3A). However, older lethal and nonlethal genes show similar degrees of expression correlation with paralogs (Ks > 2; KST, P = 0.35). These results are also consistent with previous findings in A. thaliana that, unlike other eukaryotic species, expression divergence is not strongly correlated with duplication timing (Gu et al., 2002; Ganko et al., 2007).

Figure 3.

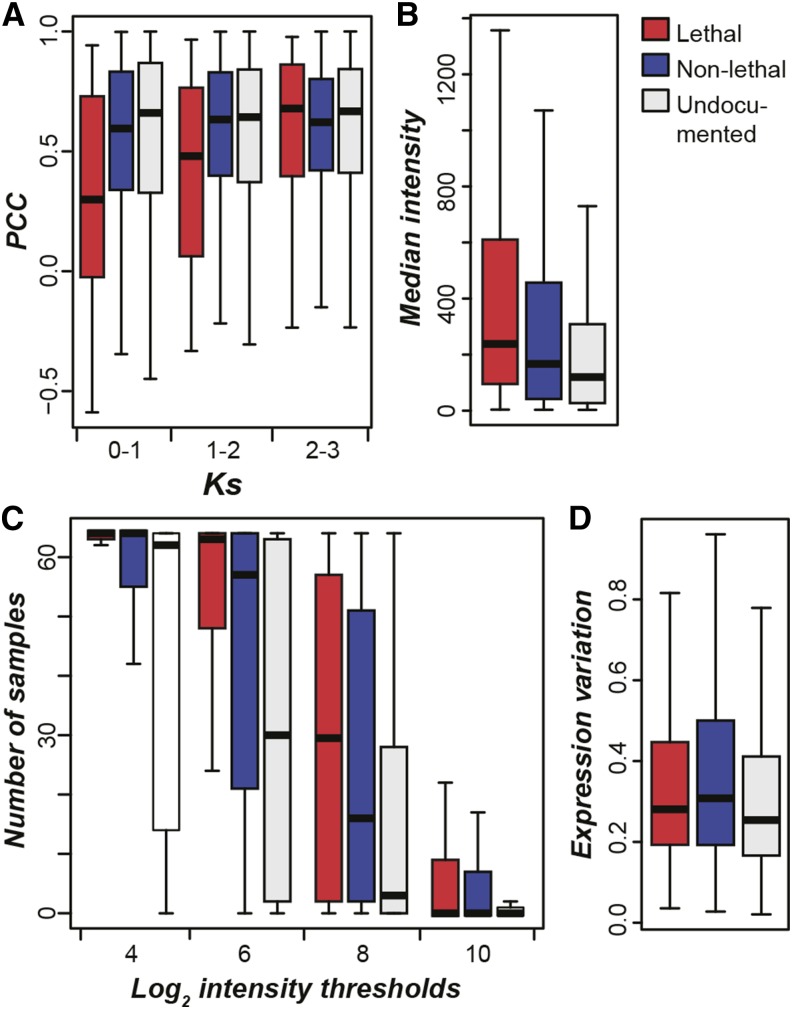
Expression Characteristics of A. thaliana Phenotype Genes.

(A) Box plots of expression correlations (PCC) of paralogous gene pairs involving three gene categories, lethal, nonlethal, and undocumented genes, across AtGenExpress developmental data set samples (Schmid et al., 2005). Lower expression correlation indicates increased degree of expression divergence for a gene pair. Genes in a paralog pair may or may not be from the same phenotype category.

(B) Box plots of median expression levels (array hybridization intensities) of genes in each category across array experiments.

(C) Box plots of numbers of samples where genes in each category were considered expressed according to multiple thresholds.

(D) Box plots of expression variation across samples (median absolute deviation/median) in each gene category.

One potential explanation for the decreasing differences in expression divergence between lethal and nonlethal duplicates over time is that greater divergence in the protein-coding sequences among older duplicates has contributed to a higher degree of biochemical divergence between duplicates. Therefore, the presence of a paralog with a similar expression profile no longer buffers against the consequences of gene loss. We found that lethal gene duplicates with Ks > 2 have a significantly higher ratio of nonsynonymous to synonymous substitution rates compared with nonlethal duplicates (Ka/Ks; KST, P < 6e-10; Supplemental Figure 3), indicating that there is increased divergence at the protein-coding level for older lethal genes compared with nonlethal genes. This raises a question: Among duplicates with Ks < 1, what underlying mechanisms contribute to the differences in expression correlation between lethal and nonlethal genes? Was there selection pressure driving the expression differences between lethal genes and/or maintaining expression similarity among nonlethals? Alternatively, were the patterns we see predominantly driven by neutral processes such as drift? In this context, the distinction between lethal and nonlethal genes may simply be how paralogs accrued mutations that contribute to expression divergence and have little to do with selection. These possibilities need to be further studied.

In addition to expression divergence, expression level of a gene may affect phenotypic severity. In S. cerevisiae and M. musculus, essential genes tended to be expressed at higher levels (Winzeler et al., 1999; Yuan et al., 2012). Consistent with findings in other species, in A. thaliana the expression levels of lethal genes across the AtGenExpress developmental expression series (n = 64; Schmid et al., 2005) are significantly higher than those of nonlethal genes (KST, P < 2e-8; Figure 3B), suggesting that transcript levels are correlated with gene essentiality. In addition to expression level, lethal genes tend to be more broadly expressed across developmental stages and organs than nonlethal genes (KST, P < 5e-19, 4e-12, 6e-05, and = 0.19 for log₂ intensity thresholds of 4, 6, 8, and 10, respectively; Figure 3C). Finally, while lethal genes show a significantly lower degree of expression variation compared with nonlethal genes, the effect size is small (KST, P < 0.01; Figure 3D). Although lethal genes tend to be highly expressed, 7% are expressed among the bottom third of all genes (defined as weakly expressed, n = 51; log₂ median intensity ≤ 4.39). Among 15 GO categories significantly overrepresented in weakly expressed lethal genes compared with highly expressed ones, 14 are related to transcriptional regulation due to the contribution of the same 15 genes across categories (Supplemental Data Set 2). These genes exhibit a broad spectrum of lethal phenotypes (gametophytic, embryo, and seedling) with notable developmental defects, including cotyledons with leaf-like characteristics (FUS3, LEC1, and LEC2), precocious seed development (FIS2 and MEA), and complete loss of the primary root (STIP). To summarize, we found that lethal gene duplicates tend to display higher expression divergence when Ks ≤ 2 and higher protein sequence divergence when Ks > 2. We also found that lethal genes tend to be more highly and broadly expressed and have lower degrees of expression variation compared with nonlethal genes. Thus, a variety of expression characteristics correlate with phenotype lethality and were incorporated into lethal-phenotype prediction models (Table 1).

Conservation of Lethal Genes

Due to their severe phenotypic consequences when lost, lethal genes likely experienced greater selective constraint compared with genes with nonlethal phenotypes. The Ka/Ks values between A. thaliana lethal genes and their homologs in five plant species tend to be significantly lower compared with cross-species nonlethal gene homolog pairs (KST, see figure legend for P values; Figure 4A). Similarly, lethal genes have a significantly lower degree of nucleotide diversity among 80 accessions of A. thaliana compared with nonlethal genes (KST, P < 7e-4; Figure 4B). Both results suggest that lethal genes are experiencing stronger purifying selection. There are two potential confounding factors. First, lethal genes tend to be expressed at higher levels than nonlethal genes (Figure 3B) and highly expressed genes often experience greater selective pressure due to disproportionate effects of toxic protein misfolding (Drummond et al., 2005). Second, expression levels can affect calculations of Ka/Ks due to codon usage bias (Duret and Mouchiroud, 1999). Thus, we analyzed the relationship between the Ka/Ks values and median expression levels. Consistent with our expectation, we found a negative correlation between median expression levels of lethal genes and Ka/Ks values in each of the five plant species (median Pearson correlation coefficient [PCC] = −0.23). However, this relationship explains only a minor component of the variation in selective pressure experienced by lethal genes (r² values range from 0.03 to 0.08). Thus, our finding that lethal genes are experiencing stronger negative selection is not simply due to their higher expression levels.

Figure 4.

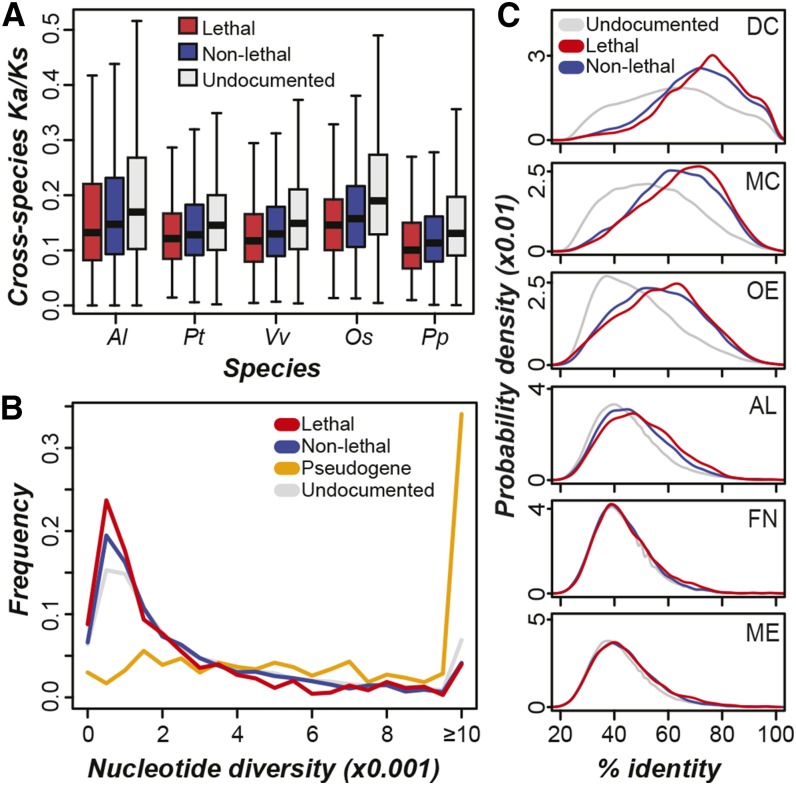
Evolutionary Rate and Cross-Species Protein Conservation of A. thaliana Phenotype Genes.

(A) Ratios of nonsynonymous substitutions (Ka) to synonymous substitutions (Ks) between A. thaliana genes and homologs in the same OrthoMCL cluster from Arabidopsis lyrata (Al; KST of lethal versus nonlethal, P < 0.02), Populus trichocarpa (Pt; P < 0.01), Vitis vinifera (Vv; P < 0.01), O. sativa (Os; P < 0.02), and Physcomitrella patens (Pp; P < 0.04). Lower Ka/Ks values are indicative of stronger negative selection pressure.

(B) Distributions of nucleotide diversity for lethal, nonlethal, pseudo-, and undocumented genes. Higher nucleotide diversity values indicate higher degree of sequence polymorphism between A. thaliana accessions.

(C) Probability density distributions of median percentage of identity of lethal, nonlethal, and undocumented genes to top BLASTP matches in dicotyledonous plants (DC; lethal versus nonlethal KST, P < 2e-6), monocotyledonous plants (MC; P < 7e-4), other embryophytic plants (OE; P = 0.05), algae (AL; P < 7e-6), fungi (FN; P = 0.07), and metazoans (ME; P = 0.25).

Similar to the Ka/Ks-based comparison, lethal genes have significantly higher sequence identities to their best matches in other plant lineages compared with nonlethal genes (Figure 4C). Although no significant difference in sequence identity is noted between lethal and nonlethal genes when considering their best matches in animal and fungal species, a significantly higher proportion of lethal genes (25%) are present in orthologous clusters consisting of genes from seven diverse eukaryotes (“core eukaryotic genes”; see Methods) compared with nonlethal genes (15.7%; FET, P < 3e-8). Lethal genes tend to be the result of older duplications and are present in fewer copies than nonlethal genes. As any set of genes with these features may be highly conserved, we assessed the effects of copy number and duplication age on the sequence conservation of lethal genes. We found that both timing of duplication (Ks value, r² = 0.01) and gene copy number (r² = 0.03) explain little of the variation in protein conservation across the plant kingdom for lethal genes. These results, along with those from the above analysis of the relationship between expression level and Ka/Ks, show that correlation between features that are expected to be dependent can be far from perfect, highlighting the need to consider them jointly for lethal-phenotype gene predictions.

Together with our finding that lethal genes tend to have homologs in rice (Figure 1B), the results from Figure 4 indicate a higher degree of conservation for lethal genes. Because evolutionary rate values and protein conservation metrics could prove useful in a prediction context, they were included in later lethal gene prediction (Table 1). However, we should emphasize that the Ka/Ks, nucleotide diversity, and cross-species sequence identity distributions between lethal and nonlethal genes overlap substantially, i.e., the effect sizes are small despite significant differences (Figure 4). One explanation is that the nonlethal genes studied here are those with observable phenotypes in loss-of-function backgrounds. These nonlethal genes thus are likely subjected to strong selection, although not as strong as the selection against lethal gene mutations. We should also note that none of the examined characteristics that distinguish between lethal and nonlethal genes are perfect. As a result, multiple characteristics are considered jointly in statistical learning models for predicting lethal-phenotype genes (described in a later section).

Network Connectivity of Lethal-Phenotype Genes

In S. cerevisiae, proteins that are highly connected in physical protein-protein interaction networks tend to be essential (Jeong et al., 2001). Similarly, analyses of S. cerevisiae and A. thaliana gene networks based on functional relatedness between genes have demonstrated that highly connected genes tend to have severe loss-of-function phenotypes (Lee et al., 2008; Mutwil et al., 2010), and identification of coexpression clusters in A. thaliana that are enriched in lethal phenotype genes was useful in selecting and validating six novel essential genes (Mutwil et al., 2010). Furthermore, an A. thaliana gene functional network (AraNet; Lee et al., 2010) was used to demonstrate that genes with embryo-lethal phenotypes tend to be connected with one another in the gene network (Lee et al., 2010). However, no formal prediction of essential genes using AraNet data has been performed. To verify that the relationship between network connectivity and gene phenotype lethality also exists in our phenotype data set, we examined coexpression networks established in this study, connections in the AraNet gene network, and protein-protein interaction data (Arabidopsis Interactome Mapping Consortium, 2011). We found that lethal genes in A. thaliana tend to be found in larger coexpression modules (median size = 19) than those containing nonlethal genes (median = 13; KST, P < 2e-34; Figure 5A). In addition, lethal genes tend to be coexpressed (PCC > 0.86; 99th percentile of all pairwise PCCs) with a greater number (median = 20) than nonlethal genes (median = 5; KST, P < 8e-8). Similarly, A. thaliana lethal genes tend to have a greater number of interactions (median = 53) in the AraNet gene functional network than nonlethal genes (median = 30; KST, P < 1e-10; Figure 5B). These results corroborate previous findings based on analysis of coexpression networks (Mutwil et al., 2010) and indicate that high interactivity in gene networks may be useful for establishing lethal-phenotype gene predictions.

Figure 5.

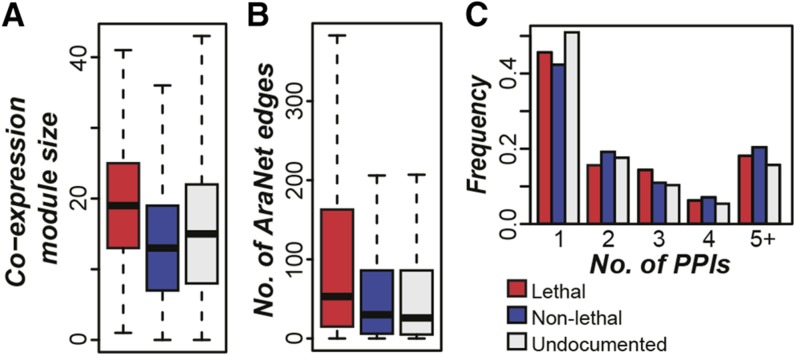
Network Connectivity of Phenotype Genes.

(A) Coexpression module sizes of lethal, nonlethal, and undocumented genes. Modules represent groups of genes clustered via K-means clustering (K = 2000) based on expression similarity across A. thaliana development samples in AtGenExpress (Schmid et al., 2005).

(B) Number of edges connected to genes in the three categories with a log likelihood ≥ 1 in the AraNet network (Lee et al., 2010). Higher numbers of edges indicate increased connectivity within the network.

(C) Distributions of the numbers of genes with 1, 2, 3, 4, or ≥5 protein-protein interactions (PPIs; Arabidopsis Interactome Mapping Consortium, 2011).

In contrast to the relationship between gene essentiality and centrality in gene networks, connectivity within a physical protein-protein interaction network does not seem to be correlated with phenotypic severity in A. thaliana (Lloyd and Meinke, 2012). There remains no clear relationship between our updated phenotype data and protein-protein interactions (KST, P = 0.73; Figure 5C). It remains to be determined if this is due to the lower coverage in the A. thaliana interactome map (12% of proteins compared with 30% in yeast; Jeong et al., 2001). Taken together, the higher connectivity among phenotype-lethal genes is consistent with the interpretation that their disruption may interfere with the function of many other genes. One additional possibility is low-connectivity genes may play more specialized roles than high-connectivity ones. Thus, low-connectivity genes would tend not to have strong phenotypic consequences when mutated.

Prediction of Lethal Genes Using a Machine Learning Framework

Based on analysis of functional annotation, gene copy number, duplicate retention patterns, gene expression, evolutionary rates, cross-species conservation, and network connectivity (Table 1), we identified a wide variety of genomic features correlated with phenotype lethality. In addition to these features, genes encoding longer proteins with a larger number of domains and those with CG gene body methylation (Takuno and Gaut, 2012) are more likely to exhibit lethal phenotypes upon disruption (Table 1). As these features do not correlate perfectly with whether disruption of a gene results in a lethal or nonlethal phenotype, it raises the question as to whether a meaningful prediction of phenotype lethality is feasible if they are jointly considered. In addition, it remains unclear how these disparate features would differ in their contribution to A. thaliana lethal-phenotype gene prediction.

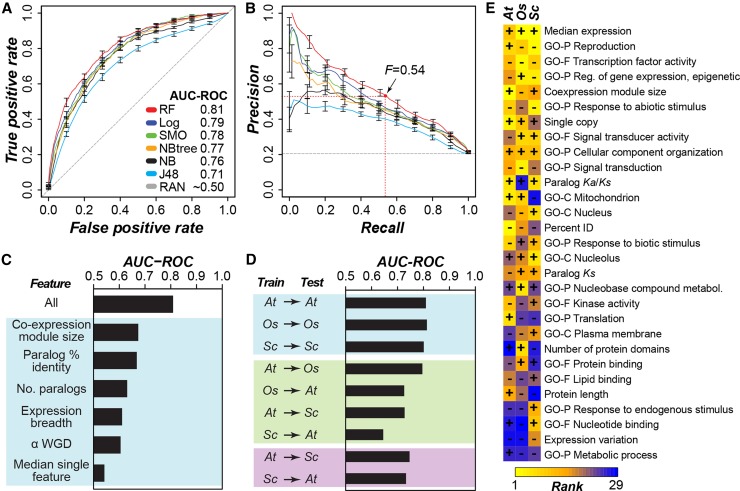
To address these questions, we applied machine learning methods that have been used for essential gene predictions in budding yeast (Seringhaus et al., 2006; Acencio and Lemke, 2009) and mouse (Yuan et al., 2012). A matrix of genes with a documented phenotype and their associated values for different features (Supplemental Data Set 3) was used as input for six machine learning classifiers (see Methods; Figure 6A). To build the classifiers, 90% of our data set was used for model building (training) and 10% was held out for testing the accuracy of the predictive model (validation). The model building process was repeated 10 times so that every gene in our phenotype data set was held out of the model building exactly one time (10-fold cross-validation). We should emphasize that the training data were completely independent from the validation data. Performance was evaluated by calculating the area under the curve-receiver operating characteristic (AUC-ROC), where the AUC-ROC of a model based on random guessing is ∼0.5 and that of a perfect model is 1.0. Using the best performing classifier, Random Forest (Ho, 1995), the lethal gene prediction model AUC-ROC is 0.81, which is significantly better than random guessing (Figure 6A; see Methods). To provide an alternative interpretation of model performance, we also examined the precision (proportion of predicted genes that are truly lethal) and recall (proportion of true lethal genes recovered) of our model (Figure 6B). Based on this analysis, to correctly recover 50% of lethal genes, our precision is at 57%. Because the proportion of lethal genes in our data set is 0.2, the precision of random guesses is expected to be ∼20% (gray line, Figure 6B), indicating that our methods perform reasonably well. By comparison, an earlier study based on coexpression clusters predicted and validated six novel essential genes out of a pool of 20 candidate genes (Mutwil et al., 2010). This represents a precision of 30%. However, this methodology applies only to essential gene-enriched clusters (357 genes, ∼1.3% of A. thaliana annotated genes). As a result, any essential genes outside of these clusters cannot be predicted using this methodology and recall is expected to be very low. This highlights the need to consider a large suite of gene features for genome-wide predictions of essential genes.

Figure 6.

Machine Learning Performance of Essential Gene Predictions.

(A) ROC curves of the predictive models based on Random Forest (RF), logistic regression (Log), SMO-SVM (SMO), Naïve Bayes tree (NBtree), Naïve Bayes (NB), and J48 decision tree (J48) using the best-performing parameter sets. AUC-ROC is indicated in the inset; an AUC-ROC value of ∼0.5 is equivalent to random guessing, while an AUC-ROC of 1 indicates perfect predictions. Diagonal dashed line: the expected performance of a model based on random guessing (RAN). Curves closer to the upper left corner of the chart represent a better predictive performance than curves that are closer to the diagonal dashed line. Error bars: se between 10 cross-validation runs.

(B) Precision-recall curves for the models from (A). Precision: the proportion genes predicted as lethal that are actual lethal genes. Recall: the proportion of actual lethal genes predicted as lethal. Horizontal dashed line: the proportion of lethal genes in the data set, which represents the expected precision based on random guessing. Error bars: se between cross-validation runs.

(C) AUC-ROC values of the best-performing Random Forest machine learning classification using all features (All; median of 10 cross-validation runs) in comparison to AUC-ROCs of the models based on each of the five most informative features (cyan background) and the median of all single feature predictions.

(D) AUC-ROC values of within-species (cyan background) and cross-species (green and magenta background) predictions in A. thaliana (At), rice (Os), and S. cerevisiae (Sc). Species on the left side of the arrows indicate the species from which data were used to train a prediction model. Independent data sets from species on the right of the arrows were used for testing. Predictions between A. thaliana and S. cerevisiae were performed both with a full feature set (green background) and with a subset of features in which the sign of SVM weights agree (magenta background).

(E) Ranks and signs of SVM weights of 29 features available in A. thaliana (At), rice (Os), and yeast (Sc). A lower number rank of a feature weight indicates greater importance for within-species predictions. A more positive weight indicates better association with phenotype lethality and a more negative weight indicates better association with non-lethality.

We next used the best performing model to classify the rest of the 23,763 undocumented genes as potentially lethal or nonlethal when lost. This provided each gene with a “lethal-phenotype score,” a value between 0 and 1 where higher values indicate higher confidence that a gene will display a lethal phenotype upon disruption. Notably, the highest lethal-phenotype score for an undocumented gene is 0.72, while the highest scoring lethal gene in our phenotype data set is almost 0.90, indicating a distinction between the lethal genes in our training data set and the rest of the genes in the A. thaliana genome and potential biases in our model. Applying the machine learning model and a lethal-phenotype score threshold resulting in the highest F-measure (harmonic mean of precision = 0.54 and recall = 0.54; arrow, Figure 6B) in the training data, we identified 1970 (8%) undocumented genes whose loss is expected to result in a lethal phenotype (Supplemental Data Set 1). Using this lethal-phenotype score threshold (0.31), we expect that 1059 (1970*precision) are correctly predicted lethal genes and that there are 885 (1059/recall-1059) additional lethal genes that we fail to detect. Thus, we anticipate an additional 1944 lethal genes in the undocumented gene set. Together with the 705 known lethal genes, 10% (∼2700) of A. thaliana protein-coding genes are expected to have lethal mutant phenotypes based on the lethal-phenotype score threshold of 0.31. As an additional validation step, we collected an independent set of 60 A. thaliana phenotype genes based on a literature search (17 with a lethal phenotype; Supplemental Data Set 1) that are not included in our initial data set of 3443 lethal and nonlethal genes. The AUC-ROC of the best-performing Random Forest model is 0.83 for this independent set. Of the 17 genes with lethal phenotypes in this 60-gene data set, 13 (77%) are correctly predicted as lethal and of the 43 nonlethal genes, 40 (93%) are correctly predicted as nonlethal.

To determine what features are among the most important to our predictions, we assessed the performance reduction resulting from the removal of each feature from prediction analysis. We found that no single feature is particularly critical for predictive performance by itself (all leave-one-out models have AUC-ROC ≥ 0.8 compared with 0.81 for the full model; Supplemental Table 4). These results are corroborated by the fact that machine learning predictions using all data types perform much better than predictions based on any single feature by itself (median AUC-ROC = 0.54, Figure 6C; Supplemental Data Set 4). We also found that 46 features (80% of all features) are required to achieve an AUC-ROC of 0.80 (Supplemental Figure 4), indicating that the contributions from most features are critical. This is consistent with our observations that, although the features we used are generally significantly distinct between lethal and nonlethal genes, in many cases the effect sizes are small (Figures 1 to 5). In addition, many features we included here are likely dependent, although correlation between features is low (see Methods). In any case, our findings indicate that the predictive models for lethal-phenotype genes are robust and draw upon a wide variety of gene features to generate meaningful classifications of lethal and nonlethal genes.

Cross-Species Predictions of Lethal-Phenotype Genes

Considering that some of the features we found to be correlated with gene lethality have been shown to be important in other species (Seringhaus et al., 2006; Yuan et al., 2012), this raises the question whether a prediction model trained with A. thaliana data (A. thaliana model) can be used to predict phenotype lethality across species boundaries. To test this, we first collected rice phenotype data for 92 genes (18 lethal; see Methods; Supplemental Data Set 1) and analogous genomics and functional annotation data (Table 1). Then, a “rice model” was generated and applied to predict lethal genes within the rice test set using 2-fold cross validation. Surprisingly, this performed as well as within-A. thaliana predictions (AUC-ROC = 0.82; Figure 6D), indicating that a significantly smaller gene set still allows lethal gene classification with comparable accuracy. We also tested if good predictions could be made in A. thaliana using a reduced gene set by randomly sampling 20 lethal and 80 nonlethal genes from our full data set and making predictions with 2-fold cross-validation. This was repeated 100 times. The AUC-ROCs of these 100 models range from 0.55 to 0.88 with a median of 0.75. The median AUC-ROC indicates that few phenotype genes can be used to establish lethal gene prediction model with reasonable performance. The rather large variance in AUC-ROCs indicates that the genes included during model building can have a significant effect, particularly if the sample size is small. Next, to test if prediction across plant species is feasible, we trained prediction models using data from one species and predicted phenotype lethality for genes in test sets from another species (see Methods). Using the A. thaliana model, we can predict rice lethal genes with an AUC-ROC of 0.80 (Figure 6D). A rice model is also capable of identifying A. thaliana lethal genes, although the performance is reduced (AUC-ROC = 0.72; Figure 6D). This is potentially because use of a model trained on a small gene set is ineffective in classifying a large number of genes in another species.

Given that cross-species phenotype prediction is feasible between A. thaliana and rice, which diverged over 200 million years ago, we sought to determine if lethal-phenotype genes were predictable across a significantly greater phylogenetic distance by predicting lethal genes in S. cerevisiae. We collected a S. cerevisiae phenotype data set consisting of 6075 genes (1189 lethal; see Methods; Supplemental Data Set 1), 11 types of genomic data (Table 1) and assignments to 25 GO terms. Similar to earlier studies, the yeast model performed well in predicting yeast lethal genes (AUC-ROC = 0.82; Figure 6D). Application of the A. thaliana model on yeast data performed reasonably well (AUC-ROC = 0.73), while an S. cerevisiae model on A. thaliana data performed worse (AUC-ROC = 0.65). The reduced performance in cross plant-fungal species predictions prompted us to investigate which features were meaningful for predictions in one species but not the other. The relative importance of features can be assessed according to a weight measure derived by the support vector machine (SVM) classifier, which indicates the importance of a feature for predicting lethal (more positive weight) or nonlethal (more negative weight) genes. Between A. thaliana and S. cerevisiae, we found that 15 out of 36 features (42%) had opposing signs on their SVM weights (Supplemental Table 1), suggesting that, despite their importance for distinguishing lethal and nonlethal genes, these features have opposite contributions. For example, genes associated with the reproduction GO term tend to be phenotype-lethal in A. thaliana, but nonlethal in S. cerevisiae. When features with opposing correlations with lethality between the two species were removed, the performance improved in predicting S. cerevisiae lethal genes with the A. thaliana model (AUC-ROC from 0.73 to 0.75) and in predicting A. thaliana lethal genes with the S. cerevisiae model (AUC-ROC from 0.65 to 0.73; Figure 6D). While not as accurate as A. thaliana-rice cross-species predictions, these results demonstrate that lethal phenotypes can be predicted between two species separated by 1.4 billion years of evolution. In addition, although many features of essential genes are similar between species, some features are predictive of lethal phenotypes in one species but of nonlethal phenotypes in another.

As lethal-phenotype genes tend to be well conserved, it may be expected that cross-species predictions would perform well. However, we should emphasize that the A. thaliana-rice cross-species predictions do not make use of any conservation-based features, and as a result, sequence conservation is unrelated to the performance of these cross-species predictions. For A. thaliana-yeast cross-species predictions, only one feature is related to gene conservation: presence as a core eukaryotic gene. While this is important for predictions (based on SVM feature weights; Supplemental Table 1), if cross-species predictions are performed using only the core eukaryotic gene feature, the AUC-ROC of predictions falls from 0.75 to 0.63 for A. thaliana-to-yeast cross-species predictions and from 0.73 to 0.55 for yeast-to-A. thaliana predictions. Furthermore, if within-A. thaliana predictions are performed using only sequence conservation and evolutionary rate features, the AUC-ROC of essential gene predictions is 0.60 (compared with 0.81 with the full feature set). These results serve to further emphasize that neither protein conservation nor any single feature can sufficiently explain gene essentiality by itself and that drawing upon a robust set of gene features provides a far more accurate prediction of essential genes.

To compare and contrast gene features important for essential gene prediction in all three species, we evaluated the importance of 29 features that are available in A. thaliana, rice, and yeast. Feature importance and relationship with phenotype lethality were assessed using the rank and sign of SVM weights that are akin to the importance of a feature for predicting lethal (more positive weight) or nonlethal (more negative weight) genes (Figure 6E). Features have generally similar importance for essential gene predictions in each species, although their relationship with lethality in each species is often not the same (i.e., opposing signs on SVM weights). We find five features that are relatively important for predictions and have the same sign in each species: median expression level, transcription factor activity, singleton status, cellular component organization, and signal transduction. These features likely represent characteristics shared by essential genes across kingdoms. Despite general similarity in feature importance, there are apparent species-specific features. For example, mitochondrial protein localization represents a feature important for predicting essential genes in plants but not in yeast. In addition, while response to endogenous stimulus and expression variation are relatively unimportant for predictions in plants, they are important for yeast predictions. Some species-specific features are not shared between more closely related taxa. For example, translation is important for lethal-phenotype predictions in A. thaliana but not in rice and yeast. For yeast, this may be due to a larger portion of translation-related genes being identified, including factors that are less central and essential to the process of protein synthesis. In rice, the smaller data set of phenotype genes may not include many genes involved in the translation process; therefore, the term is not relevant to the predictions. Thus, we cannot rule out the possibility that some of the differences we found are due to differences in how functional categories are annotated across species. It will be more informative to examine lethal phenotype status on a gene-by-gene basis by asking whether and why orthologous genes are essential in one species but not the other.

Finally, because few sequenced species have the extensive functional genomic resources found in A. thaliana, rice, and S. cerevisiae, we sought to determine if a model based only on features that can be generated from a genome sequence (Table 1) can accurately predict lethal-phenotype genes. A machine learning model without input from expression and interactome features was generated for predicting A. thaliana lethal genes and performed with an AUC-ROC of 0.74. This result suggests that essential genes can be predicted with only sequence-based features. Interestingly, it has also been shown that sequence-based features are important in the identification of functional overlap between related genes (Chen et al., 2010). Our finding represents an important step that should prove useful in analyzing newly sequenced organisms that lack robust expression and interactome data sets.

Conclusion

We identified a set of genomic features that significantly correlate with genes that have lethal phenotypes when disrupted in A. thaliana. Similar to findings in yeast and mouse (Seringhaus et al., 2006; Yuan et al., 2012), these features can be used to predict genes with lethal phenotypes in plants. We also show that lethal-phenotype gene prediction models can be applied across species with reasonable performance. This provides strong evidence that the characteristics of essential genes can be defined based on genome sequence features and large-scale functional genomics data and, in some cases, are shared between species. We found that a smaller percentage of A. thaliana genes are predicted to be essential (10%) in comparison to S. cerevisiae, M. musculus, and S. pombe (18, 19, and 26%, respectively; Kim et al., 2010; Yuan et al., 2012). Considering the presence of multiple rounds of genome duplication in the past 100 million years in the A. thaliana lineage, the presence of duplicates is likely a major contributor to the difference. We should emphasize that although individual characteristics can be used to distinguish between genes with lethal and nonlethal phenotypes, in many cases the effect sizes are rather small. Thus, despite the statistical significance, lethal-phenotype genes are more accurately predicted when many features are considered jointly.

Another consideration is that the cause-and-effect relationship between these features and phenotype lethality are not always obvious. For example, while lethal-phenotype genes tend to be single copy or have ancient duplicates, it is not known if stochastic gene loss simply results in essentiality for the remaining duplicate. Alternatively, there may be preferential loss of duplicates of essential genes, perhaps due to an inability to neo- or subfunctionalize many essential gene functions or because essential genes disproportionately function in dosage-dependent processes. While our finding that lethal-phenotype genes tend to have similar duplicate retention and loss patterns across lineages is consistent with the preferential loss possibility, a more detailed analysis on this topic is warranted. Although the machine learning model performs well with high AUC-ROC, there also remains room for improvement in essential gene prediction. For our analysis, we restricted features to those in which we could provide a priori reasoning for association with phenotype lethality. Alternatively, a more data-driven approach that includes more genomic signatures without apparent relationships to phenotype lethality (e.g., histone marks, cis-regulatory complexity, or chromatin state) may allow the discovery of previously ignored factors. Another potential way to improve prediction is to focus on more narrowly defined sets of essential genes. Because lethal phenotypes can result from the loss of a broad range of functions, we cannot necessarily expect all essential genes to possess the same sets of characteristics, as suggested by the significant association of lethal-phenotype genes with multiple characteristics but mostly with small effect sizes. As a result, it is reasonable to hypothesize that there exist distinct sets of essential genes where genes in each set share common characteristics. If this is the case, it will be intriguing to uncover the underlying reasons for the existence of such gene sets.

Taken together, our findings provide a detailed look at the factors predictive of gene phenotype lethality. Through a joint analysis of evolutionary (duplication and conservation) and functional (expression and Ka/Ks) characteristics of lethal-phenotype genes, this study advances our understanding of the evolution of essential genes. In addition, we provide genome-wide plant essential gene predictions and large-scale validation of cross-species lethal-phenotype predictions, building on earlier results focused on fungal or metazoan species and on smaller plant gene data sets. The predictive performance of our models highlights a promising avenue for prioritizing candidate genes for large-scale phenotyping efforts in A. thaliana, particularly essential genes. The feasibility of cross-species predictions suggests that model plant phenotype data can be useful for the identification of essential genes in other plant species.

METHODS

Phenotype Data Sources

Descriptions of gene-based, loss-of-function mutant phenotypes in Arabidopsis thaliana were retrieved from three sources: (1) a published phenotype data set (Lloyd and Meinke, 2012), (2) the Chloroplast 2010 Database (Ajjawi et al., 2010; Savage et al., 2013), and (3) the RIKEN Phenome database (Kuromori et al., 2006). Phenotype descriptions for genes in rice (Oryza sativa) were gathered from four sources: (1) a published phenotype data set (Lloyd and Meinke, 2012), (2) literature search and manual curation (search terms: rice, lethal, mutant, phenotype, null, and knockout), (3) Oryzabase (Kurata and Yamazaki, 2006), and (4) Gramene (Monaco et al., 2014). Saccharomyces cerevisiae (yeast) phenotype annotations were obtained from the Saccharomyces Genome Database (http://www.yeastgenome.org; Cherry et al., 2012). If a gene had conflicting phenotype assignments from multiple sources, the lethal phenotype description was given priority. For yeast, phenotypes annotated to the “inviable” phenotype ontology term were considered lethal, while those annotated to the “viable” term were considered nonlethal. Only phenotypes associated with a null allele were included. An independent set of 60 A. thaliana phenotype genes was identified from recently published literature by searching for articles in the PubMed database that included the keywords “Arabidopsis” and “lethal” and were published in 2012 or 2013. This independent data set includes 24 genes for which a homozygous single-gene mutant was viable and included in at least the attempted construction of a double knockout mutant for the GABI-DUPLO project (Bolle et al., 2013).

GO Functional Annotation

GO gene annotations for A. thaliana and yeast were downloaded from the GO database (http://www.geneontology.org/), and version 7 rice annotations were downloaded from the Rice Genome Annotation Project (Kawahara et al., 2013; (http://rice.plantbiology.msu.edu). A. thaliana and yeast annotations were mapped to the plant slim ontology using the map2slim program in the GOperl package (http://search.cpan.org/∼cmungall/go-perl/). For A. thaliana, only gene-GO terms associated with experimental or computational evidence codes (EXP, IDA, IPI, IMP, IGI, IEP, ISS, ISO, ISA, ISM, IGC, IBA, IBD, IKR, IRD, and RCA) were used, while those based only on curation and author statements were excluded. Of the 97 terms in the plant GO slim subset, three were excluded because they are the root terms (biological process, molecular function, and cellular component), 59 were excluded because they are not significantly over- or underrepresented in lethal genes, one was excluded because it is associated with few A. thaliana phenotype genes (<1%), and five were excluded because they are highly overlapping in gene membership with another significantly enriched term (PCC ≥ 0.50). Among overlapping terms, one representative term was chosen based on the lowest adjusted P value from FETs, except in the case of pairwise overlap between the “response to stress” term and “response to biotic stimulus”/”response to abiotic stimulus,” where “response to stress” was removed despite having a lower P value to maintain the distinction in functional responses to biotic and abiotic environmental factors. Because 151 of 329 genes in the embryo development term are included in our phenotype data set, it was excluded to prevent ascertainment bias. Plant GO slim terms plastid, embryo development, and pollination were excluded from analysis involving yeast data. GO enrichment analysis using the full list of terms beyond the plant slim subset was also performed in A. thaliana to determine enrichment of both highly expressed (genes with the top third expression levels) and weakly expressed (genes with the bottom third expression levels) lethal genes (Supplemental Data Set 2). In all GO analyses, P values were adjusted for multiple testing based on the Benjamini and Hochberg procedure (Benjamini and Hochberg, 1995).

Evolutionary Rate Calculations and Analysis of Duplicates and Pseudogenes

Paralogs in A. thaliana, rice, and S. cerevisiae and homologs between A. thaliana and five different plant species (Arabidopsis lyrata, Populus trichocarpa, Vitis vinifera, rice, and Physcomitrella patens) were identified with OrthoMCL (inflation parameter = 1.5). Protein sequences for A. thaliana were downloaded from The Arabidopsis Information Resource (version 10; www.arabidopsis.org), sequences for rice were downloaded from the Rice Genome Annotation Project (version 7; rice.plantbiology.msu.edu), sequences for S. cerevisiae were downloaded from the Saccharomyces Genome Database (www.yeastgenome.org), and sequences for A. lyrata, P. trichocarpa, and V. vinifera were downloaded from Phytozome (version 9; www.phytozome.net).

In Figure 1A, the paralog copy number for each A. thaliana gene equaled the size of the OrthoMCL cluster the gene in question resided in. In Figure 1B, to identify orthologs between A. thaliana and rice and to assess duplicate retention and loss, a gene-species tree reconciliation approach was used. First, protein sequences of genes in each A. thaliana-rice OrthoMCL cluster were aligned using MUSCLE (Edgar, 2004). Ten maximum likelihood trees for each aligned cluster were built using RAxML (Stamatakis, 2014) to identify the tree with the highest likelihood. The trees were midpoint rooted with retree in the PHYLIP package and parsed with Notung (Chen et al., 2000) to identify duplication and speciation nodes in the gene trees. A group of genes sharing a speciation node in a gene tree were regarded as an orthologous group.

Rates of synonymous (Ks) and nonsynonymous (Ka) substitutions were calculated between homologous gene pairs using the yn00 package in PAML (Yang, 2007). Highly similar or dissimilar sequence pairs (Ks < 0.005 and Ks > 3, respectively) were excluded from further analyses. In cross-species Ka/Ks calculations, the median Ka/Ks value between each A. thaliana gene and genes from other species in the same OrthoMCL cluster was used as a representative value. In A. thaliana, rice, and S. cerevisiae, a paralogous pair for Ks analysis only (e.g., Figure 2A) was defined by identifying a gene and its top-scoring match in BLAST similarity searches (Altschul et al., 1990). Nucleotide diversity between 80 A. thaliana accessions was calculated according to an earlier study (Moghe et al., 2013). Genes with paralogs produced in the α or βγ WGD events were identified by Bowers et al. (2003). Two genes were defined as a tandem duplicate pair if they have a BLASTP E-value < 1e-10 and are no more than 10 genes apart. Pseudogenes were identified through the pipeline described by Zou et al. (2009). Clusters of orthologous genes were downloaded from the National Center for Biotechnology Information (Tatusov et al., 2003). Core eukaryotic genes were defined as genes present in clusters that included at least one gene from each of the seven species in the analysis (A. thaliana, Caenorhabditis elegans, Drosophila melanogaster, Encephalitozoon cuniculi, Homo sapiens, S. cerevisiae, and Schizosaccharomyces pombe).

BLAST similarity searches were performed between A. thaliana protein sequences and the protein sequences of 34 other plant species present in Phytozome v9, including 26 dicotyledonous, 6 monocotyledonous, and 2 other embryophyte species. Similarity searches were also performed between A. thaliana and 8 fungal species (Aspergillus nidulans, Coprinopsis cinerea, Cryptococcus neoformans, Fusarium oxysporum f. sp lycopersici, Neurospora crassa, Puccinia graminis f. sp tritici, S. cerevisiae, and S. pombe) and 8 metazoan species (C. elegans, Ciona savignyi, Danio rerio, D. melanogaster, Gallus gallus, H. sapiens, Mus musculus, and Xenopus tropicalis). Fungal and metazoan protein sequence annotations were retrieved from FungiDB (www.fungidb.org) and Ensembl (www.ensemblgenomes.org), respectively.

Expression Data Sources and Processing

The AtGenExpress development microarray data (Schmid et al., 2005; available from https://www.arabidopsis.org/portals/expression/microarray/ATGenExpress.jsp) were used for A. thaliana. Samples involving data from mutant plants were removed and the median value of the replicates was used as a representative expression value for each gene. Preprocessed RNA-seq data from rice were downloaded from the Rice Genome Annotation Project (http://rice.plantbiology.msu.edu/expression.shtml). Data for testing differential gene expression were excluded from further analyses. For S. cerevisiae, a time-course cell cycle expression data set was used (Orlando et al., 2008). Median and maximum expression and variation of expression were calculated for each gene in the data sets. Expression variation was represented by median absolute deviation divided by the median as it is a measure that does not require a normality assumption. For rice, expression breadth was calculated by counting the number of tissues in which expression was greater than zero fragments per kilobase of exon per million reads mapped. For AtGenExpress data, a series of thresholds (log₂ intensity = 4∼10) for calling whether a gene was expressed or not was tested. The log₂ intensity threshold of 4 resulted in the lowest P value (KST) from testing if the distributions of number of data sets a gene was expressed in were significantly different between lethal and nonlethal genes and was used in machine learning analysis. Expression correlations between a gene and putative paralogs (defined as genes belonging to the same OrthoMCL cluster) were evaluated using PCC and the maximum PCC with a paralogous gene was reported in Figure 3A and used in machine learning analysis.

Network Analysis

Coexpression modules in the AtGenExpress expression data were identified through K-means clustering with K = 5∼2000. Clusters generated with K = 2000 resulted in the lowest P value from KSTs that tested whether the coexpression module size distributions for lethal and nonlethal genes were significantly different and were used in subsequent analysis. PCCs between all genes for which expression data was available were calculated. A gene pair with a PCC of 0.86 (99th percentile of all pairwise comparisons) was considered coexpressed. The AraNet gene network data set (Lee et al., 2010) was downloaded from http://www.functionalnet.org/aranet/, and any gene pair with a log likelihood score ≥ 1 was considered to be functionally related for our analyses. S. cerevisiae gene network data generated by Costanzo et al. (2010) were retrieved from the Saccharomyces Genome Database. Protein-protein interaction data from the Arabidopsis Interactome Mapping Consortium (Arabidopsis Interactome Mapping Consortium, 2011) were retrieved from the supplemental data associated with the publication. Self-interactions and interactions involving a mitochondrial or plastid gene were excluded from analysis.

Machine Learning Predictions

Phenotype predictions were performed using machine learning algorithms implemented in the Waikato Environment for Knowledge Analysis software (Hall et al., 2009). The features we used are shown in Table 1, and a complete matrix of all genes and feature values is available in Supplemental Data Set 3. We first tested if the targeted features were correlated with one another through pairwise Spearman rank correlation analysis. We found that 95 and 99% of feature pairs show a correlation of ≤0.22 and ≤0.40, respectively. This indicated that there was no extensive overlap and thus all features were used in subsequent analysis.

Six classifiers capable of handling binary, numeric, and missing data were tested: J48 decision tree, logistic regression, naïve Bayes, naïve Bayes tree, Random Forest, and sequential minimal optimization support vector machine (SMO-SVM). Ten-fold cross validation was performed for all machine learning runs, except for those involving rice phenotype data, where a low number of instances necessitated 2-fold cross-validation. A grid search was implemented to identify best-performing parameters. Grid searches for each classifier included a parameter for the proportion of lethal-to-nonlethal instances to include in each round of predictions. For the Random Forest classifier, a model trained with a 1-to-1 ratio of lethal to nonlethal genes (AUC-ROC = 0.8) performed similarly as models trained with a data set containing other ratios of lethal to nonlethal genes (maximum AUC-ROC = 0.81). Additional parameters for the following classifiers were also examined: J48 decision tree, pruning confidence; logistic regression, ridge; SMO-SVM, complexity constant; random forest, number of random features to consider. The –M option was invoked in SMO-SVM runs, which provides a confidence score between 0 and 1 with predictions and was used as the “lethal-phenotype score.” For random forest, 100 trees were built during the parameter search phase. All other parameters were default values. Best-performing parameter sets for each classifier were determined by AUC-ROC, which was calculated and visualized using the ROCR package (Sing et al., 2005). Models were built using best-performing parameter sets and randomly shuffled lethal and nonlethal gene labels. The AUC-ROC values from 100 iterations of gene label shuffling for all six classifiers ranged from 0.45 to 0.55 with a median of 0.5.

To predict whether an undocumented gene was lethal, the lethal-phenotype score resulting in the highest F-measure [harmonic mean of precision (proportion of predictions correct) and recall (proportion of true positives predicted)] was used as the threshold to call potential lethal-phenotype genes. Features most important to the prediction analysis were evaluated by leave-one-out analysis, wherein features were excluded one at a time, and effects on performance in comparison to a full feature set were recorded. To evaluate how many features are required to have comparable performance as the full model, 57 models were built and evaluated with increasing numbers of features. The order in which features were included was based on SVM weight, where features with the highest absolute weight were added first. During cross-species predictions, numeric data were discretized into quantiles (for example, data points in the lowest quantile were set to 1, while data points in the highest quantile were set to 5) to ensure that data were present in similar ranges and distinctions within data drawn by the machine learning algorithms could be applied to data from another species.

Supplemental Data

• Supplemental Figure 1. Over- and under-representation of phenotype genes in Gene Ontology categories.

• Supplemental Figure 2. Proportions of most similar paralogs produced in whole-genome duplication events.

• Supplemental Figure 3. Evolutionary rates between paralogs.

• Supplemental Figure 4. Performance of essential gene predictions with increasing numbers of features.

• Supplemental Table 1. Signs, absolute values, and ranks of support vector machine weights for A. thaliana and S. cerevisiae features.

• Supplemental Data Set 1. Lethal and nonlethal designations for A. thaliana, O. sativa, and S. cerevisiae genes.

• Supplemental Data Set 2. Gene Ontology terms with overrepresented numbers of weakly expressed lethal-phenotype genes.

• Supplemental Data Set 3. A. thaliana gene feature values.

• Supplemental Data Set 4. Performance of single-feature and leave-one-out lethal-phenotype gene prediction models.

Glossary

GO

Gene Ontology

FET

Fisher’s exact test

KST

Kolmogorov-Smirnov test

WGD

whole-genome duplication

PCC

Pearson correlation coefficient

AUC-ROC

area under the curve-receiver operating characteristic

SVM

Support Vector Machine

SMO-SVM

sequential minimal optimization support vector machine