Impact of Anchoring Groups on Ballistic Transport: Single Molecule vs Monolayer Junctions

Abstract

Tuning the transport properties of molecular junctions by chemically modifying the molecular structure is one of the key challenges for advancing the field of molecular electronics. In the present contribution, we investigate current–voltage characteristics of differently linked metal–molecule–metal systems that comprise either a single molecule or a molecular assembly. This is achieved by employing density functional theory in conjunction with a Green’s function approach. We show that the conductance of a molecular system with a specific anchoring group is fundamentally different depending on whether a single molecule or a continuous monolayer forms the junction. This is a consequence of collective electrostatic effects that arise from dipolar elements contained in the monolayer and from interfacial charge rearrangements. As a consequence of these collective effects, the “ideal” choice for an anchoring group is clearly different for monolayer and single molecule devices. A particularly striking effect is observed for pyridine-docked systems. These are subject to Fermi-level pinning at high molecular packing densities, causing an abrupt increase of the junction current already at small voltages.

Introduction

Electronic devices in which individual molecules or a molecular assembly are used as semiconducting components constitute a promising approach for ultimate miniaturization.¹⁻³ One of the key challenges in realizing such “molecular electronics” is a microscopic understanding of charge transport through metal–molecule–metal systems. An efficient way of tuning the transport properties of molecular devices is exploiting the enormous versatility of organic chemistry that is mainly achieved by chemical substitutions within the molecular backbone⁴ and via specific side groups. Another commonly used “molecular design” approach is to control charge transport in molecular junctions by changing the anchoring group linking the molecule and the metal.⁵⁻⁷ This, on the one hand, offers the possibility to tune the properties of the individual molecules, i.e., the ionization potential (IP) and electron affinity (EA). After all, from a molecular perspective, the anchoring group acts as yet another electron donating or accepting substituent. On the other hand, when assembling molecules into an actual junction, the choice of the anchoring chemistry strongly affects the coupling strength between the metal and the electrodes, crucially impacting the chemical stability of the device as well as its charge transport properties.⁸⁻³²

One of the first and to date most studied anchoring groups in gold-based junctions is thiol (−SH),⁸⁻¹⁰ mostly because of the strong covalent S–Au bond and the efficient electronic coupling associated with it. The properties of thiolate-bonded molecular junctions were, however, also shown to be quite sensitive to the binding geometry.¹¹ Furthermore, the S–Au bond seems to have some disadvantage compared to, e.g., the Se bond to coinage metals.¹² In fact, the structural details of the S–Au bond are strongly disputed in the literature,¹³⁻¹⁵ suggesting that a coexistence of several different geometries might be especially relevant for thiol-Au bonded junctions causing a wide spread of experimentally measured conductances.¹⁶⁻¹⁸ Thus, alternative anchoring groups have been studied extensively both theoretically and experimentally. These include, for example, pyridines^10,19−21, isocyanides (−NC),^7,22,23 cyanides (−CN),^5,10,22 the above-mentioned selenolates (−Se),^24,25 amines (−NH₂),^10,26−28 carboxyl-acids (−COOH),^26,29 and fullerenes (C₆₀).³⁰⁻³² These investigations showed that, depending on their donor and acceptor character, anchoring groups can have a profound impact on the level alignment,⁹ i.e., the relative energetic position of the HOMO (highest occupied molecular orbital) and the LUMO (lowest unoccupied molecular orbital) with respect to the metal Fermi level. In the coherent transport regime, this determines the tunneling barrier for charge carriers and is thus of key importance in molecular electronics.^33,34 Chemical trends of conductance and junction stability were investigated by Hong et al.¹⁰ for tolane molecules attached to gold via different anchor groups. The conductance was found to decrease following the sequence SH > NH₂ > Pyr ≫ CN, while the junction formation probability followed the chemical trend Pyr > SH > NH₂ > CN. Interestingly, a recent combined theoretical and experimental study of porphyrin single molecule junctions³⁵ found a sequence in conductance that is different, namely, Pyr > NH₂ > SO₃ > CN > COOH. Note that these investigations focused on single molecule junctions, whereas a systematic study on docking dependent transport for full monolayer junctions is currently missing. One can, however, expect on rather general grounds that the collective behavior of surrounding molecules becomes important when going from a single molecule to a SAM.³⁶⁻⁴⁸ Notably, it has recently been demonstrated that tuning the “electrostatic environment” allows for strong rectification in single-molecule junctions.⁴⁹ Furthermore, we have shown that intramolecular collective electrostatic effects are an important source of such “collectivity” in molecular junctions and that they can drastically affect the level alignment and with it important electrical characteristics.^50,51 As these electrostatic effects arise from the combined electric fields of neighboring molecules, they are especially relevant for differently linked junctions, since binding to the leads in virtually all cases involves the formation of a polar bond. Therefore, additional electric fields are generated by charge rearrangements due to metal–organic interactions. Additionally, the anchor groups themselves are often highly polar. As a consequence, collective electrostatic effects are present in virtually every multimolecular junction.

Here, we present an extensive theoretical analysis on how these additional fields caused by intramolecular polar bonds and the metal–molecule bonding impact the electronic and transport properties of molecular assemblies bonded to gold electrodes.^50,51 The focus is on the variations of collective electrostatics for commonly used anchoring groups, namely, thiol, methylthiol, isocyanide and pyridine. We will demonstrate that it is not only the “chemistry” of a specific anchoring group that determines the transport properties of molecular junctions, but also the local electrostatic environment of a molecule that plays a similarly decisive role. Most importantly, this can result in fundamentally different chemical trends in the transport properties of SAMs and single-molecule junctions, where it needs to be clarified to what extent they depend on the specific docking chemistry. This ultimately raises the question to what extent chemical design of only the molecular properties can control the characteristics of actual molecular junctions.

System Setup and Theoretical Methods

In our calculations, we study molecular junctions based on “Tour-wire”-type⁵² molecules, i.e., 1,2-bis(2-phenylethynyl)benzene attached to gold electrodes via thiolate (−S), methylthiolate (−CH₂S), isocyanide (−NC), and pyridine (−Pyr) anchor groups (see Figure 1a). These molecules differ in the electron donating/accepting properties due to the different anchoring groups, which changes the associated local dipoles, as well as in the bonding mechanism with the gold leads.

Figure 1.

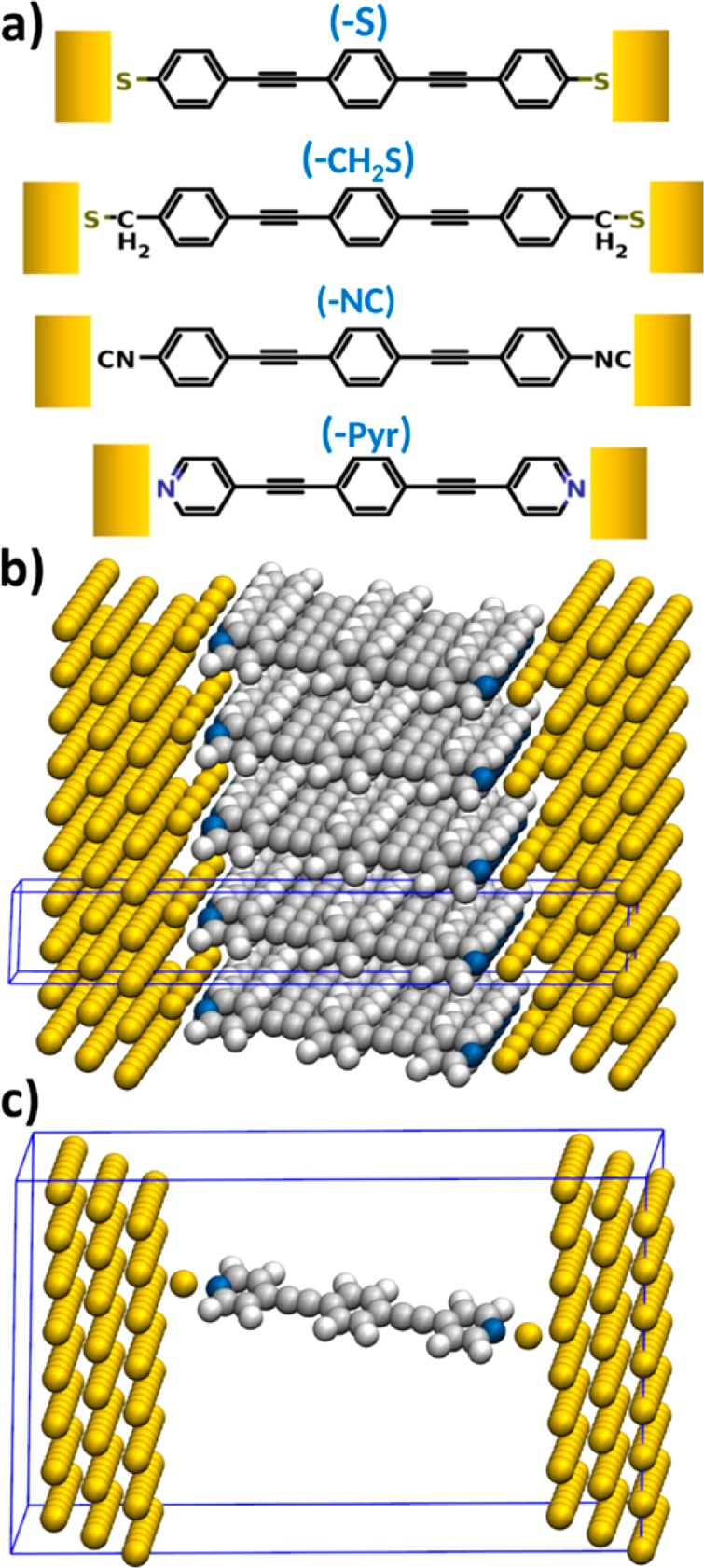
(a) Schematic representation of the chemical structure of the investigated molecules with thiolate (−S), mehtylthiolate (−CH₂S), isocyanide (−NC), and pyridine (−Pyr) anchoring groups, respectively; (b) structure of the densely packed (Θ = 1) (−Pyr_ad) junction and (c) the corresponding model system for the single-molecule situation (Θ = 1/16). The unit cells are indicated as blue boxes.

For the corresponding metal–molecule–metal junctions, we consider different molecular packing densities Θ. These span the range between the two limiting cases represented by the (periodically repeated) unit cells shown in Figure 1b and c, where the latter models a single molecule and the former a densely packed monolayer: we use one molecule in a (2 × 2) Au(111) surface unit-cell to model the Θ = 1 case (i.e., a densely packed SAM), and reduce the packing density gradually by expanding the cell laterally and removing all except one molecule. With this procedure, molecular packing densities of Θ = 1/2, 1/4, 1/8, and 1/16 are realized. The latter corresponds to a single molecule per 8 × 8 surface unit-cell of gold (for more details see Supporting Information). This we consider as the single-molecule junction limit, an assessment supported by the analysis of the changes in the electrostatic energy due to the bond formation discussed below. The metallic leads are represented by three layers of Au(111) on each side of the junction (i.e., six layers of Au separating periodic replicas of the molecules/monolayers). We optimized the structure of the SAM-based junctions (at full packing density, Θ = 1) including the innermost gold layers, and also relaxed the dimensions of the junction in the transport direction to allow for a more systematic structural setup. The geometry was not reoptimized at lower molecular packing densities, as the impact on the junction properties is expected to be minor and in this way we can also isolate the role of collective electrostatic effects. A detailed description of the geometry-optimization process employed for such junctions can be found in the Supporting Information of ref (51).

For the thiolate anchoring group, the sulfur atom was found to be situated close to the fcc hollow site, while for the methylthiolate a docking position between fcc hollow and bridge was observed, in accordance with previous findings.⁵³ The optimization for the isocyanide anchoring group also led to a docking position between fcc hollow and bridge. In the case of the pyridine anchoring group we investigated two different adsorption geometries, because the pyridine linker is characterized by a double-peak conductance signature corresponding to two distinctly different binding geometries that are present predominantly in the junction.²¹ The lower conductance feature corresponds to a vertical geometry, and the higher conductance value to a geometry where the molecule is significantly tilted and the electrode separation is smaller than the molecular length. Quek et al. further demonstrated that switching between these two conductance states can be achieved reversibly through repeated junction elongation and compression.⁵⁴ We modeled the vertical “low-conductance” pyridine structure (tilted by 5° relative to the surface normal and denoted as (−Pyr)) by a standard planar gold geometry, where after optimization the nitrogen atom is found in an on top position. A tilting of the pyridine docked molecule is energetically very costly for a flat Au surface; to overcome gold–hydrogen steric repulsion,²⁰ we studied a pyridine-docked molecule in the presence of an ad atom added to an fcc hollow site as a second structure. This results in a “high conductance” structure, tilted by 15° and denoted as (−Pyr_ad). Note that depending on the specific docking sites chosen for the electrodes and influenced also by the relative alignment of the electrodes in the experiment, of course other (higher) tilt angles are also conceivable, but the two geometries studied here already provide fundamental insight into the peculiarities of transport through pyridine docked systems (vide infra).

Geometry optimizations and electronic structure calculations were performed applying periodic boundary conditions within the framework of density functional theory (DFT) using the VASP⁵⁵ code. We employed the Perdew-Burke-Enzerhof PBE⁵⁶ exchange-correlation functional and a plane-wave basis set (cutoff: ca. 20 Ry). Geometries were optimized for the full packing density, Θ = 1, by applying the conjugate gradient scheme⁵⁷ as implemented in VASP. Charge-transport calculations were done in a three-step procedure combining DFT and nonequilibrium surface Green’s functions⁵⁸ to calculate I-V curves from (zero-bias) transmission functions in the Landauer-Büttiker formalism.^59,60 First, we used a locally modified version of the DFT based code SIESTA,⁶¹ where we applied a double-ζ polarized orbital basis set (DZP) in conjunction with a “PAO.EnergyShift” of 0.001 Ry, for extracting the Hamilton and overlap matrix of a region comprising the molecule and three gold layers at each side (a detailed discussion of why for the present study this choice of the “PAO.EnergyShift” is crucial in conjunction with the standard DZP basis functions of SIESTA can be found in ref (51)). Successively, using recursive Green’s functions we computed the self-energies of the electrodes. Finally, we obtained the zero-bias transmission function T(E) and used it to calculate the current–voltage characteristics I(V) within the Landauer-Büttiker formalism as

1

Here, f(x) is the Fermi–Dirac occupation function at 300 K and μ_left/right = E_F ± (eV/2), with E_F the Fermi energy, e the elementary charge, and V the voltage. Further details regarding the implementation of this approach can be found in the Supporting Information of ref (51). The zero-bias conductance G(E_F) also discussed in the following was calculated as G(E_F) = T(E_F)·G₀, where T(E_F) is the value of the zero-bias transmission function T at E_F, and G₀ = (2e²/h) is the quantum of conductance.

Bonding-induced charge rearrangements are defined as the difference between the charge density of the full metal–molecule–metal junction, ρ_sys, and the sum of densities of the isolated noninteracting subsystems, Δρ = ρ_sys – (ρ_mono + ρ_slab). ρ_slab is the charge density of the electrodes and ρ_mono the charge density of the free-standing monolayer. In the thiolates the charge density of the H-layers also has to be included.^62,63 The changes in the electrostatic energies due to metal–molecule bonding are calculated as differences of the electrostatic energies of the individual systems obtained from the VASP calculations. XCrySDen,⁶⁴ VMD,⁶⁵ Mayavi2,⁶⁶ and Ovito⁶⁷ were used for graphical visualization.

Results

Transport Characteristics of Single Molecule and Monolayer Junctions

The calculated current–voltage (I–V) characteristics for the differently linked molecular junctions are shown in Figure 2a for transport through single molecules (i.e., at Θ = 1/16, vide supra).

Figure 2.

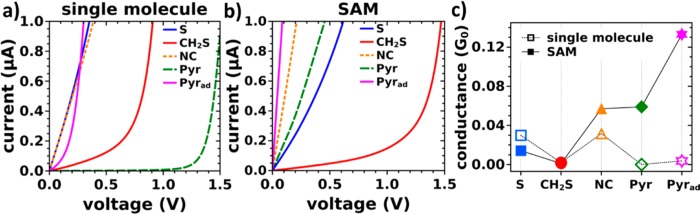
Calculated current–voltage characteristics of the (−S), (−CH₂S), (−NC), (−Pyr), and (−Pyr_ad) systems for (a) the model for a single molecule junction (i.e., a packing density of Θ = 1/16) and (b) for a SAM with Θ = 1; (c) corresponding zero-bias conductance G(E_F) = T(E_F)·G₀ for single molecule junctions (open symbols) and full monolayer junctions (closed symbols). G₀ here refers to the quantum of conductance that corresponds to 2e²/h.

Not surprisingly, we find significant differences in the current per molecule as a function of the docking chemistry. For the (−S) and (−NC) single molecule junctions, a pronounced increase of the current already at small bias voltages is observed. This indicates a strong hybridization of molecular states with states in the metal–electrode close to E_F resulting in good metal–molecule coupling. In contrast, for the (−CH₂S), (−Pyr), and (−Pyr_ad) single molecule junctions, a significant increase of the current is seen only for higher voltages. This is indicative of a weaker coupling between the (−CH₂S), (−Pyr), and (−Pyr_ad) molecules and the metal electrodes. Overall, we identify the following sequence for the current in the single-molecule junction in the studied geometry at small voltages of up to 0.25 V: S ≈ NC > Pyr_ad > CH₂S ≫ Pyr.

The situation changes markedly at full packing density (see Figure 2b; current–voltage characteristics for intermediate situations are contained in the Supporting Information). While the (−CH₂S) SAM still exhibits a close to exponential (I–V) characteristic with the onset of significant current shifted to even higher voltages, in all other systems an abrupt rise of the current with voltage is observed. This means that the performance of different anchoring groups for the single molecule and the SAM situation is very different. This is most pronounced for the (−Pyr) system, where a slowly, roughly exponentially growing current in the single molecule junction is replaced by an immediately increasing one in the respective SAM device. Hence, the ideal anchoring group for obtaining a large current per molecule is different in the case of the SAM-junctions, where we obtain the following sequence (see Figure 2b): Pyr_ad > NC > Pyr > S ≫ CH₂S.

As can be seen from Figure 2c, these trends are also reflected in the zero-bias conductance G(E_F) (see also the enlarged image of the small bias region of Figure 2a contained in the Supporting Information). Notably, for the isocyanide (−NC) and both pyridine linked junctions, the zero-bias conductance per molecule is strongly increased when going from the single molecule to the SAM, while for the junction based on the thiolate anchoring group (−S) we find a decrease of G(E_F). For the methylthiolate-based system (−CH₂S) the change in conductance between single molecule and SAM device is comparably small (increase from 0.001 G₀ at Θ = 1 to 0.002 G₀ at Θ = 1/16).

These results show that it depends on the molecular packing density which anchoring group yields the highest conductance.

Evolution of Transmission Functions with Molecular Packing Density

Current–voltage characteristics are related to transmission functions via the Landauer-Büttiker formula (cf. eq 1). Therefore, the above-discussed trends can be directly traced back to the respective transmission functions. They offer an initial handle to better understand the results presented above and are shown in Figure 3 for all investigated systems as a function of the molecular packing density Θ. Solid, darkly shaded curves correspond to the SAM situation, Θ = 1, and dotted, lightly shaded curves to the respective single molecule case, Θ = 1/16. Gray lines represent packing densities in between, namely, Θ = 1/2, Θ = 1/4, and Θ = 1/8. They are included here to better visualize the typically rather smooth packing density-dependent evolution of the electronic structure of the junctions.

Figure 3.

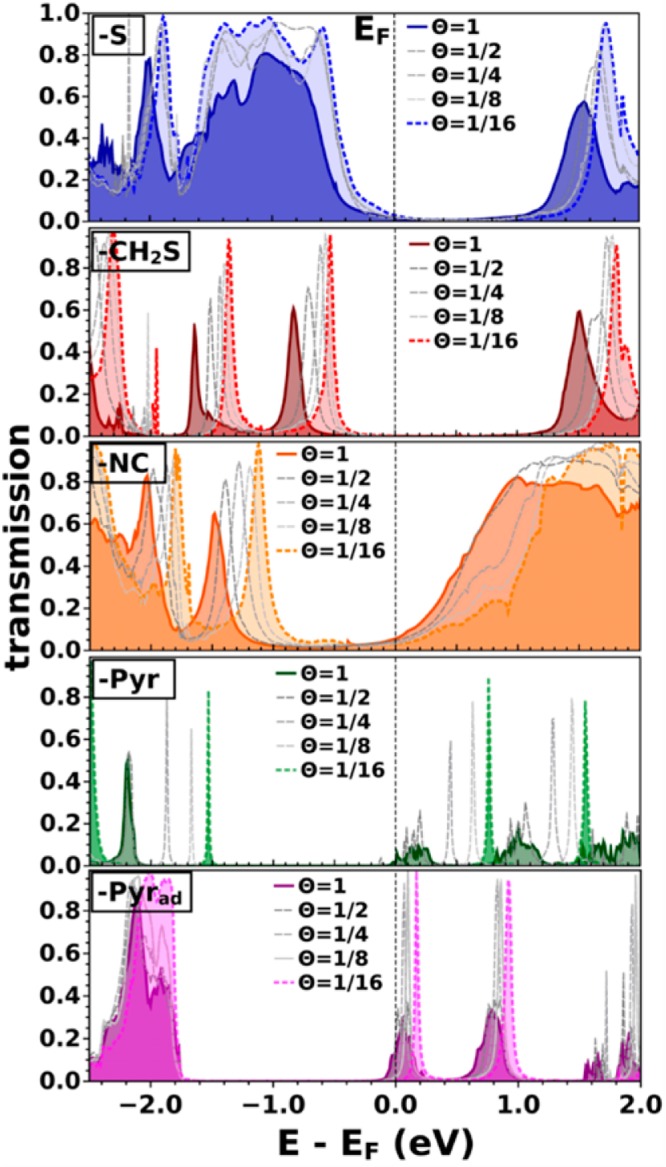
Calculated (zero-bias) transmission functions of the (−S), (−CH₂S), (−NC), (−Pyr), and (−Pyr_ad) systems at different packing densities Θ (Θ = 1 (SAM): darkly shaded, solid lines. Θ = 1/16 (single molecule): lightly shaded, dotted lines). The Fermi level E_F is used as the energy reference.

The following discussion first concentrates on the single molecule situation: When comparing the transmission functions of the differently linked systems we find two important differences. First, the energetic positions of the transmissive states with respect to the metal Femi level E_F drastically change when changing the anchoring group. Electron-donating linker groups, i.e., thiolate and methylthiolate, lift the frontier orbital energies, bringing the HOMO closer to E_F. Therefore, for (−CH₂S) and (−S) we find a pronounced p-type current with holes as the dominant charge carriers. Electron-withdrawing anchoring groups such as (−NC) and (−Pyr) push the frontier orbital energies down with respect to E_F, thus reducing the difference between the LUMO and E_F, thereby promoting an n-type current. The second apparent difference when comparing the differently docked systems is the width of the transmissive features. For the (−S) and the (−NC) system we find particularly broad and highly transmissive π-HOMO and π-LUMO-derived states. The pronounced broadening of these states is also seen in the density of states, which means that it is characteristic of the electronic structure of this molecule–metal interface and can be associated with a pronounced molecule–metal hybridization. Indeed, the width of the transmission states is a measure of the molecule–metal coupling strength,^1,68 which together with the small tunneling barrier explains the pronounced current for the (−S) and (−NC) systems. These results indicate that (−NC) and (−S) terminated molecules are especially promising for highly conductive single-molecule junctions. When introducing a methyl group between the thiolate and the conjugated backbone, the coupling between the extended states in the metal and the transmissive π-orbitals of the molecule is significantly reduced, resulting in a narrowing of the HOMO-related T(E) peak in (−CH₂S). Correspondingly, the current per molecule also decreases for the (−CH₂S) anchoring group compared to (−S), cf. Figure 2a. This finding is in agreement with several single molecule transport measurements,⁶⁹⁻⁷² where methyl spacers were shown to reduce the conductance by several orders of magnitude.⁶⁹ Similarly, Danilov et al.⁷¹ suggested a change of the transport mechanism from strong coupling with coherent tunneling for (−S) to weak coupling with sequential tunneling and Coulomb blockade behavior for (−CH₂S) due to the insertion of the CH₂ spacer.

Compared to the systems discussed so far, (−Pyr) shows extraordinarily narrow HOMO and LUMO derived peaks at Θ = 1/16 that are both >1 eV away from E_F. This explains the strongly reduced current for the (−Pyr) single molecule junction, a finding that is again in agreement with the literature, as this pyridine configuration reflects the low conductance situation, where the molecule is vertically arranged between the two electrodes.^21,54,73 When introducing an adatom in the junction geometry (−Pyr_ad) the molecule tilts and the overlap between the Au s-states and the molecular π-system is increased⁵⁴ resulting in a somewhat increased lead to molecule coupling. Moreover, the transmissive states in the single-molecule situation (Figure 3) are shifted toward the Fermi level compared to the (−Pyr) system, which is also reflected in an increased current (see Figure 2a).

When we increase the packing density from the single molecule limit to the densely packed SAM, (Θ = 1; darkly shaded, solid lines in Figure 3), the relevant transmission features strongly shift to lower energies for all investigated systems. The exact amount of this energy shift depends on the system, and its origin will be explained in detail below. The broadening of T(E) hardly changes in the case of (−S), (−CH₂S), and (−NC) junctions when increasing the packing density. For the (−Pyr) and (−Pyr_ad) systems, however, the very sharp features observed at the single molecule level broaden significantly in the SAM structure. This indicates that the metal–molecule coupling is qualitatively different for the single molecule and densely packed layer scenario of the pyridine-docked systems. The broadening concurs with the downward-shift of the LUMO-derived feature in T(E) until it aligns with the Fermi level; for (−Pyr_ad) the Fermi energy even cuts through the corresponding transmission peak. This is a manifestation of Fermi-level pinning,⁷⁴⁻⁷⁶ which due to the vanishing electron-injection barrier gives rise to the steep and immediate increase of the current observed for the pyridine linked SAM junctions (see Figure 2b). The origin of this Fermi-level pinning situation will be explained in detail below.

Relation between Level Alignment in the Junction and the Properties of the Individual Molecules

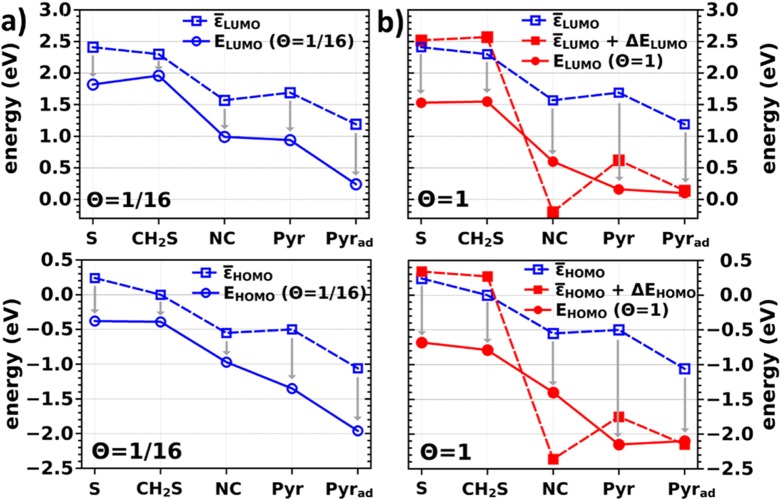
To understand the shifts of the transmission functions when changing anchoring groups and molecular packing densities, it is useful to perform an in-depth analysis of the location of the electronic states in the molecular systems relative to the states in the electrodes. The level alignment in the junction is given by the energetic positions of the peaks of the π-HOMO and π-LUMO (respectively, the corresponding bands in the SAM) relative to the Fermi level. These quantities are denoted as E_HOMO and E_LUMO. They are obtained from the densities of states projected onto the molecular region (including a Gaussian broadening). Their determination becomes somewhat ill-defined in strongly hybridized cases such as the (−S) HOMO and (−NC) LUMO.⁶² In a first approximation, we can attempt to understand the dependence of E_HOMO and E_LUMO on the molecular packing densities from three properties: (i) the energies of the frontier π-orbitals of the molecules in the gas phase (ε_HOMO and ε_LUMO), (ii) the work function of the clean Au(111) electrode (Φ), and (iii) the change in the energies of the molecular states due to intermolecular and molecule–metal interactions. The latter is denoted as δE_HOMO(Θ) and δE_LUMO(Θ) for the HOMO- and LUMO-derived states, respectively. This yields the following equations for the Θ-dependent energy level alignment in the junction, E_HOMO(Θ) and E_LUMO(Θ):

2a

2b

In passing, we note that including the work function of the electrodes in this analysis is necessary, as the relevant energy reference in the junction is the Fermi energy determined by the leads, while molecular orbitals are typically given relative to the vacuum level. The “realigned” quantities are denoted as ε̅_HOMO and ε̅_LUMO. ε̅_HOMO, ε̅_LUMO, and E_HOMO(Θ) and E_LUMO(Θ) are plotted in Figure 4 for the various molecules at full and lowest packing densities. At this point it should be mentioned that the values reported in Figure 4 have been derived from our DFT results, i.e., they include all effects that arise from the molecular packing density up to the level of the employed PBE functional (in particular, collective electrostatic effects in the focus of the present paper). Renormalization occurring within the molecular films and molecule–metal renormalization effects are, however, not accounted for in our (semi)local DFT calculations.⁷⁷

Figure 4.

(a) Energies of the molecular frontier orbitals, ε̅_HOMO (top) and ε̅_LUMO (bottom), of the isolated molecule corrected by the work-function of the electrodes (see text for details) and level alignment in the single molecule junction, E_HOMO (Θ = 1/16) and E_LUMO (Θ 1/16) as a function of the anchoring group used. Note that for Pyr_ad the work function of the Au substrate including the adatoms has been considered. (b) ε̅_HOMO (top) and ε̅_LUMO (bottom), of the isolated molecule compared to the situation in the hypothetical free-standing monolayer; ε̅_HOMO + ΔE_HOMO (top) and ε̅_LUMO + ΔE_LUMO (bottom) and level alignment in the monolayer junction, E_HOMO (Θ = 1)/E_LUMO (Θ = 1) for all studied anchoring groups.

When comparing the dotted and solid blue lines in Figure 4a, we find a reasonably close correlation between the properties that can be inferred from the isolated molecules alone, i.e., ε̅_HOMO and ε̅_LUMO, and the level alignment in the complete single molecule junction, E_HOMO(Θ = 1/16) and E_LUMO(Θ = 1/16) display a similar relative evolution. Thus, variations in the energetic positions of the transmission maxima can primarily be regarded as a consequence of a change in the molecular properties due to the chemical substitution with docking moieties. Still, it should be kept in mind that the bonding to the metal, which within our approximate framework for the single-molecule case is the only reason for finite values of δE_HOMO(Θ = 1/16) and δE_LUMO(Θ = 1/16) (cf., gray arrows), shifts the unoccupied states toward E_F and the occupied ones away from it. This has immediate consequences for the transport and is intertwined with its polarity, as will be discussed below.

To better understand the SAM situation (Θ = 1), it is useful to employ a Gedanken experiment often used for analyzing the properties of self-assembled monolayers,^62,63 namely, splitting the transition from the isolated molecule to the densely packed SAM into two steps: the formation of a hypothetical free-standing monolayer followed by the bonding of that monolayer to the substrate (where the latter in the case of thiolates also means eliminating the H atoms of the anchoring group). Consequently, δE_HOMO(Θ) and δE_LUMO(Θ) can be partitioned into

3a

3b

In this way, the energetic shifts of the states upon advancing from the isolated molecule to the monolayer bonded to two electrodes are viewed as a combination of (i) an energetic shift of the centers of the HOMO- and LUMO-derived bands due to the formation of a free-standing monolayer at a certain molecular packing density Θ (ΔE_HOMO(Θ) and ΔE_LUMO(Θ)); (ii) the modification of the energy landscape resulting from the charge rearrangements due to the bond formation between the molecules and the electrodes expressed as the bond-dipole, ΔE_BD(Θ); (iii) correction energies E_corr^HOMO and E_corr^LUMO, quantifying the change of the energy of the electronic eigenstates due to the charge rearrangements and resulting electrical fields. Effects (i) and (ii) are effectively largely electrostatic, while (iii) is a quantum-mechanical effect, which is typically small in densely packed systems due to the confinement of the energy gradients to the immediate interface region.⁶² The latter is observed also here (cf., Table 1) with the exception of (−Pyr_ad), which is an expected consequence of Fermi-level pinning (vide infra).

Table 1. Interface Energetics^a.

	ΔEHOMO	ΔELUMO	ΔEBD	EcorrHOMO	EcorrLUMO	EHOMO	ELUMO
Θ = 1
–S	0.10	0.10	–1.03	0.01	0.05	–0.68	1.53
–CH2S	0.27	0.27	–1.04	–0.02	0.02	–0.79	1.55
–NC	–1.81	–1.77	1.00	–0.04	–0.20b	–1.40	0.60
–Pyr	–1.07	–1.07	–0.29	–0.11	–0.17	–2.15	0.16
–Pyrad	–1.09	–1.05	0.37	–0.32	–0.41	–2.10	0.10
Θ = 1/16
–S	0.00	0.00	–0.24	–0.38	–0.35	–0.38	1.82
–CH2S	0.00	0.00	–0.19	–0.20	–0.15	–0.39	1.96
–NC	0.00	0.00	–0.14	–0.28	–0.44	–0.97	0.99
–Pyr	0.00	0.00	–0.19	–0.48	–0.56	–1.35	0.94
–Pyrad	0.00	0.00	–0.51	–0.39	–0.44	–1.96	0.24

^aQuantities characterizing the energetic shift of the electronic states between single molecules and molecules as part of a monolayer junction (cf., eqs 3a and 3b) for (−S), (−CH₂S), (−NC), (−Pyr), and (−Pyr_ad) junctions at full packing density, Θ = 1, and at the single molecule limit, Θ = 1/16. ΔE_HOMO and ΔE_LUMO are the energetic shifts of the centers of the HOMO- and LUMO-derived bands due to the formation of a free-standing monolayer. ΔE_BD is the bond dipole upon junction formation; E_corr^HOMO and E_corr^LUMO are correction energies, and E_HOMO and E_LUMO are the energetic positions of the peaks of the π-HOMO and π-LUMO derived bands relative to the Fermi level in the complete junctions. All quantities are given in eV. The values for the molecule-derived quantities ε_HOMO and ε_LUMO and the corresponding energies realigned relative to the Fermi level of the electrodes ε̅_Homo and ε̅_LUMO can be found in the Supporting Information.

^bNote that this value has a significant uncertainty as it is difficult to determine because the frontier unoccupied states are spread over a wide energy range (see also ref (62)).

The results of the two-step Gedanken experiment are illustrated in Figure 4b and the relevant energies are summarized in Table 1. They shall be discussed in the following for the (−CH₂S), (−S), and (−NC) junctions. For pyridine-linked molecular junctions, the underlying physics changes drastically. Thus, they will be explained separately. The origin of ΔE_HOMO and ΔE_LUMO are collective electrostatic effects that arise from the superposition of the fields generated by the polar anchoring groups at both ends of the free-standing molecular assemblies. They change the electrostatic energy and with it the energies of the frontier orbitals within the free-standing monolayer with the magnitude of the effect proportional to the dipole density.¹³ By definition, ΔE_HOMO(Θ) and ΔE_LUMO(Θ) vanish in the case of isolated molecules. As can be seen from Table 1, thiolate (−S) and methylthiolate (−CH₂S) linked molecules show an upward shift of the states in the monolayer compared to the isolated molecule, whereas for isocyanide (−NC) and pyridine, downward shifts of up to 1.8 eV are observed. This can also be retraced in Figure 4b, where we find pronounced differences in energy when comparing the blue open squares (isolated molecules) with the red filled ones (free-standing SAMs). As a consequence, we find no correlation between the molecular and monolayer properties. The particularly large shifts for isocyanide and pyridine are mostly attributed to a vertical alignment of the dipoles in these anchoring groups compared to a more tilted orientation of thiol and methylthiol dipoles.

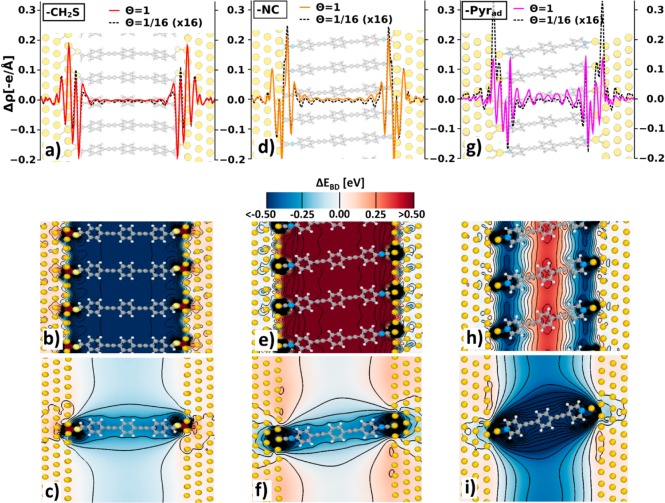
The bonding-induced shift of the energy landscape (contribution (ii)) is a consequence of charge-rearrangements, Δρ, either due to the formation of bonds between the anchoring groups and the metal surface (in the case of pyridines and isocanyides) or due to a replacement of S–H by S–Au bonds (in the case of the thiolates⁷⁸). The magnitude of the total step in the electrostatic energy due to the metal–molecule bond is typically referred to as “bond dipole”, (ΔE_BD(Θ)), and especially at high packing densities depends on the chemical nature of the anchoring group.⁶² The spatially resolved change in the electrostatic energy due to the charge rearrangements are shown in Figure 5 for several examples. In the case of (−CH₂S) and (−NC) (as well as in the thiolate case not shown here), Δρ for the isolated molecule and SAM situation is well localized at the metal–molecule interface (see Figure 5a and d). Here, one essentially deals with a succession of charge depletions and accumulations rather than with a single dipole.⁶²

Figure 5.

(a,d,g) (x,y)-integrated charge rearrangements per molecule, Δρ, along transport direction at full (Θ = 1, solid lines) and lowest (Θ = 1/16, dashed, black lines) packing density for (−CH₂S), (−NC), and (−Pyr_ad); (b,e,h) contour plot of the change in the electrostatic energy in the plane of the molecule due to metal–molecule bonding, ΔE_BD, at full packing density, Θ = 1, for (−CH₂S), (−NC), and (−Pyr_ad); (c,f,i) equivalent plots at the lowest considered packing density, Θ = 1/16. Isolines are drawn every 0.1 eV in the range from −2 eV to 2 eV.

At full packing density this behavior of Δρ results in a rigid and abrupt shift of the electrostatic energy at the immediate metal–SAM interface and in an essentially flat energy surface in between as shown in Figure 5b and e. The abruptness of that energetic jump is, on one hand, due to the localization of the charge rearrangements (vide supra) and, on the other hand, a consequence of collective electrostatics: the decay length of the electric field of a regular 2D arrangement of dipoles is nearly an order of magnitude smaller than the interdipole distance.⁴² As can be inferred from Figure 5b and e, in the case of (−CH₂S) the bond dipole shifts the orbitals down in energy, while it shifts them up for (−NC). These observations can also be retraced in Table 1, where ΔE_BD is listed as the shift of the electrostatic energy in the middle of the junction (see Supporting Information for a graphical illustration).

As ΔE_HOMO and ΔE_LUMO are small for (−S) and (−CH₂S), in these systems ΔE_BD dominates the level alignment in the junction at Θ = 1. Conversely, for (−NC) we find a strong shift to negative energies due to collective effects within the free-standing monolayer (vide supra) that is partially compensated by a strong positive shift by the bond dipole. The latter is primarily a consequence of the electron-density depletion in the top metal layer and the electron accumulation at the C atoms resulting in a dipole layer opposing the – NC dipoles. The details of the charge rearrangements can be understood from the specifics of the bond formation between the – NC groups and the Au substrate, explained in detail in the Supporting Information. Overall, the particularly strong dipole of the – NC group, on one hand, triggers a particularly large ΔE_HOMO and ΔE_LUMO, but, on the other hand, also causes a very strong compensating ΔE_BD. As a consequence, the fairly good correlation of the relative trends of ε̅_HOMO and ΔE_HOMO, respectively, ε̅_LUMO and ΔE_LUMO is recovered in Figure 4b (comparing open blue rectangles and full red circles). The shift between the two evolutions caused by the collective electrostatic effects is, however, much larger than in the case of the single-molecule junctions.

Discussing the single-molecule junction limit (i.e., Θ = 1/16) in the framework of the above Gedanken experiment provides us with certain additional insights, but also has its limitations, as will become evident below. The shape of the plane-integrated charge rearrangements remains similar but the magnitude changes (Figure 5a and d). These charge-rearrangements are localized in the vicinity of the anchoring groups. As the density of those groups is much lower at the interface, the modifications of the electrostatic energy in the single molecule case (Figure 5c and f) are fundamentally different from those in the SAMs (Figure 5b and e).³¹ Most importantly, no abrupt energetic jumps in the regions of the interfaces occur that would result in a massive and rigid shift of the molecular states. As a consequence, the values of ΔE_BD remain small (see Table 1). In contrast to the full coverage case, where the sign of the change in electrostatic energy depends on the anchoring group, for the single-molecule limit it is always negative. The more extended variations of the electrostatic energy in the direction perpendicular to the metal surface result in a quite significant modification of the molecular eigenstates. This results in the correction energies becoming rather large, i.e., in the range of 0.3–0.4 eV (see Table 1), which hints towards severe limitations of describing bonding-induced effects in terms of only the bond-dipole for a highly dilute monolayer.

Fermi Level Pinning

For the pyridine docked molecular junctions (−Pyr) and (−Pyr_ad) a different behavior is observed. This is a consequence of Fermi-level pinning,⁷⁴⁻⁷⁶ which occurs here especially at full packing density. Phenomenologically, one can consider a system in the regime of Fermi-level pinning when in the combined electrode–molecule (SAM)–electrode system the Fermi level cuts through a peak in the density of states that is associated either with the HOMO- or, in the present case, LUMO-derived bands. As a consequence, the corresponding peak of the DOS is very close to E_F, as shown for the pyridine-docked SAMs by the red circles in Figure 4b. Whether such a situation occurs in a SAM depends on (i) molecular properties (here the electron affinity approximated by the position of the LUMO realigned to account for the metal work-function, i.e., ε̅_LUMO), (ii) the shift of the molecular bands due to the formation of the (free-standing) monolayer, and (iii) the bond-dipole caused by the formation of the chemical bond between the anchoring group and the metal electrodes. Notably, (ii) and (iii) differ between isolated molecules and SAMs due to the collective electrostatic effects discussed above.

In the case where considering all these effects the LUMO-derived bands would come to lie below E_F, additional charge rearrangements are triggered to re-establish thermodynamic equilibrium. These are no longer confined to the immediate interface region, but extend onto the molecular backbone as shown in Figure 5g for (−Pyr_ad) (this also occurs in the case of (−Pyr) not shown here). Interestingly, the extended charge rearrangements are mostly not associated with charge transfer between the metal and the molecular π-system, as usually observed for flat-lying adsorbates in the case of Fermi-level pinning.^74,79,80 Rather, they correspond to a (local) polarization of the molecules⁷⁵ (see plots of the net charge transfer in the Supporting Information). For the resulting changes in the electrostatic energy at Θ = 1 (see Figure 5h), one observes an abrupt jump to negative values directly at the interface between the metal and the molecule, as in the thiolates. Deeper into the layer the extended charge rearrangements, however, cause a significant energy gradient, yielding a large positive change of the electrostatic energy in the center of the (−Pyr_ad) SAM. As a consequence, the concept of a single bond-dipole describing a rigid shift of the overall energy landscape upon bonding cannot be applied here. Thus, the values of ΔE_BD in Table 1, calculated as shifts of the plane-averaged electrostatic energy in the middle of the junction, are no longer particularly meaningful. The differences in the level alignment between (−Pyr) and (−Pyr_ad) stem from the reduced work-function of the Au-surface covered with Au adatoms (4.71 eV compared to the 5.18 eV for flat Au(111)) and the differences in chemical bonding mentioned in the description of the system setup.⁵⁴ This triggers Fermi-level pinning already at relatively low packing densities in the presence of adatoms (see Figure 3); in fact (−Pyr_ad) even at (Θ = 1/16) can be considered to be at the onset of Fermi-level pinning. This is confirmed by the more massive interfacial charge rearrangements in that system compared to (−Pyr). It also results in the comparably steep rise of the current for bias voltages above 0.2 eV (see Figure 2a).

Discussion

With all ingredients in hand, we can now reconsider the relation between chemical trends due to different anchoring groups, their impact on level alignment, and the actual transport properties. As discussed above, for the single molecule junctions the molecular trends induced by the substitution with electron withdrawing, respectively, donating anchoring groups essentially prevail. This is a consequence of the comparably small energetic shifts due to the metal–molecule bonding. They are caused by comparably weak energy shifts in the molecular region in conjunction with the resulting changes in the molecular eigenstates (E_corr), which are always negative. The situation changes dramatically in the densely packed monolayer, where collective electrostatic effects come into play that significantly shift the states in the monolayers. Interestingly, the shifts of the electrostatic energy caused by (i) the monolayer formation and (ii) the metal–SAM bonding add up such that the net effect is a strong shift of the states in all SAMs to lower energy compared to E_F. This shift is of roughly comparable magnitude and, most importantly, in all cases significantly larger than the shift for the single-molecule junction.

As a consequence, when comparing single-molecule and SAM junctions, the (zero-bias) transmission functions in the latter case are always shifted to smaller energies compared to E_F. Whether this then results in a decrease or an increase of the current per molecule depends on whether the transmissive channels at low bias arise from occupied or unoccupied states, i.e., whether hole or electron currents dominate. Consequently, the current per molecule decreases for the SAM case in (−S) and (−CH₂S), as there the increase of the barrier for holes is the relevant effect. Conversely, in (−NC) and both pyridine linked junctions, the decreased barrier for electrons at Θ = 1 results in an increase of the current per molecule. As a second effect, the coupling and hybridization at the metal–molecule interface obtained from the widths of the transmission peaks significantly influences the current, where strongly coupled junctions like (−S) and (−NC) are advantageous.

Conclusions

In conclusion, the relative energetic trends obtained for the orbital energies of the studied molecules with various anchoring groups by and large translate into trends in the level alignment of single-molecule as well as SAM-junction cases. A direct estimation of the junction properties solely on the basis of the molecular properties, however, remains difficult, if not impossible. This is a consequence of collective electrostatic effects that trigger a massive overall shift between the orbital energies in the single molecule and the SAM case. This yields an enormous increase or decrease of the junction current depending on the type of majority carriers. For pyridine-linked junctions the situation is further complicated by Fermi Level Pinning, which changes the metal–molecule bonding and the resulting energetic shifts especially at high packing densities. Thus, in such junctions a particularly steep increase of the current with rising bias voltage is observed, an effect that can be of particular interest for certain molecular electronics applications.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcc.5b06110.

• Details on the variation of molecular packing densities, (I–V) – characteristics and transmission functions for all packing densities, packing dependent peak positions of HOMO- and LUMO-derived bands (obtained from PDOS) for all investigated systems, cumulative charge transfer and bond dipole for all anchoring groups, the values for the molecule-derived quantities ε̅_HOMO and ε̅_LUMO, and a detailed description of the bond formation between (−NC) and Au substrate (PDF)

The authors declare no competing financial interest.