Crowded growth leads to the spontaneous evolution of semistable coexistence in laboratory yeast populations

Significance

The spontaneous emergence of stable coexistence between competing lineages in experimental evolution illustrates principles behind the creation and maintenance of biodiversity. Here, we present the first experimental observation of a general mechanism that leads to stable diversification in microbial populations despite competition for shared resources. Coexistence in our system depends on a tradeoff between growth and the ability to avoid cellular crowding. We elucidate the biophysical and genetic basis of this coexistence, and introduce a mathematical model that explains our results. Our analysis demonstrates that this coexistence can be perturbed by evolution on longer time scales, providing a unique quantitative example of how the interactions between ecological and evolutionary processes can create and destroy diversity in microbial populations.

Abstract

Identifying the mechanisms that create and maintain biodiversity is a central challenge in biology. Stable diversification of microbial populations often requires the evolution of differences in resource utilization. Alternatively, coexistence can be maintained by specialization to exploit spatial heterogeneity in the environment. Here, we report spontaneous diversification maintained by a related but distinct mechanism: crowding avoidance. During experimental evolution of laboratory Saccharomyces cerevisiae populations, we observed the repeated appearance of “adherent” (A) lineages able to grow as a dispersed film, in contrast to their crowded “bottom-dweller” (B) ancestors. These two types stably coexist because dispersal reduces interference competition for nutrients among kin, at the cost of a slower maximum growth rate. This tradeoff causes the frequencies of the two types to oscillate around equilibrium over the course of repeated cycles of growth, crowding, and dispersal. However, further coevolution of the A and B types can perturb and eventually destroy their coexistence over longer time scales. We introduce a simple mathematical model of this “semistable” coexistence, which explains the interplay between ecological and evolutionary dynamics. Because crowded growth generally limits nutrient access in biofilms, the mechanism we report here may be broadly important in maintaining diversity in these natural environments.

The spontaneous evolution of stably coexisting lineages has been documented in several laboratory microbial evolution experiments. Such coexistence is typically maintained by some form of resource partitioning, either through specialization to different nutrients in the environment (1–3) or cross-feeding (4–9). However, natural environments often harbor a greater diversity of microorganisms than nutrients, suggesting that many species stably coexist while competing for the same resources (10). Understanding how this diversity is maintained despite the principle of competitive exclusion has long been an important challenge in biology (11–14). An extensive body of theoretical work has sought to address this challenge by proposing a number of potential mechanisms that could maintain coexistence among lineages engaged only in exploitive competition (i.e., consumption of shared resources) (15, 16).

Some of these mechanisms have been found to evolve spontaneously in experimental systems (17, 18). For example, coexistence can be maintained by cross-feeding of secondary metabolites in homogeneous environments containing a single limiting nutrient (4). However, most experimental examples of the spontaneous evolution of coexistence on the same resources have involved spatially heterogeneous environments (19–21). For example, laboratory Pseudomonas fluorescens populations diversify from a planktonic ancestor that occupies the liquid phase of statically incubated cultures into a second type that forms a mat at the broth surface (21). This coexistence is stabilized by a tradeoff between the cost of mat formation and its benefits in conferring privileged access to oxygen (22). Coexistence based only on temporal heterogeneity is also possible (23) and has been investigated experimentally (8).

Theory has suggested another mechanism of coexistence based on crowding avoidance: If access to resources is density-dependent and competing lineages positively assort, then competition within a lineage will be more intense than competition between lineages (24, 25). Here, we describe the first experimental observation of spontaneous diversification due to this crowding avoidance effect. As in earlier studies (21), coexistence depends on spatial structure and a tradeoff between the ability to grow and maintain access to nutrients. However, nutrient access varies here according to cells’ local density rather than the spatial heterogeneity of nutrients in the environment. This type of interference competition is widespread in microbial populations, particularly in biofilms (26, 27). We introduce a simple mathematical model of this mechanism, which explains our observations and shows that this coexistence is semistable: It can be changed or destroyed by evolution on longer time scales.

Results

Spontaneous Evolution of Stable Coexistence.

In earlier laboratory evolution experiments (28, 29), we tracked the frequencies of fluorescently marked lineages over ∼1,000 generations in ∼1,000 haploid, asexual budding yeast populations propagated by serial passaging (with daily 1:2¹⁰ dilutions) in unshaken 96-well microplates. In most cases, natural selection eliminated diversity over time as these populations adapted, driving the marked lineage to either fixation or extinction. In 13 populations, however, we observed marked lineages that remained at constant intermediate frequencies for hundreds of generations.

To test the stability of this coexistence, we used sorting cytometry to perturb the frequency of each marked lineage. Specifically, we varied the frequency of the marked lineage from 0 to 1 across 24 replicates generated from each of the original 13 populations. In many cases, the marked lineages returned to their original frequencies (Fig. 1A and Figs. S1 and S2), indicating that coexistence is stably maintained by negative frequency-dependent selection in these populations. However, lineages in different populations have different equilibrium frequencies and fitness–frequency relationships (Fig. 1B and Fig. S1).

Fig. 1.

Coexistence due to negative frequency-dependent fitness. (A) Frequency of a fluorescently marked lineage over time. Colors represent independently evolved populations; each line is a replicate of the corresponding population in which the initial frequency of the marked lineage was perturbed to a given value. (B) Fitness of the marked strain as a function of its frequency, as calculated from the data in A. (C) Fluorescent image of one population shows that the marked lineage is located on the well walls, whereas the B type is located at the well bottom. (D) Microtiter wells containing isolated strains of the two types.

Fig. S1.

Coexistence due to negative frequency-dependent fitness (full data). Column 1 shows the original observation of marked lineages remaining at intermediate frequencies, suggesting frequency-dependent selection. (Insets) All these populations had dispersed pellet morphology. Columns 2 shows these lineages returned to their original frequencies after perturbation by sorting cytometry (Materials and Methods; note that the sharp decline in frequencies around generation 180 is an artifact of an experimental error, in which populations were temporarily propagated at dilution factors $\gg 2^{10}$. Column 3 shows the resulting lineage dynamics when these populations were duplicated from round-bottom into flat-bottom wells (A cells do not adhere to the vertically sloped walls of flat wells, which eliminates the crowding avoidance effect by causing both types to be similarly confined to the well bottom, and hence prevents coexistence). Column 4 shows the competition of clones, one A and one B, drawn from the source population of each row and propagated in unshaken (solid lines) and shaken (dashed lines) round-bottom wells.

Fig. S2.

B types do not exhibit frequency dependent fitness. Column 1 shows the observation of marked lineages remaining at intermediate frequencies in populations subsequently shown to lack frequency-dependent selection. (Insets) None of these populations had dispersed pellet morphologies. Column 2 shows the dynamics of these lineages after perturbation by sorting cytometry, and column 3 shows their dynamics after duplication from round-bottom to flat-bottom wells.

Identification of Adherent and Bottom-Dweller Types.

Visual inspection of these lines revealed that all populations exhibiting stable coexistence also display a “dispersed” pellet morphology, with some cells able to grow across a greater range of the well surface (Fig. 1C). When we isolate clones from these populations, we find two types: adherent (A) types that can grow on the well walls and bottom-dweller (B) types that grow in a compact pellet at the well bottom (Fig. 1D). Yeasts are nonmotile, and these populations are grown in unshaken wells of media. Hence, adherence enables cells to colonize the walls only when they are diluted into a fresh well of media and adhere to the polystyrene well walls during initial sedimentation at the start of a new cycle of growth. In other words, unlike B cells, A cells tend not to tumble down to the bottom of the well once they land on a sloped surface, as seen in Movies S1–S3.

Competition assays revealed that the relative fitness of any pair of A and B clones is negative frequency-dependent, although different pairs have different fitness–frequency relationships (Fig. S1). We found that the convergence of each marked lineage to its equilibrium frequency (Fig. 1A and Fig. S1) is recapitulated by the pair of A and B clones isolated from the same population (Fig. S1). We isolated clones from 59 other populations that had evolved dispersed morphology during the same experiment (28). All of these populations contained A types, and we found that they could arise from any of the marked lineages (i.e., founding genotypes).

Role of Spatial Structure.

The observation that cocultured A and B strains tend to occupy different regions of a microtiter well (Fig. 1C) suggests that their coexistence depends on spatial structure. In support of this view, we find that the frequency-dependent selection disappears and the A and B types no longer coexist when microtiter plates are continuously shaken during growth or have a different well geometry (flat rather than round bottoms; Fig. S1).

Genetic Basis of Adherence.

Mating of A clones to their ancestors revealed that the A phenotype is a recessive Mendelian trait that segregates 2:2. To identify these mutations, we performed bulk segregant analysis of three independently evolved A clones (30, 31), and found a single mutation linked to the phenotype in each one (enzyme ERG3 and transcription factors UPC2 and HAP1, respectively). These genes are all related to the ergosterol biosynthesis pathway, and the nature of the mutations (Dataset S1) led us to hypothesize that they reduce production of ergosterol. To test this hypothesis, we deleted ERG3 in the ancestral background, and the resulting strain is an A type that stably coexists with its B ancestor. We also found that adherence can be phenocopied by growing the ancestor at sublethal concentrations of azole antifungal drugs (Fig. S3), which inhibit another part of the ergosterol pathway (ERG11). Together, these data show that A lineages typically arise by single mutations that disrupt the ergosterol pathway and that such mutations alone are sufficient to give rise to coexistence.

Fig. S3.

Adherence phenocopied using antifungal drugs. The B ancestral strain (DBY15108) was grown at a range of drug concentrations in round-bottom wells. After saturation, cells were resuspended by shaking, allowed to settle, and imaged (Materials and Methods).

Dynamics of A-Type vs. B-Type Growth.

When cells are inoculated into a well at the beginning of each growth cycle, B cells accumulate at the bottom, whereas A cells also colonize the walls. We therefore hypothesized that adherence allows cells to escape crowding at the well bottom, dispersing them over a larger surface area, and therefore conferring a growth advantage during the high-density phase of each cycle of dilution and growth (illustrated schematically in Fig. 2). Coexistence then requires the A type to grow more slowly than the B type at low densities, as seen in Fig. 3. Accordingly, deleting ERG3 leads to a growth defect at low densities (Dataset S1) and each A clone is less fit than the B clone isolated from the same population when grown in shaken or flat-bottom microplates (Fig. S1).

Fig. 2.

Effect of crowding on the growth of A and B strains. A schematic illustration of growth during one cycle is shown.

Fig. 3.

Population dynamics within growth cycles. (A) Frequency of the A type over the course of two growth cycles. Eighteen representative populations starting with different initial frequencies are shown (of 180 total populations; complete data are provided in Fig. S4). (B) Ratio of the densities of the A type relative to the B type when each strain is grown in isolation (absolute density measurements are provided in Fig. S5). (C) Net fitness of the A type across growth cycles in all populations as a function of starting frequency, calculated from the data in A and Fig. S4. Dashed lines are the best-fit model prediction.

The mechanism of coexistence proposed here implies a biphasic approach to the equilibrium frequency: The B type increases in frequency at low densities early in each cycle, but the A type later gains an advantage by better maintaining its growth rate as density increases. To test this hypothesis, we measured the relative frequencies of cocultured A and B types over the course of two growth cycles (Fig. 3A and Fig. S4). As expected, the frequencies of A and B types oscillate, with the B strain favored at the beginning of each cycle and the A type favored at the end. These dynamics are also qualitatively consistent with the growth curves of A and B strains cultured in isolation (Fig. 3B and Fig. S5), which show that the B type grows faster at low density but slower at high densities.

Fig. S4.

A vs. B dynamics within each growth cycle. A strain frequencies in 162 populations are shown, in addition to the 18 shown in Fig. 3A.

Fig. S5.

Growth curves of A and B strains. The densities of the A and B strains in Fig. 3 (EFY5 and EFY10, respectively) as measured in 15 replicates (mean ± SEM, horizontal error bars of ±30 min). The ratio of these growth curves is shown in Fig. 3B.

Model of Coexistence.

We can describe these dynamics using a simple mathematical model. At low density, both A and B types grow exponentially, at rates r_A and r_B, respectively. However, the growth rate of the B type declines at high densities due to crowding and burial. We model this decline as a transition to linear growth at rate r_Bn_B, which reflects the continued growth of only a surface layer of n_B bottom-dwelling cells. In contrast, the A type continues to grow exponentially, because it is dispersed over a larger surface area. This mechanism does not require any differences in resource utilization, and accordingly, we find that the relative fitness of A and B types in shaken or flat-bottom plates is frequency-independent. For simplicity, we thus approximate the carrying capacity, K, of all strains to be the same. Together, this implies that during each daily growth cycle, the dynamics of the A and B types are given by

$$\frac{dA}{dt}=A{r}_A\cdot \mathrm{\Theta }\left(1-\frac{A+B}{K}\right)\hspace{0.17em},$$

$$\hspace{0.17em}\frac{dB}{dt}=B{r}_B\cdot {\left[1+\frac{B}{n_B}\right]}^{-1}\cdot \mathrm{\Theta }\left(1-\frac{A+B}{K}\right).$$

Here, A and B represent the total number of A and B cells, and Θ is the Heaviside function (which states that all growth stops when the total population size reaches K). After each growth cycle, the cells are uniformly diluted into a fresh well (reducing both A and B by a factor of 2¹⁰) and the cycle begins anew.

This model predicts that the A type declines in frequency during the initial phase of the growth cycle when the number of B cells is much less than n_B, because the B type has a faster maximum growth rate (r_B > r_A). If the A type is at higher frequency at the start of a growth cycle, this phase is prolonged (driving the A frequency down), because there are then fewer B cells initially, and hence they take longer to approach n_B. On the other hand, the A type increases in frequency later in the growth cycle, when the growth of the B type is limited by crowding. If the B type starts at high frequency, it more quickly approaches n_B and begins to feel these crowding effects, prolonging this second phase of the growth cycle (driving the A frequency up). Our mathematical model of these effects accurately reproduces the resulting biphasic convergence toward the equilibrium frequency (Fig. 3A) and the resulting fitness–frequency relationship (Fig. 3C). It also reproduces the qualitative differences in the growth curves of the two types when grown independently (Fig. 3B). To obtain these predictions, we set K = 9 ⋅ 10⁶ cells per well and r_B = ln(2)/80 min⁻¹ based on independent growth curve data (Fig. 3B and Fig. S5), and fit the free parameters r_A and n_B, finding r_A = ln(2)/89 min⁻¹ and n_B = 0.28 K. This inferred n_B corresponds to an ∼10% slowdown of the B-type growth at 3 ⋅ 10⁵ cells per well. Note that in Fig. 3B, the model overestimates the ratio of A- and B-type densities 12–20 h after inoculation; this transient discrepancy arises because we neglect the details of precisely how growth slows near saturation (Fig. S5). These details can be incorporated into the model with additional parameters but are not necessary for accurately predicting the dynamics of the two types in coculture.

Interplay Between Ecological and Evolutionary Dynamics.

Although the two types occupy different spatial niches, they compete for shared nutrients. This competition implies that interplay between evolutionary and ecological factors will affect the long-term stability of coexistence. For example, both r_A and r_B can change over evolutionary time as the A and B types adapt. Our model predicts quantitatively how the equilibrium frequency of the two strains depends on the ratio of these growth rates, r_A/r_B (dashed curve in Fig. 4). Here, we use relative fitness in flat-bottom wells as a proxy for r_A/r_B (details are provided in Materials and Methods and Fig. S6), because flat wells have vertical walls to which A cells hardly adhere, so that both types experience the same degree of crowding. Note this model prediction requires no additional fitting, because it depends only on the value of n_B/K estimated from Fig. 3. In principle, n_B and K could also evolve, and we could use our model to predict how this evolution would affect coexistence. However, we treat these parameters as constant because they are determined primarily by the fixed geometry of the microplate wells and the total nutrients in the media.

Fig. 4.

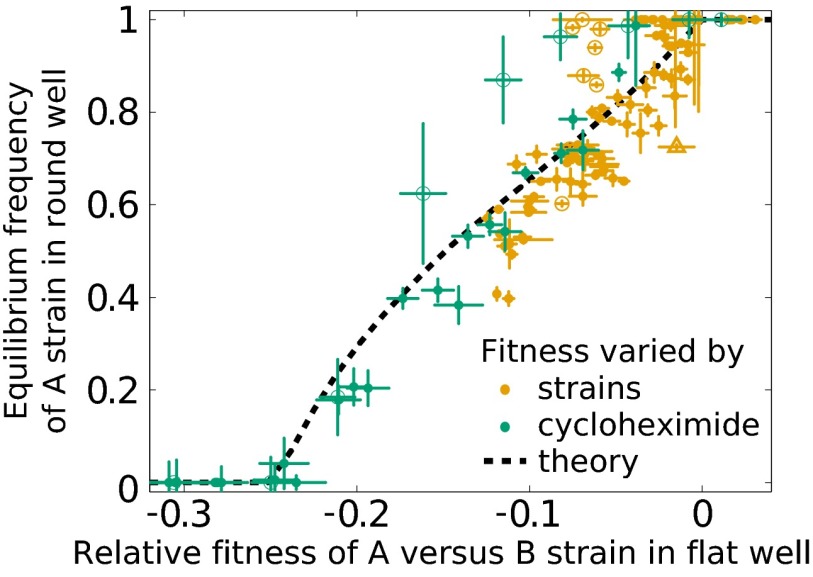
Semistability of the coexistence. We show the equilibrium frequency of A and B types as a function of their relative fitness in flat wells, which is a proxy for their ratio of growth rates, r_A/r_B. Each point represents the competition between one pair of A and B strains. Orange points are all pairwise combinations between 25 A strains and four B strains. The orange triangle is the constructed erg3$\Delta$ A strain vs. one of the B strains. Green points are competitions between four A strains and a cycloheximide-resistant B strain at a range of cycloheximide concentrations. Circled points correspond to two A strains that attained consistently higher than predicted equilibria, given their fitness. The dashed line is the model prediction; note this prediction involves no fitting.

Fig. S6.

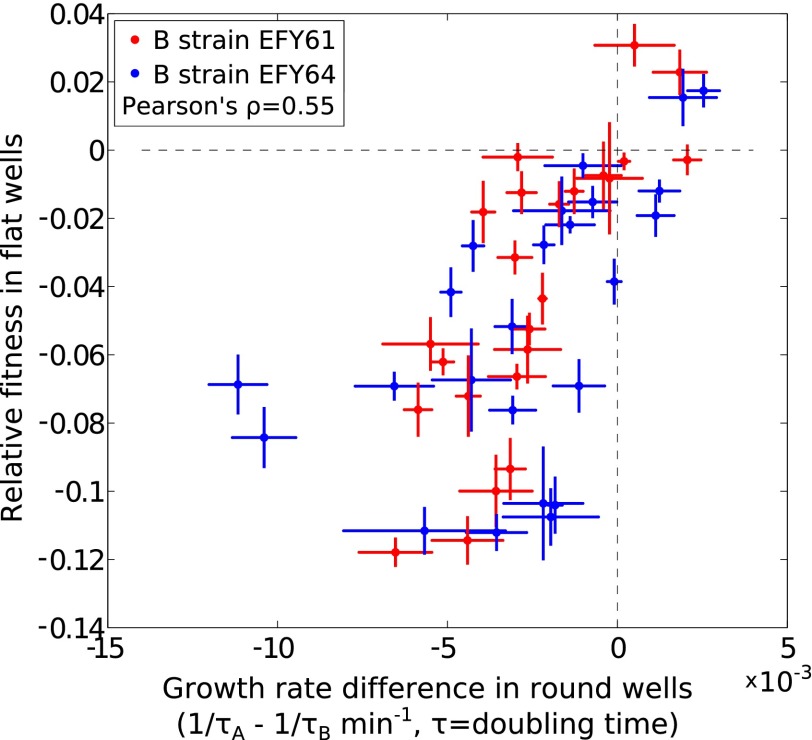
Fitness in flat wells compared with the maximum growth rate in round wells. Absolute differences in growth rate are plotted on the x axis for 48 A and B strain pairs. These strains were measured at low density (<10⁶ cells per milliliter) in round wells by mixing pairs of strains and assaying their proportions at the beginning and end of a 3-h interval (error bars are SEM for four biological replicates). The measurements of relative fitness in flat-bottom wells, plotted on the y axis, are the same as in Fig. 4.

To test our predictions for how changes in r_A and r_B affect coexistence, we considered all possible pairwise combinations of 25 A strains and four B strains chosen to span a large range of fitnesses (Dataset S1). Because we identified no A strains with fitness defects relative to B types greater than ∼10%, we also engineered a cycloheximide-resistant B strain and titrated the cycloheximide concentration in the media to decrease the relative growth rate of the A types artificially, and thus vary r_A/r_B over a broader range. For these competitions, we chose strains whose carrying capacities were unaffected by the cycloheximide for most of its concentration range (up to ∼100 nM). We found that our model accurately predicts how the equilibrium frequency depends on r_A/r_B (Fig. 4). Consistent with the model prediction, Fig. 4 shows that the B type will be driven extinct if the growth rate of the A type, r_A, evolves to match or exceed the growth rate of the B type, r_B. Conversely, the B type will drive the A type extinct if it achieves a growth rate [1-n_Bln(d)/K]⁻¹ ≈25% higher (here, d is the dilution factor) (23).

Furthermore, these data imply that adaptation within the subpopulations of coexisting A and B types tends to increase their equilibrium frequency vs. one another. To test this hypothesis, we confirmed that the fitness of A and B types, when competed against reference strains of the same type, positively correlates with their equilibrium frequency vs. strains of the opposite type (Fig. 5). We also conducted competition assays between combinations of two A strains and one B strain, and found that the A type with higher equilibrium frequency eliminates the one with lower equilibrium (Fig. 6 and Fig. S7).

Fig. 5.

Dependence of coexistence on fitness. (A) All pairwise competitions between a set of A strains (color-coded) and B strains of varied fitness. These fitness measurements were included in an earlier publication (28). (B) Similar data for A strains (strain numbers are indicated in the figure) vs. EFY64. Dashed curves show the model fit obtained by choosing the indicated values of r_B = ln(2)/τ_B. EFY5 is the A strain in Fig. 3; hence, its r_A = ln(2)/89 min⁻¹. The r_A values of the other A strains are determined by their fitness relative to strain EFY5.

Fig. 6.

Competition of two A strains and one B strain. The outcomes of competition for three combinations of strains are shown. Data points are color-coded by strain. Strain EFY64 is type B, and the other strains are type A. Dashed curves are model predictions based on the measured frequencies at generation 0, the model parameters n_B and K inferred from Fig. 3, and growth rates inferred from the equilibrium frequencies in Fig. 5B (Materials and Methods). The outcomes of other three-strain competitions are shown in Fig. S7.

Fig. S7.

Competition between two A strains and one B strain. Dynamics in populations containing all pairwise combinations between two sets of A strains, indicated by numbering of rows and columns, and one B strain (EFY64). Data points are color-coded according to strain, and symbols (×, ♢, ○, ●) correspond to independent populations. Dashed curves are model predictions based on measured initial frequencies and parameters inferred from Figs. 3 and 5B (Materials and Methods). Measurements at generations 40 and 50 were performed on samples stored for ∼24 h at 4 °C, which appears to have biased those frequencies in favor of the nonfluorescent strain (EFY64).

Discussion

The spontaneous evolution of stable coexistence between competing lineages generally involves some type of tradeoff between traits affecting fitness (14). A number of specific cases have been characterized in laboratory evolution experiments. For example, the growth of experimental P. fluorescens populations near the surface of a static broth creates an oxygen gradient, and coexistence arises between an evolved type able to colonize the oxygen-rich broth surface and an ancestral type able to grow faster but confined to oxygen-poor regions below (21, 22).

Coexistence between A and B types in our system arises due to a conceptually similar tradeoff between the ability to grow vs. maintain access to nutrients. However, in our system, the A type achieves better access through crowding avoidance (i.e., reducing its density), rather than by occupying a privileged position near a nutrient source. Because growing nonmotile cells tend to become surrounded by their progeny, density-dependent interference competition for nutrients is typically more intense among kin. Hence, the A and B types meet the classic condition for competitive coexistence: Intraspecific competition within types is greater than the interspecific competition between them (32). The two types exhibit different strategies for coping with this common form of intraspecific competition: The B type produces progeny as fast as possible but faces crowding sooner and more severely, whereas the A type mitigates crowding to grow at a slower but more sustainable rate.

Here, crowding avoidance improves access to a fixed pool of nutrients. This effect is closely related to other ecological mechanisms, such as dispersal, which, instead, typically involve gaining access to new resources. For example, the growth of microbial colonies in nutrient agar favors faster spreading away from regions of existing growth where nutrients are already depleted (33–35). If cells are nonmotile, then spreading is achieved by growth itself, and there is essentially a single selection pressure for faster growth (34). However, motile cells may face a trade-off between growth and motility, which can sustain coexistence (36). Thus, crowding avoidance and dispersal can lead to similar selection pressures and ecological consequences.

One might expect the link between adherence and slower growth to represent a fundamental tradeoff if adherence required production of proteins (e.g., adhesins) or secretion of an extracellular matrix. However, we have no evidence that such is the case in our system, and overexpression of adhesins is typically associated with flocculation (37), which we do not observe. Instead, the association between adherence and slower growth may be incidental to mutations disrupting the ergosterol pathway. Previous studies have shown that such mutations reduce growth rate (38) and that deletions of ERG3 and ERG4 can increase and decrease adherence, respectively (39). Most likely, A mutants are more hydrophobic, because adherence to polystyrene is itself a measure of cell-surface hydrophobicity (40, 41). Consistent with this speculation, pellet morphologies of A cells become indistinguishable from B cells in the presence of detergent (<0.05% Tween-20, a nontoxic concentration). However, the precise link between the ergosterol pathway and adherence is unknown (although this pathway is targeted by most antifungal drugs and adherence is a virulence factor).

Together, our findings show how an apparent tradeoff between faster growth and crowding avoidance evolves repeatedly and fosters ecologically stable coexistence that can be shifted and even eliminated by evolution on longer time scales. Here, this “semistability” is explained by a simple mathematical model that accurately predicts the full range of proportions at which the A and B types coexist as a function of their growth rate and related parameters. Semistable coexistence has also been studied in the context of cross-feeding (9). Our findings suggest the following recurring evolutionary scenario. First, A types evolve from B types by loss-of-function mutations disrupting ergosterol biosynthesis. The resulting A types stably coexist with their B-type progenitors because these mutations incur a pleiotropic growth defect or occur on unfit genetic backgrounds. Subsequently, if both types adapt at the same rate, r_A/r_B will be constant and the equilibrium frequency will not change. However, due to the inherent randomness in evolution, and possibly due to differences in the available mutational spectrum (e.g., the potential for compensatory adaptation in the A lineages), r_A and r_B will typically evolve at different rates. Thus, evolution can cause the equilibrium frequency to change over time, and potentially even destroy coexistence. These effects could explain our observations in previous work of populations sometimes gaining and then losing a dispersed pellet morphology (29). Furthermore, as these changes occur, additional A mutants can arise in the adapting B population. If the B type has been adapting more rapidly than the A type, these new mutants are likely to be able to displace the original A type [a similar phenomenon of repeated recolonization of an established niche is observed in experimental Burkholderia biofilms (42)]. These expectations are supported by competition assays between two A strains and one B strain, which show that A strains with higher equilibrium frequencies (relative to the B strain) displace those A strains with lower equilibria (Fig. 6 and Fig. S7).

Our results and mathematical model highlight a simple mechanism for semistable diversification via crowding avoidance, which arises repeatedly even in a very simple laboratory system. Although the precise form of frequency-dependent selection we observe here is specific to the details of our system, this general mechanism of coexistence is likely to be broadly relevant. For example, microbial biofilms are usually characterized by periodic growth, competition, and dispersal. Crowding and adherence are key to these processes, and play a particularly important role in pathogenicity. Opportunities to reduce crowding, and hence relieve density-dependent competition within a lineage, may therefore play an important role in maintaining the extensive diversity of microbes in nature.

However, it is important to note that our system harbors more complexity than our model describes. For example, fitness differences among some B strains are affected by well geometry (Fig. S2 and Dataset S1), which cannot be explained in terms of growth rate and saturation density. A cells also often collapse in large numbers to the well bottom during later stages of growth, suggesting that they too experience some effects of crowding and may even actively bury the B cells below (Movies S1–S3). Possibly for this reason, some A strains attain consistently higher than predicted equilibria (circled points in Fig. 4). Given these caveats and complexities, these populations are a rich and tractable system for studying microbial ecology and ecoevolutionary dynamics.

Materials and Methods

Strains.

All strains in this study are derived from a haploid MATa W303 ancestor. Specifically, strains EFY1–6, EFY50, and EFY67–85 are descendants of DBY15108 isolated from populations that evolved dispersed pellet morphology during an earlier long-term evolution experiment (28). EFY20, EFY27, EFY37, EFY38, EFY40, EFY43, and EFY46 are descendants of EFY10–17 similarly isolated from the same experiment. EFY10–17 and EFY61–64 are descendants of DBY15104 and DBY15105, respectively, which were isolated from a different evolution experiment (29). EFY10–17 were engineered to express a fluorescent reporter as previously described (28). To construct the erg3$\Delta$ strain (MJM179), we amplified regions flanking the G418 resistance cassette of the yeast deletion collection erg3$\Delta$ mutant (43) and integrated the PCR product into the ERG3 locus of DBY15108. The deletion was confirmed by PCR and Sanger sequencing.

Bulk Segregant Analysis.

To identify mutations causing the A phenotype, we sequenced three A clones and backcrossed each with an $\alpha$ ancestor, resulting in three diploids heterozygous for all mutant sites present in the corresponding clone. We sporulated these diploids and dissected tetrads to isolate 40 recombinant haploids. Each haploid was inoculated into a round-bottom well and scored for the presence or absence of the A phenotype (Materials and Methods, Assay for Adherence). These haploids were split into two pools of clones containing either only A types or B types. Genomic DNA was obtained from each pool and genotyped by Sanger sequencing at each candidate locus. Causal loci were identified as those loci for which the A pool exhibited only the mutant allele and the B pool exhibited only the ancestral allele.

Cell Culture.

Yeast populations were propagated as previously described (29), with slight modifications. Briefly, this protocol is to grow cells in 96-well polystyrene microplates containing 128 μL of rich media (YPD) at 30 °C and dilute them daily 2¹⁰-fold into fresh plates using a pipetting robot (Beckman BioMek FX). To ensure consistent dispersal of the A type, plates were shaken 10–30 s (1,100 rpm; Heidolph Titramax 100) immediately after inoculation. Microplates had round or flat bottoms and were incubated either with or without continuous shaking (1,350 rpm; Titramax 100) as indicated above.

Measurement of Lineage Frequencies and Relative Fitness.

Cell densities and frequencies of fluorescently labeled lineages were simultaneously determined by flow cytometry (BD Biosciences LSRII or Fortessa with attached high-throughput samplers). Because cytometry sample preparation requires washing cells in PBS, which disrupts population-level spatial structure, populations were assayed after their daily dilution or, in the case of Fig. 3 and Figs. S4–S6, by destructive sampling of replicates. To measure relative fitness, two strains of the same type are mixed together in equal proportion and propagated in coculture for 30 generations (29). The fitness is determined from their frequencies at generations 10 and 30 according to the formula: s = ln((f_x/f_y)_{t = T}/(f_x/f_y)_{t = 0})/T, where f_x and f_y are frequencies of lineages x and y and T is the number of population doublings (in this case, equal to 20). This formula is also used to calculate fitness from other lineage frequency data (e.g., Fig. 1A).

Direct Measurements of Maximal Growth Rates.

To measure maximum growth rates (r_A and r_B in our model) directly, we maintained strains in the same way as described above, and assayed lineage frequencies and cell densities by destructively sampling replicates before saturation. For Fig. 3B and Fig. S5, we measured total cell densities of one pair of A- and B-type strains at several time points. Because of the need to count many cells at very low densities in populations maintained in small volumes, it was not practical to measure direct growth rates accurately in this way for many strains. In addition, systematic errors can easily arise because the relevant growth rate differences are small, and these differences must be measured within the correct narrow time window during the first hours of growth before crowding effects become significant. Thus, to avoid these difficulties, we used fitness in flat-bottom wells as a proxy for r_A/r_B to test the model predictions shown in Fig. 4. To verify that these two quantities are correlated, we directly measured differences in maximum growth rates for 50 strain combinations (half of those strain combinations in Fig. 4). We did so by preparing replicates of strain pairs in coculture and assayed their relative frequencies 2 and 5 h after inoculation by destructive sampling of replicates. We then calculate (1/τ_x − 1/τ_y) = log₂((f_x/f_y)_{t = T}/(f_x/f_y)_{t = 0})/T, where T = 180 min and τ_x and τ_y are the doubling times of strains x and y. Although these measurements are noisy and may contain systematic biases for the reasons described above, we find that they are significantly correlated with relative fitness in flat-bottom wells (Pearson correlation = 0.55, P < 10⁻⁵; Fig. S6).

Measurements of Equilibrium Frequency.

Equilibrium frequency is measured by mixing A- and B-type strains at a range of ratios and propagating the populations in parallel, as shown in Fig. 1 and Fig. S1. Equilibrium and its uncertainty then equal the mean and SE of the final frequencies. For Fig. 4, the propagation was truncated before populations converged to a common ratio. In these cases, the equilibrium is estimated from the fitness-vs.-frequency data (illustrated in Fig. 1B) using least-squares linear regression, and the uncertainty is computed by bootstrapping (SD of equilibria inferred from data sampled with replacement). In Fig. 4, the fitness and equilibrium between a cycloheximide-resistant B strain (DVD101) and two sensitive A strains (EFY3, EFY5, EFY68, and EFY85) were varied by competing these strains in media supplemented with cycloheximide concentrations ranging from 12.5 to 150 nM, in 12.5 nM increments.

Imaging.

To obtain the fluorescent and time-lapse images of pellet morphologies (Fig. 1C and Movies S1–S3, respectively), we used a Zeiss LumarV12 stereoscope. For bright-field images (Fig. 1D), we used an Epson Perfection V700 transparency scanner.

Modeling.

Our model predicts that equilibrium frequencies are determined by the ratios of parameters r_A/r_B and K/n_B. To obtain the predictions in Fig. 2, we set r_B = ln(2)/80 min⁻¹ and K = 9 ⋅ 10⁶ cells per well based on the growth curve data for single-strain populations (Fig. 3B and Fig. S4). We then determined r_A and n_B by minimizing χ² error with respect to lineage frequencies and densities at the end of each cycle, assuming measurement uncertainties of 2.5% and 10% for lineage frequencies and cell densities, respectively. These computations were performed by a commercial differential equation solver and minimization algorithm [ode45 and fminsearch in MATLAB (MathWorks), version 2012a].

The value K/n_B ≈ 3.5 inferred from Fig. 3 is assumed to be the same for all B strains. The model, given this assumption, implies a one-to-one correspondence between the fitnesses of strains of the same type and their ratio of growth rates, as well as between the equilibrium frequency of strains of the opposite type and their ratio of growth rates. Consequently, data in different figures can imply different values for the same parameters. For example, in Fig. 5A, the theoretical ratio of growth rates for strains EFY1 and EFY5 is 1.09 based on their different equilibria, but in Fig. 5B, it is 1.01 based on their difference in fitness. Likewise, in Fig. 6 and Fig. S7, the predictions may be based on either the equilibria or fitnesses shown in Fig. 5B. We based predictions on the equilibria because, overall, this method produced better agreement with the data, but there are discrepancies when A strains have a larger difference in fitness than implied by their equilibria or vice versa. For example, EFY46 has a slightly lower equilibrium than EFY1, but a relatively large fitness defect (Fig. 5B). Hence, EFY46 declines faster than predicted by the model in Fig. 6 (Left).

The fitness values of the 14 A-type strains in Fig. 5B were inferred from 49 pairwise fitness measurements (Fig. S8). We chose EFY5 as the zero-fitness reference and inferred the remaining 13 fitness values by minimizing χ² error under the assumption that fitness is transitive. The horizontal error bars show the parameter variation that increases χ² error by one unit around its minimum.

Fig. S8.

Transitivity of fitness among A strains. All pairwise fitnesses between two sets of seven A strains measured in triplicate are shown. These data were used to determine the absolute fitnesses shown in Fig. 5B and were found to be consistent with transitive fitness among A strains (${\chi }^2=0.6$; Materials and Methods).

Assay for Adherence.

To produce pellet morphologies that can indicate adherence, we add >10⁵ cells to a round-bottom well, shake vigorously to suspend, and allow ∼30 min for cells to settle. B cells accumulate in a round pellet at the bottom, whereas A cells form an opaque ring around the well center. To determine whether adherence could be phenocopied by azole antifungal drugs, we grew EFY10 (a B-type strain) for 2 d in the presence of sublethal concentrations of fluconazole and miconazole, and then repeated the adherence assay described above.