Geometrically controlled snapping transitions in shells with curved creases

Significance

Shape-programmable structures have recently used origami to reconfigure using a smooth folding motion, but are hampered by slow speeds and complicated material assembly. Inspired by natural systems like the leaves of Venus flytraps and hummingbird beaks, we use curved creases to imbue elastic shells with programmable fast “snapping” motion. This deformation between preprogrammed states can be tuned to be either continuously foldable or snap discontinuously. Our results provide a purely geometrical mechanism for designing multistable structures, thus circumventing the need for complex materials or fabrication methods in creating structures with fast dynamics. This technique will find application in designing structures over a wide range of length scales, including self-folding materials, tunable optics, and switchable frictional surfaces for microfluidics.

Abstract

Curvature and mechanics are intimately connected for thin materials, and this coupling between geometry and physical properties is readily seen in folded structures from intestinal villi and pollen grains to wrinkled membranes and programmable metamaterials. While the well-known rules and mechanisms behind folding a flat surface have been used to create deployable structures and shape transformable materials, folding of curved shells is still not fundamentally understood. Shells naturally deform by simultaneously bending and stretching, and while this coupling gives them great stability for engineering applications, it makes folding a surface of arbitrary curvature a nontrivial task. Here we discuss the geometry of folding a creased shell, and demonstrate theoretically the conditions under which it may fold smoothly. When these conditions are violated we show, using experiments and simulations, that shells undergo rapid snapping motion to fold from one stable configuration to another. Although material asymmetry is a proven mechanism for creating this bifurcation of stability, for the case of a creased shell, the inherent geometry itself serves as a barrier to folding. We discuss here how two fundamental geometric concepts, creases and curvature, combine to allow rapid transitions from one stable state to another. Independent of material system and length scale, the design rule that we introduce here explains how to generate snapping transitions in arbitrary surfaces, thus facilitating the creation of programmable multistable materials with fast actuation capabilities.

Curved shells are generally used to enhance structural stability (1–3), because the coupling between bending and stretching makes them energetically costly to deform. The consequences of this coupling are seen in both naturally occurring scenarios, such as intestinal villi and pollen grains (4, 5), and find use in man-made structures such as programmable metamaterials (6–9). When these shells have multistable configurations, the transition between them is opposed by geometrically enhanced rigidity resulting from the dominant stretching energy. Often, even for relatively small range of deformation, stretching leads to the high forces and rapid acceleration associated with a “snap-through” transition in many natural and man-made phenomena (10–17). For example, Venus flytraps (Dionaea muscipula) use this mechanism to generate a snapping motion to close their leaves (11), hummingbirds (Aves: Trochilidae) twist and rotate their curved beaks to catch insect prey (14), and engineered microlenses use a combination of bending and stretching energy to rapidly switch from convex to concave shapes to tune their optical properties (12). Despite the ability to engineer bistability and snapping transitions in a variety of systems by using prestress or material anisotropy (18–24), a general geometric design rule for creating a snap between stable states of arbitrary surfaces does not exist. This stands in stark contrast to the well-known rules and consequences for folding of a flat sheet, as shown in origami design (25–27). In origami, weakening the material locally by introducing a crease allows the sheet to deform without stretching, and thus allows the sheet to access low-energy states without requiring nonlinear material strain.

Geometrical Mechanics of Folding a Shell

Inspired by these ideas from origami, we consider the folding of curved surfaces with creases. Although this concept has been realized on rare occasions in art (27–29), the continuum mechanics of a creased shell is far from fully understood. In particular, folding a curved surface along a crease often leads to large deformations of the shell. However, despite these nonlinear deformations, we show that the local geometry of the crease alone creates a large energy barrier that leads to a snapping transition in a sufficiently thin shell. Because our proposed design principle arises purely from geometry, it does not rely on special materials or anisotropy to generate rapid snap-through transitions; in practical applications, this enables one to harness the instability for fast actuations purely by design, thereby providing a simple method for the design of rapidly actuating structures from a wide range of elastic materials.

We consider a crease to be a long but narrow region of locally weak material introduced, for example, through a local thinning of the shell. This local weakening behaves as a foldable hinge in the shell, but the curvature of the rest of the shell limits the deformation of this hinge, because the shell and hinge itself must deform to accommodate folding along the creased area. When the entire shell is sufficiently thin, this deformation will be approximately isometric, meaning it is devoid of in-plane strain. Geometry and the condition of isometry combine to allow us to relate the shape of the crease to the deformation of the shell in the vicinity of the fold. To proceed, imagine an unfolded shell upon which a hinge, parametrized by arc length s and having tangent vector $\mathbf{t}\left(s\right)$, has been inscribed (Fig. 1A). The perpendicular vectors $\mathbf{t}\left(s\right)$ and $d\mathbf{t}\left(s\right)/ds$ span the osculating plane, while the space curvature $\kappa \equiv \left|d\mathbf{t}\left(s\right)/ds\right|$. If the osculating plane makes an angle ψ with respect to the shell (Fig. 1B), we can define the geodesic curvature, ${\kappa }_g=\kappa \cos \psi$, and the normal curvature, ${\kappa }_N=\kappa \sin \psi$, as the respective projections of the space curvature onto the tangent (${\hat{\mathbf{u}}}^{+}$, Fig. 1B) and normal (${\widehat{\mathbf{n}}}^{+}$, Fig. 1B) of the shell’s midsurface.

Fig. 1.

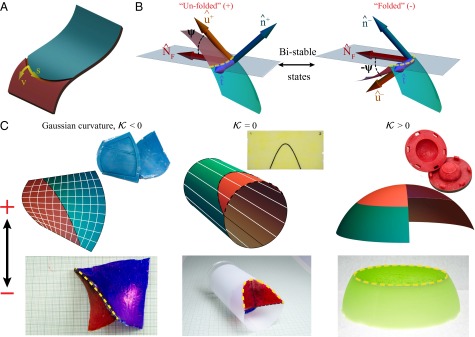
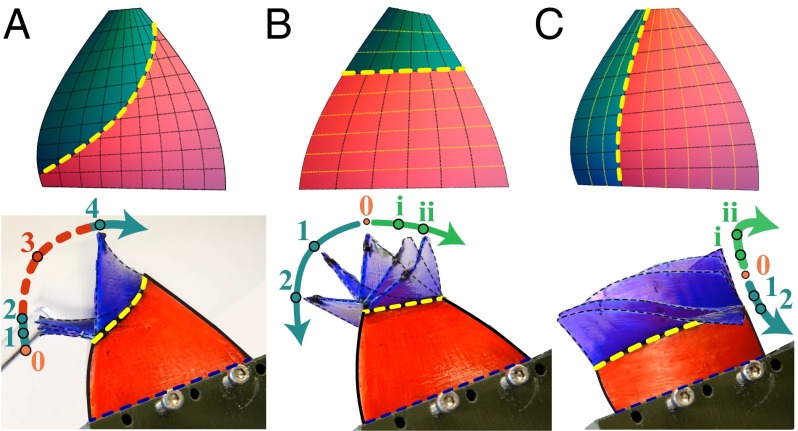
Folding of curved shells along a crease. (A) Creasing a shell involves thinning the shell locally along a curve that lies on the surface to form a “trench.” A local coordinate system $\left\{s,v\right\}$ on the crease is indicated. (B) Natural and folded states of a creased shell, denoted as the “+“ (unfolded) and ”−” (folded) conformations. Tangent and normal vectors to each surface “$\pm$” are given by ${\widehat{\mathbf{u}}}^{\pm }$ and ${\widehat{\mathbf{n}}}^{\pm }$, respectively. ${\widehat{\mathbf{N}}}_{\mathbf{F}}$ is the normal to the curve, whereas $\widehat{\mathbf{t}}$ indicates the tangent to both the crease and the surface. The angle ψ between ${\widehat{\mathbf{N}}}_{\mathbf{F}}$ and $\widehat{\mathbf{u}}$ is also indicated. (C) Schematics (for +) and creased experimental samples (for −) for all three prototypical geometries: helicoid ($K<0$), cylinder ($K=0$), and spherical shell ($K>0$). (Insets) Three-dimensional printed molds with embossed ridge to realize creases on ($K\ne 0$) geometries, and a scored sheet for the ($K=0$) case. Examples of curves with ${\kappa }_N=0$ are marked on schematics in white lines, and creases are marked on experimental samples with dotted yellow curves.

An advantage of this decomposition is that, if in-plane strains in the shell vanish, the geodesic curvature of the fold must remain unchanged after folding (30, 31), yielding the relationship ${\kappa }_N\left(s\right)={\kappa }_g\left(s\right)\tan \psi \left(s\right)$. The shape of the fold also determines, in part, the geometry of the shell on either side of the fold. In the absence of stretching, a shell cannot change its Gaussian curvature $\mathcal{K}$. A straightforward calculation (see the Supporting Information) obtains the mean curvature of the shell near the fold,

$$H=\frac{1}{2}\left({\kappa }_N+\frac{\mathcal{K}+{\left({\partial }_s\psi +\tau \right)}^2}{{\kappa }_N}\right),$$ [1]

where τ is the torsion of the fold, which measures the rate that the osculating plane twists around the hinge and, hence, the nonplanarity of the hinge (32).

A special role is played by angles along which a fold does not change its space curvature, κ, after folding. In this case we may use the definition of the geodesic curvature to solve for the angle ψ, which yields $\psi =\pm {\cos }^{-1}\left({\kappa }_g/\kappa \right)$. There are two solutions for ψ, one of which may be physically understood as a local reflection of the shell through the osculating plane of the fold. A surface can be folded by an angle $2\psi$, for example, along which the normal curvature on either side is $\pm {\kappa }_g\tan \psi$ (Fig. 1B). This “mirror reflection” is naturally an isometry of the surface in the vicinity of the fold, although the mean curvature H must switch signs on one side relative to the other. The mirror reflection isometry was noted in the seminal monograph on bending of surfaces by Pogorelov (33), whose work on spherical isometries we discuss below.

The bending energy density of a folded surface, in the vicinity of the fold, is ${\mathrm{ℰ}}_B=B/2{\left(H-H_0\right)}^2$, where B is a bending modulus and $H_0$ is the background shell curvature. An unfolded shell has ${\kappa }_N$ of the same sign on either side of the crease, and thus matches the preferred curvature $H_0$. However, the bending energy density of a shell which has been folded (Fig. 1B) is not zero because ${\kappa }_N$ will be negative on one side and positive on the other; thus, only one side of the hinge can match the preferred curvature of the shell $H_0$. Consequently, there must exist a state between the folded and unfolded states of the shell for which ${\kappa }_N=0$. At this critical value, H generically diverges (Eq. 1, see the Supporting Information). Whereas the bending energy between the folded and unfolded states is infinite for isometric deformations, in any real material as the shell bends the energy will reach a scale where stretching becomes favorable. As a result, our assumption that the shell does not stretch must have been flawed, and in-plane stresses must have developed near the fold similar to stress-focusing phenomena seen in other curved surfaces (1, 34–39). Beyond this special stressed configuration, however, in-plane stresses are no longer necessary and the surface can, at least in principle, accommodate the folding through bending deformations alone.

An important exception to the previous analysis arises when the crease has zero normal curvature everywhere. Curves with vanishing ${\kappa }_N$ can still exist when $\mathcal{K}=-{\left[{\psi }^{\prime }\left(s\right)+\tau \left(s\right)\right]}^2$ (Fig. 1C). This occurs trivially on flat paper inscribed with a curved fold because ${\psi }^{\prime }\left(s\right)$, $\tau \left(s\right)$, and $\mathcal{K}$ vanish individually. In this case, the surface can be folded with a monotonically increasing energy mediated by the bending energy alone (31, 40). Moreover, curves with vanishing ${\kappa }_N$ only exist on surfaces of nonpositive Gaussian curvature, restricting the class of shells that may be creased with this property.

General Design Principle

These considerations provide a geometrical design rule: simply by introducing a crease with finite normal curvature (${\kappa }_N$), an energetic barrier is created between a pair of locally isometric states. For any finite-thickness shell, such transitions will require stretching of the surface and can lead to violent snaps. Bending along an asymptotic curve, defined to have ${\kappa }_N=0$, however, leads to continuous deformations and the absence of a snap. Therefore, the three types of Gaussian curvature naturally divide the shell behavior under folding into one of three types. When $\mathcal{K}>0$ (such as on a sphere), there are no asymptotic curves so all creases can generate a snap-through instability. When $\mathcal{K}=0$, however, the shell is either completely flat, or has a single direction at each point with ${\kappa }_N=0$. One might imagine a cylinder, for example, which has lines of zero normal curvature along the cylinder axis. These folds are necessarily straight in space (32). Finally, surfaces with $\mathcal{K}<0$ pose a further interesting case––having two directions at each point along which ${\kappa }_N=0$, neither of which need be straight (41). Consequently, one can have both kinds of ${\kappa }_N=0$ curves on a $\mathcal{K}<0$ surface: planar and nonplanar, as we discuss here on a helicoid. All of these ${\kappa }_N=0$ curves are marked in white on respective geometries in Fig. 1C.

To test the applicability of this design rule we crease elastomeric and plastic helicoids, cylinders, and spheres, whose $\mathcal{K}$ are, respectively, negative, zero, and positive. Geometries with finite $\mathcal{K}$ were fabricated by casting samples in 3D-printed molds, with embossed ridges to realize creased areas, whereas cylindrical shells are prepared by laser-cutting and rolling a planar sheet (Fig. 1C and Materials and Methods).

Negative Gaussian Curvature: Helicoid

To explore snapping behavior and the lack thereof in negative Gaussian curvature surfaces, we specifically choose the helicoid. The helicoid is the only ruled minimal surface (such that $H=0$) with negative Gaussian curvature. As a surface with $\mathcal{K}<0$, there exist two curves of zero ${\kappa }_N$ at every point. Moreover, because the surface is minimal, these two curves are locally orthogonally to one another (32). For the helicoid specifically, one family of curves is given by the generating lines, whereas the other is given by a family of helices that have nonzero curvature and torsion. Whereas smooth deformation of a shell about a straight crease can be intuitively visualized as a composition of rigid-body rotations, deformation along a nonplanar crease is less obvious, but folding along this curve is predicted to be continuous according to our design principle (See the Supporting Information for more details). The coexistence of this set of curves makes the helicoid an ideal surface on which to validate the design rule.

Thus, we fabricate plastic helicoids with creases along three kinds of curve: (i) a ${\kappa }_N\ne 0$ curve generated by slicing the helicoid with a plane, (ii) the first ${\kappa }_N=0$ curve along the generating lines, and (iii) the second ${\kappa }_N=0$ along the helical curve orthogonal to ruling lines (Fig. 2 A, B, and C, respectively). Deforming these shells along the ${\kappa }_N\ne 0$ crease generates a discontinuous motion characteristic of a snap-through instability as predicted (Movie S1 and Fig. 2A). Moreover, for the other two planar and nonplanar creases, we observe the continuous “smooth” motion characteristic of a simple hinge as predicted for curves with vanishing normal curvature (Movie S1 and Fig. 2 B and C). Hence, the purely geometric nature of our design rule offers a way to understand the continuity or discontinuity of folding even without a detailed understanding of the complex shell mechanics.

Fig. 2.

Folding of helicoids ($K<0$). Composite image of Movie S1 demonstrates the folding behavior of a creased helicoid with a clamped edge, indented with a rigid indenter. Schematics for all cases indicate the position of the crease relative to the asymptotic curves with ${\kappa }_N=0$ (dotted black or yellow). (A) Five frames at equal time interval depict the discontinuous snap-through deformation of a helicoid possessing a crease with ${\kappa }_N\ne 0$ from initial folded state (0) to the final folded state (+4). Frame 3 falls midsnap, and is blurred. For both (B) planar (along generating line) and (C) nonplanar (or helical) ${\kappa }_N=0$ creases, a composite image is used to depict torsion along either side of the folded state (0) of the crease. As predicted, a continuous deformation characteristic of a hinge is observed for both of these cases. Frames at equal time intervals on either side are used (1, 2 on one side, and i, ii on another).

Zero Gaussian Curvature: Cylinder

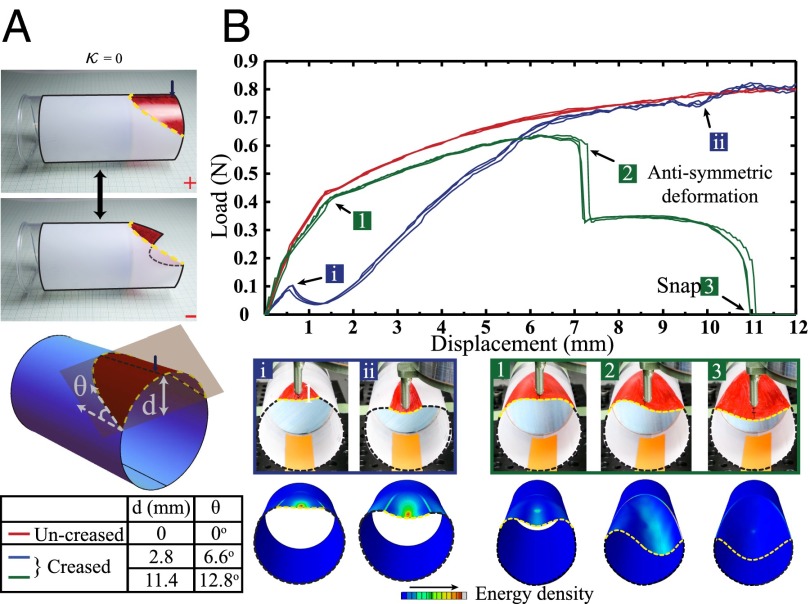
As a singly curved surface, a cylinder has only one set of planar curves with ${\kappa }_N=0$ along the axis. On the other hand, creases with finite ${\kappa }_N$ on a cylinder can be created by intersecting the surface with a plane at an oblique angle (θ) at a distance (d) from the apex, as shown in Fig. 3A and Materials and Methods. According to our hypothesis, we expect the cylinder to undergo a snapping transition when deformed along this crease. Remarkably, despite the introduction of a crease, the free cylinder displays a global bending deformation instead of snapping (Movie S2). Such global deformations arise because cylinders have $\mathcal{K}=0$, and thus can bend without stretching, so that there is a pathway accessible to the shell that costs less energy than snapping but still satisfies the constraint imposed by the indenter.

Fig. 3.

Folding of cylinders ($K=0$). (A) Bistable states (+, −) of a cylinder with appropriate planar crease. Crease parameters d (distance of the osculating plane from the apex) and angle θ (from horizontal) are shown in the schematics, along with values for $d,\theta$ for the representative samples studied in this experiment. The radius of the cylinder is 25 mm. (B) Force–displacement curves for uncreased (red), crease with $\theta =6.6\mathsf{°},\hspace{0.5em}d=2.8$ mm (blue) exhibiting monostable behavior. In contrast, a creased cylinder with $\theta =12.8\mathsf{°},\hspace{0.5em}d=11.4$ mm (green) exhibits an antisymmetric behavior leading to a bistable snapped state. Snapshots from experiments and FEA simulations show different stages of deformation. A contact-slip profile is seen at higher displacements for these samples. See, additionally, Movie S2.

These pathways can be eliminated by imposing fixed boundary conditions on one of the free ends of the cylinder by inserting a rigid cylindrical plug. We use two representative results from the parameter space consisting of $\left\{d,\theta \right\}$ for discussing the stability of indenting a creased cylinder. For creased cylinders with a small $\left\{d,\theta \right\}=\{2.8$ $\mathrm{mm},\hspace{0.5em}6.6\mathsf{°}\}$, we note that the effective stiffness of the shell is much lower for small displacements, but that the indentation profile matches the uncreased shell for large indentation. For creases with larger $\left\{d,\theta \right\}=\{11.4$ $\mathrm{mm},\hspace{0.5em}12.8\mathsf{°}\}$, the localized stretching energy can be focused entirely in the crease, so that the energy landscape is modified to allow for a fast snap. As indicated in Fig. 3B (Movie S2), a transition to an antisymmetric mode is observed before snapping completely into the mirror reflection isometry. Notably, stability of the isometric state and the presence of an antisymmetric mode in our experiments is consistent with finite-element analysis (FEA, performed using ABAQUS, Dassault Systemes).

The stability of this isometric state can be explained by considering the concentration of bending and stretching energy during the deformation. Indenting an uncreased cylinder near the free edge produces a deformation pattern that is composed of two parts: a region of mirror isometry that contains only bending, and a localized ridge (1, 33, 37, 42). The localized region, which acts as an elastic boundary layer, contains all of the stretching energy of the deformation. By weakening the material through creasing, the stretching cost for the ridge can be dramatically lowered, and the folded state may become stable. Here, we observe that for lower values of $\left\{d,\theta \right\}$ the bending energy cost of the mirror isometry is large enough that the energy gain from creasing is insufficient to result in bistability, whereas larger $\left\{d,\theta \right\}$ values lower the cost of the ridge sufficiently to induce bistability.

Positive Gaussian Curvature: Sphere

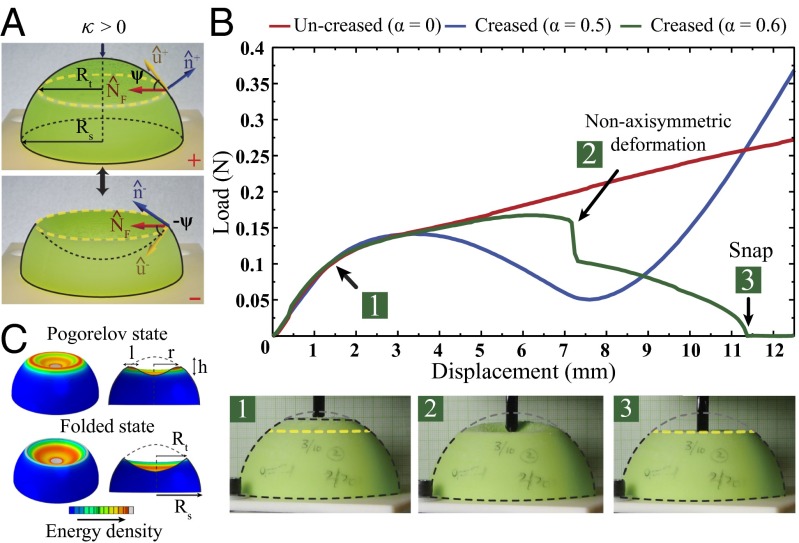
Given their axisymmetry, spherical shells are well suited to quantitative analytical, computational, and experimental analysis. Moreover, mechanisms involving pure bending are avoided in spherical shells, because surfaces with doubly curved shells naturally require stretching for many deformations of the surface (1, 43, 44). Because the spherical geometry is devoid of any ${\kappa }_N=0$ curves, we expect that intersecting a spherical surface with a plane to create a crease with finite ${\kappa }_N$ will result in a snap. Unlike previously discussed geometries, due to the symmetry of the sphere these creases have constant ${\kappa }_N$ over the whole surface, allowing analytically tractable solutions. In a systematic approach, we fabricate hemispheres with different crease radius $R_t$ and sphere radius $R_s$, and define the normalized crease radius as $\alpha =R_t/R_s$ (Fig. 4A). Upon indentation, for an uncreased shell ($R_s=35\hspace{0.17em}\text{mm},\alpha =0$) we observe a monotonically increasing load response similar to previous studies (1, 38, 45) (Fig. 4B). In a similar fashion to the cylinder, we observe a local minimum in force for lower values of α (=0.5) devoid of a stable folded state, but indenting a creased shell with higher α (=0.6) leads first to an unstable, nonaxisymmetric snap, soon followed by a well-defined stable snap (Fig. 4B, Insets and Movie S3).

Fig. 4.

Folding of spheres ($K>0$). (A) Spherical shell of thickness t, radius $R_s$, and a crease radius $R_t$ in bistable states (+, −). Vectors (${\widehat{\mathbf{u}}}^{\pm },{\widehat{\mathbf{n}}}^{\pm },{\widehat{\mathbf{N}}}_{\mathbf{F}}$, and $\widehat{\mathbf{t}}$) and parameters ($R_t,R_s$, and ψ) used in this study are overlaid on the experimental sample. (B) Spherical shells with crease radius $\alpha =R_t/R_s=0$ (red), 0.5 (blue), and 0.6 (green), and over all radius $R_s=35\hspace{0.5em}\text{mm}$. For the smaller value of α, no stable snap is observed indicating monostability, whereas for larger value of α a nonaxisymmetric deformation, followed by a stable snap, occurs under indentation (Movie S3). (C) Schematics for the Pogorelov state of a deformed spherical shell, with representative ridge (of size $\sim l$) at a radius r; and the folded state of a creased spherical shell (radius $R_s$), with a crease radius $R_t$.

Along the lines of argument we presented for stability of creased cylinders, a spherical shell poses a system which can be solved analytically. There is a well-known nearly isometric deformation of a sphere seen for displacements larger than the thickness but smaller than the crease size (33, 46). This deformation regime is characterized by an inverted bulge of radius r and bounded by a ridge of size $\ell \sim \sqrt{t{R}_s}$ (Fig. 4C). The energy for this state has a bending energy contribution from the inverted bulge that scales as $E_B\sim B{\left(r/R_s\right)}^2$, whereas the “Pogorelov ridge,” acting as an elastic boundary layer, contains all of the stretching energy (35, 47). The energy in the ridge scales as $E_P\sim Y{\left(t/R_s\right)}^{5/2}{r}^3$, with Y as the Young’s modulus of the material. Hence the total energy ($E_T$) for deformation scaled by B can be expressed as

$$\frac{E_P+E_B}{B}\approx {\left(\frac{r}{R_s}\right)}^2+{\gamma }^{1/4}{\left(\frac{r}{R_s}\right)}^3,$$ [2]

where γ is the Föppl–von Kármán number $\gamma \equiv \widehat{Y}{R}_s^2/B$, with $\widehat{Y}$ as the stretching modulus of the material (plotted schematically in Fig. 5A). For a thin shell $\widehat{Y}=Yt$, and $B=Y{t}^3/12\left(1-{\nu }^2\right)$, where ν is Poisson’s ratio, such that $\gamma \sim {\left(R_s\sqrt{12\left(1-{\nu }^2\right)}/t\right)}^2$. The Föppl–von Kármán number characterizes the balance between bending and stretching energies, and can be defined even for structures that are not technically thin shells, such as viruses and polymerized membranes (48).

Fig. 5.

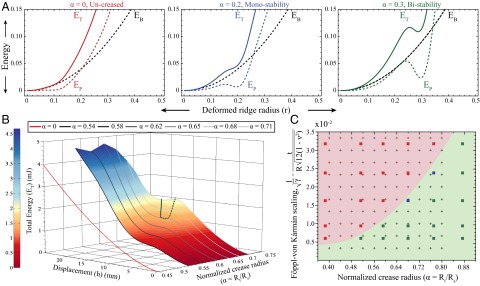
Stability of creased spherical shells (K > 0). (A) For an uncreased shell, the energy of an indented shell is composed of the bending energy $E_B$ (black dotted) and the Pogorelov ridge $E_P$ (colored dotted). For a creased shell $E_P$ takes a substantial dip localized at $r\sim R_t$, but the total energy $E_T$ (colored solid) only has a local minimum if the crease is large enough. In these schematics the function $t\left(r\right)$ is chosen to mimic the profile provided by experimental molds. (B) Numerically calculated energy landscape for a creased shell with $\gamma \approx {10}^4$ for a variety of α. The Pogorelov solution is recovered for $\alpha =0$ (red plot), whereas for small values of α the energy gain from the crease is insufficient to create a local minimum. However, above a critical α, local minima (solid green) and maxima (dashed green) bifurcate to generate a region of stability. (C) Phase diagram for snapping behavior of spherical shells over a wide range of geometrical parameters α and $1/\sqrt{\gamma }$. Stability behavior in experiments is characterized as bistable (, switches to folded state through a snapping mechanism), monostable (, prefers unfolded state), or temporarily stable (, closer to phase boundary: snap back on a timescale of seconds without external perturbations). Finite-element simulations (points solved denoted with +) provide regions of monostability (red shading) and bistability (green shading). Each experimental data point was analyzed for at least three shells of appropriate parameters.

In the case of a creased sphere, we assume that the deformation of the shell retains the same structure as this classical solution, but now the thickness of the sphere in the Pogorelov ridge is a function of the bulge radius r, such that $t\left(r=R_t\right)=\mathit{ϵ}t\left(r=0\right)$, where $\mathit{ϵ}<1$. As shown schematically in Fig. 5A, for a creased spherical shell there is a local minimum in the Pogorelov energy centered at $r=R_t$ that generates an energy barrier that competes with bending energy. However, for small values of α the monotonically increasing bending energy overcomes the energy gain from thinning the shell at the crease, and the folded state remains unstable. Evidently, for larger values of α, this gain surpasses the bending energy of the shell, resulting in bistability due to the presence of a local minimum in total energy. Thus, we infer that the stability of creased shells is governed by the competition between bending energy of the undeformed shell and stretching energy contained in the creased region.

To confirm this simple model, we again use FEA to determine the conditions under which there is a stable snap. For linear elastic materials this system is fully characterized by two dimensionless numbers, the reduced crease radius α and the Föppl–von Kármán number γ. We report the total energy for axisymmetric solutions with $\gamma ={10}^4$ (corresponding to the elastomeric hemispheres discussed here) as a function of the indenter displacement (h) and the normalized crease radius (α) in Fig. 5B. We find that, beyond a critical crease radius, there is a bifurcation of stability and the energy curves develop a well-defined local minimum (solid) and maximum (dashed), with the region between these curves denoting a basin of attraction for the folded state.

By examining creased hemispherical shells over a range of γ, we construct a phase diagram for stability of creased spherical shells (Fig. 5C). Through numerical simulations, we find that for increasing thickness, larger values of the crease radius are required to create a stable snap. Moreover, we conduct a series of experiments on spherical shells with a range of γ and α, and identify the stability of the folded state. These reveal a boundary between bistability and monostability that is in excellent agreement with our numerical calculations. Further bolstering this, for some samples we observe the presence of folded states that are temporarily stable (for times on the order of seconds)––the proximity of these samples to the predicted phase boundary further demonstrates the agreement between experiments and simulation.

Conclusion

The ability to introduce tunable bistability into a curved shell via structural inhomogeneity represents a major step in generating programmable materials with rapid actuation capabilities. While inhomogeneous shells have already been predicted to serve as a template for constructing tunable shapes (49), and used to design next-generation substances such as lock-and-key colloids (50) or controllably collapsible capsules (39), our geometric design principle adds further insight into controlling the mechanics of thin shells. Because the speed of the snap arises from stretching in the shell, inertia mediates the transition at the speed of sound in the material (Movies S1–S3), and crucially, the snap is unimpeded by poroelasticity or hydraulic damping as displayed in many natural snapping systems (51). Our work lays the foundation for developing non-Euclidean origami, in which multiple folds and vertices combine to create new structures. Indeed, smoothly deployable structures built from non-Euclidean surfaces could be engineered using origami-like principles that build upon the isometric design rules for negative Gaussian curvature surfaces that we derive here. Finally, because the principles and methods we describe are purely geometric, they open the door for developing design paradigms independent of length scale and material system.

Materials and Methods

Shell Fabrication.

Three-dimensional models of different geometries were designed in a CAD software. The non-Euclidean geometries (helicoid and hemisphere) were fabricated using a commercial 3D printer (Stratys Inc., uDimensions) to obtain two-part molds with embossed features to generate creases (Fig. 1C). The hemispherical shells were fabricated using poly(vinyl siloxane) by curing a commercially available two-part base–catalyst mixture [Zhermack SpA Elite Double 32, Elastic modulus $\left(Y\right)=1.3$ MPa]. Before filling the mold, the 1.2:1 base:catalyst mixture was degassed to remove bubbles that may otherwise serve as defects. The helicoid samples were fabricated using poly(caprolactone) (Monomer-Polymer & Dajac Labs, 1258, $Y=353$ MPa), by melting polymer in the mold at 70 °C, and allowing it to cool. The hemispherical and helicoid shells studied were 1 mm thick, and the crease had a rectangular cross-section 0.75 mm deep ($\mathit{ϵ}=0.75$) and 1 mm wide along the appropriate curve. Only samples without structural defects were included for testing. Owing to their Euclidean nature, cylinders could be fabricated using a conventional 2D technique. Here, we use a commercial laser cutter (Epilog Laser, Zing 16) to score a poly(ethylene terephthalate) sheet (Grafix Dura-Lar, 120 μm thick, $Y\sim 5$ GPa) with a curve. The shape of this plane curve is set to be sinusoidal such that when the sheet is wrapped to form a cylinder, the resulting space curve is the intersection between a plane and a cylinder at an oblique angle (θ). The scored sine wave was scaled to different amplitudes to obtain the combinations of $d,\theta$ discussed.

Helicoid Characterization.

Helicoids with different creases were clamped on one edge, and deformed along the crease using a rigid indenter by hand. Composite images using frames at equal time intervals from these movies were created by using alpha blending. For the sample with a snap-through, frames were chosen to be 300 ms apart. For the sample with a planar crease, frames are 1 and 6 s apart for deformation on either side of the torsional hinge. Lastly, for the sample with helical crease, frames were 1.5 and 1.5 s apart for deformation on either side of the torsional hinge.

Load Displacement Characterization.

A custom-built force displacement device, combining a linear translation stage (Zaber Technologies Inc., T-LSM 100) and a load cell (Loadstar Sensors Inc., RPG-10), was used to perform strain-controlled force measurements. For both cylindrical and hemispherical samples, 3D printed point indenters (radius ratio of indenter with respect to shell $\sim 0.05$) were used for indentation. All samples were deformed in strain-controlled tests at a compressive strain rate of 5 mm/min. Data collection and analysis was performed using an in-house algorithm in MATLAB (The Mathworks), without any signal processing/ filtering (components derived from ref. 52).

Differential Geometry of Curves and Surfaces

A crease placed on a surface is parametrized by a space curve $\mathit{c}\left(s\right)$, with s an arc length variable that runs along the curve. At each point on the crease we define the orthonormal Frenet frame $\left\{\mathit{t},{\mathit{N}}_F,\mathit{B}\right\}$, with the unit tangent $\mathit{t}={\partial }_s\mathit{c}$, normal ${\partial }_s^2\mathit{c}=\kappa {\mathit{N}}_F$, and binormal $\mathit{B}=\mathit{t}\times {\mathit{N}}_F$ vectors, respectively. These vectors are characterized by the following relationship:

$$\frac{d}{ds}\left(\begin{array}{c}\mathit{t}\\ {\mathit{N}}_F\\ \mathit{B}\end{array}\right)=\left(\begin{array}{ccc}0& \kappa & 0\\ -\kappa & 0& \tau \\ 0& -\tau & 0\end{array}\right)\left(\begin{array}{c}\mathit{t}\\ {\mathit{N}}_F\\ \mathit{B}\end{array}\right),$$ [S1]

where κ is the curvature of the crease and τ is the torsion. The surface of the shell is composed of two regions that are divided by the crease, each parametrized by a local orthonormal frame. In a frame of reference where one surface is fixed in space a local orthonormal frame $\left\{\widehat{\mathit{t}},\hspace{0.17em}{\widehat{\mathit{u}}}^{+},\hspace{0.17em}{\widehat{\mathit{n}}}^{+}\right\}$ defines the two surfaces in the unfolded state. When the surface is folded, another frame $\left\{\widehat{\mathit{t}},\hspace{0.17em}{\widehat{\mathit{u}}}^{-},\hspace{0.17em}{\widehat{\mathit{n}}}^{-}\right\}$ is used to signify the change from the undeformed state. These vectors are related in a similar fashion to the Frenet frame:

$$\frac{d}{ds}\left(\begin{array}{c}\mathit{t}\\ {\mathit{u}}^{\pm }\\ {\mathit{n}}^{\pm }\end{array}\right)=\left(\begin{array}{ccc}0& {\kappa }_g& {\kappa }_N\\ -{\kappa }_g& 0& {\tau }_g^{\pm }\\ -{\kappa }_N& -{\tau }_g^{\pm }& 0\end{array}\right)\left(\begin{array}{c}\mathit{t}\\ {\mathit{u}}^{\pm }\\ {\mathit{n}}^{\pm }\end{array}\right).$$ [S2]

Here we have aligned the two frames so that the tangent to the curve is one of the tangents to the surface, and we have defined the geodesic curvature ${\kappa }_g\equiv \mathit{t}\mathit{\prime }\cdot {\mathit{u}}^{\pm }$, the normal curvature ${\kappa }_N^{\pm }\equiv \mathit{t}\mathit{\prime }\cdot {\mathit{n}}^{\pm }$, and the geodesic torsion ${\tau }_g\equiv {\mathit{u}}^{\prime }\cdot \mathit{n}$. The relationship between the surface vectors and the crease vectors is given in terms of the linear combination

$$\mathit{u}=\cos \psi {\mathit{N}}_f+\sin \psi \mathit{B}\text{,}$$ [S3]

$$\mathit{n}=-\sin \psi {\mathit{N}}_F+\cos \psi \mathit{B}.$$ [S4]

The angle ψ measures the difference between the surface tangent $\mathit{u}$ and the Frenet normal ${\mathit{N}}_F$, as well as comparing the geodesic and normal curvatures directly to the crease curvature via ${\kappa }_g=\kappa \cos \psi$ and ${\kappa }_N=\kappa \sin \psi$. Using this relationship also supplies expressions for the surface quantities in terms of the crease quantities:

$${\kappa }_g=\kappa \cos \psi ,$$ [S5]

$${\kappa }_N=\kappa \sin \psi ,$$ [S6]

$${\tau }_g={\psi }^{\prime }\left(s\right)+\tau .$$ [S7]

The angle ψ is particularly important if we wish to consider folding the shells about this crease. The equation for ψ in terms of normal (or geodesic) curvature has two solutions, that is, $\psi =\pm {\cos }^{-1}\left({\kappa }_g/\kappa \right)=\pm {\cos }^{-1}\sqrt{1-{\left({\kappa }_N/\kappa \right)}^2}$. This corresponds to the folded and unfolded states shown in Fig. 1.

To determine the stability of the folded state we first write the energy for deformation of a thin shell:

$$\mathrm{ℰ}=\frac{Yt}{2\left(1+\nu \right)}{\displaystyle \int dS\left[\frac{\nu }{1-\nu }{\left(E_{\gamma }^{\gamma }\right)}^2+E_{\alpha \beta }{E}^{\alpha \beta }+\frac{t^2}{12}\left(\frac{\nu }{1-\nu }{\left(K_{\gamma }^{\gamma }\right)}^2+K_{\alpha \beta }{K}^{\alpha \beta }\right)\right]},$$ [S8]

where $E_{\alpha \beta }$ is the strain tensor, $K_{\alpha \beta }$ is the bending tensor, Y is Young’s modulus, ν is Poisson’s ratio, and t is the thickness of the shell. To describe the strain and bending tensors of the surface, we need the first and second fundamental forms, given by $\mathrm{ℐ}=g_{\alpha \beta }d{x}^{\alpha }d{x}^{\beta }$ and $\mathrm{ℐℐ}=h_{\alpha \beta }d{x}^{\alpha }d{x}^{\beta }$, where $g_{\alpha \beta }$ and $h_{\alpha \beta }$ are the metric and curvature tensors, respectively. Using these definitions, $E_{\alpha \beta }=g_{\mathrm{\alpha \beta }}^{*}-g_{\alpha \beta }$ and $K_{\alpha \beta }=h_{\mathrm{\alpha \beta }}^{*}-h_{\alpha \beta }$, where$\hspace{0.5em}{g}_{\mathrm{\alpha \beta }}^{*},h_{\mathrm{\alpha \beta }}^{*}$ refer to the fundamental forms in the deformed configuration. In general it costs more energy to stretch than to bend, so we first examine the isometric limit ($g_{\alpha \beta }=g_{\mathrm{\alpha \beta }}^{*}$), so that the only contribution to the energy comes from bending. While this limit is singular, it provides a simple geometric interpretation of nearly free deformations and yields insight into the stability and foldability of general shells.

We define a coordinate system on the shell $\left\{s,v\right\}$ using the crease as the point of origin, so that s is an arc length along the crease and v is measured orthogonal to the crease, such that

$$\mathrm{ℐ}=Ed{s}^2+2Fdsdv+Gd{v}^2,$$ [S9]

$$\mathrm{ℐ}{\mathrm{ℐ}}^{\pm }=N^{\pm }d{s}^2+2M^{\pm }dsdv+L^{\pm }d{v}^2,$$ [S10]

where we need to define $\mathrm{ℐ}{\mathrm{ℐ}}^{+},\mathrm{ℐ}{\mathrm{ℐ}}^{-}$ separately for the pieces of the surface that are divided by the crease. Because s is an arc-length parametrization, the first fundamental form may be written as $\mathrm{ℐ}=d{v}^2+{\rho }^{2}d{s}^2$, and we have that the components of the metric are $g_{vv}=1$, $g_{sv}=g_{vs}=0$, and $g_{ss}={\rho }^2$, where $\rho \left(s,\hspace{0.17em}v\right)$ is an unknown function that in general requires the full solution of the Gauss–Codazzi equations. Close to the crease, $v\approx 0$, however, because s is an arc-length variable we know that $\rho \left(0,\hspace{0.17em}s\right)=1$.

Finding the bending energy requires that we find the mean curvature of the surface, which requires us to compute the components of the curvature tensor, $h_{\alpha \beta }=\left({\partial }_{\alpha }{\partial }_{\beta }\mathit{r}\right)\cdot \mathit{n}$, where r is a parametrization of the surface. With the geometric definitions given above, we have the fairly simple results that $N^{\pm }=h_{ss}={\kappa }_N^{\pm }$ and $M^{\pm }=h_{sv}={\tau }_g^{\pm }$. To find $L^{\pm }$, we invoke Gauss’s Theorema Egregium, which states that $\det \mathrm{ℐℐ}/\det \mathrm{ℐ}=\mathcal{K}$, where $\mathcal{K}$ is the Gaussian curvature of the surface. Written using our nomenclature, this indicates that

$$\mathcal{K}=\frac{L^{\pm }{N}^{\pm }-{\left(M^{\pm }\right)}^2}{EG-F^2}=\frac{L{\kappa }_N^{\pm }-{\left(\pm {\psi }^{\prime }+\tau \right)}^2}{{\rho }^2}.$$ [S11]

Close to the crease this yields $L=\left(\mathcal{K}+{\left(\pm {\psi }^{\prime }+\tau \right)}^2\right)/{\kappa }_N^{\pm }$ if ${\kappa }_N\ne 0$. If ${\kappa }_N=0$, then the value of L is not constrained by the Theorema Egregium, and thus the shell is not constrained isometrically by the crease.

The bending energy density ${\mathrm{ℰ}}_B\sim B{\left(H^{+}\right)}^2+B{\left(H^{-}\right)}^2$, where $H=\left(1/2\right)Tr\left\{{\mathrm{ℐ}}^{-1}\mathrm{ℐℐ}\right\}$, written in terms of the crease parameters for ${\kappa }_N\ne 0$:

$$H^{+}=\frac{1}{2}\left(N^{+}+L^{+}\right)=\frac{1}{2}\left({\kappa }_N^{+}+\frac{\mathcal{K}+{\left({\psi }^{\prime }+\tau \right)}^2}{{\kappa }_N^{+}}\right),$$ [S12]

and similarly for $H^{-}$. Because the geodesic curvature ${\kappa }_g$ is invariant under isometric deformations, we may write the mean curvature in terms of isometric constants, parameters that are related only to the crease, and the folding angle ψ:

$$H^{+}=\frac{1}{2}\left({\kappa }_g\tan \psi +\frac{\mathcal{K}+{\left({\psi }^{\prime }\left(s\right)+\tau \left(s\right)\right)}^2}{{\kappa }_g\tan \psi }\right).$$ [S13]

The energy, proportional to $H^2$, diverges as ψ passes through zero, indicating that our isometric model cannot accurately describe the transition between folded shell states for creases that have finite normal curvature. The existence of an infinite barrier in this singular limit indicates that the angle ψ may not be folded continuously from the folded state to the unfolded state.

If the crease has zero normal curvature, however, the component of the second fundamental form $h_{vv}$ is unconstrained by the crease. The mean curvature is given by $H=L$, with L determined entirely by bending away from the crease that is unconstrained by the condition of isometry. The folding angle and torsion, however, are constrained by

$${\psi }^{\prime }\left(s\right)+\tau \left(s\right)=\sqrt{-\mathcal{K}\left(s\right)}.$$ [S14]

Written another way, we have that ${\tau }_g=\sqrt{-\mathcal{K}}$, i.e., that the geodesic torsion is related to the Gaussian curvature of the surface. The geodesic torsion physically corresponds to the rate of rotation of the normal to the surface along the curve.

Together, these results can be used to infer a number of things. First, finite normal curvature implies that there is an energy barrier, which implies that a subcritical bifurcation may occur. Second, zero normal curvature implies that locally, the shell may deform without stretching, and thus the angle ψ may be varied continuously without fear of approaching a stretching barrier. Furthermore, zero normal curvature explicitly means that one of the components of the curvature tensor vanishes identically; specifically, the curvature of the surface in the direction of the crease is always zero.

Example: The Helicoid

A parametrization for the helicoid is $\mathbf{\mathscr{H}}\left(u,v\right)=\left\{u\cos v,u\sin v,\alpha v\right\}$, which yields $\mathrm{ℐ}=d{u}^2+\left({\alpha }^2+u^2\right)d{v}^2$ and $\mathrm{ℐℐ}=-2L/\sqrt{{\alpha }^2+u^2}dudv$. The helicoid is a minimal surface, so $H=0$, and it has Gaussian curvature $\mathcal{K}=-{\alpha }^2/{\left({\alpha }^2+u^2\right)}^2$.

For a general surface with nonpositive Gaussian curvature, at every point there exists a pair of asymptotic curves such that the normal curvature along these curves is zero. For a curve parametrized by an arc length t, $\mathit{\beta }\left(t\right)=\left\{\xi \left(t\right),\eta \left(t\right)\right\}$, solutions to the following differential equation yield asymptotic curves:

$$N{\xi }^{\prime }{\left(t\right)}^2+2M{\xi }^{\prime }\left(t\right){\eta }^{\prime }\left(t\right)+L{\eta }^{\prime }{\left(t\right)}^2=0.$$ [S15]

For a helicoid, if we let $\xi =u,\eta =v$ then this equation is simply

$$\frac{-2\alpha }{\sqrt{{\alpha }^2+u^2}}{u}^{\prime }\left(t\right)v^{\prime }\left(t\right)=0,$$ [S16]

which has as solutions curves of constant v (straight lines) or curves of constant u (helices). Asymptotic curves of constant v are particularly simple examples, because $\tau =0$ and ${\kappa }_g=0$, so that these curves are both asymptotic lines and geodesics of the helicoid. The ability to fold the helicoid about any of these construction lines follows trivially from rigid-body rotations, and any energetic cost is associated with the fold, not the bending of the surface.

Alternatively, we could write this as ${\tau }_g=\sqrt{-\mathcal{K}}=1/R$, where $1/R$ is the magnitude of the principal radius of curvature of the helicoid. This means that ${\psi }^{\prime }=1/R$, and thus the folding of the surface only changes along the curve by the same amount that the surface naturally rotates.

Choosing curves of constant $u=u_0$ yields helices, which have a constant torsion $\tau =\alpha /\left({\alpha }^2+u_0^2\right)$, and Gaussian curvature that is constant along the helix, $\mathcal{K}=-{\alpha }^2/{\left({\alpha }^2+u_0^2\right)}^2$, so that ${\psi }^{\prime }\left(s\right)=0$ along the curve. Any constant folding angle ψ will lead to locally isometric deformations that do not necessarily result in an energy barrier to folding. These arguments are all local, and there may be global constraints that lead to an energetic barrier, but this depends specifically on the type of surface and shape of the crease.