Significance
In vitro experiments that measure relative sliding velocities between actin and myosin filaments give insight into how the muscle motor protein myosin works in muscle. We show that when the physiological filamentous myosin moves along actin filaments, the velocities cannot be explained by the prevailing theory. Instead, we propose a paradigm in which myosin heads undergo unloaded “powerstrokes” rather than work in mechanical opposition to each other during contraction. This model is consistent with unloaded shortening velocities measured in muscle.
Keywords: myosin, actin, muscle contraction, kinetics, ATPase
Abstract
It is not known which kinetic step in the acto-myosin ATPase cycle limits contraction speed in unloaded muscles (V0). Huxley’s 1957 model [Huxley AF (1957) Prog Biophys Biophys Chem 7:255–318] predicts that V0 is limited by the rate that myosin detaches from actin. However, this does not explain why, as observed by Bárány [Bárány M (1967) J Gen Physiol 50(6, Suppl):197–218], V0 is linearly correlated with the maximal actin-activated ATPase rate (vmax), which is limited by the rate that myosin attaches strongly to actin. We have observed smooth muscle myosin filaments of different length and head number (N) moving over surface-attached F-actin in vitro. Fitting filament velocities (V) vs. N to a detachment-limited model using the myosin step size d = 8 nm gave an ADP release rate 8.5-fold faster and ton (myosin’s attached time) and r (duty ratio) ∼10-fold lower than previously reported. In contrast, these data were accurately fit to an attachment-limited model, V = N·v·d, over the range of N found in all muscle types. At nonphysiologically high N, V = L/ton rather than d/ton, where L is related to the length of myosin’s subfragment 2. The attachment-limited model also fit well to the [ATP] dependence of V for myosin-rod cofilaments at three fixed N. Previously published V0 vs. vmax values for 24 different muscles were accurately fit to the attachment-limited model using widely accepted values for r and N, giving d = 11.1 nm. Therefore, in contrast with Huxley’s model, we conclude that V0 is limited by the actin–myosin attachment rate.
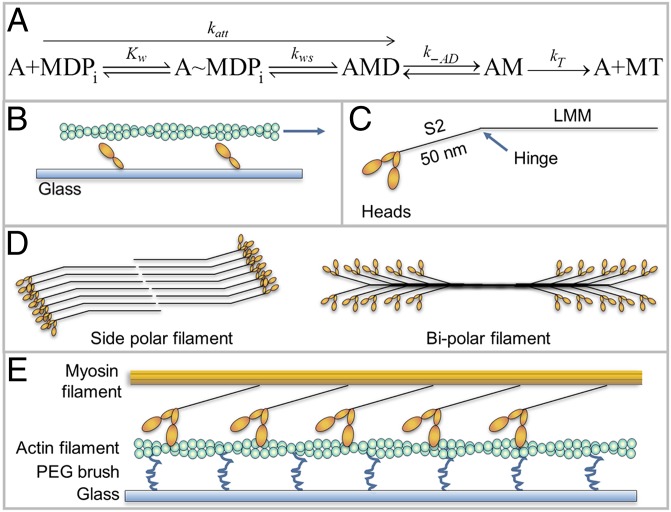
An important parameter used to characterize and compare muscle types is the maximum shortening velocity defined as the velocity of intact (1) or skinned (2) muscle fibers and myofibrils (3) shortening under no load (V0). Any model of muscle contraction must be able to quantitatively predict V0 in terms of rate constants in the acto-myosin ATPase cycle (4). Huxley’s 1957 model of muscle contraction (5), which is still the most widely accepted model, predicts that V0 is limited by the rate of detachment of myosin from actin, which is limited by the rate of ADP release from acto-myosin ((k-AD) (6) or the rate of attachment of ATP (kT·[ATP]) to acto-myosin (7) (Fig. 1A). Stated simply, Huxley’s model says that muscle contracts only as fast as the myosins at the end of their working cycle can detach from actin.
Fig. 1.
Kinetic scheme and various myosin structures. (A) Kinetic scheme for myosin (M) attachment to actin (A), D = ADP, T= ATP, Pi = phosphate. Kw is the equilibrium constant for weak binding and kws is the forward rate constant for the weak to strong transition. See the text for other rate constants. (B) Classic IVMA with actin (green), being moved by myosin heads (orange) attached to coverslip (blue). (C) Myosin II molecule. (D) Comparison of side-polar (smooth muscle) and bipolar myosin filaments (skeletal and cardiac muscle). (E) Inverted IVMA, myosin filament (orange) moves over biotinylated actin attached to the coverslip (light blue) via biotinylated PEG brush (blue) and streptavidin (not shown for clarity) (21).
In a classic study, Bárány (8) found a linear correlation between V0 and maximal ATPase rates (vmax) among different muscle types from organisms of broad evolutionary origin suggesting that V0 and ATPase are limited by the same kinetic step. However, it is well established that the ATPase rate (4) in myofibrils (9) and in purified acto-myosin in solution (4, 10) is not detachment-limited, but rather is attachment-limited, controlled by Kw·kws = katt (Fig. 1A) (4). If V0 is attachment-limited, unloaded muscles will contract essentially as fast as N myosin heads with a given step size attach weakly to actin and undergo the powerstroke to the strongly bound state.
The mechanism that limits the velocity of muscle contraction has been addressed using the classic in vitro motility assay (IVMA), where actin filaments move over surface-attached monomeric myosin (11–14) (Fig. 1B). The maximal velocity (Vf) is primarily limited by k-AD (15–17) and therefore Vf = d·k-AD. However, recent studies show that Vf exceeds the detachment limit (18–21) and that factors that specifically inhibit attachment kinetics also slow Vf, suggesting that attachment kinetics influence Vf. The effects of attachment kinetics on V0 appear to be even more significant because V0 is considerably faster than Vf (16, 22–24), which may indicate that the kinetic steps limiting Vf and V0 are not the same. However, it is difficult to draw firm conclusions because several aspects of the IVMA may lead to slower velocities: random myosin orientation on the surface (25), inactive myosin (26), low ionic strength necessary to keep actin bound to myosin (16, 22), the absence of regulatory proteins (27), and absence of the same geometry as the muscle lattice.
Because myosin II has a low duty ratio (r) (20, 28, 29), many molecules are required to generate processive motion. Therefore, the functional form of myosin in vivo is the filament (Fig. 1D). We have recently introduced an inverted IVMA in which smooth muscle myosin (SMM) filaments move over surface-attached actin [Fig. 1E (21)], which more closely mimics the geometry of a muscle lattice and minimizes surface interactions.
Here, we used this inverted assay to address which kinetic step limits V0. We prepared side-polar SMM filaments (21) that, unlike bipolar skeletal and cardiac filaments, have all heads on one side of the filament orientated in the same direction (Fig. 1D) (30–35). We examined the relationship between V and N because the N dependence of V is a powerful test to discriminate between a detachment-limited and an attachment-limited model. N was reduced at a fixed filament length by making SMM-rod cofilaments and higher N was achieved by making SMM filaments with a wide range of longer lengths. We found that within the range of N seen in essentially all types of myosin filaments in muscle, V was linearly related to N, which fits the model where V is limited by the ATPase rate (v). As N was increased far beyond the physiological N, V approached an N-independent detachment limit with V = L·k-AD (not d·k-AD) where L is the “tether length” of the region of the myosin tail that is proximal to the heads known as subfragment 2 (S2, Fig. 1C). We confirmed our findings by measuring V at several fixed N (cofilaments) as a function of [ATP]. These data make sense in the context of the nonlinear stiffness of full-length myosin II when it is measured within a myosin filament (36, 37).
The equations that fit our data are consistent with the relationship between vmax and V0 originally shown by Bárány (8), leading to the conclusion that unloaded muscles contract at velocities that are limited by their respective ATPase activities (attachment-limited).
Results and Discussion
Characterization of Filament Preparations.
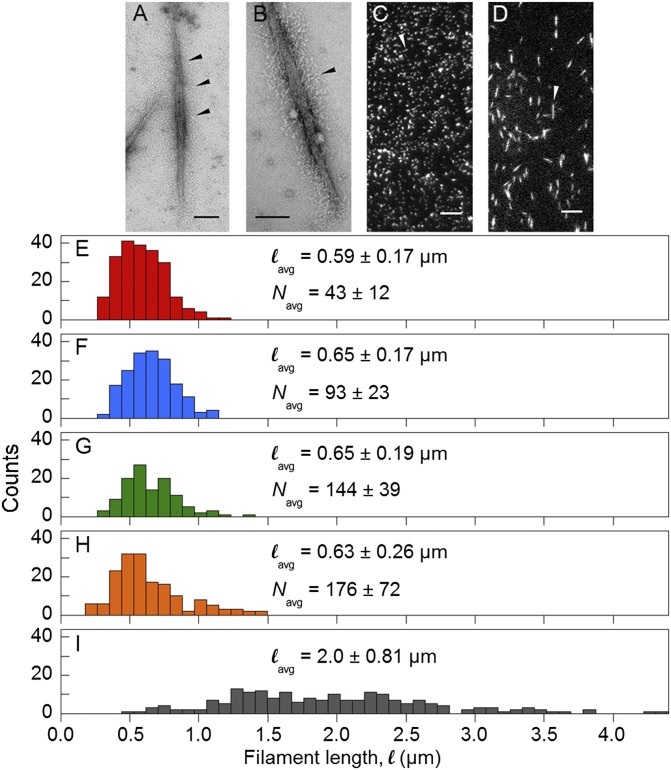
The objective of this study was to measure velocities of SMM filaments containing different numbers of heads. To vary the number of heads we used 100% SMM filaments [Fig. 2A (21)] and SMM-rod cofilaments (Fig. 2B). Electron micrographs showed that both preparations are side-polar as evidenced by the S1/S2 regions projecting continuously along the filament backbone (black arrows). Comparison of many images revealed no major differences in structure aside from fewer myosin heads in cofilaments.
Fig. 2.
Characterization of filament preparations. (A and B) Electron micrographs of negatively stained rhodamine-labeled and EDC cross-linked 100% SMM filaments from ref. 21 and 26% SMM cofilaments, respectively. (Scale bar, 100 nm.) Arrow heads point to S1/S2 regions projecting from filament backbone. (C and D) TIRF microscopy images of rhodamine-labeled, EDC cross-linked 100% SMM filaments from ref. 21 corresponding to H and 100% SMM filaments corresponding to I, respectively. (Scale bar, 5 µm.) Arrow heads point to individual filaments. (E–I) Length distributions of 26% SMM cofilaments (E, red), 51% SMM cofilaments (F, blue); 75% SMM cofilaments (G, green); 100% SMM filaments (H, orange); and variable length 100% SMM filaments (I, gray). Colors match points in Figs. 3 and 5. lavg and Navg ± SD are indicated.
The length, l, distributions measured from electron micrographs of the cofilament preparations (26%, 51%, 75% SMM) are shown in Fig. 2 E–G. We estimate that due to the side-polar structure, only one side, or 1/2 of the heads, is able to interact with actin in the inverted motility assay (21). This can be seen directly in movies (Movie S1) where the moving filaments appear to interact with actin along their full length. Therefore, N was defined as the number of heads per filament side. Because side-polar filaments have 4 myosin molecules (8 heads) per 14.3-nm repeat and there are two rods in a full-length SMM molecule (33, 34), N was calculated using Eq. 1, giving N = 43 ± 12, 93 ± 23, and 144 ± 39 for the 26%, 51%, and 75% SMM cofilaments, respectively.
| [1] |
Filaments prepared as in Haldeman et al. (21) (Fig. 2C) had an average length, lavg, of 0.63 ± 0.26 µm (Fig. 2H), giving N = 176 ± 72. Longer filaments with a wider length distribution (Fig. 2D) were prepared under conditions that limited the number of nucleation sites during assembly, giving an average length of 2.0 ± 0.81 µm (Fig. 2I). The lengths of these filaments were measured during the motility assay (Materials and Methods) and N was calculated using Eq. 1 except that lavg was replaced with l, the length of each moving filament.
Inverted Motility Assays Varying N at Saturating ATP.
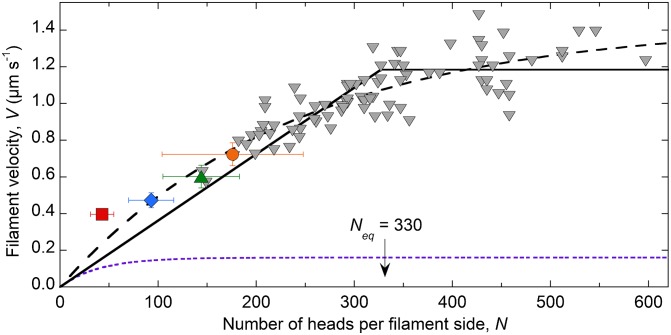
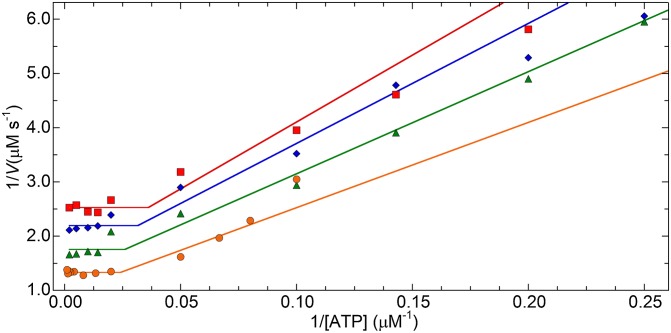
Inverted motility assays (see Movie S1, for example) were performed at saturating ATP (1 mM) and filament velocities were plotted against the calculated estimate of N (Fig. 3). The gray triangles each represent one 100% SMM filament of measured length moving at a velocity calculated from a single trajectory. Although filaments with n > 600 heads were observed moving, those velocities were not used because the longer filaments tended to interact with multiple actin filaments simultaneously. The orange point is from ref. 21 and the remaining colored points are for the cofilaments, which are the average ±SD for both length and velocity because of the relatively narrow length distributions (Fig. 2 E–H) and the inaccuracy of measuring shorter lengths by total internal reflection fluorescence (TIRF) microscopy.
Fig. 3.
N dependence of SMM filament velocities moving in the inverted motility assay at 1 mM ATP. Red square, 26% SMM cofilaments; blue diamond, 51% SMM cofilaments; green triangle, 75% SMM cofilaments; orange circle, 100% SMM filaments. All colored points, n = 10. Gray triangles, 100% SMM filaments (Fig. 2I) (total n = 82). Fit to Eq. 2, dashed line (see the text). Fit to Eqs. 5 and 7, solid sloping line and solid horizontal line, respectively. The break between the two lines is Neq = 330 heads. Fits were determined using a Levenberg–Marquardt nonlinear least-squares parameter optimization method. See Table 1 for the fixed parameters and results of the fit. Detachment-limited prediction (Eqs. 2–4; see the text), dotted purple line, using k-AD = 21 s-1, katt = 0.49 s-1 per head-1, r = 0.023, ton = 0.048 s, and d = 8 nm.
Fitting Data in Fig. 3 to the Classic Detachment-Limited Model.
Using the classic IVMA, investigators have varied N by varying the density of monomeric myosin on the surface and the length of the actin filament (38); these results fit well to a detachment-limited model [Eq. 2 (39)], where r is the duty ratio defined by Eq. 3, ton is the average attached time defined by Eq. 4, and the other rate constants are described in Fig. 1A.
| [2] |
| [3] |
| [4] |
The fit of all of the data in Fig. 3 to Eq. 2 with d fixed at 8 nm (36) is shown by the dashed line, giving R2 = 0.81, katt = 0.75 s−1, k-AD = 179 s−1, r = 0.0042, and ton = 0.0056 s. Although the fit is good, the resulting values are unreasonable for SMM. Other studies have found that r for SMM is ∼0.05 (reviewed in ref. 40) and ton = 0.047 ± 0.012 s (41). Our measured values in solution for these SMM filaments in the same buffer and at the same temperature are 0.49 s−1 per head−1 for ATPase at saturating actin, which is an estimate of katt, and 21 ± 3 s−1 for k-AD (21). Therefore, fitting the data in Fig. 3 to a detachment-limited model (Eq. 2) requires k-AD to be 8.5-fold higher and ton and r to be ∼10-fold lower than previously reported. The predicted velocity dependence on N using the above-published values and Eqs. 2–4 is shown by the dotted purple line in Fig. 3. This analysis indicates that the conventional detachment-limited model, presumably limited by the rate of ADP release, does not accurately fit the N dependence of V in Fig. 3.
We considered whether or not an increase in the rate of ADP release could account for the data in Fig. 3. Veigel et al. (42) showed that a load placed on an SMM head in the direction of motion results in an accelerated ADP release rate. According to their analysis, an ∼8.5-fold increase in the ADP release rate would require an ∼3.3-pN force. However, because the myosin is in the filamentous state, and not interacting with the coverslip surface, and the S2 region has been shown to be very flexible relative to the head (36, 37), it is free to bend or buckle, transmitting little force on the attached myosin head over a distance < twofold the length of the S2. To generate a force of ∼3.3 pN, the head would need to be pulled ∼65 nm (36). This would only occur once velocities were fast enough for the head to be pulled that far before detaching. For example, at V = 0.72 µm s−1 (orange point, Fig. 3), accounting for the acceleration in ADP release due to strain (42), the head would only be pulled ∼17 nm before detaching. For a head to be pulled the ∼65 nm needed to accelerate ADP release to 179 s−1 (see above), the filament would need to be moving at ∼10 µm s−1, a velocity that is never reached in our data (Fig. 3). This suggests that acceleration of ADP release does not account for the data in Fig. 3.
Fitting Data in Fig. 3 to an Attachment-Limited Model.
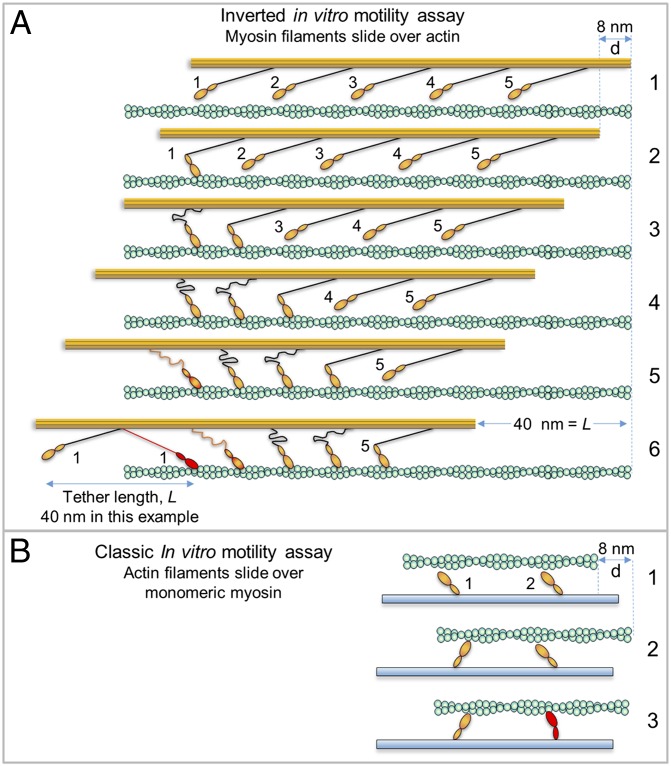
To explain our data, we propose the model illustrated in Fig. 4A. The flexible S2 region allows SMM filament velocities to be limited solely by katt (Fig. 4A, frames 1–5), until with increasing N, a high enough velocity is reached to pull an attached head to the end of the S2 tether (frame 6), resulting in a drag against driving heads. Based on Kaya and Higuchi’s work (36, 37), the S2 tether length, L, or the length over which the S2 region can be pulled back without exerting resistive strain, is ∼60–70 nm for skeletal myosin, and should be similar for SMM. This is radically different from the detachment-limited model (Fig. 4B), where a single head attached to an actin filament limits velocities (this would be the case if the S2 region is hampered by surface interactions).
Fig. 4.
Comparison of attachment- and detachment-limited models. Actin (green) affixed to coverslip (not shown for clarity), myosin filament backbone (orange) with protruding S2 (black) connecting to orange head (only one head shown). Frame numbers at right. (A) Hypothetical myosin filament moving in the inverted motility assay according to attachment-limited model. Working heads adjacent to one another are not likely (low duty ratio) and are shown as such only to illustrate the general idea. Frames: 1, no heads are attached; 2, head 1 attaches/undergoes powerstroke (A/P) moving filament d = 8 nm; 3, head 2 A/P while head 1 still attached, but head 1 places minimal drag load on filament due to flexible S2, therefore d = 8 nm once again; 4, head 3 A/P, buckling S2 of head 1 further and head 2; 5, after head 4 A/P, the S2 region of head 1 now begins to place some drag load on the filament; 6, after head 5 A/P, the S2 region of head 1 (red) is now fully stretched into a drag position, placing maximal drag load onto the filament, further heads working will not move the filament until head 1 detaches (now the filament is in a detachment-limited situation). The S2 tether length, L, is arbitrarily set to 40 nm. (B) Monomeric myosin heads in the classic IVMA. S2 (not shown) is interacting with coverslip (blue). Frames: 1, no heads attached; 2, head 1 A/P giving d = 8 nm; 3, head 2 attaches but d << 8 nm due to load placed on actin by head 1, head 2 is strained (red) because it cannot undergo full powerstroke.
According to an attachment-limited model there are no forces that resist filament sliding and so V is determined by the number of working steps of step size, d, per unit time. Thus, N myosin heads that each take a step at a rate v (ATPase rate) can move relative to the actin filament at a speed V according to Eq. 5 (attachment-limited).
| [5] |
The attachment-limited situation is valid as long as V is slow enough so that a head attached for a time ton does not reach the end of the S2 tether of length L as explained in Fig. 4A, or when V = N·v·d < L/ton. We refer to this critical value of N as Neq according to Eq. 6.
| [6] |
When V > L/ton, attached myosin heads reach the end of the S2 tether, and V becomes detachment-limited, which means that an attached myosin head moves a distance L over its attached time ton and cannot move any faster regardless of N, as in Eq. 7.
| [7] |
Eq. 7 is similar to the classic detachment limit (Eq. 2) with the important difference that d is replaced by L. Note that the model described by Eqs. 5–7 does not require us to specify certain details, such as the relationship between the two heads or their attachment positions because it is a kinetic model describing average behaviors.
The sloping solid line in Fig. 3 shows the fit to Eq. 5 fixing k-AD = 18 s−1, kT = 0.5 µM−1⋅s−1, and d = 8 nm, where n < Neq, and where n > Neq, data were fit to Eq. 7 using the same fixed values (horizontal solid line). The fit gave v = 0.44 s−1, L = 67 nm, and r = 0.024 (Table 1), which matches well with our measured vmax = 0.49 ± 0.01 s−1 (21), as well as the previously measured S2 tether length, L, of 60–70 nm (36, 37). Whereas r is twofold lower than the measured value of ∼0.05 (40), others have predicted based on simulations that r should be twofold less for myosin ensembles with high N than for monomeric myosin (43).
Table 1.
Note that Eqs. 5 and 7 do not account for any acceleration in ADP release that occurs as the myosin head is pulled in the direction of motion. Although this likely does occur, incorporating strain dependence of ADP release into our model using values from Veigel et al. (42) and Kaya and Higuchi (36, 37) resulted in a twofold decrease in L with no change in other parameters. For this reason, and to keep the model relatively simple, we assumed that k-AD was unaffected by strain.
Inverted Motility Assays Varying ATP at Fixed Numbers of Heads.
To further test our model, we performed inverted motility assays with the cofilaments (Fig. 2 E–G) and 100% SMM filaments (Fig. 2H) at varying [ATP]. The data were fit (Fig. 5, lines) to the reciprocals of Eqs. 5 and 7 with ATP as the independent variable, which results in Eqs. 8 and 9 where ATPeq is the ATP concentration at which the two functions are equal, given by Eq. 10.
| [8] |
| [9] |
| [10] |
The resulting parameters for the fits are in Table 1. All R2 values were above 0.95 and provided v, L, and N values within twofold of the expected results obtained from the data in Figs. 2 and 3 as well as our measured value of vmax. As predicted by our model, filament velocities were detachment-limited at low ATP, and attachment-limited at high ATP.
Fig. 5.
Plot of 1/ATP versus 1/V for filaments with different N. Data are 26% SMM cofilaments (red squares); 51% SMM cofilaments (blue diamonds); 75% SMM cofilaments (green triangles); 100% SMM filaments (orange circles). Each data set was fit (lines) to Eqs. 8 and 9 using a Levenberg–Marquardt nonlinear least-squares parameter optimization method. See Table 1 for a list of fit parameters. Each data point, n = 10.
An Attachment-Limited Model is Consistent with Previously Reported Measurements of ATPase and V0 in Muscle.
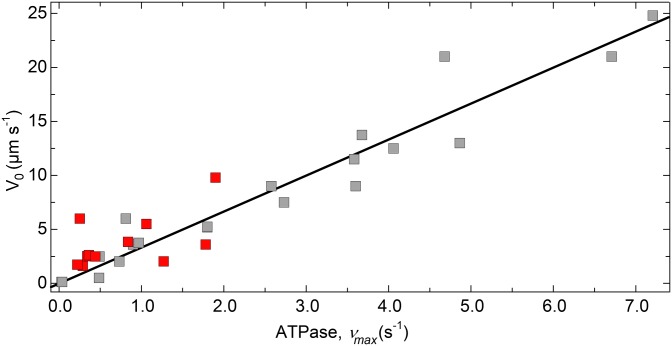
Fig. 6 shows the relationship between maximal actin-activated ATPase (vmax) and V0 for muscle fibers for which both parameters have been measured under similar conditions. The line shows the fit of these data to Eq. 5 using n = 300 (28, 44), and r = 0.025. In this case N is the number of heads per half-sarcomere in a single myosin filament because filaments are bipolar (Fig. 1D). The resulting fit (R2 = 0.96) gives d = 11.1 nm, which is within the 6–12-nm range of measured values for muscle myosins [(36, 42); reviewed in ref. 40]. Also, we can estimate the Neq for muscles in which k-AD has been measured or estimated and compare that to the actual N. For example, in frog sartorius muscle, k-AD is ∼250–300 s−1, which gives Neq ∼400–480, well above the actual N of 300. Similarly in rat cardiac muscle, k-AD = 93 s−1 (45) gives Neq = 750. This predicts that muscles operate well within the attachment-limited regime during unloaded shortening. Note that Fig. 6 does not include any smooth muscles because they are not organized into sarcomeres of uniform length (46).
Fig. 6.
Relationship between V0 and maximal ATPase (vmax) for various muscles. V0 data from experiments with muscle preparations are plotted against the respective ATPase vmax from either solution-based acto-myosin ATPase (gray) or myofibril/fiber ATPase (red) or both. See Table S1 for a list of muscle types and references for the values. Where necessary, ATPase was converted to s−1, V0 was converted to µm s−1 assuming a sarcomere length of 2.5 µm if not given. The line is a fit to Eq. 5 in which V is replaced by V0, N was fixed at 300 (half-sarcomere), giving d = 11.1 nm (R2 = 0.89).
Table S1.
Summary of values and references for Fig. 6
| Muscle type | Temperature, °C | Actomyosin ATPase vmax*, s−1 | Ref. | Myofibril or fiber ATPase vmax†, s−1 | Ref. | V0‡, µm s−1 | Ref. |
| Rabbit psoas | 15 | 0.9§ | (54) | 1.78 | (55) | 3.6 | (56) |
| Rabbit psoas | 10 | 0.73§ | (54) | 1.27 | (57) | 2.03 | (57) |
| Rat EDL | 35 | 6.71, 4.68 | (8, 58) | 21 | (8) | ||
| Rat soleus | 35 | 2.58, 3.6 | (8, 58) | 9 | (8) | ||
| Rat type I | 15 | 0.288 | (59) | 1.6 | (59) | ||
| Rat type IIa | 15 | 1.06 | (59) | 5.5 | (59) | ||
| Rat type IIb | 15 | 1.9 | (59) | 9.8 | (59) | ||
| Mouse EDL | 35 | 7.21 | (8) | 24.8 | (60) | ||
| Mouse soleus | 35 | 3.58 | (8) | 11.5 | (60) | ||
| Rat type I (control)¶ | 15 | 0.221 | (61) | 1.7 | (61) | ||
| Rat type I¶ (1 wk) | 15 | 0.342 | (61) | 2.5 | (61) | ||
| Rat type I¶ (2 wk) | 15 | 0.361 | (61) | 2.6 | (61) | ||
| Rat type I¶ (3 wk) | 15 | 0.837 | (61) | 3.8 | (61) | ||
| Rat cardiac | 25 | 0.81 | (62) | 0.252 | (63) | 6 | (64) |
| Mouse cardiac α | 22 | 1.8 | (65) | 5.2 | (66) | ||
| Rat diaphragm | 37 | 3.68 | (8) | 13.8 | (8) | ||
| Cat fast | 36 | 4.86 | (8) | 13 | (8) | ||
| Frog sartorius | 22 | 4.06 | (8) | 12.5 | (8) | ||
| Human elbow flexor | 37 | 2.73 | (8) | 7.5 | (8) | ||
| Cat soleus | 36 | 1.8 | (8) | 5.3 | (8) | ||
| Pecten striated adductor | 14 | 0.97 | (8) | 3.8 | (8) | ||
| Frog sartorius | 0 | 0.49, 0.11 | (8, 67) | 0.44 | 2.5 | (8) | |
| Dogfish coracohyoid | 0 | 0.44 | (8) | 2.5 | (8) | ||
| Tortoise iliofibularis | 20 | 0.48 | (8) | 0.5 | (8) | ||
| Tortoise iliofibularis | 0 | 0.03 | (8) | 0.13 | (8) | ||
| Mytilus posterior adductor | 14 | 0.04 | (8) | 0.13 | (8) |
Solution ATPase measurements.
ATPase measured in the same fiber/myofibril preparation that was used to measure V0.
Calculated to half-sarcomere s−1 (µm s−1) using a sarcomere length of 2.5 µm if not given.
Adjusted to temperature from 25 °C using Q10 = 2.
Rat hindlimbs were unloaded for a duration of 0, 1, 2, or 3 wk before measurements.
Although the equivalent experiment of varying N by changing filament length cannot be done in muscle, classic studies (47, 48) have examined the relationship between V0 and sarcomere length. Whereas there is minimal change in V0 over the physiological range of filament overlap, consistent with the Huxley model, it is widely recognized that passive compressive forces can compensate for reduced effective N at longer lengths and passive resistive forces can compensate for increased effective N at shorter lengths. Therefore, the results of these studies are not necessarily inconsistent with our model.
A strength of our in vitro system is that these overlying forces are not present. Our model accurately describes the relationship between V0 and vmax for a wide range of muscle types (Fig. 6). This suggests that V0 is limited only by the rate that myosin attaches to actin (katt), not by the rate at which it detaches from actin, as has been previously thought. Our model brings attention to the importance of the mechanical properties and length of S2 in relation to the speed of muscle contraction. Interestingly, the length of the S2 region is highly conserved in muscle myosins (49) and other myosin IIs. This previously unidentified importance of the S2 region may help explain the phenotypes of cardiac muscle with familial hypertrophic mutations in the S2 region. Our results, which are supported by several previous works (18–21), also suggest that many modifications to muscles that alter V0, such as mutations in myosin, or drugs that target myosin, may alter the rate that myosin attaches to rather than detaches from actin. Our findings suggest a paradigm in which myosin heads undergo unloaded “powerstrokes” rather than work in mechanical opposition to each other during contraction, and that mechanochemistry is a property of the ensemble of myosins in muscle (50), not the individual myosin heads.
Materials and Methods
Buffers and Proteins.
Filament buffer was 10 mM sodium phosphate, pH 7.0, 5 mM MgCl2, 125 mM NaCl, 0.1 mM EGTA, 1 mM DTT, and 30 nM NaN3. Actin, biotinylated actin [5% (wt/wt)], and SMM were as described in ref. 21. Rods were prepared by papain digestion of SMM (51).
Preparation and Analysis of Myosin-Rod Cofilaments.
SMM and rods were labeled with NHS-rhodamine (Thermo Scientific) in 20 mM Hepes, pH 7.2, 0.5 M NaCl, 0.1 mM EGTA, 5 mM DTT, 30 nM NaN3 (21) and mixed in varying ratios and dialyzed into DTT-free filament buffer to form cofilaments. To determine molar ratios of full-length SMM to rod, cofilaments were separated on 4–20% (wt/wt) acrylamide Tris-glycine gels (Invitrogen), stained and imaged to quantify the full-length heavy chain and rod densities compared with mixed standards. Cross-linking with 1-ethyl-3-(3-dimethylaminopropyl)carbodiimide hydrochloride (EDC), phosphorylation, and ATP removal were performed as described in ref. 21. Cofilament lengths were measured from electron micrographs (21).
Preparation of 100% SMM Filaments.
SMM filaments (100%) prepared as described in ref. 21 had a narrow length distribution (Results and Discussion). To prepare longer filaments with a wider length distribution, SMM was labeled with NHS-rhodamine and after excess dye was removed by dialysis into 10 mM sodium phosphate, pH 7.0, 5 mM MgCl2, 500 mM NaCl, 0.1 mM EGTA, 1 mM DTT, 30 nM NaN3, the SMM concentration was determined using the manufacturer’s protocol and an E280 nm (0.1%) of 0.56 for SMM. The labeled SMM was diluted to 0.5 mg ml−1 (2.1-µM heads) in filament buffer. ATP (Sigma; A3377; 2.5 µM) was added to depolymerize the myosin. After no more than 5 min, residual filamentous myosin was pelleted for 15 min at 164,000 × g at 4 °C. The supernatant was removed and incubated for 3–4 d on ice to allow filaments to assemble slowly from the monomeric 10S-ADP.Pi state. After overnight dialysis to DTT-free filament buffer with Dowex (Sigma, 217425) in the dialysate to remove ADP, filaments were cross-linked as described in ref. 21 but the final pelleting step was omitted. Phosphorylation and subsequent ATP removal were as described in ref. 21 except in 10 mM sodium phosphate, pH 7.0, 5 mM MgCl2, 125 mM NaCl, 3 mM CaCl2, 0.1 mM EGTA, 1 mM DTT, 30 nM NaN3. Lengths were estimated from TIRF microscopy images using the ImageJ line tool and 0.31 µm was subtracted to account for the point-spread function of fluorescence, determined from the average length difference between electron micrographs and TIRF images of filaments (21).
Custom Flow Cells.
An ∼1.8-mm hole was drilled in a 3 × 1′′ × 1-mm glass slide (Fisher Scientific, 12–544-1). An ∼1-cm piece of 1.8-mm o.d. × 0.055′′ i.d. PEEK tubing (IDEX, 1539) was inserted flush with the slide and glued in place with Norland Optical Adhesive 68 (Norland Products, NOA68) and allowed to cure with exposure to UV light for 15 min. Two strips of double-sided tape (3M) on three sides of Biotin-PEG coverslips (21) held it to the slide; one strip was used on the remaining side to allow fluid to drain. The resulting flow cell (∼80 µl) allowed for immediate imaging after buffer additions.
Inverted Geometry IVMAs.
Experiments were at room temperature using a Nikon TE2000 epifluorescence microscope (Technical Instruments) and a Roper Cascade 512B camera (Princeton Instruments) with TIRF excitation at 532 and 488 nm, with 565/40 and 510/20 band-pass emission filters (Chroma), and a 100× objective. Each field of view was 54 µm2 (512 pixels2) at 106 nm pixel−1. Each step was in filament buffer unless noted otherwise. Biotin-PEG flow cells were incubated with 5 mg ml−1 BSA (Sigma; A3059) for 2 min, then 4 µg ml−1 streptavidin (Invitrogen; 434302) for 15–30 s, followed by 80 µl of 5 mg ml−1 BSA. Alexa 488-phalloidin-labeled 5% (wt/wt) biotinylated actin (80 µl of 70 nM) in 50 mM imidazole, pH 7.0, 50 mM KCl, 2 mM EGTA, 8 mM MgCl2, and 10 mM DTT was added and incubated for 4 min. The flow cell was washed once with 80 µl followed by phosphorylated SMM filaments (80 µl of 25 µg ml−1) for 2 min, followed by 80 µl of filament buffer plus 0.5% methylcellulose and an oxygen scavenger system (21) with indicated [ATP]. Image sequences (0.1 s) were immediately collected with TIRF excitation (532-nm laser) to monitor moving SMM filaments for ∼1 min followed by a still image of actin filaments using TIRF (488-nm excitation laser), which was overlaid with the image sequence of the SMM filaments using ImageJ (Movie S1).
Velocity Analysis of Filament Trajectories.
Background fluorescence (if present) was removed using the subtract background filter in ImageJ. Filament motion was analyzed using custom software (52) in which regions of fluorescence were segmented from background by intensity-based thresholding levels that were determined manually for each movie. Any fluorescent region with an area less than 10 pixels was not analyzed and the centroid for each of the remaining regions was calculated (53). Filament trajectories were created by linking the centroid positions through a displacement minimization algorithm. Trajectories with pauses, usually from acute actin bends, intersections, or bundles, were not included.
Supplementary Material
Acknowledgments
We thank Juli Petereit for advice about model equations. This work was supported by National Heart, Lung and Blood Institute Grant 5R01HL110214 (to C.R.C. and J.E.B.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1510241112/-/DCSupplemental.
References
- 1.Huxley AF, Simmons RM. Mechanical properties of the cross-bridges of frog striated muscle. J Physiol. 1971;218(1) Suppl:59P–60P. [PubMed] [Google Scholar]
- 2.Goldman YE. Measurement of sarcomere shortening in skinned fibers from frog muscle by white light diffraction. Biophys J. 1987;52(1):57–68. doi: 10.1016/S0006-3495(87)83188-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Friedman AL, Goldman YE. Mechanical characterization of skeletal muscle myofibrils. Biophys J. 1996;71(5):2774–2785. doi: 10.1016/S0006-3495(96)79470-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lymn RW, Taylor EW. Mechanism of adenosine triphosphate hydrolysis by actomyosin. Biochemistry. 1971;10(25):4617–4624. doi: 10.1021/bi00801a004. [DOI] [PubMed] [Google Scholar]
- 5.Huxley AF. Muscle structure and theories of contraction. Prog Biophys Biophys Chem. 1957;7:255–318. [PubMed] [Google Scholar]
- 6.Siemankowski RF, White HD. Kinetics of the interaction between actin, ADP, and cardiac myosin-S1. J Biol Chem. 1984;259(8):5045–5053. [PubMed] [Google Scholar]
- 7.Nyitrai M, et al. What limits the velocity of fast-skeletal muscle contraction in mammals? J Mol Biol. 2006;355(3):432–442. doi: 10.1016/j.jmb.2005.10.063. [DOI] [PubMed] [Google Scholar]
- 8.Bárány M. ATPase activity of myosin correlated with speed of muscle shortening. J Gen Physiol. 1967;50(6) Suppl:197–218. doi: 10.1085/jgp.50.6.197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lionne C, Brune M, Webb MR, Travers F, Barman T. Time resolved measurements show that phosphate release is the rate limiting step on myofibrillar ATPases. FEBS Lett. 1995;364(1):59–62. doi: 10.1016/0014-5793(95)00356-e. [DOI] [PubMed] [Google Scholar]
- 10.Spudich JA. How molecular motors work. Nature. 1994;372(6506):515–518. doi: 10.1038/372515a0. [DOI] [PubMed] [Google Scholar]
- 11.Kron SJ, Spudich JA. Fluorescent actin filaments move on myosin fixed to a glass surface. Proc Natl Acad Sci USA. 1986;83(17):6272–6276. doi: 10.1073/pnas.83.17.6272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yanagida T, Nakase M, Nishiyama K, Oosawa F. Direct observation of motion of single F-actin filaments in the presence of myosin. Nature. 1984;307(5946):58–60. doi: 10.1038/307058a0. [DOI] [PubMed] [Google Scholar]
- 13.Toyoshima YY, et al. Myosin subfragment-1 is sufficient to move actin filaments in vitro. Nature. 1987;328(6130):536–539. doi: 10.1038/328536a0. [DOI] [PubMed] [Google Scholar]
- 14.Yengo CM, Takagi Y, Sellers JR. Temperature dependent measurements reveal similarities between muscle and non-muscle myosin motility. J Muscle Res Cell Motil. 2012;33(6):385–394. doi: 10.1007/s10974-012-9316-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Warshaw DM, Desrosiers JM, Work SS, Trybus KM. Effects of MgATP, MgADP, and Pi on actin movement by smooth muscle myosin. J Biol Chem. 1991;266(36):24339–24343. [PubMed] [Google Scholar]
- 16.Homsher E, Wang F, Sellers JR. Factors affecting movement of F-actin filaments propelled by skeletal muscle heavy meromyosin. Am J Physiol. 1992;262(3 Pt 1):C714–C723. doi: 10.1152/ajpcell.1992.262.3.C714. [DOI] [PubMed] [Google Scholar]
- 17.Yamashita H, et al. ADP inhibits the sliding velocity of fluorescent actin filaments on cardiac and skeletal myosins. Circ Res. 1994;74(6):1027–1033. doi: 10.1161/01.res.74.6.1027. [DOI] [PubMed] [Google Scholar]
- 18.Hooft AM, Maki EJ, Cox KK, Baker JE. An accelerated state of myosin-based actin motility. Biochemistry. 2007;46(11):3513–3520. doi: 10.1021/bi0614840. [DOI] [PubMed] [Google Scholar]
- 19.Baker JE, Brosseau C, Fagnant P, Warshaw DM. The unique properties of tonic smooth muscle emerge from intrinsic as well as intermolecular behaviors of Myosin molecules. J Biol Chem. 2003;278(31):28533–28539. doi: 10.1074/jbc.M303583200. [DOI] [PubMed] [Google Scholar]
- 20.Baker JE, Brosseau C, Joel PB, Warshaw DM. The biochemical kinetics underlying actin movement generated by one and many skeletal muscle myosin molecules. Biophys J. 2002;82(4):2134–2147. doi: 10.1016/S0006-3495(02)75560-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Haldeman BD, Brizendine RK, Facemyer KC, Baker JE, Cremo CR. The kinetics underlying the velocity of smooth muscle myosin filament sliding on actin filaments in vitro. J Biol Chem. 2014;289(30):21055–21070. doi: 10.1074/jbc.M114.564740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Elangovan R, et al. An integrated in vitro and in situ study of kinetics of myosin II from frog skeletal muscle. J Physiol. 2012;590(Pt 5):1227–1242. doi: 10.1113/jphysiol.2011.222984. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Thedinga E, Karim N, Kraft T, Brenner B. A single-fiber in vitro motility assay. In vitro sliding velocity of F-actin vs. unloaded shortening velocity in skinned muscle fibers. J Muscle Res Cell Motil. 1999;20(8):785–796. doi: 10.1023/a:1005658825375. [DOI] [PubMed] [Google Scholar]
- 24.Pellegrino MA, et al. Orthologous myosin isoforms and scaling of shortening velocity with body size in mouse, rat, rabbit and human muscles. J Physiol. 2003;546(Pt 3):677–689. doi: 10.1113/jphysiol.2002.027375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ishijima A, et al. Multiple- and single-molecule analysis of the actomyosin motor by nanometer-piconewton manipulation with a microneedle: Unitary steps and forces. Biophys J. 1996;70(1):383–400. doi: 10.1016/S0006-3495(96)79582-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Warshaw DM, Desrosiers JM, Work SS, Trybus KM. Smooth muscle myosin cross-bridge interactions modulate actin filament sliding velocity in vitro. J Cell Biol. 1990;111(2):453–463. doi: 10.1083/jcb.111.2.453. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Homsher E, Nili M, Chen IY, Tobacman LS. Regulatory proteins alter nucleotide binding to acto-myosin of sliding filaments in motility assays. Biophys J. 2003;85(2):1046–1052. doi: 10.1016/S0006-3495(03)74543-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sellers JR. 1999. Myosins (Oxford Univ Press, Oxford, UK), 2nd Ed, pp 57–67.
- 29.Cremo CR, Geeves MA. Interaction of actin and ADP with the head domain of smooth muscle myosin: Implications for strain-dependent ADP release in smooth muscle. Biochemistry. 1998;37(7):1969–1978. doi: 10.1021/bi9722406. [DOI] [PubMed] [Google Scholar]
- 30.Craig R, Megerman J. Assembly of smooth muscle myosin into side-polar filaments. J Cell Biol. 1977;75(3):990–996. doi: 10.1083/jcb.75.3.990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Cooke PH, Fay FS, Craig R. Myosin filaments isolated from skinned amphibian smooth muscle cells are side-polar. J Muscle Res Cell Motil. 1989;10(3):206–220. doi: 10.1007/BF01739811. [DOI] [PubMed] [Google Scholar]
- 32.Xu J-Q, Harder BA, Uman P, Craig R. Myosin filament structure in vertebrate smooth muscle. J Cell Biol. 1996;134(1):53–66. doi: 10.1083/jcb.134.1.53. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Cross RA, Engel A. Scanning transmission electron microscopic mass determination of in vitro self-assembled smooth muscle myosin filaments. J Mol Biol. 1991;222(3):455–458. doi: 10.1016/0022-2836(91)90487-q. [DOI] [PubMed] [Google Scholar]
- 34.Tonino P, Simon M, Craig R. Mass determination of native smooth muscle myosin filaments by scanning transmission electron microscopy. J Mol Biol. 2002;318(4):999–1007. doi: 10.1016/S0022-2836(02)00191-2. [DOI] [PubMed] [Google Scholar]
- 35.Trybus KM. Assembly of cytoplasmic and smooth muscle myosins. Curr Opin Cell Biol. 1991;3(1):105–111. doi: 10.1016/0955-0674(91)90172-u. [DOI] [PubMed] [Google Scholar]
- 36.Kaya M, Higuchi H. Nonlinear elasticity and an 8-nm working stroke of single myosin molecules in myofilaments. Science. 2010;329(5992):686–689. doi: 10.1126/science.1191484. [DOI] [PubMed] [Google Scholar]
- 37.Kaya M, Higuchi H. Stiffness, working stroke, and force of single-myosin molecules in skeletal muscle: elucidation of these mechanical properties via nonlinear elasticity evaluation. Cell Mol Life Sci. 2013;70(22):4275–4292. doi: 10.1007/s00018-013-1353-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Harris DE, Warshaw DM. Smooth and skeletal muscle myosin both exhibit low duty cycles at zero load in vitro. J Biol Chem. 1993;268(20):14764–14768. [PubMed] [Google Scholar]
- 39.Uyeda TQ, Kron SJ, Spudich JA. Myosin step size. Estimation from slow sliding movement of actin over low densities of heavy meromyosin. J Mol Biol. 1990;214(3):699–710. doi: 10.1016/0022-2836(90)90287-V. [DOI] [PubMed] [Google Scholar]
- 40.Tyska MJ, Warshaw DM. The myosin power stroke. Cell Motil Cytoskeleton. 2002;51(1):1–15. doi: 10.1002/cm.10014. [DOI] [PubMed] [Google Scholar]
- 41.Lauzon AM, et al. A 7-amino-acid insert in the heavy chain nucleotide binding loop alters the kinetics of smooth muscle myosin in the laser trap. J Muscle Res Cell Motil. 1998;19(8):825–837. doi: 10.1023/a:1005489501357. [DOI] [PubMed] [Google Scholar]
- 42.Veigel C, Molloy JE, Schmitz S, Kendrick-Jones J. Load-dependent kinetics of force production by smooth muscle myosin measured with optical tweezers. Nat Cell Biol. 2003;5(11):980–986. doi: 10.1038/ncb1060. [DOI] [PubMed] [Google Scholar]
- 43.Walcott S, Warshaw DM, Debold EP. Mechanical coupling between myosin molecules causes differences between ensemble and single-molecule measurements. Biophys J. 2012;103(3):501–510. doi: 10.1016/j.bpj.2012.06.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Spudich JA. Hypertrophic and dilated cardiomyopathy: Four decades of basic research on muscle lead to potential therapeutic approaches to these devastating genetic diseases. Biophys J. 2014;106(6):1236–1249. doi: 10.1016/j.bpj.2014.02.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Deacon JC, Bloemink MJ, Rezavandi H, Geeves MA, Leinwand LA. Identification of functional differences between recombinant human α and β cardiac myosin motors. Cell Mol Life Sci. 2012;69(13):2261–2277. doi: 10.1007/s00018-012-0927-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Seow CY. Myosin filament assembly in an ever-changing myofilament lattice of smooth muscle. Am J Physiol Cell Physiol. 2005;289(6):C1363–C1368. doi: 10.1152/ajpcell.00329.2005. [DOI] [PubMed] [Google Scholar]
- 47.Gordon AM, Huxley AF, Julian FJ. The variation in isometric tension with sarcomere length in vertebrate muscle fibres. J Physiol. 1966;184(1):170–192. doi: 10.1113/jphysiol.1966.sp007909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Edman KA. The velocity of unloaded shortening and its relation to sarcomere length and isometric force in vertebrate muscle fibres. J Physiol. 1979;291:143–159. doi: 10.1113/jphysiol.1979.sp012804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Olney JJ, Sellers JR, Cremo CR. Structure and function of the 10 S conformation of smooth muscle myosin. J Biol Chem. 1996;271(34):20375–20384. doi: 10.1074/jbc.271.34.20375. [DOI] [PubMed] [Google Scholar]
- 50.Baker JE, LaConte LE, Brust-Mascher I, Thomas DD. Mechanochemical coupling in spin-labeled, active, isometric muscle. Biophys J. 1999;77(5):2657–2664. doi: 10.1016/S0006-3495(99)77100-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.King L, Jiang MJ, Huang TS, Sheu GC. Protease-susceptible sites and properties of fragments of aortic smooth-muscle myosin. Biochem J. 1995;312(Pt 2):511–518. doi: 10.1042/bj3120511. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Carter MS. 2014. Single molecule imaging methods and novel computational motion analysis used to characterize the transitions of single molecules between multiple states of motion: Determining the biochemical kinetics of single molecules in in vitro and in vivo systems. PhD dissertation (University of Nevada, Reno, NV)
- 53.Russ JC. The Image Processing Handbook. 4th Ed. CRC Press; Boca Raton, FL: 2002. pp. 475–526. [Google Scholar]
- 54.Persechini A, Stull JT. Phosphorylation kinetics of skeletal muscle myosin and the effect of phosphorylation on actomyosin adenosinetriphosphatase activity. Biochemistry. 1984;23(18):4144–4150. doi: 10.1021/bi00313a021. [DOI] [PubMed] [Google Scholar]
- 55.Glyn H, Sleep J. Dependence of adenosine triphosphatase activity of rabbit psoas muscle fibres and myofibrils on substrate concentration. J Physiol. 1985;365:259–276. doi: 10.1113/jphysiol.1985.sp015770. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Moss RL. The effect of calcium on the maximum velocity of shortening in skinned skeletal muscle fibres of the rabbit. J Muscle Res Cell Motil. 1982;3(3):295–311. doi: 10.1007/BF00713039. [DOI] [PubMed] [Google Scholar]
- 57.Cooke R, Franks K, Luciani GB, Pate E. The inhibition of rabbit skeletal muscle contraction by hydrogen ions and phosphate. J Physiol. 1988;395:77–97. doi: 10.1113/jphysiol.1988.sp016909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Bárány M, Close RI. The transformation of myosin in cross-innervated rat muscles. J Physiol. 1971;213(2):455–474. doi: 10.1113/jphysiol.1971.sp009393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Schluter JM, Fitts RH. Shortening velocity and ATPase activity of rat skeletal muscle fibers: Effects of endurance exercise training. Am J Physiol. 1994;266(6 Pt 1):C1699–73. doi: 10.1152/ajpcell.1994.266.6.C1699. [DOI] [PubMed] [Google Scholar]
- 60.Luff AR. Dynamic properties of the inferior rectus, extensor digitorum longus, diaphragm and soleus muscles of the mouse. J Physiol. 1981;313:161–171. doi: 10.1113/jphysiol.1981.sp013656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.McDonald KS, Fitts RH. 1993. Effect of hindlimb unweighting on single soleus fiber maximal shortening velocity and ATPase activity. J Appl Physiol 74(6):2949-2957. [DOI] [PubMed]
- 62.Pope B, Hoh JF, Weeds A. The ATPase activities of rat cardiac myosin isoenzymes. FEBS Lett. 1980;118(2):205–208. doi: 10.1016/0014-5793(80)80219-5. [DOI] [PubMed] [Google Scholar]
- 63.Cappelli V, Bottinelli R, Poggesi C, Moggio R, Reggiani C. Shortening velocity and myosin and myofibrillar ATPase activity related to myosin isoenzyme composition during postnatal development in rat myocardium. Circ Res. 1989;65(2):446–457. doi: 10.1161/01.res.65.2.446. [DOI] [PubMed] [Google Scholar]
- 64.de Tombe PP, ter Keurs HE. Force and velocity of sarcomere shortening in trabeculae from rat heart. Effects of temperature. Circ Res. 1990;66(5):1239–1254. doi: 10.1161/01.res.66.5.1239. [DOI] [PubMed] [Google Scholar]
- 65.Malmqvist UP, Aronshtam A, Lowey S. Cardiac myosin isoforms from different species have unique enzymatic and mechanical properties. Biochemistry. 2004;43(47):15058–15065. doi: 10.1021/bi0495329. [DOI] [PubMed] [Google Scholar]
- 66.Fitzsimons DP, Patel JR, Moss RL. Aging-dependent depression in the kinetics of force development in rat skinned myocardium. Am J Physiol. 1999;276(5 Pt 2):H1511–H1519. doi: 10.1152/ajpheart.1999.276.5.H1511. [DOI] [PubMed] [Google Scholar]
- 67.Ferenczi MA, Homsher E, Trentham DR, Weeds AG. Preparation and characterization of frog muscle myosin subfragment 1 and actin. Biochem J. 1978;171(1):155–163. doi: 10.1042/bj1710155. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.