Broken-Symmetry DFT Computations for the Reaction Pathway of IspH, an Iron–Sulfur Enzyme in Pathogenic Bacteria

Abstract

The recently discovered methylerythritol phosphate (MEP) pathway provides new targets for the development of antibacterial and antimalarial drugs. In the final step of the MEP pathway, the [4Fe–4S] IspH protein catalyzes the 2e^–/2H⁺ reductive dehydroxylation of (E)-4-hydroxy-3-methyl-but-2-enyl diphosphate (HMBPP) to afford the isoprenoid precursors isopentenyl pyrophosphate (IPP) and dimethylallyl pyrophosphate (DMAPP). Recent experiments have attempted to elucidate the IspH catalytic mechanism to drive inhibitor development. Two competing mechanisms have recently emerged, differentiated by their proposed HMBPP binding modes upon 1e^– reduction of the [4Fe–4S] cluster: (1) a Birch reduction mechanism, in which HMBPP remains bound to the [4Fe–4S] cluster through its terminal C₄–OH group (ROH-bound) until the −OH is cleaved as water; and (2) an organometallic mechanism, in which the C₄–OH group rotates away from the [4Fe–4S] cluster, allowing the HMBPP olefin group to form a metallacycle complex with the apical iron (η²-bound). We perform broken-symmetry density functional theory computations to assess the energies and reduction potentials associated with the ROH- and η²-bound states implicated by these competing mechanisms. Reduction potentials obtained for ROH-bound states are more negative (−1.4 to −1.0 V) than what is typically expected of [4Fe–4S] ferredoxin proteins. Instead, we find that η²-bound states are lower in energy than ROH-bound states when the [4Fe–4S] cluster is 1e^– reduced. Furthermore, η²-bound states can already be generated in the oxidized state, yielding reduction potentials of ca. −700 mV when electron addition occurs after rotation of the HMBPP C₄–OH group. We demonstrate that such η²-bound states are kinetically accessible both when the IspH [4Fe–4S] cluster is oxidized and 1e^– reduced. The energetically preferred pathway gives 1e^– reduction of the cluster after substrate conformational change, generating the 1e^– reduced intermediate proposed in the organometallic mechanism.

Short abstract

IspH is a [4Fe−4S] protein that is an antibacterial and antimalarial drug target. A complete characterization of IspH catalysis is desired to better inform inhibitor design. To date there are competing hypotheses for how IspH converts its substrate HMBPP to product, particularly with respect to how HMBPP coordination changes during catalysis. Here, we present broken-symmetry DFT computations that assess different binding modes of HMBPP to IspH in the oxidized and 1-electron reduced states.

Introduction

In 2012, the World Health Organization documented 8.6 million cases of tuberculosis, of which 450 000 were multidrug-resistant (MDR TB); of these, 171 000 cases were fatal.¹ In cases of MDR TB, the use of alternative, less effectual therapies is required when the first-line drugs are no longer effective.¹ The problem associated with drug resistance is not unique to tuberculosis and, notably, also plagues efforts to curb malaria²⁻⁵ and hospital-borne bacterial infections.^6,7 The diminished efficacy of conventional therapies against the multidrug-resistant organisms that cause these illnesses necessitates the development of new drugs with novel modes of action.⁸

Recently, the isoprenoid biosynthesis pathway discovered in microorganisms has inspired the development of new antibacterial and antimalarial drugs.^9,10 Isoprenoids comprise a wide selection of essential biomolecules that includes sterols, chlorophylls and quinones, all of which are synthesized from the precursors isopentenyl pyrophosphate (IPP; 1 in Figure 1) and dimethylallyl pyrophosphate (DMAPP; 2 in Figure 1).^11,12 Rohmer and Arigoni independently discovered the methylerythritol phosphate (MEP) metabolic pathway (alternatively named the 1-deoxy-d-xylulose 5 phosphate [DOXP] pathway) that is responsible for the synthesis of isoprenoids in most eubacteria (including the pathogens Helicobacter pylori and Mycobacterium tuberculosis) and in apicomplexan protozoa such as the malaria parasite Plasmodium falciparum.¹³⁻¹⁶ Although isoprenoid synthesis is also essential in humans, all animals obtain DMAPP and IPP through a mevalonate-dependent pathway that is distinct from the MEP pathway,^12,17 which justifies the pursuit of MEP inhibitors to treat bacterial and malarial infections. The first step toward producing such drugs has recently been achieved with the approval of fosmidomycin, an antimalarial drug that targets 1-deoxy-d-xylulose 5-phosphate reductoisomerase (DOXP reductase, also referred to as Dxr or IspC), the second enzyme in the MEP pathway.¹⁸⁻²⁰

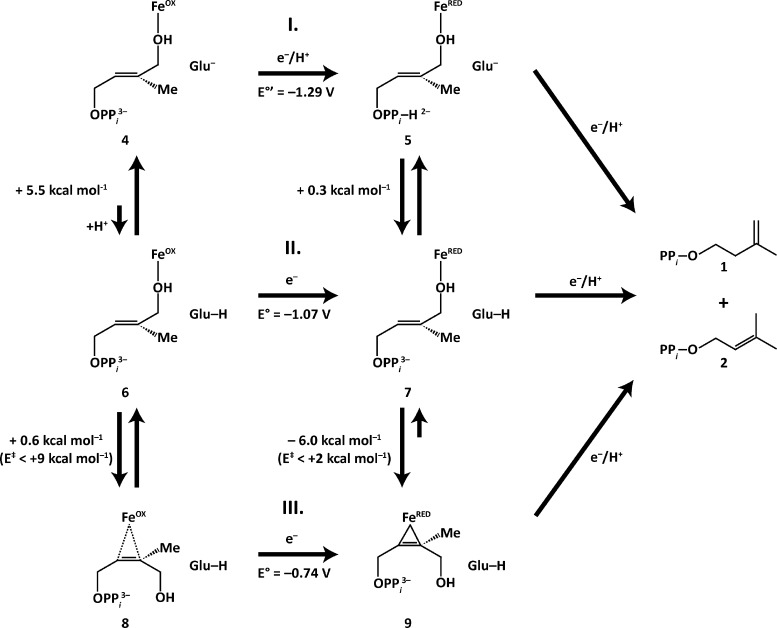
Figure 1.

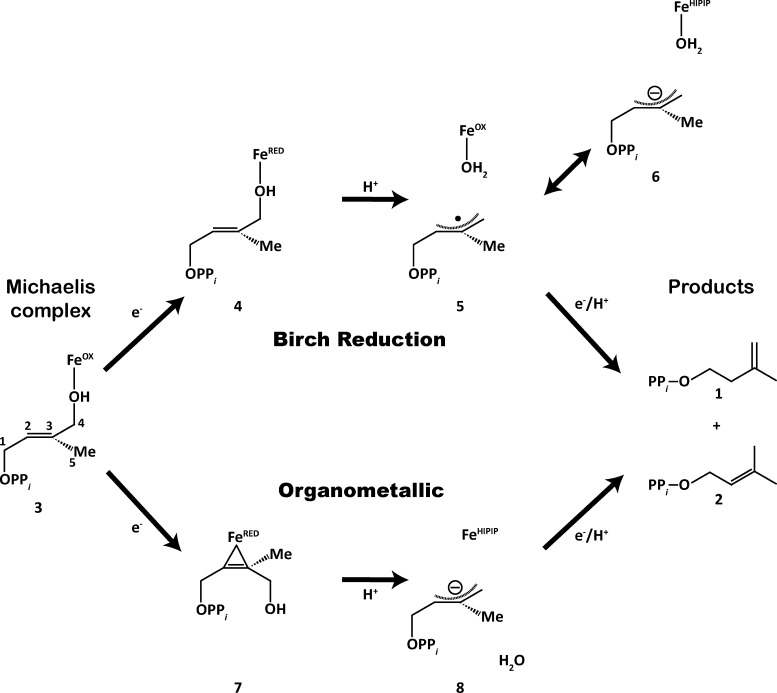
Schematic representation of the two disparate mechanisms used to explain IspH catalysis. Both the Birch reduction and organometallic mechanisms attempt to explain how IspH catalyzes the 2e^–/2H⁺ reductive dehydroxylation of HMBPP (3) to afford IPP (1) and DMAPP (2) in an approximate 5:1 ratio.

Following the success of fosmidomycin, multiple groups have worked to structurally characterize and develop inhibitors for other enzymes in the MEP pathway,¹⁰ including the IspH (LytB) protein.²¹⁻²⁷ In the final step of the MEP pathway, IspH catalyzes the 2e^–/2H⁺ reductive dehydroxylation of (E)-4-hydroxy-3-methyl-but-2-enyl diphosphate (HMBPP; 3 in Figure 1) to produce IPP and DMAPP in an approximate 5:1 ratio.²⁸⁻³² Various spectroscopic studies^{21,26,29,31,33,34} and high-resolution crystal structures^23,35,36 indicate the presence of a central [4Fe–4S] cluster in the active form of IspH. In the Escherichia coli crystal structure of IspH in complex with HMBPP (IspH:HMBPP),³⁵ three conserved cysteine residues (C12, C96, and C197) tether the cluster to the protein, leaving a single iron site, labeled Fe1 or the apical Fe, available for coordinating the C₄–OH group of the substrate HMBPP (atom numbers are labeled on 3 in Figure 1). The [4Fe–4S] cluster not only anchors the HMBPP molecule in the active site but also facilitates the transfer of 2e^– to HMBPP.^28−31,34 Additionally, the nearby E126 residue is understood to be essential in IspH catalysis.^26,37 Kinetics experiments performed on an IspH E126A mutant give a V_max that is over 40-fold lower than what is observed for wild-type (WT) IspH, indicating that the E126A mutant is nearly unable to catalyze the conversion of HMBPP to IPP and DMAPP.²⁶

Despite having reasonable knowledge of the proton and electron sources for IspH catalysis, the detailed catalytic mechanism is highly debated. Since a number of thorough review articles have catalogued recent experimental progress toward understanding IspH catalysis,^9,38−41 we briefly describe the two predominant mechanisms currently under consideration—the Birch reduction and organometallic mechanisms, borrowing the nomenclature used in the review by Liu and co-workers.⁴⁰

Proponents of the Birch reduction mechanism (top route in Figure 1) suggest catalysis is driven by the ability of Fe1 to act as a Lewis acid.^{30,32,35,39,42,43} The first mechanistic step in this mechanism is the reduction of the oxidized [4Fe–4S]²⁺ cluster (3) to its [4Fe–4S]⁺ form (4). Once reduced, the [4Fe–4S]⁺ cluster transfers an electron to HMBPP concurrent with the protonation and cleavage of the HMBPP C₄–OH group to generate a delocalized, allyl radical intermediate (5). Product generation (1 and 2) then requires the addition of both a proton and electron to the substrate intermediate. In this step, the electron is transferred either from an external source or from the [4Fe–4S]²⁺ cluster, which would then assume a [4Fe–4S]³⁺ (HiPIP-like⁴⁴⁻⁴⁶) oxidation state (6). While support for the Birch reduction mechanism derives from biochemical studies of HMBPP analogues,⁴² which do not require the formation of organometallic complexes, structures of the proposed intermediates (4–6) have not been directly observed.

In contrast with the Birch reduction mechanism, Oldfield and co-workers propose an organometallic mechanism for IspH catalysis (bottom route in Figure 1),^{26,35,41,47−49} in which the Fe1–O_C4 bond breaks and the C₄–OH group rotates away from Fe1 when the [4Fe–4S] cluster is reduced by one electron (7). Following this rotation, two electrons are transferred from the [4Fe–4S]¹⁺ cluster to the substrate, which, upon proton transfer and water loss, forms an allyl anion species (8).^48,49 This [4Fe–4S]³⁺ HiPIP state is similar to the proposed intermediate in the Birch reduction step (6), differing only in that it is formed following bond rotation. The requirement of bond rotation proposed in the organometallic mechanism is based on electron nuclear double resonance (ENDOR) spectroscopy experiments performed on an E126A mutant intermediate that showed hyperfine coupling between the HMBPP carbon atoms—likely the olefinic C₂ and C₃ atoms (Figure 1, numbering shown on 3)—and the [4Fe–4S]¹⁺ cluster.²⁶ It is unclear whether this intermediate exists in wild-type (WT) IspH, as the 1e^– reduced state has not been trapped when E126 is present.

A minor species identified in the X-ray structure of the WT IspH:HMBPP complex,³⁶ obtained shortly after irradiation of the crystals, contains HMBPP in an alternative conformation with its C₄–OH group rotated away from Fe1. In this crystal structure, HMBPP weakly coordinates Fe1 through its olefinic C₂ and C₃ atoms, and the C₄–OH group is positioned to form a hydrogen bond with the HMBPP PP_i (pyrophosphate) tail. Such HMBPP conformations are also observed in crystal structures of [3Fe–4S] T167C, E126D, and E126Q mutants³⁶ and indicate that the properties of the IspH active site can be tuned to induce HMBPP binding in a manner that is similar to what is proposed in the organometallic mechanism. Separately, ¹³C feeding studies⁴⁷ have also provided independent support for the organometallic mechanism.

Further analysis is needed to establish which IspH catalytic mechanism is preferred. Since the proposed binding modes of HMBPP in the Birch reduction and organometallic mechanisms differ when the [4Fe–4S] cluster is 1e^– reduced,⁴⁰ this report uses broken-symmetry density functional theory (BS-DFT) computations to study the geometries and energies of the different 1e^– reduced intermediates implicated by these two distinct mechanisms. We perform these computations on the same active-site model used previously to examine the different IspH oxidized states.⁵⁰ This approach enables us to obtain reduction potentials and explore the feasibility of identifying different IspH reaction intermediates in the 1e^– reduced state. We also extend our analysis of oxidized states and related reaction pathways beyond that in previous work.⁵⁰

Methods

Active-Site Model Used to Probe 1e^– Reduced States of IspH

The active-site quantum model employed in this work is identical to that used previously to successfully compute geometries and Mössbauer parameters for the IspH oxidized state.⁵⁰ Briefly, this large active-site model is constructed from the oxidized [4Fe–4S] IspH:HMBPP crystal structure solved to 1.7 Å resolution by Grawert et al. (PDB ID: 3KE8).³⁵ In addition to the [4Fe–4S] cluster, its coordinating thiolates (C12, C96, and C197), and the substrate HMBPP, we include the side chains of various residues suggested to play roles in catalysis: T167, E126, H41, and H124. Additionally, we include other residues that are ideally positioned to stabilize the highly charged HMBPP PP_i tail: H74, S225, S226, N227, and S269. Further, the model includes the backbones of A199/T200, P97/L98, and G14/V15, the side chain of T200, and a crystallographic water that cumulatively donate the only five hydrogen bonds to the cluster sulfides and thiolates observed in the [4Fe–4S] IspH/HMBPP crystal structure.³⁵ The inclusion of all hydrogen bond donors to the [4Fe–4S] cluster is necessary because of their collective role in modulating the reduction potentials of [4Fe–4S] clusters.⁵¹⁻⁵⁴ Upon addition of hydrogen atoms and capping groups, as detailed previously, the IspH active-site model contains 203–205 atoms, depending on the protonation state of C₄–O(H), E126, and the PP_i tail.⁵⁰

Practical Considerations for Broken-Symmetry Density Functional Theory Computations of the 1e^– Reduced States of IspH

In [4Fe–4S] clusters, the different Fe sites are spin-polarized and spin-coupled, with two antiferromagnetically (AF) coupled Fe–Fe pairs. Since conventional DFT methods are typically unable to obtain AF-coupled states, we employ BS-DFT computations to obtain optimized geometries and relative energies for the IspH active-site quantum cluster in the 1e^– reduced state.⁵⁵⁻⁵⁷

Previously, we considered an active-site model of the IspH oxidized state.⁵⁰ In these computations, the AF-coupled oxidized state contains two Fe–Fe spin-coupled pairs: one pair with a net spin of +9/2, and the other pair with a net spin of −9/2. Collectively, these pairs combine to give a system net spin of S_Tot = 0. To generate the AF-coupled 1e^– reduced state, we add a spin-α electron to the system to give S_Tot = +1/2. (The plus sign indicates that the ẑ-component of total spin, M_S,Tot, equals +1/2 in the BS state used; the majority spin is thus α for the quantum cluster.) In practice, generating this AF-coupled 1e^– reduced state is achieved from the optimized geometries previously obtained for the oxidized state of the IspH cluster. The AF-coupled BS state for the 1e^– reduced state is found by first computing a ferromagnetically coupled state, where all Fe atoms are high-spin with parallel net spins (S_Tot = 9/2 + 8/2 = +17/2). Then, the spin vectors on two of the four Fe atoms are rotated to generate the AF-coupled, BS state with S_Tot = +1/2, which is used as the starting point for geometry optimizations of the 1e^– reduced states.

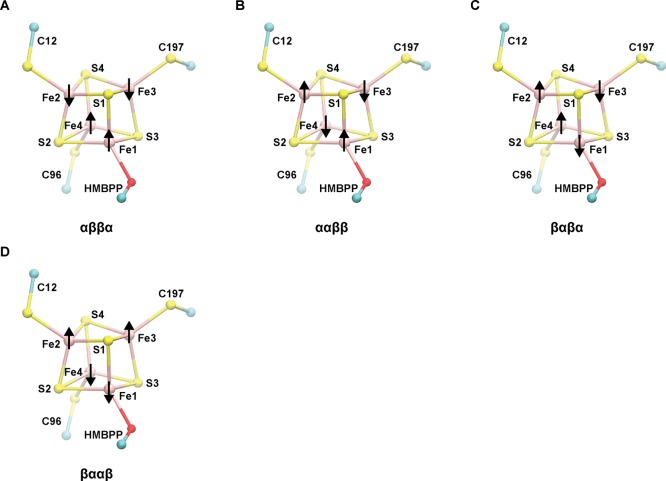
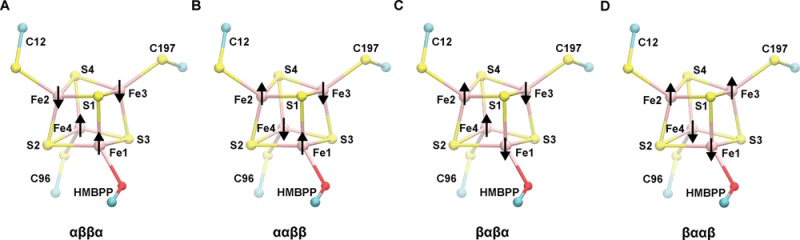
When the [4Fe–4S] cluster is 1e^– reduced, the spin-coupled Fe–Fe pair whose net spins are aligned with the total system spin (S_Tot) formally corresponds to a delocalized, mixed-valence pair (two Fe^2.5+, S = +9/2); the Fe–Fe pair whose net spins are aligned opposite to S_Tot is a ferrous pair (two Fe²⁺, S = −8/2). Because of the non-equivalency of these two Fe–Fe pairs, computations are performed on different valence isomers of the 1e^– reduced [4Fe–4S]¹⁺ cluster; that is to say, different Fe–Fe spin-coupling combinations were examined in this study. Consistent with our recent study of the IspH oxidized state,⁵⁰ we consider four of the six possible valence isomers in the 1e^– reduced state, which are named according to the net spin on each specific iron site (Fe1–Fe4): αββα, ααββ, βαβα, and βααβ (Figure 2). To effectively manage the number of computations needed to characterize the different protonation and electronic states available in the 1e^– reduced state of our active-site quantum model, we omit the αβαβ and ββαα states from our analysis, which were found to be either intermediate or higher in energy than all other states performed on a smaller active-site model.

Figure 2.

Illustration of the different valence isomers considered in this study. Atom numbering applied to [4Fe–4S] cluster irons and sulfides are used throughout this report. The naming of each valence isomer corresponds to the alignment of the net spin on each Fe atom (1–4): (a) αββα, (b) ααββ, (c) βαβα, and (d) βααβ.

Geometry Optimizations of the IspH 1e^– Reduced States

BS-DFT computations are performed using the Amsterdam Density Functional (ADF) 2009 program.⁵⁸ We choose to perform all geometry optimizations and single-point energy computations with the OLYP exchange-correlation (XC) functional,^59,60 since its use has been shown to produce good-quality geometries, spin-state energetics, and spectroscopic parameters for various Fe complexes,⁶¹⁻⁶³ including the oxidized IspH active site.⁵⁰ Geometry optimizations are performed on all valence isomers considered in this study and employ the Slater-type triple-ζ plus polarization (STO-TZP) basis set with core electrons frozen and a numerical integration accuracy of 4.0. To ensure the active-site geometry in our computations best matches that of the IspH protein, the C_α atoms of all residues, with the exception of the thiolate residues, are constrained to their crystallographic positions. All the thiolates are capped at the C_β atom, constraining one hydrogen atom attached to the C_β atom to lie along the C_β–C_α bond vector. Further details pertaining to the preparation of the model active site can be found in ref (49).

In all geometry optimizations, solvent effects are approximated using the Conductor-like Screening Model (COSMO)^64,65 with a dielectric constant (ε) of 20. This choice for ε has been validated in BS-DFT studies of ribonucleotide reductase intermediate X,⁶⁶ the oxidized states of the [4Fe–4S]-containing adenosine 5′-phosphosulfate reductase (APS reductase),⁶⁷ and IspH.⁵⁰ When energies are obtained from these geometry optimizations with COSMO solvation (ε = 20), we refer to the results as having been obtained with the DFT/COSMO method.

Single-Point Energy Calculations Using the DFT/SCRF Method

Following geometry optimizations in COSMO solvation (ε = 20), we perform single-point self-consistent reaction field (SCRF) computations (henceforth referred to as DFT/SCRF computations) on all BS states considered. In these DFT/SCRF computations, the optimized geometry obtained for the active-site region is subjected to a multi-dielectric environment that also includes the permanent charges and dipoles generated by the surrounding IspH protein point charges through a finite-difference solution to the Poisson equation.⁶⁸

To generate the protein/solvent environment included in the DFT/SCRF method, the optimized geometry of each 1e^– reduced state is embedded in the oxidized [4Fe–4S] IspH:HMBPP crystal structure.³⁵ Atoms present in both the active-site model and the protein crystal structure are omitted from the electrostatic protein region to ensure that they are represented only once—in the region described by DFT. All other protein atoms are assigned fixed point charges and atomic radii from the PARSE charge set.⁶⁹ The DFT/SCRF method then assigns different dielectric constants to describe the active-site region (ε = 1), its surrounding protein environment (ε = 4), and the solvent region outside the protein (ε = 80).

Following system preparation, DFT/SCRF computations are performed using the standard interface between a developmental version of ADF2011 and Bashford’s Macroscopic Electrostatics with Atomic Detail (MEAD)^70,71 program. (We note that all computations reported here give results that are identical to those obtained using the official release of ADF2012.⁷²) In practice, the DFT/SCRF computations are conducted iteratively, whereby the following steps are taken: (1) a gas-phase single-point energy calculation is performed on the active-site geometry obtained from an optimization using COSMO; (2) following the gas-phase single-point energy computation, point charges are obtained for the active-site atoms by fitting to the DFT-derived molecular electrostatic potential (ESP) using the CHELPG algorithm⁷³ combined with singular value decomposition;⁷⁴ (3) the total (electronic plus nuclear) charge density obtained for the active site quantum cluster is subjected to two potentials obtained by a finite-difference solution of the Poisson equation: a protein potential arising from the protein point charges screened by different dielectric media (ε = 1 for the quantum region, ε = 4 for the protein region, and ε = 80 for the solvent region) and a reaction field potential generated by the response of the different dielectric regions to the ESP charges in the quantum region; (4) the sum of the protein and reaction field potentials are then added to the Coulomb operator in the DFT scheme, and a single-point energy calculation is performed, taking into account the polarization of the quantum region by protein/solvent environment; (5) the electronic energy obtained from the single-point energy calculation is added to the protein and reaction field energies to obtain a total DFT/SCRF energy; (6) steps 1–5 are iterated until the DFT/SCRF energy does not deviate between cycles by more than 0.1 kcal mol^–1.⁶⁸

Naming Scheme for the Different Oxidized and Reduced IspH States

To facilitate the discussion of the different active-site protonation states of IspH, we adopt a naming scheme introduced previously, RO^XP^YE^Z, where X, Y, and Z are assigned either a minus sign “–” or the letter “H” to signify whether or not a proton resides on the HMBPP C₄–O(H) group, the HMBPP PP_i moiety, or E126, respectively (Table 1).⁵⁰ For example, in the state named RO^HP^–E^–, HMBPP possesses a protonated C₄–O(H) group and a fully deprotonated PP_i group (giving the ligand a net charge q of −3), whereas E126 is deprotonated. Combined with the 1e^– reduced [Fe₄S₄Cys₃]^2– cluster and the two charged imidazoles (of which each has q = +1), the model active site of the RO^HP^–E^– state carries a total charge of −4 (Table 1). We stress that the “–” sign does not specify the net charge of the PP_i group within this naming scheme, which has a −3 charge when it is deprotonated (P^–) and a −2 charge when it is singly protonated at an oxygen on the terminal phosphate group of HMBPP (P^H).

Table 1. A Description of the Nomenclature Used Throughout This Report^a.

protonation state	q	C4–O(H)	PPi	E126
RO–P–EH	–4	–	–	H
RO–PHEH	–3	–	H	H
ROHP–E–	–4	H	–	–
ROHPHE–	–3	H	H	–
ROHP–EH	–3	H	–	H
ROHPHEH	–2	H	H	H

^aThis nomenclature is identical to the scheme used previously to describe the IspH oxidized state.⁵⁰ Unless indicated with an H, the titratable moiety is assumed to be fully deprotonated and is marked by a “–”. The total charge (q) of the active-site quantum cluster when the [4Fe–4S] cluster is 1e^– reduced is also given for each state.

Additionally, since the results presented here consider different binding modes of HMBPP to Fe1, we indicate the coordinating group of HMBPP in parentheses following its protonation state when the coordination mode is ambiguous. For example, when the RO^HP^–E^– state coordinates Fe1 through its ROH group, it is denoted by RO^HP^–E^–(ROH). When the same protonation state is considered but with the HMBPP olefinic C₂ and C₃ atoms coordinating Fe1, the state is instead labeled RO^HP^–E^–(η²).

Computing Relative Energies in the 1e^– Reduced State

The relative free energy of deprotonation at pH = 7, ΔG_deprot, is obtained for an arbitrary number of titrating protons n (eq 1):

1

When using the DFT/COSMO method, E(A) and E(H_nA) are the “total” energies of the geometry-optimized BS states (ε = 20), computed with respect to a sum of atomic fragments (spin-restricted atoms).⁷⁵ Alternatively, ΔG_deprot is computed with the DFT/SCRF method using the total free energies of the active site described by DFT plus the effects of the protein/solvent environment, as obtained by a finite-difference solution of the Poisson equation.⁶⁸

We approximate the difference in zero-point energy (ZPE) between the protonated and deprotonated states, ΔZPE (eq 1), as the difference in ZPE upon deprotonation of all fragments that are titrated (e.g., the carboxylate of E126, the C₄–O(H) group of HMBPP, or the PP_i tail of HMBPP), obtained from OLYP frequency calculations performed on the two protonation states of each individual fragment. These values are computed to be −8.7, −10.4, and −8.8 kcal mol^–1 for E126, the HMBPP C₄–O(H) group, and the HMBPP PP_i moiety, respectively, using the OLYP/STO-TZP level of theory.⁵⁰

In eq 1, ΔG_ref(H⁺) is the free energy associated with the titrated proton(s), as defined by eq 2:

2

In eq 2, the energy of a proton, E(H⁺), is 292.7 kcal mol^–1, which is obtained from an empirically corrected, gas-phase OLYP calculation with respect to a spin-restricted hydrogen atom.^50,76,77 For ΔG_sol(H⁺, 1 atm), the solvation free energy of a proton, we use the value of −264.0 kcal mol^–1, which is an experimental value derived from analysis of cluster-ion solvation data.^78,79 The translational entropy of a proton, −TΔS_gas(H⁺), is chosen to be −7.76 kcal mol^–1, its value computed theoretically at 298 K and 1 atm.⁸⁰ The final term in computing the free energy of the titrating proton, 5/2 RT (1.5 kcal mol^–1), arises from the sum of the proton translational energy (3/2 RT) and the work term PV = RT.^78,80

Finally, the term ΔE_corr corrects ΔG_deprot for a neutral solvent environment (pH = 7), equal to −2.303 × k_BT × pH (equivalent to −9.6 kcal mol^–1 at pH 7). When multiple protons are titrated, the number of protons exerts a multiplicative effect on ΔG_ref(H⁺) and ΔE_corr, whereas if two states are tautomers, the variable n in eq 1 is equal to zero, and the difference in energy between states is only corrected for ΔZPE.

Computing Reduction Potentials in the 1e^– Reduced State

Reduction potentials are obtained for the general process:

3

All reduction potentials are obtained with respect to the standard hydrogen potential (ΔSHE = −4.34 V),^51,78,81 computed in the absence of proton coupling using eq 4:

4

where IP_red(RO^XP^YE^Z) is the computed ionization potential that includes solvent effects, obtained using either the DFT/COSMO or DFT/SCRF methods.⁵¹

Results

1. Geometries in [4Fe–4S]¹⁺ IspH with HMBPP Bound via C₄–O(H)

Because protonation of the C₄–O(H) group is required for catalysis, we will focus most of our discussion on the lowest-energy valence isomers computed for each protonation state having HMBPP bound to the [4Fe–4S]¹⁺ cluster via its C₄–OH group (i.e., ROH-bound states). Across three different charge states for the active-site clusters, namely, RO^HP^–E^– (q = −4), RO^HP^HE^– (q = −3), and RO^HP^HE^H (q = −2), the Fe1–O_C4 distance increases by ∼0.02–0.05 Å following 1e^– reduction of the [4Fe–4S] cluster (Figure 3, Table 2). For instance, in the oxidized state,⁵⁰ the Fe1–O_C4 distance is 2.13 and 2.21 Å for the RO^HP^HE^– and RO^HP^HE^H states, respectively; however, these respective distances become 2.15 and 2.26 Å following 1e^– reduction of the [4Fe–4S] cluster (Table 2).

Figure 3.

Optimized geometries of the lowest-energy ROH-bound states when the [4Fe–4S] cluster is 1e^– reduced with different total system charges: (a) RO^HP^–E^–, q = −4; (b) RO^HP^HE^–, q = −3; (c) RO^HP^–E^H, q = −3; (d) RO^HP^HE^H, q = −2.

Table 2. Geometric Parameters for the Lowest-Energy Valence Isomers of Three Representative Protonation States when the [4Fe–4S] Cluster Is Both Oxidized⁵⁰ and Reduced by One Electron.

		ROHP–E–(ROH)			ROHPHE–(ROH)			ROHPHEH(ROH)
	exp	ox	red	Δa	ox	red	Δa	ox	red	Δa
cluster bond lengths
Fe1–S5	2.344	2.218	2.227	0.01	2.215	2.272	0.06	2.209	2.251	0.04
Fe1–S6	2.393	2.301	2.313	0.01	2.298	2.290	–0.01	2.280	2.268	–0.01
Fe1–S7	2.364	2.328	2.338	0.01	2.317	2.319	0.00	2.313	2.325	0.01
Fe2–S5	2.217	2.323	2.304	–0.02	2.324	2.340	0.02	2.333	2.343	0.01
Fe2–S6	2.186	2.203	2.253	0.05	2.201	2.209	0.01	2.210	2.215	0.00
Fe2–S8	2.181	2.362	2.392	0.03	2.359	2.390	0.03	2.353	2.391	0.04
Fe3–S5	2.319	2.313	2.306	–0.01	2.317	2.333	0.02	2.305	2.333	0.03
Fe3–S7	2.281	2.236	2.299	0.06	2.237	2.255	0.02	2.238	2.255	0.02
Fe3–S8	2.306	2.357	2.358	0.00	2.350	2.372	0.02	2.360	2.382	0.02
Fe4–S6	2.308	2.314	2.325	0.01	2.319	2.308	–0.01	2.325	2.325	0.00
Fe4–S7	2.217	2.320	2.326	0.01	2.324	2.305	–0.02	2.326	2.310	–0.02
Fe4–S8	2.276	2.245	2.265	0.02	2.242	2.312	0.07	2.242	2.296	0.05
Fe2–SC12	2.283	2.263	2.312	0.05	2.258	2.314	0.06	2.257	2.311	0.05
Fe3–SC197	2.285	2.283	2.337	0.05	2.274	2.337	0.06	2.271	2.324	0.05
Fe4–SC96	2.264	2.295	2.357	0.06	2.290	2.348	0.06	2.291	2.353	0.06
HMBPP bond lengths
Fe1–OC4	2.046	2.108	2.161	0.05	2.133	2.148	0.01	2.254	2.282	0.03
Fe1–C3	3.039	3.627	3.639	0.01	3.551	3.629	0.08	3.399	3.431	0.03
Fe1–C2	2.913	3.267	3.306	0.04	3.266	3.310	0.04	3.220	3.241	0.02
HMBPP bond lengths
OC4–OT167	2.702	2.816	2.880	0.06	2.914	2.843	–0.07	3.179	3.161	–0.02
OT167–OE126	2.761	2.770	2.799	0.03	2.771	2.795	0.02	2.667	2.654	–0.01
OE126–OW1	2.578	3.133	3.131	0.00	2.907	3.051	0.14	3.711	3.740	0.03
OW1–OPPi	2.548	2.746	2.753	0.01	3.006	2.989	–0.02	2.836	2.841	0.01
OC4–OE126	3.526	4.337	4.473	0.14	4.358	4.472	0.11	4.200	4.155	–0.05
OC4–OPPi	4.782	4.958	4.970	0.01	4.890	4.944	0.05	4.874	4.861	–0.01
HMBPP angle
C2–C3–C4–OC4	2.046	–104.6	–103.7	0.9	–101.8	–103.7	–1.9	–99.1	–99.3	–0.2

^aThe differences in bond length (Å) or angle (deg) between the oxidized and 1e^– reduced states are given under the column labeled Δ.

The Fe–S^2– (iron–sulfide) bond lengths are similar between the oxidized⁵⁰ and 1e^– reduced geometries within the same protonation state and valence isomer; however, all Fe–thiolate distances are elongated by ∼0.05 Å in the 1e^– reduced state (Table 2). Nevertheless, identically protonated, oxidized, and 1e^– reduced geometries possess similar hydrogen-bond networks and orientations of the second- and third-sphere ligands (i.e., protein residues). These results lead to a maximum heavy atom root-mean-square deviation (RMSD) of 0.12 Å over all heavy atoms in the full quantum cluster. Additionally, there is little difference in geometry for the different valence isomers of the same protonation state when the [4Fe–4S] cluster is 1e^– reduced (RMSD < 0.18 Å).

While the results from our geometric analysis focus on three representative protonation states in the 1e^– reduced state, the other protonation states considered in this study show similar geometry changes upon reduction (Supporting Information, Table S1).

2. Distribution of Spin Density and Charge in the Oxidized and 1e^– Reduced States of IspH with HMBPP Bound to Fe1 through its C₄–OH Group

By tracking net spin populations (NSPs) using Mulliken analysis and the ESP partial charges using DFT/SCRF calculations, we can better understand how the electronic structure of the active-site quantum cluster changes following a 1e^– reduction of the [4Fe–4S] cluster. For a representative protonation state (e.g., RO^HP^HE^–), we present the NSPs and ESP charges computed for the lowest-energy valence isomers having the net spin on Fe1 aligned either with (net spin-α) or opposite (net spin-β) the overall net spin of the full active-site quantum cluster (S_Tot = +1/2). In all RO(H)-bound protonation states, the lowest-energy state having Fe1 net spin-α is the αββα state; analogously, all lowest-energy states with Fe1 net spin-β are βααβ valence isomers (Supporting Information, Table S4). The important physical distinction between these spin isomers is that they are also different valence isomers. When one adds an α-spin electron to the oxidized cluster, this process is a minority spin addition for each Fe site with net-β spin and has little effect on the net-α spin sites. This result follows because all Fe sites are high-spin and have greater than (or equal to) a half-filled Fe 3d shell in the starting oxidized state.

NSPs and ESP charges for the RO^HP^HE^– state are reported for the oxidized and 1e^– reduced states of the [4Fe–4S] cluster in Tables 3 and 4, respectively. Additionally, we report the changes in NSPs and ESP charges (ΔNSP and Δq, respectively) following from the 1e^– reduction of the [4Fe–4S] cluster to elucidate where the charge and spin density associated with the reducing electron resides.

Table 3. NSPs Given for Atoms in the [4Fe–4S] Cluster, Its Coordinating Thiolates, and HMBPP from Two Representative Valence Isomers of the RO^HP^HE^–(ROH) State When the [4Fe–4S] Cluster Is Oxidized⁵⁰ and Reduced by One Electron.

	ROHPHE–(ROH)
	αββα			βααβ
	ox	red	ΔNSPa	ox	red	ΔNSPa
Fe1	3.241	3.324	0.083	–3.247	–3.032	0.215
Fe2	–3.174	–2.904	0.270	3.170	3.284	0.113
Fe3	–3.181	–3.112	0.069	3.196	3.316	0.120
Fe4	3.206	3.272	0.066	–3.212	–3.069	0.143
sum	0.092	0.580	0.488	–0.092	0.499	0.591
S1	–0.034	0.018	0.053	0.026	0.194	0.168
S2	0.084	0.270	0.186	–0.083	–0.016	0.067
S3	0.096	0.183	0.087	–0.093	–0.036	0.056
S4	–0.047	0.007	0.054	0.049	0.157	0.108
sum	0.099	0.478	0.379	–0.101	0.299	0.399
C12	–0.224	–0.106	0.118	0.224	0.161	–0.062
C96	0.199	0.137	–0.062	–0.198	–0.086	0.112
C197	–0.191	–0.111	0.080	0.192	0.134	–0.058
sum	–0.215	–0.080	0.135	0.218	0.210	–0.008
cluster	–0.024	0.978	1.002	0.025	1.007	0.982
OC4	0.019	0.012	–0.007	–0.019	–0.012	0.008
C3	0.003	0.001	–0.001	–0.003	–0.001	0.001
C2	0.000	0.002	0.001	0.000	0.002	0.002
HMBPP	0.023	0.016	–0.007	–0.023	–0.013	0.011
cluster + HMBPP	–0.001	0.994	0.995	0.002	0.994	0.993

^aThe difference in NSP (ΔNSP) between the oxidized and 1e^– reduced atoms is indicated.

Table 4. ESP Charge Distributions Given for Atoms in the [4Fe–4S] Cluster, Its Coordinating Thiolates, and HMBPP from Two Representative Valence Isomers of the RO^HP^HE^–(ROH) State When the [4Fe–4S] Cluster Is Oxidized⁵⁰ and Reduced by One Electron.

	ROHPHE–(ROH)
	αββα			βααβ
	ox	red	Δqa	ox	red	Δqa
Fe1	0.527	0.549	0.022	0.515	0.516	0.001
Fe2	0.472	0.528	0.056	0.472	0.559	0.087
Fe3	0.548	0.617	0.069	0.575	0.698	0.123
Fe4	0.440	0.502	0.062	0.444	0.490	0.046
sum	1.987	2.196	0.209	2.007	2.263	0.257
S1	–0.491	–0.636	–0.145	–0.495	–0.678	–0.183
S2	–0.293	–0.362	–0.069	–0.278	–0.340	–0.062
S3	–0.348	–0.505	–0.156	–0.357	–0.514	–0.157
S4	–0.591	–0.798	–0.206	–0.605	–0.825	–0.220
sum	–1.724	–2.301	–0.577	–1.735	–2.357	–0.622
C12	–0.266	–0.413	–0.148	–0.261	–0.387	–0.125
C96	–0.332	–0.478	–0.146	–0.334	–0.499	–0.165
C197	–0.380	–0.539	–0.159	–0.404	–0.567	–0.162
sum	–0.977	–1.430	–0.452	–1.000	–1.453	–0.453
total cluster	–0.714	–1.534	–0.820	–0.728	–1.546	–0.817
OC4	–0.386	–0.412	–0.026	–0.388	–0.418	–0.030
C3	0.013	0.024	0.010	0.019	0.028	0.009
C2	–0.213	–0.237	–0.024	–0.241	–0.269	–0.029
total HMBPP	–0.296	–0.370	–0.075	–0.317	–0.418	–0.101
cluster + HMBPP	–1.010	–1.905	–0.895	–1.046	–1.964	–0.918

^aThe difference in charge (Δq) between the oxidized and 1e^– reduced atoms is indicated.

In the RO^HP^HE^–(ROH) αββα 1e^– reduced state, Fe1 and Fe4 (numbering illustrated in Figure 2) have NSPs of +3.32 and +3.27, respectively, which is slightly more positive than their respective values of +3.24 and +3.21 in the oxidized state (Table 3). In contrast, Fe2 and Fe3 have spin densities of −2.90 and −3.11 in the 1e^– reduced state—values that are significantly more positive than their corresponding values in the oxidized state (−3.17 and −3.18, respectively). The net spin-β Fe2–Fe3 pair has site NSPs that are reduced in magnitude relative to Fe1 and Fe4, because the spin-α electron added in the broken-symmetry scheme falls largely on Fe2 and Fe3. The magnitudes of these site NSPs support the formal assignment of the Fe1–Fe4 spin-coupled pair as being a delocalized, mixed-valence pair (S = +9/2), whereas Fe2 and Fe3 form a ferrous pair (S = −8/2). Comparing the NSPs summed over all Fe atoms in the RO^HP^HE^– αββα 1e^– reduced state relative to the RO^HP^HE^– αββα oxidized state, it is evident that approximately half of the reducing electron spin density falls on the Fe atoms (ΔNSP = 0.49, Table 3). The remaining reducing net-α spin density indicates there is significant Fe–S covalency in the system; indeed, the cluster sulfides give a ΔNSP of +0.38, and the cluster thiolates give a ΔNSP of +0.14 (Table 3).

In both the oxidized and 1e^– reduced states, it is apparent that each thiolate possesses significant net spin density that is aligned with the majority spin density on the iron to which it is coordinated. For instance, C12 (Cys12) is attached to Fe2, which has NSPs of −3.17 and −2.90 in the oxidized and 1e^– reduced states, respectively. When the [4Fe–4S] cluster is oxidized, C12 possesses an NSP of −0.22, which shifts to −0.11 (decreases in magnitude) following 1e^– reduction of the [4Fe–4S] cluster (Table 3). In both the oxidized and 1e^– reduced states, the NSP of C12 is aligned with that on Fe2, and the shift in the NSP accompanying reduction indicates that the electron density on the Fe2–Fe3 pair decreases the spin and (negative) charge transfer from C12 and C197 to the ferrous Fe2–Fe3 pair. This result is analogous to the mixed-valence Fe2–Fe3 pair in the oxidized cluster.

In the RO^HP^HE^– αββα state, there is very little spin density on HMBPP in either the oxidized or 1e^– reduced state (both having NSPs of 0.02). Consequently, nearly all of the spin density associated with the reducing electron (net-α) is localized on the [4Fe–4S] cluster and is involved in bonds to the cysteine side chains.

In the RO^HP^HE^–(ROH) βααβ 1e^– reduced state, Fe1 and Fe4 couple with lower magnitude net spins (−3.03 and −3.07, respectively, for the RO^HP^HE^– state) than Fe2 and Fe3 (+3.28 and +3.32, respectively; Table 3). Analogous to the αββα states, these NSPs indicate that Fe1 and Fe4 form a Fe²⁺–Fe²⁺ pair, whereas Fe2 and Fe3 formally correspond to a delocalized, mixed-valence pair (Fe^2.5+–Fe^2.5+). In all βααβ states, and much like the αββα states, most of the reducing net-α spin is localized on the [4Fe–4S] cluster and the coordinating thiolates (total ΔNSP = +0.98), and there is little net spin localized to HMBPP (ΔNSP = +0.01, Table 3).

Similar trends in spin density distributions, including a dependence on the net spin of Fe1, are observed for all other protonation states considered for the system that is reduced by one electron when HMBPP coordinates Fe1 through its C₄–O(H) group (Supporting Information, Table S2).

The charge distribution in the RO^HP^HE^–(ROH) βααβ state is nearly identical to that of the αββα for both the oxidized and 1e^– reduced states (Table 4). Furthermore, ESP charges on the [4Fe–4S] cluster and HMBPP are largely similar among all valence isomers for a given protonation state (RMSDs < 0.03), indicating that charge distributions have less dependence on a given valence isomer. The effects of charge transfer are directly observed, specifically, the charges on the irons, inorganic sulfides, thiolates, and ligand molecule in the RO^HP^HE^– oxidized and 1e^– reduced states. In particular, the partial charges on all Fe atoms slightly increase (i.e., become more positive) upon 1e^– reduction, whereas the inorganic sulfides, thiolates, and ligand molecule all become more negative. In the RO^HP^HE^– αββα and βααβ states, the sum of the partial charges on the Fe atoms increases by 0.21 and 0.26, respectively, whereas the sum of the partial charges on the S^2– and thiolate groups decrease (i.e., become more negative) by 1.03 and 1.08, respectively (Table 4, Δq). From these values, it is apparent that ∼0.82 e^– charge is transferred to the [4Fe–4S] cluster and its coordinating thiolates following 1e^– reduction of the cluster. The net charge of HMBPP changes less upon reduction, becoming only 0.08–0.10 e^– more negative in the RO^HP^HE^– αββα and βααβ states. The remaining difference in charge between the oxidized and reduced states is transferred to various groups that donate hydrogen bonds either to the [4Fe–4S] cluster or to the imidizolium groups of H41 and H74 that coordinate HMBPP. Consequently, we find that most of the reducing electron charge in the RO(H)-bound states is localized on the [4Fe–4S] cluster and HMBPP molecule, with large amounts of charge transfer occurring between the cluster irons and their coordinating sulfides and ligands. ESP charges obtained for the lowest-energy valence isomers of all other protonation states considered when HMBPP binds Fe1 through its C₄–OH group are presented in Supporting Information, Table S3.

3. Relative Energies of the ROH-Bound 1e^– Reduced States

To assess which protonation state is favored in the 1e^– reduced state, we apply eq 1 to obtain the relative energies of the various RO(H)-bound states considered, using both COSMO solvation with ε = 20 (DFT/COSMO) and a finite difference solution to the Poisson equation for the active-site quantum cluster embedded in the IspH protein (DFT/SCRF). The energies of the lowest-energy valence isomer for each protonation state considered along with their corresponding relative energies in the oxidized state are given in Table 5.⁵⁰ Energies for all other valence isomers considered are tabulated in the Supporting Material (Table S4).

Table 5. Relative Energies (kcal mol^–1) of the Different RO(H)-Bound States Considered in This Study When the [4Fe–4S] Is Oxidized⁵⁰ and Reduced by One Electron.

		oxidizeda		reduceda
state (charge)	qox/qred	DFT/COSMO	DFT/SCRF	DFT/COSMO	DFT/SCRF
RO–P–EH (RO–)	–3/–4	7.9	0.0	29.5	13.0
RO–PHEH (RO–)	–2/–3	0.0	2.2	16.6	10.3
ROHP–E– (ROH)	–3/–4	8.4	0.0	17.6	4.1
ROHPHE– (ROH)	–2/–3	5.3	6.1	5.8	0.0
ROHP–EH (ROH)	–2/–3	2.9	5.5	5.3	0.3
ROHPHEH (ROH)	–1/–2	0.0	13.3	0.0	4.5

^aEnergies are given relative to the lowest-energy state and are presented only for the lowest-energy valence isomer for each protonation state. The relative energies of all valence isomers are given in Supporting Information, Table S4.

Using the DFT/COSMO method, the lowest-energy 1e^– reduced state computed at pH = 7 is the RO^HP^HE^H state with a net charge (q) of −2. The RO^HP^–E^H and RO^HP^HE^– states (both q = −3) are higher in energy than the RO^HP^HE^H state by 5.3 and 5.8 kcal mol^–1, respectively. In contrast, the structure in which both the PP_i and E126 groups are deprotonated and the C₄–O(H) group is protonated (q = −4) is highly unfavorable. This so-called RO^HP^–E^– state lies 17.6 kcal mol^–1 higher in energy than the RO^HP^HE^H state. All states having HMBPP bound to Fe1 through a deprotonated C₄–O(H) group are significantly higher in energy than their ROH-bound counterparts (>15 kcal mol^–1 above the energy of the RO^HP^HE^H state, Table 5).

The RO^HP^HE^– state is lowest in energy using the DFT/SCRF method, but it is only 0.3 kcal mol^–1 lower in energy than the RO^HP^–E^H state. The proximity in energy between these isoelectric (q = −3) tautomers suggests that proton transfer between the PP_i and E126 groups is facile. The RO^HP^–E^– (q = −4) and RO^HP^HE^H (q = −2) states are higher in energy than the RO^HP^HE^– state by 4.1 and 4.5 kcal mol^–1, respectively. Similar to what is observed with the DFT/COSMO method, the RO^–P^HE^H and RO^–P^–E^H states are the highest-energy 1e^– reduced states computed with the DFT/SCRF method, which lie 10.3 and 13.0 kcal mol^–1 above the RO^HP^HE^– state, respectively.

The two lowest-energy states found using the DFT/SCRF method, namely, RO^HP^HE^–(ROH) and RO^HP^–E^H(ROH), both have a total charge of −3 and are thus more negatively charged than the active site preferentially stabilized by the DFT/COSMO method (RO^HP^HE^H, q = −2). The stabilization of 1e^– reduced states having q = −3 by the DFT/SCRF method is consistent with the results obtained for active-site models of oxidized IspH, where the RO^–P^–E^H and RO^HP^–E^– states (both having q = −3) are preferred energetically (Table 5, column 4).

4. Reduction Potentials of the C₄–OH Bound States

All reduction potentials are tabulated in Table 6 for processes where an electron is added to an oxidized state that has HMBPP bound to Fe1 through its C₄–O(H) group. It will be recalled that all reduction potentials are computed relative to the standard hydrogen electrode (ΔSHE, eq 4). Using the DFT/COSMO method, it is clear that the addition of an electron to states having a deprotonated C₄–O(H) group is very unfavorable in the absence of proton coupling, as E° = −2.39 and −2.14 V for the RO^–P^–E^H(ROH) and RO^–P^HE^H(RO^–) states, respectively (Table 6). The reduction potentials obtained with the DFT/COSMO method for the ROH-bound states are also very negative but increase (i.e., shift toward positive values) as the number of bound protons increases. For comparison, reduction of the RO^HP^–E^–(ROH) state (q = −3/–4 for oxidized/reduced states) can be achieved with a reduction potential of −1.82 V, whereas the reduction potential for the RO^HP^HE^H(ROH) state (q = −1/–2 for oxidized/reduced states) is −1.42 V. The lowest reduction potential calculated using the DFT/COSMO method is found for the RO^HP^HE^H state.

Table 6. Reduction Potentials (E°, V) Computed for RO(H)-Bound States. When Applicable, Redox Potentials Coupled to Proton Transfer (E°′, V) Are Indicated in Parentheses.

state	DFT/COSMO	DFT/SCRF
RO–P–EH(RO–)	–2.39	–1.86 (−1.29)a
RO–PHEH(RO–)	–2.14 (−1.42)	–1.64 (−1.19)c
ROHP–E–(ROH)	–1.82	–1.47 (−1.29)b
ROHPHE–(ROH)	–1.44	–1.03
ROHP–EH(ROH)	–1.52	–1.07 (−1.06)c
ROHPHEH(ROH)	–1.42	–0.91c

^aElectron transfer accompanies proton addition and a proton shift to generate the RO^HP^HE^–(ROH) 1e^– reduced state.

^bElectron transfer accompanies proton addition to generate the RO^HP^HE^H(ROH) 1e^– reduced state.

^cElectron transfer accompanies an internal proton transfer to generate the RO^HP^HE^–(ROH) 1e^– reduced state.

Using the DFT/COSMO method, we found that the RO^–P^HE^H and RO^HP^HE^H states are isoenergetic and of lowest energy when the [4Fe–4S] cluster is oxidized, whereas the RO^HP^HE^H state is the lowest-energy 1e^– reduced state. Reduction can thus occur in one of three thermodynamically equivalent processes: (1) reduction via the RO^–P^HE^H protonation state (E° = −2.14 V), followed by protonation of the C₄–O(H) group in the 1e^– reduced state (ΔE = −16.6 kcal mol^–1); (2) protonation of the C₄–O(H) group in the oxidized state that requires 1.6 kcal mol^–1, followed by reduction through the RO^HP^HE^H state (E° = −1.42 V); or (3) proton-coupled electron transfer (following eq 5), which gives an effective reduction potential of E°′ = −1.42 V (calculated from eq 6).

5

6

Regardless of the path taken, all reduction potentials calculated with the DFT/COSMO method for states having HMBPP bound to Fe1 through its C₄–O(H) group are too negative, lying outside the range expected for [4Fe–4S] ferredoxin (Fdx) proteins (−700 to −280 mV).^51,82

All reduction potentials computed in the absence of proton coupling with the DFT/SCRF method are shifted by 0.35–0.55 V in the positive direction relative to those obtained with the DFT/COSMO method (Table 6). For example, the reduction potentials obtained with DFT/SCRF for the RO^HP^–E^– and RO^HP^HE^H states are −1.47 and −0.91 V, respectively, which we can see are more positive than their analogous values of −1.82 and −1.42 V obtained with DFT/COSMO. Although the reduction potential obtained for the addition of an electron to the RO^HP^HE^H state is closer to the expected range for [4Fe–4S] Fdx proteins,^51,82 the RO^HP^HE^H state is 13.3 kcal mol^–1 above the lowest-energy RO^HP^–E^– and RO^–P^–E^H states when the [4Fe–4S] cluster is oxidized. This energy barrier, which is obtained using the DFT/SCRF method, likely prohibits reduction of the RO^HP^HE^H state. The more likely candidate for reduction in the absence of proton coupling is the RO^HP^HE^– state, which can be reached following protonation of the RO^HP^–E^– oxidized state at a cost of 6.1 kcal mol^–1 and reduction at E° = −1.03 V (Tables 5 and 6).

Since the protonation states of the lowest-energy oxidized states (i.e., RO^HP^–E^– and RO^–P^–E^H) and the lowest-energy 1e^– reduced state (i.e., RO^HP^HE^–) differ by a single proton using the DFT/SCRF method, the addition of an electron to the system may be coupled to protonation of one of the active-site residues. Starting from the RO^HP^–E^– oxidized state, coupling reduction to the protonation of the PP_i moiety (eqs 7 and 8) gives an effective reduction potential of E°′ = −1.29 V, which is positively shifted by 0.18 V relative to its uncoupled reduction potential. Alternatively, protonation of the PP_i moiety in the RO^–P^–E^H oxidized state, which requires 2.2 kcal mol^–1, can precede reduction and coupled to an internal proton transfer from E126 to the C₄–O(H) group (eqs 9 and 10, E°′ = −1.19 V).

7

8

9

10

While both the reduction potentials and effective reduction potentials that consider proton coupling indicate that reduction is more favorable when the energies used to compute the reduction potentials are calculated with the DFT/SCRF method, rather than the DFT/COSMO method, all relevant reduction potentials obtained using the DFT/SCRF method are still more negative than the typical values associated with [4Fe–4S] Fdx proteins.^51,82 This conclusion leads us to consider alternative routes for the one-electron reduction of the IspH active site.

5. Geometries of [4Fe–4S]¹⁺ IspH with HMBPP Bound via C₂ and C₃ (η²-Complex)

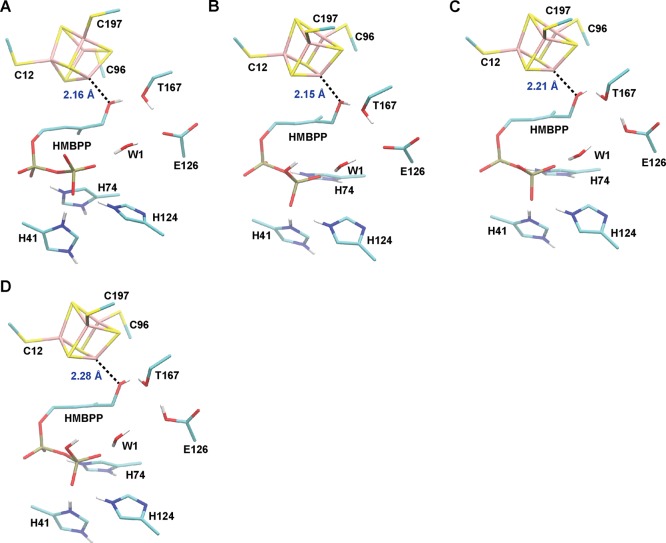
In addition to the mechanism involving RO(H)-bound intermediates in the reduction of IspH, we performed geometry optimizations of 1e^– reduced states that are consistent with the organometallic mechanism,²⁶ which have HMBPP coordinate Fe1 through its olefinic C₂ and C₃ atoms (η²-binding). The starting points for these computations are generated by rotating the C₂–C₃–C₄–OH dihedral angle (henceforth referred to as ϕ) from its C₄–O(H) bound value, which ranges from −105 to −95° in all 1e^– reduced RO(H)-bound optimized geometries, to values of either ca. +100° (Figure 4A,B) or −160° (Figure 4C,D). When ϕ ≈ +100°, the HMBPP C₄–OH group is fully rotated away from the [4Fe–4S] cluster, forming a ring conformation in which it participates in (charged) hydrogen-bond interactions with the PP_i tail of HMBPP (Figure 4A,B). This conformation is similar both to the minor species observed in the X-ray crystal structure of the [4Fe–4S] IspH:HMBPP complex after irradiation and to various [3Fe–4S] mutants in complex with HMBPP.³⁶ When ϕ ≈ −160°, the C₄–OH group is rotated under the plane of the [4Fe–4S] cluster and assumes a trans-like conformation that allows the C₄–OH group to form a hydrogen bond with the carboxylate of E126 (Figure 4C,D). Geometry optimizations of both the “ring” and “trans” η²-bound states (henceforth referred to as η²-ring and η²-trans) reveal two distinct energy minima when the C₄–O(H) group is protonated: (1) a weak complex in which the olefinic C₂ and C₃ atoms are ∼2.5–2.8 Å from Fe1, and (2) a tight coordination in which the C₂ and C₃ atom are close to Fe1 (with Fe1–C distances of ∼2.1 Å). In cases where the C₄–O(H) group is deprotonated, no local minima corresponding to η²-bound states are present.

Figure 4.

Optimized geometries of the lowest-energy η²-bound states computed with DFT/SCRF when the [4Fe–4S] cluster is 1e^– reduced. For comparison, the lowest-energy valence isomers having Fe1 net spin-α and net spin-β are considered. (A) The RO^HP^–E^H(η²-ring) ααββ state; (B) the RO^HP^–E^H(η²-ring) βααβ state; (C) the RO^HP^–E^H(η²-trans) ααββ state; (D) the RO^HP^–E^H(η²-trans) βααβ state.

To illustrate the characteristics of the computed η²-bound geometries, we use the RO^HP^–E^H protonation state as a representative case (Table 7, Figure 4), with particular consideration given to valence isomers having different net spins on Fe1. In the optimized geometry of the RO^HP^–E^H(η²-ring) ααββ valence isomer, ϕ is equal to +95.2°, which is rotated over 180° from its value when HMBPP is bound through its C₄–OH group (−101.4°, Table 7). The Fe1–O_C4 bond is broken in the η²-ring state, as the C₄–OH group is displaced >2 Å from Fe1. However, the olefinic HMBPP atoms, namely, C₂ and C₃, weakly coordinate Fe1, with Fe1–C₂/C₃ distances of ∼2.5 Å (Figure 4A). These distances suggest that the complex is stabilized mainly through weak interactions between Fe1 and the olefin, and these interactions are enhanced relative to those present in RO(H)-bound states.³⁵ With an O_C4–O_PPi distance of 2.68 Å, a charged hydrogen bond between the C₄–OH group and the HMBPP PP_i group further stabilizes the ααββ η²-ring conformation (Figure 4A, Table 7). In addition to this HMBPP intramolecular hydrogen bond, the hydrogen-bond network observed in the RO^HP^–E^H(ROH) state (Figure 3C) is largely preserved in the ααββ η²-ring state: E126 donates a hydrogen bond to T167, which directs the proton from its side chain OH group toward the cluster sulfide S3 atom (Table 7, Figure 4A). The internal geometry of the 1e^– reduced [4Fe–4S]¹⁺ cluster in the RO^HP^–E^H(η²-ring) ααββ state is quite similar to that of the RO^HP^–E^H(ROH) ααββ state, with cluster bond lengths from the two states giving an RMSD value of 0.02 Å. Despite this similarity, a superposition of the two states reveals that the position of the [4Fe–4S] cluster in the RO^HP^–E^H(η²-ring) ααββ state is shifted down toward the HMBPP olefin group relative to its position in the RO^HP^–E^H(ROH) ααββ state (Supporting Information, Figure S1). In other words, the position of HMBPP in the RO^HP^–E^H(ROH) ααββ state is largely unchanged from that in the RO^HP^–E^H(η²-ring) ααββ state. For the η² interaction to exist, the [4Fe–4S] cluster must translate toward HMBPP to bring Fe1 in proximity of the olefin (Figure S1).

Table 7. A Comparison of Key Bond Lengths (Å) and Angles (deg) between the ROH- and η²-Bound Structures in the 1e^– Reduced RO^HP^–E^H State.

binding mode	ROH		η2-ring		η2-trans
valence isomer	ααββ	βααβ	ααββ	βααβ	ααββ	βααβ
cluster bond lengths
Fe1–S1	2.282	2.245	2.307	2.285	2.309	2.289
Fe1–S2	2.279	2.267	2.284	2.291	2.279	2.299
Fe1–S3	2.229	2.324	2.241	2.384	2.238	2.375
Fe2–S1	2.336	2.333	2.330	2.316	2.332	2.321
Fe2–S2	2.298	2.213	2.302	2.194	2.307	2.200
Fe2–S4	2.283	2.395	2.270	2.373	2.277	2.370
Fe3–S1	2.260	2.328	2.248	2.311	2.250	2.313
Fe3–S3	2.312	2.258	2.340	2.271	2.331	2.259
Fe3–S4	2.368	2.382	2.362	2.367	2.364	2.366
Fe4–S2	2.272	2.321	2.270	2.312	2.273	2.316
Fe4–S3	2.314	2.307	2.332	2.307	2.327	2.302
Fe4–S4	2.339	2.301	2.343	2.246	2.343	2.252
Fe2–SC13	2.335	2.309	2.310	2.285	2.314	2.292
Fe3–SC197	2.297	2.330	2.300	2.364	2.302	2.356
Fe4–SC96	2.337	2.356	2.295	2.314	2.297	2.315
HMBPP bond lengths
Fe1–OC4	2.340	2.257	4.552	4.287	3.751	3.593
Fe1–C3	3.363	3.304	2.541	2.144	2.615	2.143
Fe1–C2	3.603	3.573	2.496	2.118	2.531	2.112
H-bond lengths
OC4–OT167	3.178	3.174	4.397	4.384	3.424	3.370
OT167–OE126	2.653	2.649	2.693	2.687	2.655	2.634
OE126–OW1	3.686	3.677	3.733	3.598	3.687	3.633
OW1–OPPi	2.730	2.734	2.782	2.774	2.732	2.723
OC4–OE126	4.156	4.154	3.620	3.621	3.149	3.137
OC4–OPPi	4.838	4.852	2.683	2.722	4.541	4.593
HMBPP angle
C2–C3–C4–OC4	–101.4	–101.9	95.2	90.3	–154.8	–158.4

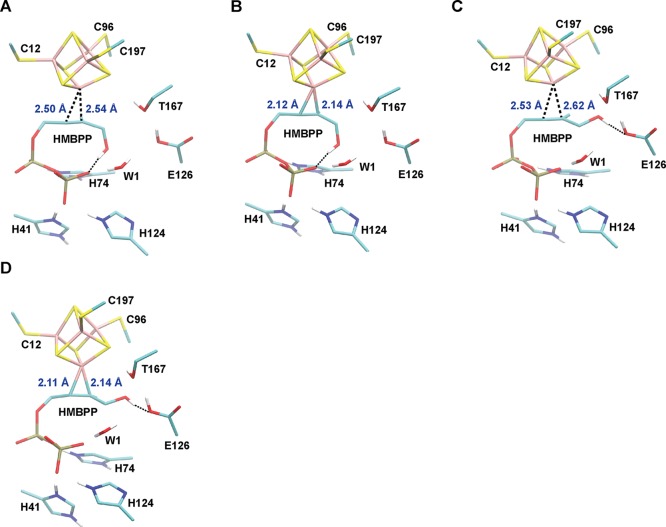
The orientation of HMBPP in the IspH active site observed in the RO^HP^–E^H(η²-ring) βααβ state is largely similar to that observed in the ααββ valence isomer, although the olefinic C₂ and C₃ atoms bind Fe1 more tightly in the βααβ valence isomer (with respective bond lengths of 2.12 and 2.14 Å). Relative to the RO^HP^–E^H(ROH) βααβ state, the geometry of the [4Fe–4S] cluster in the RO^HP^–E^H(η²-ring) state is distorted at Fe1: all Fe1–S^2– distances are elongated 0.03 to 0.06 Å (Table 7). In particular, the Fe1–S3 bond is lengthened in the RO^HP^–E^H(η²-ring) βααβ state (2.38 Å) compared with its ROH-bound counterpart (2.32 Å). This distortion of the [4Fe–4S] cluster allows for a closer interaction between Fe1 and C2/C3, as well as better interaction between the −OH group of T167 and the cluster sulfide S3. Distances between hydrogen bond partners in the RO^HP^–E^H(η²-ring) βααβ state are nearly identical to those in the RO^HP^–E^H(η²-ring) ααββ state; consequently, the “tight” and “loose” η²-complexes observed in these respective states appear to differ only in the position of the [4Fe–4S] cluster and in the local environment of the Fe1–C₂/C₃ bonds.

In geometry-optimized η²-trans states, the HMBPP C₄–OH group is rotated under the plane of the [4Fe–4S]¹⁺ cluster (Figure 4C,D). This η²-trans conformation involves a rotation of ϕ by ca. −50° from its ROH-bound value to give ϕ = −154.8° and −158.4° in the RO^HP^–E^H(η²-ring) ααββ and βααβ states, respectively. In η²-trans states, the C₄–OH group does not accept a hydrogen bond from T167 as is observed in the ROH-bound state; instead, T167 forms a hydrogen bond with the carboxylate of E126 (O_C4–O_E126 distance of ∼3.15 Å, Table 7). Similar to the RO^HP^–E^H(η²-ring) ααββ state, the C₂ and C₃ atoms form a weak van der Waals complex with Fe1 in the RO^HP^–E^H(η²-trans) ααββ valence isomer (Fe1–C2/C3 distance of ∼2.55 Å). Alternatively, the olefinic HMBPP atoms in the RO^HP^–E^H(η²-trans) βααβ state tightly coordinate Fe1 (Fe–C distances of ∼2.1 Å), which is similar to what is observed in the RO^HP^–E^H(η²-ring) βααβ state (Table 7).

Although our discussion has focused on the RO^HP^–E^H state as a representative protonation state, similar η²-ring and η²-trans geometries are also observed for the RO^HP^HE^H protonation state (Supporting Information). We note that η²-bound states having a deprotonated E126 group are significantly higher in energy than their protonated counterparts; for this reason, we omit them from further discussion.

6. Distribution of Charge and Spin in [4Fe–4S]¹⁺ IspH with HMBPP η²-Complex

From the geometric data obtained for the η²-bound states, it is apparent that two possible orientations of the C₂–C₃–C₄–OH dihedral angle exist: η²-ring and η²-trans. The strength of Fe1–C₂/C₃ coordination, however, depends only on the spin isomer considered and is independent of whether the geometry is η²-ring or η²-trans. An inspection of the Mulliken spin populations on the Fe atoms in these different η²-bound states shows that there is correlation between the alignment of the net spin on Fe1 and the Fe1–C₂/C₃ distances. Specifically, when the net spin on Fe1 is aligned with the system net spin S_Tot = +1/2, as is the case with the ααββ and αββα valence isomers, the observed η²-bound geometries have elongated Fe₁–C₂/C₃ distances. In contrast, when Fe1 possesses a net spin-β and is thus aligned opposite to S_Tot (e.g., the βααβ and βαβα valence isomers), the Fe₁–C₂/C₃ distances are much shorter (Table 7).

We consider the RO^HP^–E^H states as representative cases for comparing the NSPs and partial charges in the η²-ring and ROH-bound states following reduction (Tables 8 and 9). Specifically, we track the dependence of these electronic properties on the net spin of Fe1 by considering the αββα and βααβ states. In the RO^HP^–E^H(η²-ring) αββα state, Fe1 possesses a net spin-α. This Fe atom has an NSP of +3.17 and couples with Fe4 (NSP = +3.30) to form a delocalized, mixed-valence (Fe ^2.5+ −Fe ^2.5+) pair. The Fe2–Fe3 spin pair carries reduced (in magnitude) NSPs of −3.00 and −2.88, which are characteristic of a ferrous pair (Table 8). From summing the NSPs of the Fe atoms in the RO^HP^–E ^H(η²-ring) αββα state, it is evident that most of the system’s net spin falls on the [4Fe–4S] cluster iron atoms (+0.59). Significant spin density is also found on the cluster sulfides (+0.44) and thiolates (−0.07). Similar to what is observed in the ROH-bound states, however, there is little spin density found on HMBPP (+0.02, Table 8).

Table 8. NSPs Given for Atoms in the [4Fe–4S] Cluster, Its Coordinating Thiolates, and HMBPP from Two Representative Valence Isomers of the RO^HP^–E^H(η²-ring) State When the [4Fe–4S] Cluster Reduced by One Electron Compared with the NSPs from the Same Valence Isomers in the RO^HP^–E^H(ROH) State When the [4Fe–4S] Cluster Is Oxidized.

	ROHP–EH
	αββα			βααβ
	ox (ROH)	red (η2-ring)	ΔNSPa	ox (ROH)	red (η2-ring)	ΔNSPa
FE1	3.205	3.173	–0.032	–3.206	–2.879	0.327
FE2	–3.175	–3.000	0.175	3.174	3.204	0.030
FE3	–3.197	–2.880	0.317	3.195	3.328	0.132
FE4	3.222	3.297	0.075	–3.222	–3.194	0.029
sum	0.055	0.590	0.535	–0.059	0.459	0.519
S1	–0.013	0.050	0.062	0.014	0.218	0.204
S2	0.086	0.160	0.074	–0.085	–0.036	0.049
S3	0.101	0.220	0.119	–0.101	–0.022	0.079
S4	–0.037	0.014	0.052	0.038	0.048	0.009
sum	0.137	0.443	0.306	–0.133	0.208	0.341
C12	–0.233	–0.119	0.114	0.233	0.187	–0.046
C96	0.207	0.143	–0.064	–0.207	–0.145	0.062
C197	–0.185	–0.092	0.093	0.185	0.137	–0.048
sum	–0.211	–0.068	0.143	0.212	0.179	–0.033
total cluster	–0.019	0.965	0.984	0.019	0.846	0.827
OC4	0.013	0.006	–0.007	–0.013	0.003	0.015
C3	0.002	0.011	0.008	–0.002	0.055	0.058
C2	0.000	0.001	0.001	0.000	0.109	0.109
total HMBPP	0.019	0.020	0.001	–0.019	0.155	0.174
cluster + HMBPP	–0.001	0.985	0.985	0.000	1.000	1.001

^aThe difference in NSP (ΔNSP) between the oxidized and 1e^– reduced atoms is indicated.

Table 9. ESP Charges Given for Atoms in the [4Fe–4S] Cluster, Its Coordinating Thiolates, and HMBPP from Two Representative Valence Isomers of the RO^HP^–E^H(η²-ring) State When the [4Fe–4S] Cluster Reduced by One Electron Compared with the Charges from the Same Valence Isomers in the RO^HP^–E^H(ROH) State When the [4Fe–4S] Cluster Is Oxidized⁵⁰.

	ROHP–EH
	αββα			βααβ
	ox	red (η2-ring)	Δqa	ox	red (η2-ring)	Δqa
FE1	0.404	0.373	–0.030	0.404	0.307	–0.097
FE2	0.490	0.533	0.043	0.491	0.512	0.021
FE3	0.599	0.645	0.045	0.599	0.692	0.093
FE4	0.477	0.515	0.038	0.477	0.494	0.018
sum	1.969	2.065	0.096	1.970	2.005	0.035
S1	–0.440	–0.583	–0.143	–0.440	–0.592	–0.152
S2	–0.302	–0.328	–0.026	–0.302	–0.267	0.035
S3	–0.412	–0.597	–0.186	–0.412	–0.570	–0.158
S4	–0.600	–0.740	–0.140	–0.600	–0.691	–0.091
sum	–1.753	–2.248	–0.495	–1.754	–2.119	–0.365
C12	–0.267	–0.396	–0.129	–0.268	–0.346	–0.078
C96	–0.332	–0.434	–0.102	–0.332	–0.398	–0.066
C197	–0.393	–0.486	–0.093	–0.393	–0.460	–0.068
sum	–0.993	–1.316	–0.324	–0.993	–1.205	–0.212
total cluster	–0.777	–1.499	–0.723	–0.777	–1.319	–0.542
OC4	–0.119	–0.309	–0.189	–0.119	–0.328	–0.209
C3	–0.036	–0.016	0.020	–0.035	–0.038	–0.003
C2	–0.142	0.049	0.191	–0.142	0.068	0.210
total HMBPP	–0.430	–0.636	–0.205	–0.430	–0.784	–0.354
cluster + HMBPP	–1.207	–2.135	–0.928	–1.207	–2.103	–0.896

^aThe difference in charge (Δq) between the oxidized and 1e^– reduced atoms is indicated.

From a direct comparison between the NSPs computed for the oxidized RO^HP^–E^H(ROH) αββα state and the 1e^– reduced RO^HP^–E^H(η²-ring) αββα state (ΔNSP, Table 8), it is clear that the reducing electron is almost entirely localized on the [4Fe–4S] cluster and its coordinating thiolates (ΔNSP ≈ 0.98) and not on HMBPP (ΔNSP < 0.01).

The distribution of spin densities in the 1e^– reduced RO^HP^–E^H(η²-ring) βααβ state differs from the αββα valence isomer in the amount of spin density localized on the [4Fe–4S] cluster and HMBPP. In the 1e^– reduced RO^HP^–E^H(η²-ring) βααβ state, Fe2 and Fe3 couple with NSPs that are larger in magnitude (+3.20 and +3.33, respectively) than either member of the Fe1–Fe4 spin-coupled ferrous pair (−2.88 and −3.19, respectively). The NSPs summed over all iron atoms is +0.46, which is ∼0.1 less than what is observed for the αββα state (Table 8). Spin density found on the cluster sulfides (+0.21) and thiolates (+0.18) in the βααβ valence isomer do not compensate for the lower spin density found on the iron atoms relative to what is observed in the αββα valence isomer. Instead, HMBPP has a total NSP of 0.16 in the RO^HP^–E^H(η²-ring) βααβ state, which is indicative of majority (α) spin transfer from the [4Fe–4S] cluster to HMBPP. This spin, which is parallel to the system net spin (S_Tot = +1/2) but opposite to the net spin on Fe1 (β), is largely localized on the olefinic C₂ and C₃ atoms (+0.11 and +0.06, respectively; Table 8).

The greater net spin density found on HMBPP in the βααβ valence isomer is also accompanied by higher negative charge localized on HMBPP (Table 9). In the 1e^– reduced RO^HP^–E^H(η²-ring) αββα and βααβ states, the total charge summed over the [4Fe–4S] cluster, its coordinating thiolates and HMBPP are nearly equivalent (−2.14 and −2.10, respectively, Table 9). However, the distribution of charge on these different groups depends on the valence isomer. For example, the charge on the [4Fe–4S] cluster and its coordinating thiolates is −1.50 in the αββα isomer, whereas the charge on HMBPP is −0.64 (Table 9). In contrast, the βααβ isomer possesses less negative charge on its [4Fe–4S] cluster and coordinating thiolates (q = −1.32); however, significantly more charge is found on the HMBPP ligand (q = −0.78, Table 9).

Combining the geometric analyses of 1e^– reduced RO^HP^–E^H(η²-ring) states with a tabulation of their NSPs and ESP charge distributions, it is clear that the alignment of the net spin on Fe1 correlates with the type of coordination of HMBPP and the amount of spin and charge transfer from the [4Fe–4S] cluster to the ligand. When the net spin of Fe1 (α) is aligned with the total spin of the system (α), the HMBPP olefin coordinates Fe1 loosely, and very little spin density is transferred to HMBPP. In contrast, when the net spin of Fe1 (β) is aligned opposite the system net spin (α), the HMBPP olefin forms a tight, metallacycle complex with Fe1 and significant α spin density, and relatively more charge is transferred to HMBPP. Similar trends in geometry, NSPs, and charge distributions are observed for the RO^HP^HE^H protonation state and η² -trans states (Supporting Information, Tables S6 and S7).

7. Relative Energies of the η²-Bound 1e^– Reduced States

The relative energies of the different η²-bound states in the 1e^– reduced state are computed to further understand differences between the tightly-bound complexes found when Fe1 possesses a net spin-β (e.g., the βααβ valence isomer) and the loosely-bound complexes found when Fe1 possesses a net spin-α (e.g., the ααββ valence isomer). Considering only the lowest-energy valence isomers having Fe1 with either net spin-α or net spin-β, we examine the relative energies of the 1e^– reduced RO^HP^–E^H(η²-ring) state. Using the DFT/COSMO method, the βααβ valence isomer is 7.8 kcal mol^–1 lower in energy than the ααββ state (Supporting Information, Table S8). Similarly, using the DFT/SCRF method, the RO^HP^–E^H(η²-ring) βααβ state is 8.8 kcal mol^–1 lower than the ααββ valence isomer. Indeed, regardless of protonation and type of η² coordination, all η²-bound states having Fe1 net spin-β are 7–14 kcal mol^–1 lower in energy than states with net spin-α on Fe1 (Table S8). From these results, it is apparent that the tightly-bound metallacycle complexes formed when Fe1 is net spin-β are preferred energetically over complexes with Fe1 having net spin-α that are stabilized predominantly through van der Waals interactions.

The energies of all computed η²-bound states are further compared to the energies of RO^–- and ROH-bound states to determine which conformations of HMBPP are preferred when the [4Fe–4S] cluster is reduced by one electron (Table 10, Figure 5). We note that all relative energies discussed here are given only for the lowest-energy valence isomers computed for each protonation state and binding mode; a complete tabulation of the relative energies of all valence isomers considered can be found in Supporting Information, Table S9.

Table 10. Relative Energies (kcal mol^–1) of Different RO(H)- and η²-Bound States in Both the Oxidized and 1e^– Reduced States.

		oxidizeda		reduceda
state (charge)	q	DFT/COSMO	DFT/SCRF	DFT/COSMO	DFT/SCRF
RO–P–EH(RO–)	–3/–4	7.9	0.0	29.5	13.0
RO–PHEH(RO–)	–2/–3	0.0	2.2	16.6	10.3
ROHP–E–(ROH)	–3/–4	8.4	0.0	17.6	4.1
ROHPHE–(ROH)	–2/–3	5.3	6.1	5.8	0.0
ROHP–EH(ROH)	–2/–3	2.9	5.5	5.3	0.3
ROHPHEH(ROH)	–1/–2	0.0	13.3	0.0	4.5
ROHP–EH(η2-ring)	–2/–3	5.4	6.0	0.7	–5.7
ROHPHEH(η2-ring)	–1/–2	6.7	19.3	–10.3	–3.4
ROHP–EH(η2-trans)	–2/–3	11.6	14.1	6.4	1.5
ROHPHEH(η2-trans)	–1/–2	6.2	19.6	–1.5	3.6

^aEnergies are given relative to the lowest-energy RO(H)-bound state.

Figure 5.

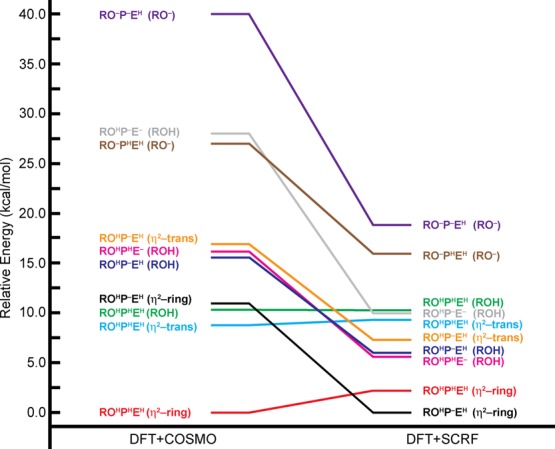
Relative energies (kcal mol^–1) of different RO(H)- and η²-bound 1e^– reduced states. Energies are given relative to the lowest-energy state.

With the DFT/COSMO method, the RO^HP^HE^H (η²-ring) state is the lowest-energy η²-bound state when the [4Fe–4S] cluster is 1e^– reduced. The energies of the isoelectric RO^HP^HE^H (η²-ring) and RO^HP^HE^H (η²-trans) states are both lower than that of the lowest-energy RO(H)-bound state (i.e., RO^HP^HE^H) by 10.3 and 1.5 kcal mol^–1, respectively (Table 10). In contrast, we find the RO^HP^–E^H(η²-ring) and RO^HP^HE^H (η²-ring) states to be the lowest-energy 1e^– reduced states computed using the DFT/SCRF method, with energies that are, respectively, 5.7 and 3.4 kcal mol^–1, lower than the lowest-energy RO(H)-bound state RO^HP^HE^–(ROH). In the DFT/SCRF computations, the η²-trans states are disfavored energetically, as the energies of the RO^HP^–E^H (η²-trans) and RO^HP^HE^H (η²-trans) states are, respectively, 1.5 and 3.6 kcal mol^–1 higher than the energies of the RO^HP^HE^–(ROH) state (Table 10, Figure 5).

Relative energies obtained using both the DFT/COSMO and DFT/SCRF methods thus indicate that η²-ring states are preferred over all RO(H)-bound geometries when the [4Fe–4S] cluster is 1e^– reduced. Similar to what was observed with the RO(H)-bound states, we find the relative energies of η²-bound states depend on the method used to calculate the energy and the charge in the active site: the RO^HP^HE^H (η²-ring) state, which has a charge of −2, is preferentially stabilized with the DFT/COSMO method, whereas the RO^HP^–E^H(η²-ring) state, which has a charge of −3, is the lowest-energy state when using the DFT/SCRF method.

8. Barrier to Rotation of the C₄–OH Group in the 1e^– Reduced State

Clearly, η²-bound states are lower in energy than all RO(H)-bound states upon 1e^–reduction of the [4Fe–4S] cluster. However, it is unclear from our computations whether these η²-bound states are catalytically relevant. More specifically, it is possible that η²-bound states may not be accessible from ROH-bound states, despite being lower in energy. To search for rotational barriers that would prevent an ROH-bound HMBPP structure from accessing η²-type geometries, we perform linear transit (LT) computations in the 1e^– reduced state along the C₂–C₃–C₄–OH dihedral angle (ϕ), which distinguishes HMBPP geometries in ROH- and η²-bound states.

LT computations are performed on the RO^HP^–E^H βααβ state since it is the lowest-energy η²-bound state computed with the DFT/SCRF method. Two different starting points are used to conduct the LT computations: (1) starting from the ROH-bound conformation with ϕ set to −100°, which is its approximate value in ROH-bound states; (2) starting from an η²-ring conformation with ϕ set to +100°. From these starting points, the transit is stepped in 20° increments forward and backward to complete the full range of the torsion. Geometry optimizations are performed along ϕ, from which energies are obtained using both the DFT/COSMO and DFT/SCRF methodologies (Figure 6A,B).

Figure 6.

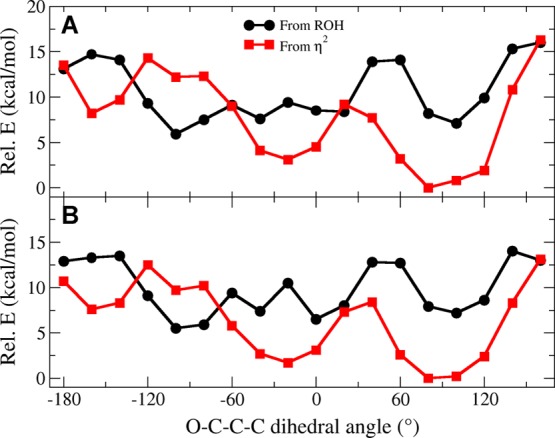
Linear transit computations performed along ϕ in the 1e^– reduced state starting from an ROH-bound geometry (black) and an η²-ring geometry (red). Energies (kcal mol^–1) are obtained using the DFT/COSMO (A) and DFT/SCRF (B) methods.

Starting with the DFT/COSMO results, we observe two different behaviors in the LT curves given in Figure 6A. When initiated from the ROH-bound state at ϕ = −100° (Figure 6A, black curve), the system increases in energy when ϕ is distorted from its approximate ROH-bound value. HMBPP remains attached to Fe1 via its C₄–OH group in the range of −120° ≤ ϕ ≤ −40°. When ϕ < −120°, HMBPP adopts its η²-trans conformation, although the geometries obtained in the LT computation contain little interaction between Fe1 and the olefinic carbons, with Fe–C₂/C₃ distances of 3.3–3.5 Å. Similarly, only weakly-bound η²-ring conformations are found at values of ϕ > −40°, with similarly elongated Fe–C₂/C₃ distances. The only local minimum corresponding to an η²-bound conformation is found at ϕ = +100°, although neither this state nor the LT state obtained near the η²-trans value of ϕ (ca. −160°) are lower in energy than the ROH-bound states found along the LT.

LT computations performed starting from the geometry-optimized η²-ring state (Figure 6A, red curve) permits computation of η²-bound states along the full ϕ reaction coordinate. In these calculations, the state computed at ϕ = +80° represents a tightly-bound η²-complex with Fe–C₂/C₃ distances of ∼2.1 Å. This structure is the global minimum among all LT states computed with the DFT/COSMO method.

Combining the LTs initialized from the ROH-bound (Figure 6A, black curve) and η²-ring (Figure 6A, red curve) states, we consider the relative energies of transitioning from an ROH-bound conformation to an η²-ring complex. Starting from the ROH-bound conformation at ϕ = −100°, the system moves along the black, ROH-bound curve until ϕ = −60°. At this value of ϕ, the orientation of HMBPP switches to an η²-type coordination of Fe1 and the system propagates along the red curve until it reaches the global minimum η²-ring state at ϕ = +80°. From these LT curves, the barrier to transition from the ROH-bound state to the η²-ring state is approximately the energy required to travel along the black curve from ϕ = −100° to ϕ = −60°. From Figure 6A, this energy barrier is ∼3 kcal mol^–1 when using the DFT/COSMO method.

From DFT/SCRF computations performed on the optimized geometries obtained along the LT paths, we obtain slightly different energies along ϕ (Figure 6B). Qualitatively, however, these DFT/SCRF LT curves are similar to those obtained using the DFT/COSMO method. The energy required to transition from the ROH-bound state to the η²-ring state can be approximated as the difference in energy between the ROH-bound state at ϕ = −100° and the point at which the black and red curves in Figure 6B intersect. This approximation gives a rotational barrier of ∼2 kcal mol^–1. Consequently, both DFT/COSMO and DFT/SCRF methods predict a small barrier that connects the ROH- and η²-ring states.

9. Geometries of [4Fe–4S]²⁺ IspH with HMBPP Bound via C₂ and C₃ (η²-Complex)

In previous sections, we obtained reduction potentials for the one-electron reduction of RO(H)-bound states (−1.4 to −1.0 V) that are more negative than the reduction potentials expected for [4Fe–4S] Fdx proteins.^51,82 Additionally, we have located η²-bound structures in the 1e^– reduced state that are both lower in energy than ROH-bound states and accessible from these states. Building on these findings, we entertain the hypothesis that the orientation of HMBPP switches from ROH- to η²-binding in the oxidized state to facilitate the 1e^– reduction of the [4Fe–4S] cluster. Using the η²-bound geometries computed in the 1e^– reduced state as a starting point, we perform geometry optimizations of oxidized active-site clusters with the C₄–OH group rotated away from Fe1. Our discussion of these states focuses on η²-ring states since they are lower in energy when the [4Fe–4S] cluster is 1e^– reduced; however, analyses of oxidized η²-trans states are provided in the Supporting Information.

Regardless of valence isomerism, all oxidized η²-ring states have elongated Fe1–C₂/C₃ distances (Table 11). We are unable to obtain tightly-bound η² complexes like those observed in the βααβ η²-bound valence isomers when the [4Fe–4S] cluster is 1e^– reduced, even when the geometry optimizations are initialized from these states. Giving consideration to the lowest-energy states having Fe1 either net spin-α or net spin-β, we find that both the αββα and βααβ RO^HP^–E^H(η²-ring) oxidized states have Fe1–C ₂/C₃ distances of ∼2.6 Å (Table 11, Figure 7). Indeed, these two states are structurally similar (with an RMSD of 0.02 Å), and both maintain the network of hydrogen bonds observed in the 1 e^– reduced η²-ring states (Table 11, Figure 7). For instance, the distance between the O_C4 and O_PPi atoms in both the oxidized and 1e^– reduced η²-ring states is ∼2.70 Å, indicating that the intramolecular hydrogen bond stabilizing the HMBPP ring conformation is not disrupted between the two oxidation states considered.

Table 11. A Comparison of Key Bond Lengths (Å) and Angles (deg) between the ROH- and η²-ring Structures in Both the Oxidized and 1e^– Reduced RO^HP^–E^H States.

	oxidized				reduced
binding mode	ROH	ROH	η2-ring		η2-ring
valence isomer	αββα	βααβ	αββα	βααβ	αββα	βααβ
cluster bond lengths
Fe1–S5	2.200	2.200	2.197	2.197	2.207	2.285
Fe1–S6	2.282	2.282	2.277	2.278	2.298	2.291
Fe1–S7	2.319	2.319	2.304	2.304	2.308	2.384
Fe2–S5	2.328	2.328	2.305	2.304	2.302	2.316
Fe2–S6	2.206	2.206	2.193	2.192	2.225	2.194
Fe2–S8	2.357	2.357	2.358	2.360	2.361	2.373
Fe3–S5	2.305	2.305	2.300	2.300	2.285	2.311
Fe3–S7	2.240	2.240	2.265	2.267	2.320	2.271
Fe3–S8	2.361	2.361	2.350	2.349	2.344	2.367
Fe4–S6	2.326	2.326	2.309	2.310	2.318	2.312
Fe4–S7	2.322	2.322	2.325	2.324	2.343	2.307
Fe4–S8	2.241	2.241	2.229	2.230	2.256	2.246
Fe2–SC12	2.256	2.256	2.241	2.238	2.290	2.285
Fe3–SC197	2.275	2.275	2.285	2.284	2.281	2.364
Fe4–SC96	2.295	2.295	2.279	2.279	2.338	2.314
HMBPP bond lengths
Fe1–OC4	2.214	2.214	4.514	4.516	4.525	4.287
Fe1–C3	3.531	3.531	2.603	2.604	2.552	2.144
Fe1–C2	3.272	3.272	2.571	2.569	2.485	2.118
H-bond lengths
OC4–OT167	3.189	3.189	4.334	4.342	4.380	4.384
OT167–OE126	2.661	2.661	2.700	2.702	2.684	2.687
OE126–OW1	3.687	3.688	3.703	3.685	3.717	3.598
OW1–OPPi	2.734	2.734	2.794	2.793	2.786	2.774
OC4–OE126	4.209	4.209	3.629	3.641	3.590	3.621
OC4–OPPi	4.875	4.875	2.695	2.695	2.703	2.722
HMBPP angle
C2–C3–C4–OC4	–101.5	–101.5	95.4	95.7	94.1	90.3

Figure 7.

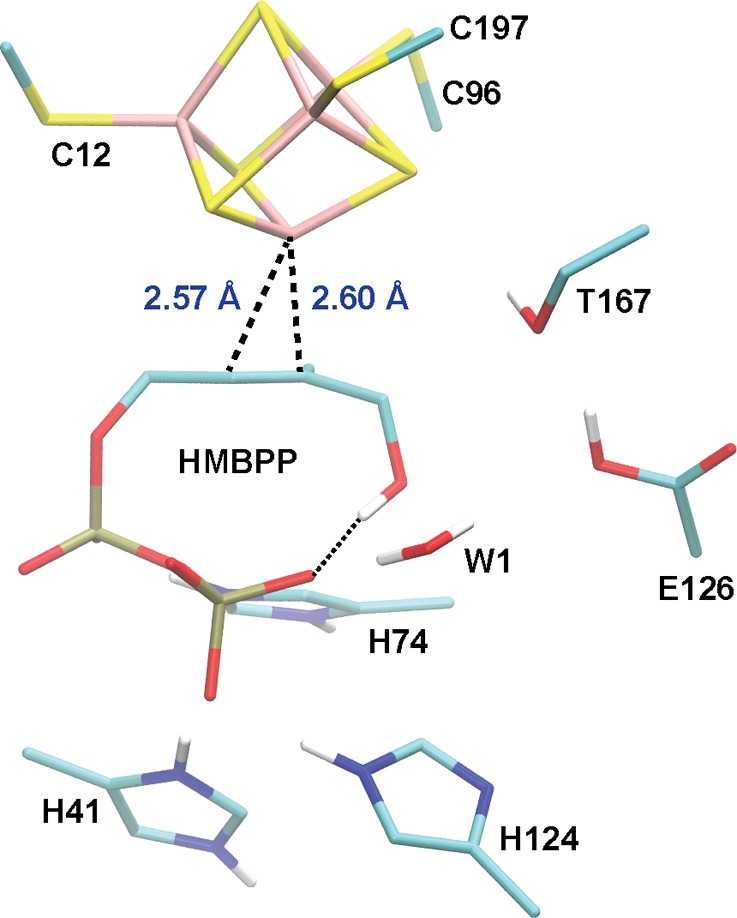
Optimized geometry of the lowest-energy η²-ring state, RO^HP^–E^H(η²-ring), when the [4Fe–4S] cluster is oxidized.

Further, comparing the oxidized η²-ring complexes to their 1e^– reduced equivalents, we observe high similarity between the oxidized complexes and the αββα 1e^– reduced state (Table 11). In the case of the RO^HP^–E^H(η²-ring) αββα valence isomer, the geometries obtained in the oxidized and 1e^– reduced states show an RMSD of only 0.08 Å. From these geometric data, it is apparent that the olefinic carbons of HMBPP can only weakly interact with Fe1 when the [4Fe–4S] cluster is oxidized. Upon 1e^– reduction, however, the olefin coordination to Fe1 can either remain elongated, as in the αββα and ααββ states, or can form a more tightly-bound complex when Fe1 is net spin-β (Table 11).

10. Distribution of Spin and Charge in η²-Bound Oxidized States

The NSPs obtained in the oxidized and 1e^– reduced states for representative valence isomers of the RO^HP^–E^H(η²-ring) state are given in Table 12. In the RO^HP^–E ^H(η²-ring) αββα oxidized state, the NSPs on the Fe atoms are similar in magnitude, which precludes an assignment of the spin-coupled ferric/ferrous and delocalized, mixed-valence pairs. Summing the spins on these Fe atoms reveals that the total NSP of ∼0.05 is localized on the Fe atoms (Table 12). Taking into account the spin densities that reside on the cluster sulfides and thiolates from the Fe atoms, we obtain a total NSP of −0.03 on the full cluster. Equal to and opposite to the spin density localized on the cluster, we find a total NSP of +0.03 on HMBPP, with individual NSPs of ca. +0.01 on each of the olefinic carbons and O_C4 (Table 12). When comparing oxidized and 1e^– reduced RO^HP^–E^H(η²-ring) αββα states, we find the reducing electron spin density falls almost entirely on the [4Fe–4S] cluster and its coordinating thiolates (summed ΔNSP of 0.99), with very little spin density transferred to the HMBPP ligand (NSP ≈ −0.01, Table 12).

Table 12. NSPs Given for Atoms in the [4Fe–4S] Cluster, Its Coordinating Thiolates, and HMBPP from Two Representative Valence Isomers of the RO^HP^–E^H(η²-ring) State When the [4Fe–4S] Cluster Is Oxidized and Reduced by One Electron.

	ROHP–EH
	αββα			βααβ
	ox (η2-ring)	red (η2-ring)	ΔNSPa	ox (η2-ring)	red (η2-ring)	ΔNSPa
FE1	3.146	3.173	0.028	–3.145	–2.879	0.266
FE2	–3.106	–3.000	0.105	3.104	3.204	0.100
FE3	–3.193	–2.880	0.313	3.190	3.328	0.137
FE4	3.198	3.297	0.099	–3.199	–3.194	0.005
sum	0.045	0.590	0.545	–0.049	0.459	0.509
S1	–0.006	0.050	0.055	0.008	0.218	0.210
S2	0.063	0.160	0.096	–0.062	–0.036	0.026
S3	0.102	0.220	0.118	–0.104	–0.022	0.082
S4	–0.029	0.014	0.043	0.030	0.048	0.017
sum	0.130	0.443	0.313	–0.127	0.208	0.335
C12	–0.239	–0.119	0.119	0.240	0.187	–0.053
C96	0.216	0.143	–0.073	–0.215	–0.145	0.070
C197	–0.181	–0.092	0.089	0.181	0.137	–0.045
sum	–0.204	–0.068	0.136	0.206	0.179	–0.027
total cluster	–0.029	0.965	0.994	0.029	0.846	0.816
OC4	0.007	0.006	–0.001	–0.007	0.003	0.009
C3	0.010	0.011	0.000	–0.011	0.055	0.066
C2	0.007	0.001	–0.006	–0.006	0.109	0.115
total HMBPP	0.026	0.020	–0.006	–0.025	0.155	0.180
cluster + HMBPP	–0.004	0.985	0.988	0.004	1.000	0.996

^aThe difference in NSP (ΔNSP) between the oxidized and 1e^– reduced atoms is indicated.

Similar to the αββα valence isomer, the summed NSP localized on the [4Fe–4S] cluster and its coordinating thiolates in the RO^HP^–E^H(η²-ring) βααβ oxidized state is equal to +0.03; the NSP localized to HMBPP in this state is equal to −0.03 (Table 12). From these data, it is clear that there is very little transfer of spin density from the [4Fe–4S] cluster to HMBPP when the system is oxidized. In contrast, upon 1e^– reduction of the RO^HP^–E^H(η²-ring) βααβ state, significant NSP (0.18) is transferred to HMBPP and, specifically, onto the olefinic carbons C₂ and C₃ (ΔNSP = 0.12 and 0.07, respectively; Table 12).

The different electronic properties of the valence isomers considered are further magnified when the ESP charge distributions following reduction of the η²-bound complexes are considered. In both the oxidized RO^HP^–E^H(η²-ring) αββα and βααβ states and the 1e^– reduced RO^HP^–E^H(η²-ring) αββα state, the total charge obtained for the HMBPP molecule is ca. −0.65 e^– (Table 13). In contrast, HMBPP has a total charge of ∼ −0.78 in the 1e^– reduced RO^HP^–E^H(η²-ring) βααβ state. From these trends, it is clear that the electronic properties of HMBPP in oxidized η²-ring states are similar to those of valence isomers in 1e^– reduced η²-ring states having Fe1 net spin-α. Differing from these states, the 1e^– reduced RO^HP^–E^H(η²-ring) βααβ state prefers tight coordination of Fe1 by the olefinic carbons and, consequently, contains greater transfer of spin and charge from the [4Fe–4S] cluster to HMBPP.

Table 13. ESP Charge Distributions Given for Atoms in the [4Fe–4S] Cluster, Its Coordinating Thiolates, and HMBPP from Two Representative Valence Isomers of the RO^HP^–E^H(η²-ring) State When the [4Fe–4S] Cluster Is Oxidized and Reduced by One Electron.

	ROHP–EH
	αββα			βααβ
	ox (η2-ring)	red (η2-ring)	Δqa	ox (η2-ring)	red (η2-ring)	Δqa
FE1	0.386	0.373	–0.012	0.387	0.307	–0.080
FE2	0.464	0.533	0.068	0.459	0.512	0.053
FE3	0.621	0.645	0.023	0.618	0.692	0.074
FE4	0.459	0.515	0.056	0.455	0.494	0.040
sum	1.930	2.065	0.135	1.919	2.005	0.087
S1	–0.458	–0.583	–0.125	–0.458	–0.592	–0.133
S2	–0.268	–0.328	–0.060	–0.268	–0.267	0.001
S3	–0.448	–0.597	–0.149	–0.446	–0.570	–0.124
S4	–0.566	–0.740	–0.173	–0.563	–0.691	–0.129
sum	–1.741	–2.248	–0.508	–1.735	–2.119	–0.385
C12	–0.243	–0.396	–0.153	–0.238	–0.346	–0.108
C96	–0.305	–0.434	–0.129	–0.305	–0.398	–0.093
C197	–0.369	–0.486	–0.117	–0.367	–0.460	–0.094
sum	–0.916	–1.316	–0.400	–0.910	–1.205	–0.295
total cluster	–0.727	–1.499	–0.773	–0.726	–1.319	–0.593
OC4	–0.334	–0.309	0.025	–0.333	–0.328	0.006
C3	–0.010	–0.016	–0.006	–0.013	–0.038	–0.025
C2	0.019	0.049	0.030	0.026	0.068	0.042
total HMBPP	–0.646	–0.636	0.010	–0.645	–0.784	–0.139
cluster + HMBPP	–1.372	–2.135	–0.763	–1.371	–2.103	–0.732

^aThe difference in charge (Δq) between the oxidized and 1e^– reduced atoms is indicated.

11. Relative Energies of the η²-Bound States in the Oxidized State

The energies of η²-bound oxidized states can be directly compared to their ROH-bound counterparts to obtain their relative energies (Table 10). Using the DFT/COSMO method, the lowest-energy η²-bound oxidized state is the RO^HP^–E^H(η²-ring) state, which is 5.4 kcal mol^–1 higher in energy than the lowest-energy RO(H)-bound oxidized states RO^–P^HE^H and RO^HP^HE^H. The RO^HP^HE^H(η²-trans) and RO^HP^HE^H(η²-ring) states are, respectively, 6.2 and 6.8 kcal mol^–1 higher in energy than the lowest-energy RO(H)-bound states (Table 10).

Using the DFT/SCRF method, the preferred η²-bound oxidized state is also the RO^HP^–E^H(η²-ring) state, which lies 6.0 kcal mol^–1 higher in energy than the lowest-energy RO(H)-bound states RO^–P^–E^H and RO^HP^–E^–. All other η²-bound oxidized states are >14 kcal mol^–1 higher in energy than the RO^–P^–E^H(ROH) and RO^HP^–E^–(ROH) states. From both the DFT/COSMO and DFT/SCRF computations, it is clear that the RO^HP^–E^H(η²-ring) state is moderately higher in energy than the lowest-energy RO(H)-bound oxidized states. We thus reason that the RO^HP^–E^H(η²-ring) state can be accessed prior to 1e^– reduction of the [4Fe–4S] cluster, provided that no kinetic barriers prohibit the C₄–OH group rotation required to achieve η² binding.

12. Reduction Potentials Computed for η²-Bound States

Having obtained the energies of η²-bound states when the [4Fe–4S] cluster is oxidized and reduced by one electron, we can obtain reduction potentials for the addition of an electron to these alternative geometries (Table 14). With the DFT/COSMO method, the computed reduction potential for the lowest-energy η²-bound state, RO^HP^–E^H(η²-ring), is −1.22 V, which is shifted ∼300 mV positive relative to the reduction potential computed for the similarly protonated RO^HP^–E^H(ROH) state (Table 6). Coupling the transfer of a proton to reduction of the RO^HP^–E^H(η²-ring) state (eq 11) generates the 1e^– reduced RO^HP^HE^H(η²-ring) state and effectively increases the reduction potential E°′ to −0.74 V.

11

Table 14. Reduction Potentials (V) Obtained for the Addition of an Electron to the η²-Bound States.

protonation state	binding mode	DFT/COSMO	DFT/SCRF
ROHP–EH	ROH	–1.52	–1.07
	η2-ring	–1.22 (−0.74)a	–0.78
	η2-trans	–1.20	–0.74
ROHPHEH	ROH	–1.42	–0.91
	η2-ring	–0.68	–0.31
	η2-trans	–1.09	–0.60

^aElectron transfer accompanies proton addition to generate the RO^HP^HE^H(η²-ring) 1e^– reduced state. Redox potential coupled to proton transfer indicated in parentheses.

Alternatively, we can consider reduction to proceed through the RO^HP^HE^H(η²-ring) oxidized state, which is 1.3 kcal mol^–1 higher in energy than the RO^HP^–E^H(η²-ring) oxidized state (Table 10). The reduction potential in this scenario is calculated to be E° = −0.68 V. Regardless of the pathway, it is evident that reduction is preferred through η²-bound states when using the DFT/COSMO method.

Using the DFT/SCRF method, the reduction potential for the addition of an electron to the RO^HP^–E^H(η²-ring) state is −0.78 V. This value is ∼300 mV more positive than that computed for the analogous RO^HP^–E^H(ROH) state and ∼600 mV more positive than the reduction potential coupled to proton transfer through the lowest-energy ROH-bound state, RO^HP^–E^–. Thus, it is easier to add an electron to the RO^HP^–E^H(η²-ring) state than to RO(H)-bound states.

13. Barrier to Rotation of C₄–OH Group in the 1e^– Oxidized State

Computed reduction potentials for η²-bound states are closer to the values expected for [4Fe–4S] Fdx proteins.^51,82 For such redox processes to occur, however, these η²-bound states must be accessible when the [4Fe–4S] cluster is oxidized. Using the DFT/COSMO method, the RO^HP^–E^H(η²-ring) state is only 5.4 kcal mol^–1 higher in energy than the lowest-energy RO(H)-bound state; with the DFT/SCRF method, the RO^HP^–E^H(η²-ring) state is 6.0 kcal mol^–1 higher in energy than the lowest-energy RO(H)-bound states (Table 10). The addition of an electron through these η²-bound intermediates is thus thermodynamically attainable. To probe whether such mechanisms are kinetically feasible, we perform linear transit computations along ϕ, following the framework applied earlier to the 1e^– reduced states, to quantify the barriers to rotate the C₄–OH group away from Fe1 in the RO^HP^–E^H state when the [4Fe–4S] cluster is oxidized (Figure 8). The protonation state is fixed throughout the computation. LT computations using the DFT/COSMO and DFT/SCRF methods give respective rotational barriers of 11.4 and 8.9 kcal mol^–1 to reach the RO^HP^–E^H(η²-ring) state when the [4Fe–4S] cluster is oxidized. These values indicate that rotation of the C₄–OH group to attain η²-bound states is feasible.

Figure 8.

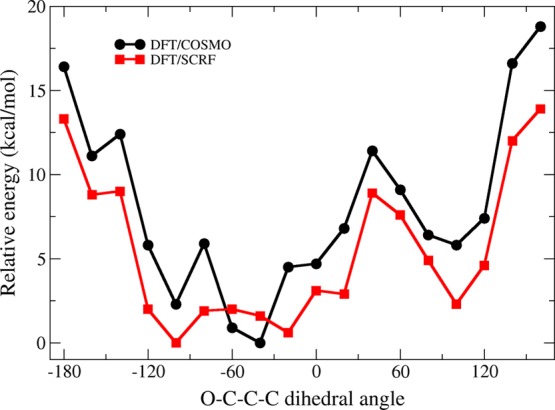
Linear transit computation performed along ϕ in the oxidized state. Energies (kcal mol^–1) are obtained using the DFT/COSMO (black) and DFT/SCRF (red) methods.

Discussion

Before discussing the computations performed in this study, we briefly summarize the results from BS/DFT computations performed on the oxidized state of our IspH active-site quantum cluster.⁵⁰ Exploring only RO(H)-bound geometries in the oxidized state, we previously found that the DFT/COSMO method favors states with less negative charge in the active site (q = −2) than the DFT/SCRF method, which preferentially stabilizes q = −3 states. More specifically, the lowest-energy RO(H)-bound states obtained using DFT/COSMO are the RO^–P^HE^H and RO^HP^HE^H, whereas the RO^–P^–E^H and RO^HP^–E^– states are the lowest energy in DFT/SCRF computations (Table 10). Furthermore, we observed that the geometry optimized structures of the RO^HP^YE^–(ROH) states, regardless of PP_i protonation, best match the active-site geometry observed in the oxidized [4Fe–4S] IspH:HMBPP crystal structure.³⁵ Moreover, Mössbauer isomer shifts^21,33 computed for ROH-bound states gave better agreement with experiment than those computed for RO^–-bound states.⁵⁰

Shifting focus to the 1e^– reduced RO(H)-bound states computed in this work, the lowest-energy state obtained using the DFT/COSMO method is the RO^HP^HE^H(ROH) state (q = −2), whereas the RO^HP^HE^–(ROH) state (q = −3) is favored using the DFT/SCRF method (Table 10, Figure 5). The propensity of these different methods to stabilize different charge states is consistent with the observed preference for q = −2 and q = −3 states by the DFT/COSMO and DFT/SCRF methods, respectively, when the [4Fe–4S] cluster is oxidized.⁵⁰ The energetic preference for maintaining certain active-site charge states ensures that protons accompany electrons when the latter are added to the system, as is required in IspH catalysis.

Combining the energetic analyses of the oxidized and 1e^– reduced RO(H)-bound states, we obtain reduction potentials using both the DFT/COSMO and DFT/SCRF methods. In our previous study of the IspH oxidized state, we proposed the preferred state to be RO^HP^–E^–(ROH). Using this state as a starting point to consider the 1e^– reduction of the IspH [4Fe–4S] cluster, we obtain reduction potentials in the absence of proton coupling of −1.82 and −1.47 V using the DFT/COSMO and DFT/SCRF methods, respectively (Table 6). As illustrated by this example, all reduction potentials computed using the DFT/SCRF method are ∼0.30–0.50 V more positive than those computed using the DFT/COSMO method (Tables 6 and 14). The tendency of the DFT/COSMO method to obtain reduction potentials that are more negative than those determined experimentally has been noted previously.^51,68 In contrast with DFT/COSMO, the DFT/SCRF method lends improvement to the computation of reduction potentials through its inclusion of the surrounding protein point charges in a multi-dielectric environment, which better accommodates the addition of an electron to the active-site cluster reduction than the simpler COSMO description of the active site surroundings.^51,68 While both DFT/COSMO and DFT/SCRF methods give reduction potentials that are too negative, those computed using the DFT/SCRF method are significantly closer to the range of reduction potentials expected for [4Fe–4S] Fdx proteins.^51,82 Combining this result with previous findings that the DFT/SCRF method also better predicts the geometry and protonation of the HMBPP ROH group in the oxidized state, we choose to limit further discussion to our results obtained using the DFT/SCRF method.

Returning to our discussion of how ROH-bound states may undergo reduction, we begin with the RO^HP^–E^–(ROH) state, which is one of the two lowest-energy oxidized states obtained with the DFT/SCRF method. The reduction potential for this state can be increased from −1.47 to −1.29 V with proton transfer to the HMBPP PP_i moiety (Table 6); however, there are no clear titratable groups available to donate this proton in our active-site model. Consequently, it is more likely that, if protonation is required for the addition of the reducing electron, the proton transfer occurs in the oxidized state prior to reduction of the [4Fe–4S] cluster. In this scenario, either E126 or the PP_i group of HMBPP can be protonated in the oxidized state at a respective energetic cost of 5.5 or 6.1 kcal mol^–1 (Table 5). Subsequent reduction of the system can be achieved with reduction potentials of −1.03 and −1.07 V for the RO^HP^HE^– and RO^HP^–E^H states, respectively (Table 6). While these reduction potentials are less negative, they still fall outside the expected range for [4Fe–4S] Fdx proteins.^49,78 To obtain reduction potentials in the −800 to −200 mV range,^51,82 it thus appears that reduction likely occurs via an alternative pathway.

We address the possibility that reduction may occur through an alternative pathway by considering the suggestions of others that HMBPP shifts to η² binding of Fe1 in the 1e^– reduced state. To this end, we find two η²-bound HMBPP rotamers (i.e., “ring” and “trans”) distinguishable by their respective C₂–C₃–C₄–OH dihedral angle (ϕ ≈ +90 and −160°, respectively) and, consequently, the orientation of the C₄–OH moiety of HMBPP in the active-site hydrogen-bond network (Figure 4). The η²-ring state is found to be the lower energy η²-bound state (Table 10), and the RO^HP^–E^H(η²-ring) state is 7.2 kcal mol^–1 lower than the energy of the lowest-energy η²-trans state, RO^HP^–E^H(η²-trans).

In both of the η²-ring and η²-trans states, two binding modes are present that differ with respect to the NSP on Fe1: (1) tight coordination of Fe1 by C₂ and C₃ with Fe–C distances of ∼2.1 Å when Fe1 is net spin-β and aligned opposite to S_Tot; and (2) a loose coordination of Fe1 by the olefin (Fe–C distances of ∼2.6 Å) when Fe1 is net spin-α and aligned with S_Tot (Tables 7–8). In both η²-ring and η²-trans states, the tighter coordination mode observed when the net spin Fe1 is aligned opposite S_Tot is favored energetically by ∼7–11 kcal mol^–1 (Supporting Information, Table S8).

The RO^HP^–E^H(η²-ring) state is 5.7 kcal mol^–1 lower in energy than all ROH-bound 1e^– reduced states considered in this study, demonstrating a thermodynamic preference for this alternative geometry in the 1e^– reduced state (Table 10). Given this finding, we restrict further discussion of η²-bound states to η²-ring states. Linear transit (LT) computations along the ϕ reaction coordinate are initiated from both ROH- and η²-ring geometries. An analysis of energies along these LTs indicate that, while ROH-bound geometries are favored at ϕ values between −120 and −80°, η²-bound states become lower in energy at all values of ϕ outside this range. From these data, the rotational barrier obtained along the ϕ reaction coordinate that permits HMBPP to transition from ROH- to η²-ring coordination of the [4Fe–4S] cluster is only ∼2 kcal mol^–1 (Figure 6B). Thus, η²-ring states are both kinetically accessible and thermodynamically favored in the 1e^– reduced state.

The stabilization of η²-bound 1e^– reduced states corroborate the organometallic mechanism proposed by Oldfield and co-workers for IspH catalysis.⁹ Coupling our finding that η²-ring geometries are favored in the 1e^– reduced state with the indirect support for the existence of such intermediates from ENDOR²⁶ and crystallographic studies³⁶ led us to consider reduction through states with HMBPP bound to Fe1 in these η²-binding modes. To obtain reduction potentials through the η²-ring state, it is necessary that such geometries preexist in the oxidized state. Starting from the geometries optimized in the 1e^– reduced state, we compute η²-bound states with the [4Fe–4S] cluster oxidized. All such states are characterized by loose coordination of Fe1 by the HMBPP olefinic carbons, similar to what is observed in 1e^– reduced η²-bound states having Fe1 net spin-α (Table 11, Figure 7). The loosely-bound RO^HP^–E^H(η²-ring) state is the lowest-energy η²-bound structure in the oxidized state at only 0.5 kcal mol^–1 above the energy of the similarly protonated RO^HP^–E^H(ROH) state, and it is 6.0 kcal mol^–1 higher in energy than the energy of the lowest-energy RO(H)-bound states RO^HP^–E^– and RO^–P^–E^H.

Reduction via η²-bound states is possible given the similar energies of RO^HP^–E^H(ROH) and RO^HP^–E^H(η²-ring) states when the [4Fe-4S] cluster is oxidized and the low energy of the RO^HP^–E^H(η²-ring) state upon 1e^– reduction. Indeed, the reduction potential obtained through the RO^HP^–E^H(η²-ring) falls near the lower bound of the expected range for [4Fe–4S] Fdx proteins at −0.74 V (Table 14). Compared to the −1.07 V reduction potential obtained for reduction through the RO^HP^–E^H(ROH) state (Table 6), reduction through the η²-ring state is preferred by over 7 kcal mol^–1. However, LT computations on RO^HP^–E^H states along the ϕ reaction coordinate when the system is oxidized suggests a rotational barrier of ∼8.9 kcal mol^–1 between ROH- and η²-ring states. This kinetic barrier required to reach the RO^HP^–E^H(η²-ring) oxidized state opposes the thermodynamic preference for reduction through η²-bound states; however, it is likely, though outside the scope of the calculations performed in this work, that the free energy barrier between these states is overestimated. The breaking of the Fe1–O_C4 bond, while shown to be enthalpically unfavorable by our DFT/SCRF LT computations, likely increases the configurational entropy of the system. Such entropic compensation, which is not quantified in this work, would lower the barrier to rotation and render reduction through η²-bound states more favorable. Additionally, the reorientation of the electric dipoles of the protein in response to this HMBPP conformational change is omitted from our model, as all DFT/SCRF computations use a static protein structure corresponding to the oxidized [4Fe–4S] IspH:HMBPP crystal structure³⁵ in which HMBPP is bound to Fe1 through its C₄–O(H) group. Thus, the rotational barrier of 8.9 kcal mol^–1 provides an upper bound to the “true” barrier separating ROH- and η²-ring states when the [4Fe–4S] cluster is oxidized.

We note that the reaction barriers observed for reduction through both of the RO(H)- and η²-bound pathways are not unfounded for the IspH enzyme. More specifically, kinetic studies of the IspH enzyme performed in vitro indicate that IspH has low catalytic turnover (k_cat = 604 s^–1).^34,39 Applying simple transition-state theory for heuristic purposes,⁸³ this turnover rate implies IspH catalysis occurs with a barrier energy of ca. 16 kcal mol^–1. Although simplistic, this view of IspH kinetics suggests the energetic penalties associated with reduction through both ROH-bound and η²-ring states are within reason.

Using Figure 9, we show how our computational work affects previous proposals for the IspH catalytic mechanism. In the oxidized state (left column, Figure 9), the HMBPP coordinates Fe1 through its C₄–OH group in the RO^HP^–E^– protonation state (4, Figure 9). From this starting point, the simplest path to the reduced state is through proton–coupled electron transfer to the RO^HP^–E^–(ROH) state (4 → 5, Path I) with E°′ = −1.29 V. Two problems exist that lead us to discard Path I: (1) the reduction potential is too negative, and (2) there is no protonated group in the active site available for this electron transfer. Consequently, the active site must be protonated (either at E126 or the HMBPP PP_i group) prior to 1e^– reduction of the [4Fe–4S] cluster. In the oxidized state, the easiest site to protonate to generate the RO^HP^–E^H(ROH) oxidized state is E126 (6), which requires 5.5 kcal mol^–1. Electron addition to the RO^HP^–E^H(ROH) state is achieved with E° = −1.07 V (Path II, Figure 9), which, although shifted positive relative to the reduction potential computed for RO^HP^–E^–(ROH), is still too negative for ferredoxins.^49,78

Figure 9.

Modifications to the catalytic mechanism proposed for IspH,⁴⁰ using energies obtained in this study. ΔE^‡ signifies an estimate of the energy barrier; all other energies are the differences in free energy between intermediates.

Thus, consistent with the findings of others,^{26,35,41,47−49} we suggest Path III is a likely alternative to Path II. Instead of reduction occurring at a high cost with HMBPP bound to Fe1 through its C₄–OH group, the C₄–OH group crosses a kinetic barrier with an upper bound of 9 kcal mol^–1 to assume an η²-ring conformation (8, at a thermodynamic cost of 0.6 kcal mol^–1). Through such an oxidized RO^HP^–E^H(η²-ring) state, electron addition is achieved with a significantly lower E° = −0.74 V (9, Figure 9). In Path III, this 1e^– reduction is gated by a substrate rotation and shift in Fe binding mode in the oxidized state. Then after 1e^– reduction, the Fe–C=C π bond strengthens and becomes shorter. Following 1e^– reduction, the terminal −OH group must be cleaved and an additional proton and electron must be added to yield IPP (1) and DMAPP (2).

While Path III appears to us to be the most likely mechanism, there may not be a single mechanism by which reduction occurs. The possible diversity of mechanisms can be explored experimentally by varying reductants, working to isolate intermediates, and examining the resulting reaction kinetics. From our computations, the RO^HP^–E^H(η²-ring) state is the lowest-energy state when the [4Fe–4S] cluster is reduced. It is possible that reduction is not gated, and instead, electron addition to the [4Fe–4S] cluster may be achieved through either ROH- or η²-bound states. Upon reduction, however, the η²-ring state is favored energetically with a much smaller rotational barrier separating it from the ROH-bound state; consequently, it is likely that the η²-ring state precedes all later steps in IspH catalysis, regardless of whether reduction occurs through ROH- or η²-bound states.

Omitted from consideration in these studies is the potential for cleavage of the −OH group attached to C₄ either accompanying or following reduction of the [4Fe–4S] cluster. While the transfer of an additional proton to the C₄–OH group (to make a C₄–OH₂ group) would likely make electron addition to the [4Fe–4S] cluster more favorable by reducing the anionic character in its immediate vicinity, we reason that having this concerted proton transfer event to the C₄–OH group prior to reduction would incur an energetic barrier greater than what is observed for the rotation of the C₄–OH group. Consequently, we suggest that the cleavage of the C₄–OH bond occurs after the C₄–OH group has rotated away from Fe1 in the 1e^– reduced state to form the η²-ring conformation.

The computations performed in this study suggest that the η²-ring state is favored following 1e^– reduction of the [4Fe–4S] cluster. This finding lends further support to development of olefin–based inhibitors.^9,24,26 It is worth noting that, in the case of IspH, olefin binding to Fe1 is favored over RO^–/ROH binding in the 1e^– reduced state. In contrast, binding through the HMBPP RO(H) group is preferred when the [4Fe–4S] cluster is oxidized. Consequently, our results suggest that inhibitor design may be considered redox-dependent. Furthermore, since the binding mode of olefinic groups changes upon reduction, we propose that docking and other structural studies must account for the different binding modes of such groups, depending on the oxidation state of the [4Fe–4S] cluster. Attempts to improve inhibitor design by leveraging structural insight from these computational studies are ongoing.

Supporting Information Available

Geometric parameters for the lowest-energy 1e^– reduced RO(H)-bound states that are omitted from Table 2; NSPs and ESP charge distributions computed for the lowest-energy 1e^– reduced RO(H)-bound valence isomers not included in Table 3; relative energies of all valence isomers considered for 1e^– reduced RO(H)-bound states; geometric parameters compared between ROH- and η²-bound geometries in the 1e^– reduced RO^HP^HE^H state; NSPs and ESP charge distributions computed for the lowest-energy 1e^– reduced η²-bound states omitted from Table 8; relative energies of tight versus loose η² complexes in the 1e^– reduced state; relative energies of all valence isomers considered for 1e^– reduced η²-bound states; geometric parameters compared between ROH- and η²-ring geometries in both the oxidized and 1e^– reduced RO^HP^HE^H states; comparisons of NSPs and ESP charge distributions computed for η²-ring geometries in the oxidized and 1e^– reduced RO^HP^HE^H states; and a superposition of ROH- (blue) and η²- (red) bound geometries in the 1e^– reduced state. The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.inorgchem.5b00751.

The authors declare no competing financial interest.