Skip to main content
PMC home page
APA Open Access logoLink to APA Open Access
. 2015 Aug 17;19(3):215–229. doi: 10.1037/gpr0000032

From Mindless Masses to Small Groups: Conceptualizing Collective Behavior in Crowd Modeling

Anne Templeton 1,*, John Drury 1, Andrew Philippides 2
Editor: Gerianne M Alexander
PMCID: PMC4568938  PMID: 26388685

Abstract

Computer simulations are increasingly used to monitor and predict behavior at large crowd events, such as mass gatherings, festivals and evacuations. We critically examine the crowd modeling literature and call for future simulations of crowd behavior to be based more closely on findings from current social psychological research. A systematic review was conducted on the crowd modeling literature (N = 140 articles) to identify the assumptions about crowd behavior that modelers use in their simulations. Articles were coded according to the way in which crowd structure was modeled. It was found that 2 broad types are used: mass approaches and small group approaches. However, neither the mass nor the small group approaches can accurately simulate the large collective behavior that has been found in extensive empirical research on crowd events. We argue that to model crowd behavior realistically, simulations must use methods which allow crowd members to identify with each other, as suggested by self-categorization theory.

Keywords: crowds, computer simulations, modeling, social identity, intragroup processes

Computer simulations are increasingly used to monitor and predict behavior at large crowd events, such as mass gatherings, festivals, and evacuations. Recent approaches to crowd modeling have proved effective in explaining patterns in aggregates of people together in the same place, such as pedestrians in a busy street (e.g., Helbing, Molnar, Farkas, & Bolay, 2001; Moussaïd, Helbing, & Theraulaz, 2011) and small group behavior within crowd flow (e.g., Köster, Seitz, Treml, Hartmann, & Klein, 2011; Moussaïd, Perozo, Garnier, Helbing, & Theraulaz, 2010; Singh et al., 2009). However, as yet, computer modelers have not created models which can adequately simulate certain key psychological features of large crowd behavior.

In a commentary on collective behavior, Turner (1987) argued that instead of treating crowds as individuals without any connections to one another, we need to explain the mental unity of real life crowds where the crowd behaves as one. As Reicher (1984) states, “the fascination of crowd psychology lies in the fact that it seeks to account for behavior that shows clear social coherence—in the sense of a large amount of people acting in the same manner—despite the lack of either pre-planning or any structured design” (p. 1). There are numerous real world examples of such collective behavior, for example football supporters performing a Mexican wave, protestors chanting together, or people coordinating their egress movements in emergencies. In each case, there is not only a physical crowd—an aggregate of individuals in the same location—but also a psychological crowd, that is, a shared psychological unity in those individuals and hence coordinated behavior (Reicher & Drury, 2011). Indeed, in some crowd events there may be more than one large psychological group which exists within a physical crowd. For example, in the case of a football match, the fans of each team make up two psychological crowds that behave differently from each other within one large physical crowd of people in the same stadium.

For a number of years, researchers modeling crowd behavior have recognized that to enhance the realism of simulations, and to better approximate collective behavior, greater granularity or psychological detail is required (for examples see Galea, 2006; Gerodimos, 2006). Thus some modelers have explicitly looked to the social sciences for both evidence and concepts for understanding collective behavior (e.g., Franca, Marietto, & Steinberger, 2009; Fridman & Kaminka, 2007; Helbing, Farkas, & Vicsek, 2002; Johnson & Feinberg, 1997). In different ways, these and other modelers have argued that more accurate simulations will require the inclusion of groups within a crowd (e.g., Aguirre, El-Tawil, Best, Gill, & Fedorov, 2011; Bruno, Tosin, Tricerri, & Venuti, 2011; Singh et al., 2009). However, this raises the question of what is meant by the concept of ‘group.’ In both psychology and computer science there are different understandings of what is meant by a ‘group.’ Some of these understandings may be better than others in helping to produce a more realistic simulation of behavior in a psychological crowd.

This article will critically examine existing crowd computer simulations by first outlining how understandings of group and collective behavior have developed within social psychology, before presenting a systematic review of the implicit and explicit assumptions in modelers’ treatment of ‘groups’ and ‘crowds’. On the basis of this review we will argue that crowd modelers will benefit from incorporating aspects of self-categorization theory (Turner, 1982; Turner, Hogg, Oakes, Reicher, & Wetherell, 1987) in to their models in order to create realistic simulations of collective behavior in line with findings from empirical psychological research.

Toward an Understanding of Collective Behavior

In early understandings of collective behavior, crowds were treated as either a mass of people under one ‘group mind,’ or a mass of numerous unconnected individuals within the crowd. In ‘group mind’ accounts, crowds were understood as homogeneous entities where upon entering a crowd individuals lost both their individual ability to reason and their personality. Here every crowd member became indistinguishable from the others as they tended toward indiscriminate violence (Le Bon, 1960). Individualist accounts, such as Allport (1924), argued that the idea of the collective is a nominal fallacy; groups and crowds are merely aggregates of individuals. Any collectivity was seen to occur only through social facilitation, whereby the presence of others stimulated behavior that was already present in each individual. Later research demonstrated that neither group mind nor individualism could explain the social form of collective behavior; the mechanisms posited by Le Bon, Allport and others to explain collectively were inherently primitive, irrational, and mindless. For both positions, collective behavior tends to indiscriminate violence. However, extensive empirical research has shown that most crowds are not violent, and that even in riots and violent crowds, behavior is rational, discriminate, and often shows a pattern which is in line with shared conceptions of legitimacy (e.g., Fogelson, 1971; Reicher, 1984, 1996; Reicher & Stott, 2011; Thompson, 1971).

In the current literature, collective behavior is often characterized as ‘contagion’ where the mere sight or sound of others’ behavior apparently influences individuals in a crowd to behave in the same way (e.g., Gallup et al., 2012; Mann, Faria, Sumpter, & Krause, 2013). However, social psychologists examining crowd behavior have argued that the concept of ‘contagion’ cannot explain group boundaries to social influence. Thus Milgram and Toch (1969) pointed out that a different model of collective behavior was required to explain why the rousing effects of a demagogue affected the behavior of protesters but not the riot police who were physically copresent in the same crowd. Psychological group boundaries in ‘contagion’ have also been demonstrated experimentally (Van der Schalk et al., 2011).

Later interactionist approaches focused on group norms and interactions, and treated groups as psychological entities. Asch (1952) claimed that to understand the individual we must pay some attention to the group they belong to on the principle that the parts get their meaning from their relationship within the whole. Sherif (1967) proposed that being in a group has psychological consequences which are separate to those of the individual, and collectivity emerged when individuals had shared meanings and beliefs. The ideas of these and other Gestalt social psychologists were crucial for influencing psychological research to view individuals as members of a shared social field which was separate from them as individuals. Some sociologists began to take up this idea of interaction and applied it to crowds by focusing upon meaning-seeking and social norms for individuals to gauge acceptable behavior in a novel situation where how to behave is not immediately obvious (Emergent Norm Theory: Turner & Killian, 1957, 1987).

Other sociologists such as Aveni (1977) criticized previous research for treating crowds as “spatially proximate collections of individuals . . . undergoing some common experience” (p. 96) and also noted that previous research has paid little attention to the structure of crowds. Aveni’s criticism of this approach was followed by research looking at the affiliation between some members of the crowd. Various studies showed that in an evacuation people will attempt to remain with the small group that they have preexistent affiliative bonds with, such as friends and family, even if this results in their evacuation time increasing or causing a hazard to themselves (Johnson, 1988; Mawson, 2005; Sime, 1983). However, approaches to crowd behavior focusing on small groups fall short of explaining large collective behavior. For example, these accounts cannot explain why in emergency situations a crowd of strangers can become united and help those who were previously strangers (Drury, 2012), or even that two large psychological crowds can exist who act together (intragroup) yet oppose one another (intergroup) (Reicher, 1996). Although there are many theories of crowd behavior, such as the individualist and contagion approaches mentioned above, one of the most widely accepted and utilized accounts of collective behavior in social psychology, which is grounded in extensive empirical research and can explain the collective behavior of psychological crowds, is self-categorization theory (Turner, 1982; Turner et al., 1987).

The Psychological Crowd: A Self-Categorization Approach

Self-categorization theory suggests that shared social identity—people’s cognitive representation of their relationship to others - is what makes collective behavior possible (Turner, 1985). Self-categorization theory can therefore explain how physical aggregates of individuals can come together psychologically within a crowd and how a single physical crowd may consist of one, two (or more) psychological crowds who each act as a large group without prior interpersonal relationships or interpersonal interaction. Self-categorization theory suggests that collective behavior occurs through the process of depersonalisation. Here, individuals self-stereotype themselves in line with the definition of a social category and see themselves as being interchangeable with others in their social category. In doing this, individuals shift from their personal identity to their identity as a member of a particular social group (Turner et al., 1987).

A plethora of crowd phenomena has been explained by self-categorization theory, such as urban riots (Reicher, 1984), mass emergency evacuations (Drury et al., 2009), religious mass gatherings (Alnabulsi & Drury, 2014), music festivals (Neville & Reicher, 2011), collective action (Drury, Reicher, & Stott, 2003), and ‘personal space’ in crowded locations (Novelli, Drury, & Reicher, 2010). An example of this behavior can be seen during the London bombings of July 7th 2005, where individual commuters became united through a shared identity in relation to the threat of the bombs. On the basis of their shared identity, the commuters helped each other and reported feelings of ‘unity,’ and felt ‘part of a group’ (Drury, Cocking, & Reicher, 2009, p. 81). The ability of self-categorization theory to explain behavior in numerous situations indicates that modelers would benefit from applying this theory to their models in order to adequately simulate a broader variety of crowd behavior.

Over the past decade, there has been an increased recognition among modelers that the concept of social identity is necessary for more realistic crowd simulations (for examples, see Aguirre et al., 2011; Köster et al., 2011; Langston, Masling, & Asmar, 2006; Smith et al., 2009). Here we examine whether any computer models of crowds have responded to this perceived need and adequately implemented a model of crowd behavior in line with empirical research in crowd psychology. The following section will address the main modeling techniques which have been used to simulate crowds before we present the analysis of the conceptions of crowd behavior found in the modeling literature.

Psychological Requirements for Modeling the Crowd

Social psychological research on crowd psychology suggests a set of theoretical criteria that computer simulations of crowds should adhere to. In particular, a simulation must be able to model individuals who have the required perceptual and cognitive abilities to recognize identities—both their own and others’. Modeling techniques such as flow-based models which treat all members of the crowd as identical (e.g., Fang, Lo, & Lu, 2003) are inappropriate as they cannot model the variable cognitive processes in individuals. Two commonly used approaches for simulating crowd behavior are social force models and cellular automata. Both model types are typically based upon set rules and equations which have the same rules for every individual. In these models, the behavior of individuals is determined by attractors and repellors such as attraction to an area in the virtual environment and repulsion from other individuals to avoid collision (e.g., Burstedde, Klauck, Schadschneider, & Zittartz, 2001; Zhao, Yang, & Li, 2008; Zhang, Zhao, & Liu, 2009).

However, other models such as agent-based models (ABMs) do have the potential to simulate these individual capacities as each agent can have different characteristics which affect their behavior. ABMs can represent varying levels of perceptual and cognitive processes. Importantly, they are also dynamic, as the behavior of the agents (people) within the crowd, their individual characteristics, and the ‘information’ that the agents receive, together drive their actions and can be updated at each time step of the simulation (e.g., Fang, Yuan, Wang, & Lo, 2008; Ji & Gao, 2007; Köster et al., 2011). ABMs thus lend themselves to modeling complex crowd behavior and, in particular, situations in which individuals’ characteristics alter as their social identities change during the simulation. They can also represent more complex abilities, specifically the ability of individuals to perceive their own group membership and the group membership of other agents in the simulation. For instance, membership has been used to alter agent behavior through governing an agent’s spatial location based on the perception of their own group membership and the group membership of others, such as in leader and follower models (e.g., Qiu & Hu, 2010; Yuan & Tan, 2007). As such, ABMS have the ability to simulate psychological components of group identity and self-categorization in crowds. In this review, we will explore how the principles of identity and categorization have been implemented in existing ABMs and similar models of crowd behavior.

Method

Reviewing the Literature

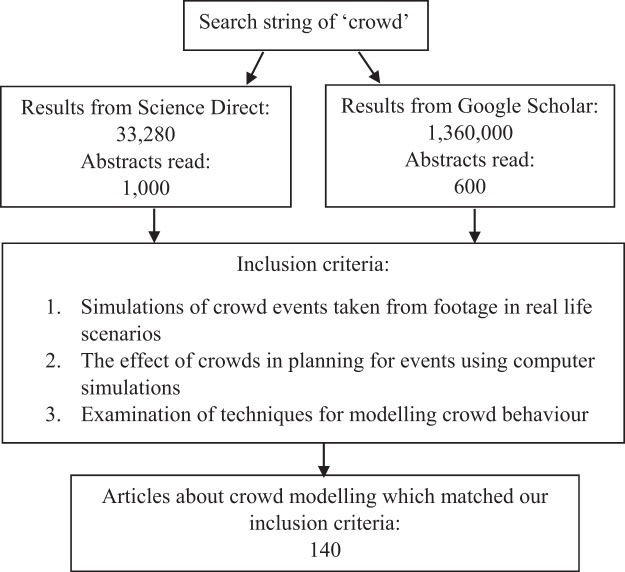
A systematic review of the crowd modeling literature was conducted, in which publications were coded according to the psychological basis used to model crowd behavior. Literature was sourced from the ScienceDirect database and Google Scholar search engine (see Figure 1). In order to locate the relevant literature, the search string of “crowd” was used. Articles and conference proceedings about crowd models were selected from the generated results. Publications recommended by ScienceDirect due to their similarity to the articles identified were also incorporated in to the collection, and the references cited in relevant literature were also used to source additional literature.

Figure 1.

Figure 1

Open in a new tab

Flow diagram of search criteria and exclusion process for relevant articles. Where the same articles were generated by both Science Direct and Google Scholar, the abstracts were read and incorporated into the corpus only once.

Crowd Modeling Typology

Each article was analyzed according to how the behavior of the crowd was treated. Where the theoretical basis for the crowd behavior being implemented was not explicitly stated by the authors, it was inferred from how the crowd behavior was modeled and what psychological literature was referenced, if any. Throughout data collection, it became evident that in the literature the crowd was conceptualized and implemented in one of five possible subtypes. These subtypes fit in to two major types. In the first type, the crowd is treated as a mass. In the second type, the crowd is treated as consisting of a number of small groups.

The prima facie validity of the subtypes was established by presenting descriptions of each category (with examples) to an audience of crowd modelers. To ascertain that the reliability of the subtypes by the first coder were correct, an interrater reliability analysis was conducted on the scheme used to divide cases into types and subtypes. Fourteen articles were randomly selected, and for each article an excerpt was chosen which represented the approach taken toward crowd behavior (minimum length of excerpt = 107 words, maximum length of excerpt = 341). These excerpts were presented to an independent judge, along with definitions of each subtype, and she assigned each article to a subtype. There was very good agreement between the allocation of the raters, Cohen’s Kappa K = .898 (p < .001) 95% CI (0.676, 1.000).

Results

The most prominent models were the mass approaches to crowd behavior, which could be divided in to two subtypes; the ‘homogeneous mass’ approach (52 articles) and the ‘mass of individuals’ approach (31 articles). Within the small groups type, small groups are included in the crowd simulations but the understanding of ‘groups’ and methods to implement group behavior varied. Thus there were three subtypes of small group simulations; ‘non-perceptual groups’ (33 articles), ‘perceptual groups’ (14 articles), ‘cognitive groups’ (10 articles). The number of articles in each subtype is shown in Figure 2, and the allocation of all models in to subtypes is shown in Table 1.

Figure 2.

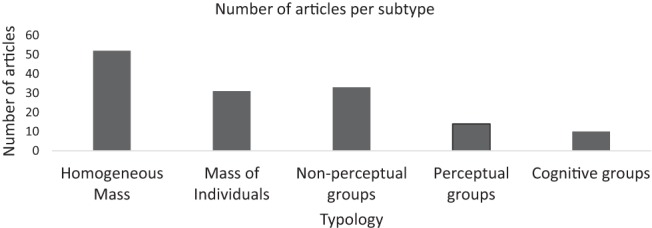
Figure 2

Open in a new tab

The number of articles published in journals and conference proceedings per subtype.

Table 1. List of the Literature Reviewed and the Allocated Subtypes.

Authors Year Typology
Aguirre, El-Tawil, Best, Gill, & Federov 2011 Perceptual groups
Andrade, Blunsden, & Fisher 2006 Homogeneous mass
Banarjee, Grosan, & Abraham 2005 Homogeneous mass
Bandini, Gorrini, & Vizzari 2014 Perceptual groups
Bicho, Rodrigues, Musse, Jung, Paravisi, & Magalhaes 2012 Non-perceptual groups
Bierlaire, Antonini, & Weber 2003 Mass of individuals
Bodgi, Erlicher, & Argoul 2007 Homogeneous mass
Bruno, Tosin, Tricerri, & Venuti 2011 Homogeneous mass
Burstedde, Klauck, Schadschneider, & Zittarz 2001 Homogeneous mass
Carroll, Owen, & Hussein 2013 Homogeneous mass
Chen & Huang 2011 Non-perceptual groups
Chen & Lin 2009 Non-perceptual groups
Chen, Wang, Wu, Chen, Khan, Kolodziej, Tian, Huang, & Liu 2013 Perceptual groups
Cho & Kang 2014 Non-perceptual groups
Chong, Liu, Huang, & Badler 2014 Non-perceptual groups
Chow 2007 Homogeneous mass
Chrysostomou, Sirakoulis, & Gasteratos 2014 Non-perceptual groups
Davidich & Köster 2013 Mass of Individuals
Degond & Hua 2013 Homogeneous mass
Dogbe 2012 Non-perceptual groups
Dou, Chen, Chen, Chen, Deng, Zhang, Xi, & Wang 2014 Mass of Individuals
Fang, Lo, & Lu 2003 Homogeneous mass
Fang, Yuan, Wang, & Lo 2008 Homogeneous mass
Fienberg & Johnson 1995 Non-perceptual groups
Franca, Marietto, & Steinberger 2009 Cognitive groups
Fridman & Kaminka 2007 Non-perceptual groups
Galea, Owen, & Lawrence 1996 Mass of individuals
Gawroński & Kulakowski 2011 Perceptual groups
Georgoudas, Kyriakos, Sirakoulis, & Andreadis 2010 Homogeneous mass
Goldenstein, Karavelas, Metaxas, Guibas, Aaron, & Goaswami 2001 Non-perceptual groups
Gutierrez, Frischer, Cerezo, Gomez, & Seron 2007 Mass of individuals
Haciomeroglu, Barut, Ozcan, & Sever 2013 Non-perceptual groups
Heïgeas, Luciani, Thollot, & Castagne 2003 Homogeneous mass
Helbing, Johansson, & Al-Abideen 2007 Mass of Individuals
Helbing, Farkas, & Vicsek 2000 Homogeneous mass
Helbing, Farkas, Molnar, & Vicsek 2002 Homogeneous mass
Helbing, Molnar, Farkar, & Bolay 2001 Non-perceptual groups
Heliövaara, Korhonen, Hostikka, & Ehtamo 2012 Homogeneous mass
Henein & White 2007 Homogeneous mass
Hu, Zheng, Wang, & Li 2013 Mass of individuals
Hughes 2000 Homogeneous mass
Hussain, Yatim, Hussain, & Yan 2011 Non-perceptual groups
Idrees, Warner, & Shah 2014 Non-perceptual groups
Ji & Gao 2007 Perceptual groups
Ji, Zhou, & Ran 2013 Homogeneous mass
Jiang, Xu, Mao, Li, Xia, & Wang 2010 Non-perceptual groups
Jiang, Zhang, Wong, & Liu 2010 Homogeneous mass
Ji-hua, Cheng-zhi, Zhi-Feng, & Bo 2013 Homogeneous mass
Johansson, Batty, Hayashi, Bar, Marcozzi, & Memish 2012 Mass of individuals
Johnson & Feinberg 1977 Perceptual groups
Johnson & Feinberg 1997 Perceptual groups
Johnson, Hart, & Hui 1999 Mass of individuals
Kamkarian & Hexmoor 2013 Mass of individuals
Karni & Schmeidler 1986 Homogeneous mass
Khaleghi, Xu, Wang, Li, Lobos, Liu, & Son 2013 Homogeneous mass
Kirchner & Schadschneider 2002 Non-perceptual groups
Kirchner, Klüpfel, Nishinari, Schadschneider, & Schreckenberg 2003 Homogeneous mass
Köster, Seitz, Treml, Hartmann, & Klein 2011 Perceptual groups
Kountouriotis, Thomopoulos, & Papelis 2014 Perceptual groups
Krausz & Bauckhage 2012 Homogeneous mass
Lachapelle & Wolfram 2011 Non-perceptual groups
Langston, Masling, & Asmar 2006 Mass of individuals
Lee & Hughes 2006 Homogeneous mass
Lee & Hughes 2007 Homogeneous mass
Lei, Li, Gao, Hao, & Deng 2012 Mass of individuals
Li & Qin 2012 Homogeneous mass
Lister & Day 2012 Homogeneous mass
Lo, Fang, Lin, & Zhi 2004 Mass of individuals
Löhner 2010 Non-perceptual groups
Lozano, Morillo, Orduña, Cavero, & Vigueras 2009 Non-perceptual groups
Ma, Lo, Song, Wang, Zhang, & Liao 2013 Homogeneous mass
Ma & Song 2013 Perceptual groups
Manfredi, Vezzani, Calderara, & Cucchiara 2014 Non-perceptual groups
Marana, Velastin, Costa, & Lotufo 1998 Mass of individuals
Maury, Roudneff-Chupin, & Santambrogio 2010 Homogeneous mass
Mazzon, Tahir, & Cavallaro 2012 Mass of individuals
Mehran, Oyama, & Shah 2009 Non-perceptual groups
Mekni 2013 Cognitive groups
Moore, Flajšlik, Rosin, & Marshall 2008 Perceptual groups
Moussaïd, Helbing, & Theraulaz 2011 Mass of individuals
Moussaïd, Perozo, Garnier, Helbing, & Theraulaz 2010 Non-perceptual groups
Mukovskiy, Slotine, & Giese 2013 Homogeneous mass
Musse & Thalmann 1997 Cognitive groups
Musse & Thalmann 2001 Cognitive groups
Musse, Babski, Çapın, & Thalmann 1998 Cognitive groups
Narain, Golas, Curtis, & Lin 2009 Homogeneous mass
Nilsson & Johansson 2009 Non-perceptual groups
Oğuz, Akaydın, Yılmaz, & Güdükbay 2010 Non-perceptual groups
Pan, Han, Dauber, & Law 2007 Cognitive groups
Parunak, Brooks, Brueckner, & Gupta 2012 Cognitive groups
Pelechano, Allbeck, & Badler 2007 Mass of Individuals
Pires 2005 Homogeneous mass
Qui & Hu 2010 Perceptual groups
Ramesh, Shanmughan, & Prabha 2014 Mass of individuals
Ran, Sun, & Gao 2014 Non-perceptual groups
Ryan, Denman, Fookes, & Sridharan 2014 Homogeneous mass
Sagun, Bouchlaghem, & Anumba 2011 Homogeneous mass
Sarmady, Haron, & Talib 2011 Homogeneous mass
Shao, Dong, & Tong 2013 Non-perceptual groups
Shendarkar, Vasudevan, Lee, & Son 2008 Perceptual groups
Shi, Ren, & Chen 2009 Mass of individuals
Shi, Zhong, Nong, He, Shi, & Feng 2012 Mass of individuals
Silverberg, Bierbaum, Sethna & Cohen 2013 Homogeneous mass
Singh, Arter, Dodd, Langston, Lester, & Drury 2009 Non-perceptual groups
Smith, James, Jones, Langston, Lester, & Drury 2009 Cognitive groups
Song, Gong, Cui, Fang, & Cao 2013 Mass of Individuals
Spieser & Davison 2009 Homogeneous mass
Tajima & Nagatani 2001 Homogeneous mass
Thiel-Clemen, Köster, & Sarstedt 2011 Non-perceptual groups
Thompson & Marchant 1995 Non-perceptual groups
Tong & Cheng 2013 Mass of individuals
Varas, Cornejo, Mainemer, Toledo, Rogan, Munoz, & Valdivia 2007 Homogeneous mass
Vasudevan & Son 2011 Cognitive groups
Vigueras, Lozano, Orduña, & Grimaldo 2010 Homogeneous mass
Wagner & Agrawal 2014 Homogeneous mass
Wang, Li, Khaleghi, Xu, Lobos, Vo, Lien, Liu, & Son 2013 Homogeneous mass
Wang, Zhang, Cai, Zhang, & Ma 2013 Mass of individuals
Wang, Zheng, & Cheng 2012 Mass of individuals
Weifeng & Hai 2011 Mass of individuals
Wu & Radke 2014 Mass of individuals
Xiaoping, Wei, & Chao 2010 Homogeneous mass
Xiong, Cheng, Wu, Chen, Ou, & Xu 2012 Non-perceptual groups
Xiong, Lees, Cai, Zhou, & Low 2010 Homogeneous mass
Yamamoto, Kokubo, & Nishiniari 2007 Homogeneous mass
Yan, Tong, Hui, & Zonghhi 2012 Mass of Individuals
Yaseen, Al-Habaibeh, Su, & Otham 2013 Non-perceptual groups
Yu & Johansson 2007 Homogeneous mass
Yuan & Tan 2007 Cognitive groups
Yücel, Zanlungo, Ikeda, Miyashita, & Hagita 2013 Perceptual groups
Zanlungo 2007 Mass of individuals
Zanlungo, Ikeda, & Kanda 2012 Homogeneous mass
Zawidzki, Chraibi, & Nishinari 2013 Mass of Individuals
Zhang, Liu, Liu, & Zhao 2007 Homogeneous mass
Zhang, Liu, Wu, & Zhao 2007 Homogeneous mass
Zhang, Weng, Yuan, & Chen 2013 Mass of individuals
Zhao, Wang, Huang, Cui, Qui, & Wang 2014 Mass of individuals
Zhao, Yang, & Li 2008 Homogeneous mass
Zheng & Cheng 2011 Non-perceptual groups
Zheng, Sun, & Zhong 2010 Homogeneous mass
Zheng, Zhao, Cheng, Chen, Liu, & Wang 2014 Non-perceptual groups
Open in a new tab

Mass Crowd Simulations

Simulations which fall in to this category treat crowds as consisting of numerous ‘individuals’ in a large mass. Despite research demonstrating that there are often small psychological groups within physical crowds and extensive research showing that collective behavior requires individuals to see themselves as part of a large psychological crowd or group, groups are not implemented in these types of models.

‘Homogeneous Mass’ Subtype

The most commonly used approach within the crowd modeling literature is the homogeneous mass subtype. In examples of this subtype, the crowd is treated as an aggregate mass where every person is allocated identical properties. Within this subtype the crowd is regarded as a very large physical mass of individuals who coincidentally share the same goal—for example evacuating their environment. Literature in this subtype is therefore also characterized by modeling very basic agent behavior, often simply avoiding collisions with one another. This approach is predominantly used in order to model the effect of crowd size and crowd density on egress in emergency evacuations and ordinary environments. For example, Fang, Lo, and Lu (2003) modeled a crowd flow pattern in an emergency situation to examine the effect of crowd density on the speed of evacuation. Similarly, to examine the effect of crowd size on the speed of egress, Lee and Hughes (2006) manipulated the size of the crowd and the complexity of the environment to determine the effect on pedestrian walking speed. Although the assumptions underlying this approach are adequate to model the movement of one psychological crowd in a specific situation, these assumptions cannot accurately capture the behavior of crowds in more complex scenarios, such as when there are two or more crowds acting in different ways or even in contraflow. When other crowds are introduced in to the model, modelers need to simulate different crowd movement and dynamic group identities. Thus, the assumptions of this subtype cannot be applied to other scenarios where there is more than one psychological crowd.

‘Mass of Individuals’ Subtype

The mass of individuals approach differs from the homogeneous mass approach in that agents are given unique properties which make them act as individuals within the crowd. Usually, individual differences are implemented in order to examine the factors that can affect evacuation egress. For example, Shi et al. (2012) assign individuals different attributes such as response time, walking speed, and endurance in order to create a more realistic simulation of pedestrian evacuation in a heterogeneous crowd in a metro station in China. Other example attributes include different pedestrian velocities or health status (e.g., Dou et al., 2014). As in the previous subtype, the crowd members act independently but with the same goal of evacuating as quickly as possible. Some models include elaborate environments which affect the egress of individuals in more realistic simulations; for example Shi, Ren, and Chen (2009) manipulate the egress time of individual agents by causing the agents to be affected by the level of smoke in the room and how injured the individuals are. However, although these models can become very intricate, the premise of the model is still that of individual behavioral differences within a ‘mass’, rather than acting as a collective.

Small Group Types

This subtype is characterized by small groups within the crowd. The small groups are usually implemented to determine the effect of groups on egress time, following Aveni’s (1977) research that suggested that crowds may be comprised of small groups and individuals. The type of groups that are implemented varied and can be divided in to three subtypes on an ordinal scale of psychological realism. However, all of these models represent sociality merely in terms of relations within small groups where collective behavior is reduced to being similar to interpersonal behavior rather than the crowd being a group itself.

‘Non-Perceptual Groups’ Subtype

Models of this subtype simulate physical groups but not psychological groups. That is, groups are implemented as homogeneous physical aggregates of people with no intragroup connection or individual knowledge of group membership. Instead, these are essentially small preexisting groups, which physically stick together in the crowd regardless of the situation. Thus, they move as one homogeneous aggregate, as though they are one large and slow individual. Simulations which fell in to this subtype model small groups in order to investigate the effect of groups on egress, particularly at bottlenecks and exits (e.g., Idrees, Warner, & Shah, 2014).

The implementation of small groups in this type of simulation is in some ways similar to the ‘mass of individuals’ approach. Instead of being an individual who acts independently within the mass, the group is an aggregate cluster of individuals which act as one within the crowd. Although no psychological connection between the groups is modeled, affiliative theories are often referenced (e.g., Aveni, 1977) to justify the inclusion of a group which stays together in a crowd situation (e.g., Feinberg & Johnson, 1995). For example, Dogbe (2012) modeled group behavior using attraction and repulsion interactions, where social groups (assumed to be friends and family in this model) are attracted to move together throughout the simulation, but are repulsed by other neighboring groups. By implementing group behavior in this way, Dogbe is simulating a crowd where the groups are essentially small numbers of people clumped together within the crowd, with no meaningful interaction other than to change formation in order to stay together as they move throughout the crowd. Although it is an advance in terms of psychological theory used that these models simulate groups which are visible through their movement, the focus on small groups neglects the fact that groups can coincide and that an entire crowd can move together as a unit.

‘Perceptual Groups’ Subtype

In contrast to the non-perceptual groups subtype, in perceptual groups individuals are able to perceive their own group membership, the identity of others within the crowd, and act according to their role. Often models which fall in to this subtype include ‘leaders’ and ‘followers’ where followers are treated as being together as a group because of their connection to leaders as the simulation unfolds (e.g., Moore, Flajšlik, Rosin, & Marshall, 2008). Although in simulations of this subtype, individuals are able to perceive their own group membership and the group identity of other individuals, their movement is derived from the idea that people will come together as a group because they are looking for signs and information about how to act in a novel situation. This approach to group behavior draws close parallels with emergent norm theory (Turner & Killian, 1957, 1987), as the agents are in a novel situation and look for leaders and social norms to discern how to act. However, a common problem with these models is that the agent’s priority is to move to the nearest leader, which causes clusters of individuals to form groups without the individuals ever having a psychological bond with any other person (e.g., Qui & Hu, 2010). This could be criticized as these groups are based upon being in the same spatial location rather than being together because they share a group identity, and agents have no perception of others aside from avoiding collision and knowing who is a ‘leader’ or a ‘follower.’

‘Cognitive Groups’ Subtype

In this subtype, individuals are able to perceive their own group membership and the group membership of others, just as in the ‘perceptual’ models. However, there is an extra component; individuals can share similar properties which are treated as ‘cognition’ by the authors. Here, agents who share the same properties are treated as being in a group. Additionally, the properties of each agent can change throughout the simulation, which causes the groups to change. As new information about the environment is given to the agents, the agents adapt their properties and seek out who they perceive to match their properties. Within this subtype, articles again tend to reference emergent norm theory (Turner & Killian, 1957, 1987) to justify why they implement interaction between crowd members. For example, Franca, Marietto, and Steinberger (2009) assign each agent certain properties. When new information is introduced to the agents, the agents begin to communicate to establish new norms. They seek out others who share their properties or are affected in the same way by information, and consequently move into groups with agents who share the same properties as them.

The principles behind simulations of the ‘cognitive’ subtype are the closest to psychological realism and lend themselves to more diverse implementations of both group and individual behavior. This approach is closest to self-categorization theory because it allows for the implementation of both individual properties and the ability to become a group member. It has also been used to simulate people acknowledging their group membership but being able to decide whether to act with their group or to act as an individual. Yuan and Tan (2007) created a scenario where a crowd of people have to evacuate a room, but agents can decide whether to leave with their group members or not. Moreover, this subtype focuses on the fact that groups exist based on shared properties, which is theoretically in line with the proposal of self-categorization theory that groups exist due to a sense of commonality between their members.

Trend Analysis

As Figure 3 shows, although the initial models of crowd behavior began with a mix of articles from all subtypes, since 2007 the ‘homogenous mass’, ‘mass of individuals’ and ‘non-perceptual’ subtypes have been more prominent. Although there was an initial spike of articles in the ‘cognitive groups’ subtype in 2001, then another in 2009, this subtype has largely been overtaken by the ‘mass’ approaches. One factor which could have contributed to the rise in crowd modeling articles over the years is increased access to crowd modeling software. The upsurge of crowd simulations—particularly in the ‘homogeneous mass’, ‘mass of individuals’ and ‘non-perceptual groups’ subtypes - over the last decade could be due to the availability of modeling software such as SIMULEX (e.g., see Thompson & Marchant, 1995) and FIREScape (e.g., see Feinberg & Johnson, 1995), which provide tools to simulate crowds without focusing on group behavior (for a detailed analysis of emergency evacuation simulation models, see Santos & Aguirre, 2004).

Figure 3.

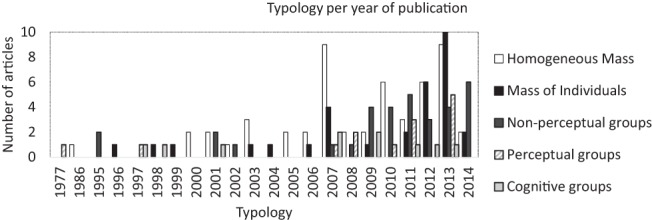
Figure 3

Open in a new tab

Prevalence of subtype per year of publication.

Discussion

Misrepresenting the Crowd

This review has discerned that a plethora of models of crowd behavior have successfully simulated crowds of individuals. Notably, the majority of models have not aimed to incorporate psychological theories in to their rationale for crowd behavior. However, to accurately monitor and predict the collective behavior exhibited in psychological crowds specifically, it is imperative that models being used for crowd safety management have an accurate understanding of collective behavior taken from empirical research. In line with what is known in crowd psychology, a realistic model of collective behavior must include the capacity to simulate the difference between physical crowds and psychological crowds. Specifically, it must be able to model both the members of a crowd categorising themselves as individuals distinct from other individuals, and the situation where the same individuals categorise themselves as members of the crowd and hence share an identity. Simulations of psychological crowds must therefore address the way in which people can identify with one another and how collective behavior emerges from this process.

This review has found that some crowd modelers have begun to approach psychological realism by incorporating groupness (e.g., Aguirre et al., 2011; Moore, Flajšlik, Rosin, & Marshall, 2008) in their models of crowd behavior, particularly those we denoted as the ‘cognitive groups’ subtype. However, these developments have not occurred at the same rate. Over the previous decade, there has been an increase in models which have implemented the ‘homogeneous mass’, ‘mass of individuals’ and ‘non-perceptual group’ approaches. The advantages and limitations of each subtype will be discussed, and we propose the theoretical advances that must be made in order for crowd models to simulate collective behavior more accurately across a variety of collective behavior scenarios.

Constructing the Relationship Between the Individual and the Group

Examples of the mass type of model support Sime’s (1985) assertion that in computer simulations people are treated as ball-bearings; they are unthinking and act at a very base level of simply moving without interacting with one another. The homogeneous mass approach is also similar to the Le Bonian (1895) notion of crowds as an unthinking mass who act at a primitive psychological level, where there is no sense of individuality and thus is reminiscent of the broader mass society narrative, where the crowd is treated as an ‘undifferentiated whole’ (Giner, 1976, p. 47); the mass lacks capacity for moral sense, or a sense of direction. Models in this subtype are not behaviorally realistic because there are no individuals, and therefore there is no room for individual cognition from which meaningful group behavior can emerge. As mentioned previously, although models in this approach can simulate one crowd where members move together in a limited number of scenarios such as evacuation through one route, this account cannot explain collective behavior in all situations, such as where there are two or more psychological crowds, or two crowds in contraflow.

In Galea, Owen, and Lawrence’s (1996) model, the importance of each member of the crowd having individual attributes which change how people act throughout the simulation is emphasized. Although this was an important development for approaching psychological realism, it was at the cost of modeling collective behavior. Granularity is obtained at the cost of collectivity. In the mass of individuals approach, there is no collective behavior because the crowd members act as individuals without any sense of the commonality which is required for collective group behavior. To create a realistic model of collective behavior, modelers need to understand how the individual can become part of a psychological crowd. Thus, modelers need to implement the capacity of crowd members to act either as an individual or as a member of the crowd depending upon whether the person categorises themselves as an individual within a physical crowd, or as a member of the psychological crowd.

The Crowd as Small Groups

Unlike the ‘mass’ type, models within the ‘small groups’ type have various levels of connections between the members of the crowd. The models in this subtype are a significant development in crowd modeling as they recognize and implement the importance of groupness and how this can affect the behavior of the crowd members. However, the ‘small groups’ type falls short of realistically modeling large crowd behavior as it only includes small groups within a crowd. Increasing granularity (small-group level variation within a physical crowd) loses the sense of ‘groupness’ at the crowd level because the focus is upon numerous small groups within the crowd. The approach therefore does not explain collective behavior where the crowd is one group. By doing this, the models are unable to simulate the behavior of large psychological crowds where the entire crowd shares one group identity. However, each subtype within the ‘small groups’ type has its own specific advantages and drawbacks.

In the ‘non-perceptual groups’ subtype of simulation, groups are treated as physical entities rather than being together due to a psychological bond between the members of the group. The original models in this subtype (e.g., Goldenstein et al., 2001; Thompson & Marchant, 1995) were very important for the development of simulations of crowd behavior because they introduced groups in to the crowd. However, groups are only incorporated in order to make simulations more realistic by claiming that the groups are families or friends. Group membership has no effect on the behavior of the group apart from staying together throughout the simulation. Although there are now groups, there is no sense of collective behavior based on a shared group identity.

Within the ‘perceptual groups’ subtype, modelers represent crowd members as being able to know their own group identity and the group identity of others. Although the ability of the crowd members to perceive group membership and act in accordance with it is in line with self-categorization theory (Turner et al., 1987), here groups are treated simply as people that are in the same spatial location. Although group membership is dependent upon group members actively categorising themselves as members of that specific group, group membership is limited and only goes as far as crowd members having roles as either a ‘leader’ or a ‘follower’ as opposed to group membership arising from a sense of common identity. Empirical research on group behavior suggests that psychological group membership is more versatile than this; when people are in a novel crowd situation they can come together through sharing a group identity and act together in a coordinated way, such as by self-organizing and helping one another (Drury, 2012; Drury et al., 2009). In addition, group membership does not need to be limited to those people within the same spatial location. The shared group identity can spread to include the entire crowd, where people have a shared social identity with others in the crowd and act in a coordinated way with them even if they are not near to each other, for example football fans in a stadium.

Incorporating Cognition for Collective Behavior

The subtype of model which comes closest to explicating the underlying components of cognitive group membership and which is consistent with psychological research is the ‘cognitive groups’ subtype. Examples of this subtype not only incorporated the perception of group membership, but also went further than the ‘perceptual groups’ subtype by incorporating what is claimed as ‘cognition.’ In this subtype ‘cognition’ is instantiated as the ability of people to perceive their own beliefs and the beliefs of others, and group membership is dependent upon shared beliefs and desired actions. Moreover, in some simulations (e.g., Yuan & Tan, 2007), the agents are able to choose whether to act with a group or to act as an individual.

The incorporation of ‘cognition’ brings this subtype closest to implementing principles of self-categorization theory in a crowd simulation. Although not explicitly stated in any of the literature that has been reviewed, it could be argued that models in this subtype actually model something of the cognitive shift from being psychologically an individual to becoming a member of a particular social group and taking on that salient identity, which is crucial for collective behavior to emerge. However, despite these advantages, this approach does not completely model a psychological crowd as the models are yet to make the leap from small ‘cognitive’ groups to large crowds where the members share the same group identity. For example - although not specifically a model of crowd behavior - van Rooy (2012) uses an ABM to examine SCT by grouping individuals depending upon their shared opinions. Within this model the individuals could communicate their opinions with others and change group affiliation to be with others who shared the same opinions. By defining groups as those who share common opinions van Rooy’s definition of groups approaches psychological realism by basing group membership on a sense of commonality. While groups are still treated as consisting of small numbers, future work could ascertain whether these principles could be extended to an entire crowd.

Toward a Cognitive Model of Collective Behavior

There are a number of factors that must be addressed in order for modelers to create an accurate simulation of collective behavior. One component that is fundamental to collective behavior is the perception of groupness: the ability of an individual to know their own group identity and perceive the group identities of others. An issue here is how to quantify the level of identification that a member feels with their group. Identification with a group is not simply a binary ‘identify’ or ‘do not identify’ scenario; modelers should create agents with the potential for variable levels of group identification which are dependent upon the context that the individual is in. Similarly, the effect of group identity upon behavior is not necessarily linear. Although an increased level of identification may cause individuals to behave in line with the norms of the group, other variables may act as moderators, such as beliefs about legitimacy of actions and levels of self-efficacy. One example of a model which has effectively employed aspects of self-categorization theory to simulate collective crowd behavior is von Sivers, Templeton, Köster, Drury, and Philippides (2014). The study described in this article is a first step toward examining the effect of self-categorization theory upon collective crowd behavior during an emergency, and could be used as a marker for future work simulating collective behavior.

This has been the first comprehensive and up-to-date review of how computer models have conceptualized groups and crowd behavior. Despite the importance that models used for crowd management and safety are able to realistically simulate crowd behavior, until now there has not been a review of how modelers approach collective behavior, or indeed whether they approach it at all. An earlier review by Sime (1985) found that the idea of ‘mass panic’ was influential in how modelers implemented crowd behavior in safety planning and the design of public spaces. However, modeling approaches have evolved since Sime’s review. There has been an upsurge in the number of crowd simulations since then, with some articles even referencing Sime in their justification for their new approaches to modeling crowd behavior (e.g., Feinberg & Johnson, 1995; Kamkarian & Hexmoor, 2013). In addition, a recent review of building evacuation simulations by Aguirre et al. (2011) found that modelers using ABMs placed an emphasis on individuality and mass panic and suggested that evacuation simulations need to include other social scientific factors such as norms, leadership, and group identification and membership.

Though both of these reviews were very important for addressing improvements the needed to be made in the crowd modeling literature, our review has gone further than this. We have comprehensively reviewed a broad scope of crowd modeling scenarios from 1977 to 2014, including simulations of crowd events taken from real life events, simulations of crowds in planning for events, literature looking at techniques for modeling crowd behavior using simulations, and articles which addressed the techniques used to model crowd behavior. Moreover, we have examined the theoretical underpinnings of each of these 140 articles to determine what assumptions modelers are making about crowd behavior. This is the first systematic comparison of the crowd modeling literature with current models of crowd behavior in social psychology.

By examining what crowd modelers are creating and comparing it to empirical research of collective behavior, we can see what future models need to change. Although models have been successful in simulating crowds without a group identity, as yet simulations have not aimed to model large psychological behavior. Modelers are yet to model the transformation of people from identifying as an individual to identifying as a member of the crowd. Without this they cannot model meaningful collective behavior where the behavior of a large crowd can be understood in terms of group membership, which is needed to explain scenarios where there is more than one crowd present (such as the football fans mentioned previously). To create a realistic model of crowd behavior, crowd modelers must look to the extensive empirical research on group and crowd behavior in social psychology.

We propose that to make more realistic simulations of collective behavior, which can be applied to a broad range of scenarios, modelers must implement aspects from self-categorization theory. Specifically, these simulations should be based on the aspects of self-categorization theory which can explain how members of a large crowd share the same group identity, the transformation from the individual identities to the identities as group members, and the subsequent actions which follow from being part of that group. While this would create more realistic models of collective behavior for modelers, this interdisciplinary work could also benefit social psychologists. By creating models which incorporate self-categorization theory and accurately simulate the behavior that we have found in empirical search, it could help to develop theories of collective behavior in social psychology. Only by incorporating these aspects that are based on extensive empirical social psychological research will crowd modelers be able to realistically simulate, monitor, and predict collective behavior in crowds across a wide range of crowd events.

References

  1. Aguirre B. E., El-Tawil S., Best E., Gill K. B., & Fedorov V. (2011). Contributions of social science to agent-based models of building evacuation. Contemporary Social Science, 6, 415–432. 10.1080/21582041.2011.609380 [DOI] [Google Scholar]
  2. Allport F. H. (1924). Social psychology. Boston: Houghton Miffin. [Google Scholar]
  3. Alnabulsi H., & Drury J. (2014). Social identification moderates the effect of crowd density on safety at the Hajj. Proceedings of the National Academy of Sciences, USA of the United States of America, 111, 9091–9096. 10.1073/pnas.1404953111 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Andrade E. L., Blunsden S., & Fisher R. B. (2006, August). Modelling crowd scenes for event detection. Paper presented at the International Conference of Pattern Recognition, Hong Kong.
  5. Asch S. (1952). Social psychology. Englewood Cliffs, NJ: Prentice Hall; 10.1037/10025-000 [DOI] [Google Scholar]
  6. Aveni A. F. (1977). The not-so-lonely crowd: Friendship groups in collective behavior. Sociometry, 40, 96–99. 10.2307/3033551 [DOI] [Google Scholar]
  7. Banarjee S., Grosan C., & Abraham A. (2005, September). Emotional ant-based modeling of crowd dynamics. In Proceedings of the Seventh International Symposium on Symbolic and Numeric Algorithms for Scientific Computing. Symposium conducted at Timisoara, Romania 10.1109/SYNASC.2005.35 [DOI]
  8. Bandini S., Gorrini A., & Vizzari G. (2014). Towards an integrated approach to crowd analysis and crowd synthesis: A case study and first results. Pattern Recognition Letters, 44, 16–29. 10.1016/j.patrec.2013.10.003 [DOI] [Google Scholar]
  9. Bicho A. D. L., Rodrigues R. A., Musse S. R., Jung C. R., Paravisi M., & Magalhães L. P. (2012). Simulating crowds based on a space colonization algorithm. Computers & Graphics, 36, 70–79. 10.1016/j.cag.2011.12.004 [DOI] [Google Scholar]
  10. Bierlaire M., Antonini G., & Weber M. (2003, August). Behavioral dynamics for pedestrians. In K. Axhausen (Chair), Moving through nets: The physical and social dimensions of travel. Symposium conducted at the International Conference on Travel Behaviour Research, Lucerne, Switzerland.
  11. Bodgi J., Erlicher S., & Argoul P. (2007). Lateral vibration of footbridges under crowd-loading: Continuous crowd modeling approach. Key Engineering Materials, 347, 685–690. 10.4028/www.scientific.net/KEM.347.685 [DOI] [Google Scholar]
  12. Bruno L., Tosin A., Tricerri P., & Venuti F. (2011). Non-local first-order modelling of crowd dynamics: A multidimensional framework with applications. Applied Mathematical Modelling, 35, 426–445. 10.1016/j.apm.2010.07.007 [DOI] [Google Scholar]
  13. Burstedde C., Klauck K., Schadschneider A., & Zittartz J. (2001). Simulation of pedestrian dynamics using a two-dimensional cellular automaton. Physica A. Statistical Mechanics and Its Applications, 295, 507–525. 10.1016/S0378-4371(01)00141-8 [DOI] [Google Scholar]
  14. Carroll S. P., Owen J. S., & Hussein M. F. M. (2013). A coupled biomechanical/discrete element crowd model of crowd-bridge dynamic interaction and application to the Clifton suspension bridge. Engineering Structures, 49, 58–75. 10.1016/j.engstruct.2012.10.020 [DOI] [Google Scholar]
  15. Chen D., & Huang P. (2011). Motion-based unusual event detection in human crowds. Journal of Visual Communication and Image Representation, 22, 178–186. 10.1016/j.jvcir.2010.12.004 [DOI] [Google Scholar]
  16. Chen D., Wang L., Wu X., Chen J., Khan S. U., Kołodziej J., et al. Liu W. (2013). Hybrid modelling and simulation of huge crowd over a hierarchical grid architecture. Future Generation Computer Systems, 29, 1309–1317. 10.1016/j.future.2012.03.006 [DOI] [Google Scholar]
  17. Chen Y., & Lin Y. (2009). Controlling the movement of crowds in computer graphics by using the mechanism of particle swarm optimization. Applied Soft Computing, 9, 1170–1176. 10.1016/j.asoc.2009.03.004 [DOI] [Google Scholar]
  18. Cho S. H., & Kang H. B. (2014). Abnormal behavior detection using hybrid agents in crowded scenes. Pattern Recognition Letters, 4, 64–70. [Google Scholar]
  19. Chong X., Liu W., Huang P., & Badler N. I. (2014). Hierarchical crowd analysis and anomaly detection. Journal of Visual Languages and Computing, 25, 376–393. 10.1016/j.jvlc.2013.12.002 [DOI] [Google Scholar]
  20. Chow W. K. (2007). “Waiting time” for evacuation in crowded areas. Building and Environment, 42, 3757–3761. 10.1016/j.buildenv.2006.08.001 [DOI] [Google Scholar]
  21. Chrysostomou D., Sirakoulis G. C., & Gasteratos A. (2014). A bio-inspired multi-camera system for dynamic crowd analysis. Pattern Recognition Letters, 44, 141–151. 10.1016/j.patrec.2013.11.020 [DOI] [Google Scholar]
  22. Davidich M., & Köster G. (2013). Predicting pedestrian flow: A methodology and a proof of concept based on real-life data. PLoS ONE, 8(12), 10.1371/journal.pone.0083355 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Degond P., & Hua J. (2013). Self-organized hydrodynamics with congestion and path formation in crowds. Journal of Computational Physics, 237, 299–319. 10.1016/j.jcp.2012.11.033 [DOI] [Google Scholar]
  24. Dogbe C. (2012). On the modelling of crowd dynamics by generalized kinetic models. Journal of Mathematical Analysis and Applications, 387, 512–532. 10.1016/j.jmaa.2011.09.007 [DOI] [Google Scholar]
  25. Dou M., Chen J., Chen D., Chen X., Deng Z., Zhang X., et al. Wang J. (2014). Modeling and simulation for natural disaster contingency planning driven by high-resolution remote sensing images. Future Generation Computer Systems, 37, 367–377. 10.1016/j.future.2013.12.018 [DOI] [Google Scholar]
  26. Drury J. (2012). Collective resilience in mass emergencies and disasters In Jetten J., Haslam C., & Haslam A. S. (Eds.), The social cure: Identity, health and well-being (pp. 195–216). Hove, England and New York, NY: Psychology Press. [Google Scholar]
  27. Drury J., Cocking C., & Reicher S. (2009). Everyone for themselves? A comparative study of crowd solidarity among emergency survivors. The British Journal of Social Psychology, 48, 487–506. 10.1348/014466608X357893 [DOI] [PubMed] [Google Scholar]
  28. Drury J., Cocking C., Reicher S., Burton A., Schofield D., Hardwick A., et al. Langston P. (2009). Cooperation versus competition in a mass emergency evacuation: A new laboratory simulation and a new theoretical model. Behavior Research Methods, 41, 957–970. 10.3758/BRM.41.3.957 [DOI] [PubMed] [Google Scholar]
  29. Drury J., & Reicher S. D. (2010). Crowd control. Scientific American Mind, 21, 58–65. 10.1038/scientificamericanmind1110-58 [DOI] [Google Scholar]
  30. Drury J., Reicher S., & Stott C. (2003). Transforming the boundaries of collective identity: From the “local” anti-road campaign to “global” resistance? Social Movement Studies, 2, 191–212. 10.1080/1474283032000139779 [DOI] [Google Scholar]
  31. Fang Z., Lo S., & Lu J. (2003). On the relationship between crowd density and movement velocity. Fire Safety Journal, 38, 271–283. 10.1016/S0379-7112(02)00058-9 [DOI] [Google Scholar]
  32. Fang Z., Yuan J. P., Wang Y. C., & Lo S. M. (2008). Survey of pedestrian movement and development of a crowd dynamics model. Fire Safety Journal, 43, 459–465. 10.1016/j.firesaf.2007.12.005 [DOI] [Google Scholar]
  33. Feinberg W. E., & Johnson N. R. (1995). FIRESCAPE: A computer simulation model of reaction to a fire alarm. The Journal of Mathematical Sociology, 20, 247–269. 10.1080/0022250X.1995.9990164 [DOI] [Google Scholar]
  34. Fogelson R. M. (1971). Violence as protest: A study of riots and ghettos. Garden City, NY: Doubleday. [Google Scholar]
  35. Franca R., Marietto M., & Steinberger M. B. (2009, August). Proposing a cognitive multi-agent model for the panic in crowds phenomenon. In Applications of Digital Information and Web Technologies (pp. 737 –742). Symposium conducted at the Second International Conference on the Applications of Digital Information and Web Technologies, London, England.
  36. Fridman N., & Kaminka G. A. (2007). Towards a cognitive model of crowd behavior based on social comparison theory. In A. Cohn (Ed.), Proceedings of the national conference on artificial intelligence (Vol. 22, Iss. 1, pp. 731–737). Twenty-second national conference on artificial intelligence.
  37. Galea E. (2006, May). Engineering crowd safety through simulation. Paper presented at the Future Technology Initiatives for the Olympics Exhibition, London.
  38. Galea E. R., Owen M., & Lawrence P. J. (1996). Computer modelling of human behaviour in aircraft fire accidents. Toxicology, 115(1–3), 63–78. http://www.ncbi.nlm.nih.gov/pubmed/9016741.10.1016/S0300-483X(96)03495-6 [DOI] [PubMed] [Google Scholar]
  39. Gallup A. C., Hale J. J., Sumpter D. J., Garnier S., Kacelnik A., Krebs J. R., & Couzin I. D. (2012). Visual attention and the acquisition of information in human crowds. Proceedings of the National Academy of Sciences, USA of the United States of America, 109, 7245–7250. 10.1073/pnas.1116141109 [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Gawroński P., & Kułakowski K. (2011). Crowd dynamics - being stuck. Computer Physics Communications, 182, 1924–1927. 10.1016/j.cpc.2011.03.005 [DOI] [Google Scholar]
  41. Georgoudas I. G., Kyriakos P., Sirakoulis G. C., & Andreadis I. T. (2010). An FPGA implemented cellular automaton crowd evacuation model inspired by the electrostatic-induced potential fields. Microprocessors and Microsystems, 34(7–8), 285–300. 10.1016/j.micpro.2010.06.001 [DOI] [Google Scholar]
  42. Gerdimos A. (2006, May). Pedestrian simulation: Recent advancements and new directions. Paper presented at the Future Technology Initiatives for the Olympics Exhibition, London, England.
  43. Giner S. (1976). Mass society. London, England: Martin Robertson. [Google Scholar]
  44. Goldenstein S., Karavelas M., Metaxas D., Guibas L., Aaron E., & Goswami A. (2001). Scalable nonlinear dynamical systems for agent steering and crowd simulation. Computers & Graphics, 25, 983–998. 10.1016/S0097-8493(01)00153-4 [DOI] [Google Scholar]
  45. Gutierrez D., Frischer B., Cerezo E., Gomez A., & Seron F. (2007). AI and virtual crowds: Populating the Colosseum. Journal of Cultural Heritage, 8, 176–185. 10.1016/j.culher.2007.01.007 [DOI] [Google Scholar]
  46. Haciomeroglu M., Barut O., Ozcan C. Y., & Sever H. (2013). A GPU-assisted hybrid model for real-time crowd simulations. Computers & Graphics, 37, 862–872. 10.1016/j.cag.2013.05.006 [DOI] [Google Scholar]
  47. Heïgeas L., Luciani A., Thollot J., & Castagné N. (2003). A physically-based particle model of emergent crowd behaviors. Paper presented at International Conference Graphicon, Moscow, Russia.
  48. Helbing D., Farkas I. J., Molnar P., & Vicsek T. (2002). Simulation of pedestrian crowds in normal and evacuation situations. Pedestrian and Evacuation Dynamics, 21, 21–58. [Google Scholar]
  49. Helbing D., Farkas I., & Vicsek T. (2000). Simulating dynamical features of escape panic. Nature, 407, 487–490. 10.1038/35035023 [DOI] [PubMed] [Google Scholar]
  50. Helbing D., Johansson A., & Al-Abideen H. Z. (2007). Dynamics of crowd disasters: An empirical study. Physical Review E: Statistical, Nonlinear, and Soft Matter Physics, 75(4 Pt. 2), 10.1103/PhysRevE.75.046109 [DOI] [PubMed] [Google Scholar]
  51. Helbing D., Molnár P., Farkas I. J., & Bolay K. (2001). Self-organizing pedestrian movement. Environment and Planning B, Planning & Design, 28, 361–383. 10.1068/b2697 [DOI] [Google Scholar]
  52. Heliövaara S., Korhonen T., Hostikka S., & Ehtamo H. (2012). Counterflow model for agent-based simulation of crowd dynamics. Building and Environment, 48, 89–100. 10.1016/j.buildenv.2011.08.020 [DOI] [Google Scholar]
  53. Henein C. M., & White T. (2007). Macroscopic effects of microscopic forces between agents in crowd models. Physica A: Statistical Mechanics and Its Applications, 373, 694–712. 10.1016/j.physa.2006.06.023 [DOI] [Google Scholar]
  54. Hu X., Zheng H., Wang W., & Li X. (2013). A novel approach for crowd video monitoring of subway platforms. Optik-International Journal for Light and Electron Optics, 124, 5301–5306. 10.1016/j.ijleo.2013.03.057 [DOI] [Google Scholar]
  55. Hughes R. L. (2000). The flow of large crowds of pedestrians. Mathematics and Computers in Simulation, 53, 367–370. 10.1016/S0378-4754(00)00228-7 [DOI] [Google Scholar]
  56. Hussain N., Yatim H. S. M., Hussain N. L., Yan J. L. S., & Haron F. (2011). CDES: A pixel-based crowd density estimation system for Masjid al-Haram. Safety Science, 49, 824–833. 10.1016/j.ssci.2011.01.005 [DOI] [Google Scholar]
  57. Idrees H., Warner N., & Shah M. (2014). Tracking in dense crowds using prominence and neighborhood motion concurrence. Image and Vision Computing, 32, 14–26. 10.1016/j.imavis.2013.10.006 [DOI] [Google Scholar]
  58. Ji Q., & Gao C. (2007). Simulating crowd evacuation with a leader-follower model. International Journal of Computer Sciences and Engineering Systems, 1, 249–252. [Google Scholar]
  59. Ji X., Zhou X., & Ran B. (2013). A cell-based study on pedestrian acceleration and overtaking in a transfer station corridor. Physica A. Statistical Mechanics and Its Applications, 392, 1828–1839. 10.1016/j.physa.2012.12.016 [DOI] [Google Scholar]
  60. Jiang H., Xu W., Mao T., Li C., Xia S., & Wang Z. (2010). Continuum crowd simulation in complex environments. Computers & Graphics, 34, 537–544. 10.1016/j.cag.2010.05.013 [DOI] [Google Scholar]
  61. Jiang Y., Zhang P., Wong S. C., & Liu R. (2010). A higher-order macroscopic model for pedestrian flows. Physica A: Statistical Mechanics and Its Applications, 389, 4623–4635. 10.1016/j.physa.2010.05.003 [DOI] [Google Scholar]
  62. Ji-hua H., Cheng-zhi Z., Zhi-feng C., & Bo W. (2013). A Research of Pedestrian Evacuation Simulation for BRT Station based on Fine Grid Method. Procedia Engineering, 52, 137–144. 10.1016/j.proeng.2013.02.118 [DOI] [Google Scholar]
  63. Johansson A., Batty M., Hayashi K., Al Bar O., Marcozzi D., & Memish Z. A. (2012). Crowd and environmental management during mass gatherings. The Lancet infectious diseases, 12, 150–156. 10.1016/S1473-3099(11)70287-0 [DOI] [PubMed] [Google Scholar]
  64. Johnson N. R. (1988). Fire in a crowded theatre: A descriptive analysis of the emergence of panic. International Journal of Mass Emergencies and Disasters, 6, 7–26. [Google Scholar]
  65. Johnson N. R., & Feinberg W. E. (1977). A computer simulation of the emergence of consensus in crowds. American Sociological Review, 42, 505–521. 10.2307/2094754 [DOI] [Google Scholar]
  66. Johnson N. R., & Feinberg W. E. (1997). The impact of exit instructions and number of exits in fire emergencies: A computer simulation investigation. Journal of Environmental Psychology, 17, 123–133. 10.1006/jevp.1997.0047 [DOI] [Google Scholar]
  67. Johnson N. F., Hart M., & Hui P. M. (1999). Crowd effects and volatility in markets with competing agents. Physica A: Statistical Mechanics and its Applications, 269, 1–8. doi: 10.1016/S0378-4371(99)00073-4 [DOI] [Google Scholar]
  68. Kamkarian P., & Hexmoor H. (2013). Exploiting the imperialist competition algorithm to determine exit door efficacy for public buildings. Simulation, 90, 24–51. 10.1177/0037549713509416 [DOI] [Google Scholar]
  69. Karni E., & Schmeidler D. (1986). Self-preservation as a foundation of rational behaviour under risk. Journal of Economic Behavior & Organization, 7, 71–81. 10.1016/0167-2681(86)90022-3 [DOI] [Google Scholar]
  70. Khaleghi A. M., Xu D., Wang Z., Li M., Lobos A., Liu J., & Son Y.-J. (2013). A DDDAMS based planning and control framework for surveillance and crowd control via UAVs and UGVs. Expert Systems with Applications, 40, 7168–7183. 10.1016/j.eswa.2013.07.039 [DOI] [Google Scholar]
  71. Kirchner A., Klüpfel H., Nishinari K., Schadschneider A., & Schreckenberg M. (2003). Simulation of competitive egress behavior: Comparison with aircraft evacuation data. Physica A: Statistical Mechanics and Its Applications, 324, 689–697. 10.1016/S0378-4371(03)00076-1 [DOI] [Google Scholar]
  72. Kirchner A., & Schadschneider A. (2002). Simulation of evacuation processes using a bionics inspired cellular automaton model for pedestrian dynamics. Physica A: Statistical Mechanics and Its Applications, 312(1–2):260–276. 10.1016/S0378-4371(02)00857-9 [DOI] [Google Scholar]
  73. Köster G., Seitz M., Treml F., Hartmann D., & Klein W. (2011). On modelling the influence of group formations in a crowd. Contemporary Social Science: Journal of the Academy of Social Sciences, 6, 387–414. 10.1080/21582041.2011.619867 [DOI] [Google Scholar]
  74. Kountouriotis V., Thomopoulos S. C. A., & Papelis Y. (2014). An agent-based crowd behaviour model for real time crowd behaviour simulation. Pattern Recognition Letters, 44, 30–38. 10.1016/j.patrec.2013.10.024 [DOI] [Google Scholar]
  75. Krausz B., & Bauckhage C. (2012). Loveparade 2010: Automatic video analysis of a crowd disaster. Computer Vision and Image Understanding, 116, 307–319. 10.1016/j.cviu.2011.08.006 [DOI] [Google Scholar]
  76. Lachapelle A., & Wolfram M. T. (2011). On a mean field game approach modeling congestion and aversion in pedestrian crowds. Transportation Research Part B: Methodological, 45, 1572–1589. 10.1016/j.trb.2011.07.011 [DOI] [Google Scholar]
  77. Langston P. A., Masling R., & Asmar B. N. (2006). Crowd dynamics discrete element multi-circle model. Safety Science, 44, 395–417. 10.1016/j.ssci.2005.11.007 [DOI] [Google Scholar]
  78. Le Bon G. (1960). The crowd (Translation of Psychologie des foules). New York, NY: Viking Press; (Original work published in 1895) [Google Scholar]
  79. Lee R. S. C., & Hughes R. L. (2006). Prediction of human crowd pressures. Accident; Analysis and Prevention, 38, 712–722. 10.1016/j.aap.2006.01.001 [DOI] [PubMed] [Google Scholar]
  80. Lee R. S. C., & Hughes R. L. (2007). Minimisation of the risk of trampling in a crowd. Mathematics and Computers in Simulation, 74, 29–37. 10.1016/j.matcom.2006.06.029 [DOI] [Google Scholar]
  81. Lei W., Li A., Gao R., Hao X., & Deng B. (2012). Simulation of pedestrian crowds’ evacuation in a huge transit terminal subway station. Physica A: Statistical Mechanics and its Applications, 391, 5355–5365. 10.1016/j.physa.2012.06.033 [DOI] [Google Scholar]
  82. Li X., & Qin W. (2012). A crowd behavior model based on reciprocal velocity obstacle algorithm. Procedia Engineering, 29, 2887–2893. 10.1016/j.proeng.2012.01.409 [DOI] [Google Scholar]
  83. Lister W. D., & Day A. (2012). Stream-based animation of real-time crowd scenes. Computers & Graphics, 36, 651–657. 10.1016/j.cag.2012.02.014 [DOI] [Google Scholar]
  84. Lo S. M., Fang Z., Lin P., & Zhi G. S. (2004). An evacuation model: The SGEM package. Fire Safety Journal, 39, 169–190. 10.1016/j.firesaf.2003.10.003 [DOI] [Google Scholar]
  85. Löhner R. (2010). On the modeling of pedestrian motion. Applied Mathematical Modelling, 34, 366–382. 10.1016/j.apm.2009.04.017 [DOI] [Google Scholar]
  86. Lott A. J., & Lott B. E. (1965). Group cohesiveness as interpersonal attraction: A review of relationships with antecedent and consequent variables. Psychological Bulletin, 64, 259–309. 10.1037/h0022386 [DOI] [PubMed] [Google Scholar]
  87. Lozano M., Morillo P., Orduña J. M., Cavero V., & Vigueras G. (2009). A new system architecture for crowd simulation. Journal of Network and Computer Applications, 32, 474–482. 10.1016/j.jnca.2008.02.011 [DOI] [Google Scholar]
  88. Ma J., Lo S. M., Song W. G., Wang W. L., Zhang J., & Liao G. X. (2013). Modeling pedestrian space in complex building for efficient pedestrian traffic simulation. Automation in Construction, 30, 25–36. 10.1016/j.autcon.2012.11.032 [DOI] [Google Scholar]
  89. Ma J., & Song W. (2013). Automatic clustering method of abnormal crowd flow pattern detection. Procedia Engineering, 62, 509–518. 10.1016/j.proeng.2013.08.094 [DOI] [Google Scholar]
  90. Manfredi M., Vezzani R., Calderara S., & Cucchiara R. (2013). Detection of static groups and crowds gathered in open spaces by texture classification. Pattern Recognition Letters, 44, 39–48. 10.1016/j.patrec.2013.11.001 [DOI] [Google Scholar]
  91. Mann R. P., Faria J., Sumpter D. J., & Krause J. (2013). The dynamics of audience applause. Journal of the Royal Society, Interface, 10, 10.1098/rsif.2013.0466 [DOI] [PMC free article] [PubMed] [Google Scholar]
  92. Marana A. N., Velastin S. A., Costa L. D. F., & Lotufo R. A. (1998). Automatic estimation of crowd density using texture. Safety Science, 28, 165–175. 10.1016/S0925-7535(97)00081-7 [DOI] [Google Scholar]
  93. Maury B., Roudneff-Chupin A., & Santambrogio F. (2010). A macroscopic crowd motion model of gradient flow type. Mathematical Models and Methods in Applied Sciences, 20, 1787–1821. 10.1142/S0218202510004799 [DOI] [Google Scholar]
  94. Mawson A. R. (2005). Understanding mass panic and other collective responses to threat and disaster. Psychiatry, 68, 95–113. 10.1521/psyc.2005.68.2.95 [DOI] [PubMed] [Google Scholar]
  95. Mazzon R., Tahir S. F., & Cavallaro A. (2012). Person re-identification in crowd. Pattern Recognition Letters, 33, 1828–1837. 10.1016/j.patrec.2012.02.014 [DOI] [Google Scholar]
  96. Mehran R., Oyama A., & Shah M. (2009). Abnormal crowd behavior detection using social force model. Conference on Computer Vision and Pattern Recognition, 1, 935–942. 10.1109/CVPR.2009.5206641 [DOI] [Google Scholar]
  97. Mekni M. (2013). Crowd simulation using informed virtual geospatial environments. 2nd WSEAS International Conference on Information Technology and Computer Networks, 1, 31–42. Retrieved from http://www.wseas.us/e-library/conferences/2013/Antalya/ITCN/ITCN-03.pdf [Google Scholar]
  98. Milgram S., & Toch H. (1969). Collective behavior: Crowds and social movements In Lindzey G., Gilbert D., & Fiske S. T. (Eds.), The handbook of social psychology (Vol. 4, pp. 507–610). Reading, MA: Addison Wesley. [Google Scholar]
  99. Moore S. C., Flajšlik M., Rosin P. L., & Marshall D. (2008). A particle model of crowd behavior: Exploring the relationship between alcohol, crowd dynamics and violence. Aggression and Violent Behavior, 13, 413–422. 10.1016/j.avb.2008.06.004 [DOI] [Google Scholar]
  100. Moussaïd M., Helbing D., & Theraulaz G. (2011). How simple rules determine pedestrian behavior and crowd disasters. Proceedings of the National Academy of Sciences, USA of the United States of America, 108, 6884–6888. 10.1073/pnas.1016507108 [DOI] [PMC free article] [PubMed] [Google Scholar]
  101. Moussaïd M., Perozo N., Garnier S., Helbing D., & Theraulaz G. (2010). The walking behaviour of pedestrian social groups and its impact on crowd dynamics. PLoS ONE, 5(4), 10.1371/journal.pone.0010047 [DOI] [PMC free article] [PubMed] [Google Scholar]
  102. Mukovskiy A., Slotine J. E., & Giese M. A. (2013). Dynamically stable control of articulated crowds. Journal of Computational Science, 4, 304–310. 10.1016/j.jocs.2012.08.019 [DOI] [Google Scholar]
  103. Musse S. R., Babski C., Capin T., & Thalmann D. (1998). Crowd modelling in collaborative virtual environments. In Proceedings of the ACM Symposium on Virtual Reality Software and Technology 1998 (pp. 115–123). Paper presented at ACM Symposium on Virtual Reality Software and Technology, Taipei, Taiwan 10.1145/293701.293716 [DOI]
  104. Musse S. R., & Thalmann D. (1997). A model of human crowd behavior: Group inter-relationship and collision detection analysis. In D. Thalmann, & M. van de Panne (Eds.), Computer Animation and Simulations ‘97. Paper presented at Eurographics workshop, Budapest, Wien.
  105. Musse S. R., & Thalmann D. (2001). Hierarchical model for real time simulation of virtual human crowds. Visualization and Computer Graphics. IEEE Transactions on, 7, 152–164. [Google Scholar]
  106. Narain R., Golas A., Curtis S., & Lin M. C. (2009). Aggregate dynamics for dense crowd simulation. ACM Transactions on Graphics, 28, 122–130. 10.1145/1618452.1618468 [DOI] [Google Scholar]
  107. Neville F., & Reicher S. (2011). The experience of collective participation: Shared identity, relatedness and emotionality. Contemporary Social Science, 6, 377–396. 10.1080/21582041.2012.627277 [DOI] [Google Scholar]
  108. Nilsson D., & Johansson A. (2009). Social influence during the initial phase of a fire evacuation-Analysis of evacuation experiments in a cinema theatre. Fire Safety Journal, 44, 71–79. 10.1016/j.firesaf.2008.03.008 [DOI] [Google Scholar]
  109. Novelli D., Drury J., & Reicher S. (2010). Come together: Two studies concerning the impact of group relations on personal space. The British Journal of Social Psychology, 49, 223–236. 10.1348/014466609X449377 [DOI] [PubMed] [Google Scholar]
  110. Oğuz O., Akaydın A., Yılmaz T., & Güdükbay U. (2010). Emergency crowd simulation for outdoor environments. Computers & Graphics, 34, 136–144. 10.1016/j.cag.2009.12.004 [DOI] [Google Scholar]
  111. Pan X., Han C. S., Dauber K., & Law K. H. (2007). A multi-agent based framework for the simulation of human and social behaviors during emergency evacuations. AI & Society, 22, 113–132. 10.1007/s00146-007-0126-1 [DOI] [Google Scholar]
  112. Parunak H. V. D., Brooks S. H., Brueckner S. A., & Gupta R. (2012, October). Apoptotic stigmergic agents for real-time swarming simulation. In AAAI Fall Symposium: Human Control of Bioinspired Swarms (pp. 59–64). Retrieved from http://www.aaai.org/ocs/index.php/FSS/FSS12/paper/viewFile/5579/5839
  113. Pelechano N., Allbeck J. M., & Badler N. I. (2007, August). Controlling individual agents in high-density crowd simulation. Paper presented at the Eurographics Symposium on Computer Animation, San Diego, CA.
  114. Pires T. T. (2005). An approach for modeling human cognitive behavior in evacuation models. Fire Safety Journal, 40, 177–189. 10.1016/j.firesaf.2004.10.004 [DOI] [Google Scholar]
  115. Qiu F., & Hu X. (2010). Modeling group structures in pedestrian crowd simulation. Simulation Modelling Practice and Theory, 18, 190–205. 10.1016/j.simpat.2009.10.005 [DOI] [Google Scholar]
  116. Ramesh M. V., Shanmughan A., & Prabha R. (2014). Context aware ad hoc network for mitigation of crowd disasters. Ad Hoc Networks, 18, 55–70. 10.1016/j.adhoc.2013.02.006 [DOI] [Google Scholar]
  117. Ran H., Sun L., & Gao X. (2014). Influences of intelligent evacuation guidance system on crowd evacuation in building fire. Automation in Construction, 41, 78–82. 10.1016/j.autcon.2013.10.022 [DOI] [Google Scholar]
  118. Reicher S. D. (1984). The St. Paul’s Riot: An explanation of the limits of crowd action in terms of a social identity model. European Journal of Social Psychology, 14, 1–21. 10.1002/ejsp.2420140102 [DOI] [Google Scholar]
  119. Reicher S. D. (1996). The Battle of Westminster: Developing the social identity model of crowd behaviour in order to explain the initiation and development of collective conflict. European Journal of Social Psychology, 26, 115–134. [DOI] [Google Scholar]
  120. Reicher S., & Drury J. (2011). Collective identity, political participation and the making of the social self In Azzi A., Chryssochoou X., Klandermans B., & Simon B. (Eds.), Identity and participation in culturally diverse societies: A multidisciplinary perspective (pp. 158–176). Oxford, England: Wiley-Blackwell. [Google Scholar]
  121. Reicher S. D., & Stott C. (2011). Mad mobs and Englishmen? Myths and realities of the 2011 riots. London, England: Constable and Robinson. [Google Scholar]
  122. Ryan D., Denman S., Fookes C., & Sridharan S. (2014). Scene invariant multi camera crowd counting. Pattern Recognition Letters, 44, 98–112. 10.1016/j.patrec.2013.10.002 [DOI] [Google Scholar]
  123. Sagun A., Bouchlaghem D., & Anumba C. J. (2011). Computer simulations vs. building guidance to enhance evacuation performance of buildings during emergency events. Simulation Modelling Practice and Theory, 19, 1007–1019. 10.1016/j.simpat.2010.12.001 [DOI] [Google Scholar]
  124. Santos G., & Aguirre B. (2004). A critical review of emergency evacuation simulation models. In Gaithersburg M. D., Peacock R. D., & Kuligowski E. D. (Eds.), Proceedings of building occupant movement during fire emergencies. Symposium conducted at the meeting of National Institute of Standards and Technology, Gaithersburg, MD.
  125. Sarmady S., Haron F., & Talib A. Z. (2011). A cellular automata model for circular movements of pedestrians during Tawaf. Simulation Modelling Practice and Theory, 19, 969–985. 10.1016/j.simpat.2010.12.004 [DOI] [Google Scholar]
  126. Shao J., Dong N., & Tong M. (2013). Multi-part sparse representation in random crowded scenes tracking. Pattern Recognition Letters, 34, 780–788. 10.1016/j.patrec.2012.07.008 [DOI] [Google Scholar]
  127. Shendarkar A., Vasudevan K., Lee S., & Son Y. J. (2008). Crowd simulation for emergency response using BDI agents based on immersive virtual reality. Simulation Modelling Practice and Theory, 16, 1415–1429. 10.1016/j.simpat.2008.07.004 [DOI] [Google Scholar]
  128. Sherif M. (1967). Group conflict and co-operation: Their social psychology. London, England: Routledge & Kegan Paul. [Google Scholar]
  129. Shi J., Ren A., & Chen C. (2009). Agent-based evacuation model of large picnic buildings under fire conditions. Automation in Construction, 18, 338–347. 10.1016/j.autcon.2008.09.009 [DOI] [Google Scholar]
  130. Shi C., Zhong M., Nong X., He L., Shi J., & Feng G. (2012). Modeling and safety strategy of passenger evacuation in a metro station in China. Safety Science, 50, 1319–1332. 10.1016/j.ssci.2010.07.017 [DOI] [Google Scholar]
  131. Silverberg J. L., Bierbaum M., Sethna J. P., & Cohen I. (2013). Collective motion of humans in mosh and circle pits at heavy metal concerts. Physical Review Letters, 110, 228701 10.1103/PhysRevLett.110.228701 [DOI] [PubMed] [Google Scholar]
  132. Sime J. D. (1983). Affiliative behaviour during escape to building exits. Journal of Environmental Psychology, 3, 21–41. 10.1016/S0272-4944(83)80019-X [DOI] [Google Scholar]
  133. Sime J. D. (1985). Designing for people or ball-bearings? Design Studies, 6, 163–168. 10.1016/0142-694X(85)90007-9 [DOI] [Google Scholar]
  134. Singh H., Arter R., Dodd L., Langston P., Lester E., & Drury J. (2009). Modelling subgroup behaviour in crowd dynamics DEM simulation. Applied Mathematical Modelling, 33, 4408–4423. 10.1016/j.apm.2009.03.020 [DOI] [Google Scholar]
  135. Smith A., James C., Jones R., Langston P., Lester E., & Drury J. (2009). Modelling contra-flow in crowd dynamics DEM simulation. Safety Science, 47, 395–404. 10.1016/j.ssci.2008.05.006 [DOI] [Google Scholar]
  136. Song Y., Gong J., Li Y., Cui T., Fang L., & Cao W. (2013). Crowd evacuation simulation for bioterrorism in micro-spatial environments based on virtual geographic environments. Safety Science, 53, 105–113. 10.1016/j.ssci.2012.08.011 [DOI] [Google Scholar]
  137. Spieser K., & Davison D. E. (2009). Multi-agent stabilisation of the psychological dynamics of one dimensional crowds. Automatica, 45, 657–664. 10.1016/j.automatica.2008.09.013 [DOI] [Google Scholar]
  138. Tajima Y., & Nagatani T. (2001). Scaling behavior of crowd flow outside a hall. Physica A. Statistical Mechanics and Its Applications, 292, 545–554. 10.1016/S0378-4371(00)00630-0 [DOI] [Google Scholar]
  139. Thiel-clemen T., Köster G., & Sarstedt S. (2011). WALK: Emotion-based pedestrian movement simulation in evacuation scenarios In Wittmann J. & Wohlgemuth V. (Eds.), Simulation in Umwelt-und Geowissenschaften: Workshop (pp. 103–112). Berlin, Germany: Shaker Verlag. [Google Scholar]
  140. Thompson E. P. (1971). The moral economy of the English crowd in the eighteenth century. Past & Present, 50, 76–136. 10.1093/past/50.1.76 [DOI] [Google Scholar]
  141. Thompson P. A., & Marchant E. W. (1995). Computer and fluid modelling of evacuation. Safety Science, 18, 277–289. 10.1016/0925-7535(94)00036-3 [DOI] [Google Scholar]
  142. Tong W., & Cheng L. (2013). Simulation of pedestrian flow based on multi-agent. Procedia: Social and Behavioral Sciences, 96, 17–24. 10.1016/j.sbspro.2013.08.005 [DOI] [Google Scholar]
  143. Turner J. C. (1982). Towards a cognitive redefinition of the social group In Tajfel H. (Ed.), Social Identity and intergroup relations (pp. 15–40). Cambridge: New York, NY: Cambridge University Press. [Google Scholar]
  144. Turner J. C. (1985). Social categorization and the self-concept: A social cognitive theory of group behavior. Advances in Group Processes, 2, 77–122. [Google Scholar]
  145. Turner J. C. (1987). The analysis of social influence In Turner J. C., Hogg M. A., Oakes P. J., Reicher S. D., & Wetherell M. S. (Eds.) Rediscovering the social group: A self-categorization theory. Oxford, England: Basil Blackwell. [Google Scholar]
  146. Turner J. C., Hogg M. A., Oakes P. J., Reicher S. D., & Wetherell M. S. (1987). Rediscovering the social group: A self-categorization theory. Oxford, England: Basil Blackwell. [Google Scholar]
  147. Turner R. H., & Killian L. (1957). Collective behaviour. Engelwood Cliffs, NJ: Prentice Hall. [Google Scholar]
  148. Turner R. H., & Killian L. (1987). Collective behaviour (3rd ed.). Englewood Cliffs, NJ: Prentice Hall. [Google Scholar]
  149. van der Schalk J., Fischer A., Doosje B., Wigboldus D., Hawk S., Rotteveel M., & Hess U. (2011). Convergent and divergent responses to emotional displays of ingroup and outgroup. Emotion, 11, 286–298. 10.1037/a0022582 [DOI] [PubMed] [Google Scholar]
  150. Van Rooy D. (2012). A connectionist ABM of social categorisation processes. Advances in Complex Systems, 15, 1–21. 10.1142/S0219525912500774 [DOI] [Google Scholar]
  151. Varas A., Cornejo M. D., Mainemer D., Toledo B., Rogan J., Muñoz V., & Valdivia J. A. (2007). Cellular automaton model for evacuation process with obstacles. Physica A. Statistical Mechanics and Its Applications, 382, 631–642. 10.1016/j.physa.2007.04.006 [DOI] [Google Scholar]
  152. Vasudevan K., & Son Y. J. (2011). Concurrent consideration of evacuation safety and productivity in manufacturing facility planning using multi-paradigm simulations. Computers & Industrial Engineering, 61, 1135–1148. 10.1016/j.cie.2011.07.003 [DOI] [Google Scholar]
  153. Vigueras G., Lozano M., Orduña J. M., & Grimaldo F. (2010). A comparative study of partitioning methods for crowd simulations. Applied Soft Computing, 10, 225–235. 10.1016/j.asoc.2009.07.004 [DOI] [Google Scholar]
  154. Von Sivers I., Templeton A., Köster G., Drury J., & Philippides A. (2014). Humans do not always act selfishly: Social identity and helping in emergency evacuation simulation. Transportation Research Procedia, 2, 585–593. 10.1016/j.trpro.2014.09.099 [DOI] [Google Scholar]
  155. Wagner N., & Agrawal V. (2014). An agent-based simulation system for concert venue crowd evacuation modeling in the presence of a fire disaster. Expert Systems with Applications, 41, 2807–2815. 10.1016/j.eswa.2013.10.013 [DOI] [Google Scholar]
  156. Wang L., Zhang Q., Cai Y., Zhang J., & Ma Q. (2013). Simulation study of pedestrian flow in a station hall during the Spring Festival travel rush. Physica A: Statistical Mechanics and its Applications, 392, 2470–2478. 10.1016/j.physa.2013.01.044 [DOI] [Google Scholar]
  157. Wang X., Zheng X., & Cheng Y. (2012). Evacuation assistants: An extended model for determining effective locations and optimal numbers. Physica A: Statistical Mechanics and its Applications, 391, 2245–2260. 10.1016/j.physa.2011.11.051 [DOI] [Google Scholar]
  158. Wang Z., Li M., Khaleghi A. M., Xu D., Lobos A., Vo C., & Son Y. J. (2013). DDDAMS-based Crowd Control via UAVs and UGVs. Procedia Computer Science, 18, 2028–2035. 10.1016/j.procs.2013.05.372 [DOI] [Google Scholar]
  159. Weifeng Y., & Hai T. K. (2011). A model for simulation of crowd behaviour and the evacuation from a smoke-filled compartment. Physica A: Statistical Mechanics and its Applications, 390, 4210–4218. 10.1016/j.physa.2011.07.044 [DOI] [Google Scholar]
  160. Wu Z., & Radke R. J. (2014). Improving counterflow detection in dense crowds with scene features. Pattern Recognition Letters, 55, 152–160. [Google Scholar]
  161. Xiaoping Z., Jiahui S., & Yuan C. (2010). Analysis of crowd jam in public buildings based on cusp catastrophe theory. Building and Environment, 45, 1755–1761. 10.1016/j.buildenv.2010.01.027 [DOI] [Google Scholar]
  162. Xiong G., Cheng J., Wu X., Chen Y.-L., Ou Y., & Xu Y. (2012). An energy model approach to people counting for abnormal crowd behavior detection. Neurocomputing, 83, 121–135. 10.1016/j.neucom.2011.12.007 [DOI] [Google Scholar]
  163. Xiong M., Lees M., Cai W., Zhou S., & Low M. Y. H. (2010). Hybrid modelling of crowd simulation. Procedia Computer Science, 1, 57–65. 10.1016/j.procs.2010.04.008 [DOI] [Google Scholar]
  164. Yamamoto K., Kokubo S., & Nishinari K. (2007). Simulation for pedestrian dynamics by real coded cellular automata (RCA). Physica A: Statistical Mechanics and Its Applications, 379, 654–660. 10.1016/j.physa.2007.02.040 [DOI] [Google Scholar]
  165. Yan L., Tong W., Hui D., & Zongzhi W. (2012). Research and application on risk assessment DEA model of crowd crushing and trampling accidents in subway stations. Procedia engineering, 43, 494–498. 10.1016/j.proeng.2012.08.085 [DOI] [Google Scholar]
  166. Yaseen S., Al-Habaibeh A., Su D., & Otham F. (2013). Real-time crowd density mapping using a novel sensory fusion model of infrared and visual systems. Safety Science, 57, 313–325. 10.1016/j.ssci.2013.03.007 [DOI] [Google Scholar]
  167. Yu W., & Johansson A. (2007). Modeling crowd turbulence by many-particle simulations. Physical Review E: Statistical, Nonlinear, and Soft Matter Physics, 76(4 Pt. 2), 10.1103/PhysRevE.76.046105 [DOI] [PubMed] [Google Scholar]
  168. Yuan W., & Tan K. H. (2007). An evacuation model using cellular automata. Physica A. Statistical Mechanics and Its Applications, 384, 549–566. 10.1016/j.physa.2007.05.055 [DOI] [Google Scholar]
  169. Yücel Z., Zanlungo F., Ikeda T., Miyashita T., & Hagita N. (2013). Deciphering the crowd: Modeling and identification of pedestrian group motion. Sensors (Basel, Switzerland), 13, 875–897. 10.3390/s130100875 [DOI] [PMC free article] [PubMed] [Google Scholar]
  170. Zanlungo F. (2007). A collision-avoiding mechanism based on a theory of mind. Advances in Complex Systems, 10(Supp. 2), 363–371. 10.1142/S0219525907001410 [DOI] [Google Scholar]
  171. Zanlungo F., Ikeda T., & Kanda T. (2012). A microscopic “social norm” model to obtain realistic macroscopic velocity and density pedestrian distributions. PLoS ONE, 7(12), 10.1371/journal.pone.0050720 [DOI] [PMC free article] [PubMed] [Google Scholar]
  172. Zawidzki M., Chraibi M., & Nishinari K. (2013). Crowd-Z: The user-friendly framework for crowd simulation on an architectural floor plan. Pattern Recognition Letters, 44, 88–97. 10.1016/j.patrec.2013.10.025 [DOI] [Google Scholar]
  173. Zhang Q., Liu M., Liu J., & Zhao G. (2007). Modification of evacuation time computational model for stadium crowd risk analysis. Process Safety and Environmental Protection, 85, 541–548. 10.1205/psep06026 [DOI] [Google Scholar]
  174. Zhang Q., Liu M., Wu C., & Zhao G. (2007). A stranded-crowd model (SCM) for performance based design of stadium egress. Building and Environment, 42, 2630–2636. 10.1016/j.buildenv.2006.06.016 [DOI] [Google Scholar]
  175. Zhang Q., Zhao G., & Liu J. (2009). Performance-based design for large crowd venue control using A multi-agent model. Tsinghua Science and Technology, 14, 352–359. 10.1016/S1007-0214(09)70051-3 [DOI] [Google Scholar]
  176. Zhang X. L., Weng W. G., Yuan H. Y., & Chen J. G. (2013). Empirical study of a unidirectional dense crowd during a real mass event. Physica A: Statistical Mechanics and its Applications, 392, 2781–2791. 10.1016/j.physa.2013.02.019 [DOI] [Google Scholar]
  177. Zhao D., Yang L., & Li J. (2008). Occupants’ behavior of going with the crowd based on cellular automata occupant evacuation model. Physica A: Statistical Mechanics and Its Applications, 387, 3708–3718. 10.1016/j.physa.2008.02.042 [DOI] [Google Scholar]
  178. Zhao L., Wang J., Huang R., Cui H., Qiu X., & Wang X. (2014). Sentiment contagion in complex networks. Physica A: Statistical Mechanics and its Applications, 394, 17–23. 10.1016/j.physa.2013.09.057 [DOI] [Google Scholar]
  179. Zheng L., Zhao J., Cheng Y., Chen H., Liu X., & Wang W. (2014). Geometry-constrained crowd formation animation. Computers & Graphics, 38, 268–276. 10.1016/j.cag.2013.10.035 [DOI] [Google Scholar]
  180. Zheng X., & Cheng Y. (2011). Modeling cooperative and competitive behaviors in emergency evacuation: A game-theoretical approach. Computers & Mathematics with Applications (Oxford, England), 62, 4627–4463. 10.1016/j.camwa.2011.10.048 [DOI] [Google Scholar]
  181. Zheng X., Sun J., & Zhong T. (2010). Study on mechanics of crowd jam based on the cusp catastrophe model. Safety Science, 48, 1236–1241. 10.1016/j.ssci.2010.07.003 [DOI] [Google Scholar]

Articles from Review of General Psychology are provided here courtesy of American Psychological Association

RESOURCES