A Simulation Study on the Performance of the Simple Difference and Covariance-Adjusted Scores in Randomized Experimental Designs

Abstract

Research by Huck and McLean (1975) demonstrated that the covariance-adjusted score is more powerful than the simple difference score, yet recent reviews indicate researchers are equally likely to use either score type in two-wave randomized experimental designs. A Monte Carlo simulation was conducted to examine the conditions under which the simple difference and covariance-adjusted scores were more or less powerful to detect treatment effects when relaxing certain assumptions made by Huck and McLean (1975). Four factors were manipulated in the design including sample size, normality of the pretest and posttest distributions, the correlation between pretest and posttest, and posttest variance. A 5 × 5 × 4 × 3 mostly crossed design was run with 1,000 replications per condition, resulting in 226,000 unique samples. The gain score was nearly as powerful as the covariance-adjusted score when pretest and posttest variances were equal, and as powerful in fan-spread growth conditions; thus, under certain circumstances the gain score could be used in two-wave randomized experimental designs.

Questions about the measurement of change in experimental and quasi-experimental designs are not new. At the heart of this matter often lies the question, what is the most appropriate way to analyze data between two points in time? This question may lead to many answers, and has been treated by Tucker, Damarin, and Messick (1966), Lord (1967, 1969), Cronbach and Furby (1970), and Rubin (1974). More recently, Rogosa, Brandt, and Zimowski (1982), Rogosa and Willett (1985), and Willett and Sayer (1994) provided general guidelines into the realm of statistical analysis of pretest-posttest data; yet despite such provisions, no consensus has yet been reached as to which statistical method is the most appropriate. The answer to this simple question traditionally comes in two forms, either the simple difference score (also synonymous with change and gain score) or the covariance-adjusted score. Relatively few guidelines exist about the appropriateness of both statistical techniques given the question of interest to the researcher, making it difficult to advocate for the utility of either.

When the effectiveness of an implemented treatment is of interest, two observation studies are reported quite frequently in the literature. Such a design may seem naturally appealing as two waves denote a starting and ending point to one’s study. Although advances in research methodology have resulted in more studies employing multiwave designs to improve the reliability of assessing treatment effects, the two-wave study remains a prevalent modality. In fact, when reviewing commonly used designs for assessing treatment effects from 2002 to 2007 in the Journal of Educational Psychology and Developmental Psychology, a variety of methods were utilized. A search for studies which assessed change or growth in these two journals yielded a total of 61 growth-based studies, of which 44% (n = 27) used a randomized pretest-posttest experimental design. Across these randomized experiments, researchers used three primary analytic procedures to answer questions about differences in change between groups. Analysis of covariance (ANCOVA) was the most prevalent method used (n = 12), followed by repeated measures ANOVA (n = 10), and posttest ANOVA (n = 5) designs. The findings suggested that not only are pretest-posttest designs widely utilized in randomized experiments, but that researchers were nearly as likely to utilize a gain score analysis as they were a covariance-adjusted score.

The Difference Score

The creation of the simple difference score was one of the earliest methods used to analyze data measured over multiple time points (Lord, 1956, 1958). The difference score is appealing because it provides, in the natural metric units of the measure, the raw gain observed by individuals, and is expressed as

$$\mathrm{\Delta }{X}_i=X_{2i}-X_{1i},$$ (1)

representing that individual i has changed between the pretest (X₁) and posttest (X₂). Although it has been a viable option for researchers to use in two-wave designs, Cronbach and Furby (1970) condemned its use. Reactions from this paper were so strong that most believed the idea that the difference score was an inherently poor method and that alternative methods of analysis should be considered. More recently, research from Rogosa et al. (1982) and Rogosa and Wilett (1983) refuted the criticisms by Cronbach and Furby, and demonstrated that the difference score is, in fact, unbiased, valid, and reliable. Despite this evidence, the idea that the difference score is unfair has continually prevailed (Zumbo, 1999).

Data Analysis Choice in the Randomized Experiment

When one is concerned about the power to detect an effect in a randomized study, Huck and McLean (1975) demonstrated that the covariance-adjusted score typically outperforms the gain score, and is a more sensitive test for detecting treatment effects. Such conclusions were based on the assumption that the between-group pretest means are equal as a function of the random assignment. When random assignment of units to conditions occurs, the between-group sum of squares (SS_(bg)) from the covariance-adjusted analysis becomes the same as the sum of squares from the gain score analysis. The within-group sum of squares for the covariance-adjusted score (SS_ωg(R_ΔX_i)) is defined as

$$S{S}_{\omega g(R_{\mathrm{\Delta }}{X}_i)}=S{S}_{\omega g(\mathrm{\Delta }X)}-{(b_{\omega }-1)}^2(S{S}_{\omega g(X_1)}),$$ (2)

where b_ω is the pooled within-group regression coefficient. When b_ω≠1, the effect size for the covariance-adjusted score (i.e., R_ΔXi) will be greater than the effect size from the gain score analysis; however, when b_ω = 1, the gain score will be at least as powerful as R_ΔXi because both will have the same SS_(bg) in the numerator and SS_ωg in the denominator of the F ratio.

Although researchers have used such proofs as evidence to use R_ΔXi several important assumptions are made when doing so; namely, that the data are normally distributed and that the pretest and posttest variances are equal. Such assumptions are often untenable, as data rarely have skew and kurtosis values of zero. Similarly, the assumption that pretest and posttest variances are equal implicitly states that the observed reliability of scores at both times is also equal, which further suggests that true score variances are equal; this also may not necessarily reflect the properties of data. Furthermore, when variances are assumed to be equal and one is interested in the power to detect an effect, the conclusion that R_ΔXi is more powerful than ΔX_i does not generalize to the situation where fan-spread growth is observed. Fan-spread growth is defined by increasing variance from pretest to posttest, and it may be stated that the degree to which the covariance-adjusted score is more powerful than the gain score in this condition is a mathematical uncertainty. Stoolmiller and Bank (1995) reported that when variances increased from pretest to posttest, the gain score model tended to be more powerful than the covariance-adjusted score model at detecting effects, but when variances were equal the covariance-adjusted score was more powerful. As the latter finding was in congruence with the mathematical proofs, it is apparent that much is still unknown about the performance of R_ΔXi and ΔX_i under certain conditions, thus precluding a comprehensive discussion of the relative efficiency of each statistical technique.

Although power to detect statistically significant effects is an optimal choice when making a decision about the method of analysis, virtually none of the recent commentaries on the gain score or covariance-adjusted score have discussed this component. Evidence such as Equation 2 has shown algebraically that the covariance-adjusted score is more powerful than the gain score, yet this assumes normally distributed data and equal pretest and posttest variances. Williams and Zimmerman (1996) noted a consistent lack of data-based investigations into the performance of the two statistical techniques, centering instead on theoretical and methodological considerations (e.g., Cronbach & Furby, 1970). As such, it is important to empirically test circumstances under which the gain score and covariance-adjusted score might be differentially powerful when the assumptions of Equation 2 are relaxed, to provide researchers a more comprehensive idea of how the choice of data analysis procedures will influence power to detect effects in their data.

METHOD

Data Simulation Design

The primary aim of the study was to use data simulation to assess the performance of the gain and covariance-adjusted scores under realistic data conditions to answer questions of interest. Monte Carlo simulation studies are useful in assessing outcomes that may not be easily or directly evaluated using a theoretical or mathematical approach. This method provided a venue for assessing quantitative questions of interest without collecting data, and allowed for the manipulation of key moments and factors of interest (Fan et al., 2000).

Selection of Manipulated Variables and Data Considerations

Normality

The dispersion of data in a population is an indication of the degree to which the population might be normally distributed. Non-normality may exist in a population for a number of reasons, such as units in the population which deviate from the mean more drastically then other units (i.e., skew). Skew is typically present in most data, yet few researchers test for the degree to which skew may impact their data structure. Malgady (2007) noted that little attention in psychological literature is given to skew, and rarely accompanies common descriptive statistics (i.e., mean and standard deviation). Ignoring this type of asymmetry in one’s sample data can lead to biased estimates of the mean. Using the Fleishman (1978) power transformation, normality was manipulated by adjusting a multivariate normal data set to have skew properties of ±.5 and 1, reflecting mild and large violations of normality.

Sample size

The relationship between sample size and power has been well documented (e.g., Cohen, 1988), and as one increases their sample size, power typically increases. Although increased power is expected as a function of the main effect of sample size manipulation, simulations have examined how sample size interacts with other manipulated variables (Zimmerman, 1987, 2003). In the context of this study, it was expected that as normality and sample size interacted, the covariance-adjusted or simple difference scores could be differentially powerful. To this end, group sample sizes of 20, 30, 50, 200, and 500 were chosen as to reflect conditions where a study would have a small, medium, or large sample.

Pretest-posttest correlation

The relationship between initial and final status is an important factor to use in the context of the proposed simulation study, as it is inversely correlated with individual differences in change. Large individual differences are marked by a low pretest-posttest correlation, whereas small interindividual differences in change are evidenced by increasingly large stability coefficients. Pretest-posttest correlations are also directly related to the functional form of change, and as the correlation increases, either fan-spread growth or no growth forms may be observed. It was expected that when the pretest-posttest correlation was large, the covariance-adjusted score would be a more powerful analysis of treatment effects than the gain score when a normal distribution was observed and variances between the pretest and posttest were equal. Conversely, when the correlation was small and the correlation between initial status and change was positive, the simple difference score was expected to be more powerful. The correlation between pretest and posttest was controlled using small (.20), moderate (.40, .60), and large (.80) values to reflect the degree of interindividual differences.

Correlation between initial status and change

The functional form of change over time is a key part of the simulation to better understand the utility of the simple difference and covariance-adjusted scores. Although research has primarily focused on the negative or zero correlation between initial status and change, the stringent assumption of equal variances at the pretest and posttest precluded an understanding of the power of the two analytic strategies. Based on findings from Stoolmiller and Bank (1995), it was expected that when the correlation between initial status and change (i.e., ρ_(X1ΔX)) is positive, the simple difference score would be more powerful than covariance-adjusted score. Conversely, when the correlation between initial status and change was zero or negative, the covariance-adjusted score would be more powerful to detect effects. Rogosa (1995) previously showed that the functional form of change over time can be defined by changing variances from the pretest to the posttest. Fan-spread growth is defined by increasing variance, mastery learning is defined by decreasing variance, and parallel growth by equal variances; therefore, ρ_(X1ΔX) was set at −.30 to mastery learning condition, ρ_(X1ΔX) = .00 was used to define parallel growth conditions, and fan-spread growth was described with ρ_(X1ΔX) = .30.

Data Generation Procedures

Replicates for the simulation were created using the interactive matrix language procedure (PROC IML) in SAS (version 9.1.3 for Windows). Reliability of the gain score or covariance-adjusted score was not proposed to be directly manipulated in the study; however, without any manipulation or introduction of measurement error, a simulation will generate conditions where the reliability of scores is equal to 1.0. This would not reflect typical occurrences in researcher’s data; thus, it was important to set the reliability of the pretest and posttest at a reasonable level. Reliability of .80 is considered to be an acceptable level for research decisions (Nunnally & Bernstein, 1994), and the data were manipulated to achieve this threshold.

The relationship among the posttest variance (σ₂), ρ_(X1ΔX), and ρ_(X1X2) is such that ρ_(X1X2) must be greater than ρ_(X1ΔX) in order for σ₂ to be a positive, meaningful value. As such, although the levels of the simulation factors constituted a 5 × 5 × 4 × 3 factorial design, resulting in 300 unique conditions, this relationship between ρ_(X1X2) and ρ_(X1ΔX) limited certain conditions from occurring (e.g., ρ_(X1X2)= .30 and ρ_(X1ΔX)) = .20). To this end, when mastery learning occurred, conditions for skew, sample size, and average treatment effect were observed over all levels of ρ_(X1X2)). When parallel growth was observed, conditions were estimated for ρ_(X1X2) = .40, .60, and .80. Finally, for fan-spread growth, conditions were estimated for ρ_(X1X2) = .60 and .80. Therefore, a mostly crossed simulation design totaling 226 unique conditions was run, with each one generating 1,000 samples. A total of 226,000 unique samples were generated from the simulation.

Data Analysis

Estimation of effect and statistical tests

The covariance-adjusted score was estimated using the general linear model procedure (PROC GLM) in SAS, whereas the gain score was estimated by using the MIXED procedure in SAS. Under each simulated condition, it was important to check that the results from the simulation approximated the population values that were manipulated for each factor. Descriptive statistics of the average ρ_(X1X2), ρ_(X1ΔX), pretest skew, and posttest skew may be used to demonstrate an incongruence between the observed results and specified population values. Such discrepancies could indicate incorrect data generation or programmatic misspecification of the simulation. The conditions under which each statistical technique had greater power to detect effects was studied by using the probability values from the F-tests in the ANCOVA and repeated measures ANOVA. The proportion of occurrences for the estimation of a significant effect for the interactions among the manipulated factors by both approaches was compared.

RESULTS

Simulation Manipulation Check

When comparing the sample replication values from the simulation results to the fixed population values of the manipulated variables, the mean replication estimates from the simulation were either identical or closely approximated the specified population value. The largest deviation of a mean sample replication from a population value were the pretest and posttest skews of ±1.0, which were .04 units away from specified values, but were not considered to be a great enough deviation to have significantly altered the results from the simulation.

Type I Error Rates

The probability of rejecting the null hypothesis when it is actually true (i.e., Type I error) was important to consider when describing results from the simulation. These values were estimated under the conditions where the average treatment effect was zero. Mean replication values for both statistical techniques under this condition should be .05, as no treatment effect should exist in the sample estimates where the population specification was 0. Results for the gain and covariance-adjusted scores showed that the mean Type I error rate for the simulation was .05. In addition, the Type I error rate was not different from .05 across any of the factors being manipulated.

Procedural Differences in Estimation of Power

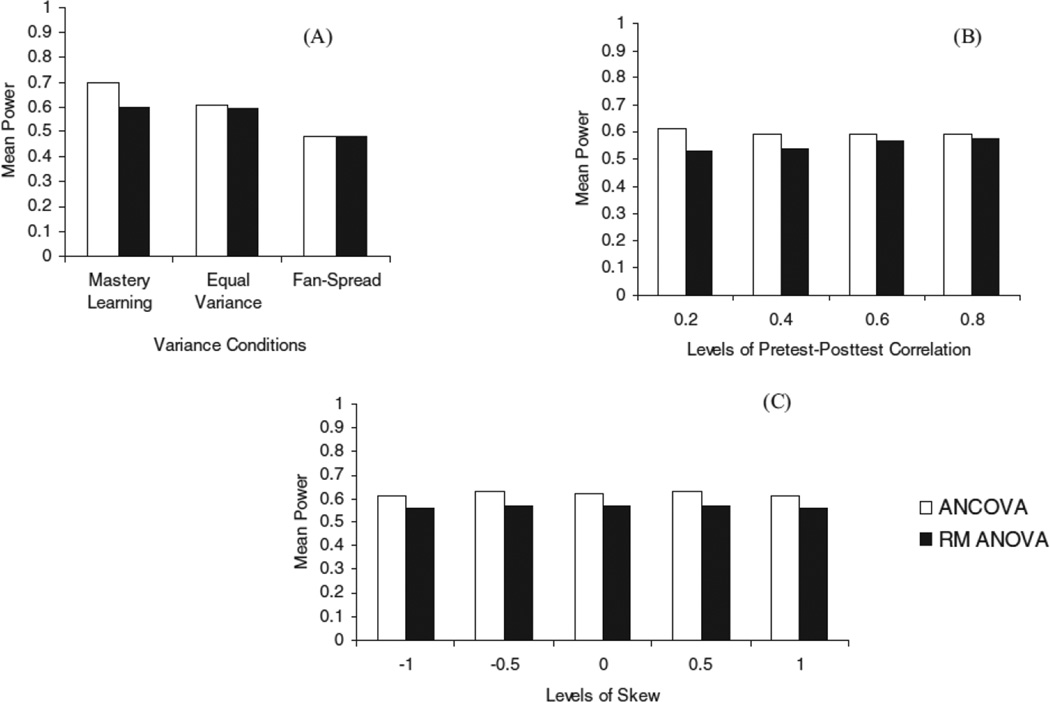
Figure 1 demonstrates the mean power rates between the two analyses across the three variance conditions (Figure 1A), the four levels of ρ_(X1X2) (Figure 1B), and the five levels of skew (Figure 1C), when averaged over all sample size conditions. Over the levels of the variance conditions (Figure 1A), the covariance-adjusted score had a strong advantage in power when mastery learning was observed (.69) compared to the gain score (.60) averaged over all other conditions. In the parallel growth condition, the covariance-adjusted score (.61), held a slight advantage over the gain score (.59), whereas both analyses produced equal levels of power under the fan-spread growth condition (.48). When considering the levels of the pretest-posttest correlation, the covariance-adjusted score was more powerful than gain by .08 when ρ_(X1X2) = .20, and as the correlation increased the differences decreased to .01 when ρ_(X1X2) = .80. Across all skew conditions, the covariance-adjusted score was more powerful by an average of .055, with relatively similar differences between the two procedures when data were either positively or negatively skewed.

Figure 1.

Mean power differences for variance conditions (A), levels of pretest-posttest correlation (B), and levels of skew (C).

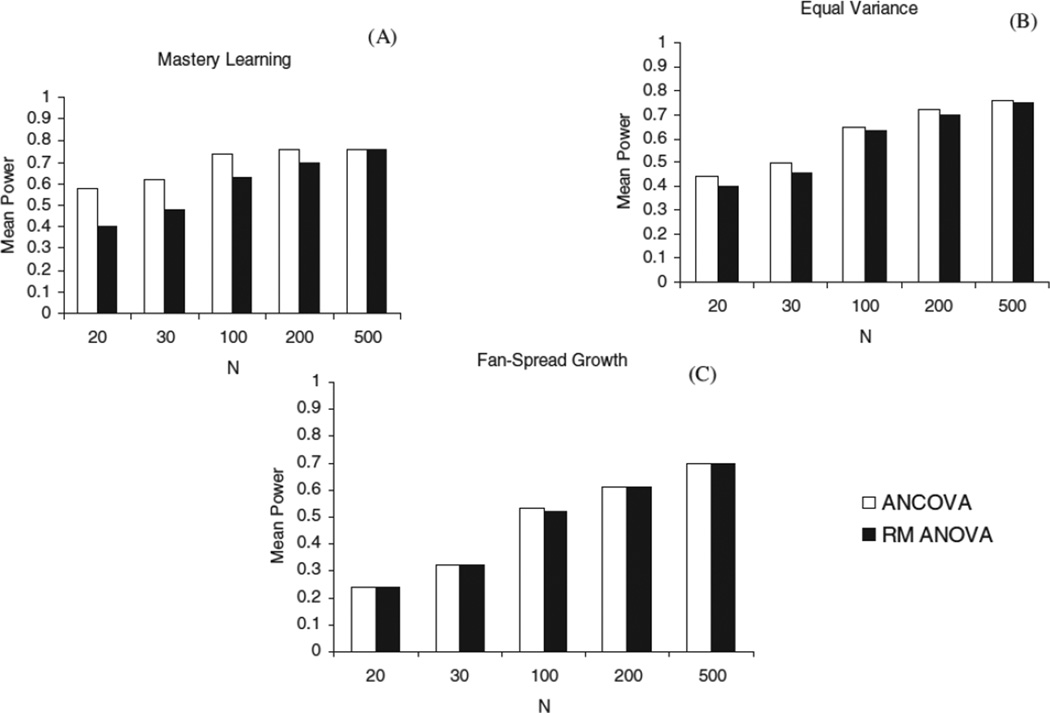
As might be expected, these patterns in the mean power between the two analyses in mastery learning conditions across the full sample were more strongly differentiated in smaller group sample sizes compared to larger samples (Figure 2). Although the relative power differences in the mastery learning conditions (Figure 2A) was .18 and .15 when N = 20 or 30 (respectively), this difference shrank to .11 and .06 when N = 100 or 200, respectively. In the context of parallel growth or fan-spread growth, regardless of the sample size, the mean power differences varied very little.

Figure 2.

Mean power differences within mastery learning (A), equal variance (B), and fan spread (C) by group sample sizes.

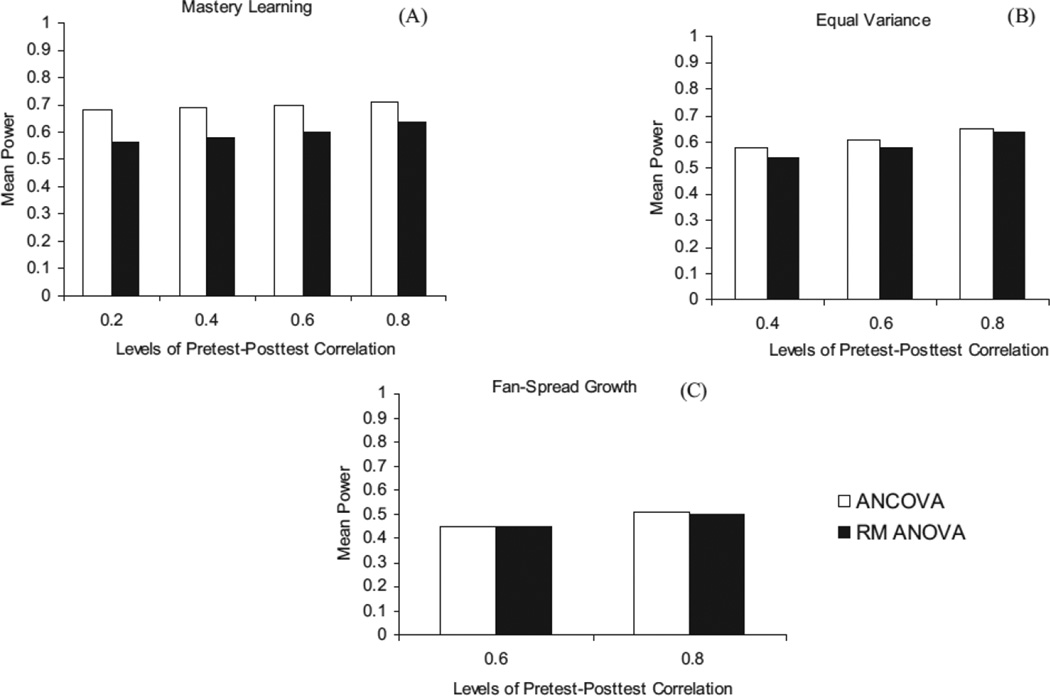
In addition to inspecting differences in power for the main effects of the factors, it was important to also examine how the gain and covariance-adjusted scores operated when looking at how the levels of ρ_(X1X2) and skew each performed over the levels of ρ_(X1ΔX) for the full sample. The relationship between ρ_(X1ΔX) and ρ_(X1X2) showed similar results as when the main effect of only ρ_(X1X2) was examined; that is, the largest differences in mean power between the two analyses were maximized at the lowest level of ρ_(X1X2) (Figure 3). The average difference in the mastery learning condition for the full sample was .10, compared with .026 for the parallel growth condition, and .005 for the fan-spread growth condition. This trend continued when disaggregated by the different sample sizes, with the largest observed difference (i.e., .21) occurring in the mastery learning condition when N = 20 and ρ_(X1X2)) = .20.

Figure 3.

Mean power differences within mastery learning (A), equal variance (B), and fan spread (C) by pretest-posttest correlation.

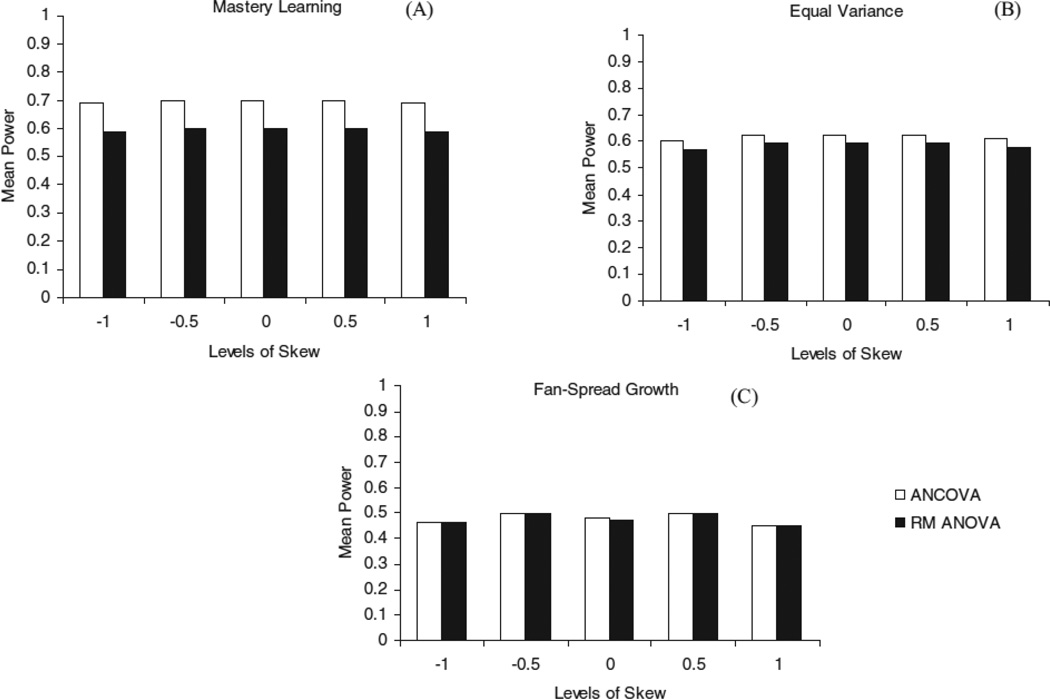
When considering the relationship between skew and ρ_(X1ΔX) (Figure 4), the results in the mastery learning condition suggested, regardless of the magnitude or direction of skew that the mean differences between the analyses were the same. Similarly, very little variability was observed in mean differences across skew conditions for parallel growth, with differences ranging from .02 to .03, as well as for fan-spread growth, where the differences were .00 across all levels of positive and negative skew.

Figure 4.

Mean power differences within mastery learning (A), equal variance (B), and fan spread (C) by levels of skew.

DISCUSSION

One of the most important decisions a researcher needs to consider when conducting a two-wave randomized experiment is the type of statistical technique to use. To date, many experimenters have been convinced by a relatively small number of published articles that the gain score should be discarded and that they should opt to use the covariance-adjusted score in an ANCOVA model. It is interesting to note that regardless of the theoretical debates that have occurred in the literature, recent publications of pretest-posttest designs demonstrate that researchers are almost equally likely to use the gain score as they are the covariance-adjusted score. No consideration was given in these studies as to why a particular statistical technique was chosen, indicating that a bridge may not yet exist between the theory of analyzing data in pretest-posttest designs and its application in experimental designs. Outside of Rogosa et al.’s (1982) work pertaining to the reliability of the gain score, few diverse arguments have been made concerning the circumstances under which the gain score should be used.

The key issue with both approaches is to gain a better understanding of the conditions under which each may maximize a particular outcome (e.g., reliability, power). Most studies have focused on conditions where each should be used when the reliability of the score produced by the analysis is the most important. Based on calls from Zumbo (1999) and Rogosa (1995) to increase the number of simulation studies, this study examined the circumstances under which the simple difference and covariance-adjusted scores may be differentially powerful in randomized experiments when a pretest-posttest design is used. Results sought to extend findings from Stoolmiller and Bank (1995), who indicated the gain score may be more powerful when fan-spread growth was observed, whereas the covariance-adjusted score may be more powerful when mastery learning occurred. What has not yet been fully developed is what power differences may exist when variances are unequal and/or data are non-normally distributed. Thus, this study was conducted to provide further data and information about the choice of data analysis when such conditions exist.

Findings from the simulation indicated that of all the manipulated factors, the relative power differences between the analyses were differentiated by the level of the correlation between initial status and change. The hypothesis that the covariance-adjusted score would be more powerful than the gain score with mastery learning was strongly supported, with average differences of .10 observed across levels of the other factors. Moreover, the covariance-adjusted score had nearly 17% more power than the gain score. Conversely, in the fan-spread growth condition, where the gain score was expected to be more powerful, results suggested that both analyses were equally powerful. Although the gain score did not prove to be more powerful where it was expected, a more interesting result was observed in the parallel growth condition. Although the covariance-adjusted score was indeed more powerful than the gain score, when variances were equal at two time points the magnitude could be construed as practically unimportant. With only a 3% advantage for the covariance-adjusted score when averaged across all samples, one is left wondering about the practical value of such a difference.

As distributions became increasingly non-normal, regardless of direction, the covariance-adjusted score demonstrated greater power over the gain score. In these non-normal conditions, the relative difference between the two statistical techniques was .05. This magnitude was similar to the difference that was observed when data were normally distributed; thus, whether data were skewed or not typically did not impact the level of difference in power between the covariance-adjusted and gain scores. When considering ρ_(X1X2), the general finding was that a greater discrepancy in power was observed as the correlation became weaker. Such a result was not surprising given the earlier discussion in which the structure of the simulation required a larger ρ_(X1X2) than ρ_(X1ΔX). Power differences when ρ_(X1X2) = .20 pertained specifically to the mastery learning condition, ρ_(X1X2)= .40 was specific to mastery learning and parallel growth, and ρ_(X1X2) = .60 and .80 were relative to all three variance conditions. As observed from the results, the differences in power between the covariance-adjusted and gain scores are small when averaged over all three variance conditions.

This observation is seemingly in contrast with the previous expectation that in the presence of a small ρ_(X1X2) the gain score would be more powerful. Rather than examining the mean power differences averaged over the three variance conditions, when the findings were viewed across each level of ρ_(X1X2), the covariance-adjusted score was more powerful (range = .06), yet when the ρ_(X1X2) and ρ_(X1ΔX) interacted, the relative differences in power from the smallest to largest pretest-posttest correlation was much smaller than when averaged. That is, the range for mastery learning was .05, .03 for parallel growth, and .01 for fan-spread growth. Disaggregating the results demonstrated that the covariance-adjusted score was, in fact, more powerful when the correlation was at least moderate across the three ρ_(X1ΔX) conditions.

Although the findings in the mastery learning and fan-spread growth conditions shed light on the research that has suggested differential power might exist between ANCOVA and repeated measures ANOVA models, the lack of a strong difference when variances were equal and the ρ_(X1ΔX) = 0 was of interest. Although the findings relative to power differences provided support for the difference that Equation 2 suggests (i.e., ANCOVA can be expected to have greater power when pretest and posttest variances are equal), the magnitude of the difference was questionable. This might be partly explained by the special condition of homogeneous growth that was considered in this study. When parallel growth was observed, both analyses were nearly equally powerful at detecting average treatment effects, both when the main effect of skew was considered, as well as when deviations from normality were observed. As the variances increased from pretest to posttest, and fan-spread growth occurred, the gain score was also approximately equal in power to the covariance-adjusted score, with a mean difference of .00. In the context of non-normality and fan-spread growth, the differences by sample size were actually closer than when skew was not zero, suggesting that increasing deviations from normality results in smaller discrepancies in mean power between procedures.

These findings are of practical value to researchers because they show that regression-based measures of change practically differ from difference scores, but that the magnitude of the difference is largely related to ρ_(X1ΔX). In the context of parallel growth, the difference in power between analytic approaches was relatively small in magnitude. It is worth attempting to understand how this finding fits with previous research from both Huck and McLean (1975) and Maxwell and Delaney (2004), both of which demonstrate greater power for covariance-adjusted scores; yet neither suggested what the expected relative magnitude of the difference should be. Equation 2 shows less error in the covariance-adjusted score compared to the simple difference score, but it is plausible that this may be the case when equal variance but heterogeneous change occurs between two time points. As the current simulation only studied equal variance and homogeneous change, it might be expected that when this condition holds, the covariance-adjusted score retains a slight, but practically unimportant advantage in power.

Guidelines for Researchers

When individuals are randomly assigned to conditions and the reliability of the pretest and posttest are approximately .80, as a general rule of thumb researchers should utilize the covariance-adjusted score when maximizing power is of interest. The ANCOVA was most powerful when mastery learning occurred, especially under conditions with small sample sizes. Regardless of the level of the pretest-posttest correlation or the amount of skew present in the data, the covariance-adjusted score consistently produced greater power than the gain score. The small differences in power between the two analyses that occurred in the parallel growth and fan-spread growth conditions may not be considered practically important; however, the lack of instances where the gain score demonstrated greater power precludes a strong recommendation for the gain score. Although the relative power differences between the two analyses decreases in the parallel growth and fan-spread growth conditions, it is still large enough that one does not necessarily need to consider the ratio of pretest variance to posttest variance when making a decision about the choice of analyses in the context of a two-wave randomized experiment.

Despite the equal power across procedures in the fan-spread growth condition and nearly equal power in the parallel growth condition, it should be of interest to reevaluate the recent trends in publication of pretest-posttest experimental designs. Based on the recent set of publications, many researchers do not report reasons for choosing an ANCOVA or repeated measures ANOVA analysis. Without such a rationale, it is difficult to understand for what reasons each may have been utilized for the randomized experiments. None of the reviewed publications mentioned the relationship between initial status and change, so it may be apparent that this was not a consideration when choosing the method of data analysis. Although some may certainly use the information from measurement literature to guide the selection of an appropriate analysis, others may choose their method based on recent or often-published practices. To this end, by using the covariance-adjusted score across a variety of data structures, very little, if any, power would be lost with a straightforward application. Although correlations between initial status and change not studied here could potentially produce an advantage of the gain score in power, a general applied framework based on the results from the simulations in these studies would advocate that the covariance-adjusted score in the ANCOVA model is the best analysis to apply. Although nearly half of recently published reports used a repeated measures ANOVA to answer questions of effectiveness in randomized pretest-posttest designs, they may have been able to achieve greater power to detect smaller effects by using the covariance-adjusted score from an ANCOVA design.