Abstract
Recent studies on Alzheimer's Disease (AD) or its prodromal stage, Mild Cognitive Impairment (MCI), diagnosis presented that the tasks of identifying brain disease status and predicting clinical scores based on neuroimaging features were highly related to each other. However, these tasks were often conducted independently in the previous studies. Regarding the feature selection, to our best knowledge, most of the previous work considered a loss function defined as an element-wise difference between the target values and the predicted ones. In this paper, we consider the problems of joint regression and classification for AD/MCI diagnosis and propose a novel matrix-similarity based loss function that uses high-level information inherent in the target response matrix and imposes the information to be preserved in the predicted response matrix. The newly devised loss function is combined with a group lasso method for joint feature selection across tasks, i.e., clinical scores prediction and disease status identification. We conducted experiments on the Alzheimer's Disease Neuroimaging Initiative (ADNI) dataset, and showed that the newly devised loss function was effective to enhance the performances of both clinical score prediction and disease status identification, outperforming the state-of-the-art methods.
1. Introduction
Alzheimer's Disease (AD) is the most common form of dementia that often appears in the persons aged over 65. Brookmeyer et al. showed that there are 26.6 million AD patients worldwide and 1 out of 85 people will be affected by AD by 2050 [1]. Thus, for timely treatment that might be effective to slow the progression, it's of great importance for early diagnosis of AD and its prodromal stage Mild Cognitive Impairment (MCI).
For the last decade, machine learning techniques have been successfully used to analyze complex patterns in neuroimaging data, especially, for AD/MCI diagnosis [5, 20, 21, 25]. The previous imaging studies mostly focused on developing classification models (e.g. [8, 11, 17]) to identify clinical labels such as AD, MCI, and Normal Control (NC). Recently, regression models have also been investigated to predict clinical scores such as Alzheimer's Disease Assessment Scale-Cognitive Subscale (ADAS-Cog) and Mini-Mental State Examination (MMSE) from individual Magnetic Resonance Imaging (MRI) and/or Positron Emission Tomography (PET) scans [15].
Unlike those studies that focused on only one of the tasks [8, 17], there have been also efforts to tackle both tasks simultaneously in a unified framework. For example, Zhang and Shen [24] proposed a method of joint feature selection for both disease diagnosis and clinical scores prediction, and showed that the features used for these tasks are highly related. In line with their work and for better understanding of the underlying mechanism of AD, our interest in this paper is to predict clinical scores and to identify disease status jointly and here we call it as a Joint Regression and Classification (JRC) problem.
In the computer-aided AD diagnosis, the available sample size is usually much smaller than the feature dimensionality. For example, the sample size used in [8, 11] was as small as 103 (i.e., 51 AD and 52 NC), while the feature dimensionality (including MRI features and PET features) was hundreds or even thousands. The small sample size makes it difficult to build an effective model, and the high-dimensional data could lead to the over-fitting issue although the number of intrinsic features may be very low [22, 26, 28]. To circumvent this challenging problem, Wang et al. used features of the predefined Region-Of-Interests (ROIs) of medial temporal lobe structures, medial and lateral parietal, and prefrontal cortical areas in predicting memory scores and discriminating between AD and NC [19].
Rather than predefining the ROIs based on the prior knowledge, it is preferable to select the informative features in a data-driven manner. In this respect, Zhang and Shen embedded an ℓ2,1-norm regularizer into the sparse re gression model, thus formulating a multi-task learning [24]. Recent studies demonstrated that the consideration of the manifold of the data can further boost the power of feature selection methods [27, 29]. However, to our best knowledge, the previous methods used mostly a loss function defined as sum of the element-wise difference between target values and predicted ones, and considered only the manifold of feature observations, not that of the target variables. Furthermore, none of the previous methods utilized manifold-based feature selection for the JRC problem.
In this paper, we propose a new loss function that uses high-level information inherent in the observations, and combine it with a group lasso [23] for joint sparse feature selection in the JRC problem. Specifically, we define a loss function as matrix similarity and impose the high-level information in the target response matrix to be preserved in the predicted response matrix. For the high-level information, we use the relations between samples and the relations between response variables, each of which we call as ‘sample-sample relation’ and ‘variable-variable relation’. Hereafter, each column and each row of a matrix correspond, respectively, to one sample and one response variable. In our work, a sample in a response matrix consists of clinical scores and a class label, and each of the clinical scores or a class label is considered as a response variable. By utilizing the high-level information inherent in the target response matrix and imposing it to be preserved in the predicted response matrix, we define a more sophisticated loss function, which affects feature selection, and thus helps enhance the prediction and classification performances in AD/MCI diagnosis.
2. Proposed Method
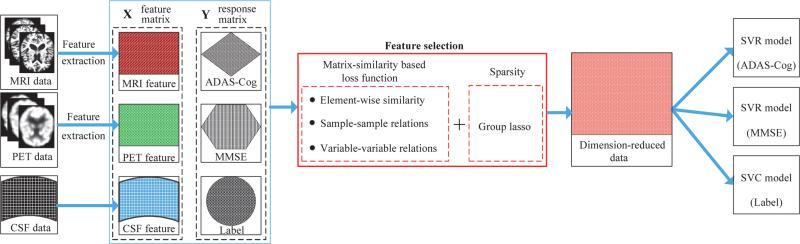
In Fig. 1, we present a schematic diagram of the proposed method to predict both clinical scores and a class label using neuroimaging data. Given MRI, PET, and CerebroSpinal Fluid (CSF) data, we first extract features from MRI and PET, while using the CSF biomarkers as CSF features. We then construct a feature matrix X with a concatenation of multi-modal features at each column, and the corresponding response matrix Y with a concatenation of clinical scores (e.g., ADAS-Cog, MMSE) and a class label at each column. With our new loss function and a group lasso method, we select features jointly used to represent clinical scores and a class label. By using the training samples but with only the selected features, we build clinical scores regression models and a clinical label identification model with Support Vector Regression (SVR) and Support Vector Classification (SVC), respectively.
Figure 1.
The framework of the proposed method.
2.1. Notations
In this paper, we denote matrices as boldface uppercase letters, vectors as boldface lowercase letters, and scalars as normal italic letters, respectively. For a matrix X = [xij], its i-th row and j-th column are denoted as xi and xj, respectively. We denote a Frobenius norm and an ℓ2,1-norm of a matrix X as ∥X∥F = and ∥X∥2,1 = , respectively. We further denote a transpose, a trace, and an inverse of a matrix X as XT, tr(X), and X−1, respectively.
2.2. Matrix-Similarity based Loss Function
Let X = [x1, ..., xn] ∈ Rd×n and Y = [y1, ..., yn] ∈ Rc×n, where n, d, and c denote the numbers of samples (or subjects)1, feature variables, and response variables, respectively. In our work, the response variables correspond to ADAS-Cog, MMSE, and a class label. We assume that the response variables can be represented by a weighted linear combination of the features as follows:
where W ∈ Rd×c is a regression coefficient matrix. By regarding the prediction of each response variable as a task and constraining the same features to be used across tasks, we can formulate a multi-task learning with a group lasso [23] as follows:
| (1) |
where f(W) is a loss function depending on W and λ is a sparsity control parameter. Note that each element in a column wk of W assigns a weight to each of the observed features in representing the k-th response variable. The ℓ2,1-norm regularizer ∥W∥2,1 penalizes all coefficients in the same row of W together for joint feature selection or unselection in predicting the response variables. Specifically, the ℓ2-norm regularizer enforces the selection of the same features across tasks, and the ℓ1-norm imposes the feature sparseness in the linear combination. Note that later in our experiments for clinical score prediction and clinical label classification, we extract one feature from each Region-Of-Interest (ROI) of the brain in MRI or PET, thus this ℓ2,1-norm has the effect of selecting ROIs that are highly relevant to the prediction of both clinical scores and a class label.
With regard to the loss function in Eq. (1), the most commonly used metric in the literature is the element-wise distance between the target response matrix Y and the predicted response matrix Ŷ as follows:
| (2) |
This element-wise loss function has been successfully used in many objective functions in the literature [18, 23, 24]. From a matrix similarity point of view, Eq. (2) measures the similarity with the sum of the element-wise differences between matrices. Note that, in this case, the lower the score is, the more similar they are. However, we believe that there exists additional information inherent in the matrices, which we can use in measuring the similarity, such as the relations between any pair of columns and the relations between any pair of rows. In our case, the columns and the rows correspond, respectively, to samples and response variables. Ideally, besides the element-wise values, those relations in the target response matrix Y should be also preserved in the predicted response matrix Ŷ. By imposing the higher-level information to be matched between two matrices, we can find an optimal regression matrix W that helps accurately predict the target response values, and thus select useful features. The selected features can be finally used in predicting clinical scores and a class label of a testing sample.
To better characterize the newly devised loss function, we explain them in terms of a graph matching. We illustrate the sample-sample (a pair of columns) relations, e.g., (yi – yj) or (ŷi – ŷj), and the variable-variable (a pair of rows) relations, e.g., (yk – yl) or (ŷk – ŷl), by means of a graph in Fig. 2(a) and Fig. 2(b), respectively. In Fig. 2(a), a node represents one sample, i.e., a column vector yi or ŷi in the respective matrices, an edge in a graph denotes the relation between the connected nodes, and different colors denote different class labels. In the graph, the samples of the same class would have a small distance, whereas the samples of different classes would have a large distance. In Fig. 2(b), a node represents a set of observations for a response variable, i.e., a row vector in the respective matrices, and an edge denotes the relation between nodes.
Figure 2.
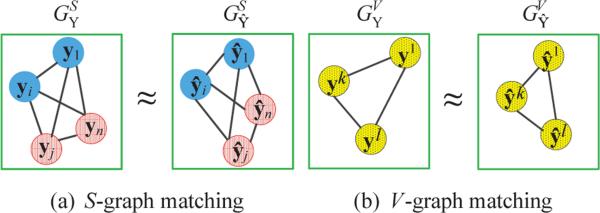
An illustration of measuring a matrix similarity by means of a graph matching. For simplicity, we showed only a small number of nodes. (a) Each node represents a column vector of the target or the predicted response matrix, edges represent the distance between nodes, and colors represent class labels. (b) Each node represents a row vector of the target or the predicted response matrix and edges denote the distance between nodes.
As mentioned above, we impose these relational properties in a target response matrix, now represented by a graph, to be preserved in the respective graph for the predicted re sponse matrix as follows:
where and denote, respectively, graphs representing the sample-sample relations for the target response matrix Y and the predicted response matrix Ŷ, and and denote, respectively, graphs representing the variable-variable relations for the target response matrix Y and the predicted response matrix Ŷ. Hereafter, we call the graphs representing the sample-sample relations and the variable-variable relations as ‘S-graph’ and ‘V-graph’, respectively. We formulate the problem of matching two graphs, i.e., S-graph and V-graph, as follows:
| (3) |
| (4) |
where MS and MV denote, respectively, the graph matching scores between and , and between and . By introducing these newly devised graph matching terms into the loss function of Eq. (2), our new loss function becomes as follows:
| (5) |
where α1 and α2 denote, respectively, the control parameters for the terms. Compared to the conventional element-wise loss function in Eq. (2), the proposed function additionally considers two graph matching regularization terms. It is worth noting that unlike the previous manifold learning methods, i.e., local linear embedding [13], locality preserving projection [7], and high-order graph matching [10], that focused on the sample similarities by imposing nearby samples to be still nearby in the transformed space, the proposed method imposes more strict constraints, i.e., sample-sample relations and variable-variable relations, in finding the optimal regression matrix W.
2.3. Objective Function Optimization
With some mathematical transformations, we can simplify MS and MV as follows:
| (6) |
| (7) |
where and , In (or Ic) is an identity matrix of size n (or c), and 1n (or 1c) is a column vector of n (or c) ones. By replacing the graph matching terms MS and MV in Eq. (5) with Eq. (6) and Eq. (7), respectively, our objective function can be rewritten as follows:
| (8) |
By setting the derivative of the objective function in Eq. (8) with respect to W to zero, we can obtain an equation of the following form:
| (9) |
where A = −(XXT)−1(XXT + 2α1XHnXT + λQ), B = 2α2Hc, C = −(XXT)−1(XYT + 2α1XHnYT + 2α2XYTHc), and Q ∈ Rd×d is a diagonal matrix with the i-th diagonal element set to
| (10) |
Although the objective function in Eq. (8) is convex, due to the non-smooth term of ∥W∥2,1, it is not straightforward to find the global optimum. Furthermore, due to the interdependence in computing matrices of W and Q, it's not trivial to solve Eq. (9). To this end, in this work, we apply an iterative approach to optimize Eq. (9) by alternatively computing Q and W. That is, at the t-th iteration, we first update the matrix W(t) with the matrix Q(t – 1) fixed and then update the matrix Q(t) with the updated matrix W(t). Due to the limited space, we don't prove the convergence of Algorithm 1, but in a nutshell, according to [29], the error value monotonically decreases in every iteration.
Algorithm 1.
Pseudo code of solving Eq. (8).
2.4. Feature Selection and Model Training
Due to the use of an ℓ2,1-norm regularizer in our objective function, after finding the optimal solution with Algorithm 1, we have some zero (or close to zero) row vectors in W, whose corresponding features are not useful in joint prediction of clinical scores and a class label. Furthermore, we believe that the lower the ℓ2-norm value of a row vector, the less informative the respective feature in our observation. To this end, we first sort rows in W in a descending order based on each row's ℓ2-norm value, i.e., ∥wj∥2, j ∈ {1, . . . , d}, to find K top-ranked rows, and then select the respective features. Note that the selected features are jointly used to predict clinical scores and a class label.
By using training samples but with only the selected features, we then train support vector machines, which have been successfully used in many fields [16, 24]. Specifically, we build two SVR models for ADAS-Cog and MMSE scores prediction, respectively, and a SVC model for a class label identification3.
3. Experimental Results
We conducted various experiments on the ADNI dataset4 to compare the proposed method with the state-of-the-art methods as detailed below.
3.1. Experimental Settings
In our experiments, we used baseline MRI, PET, and CSF data obtained from 202 subjects including 51 AD subjects, 52 NC subjects, 43 MCI Converters (MCI-C), and 56 MCI Non-Converters (MCI-NC). We preprocessed the MRI and PET images by performing spatial distortion, skull-stripping, and cerebellum removal, sequentially. We segmented MRI images into gray matter, white matter, and cerebrospinal fluid. We then parcellated MRI images into 93 ROIs based on a Jacob template [9], by means of registering via HAMMER [14]. We finally computed the gray matter tissue volumes of the ROIs as features. For the PET images, we aligned them to their respective MRI images. We obtained 93 gray matter volumes from an MRI image and 93 mean intensities from a PET image and used them as features.
We considered two binary classification problems: AD vs. NC and MCI vs. NC. We used features from MRI, PET, MRI+PET (MP for short), or MRI+PET+CSF (MPC for short) and learned feature selection models with the target responses composed of two clinical scores and one class label. We then trained regression models and a classification model using the training samples with only the selected features.
For the quantitative performance evaluation, we employed the metrics of Correlation Coefficient (CC) and Root Mean Squared Error (RMSE) between the predicted clinical scores and the target clinical scores in regression, and the metrics of classification ACCuracy (ACC), SENsitivity (SEN), SPEcificity (SPE), and the Area Under an receiver operating characteristic Curve (AUC) in classification.
We performed 10-fold cross-validation and repeated the whole process 10 times to avoid the possible bias during dataset partitioning for cross-validation. We reported the averaged performances.
3.2. Competing Methods
In order to show the validity of the proposed method, we compare our method with the following methods.
Full features based method: We conducted the tasks of regression and classification using the original full features with no feature selection step, and considered the results as baseline. In the following, we denote this method with the suffix “N”.
Single-task based method: We conducted regression and classification tasks separately but selecting features using the objective function in Eq. (8). Although here we used the same original features as the proposed method, we performed the task of regression or classification by selecting the set of features separately. In the following, we use the suffix “S” to represent the type of single-task based method.
M3T [24]: A Multi-Modal Multi-Task method includes two key steps: (1) multi-task learning for each modality to find relevant features that jointly represent multiple response variables, and (2) a multi-kernel learning to integrate decisions from multiple modalities. It is noteworthy that M3T is a special case of our method by setting α1 = α2 = 0 in Eq. (8).
HOGM [10]: A High-Order Graph Matching method uses a sample-sample relation in a matrix and applies an ℓ1-norm regularization term with a single response variable (i.e., single-task learning).
M2TFS [8]: A Manifold regularized Multi-Task Feature Selection method selects features by combining the least square loss function with an ℓ2,1-norm regularizer and a graph regularizer. It then performs multi-modality classification via a multi-task learning, in which each task focuses on each modality. This method is designed only for classification. In our experiments, we considered two versions of M2TFS depending on the way of fusing multi-modality information: M2TFS-C (simple concatenation of multi-modality features into a long vector) and M2TFS-K (combining decisions from modalities through a multi-kernel learning).
SJCR [19]: A Sparse Joint Classification and Regression method jointly uses a logistic loss function and a least square loss function along with an ℓ2,1-norm for multi-task feature selection.
3.3. Classification Results
Table 1 shows the classification performances of the methods. It is clear that the proposed method outperforms the competing methods in all experiments. Specifically, we observe the following results.
It is important to conduct feature selection on the high-dimensional features before performing classification. The worst results were obtained by the methods without feature selection, i.e., MRI-N, PET-N, MP-N, and MPC-N. For example, for MRI-based classification as shown in the first block of Table 1, even using a simple feature selection method, i.e., MRI-S, can still increase the classification accuracies by 1.7% and 8.4%, compared to MRI-N in AD vs. NC and MCI vs. NC classifications, respectively. Compared to the baseline, our method with MPC improved the classification accuracies by 5.1% and 9.5% in AD vs. NC and MCI vs. NC classifications, respectively.
It is beneficial to use joint regression and classification framework for feature selection, even only for the task of classification. As shown in Table 1, the proposed method that performed feature selection for joint regression and classification achieved better classification performance than the single-task based methods (MRI-S, PET-S, MP-S, and MPC-S). For example, in MRI-based classification, our method improved the classification accuracies by 2.6% and 3.0% compared to MRI-S based method in AD vs. NC and MCI vs. NC classifications, respectively.
To fuse multi-modal features helps improve classification performance. In all experiments, the classification performances with multi-modality data such as MP and MPC were better than the same methods with single-modality data such as MRI and PET. Also, the classification performance by MPC was generally better than MP. For example, in the discrimination between AD and NC, the proposed method with MPC achieved the classification accuracy of 95.9%, sensitivity of 95.7%, specificity of 98.6%, and AUC of 98.8%, while the best performance among other competing methods with single-modality data was 93.8% (ACC), 92.3% (SEN), 96.7% (SPE), and 97.9% (AUC), respectively, and the best performance among other competing methods with MP data was 95.3% (ACC), 94.9% (SEN), 98.1% (SPE), and 98.3% (AUC), respectively.
Table 1.
Comparison of classification performances (%) of the competing methods.
| Modality | Method | AD vs. NC | MCI vs. NC | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ACC | SEN | SPE | AUC | ACC | SEN | SPE | AUC | ||
| MRI | MRI-N | 89.5 | 82.7 | 86.3 | 95.3 | 68.3 | 92.6 | 39.2 | 82.5 |
| MRI-S | 91.2 | 85.9 | 92.5 | 96.7 | 76.7 | 93.3 | 37.6 | 83.7 | |
| HOGM | 93.4 | 89.5 | 92.5 | 97.1 | 77.7 | 95.6 | 51.4 | 84.4 | |
| M3T | 92.6 | 87.2 | 95.9 | 97.5 | 78.1 | 94.5 | 54.0 | 83.1 | |
| SJCR | 92.5 | 89.6 | 96.1 | 97.5 | 77.9 | 95.2 | 52.7 | 84.9 | |
| Proposed | 93.8 | 89.7 | 96.7 | 97.9 | 79.7 | 95.0 | 56.1 | 85.2 | |
| PET | PET-N | 86.2 | 83.5 | 84.8 | 94.8 | 69.0 | 95.0 | 30.8 | 77.9 |
| PET-S | 87.9 | 85.7 | 90.9 | 94.7 | 73.8 | 96.5 | 36.2 | 78.7 | |
| HOGM | 91.7 | 91.1 | 92.8 | 95.6 | 74.7 | 96.5 | 43.2 | 79.3 | |
| M3T | 90.9 | 90.5 | 93.1 | 96.4 | 77.2 | 94.5 | 44.3 | 80.5 | |
| SJCR | 91.6 | 83.7 | 93.6 | 95.9 | 73.8 | 96.4 | 23.2 | 80.8 | |
| Proposed | 92.3 | 92.3 | 93.9 | 96.6 | 79.1 | 96.1 | 47.2 | 81.2 | |
| MP | MP-N | 89.7 | 92.2 | 85.9 | 96.1 | 71.6 | 96.1 | 43.9 | 82.7 |
| MP-S | 90.8 | 92.6 | 93.8 | 96.7 | 76.3 | 97.0 | 39.9 | 83.4 | |
| M2TFS-C | 91.0 | 90.4 | 91.4 | 95.0 | 73.4 | 76.5 | 67.1 | 78.0 | |
| M2TFS-K | 95.0 | 94.9 | 95.0 | 97.0 | 79.3 | 85.9 | 66.6 | 82.0 | |
| HOGM | 95.2 | 92.8 | 95.4 | 97.8 | 79.5 | 96.6 | 58.6 | 84.6 | |
| M3T | 94.0 | 92.0 | 96.3 | 98.0 | 78.4 | 95.0 | 57.7 | 83.9 | |
| SJCR | 93.4 | 92.7 | 96.5 | 96.8 | 78.2 | 96.1 | 54.4 | 83.1 | |
| Proposed | 95.3 | 93.5 | 98.1 | 98.3 | 80.2 | 96.5 | 59.7 | 85.5 | |
| MPC | MPC-N | 90.8 | 93.1 | 88.3 | 96.5 | 72.5 | 96.3 | 47.1 | 84.1 |
| MPC-S | 92.5 | 94.1 | 93.8 | 97.6 | 77.1 | 97.1 | 47.5 | 83.9 | |
| HOGM | 95.6 | 94.5 | 96.9 | 98.5 | 80.6 | 96.7 | 64.7 | 86.2 | |
| M3T | 94.6 | 93.1 | 96.4 | 98.5 | 80.1 | 95.2 | 58.7 | 84.3 | |
| SJCR | 93.9 | 92.8 | 96.5 | 97.0 | 78.9 | 96.2 | 55.9 | 83.4 | |
| Proposed | 95.9 | 95.7 | 98.6 | 98.8 | 82.0 | 98.0 | 60.1 | 87.0 | |
(ACC: ACCuracy, SEN: SENsitivity, SPE: SPEcificity, and AUC: Area Under the receiver operating characteristic Curve)
3.4. Regression Results
We also evaluated the regression performances using MRI, PET, MP, and MPC. We presented the results of CCs and RMSEs of all the competing methods in Table 2. From the results, it is clear that the proposed method outperforms all the competing methods, when using any combinations of three types of data.
Table 2.
Comparison of regression performances of the competing methods.
| Modality | Method | AD vs. NC | MCI vs. NC | ||||||
|---|---|---|---|---|---|---|---|---|---|
| ADAS-Cog | MMSE | ADAS-Cog | MMSE | ||||||
| CC | RMSE | CC | RMSE | CC | RMSE | CC | RMSE | ||
| MRI | MRI-N | 0.587 | 4.96 | 0.520 | 2.02 | 0.329 | 4.48 | 0.309 | 1.90 |
| MRI-S | 0.591 | 4.85 | 0.566 | 1.95 | 0.347 | 4.27 | 0.367 | 1.64 | |
| HOGM | 0.625 | 4.53 | 0.598 | 1.91 | 0.352 | 4.26 | 0.371 | 1.63 | |
| M3T | 0.649 | 4.60 | 0.638 | 1.91 | 0.445 | 4.27 | 0.420 | 1.66 | |
| SJCR | 0.652 | 4.69 | 0.636 | 1.90 | 0.448 | 4.27 | 0.425 | 1.67 | |
| Proposed | 0.661 | 4.58 | 0.650 | 1.89 | 0.461 | 4.21 | 0.441 | 1.62 | |
| PET | PET-N | 0.597 | 4.86 | 0.514 | 2.04 | 0.333 | 4.34 | 0.331 | 1.70 |
| PET-S | 0.620 | 4.83 | 0.593 | 2.00 | 0.356 | 4.26 | 0.359 | 1.69 | |
| HOGM | 0.600 | 4.69 | 0.515 | 1.99 | 0.360 | 4.21 | 0.368 | 1.67 | |
| M3T | 0.647 | 4.67 | 0.593 | 1.92 | 0.447 | 4.24 | 0.432 | 1.68 | |
| SJCR | 0.644 | 4.65 | 0.595 | 1.97 | 0.446 | 4.23 | 0.426 | 1.68 | |
| Proposed | 0.663 | 4.64 | 0.610 | 1.89 | 0.452 | 4.21 | 0.444 | 1.66 | |
| MP | MP-N | 0.626 | 4.80 | 0.587 | 1.99 | 0.365 | 4.29 | 0.335 | 1.69 |
| MP-S | 0.634 | 4.83 | 0.585 | 1.92 | 0.359 | 4.25 | 0.371 | 1.67 | |
| M2TFS-C | 0.641 | 4.89 | 0.636 | 1.87 | 0.446 | 4.25 | 0.408 | 1.64 | |
| M2TFS-K | 0.645 | 4.59 | 0.648 | 1.82 | 0.458 | 4.21 | 0.415 | 1.63 | |
| HOGM | 0.633 | 4.64 | 0.602 | 1.83 | 0.364 | 4.20 | 0.365 | 1.65 | |
| M3T | 0.653 | 4.61 | 0.639 | 1.91 | 0.450 | 4.23 | 0.433 | 1.64 | |
| SJCR | 0.656 | 4.64 | 0.643 | 1.81 | 0.451 | 4.19 | 0.431 | 1.64 | |
| Proposed | 0.666 | 4.53 | 0.651 | 1.80 | 0.463 | 4.20 | 0.448 | 1.62 | |
| MPC | MPC-N | 0.629 | 4.79 | 0.588 | 1.97 | 0.368 | 4.29 | 0.337 | 1.70 |
| MPC-S | 0.638 | 4.81 | 0.599 | 1.92 | 0.366 | 4.25 | 0.394 | 1.66 | |
| HOGM | 0.639 | 4.63 | 0.611 | 1.81 | 0.365 | 4.20 | 0.368 | 1.65 | |
| M3T | 0.665 | 4.59 | 0.663 | 1.81 | 0.451 | 4.22 | 0.441 | 1.62 | |
| SJCR | 0.658 | 4.64 | 0.645 | 1.81 | 0.451 | 4.19 | 0.433 | 1.63 | |
| Proposed | 0.668 | 4.47 | 0.685 | 1.78 | 0.470 | 4.16 | 0.456 | 1.59 | |
(CC: Correlation Coefficient, RMSE: Root Mean Square Error)
Specifically, we observe the following: (1) Again, the regression performance of the methods without feature selection (MRI-N, PET-N, MP-N and MPC-N) was much worse than the methods with feature selection. Moreover, our method achieved the best performance compared to the competing methods. (2) Our method with MPC consistently outperformed the same method with MP on each performance measure, although the method with MP already achieved a better performance than our method with a single modality such as MRI and PET. This was also observed for all other competing methods. (3) The multi-task learning for joint feature selection to represent multiple response variables achieved better performances than the single-task learning, same as for the classification task above.
3.5. Summary
From all the experimental results, we found that (1) the proposed matrix-similarity based loss function helped enhance performances of both regression and classification; (2) the proposed method formulated in a joint regression and classification framework was superior to its counterpart that was formulated for regression and classification separately; (3) the multi-modal information fusion helped improve the performances compared to using the unimodal information.
To verify a statistical significance, we performed paired-sample t-tests between results of our method and those of the competing methods. For most of the cases, the p-values were less than 0.001, which means that our method statistically outperformed the competing methods on the tasks of predicting clinical scores (i.e., ADAS-Cog and MMSE) and identifying a class label.
3.6. Most Discriminative Brain Regions
We also investigated the most discriminative regions based on the features selected by the proposed method. Due to the application of a cross-validation technique, the selected features varied across the repeated experiments. We thus found the most discriminative regions based on the selected frequency of each region over the cross-validations. The top 10 selected regions in MCI vs. NC classification with MPC included the following brain areas: amygdala right, hippocampal formation left, hippocampal formation right, entorhinal cortex left, temporal pole left, parahippocampal gyrus left, uncus left, perirhinal cortex left, cunecus left, and temporal pole right. It is noteworthy that the top six-ranked brain regions are known to be highly related to AD and MCI in many previous studies [3, 4, 6, 11, 12, 24].
4. Conclusions
In this paper, we proposed a novel matrix-similarity based loss function. Specifically, we used high-level information inherent in the target response matrix and imposed the information to be preserved in the predicted response matrix. Our objective function for joint feature selection was formulated by combining the newly devised loss function with a group lasso. In our extensive experiments on ADNI dataset, we validated the effectiveness of the proposed method by showing the performance enhancements in both the clinical scores (i.e., ADAS-Cog and MMSE) prediction and the class label identification, outperforming the state-of-the-art methods.
Acknowledgements
This study was supported by National Institutes of Health (EB006733, EB008374, EB009634, AG041721, AG042599, and MH100217). Xiaofeng Zhu was partly supported by the Natural Science Foundation of China (NSFC) under grant 61263035.
Footnotes
In this work, we have one sample per subject.
In our work, we used the built-in function ‘lyap’ in MATLAB.
We used the LIBSVM toolbox [2].
Please refer to “www.adni-info.org” for details.
References
- 1.Brookmeyer R, Johnson E, Ziegler-Graham K, Arrighi MH. Forecasting the global burden of Alzheimer's disease. Alzheimer's & Dementia : the Journal of the Alzheimer's Association. 2007;3(3):186–191. doi: 10.1016/j.jalz.2007.04.381. [DOI] [PubMed] [Google Scholar]
- 2.Chang C-C, Lin C-J. LIBSVM: A library for support vector machines. ACM Transactions on Intelligent Systems and Technology. 2011;2(27):1–27. 27. [Google Scholar]
- 3.Chételat G, Eustache F, Viader F, Sayette VDL, Pélerin A, Mézenge F, Hannequin D, Dupuy B, Baron J-C, Desgranges B. FDG-PET measurement is more accurate than neuropsychological assessments to predict global cognitive deterioration in patients with mild cognitive impairment. Neurocase. 2005;11(1):14–25. doi: 10.1080/13554790490896938. [DOI] [PubMed] [Google Scholar]
- 4.Convit A, De Asis J, De Leon M, Tarshish C, De Santi S, Rusinek H. Atrophy of the medial occipitotemporal, inferior, and middle temporal gyri in non-demented elderly predict decline to Alzheimer's disease. Neurobiology of aging. 2000;21(1):19–26. doi: 10.1016/s0197-4580(99)00107-4. [DOI] [PubMed] [Google Scholar]
- 5.Fan Y, Rao H, Hurt H, Giannetta J, Korczykowski M, Shera D, Avants BB, Gee JC, Wang J, Shen D. Multivariate examination of brain abnormality using both structural and functional MRI. NeuroImage. 2007;36(4):1189–1199. doi: 10.1016/j.neuroimage.2007.04.009. [DOI] [PubMed] [Google Scholar]
- 6.Fox NC, Schott JM. Imaging cerebral atrophy: normal ageing to Alzheimer's disease. The Lancet. 2004;363(9406):392–394. doi: 10.1016/S0140-6736(04)15441-X. [DOI] [PubMed] [Google Scholar]
- 7.He X, Cai D, Niyogi P. Laplacian score for feature selection. NIPS. 2005:1–8. [Google Scholar]
- 8.Jie B, Zhang D, Cheng B, Shen D. Manifold regularized multi-task feature selection for multi-modality classification in Alzheimer's disease. MICCAI. 2013:9–16. doi: 10.1007/978-3-642-40811-3_35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kabani NJ. 3D anatomical atlas of the human brain. NeuroImage. 1998;7:0700–0717. [Google Scholar]
- 10.Liu F, Suk H-I, Wee C-Y, Chen H, Shenn D. High-order graph matching based feature selection for Alzheimer's disease identification. MICCAI. 2013:311–318. doi: 10.1007/978-3-642-40763-5_39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Liu F, Wee C-Y, Chen H, Shen D. Inter-modality relationship constrained multi-modality multi-task feature selection for Alzheimer's disease and mild cognitive impairment identification. NeuroImage. 2014;84:466–475. doi: 10.1016/j.neuroimage.2013.09.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Misra C, Fan Y, Davatzikos C. Baseline and longitudinal patterns of brain atrophy in MCI patients, and their use in prediction of short-term conversion to AD: results from ADNI. NeuroImage. 2009;44(4):1415–1422. doi: 10.1016/j.neuroimage.2008.10.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Roweis ST, Saul LK. Nonlinear dimensionality reduction by locally linear embedding. Science. 2000;290:2323–2326. doi: 10.1126/science.290.5500.2323. [DOI] [PubMed] [Google Scholar]
- 14.Shen D, Davatzikos C. HAMMER: hierarchical attribute matching mechanism for elastic registration. IEEE Transactions on Medical Imaging. 2002;21(11):1421–1439. doi: 10.1109/TMI.2002.803111. [DOI] [PubMed] [Google Scholar]
- 15.Stonnington CM, Chu C, Klöppel S, Jack CR, Jr, Ash-burner J, Frackowiak RS. Predicting clinical scores from magnetic resonance scans in Alzheimer's disease. NeuroImage. 2010;51(4):1405–1413. doi: 10.1016/j.neuroimage.2010.03.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Suk H-I, Lee S-W. A novel Bayesian framework for discriminative feature extraction in brain-computer interfaces. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2013;35(2):286–299. doi: 10.1109/TPAMI.2012.69. [DOI] [PubMed] [Google Scholar]
- 17.Suk H-I, Shen D. Deep learning-based feature representation for AD/MCI classification. MICCAI. 2013. :583–590. doi: 10.1007/978-3-642-40763-5_72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Suk H-I, Wee C-Y, Shen D. Discriminative group sparse representation for mild cognitive impairment classification. MLMI. 2013:131–138. doi: 10.1007/s12021-014-9241-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wang H, Nie F, Huang H, Risacher S, Saykin AJ, Shen L. Identifying AD-sensitive and cognition-relevant imaging biomarkers via joint classification and regression. MICCAI. 2011:115–123. doi: 10.1007/978-3-642-23626-6_15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wee C-Y, Yap P-T, Li W, Denny K, Browndyke JN, Potter GG, Welsh-Bohmer KA, Wang L, Shen D. Enriched white matter connectivity networks for accurate identification of MCI patients. NeuroImage. 2011;54(3):1812–1822. doi: 10.1016/j.neuroimage.2010.10.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wee C-Y, Yap P-T, Zhang D, Denny K, Browndyke JN, Potter GG, Welsh-Bohmer KA, Wang L, Shen D. Identification of MCI individuals using structural and functional connectivity networks. Neuroimage. 2012;59(3):2045–2056. doi: 10.1016/j.neuroimage.2011.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Weinberger KQ, Sha F, Saul LK. Learning a kernel matrix for nonlinear dimensionality reduction. ICML. 2004:17–24. [Google Scholar]
- 23.Yuan M, Lin Y. Model selection and estimation in regression with grouped variables. Journal of the Royal Statistical Society Series B. 2006;68(1):49–67. [Google Scholar]
- 24.Zhang D, Shen D. Multi-modal multi-task learning for joint prediction of multiple regression and classification variables in Alzheimer's disease. NeuroImage. 2012;59(2):895–907. doi: 10.1016/j.neuroimage.2011.09.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhang D, Wang Y, Zhou L, Yuan H, Shen D. Multi-modal classification of Alzheimer's disease and mild cognitive impairment. NeuroImage. 2011;55(3):856–867. doi: 10.1016/j.neuroimage.2011.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhu X, Ding W, Wu X, Zhang S. Feature selection by joint graph sparse coding. SDM. 2013:803–811. [Google Scholar]
- 27.Zhu X, Huang Z, Cui J, Shen HT. Video-to-shot tag propagation by graph sparse group lasso. IEEE Transactions on Multimedia. 2013;13(3):633–646. [Google Scholar]
- 28.Zhu X, Huang Z, Shen HT, Cheng J, Xu C. Dimensionality reduction by mixed kernel canonical correlation analysis. Pattern Recognition. 2012;45(8):3003–3016. [Google Scholar]
- 29.Zhu X, Huang Z, Yang Y, Shen HT, Xu C, Luo J. Self-taught dimensionality reduction on the high-dimensional small-sized data. Pattern Recognition. 2013;46(1):215–229. [Google Scholar]