Abstract
Concentric tube robots are catheter-sized continuum robots that are well suited for minimally invasive surgery inside confined body cavities. These robots are constructed from sets of pre-curved superelastic tubes and are capable of assuming complex 3D curves. The family of 3D curves that the robot can assume depends on the number, curvatures, lengths and stiffnesses of the tubes in its tube set. The robot design problem involves solving for a tube set that will produce the family of curves necessary to perform a surgical procedure. At a minimum, these curves must enable the robot to smoothly extend into the body and to manipulate tools over the desired surgical workspace while respecting anatomical constraints. This paper introduces an optimization framework that utilizes procedureor patient-specific image-based anatomical models along with surgical workspace requirements to generate robot tube set designs. The algorithm searches for designs that minimize robot length and curvature and for which all paths required for the procedure consist of stable robot configurations. Two mechanics-based kinematic models are used. Initial designs are sought using a model assuming torsional rigidity. These designs are then refined using a torsionally-compliant model. The approach is illustrated with clinically relevant examples from neurosurgery and intracardiac surgery.
I. INTRODUCTION
While in a few important cases, anatomical constraints can be obviated, e.g., by insufflation of the abdominal cavity, there are many sites within the body for which reducing procedural invasiveness requires inserting instruments along tortuous paths in a follow-the-leader fashion and manipulating tip-mounted tools inside small body cavities. Such situations, involving coordinated control of an instrument’s many degrees of freedom to navigate in complex 3D geometries, are well suited to robotic solutions using continuum-type (continuous curve) architectures [2]–[6].
In some interventions, such as those performed by catheters or endoscope, the robotic devices are passive along much of their length and rely on contact with the surrounding tissue to guide their advance through passageways of the body. Any compliance introduced to limit contact forces, however, also reduces tip stiffness and consequently limits what tasks can be performed at a robot’s tip. Furthermore, reliance on tissue contact for steering can result in damage to sensitive tissues. Thus, the distribution of degrees of freedom along a robot’s length together with selection of materials and desired stiffness are closely coupled to the clinical application.
Concentric tube robots are one type of continuum robot, as shown in Fig. 1, with cross sections comparable to needles and catheters. They are capable of actively-controlled lateral motion and force application along their entire length. Furthermore, the lumen of the tubes can act as a tool delivery channel and can house additional tubes and wires for controlling articulated tip-mounted tools. They can be fabricated from a variety of materials in order to achieve a range of compliances for a given diameter.
Fig. 1.
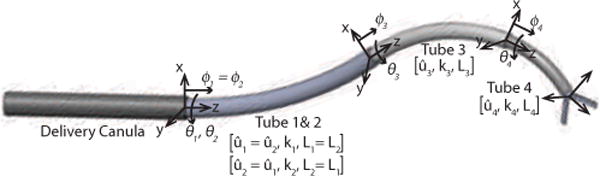
Concentric tube robot comprised of three curved telescoping sections that can be rotated and translated with respect to each other. The first section, comprising two tubes, is a variable curvature section.
While not considered here, they can also be used as steerable needles. In this way, if anatomical constraints preclude reaching a surgical site entirely through body lumens, they can be steered through through a combination of tissue and fluid-filled spaces to reach a target.
While concentric tube robots are a recent innovation, substantial progress has been made in formulating the underlying theory and in adapting the technology for specific medical applications [1], [7]–[16]. Design principles have been formulated [8] and mechanics-based kinematic and quasistatic force models have been derived [8]–[11]. Since robot shape depends on elastic deformation of the component tubes, the stability of solutions obtained from these models has also been studied [8], [9]. A variety of model-based approaches to real-time control have been formulated [8], [12], [17]. Path planning algorithms are also being developed to enable robot navigation within anatomical constraints [13], [18]. Clinical applications considered to date include neurosurgery [7], [19], lung surgery [13], [14], [18] and cardiac surgery [1], [15], [16], including in vivo demonstrations of percutaneous beating-heart intracardiac surgery in an animal model [16], [20].
A topic that has received less attention is how to design a concentric tube robot to meet the constraints imposed by a specific surgical task and anatomical environment [1], [7], [14], [21]. The robot design problem is of high computational complexity since evaluation of each candidate solution involves solving a path planning problem for a robot whose kinematic model is derived as the solution to a 3D beam-bending problem with split boundary conditions.
Tractability of the design problem can be achieved by prescribing design guidelines that constrain the free (tube) parameters, but this is challenging since, while the mathematical kinematic model and stability results for a pair of tubes are known, by themselves they do not provide any intuition about what the workspace of a specific robot will look like nor where in its workspace it will be stable.
The main contribution of this paper is a design methodology and optimization framework based on anatomical and surgical task constraints that considerably reduces the dimensionality of the design space while still providing a rich solution set. Surgical tasks are prescribed as regions of the robot workspace represented as sets of tip coordinate frames. Robot-anatomy interaction constraints are specified with respect to image-based 3D models of the anatomy. Path planning is performed implicitly by defining a sufficiently dense set of tip coordinate frames in the task description. Computational tractability is achieved using a simplified (torsionally rigid) kinematic model during the initial tube parameters search. Model refinement is then performed using the torsionally compliant kinematic model.
This paper provides a number of contributions beyond the initial design optimisation approach presented in [1]. In section IIA, geometric conditions for follow-the-leader insertion are derived to motivate the design rules. The effect of the design rules in reducing the number of design variables and thus simplifying the minimization problem is presented in section IIC. Moreover, in section IID, this paper examines for the first time the effect of section type (variable or fixed curvature) and arrangement of section types on the workspace of a concentric tube robot and defines the boundaries of the workspace in terms of the section variables. This leads to counterintuitive results crucial for understanding the robot design problem.
This is also the first paper to include elastic stability in the concentric tube robot design process. To do so, the optimization function has been adapted to include heuristics that maximise robot stability. It is demonstrated that designs exhibiting instabilities can be used as long as unstable configurations are avoided.
Another improvement is that while [1] considered a set of tip targets, it had not addressed whether the robot could reach those targets from its entry point in the anatomy nor whether it could safely move between them, i.e., path planning to the targets was not considered. Here, implicit path planning is performed by introducing a sequence of waypoints starting from the entry location (section IIE and examples). This is a crucial issue when elastic instability is considered.
While our prior work utilized a simplified kinematic model, the approach presented here uses both simplified and complete models to speed the design process without sacrificing accuracy (section IV). Also, [1] had implemented anatomical interference as a binary decision function, which necessitated the use of computationally intensive global optimization techniques. Our current submission substitutes potential fields and so greatly reduces the computational time involved in solving for a design (section IVB).
Finally, the clinical design examples presented in section V are more sophisticated and complete than prior published results. In particular, the neurosurgical example solves for a robot design that can safely navigate through both ventricles from a single insertion point while prior designs were constrained to navigating within a single ventricle [7]. We have also added an experimental validation of a robot design for intracardiac PFO closure by comparing it against a robot successfully employed in beating-heart procedures [16], [20].
This paper is structured as follows. Sec. II presents our robot design methodology that is based on the architecture of Fig. 1 in which tube sets are constrained so that the robot takes the form of a telescoping concatenation of fixed and variable curvature sections. The effect of section type and arrangement of sections on robot shape, workspace and solution stability is also explored. This section also introduces a decomposition of the design problem in which the distal sections are first designed to achieve the desired surgical workspace and, subsequently, the proximal sections are designed to navigate and position the distal sections at the surgical site. The design optimization framework is presented in Sec. III and implementation details are provided in Sec. IV. The design approach is validated for two challenging clinical procedures in Sec. V and conclusions appear in Sec. VI. All variable names used in the paper are listed in Table I and Table II.
TABLE I.
Nomenclature, pt. 1
| Symbol | Description | |
|---|---|---|
| gc | 3D curve for follow-the-leader extension | |
| t | Time instances during follow-the-leader extension | |
|
|
Physical location of a robot that follows curve s | |
|
|
Set of nonnegative integers | |
|
|
Set of real numbers | |
| n | Number of tubes in a robot design | |
| m | Number of sections in a robot design | |
| mn | Number of sections in robot navigation portion | |
| mm | Number of sections in robot manipulation portion | |
| v | Number of robot variable curvature sections | |
| ρ | Total number of arrangements of v variable curvature sections | |
| t | Number of tip task frames for specific procedure | |
| V | Binary m-vector specifying variable curvature sections | |
| Vn | Binary mn-vector specifying variable curvature sections in navigation portion of robot | |
| Vm | Binary mm-vector specifying variable curvature sections in manipulator portion of robot | |
| Vp | Binary vector specifying variable curvature sections extending from straight proximal sections | |
| s | Arc length along centerline of tube or tube set | |
| Li | Total length of tube i | |
|
|
Bending pre-curvature of ith tube about x as function of arc length, s | |
|
|
Bending pre-curvature of ith tube about y as function of arc length, s | |
|
|
Bending pre-curvature of jth tube or section | |
|
|
Vector of section pre-curvatures | |
|
|
Vector of navigation section pre-curvatures | |
|
|
Vector of manipulation section pre-curvatures |
TABLE II.
Nomenclature, pt. 2
| Symbol | Description | |
|---|---|---|
| ϕi | Relative extension of the ith tube or section | |
| Φi | Maximum relative extension of the ith tube or section | |
| ϕp, Φp | Extension variables for proximal section | |
| ϕd, Φd | Extension variables for distal section | |
| kix(s) | Bending stiffness of ith tube about x as function of arc length, s | |
| kiy(s) | Bending stiffness of ith tube about y as function of arc length, s | |
| kB | Bending stiffness of distal manipulation section | |
| kA | Bending stiffness of distal navigation section | |
| D | Stiffness ratio of a robot section with respect to proximal section | |
| θi | Rotation of the ith tube | |
| αi | Relative rotation of the ith tube with respect to tube 1 | |
|
|
Unconstrained robot tube set | |
|
|
Robot tube set satisfying design rules of Section II-A | |
| q | Set of kinematic input variables | |
| RoC | Radius of curvature, equivalent to | |
| r | Radius of a tube | |
| Bi, | The set of surgical task frames, | |
| E | Frame of entry into the anatomy | |
| Eg | Initial guess for frame of entry into the anatomy | |
| A | Frame of the manipulator base | |
| Ag | Initial guess for manipulator base frame | |
|
|
Clinician selected regions for frames E and A | |
|
|
x-axis vector for frame B | |
| Γ, Γm, Γn | Representation of the anatomy | |
| Δ, Δn | Penalty function for the anatomy | |
| v | Poisson’s ratio | |
| Rz(θ) | Rotation matrix of θ around the z-axis | |
| Ω | Occupancy volume for anatomical model | |
| Ωr | Occupancy volume eroded by radius r | |
| Ur | Distance map corresponding to Ωr | |
| Sr | Spherical structural element of radius r | |
| Pi | Point on robot centerline, i=1,…, o |
II. ROBOT DESIGN
In contrast to standard robots possessing rigid links and discrete joints, concentric tube robots are continuum robots. When their constituent pre-curved tubes are inserted inside each other, their common axis conforms to a mutual resultant curvature. By controlling relative translations and rotations of the tubes at their proximal ends, the shape and length of the robot can be varied. Thus, the tubes act as both links and flexure joints. By extending these robots telescopically, they offer the potential to act as steerable needles following curved paths through tissue while also being capable of manipulating tools inside body cavities.
Unlike hyper-redundant continuum robots, however, that are often modeled using large numbers of independently actuated revolute or universal joints that are closely spaced with respect to arc length [22], [23], concentric tube robots possess a much smaller number of degrees of freedom equal, at most, to twice the number of tubes comprising the robot. Furthermore, it is difficult to predict the workspace and arm motions produced by a robot constructed from tubes of arbitrary pre-curvature and relative stiffness since the effect of rotating or translating any individual tube is not localized in arc length and may change the shape along the entire length of the robot.
By focusing on the desired capabilities, it is possible to constrain the design space to those tube sets most likely to produce clinically relevant solutions. In particular, the following properties are desired:
The ability to follow curved paths through tissue while exerting minimal lateral forces and to navigate through narrow curved body passages, and
The ability to perform complex tissue manipulations at the interventional site while moving only distal sections.
The first property corresponds to follow-the-leader insertion as a robot extends along a desired 3D curve, typically to reach a desired site inside the body. The second property provides for the proximal portion of the robot to be used primarily for navigation to an interventional site while the distal portion is used, independently, for tissue interaction. As shown below, the design guidelines to achieve follow-the-leader insertion also provide this property.
A. Follow-the-Leader Extension
In follow-the-leader extension, a 3D curve is defined using a coordinate frame, gc(sc), parameterized by curve arc length, sc, as shown in Fig. 2. The initial frame of the curve, gc (0)=g0 is defined at the base of the robot and the curve itself is given by the solution to the differential equation
| (1) |
in which is the body frame curvature vector and vc(sc) = [0 0 1]T. Since robot cross sections slide along the curve during extension, robot arc length, sr ∈ [0, Lr] is defined independently with sr = Lr at the distal end.
Fig. 2.
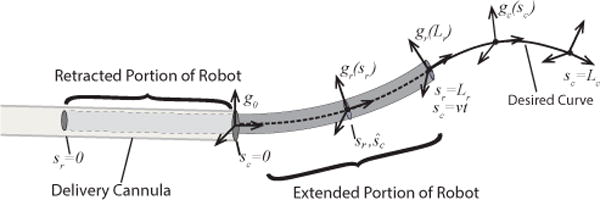
Follow-the-leader robot extension. Robot cross sections, described by gr(sr), move along desired curve, described by gc(sc) with arc length velocity, v.
Assuming constant velocity extension, v, the robot cross section, sr, is physically located along the curve at time t at
| (2) |
in which Lr − vt is the length of the retracted portion of the robot. For follow-the-leader extension, at each instant of time, t, every robot cross section in the interval of sr must satisfy (1) such that
| (3) |
Furthermore, each robot cross section must bend with time as it slides along the curve with arc length velocity, v. The temporal variation in robot curvature is
| (4) |
Recognizing time dependence of ur is through the that the kinematic input variables, q, this equation can be rewritten as
| (5) |
To satisfy this equation for all values of the continuous variable sr∈ [Lr−vt, Lr] at any time t ≥ 0 would require q to be of infinite dimension. Consequently, follow-the-leader extension along an arbitrary curve can only be performed by a robot with infinite degrees of freedom.
An alternative approach for robots with finite degrees of freedom is to constrain the set of curves to be followed. One important set of curves are those in which curvature is independent of arc length, corresponding to the trivial solution of (5) given by
| (6) |
By (4), this implies that robot curvature is independent of time and by (3) yields the solution
| (7) |
This constant-curvature solution is comprised of arcs (when the z-component of uc is zero) and helices (when the z-component is non-zero). Notice that this solution does not imply that dq/dt=0 in (5) since, for example, some kinematic variables control extension.
Thus, any robot architecture that can extend with constant curvature can perform follow-the-leader extension along curves comprised of arcs or helices. This result can be generalized if the robot design enables the trivial solution of (5) to be applied over m subintervals of sc ∈[0, Lc], each of which can be taken as constant curvature yielding an overall curve of piecewise constant curvature,
| (8) |
As shown below, applying these geometric results for follow-the-leader extension on concentric tube robots is straightforward. Follow-the-leader conditions are also considered in [24].
B. Design Guidelines
By constraining the parameter space, concentric tube robot designs can be made to provide the two desired clinical properties of follow-the-leader insertion and independent motion of the distal sections. These are achieved through the following three design rules.
The pre-curvature of each tube is piecewise constant.
The bending stiffness of each telescoping section dominates that of all distal sections.
Each telescoping section is designed to be of either fixed curvature or of varying curvature.
The first two rules, taken together, enable a design to approximately satisfy (8) for a specific piecewise-constant-curvature curve. The third rule enables a single design to satisfy (8) for a parameterized family of piecewise-constant-curvature curves. The second and third rules also provide the second desired clinical property – the ability to perform tissue manipulation at the robot tip while moving only distal sections.
The first rule is based on the result that concentrically combined tubes of piecewise constant curvature yield a telescoping shape that is also approximately piecewise constant. This has been considered in detail for arcs in, e.g., [8] and initial results for helices appear in [24]. Without loss of generality and to further reduce the number of design parameters, only arcs are considered in the remainder of this paper.
To satisfy (8), it must also be true that, during telescopic insertion, extension proceeds from the most proximal section to the most distal and, as each constant-curvature section extends, the proximal sections should not be displaced laterally from the desired curve. The same must be true to perform tissue manipulations using only the distal sections.
This can be achieved by selecting the bending stiffness (and, consequently, the torsional stiffness) of each section to be substantially larger than the combined stiffness of the distal sections. The design examples in this paper use a stiffness ratio of 10 between adjacent sections, but ratios of 6–8 have proven sufficient in practice. In addition to follow-the-leader extension, this rule is also advantageous since it produces an approximate kinematic decoupling between each telescoping section of the robot.
The third design rule prescribes each telescoping section to be of either fixed or variable curvature. A single tube is required to construct a constant curvature section while two tubes are needed to construct a variable curvature section [8].
A fixed curvature section extends along its pre-curved curvature when extended from its stiffer preceding section. In contrast, the extended portion of a variable curvature section can take on a continuous range of curvature magnitudes usually ranging between zero (straight) and a maximum value. These can be interpreted as continuum-robot analogs to prismatic and rotary joints, respectively.
In follow-the-leader extension, a section of fixed curvature can only assume its pre-curved value over its interval of arc length in (8) while a variable curvature section can assume any curvature in its permissible range, e.g., ‖ci‖ ∈ [0, ‖ci,max‖], enabling extension along a family of curves parameterized by the curvatures of these sections. For tissue manipulation using the distal sections, fixed and variable curvature sections can be combined to produce the task-prescribed workspace while respecting anatomical constraints.
Using these rules, the design problem is to solve for a telescoping arrangement of fixed- and variable-curvature robot sections in which the proximal sections are predominantly used for follow-the-leader navigation to the interventional site and the distal sections are used to perform the intervention. The effect of these rules on reducing the dimension of the design space is detailed below.
C. Design Variables
The unconstrained robot design problem consists of solving for the discrete variable, n, defining the number of tubes, and for the curvature and bending stiffness of each tube as continuous functions of arc length, s. Using Bishop coordinate frames for each tube as shown in Fig. 1, the unknown pre-curvature functions are given by . Assuming circular cross sections for the tubes, the bending stiffnesses will equate in the x and y directions such that there is a single unknown continuous stiffness function for each tube, kix(s)= kiy(s), s∈[0, Li], i= 1, 2, …, n. Together, the variables define an unconstrained robot tube set, denoted by:
| (9) |
By imposing the design rules of the preceding subsection, solving for these continuous functions is reduced to solving for a set of discrete parameters for each tube. To identify this set, consider first that constant curvature sections have two kinematic input variables, {ϕi, θi} corresponding to section extension length and tube rotation. Variable curvature sections consist of two tubes of equal bending stiffness which undergo identical translations but individual rotations. These sections possess three independent kinematic input variables {ϕi=ϕi+1, θi, θi+1} The angles { θi, θi+1} control rotation and curvature of the section and ϕi controls extension arc length.
Given that the robot comprises m telescoping sections, the pre-curvatures of the tubes comprising a section are given by
| (10) |
in which j=1, 2, …, m, m ≤ n, and is the pre-curvature over the distal length Φj of the jth section composed of tubes with total length of Lj. Note that Lj are dependent parameters since they can be computed from the maximum section lengths, Φj.
If the bending stiffnesses of the sections are selected according to a single stiffness ratio, D≫1 then the free parameters associated with stiffness reduce to two discrete values – the actual bending stiffness of any one section and the ratio, D. For example, it is often useful to specify the stiffness of the most distal section, kd, since it is the most compliant. Naturally, the stiffness, radius, and maximum possible pre-curvature of a tube are related through its mechanical properties.
The design rules also replace the selection of tube number, n, with the selection of section number m along with selection of the number of variable curvature sections, v. These are related by:
| (11) |
If v > 0 then the location of the variable curvature sections along the length of the robot must also be specified. The number ρ of arrangements is given by the permutations of m sections taken v at a time:
| (12) |
Due to the exponential nature of the equation, there is a drastic difference, for example, between using 3 sections (8 combinations) and 5 sections (32 combinations). Eq. (12) underlines this combinatorial explosion for the general robot design problem that follows the guidelines provided in this paper.
In summary, the design rules replace solving for continuous functions of curvature and bending stiffness for n individual tubes, as well as their lengths, with solving for the 2m + 2 parameters corresponding to the curvature and maximum extension length of each section along with two stiffness parameters. Together with the number and location of the variable curvature sections, these provide a complete description of the robot tube set,
| (13) |
in which the specifies the variable curvature sections.
To potentially prune the search space so as to avoid considering all 2m possible combinations of fixed and variable curvature sections, it is worthwhile to gain insight into how the number and arrangement of variable curvature sections affect robot workspace and section stability. These topics are considered in the following subsection.
D. Effect of Section Type
While workspaces of standard robot architectures, such as SCARA or PUMA arms, are well known, there are no prior results for concentric tube robots. Since the number, type and arrangement of robot sections are inputs to the design process, only by understanding the achievable workspaces can one intelligently select these inputs. For example, while variable curvature sections possess an extra degree of freedom compared to fixed curvature sections, they also require an additional tube. This can increase both the cost and diameter of the tubes comprising a robot design and potentially introduce an instability associated with straightening the variable curvature tube pair. In order to guide the design process, the effects of section type and arrangement on workspace and stability are developed below.
1) Workspace
To gain such an understanding, four two-section concentric tube robots are considered here. Listing the section type from base to tip, these are: (1) fixed-fixed curvature, (2) fixed-variable curvature, (3) variable-fixed curvature and (4) variable-variable curvature. These designs are comprised of two, three (two designs) and four tubes and possess four, five (two designs) and six degrees of freedom, respectively.
Using the elastically stable parameter set of Design 1 in Table III, the workspaces, comprising the sets of reachable tip positions, are compared in Fig. 3. It is assumed that the two sections are extended from a straight rigid vertically-oriented cannula whose tip is located at the origin. Due to the cylindrical symmetry of the workspaces, only the xz plane is plotted.
TABLE III.
Parameters of robot design examples.
| Base location [mm] | [0, 0, 0]T | ||
| Entry vector | [0, 0, 1]T | ||
| Section stiffness ratio | D = 10 | ||
|
Design 1 – Stable | |||
| Section | 1/ki [mm] | Φi [mm] | Li [mm] |
| proximal | 60 | 40 | 40 |
| distal | 25 | 20 | 60 |
|
Design 2 – Unstable | |||
| Section | 1/ki [mm] | Φi [mm] | Li [mm] |
| proximal | 40 | 40 | 40 |
| distal | 10 | 20 | 60 |
Fig. 3.
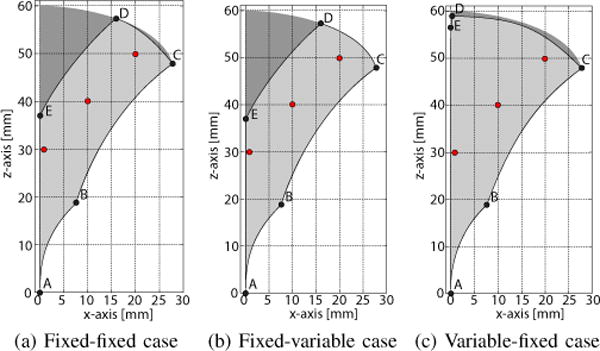
Tip position workspace for robot Design 1 of Table II showing xz-plane slices. Complete workspace is generated by rotation of slice about z axis. (a) Fixed-fixed curvature sections, (b) fixed-variable curvature sections, (c) variable-fixed curvature sections. Dark shaded area in each plot is workspace of variable-variable curvature design. Red ○ are tip positions used to generate Fig. 4
The plots were created using Monte-Carlo simulation to generate 2 million kinematic configurations using the torsionally compliant model of [8] through uniform sampling of each kinematic variable. All configurations were rotated about the z axis to place the robot tip on the xz plane. This resulted in a dense workspace point cloud, which was subsequently binned into 250×250 μm clusters. Alternative efficient methods for calculation of this workspace density can be found in [25], [26].
The curves forming the workspace boundaries are described in Table IV. Except for EA, these curves are generated as limiting values of section extension. Thus, while specific parameter values were used to generate these plots, they are representative of their designs, and researchers can use this table to compute the workspace of their robot without performing Monte-Carlo simulations, clustering, and visualisation.
TABLE IV.
Workspace Boundary Curves for Fig. 3.
| Boundary Curve | Section Variables | Boundary Curvature | ||||||
|---|---|---|---|---|---|---|---|---|
| AB | ϕp = 0 | 0 ≤ ϕd ≤ Φd |
|
|
|
|||
| BC | 0 ≤ ϕp ≤ Φp | ϕd = Φd |
|
|
|
|||
| CD | ϕp = Φp | ϕd = Φd |
|
|
- - | |||
| DE | 0 ≤ ϕp ≤ Φp | ϕd = Φd |
|
|
|
|||
| EA | 0 ≤ ϕp ≤ Φp | 0 ≤ ϕd ≤ Φd |
|
|
0 | |||
Several important observations can be made in comparing workspaces. First, the workspace of the variable-variable design, depicted as the dark shaded area in each subfigure, is a superset of all other workspaces and so provides a benchmark for comparing the other workspaces. Second, while the fixed-variable design is comprised of three tubes, its workspace is very close to that of the fixed-fixed design that requires only two tubes. Furthermore, the workspace of the three-tube variable-fixed design is close to that of the four-tube variable-variable design. In particular, it eliminates the central void located along the longitudinal z-axis.
Since these robot designs possess 4–6 degrees of freedom, it is also worthwhile to consider the range of orientations that can be achieved at each tip position in the workspace. The families of solutions for the labeled points of Fig. 3 are depicted in Fig. 4. The xz-plane views on the top show a subset of solutions for clarity. To illustrate the 3D geometry of the solution sets, the intersections of the robot configuration sets with cut planes are also plotted in the figure. The cut plane views illustrate the range of robot shapes associated with a tip position that can be used to satisfy anatomical and stability constraints. Smaller cut plane sets provide fewer solutions for satisfying these constraints. The variable-fixed design can be seen to provide the largest set of shapes.
Fig. 4.
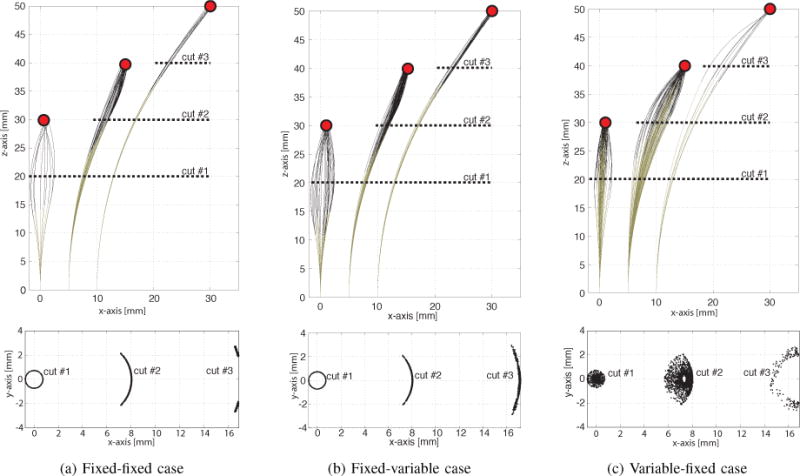
Solution sets of orientations for three tip positions labeled in Fig. 3. Cut planes show cross sections of solution sets. (a) Fixed-fixed design, (b) Fixed-variable design, (c) Variable-fixed design.
The curves forming the workspace boundaries are described in Table IV. Except for EA, these curves are generated as limiting values of section extension. Thus, while specific parameter values were used to generate these plots, they are representative of their designs, and researchers can use this table to compute the workspace of their robot without performing Monte-Carlo simulations, clustering, and visualisation.
Several important observations can be made in comparing workspaces. First, the workspace of the variable-variable design, depicted as the dark shaded area in each subfigure, is a superset of all other workspaces and so provides a benchmark for comparing the other workspaces. Second, while the fixedvariable design is comprised of three tubes, its workspace is very close to that of the fixed-fixed design that requires only two tubes. Furthermore, the workspace of the three-tube variable-fixed design is close to that of the four-tube variablevariable design. In particular, it eliminates the central void located along the longitudinal z-axis.
Since these robot designs possess 4−6 degrees of freedom, it is also worthwhile to consider the range of orientations that can be achieved at each tip position in the workspace. The families of solutions for the labeled points of Fig. 3 are depicted in Fig. 4. The xz-plane views on the top show a subset of solutions for clarity. To illustrate the 3D geometry of the solution sets, the intersections of the robot configuration sets with cut planes are also plotted in the figure. The cut plane views illustrate the range of robot shapes associated with a tip position that can be used to satisfy anatomical and stability constraints. Smaller cut plane sets provide fewer solutions for satisfying these constraints. The variable-fixed design can be seen to provide the largest set of shapes.
In summary, for two-section robot designs, the 3-tube variable-fixed curvature section design offers advantages both in workspace size and range of possible orientations at each point within the workspace. This design possesses five degrees of freedom (DOF) with the missing DOF corresponding to a roll rotation at the tip. Roll can easily be added to a tip-deployed tool through an inner rotating straight tube. Thus, the variable-fixed design can be a good choice for the manipulation portion of a robot design when using the navigation and manipulation decomposition described in Section II-E. Moreover, these results demonstrate that, counterintuitively, a distal variable curvature section provides minimal benefit over a fixed curvature section in terms of workspace.
2) Stability
When two or more curved tubes undergo relative rotation at their base, elastic energy is stored and released through twisting and bending of the tubes. As the curvatures and lengths of the tubes increase, the mapping from kinematic input variables (base rotations and extensions of tubes) to robot tip frame can fail to be injective with the extra solutions corresponding to elastically unstable solutions [8]. To uniquely describe all solutions, a robot configuration is defined here by both the kinematic input variables and by the associated tip frame.
Since the instability occurs only for specific configurations of the tubes, such designs can still be used as long as the unstable configurations are avoided. For example, Fig. 5 illustrates the case for the variable-fixed section arrangement of Design 2 in Table III. For this tube set, there is an instability associated with rotating the distal fixed curvature section while partially retracted into the curved balanced pair. Two configurations associated with the same tip position, but different extensions are shown in Fig. 5. In configuration 1, the distal curved section is substantially retracted into the proximal section and oriented so that the curvatures oppose each other. This configuration is unstable. In contrast, configuration 2 achieves the same workspace position as configuration 1, but it is stable since the distal section is substantially extended and the curvatures of the two sections are aligned.
Fig. 5.
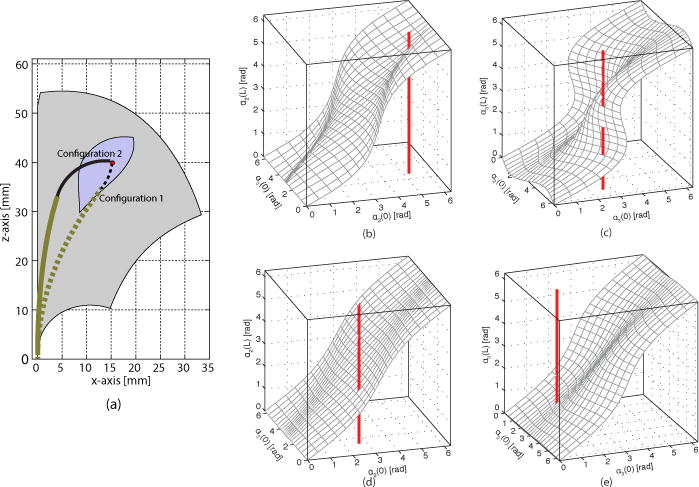
Workspace of variable-fixed design. (a) Configuration 1 (dotted) is unstable and snaps. Configuration 2 is stable. Region of workspace containing unstable configurations is indicated in blue. (b)–(c) S-surfaces of Configuration 1, (d)–(e) S-surfaces of Configuration 2.
Such instabilities can be graphically visualized for specific values of relative section extension as shown in Fig. 5. The relative twist angles at the tips of the tubes, αi(Li) are plotted with respect to the relative twist angles at the proximal end of the robot, αi(0), with αi defined by:
| (14) |
A configuration can be unstable if multiple values of αi(Li) correspond to the same value of αi(0), Graphically, this occurs when the planar cuts of the surfaces resemble s-shaped curves. For the stable configuration of Fig. 5(a), the retracted distal fixed curvature section possesses a single solution for α2(L) [Fig. 5(b)], but has multiple solutions associated with α3(L) [Fig. 5(c)]. In contrast, for the stable configuration of Fig. 5(a), substantially larger distal section extension produces unique twist angle solutions as shown in Figs. 5(d), (e). In this paper, this approach was used to evaluate the stability of specific robot configurations. A configuration was deemed unstable if any of the directional derivatives of αi(Li) with respect to αi(0)were negative.
Since each tip position in the workspace may be reachable through multiple tube configurations (associated with different orientations; see Fig. 4), the workspace can be divided as shown in Fig. 5 into sets comprising tip positions that are stable for all configurations and those that are stable for some configurations. Path planning through these positions involves solving for stable configurations.
The following heuristics can be defined to guide an optimization toward stable configurations. The first two are motivated by the examples above while the third follows from inequality (38) in [8] which relates the existence of unstable configurations to the length of a variable curvature section. As shorthand below, one configuration is defined as more or less stable than another based on their relative distance in the space of kinematic variables to an unstable configuration.
Variable curvature sections are most stable at maximum curvature.
The stability of adjacent constant curvature sections increases as the distal section is extended (assuming that the retracted transmission portion of the extended section has zero curvature).
If a variable curvature section extends from a straight dominating proximal section, stability of the variable curvature section increases as it is retracted into the straight proximal section.
E. Navigation and Manipulation Design Decomposition
As depicted in Fig. 6, minimally invasive surgery may involve navigating through narrow body lumens to reach surgical targets and, subsequently, deploying and manipulating tools in confined spaces to perform the procedure. In the case of concentric tube robots, navigation to the surgical site involves telescopic extension and steering from the entry point on the body, defined by coordinate frame E, to the entry point into the body lumen where the surgery will occur, denoted by coordinate frame A. Once inside this body lumen (e.g., a chamber of the heart), it is often desirable to control the position and orientation of the instrument’s distal tip to manipulate tools, e.g., to reach the set of tip coordinate frames, Bi, i = 1, …, t, while holding relatively immobile the proximal length responsible for navigation.
Fig. 6.
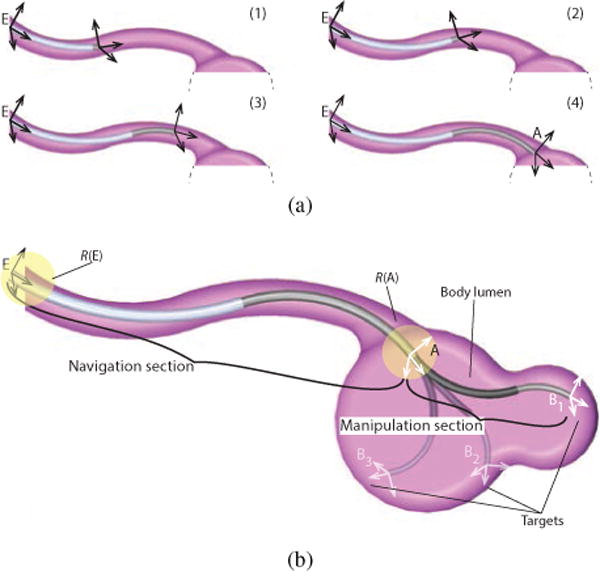
Navigation and manipulation tasks. (a) Navigation – telescopic extension and steering of proximal sections from entry frame, E, to frame A. (b) Manipulation – distal sections move from A to set of tip task frames, Bi located at surgical sites.
For concentric tube robots, this leads to a natural decomposition over the length of the robot in which the proximal sections are responsible for navigation and the distal sections are responsible for tissue manipulation [see Fig. 6(b)]. Many interventions fit this decomposition, such as those inside the heart, the fluid-filled spaces of the central nervous system, the throat, the lungs and the kidneys. Accordingly, the robot design problem can be decomposed into a sequence of two simpler problems in which the distal manipulation sections are designed first and the navigation sections subsequently.
As shown in Fig. 6, the navigation portion of the robot extends between coordinate frames E and A, and the manipulation portion of the robot extends from frame A to the set of tip task frames, . This set of t tip task frames are selected by the clinician to define the region (i.e., curve, surface or volume) of anatomical locations that the robot tip must reach to perform a procedure. This set may also include waypoints to enable safe or stable navigation of the robot tip from frame A to B1 and also between various task frames as needed. Depending on the surgical task, different components of the Bi may be unspecified, e.g., only tip position may be important.
While the tip task frames, Bi, are selected as specific locations with respect to the anatomy, there is usually some freedom in locating the navigation frames E and A. Consequently, the clinician selects regions, labeled and , in which these frames can be located and the robot design algorithm selects the specific frames within these regions.
All of these frames and regions must be defined with respect to an anatomical model that is derived from images generated, e.g., using Magnetic Resonance Imaging (MRI), Computed Tomography (CT) or 3D ultrasound, together with software tools that enable user-guided organ segmentation and rendering, e.g. ITK-Snap. Given this anatomical information, termed Γ, the anatomical constraints, termed Δ(Γ), may be specified by the clinician in accordance with the various types of tissue located along the length of the robot. For example, in the context of intracardiac surgery, constraints on the navigation portion of the robot passing through the vasculature should be defined to avoid puncture or large deflections. In contrast, constraints on the manipulation portion of the robot inside the heart should be defined to avoid contact with the heart wall.
Using this terminology, the overall robot design problem consists of solving sequentially the manipulation and navigation design problems as defined below.
1) Manipulation Design Problem
Given
a region and an initial guess Ag,
a set of tip task frames, , and
a manipulator robot architecture specifying the number of sections in the manipulator portion of the robot, mm, the number and location of variable curvature sections in the manipulator, Vm, tip tube stiffness, kB and dominating stiffness ratio, D,
Solve for the coordinate frame, , tube curvatures, and extension lengths, that minimize:
the curvatures of the manipulator sections, and
the extension lengths, Φm
such that:
the tip task frames, lie in the workspace of the robot, and
the robot satisfies the anatomical constraints, Δm(Γ).
2) Navigation Design Problem
Given
a region and an initial guess Eg,
the coordinate frame A obtained from solving the manipulation problem, and
a navigation robot architecture specifying the number of sections in the navigation portion of the robot, mn, the number and location of variable curvature sections, Vn, desired stiffness of the distal navigation section, kA and dominating stiffness ratio, D,
Solve for the coordinate frame, , tube curvatures, and extension lengths, that minimize:
the curvatures of the navigation sections, and
the extension lengths, Φn
such that:
the robot satisfies the anatomical constraints, Δn(Γ).
The resulting robot design is given by the combined solutions to the manipulation and navigation problems,
| (15) |
III. ROBOT DESIGN OPTIMIZATION
The algorithm is used to solve both the navigation and manipulation design problems, each of which can be posed as sets of nested, simpler optimization problems in which subsets of the design variables are held constant. The two constitutive optimization problems are: (1) solving the anatomically-constrained inverse kinematics problem for a given robot design and base location, (2) solving the optimal robot design and base location problem. These are defined below.
A. Anatomically Constrained Inverse Kinematics
For a given concentric tube robot architecture, , the problem involves solving for the vector of robot tube kinematic variables, q = {ϕ, θ}, that position and tangentially align the robot tip with coordinate frame , given that its base is located at frame A and imposed anatomical constraints Δ(Γ) are respected. Using homogeneous coordinates to represent coordinate frames, frame B can be written as:
| (16) |
Note that and are irrelevant since only the tangential vector will be considered. We denote the forward-kinematics mapping as:
| (17) |
where Btip is the coordinate frame of the tip. Using a penalty method to represent the tip configuration and anatomical constraints, a cost function, c, can be defined as follows, with overbars indicating fixed parameters:
| (18) |
The first two terms penalize the tip position and tangent direction. Note that an additional tube can be added to perform tip roll as needed. The third term employs the function Δ that computes the anatomical constraints, e.g., the interference between the robot and the anatomy. The scalar constants γ1, γ2, γ3 are weighting factors. Minimization of this cost function results in the kinematic variable vector q* that best solves the anatomically-constrained inverse-kinematics problem:
| (19) |
Alternate formulations of the cost function c can be useful. For example, in some applications including the neurosurgical example discussed later in the paper, the tip tangent direction may not be clinically important. Furthermore, cost criteria may be included to utilize kinematic redundancy to avoid unstable tube configurations. For example, the three rules for avoiding instabilities that are included at the end of Section II-D can be included as given in the cost function below in which the scalars are weighting factors and ∊ > 0 is included in the last term to avoid singularity.
| (20) |
B. Robot Design and Base Location Optimization
This problem involves solving for the optimal robot design that can reach a workspace defined by the set of tip coordinate frames, while satisfying anatomical constraints. Simultaneously, the optimization solves for the base coordinate frame A. Since material properties place limits on tube curvature, robot sections with smaller curvatures are preferred. In addition, robot length should be minimized in order to maximize robot stiffness. These considerations lead to the following design cost function, f, that can be written as a function of the inverse-kinematics cost, c:
| (21) |
Here, {δ1i}, and {δ2i} are scalar weights on section curvatures and lengths. In practice, the number of weights can be reduced, e.g., one can assign a single weight per design variable type. The examples of Sec. V discuss this in detail.
The optimal design satisfies:
| (22) |
where i=1, …, n. The manipulation design problem of Sec. II can be solved directly with this formulation. For the navigation problem, the kinematic cost function involves a single tip frame, A.
IV. IMPLEMENTATION
A block diagram of the design optimization appears in Fig. 7. The optimization algorithm is initialized with the robot architecture, task description, anatomical constraints and stiffness parameters. Starting with the torsionally rigid kinematic model, the robot design and base location optimization routine uses (21) to compare prospective designs.
Fig. 7.
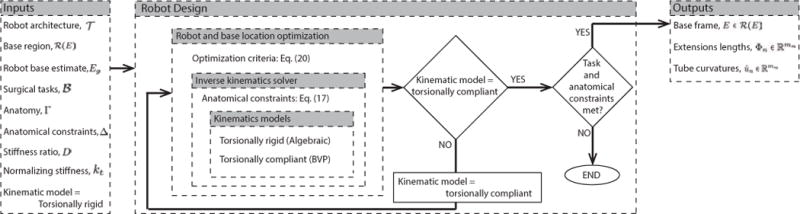
Robot design optimization framework.
When the optimization routine either converges or meets iteration limits, the routine switches to the torsionally compliant kinematic model and uses the solution from the torsionally rigid model as its initial guess. For the cases we have considered, the design obtained from the torsionally rigid model is close to meeting the anatomical and task constraints and so fewer iterations are needed for this second optimization pass.
The main code components are associated with computing the inverse kinematics and with evaluating the anatomical constraints. The kinematic and anatomic models are described in the following together with the optimization algorithm.
A. Robot Kinematic Model
Current models based on tube mechanics are boundary value problems (BVP) comprised of differential equations with respect to robot arc length that have their boundary conditions split between the robot base and tip [8], [9]. These models assume that the tubes are rigid longitudinally and with respect to shear of the cross section. Each tube, however is free to bend and twist about its axis.
For design optimization, a fast inverse kinematic solver is critical. The approach taken here is to implement inverse kinematic solvers of the both the BVP and of an approximate algebraic model that treats the tubes as torsionally rigid [8]. Both models are solved by root finding.
During the design process, the optimization routine arrives at a preliminary design using the simplified kinematic model. This design is used as the initial guess for the BVP model. This approach is intended to achieve computational efficiency while still providing the accuracy obtained from the complete model. If more accurate models are introduced in the future, they can be easily incorporated into this framework.
B. Anatomical Model
The anatomical model is generated from MRI or CT images by image segmentation and is represented as a triangulated surface. Computationally efficient encodings of spatial relationships can be achieved using KD-trees [27]. Thus, the vertices of the anatomy are used to populate a KD-tree, and the tree can be queried for the proximity and geometric relationship of the robot to the anatomy.
For fast collision detection, a linear-time algorithm was developed. First, a binarization step creates an anatomical occupancy map indicating forbidden and allowed robot regions. Second, the allowed occupancy volume is shrunk by erosion operations with spherical elements of radii corresponding to the cross sections of the concentric tube robot elements:
| (23) |
where Sr is the structural element corresponding to radius r, Ω is the allowed occupancy volume, and Ωr the eroded volume. For the cross sections of all the tubes comprising a concentric tube robot, (23) results in a pyramidal occupancy map that can be used for collision detection using only the discretized centerline/skeleton of the concentric tube robot.
The binarized anatomical model is used to extract a Euclidean distance map that simplifies the anatomically constrained inverse kinematics problem. The distance to the anatomy boundary is calculated for each point . A potential function [28] is calculated as:
| (24) |
where is the function’s value at and ∊ ensures a nonzero denominator The inverse kinematics should be calculated such that the concentric tube robot maximizes its distance from anatomical boundaries, similar to [13]. This can be satisfied by minimizing the values of along the centerline of the robot,where, depending on the radius, r, of the section under examination, the appropriate Ur is selected:
| (25) |
where is the robot centerline. The introduction of the anatomical distance-based functional smooths the cost function f of (21) and allows efficient optimization.
Querying Ur for values of 1/∊ allows collision detection in , where n are the points on the discretized concentric tube robot centerline. The number of points is held constant for each robot configuration during the evaluation of the kinematics to avoid discretisation bias. The collision detector’s complexity is lower than , which is the expectation for n nearest-neighbor queries on a KD-tree with k nodes and, consequently, is used for collision detection.
The anatomical constraints are implemented as soft constraints. While interference and constraint violation (e.g., greater than maximum allowable deflection) can be treated in a binary fashion wherein a solution is abandoned when interference is detected, a soft implementation enables implicit construction of a smooth minimisation “error map” rather than one that contains “unmapped” areas of abandoned solutions. Moreover, the selected weighting functions provide an element of robustness to model error in contrast to binary decision functions since they drive the inverse kinematic solutions away from the anatomical boundaries.
C. Optimization Algorithm
Preliminary implementations of our framework in [1], [7] required optimization using Generalized Pattern Search GPS methods [29], as the cost function was nonsmooth and nonlinear. GPS methods are effective in optimizing nonsmooth problems, since they do not require any differentiation [30]. Due to their sampling approach, however, they are computationally inefficient.
The introduction of (25) smooths the cost function, and enables the use of faster optimization methods like the Nelder-Mead downhill simplex method [31]. The implementation of the Nelder-Mead method provided by the Optimization Toolbox of Matlab® was used in the following examples.
V. CLINICAL EXAMPLES
Two examples are presented here to showcase the performance of the proposed design algorithm. The first is a neu-rosurgical example that involves choroid plexus cauterization for hydrocephalus treatment. The second example considers closure of a patent foramen ovale inside the beating heart.
A. Choroid Plexus Cauterization
Cerebrospinal fluid (CSF) is a watery fluid that surrounds the brain and spinal cord. Formed by the choroid plexus (CP), it fills the ventricular spaces within the brain (Fig. 8). Hydrocephalus is the pathologic imbalance of CSF production and absorption leading CSF accumulation. This can lead to elevations in intracranial pressure and compression of brain tissue resulting in neurologic dysfunction and even death.
Fig. 8.
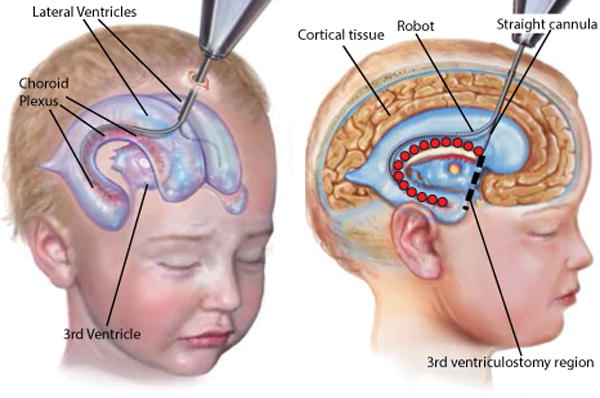
Robotic cauterization of the choroid plexus. Robot enters right lateral ventricle and also crosses over into left ventricle to perform cauterization. Red ○ define the tip task frame set indicating the cauterization points in the right lateral ventricle.
Standard treatment of hydrocephalus involves diversion of CSF from the ventricles through a catheter that drains this fluid from the ventricles to another absorptive cavity in the body (typically the peritoneal cavity or pleural cavity). Alternative methods of CSF diversion and production decrease include third ventriculostomy combined with cauterization of the CP [32]–[34]. Endoscopic third ventriculostomy involves creating a burr hole in the skull, inserting a straight endoscope, and puncturing the floor of the third ventricle to create a natural bypass for CSF drainage (see Fig. 8). CP cauterization (CPC) is performed by monopolar cautery using a Bugbee wire. The CP covers portions of the two lateral ventricles and the third ventricle (see Fig. 8). Conventional tools, flexible endoscopes included, cannot perform a thorough cauterization since they do not possess the necessary flexibility and dexterity [35].
Concentric tube robots can be employed during the cauterization process to deliver the wire to the challenging locations, and a concentric-tube-robot-based surgical platform is currently under investigation [35]. The optimal robot architecture and parameters, however, are unknown. With the framework proposed in this paper, a variety of designs using different architectures can be created and evaluated.
The brain ventricles can be reliably visualized with MRI using T1- and T2-weighted sequences. High-resolution image stacks were used to produce a model of the ventricular system of a hydrocephalic 10 month old male child. The robot must enter the ventricles along specific paths through the brain tissue in order to avoid passing through critical brain regions. Consequently, coordinate frames E and A, defining the navigation portion of the robot are clinician specified and this robot section consists of a single straight tube as shown in Fig. 8. Thus, for this example, the entire portion of the robot inside the ventricles comprises the manipulation section.
Clinician-specified anatomical targets, covering the CP on the lateral ventricles were specified (see Fig. 9) along with waypoints selected to guide the robot safely from the straight insertion tube to the CP point set, essentially coupling the robot design problem with implicit path-planning. Together these sets of points form the set of target points, . Since the surgical task to be performed is cauterization, which is largely contact angle independent, only the reachability of the targets is evaluated.
Fig. 9.
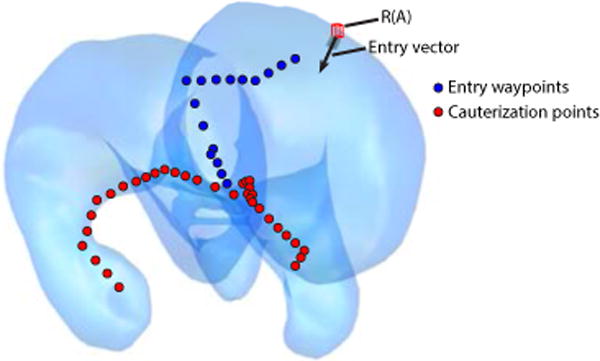
Cauterization targets and entry waypoints specified on the anatomical model of the hydrocephalic ventricles.
To avoid tissue damage, the inserted length of the manipulation section should only contact the brain at its tip and only at those locations where cauterization is to occur. In consequence, anatomical collisions are assigned a high penalty in the anatomical constraint function, Δ.
1) Manipulation Section Design
The design algorithm requires the number, type and arrangement of robot sections as inputs. The Bugbee wire for cauterization acts as the distal robot section and behaves as a straight constant curvature section that flexes when retracted into a stiffer curved tube, but returns to zero curvature when extended. The geometry of the ventricles shown in Fig. 8 indicates that at least two curved sections are needed to reach the most distal targets. Consequently, the design algorithm was run for the four robot architectures consisting of three sections: (a) variable-variable-fixed curvature, (b) variable-fixed-fixed curvature, (c) fixed-variable-fixed curvature and (d) fixed-fixed-fixed curvature.
The distal fixed section corresponds to the zero curvature cauterization wire. Owing to its extreme flexibility, the stiffness ratio for the two distal sections was taken to be D=20 while the ratio for the two proximal sections was specified as D=10. For the purposes of this design example, the bending stiffness of the Bugbee wire was normalized to kd=1. To properly expose the wire for cauterization, a minimum section extension of 10mm was also specified for the distal section.
The design variable weights of (18), (20), (21), were selected to be:
| (26) |
where is the tip position error from (18).
The weight on tip position error, γ1, was set so that errors greater than 1.5 mm are penalized exponentially, where 1.5mm corresponds to anticipated coagulation area given by the diameter d=1 mm of the Bugbee wire. This weighting heavily penalizes target errors larger than 1.5mm, which would prevent execution of the surgical task, while also ensuring that small changes in displacement about target points do not dominate the cost function. This discontinuity encodes in the optimization the importance of respecting the task constraints.
Since tip orientation is unimportant for cauterization, γ2 is set to zero. For the anatomical constraint function, a weight of γ3=1 proved sufficient. It was also sufficient to specify unit weights for all robot section curvatures and lengths. The stability-related weighting factors, γsi, were initially all set to unity and then increased by powers of ten until a stable solution set of configurations was found. Increasing the weights further increased the tip position errors.
The design code was run for four of the eight possible 3- section architectures with results provided in Table V and Fig. 10. All optimizations commenced from a robot design that did not satisfy the anatomical constraints. As shown, only the two architectures with a proximal variable curvature section can reach all of the target points in while respecting the anatomical constraints. From the table, it is observed that both designs require very similar section curvatures. This is perhaps not surprising since the workspace analysis of Section II demonstrated that variable-fixed and variable-variable designs share comparable workspaces. Note that the total lengths of these two designs (116 mm versus 126 mm) are similar and that the Bugbee wire length was minimum for all designs.
TABLE V.
Robot Design Parameters for CPC.
| Robot Architecture | 1/ki [mm] | Φi [mm] | Li [mm] |
|---|---|---|---|
| (a) (successful) | |||
| variable curvature | 18 | 54 | 54 |
| variable curvature | 18 | 52 | 106 |
| fixed curvature | ∞ | 10 | 116 |
| (b) (successful) | |||
| variable curvature | 19 | 58 | 58 |
| fixed curvature | 19 | 58 | 116 |
| fixed curvature | ∞ | 10 | 126 |
| (c) (unsuccessful) | |||
| fixed curvature | 20 | 37 | 37 |
| variable curvature | 22 | 65 | 102 |
| fixed curvature | ∞ | 10 | 112 |
| (d) (unsuccessful) | |||
| fixed curvature | 22 | 35 | 35 |
| fixed curvature | 26 | 68 | 103 |
| fixed curvature | ∞ | 10 | 113 |
Fig. 10.
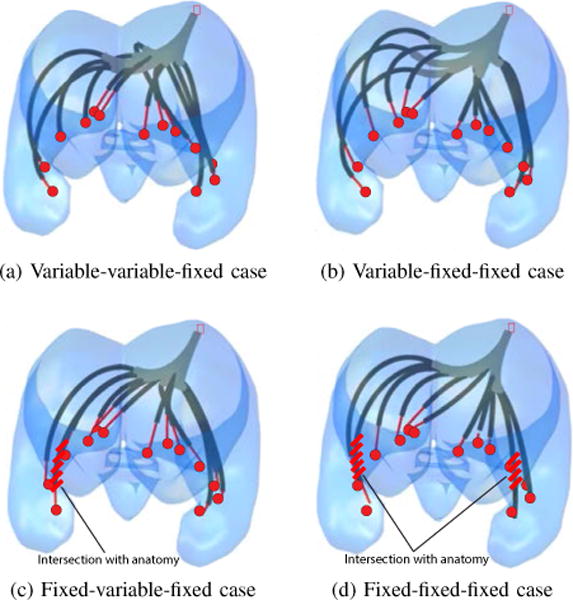
Architecture-dependent optimized robot designs. (a) Variable-variable-fixed curvature, (b) Variable-fixed-fixed curvature, (c) Fixed-variable-fixed curvature, (d) Fixed-fixed-fixed curvature. Red lines in (c) and (d) indicate violation of anatomical constraints.
Since the robot architecture composed of variable-fixed-fixed sections uses fewer tubes and yet satisfies the anatomical and surgical task constraints, it is the preferred design. This design optimisation converged in 2 h and 24 mins, after 434 design iterations. A C++ implementation would decrease computation time by a factor of ten to about 15 mins.
2) Effect of Kinematic Model
Recall from Fig. 7 that the optimization algorithm first utilizes a simplified algebraic kinematic model and then refines the design, as needed, using the complete torsionally compliant BVP model. In the case of the variable-fixed-fixed model, it was observed that the design parameters obtained using the simplified model also satisfied the BVP model constrains. Thus, the algorithm ran for a single iteration of the torsionally compliant model. Small differences in the inverse kinematic solution joint variables as well as the robot shape were present as shown in Fig. 11.
Fig. 11.
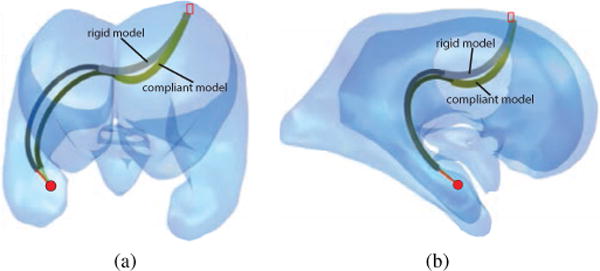
Comparison of torsionally rigid and torsionally compliant models: (a) Front view, and (b) Side view.
3) Configuration Stability
It can be shown that the variable-fixed-fixed curvature design of Table V can exhibit two types of instability. The first is associated with straightening the variable curvature section while the second arises from rotating the distal curved section while it is substantially retracted inside the proximal variable curvature section. Consequently, it is important to ensure that each of the target points and waypoints can be reached through stable configurations. The cost function of (20) is designed to guide the inverse kinematic solver away from unstable configurations. Furthermore, these configurations were explicitly tested for stability as a post-processing step using the graphical method described earlier. A path planning algorithm that explicitly considers stability can also be employed [36].
Figure 12 shows that set did include tip positions associated with unstable configurations. For each of these positions, however, there were also stable configurations. For the example illustrated, stability was achieved by further extension of the middle fixed-curvature section. The inverse kinematic cost function was effective in finding these stable configurations.
Fig. 12.
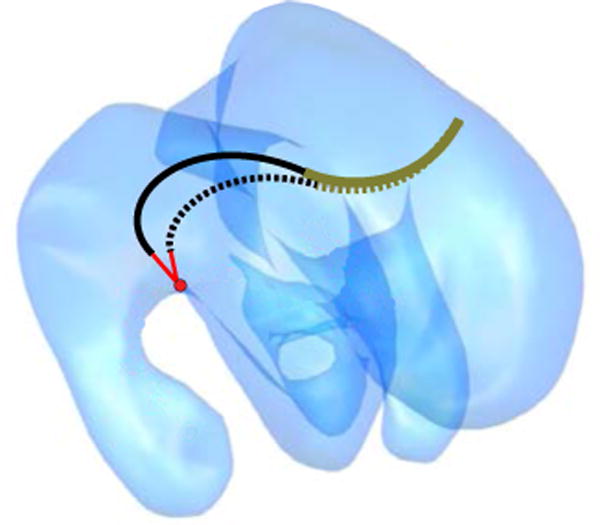
Stable and unstable configurations for a target point. Unstable configuration is shown dotted.
B. Robotic Closure of a Patent Foramen Ovale
The goal of this example is to investigate whether the design algorithm can reproduce a previously validated robot architecture and design that was successfully used on a sequence of pigs as described in [16] and [20]. This example serves not only to validate the algorithm, but also to evaluate the concept of developing a single robot design that can accommodate a group of “patients” instead of the more costly approach of having to produce a specific design for each patient.
A patent foramen ovale (PFO) is a heart defect characterized by a channel between the layers of the septum that separates the right and left atria. This channel occurs naturally in the fetus and normally seals shortly after birth. If not sealed, it can allow blood returning from the body to be recirculated to the body without filtration and oxygenation by the lungs [37].
Recently, intracardiac beating-heart repair with concentric tube robots has been successfully demonstrated in a porcine model under fluoroscopic and ultrasound imaging [16]. While all trials were performed in pigs, Fig. 13 depicts the equivalent human procedure in which the robot is introduced into the right atrium percutaneously via the internal jugular vein using telescopic extension to navigate through the internal jugular vein, the right brachiocephalic vein, and the superior vena cava into the right atrium. The actual porcine anatomy considered is shown in Fig. 16. Once the robot has reached the right atrium, the proximal sections are held fixed and the distal sections are used to manipulate the septal tissue and to deploy a tissue approximation device to seal the PFO channel.
Fig. 13.
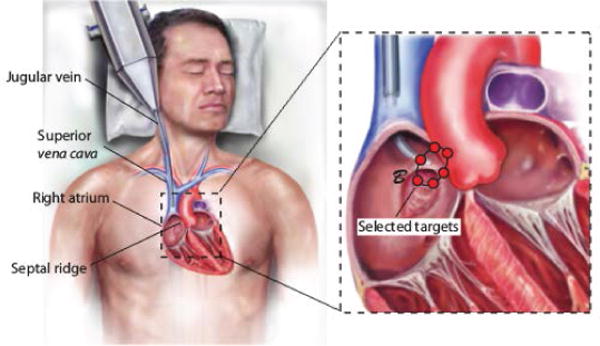
Percutaneous robotic PFO closure. Inset: Target points intended to allow treatment for a range of anatomical sizes.
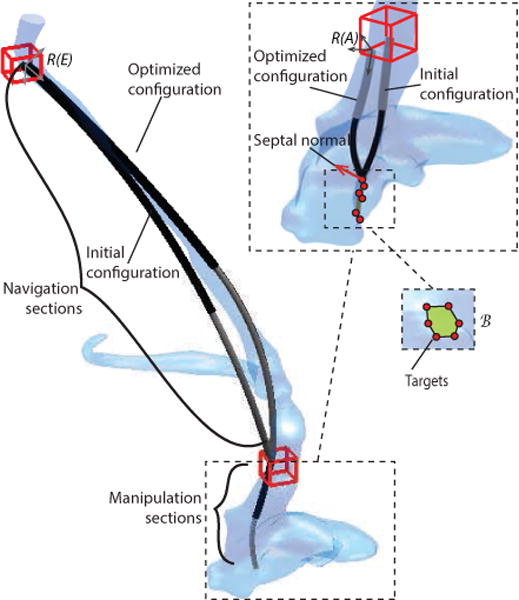
Fig. 16.
Anatomical model together with initial and optimized designs for the navigation and manipulation portions of the robot. Inset: close up of manipulation sections and target points.
The robot design used in these procedures was developed using postmortem measurements. It consisted initially of two fixed curvature sections for telescopic extension into the right atrium and a distal variable-fixed curvature architecture operating within the right atrium. During procedure development, the design was simplified to include a single section for vascular navigation resulting in a fixed-variable-fixed robot design.
The optimization algorithm was employed to solve for the section parameters for the two experimentally evaluated design architectures (fixed-fixed-variable-fixed and fixed-variable-fixed) as described below using a stiffness ratio of D=10 and a distal section stiffness normalized to kd=1.
An anatomical model of the vasculature and cardiac chambers was obtained by MRI for a 40 kg Yorkshire swine. Contrast agent was used together with respiratory and cardiac gating to obtain a sequence of 1 mm thick MRI slices. The 3D geometry was generated by threshold segmentation to each slice, followed by triangulation of the enclosed volume and Gaussian smoothing. The resulting model is shown in Fig. 16.
1) Manipulation Section Design
Sealing any specific PFO requires reaching a region on the septal ridge as shown in Fig. 13 [16]. In order to create a design that can accommodate a range of patient sizes, a set of target points has been defined that encloses an enlarged region overlapping the septal ridge, , as shown in Figs. 13 and 16. In contrast to CP ablation, orientation of the robot tip tangent with respect to the septum normal vector is important for device deployment. Consequently, a tip tangent constraint was specified to allow a maximum angle difference of 30°.
The allowable region for coordinate frame A, , was selected to be at the ostium of the superior vena cava, with a bounding box covering the full vein diameter. While the sides of the bounding box are aligned with the image coordinate directions, the z axis of frame A was constrained to be parallel to the vein’s centerline.
When operating in the right atrium, it is important that the robot avoids contact with the cardiac wall. As a result, collisions are heavily penalized by the optimization algorithm. This criterion is encoded in the anatomical constraints function Δ.
The section parameters for a variable-fixed manipulation section architecture were calculated from a random initial configuration as shown in the inset of Fig. 16 with convergence in 45 mins after 473 iterations. Notice how the location of frame A together with the shape of the manipulator sections enable the tip to achieve the desired orientation with respect to the septal surface. For the weights given below, the design parameters are provided in Table VI.
| (27) |
The weights are similar to those used for the neurosurgical example. The exponential tip error weighting threshold was reduced to 1 mm based on clinical tolerances and a high tip orientation error weight was introduced to achieve the tip tangent constraint of 30°. Having previously manually designed and tested tube sets for this example that all proved to be globally stable, we anticipated that algorithmically-obtained designs would also be stable for all configurations and so did not employ the stability cost function for this example. Anatomical and section parameter constraints match those of the previous example.
TABLE VI.
Robot Design Parameters for PFO Closure
|
Manipulation Sections
| |||
| Section type [Algorithm] | 1/ki [mm] | Φi [mm] | Li [mm]* |
| variable curvature | 75 | 28 | 28 |
| fixed curvature | 22 | 28 | 56 |
| Section type [Experiment] | 1/ki [mm] | Φi [mm] | Li [mm]* |
| variable curvature | 80 | 45 | 45 |
| fixed curvature | 24 | 35 | 80 |
|
Navigation Sections
| |||
| Section type [Algorithm] | 1/ki[mm] | Φi [mm] | Li [mm] |
| fixed curvature | 436 | 89 | 89 |
| fixed curvature | 117 | 109 | 198 |
| Section type [Experiment] | 1/ki [mm] | Φi [mm] | Li [mm] |
| fixed curvature | 600 | 170 | 170 |
Measured from frame A
2) Navigation Section Design
Using the optimized manipulator base frame A, the entry frame of the navigation section, E, is selected to be in the jugular vein, at the level of the neck, with a bounding box covering the full vein diameter as shown in Fig. 16. The z axis of frame E is prescribed to be parallel to the centerline of the jugular vein.
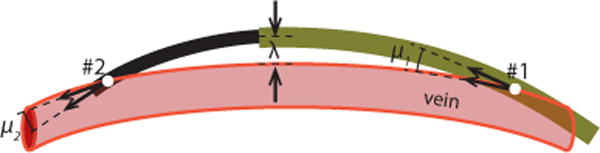
The geometry of the vessels, shown in Fig. 16, suggests that multiple curved robot sections may be needed for navigation. It is possible, however, to substantially straighten and laterally move the vessels during robot insertion. This observation is encoded in two anatomical navigation constraints (see Fig. 14):
The vessels can be laterally displaced up to λ ≤ 1cm,
During telescopic extension, the angle between the tip tangent vector and the vascular tangent vector should be μi ≤ 25° in order to avoid puncture of the vessel wall.
Fig. 14.
Anatomical constraints for vascular navigation.
To avoid computation of tissue deformation during optimization, these criteria can be approximated by comparing the shape of the extended robot with the undeformed shape of the vessels. Furthermore, the manipulation section was assumed to be fully retracted from the navigation tubes during telescopic extension to simplify kinematic calculations.
Initial design optimizations considered a single fixed curvature section for navigation, however, it was not possible to satisfy the design constraints using a single curved section. Subsequently, the design algorithm was executed for a fixed-fixed curvature architecture resulting in the design shown in Fig. 16 and detailed in Table VI. It can be seen that there is significant difference between the two section curvatures, which is expected, considering that a single fixed curvature section was inadequate.
The design weights of (27) with their heavy penalties on tip position and orientation were used to ensure that the distal point of the navigation section matches the proximal point of the manipulation section in position and orientation. Stability as well as sections curvature and length were also penalised as in the preceding examples.
The anatomical constraint function of (25), however, was modified to reflect the deformation constraints of Fig. 14. Since lateral deformation up to 1 cm is allowed, the KD-tree is queried for the distances of all robot points from the anatomy and exponentially penalises the maximum to be under 1 cm. Similarly, the robot points closer to the anatomy are investigated for their angle-of-attack to the anatomy, limiting them close to a prescribed 25°. As shown in Fig. 14, the entry and exit angles, μ1 and μ2 are limited to 25°, and the maximum displacement marked as λ must be less than 1 cm.
The navigation design problem starts from a random initial configuration, as shown in Fig. 16, and converges in 2 h and 32 minutes, after 1396 iterations.
As in the neurosurgical example, waypoints were used to guide the navigation section through the anatomy in an implicit path-planning fashion; these waypoints corresponded to the centreline of the jugular vein. The solution provided by the torsionally rigid kinematic model was found to also satisfy the torsionally compliant model constrains. Telescopic extension along the centerline of the vasculature using the two kinematic models is depicted in Fig. 15. Note that while the section parameters and centerline points are the same, the depicted configurations are obtained by solving the anatomically constrained inverse kinematics problem independently for each kinematic model.
Fig. 15.
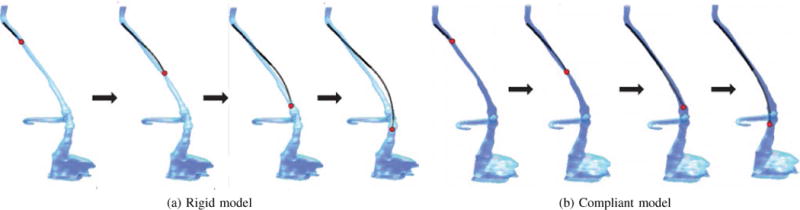
Telescopic extension through the vasculature using the optimized navigation sections. Configurations shown are solutions to the anatomically-constrained inverse kinematics problem using the: (a) torsionally rigid model, (b) torsionally compliant model.
For both the manipulation and navigation portions of the robot, the design algorithm was able to utilize the simplified algebraic kinematic model during parameter optimization and then verify the solution using the BVP model during a final iteration. In addition, it was verified that the overall robot design is stable for all configurations.
For comparison with the experimentally validated design of [16], the actual tube parameters are listed in Table VI. This robot design was used successfully for PFO closure in Yorkshire pigs varying between 45–65 kg. In these procedures, the robot was able to position its tip on the atrial septal ridge and perform the required tissue manipulation before delivery of the PFO closure device [16].
From the table, it can be observed that the curvatures of the optimized variable-fixed design closely match those used experimentally. While the lengths of the experimental sections are significantly longer than the minimum required lengths computed by the algorithm, this is not surprising since the experimental tube set was deliberately constructed to be longer than required. Furthermore, it was observed that neither curved section needed to be fully extended during any surgery.
Unlike what is shown in Fig. 16, however, the manipulator sections were not configured in an “S” shape during surgery. Instead the curvatures were aligned as shown in Fig. 13. This configuration was necessary since the surgeon rotated the pig’s heart to the left within the chest cavity, displacing the septal ridge to the left, in order to reproduce the orientation of the human heart within the chest.
For the navigation section, the algorithm was unable to solve for a single curved section that satisfied the anatomical constraints. Our initial experimental tube set also included two fixed curvature sections. During surgery, however, it was discovered that by first inserting a plastic introducer sheath through the vasculature, it was possible to displace and straighten the vasculature more substantially than was anticipated during robot insertion without causing damage. Consequently, the pair of sections was simplified to consist of a single section with a 600mm radius of curvature. Thus, while the algorithm provided a solution that closely fit the anatomy, our selected anatomical constraints proved conservative.
VI. CONCLUSIONS AND DISCUSSION
In contrast to standard robots for which the same robot design is used for all procedures, the set of tubes comprising a concentric tube robot can be easily customized to meet the task requirements and anatomical constraints of a specific procedure or class of procedures. While this design problem need only be solved once for any given procedure, the unconstrained design problem is high dimensional and computationally intensive.
To address this, this paper presents a design methodology and optimization framework that considerably reduce the dimensionality of the design space while still providing a rich solution set. In this framework, robots are constructed of telescoping sections of either fixed or variable curvature. Furthermore, it is shown how the design problem can often be decomposed into two lower dimensional problems of navigation to the surgical site and manipulation at the site.
As with any set of design rules, those proposed here represent tradeoffs. For example, implementing the sectional stiffness dominance of rule 2 requires larger tube diameters, and the variable curvature sections of rule 3 do not utilize the relative translation between the tube pair. These rules do, however, provide a systematic means to arrive at designs with the clinically-desirable capabilities of follow-the-leader insertion and kinematic decoupling of the each section from its proximal sections.
To provide insight for guiding the design process, the paper also compares the tip workspace that can be achieved by various arrangements of fixed and variable curvature sections. For two-section robots, the superiority of variable-fixed designs is clearly demonstrated.
Furthermore, it is shown that the workspace can be decomposed into regions according to the elastic stability of the configurations within the regions. In this context, it is demonstrated that tube sets exhibiting elastic instabilities within their workspace can still be safely employed by ensuring that alternate stable configurations are available within the desired task space that satisfy the anatomical constraints.
These concepts are illustrated through design examples from neurosurgery and intracardiac surgery. Since the intracardiac design is compared to previously performed in vivo robotic trials [16], it provides strong validation of the approach.
Beyond the framework presented here, there are additional design issues that must be considered. These include selecting such variables as tube diameters, thicknesses and materials. The design process can be started, for example, by selecting the inner diameter of the innermost tube to be just large enough to deliver all tools and devices needed for a procedure. The required robot tip stiffness can then be used to compute the thickness of the innermost tube. Dimensions of outer tubes can be subsequently computed.
This design process is often iterative since tube diameter and material type determine maximum bending curvature, which may or may not enable the desired workspace. Mechatronic issues also must be considered, such as the need for tubes to extend out of the body and into the drive system. While these transmission lengths can decrease torsional stiffness, this issue can be addressed by constructing the transmission lengths from an alternate stiffer material, e.g., stainless steel.
Acknowledgments
This work was supported by the National Institutes of Health under grants R01HL073647, R01HL087797 and R01HL124020.
Footnotes
C. Bergeles is now with the Hamlyn Centre, Imperial College London, London SW7 2AZ, UK.
A portion of this work has been presented at the 2011 IEEE Int. Conf. Robot. Autom. [1].
Contributor Information
Christos Bergeles, Department of Cardiovascular Surgery, Boston Children’s Hospital, Harvard Medical School, Boston, MA, 02115, USA.
Andrew H. Gosline, Department of Cardiovascular Surgery, Boston Children’s Hospital, Harvard Medical School, Boston, MA, 02115, USA
Nikolay V. Vasilyev, Department of Cardiovascular Surgery, Boston Children’s Hospital, Harvard Medical School, Boston, MA, 02115, USA
Patrick J. Codd, Department of Neurosurgery, Boston Children’s Hospital, Harvard Medical School, Boston, MA, 02115, USA
Pedro J. del Nido, Department of Cardiovascular Surgery, Boston Children’s Hospital, Harvard Medical School, Boston, MA, 02115, USA
Pierre E. Dupont, Department of Cardiovascular Surgery, Boston Children’s Hospital, Harvard Medical School, Boston, MA, 02115, USA
References
- 1.Bedell C, Lock J, Gosline A, Dupont PE. Design optimization of concentric tube robots based on task and anatomical constraints. IEEE Int Conf Robotics and Automation. 2011:398–403. doi: 10.1109/ICRA.2011.5979960. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Kwok KW, Vitiello V, Yang G-Z. Control of articulate snake robot under dynamic active constraints. Int Conf Medical Image Computing and Computer Assisted Intervention. 2010:229–236. doi: 10.1007/978-3-642-15711-0_29. [DOI] [PubMed] [Google Scholar]
- 3.Ikeuchi M, Ikuta K. Membrane micro emboss following excimer laser ablation (meme-x) process. IEEE Int Conf Micro Electro Mechanical Systems. 2008:62–65. [Google Scholar]
- 4.Jayender J, Azizian M, Patel RV. Autonomous image-guided robot-assisted active catheter insertion. IEEE Trans Robotics. 2008;24(4):858–871. [Google Scholar]
- 5.Simaan N, Xu K, Wei W, Kapoor A, Kazanzides P, Taylor RH, Flint P. Design and integration of a telerobotic system for minimally invasive surgery of the throat. Int J Robotics Research. 2009;28(9):1134–1153. doi: 10.1177/0278364908104278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Shammas E, Wolf A, Choset H. Three degrees-of-freedom joint for spatial hyper-redundant robots. Mechanism and Machine Theory. 2006;(41):170–190. [Google Scholar]
- 7.Anor T, Madsen JR, Dupont PE. Algorithms for design of continuum robots using the concentric tubes approach: a neurosurgical example. IEEE Int Conf Robotics and Automation. 2011:667–673. doi: 10.1109/ICRA.2011.5980311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Dupont PE, Lock J, Itkowitz B, Butler E. Design and control of concentric-tube robots. IEEE Trans Robotics. 2010;26(2):209–225. doi: 10.1109/TRO.2009.2035740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Rucker DC, Webster RJ, III, Chirikjian G, Cowan NJ. Equilibrium conformations of concentric-tube continuum robots. Int J Robotics Research. 2010;29(10):1263–1280. doi: 10.1177/0278364910367543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lock J, Laing G, Mahvash M, Dupont PE. Quasistatic modeling of concentric tube robots with external loads. IEEE/RSJ Int Conf Intelligent Robots and Systems. 2010:2325–2332. doi: 10.1109/IROS.2010.5651240. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rucker DC, Jones BA, Webster RJ., III A geometrically exact model for externally-loaded concentric-tube continuum robots. IEEE Trans Robotics. 2010;26(5):769–780. doi: 10.1109/TRO.2010.2062570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Mahvash M, Dupont PE. Stiffness control of continuum surgical manipulators. IEEE Trans Robotics. 2011;27(2):334–345. doi: 10.1109/TRO.2011.2105410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Lyons L, W R, III, Alterovitz R. Planning active cannula configurations through tubular anatomy. IEEE Int Conf Robotics and Automation. 2010:2082–2087. [Google Scholar]
- 14.Torres LG, Webster RJ, III, Alterovitz R. Task-oriented design of concentric tube robots using mechanics-based models. IEEE/RSJ Int Conf Intelligent Robots and Systems. 2012 doi: 10.1109/IROS.2011.6095168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Gosline A, Vasilyev NV, Veeramani A, Wu MT, Schmitz G, Chen R, Arabagi V, del Nido PJ, Dupont PE. Metal-MEMS tools for beating-heart tissue removal. IEEE Int Conf Robotics and Automation. 2012:1921–1936. doi: 10.1109/ICRA.2012.6225210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gosline A, Vasilyev NV, Butler E, Folk C, Cohen A, Chen R, Lang N, del Nido PJ, Dupont PE. Percutaneous intracardiac beating-heart surgery using metal MEMS tissue approximation tools. Int J Robotics Research. 2012;31(9):1081–1093. doi: 10.1177/0278364912443718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Xu R, Patel RV. A fast torsionally compliant kinematic model of concentric-tube robots. IEEE Int Conf Engineering in Medicine and Biology. 2012:904–907. doi: 10.1109/EMBC.2012.6346078. [DOI] [PubMed] [Google Scholar]
- 18.Lyons LA, Webster RJ, III, Alterovitz R. Motion planning for active cannulas. IEEE/RSJ Int Conf Intelligent Robots and Systems. 2009:801–806. [Google Scholar]
- 19.Burgner J, Rucker DC, Gilbert HB, Swaney PJ, Russell PT, Weaver KD, Webster RJ., III A telerobotic system for transnasal surgery. IEEE/ASME Trans Mechatronics. 2014;19(3):996–1006. doi: 10.1109/TMECH.2013.2265804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Vasilyev NV, Gosline A, Butler E, Lang N, Codd P, Yamauchi H, Feins E, Folk C, Cohen A, Chen R, del Nido PJ, Dupont PE. Percutaneous steerable robotic tool delivery platform and metal MEMS device for tissue manipulation and approximation: initial experience with closure of patent foramen ovale. Circulation: Cardiovascular Interventions. 2013;6:468–475. doi: 10.1161/CIRCINTERVENTIONS.112.000324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Burgner J, Gilber HB, Webster RJ., III On the computational design of concentric tube robots: incorporating volume-based objectives. IEEE Int Conf Robotics and Automation. 2013:1185–1190. [Google Scholar]
- 22.Chirikjian GS, Burdick JW. A modal approach to hyper-redundant manipulator kinematics. IEEE Trans Robotics. 1994;10(3):343–354. [Google Scholar]
- 23.Chirikjian GS. Variational analysis of snakelike robots. Redundancy in Robot Manipulators and Multi-Robot Systems. 2012:77–91. [Google Scholar]
- 24.Gilbert HB, Webster RJ., III Can concentric tube robots follow the leader? IEEE Int Conf Robotics and Automation. 2013:4866–4872. doi: 10.1109/TRO.2015.2394331. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ebert-Uphoff I, Chirikjian GS. Inverse kinematics of discretely actuated hyper-redundant manipulators using workspace densities. 1996:139–145. [Google Scholar]
- 26.Wang Y, Chirikjian GS. Workspace generation of hyper-redundant manipulators as a diffusion process on se (n) IEEE Trans Robotics and Automation. 2004;20(3):399–408. [Google Scholar]
- 27.Skiena SS. The algorithm design manual. 2. Springer; 2008. [Google Scholar]
- 28.Khatib O. Real-time obstacle avoidance for manipulators and mobile robots. Int J Robotics Research. 1986;5(1):90–98. [Google Scholar]
- 29.Torzcon V. On the convergence of pattern search algorithms. SIAM J Optimization. 1997;7(1):1–25. [Google Scholar]
- 30.Audet C, Dennis J., Jr Analysis of generalized pattern searches. SIAM J Optimization. 2003;13(3):889–903. [Google Scholar]
- 31.Nelder JA, Mead R. A simplex method for function minimization. The Computer Journal. 1965;7(4):308–313. [Google Scholar]
- 32.Warf B. Endoscopic third ventriculostomy and choroid plexus cauterization for pediatric hydrocephalus. J Clinical Neurosurgery. 2007;54:78–82. [PubMed] [Google Scholar]
- 33.Warf B. Hydrocephalus in uganda: the predominance of infectious origin and primary management with endoscopic third ventriculostomy. J Neurosurgery. 2005;102:1–15. doi: 10.3171/ped.2005.102.1.0001. [DOI] [PubMed] [Google Scholar]
- 34.Bondurant C, Jimenez D. Epidemiology of cerebrospinal fluid shunting. J Pediatric Neurosurgery. 1995;23:254–258. doi: 10.1159/000120968. [DOI] [PubMed] [Google Scholar]
- 35.Butler E, Hammond-Oakley R, Chawarski S, Gosline A, Codd P, Anor T, Madsen JR, Dupont PE, Lock J. Robotic neuroendoscope with concentric tube augmentation. IEEE/RSJ Int Conf Intelligent Robots and Systems. 2012 doi: 10.1109/IROS.2012.6386022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Bergeles C, Dupont PE. Planning stable paths for concentric tube robots. IEEE/RSJ Int Conf Intelligent Robots and Systems. 2013 doi: 10.1109/IROS.2016.7759636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Calvert PA, Rana BS, Kydd AC, Shapiro LM. Patent foramen ovale: anatomy, outcomes and closure. National Reviews Cardiology. 2011;8:148–160. doi: 10.1038/nrcardio.2010.224. [DOI] [PubMed] [Google Scholar]


