Transient EPR Reveals Triplet State Delocalization in a Series of Cyclic and Linear π-Conjugated Porphyrin Oligomers

Abstract

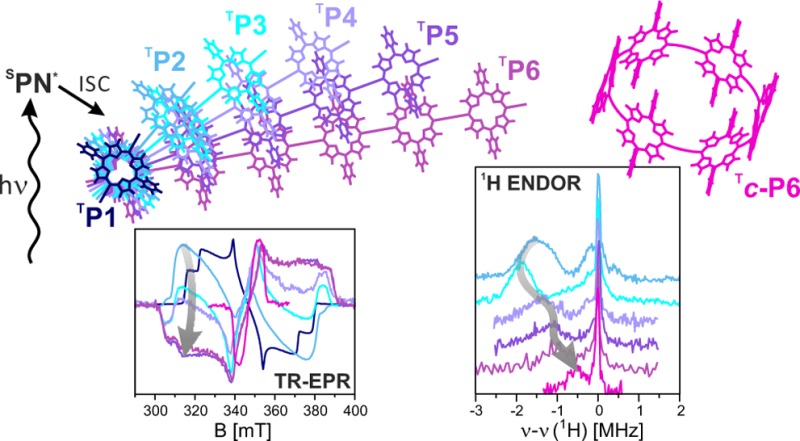
The photoexcited triplet states of a series of linear and cyclic butadiyne-linked porphyrin oligomers were investigated by transient Electron Paramagnetic Resonance (EPR) and Electron Nuclear DOuble Resonance (ENDOR). The spatial delocalization of the triplet state wave function in systems with different numbers of porphyrin units and different geometries was analyzed in terms of zero-field splitting parameters and proton hyperfine couplings. Even though no significant change in the zero-field splitting parameters (D and E) is observed for linear oligomers with two to six porphyrin units, the spin polarization of the transient EPR spectra is particularly sensitive to the number of porphyrin units, implying a change of the mechanism of intersystem crossing. Analysis of the proton hyperfine couplings in linear oligomers with more than two porphyrin units, in combination with density functional theory calculations, indicates that the spin density is localized mainly on two to three porphyrin units rather than being distributed evenly over the whole π-system. The sensitivity of the zero-field splitting parameters to changes in geometry was investigated by comparing free linear oligomers with oligomers bound to a hexapyridyl template. Significant changes in the zero-field splitting parameter D were observed, while the proton hyperfine couplings show no change in the extent of triplet state delocalization. The triplet state of the cyclic porphyrin hexamer has a much decreased zero-field splitting parameter D and much smaller proton hyperfine couplings with respect to the monomeric unit, indicating complete delocalization over six porphyrin units in this symmetric system. This surprising result provides the first evidence for extensive triplet state delocalization in an artificial supramolecular assembly of porphyrins.

Introduction

Nanoscale organic materials, such as π-conjugated oligomers, are of considerable interest in the fields of molecular electronics,¹⁻⁵ photonics,^6,7 and spintronics.^8,9 Understanding of the factors determining exciton delocalization, as well as charge and spin transport, is of fundamental importance for the design and further development of supramolecular systems with properties tailored to specific applications. The delocalization of singlet excitons has been investigated extensively using techniques such as time-resolved fluorescence anisotropy,¹⁰ whereas triplet excitons have received less attention. Understanding the behavior and spatial delocalization of the triplet excitons of conjugated oligomers and polymers has important technological applications for improving the performance of optoelectronic devices such as organic light-emitting diodes (OLEDs) and organic photovoltaics (OPVs).¹¹ Several experimental and computational studies have led to the conclusion that triplet excitons are generally less delocalized than singlet exitons,¹²⁻¹⁴ and this difference in spatial delocalization has been used to account for the fact that electron/hole recombination can lead to a nonstatistical ratio of singlet/triplet excitons.^15,16

Conjugated porphyrin oligomers have been extensively investigated using a range of different linkers to create different two- and three-dimensional supramolecular structures with varying optical and electronic properties.^6,17−23 The delocalization of unpaired electrons in these systems can be investigated by Electron Paramagnetic Resonance (EPR) in radicals generated by chemical oxidation or reduction and in triplet states obtained by photoexcitation.^6,21,24−32

Information on the delocalization of the photoexcited triplet exciton by EPR can be obtained either by measurement of the zero-field splitting (ZFS) interaction or the hyperfine couplings.³³ The former has been exploited frequently in the study of linear π-conjugated porphyrins of varying chain length.^25,29,31,34 The interpretation of the results was based on the point-dipole approximation and yielded average interelectron distances that did not exceed the dimensions of a single monomeric unit. This led to the conclusion that the triplet state is localized on a single porphyrin in most of these systems; in contrast, the corresponding radical cations typically show more extensive delocalization.³²

In a recent study, we investigated triplet state delocalization in a linear butadiyne-linked porphyrin dimer by using transient EPR, magnetophotoselection, electron nuclear double resonance (ENDOR), and hyperfine sublevel correlation spectroscopy (HYSCORE) to characterize the ZFS as well as the proton and nitrogen hyperfine interactions.³³ A reduction of the hyperfine couplings by a factor of two and an increase in the ZFS parameter D revealed complete delocalization of the triplet state in this porphyrin dimer. Our results have shown that the point-dipole approximation fails for these systems due to the extensive delocalization of the spin density in the porphyrins and on the butadiyne linkers.^33,35 The delocalization was accompanied by a reorientation of the ZFS tensor, which led to an axis of maximum dipolar coupling aligned with the long axis of the molecule and parallel to the principal optical transition moment. The study concluded that hyperfine couplings provide the most accurate estimate of the extent of triplet state delocalization, while any interpretation of the ZFS parameter D in terms of triplet state delocalization is only possible in combination with computational methods. Here, we study larger π-conjugated porphyrin arrays, in linear as well as bent and cyclic topologies, to investigate the influence of oligomer length and geometry on triplet state delocalization.

A previous study of the excess polarizability volumes of the excited states of linear butadiyne-linked porphyrin oligomers indicated that the T₁ states are much less delocalized than the singlet excited states,³⁶ and this conclusion was supported by the dependence of the energies of the T₁ and S₁ states on chain length.³⁷ The EPR results reported here provide a more detailed picture of the triplet states of these systems. In the linear oligomers, the triplet wave function is delocalized over about two to three porphyrin units, whereas in the cyclic hexamer, it is distributed evenly over all six porphyrins.

Results and Discussion

Linear Porphyrin Arrays

Transient EPR

Time-resolved EPR measurements were performed on the linear meso-to-meso butadiyne-linked porphyrin arrays with one to six porphyrin units (P1–P6, see Figure 1A)³⁸ in 2-MeTHF:pyridine 10:1 at 20 K. All photogenerated triplet states of the linear porphyrin arrays were characterized by lifetimes of the order of hundreds of microseconds at 20 K and did not show any significant time-dependent changes in spin polarization. The EPR spectra of the linear oligomers are displayed in Figure 2 and were obtained as an average of the transients up to 2 μs after a laser flash of unpolarized light at 532 nm. The ZFS parameters and the relative sublevel populations were determined from simulations of the experimental data using EasySpin³⁹ and are summarized in Table 1.

Figure 1.

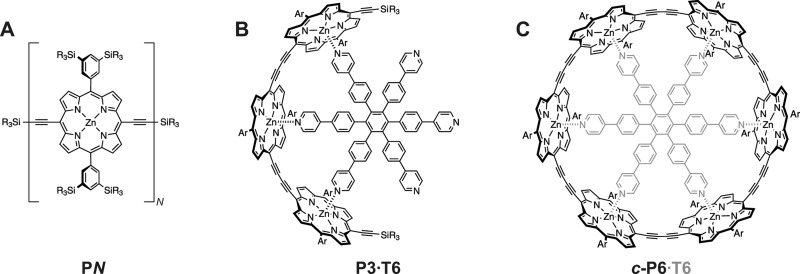
Molecular structures of the linear porphyrin oligomers, PN (N = 1–6), of the linear porphyrin trimer bound to the template T6 (PN·T6) and of the six-membered porphyrin ring (c-P6) with template indicated in gray (R = n-hexyl, Ar = phenyl rings with SiR₃ substituents at the meta positions).

Figure 2.

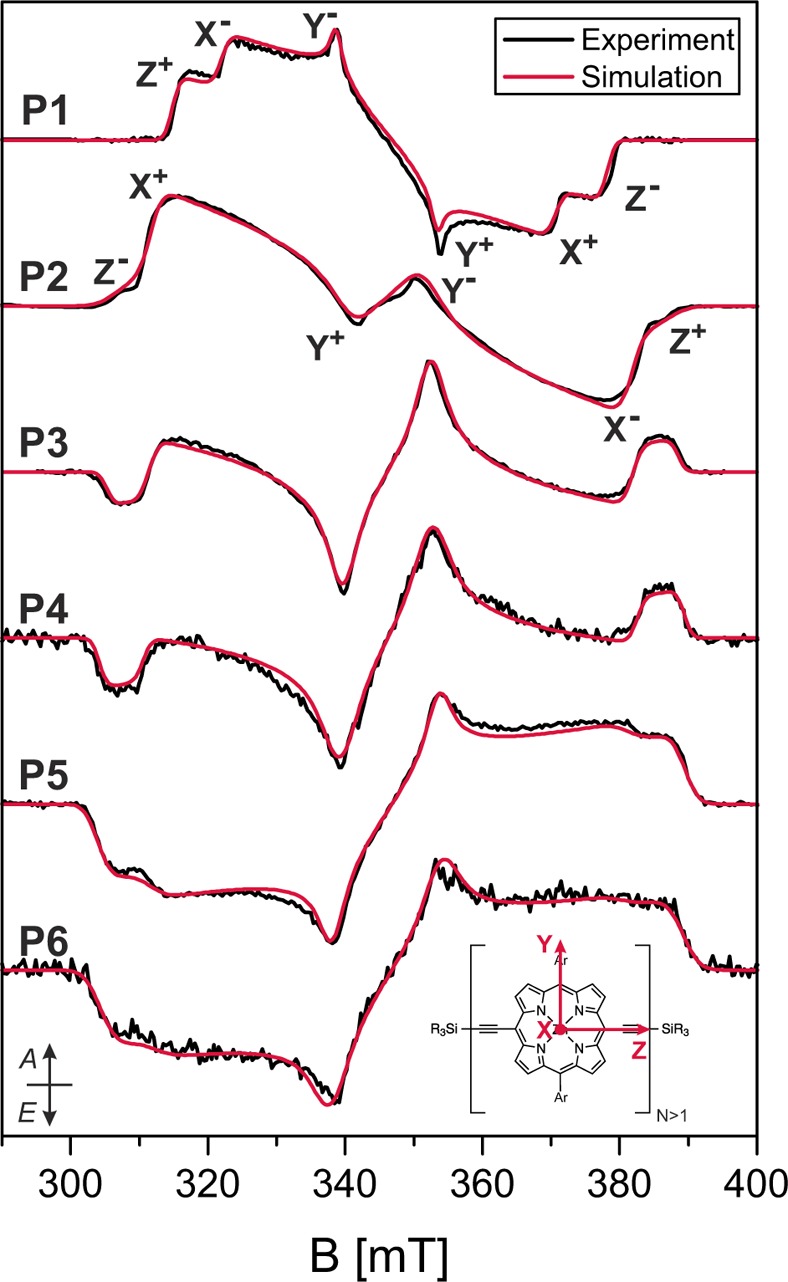
Experimental X-band transient EPR spectra of linear porphyrin chains (P1–P6) in MeTHF:pyridine 10:1 recorded at 20 K as average up to 2 μs after the laser pulse with unpolarized light at 532 nm. Simulations with the parameters reported in Table 1 are compared to the experimental data. The ordering of the triplet sublevels was chosen as |Z| > |X| > |Y|, and the six canonical positions are indicated for P1 and P2. For P3–P6, the same assignments as shown for P2 are valid (A = absorption, E = emission). The inset shows the orientation of the ZFS tensor in the molecular frame for the oligomers P2–P6.

Table 1. ZFS Parameters and Relative Zero-Field Sublevel Populations for P1 and Linear Oligomers P2–P6 Determined through Simulation of the Transient EPR Spectra Shown in Figure 2.

	|D| [MHz]	|E| [MHz]	pX:pY:pZa
P1	898 ± 5	161 ± 2	0.05:0.00:0.95
P2	1117 ± 9	284 ± 2	0.90:0.00:0.10
P3	1169 ± 7	269 ± 2	0.53:0.00:0.47
P4	1195 ± 8	273 ± 2	0.47:0.00:0.53
P5	1201 ± 8	254 ± 2	0.24:0.00:0.76
P6	1199 ± 9	260 ± 3	0.26:0.00:0.74

^aThe error on the relative sublevel populations is approximately 0.02.

The porphyrin monomer (P1) and dimer (P2) are characterized by a quite high triplet yield, and thus strong EPR signals are observed, but the triplet yield of longer linear and cyclic systems (see further) decreases significantly with increasing N.³⁷ Consequently, the EPR signals are detected with a much reduced signal-to-noise ratio for the larger systems. The lower triplet yields have been attributed to faster radiative and nonradiative decay of the first excited singlet states in the longer oligomers.³⁷

The D-values of the linear oligomers with more than two porphyrin units are similar to those of P2 with only slight increases of 5–7%. This similarity would suggest similar extents of triplet state delocalization and indicates that the ZFS tensor orientation in the longer oligomers is analogous to that determined for the porphyrin dimer, that is, the axis of maximum dipolar coupling, Z, is aligned with the long axis of the molecule, while the triplet X axis corresponds to the out-of-plane axis.³³ This assignment was confirmed by ENDOR measurements (see next section). The E-values are also very similar and indicate a similar degree of asymmetry in the plane perpendicular to the Z axis of the ZFS tensor.³³

In the case of the photoexcited triplet states of P1 and P2, DFT calculations predicted the relative changes in the ZFS parameter D correctly.³³ An increase of 24% from P1 to P2 was predicted, while experimentally an increase of 26% was found.³³ For the longer oligomers, density functional theory (DFT) predicts uneven spin density distributions with increased spin density on the central porphyrin units (see Supporting Information), and the D-values decrease slightly with respect to P2, for example, for P3 and P4, the D-values predicted with different functionals (B3LYP, BHLYP, and BP86) correspond to 75–86% of the P2D-value. This is in disagreement with the small increase observed experimentally, which, if interpreted in the framework of the point-dipole approximation (D ∝ r^–3), would indicate a decrease in the delocalization length.

While the ZFS parameters only show a small dependence on the oligomer length, the spin polarizations change significantly. The change from an AAAEEE polarization in P1 to the AAEAEE polarization in P2 was previously shown to arise from the reorientation of the ZFS tensor in P2.³³ In zinc porphyrins, the intersystem crossing (ISC) is driven by spin–orbit coupling of the zinc ion and leads to preferential population of the out-of-plane sublevel due to mixing of the zinc d-orbitals with the π-system of the porphyrin.^40,41 The out-of-plane sublevel changes from Z in P1 to X in P2, which leads to the observed change in spin polarization. In the linear oligomers with more than two porphyrin units, the spin polarization changes to EAEAEA and then progresses to an EEEAAA spin polarization for more than four porphyrin units. In terms of relative sublevel populations, this corresponds to a change from a preferential population of the X (out-of-plane) sublevel in P2 to an almost equal population of the X (out-of-plane) and Z (long axis) sublevels in P3. For even longer oligomers, a further decrease of the X (out-of-plane) sublevel population is observed, accompanied by an increase of the population of the long axis Z sublevel.

These observations indicate a change in the mechanism of triplet state formation, that is, in the ISC mechanism or formation of the final triplet state through either intra- or intermolecular triplet–triplet energy transfer. The spin polarization of a triplet state arising from triplet–triplet energy transfer can be predicted based on the sublevel populations of the donor triplet state, p_j^D (j = X,Y,Z), and the relative orientation of donor and acceptor due to the conservation of spin angular momentum.⁴²⁻⁴⁴ The sublevel populations of the acceptor, p_i (i = X,Y,Z), can be calculated as^42,43

1

where θ_ij is the angle between the principal axis j of the ZFS tensor of the donor and the ZFS axis i of the acceptor. The observed spin polarizations in the oligomers P3–P6 could not be reproduced by considering intramolecular triplet–triplet energy transfer (TTET) with conservation of spin angular momentum^45,46 between adjacent porphyrin units at varying angles with respect to each other, or intermolecular TTET between stacked porphyrin oligomers.

In terms of ISC, an alternative mechanism driving population mainly into the sublevel corresponding to the long axis of the molecule and becoming more dominant as the oligomer length increases would explain the observed spin polarizations. To test this hypothesis, transient EPR measurements were performed on the free-base oligomers, where ISC is not affected by the direct spin–orbit coupling contribution of the zinc ion.

Excitation wavelength-dependent studies, which will be discussed in detail elsewhere, have revealed contribution of different conformations of the porphyrin oligomers to the transient EPR spectrum, leading to changes in spin polarization. For this analysis, spectra recorded at a wavelength selectively exciting the planar conformation for the zinc porphyrins (645, 750, 800, and 830 nm) and for the free-base porphyrins (680, 740, 780, and 810 nm),⁴⁷ respectively, were considered (for UV–vis spectra, see Figure S1 in the Supporting Information).

The transient EPR spectra recorded for the zinc and free-base oligomers with one to four porphyrin units are compared in Figure 3, and the relative sublevel populations determined through simulation are reported in Table 2.

Figure 3.

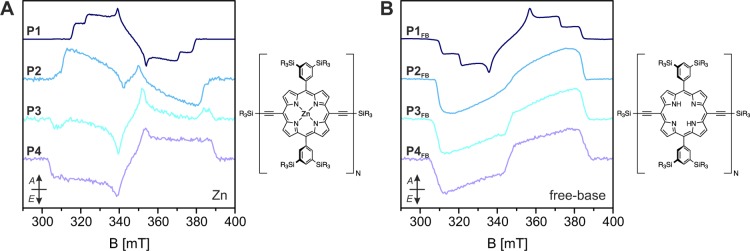
Experimental X-band transient EPR spectra of the zinc (A) and free-base (B) linear porphyrin oligomers P1–P4 in MeTHF:pyridine 10:1 recorded as average up to 2 μs after the laser pulse at 20 K. The spectra were recorded after excitation at wavelengths corresponding to the planar conformations (645, 750, 800, and 830 nm for the zinc porphyrins and 680, 740, 780, and 810 nm for the free-base porphyrins, see UV–vis data in the Supporting Information). At shorter wavelengths, the contribution of different conformations affects the spin polarization of the EPR spectrum.

Table 2. ZFS Parameters and Relative Sublevel Populations of the Zinc and Free-Base Porphyrins Determined through Simulation of the Transient EPR Spectra Recorded at Wavelengths Corresponding to the Planar Conformations.

	Zinc Porphyrins			Free-Base Porphyrins
	|D| [MHz]	|E| [MHz]	pX:pY:pZ	|D| [MHz]	|E| [MHz]	pX:pY:pZ
P1	898 ± 5	161 ± 2	0.05:0.00:0.95	1024 ± 3	144 ± 2	0.47:0.53:0.00
P2	1117 ± 9	284 ± 2	0.88:0.00:0.12	1053 ± 3	311 ± 4	0.00:0.29:0.71
P3	1169 ± 7	269 ± 2	0.46:0.00:0.54	1087 ± 3	321 ± 2	0.00:0.08:0.92
P4	1195 ± 8	273 ± 2	0.28:0.00:0.72	1116 ± 6	308 ± 5	0.00:0.04:0.96

The spin polarization of the free-base monomer corresponds to almost equal population of the two in-plane sublevels, as reported in the literature for other free-base porphyrins, and is characteristic of ISC mediated by vibronic coupling.^40,48 The progressive increase of the long axis sublevel population from the free-base monomer to the longer free-base oligomers reflects the analogous increase observed for the zinc porphyrins and supports the hypothesis of a competing ISC mechanism.

The sublevel populations of the zinc porphyrins can be calculated as linear combinations of the free-base populations, arising from ISC driven by vibronic coupling of the porphyrin rings, and the populations obtained assuming the direct zinc spin–orbit coupling to be the only populating mechanism. In the latter case, only the out-of-plane sublevel would be populated (p_Z = 1, p_X/Y = 0 for P1 and p_X = 1, p_Y/Z = 0 for the longer oligomers). The relative contribution of the vibronic mechanism to the ISC would correspond to 0.05, 0.13, 0.56, and 0.73 for P1, P2, P3, and P4, respectively. The contribution of the porphin ring to the ISC populating mechanism is governed by Herzberg–Teller vibronic coupling and is selective for the in-plane sublevels, for which nπ* and πσ* states are admixed to the ππ* states due to out-of-plane vibrations.^40,49,50 The increasing vibrational freedom of longer porphyrin oligomers could explain the increasing importance of this vibronic spin–orbit coupling contribution to the ISC mechanism and why it seems to be favored over the direct zinc spin–orbit coupling contribution in the zinc porphyrins.

¹H ENDOR

The extent of triplet state delocalization in the linear porphyrin arrays was determined based on the proton hyperfine couplings measured by ENDOR spectroscopy. Previous studies on P1 and P2 revealed that the largest proton hyperfine couplings are observed for the β proton close to the alkyne bonds (H₁, see inset in Figure 4A) along the orientation of the in-plane axis parallel to the phenyl substituents (Y). Orientation-selective Mims ENDOR measurements were therefore performed at the high-field Y canonical position for all porphyrin oligomers, and the results are shown in Figure 4A.

Figure 4.

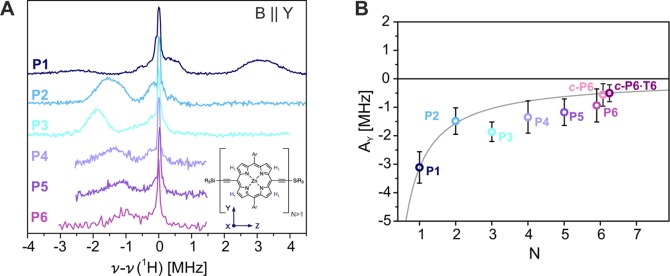
(A) Experimental Mims ENDOR spectra of P1–P6 recorded at the high-field Y position at 20 K. (B) Hyperfine couplings of the H₁ protons along the Y axis of the ZFS tensor (A_Y) determined by Gaussian fitting of the principal hyperfine peak in the experimental ENDOR spectra as a function of oligomer size; the error bars indicate the full width at half-maximum (fwhm). The gray line corresponds to the theoretical N^–1 relationship for the hyperfine couplings in case of complete delocalization. The change of the position of the hyperfine peak with respect to the Larmor frequency between P1 and P2 was explained by a change in the sign of D. The orientation of the ZFS tensor for the linear oligomers is shown in the inset; in P1, the X and Z axes are exchanged.

The hyperfine couplings determined from the position of the main hyperfine peak in the ENDOR spectra are plotted as a function of oligomer size in Figure 4B and compared to the theoretically predicted hyperfine couplings for complete delocalization (following an N^–1 dependence on the number of porphyrin units). As shown previously, the hyperfine coupling determined experimentally for P2 corresponds exactly to the predicted value since the spin density is equally distributed over both porphyrin units in this system. Because of the change in the sign of the D value accompanying the reorientation of the ZFS tensor between P1 and P2, the hyperfine peak shifts from one side of the nuclear Larmor frequency to the other.³³ Deviations from the theoretical prediction of N^–1 dependence occur for the longer oligomers: the hyperfine couplings of P3, P4, P5, and P6 correspond to 1.25, 0.90, 0.79, and 0.67 times the P2 hyperfine coupling, respectively.

The surprising increase in hyperfine coupling from P2 to P3, and the following gradual decrease for the longer linear oligomers, can be explained by an uneven spin density distribution with larger spin density on the central porphyrin units.

The ratio of spin densities on the three porphyrin units can be estimated by comparison of the hyperfine coupling observed for P3 with the corresponding hyperfine coupling in P1 since the nature of the spin density distribution on the central porphyrin unit in P3 is the same as that predicted for P1 (see Figure 5 and Figure S2 in the Supporting Information). The ratio of the experimental P3 and P1 hyperfine couplings is approximately 0.60, predicting a spin density distribution of 0.20:0.60:0.20, close to the results of the DFT calculation (0.19:0.62:0.19 with B3LYP/EPRII, see Supporting Information). The H₁ protons on the two external porphyrins would then give a hyperfine coupling of about −0.63 MHz in the Y orientation, and there is a broad shoulder at that position in the experimental spectrum. Overlap with other small hyperfine couplings prevents a definite assignment and experimental confirmation of the proposed uneven spin density distribution.

Figure 5.

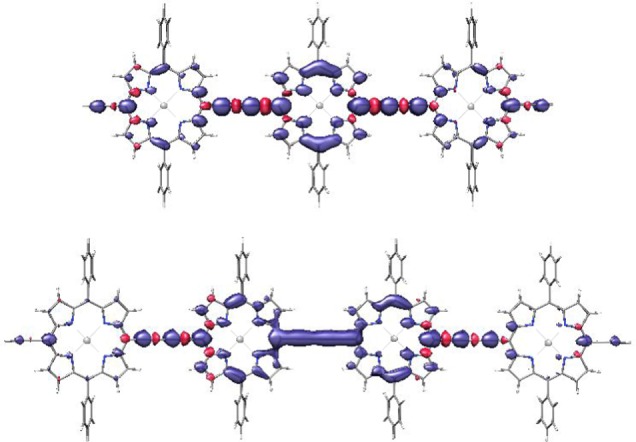
Spin density distributions in the first excited triplet state calculated at B3LYP/EPRII level for the optimized geometries of P3 and P4. The spin density distributions of the longer oligomers are shown in Figure S2 of the Supporting Information.

The amount of spin density on the central porphyrin units in P4, P5, and P6 was similarly predicted. For P5, a relative spin density contribution of 0.39 on the central porphyrin unit is predicted. For P4 and P6, the spin density distributions on the two central porphyrin units resemble the dimer spin density more than the monomer spin density, hence the dimer hyperfine couplings have been used for comparison, yielding a relative spin density contribution of 0.45 on the two central porphyrin units in P4 and of 0.34 in P6 (the values obtained based on the monomer hyperfine couplings only deviate by 0.02 from the reported values). The hyperfine couplings on the external porphyrin rings are too small to be clearly identified. Overall, the results show an increase in delocalization with the number of porphyrin units, even though it is slower than the increase expected for complete delocalization. The predictions based on the hypothesis of uneven spin density distributions in the porphyrin oligomers with three to six units agree reasonably well with the experimental results.

Porphyrin Oligomers Bound to Templates

In addition to the linear structures, oligomers bound to the template used for the synthesis of the six-membered ring were also investigated (see Figure 1B). The binding to a template places neighboring porphyrin units at angles of approximately 120° to each other and therefore allows the effect of different geometric constraints on the ZFS parameters and on triplet state delocalization to be studied.

The transient EPR spectra recorded for P2, P3, P4, and P6 in a toluene solution with an excess of T6 template are shown in Figure 6. The binding of the porphyrin to the template was verified by UV–vis measurements at room temperature.

Figure 6.

Transient EPR spectra recorded at 20 K up to 2 μs after the 532 nm laser pulse for the linear oligomers P2, P3, P4, and P6 in toluene:pyridine 10:1 and of the same oligomers bound to the T6 template in toluene without pyridine.

While the porphyrin dimer seems little affected by addition of the template, significant changes are observed for the longer oligomers. Their D-values decrease considerably, as evidenced by the reduced width of the triplet state EPR spectra (see Figure 6).

The spectra of P3·T6, and to a somewhat lesser degree also that of P4·T6, show a clearly resolved structure and spin polarization. For P6·T6, the spectrum is less well-defined, which might be due to a distribution of conformations contributing to the EPR spectrum, causing the observed broadening, especially of the outer parts of the spectrum. In all cases, a weak signal, which resembles the spectrum of the free oligomer, also seems to be present. To circumvent this problem, typically an at least five-fold excess of T6 template was used, and UV–vis data show complete binding at room temperature. Yet, EPR data indicate that partial dissociation of the porphyrin oligomer from the template does occur at low temperatures or upon freezing.

The significant decrease in D upon template binding, considered in isolation and within the framework of the somewhat ill-suited point-dipole approximation, would suggest increased delocalization. The analysis of the linear oligomers showed that this approach may lead to misinterpretation of the EPR spectra in such delocalized systems and that much more accurate information on the triplet state delocalization can be obtained from the hyperfine couplings.³³ The ENDOR spectra recorded for the free and templated porphyrin oligomers are almost identical (see Figure 7), indicating no change in the extent of the triplet state wave function upon binding of the T6 template. To understand the observed reduction of D, DFT geometry optimizations and calculations of the ZFS were performed in ORCA⁵¹ on the porphyrin oligomers bound to the template following the procedure described in ref (52). The ZFS parameters calculated at B3LYP/EPRII level are compared to the experimental results in Table 3.

Figure 7.

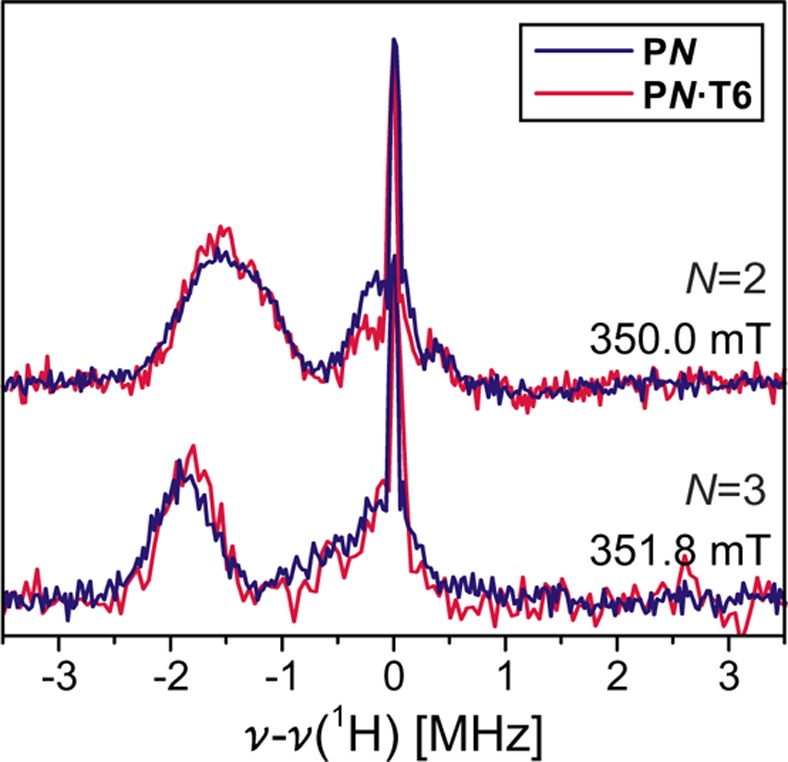
Mims ENDOR spectra recorded at the high-field Y position for the free and T6-bound P2 and P3 in toluene solution. Excitation at 532 nm was used in both cases.

Table 3. Experimental and Calculated ZFS Parameters for the Free and Bound Porphyrin Oligomers with Two to Four Porphyrin Units.

	Experiment		B3LYP/EPRII
	|D| [MHz]	|E| [MHz]	|D| [MHz]	|E| [MHz]
P2	1117 ± 9	284 ± 2	609	72
P2·T6a	890 ± 25	51 ± 15	468	51
P3	1169 ± 7	269 ± 2	456	84
P3·T6	621 ± 6	102 ± 2	270	36
P4	1195 ± 8	273 ± 2	465	60
P4·T6	486 ± 12	48 ± 3	243	6

^aZFS parameters estimated based on a simulation of the EPR spectrum as a linear combination of free (P2) and bound (P2·T6) dimer (0.85:0.15).

Although the absolute values are incorrect, the decrease in D is well reproduced by the DFT results; experimentally, the ratio of D-values for P3·T6 and P3 is 0.53 and DFT predicts a ratio of 0.59. Similarly for P4, the experimental ratio is 0.41, and DFT predicts a ratio of 0.52. For P2, the interpretation is more difficult, as only small changes are observed in the spectrum. However, some discontinuities between the X and Y transition (at about 320 mT and about 375 mT) might indicate the presence of a second contribution, and the spectrum can be simulated as a linear combination of the spectrum of the unbound P2 in toluene and an additional spectrum with a decreased D-value, assigned to P2·T6, with a ratio of 0.85:0.15 (the corresponding ZFS values are given in Table 3). The ratio of D values for P2·T6 and P2 used for this simulation (80%) is close to the ratio predicted by DFT (77%). It is established that the binding constant of the porphyrin oligomers to the template increases with the number of porphyrin units;⁵³ therefore it could be possible that even in the presence of an excess of template, the binding is not complete for P2 in frozen solution.

The origin of the decrease in D was investigated by studying the overlap of the localized singly occupied molecular orbitals (SOMOs), in analogy to the investigation in ref (35). The SOMOs were localized using the Pipek–Mezey scheme⁵⁴ (shown in the Supporting Information) and were used to separate the Coulomb and exchange contributions to the D-value. The overlap between the two localized SOMOs determines the magnitude of the D-value; increased overlap leads to an increase of both the Coulomb and the exchange contributions to the electron spin–spin interaction. The exchange contribution depends directly on the overlap integral and the Coulomb contribution depends on the distance between spin-carrying orbitals. A larger overlap of the SOMOs leads to more Coulomb contributions with small interspin distances, which correspond to larger contributions to the D-value due to the r^–3 dependence. Comparison of the populations of the SOMOs on the different porphyrin units for the linear oligomers and the oligomers bound to a template shows that there is a larger overlap for the linear systems with respect to the bent ones (Figures S3 and S4, Supporting Information), leading to larger D-values, as observed experimentally.

These results show that caution must be exerted in the interpretation of ZFS D-values in terms of triplet state delocalization in molecular-wire-type systems with extensive conjugation between the monomeric units, as changes in geometry can cause significant changes in the magnitude of D, which could be wrongly interpreted in terms of increased or decreased triplet state delocalization.

Cyclic Porphyrin Hexamer

The influence of symmetry and of the lack of end-group effects on the delocalization of the excited triplet state was investigated in the six- porphyrin ring c-P6 (see Figure 1C).^22,55

The transient EPR spectra recorded for the six-porphyrin ring without template (c-P6), the porphyrin ring with template (c-P6·T6), and the free-base porphyrin ring are shown in Figure 8A. The ZFS parameters and relative sublevel populations determined by simulation are reported in Table 4. The broadening of the transient EPR spectra prevents clear identification of the canonical positions. Echo-detected EPR spectra of triplet states typically show increased intensities at the canonical field positions due to shortened spin–spin relaxation for noncanonical orientations induced by modulation of the ZFS tensor orientation.^56,57 The Z canonical field position can be clearly identified from the echo-detected EPR spectrum, and the X canonical field position could also be assigned (see Figure S5 in the Supporting Information), allowing determination of the D- and E-values, which are summarized in Table 4.

Figure 8.

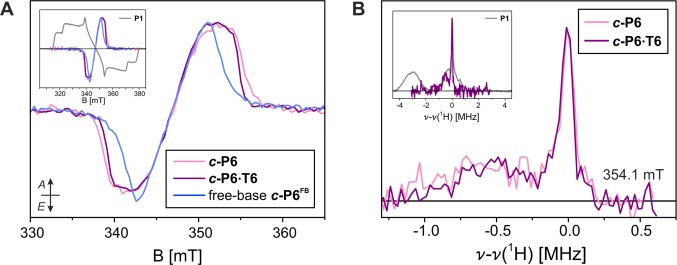
(A) Transient EPR spectra recorded at 20 K for c-P6, c-P6·T6, and free-base c-P6. The spectra are compared to the EPR spectrum of P1 in the inset. (B) Mims ENDOR spectra recorded at 20 K at a magnetic field of 354.1 mT (high-field Z transition) for c-P6 and c-P6·T6. The spectra are compared to the ENDOR spectrum of P1 (high-field Y position, corresponding to the same molecular orientation along the phenyl rings) in the inset.

Table 4. ZFS Parameters and Relative Sublevel Populations for c-P6, c-P6·T6, and Free-Base c-P6^FB Shown in Figure 8, Panel A.

	|D| [MHz]	|E| [MHz]	pX:pY:pZa
c-P6	244 ± 16	61 ± 11	0.51:0.49:0.00
c-P6·T6	230 ± 3	52 ± 1	0.57:0.43:0.00
c-P6FB	209 ± 11	29 ± 5	0.39:0.61:0.00

^aThe relative sublevel population values are affected by errors of 0.07, 0.02, and 0.03, respectively, for the three porphyrin nanorings.

The ZFS D-values of the ring systems are significantly reduced with respect to the linear oligomers, suggesting increased delocalization. The results for the oligomers bound to the T6 template have shown that a decrease in D does not necessarily imply changes in the extent of triplet state delocalization. Therefore, ENDOR measurements were performed at the high-field Z position to determine the proton hyperfine couplings, and the results are shown in Figure 8B.

The ENDOR spectra of both c-P6 and c-P6·T6 are characterized by a hyperfine peak at lower frequencies with respect to the nuclear Larmor peak corresponding to a hyperfine coupling of about 0.6 MHz, compared with values of about 3.1 MHz in P1 and 1.5 MHz in P2 (Figure 4).

The observation that the hyperfine coupling in c-P6 is approximately one-sixth of the corresponding hyperfine coupling in P1 shows that the triplet state is delocalized over all six porphyrin units in the cyclic hexamer. The ENDOR peak appears to be shifted to slightly higher hyperfine couplings in c-P6 compared to c-P6·T6, potentially indicating a slightly decreased extent of delocalization in the template-free ring.

Since the largest hyperfine couplings in the porphyrin systems investigated here are negative, the high-field Z position can be assigned to the m_S = −1 → m_S = 0 transition, and therefore the D-value can be concluded to be positive. Further, since the largest hyperfine couplings are observed in the direction of the phenyl substituents for all of the systems investigated here, the Z axis can be assigned to the out-of-plane axis of the six-porphyrin nanoring (i.e., perpendicular to the plane of the template in c-P6·T6). The sign of D and the direction of the Z axis indicate an oblate spin distribution, as expected for complete delocalization around the porphyrin nanoring. This contrasts with the prolate spin distributions in P2–P6.³³

The assignment of the Z axis as the out-of-plane axis of the porphyrin nanoring is supported by magnetophotoselection measurements performed at 810 nm, a wavelength corresponding to the center of the long wavelength absorption band in the UV–vis spectrum of c-P6·T6. The corresponding optical transitions were shown to be x- and y-polarized in the plane of the six-porphyrin nanoring; no optical transition moment is associated with the out-of-plane axis of the ring.²² The transient EPR spectra recorded at 810 nm with light polarized parallel and perpendicular to the magnetic field are shown in Figure 9. The polarization ratios P_i were calculated as a function of the magnetic field and are also shown. Alignment of an optical transition dipole moment with one of the axes of the ZFS tensor leads to a positive polarization ratio at the field positions corresponding to this orientation of the tensor with respect to the field, while negative polarization ratios are obtained for the field positions corresponding to the other two canonical orientations.^58,59 The polarization ratios for the two Z canonical field positions are clearly negative, in agreement with assignment of this orientation to the out-of-plane axis of the ring.

Figure 9.

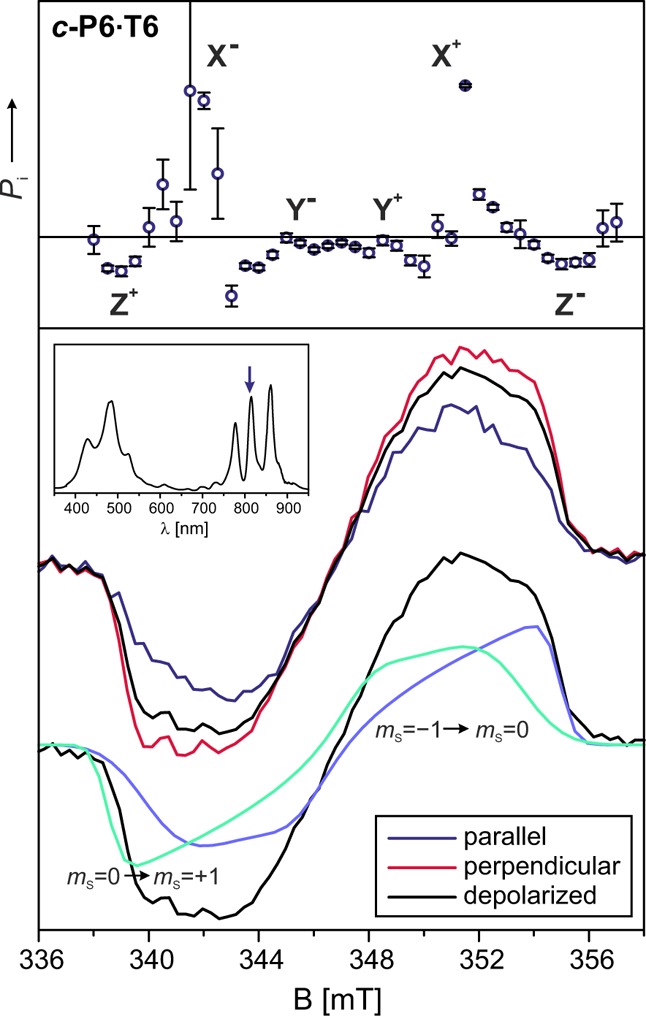
Bottom panel: Transient EPR spectra recorded for c-P6·T6 after excitation with light at 810 nm polarized parallel or perpendicular to the magnetic field. The contributions of the m_S = −1 → m_S = 0 and m_S = 0 → m_S = +1 transitions to the spectrum are shown for comparison. The simulation parameters are reported in Table 4. Top panel: The polarization ratios are shown as a function of field position above the spectra.

The assignment of the orientation of the ZFS tensor with the X and Y axes in the plane of the nanoring and with Z as the out-of-plane axis allows an attempt at explaining the observed spin polarizations. In all three cases, the EEEAAA spin polarization indicates that the triplet sublevels corresponding to the orientations in the ring plane are mainly populated. An analysis similar to that used to explain the spin polarizations in the linear oligomers can also be applied here. Assuming population of the triplet state promoted solely by zinc spin–orbit coupling yields relative sublevel populations of p_X:p_Y:p_Z = 0.46:0.54:0.00, with increasing population p_X for increasing deviations from circular symmetry (flattening of the porphyrin ring in one direction). The relative population ratios of the zinc porphyrin rings can again be calculated as linear combinations of the free-base populations and the populations for a perfectly symmetric ring for c-P6·T6. The two ISC mechanisms, direct spin–orbit coupling promoted by mixing of the zinc d-orbitals with the porphyrin π-system and vibronic spin–orbit coupling, seem to contribute to a similar extent, with a ratio of 0.57:0.43 for c-P6·T6. A similar contribution of both mechanisms seems plausible since the vibrations are restricted in the ring system, and therefore the contribution of the direct zinc spin–orbit coupling could be more important in these systems with respect to the more flexible linear oligomers, where the vibronic contribution was shown to carry more weight as the size of the systems increased. The changes in spin polarization between c-P6 and c-P6·T6 are more difficult to explain but are most likely due to the increased flexibility of the porphyrin ring without template, leading to distortions from the circular geometry that affect the selectivity of ISC.

Conclusions

The triplet state delocalization in linear, bent, and cyclic porphyrin arrays was investigated by using transient EPR to characterize the ZFS interaction and ENDOR to study the proton hyperfine couplings. Determination of the extent of delocalization from the ZFS D-value alone, using the popular point-dipole approximation, would have led to an underestimation of the delocalization length in the linear oligomers, and analysis of the hyperfine couplings was required to quantify the extent of delocalization.

The results of proton ENDOR measurements on longer linear oligomers, with three to six porphyrin units, have been interpreted in terms of triplet states with uneven spin density distributions. In each case, the triplet wave function is localized on the central porphyrin units of the oligomer rather than being uniformly distributed over the entire π-system. This behavior contrasts with that of the relaxed S₁ singlet excited state, which at room temperature is delocalized over all six porphyrin units in linear P6.¹⁰ EPR and ENDOR measurements on oligomers forced into a bent conformation by binding to a template show that the D-value is very sensitive to the geometry of the system and in isolation does not accurately reflect the extent of triplet state delocalization.

The changes in spin polarization of the EPR spectra of the longer porphyrin oligomers were attributed to the increasing importance of a competing ISC mechanism induced by molecular vibrations as the length of the oligomer increases.

In contrast to the linear oligomers P3–P6, the triplet state was found to be completely delocalized in the D_6h-symmetric cyclic porphyrin hexamer c-P6, with and without the rigid internal T6 template. This surprising result contradicts the conventional wisdom that triplet excited states of extended π-system are localized over a small region of the molecule. The following three observations provide unequivocal evidence for delocalization over all six porphyrin units in the cyclic hexamer:

• (i)The transient EPR spectra show a significant reduction of the ZFS D-value for c-P6 and c-P6·T6 with respect to the linear hexamer P6.
• (ii)The ENDOR spectra show that the proton hyperfine coupling constants in the out-of plane direction of the c-P6 and c-P6·T6 rings correspond to about 0.6 MHz, which is approximately one-sixth of the value observed for the monomer (P1) in the same direction of the molecular frame.
• (iii)Magnetophotoselection has shown that the ZFS Z-axis is perpendicular to the plane of the nanoring. Together with the assignment of a positive D-value, deduced from the ENDOR data based on knowledge of the sign of the hyperfine coupling, these results imply that the spin distribution is oblate, whereas it is prolate in the linear oligomers P3–P6.³³

The greater spatial delocalization of the triplet state of the cyclic hexamer, c-P6, compared with the linear hexamer P6 can be attributed to the equivalence of all six porphyrin sites in the cyclic hexamer together with its greater structural rigidity. This behavior illustrates the unexpected differences in electronic structure that can arise when comparing linear and cyclic π-systems.⁶⁰ The surprising discovery that the triplet wave function is delocalized over such a large π-system, with a diameter of 24 Å, suggests that triplet delocalization in yet larger π-conjugated porphyrin macrocycles^61,62 is an exciting possibility.

Supporting Information Available

Experimental details, DFT spin density distributions and molecular orbitals, and additional figures. The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.5b04511.

The authors declare no competing financial interest.