Abstract
Cost-effective study design and proper inference procedures for data from such designs are always of particular interests to study investigators. In this article, we propose a biased sampling scheme, an outcome-dependent sampling (ODS) design for survival data with right censoring under the additive hazards model. We develop a weighted pseudo-score estimator for the regression parameters for the proposed design and derive the asymptotic properties of the proposed estimator. We also provide some suggestions for using the proposed method by evaluating the relative efficiency of the proposed method against simple random sampling design and derive the optimal allocation of the subsamples for the proposed design. Simulation studies show that the proposed ODS design is more powerful than other existing designs and the proposed estimator is more efficient than other estimators. We apply our method to analyze a cancer study conducted at NIEHS, the Cancer Incidence and Mortality of Uranium Miners Study, to study the risk of radon exposure to cancer.
Keywords: additive hazards model, inverse probability weight, outcome-dependent sampling, Primary 62D05, secondary 62N01
1. INTRODUCTION
Epidemiologic studies often require a long follow-up of subjects in order to observe meaningful outcome results. The cost for a large number of subjects and a long period of follow-up time could be prohibitively expensive. Research methods that look into new efficient statistical designs that will reduce the overall cost and improve the study power under a fixed budget are always desired. For example, in the Cancer Incidence and Mortality of Uranium Miners Study conducted at the National Institution of Environment Health (Řeřicha et al., 2006), assembly of the life long record of radon exposure for a miner is a challenging and costly process. Investigators would like to maximize the study power for a given budget by strategically selecting the most informative study subjects.
The proposed ODS design for failure time data is a biased sampling scheme. Biased sampling schemes have long been recognized as cost-effective designs to improve the power of studies. Such biased designs include Case–Control designs for binary outcomes (e.g., Prentice & Pyke, 1979; Breslow & Cain, 1988; Weinberg & Wacholder, 1993; Breslow & Holubskov, 1997; Wang & Zhou, 2010), two-stage designs (e.g., White, 1982; Weaver & Zhou, 2005; Song, Zhou & Kosorok, 2009), and ODS for continuous outcomes (e.g., Zhou et al., 2002, 2007; Zhou, Qin & Longnecker, 2011).
The proposed ODS design is closely related to the well-known Case–Cohort design (Prentice, 1986) for the failure time data. The Case–Cohort design first samples a simple random sample (SRS) from the underlying population and in addition collects all remaining failures. This design is particularly effective when the failure rate is low and the number of failures is small (e.g., Self & Prentice, 1988; Cai & Zeng, 2004; Scheike & Martinussen, 2004; Sun et al., 2004; Pan & Schaubel, 2008). Variations of the Prentice (1986) Case–Cohort sampling scheme that further improve the efficiency of the designs include the stratified Case–Cohort design (e.g., Borgan et al., 2000), and generalized Case–Cohort design (e.g., Chen, 2001; Cai & Zeng, 2007; Samuelsen et al., 2007; Kang & Cai, 2009). In many studies where the failure rate may not be low and the number of failures is large, investigators may not have enough budget to sample all failures. Under these situations, it is still desirable to have a design that assembles covariates information for a subset of the failures that will increase the power of the study for a given overall budget.
The Cox proportional hazards model, which assumes the hazard ratio is constant, is commonly used in survival analysis and almost all of the aforementioned works are done under a Cox proportional hazards model framework. When the hazards ratio is varying as the study progresses, the additive hazards model, which assumes the hazards difference is constant, is a useful alternative to the Cox proportional hazards model (Cox & Oakes, 1984; Lin & Ying, 1994; Yip et al., 1999). Buckley (1984) demonstrated that the additive hazards model is biologically more plausible than the Cox proportional hazards model. In this paper, we propose an outcome-dependent sampling scheme for survival data under the additive hazards model and develop a weighted estimating equation approach to estimate the regression parameters for data generated under the proposed ODS design. The proposed design includes a SRS from the underlying cohort, as well as two supplemental samples: one from those who failed early and one from those who failed late. The intention of this sampling method is that if the exposure is related to the failure, then those who failed early and late will be more informative about the exposure-failure relationship. The Case–Cohort design can be viewed as a special case of the proposed ODS design with the selection probability of supplemental failure equal to 1. We show that parameter estimators have closed forms and are easy to compute. We provide theoretical formulas and computing software to help investigators to compute and design an optimal ODS study with the same sample size.
The rest of the paper is organized as follows. In Section 2 we introduce the proposed ODS design for failure time data and discuss suitable weights for constructing the pseudo-score function to estimate the regression parameters. A Breslow-type estimator for the cumulative baseline hazard function is also given. The asymptotic properties of the proposed estimator is presented in Section 3. In Section 4 the asymptotic relative efficiency of the proposed estimator is compared to the pseudo-score estimator under the SRS with the same sample size. A formula for calculating the optimal allocation of subsamples is provided. Section 5 presents a simulation study to evaluate the performance of the proposed methods. Section 6 provides a real data analysis. Section 7 provides some concluding remarks and discussions. The proof for theoretical results are outlined in the Appendix.
2. DATA STRUCTURE AND PSEUDO-SCORE EQUATION
2.1. ODS Design and Data Structure
Suppose that there are N independent subjects in a large study cohort. Let T be the failure time and C be the potential censoring time for T . With right-censoring, we observe the vector (X, δ) with X = min(T, C) and δ = I(T ≤ C), where I(·) is the indicator function. Let Z(t) be a possibly time-dependent p-vector of covariates. We assume that T and C are independent conditional on Z(·). Suppose the hazard function of the failure time T conditional on Z(t) follows the additive hazards model:
| (1) |
where λ0(t) is the unspecified baseline hazard and β0 denotes the p-vector of unknown regression parameters.
We propose the following general failure time ODS design, which is a retrospective design and the covariates are only measured for the selected subjects. First, we draw a simple random subcohort (SRS) from the original cohort. Let ξi indicate, by the values 1 or 0, whether or not the i-th subject is selected into SRS. Assume the sample size of SRS is n0 and n0/N → p. Secondly, we partition the domain of failure time T into a union of K̃ mutually exclusive intervals, Ãk = (ak–1, ak], k = 1,···, K̃, where {ak : k = 0, 1,···, K̃} are known constants satisfying: a0 = 0 < a1 <,···,< aK̃ = +∞. We select K exclusive intervals which are believed to be more informative to sample supplemental samples with K ≤ K̃. Let Al denote the selected exclusive interval, who is from the above partition of the failure time for l = 1,..., K. Then, the supplemental samples are selected from the subjects who occurs failure, are outside of SRS, and in each stratum Ak, k = 1,..., K. Let ηik denote whether or not the i-th subject from the stratum Ak is selected into the supplemental sample. Assume the size of supplemental samples selected form k stratum is nk, k = 1,···, K. Obviously, the above ODS design is applicable whether or not the disease rate is low and the number of failures is small.
Let Nk and n0,k denote the size of the full cohort sample and the SRS sample falling into the k-th stratum and nk/{Nk – n0,k} → rk, k = 1,···, K. Denote , i.e., n is the total size of the SRS and supplemental samples. Let n/N → ρV (validation fraction), n0/n → ρ0 (SRS fraction) and nk/n → ρk, k = 1,···, K (supplemental fraction), respectively. Let , k = 1,···, K. Then from simple calculation, the relationship between (p, rk) and (ρV, ρ0, ρk) can be expressed as following:
| (2) |
The collection of samples from these two steps whose Z(·) value is observed is referred to as the validation sample. We refer to the collection of remaining subjects whose Z(·) value is not observed as the nonvalidation sample. Hence, the observable data structure of our. proposed failure time ODS is:
where V0, Vk and V̄ are the index for the SRS, supplemental sample from the stratum Ak and the nonvalidation sample, respectively. Note that (i) when K̃ = 1 and r1 = 1, our proposed failure time ODS design is the traditional Case–Cohort design. (ii) When K̃ = 1 and r1 ∈ (0, 1), our proposed failure time ODS design is the generalized Case–Cohort design by Cai & Zeng (2007).
2.2. Weighted Pseudo-Score Estimator
Define Ni(t) = I(Xi ≤ t, δi = 1) and Yi(t) = I(Xi ≥ t). Let τ denote the study end time. If the data are completely observed, β0 of model (1) can be estimated by , the root of the following pseudo-score equation
| (3) |
where . Since not all observed data have the complete covariate history, we propose to apply the following inverse probability weight (IPW) (e.g., Horvitz & Thompson, 1951) to inference the data from an ODS design:
| (4) |
where and . We don't sample the nonvalidation sample to observe their covariates. Therefore, the sampling probability of the nonvalidation sample should be zero. The sampling probability of the supplemental sample in Ak is ρkρV/[πk(1 – ρ0ρV)], k = 1,..., K. In SRS, the sampling probability of censored subject is ρ0ρV and the sampling probability of failure is 1 if it belongs to stratum Ak, otherwise it is ρ0ρV. The above inverse probability weight (4) can achieve the following goals: (i) nonvalidation samples are eliminated by setting w = 0; (ii) the sampled censored subjects have the inverse of the sampling probability, (ρ0ρV)–1, as their weight; (iii) the sampled supplemental cases are weighted by πk(1 – ρ0ρV)/(ρ0ρV); (iv) the sampled subcohort cases are weighted by 1 if they belong to Ak (k = 1,···,K), and by (ρ0ρV)–1 otherwise.
We propose to estimate the true regression coefficients, β0, by solving the following weighted pseudo-score equation:
| (5) |
where . The resultant estimator has a closed form:
| (6) |
where for a vector a.
For the cumulative baseline hazard function , it is natural to use the fol lowing estimator:
| (7) |
To ensure its monotonicity, we make a minor modification, which still preserves the asymptotic properties, that is . Following similar arguments as Lin & Ying (1994), we can show that and are asymptotically equivalent in the sense that .
3. ASYMPTOTIC PROPERTIES
To develop large sample theory for the proposed estimators, we first introduce the following notations:
Let e(t) = E[Y(t)Z(t)]/E[Y(t)]. For i = 1, ···, N, define
We impose the following regularity conditions:
-
(C1)
Λ0(τ) < ∞.
-
(C2)
Pr(Y(t) = 1) > 0 for t ∈ (0, τ].
-
(C3)
.
-
(C4)
is positive definite.
The conditions are similar to those in Theorem 4.1 of Anderson & Gill (1982). The asymptotic properties of are stated in the following:
Theorem 1
Under the conditions (C1)-(C4), (i)(consistency) ; (ii) (asymptotic normality) is asymptotically normally distributed with mean zero and variance matrix , where is defined as in assumption (C4) and
Remark 1
The asymptotic variance of consists that of full data pseudo-score estimator's variance plus an extra term due to ODS
Remark 2
For Case–Cohort sampling. design, K̃ = 1 and r1 = 1,
and this results is the same as the variance derived by Kulich & Lin (2004).
Remark 3
For generalized Case–Cohort design, K̃ = 1 and r1 ∈ (0, 1),
and this result is the same as the variance derived by Cai & Zeng (2007).
Theorem 2
Under the conditions (C2)-(C4), the estimated variance matrixes , , and , where
with
and
Proof
the consistency follows from the law of large numbers, the uniform consistency of in Theorem 3 and the uniform convergence of Z̄w(t) to e(t) are established in the Appendix.
Define and ψ0(t) = E[Y(t)]. The follow theorem establishes the asymptotic property of the estimated cumulative baseline hazard function .
Theorem 3
Under the assumptions (C1)-(C4), (i)(uniform consistency) ; (ii)(asymptotic normality of ) , where is defined in (7), converges weakly on [0, τ] to a zero mean Gaussian process with function at (s, t) is
where
The outline of the proofs of Theorem 1 and 3 are provided in the Appendix.
4. ASYMPTOTIC RELATIVE EFFICIENCY AND OPTIMAL ODS DESIGN
4.1. Asymptotic Relative Efficiency with SRS Design with Same Sample Size
In this section, we investigate the relative efficiency of the proposed estimator to the competing estimator , where is the pseudo-score estimator from the equation (3) based on the SRS design with the same sample size. We then use those results to derive an optimal sample size allocation for future study designs.
By Theorem 1, the asymptotic relative efficiency of versus is
| (8) |
where is the total size of ODS sample. The formula of can be re-written as:
| (9) |
4.2. Optimal ODS Design
We consider the optimal subcohort allocation problem in the failure time ODS design under a fixed underlying cohort population and a fixed total budget. By optimality, we mean an allocation of n0, n1,...,nK such that the trace of matrix achieves its minimum. Recall that n = n0 + n1 + ··· + nK is total validation size where Z is observed. Let N denote the total sample size of an underlying cohort population and $B denote total budget at the disposal of the study investigators. Assume that the unit cost is $C1 to observe (X, δ) and the unit cost is $C2 to observe (Z). For given B and N, the simple random sampling design can afford to sample (B – N × C1)/C2 = nSRS subjects for assess exposure Z. The ODS design, on the other hand, can afford to sample n0, n1,..., nK to assess exposure Z, where n0, n1,...,nK are bounded by condition
| (10) |
Our goal is finding the n0, n1,...,nK allocation, such that they satisfy (10), but also minimize the trace of . We assume that N, B, C1, C2 are all fixed, which is equivalent to the condition that ρV (ρV (ρV = (n0+n1+···+nk)/N) is fixed.
From the formula (9), we known that the trace of asymptotic relative efficiency, denoted by can be written as:
| (11) |
where trace , trace , and trace , k = 1,...,K are constant and they could be consistently estimated by replacing the means with their empirical counterparts from Theorem 2. Therefore, is a function of ρV, ρ0 and ρi, 1 ≤ i ≤ K, which are dependent on our sampling scheme. It is desirable to choose values that minimize the trace of the asymptotic relative efficiency. For most ODS applications, the K̃ = 3 case is shown to be a practical and sufficient setting (Zhou et al., 2007) and the Newton-Raphson algorithm could be used to get the optimal allocation of the subsamples. We will be happy to provide interested readers with the program code we wrote for this
4.3. Optimal ODS Example
We consider the following additive hazards model:
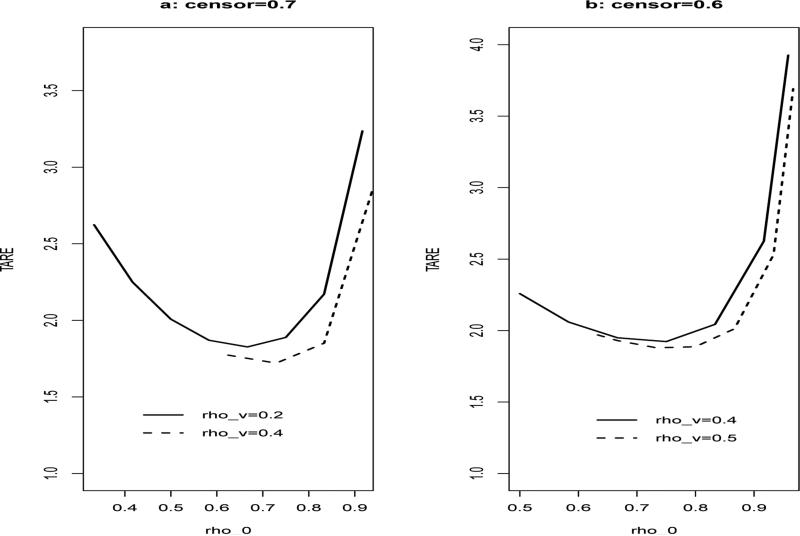
where E ~ N(0, 1), Z ~ Bern(1, 0.5), λ0(t) = 0.6, β1 = 0 and β2 = 0.5. We consider the situation where the censoring rates are 70% and 60%, and the cutpoints are (30%, 70%) quartiles of failure time. We select the supplemental samples from the high and low intervals of the failure time. Let ρ2 = 0 (ρi = ni/n and n = n0 + n1 + n3). We fix ρV and consider the trace of asymptotic relative efficiency between and under different setting of ρ0, ρ1 and ρ3. The simulation results (Figure 1) are based on the total sample size N = 600 and 1000 simulated data sets.
Figure 1.
The trace of asymptotic relative efficiency between and
In Figure 1, the X-axis represents the range of corresponding ρ0 and the Y-axis represents the trace of asymptotic relative efficiency. From Figure 1, it can be seen that: (i) the trace of asymptotic relative efficiency is decreasing as ρV is increasing. (ii) In Figure 1.a, when ρV = 0.2, 0.4, the smallest ρ0 is equal to 0.33 and 0.66, respectively. In Figure 1.b, when ρV = 0.4, 0.5, the smallest ρ0 is equal to 0.49 and 0.63, respectively. (iii) In Figure 1.a, when ρV = 0.2, 0.4, the corresponding optimal ρ0 are equal to 0.67 and 0.73, respectively. (iv) Under the situation that censoring rate is 60%, ρV = 0.4, 0.5, the corresponding optimal ρ0 are 0.75 and 0.73 in Figure 1.b. The above results suggests that: (1) when the censoring rate is high, e.g., 70%, sampling fewer SRS subcohorts (smaller ρ0) will increase the study efficiency; (2) when the censoring rate is moderate, e.g., 60%, one can find an optimal ρ0 that may be around 0.73.
5. SIMULATION STUDIES
In this section, we examine the finite sample performance of the proposed approach via simulation studies. For all simulation studies, we generated 1000 simulated datasets, each with N = 600 independent subjects. The failure times are generated from the additive hazards model:
where exposure E follows standard normal distribution and Z follows a Bernoulli distribution with Pr(Z = 1) = 0.5, λ0(t) = 0.6, β1 = 0 and β2 = 0.5. The censoring times are generated from mixture uniform distribution with c0unif[c1, c2] + (1 – c0)unif[c3, c4] with 0 < c0 < 1, where c0, c1, c2, c3 and c4 are chosen to generate around 60%, 70% censoring respectively. All the failures are partitioned into three strata with the cutpoints (30%, 70%) quartiles of failure times. Our proposed ODS design consists different sizes of SRS and supplemental sample (presented in Table 1).
TABLE 1.
Simulation results based on 1000 simulations with full cohort size N = 600 and cutpoints being (0.3, 0.7). The hazard model is λ(t) = 0.6 + β1E + β2Z with β1 = 0, β2 = 0.5 and E ~ N(0, 1), Z ~ Bernulli(0.5).
|
β
1
|
β
2
|
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Censoring | (n0,n1,n3) | Method | Mean | SE | 95%CI | Mean | SE | 95%CI | ||
| 70% | (300,65,7) | −0.002 | 0.065 | 0.062 | 0.940 | 0.502 | 0.132 | 0.130 | 0.950 | |
| −0.003 | 0.089 | 0.089 | 0.950 | 0.512 | 0.190 | 0.185 | 0.946 | |||
| −0.002 | 0.085 | 0.080 | 0.941 | 0.501 | 0.174 | 0.165 | 0.946 | |||
| −0 001 | 0.076 | 0.078 | 0.960 | 0.509 | 0.160 | 0.161 | 0.949 | |||
| −0.001 | 0.075 | 0.077 | 0.958 | 0.508 | 0.157 | 0.159 | 0.947 | |||
| (360,51,6) | −0.001 | 0.062 | 0.062 | 0.942 | 0.501 | 0.131 | 0.129 | 0.949 | ||
| −0.001 | 0.081 | 0.080 | 0.950 | 0.508 | 0.173 | 0.168 | 0.941 | |||
| −0.002 | 0.073 | 0.074 | 0.954 | 0.501 | 0.156 | 0.155 | 0.946 | |||
| 0.001 | 0.071 | 0.073 | 0.945 | 0.507 | 0.149 | 0.151 | 0.952 | |||
| −0.000 | 0.069 | 0.071 | 0.942 | 0.505 | 0.144 | 0.148 | 0.956 | |||
| 60% | (300,69,16) | −0.001 | 0.054 | 0.053 | 0.955 | 0.500 | 0.113 | 0.113 | 0.947 | |
| 0.002 | 0.074 | 0.075 | 0.954 | 0.498 | 0.170 | 0.160 | 0.938 | |||
| 0.005 | 0.067 | 0.067 | 0.943 | 0.500 | 0.142 | 0.142 | 0.954 | |||
| 0.003 | 0.065 | 0.069 | 0.962 | 0.506 | 0.142 | 0.145 | 0.958 | |||
| 0.003 | 0.064 | 0.067 | 0.957 | 0.503 | 0.137 | 0.140 | 0.961 | |||
| (360,55,13) | −0.001 | 0.053 | 0.052 | 0.950 | 0.501 | 0.115 | 0.113 | 0.951 | ||
| 0.002 | 0.069 | 0.069 | 0.944 | 0.505 | 0.148 | 0.146 | 0.948 | |||
| −0.000 | 0.064 | 0.062 | 0.948 | 0.502 | 0.138 | 0.134 | 0.939 | |||
| 0.001 | 0.063 | 0.064 | 0.952 | 0.501 | 0.132 | 0.135 | 0.953 | |||
| 0.002 | 0.060 | 0.062 | 0.952 | 0.500 | 0.129 | 0.131 | 0.953 | |||
- and are the standard pseudo-score estimator based on full cohort, SRS subcohort and SRS sample with same size as ODS design, respectively.
- and denote the proposed estimator based on the GCC design and our proposed failure time ODS, respectively.
For each setting, we compare the proposed estimator by () with four competing estimators: (1) , the estimator based on the generalized Case-Cohort design which randomly selects the SRS's of size n0 and the supplemental samples of size n1 + n3 from the cases out of SRS, respectively. (2) , the pseudo-score estimator based on the full cohort. (3) , the pseudo-score estimator based on the SRS sample. (4) , the pseudo-score based on the SRS sample with the same sample size as the ODS design. We study different scenarios including different censoring rates and different size of supplemental samples. The sample standard deviation of the 1000 estimates is given in the corresponding SE column. The column gives the average of the estimated standard error and “95% CI” is the nominal 95% confidence interval coverage of the true parameter using the estimated standard error. The simulation results are summarized in Table 1.
First, under all of the situations considered here, the five estimators are all unbiased. The proposed variance estimator provides a good estimation for the sample standard errors and the confidence intervals attain coverage closed to the nominal 95% level. Second, is the best estimator among the five estimators, because it is based on the full cohort data. Third, the proposed estimator is more efficient than the estimator, , which indicates that sampling the supplemental samples from the high and low intervals of the failure time is more efficient than simple random sampling. Finally, the proposed estimator is also more efficient than under all the situations.
6. URANIUM MINERS STUDY DATA ANALYSIS
In this section, we illustrate the proposed method using a data set from the Cancer Incidence and Mortality of Uranium Miners Study. Uranium miners are chronically exposed to ionizing radia tion, which is a known carcinogen. Therefore, miners are at risk of developing radiation-related cancer because they are chronically exposed to alpha particles emitted by radon and its progeny (referred to as radon), which will increase the risk of cancer through the resulting biological damage. Lung cancer has been long acknowledged as an occupational disease in uranium miners (BEIR VI, 1999). Furthermore, most studies investigated mortality rather than cancer incidence (Tirmarche et al., 1993; Vacquier et al., 2008; Kreuzer et al., 2008, 2010). However, they miss a substantial number of cases when the cancers have low fatality rates (Řeřicha et al., 2006; Kulich et al., 2011). So, we investigate incidence of various types of cancer excluding lung cancer rather than mortality and evaluate associations of working exposures to radon with the incidence of non-lung solid cancers.
To illustrate our methods, we consider the following ODS design. The full cohort used for cancer incidence follow-up includes 16, 434 miners. The follow-up period for case ascertainment was January 1, 1977 to December 31, 1996. A total of 2, 506 subjects with incident cancers were identified, of which 1, 575 had a cancer type of interest. The cohort was classified according to age on 1/1/1977 (5-year age groups). The subcohort was simple random sampled from each of the resulting strata so that the number of a subcohort sampled from a stratum was approximately equal to the total number of all cancer cases in the stratum. Therefore, we used the bootstrap method to obtain the variance estimation with the number of bootstraps being 300. The size of SRS, n0, is 1, 930. Let C3, C7 denote the 30% and 70% quantiles of the incidence time, respectively. We sample n1 = 236 and n3 = 236 supplemental samples from the intervals (0, C3] and (C7, ∞), respectively. The total size of ODS sample is 2, 402. We observe the following four covariates: total radon exposure (Trad) is measured as working level months (WLM, 1WLM = 3.5 × 10–3Jhm–3), Age (years), period of entering workforce (Dummy1 = 1, if subject started work between 1957 and 1966, and 0 otherwise; Dummy2 = 1, if subject started work between 1967 and 1976, and 0 otherwise) and Smoking (0 denotes non-smokers and light smokers who smoked less than 10 cigarettes a day for a period not exceeding 5 years; 1 denotes moderate and heavy smokers).
We consider the following additive hazards model:
The three methods including SRS (), GCC () and ODS () with the same size of sample are used to evaluate the association between incident and above covariates. The results for Cancer Incidence and Mortality of Uranium Miners Study are summarized in Table 2.
Table 2.
Analysis results for Cancer Incidence and Mortality of Uranium Miners Study: the listed values are the original values ×10–5
| Methods | 95%CI | ||
|---|---|---|---|
| Trad | 0.358 | 0.080 | (0.201, 0.516) |
| Age | 11.400 | 0.774 | (9.900, 12.900) |
| Smoking | 115.300 | 12.600 | (90.700, 140.000) |
| Dummy1 | 17.900 | 16.800 | (−15.000, 50.800) |
| Dummy2 | 27.500 | 21.900 | (−15.000, 70.500) |
| Trad | 0.401 | 0.063 | (0.277, 0.525) |
| Age | 7.940 | 0.721 | (6.530, 9.350) |
| Smoking | 125.500 | 11.500 | (103.000, 148.000) |
| Dummy1 | 3.380 | 13.600 | (−23.000, 29.900) |
| Dummy2 | 6.590 | 21.600 | (−36.000, 48.900) |
| Trad | 0.367 | 0.059 | (0.251, 0.483) |
| Age | 10.200 | 0.709 | (8.840, 11.600) |
| Smoking | 129.800 | 10.500 | (109.200, 150.400) |
| Dummy1 | 5.680 | 13.300 | (−20.000, 31.800) |
| Dummy2 | 7.330 | 20.500 | (−33.000, 47.400) |
Note: Trad is the total radon exposure. : the estimator obtained by simple random sampling; : the estimator obtained by generalized Case-Cohort sampling; : the estimator obtained by ODS sampling. The three methods base on the same size of the sample.
Results in Table 2 show that Trad under various methods is significantly related to the incidence of non-lung solid cancers. Nevertheless, a more precise 95% confidence interval (0.251 × 10–5, 0.483 × 10–5) is achieved for the estimator of Trad by the method . The standard deviations for Trad are 0.802 × 10–6, 0.634 × 10–6 and 0.590 × 10–6 from , and , respectively. The estimators for the remaining covariates under various methods are all almost the same as Trad. All the methods considered confirm that Trad has a positive impact on the incidence of non-lung solid cancers.
7. CONCLUDING REMARKS AND DISCUSSIONS
We proposed an ODS design for right censored failure time data under the additive hazards model. With a right censored response variable, the ODS sampling scheme is not only dependent on the value of observed failure time but also on the failure indictor. Under the framework of the additive hazards model we introduced the inverse probability weight (IPW) to the standard pseudo-score equation to estimate the regression coefficients. Our proposed estimators have a closed form and are easy to compute. The proposed estimators are shown to be consistent and asymptotically normal. Simulation studies show that the proposed estimator and design is more efficient than both the SRS estimator and the generalized Case–Cohort estimator with the same sample size.
We investigated the asymptotic relative efficiency and optimal allocation of subsample by evaluating the trace of the asymptotic relative efficiency between our proposed estimator and the standard pseudo-score estimator from SRS design with the same sample size under a fixed total sample size and a fixed total budget. We found that the proposed method performs well and is more efficient than the SRS design. When the censoring rate is high, sampling less SRS subcohort will increase the study efficiency. The simulation study suggests that greater efficiency can be gained in estimating the exposure effect on the outcome using our proposed ODS design. A real data analysis is provided to illustrate our proposed method.
Throughout this study, we have assumed Bernoulli sampling for the subcohort and cases outside the subcohort. Borgan et al., (2000) and Samuelsen et al., (2007) found that a stratified sampling SRS could improve the study efficiency. Future study focusing on developing efficient analysis methods for the stratified outcome-dependent sampling is justified.
ACKNOWLEDGEMENTS
The authors are grateful for the valuable comments and suggestions from the associate editor and the referees which drastically improved the article. This work is supported by the Fundamental Research Fund for the Central Universities 31541311216 (for Yu), National Science Foundation of China grant 11171263 (for Liu), and NIH R01 ES021900, P01 CA142538 (for Zhou).
APPENDIX
We first introduce the following lemmas which will be useful in proving the asymptotic properties of our estimators.
Lemma 1
Under the conditions (C2) to (C4), we have,
Proof
The result holds by application of the law of large numbers and Corollary III.2 of Anderson and Gill (1982).
Lemma 2
Let An(t), and Bn(t) be three sequences of bounded processes on [0, τ]. Suppose that (a) Bn(t) converges weakly to a tight limit B(t) with almost surely continuous sample paths; (b) An(t) and are monotone in t; and (c) there exist processes A(t) and A* (t) both right continuous at 0 and left continuous at τ, such that supt∈[0,τ] and . Then
This lemma's proof can be found in Kulich and Lin (2000).
Proof of Theorem 1
From the (6) and a simple algebraic manipulation, we can get that
We can show
by application of the law of large numbers and the Lemma 1.
We have
Frist, we will show the second part of (1) is asymptotical negligible,
| (1) |
Without loss of generality, assume that Zi(t) ≥ 0 for all t; otherwise, decompose each Zi(·) into its positive and negative parts. for each i, the process wiMi(t) has mean zero and can be expressed as the sum of two monotone processes on [0, τ]. Thus, by van der Vaart and Wellner (1996, Example 2.11.16), converges weakly to a tight Gaussian process B(t) with continuous sample paths on [0, τ]. Since Z̄ (t) is a product of two monotone processes which converge uniformly in probability to π1(t) and , where . We can prove (2) by the Lemma 2.
Second, the first part of (1) is equal to
| (2) |
By the define of Si(β0), the (3) is equal to
| (3) |
and
| (4) |
and the mean of them are both equal to zero. So, the two parts of (4) are uncorrelated. We rewrite the second part of (4) as:
| (5) |
It is easy to prove the three parties of (5) are uncorrelated. We can obtain the asymptotic normality of by the multivariate central limit theorem. Obviously, the consistency of holds immediately.
Proof of Theorem 3
From the (7) and a simple algebraic manipulation, we can get that we have
| (6) |
The third term is obviously op (1) uniformly in t. So,
| (7) |
From the consistency of and h(t) being bounded on [0, τ], we can obtain . We have by the method of quation (2)'s proof. Therefore,
From (6), we obtain
By the method of Theorem 1's proof, we have
and
| (8) |
Obviously, Mi(t) is the difference of two monotone function in t and ψ0(·) > 0. Thus, is also a difference of two monotone function in t. Because monotone functions have pseudo-dimension 1 (Pollard, 1990; page 15), the process is manageable (Pollard, 1990;page 38). It then follows the functional central limit theorem (Pollard, 1990; page 53) that is tight and thus converges weakly to a Gaussian process with mean zero. This weak convergence also follows van der Vaart and Wellner (1996, Example 2.11.16, page 215). The tightness of follows from the Theorem 1.
Obviously, is uniformly in t. Therefore, we have
which converges weakly to a zero-mean Gaussian process. Thus, we prove Theorem 3.
BIBLIOGRAPHY
- Andersen PK, Gill RD. Cox's regression model for counting processes: A large samle study. Annals of Statistics. 1982;10:1100–1120. [Google Scholar]
- Borgan O, Langholz B, Samuelsen SO, Goldstein L, Pogoda J. Exposure stratified case-cohort Designs. Lifetime Data Analysis. 2000;6:39–58. doi: 10.1023/a:1009661900674. [DOI] [PubMed] [Google Scholar]
- Breslow NE, Cain KC. Logistic regression for two-stage case-control data. Biometrika. 1988;75:11–20. [Google Scholar]
- Breslow NE, Holubkov R. Maximum likelihood estimation of logistic regressiion parameters under two-phase, outcome-dependent sampling. Journal of the Royal Statistical Society, Series B. 1997;59:447–461. [Google Scholar]
- Buckley JD. Additive and multiplicative models for relative survival data. Biometrics. 1984;40:51–62. [PubMed] [Google Scholar]
- Cai J, Zeng D. Sample size/power calculation for case-cohort studies. Biometrics. 2004;60:1015–1024. doi: 10.1111/j.0006-341X.2004.00257.x. [DOI] [PubMed] [Google Scholar]
- Cai J, Zeng D. Power calculation for case-cohort studies with nonrare events. Biometrics. 2007;63:1288–1295. doi: 10.1111/j.1541-0420.2007.00838.x. [DOI] [PubMed] [Google Scholar]
- Chen K. Generalized case-cohort sampling. Journal of the Royal Statistical Society, Series B. 2001;63:791–809. [Google Scholar]
- Cox DR, OAKES D. Analysis of Survival Data. Chapman & Hall; London: 1984. [Google Scholar]
- Horvitz D, Thompson D. A generalization of sampling without replacement from a finite universe. Journal of the American Statistical Association. 1951;47:663–685. [Google Scholar]
- Kang S, Cai J. Marginal hazards model for case-cohort studies with multiple disease outcomes. Biometrika. 2009;96:887–901. doi: 10.1093/biomet/asp059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kreuzer M, Grosche B, Schnelzer M, Tschense A, Dufey F, Walsh L. Radon and risk of death from cancer and cardiovascular diseases in the German uranium miners cohort study : follow-up 1946-2003. Radiation and Environmental Biophysics. 2010;49:177–185. doi: 10.1007/s00411-009-0249-5. [DOI] [PubMed] [Google Scholar]
- Kreuzer M, Walsh L, Schnelzer M, Tschense A, Grosche B. Radon and risk of extrapulmonary cancers: results of the German uranium miner's cohort study. British Journal of Cancer. 2008;99:1945–1953. doi: 10.1038/sj.bjc.6604776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kulich M, Řeřicha V, Řeřicha R, Shore DL, Sandler D. Incidence of non-lung solid cancers in Czech uranium miners: a case-cohort study. Enviromental Health. 2011;111:400–405. doi: 10.1016/j.envres.2011.01.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kulich M, Lin DY. Additive hazards regression with covariate measurement error. Journal of American Statistical Association. 2000;95:238–248. [Google Scholar]
- Kulich M, Lin DY. Improving the efficiency of relative-risk Estimation in case-cohort Studies. Journal of American Statistical Association. 2004;99:832–844. [Google Scholar]
- Lin DY, Ying Z. Semiparametric analysis of the additive risk model. Biometrika. 1994;81:61–71. [Google Scholar]
- National Research Council . Committee on the Biological Effects of lonizing Radiation (BEIR VI), Health effects of exposure to radon. National Academy Press; Washingtou DC.: 1999. [Google Scholar]
- Pan Q, Schaubel DE. Proportional hazards models based on biased samples and estimated selection probabilities. The Canadian Journal of Statistics. 2008;36:111–127. [Google Scholar]
- Pollard D. Empirical processes: theories and applications. Institute of Mathematical Statistics; Hayward: 1990. [Google Scholar]
- Prentice RL. A case-cohort design for epidemiologic cohort studies and disease prevention trials. Biometrika. 1986;73:1–11. [Google Scholar]
- Prentice RL, Pyke R. Logistic disease incidence models and case-control studies. Biometrika. 1979;66:403–412. [Google Scholar]
- Řeřicha V, Kulich M, Řeřicha R, Shore DL, Sandler D. Incidence of leukemia, lymphoma, and multiple myeloma in Czech uranium miners: a case-cohort study. Enviromental Health Perspect. 2006;114:818–822. doi: 10.1289/ehp.8476. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Samuelsen S, Ȧnestad H, Skrondal A. Stratified case-cohort analysis of general cohort sampling designs. Scandinavian Journal of Statistics. 2007;34:103–119. [Google Scholar]
- Scheike T, Martinussen T. Maximum likelihood estimation in Cox's regression model under case-cohort sampling. Scandinavian Journal of Statistics. 2004;31:283–293. [Google Scholar]
- Self SG, Prentice RL. Asymptotic distribution theory and efficiency results for case-cohort studies. Annals of Statistics. 1988;16:64–81. [Google Scholar]
- Song R, Zhou H, Kosorok M. A note on semiparametric efficient inference for two-stage outcome-dependent sampling with a continuous outcome. Biometrika. 2009;96:221–228. doi: 10.1093/biomet/asn073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun J, Sun L, Flournoy N. Additive hazards model for competing risks analysis of the case-cohort Design. Communications in Statistics – Theory and Methods. 2004;33:351–366. [Google Scholar]
- Tirmarche M, Raphalen A, Allin F, Bredon P. Mortality of a cohort of French uranium miners exposured to relatively low randon concentrations. British Journal of Cancer. 1993;67:1090–1097. doi: 10.1038/bjc.1993.200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vacquier B, Caer S, Rogel A, Feurprier M, Tirmarche M, Luccioni C, Quesne B, Acker A, Laurier D. Mortality risk in the French cohort of uranium miners: extended follow-up 1964-1999. Occupational Environmental Medicine. 2008;65:597–604. doi: 10.1136/oem.2007.034959. [DOI] [PubMed] [Google Scholar]
- van der Vaart AW, Wellner JA. Weak convergence and empirical processes. Springer-Verlag; New York: 1996. [Google Scholar]
- Wang X, Zhou H. Design and inference for cancer biomarker study with an outcome and auxiliary-dependent subsampling. Biometrics. 2010;66:502–511. doi: 10.1111/j.1541-0420.2009.01280.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weaver MA, Zhou H. An estimated likelihood method for continuous outcome regression models with outcome-dependent sampling. Journal of The American Statistical Association. 2005;100:459–469. [Google Scholar]
- Weinberg CR, Wacholder S. Prospective analysis of case-control data under general multiplicative intercept risk models. Biometrika. 1993;80:461–465. [Google Scholar]
- White J. A two stage design for the study of the relationship between a rare exposure and a rare disease. American Journal of Epidemiology. 1982;115:119–128. doi: 10.1093/oxfordjournals.aje.a113266. [DOI] [PubMed] [Google Scholar]
- Yip PF, Zhou Y, Lin D, Fang X. Estimation of population size based on additive hazards models for continuous-time recapture experiments. Biometrics. 1999;55:904–908. doi: 10.1111/j.0006-341x.1999.00904.x. [DOI] [PubMed] [Google Scholar]
- Zhou H, Chen J, Rissnen T, Korrick S, Hu H, Salonen J, Longnecker MP. Outcome-dependent sampling: an efficient sampling and inference procedure for studies with a continuous outcome. Epidemiology. 2007;18:461–468. doi: 10.1097/EDE.0b013e31806462d3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou H, Qin G, Longnecker M. A partial linear model in the outcome-dependent sampling setting to evaluate the effect of prenatal PCB exposure on cognitive function in children. Biometrics. 2011;67:876–885. doi: 10.1111/j.1541-0420.2010.01500.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou H, Weaver M, Qin J, Longnecker M, Wang MC. A semiparametric empirical likelihood method for data from an outcome-dependent sampling scheme with a continuous outcome. Biometrics. 2002;58:413–421. doi: 10.1111/j.0006-341x.2002.00413.x. [DOI] [PubMed] [Google Scholar]