Income Inequality and Intergenerational Income Mobility in the United States

Abstract

Is there a relationship between family income inequality and income mobility across generations in the United States? As family income inequality rose in the United States, parental resources available for improving children’s health, education, and care diverged. The amount and rate of divergence also varied across US states. Researchers and policy analysts have expressed concern that relatively high inequality might be accompanied by relatively low mobility, tightening the connection between individuals’ incomes during childhood and adulthood. Using data from the Panel Study of Income Dynamics, the National Longitudinal Survey of Youth, and various government sources, this paper exploits state and cohort variation to estimate the relationship between inequality and mobility. Results provide very little support for the hypothesis that inequality shapes mobility in the United States. The inequality children experienced during youth had no robust association with their economic mobility as adults. Formal analysis reveals that offsetting effects could underlie this result. In theory, mobility-enhancing forces may counterbalance mobility-reducing effects. In practice, the results suggest that in the US context, the intergenerational transmission of income may not be very responsive to changes in inequality.

How tightly linked are economic inequality between families and economic mobility across generations in the United States? Since the 1970s, disparities have grown in hourly wages, annual earnings and, most substantially, family incomes (McCall and Percheski 2010). Rising inequality has stimulated concern about how inequality persists. One widely discussed hypothesis maintains that high inequality inhibits intergenerational mobility (e.g., Ermisch et al. 2012; Wilkinson and Pickett 2010; Neckerman and Torche 2007; Solon 2004). Alan Krueger (2012), as Chairman of the Council of Economic Advisers, stated that “it is hard to … not be concerned that rising inequality is jeopardizing our tradition of equality of opportunity. The fortunes of one’s parents seem to matter increasingly in American society.”

While inequality trends generated policy interest, academic interest derives from variation over both time and space. Sociologists have long studied cross-country differences in how socioeconomic status persists on the hypothesis that different economic, social, and political contexts create different mobility opportunities (e.g., Lipset and Zetterberg 1956; Grusky and Hauser 1984; Erikson and Goldthorpe 1992). Today, in what Krueger (2012) calls “The Great Gatsby Curve,” relatively unequal countries tend to have less economic mobility than relatively equal countries (Corak 2013a; Blanden 2013; Björklund and Jäntti 2009; Andrews and Leigh 2009).

Yet, cross-national associations may not apply within every country because countries differ in how families, labor markets, and public policies shape children’s mobility prospects (Corak 2013b). Within the United States as inequality rose, income mobility appears to have remained stable (Chetty, Hendren, Kline, Saez, and Turner 2014; Lee and Solon 2009; Hertz 2007), though some uncertainty remains because studies using different data, measures, or birth cohorts find that mobility decreased (Aaronson and Mazumder 2008; Levine and Mazumder 2002), increased (Fertig 2003), or decreased and then increased (Mayer and Lopoo 2005). Beyond these trend studies, investigations of the inequality-mobility relationship within the United States remain sparse (Hout 2004). This paper elucidates this relationship by exploring differences within and across US states. It investigates the association between family income inequality and intergenerational income mobility in the contemporary United States by exploiting both temporal and geographic variation. It addresses whether children raised in relatively high-inequality eras or areas experienced more, less, or about the same level of mobility as children raised in less unequal times or places.

A state-centered analysis provides a US-specific analogy to cross-national research. States differ along many economic and demographic dimensions. More significantly, states represent stable political jurisdictions that shape children’s economic prospects via policies including tax rates and redistributive spending on welfare, education, and health. By studying state differences and time trends, this paper more fully exploits the variation available for learning about how inequality shapes mobility; previous research has been either purely cross-national or purely historical. Two recent working papers examine metropolitan differences in US income mobility; neither extensively explores the inequality-mobility relationship (Chetty, Hendren, Kline, and Saez 2014; Sharkey and Graham 2013). The family income Gini coefficient rose from .361 to .434 between the 1970–2000 censuses. State differences in 1970 were even larger than this change (with state Ginis ranging from .317 to .427 in 1970). Furthermore, inequality rose at different rates in different states (US Census Bureau 2012). Exploring variation across states and time provides a more powerful design and allows greater insight into how inequality and mobility are linked in the United States.

The intuition that high inequality undermines intergenerational mobility is widely shared. When parents’ investments in their children’s development shape children’s future achievement, large income differences between affluent and poor parents may generate large differences between their children’s adult incomes, helping affluent (poor) children remain affluent (poor) (Neckerman and Torche 2007). However, complex interactions between the family, state, and market in shaping children’s opportunities make the net relationship between inequality and mobility theoretically uncertain. For example, if Americans perceive that high inequality undermines mobility, they may support redistributive public investments in children’s development to offset the negative mobility consequences of inequalities in parents’ resources (Solon 2004). This is especially likely if Americans view mobility as an antidote to inequality, wherein inequality is acceptable when individuals “take turns” being rich and poor (Benabou and Ok 2001). Inequality may reduce mobility through some paths while boosting it through others. Alternately, inequality may have no independent causal impact; cross-national evidence might reflect common causes of inequality and mobility, not inequality’s mobility-reducing force. Empirical investigation is needed to resolve theoretical ambiguity.

This paper both provides a formal theoretical framework for understanding why the common hypothesis that inequality reduces mobility may not hold empirically, and estimates the inequality-mobility association in the contemporary United States. The empirical analysis improves on previous research in three ways. First, while previous mobility studies are either historical or comparative, this paper leverages comparisons across both time and space. Using data from the Panel Study of Income Dynamics (PSID) and various government sources, this paper examines how the relationship between parents’ and children’s family incomes varies with inequality, exploiting state and cohort differences. This design is not only statistically more powerful than previous studies (yielding greater variation in inequality and mobility). By examining geographic variation in mobility within the United States, it also provides new insights into within-country dynamics.

Second, this paper employs multiple longitudinal datasets, generating substantially more information about how inequality and mobility covary than possible from any single source.¹ The PSID is widely used in mobility studies; it provides the longest time series for analyzing trends. However, the sample is relatively small. Consequently, this paper also studies the National Longitudinal Survey of Youth 1979 cohort (NLSY79), whose larger sample yields greater power for detecting differences. It also explores Internal Revenue Service (IRS) data to capture mobility differences across smaller geographic areas than possible from national surveys. Third, this paper uses modeling techniques not previously applied to comparative mobility studies (including random coefficient models) that substantially reduce estimation uncertainty. This paper thus improves upon previous estimates, narrowing our confidence intervals and better pinpointing the size of the inequality-mobility relationship. It provides new insight into how inequality shapes mobility in the United States.

How Might Inequality Shape Mobility?

Like many previous intergenerational mobility studies, this paper provides descriptive evidence rather than testing specific theories about why inequality and mobility might relate. A formal theoretical framework provides context for this descriptive undertaking.

To understand how inequality might influence mobility, we must understand how income persists; greater persistence implies lower mobility. Any skill that is correlated across generations and rewarded in the labor market (or marriage market, when considering family income) contributes to economic persistence.² Variations in economic mobility across time, place, or subpopulation result from (1) different distributions of these skills; (2) different levels of intergenerational skill transmission; or (3) different rates of return to these skills. Inequality can shape mobility by affecting these three factors (defined formally below). Many skills correlated across generations are malleable. Consequently, their distributions and transmission rates may shift with social circumstances. Returns may vary across settings for both fixed and malleable traits.

The hypothesis that inequality reduces mobility, though often articulated, may not hold empirically because inequality may have offsetting effects. Offsetting effects manifest in two ways. First, for any given skill, mechanisms linking inequality to its distribution may reduce mobility while mechanisms linking inequality to its transmission or returns may enhance mobility. Second, inequality may affect different skills differently, making the net inequality-mobility association uncertain.

Duncan’s (1966) theorem of path analysis provides a formal framework for understanding offsetting effects. It also clarifies the distinction between transmission and returns. The theorem states that the correlation between variables k and j (here, individuals’ incomes during adulthood and childhood), ρ_kj, decomposes into contributions from {q} sources of similarity,³

$${\mathrm{\rho }}_{\text{kj}}={\mathrm{\sum }}_{\mathrm{q}}{\mathrm{\alpha }}_{\text{kq}}{\mathrm{\rho }}_{\text{qj}}.$$

Each source’s contribution further decomposes into its “transmission” (ρ_qj, the correlation between parental income and children’s skill q—e.g., educational attainment) and its “return” (α_kq, the standardized coefficient from a multiple regression predicting children’s adult income—e.g., the coefficient on children’s educational attainment). Economic persistence varies with the strength of the {q} skills’ relationships to parental income (transmission) and to adult income (return).⁴

Skill distributions may also affect mobility, in addition to skill transmissions and returns. Sociologists have gained analytic purchase by separating distributional and associational effects, particularly when studying education’s role in mobility (Breen 2011; Hout 1988). When considering correlations and standardized coefficients (as in Duncan’s theorem above), distributional shifts collapse to transmission changes. If children’s standardized skill distribution becomes less equally dispersed across parental income, then the correlation between skill and parental income rises and, by definition, transmission increases. But, when considering unstandardized coefficients, distributional shifts have unique effects (separate from transmission). Increasing skill variability raises (unstandardized) skill transmission and decreases (unstandardized) skill return, all else equal.⁵

Offsetting inequality effects along one path from parents’ to children’s incomes (in a skill’s distribution, transmission, and return) and across multiple paths generates theoretical ambiguity. Only our sociological imaginations limit the paths we could consider. Below, several examples of how inequality may decrease, increase, or fail to affect mobility illustrate how this ambiguity manifests in the United States today.

Increasing Inequality, Decreasing Mobility?

Private human-capital investments

High-income parents have more resources to invest in their children’s education than low-income parents. As inequality rose, budget constraints fell more among affluent than poor parents (Alderson, Beckfield, and Nielsen 2005). Affluent parents’ investment increases may have shifted their children’s academic skills distribution, raising affluent children’s chances of remaining affluent. Indeed, high- and low-income children’s test scores diverged with rising inequality (Reardon 2011).

Human-capital rewards

As inequality rose, higher education’s income returns grew (Autor, Katz, and Kearney 2008). Rising returns decrease mobility, since education better predicts adult income and education depends on parental income. Inequality may reduce mobility by strengthening the path between parents’ and children’s incomes through children’s education, via both private educational investments and their returns.

Labor-market opportunities

High unemployment may generate high inequality through large jobless populations and workers’ limited bargaining power (Barker and Bernstein 2013). Unemployment-driven inequality may also increase the persistence of low income. Early unemployment depresses workers’ future wage trajectories (Mroz and Savage 2006); non-college youth entering slack labor markets may struggle to climb the economic ladder.

Segregation

Inequality and residential segregation by income increased together (Watson 2009). As children’s developmental environments diverged, their chances of moving out of poverty (or affluence) may have declined due to augmented exposure to social and organizational (dis)advantages (Wilson 1987).

Increasing Inequality, Increasing Mobility?

Public human-capital investments

Progressive public spending can increase mobility by tying children’s educational achievements to public provisions, reducing their dependence on parental income and decreasing skill transmission (Solon 2004).⁶ Redistributive state spending on programs benefiting children increased with inequality (Mayer and Lopoo 2008). Likewise, real federal spending on means-tested programs jumped more than 25-fold per person in poverty between 1962 and 2011 (Haskins 2012). Public investments may have boosted mobility by improving poor children’s prospects.⁷

Public labor-market interventions

States’ incentives for businesses to relocate or expand within their jurisdictions—including loans and tax breaks—may increase both inequality and mobility through low-wage job growth in new firms, employment loss in preexisting firms that close, and employment gain in preexisting firms that survive (Bondonio and Greenbaum 2007). Similarly, state policies discouraging collective bargaining could increase inequality and (downward) mobility, since reduced unionization polarizes wages and obstructs pathways to sustained middle-class incomes via shared union memberships across generations (Western and Rosenfeld 2011).

Demographic shifts

Single-mother families’ increasing prevalence both raised family income inequality (Martin 2006) and shifted children into families with high (downward) mobility rates; parental absence weakens the processes reproducing high SES (Martin 2012; Björklund and Chadwick 2003). Middle-class children are more downwardly mobile if raised by one parent (DeLeire and Lopoo 2010). Other shifts may have raised upward mobility. As inequality grew, teen fertility declined (Hamilton and Ventura 2012), potentially boosting mobility by improving the prospects of young women and their children.⁸

Increasing Inequality, Stable Mobility?

Offsetting effects

Inequality’s mobility-depressing and mobility-enhancing effects may counterbalance across different paths linking parents’ and children’s income (e.g., children’s unemployment risk and fertility timing) or along a single path. Along the path through children’s education, offsetting public and private human-capital investments could help explain the stable, or even declining, association between children’s educational attainment and socioeconomic background (Breen 2011; Hout and Janus 2011).

Declining investment returns

Investments in children may generate declining marginal returns, limiting the skills additional income can produce (Downey 1995). If so, greater inequality in parents’ investments in children’s education driven by a rising top tail may not create additional skill inequality.⁹ Moreover, affluent parents provide non-economic resources that equip their children to negotiate middle-class educational and professional organizations (Laureau 2003; Mayer 1997). If income inequality does not influence class-specific cultures and cultural influences are much more important for mobility than economic resources, then inequality and mobility will not be associated.

Common causes

Inequality and mobility may not covary within the United States if inequality has no causal effect on mobility. Common causes of inequality and mobility may drive their negative cross-national association. Features distinguishing varieties of capitalism—including comprehensive publicly funded welfare systems, government-regulated employment security, and institutionalized collective bargaining—shape cross-country inequality trends and likely also mobility (Rueda and Pontusson 2000). These institutional structures vary less within the United States than between nations. If they drive a spurious cross-national inequality-mobility association, this association will not appear here.

In sum, while many worry about inequality’s mobility-depressing potential, null or positive associations are plausible. Resolving this uncertainty requires empirical evidence.

Inequality, Where and When?

Income inequality may shape intergenerational income mobility differently at different geographic levels and life stages. Theory does not identify one optimal geographic grouping or timing; thus, I investigate inequality at four geographic levels and two life stages.

I explore national-level time trends and state, county, and commuting-zone differences. Previous studies examined cross-country variation on the hypothesis that inequality shapes mobility through national-level policies affecting children’s opportunities (e.g., Blanden 2013). I allow for this possibility while focusing on the United States by examining national trends. Other research suggests that inequality may shape mobility within smaller regions, including through the local concentration of affluence and poverty (Wilson 1987). Thus, I also study inequality within counties and commuting zones (for the largest cities, commuting zones correspond to MSAs; they also cover non-metropolitan areas). Yet, I focus primarily on state-level inequality for theoretical and methodological reasons.

Theoretically, state-level measures capture important mechanisms potentially linking inequality and mobility, especially public spending on mobility- enhancing programs. States play major roles in determining healthcare spending on children and poor parents, and until 1996 they set cash assistance levels for the poor. State governments also largely controlled educational policy and spending during my study years. Educational spending varies within states. Yet, between-state variation is much larger than within-state and, as inequality rose, states differed in how they equalized district disparities (Murray, Evans, and Schwab 1998). These decisions were made in state capitals.

Methodologically, states’ shared national context reduces spurious variation present in cross-country analyses. Yet, as stable political jurisdictions, state borders have not changed; county and MSA borders shifted. MSAs’ population share also increased with inequality; studying within-MSA trends entails comparing different subpopulations across time. Further, small-area inequality reflects selection through local migration. If unobserved characteristics driving parents to select school districts or MSAs influence children’s mobility, inequality effect estimates will be biased. State-level inequality suffers far less from this selection bias; families are much less likely to move between than within states to improve children’s prospects (Frey 2009). Thus, I study state-level inequality, but also assess the results’ robustness using national trends and more local differences.

I also study inequality at two life stages, the teen years and early childhood. Inequality during children’s teen years may shape mobility via public education funding or socialization in segregated neighborhoods. Young high-schoolers are starting to make decisions affecting their adult educational attainment, and high college tuition (rising with inequality) may increase educational disparities (Murnane 2013; Bailey and Dynarski 2011). (Studying the teen years also has methodological advantages; see Data and Measures section.) However, other research suggests that early life investments are especially important, setting the stage for children’s future development (Cunha and Heckman 2009). Thus, I study inequality in early childhood and the teen years.

Empirical Methods

Intergenerational income mobility studies typically employ the model

$$ln{Y}_{\mathrm{i}}^{\text{child}}=\mathrm{\alpha }+\mathrm{\beta }\text{ln}{Y}_{\mathrm{i}}^{\text{parent}}+{\mathrm{\epsilon }}_{\mathrm{i}},$$ (1)

where Y is income (adjusted for age and measurement error) and β is the elasticity of children’s income with respect to their parents’ income (e.g., Mayer and Lopoo 2005; Mazumder 2005). An elasticity of 0.5 implies that 10 percent differences between families’ incomes translate into average differences of roughly 5 percent between their children’s incomes. The elasticity (β) measures persistence; its complement (1−β) measures mobility: 1−β represents the fraction children may expect to be closer to the mean than their parents.

To examine the relationship between inequality and mobility, I allow the elasticity to depend on the income inequality children experienced in their states during youth using three models: OLS with interactions, fixed effects, and random effects. Equation 1 assumes a single elasticity, implicitly averaging over heterogeneity in income persistence. To relax this assumption, I first introduce an interaction between parents’ income and state-year inequality. For parent-child pair i living in state s at time t, the model is

$$ln{Y}_{\text{ist}+20}^{\text{child}}=\mathrm{\alpha }+{\mathrm{\gamma }}_{\mathrm{a}}{\text{Gini}}_{\text{st}}+\mathrm{\beta }\text{ln}{Y}_{\text{ist}}^{\text{parent}}+{\mathrm{\gamma }}_{\mathrm{b}}\left(ln{Y}_{\text{ist}}^{\text{parent}}\times {\text{Gini}}_{\text{st}}\right)+{\mathrm{\epsilon }}_{\text{ist}}.$$ (2)

The coefficient γ_b reveals whether the relationship between parents’ and children’s incomes depends on the inequality children experienced while growing up.

Equation 2 pools all variation (across individuals growing up in different states in different years) for parameter estimation. An alternative, fixed-effects specification utilizes variation only within states and years:

$$ln{Y}_{\text{ist}+20}^{\text{child}}=\mathrm{\alpha }+{\mathrm{\gamma }}_{\mathrm{a}}{\text{Gini}}_{\text{st}}+\mathrm{\beta }\text{ln}{Y}_{\text{ist}}^{\text{parent}}+{\mathrm{\gamma }}_{\mathrm{b}}\left(ln{Y}_{\text{ist}}^{\text{parent}}\times {\text{Gini}}_{\text{st}}\right)+{\mathrm{\mu }}_{\mathrm{s}}+{\mathrm{\mu }}_{\mathrm{t}}+{\mathrm{\epsilon }}_{\text{ist}},$$ (3)

where μ_s (μ_t) represent state (year) fixed effects and ε_ist are family-specific errors.¹⁰

Random-effects models compromise between OLS interaction and fixed-effects models by partially pooling variation across contexts:

$$ln{Y}_{\text{ist}+20}^{\text{child}}={\mathrm{\alpha }}_{\text{st}}+{\mathrm{\beta }}_{\text{st}}ln{Y}_{\text{ist}}^{\text{parent}}+{\mathrm{\epsilon }}_{\text{ist}}$$ (4a)

$${\mathrm{\alpha }}_{\text{st}}={\mathrm{\alpha }}_0+{\mathrm{\gamma }}_{\mathrm{a}}{\text{Gini}}_{\text{st}}+{\mathrm{\mu }}_{\text{st}}$$ (4b)

$${\mathrm{\beta }}_{\text{st}}={\mathrm{\beta }}_0+{\mathrm{\gamma }}_{\mathrm{b}}{\text{Gini}}_{\text{st}}+{\mathrm{\nu }}_{\text{st}}.$$ (4c)

The elasticity, β_st, depends on the average slope, the Gini in state s in year t, and a random component ν_st. The relationship between parents’ and children’s incomes varies with both observed and unobserved state-year characteristics. The coefficient of interest is γ_b. The intercept, α_st, also varies across contexts, depending on fixed state-year characteristics and a random state-year deviation, μ_st. The intercept’s and slope’s random components come from a multivariate normal distribution and are allowed to covary.

I present results from OLS and fixed-effects models, but I focus primarily on the random-coefficient models for several reasons. The β_sts are optimal shrinkage estimators, being weighted averages of within- and between-state-year estimators. Borrowing strength across contexts improves the raw state-year estimators (reducing their mean squared error). MSE reductions are valued for the additional information they provide via narrower confidence intervals, compared to wider, less informative intervals. Since Stein (1956) recognized shrinkage estimators’ dominance, researchers have developed random-effects models to study situations where both micro- and macro-level observations play important roles. Moreover, random components coherently account for observations’ clustering within shared contexts in the likelihood function, rather than requiring post-hoc corrections. However, for robustness, I explore many model specifications.

All models described so far exclude covariates beyond parental income and inequality. The elasticities thus capture the full association between parents’ and children’s incomes, and the interactions capture the full association between mobility and inequality. However, I also explore models including covariates, both to increase observations’ comparability and to explain any observed inequality-mobility relationship. I sometimes adjust for family covariates at the individual level and for state covariates at the macro level. Online Appendix A provides covariate information.

Finally, I explore an alternate mobility measure: the intergenerational correlation. In a bivariate regression, the elasticity β = ρ(σ_y^child/σ_y^parent), where ρ is the intergenerational correlation and (σ_y^child/σ_y^parent) is the ratio of the logged incomes’ standard deviations. I sometimes standardize log incomes to mean zero, standard deviation one, equalizing the elasticity and correlation. Standardized measures are preferable if we are interested in the inequality-mobility relationship, abstracting from the sample income dispersions. However, the substantive conclusions do not depend on this choice.

Data and Measures

To study how intergenerational mobility and income inequality covary, I combine parent-child pairs from the Panel Study of Income Dynamics (PSID) with government data on state characteristics. I use the National Longitudinal Survey of Youth 1979 cohort (NLSY79) to replicate the PSID analysis, though survey-design differences require some analytic differences. I also briefly study Internal Revenue Service (IRS) mobility data.

The PSID is the longest-running national survey providing family income data. Beginning in 1968 with approximately 5,000 families, interviews continued annually until 1997, and biannually thereafter. Children and parents were followed, permitting comparisons between individuals’ incomes in childhood and adulthood. I analyze incomes between 1967 and 2006 (survey years 1968–2007) for children born 1954–1974 living in the United States as teenagers during the late 1960s to early 1990s, a period of rising inequality.¹¹ Results cannot be generalized to populations not present in large numbers when the PSID began, including recent immigrants. Initially, the PSID’s core sample was composed of the Survey Research Center (SRC) national sample and the Survey of Economic Opportunity (SEO) low-income oversample. Serious sampling irregularities preclude easy generalization from the SEO to any well-defined population (Brown 1996), so I study the SRC. However, results are unchanged when the SEO sample is included with sampling weights.

Like several recent mobility studies using the PSID, I examine total family income (Chadwick and Solon 2002; Mayer and Lopoo 2005). Many mobility studies compare fathers’ and sons’ labor earnings, but children’s development and adult well-being depend more heavily on their family’s total resources. Family income also improves inferences for single parents’ children and married daughters, whose spouses’ earnings strongly affect their family incomes.¹² Further, family income reduces omitted-variable biases created by ignoring mothers, an important concern as assortative mating rises (Beller 2009).¹³ Family income includes income from labor earnings, assets, and transfers such as AFDC accruing to heads, spouses, and other family members.¹⁴ I adjust for inflation with the CPI-U-RS. I obtain consistent topcodes and eliminate outliers by excluding individuals with incomes in the top or bottom 2 percent within age-gender-year cells (Winship 2009).¹⁵

Since income fluctuates, I average over five years to capture permanent incomes (Mazumder 2005).¹⁶ Because young-adult income is especially unstable, intergenerational elasticities are best measured when children at least 30 (Haider and Solon 2006). I compare individuals’ family incomes when they were 30–34 to their childhood family incomes when they were 13–17. Restricting the ages ensures that cohort differences are not driven by differences in the ages when income is observed. I study income both unadjusted and adjusted for need (using the square root of family size). Adjusting for need helps capture resource availability in children’s origin families. Yet, it mixes children’s adult income measures with their family-size choices. Both adjusted and unadjusted measures are substantively interesting. Table 1 contains descriptive income statistics. Income variance increased across generations and is relatively high in Southern states.

Table 1.

Descriptive Statistics for Parents’ and Children’s Log Family Incomes (2007 dollars) and State Family Income Inequality. PSID, NLSY79 and Census Data

		Northeast	Midwest	West	South	US
PSID
Adult Income, Child Age 30–34
Not Adjusted for Family Size
	Mean	11.14	11.00	11.03	10.82	10.98
	SD	.59	.61	.58	.69	.64
Adjusted for Family Size
	Mean	10.64	10.46	10.51	10.33	10.47
	SD	.60	.62	.59	.68	.64
Parental Income, Child Age 13–17
Not Adjusted for Family Size
	Mean	11.15	11.05	11.14	10.89	11.04
	SD	.51	.50	.47	.59	.53
Adjusted for Family Size
	Mean	10.39	10.31	10.42	10.16	10.30
	SD	.51	.50	.47	.63	.55
State Family Income Gini, Child Age 13–17
	Mean	.360	.351	.366	.388	.366
	SD	.022	.018	.021	.017	.024
N individuals		504	817	376	699	2396
N states		7	12	8	16	43
NLSY79
Adult Income, Child Age 30–49
Not Adjusted for Family Size
	Mean	10.80	10.78	10.72	10.62	10.71
	SD	.90	.83	.83	.81	.84
Adjusted for Family Size
	Mean	10.34	10.30	10.21	10.15	10.23
	SD	.86	.79	.80	.78	.80
Parental Income, Child Age 13–19 in 1979
Not Adjusted for Family Size
	Mean	10.69	10.82	10.67	10.45	10.63
	SD	.69	.62	.63	.72	.69
Adjusted for Family Size
	Mean	9.93	10.06	9.89	9.66	9.86
	SD	.70	.63	.65	.75	.71
State Family Income Gini, Child Age 13–19 in 1979
	Mean	.360	.346	.367	.379	.365
	SD	.014	.008	.010	.013	.018
N individuals		1092	1481	1096	2244	5913
N states		6	11	9	16	42

The PSID is perhaps the most widely used American data set for studying intergenerational mobility. It includes many birth cohorts, enabling exploration of how mobility varies across time and space. Yet, the sample is fairly small. Statistical power may be low, and relatively strong relationships between inequality and mobility may be statistically indistinguishable from zero. I thus complete a parallel study with the NLSY79, using an analytic sample 2.5 times larger than the PSID sample (table 1).

The NLSY79 began with a national sample of over 12,000 youths age 14–22 in 1979. Respondents were reinterviewed annually through 1994, biannually thereafter. I study income between 1978 and 2009 (survey years 1979–2010). Early on, when respondents were young and many lived in their parents’ households, parents reported income. To obtain parental reports without overrepresenting late home-leavers, I exclude those older than 19 in 1979. Since birth year varied little (1960–1965) and state is first observed in 1979, I focus on cross-state differences. The NLSY79 contains a nationally representative sample and oversamples of African Americans, Hispanics, and poor whites. To maximize sample size, I include these oversamples using weights, but I also explore models excluding them.

As in the PSID, I study total family income in the NLSY79, handling inflation, family size, and topcoding as described above. I also focus on multiyear averages, though the included ages differ slightly from the PSID analysis. I measure parental income using the 1979–1983 surveys, averaging all years when parents reported their family income for children age 14–19 in 1979. Because the NLSY79’s cohort design eliminates concern about cross-cohort differences in the ages when adult income is observed, I do not restrict to 30–34 (as in the PSID), but rather maximize the sample size by averaging all available observations age 30 and above. Income variance increased substantially across generations (table 1).

I augment PSID and NLSY79 mobility data with state-level measures of family income inequality. Using state-of-residence indicators, I assign children the inequality level in the state where they lived when they were about 14—around the same time I measure parental income. In the PSID, the calendar year varies across cohorts. In the NLSY79, it is 1979 for all. Measuring inequality simultaneously with parental income not only focuses on developmentally shared income transmission paths. It also maximizes sample size. In the PSID, earlier measurement would eliminate children from less recently born cohorts, whose early state of residence is not observed. However, I also explore inequality earlier in life: in the NLSY79, I use respondents’ state and year of birth (as reported in 1979). In the PSID, I explore respondents’ state of residence at age 14, but in the year when they were 4 (imperfectly capturing age-4 state inequality while analyzing all cohorts).

Decennial Census data provide the most reliable estimates of state inequality due to large samples, even in less populated states. I linearly interpolate family income Gini coefficients for intercensal years by state. For robustness, I also calculate Ginis annually from Current Population Survey (CPS) data (though small state-year samples make these estimates less stable). I also examine 90/50 and 50/10 ratios and top 1 percent income shares, to see if upper- or lower-tail inequality is especially influential. I estimate the ratios from Census and CPS data. Frank (2008) provides top 1 percent shares from IRS records.¹⁷

Finally, I construct additional variables from the PSID, NLSY79, and various government sources to examine how micro- and macro-level forces shape the inequality-mobility association. At the family level, I measure parental age, education, race, marital status, and child’s sex. At the state level, I measure several potential confounders and mediators. Confounders that could drive spurious inequality-mobility associations include percent African American, percent Hispanic, percent foreign born, percent poor, median income, unemployment rate, and region. Including all these measures provides a very conservative test of inequality’s association with mobility, since some reflect endogenous processes (e.g., high inequality may reflect high prevalence of low-wage jobs, which might draw African American or Hispanic workers and increase minority population shares). Consequently, most specifications exclude these covariates; some include them for robustness. State-level mediators that might help explain any observed inequality-mobility relationship include per-capita health spending, per-capita welfare spending, per-child education spending, and residential segregation by income. Online Appendix A describes these measures; tables A2–A3 contain descriptive statistics. Separate literatures examine the relationships between inequality and many of my measured confounders and mediators; I focus not on the relationships between inequality and potential mobility pathways but rather on the reduced-form empirical relationship between inequality and mobility.

Using PSID and NLSY79 data, I study the inequality-mobility nexus using national- and state-level variation. As a robustness check, I also use newly released IRS data to examine mobility by county and Census commuting zone (see Chetty, Hendren, Kline, and Saez 2014). Online Appendix A provides an overview of these data.

Results

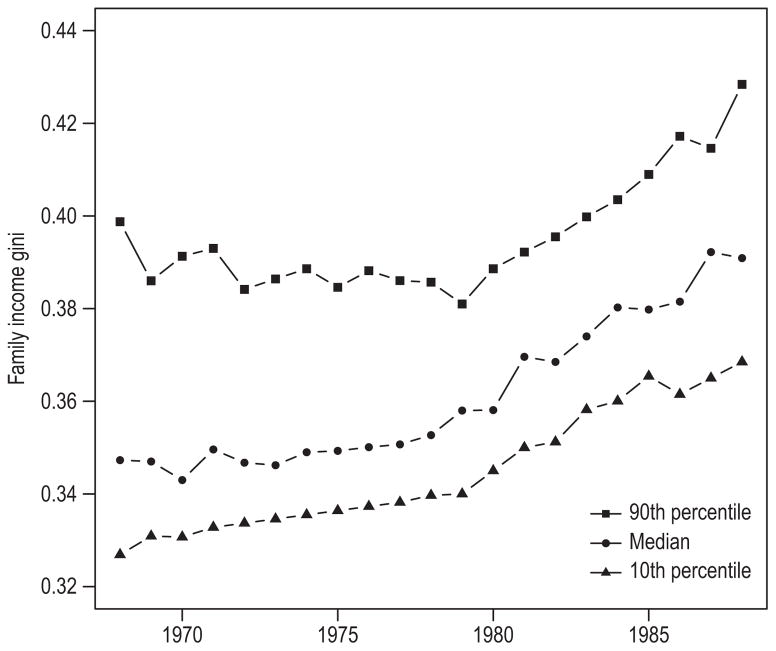
Figure 1 shows a large upward shift in state inequality over time. Members of more recently born cohorts experienced substantially more inequality when growing up than members of earlier-born cohorts. Research has focused on national trends, but states also vary considerably in their inequality levels and trends (see also Online Appendix table A1). Both longitudinal variation across years and cross-sectional variation across states provide useful information for estimating the relationship between inequality and mobility.

Figure 1.

90^th, 50^th, and 10^th Percentiles of the Distribution of Family Income Gini Coefficients Across States, by Year. State-Years Included are those in which PSID Respondents (SRC Birth Cohorts 1954–1974) are Observed in their Teen Years. Census Data

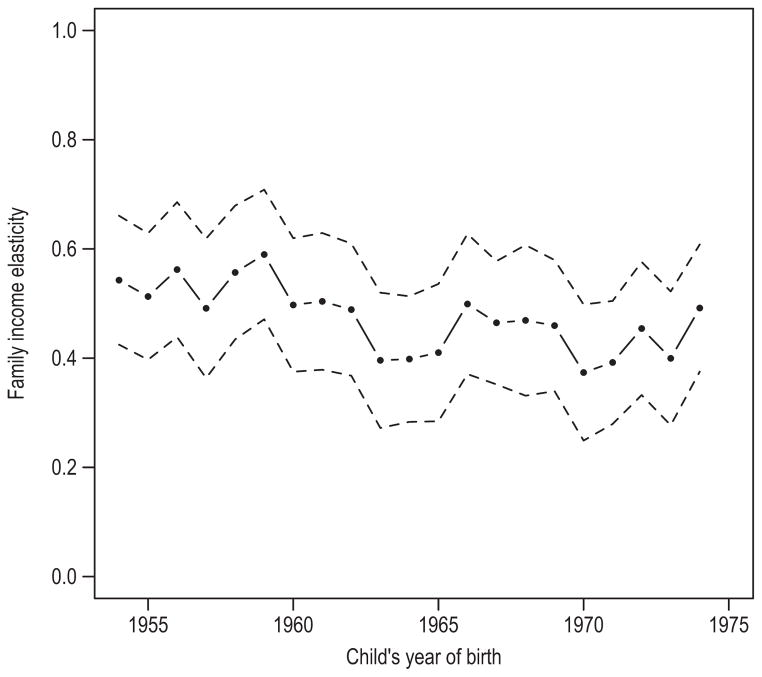
Turning first to national trends, US family income inequality rose monotonically (and dramatically, relative to historical standards) between the late 1960s and the early 1990s, when the PSID children were teenagers. If inequality hampered mobility, we would expect income elasticities to increase across cohorts. Yet, figure 2 shows no consistent trend. Across 20 birth cohorts (with age-30 income in 1984–2004), the elasticities ranged unsystematically between .38 and .59.¹⁸ This finding aligns with previous PSID analyses (Lee and Solon 2009; Hertz 2007). However, these results also improve upon previous PSID-based estimates of national-level mobility trends. My point estimates and Lee and Solon’s (2009) are extremely similar, but by optimally pooling the data using random-coefficient models, mine are more precise. I reduce the width of the estimates’ confidence intervals by more than half, excluding many extreme values (Online Appendix table A4).¹⁹ The data provide no evidence of national mobility trends that align with inequality trends.

Figure 2.

Family Income Mobility by Cohort, Random Coefficient Estimates. Posterior Medians of Cohort Slopes with Pointwise 95% Confidence Intervals. SRC Birth Cohorts 1954–1974, PSID Data

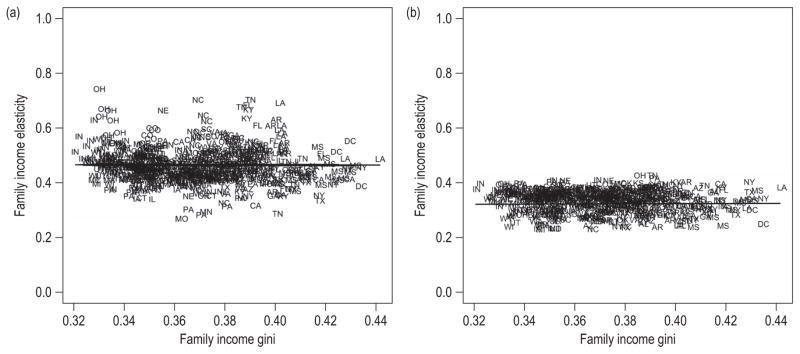
However, national trends obscure important information on the inequality-mobility relationship by averaging over state differences. I improve on previous investigations by examining inequality and mobility by state and year. Figure 3 plots the relationship between state-year family income inequality and state-year family income mobility. Panel A provides elasticity estimates from equation (4), plotting medians from the random coefficients’ posterior distributions. Examining the horizontal spread, Census data reveal significant variation in the Gini across states and years. Examining the vertical spread, PSID data show substantial differences in the intergenerational elasticity. These differences are larger than purely cross-cohort differences, ranging between .27 and .74. Yet, there is no apparent relationship between family income inequality and family income mobility. State-years with higher inequality do not exhibit higher levels of income persistence. However, the state-level estimates shown in figure 3, panel A may be misleading because the PSID was not designed to be representative at the state level. When survey respondents differ demographically from their states’ populations and mobility varies markedly across demographic groups, state-level estimates may be substantially biased.

Figure 3.

Family Income Mobility and Inequality by US State and Year. Standard Random Coefficient Estimates in (a), Random Coefficient Estimates using Multilevel Regression and Poststratification (MRP) in (b). Posterior Medians of State-Year Slopes versus State-Year Inequality. SRC Birth Cohorts 1954–1974, PSID and Census Data

Consequently, figure 3, panel B provides estimates from a technique called multilevel regression with poststratification (MRP) developed to provide subnational estimates from national surveys (Gelman and Little 1997; Park, Gelman, and Bafumi 2006). MRP helps compensate for (1) small within-state sample sizes by leveraging demographic and geographic correlations in the multilevel model (expanding equation (4) so both random intercept and slope vary not only by state-year but also by region and demographic group); and (2) the fact that the PSID sample is representative at the national (not state) level by appropriately weighting (poststratifying) each geographic-demographic respondent group by that group’s share of the true state population (Lax and Phillips 2009). I derive the poststratification weights from Census data.²⁰ Just like the standard random coefficient estimates shown in figure 3, panel A, the MRP estimates shown in panel B reveal that the inequality that children experienced in their state growing up provides no information about the mobility they experienced as adults. The MRP estimates are generally smaller and less variable (because the parent-child income association is partially explained by the demographic characteristics included in the MRP model—including sex, race, and parents’ age, education, and marital status—and additional cross-group pooling pulls outlying estimates toward the grand mean). Yet, both figure 3 panels reveal that the inequality-mobility slope is flat.²¹

But how sensitive are these results to the data, measurement, and modeling choices underlying figure 3? Sensitivity analyses generally focus on protecting against false positives when estimating causal effects (Young 2009; Leamer 1983). Yet, it is also important to guard against false negatives when estimating descriptive correlations. Especially when investigating macro-level questions—where the number of cases is relatively small and sharp designs for estimating causal relationships are seldom available—establishing the credibility of simple associations is crucial for building social-scientific understanding. Likewise, although sensitivity analyses typically focus on model specification (Sala-i-Martin 1997), investigating the fragility of conclusions to data and measurement choices is equally important. Replicating results using new datasets, particularly, provides more validation than testing multiple models on a single dataset (Freedman 1991). Consequently, I next explore different measures, models, and datasets to obtain the best possible descriptions of the relationship between inequality and mobility in the United States.

Tables 2–3 report results from PSID and NLSY79 data. Model 1 reports that the intergenerational income elasticity is .482 in the PSID and .477 in the NLSY79 (tables 2–3, top panels), typical of estimates reported in the literature (Black and Devereux 2011). They can be interpreted as averages over the cohort and state-by-cohort estimates presented above. In the PSID, the estimated elasticity is substantially higher when income is adjusted for family size, at .540 (table 2, bottom panel). Hertz (2007, table 2) also finds this pattern. Yet, adjusting for family size does not substantially alter the NLSY79 elasticity (table 3). The two surveys’ different designs and sampling schemes provide many reasons why the estimates might differ. These differences are not of primary importance here. Rather, the goal is to assess the relationship between inequality and mobility with independent samples, although they represent somewhat different US populations.

Table 2.

Family Income Elasticity-Family Income Gini Models. Gini Standardized to Mean 0, Standard Deviation 1. PSID and Census Data

	OLS			Random Effects				Fixed Effects
	Model 1	Model 2	Model 3	Model 4	Model 5	Model 6	Model 7	Model 8	Model 9
Income Not Adjusted for Family Size
Parental Income	.482 (.022)	.474 (.035)	.199 (.074)	.444 (.023)	.194 (.080)	.446 (.031)	.208 (.086)	.415 (.033)	.244 (.033)
Parental Income × Gini		.052 (.028)	.033 (.058)	.042 (.023)	.035 (.054)	.051 (.026)	.020 (.061)	.029 (.032)	−.003 (.065)
Gini		−.570 (.320)	−.383 (.636)	−.485 (.251)	−.398 (.598)	−.583 (.291)	−.241 (.678)	−.393 (.376)	−.068 (.708)
Intercept	5.664 (.246)	5.748 (.388)	8.826 (.807)	6.070 (.258)	8.878 (.885)	6.056 (.347)	8.734 (.954)	6.284 (.345)	8.475 (.383)
State-year Intercept				✓	✓	✓	✓	✓	✓
State-year Slope						✓	✓
Additional Covariates			✓		✓		✓		✓
AIC	4208.640	4207.059	3564.104	4215.783	3759.139	4217.471	3765.634	4194.975	3613.451
Income Adjusted for Family Size
Parental Income	.540 (.021)	.535 (.033)	.243 (.068)	.507 (.022)	.240 (.075)	.509 (.029)	.249 (.080)	.479 (.034)	.292 (.031)
Parental Income × Gini		.037 (.031)	.019 (.048)	.029 (.022)	.021 (.051)	.032 (.025)	.006 (.057)	.015 (.034)	−.008 (.051)
Gini		−.368 (.323)	−.202 (.485)	−.298 (.222)	−.225 (.529)	−.333 (.263)	−.067 (.592)	−.200 (.366)	.030 (.494)
Intercept	4.902 (.219)	4.958 (.348)	7.993 (.682)	5.243 (.231)	8.014 (.773)	5.228 (.308)	7.926 (.825)	5.483 (.329)	7.506 (.305)
State-year Intercept				✓	✓	✓	✓	✓	✓
State-year Slope						✓	✓
Additional Covariates			✓		✓		✓		✓
AIC	4086.374	4085.556	3394.159	4089.411	4091.043	4092.390	3600.272	4074.602	3448.951
N individuals	2396	2396	2096	2396	2096	2396	2096	2396	2096
N state-years	689	689	621	689	621	689	621	689	621
N states	43	43	41	43	41	43	41	43	41

Note: Standard errors in parentheses (robust, clustered by state and year). All continuous variables except parental and adult income are transformed to mean 0, standard deviation 1. Random effects models fit with restricted maximum likelihood (REML). Because this method is based on error contrasts, AIC can be compared only across REML models with the same fixed components. Additional covariates included in Models 3, 5, 7, and 9 include all state-level variables listed in Online Appendix Table A2, plus interactions between parental income and these state-level variables, plus all individual-level parental covariates listed in Online Appendix Table A2.

Table 3.

Family Income Elasticity-Family Income Gini Models. Gini Standardized to Mean 0, Standard Deviation 1. NLSY79 and Census Data

	OLS			Random Effects				Fixed Effects
	Model 1	Model 2	Model 3	Model 4	Model 5	Model 6	Model 7	Model 8	Model 9
Income Not Adjusted for Family Size
Parental Income	.477 (.018)	.470 (.017)	.255 (.029)	.486 (.015)	.349 (.050)	.473 (.023)	.340 (.056)	.468 (.018)	.233 (.037)
Parental Income × Gini		.006 (.015)	−.004 (.032)	−.025 (.015)	−.070 (.059)	−.026 (.021)	−.058 (.064)	.003 (.018)	−.039 (.034)
Gini		−.095 (.167)	.012 (.362)	.256 (.163)	.719 (.629)	.257 (.225)	.588 (.694)
Intercept	5.701 (.192)	5.777 (.181)	8.084 (.320)	5.548 (.161)	7.160 (.530)	5.682 (.241)	7.258 (.606)	.055 (.006)	.007 (.003)
State Intercept				✓	✓	✓	✓	✓	✓
State Slope						✓	✓
Additional Covariates			✓		✓		✓		✓
AIC	14549.445	14546.833	12374.333	13677.673	11847.162	13671.774	11849.773	14481.324	12325.147
Income Adjusted for Family Size
Parental Income	.472 (.016)	.465 (.013)	.245 (.024)	.485 (.014)	.322 (.046)	.479 (.018)	.316 (.052)	.462 (.014)	.221 (.029)
Parental Income × Gini		.009 (.011)	.042 (.023)	−.020 (.014)	−.012 (.054)	−.021 (.017)	−.002 (.059)	.002 (.013)	.008 (.022)
Gini		−.112 (.114)	−.451 (.252)	.197 (.140)	.107 (.530)	.200 (.171)	.003 (.588)
Intercept	5.622 (.164)	5.688 (.125)	7.844 (.238)	5.458 (.139)	7.131 (.462)	5.514 (.179)	7.199 (.527)	.041 (.004)	.005 (.003)
State Intercept				✓	✓	✓	✓	✓	✓
State Slope						✓	✓
Additional Covariates			✓		✓		✓		✓
AIC	1376.132	13757.161	1170.982	13012.892	11315.400	13012.403	11317.765	13669.153	11653.184
N individuals	5913	5913	5249	5913	5249	5913	5249	5913	5249
N states	42	42	41	42	41	42	41	42	41

Note: Standard errors in parentheses (robust, clustered by state). All continuous variables except parental and adult income are transformed to mean 0, standard deviation 1. Random effects models fit with restricted maximum likelihood (REML). Because this method is based on error contrasts, AIC can be compared only across REML models with the same fixed components. Additional covariates included in Models 3, 5, and 7 include all state-level variables listed in Online Appendix Table A3, plus interactions between parental income and these state-level variables, plus all individual-level parental covariates listed in Online Appendix Table A3. Additional covariates included in Model 9 include all interactions between parental income and state-level variables, plus individual-level parental covariates. Model 9 cannot estimate main effects for the state-level variables due to the state fixed effects (unlike Table 2 Model 9, which uses PSID data and thus includes variation within states over time).

Models 2–9 in tables 2–3 examine how the average income elasticity reported in model 1 varies with income inequality. Models 2–3 are OLS interaction models, models 4–5 are random-intercept models, models 6–7 are random-coefficient models, and models 8–9 are fixed-effects models. Within each specification, the first model (models 2, 4, 6, and 8) allows the income elasticity to vary only with income inequality. The second model (models 3, 5, 7, and 9) also allows it to vary with other macro-level characteristics (e.g., state racial composition) and includes additional individual- and state-level covariates.

As expected, including covariates substantially reduces the estimated elasticities; covariates help explain intergenerational income similarity. Including covariates also often reduces γ_b, the coefficient quantifying how parent-child income elasticities vary with the inequality experienced during youth. Yet, whether or not covariates are included and no matter the model’s error structure, γ_b is quite small and almost always statistically indistinguishable from zero. There is very little evidence of a relationship between the state inequality children experienced growing up and their later economic mobility.

In the PSID, when income is adjusted for family size, the ratio of γ_b to its standard error is between −0.157 and 1.318 (table 2). When income is not adjusted for family size, the ratio is 1.962 in one model specification (model 6). Yet, even in this specification, the magnitude of the relationship is quite small. The magnitude is easy to assess because the Gini is measured in standard-deviation units. (Inference is not sensitive to this standardization.) The elasticity is about .446 in states and years with average inequality and about .497 (.446 + .051) in moderately unequal states and years (inequality one standard deviation above the mean). This difference is smaller than the difference between elasticities estimated with income-adjusted versus unadjusted for family size (model 1).

Using the PSID, I find no systematic variation in mobility across cohorts growing up through a period of rising inequality at the national level. When incorporating information on state inequality levels and trends, I still find no strong link between inequality and mobility. As figure 3 illustrates (displaying table 2, model 6 estimates in panel A and modified MRP estimates in panel B), differences in income inequality cannot explain mobility’s variation across state-year contexts.²²

One limitation of the PSID, however, is its relatively small sample. Consequently, inequality-mobility associations may not be detectable. To address this concern, I turn to the NLSY79, whose sample is about 2.5 times larger. Yet, even with this increased power, there is no evidence of an inequality-mobility association (table 3). Regardless of whether the models are specified with simple interaction terms, random effects, or fixed effects, regardless of whether covariates are included, and regardless of whether income is adjusted for family size, the coefficient of interest γ_b is quite small and statistically indistinguishable from zero.²³ The estimates are also generally smaller than the PSID estimates: their simple average is about −.013 (table 3), versus about .026 (table 2). Combining these NLSY79 findings with the PSID results, the best available data cannot confirm the hypothesis that inequality and mobility are systematically linked in the United States.

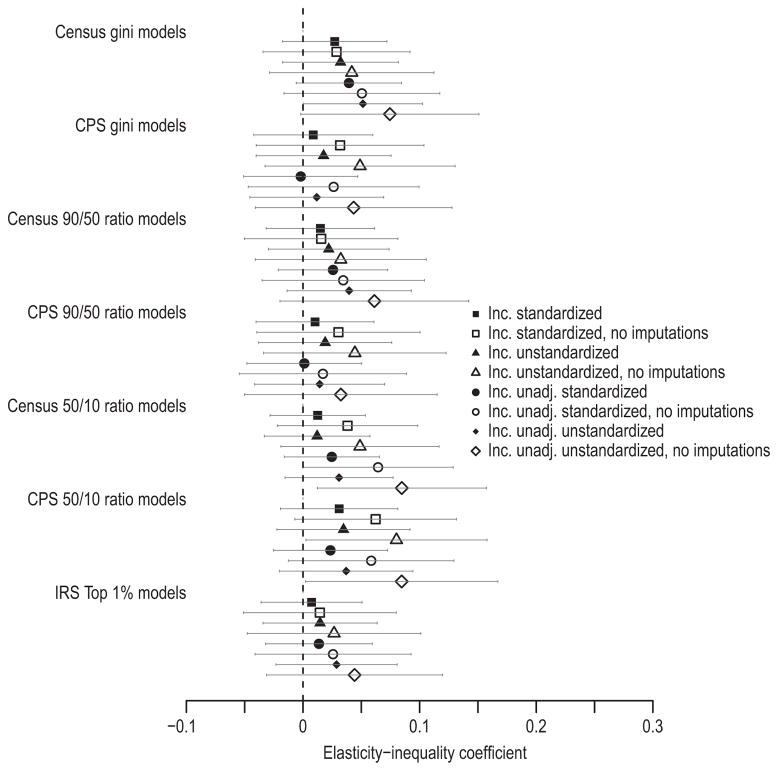
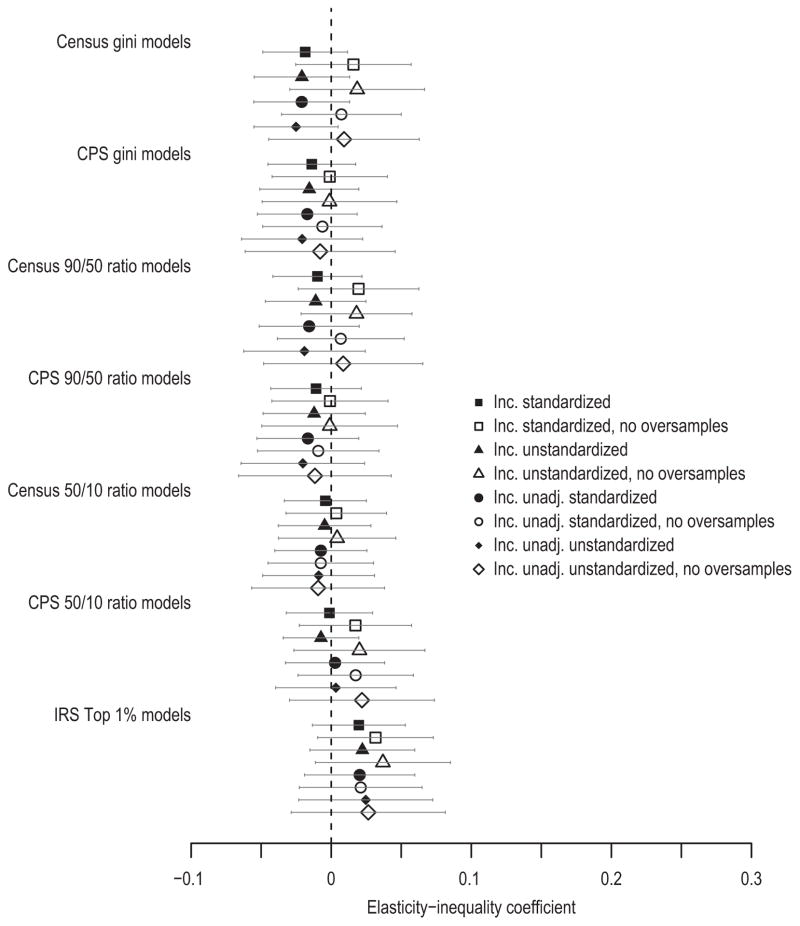
Figures 4–5 investigate whether the dearth of supporting evidence reflects poor measurement.²⁴ Measurement issues are especially important when effect magnitudes are small, due to difficulties separating weak signals from noise. I have measured inequality with the Gini, following cross-national studies (e.g., Corak 2013a). Yet, mobility might vary across US contexts only in response to changes in the upper or lower parts of the income distribution (e.g., see end-note 7). Thus, I reestimate the mobility-inequality relationship using the top 1 percent’s income share and 90/50 and 50/10 percentile ratios. Figures 4–5 also explore different data sources. Particularly in the PSID analysis, the benefits of using inequality estimates derived from large Census samples may be outweighed by the errors introduced by linear interpolation for intercensal years. CPS data provide annual state-specific Gini estimates and 90/50 and 50/10 ratios. (Annual IRS data furnish top 1 percent shares; they are never interpolated.) Finally, figures 4–5 also explore three income measurement decisions: whether to adjust for family size; whether to standardize incomes (to measure intergenerational correlations instead of elasticities); and whether to exclude imputed income components or minority oversamples.

Figure 4.

Measurement Robustness Checks for Mobility-Inequality Relationship. PSID, Census, CPS, and IRS Data. Estimates (with 95% confidence intervals) of Elasticity-Inequality Coefficient from Random Coefficient Models. Models explore (a) Different Inequality Measures, (b) Different Sources of Inequality Data, (c) Different Income Codings (un/standardized, un/adjusted for family size), and (d) Different Subsamples (including/excluding imputed income). All Inequality Measures Standardized (mean 0, sd 1)

Figure 5.

Measurement Robustness Checks for Mobility-Inequality Relationship. NLSY79, Census, CPS, and IRS Data. Estimates (with 95% confidence intervals) of Elasticity-Inequality Coefficient from Random Coefficient Models. Models Explore (a) Different Inequality Measures, (b) Different Sources of Inequality Data, (c) Different Income Codings (un/standardized, un/adjusted for family size), and (d) Different Subsamples (including/excluding minority oversamples). All Inequality Measures Standardized (mean 0, sd 1)

Figures 4–5 suggest that measurement decisions do not drive the null inequality-mobility relationship reported in tables 2–3. These figures display point estimates and 95 percent confidence intervals for γ_b, which quantifies how income mobility varies with a standard-deviation difference in income inequality. Using PSID data, figure 4 shows that only four of 56 models have 95 percent confidence intervals excluding zero (about one more than expected, given a 5 percent false discovery rate). All four use unstandardized income. Point estimates are generally larger when income is unstandardized (as expected, because unstandardized elasticities rise when income inequality in the children’s generation exceeds inequality in the parents’ generation). However, differences between standardized and unstandardized estimates are small; neither provide much evidence of an inequality-mobility association. Estimates are also somewhat larger when imputed income observations are excluded, though inference is identical. No strong patterns emerge across inequality measures. No matter the measures used, the inequality-mobility association is small and rarely statistically distinguishable from zero. NLSY79 results bolster this conclusion. None of figure 5’s 56 estimates are statistically distinguishable from zero. They are also generally smaller in magnitude and more precise than the PSID estimates. The larger sample decreases the confidence intervals’ widths.

Online Appendix figures A1–A2 further confirm that results do not depend on the model’s covariate vector. Tables 2–3 examine the Gini-by-parental-income interaction in two ways: first, conditional on only Gini and parental income main effects, and second, conditional on Gini and parental income main effects plus all other state- and individual-level main effects and interactions. Exploring only these two covariate vectors raises concerns about both under- and overcontrolling.²⁵ However, figures A1–A2 reveal that whatever the model’s covariate vector, there is very little evidence to support the conclusion that income inequality and income mobility are associated in the United States.

The inequality children experienced in their states as teenagers does not predict their income mobility. Neither does inequality earlier in the life course negatively predict mobility. PSID results are similar across table 2 (which explores teen inequality) and Online Appendix table A5 (which explores inequality around age 4). Surprisingly, NLSY79 results suggest that, if anything, children exposed to higher income inequality in their states at birth experience significantly more intergenerational mobility than children from lower-inequality states.²⁶ The γ_bs in Online Appendix table A6 are all negative (suggesting lower elasticities accompany higher inequality); several are statistically distinguishable from zero. In contrast, table 3’s γ_b estimates are smaller, almost never statistically significant, and of mixed sign. Altogether, no strong evidence emerges from the PSID or NLSY79 to confirm that higher inequality is systematically associated with lower mobility in the United States, whether inequality is measured during children’s teen years or much earlier.

Finally, estimates from IRS data suggest that even across smaller geographic areas—comparing counties and Census commuting zones, not states or national trends—income inequality and intergenerational income mobility are not robustly associated. Online Appendix figure A3 shows that when measuring inequality by the top 1 percent’s income share, the slope of the inequality-mobility line is flat. Children from high upper-tail inequality areas appear no more or less mobile than children from low upper-tail inequality areas.²⁷ When measuring inequality by the Gini or the Gini of the parents with incomes in the bottom 99 percent, there is a slight positive association between inequality and intergenerational income persistence. Yet, once each area is weighted by the number of children hailing from that location, the inequality-mobility slope appears flat again. (Weighting allows us to make statements about the population of children—rather than the population of counties/commuting zones—and is statistically efficient.) These patterns hold across both counties and commuting zones, confirming earlier national- and state-based results suggesting little robust association between inequality and mobility in the United States.

Examining directional mobility relative to parents’ economic position further suggests a null inequality-mobility relationship. Different social processes may be operating if a null relationship is driven by offsetting directional trends than if neither upward nor downward moves relative to parents’ income rank increase with inequality. Yet, PSID and NLSY79 data provide little evidence that offsetting directional trends generated the null inequality-mobility relationship. I do not find inequality-mobility associations when I study mobility between income quintiles.²⁸ Moreover, if offsetting directional trends were important, we would expect different inequality-mobility associations for different groups (e.g., race or class groups). I find no evidence that inequality associations differed across demographic subgroups, though my estimates are imprecise. (Results are available upon request.) It is possible that nonlinearities in mobility that vary with inequality are present at the extreme tails of the distribution, but could not be detected due to sparsity of cases among the very poor or wealthy. Future research might use larger data sets or alternate statistical techniques to address this possibility.

Conclusions

As family income inequality rose, parental resources available for children’s development diverged. These shifts renewed interest in intergenerational mobility among scholars and policymakers. Many speculated that high inequality would undermine economic mobility. This paper investigates the relationship between family income inequality and intergenerational income persistence in the contemporary United States. It provides the first systematic analysis of how inequality and mobility covary across contexts within the United States, exploiting variation across cohorts, across states, and within states over time.

Combining PSID data with information on state characteristics, I find little evidence that individuals’ economic mobility depends on the income inequality they experienced growing up. Over 20 years when inequality rose continuously, the intergenerational income elasticity showed no consistent trend. My national trend estimates improve upon previous estimates by shrinking the confidence intervals and excluding previously plausible trend values. I also provide the first evidence that within-state inequality trends do not predict within-state mobility trends. Neither do between-state inequality differences predict mobility, a result confirmed by NLSY79 data. IRS data further suggest that no robust inequality-mobility association exists across counties or commuting zones.

The null inequality-mobility association across political jurisdictions within the United States appears to conflict with the negative association across larger political units documented in cross-national studies (Corak 2013a; Björklund and Jäntti 2009; Andrews and Leigh 2009). One explanation of this difference highlights that inequality varies more between countries than within. Perhaps if some US states were as equal as Denmark, we would observe a relationship. Yet, even restricting comparisons to countries with inequality in the range observed within the United States, cross-country analyses reveal a substantial inequality-mobility association. A second explanation suggests that cross-country inequality differences are more long-standing and, therefore, the consequences are more institutionalized. Perhaps the mobility consequences of recent inequality trends will not be evident until institutional responses have more time to take effect. However, cross-state inequality differences are long-standing. Nunn (2008, 170) reports a strong relationship between state-level Gini coefficients of land inequality in 1860 and Gini coefficients of income inequality in 2000. Nevertheless, there is little evidence for a relationship between state-level inequality and mobility in the contemporary United States. Consequently, perhaps the best explanation for why the cross-country inequality-mobility association is not replicated within the United States is that the forces driving the cross-county association may not apply within this country.

Heterogeneity in the roles of the family, state, and market may induce different relationships between inequality and mobility in different countries. Likewise, research on educational spending and mobility suggests that the United States’ unique institutional arrangements prevent cross-country relationships from manifesting here. Blanden (2013) reports a strong, negative cross-country correlation between education spending and father-son elasticities; mobility appears to rise with educational investments. However, Grawe (2010) finds that US states with lower student-teacher ratios have lower earnings mobility, and Mulligan (1999) finds no significant relationship between state student-teacher ratios or per-student education spending and earnings mobility. Research using within-US comparisons suggests that the cross-national education spending-mobility association may not apply here. Similarly, this paper suggests that the cross-national relationship between inequality and mobility may not extend to the US context.

My results provide very little support for the hypothesis that income inequality between families shapes income mobility across generations in the United States. Yet, the nature of scientific inference does not permit the conclusion that there is absolutely no relationship. The imprecision of the PSID estimates cannot rule out a modest relationship.

I increase precision in three ways. First, I more fully exploit variation in inequality and mobility to gain power (looking across states and years, unlike previous studies). Second, I use random-coefficient models to optimally pool information from different contexts and reduce mean squared error (though other models generate similar conclusions). Third, I combine PSID with NLSY79 and IRS data, which offer larger samples (including over 9.8 million children in the IRS microdata underlying county/commuting-zone statistics). These approaches reduce our uncertainty about how US inequality and mobility associate.

Across hundreds of models, several produce inequality-mobility associations that are statistically distinguishable from zero. Yet, results are fragile. Inferential decisions are easily reversed by changing error specifications, covariate vectors, or family-size adjustments. Readers must be firmly convinced of a specific generative model’s accuracy to conclude that these data provide strong evidence that mobility depends negatively on inequality. The data cannot reject the possibility that mobility is relatively low for individuals who grew up where inequality was relatively high, nor that mobility is relatively high. Yet, if there is a non-zero association between US inequality and mobility that the best available data cannot detect, its strength is likely quite modest.

The lack of association between inequality and mobility may derive from countervailing trends in the family, state, and market forces shaping income persistence. For example, parents’ unequal private investments in their children’s education could be counterbalanced by the state’s redistributive public investments in children’s human capital. Offsetting effects are especially likely if inequality’s influence on mobility is relatively weak. Forces affecting income persistence may respond to changing inequality slowly, or not at all (e.g., genetic resemblance, parenting traditions, or state policies that progress through legislatures at unpredictable rates). Even along “susceptible” paths, inequality’s effects may be weak compared with other family or environmental characteristics. Larger inequality changes may be required to generate significant effects. The inequality variation studied here is substantial by historical standards; it covers a period of rapid increase, and differences across states were just as large. Nevertheless, the “treatment dosage” may be too weak to generate marginal effects. But, perhaps more plausibly, we may not observe a robust inequality-mobility association because income inequality per se is not a treatment that directly affects mobility, and the indirect pathways or common causes of inequality and mobility may have changed insufficiently or in offsetting ways.

Countervailing trends mean that studies of how inequality affects one path linking parents’ and children’s incomes can generate misleading intuitions about the overall inequality-mobility relationship. Nevertheless, focused studies help provide information about opportunity, as distinct from mobility. The data studied here reflect the distribution of economic outcomes, not opportunities. They suggest no net association between inequality and mobility in the contemporary United States. Nevertheless, we might be concerned if, for example, rising inequality reduced low-income children’s ability to complete college, even if this effect were counterbalanced by inequality’s incentive effects boosting college entrance rates by convincing more people to try to earn a BA. From an opportunity perspective, the obstacles people face matter. Yet, investigations of single pathways linking parents’ and children’s incomes will continue to benefit from studies, like this one, that capture net effects and contextualize many mechanisms within a broader system.

This analysis finds little evidence of a systematic connection between family income inequality and intergenerational income mobility in the United States. Of course, results may not apply to children growing up during the most recent period of persistently high inequality, particularly in the extreme upper tail. We will see in 5–15 years, when these children’s and parents’ incomes can be fruitfully compared (though the 1980–1982 birth cohorts’ experiences, documented with IRS data, suggest that the null inequality-mobility association may persist). Future research might also explore how other dimensions of intergenerational stratification vary with inequality. Inequality may affect wealth mobility or occupational mobility even if it does not shape income mobility, since the mechanisms linking parents’ and children’s incomes differ from those linking their net worth or careers. Moving beyond inequality, future research might explore what state- or local-level characteristics strongly shape children’s mobility chances; further study of some of the mediators identified here, such as social spending or residential segregation, would be useful. Yet, currently available data provide reason to question the rhetoric linking US income inequality and income mobility. Inequality may not reproduce itself by tying children more closely to their parents’ positions on the economic ladder. At the same time, there is little evidence to suggest that rising mobility accompanies rising inequality; as the distance between rungs on the economic ladder grows, movement between rungs may not get harder, but it also does not get easier. Thus, the economic consequences of growing up rich or poor have risen, simply because the distance between rich and poor has increased.

Biography

Deirdre Bloome is an Assistant Professor in the Department of Sociology and a Faculty Associate of the Population Studies Center and the Survey Research Center at the University of Michigan, Ann Arbor. Her research interests include economic and racial stratification, social mobility, family demography, social policy, and statistical methodology.