Skip to main content
PMC home page
Nature Portfolio logoLink to Nature Portfolio
. 2015 Sep 1;6:8180. doi: 10.1038/ncomms9180

Observation of intervalley quantum interference in epitaxial monolayer tungsten diselenide

Hongjun Liu 1, Jinglei Chen 1, Hongyi Yu 1,2, Fang Yang 3, Lu Jiao 1, Gui-Bin Liu 4, Wingking Ho 1, Chunlei Gao 3,5, Jinfeng Jia 3,5, Wang Yao 1,2, Maohai Xie 1,a
PMCID: PMC4569794  PMID: 26324205

Abstract

The extraordinary electronic structures of monolayer transition metal dichalcogenides, such as the spin–valley-coupled band edges, have sparked great interest for potential spintronic and valleytronic applications based on these two-dimensional materials. In this work, we report the experimental observation of quasi-particle interference patterns in monolayer WSe2 using low-temperature scanning tunnelling spectroscopy. We observe intervalley quantum interference involving the Q valleys in the conduction band due to spin-conserving scattering processes, while spin-flipping intervalley scattering is absent. Our results establish unequivocally the presence of spin–valley coupling and affirm the large spin splitting at the Q valleys. Importantly, the inefficient spin-flipping scattering implies long valley and spin lifetime in monolayer WSe2, which is a key figure of merit for valley-spintronic applications.

Inline graphicMonolayers of transition metal dichalcogenides have many of the properties required for applications in spintronics and valleytronics. Here, the authors experimentally observe intervalley quantum interference involving conduction band Q-valleys in tungsten diselenide.

Monolayer (ML) transition metal dichalcogenides (TMDs) are attracting great research interests for their extraordinary properties, in particular the exotic spin–valley-coupled electronic structures that promise future spintronic and valleytronic applications1,2,3. The energy bands of ML TMDs have well-separated valleys that constitute effectively an extra internal degree of freedom for low-energy carriers. Besides the well-studied K valleys3,4,5,6,7,8,9,10,11,12, the conduction band also has six Q valleys located approximately midway between the Γ and K points of the first Brillouin zone (BZ), where interesting valley physics is also discovered3,11,12. The large spin–orbit coupling in the TMDs makes the spin index locked to the valley index for low-energy carriers, which has some interesting consequences such as the magnetoelectric effects in 2H bilayers13. Direct experimental characterizations of the spin–valley-coupled electronic structures are of great interests for both fundamental physics and device applications.

Scanning tunnelling microscopy/spectroscopy (STM/S) is a known powerful method for probing electronic structures of thin films and its studies have already been implemented to extract the quasi-particle band gaps and band edges in ML TMDs14,15,16,17,18. Quantum quasi-particle interference (QPI) has been studied by STM/S for metals19,20, topological insulators21,22 and graphene23. A defect elastically scatters electrons from wave vector ki to kf on the constant energy contour (CEC), and quantum interference of the incoming and scattered waves form standing waves of wave vector q=kf−ki that are detected by low-temperature STS mapping. For multi-valley bands such as that in graphene and ML TMDs, the scattering by a point defect can give rise to rich QPI patterns arising from quantum interference within a valley as well as between well-separated inequivalent valleys. Fourier transform of the STS maps (FT-STS) can then directly reveal the valley locations and the band dispersion relations24,25, for example.

Here we report the experimental observation of the QPI pattern of electrons in ML WSe2 using a low-temperature STS. We observe intervalley quantum interference involving the Q valleys due to spin-conserving scattering processes, while spin-flipping intervalley scattering is absent. Our experiment establishes unequivocally the presence of spin–valley coupling and affirms the large spin splitting at the Q valleys. Importantly, the inefficient spin-flipping intervalley scattering implies long valley and spin lifetime in ML WSe2, which represents a key figure of merit for valley-spintronic applications.

Results

STM/S of MBE-grown WSe2

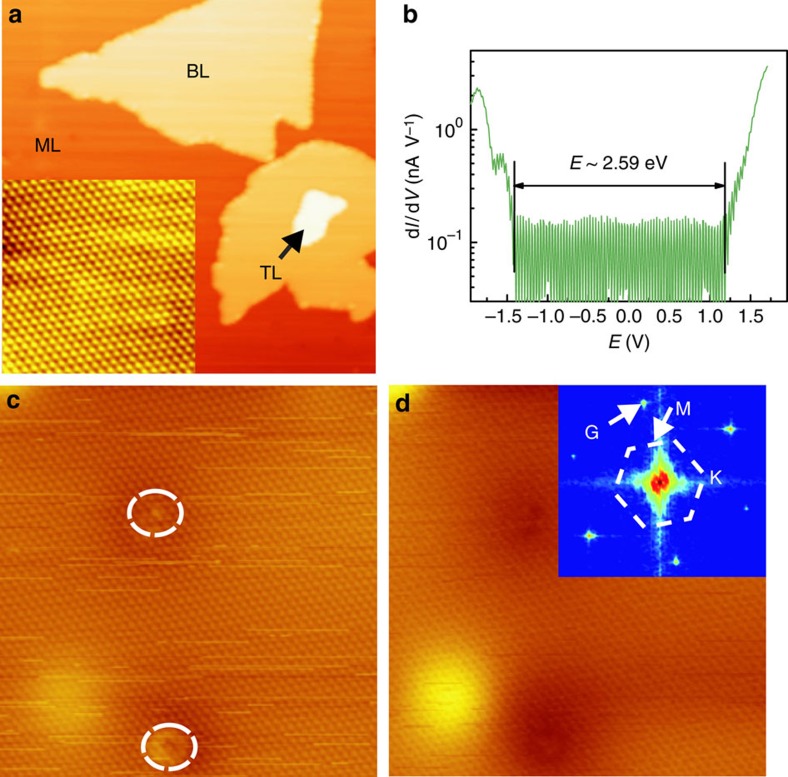
Figure 1a shows a topographic image of an as-grown WSe2 sample. It reveals a characteristic terrace-and-step morphology of an atomically flat film (refer to Supplementary Figure 1 for the reflection high-energy electron diffraction (RHEED) patterns). The sample of Fig. 1a has the nominal coverage of 1.2 MLs, so in addition to the ML film over large surface areas, there are also bilayer and even trilayer high islands. Comparing with the molecular-beam epitaxy (MBE)-grown MoSe2 films18, the most striking feature in Fig. 1a is the absence of inversion domain boundary network commonly seen in epitaxial MoSe2. This has given us an opportunity to study the quantum interference effect in ultrathin WSe2 by STM/S, thereby allows probing the electronic structure as well as the spin splitting in ML TMDs. The inset in Fig. 1a is a close-up atomic resolution image of the ML region of the sample. Fig. 1b shows the differential conductance spectrum measured at a fix point on ML WSe2 by STS at 77 K. It reveals an energy gap of 2.59±0.07 eV, in agreement with the previous report16. The Fermi level is found slightly above the mid-gap energy, suggesting the sample is slightly electron doped, likely by some native defects such as Se vacancy.

Figure 1. STM/S of MBE-grown WSe2.

Figure 1

Open in a new tab

(a) STM topographic image (size: 75 × 75 nm2, sample bias: 2.4 V) of a MBE-grown WSe2 sample on highly ordered pyrolytic graphite with the nominal coverage of 1.2 MLs, revealing dominantly ML WSe2, bilayer (BL) and trilayer (TL) islands. Inset: an atomic resolution image (size: 7.5 × 7.5 nm2, sample bias: −1.5 V) of ML WSe2. (b) STS spectrum (averaged over 50 scans) taken at a fixed position on a defect-free ML WSe2, revealing an energy gap of 2.59 eV. (c) Topographic STM image and (d) STS map of ML WSe2 measured simultaneously at −1.5 eV (size: 14 × 14 nm2). The white dashed circles in (c) mark two point defects, which show darker contrast in (d). The inset in (d) is the FT-STS map showing the reciprocal lattice (the points labelled by G). The first Brillouin zone (the white dashed hexagon) and its high symmetry points (K and M) are also shown for reference.

QPI in the valance band

To search for the QPI in ML WSe2, we first locate a surface area that contains point defects. An example is given in Fig. 1c, which shows two point defects in the field of view. In this region of the surface, quantum interference stands high chance to be observed by low-temperature STM/S. We began our search of the QPI by taking the STS maps at energies close to the valence band maximum (≤−1.4 eV). Figure 1d shows one of the STS maps obtained and the inset presents the power spectrum through Fourier transform. For all the STS maps taken in the energy range of −1.4 to −1.5 eV, including Fig. 1d, no sign of intervalley QPI is seen and the FT-STS only reveal the reciprocal lattice vectors (G) of WSe2. The latter has, nevertheless, allowed one to determine the Brillouin zone as marked by the white dashed hexagon in the figure.

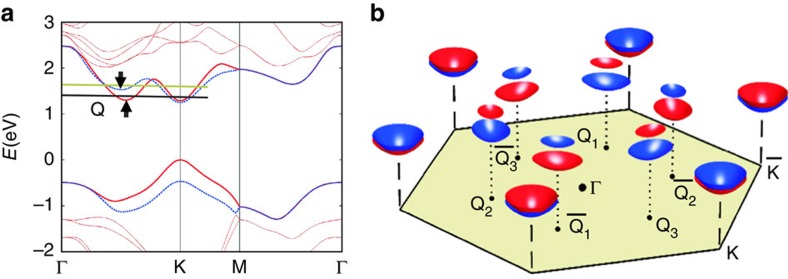
The absence of intervalley QPI in the valence band implies that spin-flipping scattering between K and 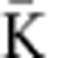Inline graphic valleys is inefficient. In ML WSe2, the ultra-strong spin–orbit coupling in the 5d orbitals of the metal atoms give rise to large spin splitting in both the conduction and valence bands, which are dictated by the mirror symmetry and time-reversal symmetry to be in the opposite out-of-plane directions at a time-reversal pair of either K or Q valleys3. In Fig. 2a, we show electronic bands of ML WSe2 calculated by the density functional theory (DFT), in which the red solid and dotted blue lines represent the spin-split bands due to spin–orbit coupling. The valence band edge at the K points has a large spin splitting17,26 with opposite signs at K and 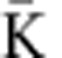Inline graphic as required by the time-reversal symmetry3,27. Consequently, QPI between K and 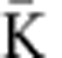Inline graphic valleys will be prohibited by the time-reversal symmetry if the scattering defects are non-magnetic. Furthermore, a recent study has shown that STM/S is not very sensitive to the K-valley states as compared with the Γ and Q valleys17, which may be another cause for the absence of the QPI in STS near the valence band maximum.

Figure 2. K and Q valleys in ML WSe2.

Figure 2

Open in a new tab

(a) Electronic bands of ML WSe2 calculated by DFT. In the bottom conduction and top valence bands, the spin-down and -up subbands are denoted by red and blue colour, respectively. The vertical arrows point to the minima of the spin-split bands at Q valley. The two horizontal lines mark the energies at which the constant energy contour maps in Figs 3d and 4c are obtained. (b) Schematic illustration of the spin–valley-coupled conduction-band edges, where the blue and red colours denote the spin-up and spin-down bands, respectively.

QPI of conduction-band electrons

Conduction band electron has a completely different story. The spin splitting is much smaller at the K-point (∼0.03 eV), and the largest spin split of ∼0.2 eV occurs in the Q valley (cf. Fig. 2a). The energy minimum at Q is close to that at K for ML WSe2 (refs 3, 11, 17, 28, 29, 30, 31). Besides, Q valley can have a much larger weight in STM/S measurements than the K valley due to the larger density of states (DOS) as well as a larger tunnelling coefficient. Therefore, the Q valleys are expected to play a significant role in the STS mapping of the empty states. As illustrated in Fig. 2b, the six-fold degenerate Q valleys form two groups. 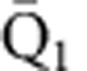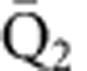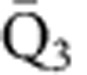Q1, Q2 and Q3 have the same spin and Inline graphic, Inline graphic and Inline graphic are their time reversals. QPIs by the spin-conserving intervalley scattering are possible within each group. In addition, as the spin splitting is small at K while the energy difference between Q and K is also small, QPIs by the spin-conserving scatterings between K and 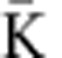Inline graphic, and between Q and K valleys may also occur (cf. Fig. 3d).

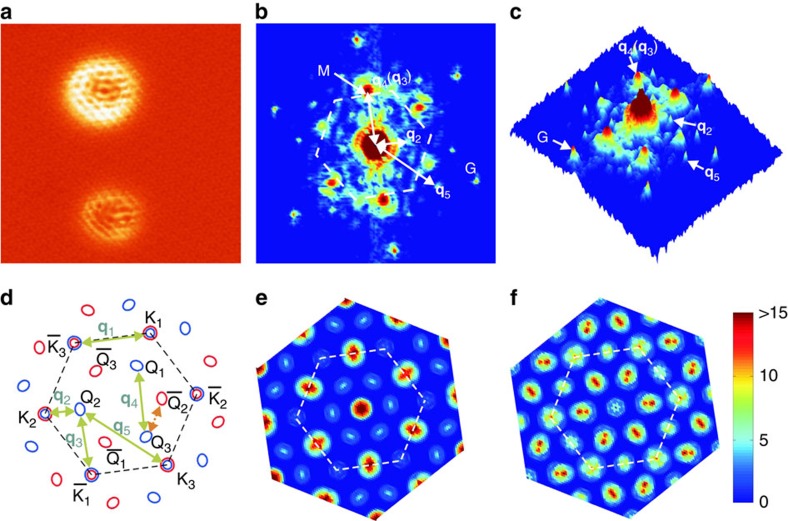
Figure 3. Intervalley quantum interference at defects.

Figure 3

Open in a new tab

(a) STS map of ML WSe2 at +1.0 eV of the same surface as in Fig. 1c, showing QPI patterns in the vicinity of the two point defects. (b,c) The FT-STS map in (a) presented in the top and perspective views, respectively. The white dashed hexagon in (b) shows the first Brillouin zone . The observed scattering wave vectors (qis) are exemplified by arrowed solid white lines in (b) and pointed in (c). The central ring-like feature as highlighted by the yellow dotted circle in (b) may reflect the intravalley scattering. (d) Constant energy contour at the energy marked by the black horizontal line in Fig. 2a. The blue (red) colour denotes the up (down) spin states. The solid green arrows indicate five possible spin-conserving scattering channels with the resulting interference wave vectors qi. The dashed orange arrow indicates a spin-flipping scattering channel. (e,f) Calculated joint density of states for, respectively, spin-conserving and spin-flipping scatterings at the same energy as in (d).

Figure 3a presents an example of the STS maps obtained over the same surface area as in Fig. 1c but at an energy of E=+1.0 eV. Unlike the filled-state STS map of Fig. 1d, the empty-state image reveals clearly the QPI patterns in the vicinity of the two defects. Figure 3b,c show the corresponding FT-STS maps presented in the top and perspective views, respectively, from which one notes distinct intensity spots besides the reciprocal lattice (G), signifying the various scattering channels and the corresponding standing wave vectors q as labelled. To identify the relevant scattering processes, we show in Fig. 3d a CEC map derived from the DFT calculations. This CEC map corresponds to an energy that is slightly above the conduction-band minimum (that is, the black horizontal line in Fig. 2a), where the spin texture of the Q valley is clearly resolved. For the K valley, on the other hand, both spin-up and spin-down bands are present with a small difference on the CEC. On the basis of this CEC, we may identify a number of possible spin-conserving intervalley scatterings as indicated by the green arrows. A spin-flipping inter-Q valley scattering is also marked by a dotted orange line. By comparing with the experimental data, we may assign the strongest scattering with the wave vector close to the M point of the Brillouin zone (that is, the middle point on the edge of the dashed white hexagon) is of the spin-conserving inter-Q valley scattering, that is, q4 in Fig. 3d.

A possible complication, however, is the presence of scattering between Q and K valleys, which would result in a wave vector (q3 in Fig. 3d) that is very similar to q4. With the resolution of the experimental data, we cannot discriminate one from the other, and indeed both could occur. Nevertheless, according to the band structure calculations3,11,17,28,29, the Q valley is situated slightly off the midpoint of Γ–K and closer to K (see Fig. 2a), so q4 would be slightly larger than 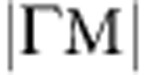Inline graphic, which appears consistent with the experimental data. Moreover, as mentioned earlier, the STM/S measurement should be more sensitive to Q states than the K states, therefore the Q–Q QPI has a larger chance to be picked up in the STM/S images compared with the Q–K one. We therefore believe that Q–Q scattering 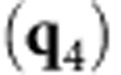Inline graphic is the dominating contributor to the experimentally observed spot next to M in Fig. 3b,c.

With the presence of both spin-up and -down subbands at K valleys and the six-fold degenerate Q valleys on the CEC, Q–K QPI at another two wave vectors, q2 and q5, and 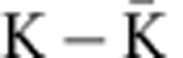Inline graphic QPI at wave vector q1 are also possible through the spin-conserving scattering (cf. Fig. 3d). Though weak, intensity spots are indeed observed at q2 and q5 as shown in Fig. 3b,c. Intensity spot at wave vector q1 may not be discernable in Fig. 3b or c, which may again be attributed to the sensitivity of STM/S to K-valley electrons. However, we did observe hint of such scatterings at some other energies (Supplementary Fig. 2).

JDOS maps

We have performed calculations of the joint density of states (JDOS), 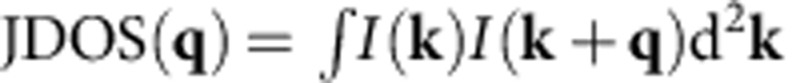Inline graphic, where I(k) represents the DOS derived from the DFT calculated energy bands. Figure 3e,f shows two JDOS maps at the energy of Fig. 3d but for spin-conserving and spin-flipping scatterings, respectively. For comparison and completeness, Fig. 4 presents another CEC map (4c) and the corresponding JDOS (4d and 4e for the spin-conserving and spin-flipping scatterings, respectively) for a higher energy (the green line in Fig. 2a) and compared with an experimental FT-STS obtained at 1.2 eV (4a and 4b for the top and perspective view, respectively).

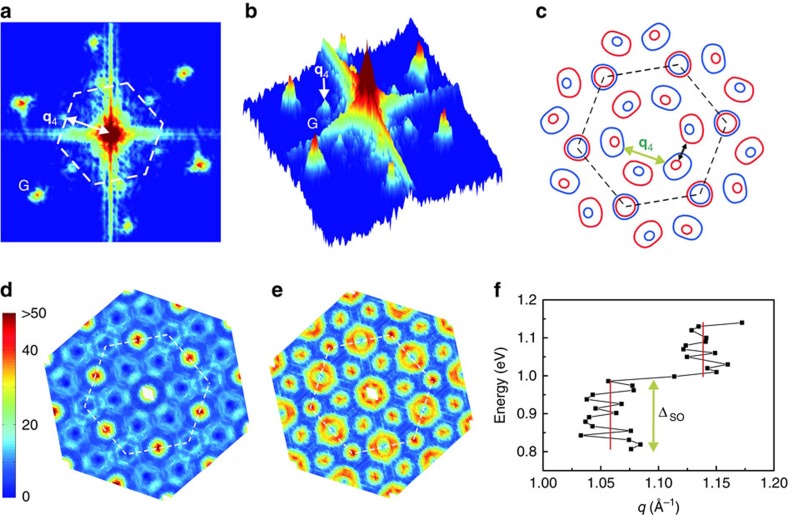
Figure 4. Energy dependence of the quantum interference pattern.

Figure 4

Open in a new tab

(a,b) FT-STS map of the surface as in Fig. 3 but measured at energy +1.2 eV and presented in the top and perspective views, respectively. (c) Constant energy contour at an energy marked by the horizontal green line in Fig. 2a, where the blue (red) line denotes the up (down) spin states. The solid green arrow indicates a spin-conserving Qi−Qj scattering channel. The black arrow indicates a spin-conserving 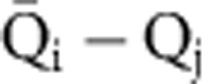Inline graphic intervalley scattering channel, as both spin-up and -down subbands at Q valleys are relevant at this higher energy. (d,e) The joint density of state maps calculated for, respectively, spin-conserving and spin-flipping scatterings at same the energy as in (c). (f) Experimentally derived wave vectors (q4) from the FT-STS maps at different energies (from 0.7 to 1.2 eV), revealing two branches as highlighted by the solid red lines. The vertical green arrow indicates the magnitude of spin splitting at Q.

Discussion

Comparing the JDOS maps with experimental FT-STS, it is clear that the spin-conserving scattering captures well the experimental results, elucidating the non-magnetic nature of the defect. Should spin-flipping scattering processes be efficient, one would expect different FT-STS (that is, Figs 3f and 4e). Our experiment therefore affirms the spin-conserving scattering processes are much more efficient than the spin-flipping ones in ML WSe2. Together with the absence of inter-K valley scattering in the valence band as described earlier, it implies long valley lifetime, promising valleytronics applications based on valley polarization of the Q-valley electrons and K-valley holes.

The agreement between Fig. 3b,e also evidences the large spin splitting at Q in ML WSe2, as otherwise spin-conserving 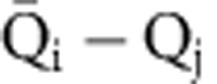Inline graphic scattering channels would be present over most of the energy range, contradicting to the experiment. By examining the STS maps obtained at different energies, we derive an energy dependence of the 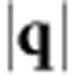Inline graphic's (peak-to-peak distances in FT-STS maps). Figure 4f summarizes the data for the wave vector q4. There are apparently two branches, corresponding to 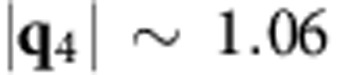Inline graphic Å−1 and 1.14 Å−1, respectively. According to the first-principle band structure, the exterma of the upper and lower spin subbands at the Q valley show a relative shift in momentum (as indicated by two short vertical arrows in Fig. 2a). Therefore, we are tempted to attribute the two branches in Fig. 4f to be scatterings dominantly in the lower and upper spin subbands, respectively. If this is indeed the case, we may further estimate the magnitude of the spin-split ΔSO at Q, which is about 0.2 eV. This is an appreciable spin splitting as pointed out above, which compares well with the first-principle calculation estimations11. We, however, note a discrepancy between theory and the experiment, where most first-principle calculations suggest the upper spin subband at Q has a smaller momentum than the lower one, which is opposite to the finding of Fig. 4f. Besides, the experimental data can have contributions of the other scattering channels (for example, the Q–K scattering q3). Hence the two momentum branches observed in Fig. 4f may reflect a change of dominance of the different scattering processes when the energy is changed. Further studies by higher-resolution STM/S may resolve this ambiguity.

Finally, we would like to draw attention of the seemingly ring feature in the FT-STS map at the centre (see Fig. 3b,c). It may reflect intravalley scattering of electrons. Unfortunately, because of long wavelength (and thus small q), the ring feature cannot be separated well from the central bright spot often affected by the random noise of the STS maps. So we have not been able to derive the dispersion relation of the Q valley in this experiment.

It should also be noted that, during the review of this article, a study on exfoliated WSe2 with similar results for intervalley scattering was reported32.

Methods

Film growth

Ultrathin WSe2 films were grown on freshly cleaved highly ordered pyrolytic graphite in a customized Omicron MBE reactor with the base pressure of 10−10 mbar. Elemental Tungsten (W) of purity of 99.99% and Selenium (Se) of 99.999% in purity were used as the sources, and their fluxes were generated from an e-beam evaporator and a dual-filament Knudsen cell, respectively. A flux ratio of 1:15 between W and Se was used. The substrate temperature during film deposition was ∼400 °C and the deposition rate was 0.5 MLs per h. During growth, the film surface was monitored in situ by the RHEED operated at 10 KeV, which showed streaky patterns signifying two-dimensional layer-by-layer growth mode of WSe2 on highly ordered pyrolytic graphite. After a preset coverage of the deposit was grown, the source fluxes were cutoff by mechanical shutters. The film was subsequently annealed at ∼500 °C for 1 h before being brought to room temperature by natural cooling on shutting off the power to the sample manipulator.

STM measurement

Room-temperature STM measurements were performed in situ using an Omicron VT-STM system while the low-temperature STM measurements were carried out at 77 K in a Unisoku low-temperature STM system ex situ. For the latter, the sample surface was protected by an amorphous Se layer deposited at room temperature until the RHEED pattern became featureless but a diffusive background. After transferred to the Unisoku low-temperature STM system, the sample was gently annealed at 300 °C until the streaky RHEED patterns reappeared and the same flat surface morphology recovered according to STM examinations. For both room-temperature and low-temperature STM measurements, the constant current mode was used. For STS measurements, the lock-in technique was employed using a modulation voltage of 15 mV and frequency of 985 Hz.

DFT and JDOS calculations

The DFT calculations were done by the Vienna Ab-initio Simulation Package (VASP) code33 using the projector-augmented wave34 as well as the Perdew–Burke–Ernzerhof exchange-correlation functional35. Relaxed lattice parameters were used for WSe2 monolayer28. Spin–orbit coupling was considered in the calculation. The energy cutoff of the plane-wave basis was set to 400 eV and the energy convergence was 10−6 eV. Vacuum layer was >15 Å to separate neighbouring periodic images. A Γ-centred k-mesh of 10 × 10 × 1 was used to obtain the ground-state density and a 51 × 51 k-mesh was used to calculate the band energies in the rhombus reciprocal cell.

After getting the conduction-band dispersion 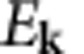Inline graphic of the two-dimensional first Brillouin zone, the 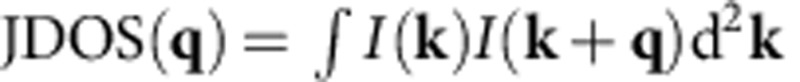Inline graphic at the Fermi level EF was calculated using the approximation 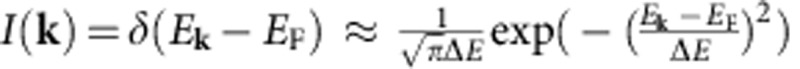Inline graphic. We set the energy resolution ▵E=30 meV, which suited well our 51 × 51 reciprocal cell mesh grid.

Additional information

How to cite this article: Liu, H. et al. Observation of intervalley quantum interference in epitaxial monolayer tungsten diselenide. Nat. Commun. 6:8180 doi: 10.1038/ncomms9180 (2015).

Supplementary Material

Supplementary Information

Supplementary Figures 1-2

ncomms9180-s1.pdf (276.6KB, pdf)

Acknowledgments

The work described in this paper was supported by a Collaborative Research Fund (HKU9/CRF/13G) sponsored by the Research Grant Council (RGC), Hong Kong Special Administrative Region. M.X. and J.J. acknowledge the support from a grant of the SRFDP and RGC ERG Joint Research Scheme of Hong Kong RGC and the Ministry of Education, China (No. M-HKU709/12). The work in SJTU was supported by the MOST (2013CB921902, 012CB927401) and the NSFC (11227404, 11374206 and 11304014) of China. G.-B. L. was supported by the NSFC (No. 11304014) of China.

Footnotes

Author contributions M.X. and H.L. conceived and designed the experiments; H.L., J.C., F.Y., L.J. and W.H. performed the growth and STM experiments; H.Y., G.-B. L. and W.Y. calculated the energy bands and the JDOS; M.X., W.Y., H.L., H.Y. and J.C. analysed the data: M.X., C.G. and J.J. contributed the experimental equipment; M.X. and W.Y. co-wrote the paper.

References

  1. Wang Q. H., Kalantar-Zadeh K., Kis A., Coleman J. N. & Strano M. S. Electronics and optoelectronics of two-dimensional transition metal dichalcogenides. Nat. Nanotechnol. 7, 699–712 (2012). [DOI] [PubMed] [Google Scholar]
  2. Xu X. D., Yao W., Xiao D. & Heinz T. F. Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 10, 343–350 (2014). [Google Scholar]
  3. Liu G. B., Xiao D., Yao Y., Xu X. D. & Yao W. Electronic structures and theoretical modelling of two-dimensional group-VIB transition metal dichalcogenides. Chem. Soc. Rev. 44, 2643–2663 (2015). [DOI] [PubMed] [Google Scholar]
  4. Mak K. F., He K., Shan J. & Heinz T. F. Control of valley polarization in monolayer MoS2 by optical helicity. Nat. Nanotechnol. 7, 494–498 (2012). [DOI] [PubMed] [Google Scholar]
  5. Zeng H. L., Dai J. F., Yao W., Xiao D. & Cui X. D. Valley polarization in MoS2 monolayers by optical pumping. Nat. Nanotechnol. 7, 490–493 (2012). [DOI] [PubMed] [Google Scholar]
  6. Cao T. et al. Valley-selective circular dichroism of monolayer molybdenum disulphide. Nat. Commun. 3, 887 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Jones A. M. et al. Optical generation of excitonic valley coherence in monolayer WSe2. Nat. Nanotechnol. 8, 634–638 (2013). [DOI] [PubMed] [Google Scholar]
  8. Zhang Y. et al. Direct observation of the transition from indirect to direct bandgap in atomically thin epitaxial MoSe2. Nat. Nanotechnol. 9, 111–115 (2014). [DOI] [PubMed] [Google Scholar]
  9. Riley J. M. et al. Direct observation of spin-polarized bulk bands in an inversion-symmetric semiconductor. Nat. Phys. 10, 835–839 (2014). [Google Scholar]
  10. Alidoust N. et al. Observation of monolayer valence band spin-orbit effect and induced quantum well states in MoX2. Nat. Commun. 5, 4673 (2014). [DOI] [PubMed] [Google Scholar]
  11. Kormányos A. et al. k⋅p theory for two-dimensional transition metal dichalcogenide semiconductors. 2D Mater. 2, 022001 (2015). [Google Scholar]
  12. Yuan H. et al. Generation and electric control of spin–valley-coupled circular photogalvanic current in WSe2. Nat. Nanotechnol. 9, 851–857 (2014). [DOI] [PubMed] [Google Scholar]
  13. Gong Z. et al. Magnetoelectric effects and valley-controlled spin quantum gates in transition metal dichalcogenide bilayers. Nat. Commun. 4, 2053 (2013). [DOI] [PubMed] [Google Scholar]
  14. Ugeda M. M. et al. Giant bandgap renormalization and excitonic effects in a monolayer transition metal dichalcogenide semiconductor. Nat. Mater. 13, 1091–1095 (2014). [DOI] [PubMed] [Google Scholar]
  15. Zhang C., Johnson A., Hsu C. L., Li L. J. & Shih C. K. Direct imaging of band profile in single layer MoS2 on graphite: quasiparticle energy gap, metallic edge states, and edge band bending. Nano Lett. 14, 2443–2447 (2014). [DOI] [PubMed] [Google Scholar]
  16. Chiu M.-H. et al. Determination of band alignment in the single-layer MoS2/WSe2 heterojunction. Nat. Commun. 6, 7666 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Zhang C. et al. Measuring critical point energies in transition metal dichalcogenides. Preprint at http://arxiv.org/abs/1412.8487 (2014).
  18. Liu H. J. et al. Dense network of one-dimensional midgap metallic modes in monolayer MoSe2 and their spatial undulations. Phys. Rev. Lett. 113, 066105 (2014). [DOI] [PubMed] [Google Scholar]
  19. Crommie M. F., Lutz C. P. & Eigler D. M. Confinement of electrons to quantum corrals on a metal surface. Science 262, 218–220 (1993). [DOI] [PubMed] [Google Scholar]
  20. Fiete G. A. & Heller E. J. Colloquium : theory of quantum corrals and quantum mirages. Rev. Mod. Phys. 75, 933–948 (2003). [Google Scholar]
  21. Zhang T. et al. Experimental demonstration of topological surface states protected by time-reversal symmetry. Phys. Rev. Lett. 103, 266803 (2009). [DOI] [PubMed] [Google Scholar]
  22. Roushan P. et al. Topological surface states protected from backscattering by chiral spin texture. Nature 460, 1106–1109 (2009). [DOI] [PubMed] [Google Scholar]
  23. Rutter G. M. et al. Scattering and interference in epitaxial graphene. Science 317, 219–222 (2007). [DOI] [PubMed] [Google Scholar]
  24. Petersen L., Hofmann P., Plummer E. W. & Besenbacher F. Fourier transform–STM: determining the surface Fermi contour. J. Electron. Spectros. Relat. Phenom. 109, 97–115 (2000). [Google Scholar]
  25. Simon L., Bena C., Vonau F., Cranney M. & Aubel D. Fourier-transform scanning tunnelling spectroscopy: the possibility to obtain constant-energy maps and band dispersion using a local measurement. J. Phys. D Appl. Phys 44, 464010 (2011). [Google Scholar]
  26. Zeng H. L. et al. Optical signature of symmetry variations and spin-valley coupling in atomically thin tungsten dichalcogenides. Sci. Rep. 3, 1608 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Xiao D., Liu G.-B., Feng W., Xu X. D. & Yao W. Coupled spin and valley physics in monolayers of MoS2 and other group-VI dichalcogenides. Phys. Rev. Lett. 108, 196802 (2012). [DOI] [PubMed] [Google Scholar]
  28. Liu G. B., Shan W. Y., Yao Y., Yao W. & Xiao D. Three-band tight-binding model for monolayers of group-VIB transition metal dichalcogenides. Phys. Rev. B 88, 085433 (2013). [Google Scholar]
  29. Roldán R. et al. Momentum dependence of spin–orbit interaction effects in single-layer and multi-layer transition metal dichalcogenides. 2D Mater. 1, 034003 (2014). [Google Scholar]
  30. Qiu D. Y., da Jornada F. H. & Louie S. G. Optical spectrum of MoS2: many-body effects and diversity of exciton states. Phys. Rev. Lett. 111, 216805 (2013). [DOI] [PubMed] [Google Scholar]
  31. Ramasubramaniam A. Large excitonic effects in monolayers of molybdenum and tungsten dichalcogenides. Phys. Rev. B 86, 115409 (2012). [Google Scholar]
  32. Yankowitz M. et al. Local Spectroscopic Characterization of Spin and Layer Polarization in WSe2, Preprint at http://arxiv.org/abs/1505.00245 (2015). [DOI] [PubMed]
  33. Kresse G. & Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996). [DOI] [PubMed] [Google Scholar]
  34. Blöchl P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994). [DOI] [PubMed] [Google Scholar]
  35. Perdew J. P., Burke K. & Ernzerhof M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996). [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information

Supplementary Figures 1-2

ncomms9180-s1.pdf (276.6KB, pdf)

Articles from Nature Communications are provided here courtesy of Nature Publishing Group

RESOURCES