A microfluidic model to study fluid dynamics of mucus plug rupture in small lung airways

Abstract

Fluid dynamics of mucus plug rupture is important to understand mucus clearance in lung airways and potential effects of mucus plug rupture on epithelial cells at lung airway walls. We established a microfluidic model to study mucus plug rupture in a collapsed airway of the 12th generation. Mucus plugs were simulated using Carbopol 940 (C940) gels at concentrations of 0.15%, 0.2%, 0.25%, and 0.3%, which have non-Newtonian properties close to healthy and diseased lung mucus. The airway was modeled with a polydimethylsiloxane microfluidic channel. Plug motion was driven by pressurized air. Global strain rates and shear stress were defined to quantitatively describe plug deformation and rupture. Results show that a plug needs to overcome yield stress before deformation and rupture. The plug takes relatively long time to yield at the high Bingham number. Plug length shortening is the more significant deformation than shearing at gel concentration higher than 0.15%. Although strain rates increase dramatically at rupture, the transient shear stress drops due to the shear-thinning effect of the C940 gels. Dimensionless time-averaged shear stress, T_xy, linearly increases from 3.7 to 5.6 times the Bingham number as the Bingham number varies from 0.018 to 0.1. The dimensionless time-averaged shear rate simply equals to T_xy/2. In dimension, shear stress magnitude is about one order lower than the pressure drop, and one order higher than yield stress. Mucus with high yield stress leads to high shear stress, and therefore would be more likely to cause epithelial cell damage. Crackling sounds produced with plug rupture might be more detectable for gels with higher concentration.

I. INTRODUCTION

Human lung airways are coated with a viscous mucus layer above a watery serous layer. In normal healthy airways, the mucus layer traps particles entering into the lung and is continuously moved toward the mouth through ciliary beating in the serous layer. Such a mucociliary clearance system acts as one of the major mechanisms for mucus clearance, besides gravitational drainage and cough (King, 2006; Fink, 2007). Human lung mucus has non-Newtonian properties of viscoelasticity, shear-thinning, and yield stress, which significantly influence lung physiology. For example, shear-thinning leads to less viscous and more flowable mucus through rapid cough or high frequency oscillation (to generate a flow with higher shear rate), which brings advantages to mucus clearance (Rubin et al., 1990; Zahm et al., 1991; King, 1998; King, 2006; and Ragavan et al., 2010). In lung diseases such as cystic fibrosis (CF) and chronic obstructive pulmonary disease (COPD), mucus is hypersecreted and unhealthy (Button et al., 2008). CF mucus may have viscoelastic properties similar to normals (Serisier et al., 2009), but the infectious process with cellular debris increases mucus viscoelasticity and reduces clearance. COPD mucus usually has high viscoelasticity, which weakens mucus clearance (Button et al., 2008). Besides damage of mucus clearance mechanism, mucus hypersecretion reduces gas exchange and incurs inflammation (Lai et al., 2009). Furthermore, plugs are more likely to form in the situation of mucus hypersecretion, blocking airways partially or totally (Kant et al., 2007). Plugging also happens in normal small airways. Small airways have diameter less than 2 mm. For adults, it is about the 9th generation and above (Ranga and Kleinerman, 1978). With no or few cartilage surroundings, small airways tend to collapse near the end of expiration, which causes mucus to form plugs closing airways (Hughes et al., 1970; Macklem et al., 1970; and Kamm and Schroter, 1989). Gravity in real life is another factor that can make airways close in deeper lung regions (Prisk et al., 1995a; 1995b; Howell et al., 2000).

Reopening the airway requires the plug to propagate and rupture, usually driven by the imposed air pressure during breathing. The propagating plug gains liquid from its precursor film (the airway lining of mucus in front of the plug) and deposits liquid to its trailing film (the airway lining of mucus behind the plug). As the trailing film is thicker than the precursor film, the plug deposits more into the film than it picks up. This decreases its volume and may eventually lead to rupture (Fujioka et al., 2008; Hassan et al., 2011). Studies on a single Newtonian liquid plug using a rigid airway model show that higher pressure drop along the plug results in faster plug propagation, thicker trailing film, and faster rupture if rupture happens (Fujioka and Grotberg, 2004; Fujioka et al., 2008; and Hassan et al., 2011). The plug rupture process introduces extra stresses on airway walls from the snapping open of the interfaces and their coalescence to the wall layer interface. Shear stress and pressure at walls are maximal at the front meniscus of the plug (Fujioka and Grotberg, 2004). Stresses reach their peaks shortly after the rear meniscus catches up with the front meniscus and rupture happens (Hassan et al., 2011). The high shear stress and pressure may cause lethal damage to underlying epithelial cells, especially at the rupture location (Huh et al., 2007). Existence of yield stress in mucus reduces shear stress but increases the gradients of shear stress and pressure at the airway walls; yield stress of mucus increases the possibility of damage to the airway epithelial cells as the plug propagates (Zamankhan et al., 2012). With plug rupture, pressure waves are produced (Huh et al., 2007). The transient pressure waves might be detected by a stethoscope and used as crackling sounds to indicate lung injury in clinic practice (Piirila and Sovijarvi, 1995a; 1995b; Vena et al., 2011).

Using a two-dimensional polydimethylsiloxane (PDMS) microfluidic channel model, we already studied plug rupture at a critical pressure drop, the minimum pressure drop needed for a mucus plug to rupture (Hu et al., 2013). Carbopol 940 (C940) gels at concentration of 0.1%–0.3% were used as mucus simulant for their properties of viscoelasticity and yield stress similar to normal/abnormal human lung mucus. For initial plug length of 0.5–3.0 times the half channel width, the critical pressure drop falls into the range of 800–1000, 800–1200, 950–1550, and 1000–1900 Pa, for gel concentration of 0.1%, 0.15%, 0.2%, and 0.3%. Such pressures are generally higher than the normal transpulmonary pressure of 600–800 Pa (6–8 cm H₂O) (Hall, 2010), and partially comparable with positive-end expiratory pressure (PEEP) of 1500–3000 Pa (15–30 cm H₂O) in high-PEEP mechanical ventilation (Sugerman et al., 1972; Brower et al., 2004; and El-Khatib and Chatburn, 2013). We found a simple linear relationship between the reciprocal Bingham number (defined through the critical pressure drop) and the dimensionless initial plug length (scaled by the half channel width). That is, the critical pressure drop increases linearly with yield stress and quadratically with initial plug length. The plug yields at a position about one-third of the half channel width away from channel walls. With rupture, shear stress at channel walls might become high enough to damage epithelial cells. The film left in the airway after rupture is generally thinner than one-fifth of channel width.

Focusing on critical pressure drops for plugs to rupture in the previous study, we have not sufficiently investigated fluid dynamics in plug deformation and rupture. Here, using the similar method in the previous study (Hu et al., 2013), we defined and introduced fluid dynamic quantities, for example, strain rates and shear stress, to investigate plug deformation and rupture beyond the critical pressure drop condition. A detailed picture was provided on plug deformation and rupture with velocity and time features. The shear-thinning and yield stress effects on strain rates and shear stress were studied. Particularly, the Bingham number was introduced to study the yield stress effects. We also tried to reveal effects of non-Newtonian properties of mucus on plug rupture and impacts of plug rupture on clinic implications of mucus clearance and epithelial cell damage.

II. METHOD

A. Experimental setup

We mainly followed the method used in our previous study on critical pressure drops for mucus plugs to rupture (Hu et al., 2013). C940 gels were used as lung mucus simulant at concentration c = 0.15%, 0.2%, 0.25%, and 0.3% (weight/weight). The storage modulus G′ and loss modulus G″ of the complex modulus of C940 gels G* = G′ + iG″ were measured with an AR1000 rheometer (TA Instruments Ltd.) at temperature of 22 °C. The 60 mm-2° cone-plate with a truncation gap of 58 μm was used in the oscillatory measurement mode over an angular frequency range of 0.015 < ω < 500 rad/s. The frequency sweep was run at a fixed strain of 0.01 for three times (Hu et al., 2013). The moduli generally increase with the gel concentration. The gels are more elastic with G′ far larger than G″, which is also observed in human lung mucus (Dawson et al., 2003). The storage modulus G′ of human lung mucus in different physiological and pathological conditions varies in the range of 0.4–204 Pa at 1 ≤ ω ≤ 100 rad/s (Jeanneret-Grosjean et al., 1988; Rubin et al., 1990; Dawson et al., 2003; Rancourt et al., 2004; and Serisier et al., 2009), which is smaller than that of the gels, 215–545 Pa, at c = 0.15%–0.3% and the same angular frequency. The gels with low concentration are comparable to some diseased lung mucus. For example, the complex modulus of the 0.15%-gel, |G*| = 237 Pa, at ω = 10 rad/s, is close to CF sputum, |G*| = 204 Pa, at the same angular frequency (Rancourt et al., 2004).

The complex viscosity is defined as η* = G*/(iω) = η′ − iη″ (η′: dynamic viscosity and η″: elasticity). The viscosities also increase with the gel concentration. The non-Newtonian property of shear-thinning was fitted through the power-law relationship, |η*|∝ω^m−1,

$$|{\eta }^{*}{|}_{0.15\%}=221{\omega }^{-0.97}\hspace{0.17em}(R^2=0.9998),$$

$$|{\eta }^{*}{|}_{0.20\%}=311{\omega }^{-0.97}\hspace{0.17em}(R^2=0.9999),$$

$$|{\eta }^{*}{|}_{0.25\%}=398{\omega }^{-0.96}\hspace{0.17em}(R^2=0.9999),$$

$$|{\eta }^{*}{|}_{0.30\%}=454{\omega }^{-0.96}\hspace{0.17em}\hspace{0.17em}(R^2=1),$$

in which R² is the coefficient of determination, and 44–48 values were used in each formula fitting process. The flow behavior index, m, varies from 0.09 to 0.16, which is within the m-range of human mucus, 0–0.5 (average: 0.15) (Yeates et al., 1997). Human lung mucus has the dynamic viscosity η′ about 2–20 Pa·s at ω = 1 rad/s, and 0.14–1.3 Pa·s at ω = 100 rad/s (Jeanneret-Grosjean et al., 1988; Rubin et al., 1990; Dawson et al., 2003; and Serisier et al., 2009). The C940 gels at the four concentrations have dynamics viscosity within 19–28 and 0.44–0.7 Pa·s at ω = 1 and 100 rad/s, respectively, which are comparable with human lung mucus.

Yield stress of the C940 gels, τ_y, a viscoplasticity parameter, was measured with a rate-controlled RVDV-III Ultra rheometer (Brookfield Engineering Laboratories Inc.) at 0.7 rpm in normal room conditions. The vane spindle-74 was used in the static yield stress measurement. The yield stress in the current experiments is 36.8, 54.6, 69.0, and 90.4 Pa for the four gel concentrations increasing from 0.15% to 0.3%, respectively. The yield stress at c = 0.15%–0.25% is comparable with that of normal human lung mucus around 40–60 Pa (Davis, 1973).

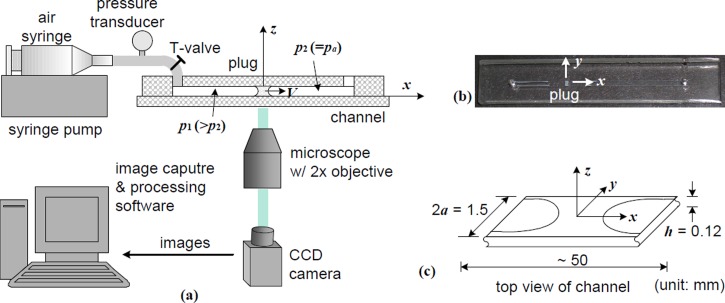
Figure 1 shows the complete experiment setup for mucus plug rupture in a collapsed small lung airway simulated in a channel made of PDMS (Slygard 184, Dow Corning Corp.). The channel geometry is 50 mm long, 1.5 mm wide, and 0.12 mm high in the x-, y-, and z-direction, respectively, as shown in Fig. 1(c). The origin of the coordinate system is on the channel centerline located at the half channel width a and half channel height h/2. The channel is placed in a horizontal xy-plane with the z-direction vertically upward. The channel walls parallel to the zx- and xy-plane are defined as the lateral (at y = ±a) and top/bottom (at z = ±h/2) walls, respectively. Such a channel has the similar perimeter to the airway of the 12th generation (Weibel, 1963). The aspect ratio (width to height), 12.5, is optically convenient to observe plug deformation and rupture. Standard soft lithography procedures were used to fabricate the PDMS channel (Xia and Whitesides, 1998). SU-8 patterns of the channel were first photo-plotted onto a photo-mask, and then the 120 μm-thick positive relief patterns were etched onto a 4-in.-diameter silicone wafer. PDMS was well mixed with the curing agent at a weight ratio of 10 to 1. Our tests showed this PDMS recipe was hydrophilic for C940 gels (Xia and Whitesides, 1998; Plachetka et al., 2004), which would be physiologically favorable. The mixture was kept in a vacuum degassing chamber for 20 min and then cast into the silanized silicon wafer. After being cured in a 60 °C oven for 2 h, the PDMS layer was peeled from the silicon wafer. Holes of 2 mm in diameter were punched at the two ends of the channel in the pattern PDMS layer, which was then sealed together with a non-pattern PDMS layer after the two layers were treated in a plasma oxidizer. This procedure ensures that the entire channel has the same surface properties.

FIG. 1.

(a) The experiment setup to simulate mucus plug dynamics in a collapsed lung airway of the 12th generation. (b) A C940-gel plug in the PDMS channel. (c) The channel dimensions: $a$—half channel width and $h$—channel height. From Hu et al., Fluid-Structure-Sound Interactions and Control. Proceedings of the 2nd Symposium on Fluid-Structure-Sound Interactions and Control, Lecture Notes in Mechanical Engineering 2014, Hong Kong, Macau, May 20–May 23 2013, edited by Y. Zhou, Y. Liu, L. Huang, and D. H. Hodges. Copyright 2013 Springer Science and Business Media. Reproduced with permission from Springer Science and Business Media.

The mucus plug in a real lung airway has precursor and trailing films attached to it. The film thickness is a quantity concerned in liquid plug studies (Halpern and Grotberg, 1992), but it is hard to control in experiments. To reduce experimental uncertainty, we made plugs without precursor/trailing films. With a syringe, we infused a C940 gel into the channel through a hole until the gel filled the channel about 1 cm in length. Then, we used another empty syringe to infuse air quickly from the same hole so as to break the gel filling into two thin films attached to the lateral channel walls. Next, we used a micro spatula to slowly press the PDMS channel downward until the film layers partially touched each other to form a plug. If the plug was connected to films, we put the spatula on the channel top above the films and somewhere away from the plug, pressed and released the channel repeatedly with the spatula until no film was connected to the plug, as shown in Fig. 1(b). Sometimes a syringe pump was run to adjust the plug position slightly forward or backward to make sure there was enough clean space for the plug to move in the channel. The length of plugs used in the experiments is within the range of 0.59–2.27a. The following results in Figs. 4, 5, 7, 8, and 9 were processed from 61, 78, 110, and 60 plug rupture experiments done at the gel concentration of 0.15%, 0.2%, 0.25%, and 0.3%, respectively.

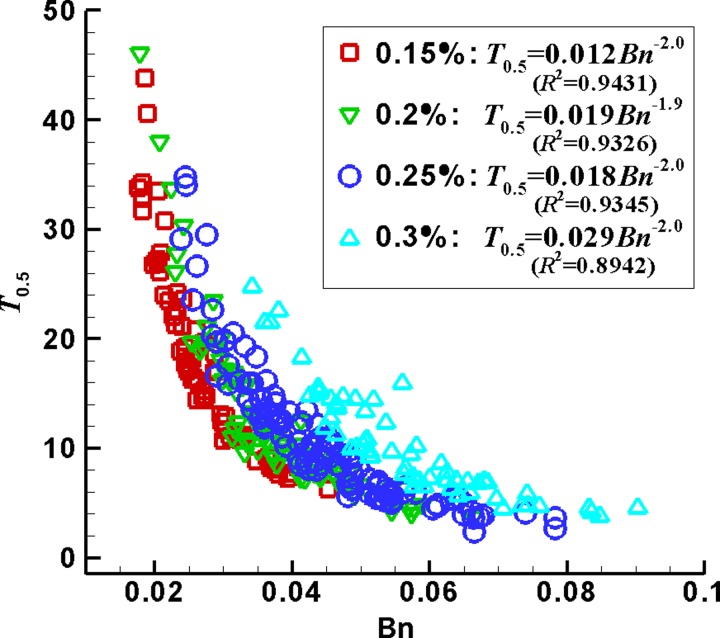
FIG. 4.

Dimensionless time T_0.5 varies with the Bingham number Bn at c = 0.15%, 0.2%, 0.25%, and 0.3%.

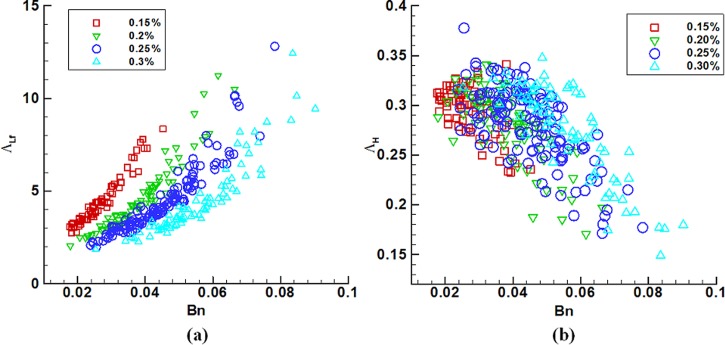
FIG. 5.

(a) The dimensionless film length Λ_Lf and (b) film thickness Λ_H as functions of Bn at c = 0.15%, 0.2%, 0.25%, and 0.3%.

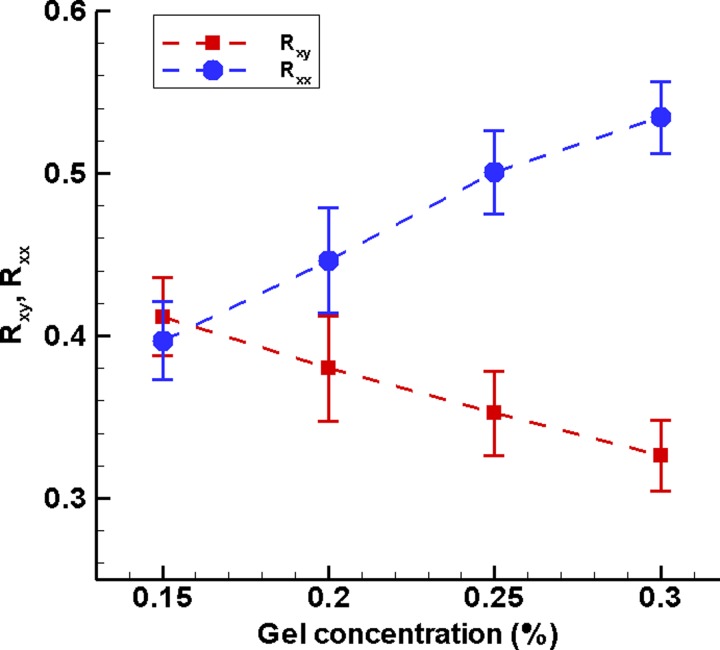
FIG. 7.

The deformation ratios, $R_{\mathit{x}\mathit{y}}$ and $R_{\mathit{x}\mathit{x}}$, at c = 0.15%, 0.2%, 0.25%, and 0.3%.

FIG. 8.

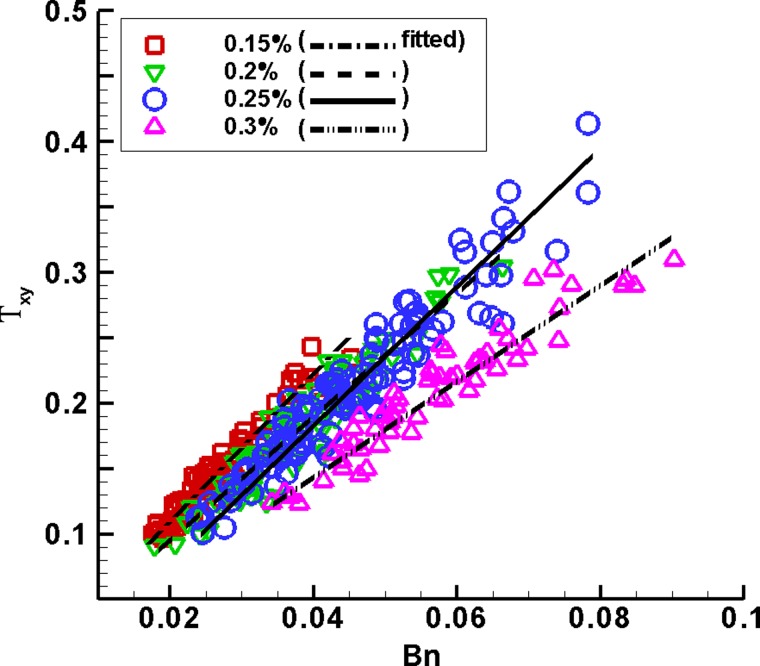
The dimensionless shear stress $T_{\mathit{x}\mathit{y}}$ as a function of the Bingham number Bn.

FIG. 9.

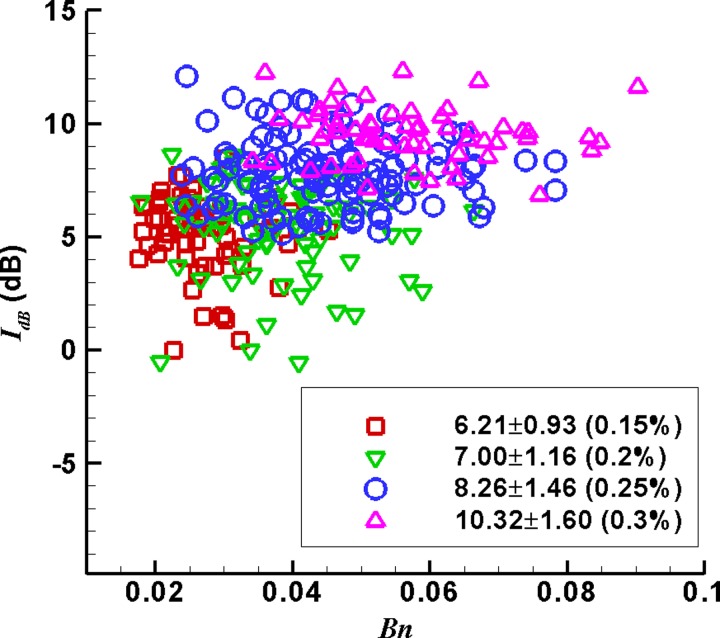
The distribution of sound intensity I_dB with Bn at the gel concentration c = 0.15%, 0.2%, 0.25%, and 0.3%.

One end of the channel was connected to a syringe pump (Harvard Apparatus PHD2000) through tubing, and the other end was open to the atmosphere. The syringe pump was used to compress air to build up a pressure drop across the plug, $\Delta p=p_1-p_2$ ($p_2$: the normal atmosphere pressure), in the range of 1600–2100 Pa, as shown in Fig. 1(a). Before the pressure drop was imposed on the plug, the piston of the air syringe was set at a zero position (in our experiments, the capacity mark of 20 ml on the syringe taken as the zero position), and any remaining pressure in the channel system was fully released. The imaging program was turned on, ready to capture images of plug rupture as soon as the plug was driven by the pressure drop. Images of plug rupture were captured by a high-speed CCD camera (CoolSnap EZ, Photometrics) at 28 frames per second (fps), and processed using the imaging program, MetaMorph (Universal Imaging Co.).

B. Quantities, parameters, and scales

In the experimental study, yield stress was still a major concern among mucus properties as the previous numerical study (Zamankhan et al., 2012). The dimensionless parameter related to yield stress is the Bingham number (ratio of yield stress to viscous stress), $Bn={\tau }_y/(\mu U/a)$, in which $\mu$ is viscosity and U is the characteristic velocity. The narrow space of the channel in the z-direction makes plug deformation and rupture discernible mainly on the xy-plane. Correlated to Poiseuille flow, we simplified momentum balance in the x-direction to be $\Delta p/L_0\sim \mu U/a^2$, and therefore the characteristic velocity is $U=\Delta p{a}^2/(\mu L_0)$, in which L₀ is the initial plug length. Thus, the Bingham number is written as $Bn={\Lambda }_{L0}{\tau }_y/\Delta p$, where Λ_L0 is the dimensionless initial plug length Λ_L0 = L₀/a (Hu et al., 2013). In our study, Bn varies from 0.018 to 0.1.

Strain rate and stress are two major quantities demonstrating the plug deformation and rupture. Previous studies in our group show that the lateral motion component in the y-direction is insignificant, compared with the x-component (Fujioka and Grotberg, 2005; Fujioka et al., 2008; Zamankhan et al., 2012; and Hu et al., 2013). The lateral motion component in the experiments was therefore neglected. We defined the transient shear strain rate ${\dot{\gamma }}_{\mathit{x}\mathit{y}}^t$ and normal strain rate ${\dot{\gamma }}_{\mathit{x}\mathit{x}}^t$ to describe the global deformation of the plug,

$${\dot{\gamma }}_{\mathit{x}\mathit{y}}^t=\frac{V_A-V_{\mathit{C}\mathit{D}}}{2a}\hspace{1em}\text{and}\hspace{1em}{\dot{\gamma }}_{\mathit{x}\mathit{x}}^t=\frac{V_B-V_A}{L},$$

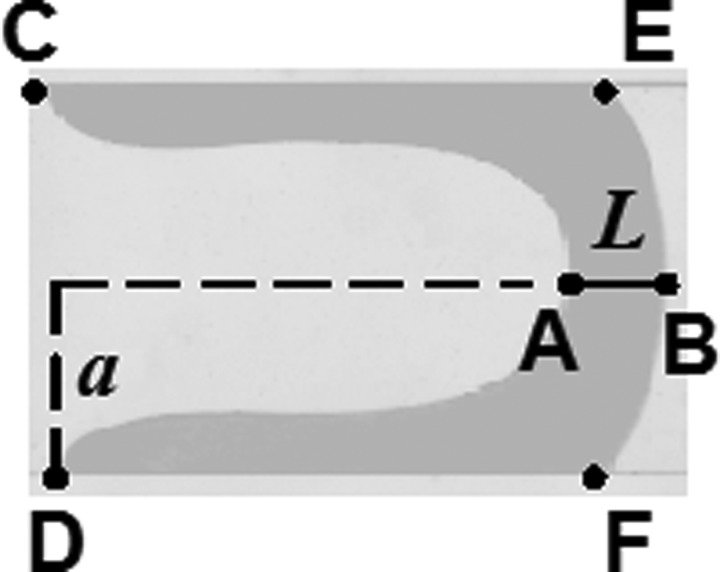
in which $V_{\mathit{C}\mathit{D}}$ is the velocity averaged at positions C and D, $V_{\mathit{C}\mathit{D}}=(V_C+V_D)/2$. The positions, C and D, together with the other four, A, B, E, and F, are denoted in Fig. 2, which shows a typical plug shape at an instant in the deformation-rupture process. The global transient shear stress is calculated through ${\tau }_{\mathit{x}\mathit{y}}^t=2\mu ({\dot{\gamma }}^t){\dot{\gamma }}_{\mathit{x}\mathit{y}}^t$, in which the transient nominal shear rate ${\dot{\gamma }}^t=\sqrt{2{{\dot{\gamma }}_{\mathit{x}\mathit{x}}^t}^2+4{{\dot{\gamma }}_{\mathit{x}\mathit{y}}^t}^2}$, and the viscosity follows the Cox-Merz rule, $\mu ({\dot{\gamma }}^t)=|{\eta }^{*}(\omega ){|}_{\omega ={\dot{\gamma }}^t}$ (Cox and Merz, 1958).

FIG. 2.

Definition of six positions on a deformed plug. Positions A and B are defined at the plug meniscus and at the centerline of the channel, denoting the transient plug length, L. C and D: the rear positions of the films attached to channel walls. E and F: the front positions of the films attached to channel walls. a: half channel width.

To quantitatively estimate plug deformation and rupture in general, we introduced time-averaged strain rates. The time interval is set from the moment t_0.5 as the dimensionless plug length is Λ_L = 0.5 (Λ_L: transient plug length L scaled by half channel width a) to the rupture moment t₀ = 0 as Λ_L = 0 (rupture). The time-averaged strain rate is defined as ${\dot{\gamma }}_{\mathit{i}\mathit{j}}=({\int }_{t_{0.5}}^{t_0}{\dot{\gamma }}_{\mathit{i}\mathit{j}}^{t}dt)/(t_0-t_{0.5})$ (i,j = x,y). The time-averaged shear stress, ${\tau }_{\mathit{x}\mathit{y}}$, is calculated from ${\tau }_{\mathit{x}\mathit{y}}=2\mu (\dot{\gamma }){\dot{\gamma }}_{\mathit{x}\mathit{y}}$, in which the nominal shear rate $\dot{\gamma }=\sqrt{2{\dot{\gamma }}_{\mathit{x}\mathit{x}}^2+4{\dot{\gamma }}_{\mathit{x}\mathit{y}}^2}$. The strain rates and stress are scaled by $U/a$ and $\mu U/a$, respectively. The dimensionless form of the time-averaged shear rate ${\dot{\gamma }}_{\mathit{x}\mathit{y}}$ is denoted as ${\dot{\Gamma }}_{\mathit{x}\mathit{y}}$, and the dimensionless form of the time-averaged shear stress τ_xy as T_xy. Thus, a simple relationship yields $T_{\mathit{x}\mathit{y}}=2{\dot{\Gamma }}_{\mathit{x}\mathit{y}}$.

The characteristic time is defined as t₀ = L₀/U $=\mu {\Lambda }_{L0}^2/\Delta p$, which nominally represents the total time needed by a plug to overcome yield stress, deform, and finally rupture. The dimensionless time T_0.5 = −t_0.5/t₀ therefore estimates how fast a plug ruptures from the length Λ_L = 0.5 to 0, relative to the whole deformation-rupture process from Λ_L = Λ_L0 to 0 (since the plug might deform slightly as it yields, deformation in the study includes plug yielding if no specification).

Plug rupture may be accompanied with sound emission (Huh et al., 2007). We introduced the parameter of sound intensity, $I_{\mathit{d}\mathit{B}}=10\hspace{0.17em}{\text{log}}_{10}({\dot{\psi }}_{{\Lambda }_L=0}/{\dot{\psi }}_{{\Lambda }_L=0.5})$, to represent potential contribution of plug deformation in sound at rupture, in which ${\dot{\psi }}_{{\Lambda }_L=0}$ and ${\dot{\psi }}_{{\Lambda }_L=0.5}$ are strain energy rates at the plug length Λ_L = 0 and 0.5, respectively, and the strain energy rate $\dot{\psi }=\tau \dot{\gamma }/2=\mu (\dot{\gamma }){\dot{\gamma }}^2/2$.

III. RESULTS

A. Plug deformation and rupture

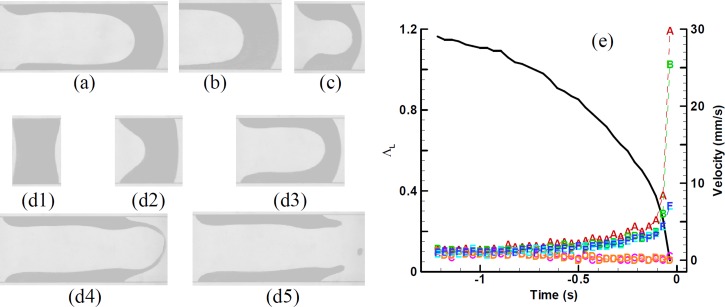
From more than three hundred experiments of plug rupture, we noticed the plug deformed and ruptured in a similar manner. At different gel concentration, Figs. 3(a)–3(d5) show the typical instant shape of a deformed plug with relative low pressure drop (Fig. 3(a)), long initial plug length (Fig. 3(b)), short initial plug length (Fig. 3(c)), or moderate parameters (Figs. 3(d1)–3(d5)). Figures 3(d1)–3(d5) display more details of plug deformation and rupture. The plug propagates, slips along the channel, and deforms with meniscus tips protruding forward (Figs. 3(d1)–3(d4)). When deformation at the rear interface is large enough, the pressure normal to the interface has a high enough y-component to pin the rear film to the lateral wall, as shown in Figs. 3(d2) and 3(d3), and to stop slippage, which initiates the rupture deformation in Fig. 3(d4). After rupture, at least one satellite droplet is formed in this case (in Fig. 3(d5)). The whole process lasts 1.64 s from the pressure drop imposed upon the plug (Fig. 3(d1)) to final rupture (Fig. 3(d5)). The plug deforms in a manner of acceleration. As the plug length Λ_L = 0.5, time is t = −0.18 s (Fig. 3(d3). That is, the plug takes 89% of the whole time to shorten 58% of its initial length, and needs only 11% of the whole time to shorten the left 42% of its initial length.

FIG. 3.

The deformation and rupture of four plugs at (a) c = 0.15%, Λ_L0 = 1.58, Δp = 1600 Pa, (b) c = 0.2%, Λ_L0 = 2.11, Δp = 2000 Pa, (c) c = 0.25%, Λ_L0 = 0.61, Δp = 1700 Pa, and (d1)–(d5) c = 0.3%, Λ_L0 = 1.18, Δp = 1900 Pa. (d1) The initial plug at the moment when the pressure drop is imposed. (d2) and (d3) The plug propagates, slips, and deforms. (d4) and (d5) The plug ruptures. From (d1)–(d5), the plug length and time moment are Λ_L = (d1) 1.18, (d2) 1.0, (d3) 0.5, (d4) 0.05, (d5) 0, and t = (d1) −1.64 (time t = 0 at rupture), (d2) −0.79, (d3) −0.18, (d4) −0.036 s, (d5) 0. (e) Transient plug length and velocities at positions A–F (defined in Fig. 2).

Figure 3(e) more clearly shows the accelerated deformation-rupture process through the plug length and velocities at six positions of A–F (defined in Fig. 2) varying with time. At the early beginning, velocities of the six positions A to F differ little, and the plug generally moves as a whole. With the process development, the velocities of A and B at the plug meniscuses increase the most rapidly, followed by E and F at the front film tips. The rear film tips, C and D, however, gradually slow down, and stop moving before rupture. The rear meniscus A moves faster than the front meniscus B; so finally the plug ruptures. The velocities of A and B dramatically increase around the rupture moment, for example, from about 3 to 25 and 30 mm/s, respectively.

The dimensionless time T_0.5 = −t_0.5/t₀ is used to approximately estimate how fast a plug ruptures from Λ_L = 0.5 to 0. Figure 4 plots T_0.5 decreasing with Bn and increasing with the gel concentration. That is, at higher Bn and lower gel concentration, the time needed for the plug to rupture is shorter, relative to the total time needed for the plug to yield, deform, and rupture. The curve-fitting further shows T_0.5 linearly increases with Bn^−2.0.

After rupture, two films are deposited onto the channel walls, as shown in Fig. 3(d5). Figure 5(a) plots the dimensionless film length Λ_Lf varies with Bn for all plugs used in experiments, in which Λ_Lf is the film length L_f scaled by the half channel width a and averaged from two film lengths. The film length Λ_Lf is generally larger than 2.0 and non-linearly rises with Bn. The dimensionless film thickness is estimated from mass conservation, Λ_H = H/a = L₀/L_f. It non-linearly decreases with Bn and generally Λ_H < 0.35, as shown in Fig. 5(b).

B. Strain rates and shear stress

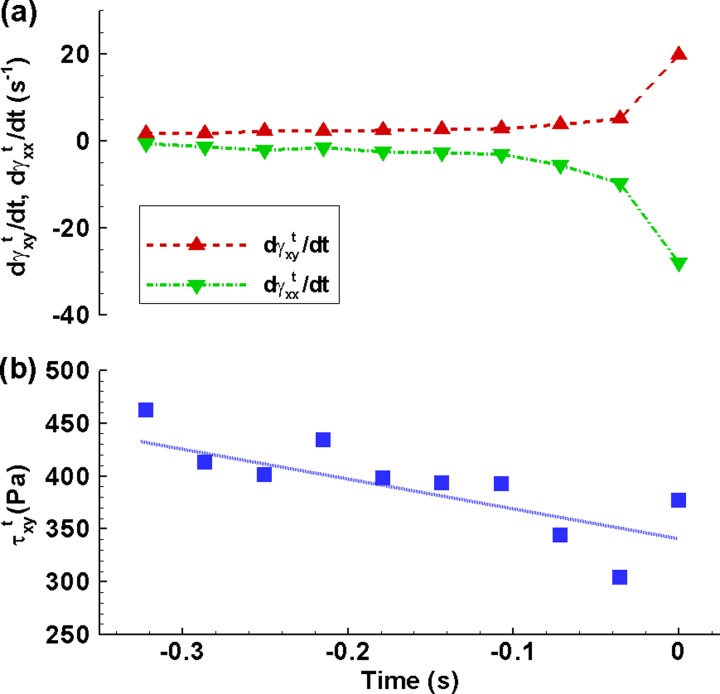
We took the plug rupture experiment shown in Figs. 3(d1)–3(d5) as a sample to obtain basic idea on transient strain rates and shear stress in mucus plug rupture. Figure 6 plots the transient shear strain rate, normal strain rate, and shear stress of the plug developing with time. The magnitudes of the transient shear and normal strain rates in Fig. 6(a) dramatically increase by 11 and 42 times from t = −0.32 s to rupture, respectively. By contrast, the transient shear stress drops by 18% from 461.9 Pa at t = −0.32 s to 376.7 Pa at rupture in Fig. 6(b). The reason is that, though the transient strain rates (also the transient nominal shear rate ${\dot{\gamma }}^t$) sharply rise at rupture, the viscosity greatly reduces due to the shear-thinning effect. The decreased viscosity significantly offsets the contribution of the increased strain rates to the resultant shear stress.

FIG. 6.

(a) The transient global shear and normal strain rates and (b) the transient global shear stress vary with time from t = −0.32 s (Λ_L = 0.69) to rupture t = 0 for the plug at c = 0.3%, Λ_L0 = 1.18, and Δp = 1900 Pa in Figs. 3(d1)−3(d5).

The ratios of ${\dot{\gamma }}_{\mathit{x}\mathit{y}}/\dot{\gamma }$ and $\left|{\dot{\gamma }}_{\mathit{x}\mathit{x}}\right|/\dot{\gamma }$ are used to evaluate the relative importance of the two major components of deformation, shearing and length shortening, in the plug deformation-rupture process. The two ratios are functions only of gel concentration. Figure 7 plots the averaged ratios, $R_{\mathit{i}\mathit{j}}=\left|{\sum }_{k=1}^K{({\dot{\gamma }}_{\mathit{i}\mathit{j}}/\dot{\gamma })}_k\right|/K$ (ij = xy and xx, K: plug number), at each gel concentration. With the gel concentration increasing, $R_{\mathit{x}\mathit{y}}$ decreases, and $R_{\mathit{x}\mathit{x}}$ increases. The dropping ratio of $R_{\mathit{x}\mathit{y}}$/$R_{\mathit{x}\mathit{x}}$( = ${\dot{\gamma }}_{\mathit{x}\mathit{y}}$/$\left|{\dot{\gamma }}_{\mathit{x}\mathit{x}}\right|$) from 1.04, 0.79, 0.72 to 0.61 for c = 0.15% to 0.3% suggests that plug length shortening is generally dominant over shearing deformation as the gel concentration is higher than 0.15%. At c = 0.15%, the shearing deformation is more significant than plug length shortening.

Due to the simple linear relationship between the dimensionless shear stress and shear rate, $T_{\mathit{x}\mathit{y}}=2{\dot{\Gamma }}_{\mathit{x}\mathit{y}}$, we investigated only the dimensionless time-averaged shear stress $T_{\mathit{x}\mathit{y}}$. Figure 8 shows $T_{\mathit{x}\mathit{y}}$ linearly increases with the Bingham number Bn at each gel concentration. With the gel concentration increasing, the Bn-range shifts rightward to the higher values. Assuming $T_{\mathit{x}\mathit{y}}=\alpha Bn$, we obtained the coefficient $\alpha$ = 5.56 (R² = 0.933), 4.73 (R² = 0.892), 4.69 (R² = 0.910), and 3.66 (R² = 0.905), decreasing with the gel concentration increasing from 0.15% to 0.3%. That is, $T_{\mathit{x}\mathit{y}}$ is 3.7–5.6 times Bn, and ${\dot{\Gamma }}_{\mathit{x}\mathit{y}}$ is 1.85–2.8 times Bn at $0.15\%\le c\le 0.3\%$.

C. Sound intensity

Figure 9 shows the distribution of sound intensity I_dB with Bn at the four gel concentrations. The data of sound intensity scatter in a limited region without definite relationship with Bn. Averaging sound intensity at each gel concentration, we found the mean sound intensity grows from 6.21, 7.00, 8.26 to 10.32 dB with the gel concentration increasing. The corresponding standard deviations are 0.93, 1.16, 1.46, and 1.60 dB, about 15%–18% of their mean values.

IV. DISCUSSION

A. Experimental methods

The microfluidic PDMS channel in the study was used to simulate an airway in the 12th generation, belonging to non-respiratory bronchioles in the conducting zone. According to the Weibel model of lung airways (Weibel, 1963), the airway diameter in the n-th generation is d_n = d₀ 2^−n/3, in which d₀ is the trachea diameter and here supposed to be 1.6 cm for the normal adult. Thus, the channel perimeter, 3.24 mm, is comparable to the airway perimeter of the 12th generation, 3.14 mm. The aspect ratio of the channel of 12.5 was a compromise of visualization and technique of PDMS channel fabrication, besides the physiological phenomenon of small airways in vivo collapsing (Hughes et al., 1970; Macklem et al., 1970; and Kamm and Schroter, 1989). Our tests of plug rupture in circular transparent tubes showed that it was almost impossible to visually observe the process of plug rupture through the CCD camera. Plug films generated with rupture tended to coat the whole inside tube walls, which blocked view through the tube walls. The current aspect ratio of 12.5 provided optical clarification of plug deformation and rupture on a horizontal plane, in which the plug films coated only the lateral walls with partial clean top/bottom walls around the middle. But to make a PDMS channel with a high aspect ratio, for example, 17.5, is still a challenge to avoid tearing damage in fabrication (Park et al., 2010). Our tests showed the channel with a higher aspect ratio also tended to collapse longitudinally around the middle, blocking the channel passage. Therefore, the current aspect ratio of 12.5 was out of comprehensive consideration and met the requirements of our study.

After a plug ruptures, the surfaces of the top/bottom walls around the middle become clean without any C940 gel attachment, which indicates that PDMS channel walls are somewhat slipping for C940 plugs. The small distance in the z-direction increases blockage of plug motion along the lateral walls. The U-shaped confinement around the lateral walls makes the films stop slipping and attach at the lateral walls. With correlation of plug deformation and rupture to a two-dimensional Poiseuille flow, the strain rates and shear stress defined in this study include the three-dimensional effects near the lateral walls, and therefore are resultant projections onto the xy-plane.

The pressure drops in this study, 1600–2100 Pa, are roughly higher than the critical pressure drops needed by plugs to rupture, 800–1900 Pa (with certain overlap at the higher critical pressure drop) (Hu et al., 2013). Such a pressure drop range is beyond the normal transpulmonary pressure about 600–800 Pa (Hall, 2010), and within the PEEP range of 1500–3000 Pa in high-PEEP mechanical ventilation (Sugerman et al., 1972; Brower et al., 2004; and El-Khatib and Chatburn, 2013).

Rupture of mucus plugs with rheology has not been studied sufficiently. A previous numerical study in our group shows yield stress is one of the major properties that determine stress generated with plug rupture (Zamankhan et al., 2012). We also took the yield stress as the major property parameter in this experimental study on flow dynamics in mucus plug rupture. The magnitude of the Bingham number weighs effects of yield stress relative to inertia. According to the Bingham number defined in this study, long initial plug length and low pressure drop also manifest yield stress effects, besides yield stress itself. Here, the Bingham number is within the range of 0.018 and 0.1, smaller than Bn ∼ 1.5, which is regarded as the Bingham number of mucus flow in normal human lung conditions of adults (Zamankhan et al., 2012). It should be pointed out that the characteristic velocity in this study is estimated from Poiseuille flow, and the viscosity follows the shear-thinning fluid model, both of which differ from those in the study of Zamankhan et al. (2012), constant flow rate-based velocity and constant viscosity in the Bingham fluid model.

B. Plug deformation and rupture

Plug deformation and rupture are an accelerated process. A plug needs to overcome yield stress before deformation. Yielding starts somewhere between the centerline and the lateral walls; then the yielding region grows until deformation is large enough to be observed or even rupture happens (Zamankhan et al., 2012). Such a process of overcoming yield stress corresponds to the experimental observation that a plug slowly moves and slightly deforms for a rather long period of time, compared with its obvious, rapid deformation and rupture in the later period, as the six velocities show in Fig. 3(e). Concentrated on dynamics of plug deformation around the rupture moment, we introduced time t_0.5 at Λ_L = 0.5 as the time interval cutoff to exclude the yield-stress overcoming period, to specify the rapid deformation-rupture period, and meanwhile to cover all plugs used in experiments (the shortest initial plug length Λ_L0 = 0.59). For short plugs, for example, Λ_L0 < 1.0, most of the process is taken into account, since the period of overcoming yield-stress is also short, and the plug deforms and ruptures quickly after the pressure drop is applied.

The dimensionless time T_0.5 decreases with Bn in the power-law manner at each gel concentration, as shown in Fig. 4. At a gel concentration, the larger Bn corresponds to the larger value of ${\Lambda }_{L0}/\Delta p$, which includes several situations, longer initial plug length, lower pressure drop, and so on. Either the longer initial plug length or the lower pressure drop makes the plug take longer time to overcome yield stress, and relatively shorter time to rupture, i.e., smaller T_0.5, as shown in Fig. 4. For the initial plug length and pressure drop that are both small (large), as long as the value of ${\Lambda }_{L0}/\Delta p$ is larger, i.e., the pressure drop is far smaller (the initial plug is far longer), the plug still needs relatively longer time to yield and shorter time to rupture. This is also the reason that, for the same Bn, the plug with the lower gel concentration (smaller yield stress) corresponds to the smaller T_0.5, in which the value of ${\Lambda }_{L0}/\Delta p$ needs to be larger to maintain the fixed Bn value.

After rupture, two films are left in the channel, attaching to the lateral walls. That the film length Λ_Lf increases with Bn (Fig. 5(a)) means the film would be long at high yield stress, small pressure drop, and long initial plug. The reason is that each of the three conditions results in slow plug motion, and the film is thin and therefore long as the plug moves slowly (Fujioka and Grotberg, 2004; Fujioka et al., 2008; and Hassan et al., 2011). For the plug studied here with initial length no shorter than 0.59a, the film is generally longer than 2a (the channel width). An airway is three times as long as its diameter (Weibel, 1963). For the collapsed channel model, a channel length of 4.1a is equivalent to the length of a real airway in the 12th generation. The plug often propagates as a whole for a distance before rupture. The distance covered due to plug propagation possibly exceeds the real airway length of this generation. The length of the bottom film left at the channel wall in Fig. 3(d5) is 4.1a, equivalent to the airway length in the 12th generation. Therefore, the plug may enter into an adjacent generation in the real airway condition even before rupture. Estimated from an empirical function for film thickness of Newtonian plugs, film thickness is no more than an asymptote of 0.36a (Halpern and Gaver, 1994; Halpern et al., 1998). For the plugs studied here, the films are usually thinner than 0.35a, slightly smaller than the Newtonian films. Compared with thick films, thin films reduce chances of new plug formation in the next breath cycle, and thereby are favorable for mucus clearance.

C. Strain rates and shear stress

The plug deforms dramatically at rupture with sudden rise in strain rates (Fig. 6(a)). But the shear-thinning effect of the C940 gels, reducing viscosity as strain rates increase, greatly moderates stress generated in the deformation-rupture process so that the resultant stress drops to a considerable degree (Fig. 6(b)). This is a favorable feature for human lung mucus with the similar shear-thinning effect in that the stress transferred from the plug to epithelial cells may have no significant increase as the plug intensely deforms at rupture during airway reopening.

We defined time-averaged shear and normal strain rates, ${\dot{\gamma }}_{\mathit{x}\mathit{y}}$ and ${\dot{\gamma }}_{\mathit{x}\mathit{x}}$, to evaluate two deformation components of the plug, shearing and length shortening. The only gel concentration-dependence of the ratio of the two strain rates in Fig. 7 indicates that all plugs at the same concentration have similarity in deformation. Plug length shortening is predominant at gel concentration higher than 0.15%. In terms of the magnitudes of ${\dot{\gamma }}_{\mathit{x}\mathit{x}}$ and ${\dot{\gamma }}_{\mathit{x}\mathit{y}}$, plug length shortening can be 1.6 times as much as shearing deformation at c = 0.3%. Figure 5(b) shows the plug film thickness roughly increases with gel concentration. The longer and thinner film at c = 0.15% implies that the plug with less viscosity tends to stretch over a larger distance and more slowly deposits to films before rupture. This may be a reason that the shearing deformation is more significant than length shortening at c = 0.15%.

The dimensionless shear rate and shear stress are simply correlated, $T_{\mathit{x}\mathit{y}}$ = 2 ${\dot{\Gamma }}_{\mathit{x}\mathit{y}}$. The simplified formula $T_{\mathit{x}\mathit{y}}=\alpha Bn$ (α = 3.7–5.6 at 0.15% ≤ c ≤ 0.3%) suggests that $T_{\mathit{x}\mathit{y}}$ linearly grows with Bn, as shown in Fig. 8. The similar linear relationship in dimension, ${\tau }_{\mathit{x}\mathit{y}}=\alpha {\tau }_y$, means the time-averaged shear stress depends mainly on yield stress. Since yield stress varies with gel concentration, the time-averaged shear stress can be taken as a constant, 204.0 ± 12.6, 258.0 ± 23.9, 322.0 ± 26.2, and 332.0 ± 23.0 Pa at the gel concentration of 0.15%, 0.2%, 0.25%, and 0.3%, respectively. The standard deviation is only 6%–9% of the mean shear stress. For human lung mucus, these results imply that high yield stress of mucus would lead to high shear stress, and consequently would be more likely to cause epithelial cell damage. Another related consequence is that high shear stress may induce more mucus secretion (Even-Tzur et al., 2008), which would increase chances of plug formation and airway blockage.

Compared with the pressure drop, the shear stress is about one order of magnitude smaller, τ_xy/Δp ∼ O(10⁻¹), and the yield stress about two orders of magnitude smaller, τ_y/Δp ∼ O(10⁻²). A numerical study shows the ratio of the maximum shear stress to the pressure drop is τ_max/Δp ∼ O(10⁻¹), in which τ_max is the von Mises stress (Zamankhan et al., 2012). In the terms of the magnitude order, the shear stress from the current study is comparable to the numerical results. It should be pointed out that the comparison here is made qualitatively, since the physical conditions are not exactly the same between the experimental and numerical study. In the numerical study, the Bingham fluid model is assumed, and the Bingham number range is 0–1.5. Generally, the pressure drop, as the force that drives the plug to rupture, is still the major influential factor in mucus plug rupture. Proper pressure drop control should be the major concern in clinical practice to avoid extra lung injury when using pressured gas to remove mucus or mucus plugs from lung airways.

In clinic practice, crackling sounds are used to detect lung injury due to diseases or mechanical reasons. An experimental study shows pressure waves accompanied with plug rupture can be taken as an indicator of crackling sounds (Huh et al., 2007). The sound intensity in this study is an indirect parameter defined by strain energy rate to estimate potential effects of plug deformation and rupture on crackling sounds. The results in Fig. 9 imply that strong crackling sounds would be most possibly detected in pathologic lung conditions with thick mucus.

D. Limitations of the study

The study on mucus plug in small airways is still at the preliminary stage. There were several limitations in the current study. We used non-biological materials, PDMS and C940 gels, to simulate the lung airway and mucus, respectively. PDMS channels have been wide practice in biological studies in vitro. The C940 gels have viscoelastic and viscoplastic properties close to human lung mucus at some concentration. However, their biological properties to cells have not been investigated. A study on plug rupture in PDMS channels with cells demonstrates damage to cells due to plug rupture (Huh et al., 2007). But the liquid plugs used in the study were made of Newtonian biological media, while human lung mucus is non-Newtonian. Currently, our efforts were made on fluid flow dynamics of mucus plug rupture, and we reduced requirements to biological similarity between our study and in vivo/in vitro situations of lung airways. Furthermore, we simplified the layered structure of lung airways, for example, neglecting the serous layer, to emphasize rupture dynamics of plugs with non-Newtonian properties. The in vivo or in vitro implications of the study were limited.

The properties of C940 gels (as well as mucus) are more than yield stress and shear-thinning, the main concerns in this study. In studies on Newtonian plug rupture, surface tension is one of the properties that determine stress in plug deformation and rupture (Halpern and Grotberg, 1993; Ghadiali and Gaver, 2003; and Wei et al., 2005). However, there have been no reliable methods to measure surface tension of C940 gels. C940 gels have yield stress and are not pervious to platinum measuring elements, both of which break down most current standard measurement techniques of surface tension (Goldin et al., 1972; Balmforth et al., 2010). Therefore, the surface tension was not included yet in the study.

The maximum transient normal strain rate at rupture, $\left|{\dot{\gamma }}_{\mathit{x}\mathit{x}}^t\right|$ = 28 s⁻¹ (Fig. 6(a)), was limited by the camera speed of 28 fps. Resolution of a CCD camera decreases with the camera speed increasing. For the CCD camera we used, 12-bit CoolSnap EZ, the speed of 28 fps was the highest feasible speed with a large enough view field. For the camera speed higher than 28 fps, the view region would be too small to cover the major part of a plug. A more advanced CCD camera with both high speed and large view would sure improve the results. Therefore, the current study was focused much on the time-averaged values, instead of the transient ones.

We supposed the plug deforms and ruptures in a quasi-two-dimensional channel with the aspect ratio of 12.5. The real deformation-rupture process could be three-dimensional, especially in the vicinity of the lateral walls. The definition of strain rates and shear stress in the current study combines with three-dimensional effects around the lateral walls, which have not been separated from the components on the xy-plane.

The sound intensity was defined based on the original dB-definition of sound, the ratio between two physical quantities. Here, the two quantities are the strain energy rates at the moments as the plug length Λ_L = 0 and 0.5. The sound intensity was introduced as an indication of potential sound emission, not a direct parameter to represent crackling sounds. The effective measurement of crackling sounds might still be sound waves, which however was not accessible to us yet. Crackling sounds can be caused by diseases or mechanics phenomena. Plug rupture might be one of the sources that send out crackling sounds. However, plug rupture has not been separated from other sources.

V. CONCLUSION

The C940 gels at low concentration, for example, 0.15%, can simulate diseased lung mucus with similar storage modulus, viscosity, or yield stress. The pressure drops applied upon plugs in the study are comparable to PEEP in the high-PEEP mechanical ventilation.

A plug needs to overcome yield stress before deformation and rupture. The plug takes relatively long time to yield as the Bingham number is large. We defined global strain rates to describe plug deformation and rupture. Plug length shortening is the more important deformation than shearing as gel concentration is higher than 0.15%. By contrast to sharp increase of strain rates at plug rupture, shear stress decreases due to the shear-thinning effect of the C940 gels. The human lung mucus with the similar shear-thinning property may reduce otherwise high shear stress transferred to epithelial cells, and therefore reduce epithelial cell damage. The films left at the channel walls might be long enough to enter into the neighbor airway, and form new plugs in the next breath cycle. The thickness of the films with non-Newtonian properties of shear-thinning and yield stress is smaller than that of the Newtonian films, which is favorable to mucus clearance.

The dimensionless time-averaged global shear rate and shear stress linearly increase with the Bingham number. In our study, the dimensionless shear stress is 3.7–5.6 times the Bingham number. In dimension, the shear stress magnitude is roughly one order lower than the pressure drop, and one order higher than the yield stress. Yield stress is a major property parameter that determines shear stress. The plug with higher yield stress would be more likely to cause epithelial cell damage. Crackling sounds emitted with plug rupture might be more detectable at higher gel concentration.