Engineering trypsin for inhibitor resistance

Abstract

The development of effective protease therapeutics requires that the proteases be more resistant to naturally occurring inhibitors while maintaining catalytic activity. A key step in developing inhibitor resistance is the identification of key residues in protease-inhibitor interaction. Given that majority of the protease therapeutics currently in use are trypsin-fold, trypsin itself serves as an ideal model for studying protease-inhibitor interaction. To test the importance of several trypsin-inhibitor interactions on the prime-side binding interface, we created four trypsin single variants Y39A, Y39F, K60A, and K60V and report biochemical sensitivity against bovine pancreatic trypsin inhibitor (BPTI) and M84R ecotin. All variants retained catalytic activity against small, commercially available peptide substrates [k_cat/K_M = (1.2 ± 0.3) × 10⁷ M⁻¹ s⁻¹. Compared with wild-type, the K60A and K60V variants showed increased sensitivity to BPTI but less sensitivity to ecotin. The Y39A variant was less sensitive to BPTI and ecotin while the Y39F variant was more sensitive to both. The relative binding free energies between BPTI complexes with WT, Y39F, and Y39A were calculated based on 3.5 µs combined explicit solvent molecular dynamics simulations. The BPTI:Y39F complex resulted in the lowest binding energy, while BPTI:Y39A resulted in the highest. Simulations of Y39F revealed increased conformational rearrangement of F39, which allowed formation of a new hydrogen bond between BPTI R17 and H40 of the variant. All together, these data suggest that positions 39 and 60 are key for inhibitor binding to trypsin, and likely more trypsin-fold proteases.

Introduction

Proteases are essential for nearly all biological processes. Their function and malfunction have been implicated in both the proliferation and treatment of medical conditions such as thrombus, cystic fibrosis, pancreatitis, hemophilia and many others.¹ The field of protease-based drug discovery has traditionally been focused on proteases as drug targets. However, growing attention has been concentrated on using proteases as therapeutic agents.^1–3 Several protease therapeutics have been approved by the Food and Drug Administration, and include treatments for several diseases including thrombus, stroke, myocardial infarction, hemophilia, sepsis, and exocrine pancreatic insufficiency.^1,4 Many other therapeutic proteases are currently in clinical and preclinical development, providing additional progression in treatments for conditions such as cystic fibrosis, vitreomacular adhesion, coeliac disease, psoriasis, and replacement gene therapy for calpainopathy (a limbgirdle muscular dystophy).¹ Some of these therapies use proteases in their endogenous form, while others use engineered and recombinant forms. One of the inherent difficulties in developing and advancing such therapeutics, however, is the natural occurrence of protease inhibitors that serve to regulate proteolytic activity. For example, serpins, which are tight-binding inhibitors that often target serine proteases, form serpin-protease complexes that are rapidly cleared from circulation.^5–8 Because of this, serpins often cause very short half-lives of protease therapeutics, especially those administered intravenously. Bypassing inhibition while maintaining catalytic activity will be crucial to the progression and development of potent protease therapeutics.

Trypsin is a canonical serine protease and the trypsin-fold is the most prevalent protease fold known in higher organisms.⁹ Furthermore, the majority of the currently marketed proteases use the trypsin-fold as a scaffold for therapeutic design¹ making trypsin itself the ideal model for further development of protease therapeutics. Consequently, identifying amino acid residues that specifically affect the interaction between trypsin and certain macromolecular inhibitors may guide and advance the development of trypsin-fold serine protease variants with increased half-lives. The co-crystal structures of trypsin and various macromolecular inhibitors reveal several conserved hydrogen bond interactions between the protease and the bound inhibitors. These interactions are often extended to P4′ of the inhibitor (Schechter and Berger notation¹⁰). In all the trypsin:inhibitor complexes compared, a consistent hydrogen bond occurs between the backbone atoms of both residue 41 of the protease and the P2′ residue of the inhibitor. In the trypsin:BPTI complex (PDB ID: 1TPA¹¹), an additional hydrogen bond exists between the P2′ R17 side chain and the H40 peptide oxygen (the S4′ subsite), possibly aiding in the stabilization of its interaction with the P2′ backbone carbonyl oxygen. Inspection of the crystal structure of tryspin bound to alaserpin (PDB ID: 1K9O¹²) shows that the hydroxyl group of trypsin residue Y39 hydrogen bonds to the P4′ peptide oxygen of alaserpin residue L355. Similar hydrogen bonds are formed with antithrombin-III bound to thrombin and Factor Xa (PDB IDs: 1SR5 and 2GD4). The same interaction is observed in complex between trypsin and bovine pancreatic trypsin inhibitor (BPTI) [PDB ID: 1TPA; Fig. 1(A)]. Ecotin, a serpin from Escherichia coli, differs from the other inhibitors in that it has a proline at the P4′ position, preventing similar hydrogen bond formation with Y39 of trypsin [PDB ID: 1EZS; Fig. 1(B)]. Additionally, K60 and Y39 of trypsin interact with each other through a charged hydrogen bond in all three of the previously mentioned trypsin-inhibitor complexes, regardless of the P4′ hydrogen bond presence, suggesting that K60 may influence the interaction between Y39 and the inhibitor.

Figure 1.

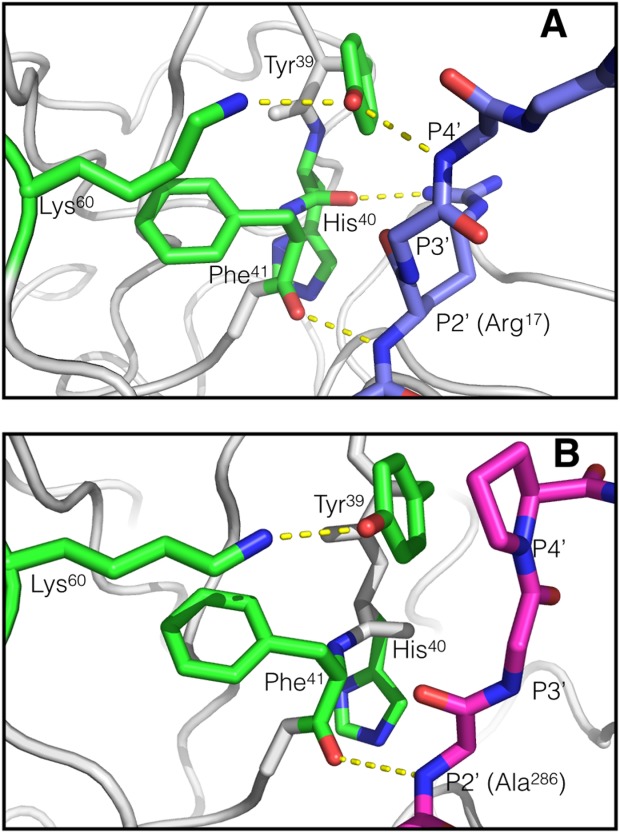
Structures of trypsin-inhibitor complexes. A. Trypsin-BPTI (derived from PDB ID: 1TPA¹¹). Trypsin residues are green and BPTI residues are blue, hydrogen bond interactions are in yellow dashed lines. There are two endogenous macromolecular inhibitor prime-side backbone interactions available when there is a hydrogen bond available at P4′. One prime-side side chain interaction (Arg¹³ of the inhibitor) is also apparent. B. Trypsin-ecotin (derived from PDB ID: 1EZS¹⁴). Trypsin is green and ecotin is magenta. The only prime-side backbone inhibitor interaction observed in ecotin is at P2′. The proline eliminates the possibility of hydrogen bond donation at P4′. Comparison of these two inhibitors provides a good assessment of the role of the P4′ hydrogen bond. Images were created using MacPyMol.¹⁵

In this article, we show that residues 39 and 60 are indeed important in the binding and modulation of interactions between BPTI and ecotin with trypsin. Based on computational data together with biochemical results, we demonstrate that substitutions at position 39 can increase (Y39F) or decrease (Y39A) sensitivity to BPTI. The data show that modifying prime side interactions can largely affect association with macromolecular inhibitors. Because BPTI offers a similar prime side binding interface to serpins, this work could be applied to current knowledge of trypsin-serpin interactions and provide important insight in developing other protease therapeutics with increased serpin resistance.

Results

Steady-state kinetics of Z-GPR-pNA hydrolysis

Because of its length, the chromogenic tripeptide N-α-benzoyloxycarbonyl-glycylprolylarginine p-nitroanilide (Z-GPR-pNA) cannot interact significantly with the S2′ subsite. The scissile bond in Z-GPR-pNA is between the arginine residue and the p-nitroanilide leaving group, which would place the pNA group in the P1′ position. Therefore, this substrate should interact with the enzyme at the S3-S1′ positions, which have not been altered in this study. The amino acid substitutions were made on P4′ prime-side binding interface and therefore should not alter the hydrolytic activity of the variants towards Z-GPR-pNA. To confirm this hypothesis, the hydrolytic activities of wild-type (WT) and trypsin variants Y39A, Y39F, K60A, and K60V towards Z-GPR-pNA were measured as described in Materials and Methods. The initial rate data for WT, Y39A, and K60A trypsin variants are shown in Figure 2. The steady-state Michaelis-Menten rate equation [Eq. (1)] was used to fit initial rates to determine steady-state kinetic constants for the hydrolysis of Z-GPR-pNA. Kinetic constants for WT, Y39F, Y39A, K60V, and K60A are summarized in Table I. As the data demonstrate, all trypsin variants that were characterized in this study were similar to wild-type trypsin in hydrolysis of Z-GPR-pNA. These results suggest that the respective active sites and overall tertiary structures of the S3-S1′ positions in the variants have not been significantly affected by the substitutions introduced at positions 39 and 60.

Figure 2.

Michaelis-Menten plot of WT (▪), Y39A (◆), and K60A trypsin (•) catalyzed hydrolysis of Z-GPR-pNA. All variants were similar to wild-type trypsin with respect to the kinetics of hydrolysis of the tripeptide substrate. Kinetic constants obtained from the described fits are summarized in Table I. Error bars represent the standard deviation of four trials.

Table I.

Steady-State Kinetic Constants for the Hydrolysis of Z-GPR-pNA by Trypsin Variants^a

Variant	kcat (min−1)	KM (µM)	kcat/KM (µM−1 min−1)
WT	4900 ± 100	8 ± 1	610 ± 80
Y39F	6890 ± 90	8.1 ± 0.6	720 ± 60
Y39A	4400 ± 100	7.6 ± 0.9	770 ± 90
K60V	6900 ± 100	9 ± 1	720 ± 90
K60A	5430 ± 80	9 ± 1	600 ± 70

^aKinetic constants were determined at 25°C in 50 mM HEPES, 100 mM NaCl, 20 mM CaCl₂ (pH 8.0) by fitting initial-rate data to the steady-state Michaelis-Menten rate equation [Eq. (1)]. Errors represent the standard deviations described in Figure 1.

Equilibrium inhibition studies

The short half-lives of current protease therapeutics are in large part due to the abundance of serpin inhibitors and corresponding receptors that remove the protease-serpin complexes.^1,16 To investigate the role of prime-side residues in the formation of such complexes, two inhibitors, BPTI and M84R ecotin, were selected based on their binding interfaces compared with other trypsin-inhibitor complexes. To determine the time it took to reach equilibrium, each trypsin variant was mixed with 10 to 100 nM BPTI or 1 to 6 nM M84R ecotin at saturating concentrations of the tripeptide substrate Z-GPR-pNA and monitored spectrophotometrically for 1 hour. Equilibrium was considered to have been reached when the change in absorbance at 410 nm no longer increased over time. To ensure that the Z-GPR-pNA concentrations remained at saturating levels throughout the assay, the activity of the uninhibited trypsin variant was monitored simultaneously. The fraction of free enzyme at equilibrium was calculated by comparing the initial rates of the variants after being incubated with inhibitor to the initial rates observed by equal total concentrations of the respective variants in the absence of inhibitor [Eq. (2)]. The fraction of free enzyme in presence of BPTI and M84R ecotin are illustrated for the variants in Figure 3(A,B), respectively. All prime-side trypsin variants described in this article interacted with the inhibitors differently than wild-type trypsin, suggesting that these residues play a role in macromolecular inhibitor binding.

Figure 3.

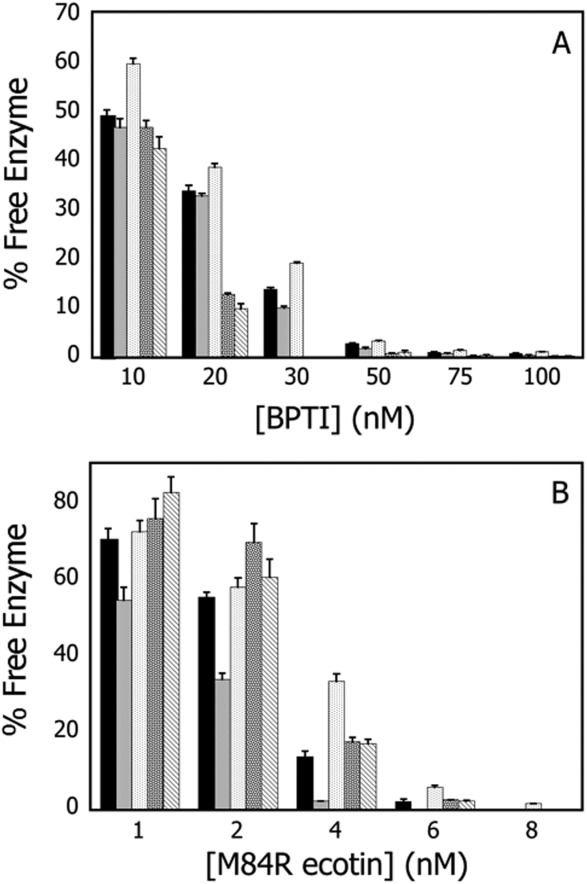
Equilibrium inhibition kinetics: BPTI and M84R ecotin. Amount of free trypsin after equilibration with BPTI and M84R ecotin for (left to right at each inhibitor concentration) WT, Y39F, Y39A, K60V, and K60A. A. BPTI. Amount of free trypsin after equilibration with 10 to 100 nM BPTI. B. M84R ecotin. Amount of free trypsin after equilibration with 1 to 8 nM M84R ecotin. Data are summarized in Tables II and III.

Equilibrium kinetics

Compared with all trypsin variants characterized in Figure 3, Y39A was the only variant less sensitive to inhibition than WT after incubation with BPTI. After a 10-min incubation at 25°C with 10 to 100 nM BPTI, WT trypsin displayed 51 to 99% inhibition (Table II). The Y39A substitution also resulted in a less favorable association with M84R ecotin. After a 20-min incubation at 25°C with 1 to 8 nM M84R ecotin, WT trypsin showed 30 to 100% inhibition. Thus Y39A displayed a decreased interaction with M84R ecotin in comparison with WT trypsin as demonstrated by the relative increased amounts of free enzyme after incubation (Table III). Conversely, Y39F showed less free enzyme in the presence of either BPTI or M84R ecotin than WT trypsin, suggesting that this substitution increased the favorability of interaction between the enzyme and the inhibitors. (Tables II and III).

Table II.

Percentage of Free Trypsin Variant after Equilibration with BPTI^a

	% Free enzyme after BPTI incubation
Variant	10 nM BPTI	20 nM BPTI	30 nM BPTI	50 nM BPTI	75 nM BPTI	100 nM BPTI
WT	49 ± 1	34 ± 1	13.9 ± 0.3	2.8 ± 0.1	1.05 ± 0.07	0.79 ± 0.03
Y39F	47 ± 2	33.0 ± 0.5	10.1 ± 0.4	1.8 ± 0.3	0.7 ± 0.1	0.41 ± 0.05
Y39A	60 ± 1	38.9 ± 0.8	19.2 ± 0.3	3.2 ± 0.1	1.45 ± 0.02	1.10 ± 0.02
K60V	47 ± 1	12.8 ± 0.4	–	0.72 ± 0.09	0.29 ± 0.11	0.17 ± 0.02
K60A	43 ± 2	10 ± 1	–	1.0 ± 0.4	0.35 ± 0.08	0.24 ± 0.03

^a% Free enzyme was determined at 25°C in 50 mM HEPES, 100 mM NaCl, 20 mM CaCl₂ (pH 8.0) using the fraction of initial rates [Eq. (2)]. Errors were determined from four trials.

Table III.

Percentage of Free Trypsin Variant after Equilibration with M84R Ecotin^a

	% Free enzyme after M84R ecotin incubation
Variant	1 nM M84R	2 nM M84R	4 nM M84R	6 nM M84R	8 nM M84R
WT	71 ± 3	55 ± 1	14 ± 2	2.0 ± 0.7	N/D
Y39F	55 ± 1	34 ± 2	2.1 ± 0.1	N/D	N/D
Y39A	73 ± 4	58 ± 2	34 ± 2	5.8 ± 0.4	1.48 ± 0.05
K60V	83 ± 4	61 ± 5	17 ± 1	2.2 ± 0.14	N/D
K60A	76 ± 3	70 ± 5	18 ± 1	2.4 ± 0.1	N/D

^a% Free enzyme was determined at 25°C in 50 mM HEPES, 100 mM NaCl, 20 mM CaCl₂ (pH 8.0) using the fraction of initial rates [Eq. (2)]. Errors were determined by four trials.

N/D = not detected; describes a signal that was less than three times that of the noise.

The K60 variants showed the lowest amount of free enzyme after incubation with BPTI in comparison with WT and the Y39 variants described in Figure 2, indicating that these variants are more sensitive to inhibition by BPTI. K60V was more strongly inhibited by BPTI than K60A (Table II). In contrast to the results found with BPTI, the K60 trypsin variants were less inhibited by M84R ecotin than WT trypsin. After incubation with 1 to 8 nM M84R ecotin, K60A displayed 24 to 97.6% inhibition, while K60V displayed 17 to 97.8% inhibition compared with wild-type trypsin under the same conditions, the K60 variants show a relative increase in free enzyme ranging from 8 to 30% (Table III).

Burst inhibition studies

Equilibrium inhibition studies provide insight to protease-inhibitor interaction after association has been established. Many protease therapeutics currently approved by the Food and Drug Administration have half-lives shorter than the time it takes to reach binding equilibrium, and therefore it is not likely that binding equilibrium is established under biological conditions. One means to having an effective therapeutic agent is to the rate of association or increase the rate of dissociation of the protease-inhibitor complex. Burst kinetic methods reveal kinetic details about the trypsin-inhibitor association in the form of on/off rates. An observed rate, k_obs as described by the slow, tight-binding burst equation [Eq. (3)], can be extracted from the data obtained by monitoring the cleavage of Z-GPR-pNA in the presence of the inhibitor. When performed under saturating substrate conditions, the observed change in rate will reflect the changing amount of free enzyme. Plotting these extracted k_obs rates against inhibitor concentrations can be used to determine the association rate (k_on) and dissociation rate (k_off) with BPTI under specific conditions (described in Materials and Methods). Determining the association rates of trypsin with BPTI provides important information since proteases often have short half-lives due to effective tight binding inhibitors such as serpins. Studying inhibition association without prolonged incubation can help design therapeutic agents, which result in a longer half-life. The trypsin variants tested in this work were mixed with BPTI under saturating substrate concentrations in order to determine how rapidly BPTI associates and dissociates with the different prime-side variants.

Wild-type trypsin was mixed with saturating concentrations of Z-GPR-pNA and 1 to 10 μM BPTI in order to determine k_obs. Plotting k_obs against inhibitor concentration revealed a k_on and k_off of 5.5 × 10⁻³ μM⁻¹ s⁻¹ and 2.5 × 10⁻³ s⁻¹, respectively (Table IV). The burst data obtained for position 39 variants showed that Y39A is the only variant that, compared with WT, had a lower association rate (4.1 × 10⁻³ μM⁻¹ s⁻¹) and faster dissociation rate (3.3 × 10⁻³ s⁻¹) with BPTI, while Y39F appears to have a slightly faster association rate (6.7 × 10⁻³ µM⁻¹ s⁻¹) and a slower dissociation rate (2.4 × 10⁻³ s⁻¹) (Table IV).

Table IV.

Burst Kinetic Constants for Hydrolysis of Z-GPR-pNA in Presence of BPTI by Trypsin Variants^a

	Burst kinetic constants
	kobs (×10−2)
Variant	1 µM BPTI	2 µM BPTI	4 µM BPTI	10 µM BPTI	kon (µM−1 s−1)	koff (s−1)
WT	0.87b	1.25 ± 0.03	3.0 ± 0.1	1.3 ± 0.1	5.5 x 10−3	2.5 x 10−3
Y39F	0.88b	1.61b	3.57 ± 0.04	5.22 ± 0.2	6.7 x 10−3	2.4 x 10−3
Y39A	0.64 ± 0.04	1.18 ± 0.05	2.56 ± 0.03	4.4 ± 0.1	4.1 x 10−3	3.3 x 10−3
K60V	1.41 ± 0.01	3.5 ± 0.1	7.5 ± 0.4	N/D	1.48 x 10−2	2.0 x 10−4
K60A	1.23 ± 0.01	2.70 ± 0.05	5.5 ± 0.4	N/D	1.04 x 10−2	3.8 x 10−3

Standard deviation of these values was less than 1%.

^a% Free enzyme was determined at 25°C in 50 mM HEPES, 100 mM NaCl, 20 mM CaCl₂ (pH 8.0) using the fraction of initial rates [Eq. (2)]. Errors were determined by four trials.

^bErrors of these values were less than 1%.

N/D = not detected; describes a signal that was less than three times that of the noise.

The k_on and k_off values for trypsin variants at position 60 were calculated from burst inhibition studies as described in Materials and Methods. In comparison with all other trypsin variants described in this work, the position 60 variants had both the highest k_on by nearly three times and lowest k_off with BPTI. K60V had both the highest association rate of 1.5 × 10⁻² s⁻¹ μM⁻¹ and lowest dissociation rate of 1.9 × 10⁻⁴ s⁻¹ compared with K60A (Table IV).

Molecular dynamics

Molecular dynamics (MD) simulations and the molecular mechanics-Generalized Born surface area (MM-GBSA) method were employed to examine conformational dynamics and binding energies of BPTI to WT, Y39A, and Y39F variants. The conformational stability of the MD simulations was evaluated by calculating main chain RMSD values for the protein:BPTI complexes. Figure 4 shows the evolution of the RMSD values from the crystal structure for the WT:BPTI, Y39A:BPTI, and Y39F:BPTI complexes. Based on the RMSD values, the conformational stability was achieved right after the equilibration phase (first 20 ns) and showed a plateau for the rest of the 1 μs simulation, indicating that the model structure had reached a conformational steady state. The RMSD deviations were in the range expected for the system of that size (less than 0.6Å). The calculation of binding free energies between BPTI and its receptors (WT, Y39A, and Y39F) showed that the lowest binding energy was observed for the Y39F:BPTI complex. The relative binding free energy difference for this complex was 3.58 kcal/mol lower than the WT:BPTI complex (Table V). ΔG_WT:BPTI and ΔG_Y39F:BPTI were −184.9 and −188.5 kcal/mol, respectively. The loss of the hydrogen bond interaction between Y39A at the P4′ position was reflected by Y39A's higher binding energy to BPTI (−170.7 kcal/mol) compared with binding energy of the WT:BPTI complex (ΔΔG = 14.18 kcal/mol; Table V). In order to confirm statistical significance of the reported energies differences we performed t-test analysis. The statistical analysis showed that P values for ΔG comparison of means were less that 0.0005 indicating that described differences are statistically significant. For example, for the WT/Y39A comparison the t = −33.09 with p < 0.0001, for the WT/Y39A comparison t = −3.89 with p = 0.0003 and for the Y39A/Y39F comparison t = 29.18 with p < 0.0001.

Figure 4.

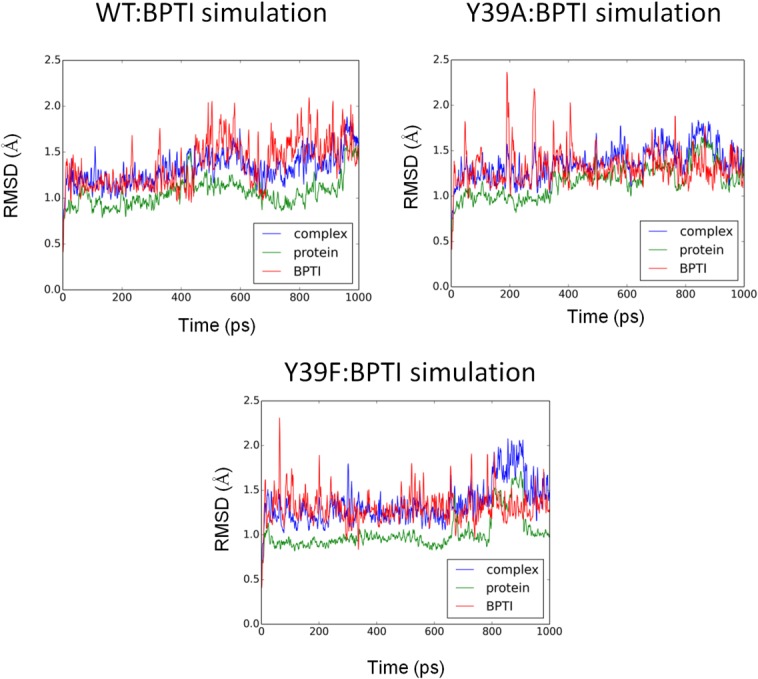
The evolution of the RMSD values from the crystal coordinates as a function of the simulation time for the complex, protein and BPTI of the WT:BPTI, Y39A:BPTI, and Y39F:BPTI structures. The average values for the WT:BPTI simulations: complex 1.32 ± 0.20 Å, protein 1.06 ± 0.17 Å, and 1.37 ± 0.28 Å, for the Y39A:BPTI simulations: complex 1.37 ± 0.19 Å, protein 1.16 ± 0.18 Å, and 1.32 ± 0.23 Å and for the Y39F:BPTI simulations: complex 1.35 ± 0.25 Å, protein 1.02 ± 0.18 Å, and 1.31 ± 0.21 Å.

Table V.

Calculated Relative Binding Free Energies Between BPTI and Trypsin Variants

	Binding energy (kcal/mol)
	WT	Y39A	Y39F
Complex	−5554.41	−5524.57	−5529.65
Enzyme	−3699.20	−3683.54	−3670.86
BPTI	−1670.29	−1670.29	−1670.29
ΔG	−184.92	−170.74	−188.50
ΔΔGY39→X	0 (X = Y39)	14.18 (X = A39)	−3.58 (X = F39)

The residue at position 39 showed distinctly different conformational behavior in Y39F:BPTI compared with Y39 or A39 in the WT:BPTI and Y39A:BPTI simulations. The loss of the hydrogen bond at position P4′ of BPTI and Y39 of trypsin (occupied 73% in the WT:BPTI complex during MD simulations) resulted in conformational freedom of the F39 residue. This residue rotates out of the position normally occupied by Y39 in the WT:BPTI complex and positions its side chain against the R17 side chain at position P2′ of BPTI for 68% of the simulation. Figure 5 shows representative conformations for the WT:BPTI [Fig. 5(A)] and Y39F [Fig. 5(B)] complexes. Three distinct conformational families were identified for F39 based on the Hα-Cα-Cβ-Cγ dihedral angle [Fig. 6(A)]. The conformation allowing direct contact between F39 and R17 was 68% occupied. The 18% occupancy corresponds to solvent exposed conformation and the remaining 14% corresponds to the position of F39 near BPTI I19, which is similar to position Y39 in the WT:BPTI complex.

Figure 5.

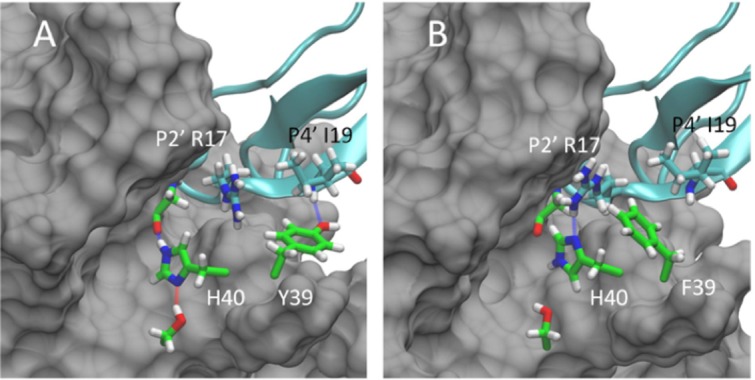
Representative conformations for the WT:BPTI (A) and Y36F:BPTI (B) complexes based on separate 500 ns MD simulations. In the WT:BPTI complex Y39 (shown in green, panel A) is positioned near P4′ I19 and forms a stable hydrogen bond interaction with the backbone amine. In the Y36F complex F39 (shown in green, panel B) moves out of position near I19 toward P2′ R17 in BPTI. This reposition allows R17 to form a new hydrogen bond with H40 of trypsin (blue line, panel B), which is absent in the WT:BPTI complex (panel A). The formation of the new hydrogen bond and the position of F39 against the R17 side chain both stabilize the Y39F:BPTI complex. The binding free energy for the Y39F:BPTI complex is 3.58 kcal/mol lower than the WT:BPTI complex and 17.76 kcal/mol lower than the Y39A:BPTI complex. The improved stability of the Y39F:BPTI complex correlates with the biochemically observed higher sensitivity of Y39F relative to WT and Y39A.

Figure 6.

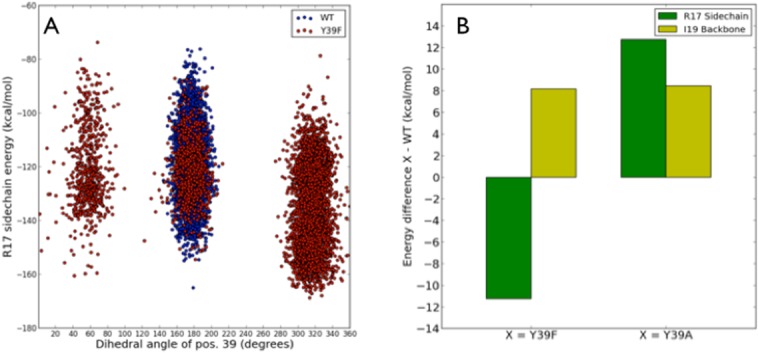
(A) Plot of the F39 Hα-Cα-Cβ-Cγ dihedral angle values against the BPTI R17 side chain energy. The three conformational families observed for the Y39F:BPTI complex had occupancies of 18% (solvent exposed), 14% (similar to position of Y39 in WT), and 68% (against R17) from left to right, respectively. The highest occupied family corresponds to F39 in direct contact with R17. (B) The energy difference for the BPTI R17 side chain and the BPTI I19 backbone for Y39F and Y39A:BPTI complexes relative to the WT:BPTI complex. The green bars represent the energy of the R17 side chain in the Y39F and Y39A complexes relative to WT. Yellow bars represent the energy of the I19 backbone in the above variants relative to WT. The most favorable binding energy was observed for the R17 side chain in the Y39F complex due to formation of the hydrogen bond between the amine group of BPTI R17 and imidazole Nδ of H40 in the trypsin variants. The loss of the hydrogen bond interaction between BPTI I19 and trypsin variants results in the unfavorable binding energy relative to WT.

In the WT:BPTI simulation, BPTI R17 forms no specific interaction with trypsin and displayed noticeable conformational flexibility, described by the root mean squared deviation (RMSD 2.06 ± 0.72 Å). The RMSD values were measured relative to the position of R17 in the crystal structure. In the Y39F:BPTI complex the rotation of F39 pressed R17 against trypsin at residues Y151, P152, and D153, reducing R17 flexibility (RMSD 1.50 ± 0.56 Å). In this conformation, the side chain of R17 forms a new hydrogen bond with the side chain Nδ of trypsin H40 [Fig. 5(B), blue line] which was not observed in the WT:BPTI simulation. This hydrogen bond was occupied at least 38% of the simulation time in the Y39F:BPTI simulation. In the WT:BPTI simulation, the imidazole ring of H40 forms two hydrogen bonds with adjacent trypsin residues (hydroxyl of S32 [red line, Fig. 5(A)] and peptide oxygen of G193 [blue line, Fig. 5(A)], while these two hydrogen were broken in Y39F.

Using MM-GBSA energy analysis, we extracted the energies of the R17 side chain and the P4′ site (I19 backbone) of BPTI to examine the character of the two hydrogen bond sites. Figure 6(B) shows the energy differences for the R17 side chain and the I19 backbone for Y39F and Y39A complexes relative to the WT complex. The mean energy of the I19 backbone was 1.237 kcal/mol for WT and 9.392 and 9.672 kcal/mol for Y39F and Y39A complexes, respectively. When considering the R17 side chain, the lowest energy was calculated for the Y39F complex (−148.1 kcal/mol) which is 11.30 kcal/mol lower than the WT complex (−136.8 kcal/mol) [Fig. 6(B)], while the R17 side chain energy for the Y39A complex (−124.1 kcal/mol) is 12.70 kcal/mol higher than the WT complex.

Discussion

An unavoidable impediment to the development of protease therapeutics is the presence of naturally occurring protease inhibitors. Such inhibitors exist to regulate normal proteolytic activity, but also decrease the half-life of therapeutic proteases that are artificially introduced. Any advances to be made in this area must circumvent this problem. By inspecting structures of existing trypsin-inhibitor complexes found in the protein data bank, we have identified two conserved residues, tyrosine 39 and lysine 60, whose substitution offer promise in this area. Data from our equilibrium inhibitor experiments with the Y39A trypsin variant and BPTI showed an increased amount of free enzyme at equilibrium suggesting that interactions between it and BPTI were weakened compared with wild-type trypsin. Structurally, the removal of the phenol side chain eliminates hydrogen bond capability with both the inhibitor residue at the P4′ position and K60 in trypsin itself. The removal of these two prime-side hydrogen bonds resulted in an increase of active Y39A trypsin concentration after incubation with BPTI. The Y39F variant was expected to exhibit similar behavior to Y39A since both variants eliminate the two hydrogen bonds. However, the equilibrium kinetics, burst kinetics, and binding energy simulation results indicate that Y39F binds more tightly to BPTI than WT. Molecular dynamics revealed that, although the P2′ hydrogen bond with trypsin was indeed eliminated, it was replaced by a new hydrogen bond between the P2′ R17 side chain and the trypsin H40 side chain. The replacement of the P4′ hydrogen bond with an H40-R17 hydrogen bond appears to account for the ability of Y39F to bind BPTI at least as tightly as WT. This hydrogen bond, as well as the “pinching” of R17 by F39, stabilizes the Y39F:BPTI complex relative to the WT:BPTI and Y39A:BPTI complexes. This agrees well with the biochemical data showing the Y39F variant to be more sensitive to inhibition by BPTI than WT and F39A. The relative decrease in the binding energy correlates with biochemically observed increased inhibitor sensitivity for the Y39 variants. These data provide insight into the importance of the P2′ R17 side chain in the sensitivity of trypsin to BPTI. The role of the P3 arginine in the stabilization of the protease:inhibitor complex has been previously demonstrated for the BPTI Kunitz-type inhibitor complexed with the serine protease bovine pancreatic trypsin.¹⁷

Due to the proline at position P4′ of ecotin, it is chemically impossible for the backbone amide to donate a hydrogen bond to the hydroxyl group of Y39 in trypsin, although it could be a hydrogen bond acceptor [Fig. 1(B)]. However, the distance between the backbone nitrogen of the P4′ proline of ecotin is 4.0 Å from the hydroxyl oxygen of Y39 making it unlikely that Y39 is donating a hydrogen bond to the proline nitrogen. Additionally, the proline and tyrosine rings are positioned such that hydrophobic stacking interactions are maximized. This absence of hydrogen bonding capability suggests that the differences in ecotin interaction between WT and Y39A likely come from the steric and possibly stabilizing presence of tyrosine at position 39, and not from the ability to hydrogen bond to position P4′ of its inhibitor. The phenyl ring of Y39, which is absent in Y39A, interacts favorably with the P4′ proline through hydrophobic stacking interactions, leading to stronger bind of ecotin by wild type. The increased sensitivity of the Y39F variant to ecotin may be explained similarly. The hydrophobic stacking interaction is conceivably strengthened since the hydroxyl group is no longer present to be attracted to K60.

Residues Y39 and K60 in trypsin interact with each other through a charged hydrogen bond between their side chains. When bound to BPTI, the hydroxyl group of Y39 simultaneously participates in hydrogen bonding with the inhibitor. Interestingly, in contrast to the Y39 variants, the K60 variants showed increased sensitivity to BPTI inhibition and decreased sensitivity to ecotin inhibition. In these variants, the P4′ hydrogen bond between the Y39 hydroxyl group and BPTI is still possible. Therefore, the differences in affinity observed with the K60 variants arise from the loss of the influence K60 had on Y39. Substitutions at position 60 resulted in variants that bound more tightly to BPTI, indicating the role of K60-Y39 interaction in the trypsin-BPTI complex. In the absence of the P4′ hydrogen bond in the case of ecotin, K60 variants showed less sensitivity than WT. The K60V variant is less sensitive to inhibition than the K60A variant, suggesting that increasing the size of the side chain moiety negatively affects ecotin binding. The loss of the charged hydrogen bond interaction likely allows Y39 more conformational flexibility which would reduce the strength of the interactions between this residue and the inhibitors. The resulting weakened interaction between Y39 and P4′ proline of ecotin could explain the reduced sensitivity of the K60 variants. Furthermore, increased Y39 fluctuation could have an impact on the P2′ hydrogen bond, which was present in all protease-inhibitor crystal structures examined. Molecular dynamics simulations of the Y39F:BPTI complex showed that F39, a hydrophobic residue, spent 18% of the simulation immersed in solvent. With the loss of the K60-Y39 hydrogen bond interaction to restrict its motion, one could predict that Y39, a more hydrophilic residue, would spend more time fluctuating in solvent compared with F39. Increased Y39 fluctuation caused by K60 mutations could have a detrimental impact on P4′ interactions and the P2′ hydrogen bond, causing an overall destabilization of trypsin:ecotin interactions.

Y39A was the only trypsin variant that was less inhibited than wild type in the presence of both BPTI and ecotin. Computational analysis presented in this work suggests that the lower inhibition of Y39A by BPTI corresponds with the absence of the hydrogen bond at the P4′ position, resulting in a 14.18 kcal/mol relative binding energy increase compared with wild-type. Substitution of Y39 with F39 unexpectedly increased sensitivity to BPTI, which correlated with the lowest calculated binding free energy reported here. In the Y39F:BPTI complex, F39 undergoes a conformational shift due to its inability to form a hydrogen bond with position P4′. This allows for closer contact between Y39F trypsin and the inhibitor resulting in a new hydrogen bond between P2′ R17 and trypsin H40 that further stabilizes the Y39F:BPTI complex relative to Y39A:BPTI and WT:BPTI complexes.

Of the variants tested in this study, Y39A appears to be the most promising trypsin variant to be considered in protease therapeutic scaffold design with overall increased inhibitor-resistance in comparison with wild type. In addition, the biochemical data with K60 variants suggests that increased and decreased interactions with BPTI versus M84R ecotin, respectively, in comparison with wild type, demonstrate potential for one to control the degree of serpin-resistance through specific prime-side interactions. The difference in inhibition between the K60 variants and the Y39 variants support the hypothesis that a single residue within the prime-side binding interface can significantly influence macromolecular inhibitor interactions. Evaluation of these substitutions in relation to their corresponding inhibitor complex interactions may provide useful insight for the development of additional engineered trypsin-fold proteases with inhibitor-resistance towards specific inhibitors, including serpins. Fine-tuning desired inhibitor-binding characteristics of trypsin-fold proteases will be essential for the advancement of protease therapeutics.

Materials and Methods

Generation of wild-type and variant zymogens

Trypsinogen variants were expressed as previously described.¹⁸ Postexpression, P. pastoris X-33 yeast cells were removed from growth media by centrifugation. The supernatant was collected and NaCl and MES were added to final concentrations of 3 M and 20 mM, respectively. The final buffered supernatant was adjusted to pH 6.0. The high-salt supernatant was then loaded onto a phenyl sepharose hydrophobic interaction chromatography column (GE Healthcare) that was equilibrated with high-salt equilibration buffer (3 M NaCl, 20 mM MES, pH 6.0) on a Pharmacia FPLC system. The column was then washed with the high-salt equilibration buffer and eluted in 5 mL fractions using a negative linear salt gradient (3-0 M NaCl in 20 mM MES, pH 6.0). Trypsinogen-containing fractions were identified by zinc-imidazole staining of 10% tricine-PAGE gels. The trypsinogen-containing fractions were combined and dialyzed into 10 mM glycine, pH 3.0, overnight at 4°C and stored at −20°C until further use.

Autoactivation of trypsin variant zymogens

Zymogen variants were dialyzed into an activation buffer composed of either 20 mM HEPES or Tris and 2 mM CaCl₂ (pH 8.0) at room temperature. Activation was considered to be complete when time-course active-site titrations showed no increase in active enzyme concentrations.

Active-site titration

The active-site concentrations of the trypsin variants were determined by monitoring the cleavage of the fluorogenic titrant 4-methylumbelliferyl p-guanidinobenzoate (MUGB, λ_ex = 360 nm, λ_em = 450 nm) as described.¹⁸ The titration was performed in kinetic assay buffer (50 mM HEPES, 100 mM NaCl, 20 mM CaCl₂, pH 8.0) at 25°C. After 30 s of data collection, 10 µL of trypsin variant was added to a final volume of 500 µL. The difference in fluorescence before and after the addition of the trypsin variant was used in conjunction with a standard curve constructed with 4-methylumbelliferone to calculate the concentration of the active enzyme.

Separation of mature trypsin from trypsinogen variants

Mature trypsin was purified from the trypsin/trypsinogen mixture via a 2 mL p-amino benzamidine (pAB) affinity column. The active trypsin was eluted from the pAB resin using 3 to 5 mL of 0.1 M acetic acid wash. The fractions were collected and quantified by active-site titration as previously described.¹⁸ The fractions with the highest concentrations of active enzyme were combined and dialyzed into 10 mM glycine, pH 3.0 overnight at 4°C. The final products were evaluated for purity by 14% tricine-PAGE.

Kinetic characterization

Stock solutions of the tripeptide N-α-benzoyloxycarbonyl-glycylprolylagrinine p-nitroanilide (Z-GPR-pNA) were prepared in 100% DMF, and concentrations were determined by total hydrolysis as previously described.¹⁸ Cleavage of Z-GPR-pNA was monitored spectrophotometrically for 3 to 5 min at 410 nm using a Spectramax M5 and M2 spectrophotomters (Molecular Devices, Sunnyvale, CA). All assays were carried out in a final volume of 250 µL using kinetic assay buffer at pH 8.0 and 25°C, 0.5 nM trypsin variant and 5 to 300 µM Z-GPR-pNA in a clear, flat-bottom 96-well assay plate (Costar). Kinetic reactions were initiated by the addition of 2 to 30 µL of substrate.

Equilibrium inhibition studies

Trypsin variants were incubated with various concentrations of BPTI or M84R ecotin in 50 mM HEPES, 100 mM NaCl, and 20 mM CaCl₂ buffer at pH 8.0 in a 25°C water bath for 10 to 20 min. Hydrolytic activity of the enzyme:inhibitor solution toward Z-GPR-pNA was monitored. Kinetic reactions were initiated by the addition of 2 to 10 µL of substrate to the enzyme:inhibitor mixture and equilibrium was taken to have been established when there was no longer a change in the rate of substrate cleavage.

Burst bovine pancreatic trypsin inhibitor (BPTI) inhibition studies

Trypsin variants and approximately 200 µM Z-GPR-pNA were mixed in 50 mM HEPES, 100 mM NaCl, and 20 mM CaCl₂ buffer at pH 8.0 and 25°C and combined with 1 to 10 µM BPTI in a clear, flat-bottom Costar 96-well assay plate. Rates of cleavage were monitored as described for kinetic characterization.

Kinetic data analysis

Kinetic constants, k_cat, K_M, and k_cat/K_M for steady-state conditions were determined using the graphing and data analysis software program KaleidaGraph (Synergy Software) and the Michaelis-Menten equation [Eq. (1)].

(1)

The amount of free enzyme was determined by spectrophotometrically monitoring the rate of cleavage of Z-GPR-pNA at 410 nm for 3 to 5 min before and after the incubation using Eq. (2) where V_i is the cleavage rate of the inhibited enzyme and V₀ is that of the uninhibited enzyme.

(2)

To determine k_on and k_off rates, burst kinetic analysis was plotted and fit for a slow, tight-binding inhibitor to determine different rate constants using Eqs. (3) and (4) where V_o is the initial rate, ΔV is the difference in velocity, and k_obs is the observed rate constant, x is time, k_on is the on rate, and k_off is the off rate:

(3)

(4)

Molecular dynamics

The binding free energies between BPTI and wild-type/variants were calculated by using the Generalized Born (GB) implicit solvent method based on molecular dynamics (MD) explicit water simulations. The MM-GBSA program in AMBER 12^13,19–22 was used to calculate the energy difference, defined as ΔG = <G_R•L> − <G_R> − <G_L> where <G_R•L>, <G_R>, and <G_L> are the mean energies of three different simulations for trypsin:BPTI complex (R•L), trypsin (R), and BPTI (L), respectively. <G_R•L> was calculated based on MD simulation of the three trypsin BPTI complexes (WT:BPTI, Y39F:BPTI, and Y39A:BPTI), while <G_R> and <G_L> were calculated from the separate simulations of trypsins and BPTI. A total of seven independent simulations were needed to compare the binding energies of WT, Y39F, and Y39A, using the same energy term for <G_L> for each variant ΔG calculation. After simulation, each system was reprocessed using MM-GBSA in order to determine the energy corrections due to solvation using the second GB OBC model as described by Onufriev et al.²³

The MD simulation setup used in this work is similar to procedures previously reported by us and others for various proteases including trypsin variants.^24–29 The initial coordinates for the WT:BPTI complex were obtained from the PDB (PDB ID: 1TPA¹¹). For each binding energy calculation, R•L, R, and L systems were created based on cattle trypsin bound to BPTI since this trypsin-fold is largely identical to rat trypsin. Each system was solvated using TIP3 explicit water box with at least 8 Å of surrounding water on each side, with chloride ions added to neutralize the system. The Particle Mesh Ewald (PME) method was used to treat long-range electrostatics using a cutoff of 10 Å.³⁰

The MD procedure consisted of five preproduction steps using the isobaric-isothermal ensemble (NPT) before production level simulation using the canonical ensemble (NVT). The procedure used is as follows: minimization with restraints, minimization with no restraints, heating from 100 to 300 K, equilibration with restraints, and finally equilibration with no restraints. The initial minimization used 500 steps of steepest descent followed by 500 steps of the conjugate gradient method with a restraint of 100 kcal/mol on the solute. This was followed by 500 steps of no restraint steepest descent and conjugate gradient minimization. The system was then heated to 300 K starting from 100 K over a 50 ps time frame using a 2 fs time step throughout. Where applicable, stages used Langevin dynamics with a 5 ps coupling parameter. Equilibration with restraints used a 1.0 ps weak-coupled barostat and a 20 kcal/mol restraint on solute over the course of 5 ns. Another 5 ns of equilibration followed with no restraint putting the total amount of preproduction simulation time at 10 ns for each system. All systems were submitted to 500 ns production simulation. A total of seven simulations were run with a combined simulation time of 3.5 μs. The trajectories were sampled at 0.1 ns intervals to calculate the binding energy, for a total of 5000 data points per simulation. All MD simulations were performed using a 4× NVIDIA M2090 GPU machine.

Glossary

BPTI

bovine pancreatic trypsin inhibitor

MD

molecular dynamics

MM-GBSA

molecular mechanics generalized born surface area

WT

wild-type

Z-GPR-pNA

N-α-benzoyloxycarbonyl-glycylprolylagrinine p-nitroanilide