Abstract
Motivated by data recording the effects of an exercise intervention on subjects’ physical activity over time, we develop a model to assess the effects of a treatment when the data are functional with 3 levels (subjects, weeks and days in our application) and possibly incomplete. We develop a model with 3-level mean structure effects, all stratified by treatment and subject random effects, including a general subject effect and nested effects for the 3 levels. The mean and random structures are specified as smooth curves measured at various time points. The association structure of the 3-level data is induced through the random curves, which are summarized using a few important principal components. We use penalized splines to model the mean curves and the principal component curves, and cast the proposed model into a mixed effects model framework for model fitting, prediction and inference. We develop an algorithm to fit the model iteratively with the Expectation/Conditional Maximization Either (ECME) version of the EM algorithm and eigenvalue decompositions. Selection of the number of principal components and handling incomplete data issues are incorporated into the algorithm. The performance of the Wald-type hypothesis test is also discussed. The method is applied to the physical activity data and evaluated empirically by a simulation study.
Keywords: Longitudinal data, Mixed-effects model, Penalized splines, Physical activity measurement, Principal components
1. Introduction
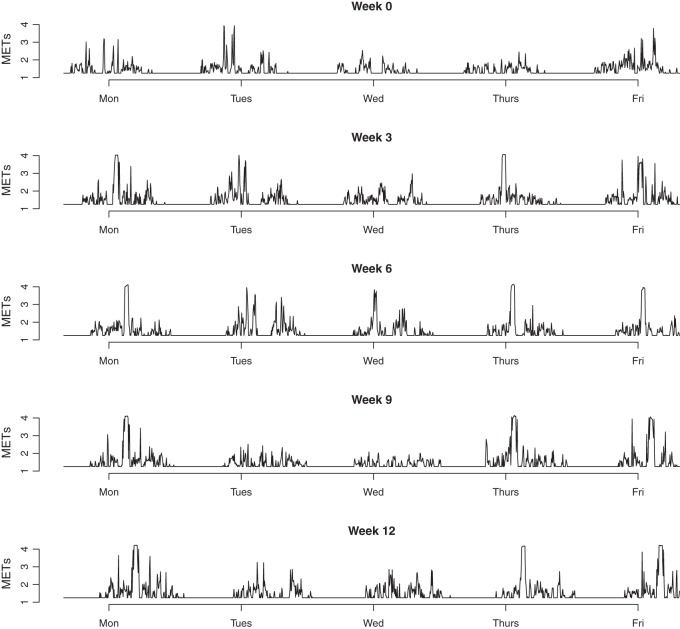
Motivated by data from an exercise intervention trial, we consider the problem of evaluating the effects of the intervention in the presence of 3-level functional data, with possibly missing, or unbalanced, observations. The data are from Kozey-Keadle and others (2014) and consist of estimates of relative energy expenditure (metabolic units, or METs) on 63 inactive individuals every 5 min. We consider data from 5 days a week (Monday through Friday) for 5 separate weeks (study weeks 0, 3, 6, 9 and 12). Figure 1 displays data from one subject as an example. The treatment assignment was made after the baseline week and consisted of assignment to either a control arm or an exercise intervention where subjects completed a standardized aerobic exercise program. The data come from electronic monitors worn by each subject, and incomplete data occur; a subject's record may be missing for some time points, days or weeks.
Fig. 1.
An example of the estimates of METs for a subject in the exercise group.
Our goal is to evaluate the effects of the intervention by comparing the change in relative energy expenditure in weeks 3, 6, 9 and 12 to that of the baseline across the treatment groups. Additionally, we are interested in the patterns of physical activity for individuals at different time scales (within days, across days of week and across weeks) and how these patterns vary across the treatment groups. As a result, our goal is to model the responses influenced by 2 factors, days within weeks, while also addressing the fact that these are nested within a third factor, subject.
The data are functional, and we approach this problem using a combination of linear mixed models, penalized B-spline smoothing, and principal component-based dimension reduction. The paper's primary contribution is in its application. Combined with functional data analysis methods, emerging physical activity monitor technology provides a surprising amount of insight into personal behaviors, and these detailed data give a new way to test for the effects of a physical activity intervention. In addition, the 3-level model in our motivating example, presents computational challenges. Current studies have mainly focused on 2-level models. For example, Di and others (2009), Zipunnikov and others (2011) and Serban and Jiang (2012) discuss 2-level multilevel functional analysis approaches with subunit data nested within each unit. Methodology for the analysis of 3-level functional data is limited, and developing a general methodology for 3-level functional data is necessary.
Although the extension from a 2-level to a 3-level model may seem straightforward, our saturated 3-level model involves much more complicated structures, ones that present non-trivial modeling and computational challenges. To be specific, the fixed effects in the 3-level model involve functional curves on different weeks and days: importantly, we allow the possibility of interactions between them and stratify by treatment. In addition, besides the random effects for the subject level, our model includes random curves for the week, the day of the week and interactions between days and weeks. We thus propose a general model with mean structures for week-specific, day-specific and week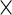 day interaction effects stratified by treatment, and random effects structures for subject-specific, week-specific, day-specific and week
day interaction effects stratified by treatment, and random effects structures for subject-specific, week-specific, day-specific and week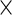 day interaction variation.
day interaction variation.
Since we employ a 3-level structure of random curves, dimensionality problems arise that can affect computation and model explanation. The problem can be handled via the dimension reduction approach discussed by Zhou and others (2008); see also Zhou and others (2010), which uses a few important principal components to summarize random curves. A typical issue for using dimension reduction techniques is to determine the number of principal components and estimate the principal component vectors. Zhou and others (2008) use a model-based approach, which estimates the parameters with an EM algorithm. For improved computational efficiency, we propose a new algorithm that includes features of a likelihood approach and eigen-decomposition.
Current functional data frameworks focus on complete data (Zhou and others, 2010). Missing or incomplete data are common in applications though, and estimation methods developed for complete data scenarios may fail in that case. Assuming our model specification is correct, we only require that the data be missing at random (Little and Rubin, 2002), and we develop a modified estimation algorithm to accommodate the incomplete data. In particular, for each person, complete data have identical dimensions of design matrices in both fixed and random effects. All individuals also have the same covariance structures. However, missing data may not have such features. Thus, our algorithm is updated to adjust the differences in design matrices and variance structures between subjects.
Since our model involves a treatment and week-specific, day-specific and week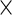 day interaction effects for the fixed effects mean structure, techniques to test whether these fixed effect mean components are necessary. We study the performance of the Wald test under our model settings. We show that care must be taken when the parameter estimates are obtained from the penalized likelihood. The statistics from the penalized likelihood method lead to systematically anti-conservative
day interaction effects for the fixed effects mean structure, techniques to test whether these fixed effect mean components are necessary. We study the performance of the Wald test under our model settings. We show that care must be taken when the parameter estimates are obtained from the penalized likelihood. The statistics from the penalized likelihood method lead to systematically anti-conservative 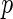 -values, but we use simulation to demonstrate that a Wald statistic based on an unpenalized likelihood can have an acceptable test level.
-values, but we use simulation to demonstrate that a Wald statistic based on an unpenalized likelihood can have an acceptable test level.
The paper is organized as follows. Section 2 describes the model, and Section 3 describes our algorithm for model fitting. Section 4 gives an updated algorithm for incomplete data, Section 5 discusses hypothesis testing issues, and simulation studies are in Section 6. We analyze data from the physical activity intervention trial in Section 7. Concluding remarks are given in Section 8. R programs are available from the first author.
2. Model setup
2.1. The mixed effects model
In this section, we establish notation for our data, specify the functional data model's fixed and random effects, and describe the covariance structure that the model induces. Let 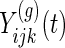 be the outcome observation at time
be the outcome observation at time 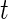 for subject
for subject 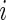
 in week
in week 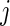
 on day
on day 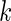
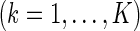 in treatment group
in treatment group 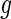
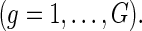 Our model is
Our model is
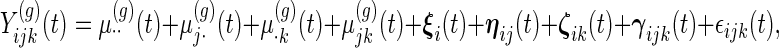 |
(2.1) |
where the superscript 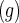 denotes treatment group,
denotes treatment group, 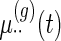 are the population mean curves,
are the population mean curves, 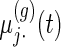 ,
, 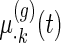 and
and 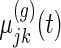 are week-specific, day-specific and week
are week-specific, day-specific and week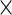 day interaction mean curves,
day interaction mean curves, 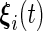 ,
, 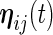 ,
, 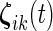 and
and 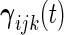 are mutually independent subject-specific, week-within-subject, day-within-subject and week
are mutually independent subject-specific, week-within-subject, day-within-subject and week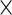 day interaction-within-subject random effects curves, and
day interaction-within-subject random effects curves, and 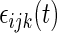 denotes random noise with mean zero and variance
denotes random noise with mean zero and variance 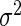 . Although there is a single curve for each subject-day-week combination, similarly to random effects linear regression with random slopes, the smooth reduced rank modeling strategy allows the model to include both this curve and a residual error. We do not vary the random effect distributions by group, but we implement a model to investigate that possibility in our application in Section 7. For ease of notation, we present the model for the case when each subject contributes data from
. Although there is a single curve for each subject-day-week combination, similarly to random effects linear regression with random slopes, the smooth reduced rank modeling strategy allows the model to include both this curve and a residual error. We do not vary the random effect distributions by group, but we implement a model to investigate that possibility in our application in Section 7. For ease of notation, we present the model for the case when each subject contributes data from 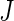 weeks and
weeks and 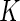 days. Necessary modifications to the model and algorithm to accommodate the situation when this is not the case are in Section 4. Motivated by our application, we consider the case where each subject is only in one treatment group. For identifiability, we constrain
days. Necessary modifications to the model and algorithm to accommodate the situation when this is not the case are in Section 4. Motivated by our application, we consider the case where each subject is only in one treatment group. For identifiability, we constrain 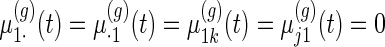 for all
for all 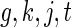 .
.
Each subject is only in one group, and observations from different subjects are modeled to be independent. Within subject, the covariance structure depends on whether observations are from the same week and/or day. The 4 covariance structures are:
- same subject, week and day:
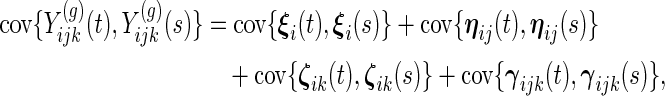
- same subject, week, different day (
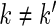 ):
):
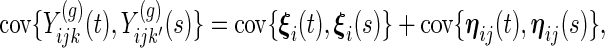
- same subject, day, different week (
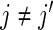 ):
):
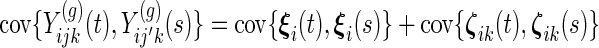
- and, same subject only (
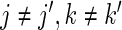 ):
):
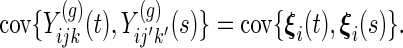
2.2. Principal component form of the random effects
We write the random effects in principal component form in this section. This allows us to consider the possibility that subject-to-subject variability is a linear combination of a limited number of principal component functions:
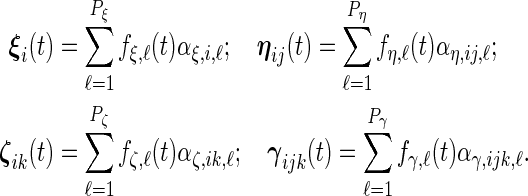 |
The 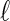 th principal component functions for subject-specific, week-specific, day-specific and week
th principal component functions for subject-specific, week-specific, day-specific and week day interaction random effects curves are
day interaction random effects curves are 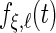 ,
, 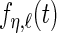 ,
, 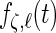 ,
, 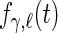 , respectively,
, respectively, 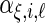 ,
, 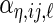 ,
, 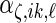 ,
, 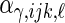 are the corresponding components’ random loadings, and
are the corresponding components’ random loadings, and 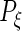 ,
, 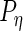 ,
, 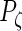 ,
, 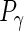 are the numbers of principal components for the 4 random effect variables. The principal components functions are orthogonal if
are the numbers of principal components for the 4 random effect variables. The principal components functions are orthogonal if 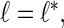
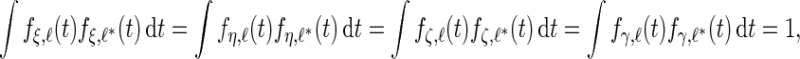 |
and the integrals are  otherwise. As is standard in an eigenvalue decomposition, we order indices so that
otherwise. As is standard in an eigenvalue decomposition, we order indices so that 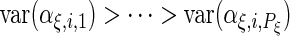 ,
, 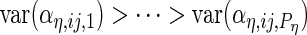 ,
, 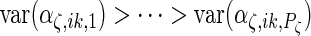 and
and 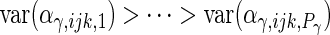 which makes the model identifiable.
which makes the model identifiable.
In order to model the correlation of each random effect using only the principal component functions, we assume that the 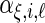 ,
, 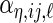 ,
, 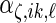 and
and  are mutually independent random effects variables, and different instances of each from the 4 levels are assumed to be independent and identically distributed. The model is specified with notation in the next subsection where we also describe how we represent the functions.
are mutually independent random effects variables, and different instances of each from the 4 levels are assumed to be independent and identically distributed. The model is specified with notation in the next subsection where we also describe how we represent the functions.
2.3. Modeling with B-splines
We model the fixed effect and principal component functions using B-splines which we chose because our application requires a smooth function and their compact support can prevent computational instability. We define them as follows. Let 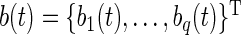 be the
be the 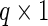 vector of B-splines basis functions evaluated at
vector of B-splines basis functions evaluated at 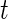 . Define
. Define 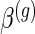 ,
,  ,
, 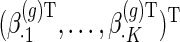 and
and 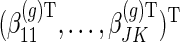 to be group-specific fixed effects coefficients for population, week-specific, day-specific and week
to be group-specific fixed effects coefficients for population, week-specific, day-specific and week day interaction mean structures, respectively. For identifiability, we set
day interaction mean structures, respectively. For identifiability, we set 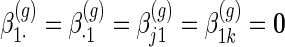 for all
for all 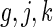 . The non-zero fixed effects coefficients are grouped together in
. The non-zero fixed effects coefficients are grouped together in 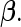 We let
We let 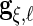 ,
, 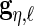 ,
, 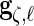 and
and 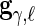 denote
denote 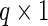 principal components vectors. Then we have
principal components vectors. Then we have
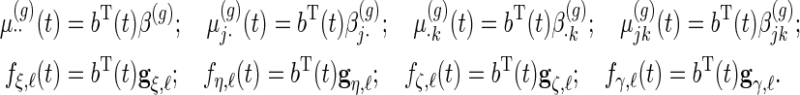 |
To maintain the orthogonality restrictions in Section 2, 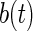 ,
, 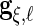 ,
,  ,
, 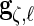 and
and 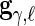 are restricted to be orthogonal. We use orthogonal B-spline basis functions from the R package “orthogonalsplinebasis”.
are restricted to be orthogonal. We use orthogonal B-spline basis functions from the R package “orthogonalsplinebasis”.
Model (2.1) then becomes
 |
(2.2) |
where 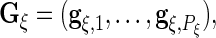
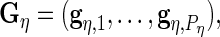
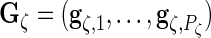 and
and 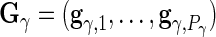 are
are 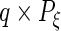 ,
, 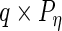 ,
, 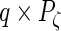 and
and 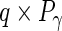 matrices, respectively, and
matrices, respectively, and 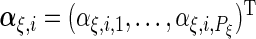 ,
, 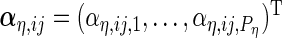 ,
,  and
and 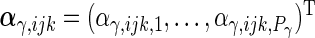 are
are 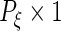 ,
, 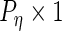 ,
, 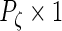 and
and 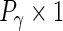 vectors. The orthogonality restrictions mean that
vectors. The orthogonality restrictions mean that  ,
, 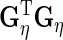 ,
, 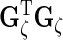 and
and  are identity matrices.
are identity matrices.
Next, we develop notation for the variance components of the component loadings. Let 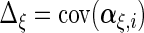 ,
, 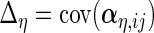 ,
, 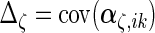 and
and  . With the restrictions and independence assumptions described in Section 2,
. With the restrictions and independence assumptions described in Section 2, 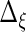 ,
, 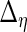 ,
, 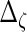 and
and 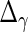 are
are 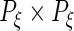 ,
, 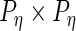 ,
, 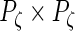 and
and 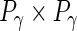 diagonal matrices with decreasing positive diagonal elements.
diagonal matrices with decreasing positive diagonal elements.
To obtain the fixed and random effects curves, we need estimates of 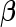 ,
, 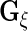 ,
, 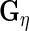 ,
,  and
and 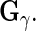 Estimates of
Estimates of 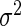 ,
, 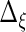 ,
, 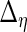 ,
, 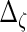 and
and 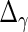 are also needed in order to estimate the random effects covariance structure and to make inferences.
are also needed in order to estimate the random effects covariance structure and to make inferences.
2.4. Link to the linear mixed model
In this section, we demonstrate that our model is in fact related to the familiar linear mixed model. If we build 4 sets of 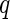 -dimensional random variables,
-dimensional random variables,
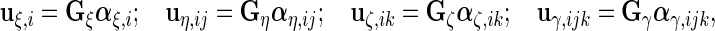 |
then model (2.2) can be rewritten as
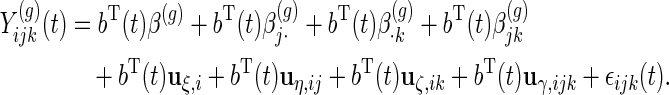 |
(2.3) |
The variance components are 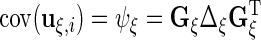 ,
, 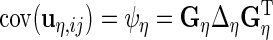 ,
,  and
and 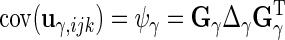 . If
. If 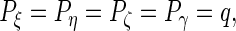 then
then 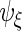 ,
, 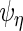 ,
, 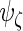 and
and 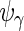 would be full rank, and (2.3) is equivalent to a 3-level linear mixed model with unstructured random effect covariance matrices (Laird and Ware, 1982). Exploiting that connection, our estimation algorithm for (2.2) iteratively combines 2 steps which we describe in the next section. The algorithm takes
would be full rank, and (2.3) is equivalent to a 3-level linear mixed model with unstructured random effect covariance matrices (Laird and Ware, 1982). Exploiting that connection, our estimation algorithm for (2.2) iteratively combines 2 steps which we describe in the next section. The algorithm takes 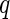 as an initial value for
as an initial value for 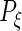 ,
, 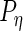 ,
, 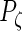 and
and 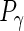 . The latter are then updated during the iterations.
. The latter are then updated during the iterations.
3. Algorithm
The previous section demonstrates that our model is a linear mixed model with reduced rank variance component matrices for the random effects. As a result, our estimation method iterates 2 steps. The first step uses the ECME algorithm (Schafer, 1998) to obtain updates of 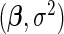 and full rank versions of
and full rank versions of 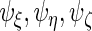 and
and 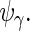 The second step reduces the rank of
The second step reduces the rank of 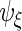 ,
, 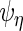 ,
, 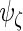 and
and 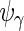 to obtain
to obtain 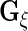 ,
, 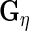 ,
, 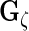 ,
, 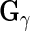 ,
, 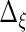 ,
, 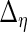 ,
,  and
and 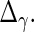 These steps are described in more detail in the next 2 subsections, and the steps are repeated until convergence. Liu and Rubin (1994) discuss convergence properties of the algorithm in general.
These steps are described in more detail in the next 2 subsections, and the steps are repeated until convergence. Liu and Rubin (1994) discuss convergence properties of the algorithm in general.
We note that in this section, we present results rather than derive them since the steps are based on existing methods. That said, care must be taken to avoid bottlenecks caused by large matrix inversions, and methods to address these non-trivial problems are in Section S.2 of Supplementary Material available at Biostatistics online.
3.1. ECME update step
Using notation described in Section S.1 of Supplementary Material available at Biostatistics online, model (2.3) can be expressed as
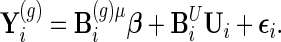 |
(3.1) |
We further define 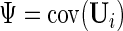 ,
, 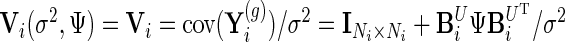 and
and 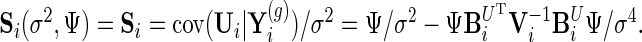 Let the current parameters be
Let the current parameters be 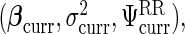 leading to
leading to 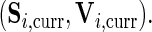
Using that notation, parameter updates are
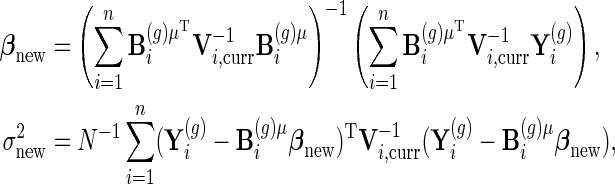 |
and
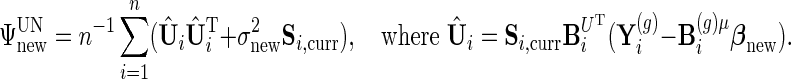 |
The first two updates come from maximizing the likelihood with other parameters held fixed, and the third update is an EM step.
The variance component matrices 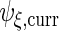 ,
, 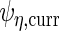 ,
, 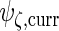 and
and 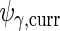 can be extracted from the block diagonal elements of
can be extracted from the block diagonal elements of 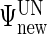 with indices that correspond to the subvectors in
with indices that correspond to the subvectors in 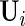 as described in Section S.1 of Supplementary Material available at Biostatistics online. We describe the rank reduction step which leads to
as described in Section S.1 of Supplementary Material available at Biostatistics online. We describe the rank reduction step which leads to 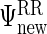 in the next subsection. After that step, we update
in the next subsection. After that step, we update 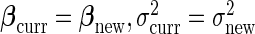 and
and 
3.2. Reduced rank model implementation
We obtain 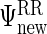 , eigenvalue decompositions of
, eigenvalue decompositions of  These are
These are
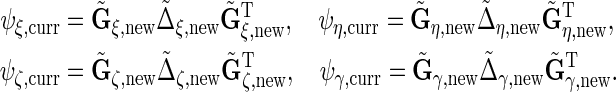 |
The tildes denote that these are full rank decompositions, and we describe the properties of the terms in these decompositions in Section 2.1.
Next, to select the number of principal components 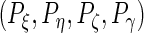 , we set a threshold
, we set a threshold 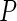 and select by defining
and select by defining
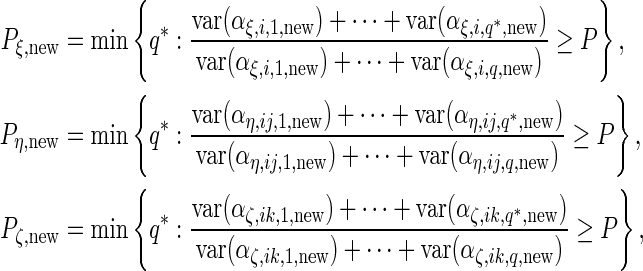 |
and
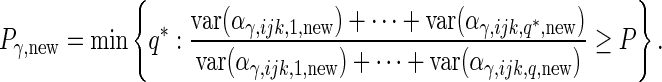 |
(3.2) |
For each of the 4 random effect groups (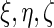 and
and 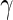 ) we then retain that many of each of the columns for the corresponding eigenvectors (
) we then retain that many of each of the columns for the corresponding eigenvectors (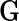 s) and the rows and columns for random loadings (
s) and the rows and columns for random loadings (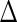 s) to define
s) to define 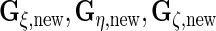 and
and 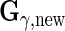 and
and 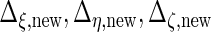 and
and 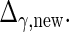
Finally, we obtain the updated reduced rank matrices
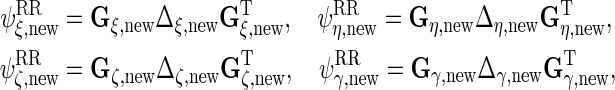 |
and these are combined into 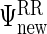 as described in Section S.1 of Supplementary Material available at Biostatistics online.
as described in Section S.1 of Supplementary Material available at Biostatistics online.
To choose 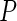 , a subjective choice is usually satisfactory and is often used. We use
, a subjective choice is usually satisfactory and is often used. We use 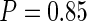 in our simulation studies which works very well in our experience. Alternatively, cross-validation or model selection methods such as BIC could be used.
in our simulation studies which works very well in our experience. Alternatively, cross-validation or model selection methods such as BIC could be used.
3.3. Maximum penalized likelihood
The previous discussion focuses on the modeling of the response variables using basis functions, but it is important to introduce roughness penalties to regularize the function fits.
We use penalized maximum likelihood for parameter estimation with maximization of
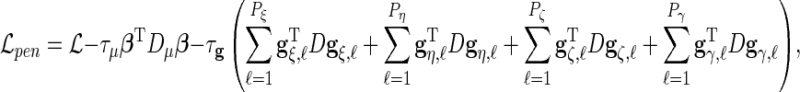 |
(3.3) |
where 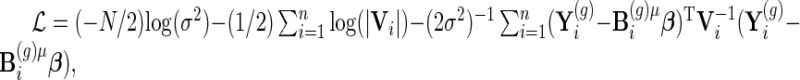 the penalty parameters are
the penalty parameters are 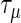 and
and 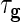 ,
, 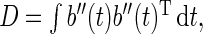 and
and 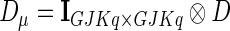 .
.
Using maximum penalized likelihood has minor effect on the equations that are used to update 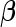 and
and 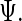 The technical details are in Section S.3 of Supplementary Material available at Biostatistics online. A search over a candidate set of parameters is a feasible way to choose the penalty parameters
The technical details are in Section S.3 of Supplementary Material available at Biostatistics online. A search over a candidate set of parameters is a feasible way to choose the penalty parameters 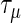 and
and 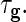 We used that approach and 5-fold cross-validation in our numerical work. It would be possible to model the penalty parameters as variance components and estimate them by REML as well.
We used that approach and 5-fold cross-validation in our numerical work. It would be possible to model the penalty parameters as variance components and estimate them by REML as well.
4. Algorithm for incomplete data
The model and algorithm discussed in Sections 2 and 3 assume that all subjects contribute the same numbers of weeks and days within each week. Although the observed data likelihood is proper for the missing data, the estimation algorithm and notation need to be modified to accommodate the data incompleteness. Define  ,
, 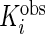 ,
, 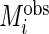 and
and 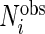 to be number of observed weeks, days, week-days and observed records for subject
to be number of observed weeks, days, week-days and observed records for subject 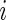 , respectively. We write
, respectively. We write 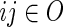 ,
, 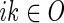 and
and  to represent that week
to represent that week 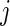 , day
, day 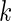 and week-day
and week-day 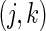 are observed for subject
are observed for subject 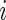 , respectively. Let
, respectively. Let 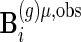 and
and 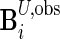 to be the
to be the 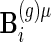 and
and 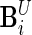 matrices with unobserved block rows removed, respectively. Define
matrices with unobserved block rows removed, respectively. Define 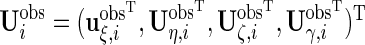 to be the
to be the 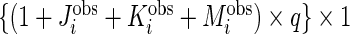 vector corresponding to subject-specific, week-specific, day-specific and week
vector corresponding to subject-specific, week-specific, day-specific and week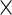 day interaction random effects for the observed data. Then define
day interaction random effects for the observed data. Then define 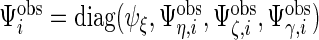 , where
, where 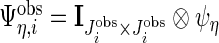 ,
, 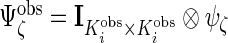 , and
, and 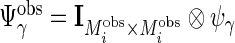 . Because of different missing patterns for each subject,
. Because of different missing patterns for each subject, 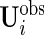 and
and 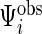 may not have identical dimensions across
may not have identical dimensions across 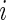 .
.
We define  and
and 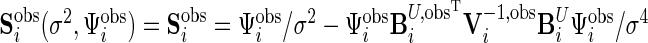 . The joint log-likelihood function for the available data becomes
. The joint log-likelihood function for the available data becomes
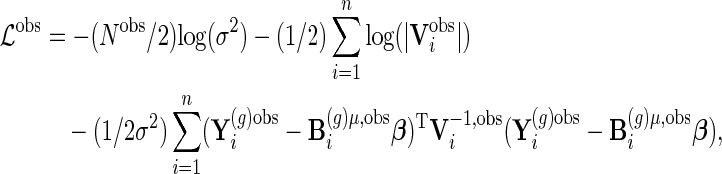 |
where 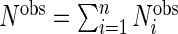 .
.
Updates for  and
and  follow the complete data strategy. On the other hand, since subject-specific
follow the complete data strategy. On the other hand, since subject-specific 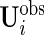 and
and 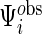 may have different dimensions, additional modification of the algorithm for updating
may have different dimensions, additional modification of the algorithm for updating 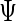 is necessary. For each subject
is necessary. For each subject 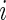 , we can obtain unstructured
, we can obtain unstructured 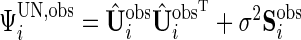 , where
, where 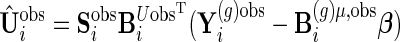 .
.
Similar to the algorithm used for complete data, we extract the diagonal blocks from 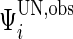 . For the complete data case,
. For the complete data case, 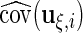 ,
, 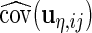 ,
, 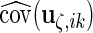 and
and  can be extracted directly from
can be extracted directly from 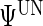 because each
because each 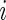 contributes 1,
contributes 1, 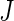 ,
, 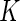 and
and 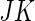 components, respectively. However, the incomplete data
components, respectively. However, the incomplete data 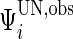 contributes 1,
contributes 1, 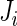 ,
, 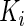 and
and 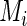 components for
components for 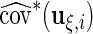 ,
, 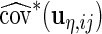 ,
, 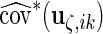 and
and 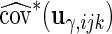 , respectively, which may be different among subjects. Thus, we calculate
, respectively, which may be different among subjects. Thus, we calculate  ,
, 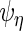 ,
, 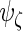 and
and 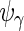 by considering the different number of complete cases for each subject:
by considering the different number of complete cases for each subject:
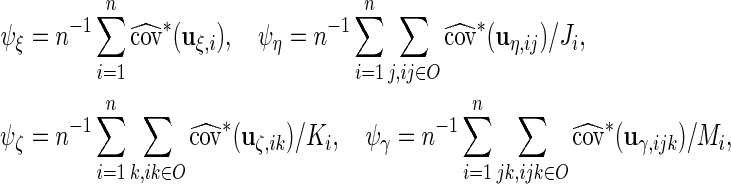 |
which leads to the updated values of 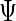 . The estimators of
. The estimators of 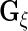 ,
, 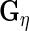 ,
, 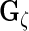 ,
, 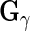 ,
, 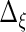 ,
, 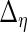 ,
,  and
and 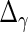 are identical to the method in Section 3.
are identical to the method in Section 3.
5. Hypothesis tests for mean curves
In this section, we discuss testing for the fixed effects mean structures, while keeping the random effects structures as previously specified. Model (2.1) involves mean curves for treatments and week-specific, day-specific and week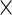 day interaction effects for each treatment. We next discuss testing whether these effects equal zero. Using the parameterization in model (2.3), inference is equivalent to testing whether a subvector of
day interaction effects for each treatment. We next discuss testing whether these effects equal zero. Using the parameterization in model (2.3), inference is equivalent to testing whether a subvector of 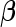 equals zero, and we discuss the Wald test approach with null hypothesis
equals zero, and we discuss the Wald test approach with null hypothesis  where
where 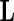 is a known matrix constructed for a specific hypotheses test. Thus, the Wald statistics can be written as
is a known matrix constructed for a specific hypotheses test. Thus, the Wald statistics can be written as 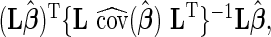 where
where 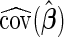 is an estimate of the covariance matrix of
is an estimate of the covariance matrix of  .
.
The hypothesis test is based on the model discussed in Section 2 and the estimation results obtained from the algorithm discussed in Section 3. When 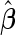 is obtained from the unpenalized likelihood function,
is obtained from the unpenalized likelihood function, 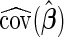 can be calculated as
can be calculated as 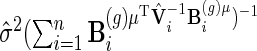 with
with 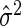 and
and 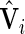 obtained from the algorithm. The Wald statistic then follows asymptotically a
obtained from the algorithm. The Wald statistic then follows asymptotically a 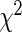 distribution with degrees of freedom equal to the rank of
distribution with degrees of freedom equal to the rank of 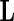 . In the simulation reported below in Section 6, this test has acceptable level for a small to moderate number of basis functions, and for both complete and missing data. When the model involves a large number of knots, the test levels deteriorate, especially with incomplete data and a small sample size, but this problem does not occur if the sample size is large.
. In the simulation reported below in Section 6, this test has acceptable level for a small to moderate number of basis functions, and for both complete and missing data. When the model involves a large number of knots, the test levels deteriorate, especially with incomplete data and a small sample size, but this problem does not occur if the sample size is large.
An alternative is to use the penalized likelihood. For  obtained from penalized likelihood (3.3),
obtained from penalized likelihood (3.3), 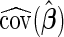 can be estimated by
can be estimated by
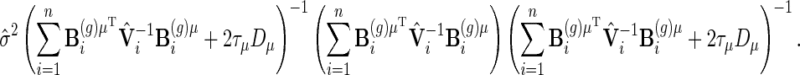 |
However, the resulting Wald test performs poorly in terms of test level, leading to too many false positives. An alternative is to use the so-called Bayesian variance estimator 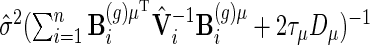 as the asymptotic covariance matrix, see Ruppert and others (2003), Equation (6.13). However, we have found that this leads to much too conservative a test and with little power. Ruppert and others (2003) suggest using
as the asymptotic covariance matrix, see Ruppert and others (2003), Equation (6.13). However, we have found that this leads to much too conservative a test and with little power. Ruppert and others (2003) suggest using  to
to  Monte Carlo simulations to calculate the
Monte Carlo simulations to calculate the 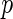 -values. However, the Monte Carlo approach is very computationally expensive for our 3-level model.
-values. However, the Monte Carlo approach is very computationally expensive for our 3-level model.
6. Simulation studies
In this section, we illustrate the performance of our methodology. In each simulation run, we have 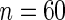 subjects for
subjects for  weeks with
weeks with  days, and each day has
days, and each day has 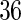 measurement times. The probability that a day's records is observed is 50%. Here, we report the setting with
measurement times. The probability that a day's records is observed is 50%. Here, we report the setting with  , but we also implement the setting with
, but we also implement the setting with 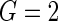 and the results are very similar. A measurement at time
and the results are very similar. A measurement at time  on day
on day 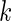 in week
in week 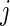 for subject
for subject 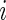 results in observation
results in observation 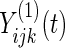 which is generated according to
which is generated according to
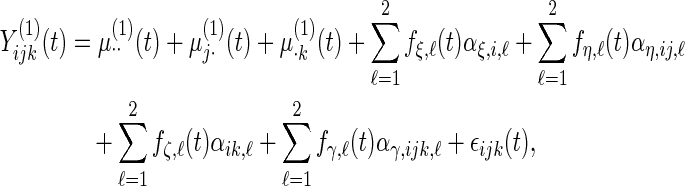 |
with detailed settings of curves and parameters listed in Table 1.
Table 1.
Settings and parameter estimation results for the simulation study in Section 6. The first part of the table displays the true curves used in the model. The second part of the table displays the true value, the average estimates and the mean squared errors (MSE) of the parameters in the joint model. 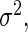
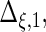
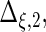
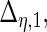

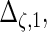
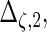
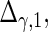
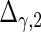 are the variances of
are the variances of 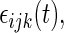
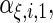
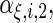
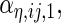
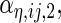

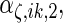
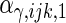 and
and 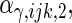 respectively. The number marked with an asterisk is the actual number multiplied by
respectively. The number marked with an asterisk is the actual number multiplied by 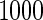 . The lower part of the table displays the rate of true null hypothesis for 4 methods with
. The lower part of the table displays the rate of true null hypothesis for 4 methods with 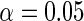 . PEN
. PEN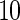 represents the penalized likelihood with
represents the penalized likelihood with 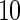 knots. UN
knots. UN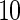 , UN
, UN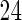 and UN
and UN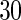 are the unpenalized likelihood methods with
are the unpenalized likelihood methods with 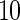 ,
, 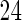 and
and 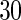 knots, respectively
knots, respectively
 |
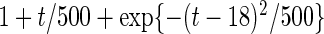 |
||||||||
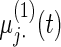 |
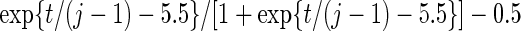
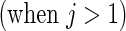
|
||||||||
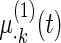 |
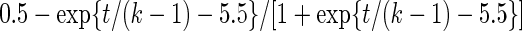

|
||||||||
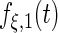 |
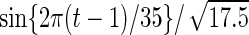 |
||||||||
 |
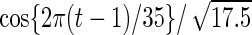 |
||||||||
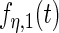 |
 |
||||||||
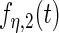 |
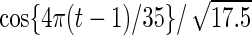 |
||||||||
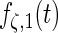 |
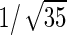 |
||||||||
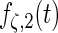 |
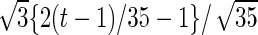 |
||||||||
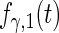 |
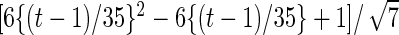 |
||||||||
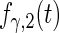 |
 |
||||||||
| Parameter | 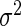 |
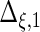 |
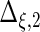 |
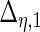 |
 |
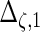 |
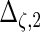 |
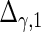 |
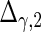 |
| True | 1.00 | 8.00 | 4.00 | 6.00 | 3.00 | 4.00 | 2.00 | 2.00 | 1.00 |
| Mean | 1.00 | 8.33 | 3.86 | 6.00 | 2.86 | 3.89 | 2.00 | 1.95 | 0.93 |
| MSE | 0.08
|
2.11 | 0.55 | 0.26 | 0.11 | 0.18 | 0.04 | 0.03 | 0.02 |
| Complete data | Missing data | Complete data | Missing data | ||||||
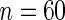 |
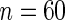 |
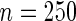 |
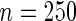 |
||||||
| PEN10 | 0.37 | 0.32 | 0.62 | 0.46 | |||||
| UN10 | 0.06 | 0.08 | 0.07 | 0.06 | |||||
| UN24 | 0.06 | 0.15 | 0.05 | 0.07 | |||||
| UN30 | 0.10 | 0.23 | 0.04 | 0.07 | |||||
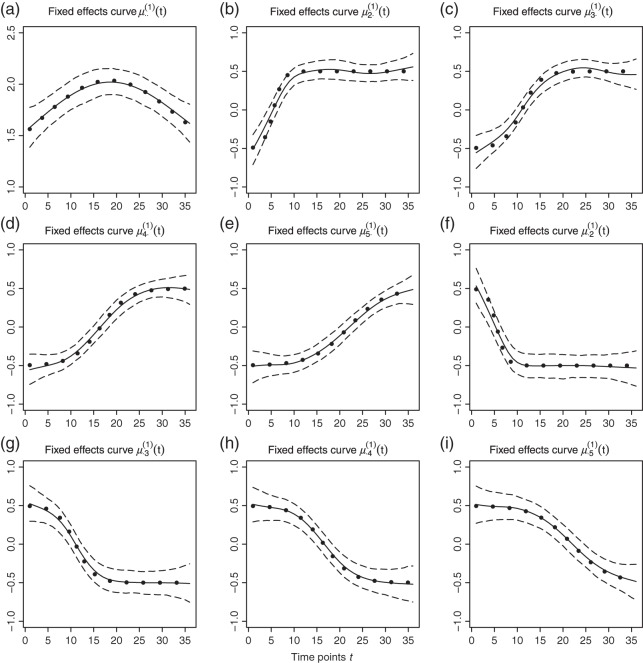
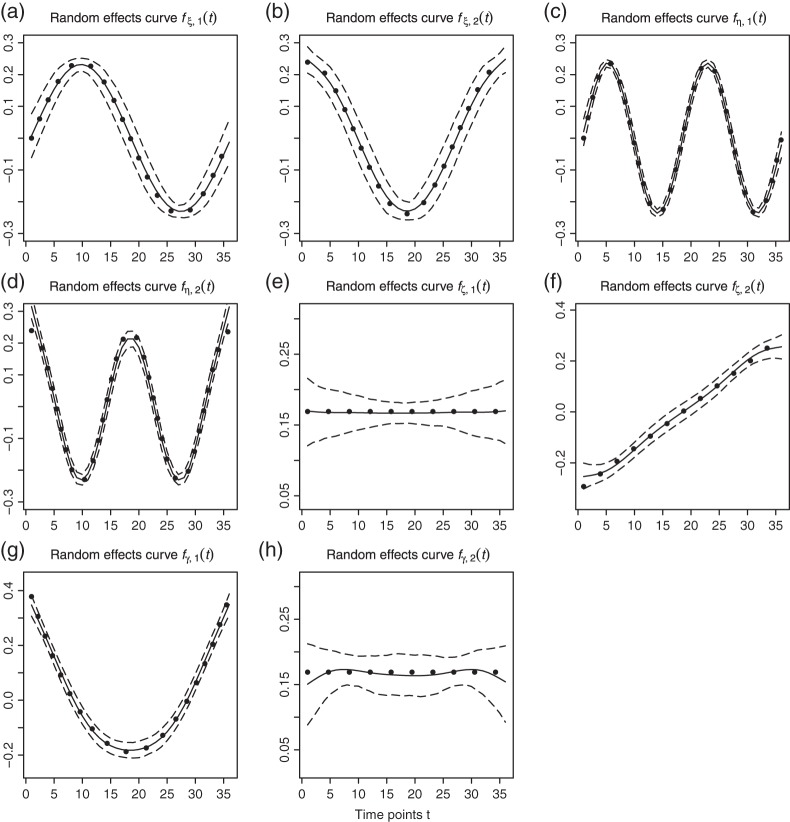
We use B-spline basis functions with 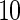 equispaced knots to fit the data. Figures 2 and 3 give results for the fixed effects and principal component curves, respectively. Parameter estimation results are shown in Table 1. The results suggest that our method has excellent performance.
equispaced knots to fit the data. Figures 2 and 3 give results for the fixed effects and principal component curves, respectively. Parameter estimation results are shown in Table 1. The results suggest that our method has excellent performance.
Fig. 2.
Fitted fixed effects curves for 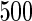 simulated data sets: (a) fixed effects curve
simulated data sets: (a) fixed effects curve 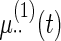 , (b)–(e) fixed effects curves
, (b)–(e) fixed effects curves 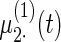 ,
, 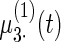 ,
, 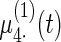 ,
, 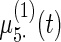 , (f)–(i) fixed effects curves
, (f)–(i) fixed effects curves 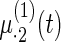 ,
, 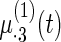 ,
, 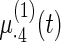 ,
, 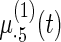 . Dotted lines denote true curves. Solid lines represent the averaged values of fitted curves. The upper and lower dashed lines are the 10% and 90% quantiles of the fitted values in 500 simulation studies.
. Dotted lines denote true curves. Solid lines represent the averaged values of fitted curves. The upper and lower dashed lines are the 10% and 90% quantiles of the fitted values in 500 simulation studies.
Fig. 3.
Fitted principal components curves for 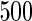 simulated data sets: (a) and (b) principal components curves
simulated data sets: (a) and (b) principal components curves 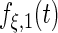 and
and 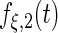 , (c) and (d) principal components curves
, (c) and (d) principal components curves 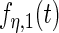 and
and 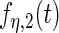 , (e) and (f) principal components curves
, (e) and (f) principal components curves 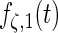 and
and 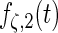 , (g) and (h) principal components curves
, (g) and (h) principal components curves 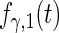 and
and 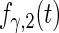 . Dotted lines denote true curves. Solid lines represent the averaged values of fitted curves. The upper and lower dashed lines are the 10% and 90% quantiles of the fitted values in 500 simulation studies.
. Dotted lines denote true curves. Solid lines represent the averaged values of fitted curves. The upper and lower dashed lines are the 10% and 90% quantiles of the fitted values in 500 simulation studies.
We next study the performance of the Wald statistics discussed in Section 5 to test the null hypothesis that 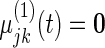 for all
for all 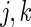 . The nominal rejection rate is set to
. The nominal rejection rate is set to 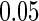 . Four methods are studied: penalized likelihood with 10 knots (PEN10), unpenalized likelihood with 10 knots (UN10), unpenalized likelihood with 24 knots (UN24) and unpenalized likelihood with 30 knots (UN30). For each method, Table 1 displays the rejection rate of
. Four methods are studied: penalized likelihood with 10 knots (PEN10), unpenalized likelihood with 10 knots (UN10), unpenalized likelihood with 24 knots (UN24) and unpenalized likelihood with 30 knots (UN30). For each method, Table 1 displays the rejection rate of 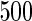 replicates under complete and incomplete data scenarios with sample size
replicates under complete and incomplete data scenarios with sample size 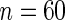 , and the rejection rate of
, and the rejection rate of  replicates for sample size
replicates for sample size 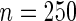 . With complete data, unpenalized likelihood works well in terms of test level with 10 and 24 knots, but has an inflated rejection rate if 30 knots are used. Under the missing data scenario, unpenalized likelihood with small sample size performs poorly in terms of rejection rate when more knots are added, but this problem does not occur with large sample size. On the other hand, testing based on penalized likelihood leads to unacceptable Type I errors in all scenarios.
. With complete data, unpenalized likelihood works well in terms of test level with 10 and 24 knots, but has an inflated rejection rate if 30 knots are used. Under the missing data scenario, unpenalized likelihood with small sample size performs poorly in terms of rejection rate when more knots are added, but this problem does not occur with large sample size. On the other hand, testing based on penalized likelihood leads to unacceptable Type I errors in all scenarios.
7. Application
7.1. Background
In this section, we apply our model to data from the physical activity intervention trial described in Section 1, which uses an activity monitor to estimate the physical activity levels of subjects over time. For this paper, the outcome of interest is energy expenditure, which is expressed in units of metabolic equivalents (METs). A person's MET value for an activity is defined as the ratio of energy expenditure during an activity to resting energy expenditure. The unit for both numerator and denominator of a MET is oxygen consumption per kilogram of body weight per minute, and the ratio makes a MET value independent of body weight or time. A MET value of at least 3 defines moderate to vigorous physical activity (MVPA). The gold-standard for measuring energy expenditure is doubly labeled water, but it is expensive and estimates only total daily energy expenditure; thus, the patterns and temporal distribution of intensity (of interest in our application) cannot be estimated. Another approach is to use indirect calorimetry where a person wears a mask and an electronic device that analyzes inhaled and exhaled gases to measure energy expenditure over time. This approach provides temporal detail, but it is impractical for large scale monitoring outside of controlled settings since the mouth is covered and the equipment is bulky and expensive. As a result, accelerometer-based activity monitoring is widely used in the physical activity and health literature. Accelerometers are small, unobtrusive and provide time-stamped estimates of acceleration. Estimates of energy expenditure from those measurements are based on the principle that acceleration is proportional to net external forces, therefore reflective of the energy cost of movement. Freedson and others (2012) provide a recent review of this work, and introduce a special issue of a journal that is devoted to this topic.
The activPAL (www.paltech.plus.com) accelerometer activity monitor was used in this study. This device were taped to the front of the thigh and used accelerometers to assess the angle of the thigh and movement. The angle differentiates sitting from standing, and the movement differentiates standing still from stepping. Those measurements are then used by an algorithm in the device to estimate energy expenditure. The algorithm is proprietary, but it appears to yield constant values for sitting and standing, and to be a linear function of a summary of total acceleration when stepping. The calibration is based primarily on locomotive activities, thus for some activities that involve significant upper body movement, energy expenditure may be underestimated. Additionally, it should be noted that acceleration tends not to be a smooth function of time, and the activPAL
(www.paltech.plus.com) accelerometer activity monitor was used in this study. This device were taped to the front of the thigh and used accelerometers to assess the angle of the thigh and movement. The angle differentiates sitting from standing, and the movement differentiates standing still from stepping. Those measurements are then used by an algorithm in the device to estimate energy expenditure. The algorithm is proprietary, but it appears to yield constant values for sitting and standing, and to be a linear function of a summary of total acceleration when stepping. The calibration is based primarily on locomotive activities, thus for some activities that involve significant upper body movement, energy expenditure may be underestimated. Additionally, it should be noted that acceleration tends not to be a smooth function of time, and the activPAL 's estimates of energy expenditure (oxygen use) also tend not to be smooth. However, a person's actual use of oxygen and the resulting MET value are smooth functions of time for physiological reasons (Powers and Howley, 2001, Chapter 4).
's estimates of energy expenditure (oxygen use) also tend not to be smooth. However, a person's actual use of oxygen and the resulting MET value are smooth functions of time for physiological reasons (Powers and Howley, 2001, Chapter 4).
7.2. Analysis of daily METs
In the study, 63 individuals wore the activPAL for 5 weeks (denoted weeks 0, 3, 6, 9, 12), 5 days in a week (Monday to Friday) and measurements were recorded every 5 min during each day. After week zero each individual was assigned randomly to either the treatment group or the control group. Each member of the treatment group received a personal trainer who developed an exercise program for them and supervised 40 min exercise sessions 5 days a week. Members of the control group were instructed to continue their lives as before.
for 5 weeks (denoted weeks 0, 3, 6, 9, 12), 5 days in a week (Monday to Friday) and measurements were recorded every 5 min during each day. After week zero each individual was assigned randomly to either the treatment group or the control group. Each member of the treatment group received a personal trainer who developed an exercise program for them and supervised 40 min exercise sessions 5 days a week. Members of the control group were instructed to continue their lives as before.
We analyze these data with model (2.1) with 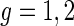 denoting the control and treatment groups, respectively. We also fit models that allow the distributions of the random effects to vary by group, but the results do not change appreciably and are not shown. The model's response is METs over time, and, as discussed in Section 7.1, the activPal's estimate of METs is less smooth in time than actual oxygen consumption. Figure S.1 in Supplementary Material available at Biostatistics online shows the activPal METs over time for a particular day and subject overlaid with the model fit, where the fit includes the maximum likelihood estimates of the
denoting the control and treatment groups, respectively. We also fit models that allow the distributions of the random effects to vary by group, but the results do not change appreciably and are not shown. The model's response is METs over time, and, as discussed in Section 7.1, the activPal's estimate of METs is less smooth in time than actual oxygen consumption. Figure S.1 in Supplementary Material available at Biostatistics online shows the activPal METs over time for a particular day and subject overlaid with the model fit, where the fit includes the maximum likelihood estimates of the 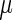 functions and the empirical best linear predictions of the random effects.
functions and the empirical best linear predictions of the random effects.
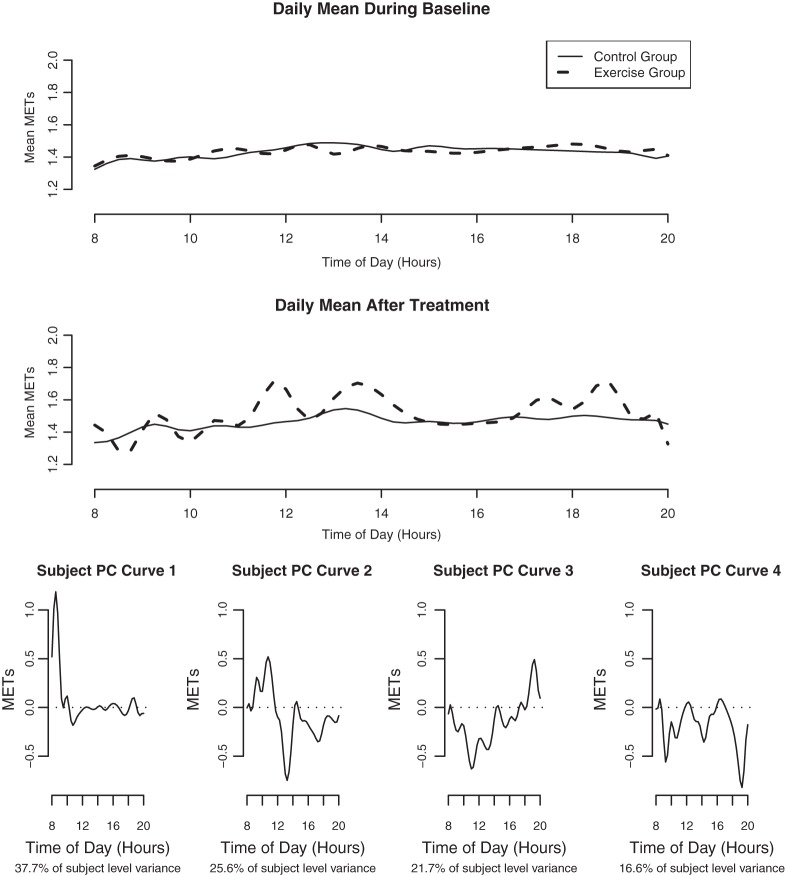
We next describe figures for the analysis of MET levels over the course of the entire day, 8:00 (8AM) to 20:00 (8PM). The top panel in Figure 4 illustrates that the mean MET levels in the treatment and control groups are similar before treatment assignment (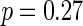 ), and the next panel shows the different means (
), and the next panel shows the different means (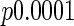 ) in the 2 groups after treatment assignment. Both are averaged over days and the second panel is averaged over weeks. It is likely that the modes in the treatment group correspond to times when the treatment group subjects tend to schedule their exercise sessions.
) in the 2 groups after treatment assignment. Both are averaged over days and the second panel is averaged over weeks. It is likely that the modes in the treatment group correspond to times when the treatment group subjects tend to schedule their exercise sessions.
Fig. 4.
The estimated mean METs over the course of the day for each treatment group before and after the treatment assignment.
The individual level daily random effect principal components are in the bottom 4 panels of Figure 4. These components are readily interpretable as the times of day when there is likely to be subject level variability in METs irrespective of day and week. The principal components for the other levels of variation are similar to the ones in this figure. One exception is that the other levels of variation show more variation in the evening (not shown).
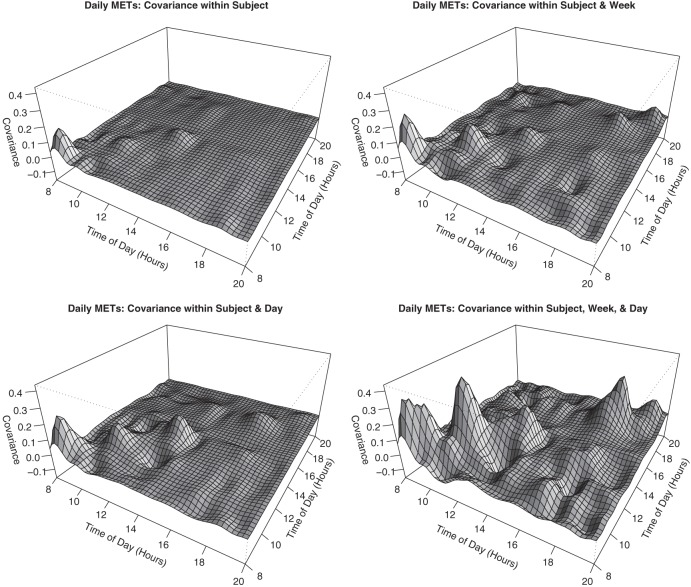
The 4 levels of the covariance matrix described in Section 2.1 are shown in Figure 5. The top left panel shows that, independent of day and week, some subjects tend to be more or less active early in the morning with periods of relatively smaller variation just before and just after noon. The other panels show that week, day, and week-by-day levels of variation increase these peaks and also add variation in the evening. In contrast to the morning variation that is purely subject-specific, this variation suggests that the subject level variation in the evening tends to be week- or day-specific. Additionally, we note that most of correlation is positive and off-diagonal regions of the matrix are close to zero.
Fig. 5.
Plots of the estimated covariance matrix of the subject random effects, including the contributions from the weeks, days and their interactions.
We also did an analysis using data before and after the first event of MVPA. See Figures S.2 and S.3 in the Supplementary Material available at Biostatistics online.
8. Conclusion
We have proposed a general modeling and estimation strategy for a treatment effect in the presence of 3-level correlated functional data. Our algorithm can handle incomplete data and employs a data-based method to select the number of principal components for the random curves. Simulation results for the model fitting strategy are encouraging and indicate little bias. We also discuss the performance of the Wald test to assess the evidence that linear combinations of mean structure parameters are zero. Our simulation results suggest that the Wald test works well for the unpenalized likelihood, but the number of knots should be restricted to be moderate, especially when the data are incomplete and the sample size is small.
The Wald test leads to biased results when using penalized likelihood. Wood (2006, 2013) discusses a modified Wald statistic based on the Bayesian variance estimator described in Section 5. However, his modifications assume that the data responses are independent, and in our case they are correlated with a complicated structure. It is an interesting problem for future research to extend the modified Wald statistic to accommodate the data associations inherent in our model.
We applied our model to analyze data from a physical activity intervention trial. The response data from this trial consisted of measurements of relative energy expenditure (MET level) every five minutes during the day for 5 days during 5 weeks from 63 individuals. The individuals in the trial were randomized into a treatment group that engaged in structured exercise and a control group. The detailed functional data analysis revealed how the patterns of activity in these groups differ in terms of timing and intensity.
Supplementary Material
Supplementary Material is available at http://biostatistics.oxfordjournals.org.
Funding
H.L. and R.J.C. were supported by a grant from the National Cancer Institute (R37-CA057030). This research has been partially supported by the Spanish Ministry of Science and Innovation (project MTM 2011-22664 which is co-funded by FEDER). H.A. was supported by a postdoctoral training grant from the National Cancer Institute (R25T-CA090301). S.K.K. and J.S. were supported by a National Cancer Institute grant (R01-CA121005). J.Z.H. was supported by a NSF grant (DMS-1208952).
Supplementary Material
Acknowledgements
Conflict of Interest: None declared.
References
- Di C. Z., Crainiceanu C. M., Caffo B. S., Punjabi N. M. (2009). Multilevel functional principal component analysis. The Annals of Applied Statistics 3, 458–488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Freedson P., Bowles H. R., Troiano R., Haskell W. (2012). Assessment of physical activity using wearable monitors: recommendations for monitor calibration and use in the field. Medicine and Science in Sports and Exercise 44, S1–S4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kozey-Keadle S., Libertine A., Lyden K., Staudenmayer J., Freedson P. S. (2014). Changes in sedentary time and spontaneous physical activity in response to an exercise training and/or lifestyle intervention. Journal of Physical Activity and Health 11, 1324–1333. [DOI] [PubMed] [Google Scholar]
- Laird N. M., Ware J. H. (1982). Random-effects models for longitudinal data. Biometrics 38, 963–974. [PubMed] [Google Scholar]
- Little R. J. A., Rubin D. B. (2002) Statistical Analysis with Missing Data, 2nd edition Wiley-Interscience, United States. [Google Scholar]
- Liu C., Rubin D. B. (1994). The ECME algorithm: a simple extension of EM and ECM with faster monotone convergence. Biometrika 81, 633–648. [Google Scholar]
- Powers S. K., Howley E. T. (2001) Exercise Physiology. Boston: McGraw-Hill. [Google Scholar]
- Ruppert D., Wand M. P., Carroll R. J. (2003) Semiparametric Regression. New York: Cambridge University Press. [Google Scholar]
- Schafer J. L. (1998). Some improved procedures for linear mixed models. Technical Report. The Methodological Center, The Pennsylvania State University. [Google Scholar]
- Serban N., Jiang H. (2012). Multilevel functional clustering analysis. Biometrics 68, 805—814. [DOI] [PubMed] [Google Scholar]
- Wood S. N. (2006). On confidence intervals for generalized additive models based on penalized regression splines. Australian and New Zealand Journal of Statistics 48, 445–464. [Google Scholar]
- Wood S. N. (2013). On p-values for smooth components of an extended generalized additive model. Biometrika 100, 221–228. [Google Scholar]
- Zhou L., Huang J. Z., Carroll R. J. (2008). Joint modelling of paired sparse functional data using principal components. Biometrika 95, 601–619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou L., Huang J. Z., Martinez J. G., Maity A., Baladandayuthapani V., Carroll R. J. (2010). Reduced rank mixed effects models for spatially correlated hierarchical functional data. Journal of the American Statistical Association 105, 390–400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zipunnikov V., Caffo B., Yousem D. M., Davatzikos C., Schwartz B. S., Crainiceanu C. (2011). Multilevel functional principal component analysis for high-dimensional data. Journal of Computational and Graphical Statistics 20, 852–873. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.