Effects of Acids, Bases, and Heteroatoms on Proximal Radial Distribution Functions for Proteins

Abstract

The proximal distribution of water around proteins is a convenient method of quantifying solvation. We consider the effect of charged and sulfur-containing amino acid side-chain atoms on the proximal radial distribution function (pRDF) of water molecules around proteins using side-chain analogs. The pRDF represents the relative probability of finding any solvent molecule at a distance from the closest or surface perpendicular protein atom. We consider the near-neighbor distribution. Previously, pRDFs were shown to be universal descriptors of the water molecules around C, N, and O atom types across hundreds of globular proteins. Using averaged pRDFs, a solvent density around any globular protein can be reconstructed with controllable relative error. Solvent reconstruction using the additional information from charged amino acid side-chain atom types from both small models and protein averages reveals the effects of surface charge distribution on solvent density and improves the reconstruction errors relative to simulation. Solvent density reconstructions from the small-molecule models are as effective and less computationally demanding than reconstructions from full macromolecular models in reproducing preferred hydration sites and solvent density fluctuations.

INTRODUCTION

Although the nature of hydration for protein function is well established, the hydration structures and patterns around proteins, particularly the charged sites¹ can be a challenge to quantify. Perturbation of the solvent distribution by the protein and consequently the effect on the protein conformational changes are important for experimental structure refinements and for computing thermodynamics.^2,3 Different hydration structures around proteins are results of the physical and chemical interactions at the protein–water interface. Water correlations show a rich variety at the various heterogeneous surface sites of proteins.⁴ The polar side chains (charged or partially charged) establish strong electrostatic interactions and layering of the water molecules. Experimental methods of studying structure, such as solution NMR and X-ray diffraction crystallography, generally agree on the atomic structures of the proteins, however such methods detect hydration water molecules and their effects differently.^5,6 A classic study of protein hydration in aqueous solution using high resolution NMR⁶ showed that the locations of trapped water in protein cavities can be essentially identical to that in the crystal structure of the same protein. Crystal structures can suffer from variability of less well-resolved waters of hydration.⁷ Efforts to assemble the different experimental observables together with computed results^8-10 including other inhomogeneous solvation methods¹¹ for DNA¹² and protein hydration¹³ have been made. Using molecular dynamics (MD) simulations, studies have analyzed the model dynamics of water molecules at the interface in terms of local water mobility and probability distribution using the pair correlation function.¹³

In order to explicitly quantify the effects of the protein surface on the protein-water pair correlation function, we consider a conditional pair correlation function that describes the solvent structure closest to a protein atom at a distance r or equivalently perpendicular to the protein surface, g_⊥(r).¹⁴ This is the first member of a physical cluster hierarchy form of the partition function written in terms of near-neighbors, next nearest-neighbors, etc.¹⁵ Here, we consider the first term as an approximation to the full probability distribution. The convergence of the series has been considered previously, and generally the suitably normalized first member of the hierarchy captures the major features of the distribution of solvent.¹⁴ The distribution of solute around solvent converges much differently.¹⁶

Depending on the thermodynamic averages sought, one can consider the water averaged around a fixed protein¹⁷ or around a flexible protein.¹³ Some have even considered a flexible reference where local protein structure is used as a reference and the rest of the protein and water is averaged.¹⁸ Such techniques quantitatively reflect the different systems aspects of the protein–water interface and project the effects each reference state has on the pair correlation functions characterizing the whole protein.

These perpendicular radial distribution functions (pRDFs), once determined can later be used to reconstruct the three-dimensional solvent density distribution around an arbitrary protein surface.^13,14,19 Although the total solvent density distribution may be unique to individual proteins, the pRDFs, are approximately transferable among broad families of proteins.^13,14,17 A promising application utilizing the universality of the pRDFs is predicting the hydration structure and thermodynamics around complex biological assemblies. Successfully reconstructing the water density distribution at the protein–water interface using the pRDFs can provide a model for the solvent distribution even in a crystal lattice or other confined situations for macromolecules. The accuracy of the hydration structure determines the reliability for further thermodynamically investigations. The pRDF method has been used for calculating solvation entropy changes during the intercalation process of an anticancer drug.²⁰

Early work considered the reconstruction of an aqueous salt solution around triple helical DNA.¹⁹ That study identified the minimum number of solute atom types needed for solvent reconstruction with a specified precision. The solute atoms were classified into various size groups based on chemical identity, chemical situation, electrostatic properties, and atomic partial charges. The results showed that errors in reconstruction at the near-neighbor level were modestly sensitive to the complexity of class. As expected the class where every solute atom was considered as unique gave a significantly better reconstruction. The other groupings varied somewhat in terms of percent difference from the reference solvent distribution obtained directly from MD simulation of DNA.

Protein amino acid side-chain and backbone atoms possess a wider variety of properties than do those of nucleic acids. Early pRDF reconstructions used a simplified model of the protein atoms using only C, N, and O atom sites.¹³ The first work that reconstructed the protein-water pair correlation function noted that protein backbone and side-chain oxygen and nitrogen atoms behaved differently in term of peaks heights, secondary peaks, and distance at which the first minimum appeared.¹³

Here, we characterize the effects on solvent reconstructions of different solute atom categories of the side-chain analogs versus that from the averaged environment of the protein. Ultimately, we want to develop the most generalized data set for reconstructions with minimum computational effort and best precision. In this work, we first examine the solvation structure for side-chain analogs of sulfur-containing amino acids and charged amino acids from small-molecule environments. We also compute the pRDF components for the sulfur-containing and charged amino acid side-chain atom types within the protein environment. These functions from averaged protein-water pairs and small model-water pairs are used to reconstruct the water distributions around azurin. We reconstruct the three-dimensional solvent density distribution using C, N, and O atom types and using additional sulfur and charged amino acid side-chain atom types. We focus on the different effects that charged surface residues have on hydration structures compared to the simpler schemes. We also discuss the difference between the average protein-water pair and small models-water pair pRDFs in the reconstructed solvent density.

METHODS

In this section we briefly review the theory underlying the pRDF and the additional criterion in the proximal search algorithm, followed by a summary of the underlying MD simulations used to obtain the solute–solvent distributions.

Distribution Functions

The proximal distributions are a near-neighbor case of the quasi component distributions.^13,15,21,22 Consider a solution containing a polyatomic solute molecule and N solvent molecules. The solute−solvent pair correlation function g_ij(r) describes the relative probability of finding a solvent molecule i at a given distance r away from a specific solute atom j. It is routinely computed from a trajectory according to eq 1:

$$g_{ij}\left(r\right)=\frac{1}{4\pi r^2\Delta rN}\sum _{t=0}^T\sum _{j=1}^N\delta [\mid {\overrightarrow{r}}_i\left(t\right)-{\overrightarrow{r}}_j\left(t\right)\mid -r]$$ (1)

Where T is the total of simulated or analyzed time steps, ${\stackrel{\rightharpoonup }{r}}_i\left(t\right)$ and ${\stackrel{\rightharpoonup }{r}}_j\left(t\right)$ represent the position vectors of solute atom i and solvent atom j at time t, respectively, and (1/4πr²Δr) is the normalization volume of a spherical shell of width Δr. For large, nonspherical proteins, the ease of use and interpretation for g_ij(r) can suffer complications from the volume element as well as coupled correlations since the g_ij(r) implicitly depends on the distribution of other protein atomic sites.

To condition on the local protein correlations and avoid distortion from the normalization of the volume for non-spherical solute, we use a perpendicular or proximal radial distribution, g_⊥(r), which gives the probability of finding the protein atom closest to a solvent atom which roughly defines the perpendicular to the protein surface or a Voronoi construction of the space around the protein. This reflects the protein surface closest to any given solvent molecule. Moreover, while the angularly averaged g_ij(r) suffers from the excluded volume of the protein in normalization of solvent distribution around protein surface atoms (the radial distribution approaches unity after a distance corresponding to or greater than the radius of gyration), g_⊥(r) enhances local characteristics of the protein surface and does not strongly depend on the rest of the protein volume. We define the pRDF as

$$g_{\perp }\left(r\right)=\sum _{t=0}^T\sum _{j=1}^N\frac{\delta \left(Inf{[\mid {\overrightarrow{r}}_i\left(t\right)-{\overrightarrow{r}}_j\left(t\right)\mid ]}_{i=1,N_{\mathrm{P}}}\right)}{\delta \tau ({\stackrel{\rightharpoonup }{r}}_j\left(t\right),k)}$$ (2)

where N_P is the number of protein atoms, and $\delta \tau ({\stackrel{\rightharpoonup }{r}}_j\left(t\right),k)$ is the volume around a solvent molecule j at instantaneous time t defined by all $\stackrel{\rightharpoonup }{r}$ vectors, where $\mid {\stackrel{\rightharpoonup }{r}}_k-\stackrel{\rightharpoonup }{r}\mid \le \mid {\stackrel{\rightharpoonup }{r}}_i-\stackrel{\rightharpoonup }{r}\mid .Inf[\mid {\stackrel{\rightharpoonup }{r}}_i\left(t\right)-{\stackrel{\rightharpoonup }{r}}_j\left(t\right)\mid ]$ yields the minimum distance vector between any solvent molecule j and the collection of solute atoms i at instant t, while k is the protein atom that is closest to the solvent atom j:

$$Inf[\mid {\overrightarrow{r}}_i\left(t\right)-{\overrightarrow{r}}_j\left(t\right)\mid ]=\mid {\stackrel{\rightharpoonup }{r}}_k\left(t\right)-{\stackrel{\rightharpoonup }{r}}_j\left(t\right)\mid$$ (3)

It is computationally nontrivial to compute the g_⊥(r) described in eq 2 because the normalized volume element has to be solved for each solvent molecule j at any instant t. A computationally effective solution is to compute the solvent positions with respect to a reference position and orientation prior to computing an averaged perpendicular distribution function. The pair correlation function computed in this way defines a water distribution at distance r perpendicular to the protein surface, measured with respect to a reference frame attached to the protein. The g_⊥(r) in this sense is considered to be a conditional pair distribution function between a protein surface (a fixed condition) and the water around it. This water distribution is straightforward to compute on a grid. The detailed theory and computational procedure is described in the literature.^10,14,21,22

We have found that the hydration pattern around particular atom types on the surface of a globular protein is often transferable to other proteins.^14,19 Here we will also test smaller molecule analogs. From the precomputed pRDF for specific protein atom types, one can reconstruct a model for a three-dimensional solvent density distribution ρ(${\overrightarrow{r}}_{uvw}$) around another solute protein using the surface atom-specific functions. Because the pRDF volume was normalized for each grid point, reconstruction also required at the same resolution normalization. This results in a smoother water distribution compared to that obtained from collocation of the macro-molecular simulation.

$$\rho \left({\overrightarrow{r}}_{uvw}\right)=\sum _{\mathrm{X}}{g}_{\perp }^{\mathrm{X}}\left(r^{\prime }\right)$$ (4)

where r′ takes the minimum value of $\mid {\overrightarrow{r}}_i-{\overrightarrow{r}}_{uvw}\mid$ for each grid point for all protein atoms i. X is the atom type of protein atom k, for which $r^{\prime }=\mid {\overrightarrow{r}}_i-{\overrightarrow{r}}_{uvw}\mid$ (e.g., X= C, N,O, S, etc.). The indices u, v, w denote the grid points along the x, y, and z directions, respectively. Since the water distribution for each atom class is different depending on their location on the grid, r′ may be slightly different for different X. We have tested and found the grid spacing, 0.5 Å, is adequate for this purpose.¹⁴

In this current work, we specifically want to examine the effects of the sulfur-containing and charged side-chain amino acid atomic sites on the $g_{\perp }^{\mathrm{X}}\left(r\right)$ functions within the context of different solute local covalent environments. We considered solutes which are side-chain analog mimics and a whole protein. We require the $g_{\perp }^{\mathrm{X}}\left(r\right)$ as a functions of different solute atomic species. The protein is decomposed into various atomic type sets. We will consider nonpolar carbon C, backbone nitrogen N, and oxygen O, negatively charged amino acid side-chain oxygen OE and OD, polar positively charged amino acid side-chain nitrogen NZ, NH, and sulfur S as a set with more specificity than the {C,H,N,O} set used previously.^13,14

We will discuss the different effects the sulfur and charged amino acid side-chain distributions on the protein surface have on reconstructions of water density distributions in this near-neighbor scheme.¹⁵ We compare the differences between reconstructions of water density from the side-chain analogs–water distribution functions and the average protein-water distribution functions to determine the effects of intramolecular correlations and context.

We use the real space R-factor and root-mean-square deviation (RMSD) defined on the reconstruction grid²³ to compare the precision between our near-neighbor reconstructed solvent density distribution and the full solvent density distribution obtained directly from MD simulations. The R-factor and the RMSD are shown below in eqs 5 and 6, respectively:

$$R=\frac{{\Sigma }_{i,j,k}\mid {\rho }_0-\rho \mid }{{\Sigma }_{i,j,k}\mid {\rho }_0+\rho \mid }$$ (5)

$$\mathrm{RMSD}=\frac{\sqrt{{(1∕N)}^2{\Sigma }_{i,j,k}{({\rho }_0-\rho )}^2}}{(1∕N){\Sigma }_{i,j,k}{\rho }_0}$$ (6)

where ρ₀ is the solvent density obtained from MD simulation and ρ is the reconstructed solvent density distribution on a grid at indices i, j, and k along x, y, and z directions, respectively.

MD Simulations

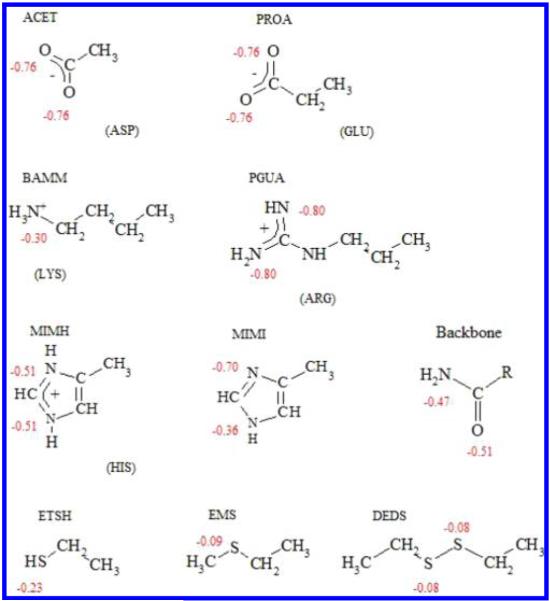
In this current work, we use the NAMD molecular dynamics package²⁴ and the CHARMM 27 force field parameters.^25,26 The initial protein coordinates were obtained from X-ray crystal structures with PDB codes 2mgk²⁷ for myoglobin and 4azu²⁸ for azurin to be consistent with our previous work.^9,13,14,16 Periodic boundary condition was used. The proteins were solvated with TIP3P²⁹ in a box with a 10 Å layer of water in all three directions. The total number of water molecules for myoglobin and azurin are 18,402 and 14,898, respectively. Counterions were added to neutralize each system; three sodium for azurin and one chloride for myoglobin. The system was subject to energy minimization and gradual heating to 300 K over 30 ps, followed by 200 ps of equilibration. Simulations to determine the solvation were carried out with 1 fs time step for 30 ns with the protein held rigid. Conformations were saved every 1 ps for analysis. The short-range nonbonded interactions were calculated for every time step. The electrostatic energy was computed using the particle mesh Ewald implementation in NAMD every two time steps.²⁴ MD simulations for the side-chain analogs (Table 1) were done with the same procedure. The method was tested on both azurin and myoglobin. The results for myoglobin are discussed in another article.³⁰

Table 1.

Corresponding Amino Acid, Their Side-Chain Analogs, and Their Atomic Partial Charges

RESULTS AND DISCUSSION

We obtained the solvent distributions around specific atoms for various amino acid side-chain analogs and proteins from MD simulations with fixed solutes. Routine checks of properties including the water distribution itself indicated satisfactory convergence after equilibration and no ion condensed near charged residues at any time. Statistical uncertainty of the pRDFs may be inferred from the smoothness of the functions as presented below. Other error sources will be discussed separately.

Here we consider ionizable and sulfur-containing residues. The solvent distributions around these particular atom types will be compared between conditions in the small models versus in the protein. While three atom {C, N, O} and four atom{C, H, N, O} sets were the focus of the previous work^13,14 in this current study, we consider a richer set of atom types in our basis set for reconstruction. The oxygen type is divided into backbone carbonyl oxygen and negatively charged Asp and Glu side-chain oxygen, OD and OE. In a similar way, the nitrogen type is divided into backbone amide nitrogen and positively charged Lys and Arg side-chain nitrogen, NZ and NH. For the sulfur atom, we examine thiol, alkyl thiol, and disulfide groups. The corresponding partial charges from the force field are shown for reference in Table 1.

Water Distributions around Negatively Charged Oxygen in Aspartic and Glutamic Side-Chain Mimics and in Azurin

The pRDFs that describe solvent distribution around OD and OE oxygen of side-chain Asp and Glu analogs, respectively, are calculated to be identical and very similar to those calculated in azurin. Figure 1 compares solvent distributions characterized by pRDFs for atom OE of the negatively charged Glu side chains, in the propionate analog (PROA) and in azurin to the backbone oxygen from the peptide Ala₁₀ and to the averaged protein oxygen atom. Our results for Ala₁₀ are essentially identical to previous work.³¹

Figure 1.

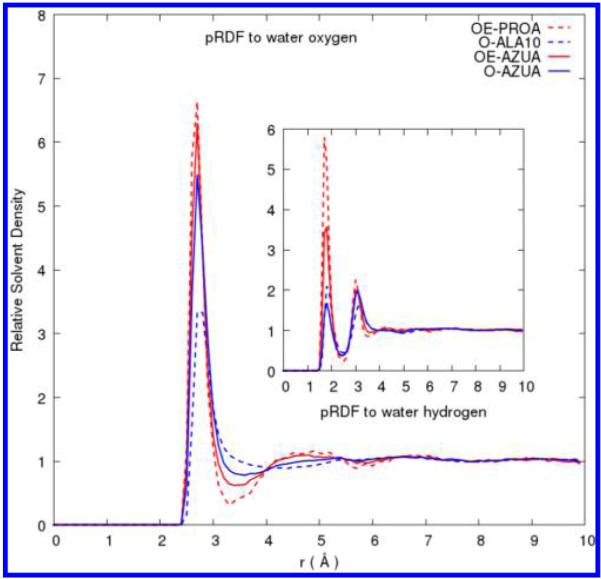
Comparison of pRDFs for solute oxygen atoms from side-chain analog models, peptide, and protein simulations. Solute oxygen negatively charged atom type OE of Glu side-chain analogs and of the protein AZUA are shown as red dotted and solid lines, respectively. O oxygen atoms of deca-alanine and the averaged O of the protein AZUA are shown as a blue dotted and solid line, respectively.

Not surprisingly, the more negatively charged the atoms, the greater the first peak heights. The pRDFs for OD and OE in ACET and PROA have almost identical peak heights by the symmetry. Their peaks heights are almost double that of a backbone carbonyl O of Ala₁₀ polypeptide. Peptides have been noted to be different in this regard from proteins.¹⁷ Note that oxygen atoms in deca-alanine only represent the backbone oxygen type and are different from the averaged oxygen atom type of the folded protein azurin.

One noteworthy characteristic of the pRDF for oxygen water distribution for the acid side-chain analogs is a pronounced minimum at distance r = 3.3 Å. Relative water density at this distance is 0.3 compared to that of bulk water at 1. This feature is washed out of the pRDF for the averaged oxygen atoms. The water hydrogen pRDFs for the side-chain analogs also show a significant difference in the peak heights between the first and second peaks compared to the water hydrogen pRDFs with backbone oxygen. The negatively charged side-chain analogs ACET and PROA have the first peak in the water hydrogen–oxygen distribution at the expected hydrogen-bonding distance.

While the all-oxygen type of deca-alanine is only backbone oxygen, the corresponding type of azurin averages various backbone and side-chain oxygen atoms. Combining all oxygen atoms into a single class results in the disappearance of features. This leads us to compare the reconstruction of solvent density distributions between reconstructions from the mimetic-water pair and the protein-water pair distribution functions. Using only the solvent distribution of categories for C, N, and O, in either small models or protein is sufficient for solvent reconstructions at a certain level of accuracy. However, information about the water depleted regions is inaccurate without the diversity of the extra categories or types of oxygen.

By symmetry, the aspartic acid and glutamic acid side-chain oxygen OD and OE, respectively, are the same. Due to incomplete averaging we find statistically different peak heights of the protein-water pair pRDFs which consequently alter the solvent reconstruction. In contrast, the mimetics-water pair pRDFs of OE and OD are essentially identical, and thus reconstruction from these distribution functions can be done with one additional acidic oxygen atom class for both Asp and Glu residues as well as the carboxylate terminus. Reconstruction from protein-water pairs with more than one oxygen group better captures the hydration structure. The optimal number of atom classes is necessary for accurate and economically inexpensive reconstruction. The simple calculation of the mimetic-water pair distribution functions more than compensates for the larger basis set of pRDFs being used in reconstruction.

Positively Charged Nitrogen of Lysine, And Arginine Side Chain in Small Models and Azurin

We computed water pRDFs for different nitrogen categories. The water distributions around the side-chain analogs were compared with one another and with the corresponding distributions in azurin. Figure 2 shows the nitrogen-water pRDFs. Unlike the solvent distribution around charged oxygen characterized by pRDFs, due to chemical diversity in the N types (see Table 1) there is less correlation between atomic charges and peak heights for the charged side-chain nitrogen atoms. We notice that although their peak heights are profoundly different, the water O pRDFs for NZ and NH have the same r distance of 2.8 Å; that for the backbone N of the Ala₁₀ peptide is markedly different as expected.

Figure 2.

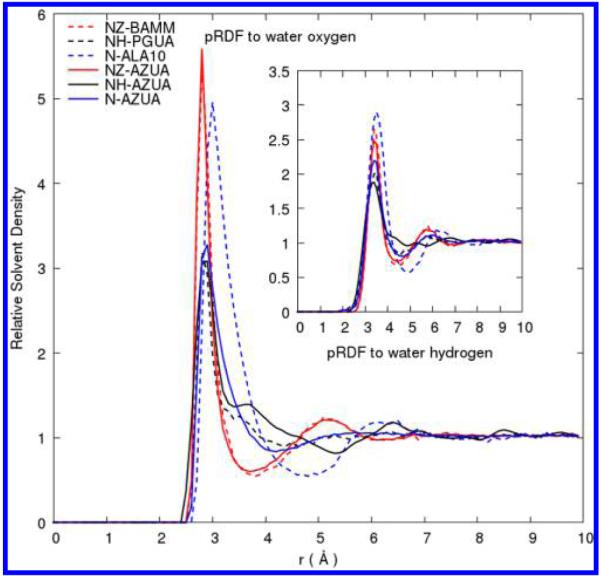
Comparison of pRDFs for nitrogen atoms from side-chain analog models, peptide and protein simulations. Positively charged NZ and NH of Lys and Arg side-chain analogs are shown in dotted red and black lines, respectively, while pRDFs for NZ and NH of the protein residue Lys and Arg side chain are shown in solid red and black lines. Peptide backbone nitrogen atoms of deca-alanine and the averaged N of the protein AZUA are showed in blue dotted and solid lines, respectively.

The water distribution around different nitrogen types shows the presence or absence of a secondary peak before the minimum and the different distances where the minima appear. Although both NZ and NH type belong to the positively charged side-chain groups, the different orientational and bonding correlations with neighboring atoms are reflected in different solvent distributions around them. The water distribution around NH of Arg side chain shows a secondary peak at distance r = 3.8 Å away from the protein. At this same distance, the water distribution around Lys side-chain NZ shows a minimum. Additionally, at distance 5.2 Å away from the protein, where water distribution around NZ exhibit a secondary peak, water distribution around NH exhibits the first obvious minimum.

In simply defining the first hydration shell to terminate at a distance where the distribution function has its first minimum, the first hydration shell around Arg side-chain nitrogen atoms is much larger than that of Lys side-chain nitrogen. The size of the Arg side chain being much greater than that of Lys side-chain nitrogen leads to a very different solvation pattern. In terms of chemical environment around the different charged side-chain nitrogen atoms, Arg side chain includes three times more electronegative atoms than Lys. The CHARMM force field^25,32 assigns partial charges of −0.80 for Arg side-chain nitrogen atoms and −0.30 for Lys side-chain nitrogen atom with the polar hydrogens carrying an impressive variety of balancing positive charges. Presumably, interactions of the Arg side-chain nitrogen atoms with water within their local side-chain context are stronger than that of Lys side chain. The solvation free energy of the Arg side-chain analog was experimentally measured to also be larger (more negative) than any other amino acid side-chain analogs, including the similarly charged Lys side-chain analog.³³

In contrast to the observation of different peak positions in the distributions for water oxygen, the pRDFs for water hydrogen with the various N types have peaks occurring at the same distance. Also while the pRDF for nitrogen of the positively charged lysine side-chain analog and the lysine side chain in azurin both have a minimum at a closer distance to the protein, the arginine side-chain nitrogen pRDF minimum appears at a further distance, confirming a larger first hydration shell. Additionally, the average nitrogen atom category in the protein results in a smooth and gradual decrease in the water distribution with no distinct minimum or secondary peak. The effects of next nearest-neighbors can be significant.¹⁶

Figure 2 also shows solvent distributions around the different nitrogen categories in the protein in comparison with the corresponding distributions in the analog models. In both cases, the solvent distributions are essentially identical around the positively charged nitrogen NZ and NH, particularly for NZ, lysine side-chain nitrogen. While the solvent distribution around deca-alanine describes how water molecules occupy a configuration space around the backbone nitrogen atoms, that of azurin describes a spatial and compositional average of water around both backbone and side-chain nitrogen types. The difference is an absence of a minimum in the averaged result for azurin, while that for deca-alanine retained its minimum. This feature consequently results in a difference in solvent reconstruction using small model-water pRDFs versus averaged protein-water pRDFs.

Water Distribution around Sulfur Atoms

Studies have been made on the pRDFs for solute C, H, N, and O atom types^13,14,17,19 as well as some initial work for the phosphorus atom type of DNA.¹⁹ However, less attention has been paid to the sulfur atom, which can be significant if proteins contain Cys and/or Met especially on their surfaces. We considered various sulfur-containing amino acid side-chain analogs in aqueous solution to examine the effects that local covalent environments of thiol, sulfide, and disulfide have on water density distributions (see Table 1).

Figure 3 shows the pRDFs for sulfur atoms of cysteine side-chain analog, ethane-thiol (ETSH), methionine side-chain analog, ethylmethylsulfide (EMS), disulfide-bond analog, diethyldisulfide (DEDS), and the averaged sulfur atom in azurin. All the peaks appear at almost the same distance r and have essentially the same peak heights in both the small models and in the azurin macromolecular environment. These functions should be useful for solvent reconstructions around any macromolecule-containing sulfur atom classes.

Figure 3.

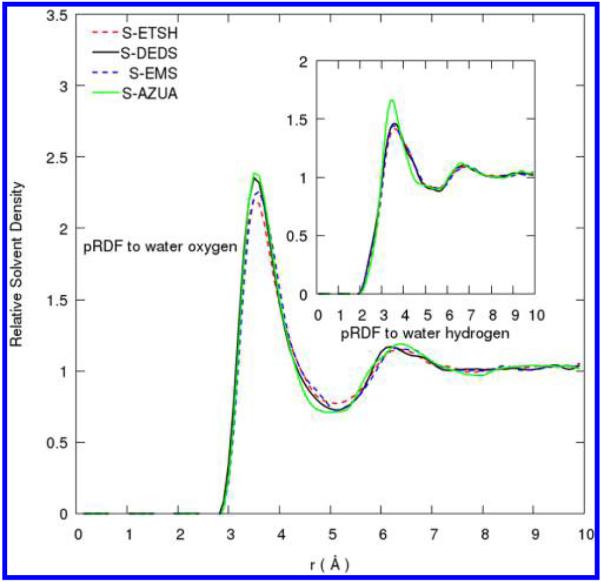
Proximal radial distribution functions around sulfur atom type of Cys and Met side-chain analogs and of disulfide bond. Data are plotted with natural smoothing spline.

We also notice that the pRDFs of all three analogs and the protein have a distinct minimum at a distance r = 5.2 Å where the relative water density is only about 60% of bulk solvent. Whether it is a thiol, sulfide, or disulfide group, it appears that sulfur-containing functional groups perturb the water density beyond the solute–water interface. In the next section, we show that this kind of behavior contributes significant improvement beyond the protein–water interface in reconstructions of water density distributions.

We also computed the pRDFs around various carbon atom types from the different sulfur-containing side-chain analogs, the charged amino acid side-chain analogs, and the all-carbon single type. All the pRDFs for different carbon types show almost identical behavior comparing to one another in both the small models and in the protein. The solvent distribution around different carbon atom types appears to be less varying across all amino acid side chains, backbones, in small-molecule models as well as in proteins.

Reconstructions of the 3D Solvent Density Distribution Using pRDFs with Different Atom Categories

Among the simplest approximations to produce a three-dimensional hydration map around a given protein at a reasonable accuracy is to group all nitrogen, all oxygen, and all carbon each in to single class of protein atom type, followed by using the proximal radial distribution function for each class to reconstruct the solvent density distribution. Several studies have used the pRDFs for three classes of protein atoms C, N, and O to reconstruct at given precisions the solvent density distribution around different proteins.^13,14

We consider three features of solvent density reconstructions from pRDFs. The first one is reconstruction of water density distribution using the pRDFs for protein C, N, O atoms with the addition of sulfur atoms (Figure 4). The second noteworthy feature is an improvement of solvent reconstruction with the additional charged side-chain atom types (Figure 5). The third finding is an improvement in reconstruction of water distribution around azurin when performed with the side-chain analog mimetic pRDFs instead of averaged atom-type protein-water pRDFs.

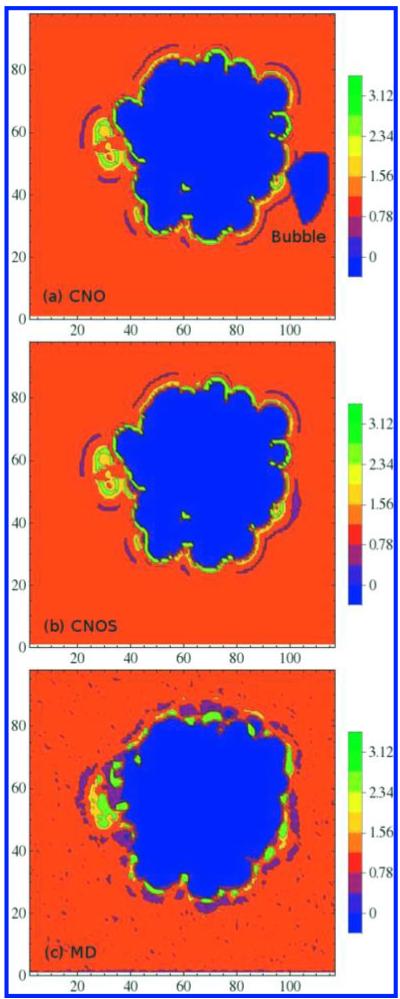
Figure 4.

(a) Solvent density reconstruction from the proximal radial distribution functions around C, N, O atom types (b) and with the addition of S atoms of Cys and Met side-chain analogs and of disulfide bond. (c) Solvent density distribution from the MD simulation.

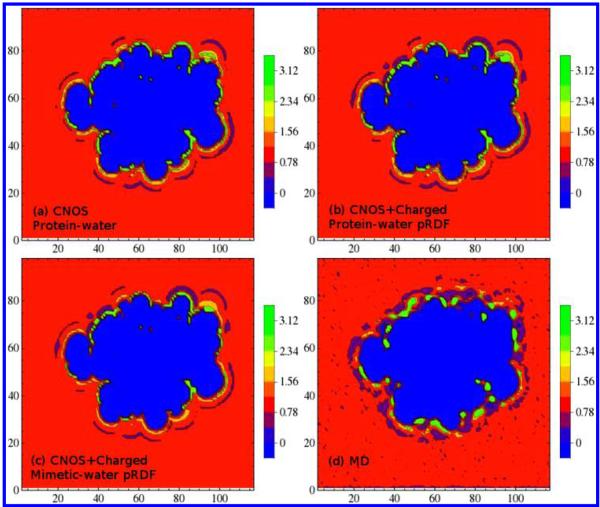
Figure 5.

(a) Solvent density reconstruction from the protein-water pair proximal radial distribution functions around C, N, O, and S atom types; (b) same as (a) with the addition of explicit charged amino acid side-chain O and N atoms. (c) Solvent density reconstruction from the mimetic-water pair proximal radial distribution functions around C, N, O, S, and explicit charged amino acid side-chain O and N atoms. (d) Solvent density distribution from the simulation.

Reconstructions Including S Atom Categories

Cysteine and methionine are important in terms of protein structure, stability and function.³⁴ The oxidizable Cys and Met are often surface exposed. Because of the recent progress in understanding the importance of sulfur-containing residues, particularly Met in terms of function and location, it is necessary to include the sulfur-water pair radial distribution in solvent density reconstruction. In the case of azurin with nine sulfur-containing amino acids, reconstruction of water distributions with pRDFs using only three atom classes C, N, and O (Figure 4a) creates a bubble in the density map where Met 64 resides. In contrast, by reconstruction with the additional pRDF for the sulfur atom type (Figure 4b), the bubble disappears.

Figure 4 shows a cross-sectional plane cut through azurin along the z axis to compare solvent reconstructions involving C, N, and O atom types (Figure 4a) to that with the addition of S atoms (Figure 4b) to the solvent distribution from MD simulation (Figure 4c). Although some of the contour levels of the predicted preferred-hydration sites are smaller than what observed from MD simulation, their locations are in good agreement. The simulated distributions occasionally show peaks (in green) due to the effects of next nearest-neighbors on localization. The reconstructed solvent density from the pRDFs also shows a localized density peak in the interior of the protein that is not observed in the MD solvent density.

This feature highlights a feature of using pRDFs reconstructions in capturing the interior hydration sites that could otherwise take a very long simulation time for water to diffuse in.³⁰ The reconstructed water density can calculate the probability of finding water near a specific atom type based on interactions and spatial availability.

Reconstructions Using the Mimetic-Pair pRDFs

Reconstruction of the water density distribution from probabilities obtained from small-molecule side-chain mimetics is demonstrated in Figure 5. At the same contour levels, reconstruction with additional pRDFs for the charged side-chain atom types (Figure 5b,c), shows water density fluctuations that more closely resemble that observed in the simulation (Figure 5d) compared to reconstructions with only C, N, O, and S pRDFs (Figure 5a). Simulated water density distributions show distinct hydration patterns at the protein–water interface and a first solvation shell defined by the water depletion before approaching bulk water. Recall that the pRDFs for charged side-chain atom types in both model analogs and in the two proteins show a clear minimum and secondary hydration peaks before approaching bulk density. In contrast, using one class of averaged distributions for each C, O, and N, the pRDFs are flattened out by averaging, and there are neither minima nor well-defined secondary peaks. Including the charged atom-type pRDFs in solvent reconstructions results in more accurate solvent distributions whether using the protein-water pair pRDFs (Figure 5b) or the side-chain analog-water pairs distribution functions (Figure 5c).

While adding the sulfur atom pRDF removed the bubble and improved relative error in reconstruction, the use of charged side-chain atom pRDFs captured the less dense regions more closely resembling simulation. This feature is a direct reflection of the presence of minima in the small model pRDFs that were averaged out of the protein pRDFs. There are certain areas where the effect may be exaggerated. These areas correspond to the volume where a carboxamide-containing amino acids are located. The result implies that it is necessary to treat the backbone and side-chain nitrogen–water pair $g_{\perp }^{\mathrm{X}}\left(r\right)$ explicitly in solvent reconstruction.

Some density regions in the simulated protein are more intense than in the reconstructed density for this particular slice along the z-axis. The present method is an average among the hydration sites which may have higher or lower proximal water density. It can result in a lower density when averaged. The more smeared out regions are often better captured by the small-molecule systems since the next nearest-neighbor effects are smaller. The protein next nearest-neighbors can more effectively trap water molecules. A next nearest-neighbor approximation may result in better precision, with an appropriate treatment for the multibody effects.

A concern of models for hydration structure is the tendency to overpredict.³⁵ While including the charged side-chain atom classes in reconstructions improves the water density fluctuations, particularly in the less than bulk water regions, including the mimetic-water pair distribution function also improves aspects the prediction of the preferred hydration sites.

A cluster of water density in the protein cavity is captured in all water density distributions either from reconstructions or MD simulation. The reconstructions present a slightly larger density cluster compared to that observed in the simulation. Solvent density from reconstructions, with or without the explicit charged atoms, also shows a second significantly smaller density cluster in the protein cavity that is not observed in the MD solvent density. While for such a deep buried hydration site, it would require a significant longer simulation time in order for water molecule to diffuse in.³⁰ In this study, a 30 ns MD simulation might not be long enough.

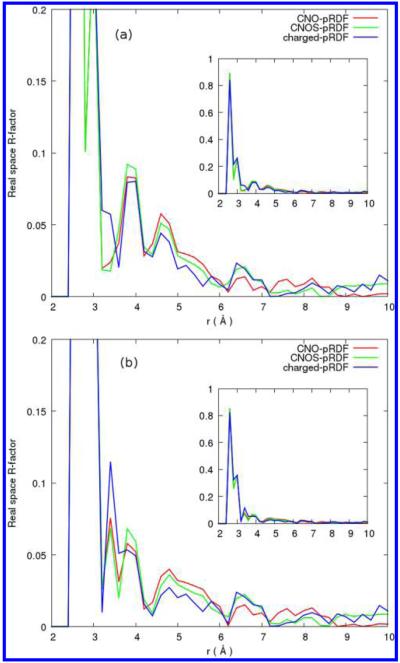
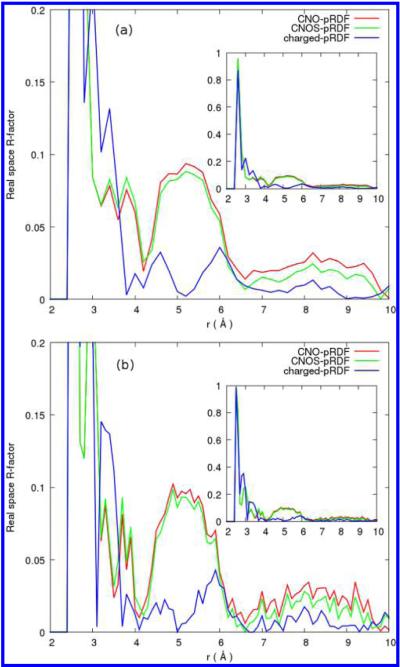
We computed the real space R-factor²³ and a grid RMSD^19,23 to quantitatively compare between our reconstructed solvent density distribution and the solvent density distribution obtained from MD simulations. Figures 6 and 7 show the R-factors for reconstructions from the protein-water and small-molecule-water pRDFs, respectively. The R-factor represents a measure of real space fitting for the three-dimensional reconstructed density on a grid compared to the solvent density distribution obtained from MD simulations. Figure 6a,b shows modestly lower R-factors around protein side-chain and heavy atoms, respectively, for the reconstruction with charged side-chain atom types compared to that with the four atom types C, N, O, and S, and the three atom types C, N, and O. There is no oxygen water density within 2.6 Å away from the protein heavy atoms. The highest R value is at distance r = 2.6 Å and is statistically less important due to low counts. The R-factor drops dramatically after that, and R values vary between 0.27 and go as low as 1.0 × 10⁻⁴. At distances up to 8 Å away from the protein side chain and 9 Å away from the protein backbone there is a small improvement for the addition of charged side-chain residues compared to the four atom types pRDFs, C, N, O, and S. Very similar behaviors are observed in the R-factors for reconstructions using the small-molecule distribution functions which are less computationally intensive to obtain. The improvement when adding charged atom types, however, is more profound in the shell between 4 and 6 Å away from the protein. Figure 7a,b shows lower R-factors around protein side-chain and heavy atoms, respectively, for charged side-chain atom types compared to that with the four atom types C, N, O, and S, and the three atom types C, N, and O only. The improvement in R-factors that comes with adding more atom categories is more for reconstructions using small models pRDFs than that with protein-water pair pRDFs.

Figure 6.

Relative error versus distance around (a) amino acid side chains and (b) protein non-hydrogen atoms from reconstruction with protein averaged distributions for three atom types C, N, and O (red) and four atom types C, N, O and S (green) and with charged side-chain oxygen and nitrogen atom types (blue).

Figure 7.

Relative error around (a) amino acid side-chain and (b) protein non-hydrogen atoms from reconstruction with mimetic-water pRDFs for only three atom types C, N, and O (red) and four atom types C, N, O and S (green) and with charged side-chain oxygen and nitrogen atom types (blue).

Table 2 gives the relative error represented by the real space R-factor²³ around all the protein side-chain, backbone, and all heavy atoms. For reconstruction from the protein-water pair $g_{\perp }^{\mathrm{X}}\left(r\right)$, the additional atom type for sulfur and the charged side chains improves the R-factor for solvent density around protein heavy atoms within the 4–6 Å shell away from the protein from 0.53 to 0.36. We chose a shell of 6 Å to compute the errors within to ensure that the protein volume and its interface with solvent is included but excluding most bulk (trivial) water. Moreover, the distance between 4 and 6 Å away from the protein is where the minimums and the secondary peaks for charged side-chain atom types are most often observed. For reconstructions from protein-averaged distributions we find an interesting trend reversal in that the total relative error of the protein heavy atoms is 4.34% using charged side-chain atom types, compared to 4.27% when using only C, N and O types. In contrast, reconstructions with small-molecule functions have a total relative error of 4.19% when including the additional charged atom types and 5.42% when using only C, N and O atoms.

Table 2.

Relative Errors for Solvent Reconstructions from the Different pRDF Atom Sets

		CNO-pRDFs	CNOS-PRDFs	side chain-pRDFs
	Reconstructions from Protein Averaged Distributions
relative error within 4–6 Å shell	side chain	0.599%	0.574%	0.427%
	backbone	0.841%	0.847%	0.888%
	heavy atom	0.53%	0.51%	0.36%
total relative error	side chain	4.43%	4.44%	4.41%
	backbone	6.44%	6.39%	6.43%
	heavy atom	4.27%	4.27%	4.34%
RMSD	side chain	0.38%	0.37%	0.39%
	backbone	0.51%	0.51%	0.52%
	heavy atom	0.71%	0.71%	0.73%
	Reconstructions from Small-Molecule Distributions
relative error within 4–6 Å shell	side chain	1.37%	1.34%	0.444%
	backbone	1.05%	1.01%	0.958%
	heavy atom	1.3%	1.3%	0.39%
total relative error	side chain	5.76%	5.62%	4.42%
	backbone	6.65%	6.48%	6.05%
	heavy atom	5.42%	5.29%	4.19%
RMSD	side chain	0.37%	0.37%	0.37%
	backbone	0.50%	0.50%	0.50%
	heavy atom	0.70%	0.70%	0.71%

The RMSD is essentially the percent error considering the MD water density distribution to the true value. The RMSD reffects mostly on regions with high density. The fact that additional atom types in solvent distribution reconstructions reveal a more precise feature of the less dense regions results in insignificant effects on the RMSD. The similarity in errors between small-molecule mimetics and those from full protein simulations indicates that the mimetics do not damage the overall statistics.

Overall, reconstructions of water density distribution around azurin match the water density from MD simulations statistically as well when using the small molecule derived $g_{\perp }^{\mathrm{X}}\left(r\right)$ functions. The conditional pair radial distribution function between solute atom X and water has previously been calculated from either a single protein or of an average over a series of proteins.^13,14,17 In either case, we find that the averaging procedure can yield functions with somewhat poorer performance.

For nonspherical macromolecule solutes, in this case globular proteins, averaged water distributions around specific atom types from a series of similar-shaped proteins presumably give a measure of how these functional groups commonly perturb the solvent environment. However, this parametrization is necessarily confounded by an extensive variety of next nearest-neighbor effects. In contrast, using the small-molecule-water distribution functions reflect the water correlations around given atom categories while minimizing the effects of a nearly random and therefore the nonspecific set of next nearest-neighbors.

Figure 8 shows a water configuration around the negatively charged oxygen atoms of Asp side chain in the small-molecule analog (Figure 8a) and in the protein (Figure 8b). We see the side chain of azurin Asp 71 with two oxygen atoms (OD) exposed to solvent but partially shielded by the rest of the protein. However, throughout the simulation, the Voronoi polyhedron of OD, defined by the distance from a given water molecule that is closest to OD than any other solute atoms, is much smaller and more limited in configuration space compared to that of the OD in the small models. Voronoi polyhedron of a particular atom type in a small molecule is less affected due to fewer next nearest-neighbors. Consequently, using the structural parameter $g_{\perp }^{\mathrm{X}}\left(r\right)$ characterizes hydration structure around a given atom type within its side-chain analog, yielding a more representative near-neighbor solvent density distribution than using $g_{\perp }^{\mathrm{X}}\left(r\right)$ from the protein averaged molecular context. That the MD simulations show some larger peaks demonstrates that the near-neighbors must also contribute to produce smaller peaks to obtain the average distributions seen.

Figure 8.

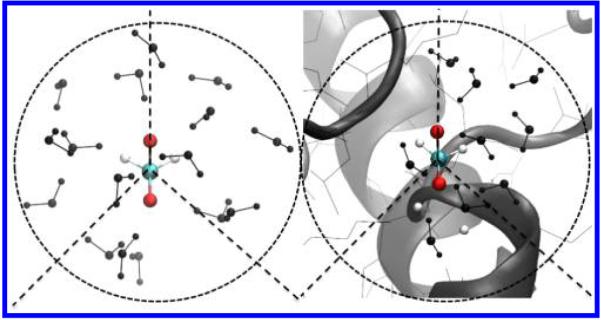
Water distribution in a shell 4 Å away from the negatively charged oxygen atom of Asp side chain in (a) the small-molecule model and (b) the protein.

CONCLUSIONS

In this work, we examined hydration structures around different amino acid side-chain atom categories in the side-chain models and in a whole protein. The atomic charge distribution and structural context of different amino acid side-chain atom categories show a variety of influences on the water. The hydration structural factors characterized by pRDFs of the small-molecule-water pairs including explicit side-chain charged groups, backbone oxygen, and backbone nitrogen groups were found to be best for solvent density reconstructions. The side-chain mimetics allow a given atom type to have a more representative Voronoi polyhedron because of fewer next nearest-neighbors than within the protein. Including the pRDF for backbone nitrogen group separately allows certain of the depletion regions of the proximal water density distribution to be better modeled. Consequently, solvent reconstructions from small-molecule mimetic-water pair pRDFs with explicit charged side-chain and backbone groups better resemble solvent distribution from whole protein simulations.

The results from this work also show that regions of water with density less than bulk solvent are better reconstructed when the charged side-chain atoms and the backbone atoms are explicitly included. The additional groups of solute atom types enable solvent reconstructions using pRDFs to better resemble the hydration patterns obtained from MD simulations in the less dense regions. The addition of sulfur atoms completes reconstructions where sulfur-containing residues reside on the protein surface.

The mimetic-water pair pRDFs of charged side-chain analogs improve the estimation of preferred hydration sites at the protein–water interface. With optimal groupings of solute atoms within a given local covalent environment, such as side-chain analogs, the solute-water pair $g_{\perp }^{\mathrm{X}}\left(r\right)$ serves as an intrinsic property of protein hydration that can be used to calculate the hydration structure around macromolecule assemblies. This method is easily expanded to other atom types. Future investigation will be done on solvent distribution around a variety of other moieties to consider post-translational modifications. The hydration structure can then be used to conveniently evaluate solution thermodynamics of an arbitrary protein system with a variety of methods at very low computational cost.^26,32