Breast Density Analysis Using an Automatic Density Segmentation Algorithm

Abstract

Breast density is a strong risk factor for breast cancer. In this paper, we present an automated approach for breast density segmentation in mammographic images based on a supervised pixel-based classification and using textural and morphological features. The objective of the paper is not only to show the feasibility of an automatic algorithm for breast density segmentation but also to prove its potential application to the study of breast density evolution in longitudinal studies. The database used here contains three complete screening examinations, acquired 2 years apart, of 130 different patients. The approach was validated by comparing manual expert annotations with automatically obtained estimations. Transversal analysis of the breast density analysis of craniocaudal (CC) and mediolateral oblique (MLO) views of both breasts acquired in the same study showed a correlation coefficient of ρ = 0.96 between the mammographic density percentage for left and right breasts, whereas a comparison of both mammographic views showed a correlation of ρ = 0.95. A longitudinal study of breast density confirmed the trend that dense tissue percentage decreases over time, although we noticed that the decrease in the ratio depends on the initial amount of breast density.

Introduction

Mammographic density represents the amount of fibroglandular tissue, which is radiographically dense, in contrast to fat tissue, which appears lucent in a mammogram [1]. Breast density is one of the strongest risk factors for breast cancer [2, 3], and women with highly dense tissue have a threefold to sixfold increase in breast cancer risk [4]. Additionally, dense breast tissue also affects methods used for automatic tumour detection [5, 6]. Specifically, studies have shown that either the sensitivity of computer-aided detection (CAD) systems is significantly decreased as breast density increases (whereas the specificity of the system remains relatively constant) [7, 8] or when specificity is decreased [9].

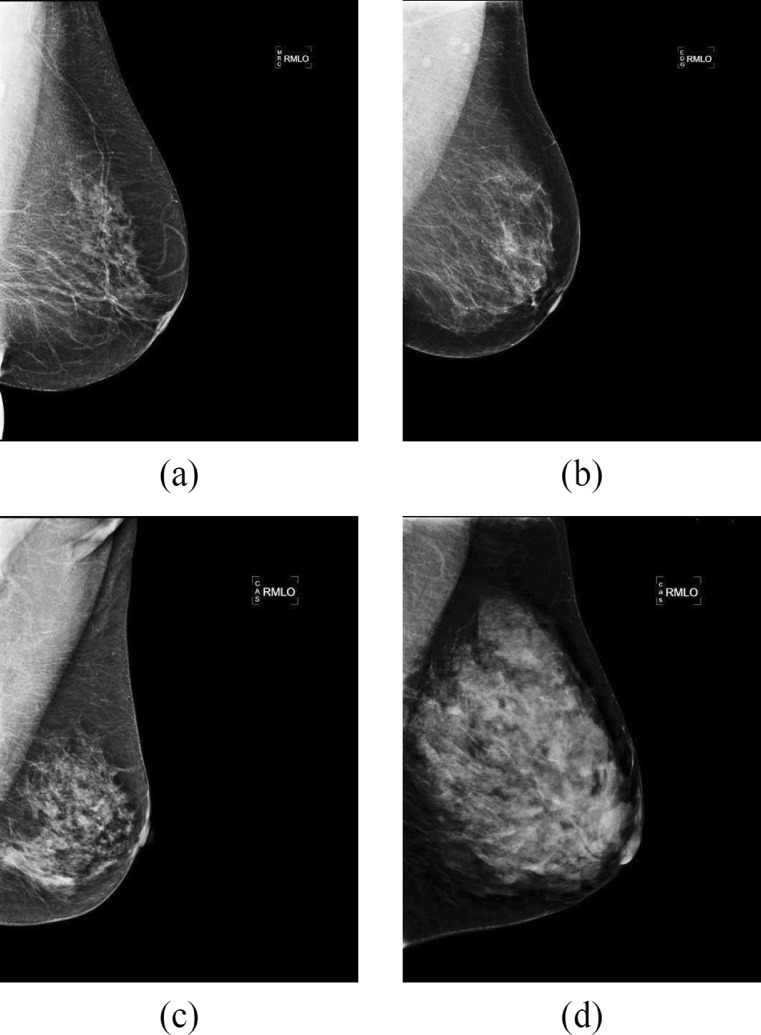
Several risk assessment metrics have been proposed in the literature to classify mammograms according to their internal density [10]. Currently, the American College of Radiology (ACR) Breast Imaging-Reporting and Data System (BI-RADS) has become a standard in the medical community. According to the BI-RADS protocol, mammograms can be classified into four categories: I (almost entirely fat), II (scattered fibroglandular densities), III (heterogeneously dense) and IV (extremely dense). Figure 1 shows four mammograms, one of each density class. The amount of fibroglandular tissue increases with each category.

Fig. 1.

Four full-field digital mammograms of increasing internal density. a BI-RADS I, b BI-RADS II, c BI-RADS III and d BI-RADS IV

There are automatic approaches that can qualitatively classify mammograms according to the above metrics [11, 12]. However, a quantitative segmentation of the breast into fatty and dense tissues provides more information at the local level than breast classification; nonetheless, manual breast density segmentation is difficult, time-consuming and prone to inter-/intra-rater subjectivity. The semiautomated Cumulus software¹ can perform an interactive intensity threshold [13, 14] and is considered one of the best methods for obtaining a quantitative segmentation [3]. However, the use of thresholds may not be sufficient to distinguish all of the dense parts of the breast. Fully automated techniques are currently being developed for obtaining a more objective and quantitative evaluation of breast density. For instance, the Volpara software² [15, 16] returns the percentage of dense tissue by means of a volumetric estimation of the breast.

In contrast with the above approaches, supervised approaches allow training of the algorithms using the experts’ knowledge. In our previous work [17], we reported the benefits of using a statistical approach in contrast to various threshold-based approaches. The approach was based on modelling the intensity of the pixel and its neighbourhood information (texture). Kallenberg et al. [18] extended the approach using a neural network classifier and by also modelling pixel position. The approach presented here extends this work by using additional features as well as a different classifier. Instead of using a neural network, we used a support vector machine (SVM) classifier, which has been proven to be a more robust and stable classifier in a variety of applications, including mammography [19, 20].

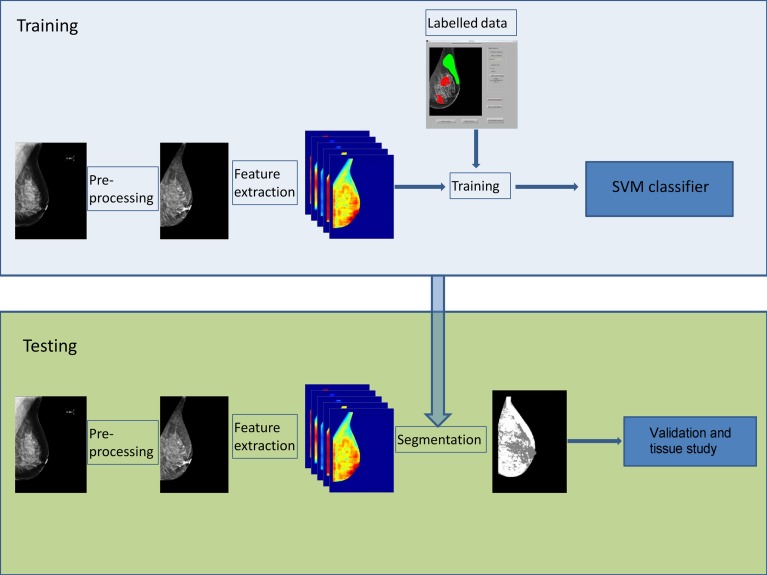
Figure 2 graphically shows our proposal for breast density segmentation. Two main parts, training and the testing, can be distinguished. During training, the classifier learns to distinguish between fatty and dense pixels from manually annotated data, whereas in testing, the classifier assigns a fatty or dense tissue label to each pixel of the input image. The results of the approach are analysed qualitatively based on the BI-RADS analysis and quantitatively by comparing the dense tissue percentage segmented in the four views of the same transversal study. Finally, a longitudinal analysis is performed by analysing the evolution of dense tissue percentage in different temporal studies. In this paper, we report the first longitudinal analysis of breast density performed by a fully automated algorithm.

Fig. 2.

Our approach follows a pixel-based classification scheme. Firstly, the algorithm learns to distinguish between fatty and dense tissue (blue box), and subsequently, it is used to segment new images (green box)

Materials and Methods

Database

The data used in this paper consists of complete and temporal full-field digital mammographic studies from 130 patients, properly anonymised and acquired following the Spanish screening programme specifications [21]. Each study includes both mediolateral oblique (MLO) and craniocaudal (CC) views from both breasts of a patient. The initial exam was followed by two additional exams every 2 years. Hence, the total number of mammograms analysed was 1560. The organisation of Spain’s NHS is decentralised, with the responsibility being delegated to each regional health system. Specifically, in Catalonia, this program affects all women between 50 and 69 years of age; thus, the ages of the patients are in this range. All mammograms were acquired from a Hologic Selenia full-field digital mammogram, with a pixel resolution of 70 μm and 12 bits per pixel. The images have a size of 4096 × 3328 pixels or 3328 × 2560 pixels, depending on the breast size. All images were bicubically downsampled by a factor of 4. This step reduced not only the computational cost but also the image noise without having an impact on the final density estimation.

A proper ground truth for the aim of this work would consist of a manual breast density segmentation of mammograms by an expert team. However, this approach is not feasible because it is challenging and time-consuming and is not necessary in real practice. Instead, a BI-RADS density score was assigned to each mammogram of the patients by three different expert radiologists with vast experience in mammography, and the majority vote was taken as the ground truth [12]. It is important to note that for each patient, the classification was performed only during the first examination; therefore, further evolution of the tissue cannot be accounted for. The database was composed of 29, 38, 30 and 33 cases belonging to BI-RADS I, II, III and IV density categories, respectively. Although this uniform distribution does not represent the real distribution of breast densities among women in screening programmes, it was appropriate for the development of our objectives.

Pre-processing

The background of a digital mammography image is homogeneous and completely black; thus, the only part of the image that interferes with automatic algorithms is the pectoral muscle (only in MLO images). The pectoral muscle is brighter than the fatty tissue and may have a similar intensity as dense areas of the breast and thus obstruct the performance of automatic density segmentation algorithms. In our work, the pectoral muscle was automatically detected using the approach of Kwok et al. [22], which was originally developed for digitised mammograms, and we adapted it for digital mammograms. However, this method failed for a few images, and thus, the pectoral muscle was manually removed.

During mammographic acquisition, the breast is compressed with a tilting compression paddle; hence, breast thickness during a mammogram is non-uniform, being lower in the periphery. This implies that pixels near the skin line are overexposed, and in a mammogram, those pixels appear darker than other breast pixels (see Fig. 1). As such, an enhancement step is necessary to correct this issue. To solve this, we applied a peripheral enhancement based on the work of Tortajada et al. [23, 24]. Specifically, from the furthest overexposed pixel from the skin line boundary to the closest, the intensity of each pixel was iteratively corrected using the following formula:

$$I^{\prime }\left(x\right)=I\left(x\right)\ast \frac{\overline{I_{N_{\mathit{in}}}\left(x\right)}}{\overline{I_N}\left(x\right)}$$ 1

where $\overline{I_N}\left(x\right)$ refers to the mean intensity of the neighbourhood of pixel x and $\overline{I_{N_{\mathit{in}}}\left(x\right)}$ and the mean intensity of the neighbourhood located one pixel inside the breast.

Feature Extraction

The most common feature used for breast density segmentation is the image’s own intensity. However, this information alone might not be enough for correct classification. Texture information allows to introduce neighbourhood information in the segmentation algorithm [25]. Additionally, a recent report also suggested the use of morphological features, which incorporates information on the likely locations of dense tissue into segmentation algorithms [18]. Our proposed tool combines intensity, texture and morphological features.

We computed all of the features shown in Table 1 using two mammograms of each BI-RADS class (i.e. eight mammograms in total) and a large variety of scales. To compute the texture features, a search window was centred on a pixel to define a region of interest. Textural features were computed inside this region and assigned to the corresponding central pixel. This process was repeated for all pixels on the image, except for pixels located at the border of the image where the window could not be placed; these pixels were excluded from further processing. The size of the window allowed experimentation with different texture scales. Small windows allowed detection of small tissue patterns whereas large windows allowed detection of bigger patterns. The range of sizes used enabled the detection of most textural patterns present in the breast density.

Table 1.

Features initially analysed for breast density segmentation. The different window sizes used when computing each textural feature are indicated

Type	Feature	Window size (in mm)
Intensity	Original
	Corrected
Morphologic	Position x, y
	Distance to skin
	Distance to nipple
	Angle to nipple
Texture	Histogram moments 1, 2, 3	0.84, 1.96, 4.20, 5.88, 9.80, 14.28, 19.88
	Histogram entropy	0.84, 1.96, 4.20, 5.88, 9.80, 14.28, 19.88
	Laplacian moments 1, 2, 3	0.84, 1.96, 4.20, 5.88, 9.80, 14.28, 19.88
	Laplacian homogeneity and entropy	0.84, 1.96, 4.20, 5.88, 9.80, 14.28, 19.88
	Co-occurrence matrices	1.96, 4.20, 9.80, 11.48, 19.88
	Fractal dimension	1.96, 4.20, 9.80, 11.48, 19.88
	Quaternion wavelets	1.96, 4.20, 9.80, 11.48, 19.88
	Local binary patterns	4.20, 11.48

From the complete feature set, the team of experts visually selected the features that best distinguished between dense and fatty tissue (notice that the lack of a proper ground truth prevents the use of automatic feature selection algorithms). This led us to a smaller set of features, which are summarised in Table 2 along with the scale used. In total, 51 features were used: original and corrected intensities, position x and y, distance to skin, the three first histogram moments and histogram entropy (computed at four different scales), the three first Laplacian moments and Laplacian homogeneity and entropy (also at four different scales) and local binary patterns [26] (we used 10 bins), which were computed using an elliptical neighbourhood. As Nanni et al. [27] observed, using an anisotropic neighbourhood rather than an isotropic one is usually more useful in medical imaging, as anisotropic distributions are more common in these types of images.

Table 2.

Features used for breast density segmentation, including the scale used to compute them

Feature	Window size (in mm)
Original intensity
Corrected intensity
Position x, y
Distance to skin
Histogram moments 1, 2, 3	1.96, 4.20, 9.80 and 19.88
Histogram entropy	1.96, 4.20, 9.80 and 19.88
Laplacian moments 1, 2, 3	1.96, 4.20, 9.80 and 19.88
Laplacian homogeneity and entropy	1.96, 4.20, 9.80 and 19.88
Local binary patterns	11.48 (10 bins)

Segmentation

The segmentation step was performed for classification at the pixel level by means of a SVM classifier [28]. An SVM is a binary classifier that represents the already known samples as data points in space and looks for the gap that separates the two categories (fatty pixel or dense pixel) as wide as possible. Therefore, new samples are mapped into that space and predicted to belong to a category based on the side of the gap they fall on.

To train the SVM, dense and fatty regions were manually selected from a set of eight mammograms (two for each BI-RADS category), where they were removed from the dataset and not used for further testing and subsequent analysis. Therefore, each pixel was characterised using its intensity, neighbourhood texture and morphological information and was used as an input for training the classifier. To extract the training data, we combined two different strategies:

• Manual selection of regions of interest (ROIs) being clearly dense or fatty. However, using only these regions, the classifier had the lack of data from those regions where the tissue is not clearly dense or fatty.

• Manual selection of ROIs from regions containing fatty and dense tissue. The pixels in these ROIs were divided using an automatic threshold [29]. Pixels with intensity higher than this threshold were considered as dense, whereas pixels with lower intensity than the threshold were considered as fatty.

One of the main drawbacks of SVM is its large computational time for training. Notice that the training step is performed prior to the testing step, hence allowing a fast segmentation of the mammograms.

Evaluation

To evaluate the performance of the tool, we used three different strategies. Firstly, using a box plot, we compared the percentage of dense tissue clustered according to its BI-RADS class. Ideally, the denser the class, the higher the mean percentage of dense tissue should be. This analysis allows us to manually correlate the ground truth labelled by the experts with the results of the tool, and it provides a strong evaluation of the tool due to the absence of manually segmented images.

To provide a complementary evaluation, we estimated the dense tissue percentage in bilateral breasts (left and right) and in ipsilateral views (MLO and CC views). In the first case, it is well known that the internal tissue distribution is similar, despite being two different breasts, and therefore, the percentage of dense tissue should be highly correlated. In the second case, we are comparing the tissue distribution of the same breast but using different points of view, which should also be closely correlated. These analyses allow us to test the repeatability of the tool.

Longitudinal Analysis

As a potential use of this tool, we analysed the evolution of breast density during three screening exams. The result of our study was compared with the three different models that Boyd et al. [3] proposed to describe density change over time. Specifically, these models use the 25th and 75th percentiles (i.e. first and third quartiles) of the distribution of density percentage to describe the different density behaviours. In all models, the percentage of breast density decreases when age increases, but changes in the interquartile range (IQR) vary depending on the model. The IQR increases with age in model A, does not change in model B and decreases in model C.

Results

Transversal Analysis

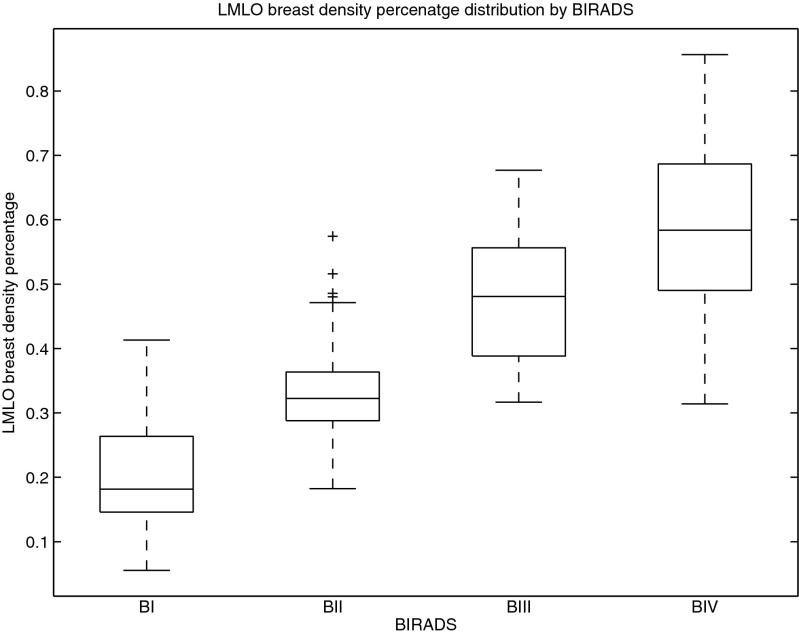
Figure 3 presents a box-and-whisker plot representation of the mammographic density percentage according to the BI-RADS classification given by the experts. In this type of plot, a box is drawn enclosing the first and third quartiles of the data, and the median value divides the box into two parts. Moreover, the whiskers show the variability outside the upper and lower quartiles. Therefore, each box represents the variability of the automatic estimation of the dense percentage clustered according to the experts’ manual annotation. It can be observed in the figure that the dense percentage increases as the BI-RADS class increases, showing high correlation between manual annotations and automatic estimations. Moreover, the distinction between BI-RADS I, II and III is very clear (the boxes are well-separated). In contrast, the boxes of BI-RADS III and IV partly overlap, although the median for BI-RADS IV is outside the enclosed area in BI-RADS III. Additionally, this figure seems to indicate that it is easier to segment dense tissues in low dense mammograms than in highly dense mammograms, where dense regions can be distributed along the mammogram. These claims are reinforced numerically based on analysis of the mean density of each BI-RADS class. Specifically, we obtained the following results: BI-RADS I: 0.20 ± 0.08, BI-RADS II: 0.32 ± 0.09, BI-RADS III: 0.47 ± 0.10 and BI-RADS IV: 0.58 ± 0.13. Upon analysis of the independence of each class using pairwise t tests, we found that the distributions were significantly different (p value <0.01).

Fig. 3.

Box plot between BI-RADS and density percentage of the segmentation result

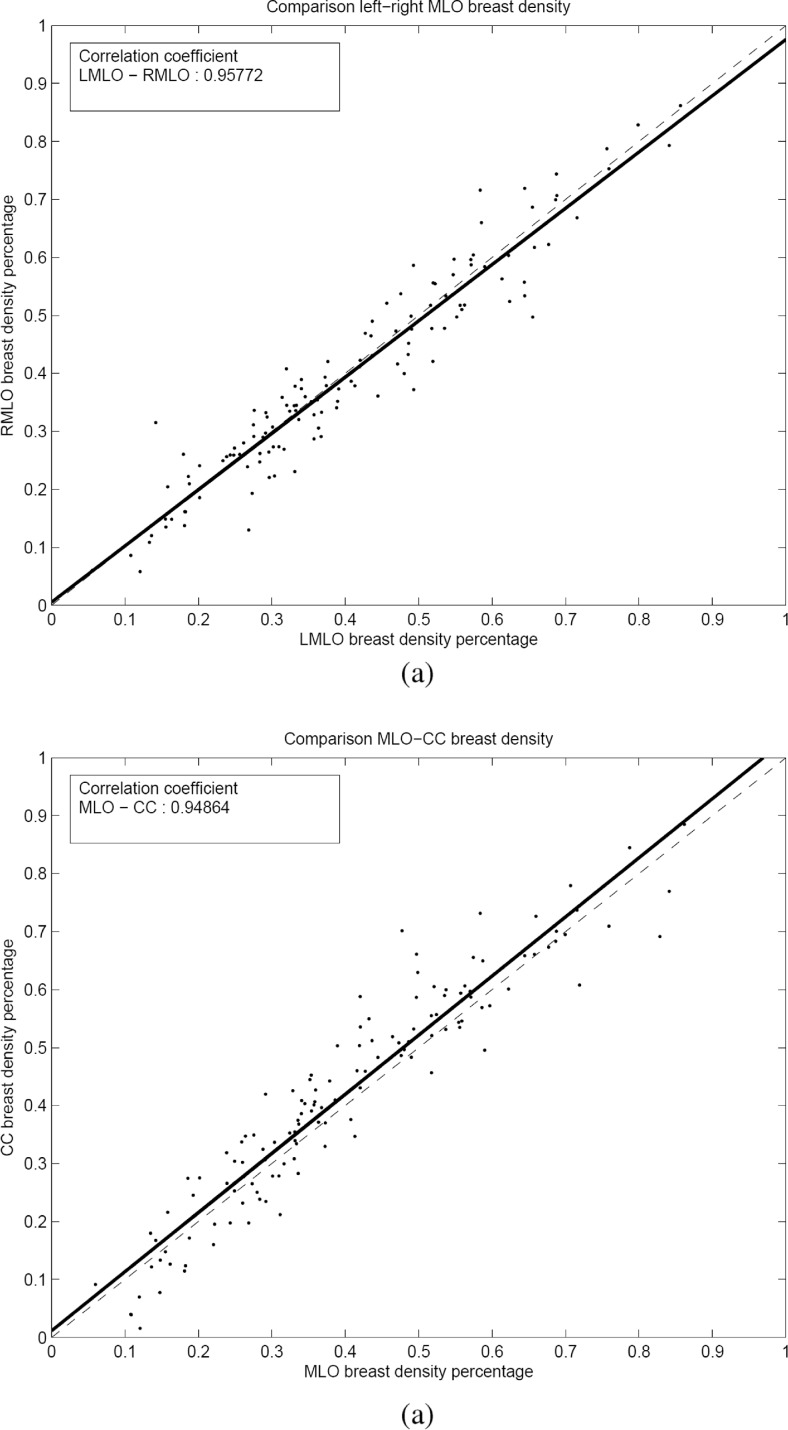
Figure 4 compares the percentages of dense tissue in the transversal study. Figure 4a shows the results of the comparison between dense percentage of all left and right MLO mammograms for the basal exploration (bilateral comparison), whereas Fig. 4b shows the relationship between both views of the same breast (ipsilateral comparison). Note that in each graph, a point corresponds to a particular case. As expected, the segmentation results for the bilateral comparison are highly correlated, as indicated by the plotted regression line ρ = 0.958 (p value <0.05). These results can be extrapolated to the fact that mammograms with similar tissue density are segmented with similar percentages of dense areas. Regarding the ipsilateral comparison, the correlation between dense area segmentation in both views is also very strong (p value <0.05). However, in contradiction to the bilateral comparison, the slope of the regression line is greater than 1, indicating that the density percentage in MLO mammograms is slightly lower than the CC view. This fact agrees with the results reported in other studies, where a high correlation between both views and a lower dense percentage for MLO view were observed [30, 31].

Fig. 4.

Summary of the results. a Bilateral comparison and b ipsilateral comparison

Longitudinal Analysis

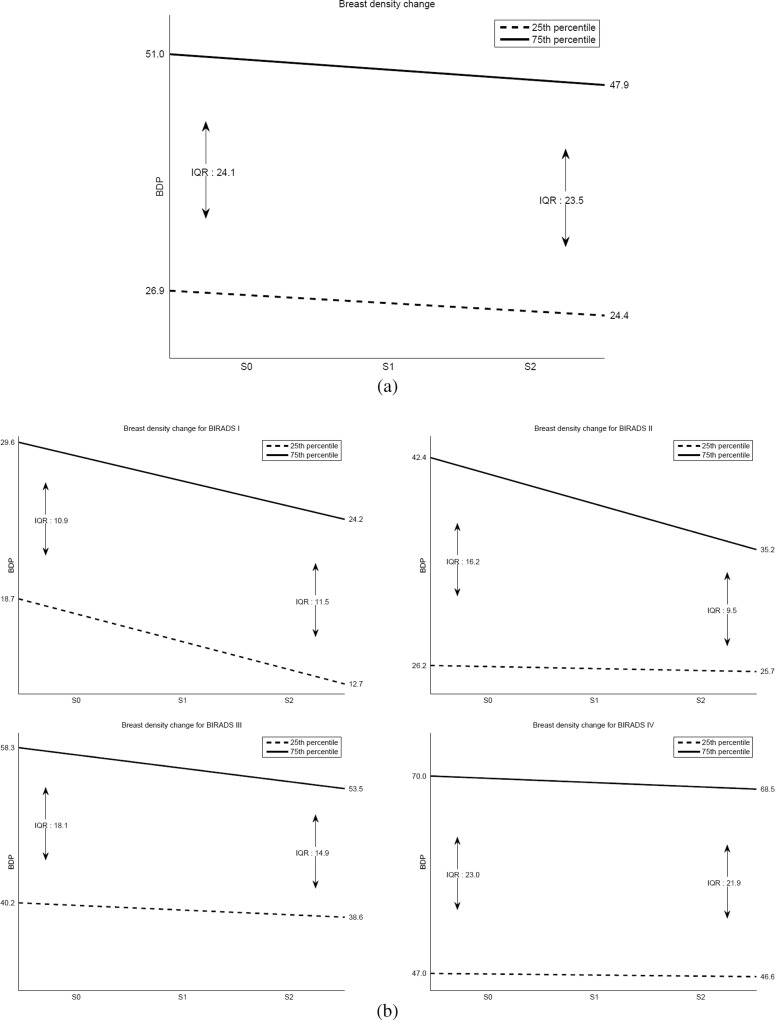
Regarding the analysis of the density evolution, we computed the density percentage of all patients in the first, second and third acquired studies. Afterwards, and similarly to the box plot analysis, we derived the first and third quartiles at each time to obtain the evolution of the breast density, as performed by Boyd et al. [3]. Figure 5a shows the regression line for the first and third quartiles when including the whole dataset in the study. As expected, breasts tend to decrease their density with time, and it seems that the decrease in the first quartile is slightly slower than the decrease in the third quartile.

Fig. 5.

First (dotted line) and third (continuous line) quartile evolution of breast density percentage when using a the entire database or b split according to the BI-RADS categories (from left top to bottom right: BI-RADS I, BI-RADS II, BI-RADS III and BI-RADS IV). S0 contains the initial follow-up exams, S1 contains the second follow-up and S2 contains the third follow-up. Note the differences between the density categories

We repeated the same procedure for all of the patients but clustered the mammograms according to the BI-RADS density categories assigned by the experts in the first study. These results are shown in Fig. 5b. Notice that although both quartiles decrease their density in all categories, the behaviour is different in each of these categories. Specifically, for BI-RADS I, the decrease in the ratio of both quartiles is significant and almost parallel, although the decrease of the first quartile is slightly greater than that of the third one. For BI-RADS II and III, the decrease in the third quartile is significant, whereas the first quartile remains almost unaffected. Finally, for BI-RADS IV, there is only a slight decrease in both the first and third quartiles.

Furthermore, for each case within the database, we computed a line of best fit for density percentage variation over time, and we analysed the different slopes. As expected, the mean slope for all women in the database was negative (−0.02), indicating a density decrease. Upon analysing the data in terms of BI-RADS category, the mean slope was also negative. Specifically, for BI-RADS IV, we obtained the lowest mean slope (−0.003).

Discussion

A novel automatic tool developed for breast density tissue segmentation has been validated in this work. The bilateral comparison of the results has shown a very strong correlation that agrees with previous studies that analysed manually segmented mammograms. Additionally, the ipsilateral comparison also showed a very strong correlation between both views and with almost the same slope reported in previous studies performed with manually segmented images.

Comparisons with other automatic approaches that segment the breast according to its density is not an easy task because it is not feasible to obtain a ground truth detailing all the dense regions in a large set of mammograms. In addition to this difficult computational task, inter- and intra-expert variability is very high when looking at breast densities [12]. However, we claim that our approach outperforms threshold-based approaches or clustering approaches that just use image intensities because the location of dense areas also plays a key role in its classification. We also tested the use of different classifiers typically used in mammography, such as a neural network [18] and a boosting algorithm [32]. The performance of both classifiers was worse than that obtained with SVM, with slightly better results obtained using the neural network compared to the boosting classifier. The main drawback of SVM is its computational cost, mostly due to the amount of time needed to compute the features. Note that once the features are computed for each pixel, the classification can be quickly performed by parallelising techniques.

The longitudinal analysis confirms the well-known fact that breast density decreases with age. Although there are other factors involved in breast density variations, such as menopause status, pregnancy and childbearing [33], in this work, we focused on the evolution with age, comparing our results with the theoretical models proposed by Boyd et al. [3] based on the IQR. According to the results obtained with our database and graphically shown in Fig. 5a, we observed that breast densities decreased over time, whereas the IQR slightly decreased. Therefore, our data seems to be congruent with model C, although the decrease is so slight that it could also be congruent with model B. However, depending on the BI-RADS score, no single model always described the density behaviour of all of the women. Specifically, for BI-RADS I, densities decreased with age, whereas IQR increased; therefore, model A or B should have been assigned in this case. On the other hand, BI-RADS II and III were clearly well-described by model C. Finally, the BI-RADS IV category label should be assigned to model B or C. Our database was composed by only three screening studies per woman, which limits the fitting of this model. More studies for each patient are required to provide a better adjustment. Additionally, the lower average slope obtained for high-density breasts indicates that the group with an increased risk of breast cancer [14] has a slower decrease in the density of the breast.

There are some limitations in our study. The lack of manual annotations of dense regions in a large dataset of mammograms prevents not only the comparison between manual and automatic segmentations using quantitative overlapping measures but also the use of automatic feature selection algorithms. On the other hand, regarding the longitudinal analysis, 6 years is a short time to detect changes in breast density, and this does not allow significant clinical conclusions to be made. However, automatic tools allow the detection of density changes in this short period of time.

Automatic tools based on computational approaches allow accurate estimation of breast density and quantification of changes with time. Longitudinal changes in breast density are dependent on the internal density of each breast, in addition to other factors. In our experiments, density changes in low-density breasts presented a more heterogeneous behaviour than those in high-density breasts, where the percentage of dense tissue seemed to be more stable over time.