Abstract
Breast cancer is becoming a leading death of women all over the world; clinical experiments demonstrate that early detection and accurate diagnosis can increase the potential of treatment. In order to improve the breast cancer diagnosis precision, this paper presents a novel automated segmentation and classification method for mammograms. We conduct the experiment on both DDSM database and MIAS database, firstly extract the region of interests (ROIs) with chain codes and using the rough set (RS) method to enhance the ROIs, secondly segment the mass region from the location ROIs with an improved vector field convolution (VFC) snake and following extract features from the mass region and its surroundings, and then establish features database with 32 dimensions; finally, these features are used as input to several classification techniques. In our work, the random forest is used and compared with support vector machine (SVM), genetic algorithm support vector machine (GA-SVM), particle swarm optimization support vector machine (PSO-SVM), and decision tree. The effectiveness of our method is evaluated by a comprehensive and objective evaluation system; also, Matthew’s correlation coefficient (MCC) indicator is used. Among the state-of-the-art classifiers, our method achieves the best performance with best accuracy of 97.73 %, and the MCC value reaches 0.8668 and 0.8652 in unique DDSM database and both two databases, respectively. Experimental results prove that the proposed method outperforms the other methods; it could consider applying in CAD systems to assist the physicians for breast cancer diagnosis.
Keywords: Computer-aided detection, Mammography, Automated mass segmentation, Classification, Random forest
Introduction
Breast cancer in females is the most common diagnosed cancer and leading cause of death in both developed and developing countries [1]. In 2008, about 1.38 million (23 % of the total cancer cases) women were diagnosed with breast cancer, and this incidence had increased by more than 20 % in 2012, which reached 1.7 million. According to the latest cancer statistics of the USA, breast cancer incidence rate was expected to account for 29 % of new cancer cases among women in 2013 [2]. Mammography is a preferred method for early detection, and it is also the most efficient and reliable tool for early prevention and diagnosis of breast cancer. For mass detection procedure on a mammogram, the radiologist needs to find out the lesion, estimate the malignancy probability, and recommend further investigations. However, it is a difficult task to classify benign and malignant mass tumors and not practical in the clinical procedure. Thus, computer-aided diagnosis (CAD) system is urgently needed to provide a second suggestion for the radiologists to better detect breast masses in mammogram images.
To accomplish mass recognition procedure, we should detect the suspicious region and obtain the region of interest (ROI) on films, extract features, and distinguish ROI between mass and normal tissue, and finally classify the decided mass into benign or malignant. Mass segmentation is crucial to the latter feature extraction and classification. Different algorithms for early lesion area detection have been widely studied, and the most common used are classical threshold method, active contour model [3–8], region growing [4], watershed [3, 4], and template matching [4, 9] methods. Dubey et al. [3] used the level set and marker-controlled watershed methods respectively to segment mass, and experimental results showed that watershed could achieve better results. Maciej [9] presented a competitive and robust CAD system for mass detection which employing the mutual information-based template matching scheme. Generally, the performance of this segmentation process was usually evaluated using detection rate and accuracy.
The next stage after mass segmentation is feature extraction and selection. The features can be calculated from the mass region contain such as the density, texture, morphologic, shape, and size [5, 6, 10, 11]. Besides, several methods using multiresolution analysis have been proposed for feature extraction in mammograms [10, 12]. Moayedi et al. [12] employed the contourlet transform to obtain the contourlet coefficient as a feature and Nascimento et al. [10] extracted multiresolution analysis features by using wavelet transform. In general, the feature space is large, complex, and with redundancy that the excessive features may decrease the classification accuracy and waste time. Thus, the redundant features should be removed to improve the performance of the algorithm. While it is difficult to select an optimized combination of features from the whole features, the genetic algorithm (GA) and stepwise method are the most frequently used method to select feature [6, 12].
Once the features related to the mass are extracted and selected, these will be as the input of a classifier to decide whether the suspicious region is benign or malignant. The classifier is a tool that provides as output the risk degree related to the tissue. Classifiers like support vector machine (SVM) [5, 6, 12, 13], decision tree [5], neural network [5, 11], and linear discriminant analysis (LDA) [5, 14] have been widely used and performed well. Wu et al. [6] segmented the breast tumor by level set method, and the auto-covariance texture features and morphologic features were extracted, then they used the genetic algorithm to detect the significant features and identified the tumors by SVM, which get the accuracy of 95.24 %. Delogu [11] employed a gradient-based algorithm to segment the mass, and 12 features were selected from the extracted 16 features based on shape, size, and intensity and, as the input of a neural classifier, finally obtained the highest classification accuracy of 97.8 % on the acceptably segmented masses assigned by radiologists.
Besides, there were some other approaches for breast cancer diagnosis research without depending on any films. For example, Dong et al. [15] gave a research based on morphological characteristics parameters of breast tumor cell; this paper stated some characteristics and the relationship to the breast cancer diagnosis in detail. Issac Niwas et al. [16] extracted feature on fine needle aspiration cytology (FNAC) samples of breast tissue using complex wavelets, then the features extracted are used as input to a k-nn classifier, which obtained the correct classification results with 93.9 %. Karakıs et al. [17] proposed a genetic algorithm model to predict the status of axillary lymph node which is important to assess metastatic breast cancer. In the study of Lacson et al. [18], they presented the prevalence of each data element from breast imaging reports and automatically validated the extracted imaging findings compared to a “gold standard” using manually extracted data from randomly selected reports.
In this work, we propose a novel and efficient classification approach based on the auto-segmented mass [7]. Firstly, the breast mass is auto-segmentation adopted by an improved integrated method, secondly, we focus on extracting features such as shape, margin, texture, and intensity from the segmented mass and its surroundings and then we set up a new feature database based on the extracted features, finally we distinguish benign and malignant based on the established feature database with the classifier of random forest. The validation procedure is performed using images not only from Digital Database for Screening Mammography (DDSM) [19] but also from Mammography Image Analysis Society (MIAS) [20], whereas which rarely appeared in the other literatures.
The rest of this paper is structured as follows: We introduce the “Materials and Methods,” and then in the “Classification” section, comprehensive evaluation criteria for the performance of mass classification are presented. Later, the results obtained by our method and the comparison with other researchers are listed in “Assessment Measures” section. Finally, the conclusion and prospect are summarized.
Materials and Methods
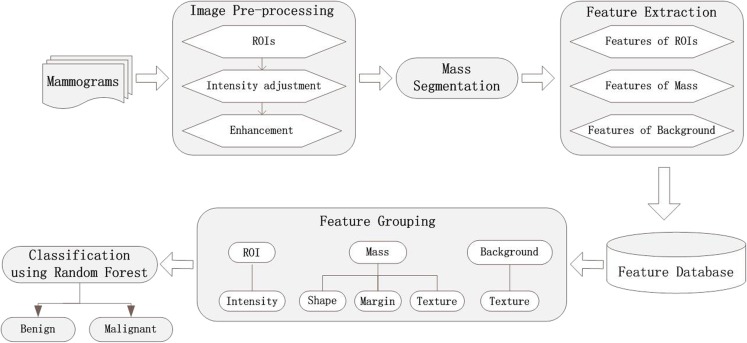
The proposed methodology for breast mass diagnosis procedure can be schematically described in Fig. 1. We can see that our approach mainly contains four stages: image preprocessing, mass segmentation, feature selection, and classification. The features are respectively extracted from the ROIs, the detected masses, and the background around the mass. After obtaining the feature database, the features are grouped into three classes with different descriptors. Finally, the random forest is used as the classifier and achieves the best performance comparing to the other classifiers.
Fig. 1.
Framework of the proposed method
Data Set
The mammograms used in this work are taken from the Digital Database for Screening Mammography (DDSM) and the Mammography Image Analysis Society (MIAS) respectively. These two databases have been widely used in studying on mammography analysis; it is due to that they are freely available. The MIAS database offered some corresponding information of lesion area such as type, location, severity, central coordinate, and radius by experts, and each image was 1024 × 1024 pixels. The resolution of the mammograms from the DDSM database was much higher than the MIAS database, and the cases were mainly divided into four pathology types: normal, cancer, benign, and benign without callback. A case collects the mammographic images of one patient and its corresponding information, and each breast consists of a mediolateral oblique and craniocaudal view mammogram.
For each case, there is a header file, with the extension “.ics,” containing the filename, the date of study and digitization, the film type, digitizer, and the density of breast. If any mammogram in the case consists lesion areas, there is a corresponding ground truth file, with the extension “.overlay,” including the shape, margin of the lesion, assessment categories, subtlety rating, pathology type, and the chain codes of suspicious region boundary, which obtained by using the 21Breast Imaging Reporting And Data System (BI-RADS) [21] lexicon. In this work, we mainly focus on mass segmentation, feature extract, and classification.
Preprocessing and Segmentation
With the chain codes offered by DDSM and the coordinate information of lesions in MIAS, we can easily identify the location and size of a mass, which enable us to extract the regions of interests (ROIs) from the full raw images. In this work, we do the experiments using the cropped subimages with size of 140 × 140, whose centers correspond to the centers of the lesions. For the mammograms of MIAS, the gray intensity is between 0 and 255, while the original images in DDSM are also with wide variation intensities of 4096 gray level, which is somewhat complicated and may cause inaccuracy in mass feature analysis like texture extraction. Therefore, we map the intensity value linearly to new values distributed in the gray level range [0–255] by using brightness adjustment methods. The frequency of masses with different shapes and margins selected in this paper is illustrated in Table 1.
Table 1.
Frequency of masses with different shape and margin
| Mass margin | Mass shape | Total | |||
|---|---|---|---|---|---|
| Round | Oval | Lobular | Irregular | ||
| Circumscribed | 18 | 26 | 30 | 1 | 75 |
| Obscured | 5 | 12 | 4 | – | 21 |
| Microlobulated | 2 | 5 | 6 | 2 | 15 |
| Ill-defined | 4 | 15 | 9 | 16 | 44 |
| Spiculated | 7 | 4 | 2 | 32 | 45 |
| Total | 36 | 62 | 51 | 51 | 200 |
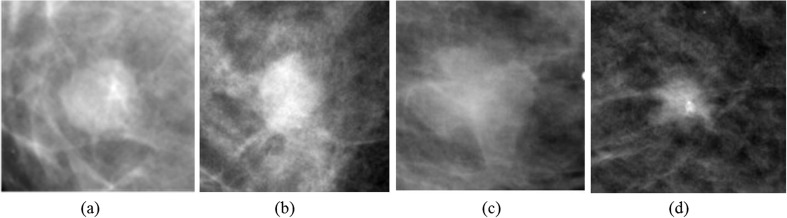
Figure 2 demonstrates some ROIs cropped from the full mammograms of DDSM. Figure 2a, b is pathologically benign, whose shapes are round and oval and margin types are circumscribed and obscured orderly; Fig. 2c, d is pathologically malignant, whose shapes are lobulated and irregular and margin types are ill defined and spiculated respectively. In general, masses with regular shapes and circumscribed margins are probably benign, while irregular-shape and speculated-margin masses are more likely to be malignant. Thus, the shape and margin features can be used to classify the masses into benign or malignant. Besides, the texture and intensity information of the ROIs are somewhat different between each image.
Fig. 2.
ROIs cropped from full mammograms of DDSM: a–b pathologically benign and c–d pathologically malignant
Before detecting the masses, we enhance the ROIs using the rough set (RS) [22] theory considering the following: (1) In ROIs, the gray value between the lesion and gland tissue is sometimes similar, and it is hard to find a suitable threshold by gray transform method; (2) the gray level is different between the mass and its surroundings, by augmenting the edge gradient, we can reserve the object information; and (3) the RS method can deal with the vagueness and uncertainty.
Here, we choose the image gradient attribute C1 and noise attribute C2 as the condition attributes of the RS method. According to the indiscernibility relation concept, each ROI is divided into two subimages:
| 1 |
| 2 |
where P is the gradient threshold, Q is the noise threshold, f(i, j) is the gradient value calculated from the cropped ROIs, and s denotes the subblock with size of 3 × 3, examining the average intensity value of each subblock and comparing the difference between the central subblock and its surrounding subblocks, if the difference satisfies condition (2), then eliminate the noise by replacing the pixel value with Q. Here, RC1 represents the points whose gradient is larger than the threshold P, RC2 represents the subblocks whose average intensity is larger than its surroundings. The subimages which need to be enhanced are defined as follows:
| 3 |
| 4 |
Next, we enhance I1 and I2 respectively and get the final image by merging the subimages: I2 is enhanced by histogram equalization method and I1 is transformed below:
| 5 |
As the gradient of boundary is generally much higher than the smooth, in this experiment, we want to enhance the boundary, then β should be bigger than 1. Here, we set α = β = 1.5 according to the experimental results. After enhancement, the boundary contrast between the mass and surrounding tissue becomes more obvious.
The mass segmentation procedure is realized by applying the active contour model [23] (snake). The snake model defined a parametric curve guided by external forces and internal forces that pull it toward the edge of the object until the energy function achieves the minimum. The curve v(s) and the minimizing energy function E(v) forms are:
| 6 |
| 7 |
| 8 |
where Eint is the internal energy decided by the curve, α and β control the smoothness and continuity, respectively, and Eext is the external energy decided by the image information. To get a minima of energy function E(v), the contour must satisfy the Euler Lagrange equation:
| 9 |
Equation (9) can be considered as a force balance equation:
| 10 |
| 11 |
where fint is the internal force and fext is the external force. The vector field convolution (VFC) snake [24] is an active contour model whose external force is VFC field. First defined a vector field kennel:
| 12 |
where m(x, y) is the vector magnitude and n(x, y) is the unit vector pointing to the kennel origin (0, 0).
| 13 |
| 14 |
Here, r = (x2 + y2)1/2. The external force is calculated by convoluting the vector field kennel k(x, y) and the edge map f(x, y), defined as
| 15 |
From the ahead-proposed paper [7], it has been proved that the external force obtained by the improved VFC Snake model turned to be more regular and the segmented results appeared to be more accurate. Thus in this paper, the external force fvfc is computed by convoluting the vector field kennel with the edge map f(x, y), which is calculated by performing the Canny operator on the RS-processed image, and then executes the deformation on the original ROIs. Since the initialization of VFC Snake would somewhat affect the performance of deformation, we initialize the model with a circle formed by the center and the biggest radius of the lesion obtained by chain codes.
The preprocessing and segmentation procedure is finished by the following steps: (1) getting the mass position and extracting the ROIs with the chain codes, (2) mapping the intensity value linearly to new values distributed in the gray level range (0–255), (3) using the RS method to perform enhancement, (4) initializing the deformable model with a circle, and (5) segmenting the mass from ROIs by the VFC Snake method.
Feature Extraction
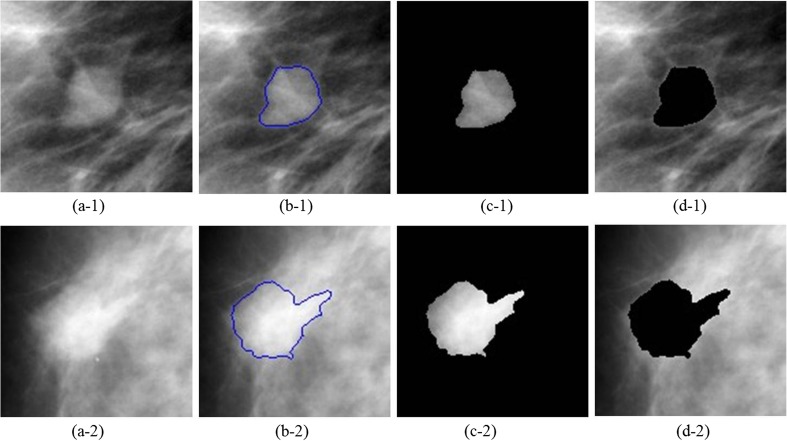
Once the mass is segmented from the normal tissues in ROIs, features are extracted in order to determine the severity of abnormity that whether the lesion is likely to be benign or malignant. Xu [25] has studied on the mass detection approaches in mammograms, which contained mass segmentation, features extraction and selection, and classifying to benign and malignant procedures. Xu also summarized features and the corresponding expressions to describe the mass in detail. According to the characteristics of BI-RADS lexicon and Xu’s description, here, we mainly extract the shape, margin, texture, and intensity features. For a comprehensive description of the ROIs, we divide each ROI into three portions: ROI, segmented mass area, and the background region in ROI, which are shown in Fig. 3, where Fig. 3a-1 is pathologically benign and Fig. 3a-2 is pathologically malignant. We extract features from each portion respectively, and the features categorized are listed in Table 2 below.
Fig. 3.
The segmented results and divided regions from DDSM: a the ROIs, b the segmented results, c the mass regions, and d the background regions of ROIs
Table 2.
Features extracted from the divided regions
| ID | Reference | Feature description | Category description | Region |
|---|---|---|---|---|
| 1–4 | [26–28] | Area, perimeter, circularity, and shape factor | Mass Shape and margin |
|
| 5–9 | [27–29] | NRL mean, NRL standard deviation, NRL entropy, NCPS, ratio of standard deviation of NRL and average RL |
NRL | |
| 10–12 | [26, 30] | Gradient mean, gradient standard deviation, and gradient skewness | Margin gradient | |
| 13–19 | [26, 30, 31] | Mean of mass, standard deviation of mass, smoothness of mass, skewness of mass, entropy of mass, uniformity of mass, and kurtosis of mass |
Gray-level histogram | |
| 20–21 | [30] | Fluctuation mean of ROI and fluctuation standard deviation of ROI | Pixel value fluctuation | ROI |
| 22–28 | [26, 28, 30] | Mean of background, standard deviation of background, smoothness of background, skewness of background, entropy of background, uniformity of background and kurtosis of background |
Gray-level histogram | Background |
| 29–32 | [30, 32] | Fluctuation mean of background, region conspicuity, fluctuation standard deviation of background and average gray value difference of mass and background |
Pixel value fluctuation |
NRL normalized radial length, NCPS normalized central position shift, RL radial length, ROI region of interest
Shape and Margin
Mass shape and margin are the primary characteristics. According to the BI-RADS lexicon, the shape of mass could be round, oval, lobular, and irregular, and the margin type of mass contains circumscribed, obscured, microlobulated, indistinct, and spiculated, while there are always interaction between the shape and margin. For example, masses with circumscribed margin are always with round or oval shape and probably to be benign. Shapes of spiculated-margin masses are often irregular, and those masses are more likely to be malignant. To describe the shapes of masses, we use the features like area, perimeter, circularity, shape factor, normalized radial length (NRL), and normalized central position shift (NCPS) to evaluate the regularity. Besides, the gradient between the mass and its surrounding tissues is useful to estimate the gray value variation, which can express the margin types, such as distinguishing circumscribed masses and obscured margin masses when their shapes appear regular.
The formulas below are the features computed on the segmented masses:
Area: the number of pixels inside the boundary of the mass.
Perimeter: the number of pixels on the boundary of the mass.
-
Circularity
16 where A is the area and P is the perimeter, for a circular shape mass, C = 0.
-
Shape factor: this feature can effectively evaluate the burr around the lesions
17 where A is the area and P is the perimeter.
- Radial length (RL): Euclidean distance from the mass center (cx, cy) to the position of boundary pixel (i, j):
18 - Normalized radial length (NRL):
19 - Mean of NRL:
20 - Standard deviation of NRL:
21 -
Entropy of NRL:
22 Here, pk is the probability of a certain normalized radial length to the number of whole radials, and P is the perimeter.
-
Normalized central position shift (NCPS): the Euclidean distance from the mass center (cx, cy) to the position of pixel with minimum gray value and divide the mass area:
23 The (a, b) is the coordinate position of the pixel whose gray value is the minimum inside the mass.
-
Gradient: gradient is the gray value difference between the boundary pixel and the 10th pixel from this pixel along the radial direction.
24 where I(i, j) is the gray value of the boundary pixel and I(x0, y0) is the gray value of the 10th radial pixel.
Gray-Level Histogram
Texture feature is another crucial feature in image classification. In the cropped ROIs from mammograms, the intensity and its variation of the lesions and its surrounding tissues are different, and the gray value of the lesions is often much higher. Here, we compute the texture features of the mass and the background region respectively based on the gray-level histogram statistic property, like mean, standard deviation, smoothness, skewness, uniformity, entropy, and kurtosis.
For a certain region, rk is a random variable to express the intensity, p(r) is the gray-level histogram, and L is the gray level.
- Mean of the intensity:
25 - Standard deviation:
26 - Smoothness:
27 - Skewness:
28 - Uniformity:
29 - Entropy:
30 - Kurtosis:
31
Pixel Value Fluctuation
The fluctuation of the pixel value could prime reflect the intensity variation inside a certain region. It is defined as the value difference between the pixel and its surroundings; for pixel I(i, j), its fluctuation is indicating
| 32 |
| 33 |
where F(i, j) is the fluctuation value of pixel I(i, j) and S(i, j) is the subblock with the size of 3 × 3 surrounding the pixel. The means to compute the means and standard deviation is the same as formulas (22) and (23).
Another relevant and significant feature is region conspicuity which is defined as follows:
| 34 |
where Īmass and Ībackground are the mean gray value of the mass and background region, respectively. is the mean fluctuation of the background.
Classification
Classification is crucially to CAD system in diverse fields, and the performance of classification depends directly on how well the discriminant features and the choice of classifier perform. Machine learning methods are widely used in medical imaging, pattern recognition, etc. As can be seen, SVM and decision tree have been used to diagnosis of breast cancer and obtain the considerable classification accuracy. However, we believe that the SVM has really not fully shown its advantage; hence in our work, we optimize SVM with genetic algorithm (GA) and particle swarm optimization (PSO) [33] and compare the classification results with random forest. Following, we shortly introduce these classification methods.
Random Forest
Random forest is proposed by Breiman [34]. It combines with the thought of “bootstrap” and the method of “random subspace,” and it can be seen as an ensemble of unpruned classification trees because it uses multiple models to obtain better predictive performance. Random forest combines many decision trees to make predictions, and these decision trees are constructed of bagging classification trees, where each tree is independent. In standard trees, each node is generated by using the best split among all the variables. In the process of classification, the testing data is classified by every individual decision tree, and the majority vote of the trees is taken as prediction.
The random forest algorithm can be summarized as follows:
Generate bootstrap samples and build one tree per bootstrap sample.
Increase diversity via additional randomization: At each node, randomly pick a subset of features to split.
-
Predict new data by executing the different prediction trees and select the most votes as prediction.
Random forest is efficient and easy to implement, and it can be used for highly accurate predictions especially for large number of input variables.
Decision Tree
Decision tree [35] is a classification technology which composed of a root node, a set of internal nodes, and a set of terminal nodes. In a decision tree, every node has only one parent node and two or more child nodes. In the process of classification, the data set is classified according to the decision framework defined by the tree in sequence, and every class label is assigned to the observation according to the terminal node into which the observation falls. Decision trees have a lot of advantages over traditional supervised classification methods especially with its explicit classification structure and the easily interpretable characteristic. It has been widely used in classification.
Support Vector Machine
Support vector machine (SVM) [36] developed by Vapnik is based on the Vapnik-Chervonenkis (VC) and structural risk minimization (SRM) principle [36, 37]. It achieves the best generalization ability by trying to find an optimal separating hyper-plane and maximize the margin between different classes. SVM with advantage of versatility and effectiveness is widely used in many segmentation and classification areas. More details and complete description of SVM can be found in the study of Zhang [38].
Assessment Measures
The objective evaluation criterion is measured by classification sensitivity, specificity, accuracy, positive predictive value (PPV), negative predictive value (NPV), Matthew’s correlation coefficient (MCC), and receiver operating characteristic (ROC). Sensitivity and specificity are statistical measures of the performance of a binary classification test. They are defined in Table 3.
Table 3.
The concept of confusion matrix
| Actual test | Predict result | |
|---|---|---|
| Positive | Negative | |
| Positive | TP | FN |
| Negative | FP | TN |
Sensitivity deals only with positive cases; it indicates the proportion of the detected positive cases over the actual positive cases.
| 35 |
Specificity deals only with negative cases; it indicates the proportion of the detected negative cases over the actual negative cases.
| 36 |
PPV deals with all cases; it can be calculated as the correct detected positive cases over all detected positive cases.
| 37 |
NPV deals with all cases; it can be calculated as the correct detected negative cases over all detected negative cases.
| 38 |
Accuracy deals with all cases, and it is the most commonly used indicators; it reflects the precision of predict results.
| 39 |
MCC is an effective accuracy evaluation indicator of machine learning approaches. Especially for the case of the negative sample numbers that are obviously unbalanced compared with the positive sample numbers, MCC provides a better evaluation than the overall accuracy.
| 40 |
The ROC curve is used for measuring the predictive accuracy of the proposed model. It indicates the true positive rate and false positive rate. The area under the ROC curve which is called AUC is one of the best methods for comparing classifiers in two-class issues. If the ROC curve rises quickly toward the upper left corner of the graph or if the value of AUC is larger, the test results can be said to perform better. An area close to 1.0 indicates that the diagnostic test is reliable; on the contrary, an area close to 0.5 demonstrates the unreliable test result.
Results and Discussion
Classification Tested on DDSM Database
In order to guarantee that the present results are valid, we use the fivefold Cross Validation (5-CV) [39] to evaluate the classification accuracy. The feature data (positive 115, negative 85) are divided into five groups randomly, every time one group is chosen as testing set and the other four groups are used to forming training set; so looping five times, we can compute the average classification accuracy. In order to reduce the deviation, we repeat the above procedure five times. The advantage of this method is that all of the test sets are independent and, there, liability of the results could be improved.
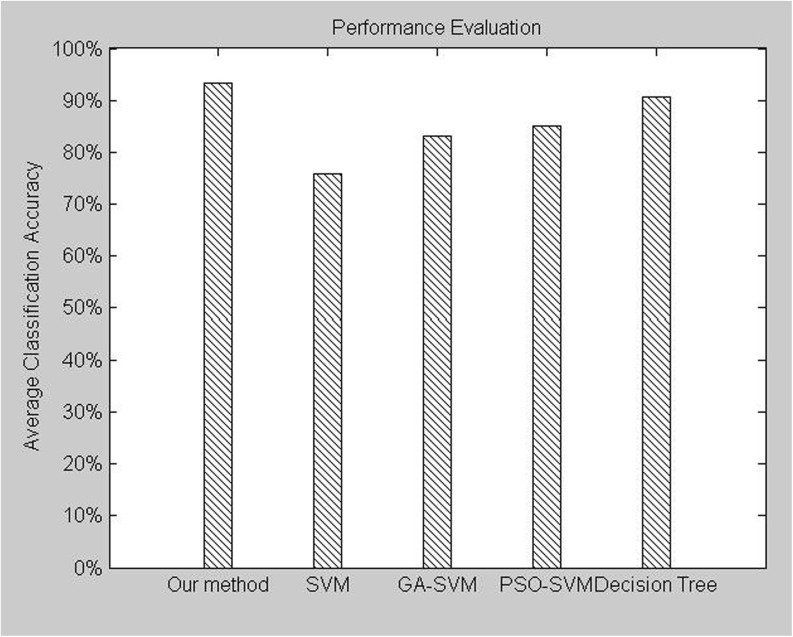
We do classify experiment with three data sets including only shapes features, shape-texture features, and shape-texture-intensity features (all features). The performance of the proposed method, approach with only shape features (SVM), approach with only shape and texture features (SVM), approach with all features (SVM), approach with all features (GA-SVM), approach with all features (PSO-SVM), and approach with all features (decision tree), is listed in Table 4 and shown in Fig. 4. We calculate the average accuracy of each repeat processing which is shown in italic fonts; the average accuracy of five times is calculated in the last line of Table 4.
Table 4.
Average classification accuracy (%) using fivefold cross validation five times from DDSM database
| Fold no. | Our method | SVM | GA-SVM | PSO-SVM | Decision tree | ||
|---|---|---|---|---|---|---|---|
| All features | Shape features | Shape-texture | All features | All features | All features | All features | |
| Fold 1 | 88.89 | 63.89 | 69.44 | 72.22 | 86.11 | 86.11 | 88.89 |
| Fold 2 | 95.74 | 63.83 | 80.85 | 80.85 | 87.23 | 87.36 | 97.87 |
| Fold 3 | 94.44 | 66.67 | 75.00 | 77.78 | 77.78 | 77.78 | 97.22 |
| Fold 4 | 93.33 | 66.67 | 76.67 | 76.67 | 93.33 | 93.33 | 90.00 |
| Fold 5 | 92.16 | 66.67 | 72.55 | 74.51 | 84.35 | 84.31 | 88.24 |
| Accuracy 1 | 92.91 | 65.55 | 75.85 | 76.41 | 85.36 | 86.18 | 92.44 |
| Fold 1 | 94.74 | 60.53 | 78.95 | 84.21 | 92.11 | 92.11 | 92.11 |
| Fold 2 | 97.44 | 61.54 | 71.80 | 71.80 | 74.36 | 76.92 | 94.87 |
| Fold 3 | 90.07 | 65.12 | 72.09 | 74.42 | 81.40 | 83.72 | 90.07 |
| Fold 4 | 97.56 | 53.65 | 75.61 | 75.61 | 85.36 | 87.80 | 92.68 |
| Fold 5 | 92.31 | 71.80 | 76.92 | 76.92 | 74.36 | 87.18 | 89.74 |
| Accuracy 2 | 94.42 | 62.53 | 75.07 | 76.59 | 81.52 | 85.55 | 91.89 |
| Fold 1 | 90.91 | 72.73 | 81.82 | 84.85 | 87.88 | 87.88 | 87.88 |
| Fold 2 | 92.50 | 65.00 | 80.00 | 80.00 | 87.50 | 87.5 | 92.50 |
| Fold 3 | 92.68 | 53.66 | 68.29 | 68.29 | 75.61 | 73.17 | 87.80 |
| Fold 4 | 91.43 | 62.86 | 74.29 | 74.29 | 80.00 | 80.00 | 91.43 |
| Fold 5 | 96.08 | 60.78 | 70.59 | 72.55 | 84.31 | 90.20 | 84.31 |
| Accuracy 3 | 92.72 | 63.02 | 75.00 | 76.00 | 83.06 | 83.75 | 88.78 |
| Fold 1 | 97.73 | 75.00 | 81.82 | 86.36 | 86.36 | 86.36 | 95.45 |
| Fold 2 | 95.35 | 51.16 | 65.12 | 67.44 | 79.07 | 83.72 | 90.70 |
| Fold 3 | 91.67 | 61.11 | 72.22 | 72.22 | 86.11 | 86.11 | 88.89 |
| Fold 4 | 86.49 | 62.16 | 75.68 | 72.97 | 86.49 | 86.49 | 81.08 |
| Fold 5 | 95.00 | 65.00 | 77.50 | 80.00 | 77.50 | 85.00 | 92.50 |
| Accuracy 4 | 93.25 | 62.89 | 74.47 | 75.80 | 83.11 | 85.57 | 89.72 |
| Fold 1 | 91.43 | 65.71 | 82.86 | 82.86 | 92.48 | 94.28 | 88.57 |
| Fold 2 | 93.48 | 71.74 | 84.78 | 84.78 | 80.43 | 80.43 | 91.30 |
| Fold 3 | 95.56 | 62.22 | 68.89 | 71.11 | 82.22 | 86.67 | 97.78 |
| Fold 4 | 90.00 | 70.00 | 70.00 | 67.50 | 72.50 | 75.00 | 85.00 |
| Fold 5 | 94.12 | 55.89 | 64.70 | 64.70 | 82.35 | 82.35 | 88.24 |
| Accuracy 5 | 92.92 | 65.11 | 74.25 | 74.69 | 82.36 | 83.75 | 90.19 |
| Ave-acc | 93.24 | 63.82 | 74.93 | 75.90 | 83.08 | 84.96 | 90.60 |
Bold font number indicates the best performance in each line
SVM support vector machine, GA-SVM genetic algorithm support vector machine, PSO-SVM particle swarm optimization support vector machine
Italics font data indicates the average accuracy of every fold
Fig. 4.
Average classification accuracy of the various classified methods tested on DDSM database
It is well known that in breast cancer diagnosis, the classification accuracy is more crucial since the ramifications of an incorrect diagnosis may cause undue surgery or even lead to death. From Table 5 and Fig. 4, we can see that the average classification accuracy rates of the methods are 93.24, 63.82, 74.93, 75.90, 83.08, 84.96, and 90.60 %, respectively. Only using shape features to distinguish breast tumor between benign and malignant seems one-sided, it cannot provide reliable classification accuracy. When adding texture features to shape features, the classification accuracy has increased significantly with 9 %; when adding intensity features to shape-texture features, it achieves the highest classification accuracy. The best classification accuracy rate is 97.56 % provided by the random forest in the second times repeat of fold 4. It is to say our method achieves the highest classification accuracy rate; in other words, our method is more suitable for CAD systems.
Table 5.
Performances of different classifiers tested on DDSM database
| Our method | SVM | GA-SVM | PSO-SVM | Decision tree | |
|---|---|---|---|---|---|
| Sensitivity | 0.9478 | 0.7826 | 0.8261 | 0.8522 | 0.9130 |
| Specificity | 0.9176 | 0.7294 | 0.8353 | 0.8471 | 0.8941 |
| PPV | 0.9397 | 0.7965 | 0.8716 | 0.8829 | 0.9211 |
| NPV | 0.9286 | 0.7126 | 0.7802 | 0.8090 | 0.8837 |
Bold font number indicates the best performance in each line
SVM support vector machine, GA-SVM genetic algorithm support vector machine, PSO-SVM particle swarm optimization support vector machine, PPV positive predictive value, NPV negative predictive value
To further fully confirm the effectiveness of our method, we also calculated the sensitivity, specificity, PPV, and NPV of all the methods based on the above simulation results, and they are listed in Table 5. The values of sensitivity and specificity reflect another measure of the diagnosis accuracy which takes into account the variance in diagnostic consequences. The higher the values for sensitivity and specificity, the better the performance of the system is. While in many cases, a higher sensitivity value can be always at the cost of a lower specificity value. In our work, Table 5 shows that the values of both sensitivity and specificity obtained by our method are higher than for the other approaches (about 0.02∼0.20 improvement). That is to say that our method is significantly superior to the other methods. SVM performed the worst, the method based on GA-SVM and PSO-SVM performed better than that of SVM, which is just consistent with the result of parameter optimization, and the method based on decision tree overmatches the former methods, but it is still inferior to the random forest. Our method achieves the sensitivity of 0.9478, specificity of 0.9176, PPV of 0.9397, and NPV of 0.9286, it performed much better than the other classifiers.
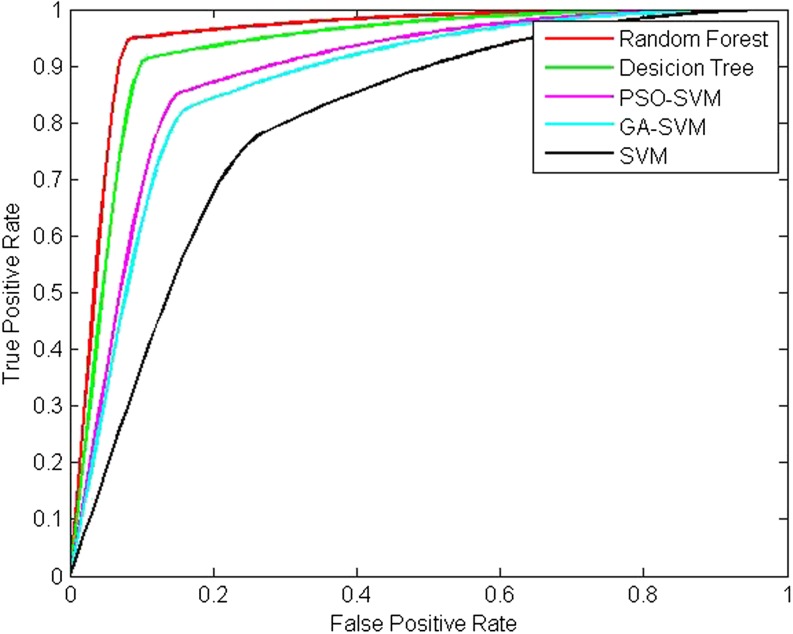
The ROC curve is also used to evaluate the performance of accuracy, and the ROC curve and the AUC of all the methods are shown in Fig. 5 and listed in Table 6, respectively. We can see that a high ROC of 0.9505 has been achieved. This proves once again the superiority of our method over the others.
Fig. 5.
ROC curve analysis of the various classified methods tested on DDSM database
Table 6.
ROC area and MCC indicators of the various classified methods tested on DDSM database
| Our method | SVM | GA-SVM | PSO-SVM | Decision tree | |
|---|---|---|---|---|---|
| AUC | 0.9505 | 0.8015 | 0.8719 | 0.8871 | 0.9294 |
| MCC | 0.8668 | 0.5106 | 0.6566 | 0.6955 | 0.8540 |
Bold font number indicates the best performance in each line
SVM support vector machine, GA-SVM genetic algorithm support vector machine, PSO-SVM particle swarm optimization support vector machine, AUC area under the curve, MCC Matthew’s correlation coefficient
MCC describes the correlation of data on a particular feature classification which has rarely been used for breast cancer CAD performance evaluation. The value of MCC is between −1 and 1, and if this value is close to 1, that is to say the diagnosis result is more reliable. In order to measure the effectiveness of our method more comprehensively, we calculate the value of MCC and list it in Table 6. It can be seen that our method achieves the best MCC value of 0.8668 compared to other classified methods. The result emphasizes the potential of our method to be used as a breast cancer classifier.
On the whole, the best specificity of 98 % and sensitivity of 92.5 % have been obtained for the proposed method. Compared to other state-of-the-art classified methods, our method shows a low computational cost, easy implementation, and high accuracy.
Classification Tested on Both DDSM Database and MIAS Database
To test and verify the feasibility and efficiency of our method on breast cancer diagnosis comprehensively, MIAS database is also employed. Here, there exists 242 images including DDSM database (200) and MIAS database (42), and we conduct experiment as follows. Firstly, the feature from DDSM database and MIAS database is divided into five groups on average, every time one group is chosen as testing set and the other four groups are used to forming training set; so looping five times, all the feature data are used to train and test the classifier. The experimental results are listed in Tables 7 and 8 and shown in Fig. 6 based on the average with five times.
Table 7.
Performances of different classifiers tested on DDSM database and MIAS database
| Our method | SVM | GA-SVM | PSO-SVM | Decision tree | |
|---|---|---|---|---|---|
| Sensitivity | 90 | 80 | 82.5 | 85 | 87.5 |
| Specificity | 96 | 82 | 86 | 86 | 96 |
| PPV | 94.87 | 78.05 | 82.5 | 82.93 | 94.59 |
| NPV | 92.31 | 83.67 | 86 | 88 | 90.57 |
| Accuracy | 91.73 | 73.03 | 79.73 | 80.13 | 90.00 |
Bold font number indicates the best performance in each line
SVM support vector machine, GA-SVM genetic algorithm support vector machine, PSO-SVM particle swarm optimization support vector machine, PPV positive predictive value, NPV negative predictive value
Table 8.
ROC area and MCC indicators of the various classified methods tested on DDSM database and MIAS database
| Our method | SVM | GA-SVM | PSO-SVM | Decision tree | |
|---|---|---|---|---|---|
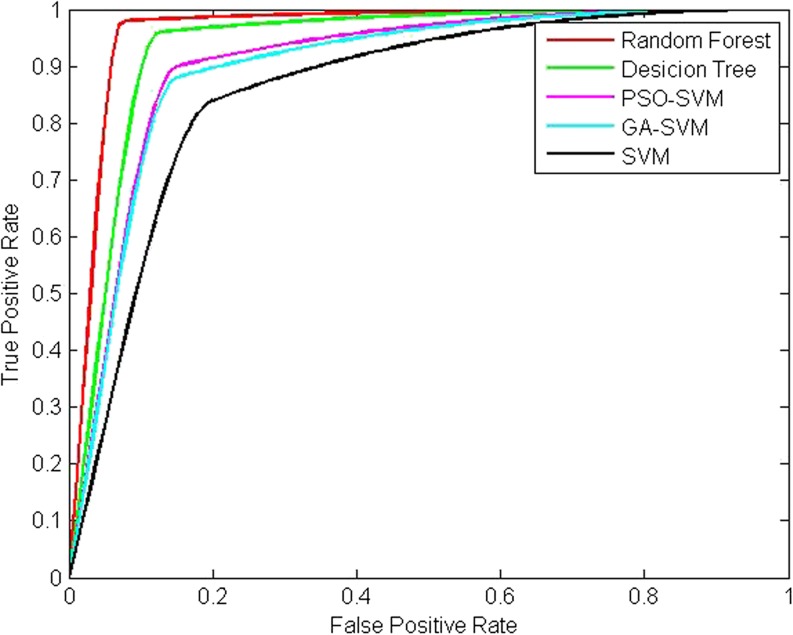
| AUC | 0.9467 | 0.8522 | 0.8794 | 0.8912 | 0.9362 |
| MCC | 0.8652 | 0.7750 | 0.7084 | 0.6850 | 0.6186 |
Bold font number indicates the best performance in each line
AUC area under the curve, MCC Matthew’s correlation coefficient
Fig. 6.
ROC curve analysis of the various classified methods tested on DDSM database and MIAS database
From Tables 7 and 8 and Fig. 6, it can be concluded that our method is effective both on DDSM database and MIAS database. It can achieve better performance compared to other classification methods. This indicates that the proposed method can detect a malignant mass with high probability. In addition, the higher PPV and NPV mean that the number of biopsies for benign lesions can be reduced. This could enable offering of a second reading to help reduce the misdiagnosis and the overall cost of diagnosis breast disease in practical application.
The promising results should be due to both the precise segmentation method and the effective classification technology. Firstly in segmentation, rough set method not only removes the noise in the mammograms but also enhances the contrast of the boundary which makes the VFC contour directly deform to the object rather than interferential tissue, and this improves the accuracy of segmentation and lays a foundation to feature extraction. Following random forest is used to overcome the state-of-the-art classifiers with its better accurate classification, and the higher accurate of classification should be due to the randomized processing reducing the correlation between distinctive learners in the ensemble and the variance reduction through averaging over learners. This superior performance makes our method suitable for distinguishing between benign and malignant of mass in mammograms efficiently.
Conclusion and Prospect
CAD plays an important role in predicting breast disease recently. In this paper, an automatic mass segmentation and classification method is presented; the aim is to overcome the accuracy and sensitivity limitations of the current solutions in mammograms for breast cancer diagnosis, firstly, the breast mass is auto-segmentation adopted by a novel integrated method, then the mass features including the characteristic of mass, ROI, and background are extracted, and finally, we distinguish the mass between benign and malignant with random forest classifier.
Experimental results are very encouraging: with respect to other existing state-of-the-art classification method including SVM, GA-SVM, PSO-SVM, and decision tree, the proposed approach has achieved the best classification accuracy of 97.73 % on the database of DDSM. When conducting experiment on both DDSM database and MIAS database, our method is also proved to be the best. The values of sensitivity, specificity, NPV, and PPV are much better than those obtained with the other methods. To evaluate the availability of the feature data and the classification accuracy more comprehensively, we also use the AUC of ROC and MCC as assessment indicators. All of these measured indicators verify the effectiveness of the proposed method in this paper.
The promising results may be due to the following aspects: The first is the improved segmentation approach, and it can locate and segment not only the mass automatically but also with lower dependence on the initial active contour at the same time with stronger capability of convergence; moreover, this segmentation method is robust to the interference of blurry areas and tissue and able to converge to the object precisely. It is the important foundation of the follow-up work; secondly, the feature extraction method is also essential, and this process is based on the accurate segmentation mass area and the extraction feature including the characteristic of mass, ROI, and background. The 32 extraction features represent the characteristic of mass area comprehensively. It does great influence on the following classification process. Last and most important, the random forest classifier used in this work improves the classification accuracy significantly. The random forest is selected for classification because of its interesting properties: (1) deal with high dimension feature without feature selection, (2) accommodate many predictor variables, (3) during creating random forests, generalization error using unbiased estimation, and (4) run new data through previously generated forests to generate classifications.
These promising results clearly demonstrate the great potential of the proposed approach in the automatic segmentation and classification of biomedical data. The proposed approach can assist the radiologist in performing an in-depth exploration of the breast tumor within a short time and improve the accurate diagnosis of breast disease. These experimental results are based on a limited sample size database, and the future investigation will pay much attention to creating a larger mammographic database. Then, we are committed to augment the present work to develop a CAD system for the early detection of the breast cancer, and we also would like to extend the CAD system on other medical diagnosis problems for consistency.
References
- 1.Jemal A, et al. Global cancer statistics. CA: Cancer J Clin. 2011;61(2):69–90. doi: 10.3322/caac.20107. [DOI] [PubMed] [Google Scholar]
- 2.Siegel R, Naishadham D, Jemal A. Cancer statistics, 2013. CA: Cancer J Clin. 2013;63(1):11–30. doi: 10.3322/caac.21166. [DOI] [PubMed] [Google Scholar]
- 3.Dubey R, Hanmandlu M, Gupta S. A comparison of two methods for the segmentation of masses in the digital mammograms. Comput Med Imaging Graph. 2010;34(3):185–191. doi: 10.1016/j.compmedimag.2009.09.002. [DOI] [PubMed] [Google Scholar]
- 4.Oliver A, et al. A review of automatic mass detection and segmentation in mammographic images. Med Image Anal. 2010;14(2):87–110. doi: 10.1016/j.media.2009.12.005. [DOI] [PubMed] [Google Scholar]
- 5.Cheng H, et al. Automated breast cancer detection and classification using ultrasound images: A survey. Pattern Recogn. 2010;43(1):299–317. doi: 10.1016/j.patcog.2009.05.012. [DOI] [Google Scholar]
- 6.Wu W-J, Lin S-W, Moon WK. Combining support vector machine with genetic algorithm to classify ultrasound breast tumor images. Comput Med Imaging Graph. 2012;36(8):627–633. doi: 10.1016/j.compmedimag.2012.07.004. [DOI] [PubMed] [Google Scholar]
- 7.Lu X, Ma Y, Xie W, et al: Automatic Mass Segmentation Method in mammograms based on improved VFC Snake model. in The 2014 International Conference on Image Processing, Computer Vision, and Pattern Recognition. 2014
- 8.Ma Y, Xie W, Wang Z, et al: A level set method for biomedical Image segmentation. in The 2013 International Conference on Image Processing, Computer Vision, and Pattern Recognition. 2013
- 9.Mazurowski MA, et al. Mutual information-based template matching scheme for detection of breast masses: From mammography to digital breast tomosynthesis. J Biomed Inform. 2011;44(5):815–823. doi: 10.1016/j.jbi.2011.04.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Nascimento MZD, et al. Classification of masses in mammographic image using wavelet domain features and polynomial classifier. Expert Syst Appl. 2013;40(15):6213–6221. doi: 10.1016/j.eswa.2013.04.036. [DOI] [Google Scholar]
- 11.Delogu P, et al. Characterization of mammographic masses using a gradient-based segmentation algorithm and a neural classifier. Comput Biol Med. 2007;37(10):1479–1491. doi: 10.1016/j.compbiomed.2007.01.009. [DOI] [PubMed] [Google Scholar]
- 12.Moayedi F, et al. Contourlet-based mammography mass classification using the SVM family. Comput Biol Med. 2010;40(4):373–383. doi: 10.1016/j.compbiomed.2009.12.006. [DOI] [PubMed] [Google Scholar]
- 13.Wu W.-J., S.-W. Lin, and W.K. Moon: An Artificial Immune System-Based Support Vector Machine Approach for Classifying Ultrasound Breast Tumor Images. J Digit Imaging: p. 1–10, 2014 [DOI] [PMC free article] [PubMed]
- 14.Cheng H, et al. Approaches for automated detection and classification of masses in mammograms. Pattern Recogn. 2006;39(4):646–668. doi: 10.1016/j.patcog.2005.07.006. [DOI] [Google Scholar]
- 15.Dong M, Ma Y: Breast cancer diagnosis development research based on morphological characteristics parameters of breast tumor cells. Chin J Clin 7(11):5023–5026, 2013
- 16.Issac Niwas S, et al. Analysis of nuclei textures of fine needle aspirated cytology images for breast cancer diagnosis using Complex Daubechies wavelets. Signal Process. 2013;93(10):2828–2837. doi: 10.1016/j.sigpro.2012.06.029. [DOI] [Google Scholar]
- 17.Karakıs R, Tez M, Kılıc YA, et al. A genetic algorithm model based on artificial neural network for prediction of axillary lymph node status in breast cancer. Eng Appl Artif Intell. 2013;26(3):945–950. doi: 10.1016/j.engappai.2012.10.013. [DOI] [Google Scholar]
- 18.Lacson R, et al: Evaluation of an Automated Information Extraction Tool for Imaging Data Elements to Populate a Breast Cancer Screening Registry. J Digit Imaging: p. 1–9, 2014 [DOI] [PMC free article] [PubMed]
- 19.Bowyer K, et al: The digital database for screening mammography. in Third International Workshop on Digital Mammography. 1996.
- 20.Suckling J, et al: The mammographic image analysis society digital mammogram database. 1994
- 21.Starren J, Johnson S.M: Expressiveness of the Breast Imaging Reporting and Database System (BI-RADS). in Proceedings of the AMIA Annual Fall Symposium. : American Medical Informatics Association, 1997 [PMC free article] [PubMed]
- 22.Pawlak Z. Rough set approach to knowledge-based decision support. Eur J Oper Res. 1997;99(1):48–57. doi: 10.1016/S0377-2217(96)00382-7. [DOI] [Google Scholar]
- 23.Kass M, Witkin A, Terzopoulos D. Snakes: Active contour models. Int J Comput Vis. 1988;1(4):321–331. doi: 10.1007/BF00133570. [DOI] [Google Scholar]
- 24.Li B, Acton ST. Active contour external force using vector field convolution for image segmentation. IEEE Trans Image Process. 2007;16(8):2096–2106. doi: 10.1109/TIP.2007.899601. [DOI] [PubMed] [Google Scholar]
- 25.Xu X: Research on detection of breast mass in mammography. Huazhong University of Science and Technology, 2010.
- 26.Li, L., et al., False-positive reduction in CAD mass detection using a competitive classification strategy. Medical Physics 28(2):250–258, 2001 [DOI] [PubMed]
- 27.Petrick N, et al: Automated detection of breast masses on mammograms using adaptive contrast enhancement and texture classification. Med Phys 23(10):1685–1696, 1996 [DOI] [PubMed]
- 28.Catarious Jr, DM: A.H. Baydush, and C.E. Floyd Jr, Characterization of difference of Gaussian filters in the detection of mammographic regions. Med Phys 33(11):4104–4114, 2006 [DOI] [PubMed]
- 29.Petrick N, et al: Combined adaptive enhancement and region-growing segmentation of breast masses on digitized mammograms. Med Phys 26(8):1642–1654, 1999 [DOI] [PubMed]
- 30.Zheng B, et al: A method to improve visual similarity of breast masses for an interactive computer-aided diagnosis environment. Med Phys 33(1):111–117, 2006 [DOI] [PubMed]
- 31.Christoyianni I, Dermatas E, Kokkinakis G: Fast detection of masses in computer-aided mammography. IEEE Signal Proc Mag 17(1):54–64, 2000
- 32.Ma Y, Gu X, Wang Y: Histogram similarity measure using variable bin size distance. Comput Vis Image Underst 114(8):981–989, 2010
- 33.Melgani F, Bazi Y: Classification of electrocardiogram signals with support vector machines and particle swarm optimization. IEEE Trans Inf Technol Biomed 12(5):667–677, 2008 [DOI] [PubMed]
- 34.Breiman L: Random forests. Mach Learn 45(1):5–32, 2001
- 35.Friedl MA, Brodley CE: Decision tree classification of land cover from remotely sensed data. Remote Sens Environ 61(3):399–409, 1997
- 36.Valdimir V. and N. Vapnik: The nature of statistical learning theory. 1995, Springer
- 37.Vapnik VN, Vapnik V: Statistical learning theory, vol. 2. Wiley, New York, 1998
- 38.Zhang T: An introduction to support vector machines and other kernel-based learning methods. AI Mag 22(2):103, 2001
- 39.Braga-Neto UM, Dougherty ER: Is cross-validation valid for small-sample microarray classification? Bioinformatics 20(3):374–380, 2004 [DOI] [PubMed]