Microconstriction Arrays for High-Throughput Quantitative Measurements of Cell Mechanical Properties

Abstract

We describe a method for quantifying the mechanical properties of cells in suspension with a microfluidic device consisting of a parallel array of micron-sized constrictions. Using a high-speed charge-coupled device camera, we measure the flow speed, cell deformation, and entry time into the constrictions of several hundred cells per minute during their passage through the device. From the flow speed and the occupation state of the microconstriction array with cells, the driving pressure across each constriction is continuously computed. Cell entry times into microconstrictions decrease with increased driving pressure and decreased cell size according to a power law. From this power-law relationship, the cell elasticity and fluidity can be estimated. When cells are treated with drugs that depolymerize or stabilize the cytoskeleton or the nucleus, elasticity and fluidity data from all treatments collapse onto a master curve. Power-law rheology and collapse onto a master curve are predicted by the theory of soft glassy materials and have been previously shown to describe the mechanical behavior of cells adhering to a substrate. Our finding that this theory also applies to cells in suspension provides the foundation for a quantitative high-throughput measurement of cell mechanical properties with microfluidic devices.

Introduction

Mechanical properties of living cells are important for essential cell functions including cell contraction (1,2), crawling and invasion (3), differentiation (4–6), and wound healing and division (7,8). Moreover, alterations of cell mechanical properties have been linked to common human diseases such as cancer (9,10), inflammation and sepsis (11), asthma (2), malaria (10,12), and cardiovascular disorders. To measure cell mechanical properties, numerous techniques have been developed including atomic force microscopy (13), micropipette aspiration (14,15), particle tracking microrheology (16), and magnetic tweezer microrheology (17). However, these techniques suffer from low measurement throughput of ∼10–100 cells/h. By contrast, microfluidic technologies can achieve a much higher throughput, for example by shear flow stretching (18,19) or by measuring the entry or transit time of cells through micronscale constrictions (microconstrictions). Such microconstriction setups have been used to investigate suspended erythrocytes (20), leukocytes (11), neutrophils (21), and invasive and noninvasive cancer cell lines (22–24). Although the cell entry time into microconstrictions correlates with cell stiffness and viscosity, it also depends on the externally applied pressure, cell size, and friction between the cell and the channel walls (25). Therefore, we believe that quantitative measurements of cell mechanical properties have thus far not been achieved with such setups.

In this article, we describe a quantitative, high-throughput method to measure the mechanical properties of cells in suspension (suspended cells or adherent cells that have been detached and brought in suspension) with a parallel microconstriction device. We use constrictions that are smaller than the nucleus of the cell and therefore deform and probe both the nucleus and the cytoskeleton, resulting in a bulk measurement of the whole cell. Our approach is to measure for each cell and each microconstriction not only the entry time, but also the cell size and the applied pressure. Using a high-speed charge-coupled device camera in combination with automated image analysis, we achieve a throughput of ∼10,000 cells/h.

We find that the relationship among entry time, cell deformation, and driving pressure conforms to power-law rheology. Power-law rheology describes the mechanical properties of cells with only two parameters: cell elasticity (stiffness) and cell fluidity (the power-law exponent). Moreover, we find that elasticity and fluidity data from cells treated with a wide range of chemicals that alter the cytoskeletal (actin, microtubule) or the nuclear structure (chromatin packing) all collapse onto a master curve. This master curve establishes that the mechanical properties of cells in suspension are governed by only a single parameter, namely cell fluidity. Therefore, with only a single measurement, we can quantitatively characterize the mechanical state of each cell.

Materials and Methods

Design of the device

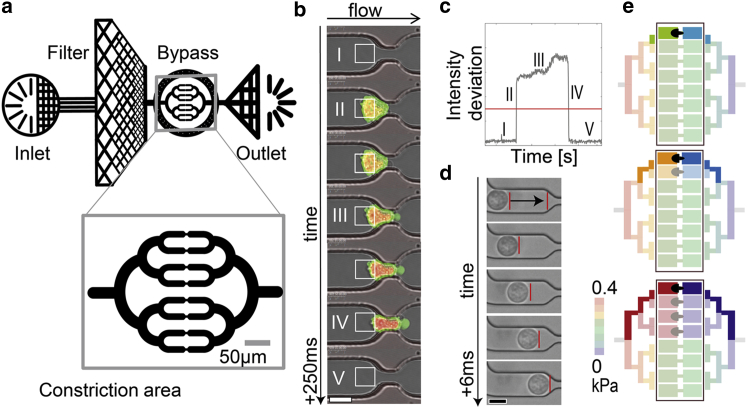
The microfluidic device consists of eight parallel constrictions connected to a single inlet and outlet with a low-resistance pressure-equalizing bypass, similar to previously published designs (11,21) (Fig. 1 a). Cells in suspension first have to pass through a filter mesh before the flow is divided into eight parallel constriction branches. The height of the device is chosen to be in the range of the cell diameter (17 μm for K562 cells). The width and height of the constrictions are chosen to be smaller than the nuclear diameter. For the K562 leukemia cells used in this study, we empirically find a good compromise between high throughput (wide constrictions) and high sensitivity (narrow constrictions) for a constriction width of 5 μm and a height of 9 μm (Fig. S1 a in the Supporting Material). With these dimensions, an average entry time between 5 and 1000 ms can be achieved. The length and shape of the constriction (Fig. 1, b and d) is chosen so that the passage time is dominated by the time the cell needs to deform to the width of the channel. Once fully deformed, the cell slides through the constriction channel in <1.4 ms, which is the temporal resolution of the camera. Therefore, cell friction at the constriction walls can be neglected. The microfluidic device is mounted on a glass coverslip and imaged from below using an inverted microscope.

Figure 1.

(a) Schematic of the microfluidic device with inlet, debris filter, constriction area surrounded by a bypass, and outlet. (Inset) Magnified view of the symmetric constriction area with eight parallel channels. (b) Sequential micrographs of a cell entry into a constriction. The actin cytoskeleton is stained with LifeAct (green); the DNA is stained with DRAQ5 (red). The white squares mark the regions of interest (ROI) for estimating the cell’s entry time. Scale bar is 10 μm. (c) The standard deviation (SD) of the brightness within the ROI is used to detect the time points when the cell enters a microconstriction (rise of the signal) and when it has fully deformed to pass through the microconstriction (fall of the signal). The entry time is calculated by thresholding (red line). Roman numbers correspond to the numbered ROIs from (b). (d) By tracking the cell before it enters the constriction, we obtain the flow speed and thus can calculate the pressure drop over each constriction with Hagen-Poiseuille’s law. Scale bar is 10 μm. (e) Changing occupational states in all constrictions are monitored continuously to calculate the pressure drop across each microconstriction during a cell’s entry. The figure depicts three examples of how the pressure across the leftmost constriction (color-coded in saturated colors) changes when cells block the fluid flow through neighboring constrictions (the pressure in the remaining system is color-coded in light colors). The 256 different combinations of blocked and free microconstrictions give rise to six possible pressure drop combinations that can differ by up to a factor of 2. To see this figure in color, go online.

Devices are fabricated using standard PDMS molding techniques from a photolithographically developed SU8 master. Briefly, SU8-2025 Photoresist (MicroChem, Westborough, MA) is spin-coated onto 3″ Si wafers (Silicon Materials, Pittsburgh, PA) to form layers of 17 μm height. Due to light diffraction during ultraviolet exposure of the Photoresist through a chrome mask, the constrictions have a decreased height of 9 μm (Fig. S1 a). Devices are produced from a 10:1 ratio of elastomer/curing agent (Sylgard 184; Dow Corning, Midland, MI), which is mixed and poured onto the SU8 master. After baking for at least 2 h at 65°C, the device is peeled from the SU8, plasma-bonded to a microscope coverslip using air plasma generated by a plasma oxidizer (Zepto; Diener Electronic, Nagold, Germany), and further baked for 1 h at 65°C.

Cell culture

K562 cells (No. CCL-243; American Type Culture Collection, Manassas, VA) are cultured at 37°C and 5% CO₂ in Iscove’s modified Dulbecco’s medium (IMDM, Gibco Cat. No. 12440053; Life Technologies/Thermo Fisher Scientific, Waltham, MA) containing 10% FCS (fetal calf serum, Gibco, Cat. No. 16000-036) and 1% PSG (Penicillin-Streptomycin-Glutamine, Gibco Cat. No. 10378-016). MDA-MB-231 cells (No. HTB-26; American Type Culture Collection), U2OS cells (No. CRL-1573; American Type Culture Collection), and HEK293T cells (No. ACS-4500; American Type Culture Collection) are cultured in Dulbecco’s modified Eagle Medium (Gibco Cat. No. 11960044), also containing 10% FCS and 1% PSG. Cells are passaged every third day. Nuclear staining is performed with DRAQ5 (Cat. No. ab108410; Abcam, Cambridge, MA) according to the manufacturer’s guidelines. Whole cell staining for size measurements is performed with calcein (Cat. No. C0875; Sigma-Aldrich, St. Louis, MO). Life-death staining is performed with calcein and propidium iodide (Cat. No. P4170; Sigma-Aldrich).

Transfection

For the generation of K562 and MDA-MB-231 cells expressing eGFP-lamin A, we use lentiviral transduction. For producing lentiviral particles, HEK293T cells are cotransfected with the vectors pMD2.G, psPAX2, and pLVX containing the coding sequence of lamin A N-terminally fused to eGFP using lipofectamine LTX (Gibco Cat. No. 15338100). The cell culture supernatant is collected daily and replaced with fresh Dulbecco’s modified Eagle’s medium for the next four days. The collected medium containing assembled virus particles is pooled and filtered through 0.45 μm pores, supplemented with 8 μg/mL polybrene (Cat. No. 107689; Sigma-Aldrich) and added to K562 and MDA-MB-2331 cells for 18 h. Starting from Day 2 after lentiviral infection, cells are selected using 2.5 μg/mL puromycin. After 10 days, eGFP-lamin A-expressing K562 cells are sorted using a MoFlo Legacy cell sorter (Dako Cytomation, Carpinteria, CA).

For the generation of U2OS cells stably expressing the fluorescent F-actin marker LifeAct-TagGFP2, we transfect the expression vector using lipofectamine LTX (Gibco Cat. No. 15338100) according to the manufacturer’s instructions. Starting from Day 2 after transfection, stably expressing cells are selected using 1 mg/mL G418 (Cat. No. 83768; Sigma-Aldrich). These cells are used only for visualizing the cell entry with confocal microscopy (Fig. 1 b), but not for evaluation of mechanical properties.

Drug treatments

To condense nuclear chromatin, K562 cells are treated for 30 min with Ca²⁺ ions (2 mM, C8106; Sigma-Aldrich) and Mg²⁺ ions (2 mM, Cat. No. 2444-05; J.T. Baker, Center Valley, PA). To decondense the chromatin, cells are treated for 3 h with 5 μM 5-AZA-2′-deoxycytidine (Cat. No. A3656; Sigma-Aldrich). To inhibit actin polymerization at the barbed end, cells are treated for 30 min with 10 μM cytochalasin D (Cat. No. C8273; Sigma-Aldrich). To permanently cross-link cell components, cells are treated for 30 min with 500 μM glutaraldehyde (Cat. No. G5882; Sigma-Aldrich). To inhibit microtubule polymerization, cells are treated for 3 h with 500 nM nocodazole (Cat. No. M1404; Sigma-Aldrich). To inhibit microtubule depolymerization, cells are treated for 1 h with 5 μM paclitaxel (Cat. No. T7191; Sigma-Aldrich). To agglomerate the vimentin and keratin intermediate filament network, cells are treated for 3 h with 5 mM acrylamide (Cat. No. A8887; Sigma-Aldrich). All drug concentrations are maintained during measurements.

Cell size and viability remain unchanged after drug treatment (Fig. S2, a and b), confirming that mechanical responses are not biased by dead or damaged cells.

Device operation

Flow through the device is created by applying a hydrostatic pressure. Before measurements, the device is flushed using an air-over-liquid pump (Bellofram, Newell, WV) with pressures ranging between 2 and 50 kPa. Microfluidic flow during measurements is manually adjusted for optimal throughput between 0.1 and 3 kPa by lifting or lowering the cell reservoir connected to the device inlet. Rigid polyether-ether-ketone tubing (PEEK tubing; VWR, Radnor, PA) is used to connect the cell reservoir to the device.

Before measurements, the device is filled with PBS (phosphate-buffered saline, Gibco Cat. No. 10010) containing 1% Pluronic (BASF, Ludwigshafen, Germany; Cat. No. P2443, Sigma-Aldrich) to coat the surfaces of the PDMS and reduce unspecific cell and protein adhesion to the surfaces of the device.

The cell suspension (100,000 cells in 1 mL of medium with 1% Pluronic; BASF) is flushed into the device, and the entry of the cells into the constrictions is monitored using either a high-speed charge-coupled device camera operated at a frame rate of 700 fps (model No. GE480; Allied Vision Technologies, Stadtroda, Germany), or a laser-scanning confocal microscope (SP5; Leica Microsystems, Wetzlar, Germany) (Fig. 1, b and d). Video sequences are recorded for further analysis with the software MATLAB (The MathWorks, Natick, MA).

We verify that incubating the cells with 1% Pluronic (BASF) for up to four days does not change cell viability and proliferation rate (Fig. S2 c). Importantly, the exposure of the cells to shear forces during their passage through the microconstriction device does not impair cell viability or cell growth (Fig. S2 c). These results suggest that our device is also suitable for repeated measurements of the same cell population over longer time periods.

Measurement of cell deformation, cell speed, and entry time

Before the cell enters the constriction, we record and analyze between three and five images of the undeformed cell, depending on the flow rate (Fig. 1 d). Bright-field images are background-subtracted, Sobel-filtered for edge detection, and the outline of the cell is segmented by thresholding. For quantifying the cell radius R, a circle is fitted to the cell contour. The change in the position of the circle over subsequent images is used to compute the cell speed. Cell entry time $t_{\text{entry}}$ into the constriction is measured by monitoring brightness changes (SD) within a region of interest (ROI) at the opening of the microconstriction (Fig. 1 c). The SD of brightness intensities within the ROI increases sharply (within one frame) when a cell enters the constriction, and drops equally sharply when it leaves the constriction (Fig. 1, b and c). An empirical threshold (constant for all experiments) is applied to define the beginning and end of the entry. To quantify the maximum cell deformation ${\epsilon }_{\text{max}}$ during the cell’s entry into the microconstrictions, we consider the cell as being incompressible during the relatively short entry time. Further, we approximate the stress as a simple one-dimensional compression. The maximum strain of the cell is calculated from the relative difference between its uncompressed radius R and the effective radius of the microconstriction $R_{\text{eff}}$, which is the radius of a circle with the same cross-section area ($R_{\text{eff}}=\sqrt{h\cdot w/\pi }=3.8\mu \text{m}$, Fig. S1 a),

$${\epsilon }_{\text{max}}=\frac{R-R_{\text{eff}}}{R},$$ (1)

for $R>R_{\text{eff}}$. We confirm that the dimensions of the constrictions remain constant for the pressure range applied in this study (1–10 kPa) (Fig. S1 b).

Pressure calculation

To calculate cell mechanical properties, the applied pressure across the constriction needs to be known. Due to the finite resistance of the microfluidic channels, however, the hydrostatic pressure is not constant throughout the device. Moreover, the pressure fluctuates on long and short timescales when parts of the inlet and outlet channel system or the microconstrictions themselves are blocked by cells. Therefore, the pressure across each individual microchannel is calculated continuously. To do so, we track the movement of each cell before it enters a microconstriction (Fig. 1 d). To relate the cell speed to the average flow speed, in a preliminary study we reconstructed the flow profile in the channels by measuring the speed of spherical beads (diameter = 1 μm) suspended in the medium together with cells (Fig. S3 a). At the same time, we measured the speed of the suspended cells and found that it was systematically lower than the average flow speed. Furthermore, the relative cell speed decreased slightly with increasing cell size (Fig. S3 b), as has been previously reported in Hetsroni et al. (26) and Belloul et al. (27). For all subsequent experiments, we compute the average flow speed $v_{\text{avg}}$ from the measured cell speed $v_{\text{cell}}$ according to $v_{\text{avg}}=v_{\text{cell}}/\left(1.22-0.46\left(r_{\text{cell}}/r_{\text{hyd}\left(\text{channel}\right)}\right)\right)$ (Fig. S3 b), where the hydrodynamic radius of the channel of width w and height h is $r_{\text{hyd}\left(\text{channel}\right)}=(h\times w)/(h+w)$. Because the cells occupy most of the channel cross section ($r_{\text{cell}}/r_{\text{hyd}\left(\text{channel}\right)}$ ∼ 0.9), cells move along the center of the channel with a SD of ±1.49 μm. We find experimentally that errors in calculating $v_{\text{avg}}$ from off-centered cells are negligibly small (data not shown).

The flow rate can then be calculated as $v_{\text{avg}}$ times the cross-sectional area of the channel. From the flow rate, we calculate the pressure drop $\text{Δ}p$ across that particular microconstriction from Hagen-Poiseuille’s law for rectangular channels. The pressure across the microconstrictions in each of the other seven segments is then computed according to Kirchhoff’s laws. When a cell blocks a microconstriction, the flow in that particular segment is taken as zero, and the pressure in all other segments is updated depending on their cell occupancy. From the speed of the next cell that is tracked before it enters a microconstriction, we verify the pressure from the previous update and find for a mean pressure of 400 Pa a small error of −0.12 ± 9 Pa (mean ± SD), which arises when one of the cells has not completely blocked a microconstriction, or when a larger cell cluster has partially blocked the inlet filter between the pressure updates. We then compute the mean pressure that each cell experiences during its entry, $\text{Δ}\overline{p}=1/t_{\text{entry}}\int \text{Δ}p\left(t\right)dt$. Using the mean pressure instead of the exact time course of the fluctuating pressure across the microconstrictions (Fig. 1 e) introduces a negligible error for the subsequent analysis of cell mechanical properties (Fig. S4, a–d).

Calculation of cell mechanical properties

The pressure applied to a cell in a microconstriction deforms the cell over time. We treat the cell as a visco-elastic homogeneous body and apply power-law rheology (28) to describe changes in cell strain ε over time, t:

$$\epsilon =\frac{\text{Δ}\overline{p}}{E}{\left(\frac{t}{t_0}\right)}^{\beta }.$$ (2)

Here, E is the cell’s stiffness (elastic modulus) evaluated at t₀ = 1 s, a commonly used arbitrary choice. The power-law exponent β reflects the mechanical stress dissipation in the cell. A power-law exponent of $\beta =0$ is indicative of a purely elastic solid, and $\beta =1$ is indicative of a purely viscous fluid. In cells, the power-law exponent usually falls in the range between 0.1 and 0.5, whereby higher values have been linked to a higher turnover rate of cytoskeletal structures (29). Therefore, in the following we refer to the power-law exponent also as cell fluidity.

When the cell is deformed to the size of the microconstriction so that $\epsilon ={\epsilon }_{\text{max}}$, it is flushed out. The total entry time $t_{\text{entry}}$ is thus

$$t_{\text{entry}}={\left(\frac{{\epsilon }_{\text{max}}E}{\text{Δ}\overline{p}}\right)}^{\frac{1}{\beta }}.$$ (3)

Statistical analysis

We fit Eq. 3 with the fit parameters E and β to the measured data ($t_{\text{entry}}$, ${\epsilon }_{\text{max}}$, and $\text{Δ}\overline{p}$) from several hundreds or thousands of cells. Thus, E and β are average values representative for the whole cell population. Before fitting Eq. 3 to the data with a bivariate error weighting using a Levenberg-Marquardt algorithm implemented in the software MATLAB, the data are logarithmically transformed to obtain a linear relationship between $\text{log}\left(t_{\text{entry}}\right)$ and $\text{log}\left({\epsilon }_{\text{max}}/\text{Δ}\overline{p}\right)$. SDs of the fit parameters are calculated by bootstrapping, where we repeat the fit on ensembles of randomly selected cells. Comparisons between different pharmacological treatments are performed using Student’s t-test. Differences are considered statistically significant for p < 0.05.

Results and Discussion

Entry time into microconstrictions

With a high-speed camera, we record the movement of the cells as they pass through the microconstrictions. For each cell, we compute the cell radius R before it enters the channel, the average pressure difference $\text{Δ}\overline{p}$ across the microconstriction during cell entry, and the entry time $t_{\text{entry}}$ for entering into the constriction.

The cell entry time tends to decrease with increasing pressure across the microconstriction (Fig. 2 a). The data of several thousand cells, after binning and averaging, show an inverse power-law relationship between $t_{\text{entry}}$ and $\text{Δ}\overline{p}$ according to $t_{\text{entry}}\sim \text{Δ}{\overline{p}}^{-1/\beta }$ (Fig. 2 a; Fig. S5 a). Moreover, when we select cells that are measured over a narrow pressure range and plot the entry time versus the maximum cell deformation in the microconstriction (${\epsilon }_{\text{max}}$) (Fig. 2 b; Fig. S5 b), we find a power-law relationship with the same exponent according to $t_{\text{trans}}\sim {\epsilon }_{\text{max}}^{1/\beta }$. Taking the power-law relationships for $t_{\text{entry}}$ together, the entry time depends on both ${\epsilon }_{\text{max}}$ and $\text{Δ}\overline{p}$, according to $t_{\text{entry}}={\left({\epsilon }_{\text{max}}E/\text{Δ}\overline{p}\right)}^{1/\beta }$ (Eq. 3) with the cell’s elastic modulus E (evaluated at t = 1 s) and fluidity β.

Figure 2.

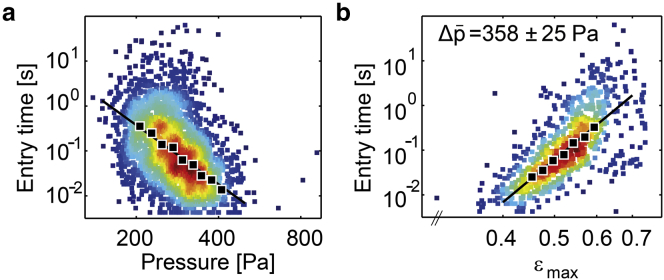
Mechanical properties of K562 leukemia cells: entry timescales with applied pressure and maximum cell deformation according to a power law. (a) Scatter plot of entry time versus pressure data for a typical experiment. The variance in pressure from 100 to 800 Pa arises from a combination of slow manual changes of the externally applied pressure, and stochastic pressure fluctuations due to different clogging configurations. Each marker represents the data from an individual cell. As a guide to the eye, the local density of data points is indicated by the marker color. (Solid markers) Geometric mean of ∼300 cells binned according to pressure. (Solid line) Fit of Eq. 3 to the nonbinned data. (b) Scatter plot of entry time versus maximum cell deformation (${\epsilon }_{\text{max}}$). Only cells from (a) that experienced an average pressure of 358 ± 25 Pa (mean ± SD) are shown. (Solid markers) Geometric mean of 70 cells binned according to cell deformation. (Solid line) Fit of Eq. 3 to the nonbinned data. To see this figure in color, go online.

Influence of cytoskeletal and nuclear structures on cell mechanical properties

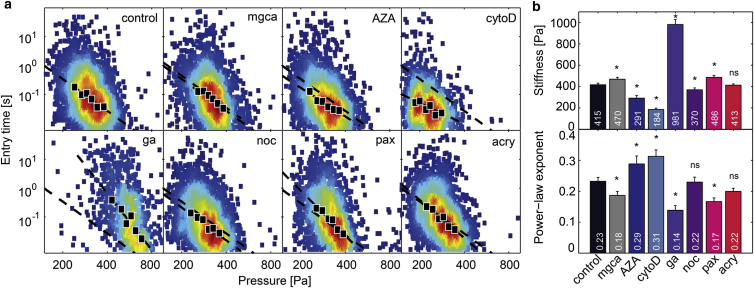
With our setup, we measure a stiffness of 415 Pa for K562 leukemia cells under control conditions. This value is in good agreement with previously published data (see Conclusions). We then treat K562 cells with a series of chemicals that are widely known to affect the deformability of cytoskeletal or nuclear structures. Cell stiffness has been shown to be mainly determined by the concentration and mechanical tension of polymerized actin (30–33). In agreement with other articles, we find that the disassembly of filamentous actin after treatment with cytochalasin D results in a dramatic decrease of cell stiffness by >50% (3,4,34). Simultaneously, cell fluidity increases, as seen by the 35% increase of the power-law exponent (Fig. 3, a and b). The opposite effect is observed after treating the cells with glutaraldehyde, which indiscriminately cross-links cytoskeletal and other cellular components and thereby stiffens the whole cell (34). Cell stiffness increases by 135%, and fluidity decreases by ∼40% (Fig. 3, a and b). Similar but smaller effects are expected from chemically altering the microtubule network of the cells (5,33). Depolymerization with nocodazole decreases cell stiffness by 11%, and increases fluidity slightly but not significantly (p = 0.22). Stabilization of the microtubule network with paclitaxel has the opposite effect: cell stiffness increases by 17%, and cell fluidity decreases by 25% (Fig. 3, a and b). Compared to changes induced by altering actin polymerization, however, these changes are considerably smaller, demonstrating that the microtubule network is of only minor importance for the deformability of K562 leukemia cells for strains between $0.3\le {\epsilon }_{\text{max}}\le 0.7$ and on timescales between 5 ms and 10 s. Disrupting the intermediate filaments vimentin and keratin by acrylamide (33,35–37) induces no significant changes in cell stiffness or fluidity (Fig. 3, a and b), demonstrating that the intermediate filament network is not important for the overall deformability of K562 cells for the strain and timescales investigated in this study.

Figure 3.

Change in stiffness and fluidity of K562 leukemia cells after drug treatment. (a) Scatter plots of entry times versus applied pressure for control cells and for cells treated with Mg²⁺Ca²⁺-ions (mgca), 5-AZA-2′-deoxycytidine (AZA), cytochalasin D (cytoD), glutaraldehyde (ga), nocodazole (noc), paclitaxel (pax), and acrylamide (acry); n > 2000 cells for each measurement. (Solid markers) Geometric mean of ∼200–400 cells binned according to pressure. (Solid lines) Fit of Eq. 3 to the binned data. Fit to control data is shown in all other plots for comparison (dashed line). (b) Population average of cell stiffness (top) and cell fluidity (bottom) for different drug treatments. Error bars represent SDs calculated by bootstrapping. (Asterisks) Significant differences with p < 0.0005. To see this figure in color, go online.

To determine if the cell entry into microconstrictions is sensitive to changes in the mechanical properties of the nucleus, cells are treated with Ca²⁺ and Mg²⁺ divalent cations, which condense the nucleus (38). This results in an increase of cell stiffness by 13% and a decrease of fluidity by 22%. Conversely, treating the cells with AZA (5-AZA-2′-deoxycytodine), which decondenses the nucleus (38,39), results in a decrease of cell stiffness by 30% and an increase of fluidity also by 25% (Fig. 3, a and b). Quantitative values of cell stiffness and fluidity for all treatments are given in Fig. 3 b.

Influence of the nuclear envelope on cell mechanical properties

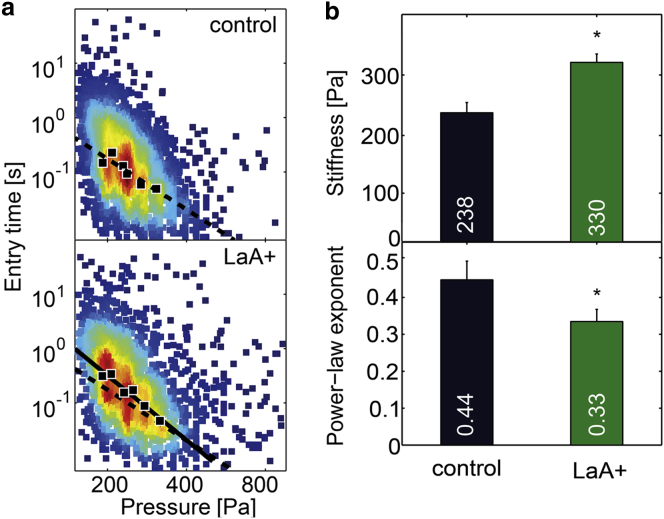
The dominant intermediate filament protein of the nuclear envelope, lamin A/C, has been shown to influence the cells’ entry time through microconstrictions (21) and to contribute to the stiffness of the nucleus (40,41). To test the influence of lamin A-overexpression on overall cell mechanical properties, we measure the stiffness and fluidity of cells overexpressing GFP-lamin A. Compared to wild-type cells, the stiffness of lamin A-overexpressing cells increases by 40% (Fig. 4, a and b), and this is accompanied by a decrease of the power-law exponent by 33% (Fig. 4, a and b). Thus, our data confirm that lamin A contributes greatly to cell stiffness, but because our method does not discriminate between the stiffness of the cell nucleus and that of the cytoskeleton, we cannot exclude the possibility that lamin A-overexpression leads to an altered cytoskeletal structure and mechanics.

Figure 4.

Effect of lamin A-overexpression on cell mechanics. (a) Scatter plots of entry times versus applied pressure for control cells and for GFP-lamin A-induced K562 cells. (Solid markers) Geometric mean of ∼300–500 cells binned according to pressure. (Solid lines) Fit of Eq. 3 to the binned data. Fit to control data is shown for comparison in the LaA+ plot (dashed line). (b) Population average of cell stiffness (top) and cell fluidity (bottom) for lamin A-overexpressing cells differ significantly (p < 0.0005 as indicated by asterisks) from control. Error bars represent SDs calculated by bootstrapping. To see this figure in color, go online.

K562 cells are nonadherent and can be permanently cultured in a suspended state. To test our method on normally adherent cells, we overexpress lamin A in MDA-MB-231 breast carcinoma cells and measure the resulting mechanical changes (Fig. S6). MDA-MB-231 cells also show power-law behavior and a similar increase in stiffness and reduction in the power-law exponent after lamin A-overexpression. These data demonstrate that our method is also suitable for measuring normally adherent cell populations.

Nonlinear mechanical properties of cells

The relatively large mechanical pressure (100–800 Pa) and strain ($0.3\le {\epsilon }_{\text{max}}\le 0.7$) acting on the cells during their entry into microconstrictions can potentially lead to an increase in stiffness, to an increase of the power-law exponent (fluidization), or both (42,43). To test if cell mechanical properties depend on the applied pressure, we bin the measured data into three pressure groups with equal number of cells in each bin, and calculate the mean cell stiffness E and the mean power-law exponent β for the cells in these bins separately. We find no systematic change of the power-law exponent with the applied pressure (Fig. S5 d). By contrast, we do find a small systematic increase in cell stiffness with increasing pressure, with a Pearson correlation coefficient of r = 0.16 (Fig. S5 c).

To test if cell mechanical properties depend on the maximum strain, we bin the measured data into three strain groups and calculate E and β for the cells in these bins separately. We find a systematic strain stiffening, with a Pearson correlation coefficient of r = 0.92 (Fig. S5 e) and a slight, systematic change in the power-law exponent β with strain (r = −0.2) (Fig. S5 f).

Despite a statistically significant strain stiffening, these effects are relatively small. We find a substantial increase of E with pressure or strain only for glutaraldehyde-treated cells. Therefore, the approximation of pressure- and strain-independent cell mechanical properties is well justified by the simplicity and robustness of the data analysis that it affords.

Collapse of cell mechanical parameters

For all treatment conditions, we find an inverse relationship between cell stiffness E and the power-law exponent β (Fig. 5 a). Treatments that increase cell fluidity cause the stiffness to decrease, and vice versa. When the logarithm of E for different treatment conditions is plotted versus the power-law exponent β, all data points collapse onto a line. This relationship thus represents a master curve in that a single parameter, β, defines the elastic and dissipative behavior of K562 leukemia cells for different manipulations of cytoskeletal or nuclear cell components.

Figure 5.

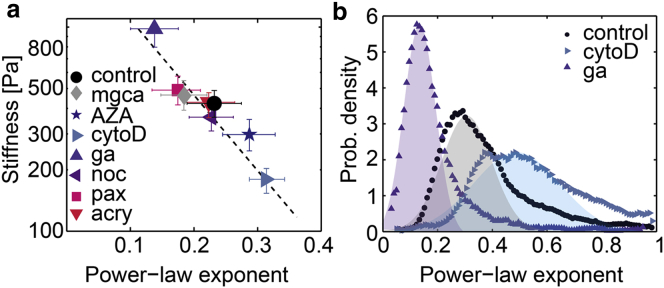
Collapse of cell mechanical properties onto a master curve allows for estimation of single cell mechanics of K562 leukemia cells. (a) Inverse relationship between cell stiffness E and power-law exponent β. Data for all treatments collapse onto a master curve. Error bars are one geometric SD. (Dashed line) Fit of the relationship $E=E_0\text{exp}\left(a\beta \right)$ to the data. (b) Distribution (probability density) of the power-law exponent β of individual cells under control conditions and after treatment with cytochalasin D or glutaraldehyde. To see this figure in color, go online.

The presence of such a master curve has been previously identified in a variety of adherent cells measured with different deformation methods (1,29,44,45). Here, we show that the same collapse of cell mechanics onto a master relationship also holds for suspended cells. Collapse of cell mechanical data onto a master curve, together with power-law behavior of cell deformations in response to stepwise-increasing mechanical stress, has been interpreted as a signature of soft glassy rheology (29,46). Accordingly, the power-law exponent describing the cell fluidity can be understood as an effective temperature that controls the dynamics of the mechanically active cell components such as actin, microtubules, or motor proteins. In the living cell, these components undergo transient binding interactions with a complex binding energy landscape. Hence, the effective temperature describes the degree of molecular agitation within this energy landscape. When the effective temperature is increased (high β) e.g., by cytochalasin D treatment, the binding interactions between cell components become less stable, and the cell softens and fluidizes. By contrast, when the effective temperature is decreased (low β), e.g., by crosslinking with glutaraldehyde, the binding interactions between cell components become more stable, and the cell stiffens and exhibits more solidlike characteristics (Fig. 5 a).

Mechanical properties of single cells

Thus far, we have measured an average stiffness and fluidity of a population of cells under a given condition. Because cell mechanical properties are described by two possibly independent parameters, E and β, we need to perform at least two independent measurements on the same cell, e.g., at two different pressure values, to extract stiffness and fluidity values for each individual cell. However, as we have demonstrated above, E and β are not independent. Rather, the mechanical properties of a cell depend only on cell fluidity β, from which the cell stiffness follows as $E=E_0\text{exp}\left(a\beta \right)$. The parameter a sets the slope of the E-versus-β curve and describes how quickly the cell exhibits a melting-type behavior when the fluidity β increases. The parameter E₀ is the intercept of the curve at the glass transition ($\beta =0$) and describes the maximum stiffness of the cell that cannot be exceeded by further cross linking (29). For K562 cells, we find a = −2.52, and E₀ = 1640 Pa.

Assuming that the same relationship holds not only for the cell population but for every cell, as was shown experimentally by atomic-force microscopy (AFM) measurements of adherent fibroblasts (44), we can estimate the mechanical properties of an individual cell from a single measurement of $\overline{\text{Δ}p}$, $t_{\text{entry}}$, and ${\epsilon }_{\text{max}}$:

$$\beta =\frac{\text{ln}\left(\frac{\text{Δ}\overline{p}}{E_0{\epsilon }_{\text{max}}}\right)}{a-\text{ln}\left(t_{\text{entry}}\right)}.$$ (4)

Thus, it is possible to describe the mechanical behavior of individual cells and to analyze the distribution of β within a cell population (Fig. 5 b). We find that the fluidity of individual K562 cells under control conditions follows a normal distribution with a SD of 0.11 centered at $\beta =0.29$. This is consistent with previous reports of a normal distribution of cell fluidity in populations of adherent cells (2,44,47). For cells treated with glutaraldehyde, the β-distribution shifts to smaller values with a smaller SD at $\beta =0.18\pm 0.05$. By contrast, in cells treated with cytochalasin D, both the average fluidity and its SD are increased to $\beta =0.42\pm 0.15$ (Fig. 5 b).

Conclusions

In this study, we measure the mechanical properties of cells in suspension using a microconstriction array. We demonstrate that measurements with this microconstriction array are highly sensitive to changes in subcellular properties induced by a range of treatments that act on the cytoskeleton or the nucleus.

Mechanical properties of K562 cells have been previously measured using different techniques. Indentation of optically trapped beads into cells immobilized on a fibronectin-coated glass surface gave a stiffness of 160 Pa (48). AFM measurements of cells trapped in microwells gave stiffness values at ∼50 Pa (11). Another AFM study of cells immobilized on a poly-L-lysine-coated glass surface reported a stiffness of 400 Pa (49). Moreover, this study also measured cells after cytochalasin D treatment and reported a 50% decrease in cell stiffness, which is in agreement with our findings. Considering that these measurements have been carried out under different strains and strain rates and over different timescales, our stiffness value of 415 Pa is in good agreement with published data.

The stiffness of normally adherent MDA-MB-231 breast cancer cells has also been measured with different techniques. Data reported for AFM measurements range from 257 (50) to 690 Pa (51). Data reported for magnetic tweezer measurements range from 400 to 1000 Pa, depending on the applied force (52). Measurements of MDA-MB-231 cells in suspension using a microfluidic micropipette aspiration assay gave stiffness values at ∼200 Pa (53). Taken together, our stiffness value of 617 Pa is in reasonable agreement with published data on adherent MDA-MB-231 cells. The fact that adherent cells need to be trypsinized and can only be measured in suspension with our measurement technique, however, implies several fundamental differences from measurements of cells in their adherent state. Cell stiffness of adherent cells is mostly governed by the cytoskeletal prestress that arises from the cell cortex and stress fibers (54), and this prestress is balanced through matrix adhesions by the substrate. Cells in suspension lack stress fibers, and the cortical tension is balanced by the hydrostatic pressure. Despite these differences, mechanical changes in response to different drugs that we measure for cells in suspension qualitatively mirror those reported for adherent cells (33).

With our microconstriction setup, we achieve high-throughput (10,000 cells/h) and at the same time a quantitative readout of cell mechanical properties using two strategies. First, we measure the size of each cell and the driving pressure in each of the parallel microconstrictions, from which we obtain a quantitative estimate of the mechanical stress and strain. Second, we apply the theory of soft glassy rheology to extract cell mechanical properties from the measurements. Soft glassy rheology predicts a power-law dependence of entry time on driving pressure and cell deformation. This power law implies a timescale-free cell mechanical behavior, which greatly simplifies the task of quantitatively estimating cell mechanical parameters because measurements can be performed either slowly or rapidly yet they give identical results. It is this timescale invariance that makes quantitative high-speed measurements of cell mechanical properties possible in the first place. Moreover, a power law is fully characterized by only two parameters, namely stiffness and fluidity. A two-parameter estimation further simplifies the task of measuring cell mechanical parameters. Finally, soft glassy rheology predicts that cell stiffness and fluidity collapse onto a single master relationship, implying that cell mechanical properties are governed by only a single parameter, which in turn can be calculated from a single set of measurements (e.g., pressure, entry time, and size). We find both predictions of soft glassy rheology, power-law behavior and collapse of the data onto a master curve, confirmed by our measurements.

Author Contributions

J.R.L., B.F., and G.W. designed the setup and experiments; J.R.L. and G.W. developed the data acquisition and analysis software; J.R.L., B.F., J.S., and G.W. performed the data analysis; I.H. designed and produced the chrome mask; T.K. and L.A.L. transfected and provided the cells; and J.R.L., B.F. and G.W. wrote the article.

Editor: Cecile Sykes.

Supporting Citations

Reference (55) appears in the Supporting Material.