Tuning Membrane Thickness Fluctuations in Model Lipid Bilayers

Abstract

Membrane thickness fluctuations have been associated with a variety of critical membrane phenomena, such as cellular exchange, pore formation, and protein binding, which are intimately related to cell functionality and effective pharmaceuticals. Therefore, understanding how these fluctuations are controlled can remarkably impact medical applications involving selective macromolecule binding and efficient cellular drug intake. Interestingly, previous reports on single-component bilayers show almost identical thickness fluctuation patterns for all investigated lipid tail-lengths, with similar temperature-independent membrane thickness fluctuation amplitude in the fluid phase and a rapid suppression of fluctuations upon transition to the gel phase. Presumably, in vivo functions require a tunability of these parameters, suggesting that more complex model systems are necessary. In this study, we explore lipid tail-length mismatch as a regulator for membrane fluctuations. Unilamellar vesicles of an equimolar mixture of dimyristoylphosphatidylcholine and distearoylphosphatidylcholine molecules, with different tail-lengths and melting transition temperatures, are used as a model system for this next level of complexity. Indeed, this binary system exhibits a significant response of membrane dynamics to thermal variations. The system also suggests a decoupling of the amplitude and the relaxation time of the membrane thickness fluctuations, implying a potential for independent control of these two key parameters.

Introduction

Lipids are the major component of biological membranes through which a delicate balance of nutrients within and outside the cell is maintained. For a long time, this complex functionality in cell membranes was mainly attributed to membrane proteins while lipid bilayers were overlooked as structureless support matrices. Over the last few decades, however, more focus has been directed to the role of lipids in mediating membrane functions (1–3). Conclusions of recent experimental and numerical studies support a growing consensus that lipid bilayers are far from inert and can have an essential role in determining the function of membrane proteins (4,5). The results of such studies clearly show that the behavior of membrane proteins can be severely compromised depending on their structural response to the thickness and curvature of the host bilayer (1,6,7). Unfortunately, much less is known about the dynamical interactions between proteins and lipid membranes despite the recognition that protein functions are ultimately governed by their local dynamics and that protein binding mechanisms are most likely driven by dynamical synergy between the proteins and the bilayer. Based on the energy landscape of membrane proteins, one would expect the synergistic dynamics to not only be important at the longer timescales of microseconds to milliseconds, but also at the much faster picosecond-to-nanosecond timescales. While these are more difficult to experimentally probe, it is becoming increasingly clear that they play a significant role in protein functionality (8), protein-protein binding (9), and enzyme catalysis (10). Indeed, there is growing realization that a number of biological functions, while being directly linked to slow protein dynamics, have their origins in the faster dynamics through solvent interactions (11) or through a dynamical hierarchy in which faster motions control the slower ones (8). However, the full extent of the role of fast dynamics is still poorly understood due to the experimental difficulties in probing this time regime. Interestingly, these timescales coincide with those of collective thermal fluctuations in lipid bilayers (12,13), which starts to suggest that tuning these fluctuations is critical for medical applications requiring selective macromolecule binding. Of particular interest in this context are membrane thickness fluctuations whose dynamics are on the same timescale as conformational transitions in proteins (8) and that have been associated with other membrane functions such as pore formation (14) and passive permeation (15).

Efforts in studying bilayer thickness fluctuations have been hindered by limitations of experimental techniques that can simultaneously access the proper length and timescales. In most cases, the experimental evidence for local membrane fluctuations has been rather indirect (16,17) or inferred from simulations (18,19). More recently, neutron spin-echo (NSE) spectroscopy was effectively used for direct observation of membrane fluctuations in oil-swollen surfactant bilayers (20) and unilamellar lipid vesicles (12). The NSE studies on single-component lipid bilayers with different lipid tail lengths, i.e., DMPC (dimyristoylphosphatidylcholine), DPPC (dipalmitoylphosphatidylcholine), and DSPC (distearoylphosphatidylcholine), revealed some interesting membrane dynamics. Membrane thickness fluctuations were only observable in the fluid phase of the bilayer, implying that such fluctuations are either completely suppressed in the gel phase of the membrane (19) or are slowed down beyond the temporal resolution of the NSE technique. The study also showed almost identical thickness fluctuation patterns (12) in the bilayers, regardless of the length of the lipid molecules used. This invariability in the dynamical behavior relative to lipid tail-length can be attributed to geometrical constraints caused by the minimalistic bilayer composition in this overly simplistic system, which favors uniform bilayer thickness and lateral membrane homogeneity.

However, if the lateral and/or normal symmetry in the membrane is broken, as in biological membranes, one would expect the change in the membrane energetics to drive the system into a more dynamic state. In this study, we investigate the effect of lipid tail-length mismatch in breaking the symmetry and regulating membrane dynamics. We consider as a model system a mixture of length-mismatched DMPC and DSPC molecules characterized by four additional carbon atoms in DSPC tails. The two molecules experience distinct transition temperatures, T_m, at which the tails change from a stiff stretched configuration (gel phase) to a flexible, more coiled configuration (fluid phase). For tail-deuterated (dt) lipids, the transition temperatures are T_m (dtDSPC) = 50.5°C and T_m (dtDMPC) = 20.5°C (12), yielding a broad thermal range of gel-fluid coexistence in DMPC/DSPC mixtures (21,22). Additionally, the two lipid molecules experience dramatic changes in their tail-length mismatch of ≈1 nm in the fluid and gel phases and ≈2 nm in the gel-fluid coexistence phase (12). These remarkable disparities in the transition temperatures and the tail-length mismatch render DMPC/DSPC mixtures an ideal model for these investigations. The broadest gel-fluid coexistence phase (21) is obtained for an equimolar mixture of DMPC and DSPC, which is the focus of this study. Due to neutron scattering sensitivity to deuterium labeling, we employ selective deuteration to probe different bilayer features. For example, thickness fluctuation parameters are best obtained from tail-contrast-matched vesicles of primarily perdeuterated-tail forms of DMPC and DSPC such that the tail region in the bilayer contrast-matches the carrier solvent (D₂O) (see Table S1 in the Supporting Material). This is the main system used in this work unless otherwise noted.

Materials and Methods

Materials

The lipids were purchased from Avanti Polar Lipids (Alabaster, AL) and used without any further purification. The equimolar mixture of DMPC and DSPC was prepared as discussed in Section S1 in the Supporting Material. The lipids were weighed in powder form and dissolved into chloroform for good dissociation, after which the chloroform was evaporated under flow of nitrogen gas. The lipid mixture was then put under vacuum overnight to ensure full evaporation of the chloroform. The dried lipids were then dispersed in D₂O above T = 55°C. Unilamellar vesicles were obtained by extruding the mixture, at T = 60°C, through polycarbonate filters with pore sizes 400, 200, and 100 nm, consecutively. The extruded solutions were kept above T = 55°C until measured.

Methods

Density measurement

To determine the transition temperatures of the mixed lipid bilayers, the solution density was measured using a model No. DMA5000 density meter (Anton Paar, Ashland, VA). Knowing that the lipid molecular density changes dramatically at the gel-fluid transition temperature, temperature-dependent density measurements were conducted over a temperature range from T = 65°C to T = 15°C with a step of 0.2°C.

Small-angle neutron scattering measurement

Small-angle neutron scattering (SANS) experiments were performed at the NG7-30-meter SANS at the National Institute of Standards and Technology (NIST) (23,24). The selected q range was from 0.03 to 5 nm⁻¹ with the use of a 0.6-nm neutron wavelength. The samples used were put in 1-mm-thick quartz cells. The sample temperature was decreased from T = 65°C to T = 15°C using a circulation bath with an accuracy better than 0.5°C. The raw data were processed via an established reduction protocol to obtain absolute scattering intensity in units of cm⁻¹ (25). Data fitting was performed using the software SasView (www.sasview.org).

Small-angle x-ray scattering measurement

Small-angle x-ray scattering (SAXS) measurements were performed at the x27c beam line at Brookhaven National Laboratory (Upton, NY). The accessed q range was 1 to 3.5 nm⁻¹ using a wavelength of 0.137 nm at a sample-to-detector distance of 95.7 cm. The scattered photons were collected by a charge-coupled device camera. The detector distance and q value were calibrated using silver behenate. The samples were measured in a 1-mm-diameter capillary tube taped to a temperature-controlled stage. The measurements were done over a temperature range of 65–25°C with an accuracy of ±1°C. Data reduction, including background subtraction, was performed using the xPOLAR software developed at Precision Works NY, Inc. (East Setauket, NY).

NSE measurement

NSE experiments were performed using the NG5-NSE spectrometer at NIST (26) at neutron wavelengths of 0.6 and 0.8 nm with a wavelength spread of ∼18%. The measured q ranges spanned from 0.4 to 1.8 nm⁻¹ and Fourier times, t, from 0.05 to 40 ns. The tail-contrast-matched sample was measured in a 4-mm-thick cell and the hydrogenated sample in a 1-mm-thick cell. The temperature was varied from T = 65°C to T = 15°C using a circulating bath with an accuracy better than ±0.1°C. The obtained NSE signals were reduced to the intermediate scattering function using the software DAVE (27), which properly accounts for background and resolution corrections.

Results and Discussion

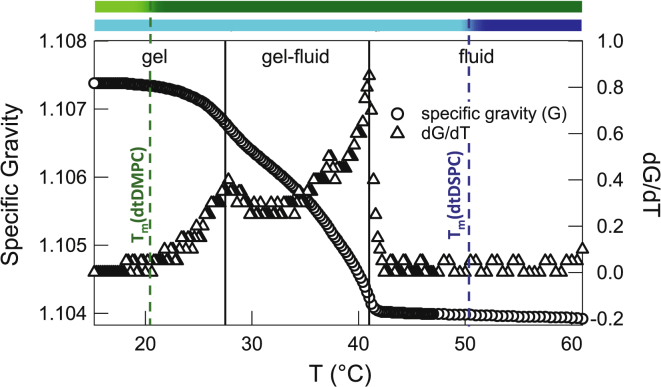
Due to strong coupling between the gel-fluid transition and membrane structure and dynamics (12), a precise determination of the phase boundaries was made. Temperature-controlled density measurements on the equimolar tail-contrast-matched vesicles show an upper and a lower transition temperature, T_u ≈ 41°C and T_l ≈ 27.5°C, as defined from the two maxima in the density gradient (Fig. 1). The analogous fully hydrogenated-lipid sample shows a similar trend with an upward shift of 2.7°C in the transition temperatures, in accord with literature values (see Table S1). In contrast with the sharp transition observed in single-lipid bilayers (12), the density in the binary system shows gradual changes around the phase boundaries. This behavior, along with the shifts in the transition temperatures (phase transition bars in Fig. 1), is attributed to a thermal delay in the collective gel-fluid transition of individual species induced by lateral rearrangements of lipid molecules (22,28).

Figure 1.

Temperature dependence of specific gravity and its gradient for the tail-contrast-matched equimolar DMPC/DSPC mixture. (Solid vertical lines) Upper and lower phase boundaries. (Phase transition bars) Gel (light) or fluid (dark) state of single-component DMPC (upper bar) and DSPC (lower bar) bilayers, as determined from the melting temperatures of the two lipids (dashed lines). To see this figure in color, go online.

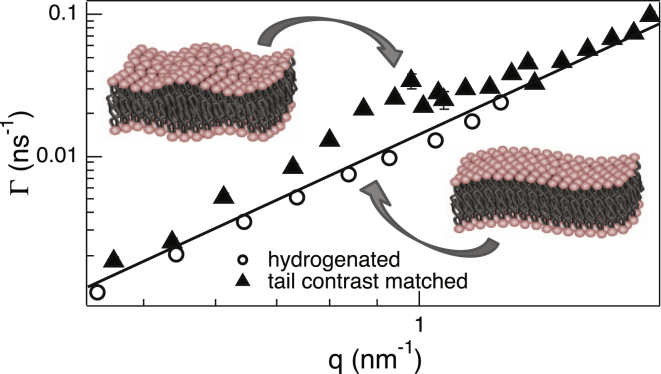
The dynamical response of the bilayer in the different phases of Fig. 1 is measured using neutron spin echo (see Fig. S1 in the Supporting Material). The NSE measurements directly yield the decay rate, Γ, of the dynamics probed at well-defined length scales determined by the wavevector transfer, q. The q-dependence of the decay rate depends on the nature of the membrane dynamics as shown in Fig. S2. If the membrane only experiences bending fluctuations, the decay rates should exhibit a simple q³ dependence, as shown by Zilman and Granek (29). However, the measured decay rates of the tail-contrast-matched bilayers (Fig. 2) show a remarkable deviation from such a q³ behavior at q ≈ 1 nm⁻¹. More precisely, the q values at which the thickness fluctuations are most prominent correspond to the membrane thickness at that temperature, as shown in Fig. S3. Previous reports on similar systems have attributed this enhancement to thickness fluctuations (12) and showed that the dynamics in such systems can be described by a linear combination of bending and thickness fluctuation contributions (12,20) such that

$$\text{Γ}=0.0058\frac{k_{\text{B}}T}{{\eta }_{D_{2}O}}\sqrt{\frac{k_{\text{B}}T}{\kappa }}{q}^3+\frac{{\left({\tau }_{TF}{q}_0^3\right)}^{-1}}{1+{\left(q-q_0\right)}^2{\xi }^2}{q}^3,$$ (1)

where k_BT is the thermal energy, ${\eta }_{{\text{D}}_2\text{O}}$ is the viscosity of D₂O, κ is the bending modulus, τ_TF is the relaxation time of thickness fluctuations, q₀ is the peak position of Γ/q³, and 1/ξ is the half-width at half-maximum of the Lorentz fit function. The first term captures noninteracting membrane bending fluctuations proposed by Zilman and Granek (29) including the refinement by Watson and Brown (30) and Lee et al. (31). The second term is an empirical expression for thickness fluctuations (12,20,32).

Figure 2.

The q dependence of Γ for hydrogenated and tail-contrast-matched samples at T = 65°C. (Solid line) The q³ behavior of bending fluctuations is represented by the first term in Eq. 1. The enhancement in the decay rates of the tail-contrast-matched sample corresponds to membrane thickness fluctuations. Error bars represent ±1 SD in the entire article and are smaller than the symbol size in this figure. To see this figure in color, go online.

For fully hydrogenated bilayers, due to the much lower contrast between the headgroups and the tail region, the enhancement occurs at much higher q values and is outside the q range of the measurement. This is clearly reflected in the simple q³ dependence of the decay rate for the hydrogenated bilayers (Fig. 2), whose dynamics are dominated by membrane bending fluctuations over the accessed q range. Because both hydrogenated and tail-contrast-matched bilayers exhibit the same bending fluctuation behavior, as manifested by the identical q³ component of their decay rates (Fig. 2), the most reliable determination of the bending properties is obtained from the data on the hydrogenated bilayers.

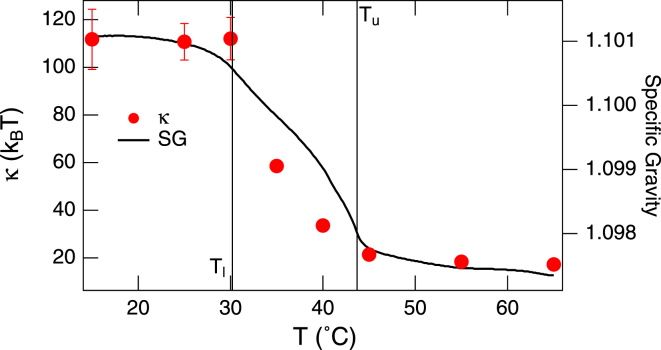
The bending modulus κ, found from the fits of the first term in Eq. 1 to the decay rates, exhibits a gradual change at the transition temperatures as shown in Fig. 3, in contrast with the sharp transition reported in single-component bilayers (12,33). At high T, both binary and single-lipid bilayers have the same asymptotic value of the bending modulus κ ≈ 20 k_BT. More pronounced differences, however, are observed in the gel-fluid coexistence region and at low temperatures. We attribute these discrepancies to the lateral phase separation of the DMPC and DSPC molecules into domains with different stiffness coefficients. For instance, in the gel-fluid coexistence region, the fluid DMPC domains are expected to maintain a certain level of flexibility in the membrane despite the presence of stiff DSPC gel domains. The strong correlation between the bending modulus and the membrane density as shown in Fig. 3 corroborates this conclusion and suggests that the average lateral membrane compressibility (directly related to κ (34,35)) is controlled by the bilayer density.

Figure 3.

Temperature dependence of κ on the hydrogenated DMPC/DSPC vesicles. (Vertical lines) Transition temperatures T_u and T_l; (solid line) measured specific gravity. To see this figure in color, go online.

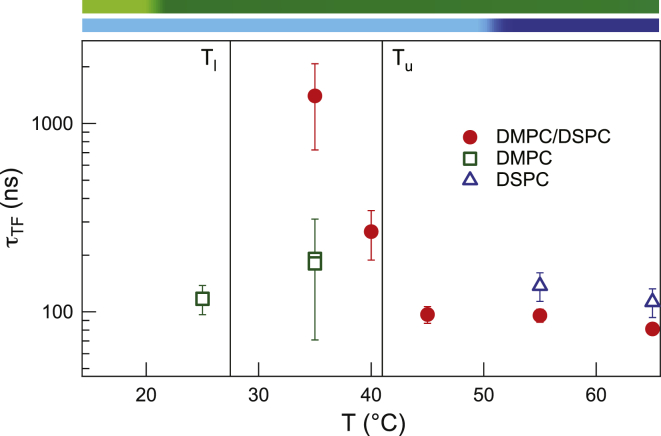
Fits of the second term of Eq. 1 to the decay rates on the tail-contrast-matched vesicles yield the two parameters, τ_TF and ξ, that describe thickness fluctuations. Fig. 4 shows the thermal dependence of the relaxation time, τ_TF, of thickness fluctuations in the binary membranes along with the previously estimated τ_TF values for the DMPC and DSPC bilayers (12). In the fluid phase, i.e., above T = 45°C, τ_TF ≈ 100 ns and is comparable to the relaxation times observed in the single-lipid bilayers (12). In the gel-fluid coexistence region, however, thickness fluctuations experience a remarkable slowdown, in agreement with our previous suggestion (12) that the thickness fluctuations in single-component bilayers may not be totally suppressed below the main transition temperature but are slowed down beyond the temporal resolution of NSE.

Figure 4.

Thermal dependence of the relaxation time of thickness fluctuations in single-component DMPC and DSPC bilayers and the equimolar DMPC/DSPC mixture. (Vertical lines) T_u and T_l; (phase transition bars) are the same as in Fig. 1. To see this figure in color, go online.

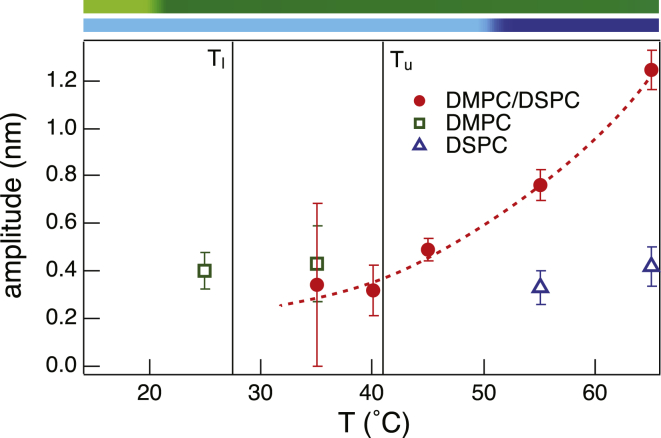
An estimate of the fluctuation amplitude for tail-contrast-matched vesicles can be extracted from ξ using the following expression, d_mξ⁻¹/q₀, as discussed in Nagao et al. (32). Unlike the fluctuations in single-lipid bilayers (12), which lack any temperature dependence above T_m, the equimolar mixture shows strong enhancement of the fluctuation amplitude at high-T (Fig. 5). In fact, at temperatures >>T_u, the thickness fluctuation amplitude in equimolar vesicles is ∼2–3 times that observed in the single-component vesicles (12). We should note that the average radius of the vesicles and the vesicle concentration are almost identical in all the samples studied so far, which rules out membrane curvature and intervesicle interaction as the source of the observed differences.

Figure 5.

Thermal behavior of thickness fluctuation amplitudes for DMPC and DSPC bilayers and their equimolar mixture. (Vertical lines and phase transition bars) Gel and fluid transitions in the mixed and pure systems, respectively, as described in Fig. 1. To see this figure in color, go online.

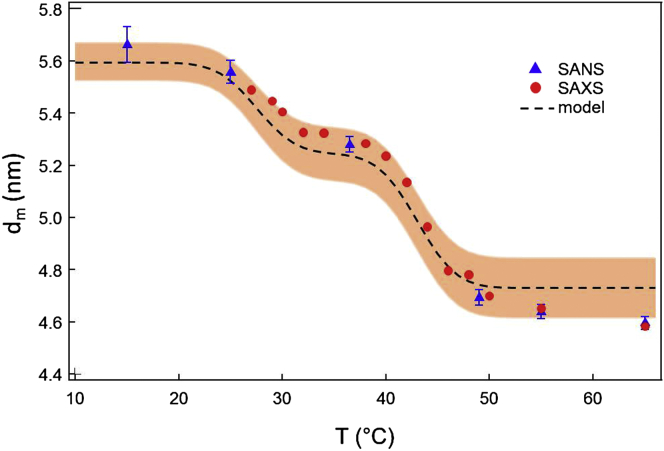
To better understand the thickness fluctuation behavior, we examine the temperature dependence of the membrane thickness. The bilayer thickness, extracted from SANS and SAXS data, fits to a three-shell vesicle model (36) (see Fig. S4), is shown in Fig. 6 over a wide thermal range. In the absence of compression, extension, or interdigitation, conservation of volume arguments require the average membrane thickness to be the mean value of the thicknesses of the pure component bilayers. We model the thickness of DMPC and DSPC bilayers by an error-function (sigmoidal distribution) that is centered at the corresponding transition temperature (as defined from density measurements) and which approaches the thickness of the gel (fluid) membrane below (above) the transition. The values for gel and fluid DMPC and DSPC membrane thickness, obtained from SANS data on single-component vesicles using the same fitting routine, are d_m (DMPC) = (5.0 ± 0.1) nm and d_m (DSPC) = (6.2 ± 0.1) nm in the gel phase and d_m (DMPC) = (4.3 ± 0.1) nm and d_m (DSPC) = (5.1 ± 0.1) nm in the fluid phase, in agreement with previous reports on these systems (37). From these values we then model the thickness of the DMPC/DSPC bilayers as the mean of the two sigmoidal distributions (dashed line in Fig. 6). The SANS/SAXS fit values of the binary membrane thickness nicely follow the three-plateau pattern, which naturally results from the hypotheses of sigmoidal distribution discussed earlier. Thus, in the high temperature region, where both DMPC and DSPC lipids are expected to be fully fluid and relatively well mixed (22,28), both must experience a nonoptimal tail packing geometry. The resulting additional entropic stretching/shrinking motions of the lipid molecules could then manifest in fluctuations normal to the bilayer surface, leading to larger thickness fluctuation amplitudes. More insight into the energetics behind this behavior can be obtained from deformation free energy calculations (38) in which such motions are generally captured by a compression-expansion energy term. Such calculations on this equimolar mixture, in the fluid phase, show an increase in the membrane compressibility compared to the single-component analogs (M. Nagao and R. Ashkar, unpublished). This increase in membrane compressibility would naturally result in an enhancement in the fluctuation amplitude observed here (Fig. 5), in accord with previous findings on similar systems (39).

Figure 6.

Temperature dependence of the thickness of equimolar DMPC/DSPC bilayers as obtained from SANS and SAXS data. (Dashed line) Based on the model described in the text; (shaded area) margin of error. To see this figure in color, go online.

As the temperature decreases toward T_u, the membrane experiences a damping in the thickness fluctuations as manifested by the gradual decrease in the fluctuation amplitude (Fig. 5). It is important to point out that in the thermal region between T_u and T_m (DSPC), DSPC molecules are below their melting transition temperature. In this region, we conjecture the possible existence of small transient DSPC clusters that reduce the area of fluid domains that can support enhanced thickness fluctuations, and may even anchor the surrounding molecules, limiting their extensions or compressions and consequently lowering the average amplitude of the membrane thickness fluctuations. Such clusters have been reported in contrast-matched SANS experiments near the upper gel-fluid transition of the mixture (22) and in Monte Carlo simulations on fluid DMPC/DSPC bilayers (21).

In the gel-fluid coexistence region, the thickness fluctuation amplitude of equimolar DMPC/DSPC membranes becomes comparable to that of the single-component bilayers, which agrees with our previous hypothesis (12) that the thickness fluctuation amplitude is determined by geometrical constraints. Indeed, in this region we expect the two lipids to be mostly segregated into DSPC gel domains and DMPC fluid domains (40,41). From our previous results, we expect only the fluid DMPC domain fluctuations to be measurable and their amplitude to be ≈0.4 nm, which matches the amplitude measured in this coexistence region within the experimental error. On the other hand, we would expect the growth of the DSPC gel domains in this region to force a cutoff on the longer wavelength modes of the thickness fluctuations. Clearly this is not impacting the amplitude within our experimental resolution, suggesting that either the size of the domains are larger than the lateral extent of the fluctuations, or that the amplitude is not affected by the contribution from longer wavelengths. We would also expect a reasonable interfacial region between the domains with significantly altered tail states. If one postulates that the fluctuations are only slowed down and not suppressed in the gel phase (12), this interfacial region, somewhere between the gel and fluid states, could easily lead to the measurable slowdown in thickness fluctuations. In this case, the data suggest the amplitudes remain the same in the gel phase, in agreement once again with the concept of geometric constraints.

To summarize, this work utilizes NSE to access unique collective membrane dynamics in binary lipid bilayers of equimolar DMPC/DSPC mixtures, along with SANS and SAXS studies for complementary structural characterization. The main findings are briefly listed below.

• 1)The phase boundaries of the mixture, determined by density measurements, indicate a shift in the transition temperatures, T_u and T_l, relative to the pure components and show a broad thermal range of gel-fluid coexistence phase, in agreement with previous studies.
• 2)In the high temperature fluid phase (T >> T_u), the system shows a dramatic enhancement in the thickness fluctuation amplitude (while maintaining the same relaxation times as in the single-component analogs).
• 3)As the temperature decreases toward the upper transition temperature, T_u, the thickness fluctuation amplitude decreases to its previously reported value in single component bilayers.
• 4)In the gel-fluid coexistence region (T₁ < T < T_u), a significant increase in the relaxation time of the membrane thickness fluctuations is observed with decreasing temperature.

Conclusions

We demonstrate that the simple addition of a second lipid component to a lipid bilayer system can introduce the tunability requisite for biological function. The membrane heterogeneity, caused by lipid tail-length mismatch in this minimalistic two-component system, allows us to begin probing the molecular and mesoscale origins of membrane dynamics that is so important to real-world function and materials engineering. Indeed, while tail lengths in single-component systems do not have any noticeable effect on thickness fluctuation parameters, an equimolar mixture of length-mismatched lipids is more responsive to thermal variations over a wide range of temperature. Among the rich dynamics in this DMPC/DSPC mixture, the most intriguing is the dramatic amplification of the thickness fluctuation amplitude in the fluid state, which is of significant relevance to critical membrane phenomena such as budding (42) and pore formation (35,43). The decrease of the fluctuation amplitude to previously reported values as the temperature is lowered from T_m (DSPC) to T_u is attributed to transient DSPC clusters that are expected to form below the main transition of DSPC. In this picture, the size of such clusters is anticipated to be on the nanoscale due to the surrounding molten lipids. Such clusters are reminiscent of the raftlike domains observed in simulations on a similar binary system (44). It is important to point out that the domains formed in the coexistence region do not fall under the same description.

The other striking feature in our results is the decoupling in the thermal response of the amplitude and the relaxation time of thickness fluctuations. While the amplitude exhibits a strong temperature dependence in the fluid phase, the relaxation time is almost constant in this temperature range. The pattern is reversed in the gel-fluid phase of the membrane. Such a decoupling would imply the possibility of independent control of the time and space components of thickness fluctuations, which would be extremely valuable in tuning membrane fluctuations, whether for regulating biological function or delivering therapeutic agents.

We hope that this direct and clear evidence of the unique thermal response of thickness fluctuations in binary lipid membranes will encourage more simulations and experiments targeted toward understanding collective dynamics in multicomponent soft membranes with varying degrees of complexity. At the next level of complexity one might ask how the local equilibrium dynamics couple to longer length and timescale dynamics. In fact, in that context, an intriguing question would be what the response of the dynamics on one length scale would be to a rapid perturbation, say from an external stimuli, on the dynamics at the other length scale. One could in fact envisage the creation of a feedback loop that could provide either an avenue to buffering harmful effects or, conversely, could lead to catastrophic consequences. We believe that using these minimalistic systems, coupling simulation to experiment, and using the NSE technique offer an exciting opportunity to begin carefully and systematically probing these important dynamic phenomena that govern the activity of biological membranes.

Author Contributions

R.A. performed SANS and SAXS experiments, analyzed the data, and wrote the article. M.N. designed the research, performed SANS, SAXS, and NSE experiments, analyzed the data, and wrote the article. P.D.B. performed SANS experiments, analyzed the data, and wrote the article. A.C.W. performed NSE experiments and analyzed the data. M.K.S. and T.K. performed SAXS experiments and the data analysis.

Editor: Dr. Francesca Marassi.

Supporting Citations

Reference (45) appears in the Supporting Material.