A Simple Network Architecture Accounts for Diverse Reward Time Responses in Primary Visual Cortex

Abstract

Many actions performed by animals and humans depend on an ability to learn, estimate, and produce temporal intervals of behavioral relevance. Exemplifying such learning of cued expectancies is the observation of reward-timing activity in the primary visual cortex (V1) of rodents, wherein neural responses to visual cues come to predict the time of future reward as behaviorally experienced in the past. These reward-timing responses exhibit significant heterogeneity in at least three qualitatively distinct classes: sustained increase or sustained decrease in firing rate until the time of expected reward, and a class of cells that reach a peak in firing at the expected delay. We elaborate upon our existing model by including inhibitory and excitatory units while imposing simple connectivity rules to demonstrate what role these inhibitory elements and the simple architectures play in sculpting the response dynamics of the network. We find that simply adding inhibition is not sufficient for obtaining the different distinct response classes, and that a broad distribution of inhibitory projections is necessary for obtaining peak-type responses. Furthermore, although changes in connection strength that modulate the effects of inhibition onto excitatory units have a strong impact on the firing rate profile of these peaked responses, the network exhibits robustness in its overall ability to predict the expected time of reward. Finally, we demonstrate how the magnitude of expected reward can be encoded at the expected delay in the network and how peaked responses express this reward expectancy.

SIGNIFICANCE STATEMENT Heterogeneity in single-neuron responses is a common feature of neuronal systems, although sometimes, in theoretical approaches, it is treated as a nuisance and seldom considered as conveying a different aspect of a signal. In this study, we focus on the heterogeneous responses in the primary visual cortex of rodents trained with a predictable delayed reward time. We describe under what conditions this heterogeneity can arise by self-organization, and what information it can convey. This study, while focusing on a specific system, provides insight onto how heterogeneity can arise in general while also shedding light onto mechanisms of reinforcement learning using realistic biological assumptions.

Introduction

Many actions performed by animals and humans depend on an ability to precisely predict and produce temporal intervals. This is particularly relevant when these intervals relate to the time of expected rewards because inaccurately estimating and producing these intervals can decrease the total amount of rewards obtained. If, as assumed in many reinforcement learning approaches, animals are agents trying to maximize these future rewards (Sutton and Barto, 1998; Gershman et al., 2014), then the brain must have evolved strategies to not only associate predictive cues with future behavioral outcomes but also to represent the duration of time between these cues and the delayed reward. These strategies must also account for the fact that behavioral outcomes are often temporally displaced from predictive cues, which might introduce an ambiguity as to which cue or action is predictive of the delayed reward, a problem known as the temporal credit assignment problem (Sutton and Barto, 1998; Dayan and Abbott, 2005; Wörgötter and Porr, 2005). Although the ability to represent temporal intervals is behaviorally evident, the neural mechanisms underpinning this ability to estimate, represent, store, and produce time intervals, which may span different scales from microseconds to hours (Mauk and Buonomano, 2004), is not well understood.

Prominent lines of inquiry have centered on the role played by the basal ganglia and its dopamine innervation in interval timing (Buhusi and Meck, 2005; Merchant et al., 2013), including computational models based on reinforcement learning approaches (Montague et al., 1996; Alexander and Brown, 2011, 2014; Gershman et al., 2014). However, timing on the scale of hundreds to thousands of milliseconds can also be represented in primary sensory areas (Supèr et al., 2001; Moshitch et al., 2006). Furthermore, cued delayed rewards have been observed to modify V1 neuronal responses to image features (Goltstein et al., 2013) and reward timing can be represented in primary visual cortex, both in vivo (Shuler and Bear, 2006; Chubykin et al., 2013; Liu et al., 2015) and in slice (Chubykin et al., 2013). Moreover, recent experimental results indicate that the activity of these neurons may directly inform timing behavior (Namboodiri et al., 2015).

Of relevance here is the observation that training, in which a brief visual stimulation is paired with a reward occurring 1 or 2 s later, modifies the responses of V1 neurons such that many of them represent expected reward time. The responses of these neurons are heterogeneous and can be organized into three qualitatively distinct classes, namely, sustained increase (SI), sustained decrease (SD), and peaked (P) (Shuler and Bear, 2006; Chubykin et al., 2013; Liu et al., 2015) (see Figure 1).

Figure 1.

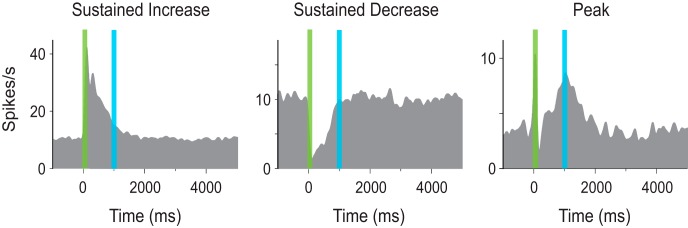
Cue-evoked responses following optogenetic conditioning. Examples of SI (left), SD (middle), and P (right) response forms. The response profiles develop in V1 after pairing a visual cue with a laser pulse 1000 ms later (blue bar) that activated axon terminals projecting from nucleus basalis. Vertical green bars represent cue presentations. Figure adapted from Liu et al. (2015) with permission.

In a previous publication (Gavornik et al., 2009), we presented a model that used reward-modulated synaptic plasticity of lateral excitatory connections to account for the SI responses. Here we build on this approach by showing how the introduction of inhibitory neurons and simple connectivity rules give rise to a diversity of interval-timing response profiles mimicking reward-timing responses observed experimentally. In doing so, we provide a detailed accounting of the important role played by inhibitory elements in shaping these responses. Additionally, the present model exhibits robustness against variations in key parameters, such as the strength of the static synaptic weights, and the presence of noise. We also analyze the emergent network structure and simplify it to obtain intuition into its operation, gaining insight into how the network achieves its robustness and suggesting additional experimental tests of the purported mechanism. Finally, we show that the network can also represent reward magnitude at the expected delay and that the P response might be specialized for this representation.

Materials and Methods

Model.

Previously (Gavornik et al., 2009; Gavornik and Shouval, 2011), we developed a model network consisting of excitatory neurons with recurrent plastic synaptic connections in an effort to understand how, in principle, such a network could learn to associate a cue with a delayed reward, and, in so doing, generate the temporal interval to the expected reward. Such a model was able to capture, nontrivially, the main characteristics of one response type observed experimentally, namely, the SI response. However, that work did not aim at explaining all the diverse forms of reward-timing responses observed experimentally. Moreover, the model lacked a biological realism, in that it did not also include the effects of inhibitory neurons.

The present model builds upon our previous work and addresses specific questions regarding the role played by inhibition in shaping the responses of the excitatory population. Specifically, it addresses questions regarding network architecture, both its structure and strength of synaptic connections, as well as the robustness of the responses to changes in key parameters pertaining to the effects of inhibition. Importantly, it explores how inhibition extends the capabilities of the network itself to not just reporting when to expect a reward but critically, to reporting its expected magnitude as well.

Therefore, our present model includes both representations of excitatory and inhibitory units, which, as before, are described as conductance based integrate-and-fire neurons. This simple model, although not capturing all properties of V1 neurons, does account for key properties.

One such property is the dynamics of the membrane potential, being described by a leak current that, in the absence of synaptic input, will keep the neuron at its resting membrane potential of −60 mV and that has a characteristic membrane time constant of 20 ms. In the presence of synaptic input, changes in the membrane potential are described by the following equations:

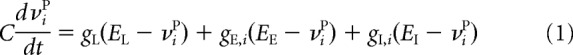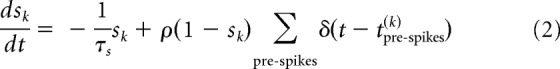where ν_i^P represents the membrane potential of the i-th neuron in population p, which can be either excitatory (E) or inhibitory (I), and where s_k is the synaptic activation of the k-th presynaptic neuron. Other parameters are as follows: membrane capacitance (C); leak, excitatory, and inhibitory conductances (g_L, g_E,i, g_I,i); leak, excitatory, and inhibitory reversal potentials (E_L, E_E, E_I); percentage change of synaptic activation with input spikes (ρ) and time constant for synaptic activation (τ_s), where we have used here as in our previous model (Gavornik et al., 2009) a value of 80 ms for recurrent excitatory NMDA currents. In the present model, we consider only fast inhibitory synapses with a time constant of 10 ms. The δ function in Equation 2 indicates that these changes occur only at the moment of the arrival of a presynaptic spike at t_pre-spikes^(k) from the k-th presynaptic neuron.

The total excitatory and inhibitory conductances are computed from the individual outgoing synaptic activations, s_k, and the synaptic strength, Ω_ik, between the postsynaptic neuron i and the presynaptic neuron k. Thus, for both excitatory and inhibitory currents, we have the following:

where the index k runs over all presynaptic neurons (either from the excitatory or inhibitory populations accordingly) contacting the postsynaptic neuron i, which for g_E,i is either an excitatory or an inhibitory neuron and for g_I,i is an excitatory neuron.

As described in prior experimental observations (Shuler and Bear, 2006; Chubykin et al., 2013; Liu et al., 2015), only one visual stimulus was presented before the delivery of the reward; thus, our simulations mimic this experimental condition. The stimulus was modeled as feedforward excitation delivered by simulated spikes that arrive from the lateral geniculate nucleus as the result of a full-field visual stimulation (compare Gavornik et al., 2009).

In an effort to introduce the least number of assumptions into our model, we consider that the only plastic synapses are those associated with recurrent excitation, which have been implicated in the role of modulating feedforward inputs (Lamme and Roelfsema, 2000). All other synapses are consider static. Thus, in the text, we will differentiate the various connections (Ω_ij^E/I), as L_ij, for those that are plastic, and as W_ij, for those that are static. Plasticity in inhibitory synapses cannot be ruled out (Holmgren and Zilberter, 2001; Haas et al., 2006; Vogels et al., 2011; Wang and Maffei, 2014). Although there is evidence for the role of ACh in depressing inhibitory synapses in the auditory cortex (Froemke et al., 2007), the effects of ACh in synapses involving interneurons in V1 are not as clear as for excitatory synapses (Gulledge et al., 2007; Alitto and Dan, 2013), and thus will not be modeled here.

Changes in the recurrent excitatory synaptic weights occur only at the time of reward, and the changes are computed following the reward-dependent expression (RDE) of synaptic plasticity (Gavornik et al., 2009). Briefly, RDE assumes the existence of synaptic biochemical processes, which we will refer to as “synaptic eligibility traces” (the term “proto-weight” was used in our previous work) that are driven by the coactivation of presynaptic and postsynaptic neurons. These traces are equivalent to the “eligibility traces” used in reinforcement learning algorithms (Sutton and Barto, 1998; Gershman et al., 2014); however, here we emphasize the term synaptic to stress the locality of these traces to the synapse, differentiating other ways in which eligibility traces could manifest in biological systems (Pan et al., 2005). In the absence of neuronal activity, these traces decay with a slow time constant (τ_p). Changes in synaptic weights depend on the activity level of the synaptic eligibility traces at the moment of the reward (for another formulation, see Izhikevich, 2007).

Mathematically, the dynamics of these “synaptic eligibility traces” at the synapse between the presynaptic neuron j and the postsynaptic neuron i, L_ij^p, where p indicates that this is a potentiating trace, are described by the following differential equation:

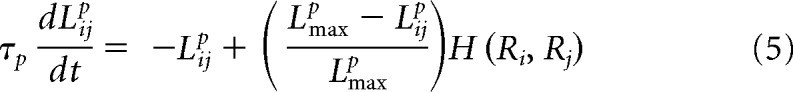where τ_p represents the slow decay time constant (here we use 5000 ms) and L_max^p is a saturating value. This addition limits the maximum value of the synaptic eligibility trace. The last term represents the trace's dependence on neuronal coactivation. In all simulations, we use a rate-based Hebbian expression, which under some conditions is a valid representation of spike-time-based learning rules (Kempter et al., 1999), composed of the presynaptic and postsynaptic firing rates R_j, R_i, respectively. Specifically, we use the function H(R_i, R_j) = R_i (R_j − θ), with θ a firing rate threshold. This threshold is set at a value of 10 Hz and was included to prevent activation of the synaptic eligibility traces by the spontaneous activity of the network, which was ∼5 Hz. The firing rates R_i are window estimates and are computed using the following equation:

where τ_w = 50 ms, and t_i stands for the time of occurrence of a spike.

As described above, in RDE, the rate of change of the synaptic weights (for recurrent excitation) is proportional to the magnitude of the synaptic traces at the time of reward. Mathematically, these changes are expressed by the following equations (one for every pair of presynaptic and postsynaptic neurons):

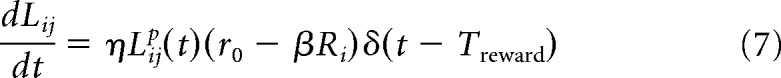where r₀ represents the magnitude of the reward, R_i is the postsynaptic firing rate of neuron i, β is a scaling factor, and η is the learning rate. The effect of neuromodulators in long-term potentiation is not typically addressed in physiological studies, less so in in vivo studies; however, there is evidence of their effect when these are bath applied and timed with the induction protocols (Cassenaer and Laurent, 2012; Chubykin et al., 2013; Yagishita et al., 2014). Regarding the mechanism of the suppression of synaptic plasticity, as in Equation 7, there is little or no evidence to either support or reject the assumption that high cortical activity at the time of reward can suppress changes in synaptic strength.

In all simulations, reward is assumed to be received at a single point in time; thus, the presence of the δ function in Equation 7. In most cases, the magnitude of the reward is considered uniform for all neurons in the excitatory population, although different values can be assigned for different excitatory subpopulations, as described in Learning expected reward magnitude at the expected delay, below.

Although spurious releases of the neuromodulator (i.e., ACh) proposed to convey the rewarding signal can, in principle, occur between the presentation of the stimulus and the delivery of the reward, here we are implicitly assuming that the amount released during reward is significant to activate (Kuczewski et al., 2005) the receptors mediating plasticity (i.e., muscarinic ACh receptors) (Chubykin et al., 2013).

To prevent unbounded increases of synaptic strength, we could have considered saturating synaptic weights L_ij as in Izhikevich (2007); however, this approach will in most cases saturate at the upper allowed value and will fail to convene to the appropriate L_ij and thus will not represent the appropriate temporal delay (compare Fig. 6). In contrast, and drawing from the reinforcement learning literature (Montague et al., 1996; Sutton and Barto, 1998), changes in synaptic weights stop when the “expected reward,” being proportional to the firing rate at the time of reward (βR_i), equals the “actual reward” magnitude (r₀) as in Equation 7. This implies that learning will stop when the firing rate reaches the target value (i.e., R_i^* = r₀/β). The dependence on high firing rates to stop the effects of the rewarding signal might suggest a possible feedback mechanism for inhibiting the rewarding nucleus. However, this hypothesis has not been experimentally verified in the case of the cholinergic system. Together, Equations 5 and 7 define the RDE learning rule.

Figure 6.

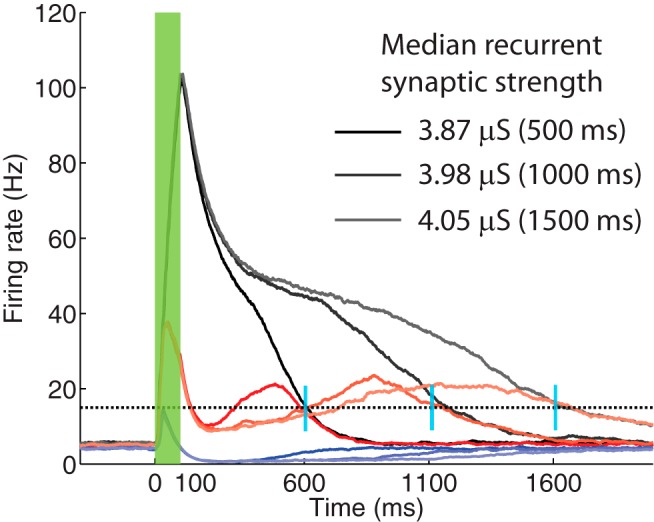
Core neural network trained to report different time intervals. The network of neurons was first trained to report a 500 ms time interval after the stimulus offset. The trial-averaged population firing rates are shown, corresponding to SI (black), SD (blue), and P (red) responses. The network was then trained to report a 1000 ms time interval, using the same cue, and starting from the previously learned synaptic weights. The firing rates corresponding to these new reported times are shown in lighter colors. Finally, the network was trained to learn a 1500 ms time interval, starting also from the network conditions corresponding to 500 ms. These firing rates are plotted in a lighter shade. Black dotted line at 15 Hz indicates the target value. Vertical blue bars represent the actual reward times used to train the network. Green bar represents the duration of the stimulus.

Network architecture.

Regarding network architecture, we use two qualitatively different but related models, which we will refer to as the “nonspecified neural architecture” (NNA) and “core neural architecture” (CNA). Both architectures entail sparse connections with fixed and finite probabilities of contacting a postsynaptic neuron, and in neither of these are recurrent connections included between inhibitory neurons.

In the NNA model, we consider two cases regarding the distribution of projections from the inhibitory units back to the excitatory units: (1) we assign a 50% probability of connecting one inhibitory neuron to an excitatory neuron, which results in a narrow, binomial distribution (narrow distribution); and (2) the number of inhibitory projections each excitatory neuron receives is drawn from a gamma distribution, Γ(k, θ), with shape parameter k = 10 and scale parameter θ = 7.5 (broad distribution).

In the CNA model, the excitatory population is divided into three subpopulations that will represent neurons with specific response types corresponding to SI, SD, and P responses. Cells between these subpopulations are connected in a predefined way, based on the converged network architecture obtained from the NNA model with a broad inhibitory strength distribution achieved after training (see Fig. 4's legend). In this case, the distribution of inhibitory projections to the excitatory population is again chosen to be narrow.

Figure 4.

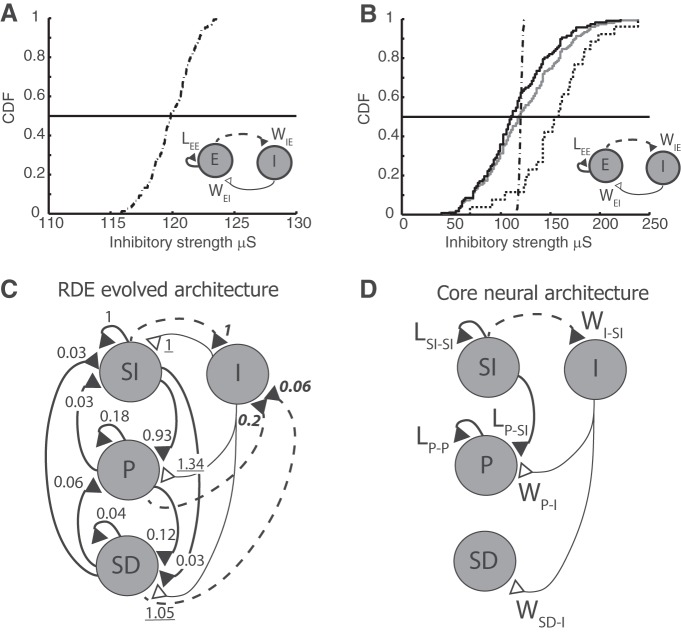
Evolved and core network architectures. A, B, Cumulative distribution function (CDF) of inhibitory projection strengths used in simulations. Insets, Network architecture. A, CDF used in Figure 2. B, CDF used in Figure 3, where the gray trace represents the distribution of all inhibitory projections and the black solid and black dotted traces represent the inhibitory projections that specifically synapse onto SI and P neuronal populations, respectively. The distribution in the latter case is shifted toward higher values with a mean that is ∼30% larger than that of the gray trace. For comparison, the trace shown in A is also plotted in B (dot-dashed); note, however, the change in scale. C, Evolved network architecture after training using the RDE rule, which results in the emergent subpopulations: SI, P, and SD. Numbers indicate relative strength of connection: L_EE connections are normalized to the SI-to-SI strength, W_EI connections to the I-to-SI strength (underlined numbers), and W_IE connections to the SI-to-I strength (bold italic numbers). D, Core neural network architecture that retains the strongest connections between subpopulations.

The CNA model represents a simplification of the NNA model. It contains only the strongest connections between neurons exhibiting the different response types and the inhibitory population, and its justification is done a posteriori. Because of its simplified form, it is mathematically more tractable and will be used to study the properties of the network.

Classification procedure.

After the NNA model has been trained to report a time interval between stimulus and reward (compare Figs. 2 and 3), neurons in the excitatory population are classified according to their response type: SI or SD until expected reward time, or peak firing (P) at expected reward time. The classification uses the trial-averaged firing rate of each neuron. Between the stimulus offset and the arrival of the reward, the trial-averaged firing rate is described by the function f(t). We calculate the time-averaged value of f(t) during the first half of the interval between the stimulus offset and the reward, 〈f(t)〉₁, and during the second half, 〈f(t)〉₂. Neurons are then classified using the following criteria:

1. SI, if 〈f(t)〉₁ > 〈f(t)〉₂ > f_BL or

2. SD, if 〈f(t)〉₂ < f_BL or

3. P, if 〈f(t)〉₁ < 〈f(t)〉₂ and 〈f(t)〉₂ > f_BL

where f_BL is the time-averaged firing rate before the stimulus onset, or equivalently its baseline firing rate. The same criteria were used to segregate the neuronal responses shown in Figures 2 and 3. Neurons corresponding to the SI population will be denoted as SI neurons, and similarly for neurons pertaining to the populations of the other response types.

Figure 2.

Network of excitatory neurons with feedback inhibition trained to report a time interval under a narrow distribution of inhibitory projection strengths. A, Trial-averaged firing rate after training to report a 1000 ms time interval between stimulus (green bar) and reward (blue bar). Black and blue traces represent neurons identified as producing SI and SD responses, respectively. Orange trace represents neurons responding only to the visual cue. Cyan trace represents the firing rate of the inhibitory population. Shaded areas represent the level of variability over trials: upper and lower bounds correspond to ±1 SD from the mean, respectively. For clarity, we have omitted the large variability of the inhibitory neurons. Only SI and SD responses show a clear difference with baseline firing rate. Inset on left, Network architecture (E, Excitatory population; I, inhibitory population). Inset on right, Distribution of the strength of inhibitory projections. B, Raster plot represents an example of the spike times of the activity of the excitatory population (E) in the last trial of training. Neuron responses show little heterogeneity in their response.

Figure 3.

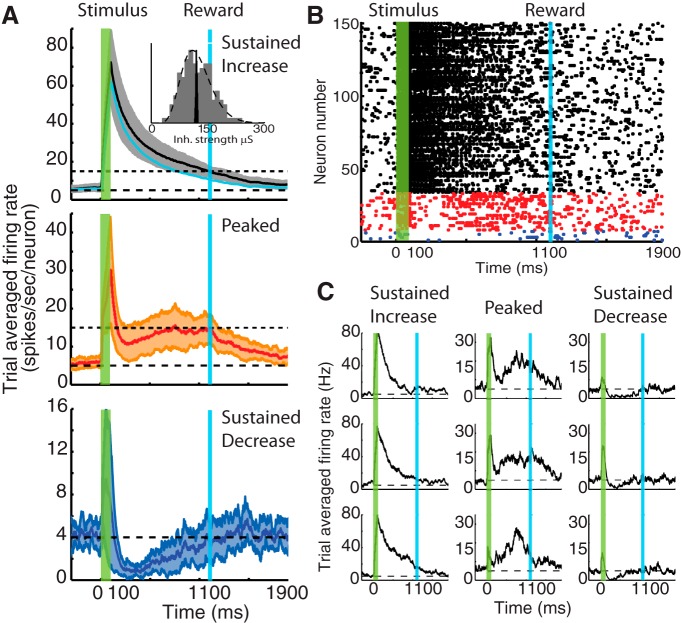
Network trained to report a time interval under a broad distribution of inhibitory projection strengths. Network architecture similar to that in Figure 2A (inset). A, Trial-averaged firing rate of three emerging subgroups of neurons corresponding to SI (black), P (red), and SD (blue) responses. The average firing rate from the inhibitory subpopulation (cyan) is also shown. Inset in top panel, Comparison between the narrow (black histogram) and broad (gray histogram) distributions of inhibitory projection strength. The broad distribution is drawn from a gamma probability density function (dashed line). B, Example raster plot at the end of a trial during training. The responses of the neurons that were identified are color coded as in A and have been rearranged accordingly for clarity. C, Examples of single-neuron trial-averaged responses showing SI, P, and SD profiles.

Results

Previously (Gavornik et al., 2009), we proposed a formal model demonstrating how cued interval timing can arise in a recurrent excitatory network as a consequence of our learning rule (i.e., RDE of synaptic plasticity). The model network consisted of excitatory neurons with recurrent plastic synaptic connections, designed to address how, in principle, such a network could learn to associate a cue with a delayed reward and generate the temporal interval to the expected reward when presented with the predictive cue. The model exhibited only one response type, namely, the SI response, although SD responses could be accounted for, but in a trivial, ad hoc way as explained below.

Here, to move toward greater biological realism, we expand upon this model by adding inhibitory elements and simple connectivity rules. By adding a small number of assumptions, we aim to do the following: (1) replicate the full diversity of reward-timing responses observed experimentally (Fig. 1); (2) derive a minimal or “core” network architecture; and (3) explain how such a network learns to express not just when to expect reward, but how much to expect following a predictive cue. In addition, we provide insight into the critical role played by inhibition in shaping the P responses by perturbing the dynamics of inhibitory neurons.

Together, these computational observations motivate future experimental work probing the capabilities of cortical circuits as well as addressing what particular circuit elements are thought to do.

Learning interval timing in a recurrent network with excitatory and inhibitory neurons

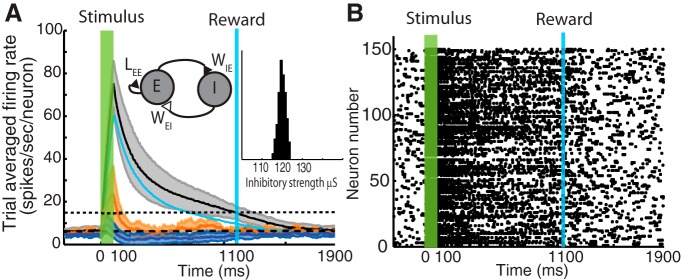
To increase the biological realism of our model, we begin by adding a population of inhibitory units (labeled I) that provide feedback inhibition to an excitatory population (labeled E), both of which consist of 150 units each. The full network was then trained to report an expected time of reward that was delayed by 1000 ms after the stimulus offset. We assume that connections between excitatory and inhibitory neurons are random, with a 50% connection probability. This results in a narrow distribution of inhibitory synaptic strengths converging onto excitatory neurons with a mean of 120 μS and an SD of 1.8 μS. The schematic of the model and the distribution of inhibitory strengths are shown as insets in Figure 2A. The architecture of this model will be referred to as the NNA.

The first question to be addressed was whether the addition of inhibitory elements would break the ability of the network to learn (using RDE) the interval to the expected reward time given a predictive cue. The addition of an inhibitory population did not change the ability of the excitatory neurons to learn to report a time interval, as illustrated by the black trace in Figure 2A representing an SI response. The traces plotted here represent the trial-average firing rate over 30 trials, and the shaded area represents the trial-by-trial variability of the response: upper and lower boundaries correspond to adding and subtracting 1 SD, respectively. The trial-averaged firing rate of the inhibitory population is also shown (cyan), which has a profile similar to that of the SI (we have omitted, for clarity, the corresponding shaded areas illustrating the large variability in the inhibitory response).

As described in Materials and Methods, changes in synaptic strength stop when the firing rate reaches a target value that is proportional to the magnitude of the reward (see Eq. 7). In this simulation, this corresponded to 15 Hz and is indicated in Figure 2A (horizontal dotted line). We assert that training has converged when the trial-average firing rate crosses this target at the time of reward (in individual trials, this firing rate fluctuates about this time), as illustrated by the black trace at 1100 ms.

To assess whether excitatory neurons exhibited a response profile that matched the qualitative features of those observed experimentally, as in Figure 1, we applied the classification procedure described in Materials and Methods to each trial-averaged neuronal response and plotted each result in a different color. Thus, from 150 neurons in the excitatory population, 86% exhibited a SI profile (black trace). Additionally, we observed simultaneously the emergence of a population of neurons with a firing rate that resembles the SD response (blue trace). The mean firing rate of the SD neurons goes below baseline, which is indicated by the horizontal black dashed line at ∼5 Hz. Finally, the orange trace, which corresponds to 5% of the neurons, exhibited activity that is similar to baseline soon after the stimulation period; these neurons did not change their dynamics as a result of training.

Our previous work (Gavornik et al., 2009) was designed to produce SI response types. Other response types, like the SD response, could only be accounted for by ad hoc changes to the original network. Specifically, a separate excitatory population that received feedforward inhibition from the original SI neurons through an added inhibitory population produced the SD response. This additional excitatory population received no excitatory drive other than feedforward background activity. However, these changes to the model did not contribute to explaining the emergence of the SD response, which was obtained only by construction. Here, in contrast, both types of neurons form part of a single population and constitute different responses as a result of the RDE learning rule and the presence of feedback inhibition. Because all excitatory neurons interact through recurrent connections, the emergence of these two responses results from some synapses being weakened and others strengthened in such a way that those neurons responding with a SD profile are those with weaker projections from the SI neurons. For instance, as the firing rate from inhibitory units decays, the SD response returns to baseline. Thus, the present model gives insight into the plausible mechanisms that contribute to diverse responses within a single population of interconnected excitatory neurons.

The addition of feedback inhibition with a narrow distribution of synaptic strengths, although not adversely affecting the ability of a recurrent network to learn cued interval timing (mostly of the SI type), did not, however, contribute to the emergence of the heterogeneous activity seen in Figure 1. This suggests that inhibition alone is not sufficient to account for the observed responses in V1.

Provided an inhibitory connectivity with a broad distribution of strength, all experimentally observed response types develop

In this section, we examine the effect of broadening the distribution of inhibitory connectivity, and determine that it is sufficient to give rise to all three reward-timing response profiles observed experimentally. The distribution of projections connecting inhibitory to excitatory units (described in Materials and Methods) results in a net inhibitory drive with the same mean as before (120 μS) but with a larger SD (40 μS) (Fig. 3A, inset). Such a broad distribution, rather than the narrow one used in the previous section, is consistent with distributions of IPSCs recorded in rat visual cortex (Xue et al., 2014). The network is robust against this change in that it is still capable of learning to report the time interval between stimulus and reward; however, there now emerges a third population of neurons that exhibit a peak-like response as observed experimentally (compare Fig. 1). In Figure 3A, the trial-average firing rate of three populations of neurons is shown, corresponding to SI, P, and SD responses. The firing rate of the inhibitory population is shown in cyan in Figure 3A. We used here the same classification scheme used in Figure 2A. A raster plot of the networks response after training for a single trial is shown in Figure 3B, grouping neurons according to their response type classification and color-coded as in Figure 3A (i.e., black, SI; red, P; and blue, SD). The proportion of excitatory neurons in each response group, in this example, was as follows: SI (78%), P (17%), and SD (7%). When a different, but also broad, distribution of inhibitory projection strengths is used, we obtain similar fractions of neurons in each response group, indicating that this effect depends primarily on the broadness of the distribution (data not shown). We note that, even within each group, there is a wide variety of single-neuron dynamics, as observed experimentally. This can be seen in Figure 3C, in which we plotted for each of the three response types (SI, SD, and P), three trial-averaged single-neuron responses.

These results show that modifying the distribution of synaptic strengths from a narrow to a broad one is sufficient for the emergence of the three response types observed in experimental recordings (Fig. 1). Although the specific fraction of neurons in each subpopulation might be dependent on other details of the distribution of inhibitory projections, quantification of this effect lies outside the scope of the present manuscript, and here we concentrated on establishing plausible conditions that could give rise to such dynamics. It is important to emphasize that the emergence of response types occurs naturally during training and is not the result of a priori knowledge of which neurons will evolve into each of the response types.

A simplified CNA

In the last two sections, we have shown that inhibition contributes to the emergence of heterogeneous responses in a network of excitatory neurons trained to report a time interval between a stimulus and its delayed reward. Moreover, in the last section, we showed that one key characteristic of the inhibitory input in producing the peak response profile is a broad distribution of inhibition strengths acting on the excitatory neurons. Here we investigate the characteristics of the circuit architecture that evolves as a consequence of the RDE learning rule.

Figure 4A, B shows the cumulative distribution of the inhibitory strengths used to obtain the results shown in Figures 2 and 3, respectively. The insets in each panel are meant to indicate that, except for the characteristics of the inhibitory connections, both model architectures are the same, namely, both are of the NNA type. In Figure 4B, the gray trace corresponds to all inhibitory connections, whereas the black solid and dotted traces represent the cumulative distributions of total inhibitory input to excitatory units that exhibited SI and P response types, respectively. As a comparison, the distribution plotted in Figure 4A is replotted here (black dot-dashed trace). However, the scales for the abscissa in Figure 4A, B are different.

The distribution of inhibitory projection strengths onto SI neurons (Figure 4B, black line) is slightly shifted to the left, whereas those of connections onto P neurons are shifted significantly to the right, suggesting that peak responses arise in part from a stronger inhibitory input (median is 34% larger than that onto SI neurons).

The emergence of subpopulations of neurons within the excitatory population after training suggests that the strengths of the recurrent excitatory connections might also become diversified. The network architecture used in the previous sections does not assume any internal subpopulations or impose any distribution of excitatory projection strengths.

During training, the excitatory population rearranges into subpopulations, as shown in Figure 3. This post-training classification suggests a more detailed representation of the final trained architecture as shown in Figure 4C (RDE evolved architecture). Here, the simple recurrent loop of the lateral connection L_EE (Figure 4A,B, insets) (i.e., the synaptic weight of recurrent excitatory connections) has been expanded to show explicitly the interactions between SI, P, and SD populations. Similarly, the connections W_IE and W_EI (i.e., excitatory-to-inhibitory and inhibitory-to-excitatory, respectively) have been expanded to show explicitly the projections between these subpopulations and the inhibitory neurons.

When the magnitudes of the recurrent excitatory connections are compared, we observe a nonuniform distribution of synaptic strengths as the result of the learning rule (thick solid lines). By normalizing the average magnitude of the excitatory connection strengths between populations to that of the recurrent SI-to-SI connection (1), we find that some subpopulations become weakly connected: SI-to-SD (0.03), SD-to-SI (0.03), P-to-SI (0.03), SD-to-SD (0.04), and SD-to-P (0.06). Here we attempt to simplify the network architecture by removing these weak connections, as illustrated in Figure 4D, to derive a simplified network architecture. Although a more rigorous mathematical approach could be applied, this pruning process is justified, a posteriori, based on the ability of the new network to produce the three response types.

A similar comparison can be applied to the excitatory projections from E to I (i.e., dashed lines) and, when the magnitude of these connections is measured relative to the strength of the SI-to-I connections (numbers in bold italics), we find that projections from P and SD neurons to inhibitory neurons are weaker. Hence, we could further simplify the architecture by eliminating these projections as illustrated in Figure 4D. Because the number of projections from the excitatory to the inhibitory neurons is uniform, the relative strengths shown in the trained network (Fig. 4C) reflect the fractional number of excitatory neurons present in each subpopulation. Finally, looking at the strengths of the connections between the I and E populations (i.e., W_EI), we find that the relative strengths to the three subpopulations show less variation (underlined numbers).

As shown previously in Figures 2 and 3, the presence of inhibitory input does not prevent the network from exhibiting the SI response; therefore, we will assume that the I-to-SI connection can be ignored without affecting the overall qualitative characteristics of the various responses, leaving only the remaining two connections. Indeed, the presence of the inhibitory input to the SI neurons only affects the final learned synaptic strengths, although the temporal profile of the SI firing rate can be overall smaller (compare SI response in Figs. 3 and 5). Removing this connection leaves the SI subpopulation with only its recurrent excitatory connections, which is the original architecture used in our previous efforts (Gavornik et al., 2009).

Figure 5.

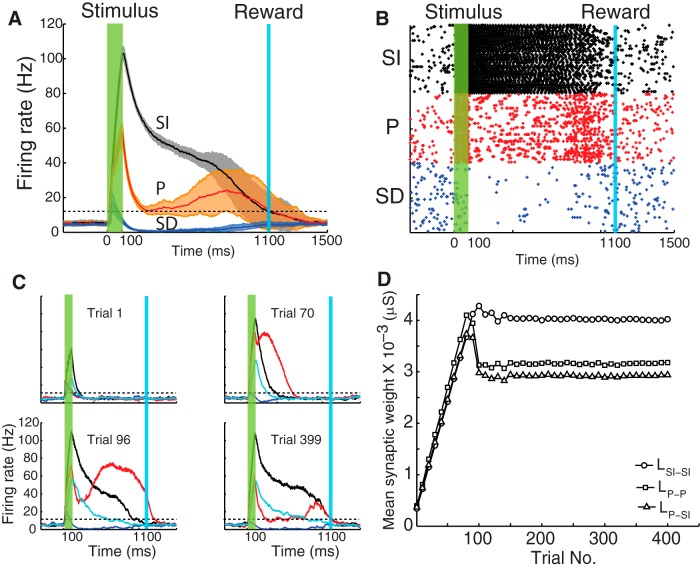
Core neural architecture network exhibits main response types. A, Trial-averaged mean population firing rate after training to report a 1000 ms time interval. Black, red, and blue traces represent the SI, P, and SD populations, respectively. The extension of the shaded areas indicates the variability of responses over trials after training (±1 SD). Horizontal dotted line indicates the target firing rate value for learning cessation (15 Hz for both SI and P populations). The trial-averaged traces cross the target values at the time of reward. B, Example raster plot showing the spontaneous activity of each population and their responses during stimulus and before the arrival of reward, after which all populations return to the basal firing rate. Colors correspond to those shown in A. C, Population firing rate of excitatory and inhibitory neurons during different trails while learning to report a 1000 ms time. Colors identify populations as in A. Cyan trace represents the activity of the inhibitory population. Horizontal dotted lines indicate the firing rate target level. D, Time evolution of the plastic synaptic weights L_SI-SI, L_P-P, and L_P-SI (Fig. 4D) over the training period.

A final simplification can be made by comparing the net excitatory and inhibitory input into each subpopulation. As noted above, the inhibitory input is very similar in magnitude: 1, 1.34, and 1.05; however, the total excitatory drive is highest for the SI and P populations, 1.06 and 1.17, respectively, compared with 0.19 onto the SD neurons. Therefore, the net input on the SD subpopulation is inhibitory; we will thus neglect the P-to-SD connection. The final reduced network architecture is depicted in Figure 4D.

A simplified network architecture can thus be derived from the relative strengths of connections evolved by the RDE learning rule. This simplified circuit will be referred to as the CNA. Figure 5 shows the result of a simulation of neurons using the CNA. In this case, because the populations of neurons with specified response types have been predefined, there is no need for a broad distribution of inhibitory projections and so those projections to the P and SD subpopulations are now chosen from a narrow distribution (i.e., as the one illustrated in Fig. 2A, inset). These results show that the main response types (SI, SD, and P) observed experimentally in rodents can arise from this CNA.

Figure 5A shows the trial-average response, and Figure 5B shows a raster plot during one selected trial. In contrast to the raster plot shown in Figure 3B, there are equal numbers of neurons in each population because now the network architecture has been specified rather than emerging naturally during training.

Figure 5C shows the average population firing rate as a function of time during the course of one trial for four selected trials during the training process. The different traces correspond to the SI (black), P (red), SD (blue), and I (cyan) populations. The horizontal black dashed lines indicate the value of reward (or equivalently, the target firing rate) for the SI and P populations, respectively. When the network is naive (Trial 1), the population activity responds only to the feedforward drive from the stimulus and then decays quickly as the stimulus ends. As the training progresses (Trials 70–399), lateral connections between excitatory neurons (e.g., L_SI-SI) are strengthened, causing the firing rate of SI neurons to extend for a longer duration due to reverberations between reciprocally connected neurons. This process continues over many trials and stabilizes when the firing rate reaches the target value at the time of reward (Trial 399) as in Gavornik et al. (2009). Simultaneously, the inhibitory neurons (cyan) also exhibit a sustained activity due to the feedforward drive from the SI population. Their firing rate returns to baseline earlier than that of the SI population because of the particular value chosen for the parameter W_I-SI (see next section) and the time constant of inhibitory conductances.

While the inhibitory neurons are sufficiently active, they suppress the P neurons, causing them to become silent after the stimulus offset. As the firing rate of these inhibitory neurons decreases, the activity of the P neurons rises due to the excitatory drive from SI neurons (L_P-SI). The height of the peak firing rate of these neurons depends on the strength of their reciprocal connection L_P-P. At Trial 96, the SI population has nearly stabilized, but the population of P neurons is still very active right after the stimulus. By Trial 399, the population activity of the P neurons after the stimulus has been completely silenced. During the intermediate trials, the magnitude of L_P-P is adjusted so that the firing rate of P neurons matches the target firing rate represented by the horizontal black dashed line. Once this target has been reached, no further changes in synaptic strength occur (see Eq. 7).

Finally, Figure 5D shows the evolution over trials of the average synaptic weights L_SI-SI, L_P-P, and L_P-SI. The different traces correspond to the average value of the synaptic weight associated with a particular presynaptic and postsynaptic neuron connected between the SI and P populations. Initially, all synaptic weights increase rapidly. Once the SI population approaches its target value at the reward time (which occurs between Trial 100 and Trial 150), further adjustments to the synaptic weights progress more gradually, slowing to converge to their final values. These results show the interplay between the dynamics of the inhibitory population and the dynamics of the excitatory drive from the SI population that gives rise to the peak response. Similar results are obtained when the network is trained to different target times.

Figure 6 shows a superposition of the trial-averaged population firing rates corresponding to the three response types, SI (black), SD (blue), and P (red), after training for different time intervals. Lighter shades represent longer times. Darker colors represent the results of training to 500 ms. In this set of simulations, the network was first trained to report this time, then training continued to report the 1000 and 1500 ms intervals, using as initial conditions the learned synaptic weights corresponding to the 500 ms interval. As can be observed here, as the expected reward was further delayed, the firing rate profile of the SI population extended in time, which is reflected also in the increase of the strength of the recurrent excitation. The median of the distribution of synaptic strengths corresponding to L_SI-SI went from 3.87 μS (at 500 ms), to 3.98 (at 1000 ms), to 4.05 (at 1500 ms), whereas those corresponding to L_P-P and to L_P-SI were approximately the same for the three times (3.4, 3.4, 3.34 μS, and 3.07, 3.10, 3.06 μS, respectively). This further emphasizes the role played by the SI population in driving the dynamics of the full network, and thus could function as time keepers (see below). The changes in L_SI-SI when the network trains from 500 to 1000 ms are larger than from 1000 to 1500 ms, which is in agreement with the theoretical predictions made previously (Gavornik and Shouval, 2011; their Fig. 5).

In summary, the simplified CNA, which is more amenable to analysis, captures the main features of the trained NNA architecture, reproduces the three response types observed experimentally, and learns to report different time intervals. Therefore, in addition to deepening an understanding of how distinct classes of cellular dynamics are generated, the CNA can be used to (1) investigate network robustness, (2) predict response behavior under selective element perturbation, and (3) propose additional capabilities, such as reporting the expected reward magnitude at the expiry of the delay, as addressed in the following sections.

Robustness against variation in synaptic weights to and from inhibitory neurons

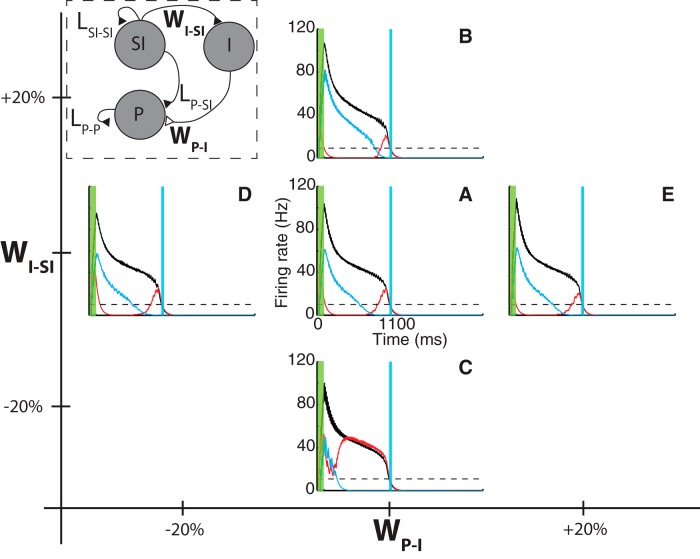
The population of P neurons exhibits its characteristic response (Fig. 5A) after training through changes in the excitatory weights (L_P-SI and L_P-P), which are modified according to the RDE learning rule. The response of the P neurons, however, depends also on the magnitude of the static synaptic weights connecting the excitatory (SI neurons) to the inhibitory population (W_I-SI), and connecting the inhibitory to the excitatory (P neurons) population (W_P-I) (Fig. 7, diagram inset). Here we explore the dependency of the P neurons response on these parameters. For this, we reduce the CNA illustrated in Figure 4D by removing the SD population, as we are interested only in the peak response, and this population does not contribute to its dynamics in this context. Furthermore, we remove the spontaneous activity of the neurons necessary for observing the SD but not the P response.

Figure 7.

Core neural architecture model exhibits robustness against changes in magnitude of static synaptic weights. Model network exhibits qualitatively similar responses for different values of the strength of the projections from excitatory-to-inhibitory (W_I-SI) and from inhibitory-to-excitatory populations (W_P-I) (inset). Results show the converged solution to training for 1000 ms for selected values of these synaptic weights (±20% of standard parameters). Black, red, and cyan traces represent the firing rate of SI, P, and I populations, respectively. A, Response corresponding to reference parameters that lead to SI and P responses. B, C, Results obtained by varying W_I-SI by 20% (B) and −20% (C). D, E, Results obtained by varying W_P-SI by −20% (D) and 20% (E).

The response of the resulting network model shows robustness against variations of these parameters (W_I-SI and W_P-I) as clearly illustrated in Figure 7. Static weights were varied by ±20%, and in each case the network responded in a qualitatively similar way in that it continued to terminate at the expected delay. The parameters used in generating the firing rate traces shown in Figure 7A are the same as those used in generating the results in Figure 5.

Changes in W_I-SI modify the response of the inhibitory population by controlling the strength of the excitatory drive from SI neurons, thus influencing the decay in firing rate for the P population after the end of the stimulus. As the magnitude of W_I-SI decreases in the sequence B-A-C in Figure 7, the firing rate of the inhibitory population decays faster to baseline (cyan trace). In Figure 7C, this effect is more pronounced with the inhibitory population, causing only a small dip in the P population firing rate; however, one can still distinguish a broad peak response. Clearly, Figure 7C lies close to the maximum decrease of W_I-SI that would still produce peak responses.

Changes in W_P-I control the strength of the inhibitory input into the P population. In this case, changes by ±20% do not exhibit significant qualitative changes in the response as the amount of inhibitory strength is already large enough to produce a noticeable reduction in the P neurons firing rate after the stimulus. Significantly larger changes to these parameters still leave the dynamics of the trained network qualitatively unchanged, although the height of the peak firing rate response varies.

It is important to note that, although the neural dynamics are robust to these variations, the final values of the plastic weights (L_ij) in each case are different, showing how, through the RDE rule, the system adjusts and compensates for different values of W_I-SI and W_P-I. These results demonstrate that the RDE learning rule robustly compensates for the changes in the static connections to obtain similar temporal dynamics.

Learning expected reward magnitude at the expected delay

In our previous model (Gavornik et al., 2009; Gavornik and Shouval, 2011), we focused on the basic mechanism that could explain how cued interval timing can arise in a recurrent excitatory network due to the arrival of reward using RDE as the learning rule describing synaptic changes. In that model, reward magnitude was used to reflect the target firing rate that the SI response should achieve at the time of the expected reward (see Eq. 7), such that reaching this target firing rate prevented further changes in synaptic weight. In this sense, this target firing rate was arbitrary, and in that model it was chosen to be close to the baseline firing rate in correspondence to the experimental observations (Figure 1).

However, this approach, which is also used in the present model, poses a potential conflict in the sense that, if different reinforcement signals scale with the reward magnitude, these signals would translate into different firing rate targets at the time of reward, leading to responses that do not predict the reward delay. Here we propose a mechanism to solve the problem of encoding the delay and the magnitude of the expected reward.

In Figure 8A, we illustrate the problem that arises if both SI and P neurons are equally sensitive to the reward magnitude. Black and red traces represent the population firing rate representing SI and P responses, respectively. In these simulations, the magnitude of the reward, as experienced by the SI and P populations, is the same, as reflected by the same target firing rate that is indicated by the black dashed line. The different panels show increasing reward magnitudes from an equivalent target value of 10 Hz (small reward) to 40 Hz (medium reward) to 50 Hz (large reward).

Figure 8.

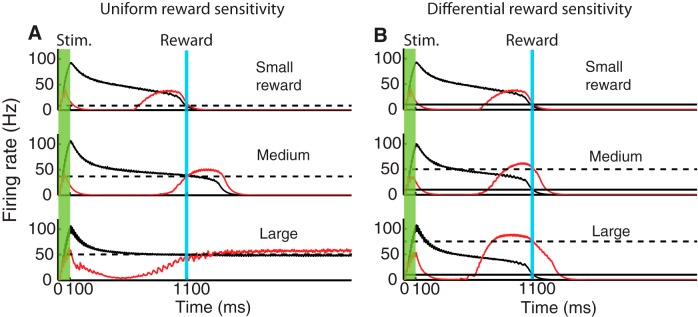
Encoding and reporting expected reward magnitude by differential reward sensitivity of SI and P populations. All traces correspond to population firing rates obtained from the network architecture shown in Figure 7 (inset). Black represents response of SI population. Red represents response of P population. The activity of the inhibitory population has been omitted for clarity. A, The sensitivity to the magnitude of the reward is uniform for neurons in the SI and P populations. As the magnitude of the reward is increased from an equivalent target firing rate of 10 Hz (small reward) to 40 Hz (medium reward) and to 50 Hz (large reward), the SI response becomes bistable and cannot follow these changes. B, If there is a differential reward sensitivity, with SI neurons responding to a fixed equivalent target rate of 10 Hz, and P neurons to increases in reward magnitude, from 10 Hz (small reward) to 50 Hz (medium reward) and 70 Hz (large reward), then these neurons are capable of encoding differences in expected reward magnitude. In this case, the magnitude of the firing rate for the P population can surpass the limit of 50 Hz observed in A (black dashed line).

As the magnitude of the reward increases, the network's response adjusts to match the new target values; however, in doing so, the SI neurons return to baseline several hundreds of milliseconds past the time of reward (see medium reward), whereas the P neurons increase their peak response to match this new target value. For a small reward, the P neuron firing rate crosses the target value after the maximum has been reached; however, as the magnitude of the reward increases, they cross the target level before they reach the peak. This occurs because the firing rate of the inhibitory population also decays later due to the feedforward drive from SI neurons, delaying the rise in the response of the P population.

When the size of the reward is further increased (large reward), this overshooting continues until the network response transitions into a new stable regimen that is characterized by a continuous firing rate with no return to baseline. P neurons, which are driven by the SI population, exhibit also a steady firing rate. The response of the SI population is consistent with the analysis shown previously (Gavornik and Shouval, 2011) in which the SI population can operate in a bistable mode, where one of the stable solutions corresponds to a steady, non-zero, firing rate. In this sequence of simulations, it becomes clear that the network loses its ability to represent the delayed reward.

In contrast to this situation, in Figure 8B we show results of simulations where SI and P neurons have different sensitivity to the reward magnitude. Here we assume that the SI population is insensitive to changes in reward magnitude and its target firing rate to be fixed at 10 Hz (which is indicated by the horizontal black line), whereas the P population is sensitive to changes in reward magnitude, reflected in the different target firing rate values from 10 (small reward), to 50 (medium), to 70 Hz (large). In this case, the response of the P population is able to track the increases in reward magnitude beyond the value of 50 Hz observed in Figure 8A, where the bifurcation occurred, whereas the SI responses remained unchanged.

These results suggest that, if SI and P neurons show this differential sensitivity to the magnitude of the reward, then these two populations of neurons might work together to signal not only the delayed reward but also convey information about its magnitude and the expiry of the expected delay. It is unclear at the moment which biophysical mechanisms could be involved in differentiating between these two populations of neurons.

Effects of perturbing inhibition

A central theme in this paper is the role played by inhibition in the emergence of heterogeneous neuronal responses in a network trained to represent reward timing using reinforcement learning. Although increases in GABA concentration in the visual cortex can have an influence in the perceived duration of subsecond intervals, as observed in humans (Terhune et al., 2014), it is altogether unclear how inhibition might influence not only the reported time, but the value of the reward. Specifically, there is no experimental evidence of how changes in inhibitory activity might modify the diverse types of single-neuron responses observed (i.e., SI, P, and SD).

Here we explore the consequences of perturbing inhibition, in a trained network, after the presentation of the cue. The purpose is to assess the key role played by inhibition in the emergence of the peak response. However, an overall decrease in inhibition, as could be achieved by a bath application of a neuromodulator, might not be a suitable manipulation of the network in this case. The main reason is that the strength of the recurrent excitation, obtained during training, also reflects the amount of inhibitory strength acting on the excitatory neurons; thus, reducing inhibition globally without further training will lead to an epileptic state in which neurons exhibit a sustained and permanent activity without returning to baseline, similar to that shown in Figure 8A for large reward (for a discussion, see also Gavornik et al., 2009; Gavornik and Shouval, 2011). To avoid this, we simulated a more subtle manipulation of silencing only 20% of the inhibitory neurons. This was achieved by clamping their membrane potential to a fixed voltage of −80 mV during a 300 ms interval. In these simulations, we first hold constant the converged values of the synaptic strengths, that is, we make the learning rate equal to zero (η = 0 in Eq. 7), to prevent further synaptic changes. The results are presented in Figure 9.

Figure 9.

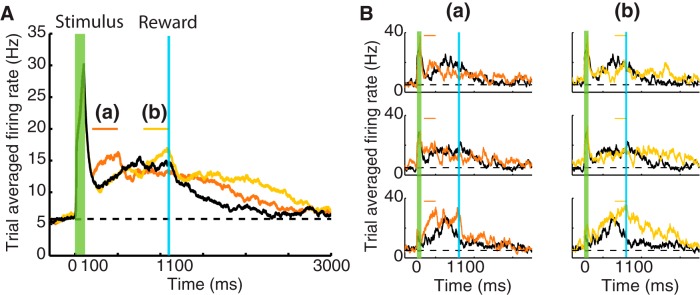
Perturbations of the inhibitory population modify P responses in a trained network. A, Results correspond to simulations showing the P response (black) after the network has been trained to report a 1000 ms time interval for the network model in Figure 3. Orange and yellow traces represent the changes in P response after inactivating 20% of the inhibitory neurons during a 300 ms interval: (a), 100 ms after the stimulus offset; (b), during the last 300 ms before the arrival of the reward. In these simulations, the network is prevented from learning (i.e., η = 0 in Eq. 7). B, Changes in individual responses of P neurons in A. Panels represent the response of individual neurons in the P population after silencing the inhibitory neurons either after the stimulus offset (a) or before the arrival of the reward (b) (compare Fig. 3C).

In Figure 9A, the black trace represents the P response of the network shown in Figure 3 after training to represent a 1000 ms timing reward. The orange trace shows the changes in the P response after silencing the inhibitory neurons 100 ms after the stimulus offset (see orange line on top). This perturbation of inhibition causes an immediate increase in the firing rate of the P neurons eliminating the initial dip in activity observed after the stimulus offset, clearly demonstrating that the P response is in part due to the effect of a stronger inhibition. The increase in activity is a consequence of breaking the balance between the continuous excitatory drive from other excitatory units and the reduction of the effectiveness of inhibition.

Another consequence of this perturbation is a broadening of the P response. After the perturbation interval is over, the firing rate does not immediately follow the course observed in the control case (black trace), but the activity returns to baseline later. This broadening arises because SI neurons overshoot the target time (data not shown) since they also receive now less inhibition than during the control case, resulting in driving the P population beyond the expected reward time. As a consequence of this overshooting, the network loses its predictive power to report the learned interval time between stimulus and reward (compare Fig. 8, medium reward, although the mechanism here is different).

The effect of applying the perturbation of inhibition 700 ms after the stimulus offset (yellow bar) is represented by Figure 9A (yellow trace). This delay in the application of the perturbation has no effect on the initial dip in activity seen before but still causes an increase of firing rate which, as before, leads to an overshooting and broadening of the P response.

Figure 9B shows examples of the firing rate of individual neurons from the trained network (black) and compares them with their responses after the described perturbation; columns (a) and (b) show the cases of an early (orange) and late (yellow) silencing of the inhibitory neurons, respectively. The neurons selected as examples are the same as those presented in Figure 3C, the heterogeneous response of these neurons in each case. The effect of the perturbation in these neurons is notably different; however, one can clearly observe the initial increase in firing rate in the early perturbations (a) and a significant broadening for the later perturbation (b).

The above results indicate at least two direct effects of a reduction in inhibition: (1) the network will be unable to accurately predict the timing of reward interval for which it was trained; specifically, it will report a longer delay; and (2) if the P response conveys information about magnitude of reward (as discussed in the previous section), then it will report either a smaller magnitude if the perturbation occurs early (orange trace) or a higher one if it occurs later (yellow trace). Therefore, if the timing encoded by this network (i.e., V1) informs downstream centers controlling behavior, as recently suggested in rats (Namboodiri et al., 2015), perturbation of the inhibitory signal, which might be implemented using optogenetic methods to target inhibitory interneurons, will cause a delayed action and a reevaluation of the expected reward.

Discussion

The ability to forecast the occurrence of an expected reward based on prior predictive cues is important to the survival of animals and humans. For this, the brain evolved strategies at the network and synapse level to represent the duration of temporal intervals. A large effort been placed in the medial prefrontal cortex (mPFC) for its role, among others, in control of action timing (Narayanan and Laubach, 2006, 2009; Singh and Eliasmith, 2006; Bekolay et al., 2014) and during two-stimulus-interval discrimination tasks (Machens et al., 2010), and in general theoretical models inspired in reinforcement learning theories to account for its outcome predicting capabilities (Alexander and Brown, 2011, 2014). However, temporal representations are also expressed in primary sensory cortices (Supèr et al., 2001; Moshitch et al., 2006); specifically, neurons from the primary visual cortex (V1) in rodents can become predictive of the expected time of a reward (Shuler and Bear, 2006; Chubykin et al., 2013; Liu et al., 2015).

Previously, we presented a theoretical framework of how the SI response could arise from potentiating synapses of lateral connections (Gavornik et al., 2009; Gavornik and Shouval, 2011), via an RDE of synaptic plasticity. Our model, in contrast to much of the timing literature, is closely related to physiology; however, it is not a detailed biophysical model, and some of its components may not have complete experimental support. As in most working memory models (Wang, 1999; Wang et al., 2013), we use relatively long excitatory time constants associated with NMDAR type currents. Although this assumption makes our model more robust, it is not fully experimentally justified. Specifically, the time constant of the synaptic conductances modified by the reinforcement signal in our experimental system is currently unknown.

Our approach contains elements similar to those used in reinforcement learning models. For instance, changes in synaptic strength are proportional to the magnitude of the synaptic eligibility trace and the prediction error term (r₀ − βR_i in Eq. 7). This term compares the expected reward (here equated to the network's activity, R_i) with the actual reward (r₀) at the reward time. However, it differs from temporal difference (TD) models like those implemented, for example, for mPFC (e.g., Alexander and Brown, 2014), where it is very difficult to formulate how different variables are mapped onto a physiological process. Moreover, in these models, a temporal representation is assumed and not learned. Typically, a unique state vector is postulated at each time step (Montague et al., 1996), but its meaning is less clear for a neural system. Indeed, much work has been done to make TD more biologically plausible. In the work surveyed by Gershman et al. (2014), it is assumed that a whole set of temporal basis functions exists in the brain, presumably residing in the striatum. In contrast, in our formulation, there are no assumptions of preexisting basis functions; instead, the network learns the temporal representations.

In our system, the main neuromodulator conveying the rewarding signal is not dopamine but ACh (Wilson and Rolls, 1990; Santos-Benitez et al., 1995; Chubykin et al., 2013). Although a TD model could in principle be implemented using ACh, as noted above, it alone cannot account for the emergence of the types of cortical dynamics explored here, unless two conditions are met as follows: (1) the cholinergic signal represents a reward prediction error; and (2) there exist temporal basis functions arising from other cortical areas that are used to learn these dynamics. However, because these dynamics can also be learned in slice, the option of external basis functions is ruled out. Furthermore, these temporal representations can be learned when the cholinergic signal is activated externally, conveying reward and not prediction error information. Thus, at least in V1, it seems that the TD approach is inconsistent with existing experimental data, and a direct comparison between our present approach and those models is difficult and in general inappropriate.

Recordings in mPFC in rodents show that neurons have a differential response during a trial based on whether the previous one was rewarded or not (Narayanan and Laubach, 2006, 2009; Bekolay et al., 2014), suggesting that this information is encoded in their activity and serves to make corrections from previous errors. In the experiments modeled here, animals were trained to report the expected time of reward by rewarding only 50% of the trials. Clearly, the reported activity of V1 neurons in probe trials showed the same distinct time representation of the cue-reward interval, suggesting that synaptic weights did not vary in unrewarded trials. In our model, changes in synaptic weight would be in the direction to correct any overshooting or undershooting of the target time, thus adjusting for errors (data not shown).

A central finding of this paper is that the addition of feedback inhibition, by itself, is insufficient to produce the variety of responses observed in the experiments. However, allowing a broad distribution of inhibitory projection strengths, some being stronger than the rest, the resulting network is then sufficient to produce heterogeneous responses as demonstrated in Figure 3, mimicking the SI, SD, and P responses observed experimentally. The presence of P responses seemed to require a stronger inhibitory influence, which these broad distributions provide. This was demonstrated by silencing 20% of inhibitory units early after the stimulus offset, which reduced significantly the initial dip in firing rate seen in the control case, demonstrating the role of the strong inhibitory input. Such manipulations could be further explored experimentally using optogenetic methods and silence interneurons at specific times and observe the effects on P responses.

The CNA, derived from the evolved network when combined with the RDE learning rule, reproduces the three response types. From it, we extract that SI neurons act as drivers of the rest of the dynamics such that increases in the strength of the recurrent excitation leads to longer reported times. The CNA shows robustness against variations (±20%) in W_I-SI and W_P-I that control the strength of the inhibitory drive to the excitatory P neurons, illustrating also that the RDE learning rule is flexible. Although not explored here, variations in the strength of connection between the inhibitory to SI population (i.e., W_SI-I) could impose new boundaries to this parameter study. For instance, an increase in W_SI-I would produce a lower overall SI firing rate, which in turn will be less effective in recruiting inhibitory neurons, thus making the emergence of a peak response more difficult, without further changes in either W_I-SI and W_P-I.

The correlation between the strength of the recurrent excitation in SI neurons and the reported time suggests that this population could be encoding only timing information, regardless of reward magnitude. However, if SI and P neuronal populations have different sensitivities to the reward magnitude (e.g., from variations in the dynamic range for sensing the presence of neuromodulator), then they could convey different aspects of the reward expectancy: expected reward delay and magnitude. As illustrated here, if SI neurons are insensitive and if P neurons are sensitive to the amount of reward received, then these populations can separately provide for the timing and the amount of reward expected. The differential sensitivity to the reward magnitude might hint to a possible role for each response type (i.e., the network uses different populations of neurons to keep track of “when” and “how much” reward is to be received). This would be in contrast to the results obtained by Machens et al. (2010) where the time information contained in the stimulus discrimination data recorded from mPFC is better explained by considering this to come from external sources and is not computed by the network. In our model, on the other hand, the same network would provide both the “when” and the “how much” through the different neuronal responses. Perhaps the timing signal provided to the mPFC arises from mechanisms similar to those presented here.

In conclusion, we have shown how an elementary network architecture of excitatory and inhibitory neurons with a broad distribution of inhibitory strengths, combined with the RDE learning rule, can give rise to a spontaneous breakup of the neuronal activity into the main response types observed in rodent V1 neurons trained to report the expected time of reward. The model exhibits robustness against variations in static synaptic strengths and noise and thus shows flexibility in learning to report time. Additionally, we propose that different neuronal responses could also convey information on the magnitude of the rewarding signal and that differential sensitivity to reward magnitude might play a role. Finally, we suggest that a reduction of inhibition could lead to an overestimation of the reported time and thus could lead to change in actions taken by the animal downstream (Namboodiri et al., 2015). Together, these observations advance an understanding of how simple connectivity and plasticity rules can sculpt a network so that the network comes to report expected reward magnitudes at their expected delays.