Neural circuit basis of visuo-spatial working memory precision: a computational and behavioral study

Abstract

The amount of information that can be retained in working memory (WM) is limited. Limitations of WM capacity have been the subject of intense research, especially in trying to specify algorithmic models for WM. Comparatively, neural circuit perspectives have barely been used to test WM limitations in behavioral experiments. Here we used a neuronal microcircuit model for visuo-spatial WM (vsWM) to investigate memory of several items. The model assumes that there is a topographic organization of the circuit responsible for spatial memory retention. This assumption leads to specific predictions, which we tested in behavioral experiments. According to the model, nearby locations should be recalled with a bias, as if the two memory traces showed attraction or repulsion during the delay period depending on distance. Another prediction is that the previously reported loss of memory precision for an increasing number of memory items (memory load) should vanish when the distances between items are controlled for. Both predictions were confirmed experimentally. Taken together, our findings provide support for a topographic neural circuit organization of vsWM, they suggest that interference between similar memories underlies some WM limitations, and they put forward a circuit-based explanation that reconciles previous conflicting results on the dependence of WM precision with load.

working memory (WM) refers to the ability to actively retain stimulus information over a short period of time, and it is thought to be a core component of cognitive functions (Baddeley 1986; Conway et al. 2003). A hallmark of WM is that the information retained is limited. Currently, a significant effort is being devoted to characterizing the nature of WM capacity limitations, but their bases remain controversial (Luck and Vogel 2013; Ma et al. 2014). Important points of discordance have been whether or not the number of items in WM can be increased at a cost in precision (Bays and Husain 2008; Zhang and Luck 2008) and whether the similarity of the items to memorize improves (Johnson et al. 2009; Lin and Luck 2009) or degrades (Elmore et al. 2011) WM performance.

Recently, a neuronal circuit perspective is entering these debates: Electrophysiological experiments have started to investigate the neural basis of multiple-item WM (Buschman et al. 2011; Lara and Wallis 2014; Warden and Miller 2007), and neural circuit modeling has been used to link cellular and network mechanisms with behavior to understand WM capacity limitations (Bays 2014; Edin et al. 2009; Macoveanu et al. 2006, 2007; Papadimitriou et al. 2015; Wei et al. 2012; Wimmer et al. 2014). Most of these models are variations of a model (Compte et al. 2000) developed to be consistent with neurophysiological data from behaving monkeys (Funahashi et al. 1989). They rely on the assumption that there is a topographic structure in the circuits supporting visuo-spatial WM (vsWM), which implements a continuous attractor mechanism responsible for the retention of spatial memory. Some evidence from fMRI (Kastner et al. 2007; Schluppeck et al. 2006) and electrophysiology (Constantinidis et al. 2001; Inoue and Funahashi 2002) studies supports a coarse degree of spatial WM maps in parietal and prefrontal cortex. Recently, neural evidence for attractor dynamics on a fine vsWM spatial map in prefrontal cortex has also been found (Wimmer et al. 2014). However, additional implications of such a spatial memory map for the relation between vsWM precision, capacity, and stimulus similarity remain untested. We aimed here to advance our understanding of the neuronal underpinnings of vsWM by explicitly testing the assumption of a topographic structure of the vsWM buffer. One implication of this structure is that the efficiency with which different items are memorized should depend on their relative locations, since stronger interference of memory traces would be expected for nearby items. Using simulations, we predicted an attractive bias when remembering locations of two nearby items, for very short interitem distances. This prediction was validated in behavioral experiments in humans. We then sought to address how these interferences affected the relationship between memory load and precision. In our model, the effect of load on memory precision was largely accounted for by changes in interitem distance with load. Behavioral data confirmed this prediction. We finally tested in an additional experiment whether behavioral data were better explained by memory attraction than by memory swapping (Bays et al. 2009), and we also confirmed that intermediate distances between memorized items were characterized by a repulsive memory bias. The importance of our work is threefold. First, we provide new experimental evidence concerning interference in vsWM. Second, we test a critical assumption of an important class of models of vsWM. Third, we put forward a plausible explanation reconciling previous results concerning the dependence of memory precision on load and concerning similarity effects on performance.

MATERIALS AND METHODS

Model

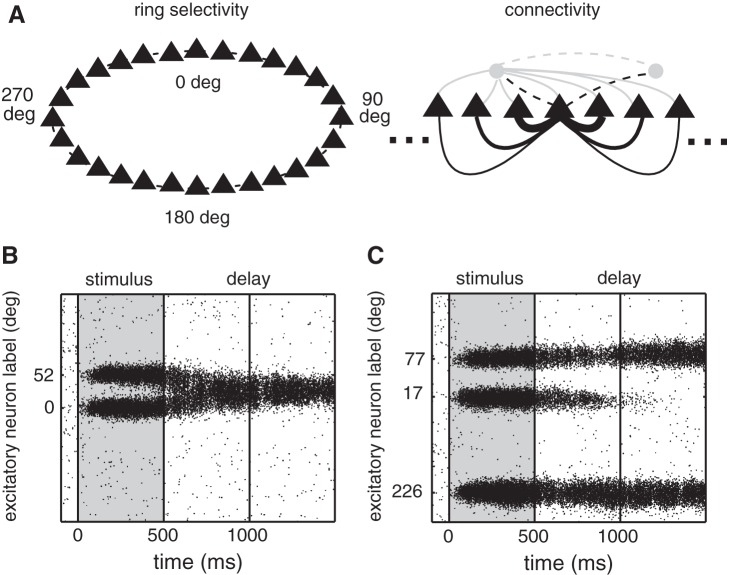
We used a previously proposed computational model (Compte et al. 2000; Edin et al. 2009) to study the precision of vsWM of multiple items. The model (Compte et al. 2000) was originally developed to account for a candidate neuronal mechanism for vsWM, namely, the selective sustained elevated neuronal firing of the prefrontal cortical neurons of monkeys performing a vsWM task (Funahashi et al. 1989). The model consists of a network of interconnected excitatory and inhibitory spiking neurons. The neurons encode the spatial location of fixed-eccentricity visual stimuli in angle θ. That is, they encode positions (in angle) on a circle. Presentation of a stimulus at location θ is simulated by increasing the external input to the corresponding excitatory neurons. The selective response of the neurons in the network is maintained because of the structured connectivity of the network. Excitatory neurons encoding for nearby angles have stronger than average connections, which is essential for a selective group of neurons to sustain elevated spiking after stimulus cessation (Compte et al. 2000).

The parameter values used were as in the intraparietal sulcus (IPS) circuit described in Edin et al. (2009), for a network capacity of two items. The model had 1,024 excitatory and 256 inhibitory leaky integrate-and-fire neurons (Tuckwell 1988). The neuronal selectivity was imposed by external inputs, assumed to originate in upstream areas of the dorsal pathway. Specifically, the presence of a visual stimulus at an angle θ_stim was modeled by increasing the external input to excitatory neurons with preferred direction around θ_stim. The strength of the external input to a neuron encoding θ decayed with the distance to θ_stim according to I_stim(θ,θ_stim) = αexp(μ[cos(2π/360(θ − θ_stim)) − 1]), where α = 0.025 nA and μ = 39.

The integrate-and-fire neuron model describes how the membrane voltage V_m integrates incoming inputs until a certain threshold value V_th is reached and an action potential or spike is fired. After reaching the threshold, V_m is reset to V_res for a refractory time period τ_ref before continuing to integrate inputs. The equation describing the subthreshold changes in V_m is

$$C_{\text{m}}\frac{\text{d}{V}_{\text{m}}}{\text{d}t}=-g_{\text{L}}\left(V_{\text{m}}-E_{\text{L}}\right)-I_{\text{syn}}-I_{\text{ext}}$$

Each cell is then characterized by the total membrane capacitance C_m, the total leak conductance g_L, and the leak reversal potential E_L and by V_th, V_res, and τ_ref. For excitatory neurons the values used were C_m = 0.5 nF, g_L = 25 nS, E_L = −70 mV, V_th = −50 mV, V_res = −60 mV, τ_ref = 2 ms and for inhibitory neurons C_m = 0.2 nF, g_L = 20 nS, E_L = −70 mV, V_th = −50 mV, V_res = −60 mV, τ_ref = 1 ms.

The network of neurons was organized according to a ring structure: Excitatory and inhibitory neurons were spatially distributed on a ring so that nearby neurons encoded nearby spatial locations. An illustration of this structure is shown in Fig. 1A. Connections between neurons were spatially tuned so that nearby neurons with similar preferred directions had stronger than average connections, while distant neurons had weaker connections. The distance-dependent connection strength g_syn,ij between cells i and j was described by g_syn,ij = W(θ_i − θ_j)G_syn, where

$$W\left({\theta }_i-{\theta }_j\right)=J^{-}+\left(J^{+}-J^{-}\right)e^{-{({\theta }_i-{\theta }_j)}^2/{2\sigma }^2}$$

Fig. 1.

The biophysical network model. A: schematic representation of the ring structure of the network model (left) and of the connectivity structure (right) between excitatory (black triangles) and inhibitory neurons (gray circles). Neurons encoding similar angles were strongly connected as illustrated by the width of the lines connecting cells. Connections onto excitatory neurons are indicated with a solid line and connections onto interneurons with a dashed line; excitatory connections are indicated in black and inhibitory connections in gray. B: example activity of excitatory neurons in the network, when items were located in the vicinity of each other, leading to attraction of the memory traces. C: example activity of excitatory neurons in the network in a trial with 3 presented items, illustrating the loss of a memory trace during the delay period.

and J⁻ was set to satisfy a normalization condition (see Compte et al. 2000). The parameters used were σ_E→E = 9.4°, σ_E→I = σ_I→E = 32.4°, J_E→E⁺ = 5.7, J_E→I⁺ = J_I→E⁺ = 1.4, and J_I→I⁺ = 1.5. Thus the connectivity between excitatory and inhibitory neurons was wider and flatter than that between excitatory neurons. The connectivity between inhibitory neurons was not spatially tuned. The strengths of the connections were G_E→E = 0.7 nS, G_E→I = 0.49 nS, G_I→E = 0.935 nS, and G_I→I = 0.7413 nS. Apart from stimulus-selective inputs, all neurons received uncorrelated random background excitatory input. The times of incoming action potentials were modeled according to a Poisson process with rate 1,800 sp/s. The conductances of this input were g_ext→E = 6.5 nS and g_ext→I = 5.8 nS. The effect of incoming action potentials was modeled through conductance-based synapses. Thus postsynaptic currents followed the equation

$$I_{\text{syn}}=g_{\text{syn}}s\left(V_{\text{m}}-V_{\text{syn}}\right)$$

where g_syn is the synaptic conductance, s is the synaptic gating variable, and V_syn is the synaptic reversal potential (V_syn = 0 for excitatory synapses, V_syn = −70 mV for inhibitory synapses). Recurrent excitatory connections were modeled to follow the dynamics of NMDA receptor (NMDAR)-mediated transmission, external excitatory inputs to follow AMPA receptor (AMPAR)-mediated transmission, and inhibitory inputs to follow GABA_A receptor (GABA_AR) transmission. The dynamics of the AMPAR and GABA_AR synaptic gating variables were modeled as an instantaneous jump of magnitude 1 when a presynaptic action potential occurred, followed by an exponential decay with time constant 2 ms for AMPA and 10 ms for GABA_A. The NMDAR conductance was voltage dependent, and this was modeled by multiplying g_syn by 1/(1 + [Mg²⁺]exp(−0.062V_m)/3.57), with [Mg²⁺] = 1.0 mM. The dynamics of the NMDAR synaptic gating were modeled by

$$\frac{\text{d}s}{\text{d}t}=\frac{-s}{{\tau }_s}+{\alpha }_{s}x\left(1-s\right),\hspace{0.17em}\frac{\text{d}x}{\text{d}t}=\frac{-x}{{\tau }_x}+{\displaystyle \sum _i\delta \left(t-t_i\right)}$$

where s is the gating variable, x is a synaptic variable proportional to the neurotransmitter concentration in the synapse, t_i are the presynaptic action potential times, τ_s = 100 ms is the decay time, τ_x = 2 ms controls the rise time, and α_s = 0.45 kHz controls the saturation properties of NMDAR channels.

Predictions from the model were derived from simulation results. Each simulation started with 100 ms of baseline activity, followed by stimulus-specific stimulation during 500 ms, and ended with a 500 ms-delay period (Fig. 1, B and C). The locations of the memories for each item were read out with Bayesian or maximum a posteriori decoding assuming an extended Poisson model as described by Zemel et al. (1998). This encoding-decoding framework was developed to handle situations where more than a single value (for example, several locations) should be encoded and decoded from the neural activity of a population of neurons. With this method, from the neuronal activity one determines a whole probability distribution over possible locations instead of a single most likely location. This allows for the encoding and decoding of different locations. The decoding distribution of items, that is, the probability distribution of angular locations ϕ_j, was estimated given the activity of the excitatory neurons in the last 100 ms of the delay period. For this, we used the function sqp from the software package GNU Octave (Eaton et al. 2009) to maximize an approximation of the logarithm of the probability distribution of angular locations ϕ_j (Eq. 17 of Zemel et al. 1998):

$$\text{AP}\left(\right\{{\varphi }_j\})={\displaystyle \sum _i{r}_i\log \left[{\displaystyle \sum _j{\varphi }_{j}f\left(x_{ij}\right)}\right]}-\epsilon \sum _j{\left({\varphi }_j-{\varphi }_{j+1}\right)}^2$$

where r_i is the activity of neuron i, x_ij is the difference between the preferred angles of neurons i and j, f(x_ij) is a neuronal tuning function assumed to be Gaussian with standard deviation 10°, set to match the dispersion of the network response to one item (the tuning), and ε = 10⁻⁷ is a weighting coefficient of the smoothness prior ∑(ϕ_j − ϕ_j+1)², which imposes smoothness across angular locations ϕ_j. Single values for the estimated locations of memorized items were found by determining the locations ϕ_j corresponding to the local maxima of AP({ϕ_j}). Before estimation, the spiking activity was resampled to a resolution of 360 for efficiency. Memory imprecision for each stimulus item was quantified as the distance in angle between that item location and the closest local maximum of the posterior probability of item locations, with the restriction that the distance had to be smaller than 35°. This restriction ensured that in cases where the memory trace vanished during the delay period the particular item was not attributed to a memory trace and instead it was counted as forgotten. In these cases the readout was taken to be a random location on the circle to mimic a subject guessing a forgotten spatial location. In cases where memory traces merged, the items were attributed to the same local maximum of the posterior probability. To study the effect of the distance between two simultaneously presented items on WM performance, we ran 100 simulations for different angular distance Δθ between the two items (Fig. 2A; Δθ from 45° to 90°). From these simulations we calculated the angular distance between remembered locations and corresponding item locations. This angular distance is a measure of error or bias in remembered location. If this bias was in the direction of the location of other memorized items (Fig. 1B) we defined it as a positive memory bias, corresponding to the attraction of memory traces. If the bias was in the direction opposed to close-by memorized items we defined it as a negative memory bias, corresponding to the repulsion of memory traces. To study the relation between precision and load for different positions of the items we ran 300 simulations for each load and for each stimulus distribution (far or random cases; Fig. 2B). For trials labeled “random,” items were simulated at random around a circle, with the restriction that they could not be closer than 33°. In trials labeled “far,” we applied the additional condition that at least one item per simulation (far item) was >80° apart from all other items. The results were then calculated, probing these far items. In particular, we computed standard deviations of the angular distances between remembered locations and corresponding item locations. We also calculated psychometric curves for each load and stimulus distribution. To this end, we counted for all simulations and for a given probed angular distance how many memory traces were counterclockwise in relation to the probed distance. The results are presented as proportion of memories counterclockwise to the probed location, as a function of angular distance between the probe and item. We fitted these proportions using probit models with angular distance as independent variable. The probit models were estimated with the Statistics Toolbox of MATLAB.

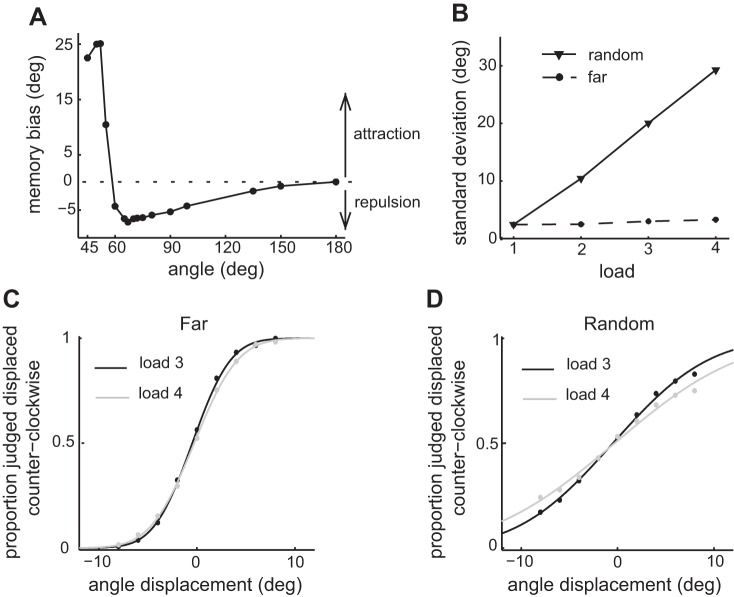
Fig. 2.

The biophysical network model predicts behavioral effects in multi-item visuo-spatial working memory (vsWM) tasks. A: memory bias as a function of angle between 2 items simultaneously presented. The results are averages over 100 simulations and are based on memory traces after 500 ms from stimulus offset. Memory biases toward the other presented item (attraction) were defined as positive, while biases away from the other presented item (repulsion) were defined as negative. The bias for small angles is easier to explore experimentally and leads to the formulation of the prediction of attraction biases. B: standard deviation error of the memory trace after 500 ms as a function of load. The standard deviation error was relatively constant for far items and increased with load for randomly located items, leading to the prediction of conditional dependence of precision on load. C: proportion of probes judged to be displaced counterclockwise from the memorized item. The results are for far items and loads 3 and 4 and were fitted with a probit model with displacement of the probe as independent variable. D: same as C but for randomly located items. C and D use the same simulations as in B and show that for far items there is no decrease in precision with load, which is observed for randomly located items. This observation also leads to the prediction of conditional dependence of precision on load.

The integration of the model equations was done with a second-order Runge-Kutta algorithm. The simulations were performed with code implemented in C++.

Behavioral Experiments

We used a vsWM task in which the subjects were presented with a set of dots and had to judge after a blank delay period whether a reappearing dot had been displaced clockwise or counterclockwise. The experimental paradigm is schematically illustrated in Fig. 3A. The stimuli were displayed on a computer screen, on a gray background. Participants sat ∼60 cm from the screen and were asked to fixate the central black square present during the whole trial time. Participants were also asked to memorize each item per se and avoid remembering the dots as a pattern. To limit the efficacy of pattern encoding strategies, we introduced specific constraints for the location of the items in each trial so that geometric symmetries or cardinal directions were avoided (see below).

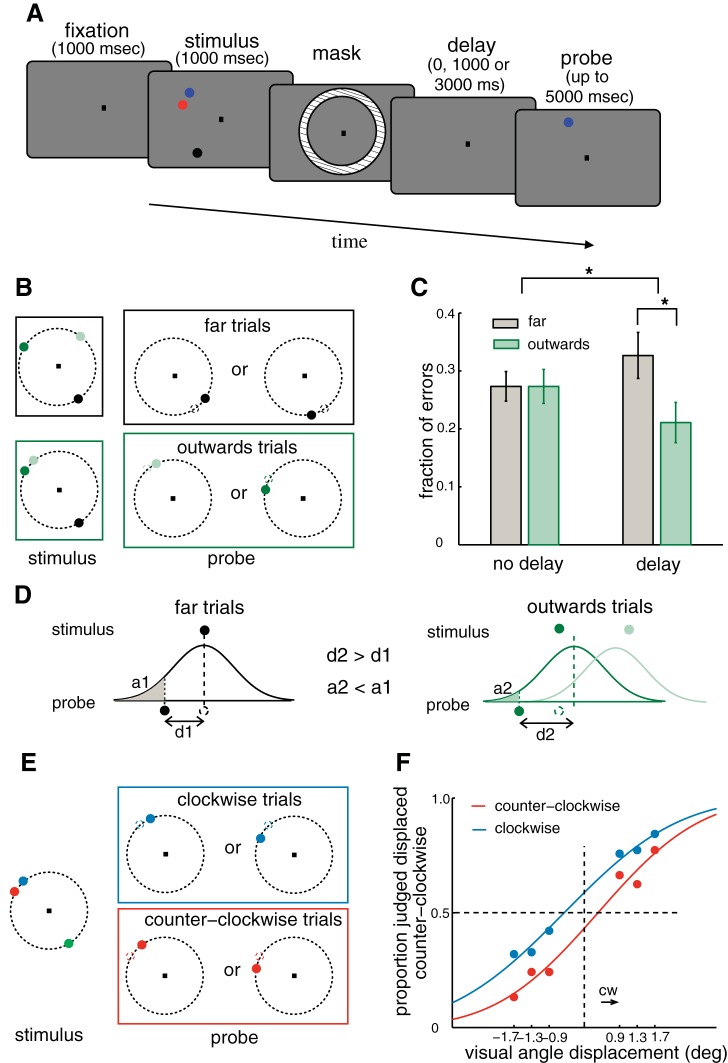
Fig. 3.

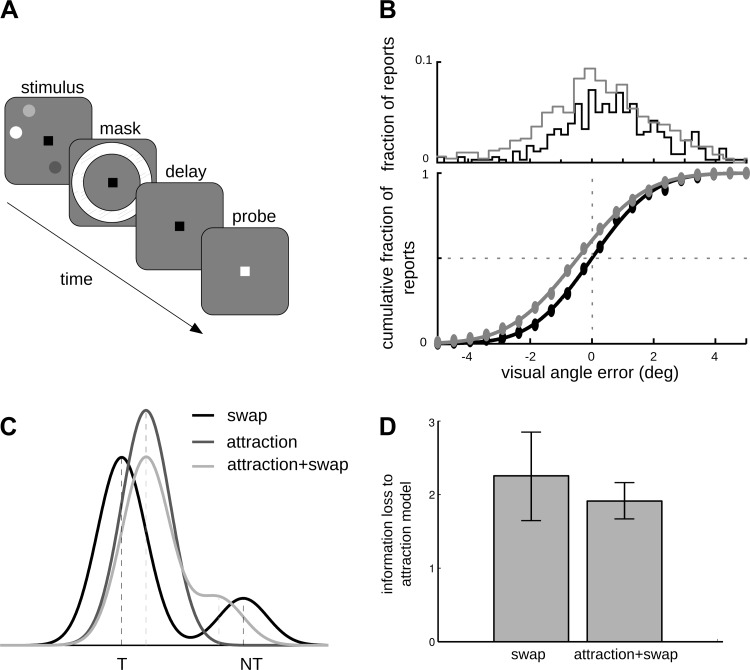
Behavioral data support the model-derived prediction of attraction biases. A: schematic illustration of the paradigm used in the behavioral experiment. B: illustration of the sorting of trials according to relative positions of the items. In one case, items were far from each other (far trials, framed in black). In the other case, the target item was presented close to another item and was displaced away from its neighbor during probing (outward trials, framed in green). C: fraction of errors averaged over participants (n = 8) in 48 trials of each trial type (delay/no delay and far/outward). Data were analyzed with a probit model. There was a significant interaction between delay and trial type. For no-delay trials there was no difference between the fraction of errors for far and outward trials, while there was a significant difference for delay trials. *Significant differences. Error bars indicate SE. D: schematic illustration of the mechanism thought to underlie the decrease in errors for outward trials compared with far trials. Bell-shaped curves represent the probability distribution of the remembered locations. The probed item defines an area under the probability function. This area is the probability of incorrectly judging the direction of displacement of the probe and is larger for far than outward trials (a2 < a1). The distance between location of the item and the location of the probe is larger for outward trials (d1 < d2). Hence, the probability of a correct response in outward trials is larger than in far trials, as observed experimentally. E: illustration of another sorting of trials, all containing the probed item in the vicinity of another item. Trials were sorted according to the clockwise or counterclockwise location of the probed item relative to the neighboring item. F: psychometric curves for clockwise and counterclockwise trials were horizontally displaced in relation to each other. Curves resulted from a probit model fit to data from all participants (n = 8). The results of C and F are consistent with the prediction of attraction biases.

Each trial started with the presentation of a central fixation cue for 1 s, followed by the presentation of the visual stimulus for 1 s. The stimulus consisted of a set of three or four colored dots (items) presented on an invisible circle centered on the fixation point and with a radius subtending a visual angle of 12.4°. The items were never presented on the horizontal and vertical diameters of the circle. The colors were attributed randomly to the different items for each trial. The stimulus was followed by 100-ms presentation of a mask consisting of an annulus (radii in visual angle 11.5° and 13.2°) of a pixelized noise pattern in a gray scale. The mask was followed by the presentation of a probe (in no-delay trials) or by a delay of 1 or 3 s (in delay trials) followed by presentation of a probe. The probe stimulus consisted of one of the stimulus dots displaced clockwise or counterclockwise on the invisible circle relative to the original stimulus location. The task consisted of judging the direction of displacement and reporting it by pressing one of two possible keys on a keyboard. Participants were given 5 s to respond and always responded before this time had elapsed. The probe was displayed until the subjects responded. Participants were trained until they showed no problems in associating the directions with the respective keys. It always took fewer than 48 trials to automatize the association. The amount of displacement in visual angle of the probe item was 0.9°, 1.3°, or 1.7° (4°, 6°, and 8° along the circle), and the probe could not be in a different hemifield than the corresponding target item. In half of the trials the memory of an item that was far from all other items was probed. For these trials, half showed all items far from each other (minimal distance between items was 70° along the circle for load 3 and 50° for load 4). These trials are referred to as far trials in Fig. 3 and as balanced trials in Fig. 4. The other half of trials where an item far from all others was probed had two nonprobed items close to each other (minimal distance along the circle from the probed item to another item was 90° for load 3 and 50° for load 4). These trials are referred to as unbalanced trials in Fig. 4. Different restrictions on distances were imposed on trials with loads 3 and 4 to ensure that a substantial part of the circle was spanned by the locations (in angle) of the items. With this, we wanted to minimize possible effects of attention that could appear if subjects could focus on a small portion of the circle and strategies to store items as geometric patterns. These restrictions resulted in trial types with balanced (invariant) and unbalanced (varying) distances across loads, which we used to demonstrate the prediction of conditional dependence of precision on load (see results). In half of the total number of trials the memory of an item located close to another item was probed (the distance between nearby items was between 10° and 20° along the circle, corresponding to a visual angle between 2.2° and 4.2°). In half of these trials the probe was displaced outward or away from the nearby item, and in the other half of trials the probe was displaced inward or toward the nearby item. For each trial type, trials were balanced in relation to relative positions of the dots in the stimulus, the displacements of the probe, the number of items, and the presence or absence of a delay period. The experiment was run in sessions of 48 trials, lasting ∼5 min. Within each session the delay was fixed, and each participant ran four sessions for each of three possible delays (no delay, 1 s, or 3 s). Type of trial, direction and amount of displacement, color of dots, and hemifield of the probed dot were randomized and balanced within each session. The order of the sessions was randomized across participants. Eight healthy participants (4 women, 4 men) took part in the experiment, with ages between 23 and 37 yr and normal or corrected-to-normal vision.

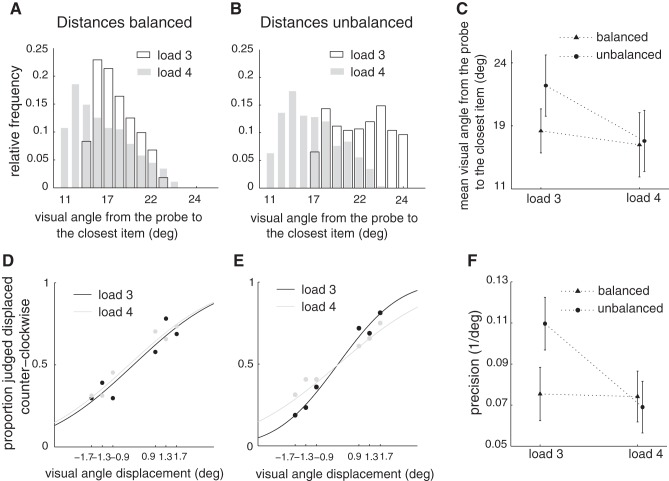
Fig. 4.

Behavioral data support the model-derived prediction of conditional dependence of precision on load. A and B: histograms of the distances between the target or probed item to the nearest nonprobed item for loads 3 and 4 for the case of balanced or invariant distances across load (A) or for the case of unbalanced or varying distances across load trials (B) (see results). Each combination of load and trial type (balanced/unbalanced) included 384 trials. C: mean distances from the target to the nearest neighbor for loads 3 and 4 and for balanced and unbalanced distances. Error bars indicate SD. D: psychometric curves for loads 3 and 4 for the case of balanced distances. Curves resulted from a probit model fit to data from all participants (n = 8). E: same as in D for unbalanced distances. F: precision derived from D and E decreased with load for unbalanced distances, while it remained unchanged for balanced distances. Error bars indicate SE.

To check for evidence of errors due to misremembering the colors of the items (Bays et al. 2009; Ma et al. 2014; Pertzov et al. 2012), we conducted a variant of this vsWM experiment. The experimental paradigm is schematically illustrated in Fig. 5A. The experiment was exactly as the one described above, except for the response period. After the delay period, the fixation dot changed from black to the color of one of the previously presented items. The subject was required to respond by indicating the remembered position of the item matching the color of the fixation mark. To indicate the remembered position, the subjects used a pressure-sensitive tablet and pen. The movement of the pen was reproduced in the visual display as a cursor so that the subject saw the colored fixation dot moving from the fixation spot to the remembered position. The subject indicated the reported position by releasing the pen from the tablet. All trials had a delay of 3 s, and separation between nearby items ranged from 3.1° to 4.4° of visual angle (14–20° on the circle). Data were acquired from four to eight sessions from each of nine healthy participating subjects (4 women, 5 men) aged between 21 and 27 yr and showing normal or corrected-to-normal vision. For each subject, sessions were typically acquired in different days. Some participants completed fewer sessions because they were not available for more data collection. The trials where the probed item was near another item were classified into two trial types, according to the probed item being clockwise or counterclockwise relative to the nearby item.

Fig. 5.

Behavioral data suggest that attraction of memory representations and not swap error is responsible for memory biases observed in close trials. A: schematic illustration of the modified experimental paradigm, where participants indicated the remembered target location upon appearance of a colored cue in the center of the screen. B, top: distributions of error to target for clockwise (gray) and counterclockwise (black) trials differed significantly (P < 0.00005, data from all participants n = 9), revealing an attractive bias. Bottom: cumulative proportion of errors to target from the distributions at top, to compare with psychometric curves in Fig. 2E. Data were fitted with a cumulative normal function. C: schematic illustration of the probability density function for each of the 3 models tested: swap, attraction, and attraction + swap models. D: average information loss ΔAIC across subjects (n = 8) for swap and attraction + swap models compared with the attraction model, the best model for data from these participants.

Participants for both experiments were recruited among a local community of researchers and students from the Institut d'Investigacions Biomèdiques August Pi i Sunyer (IDIBAPS). The experiments were conducted with the approval of the Comité Ético de Investigación Clínica (CEIC) at the Hospital Clínic in Barcelona, and informed consent was obtained from all participants before the experiments took place.

Behavioral Data Analysis

Behavior from the first experiment was measured as the number of correct trials. The results were analyzed with generalized mixed probit models in R (R Development Core Team 2013), MASS package (Venables and Ripley 2002), with participant as a random factor. For the first test of our first prediction (see results), trial type, delay, and the interaction between trial type and delay were used as independent variables or predictors. For the second test of this prediction, the amount of probe displacement was also included.

Since the interaction term was significant in both cases, the data were separated according to delay and a model was fitted using trial type as predictor for test 1 and trial type, amount of probe displacement, and the interaction between these two variables as predictors for test 2. For the test of the second prediction (see results), trial type, delay, load, and amount of probe displacement were used as independent variables. The model also included interactions between these variables. Since an interaction between delay, trial type, and displacement was found to be significant, the data were separated according to delay. A new model without the delay variable was fitted. Since for the delay trials we found an interaction between displacement, load, and trial type, the data were further divided according to trial type. For these new data partitions, a model was fitted using amount of probe displacement, load, and the interaction between these two variables as predictors.

Behavior in the second experiment was analyzed in three ways. For testing the prediction of attraction, the data were analyzed with a linear mixed model, with participant as a random factor and trial type as a predictor. To test the dependence of memory biases on interitem distance (Fig. 6), we fitted cumulative Gaussians to the cumulative fraction of error reports (Fig. 5B), collapsing clockwise and sign-inverted counterclockwise errors, and we used the fitted mean as an estimate of the memory bias (Fig. 6A). Positive biases thus reflected attraction, and negative biases reflected repulsion of the two memories. In Fig. 6B we assessed the significance of each participant's memory bias with a two-sample t-test on the error distributions of clockwise and counterclockwise trials. We used a multinomial regression model to test whether the relative incidence of significant repulsion biases compared with attraction biases increased with interitem distance in our subject population (Fig. 6B). The dependent variable could take three possible values: attraction, repulsion, or no effect. For each subject, we got three measurements of the dependent variable, corresponding to three bins of distances between items (Fig. 6). The model included an intercept and the interitem distance (taking values 3, 3.75, 4.2) as predictors. The link function was a generalized logit function.

Fig. 6.

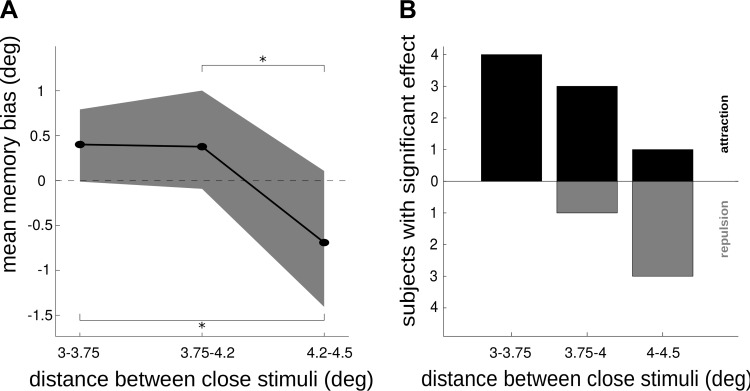
Memory repulsion emerges for intermediate distances between close-by items. A: subject-averaged memory bias (materials and methods) for trials with different distances between memorized close-by items (x-axis). Shading indicates bootstrap-derived 95% confidence intervals. *Significant difference as evaluated with 1-tailed paired t-test at P < 0.05. B: no. of subjects with significant (t-test P < 0.05) attractive and repulsive memory bias in trials with different interitem distance.

Finally, to test alternative statistical models, the data were fitted to three statistical models detailed below using a custom expectation maximization algorithm for the maximum likelihood estimation (Dempster et al. 1977) based on publicly available code (Bays et al. 2009; http://www.paulbays.com). Model comparison was done with the Akaike information criterion (AIC) (Akaike 1974), which is a measure of the relative quality of a statistical model for a given data set. Information loss of one model relative to another was then calculated by the differences between AIC values (Burnham and Anderson 2004). The information loss ΔAIC of each model compared with the best (that with the lowest AIC) was calculated for each subject and then averaged across subjects. The relative likelihood of model i relative to the best model was computed as exp(ΔAIC_i/2).

Statistical Models

A possible explanation for the errors in the task could be a wrong association (or binding) of color and location of the items (Bays et al. 2009; Ma et al. 2014; Pertzov et al. 2012). To access whether interference (attraction) between memory traces of item locations or misbinding best explains our experimental results we used three statistical models, here called swap, attraction, and attraction + swap models. All the models assume that the experimental distribution f_EXP(Δθ) of errors in reported angle Δθ can be described as a mixture of von Mises components (Fig. 5C), a circular analog of the Gaussian distribution with dispersion parameter σ, defined as ϕ_σ(Δθ) = exp[cos(Δθ)/σ²]/(2πI₀(1/σ²)), with I₀ the modified Bessel function of order 0.

Swap model.

This model is the one introduced by Bays et al. (2009) to account for performance on a recall task in which both stimuli and responses are chosen from a circular parameter space. The model assumes that the experimental distribution can be described as a mixture of three components:

$$f_{\text{EXP}}\left(\Delta \theta \right)=p_{\text{t}}{\varphi }_{\sigma }\left(\Delta \theta \right)+p_{\text{nt}}\frac{1}{n}{\displaystyle \sum _i{\varphi }_{\sigma }\left(\Delta {\theta }_i^{\ast }\right)+p_{\text{u}}\frac{1}{2\pi }}$$

The first component, weighted by p_t, describes the responses to correctly remembered items, where the subject reports the remembered position with some uncertainty around the error to the actual location of the target item. This is modeled using the von Mises distribution centered around the error to the target Δθ, with dispersion parameter σ. The second component, weighted by p_nt, describes the responses to nearby nontarget items, i.e., responses indicating the remembered location of a nontarget item (item with a color different from the probed color). Such responses reflect errors in the binding of color and location of an item (swap errors; Bays et al. 2009). This is also modeled using a von Mises distribution with dispersion parameter σ, but now centered on the error to the nontarget location Δθ* = θ − θ_nt. Finally, the third component describes the situation where the item location is forgotten and the subject guesses according to a uniform distribution. The model has three parameters p_t, p_nt, and σ, which can be estimated to fit the experimental data.

Attraction model.

In this model the subjects' reports are described by a unimodal von Mises distribution centered on a location intermediate between the target and nontarget items. This displacement would occur as a result of the attraction of coding bumps in our more detailed model of Fig. 1. This model drops one of the components, the possibility of having swap errors, and introduces a bias b in the mean, representing the attraction effect:

$$f_{\text{EXP}}\left(\Delta \theta \right)=p_{\text{t}}{\varphi }_{\sigma }\left(\Delta \theta +b\right)+p_{\text{u}}\frac{1}{2\pi }$$

Since nearby items were separated by different distances δ_i, the bias b_i in individual trials was constrained to be a fraction of δ_i: b_i = b′δ_i, and we estimated the constant factor b′. In total, the model has three parameters p_t, σ, and b′, which can be estimated to fit the measured data.

Attraction + swap model.

Finally, both errors might coexist: In some trials the two features of the stimulus are misbound, but in any case reports (to target or to nontarget items) are biased toward the nearby stimulus. This model is the same as the swap model but with one more parameter for the bias:

$$f_{\text{EXP}}\left(\Delta \theta \right)=p_{\text{t}}{\varphi }_{\sigma }\left(\Delta \theta +b\right)+p_{\text{nt}}\frac{1}{n}{\displaystyle \sum _i^n{\varphi }_{\sigma }\left(\Delta {\theta }_i^{\ast }-b\right)+p_{\text{u}}\frac{1}{2\pi }}$$

Note that the bias b (as above, b_i = b′δ_i) affects equally the responses to both target and nontarget items. This model has four parameters p_t, p_nt, σ, and b′ that can be estimated to fit the experimental data.

RESULTS

Predictions from Computational Model

We used an existing computational model (Compte et al. 2000; Edin et al. 2009) to study vsWM of several simultaneously presented items. For simplicity, we considered only the memory storage of locations at equal eccentricity, so that the item locations could be labeled by an angle θ. The model consists of a one-dimensional network of neurons connected in a topographic manner (Fig. 1A), so that neurons encoding nearby locations have stronger connections than neurons encoding far-apart locations. This structure enables the network to sustain stimulus-selective activity during a delay period (Compte et al. 2000). When plotting the activity of excitatory neurons organized according to their selectivity (Fig. 1, B and C), the sustained spiking corresponding to a memory trace is visualized as a spatially localized bump of activity in the network (y-axis) that is persistent over time (x-axis). The continuous topographic structure of the network connectivity implies that memory traces maintained simultaneously are not independent and interfere with each other. It further implies that the interference is dependent on the relative locations of the angles memorized, more interference being expected for nearby items than for far-apart items. Possible types of interference of memory traces are attraction (Fig. 1B), repulsion, and extinction (Fig. 1C). To study the effects of interference on vsWM for several items we started by considering two items and we systematically changed the angle Δθ separating them. We measured memory bias as the angular distance between cued locations and memory locations encoded in network activity 0.5 s after stimulus extinction (materials and methods). Furthermore, we defined memory bias as being positive when it reflected attraction between memory traces and negative when it reflected repulsion between memory traces. Figure 2A shows that there is a large attraction effect for angles smaller than 60° and an intermediate repulsion effect for intermediate angles, which disappears as Δθ increases. Our simple model cannot match quantitatively the conditions of a real cortical circuit, and hence we do not know in what range of Δθ we should expect the different behaviors, attraction and repulsion. However, we do know that for small angles between items we should have an attraction effect, while for very large angles we should have no effect. Based on this we sought to mainly test our model by using items very close by or in relative isolation, where we would not need to search for subject-dependent angles leading to repulsion. Hence, the first prediction we aimed at testing in behavioral experiments was that vsWM for adjacent locations should show biases consistent with a perceived attraction between the two items. We refer to this prediction as the “prediction of attraction biases.” We have, however, also checked a posteriori our experimental data for evidence of the predicted repulsive effects at intermediate interitem distances (see Testing Repulsion Biases).

We then studied how interference affected precision in our network model when the number of items to be memorized (the load) increased. We measured the standard deviation over trials of report errors σ in simulation series where different numbers of items (from 1 to 4) were presented to the network for memorization. We considered two cases. In the first case, we minimized interference by keeping distances between items large (far case). In the second case, the items were located at random (random case). We found that σ depended markedly on load in the random case, while it remained relatively constant as load changed in the far case (Fig. 2B). This was because when items were randomly placed the probability of having items separated in the range of interference (Fig. 2A) increased with load. When this probability was only allowed to change minimally with load, as in the far case, σ remained practically constant.

This effect can be demonstrated in the shape of psychometric curves. We used the same simulations as above to derive psychometric curves showing the proportion of items that are judged counterclockwise to a probed location (materials and methods) as a function of angular distance between probed location and item location (Fig. 2, C and D). For the simulations where only far items were probed, the psychometric curves changed minimally with load (Fig. 2C). For the simulations where items were randomly placed, the psychometric curves for loads 3 and 4 showed greater difference (Fig. 2D). The different slopes of the psychometric curves reflect different memory precisions for loads 3 and 4, consistent with greater interference of neighboring bumps in load 4 trials. Therefore, our second prediction was that the previously reported loss of precision with load (Bays and Husain 2008) would largely depend on the relative positioning of the items to be memorized, being minimized when the minimal distances between the items in the visual stimuli are large. We refer to this prediction as the “prediction of conditional dependence of precision on load.”

Testing Prediction of Attraction Biases

To test the predictions from the model, we used the behavioral experiment illustrated in Fig. 3A. The experimental paradigm was adapted from a previously reported paradigm (Bays and Husain 2008) used to investigate the loss of precision with load in a vsWM task in humans. For each trial the subjects were required to keep in mind the locations of three or four colored dots positioned on an invisible circle (stimulus). After presentation of a visual mask, and in some trials after an additional short delay period (1–3 s), one colored dot reappeared on the invisible circle (probe) and the task was to judge whether it had been displaced clockwise or counterclockwise. The average accuracy on this task was 70% correct. All subjects performed significantly above chance level, with accuracies ranging from 59% to 79%.

We conducted two tests of the prediction of attraction biases. For the first test we used the trial types depicted in Fig. 3B and labeled them as far and outward trials. In the far trials all items were located far apart from each other. In the outward trials the probed item was presented within a visual angle of 4.2° from another item, and it was displaced outward (or away) from the nearby item (see materials and methods). In such trials, if the predicted attraction between bumps of activity corresponding to neighboring items occurred (Fig. 1B, Fig. 2A), we expected the memory of any one of these two adjacent items to be biased toward the middle point between them. As a result, a probe displaced outward from the corresponding target, whose memorized location has been attracted to the neighboring item, would appear to have been subject to a larger displacement than the actual one. This would help the subject to judge correctly the displacement as outward as opposed to inward. This is schematically depicted in Fig. 3D. The bell-shaped curves in Fig. 3D represent the probability distributions of the locations stored in memory over multiple trials of two fixed-cue stimulus configurations, corresponding to far and outward trial categories, respectively. One can see that the distance between the mean location of the remembered item and the location of the probe is smaller for far trials (distance 1) than for outward trials (distance 2). The location of the probed item defines an area under the tail of the probability function that is larger for the far trials (area 1) than for the outward trials (area 2), and this determines the probability of incorrectly judging the direction of displacement of the probe. This should result in better performance for outward trials than in a control condition without interference, as in far trials. This is indeed what we observed in our behavioral data set: The fraction of behavioral errors for far trials was significantly larger than that for outward trials (P = 0.01) (Fig. 3C). However, the effect observed could have occurred before the delay period, during encoding of the visual stimulus. We rejected this explanation by testing for a difference between trials with and without intervening delay between visual stimulation and response. We found a significant interaction between trial type (far or outward) and delay (P = 0.03) and no significant difference between trial types for no-delay trials (Fig. 3C).

For the second test of the prediction of attraction biases we used the trial types depicted in Fig. 3E and labeled them as counterclockwise and clockwise trials. In both trial types the probed item was located adjacent to another item. For counterclockwise item trials the probed item was located counterclockwise to the neighboring item, and for clockwise item trials the opposite was verified. If attraction occurred, we expected the memory to be biased and the psychometric curves of the two trial types should be horizontally displaced instead of centered at zero probe displacement. The predicted displacement would be clockwise (counterclockwise) for counterclockwise (clockwise) item trials, indicating that nearby items were perceived to be attracted to each other. The data confirmed this prediction (Fig. 3F). The two psychometric curves were significantly different from each other (P < 0.0001), and the effect appeared with delay, as verified by a significant interaction (P < 0.0001) between trial type and delay. Note that the magnitude of the attractive bias was indicative of a partial attraction, not a complete merge of the memories (mean distance between close-by items was 3.2 ± 0.14° of visual angle, so a complete merge would correspond to a horizontal displacement by 1.6 ± 0.14° of visual angle in Fig. 2E).

Testing Prediction of Conditional Dependence of Precision on Load

To test this prediction we used two different trial types having in common that the probed item was not in close vicinity to any other item (>50° along the circle). These different trial types result from the following considerations on the experimental design (for details see materials and methods). We designed the experiment such that each load condition included a balanced number of trials with the probed item far from or close to neighboring items. The former trials (probed item far) contained a balanced number of trials with nonprobed items in a far or close configuration, giving rise to the two trial types used in this section. Furthermore, a relatively large part of the circle was covered by the items in each trial by experimental design, in order to minimize possible effects of focusing the attention on a restricted arc. Given these constraints, the two trial types had different interitem distance properties in relation to load, which we took advantage of to test our second model prediction. In one trial type (far nonprobed items) the minimal distance from the probed item to other simultaneously presented items was relatively invariant with load (Fig. 4A), and therefore these trials are referred to as balanced trials. In the other trial type (close nonprobed items) the minimal distance between the probed item and other items varied markedly between loads (Fig. 4B), and therefore they are referred to as unbalanced trials. Note that the labels “balanced” and “unbalanced” refer to the distance between probed item and the nearest item being practically invariant (balanced) or varying significantly (unbalanced) across loads. This difference is summarized in Fig. 4C, showing the mean of the minimal distances for the two loads, which is the same for balanced trials but differs for unbalanced trials. With this set of trials that dissociate load changes from changes in interitem distances, we went on to test behavioral performance in the task to validate the model's prediction. We found that there was a significant interaction of trial type (balanced/unbalanced) and probe displacement on the fraction of correct responses (P = 0.05). Furthermore, we found no difference between the psychometric curves for loads 3 and 4 for balanced trials (Fig. 4D), but a difference emerged (P = 0.03) for unbalanced trials (Fig. 4E). The difference between the psychometric curves for loads 3 and 4 in unbalanced trials corresponded to a loss of precision with load (Fig. 4F). Precision is here defined as the inverse of the standard deviation of the cumulative normal curves fitted to the data (Bays and Husain 2008), and it quantifies the slope of the psychometric curve at zero probe displacement. This loss of precision was not observed when the distances were balanced across loads (Fig. 4F), thus confirming our second prediction. The observed differential loss of precision with load for unbalanced trial types appeared with delay: We verified that there was a significant interaction between delay, displacement, and trial type (P = 0.05) and that for the cases with no delay there was no interaction between trial type and displacement or load. That is, the differences in psychometric curves observed in trials with delay were not present with no delay.

Testing a Swap-Error Model

An alternative explanation for the results in Fig. 3, C and F, is that in some error trials the subjects swapped the colors and locations of the two memorized nearby items (Bays et al. 2009; Ma et al. 2014; Pertzov et al. 2012). Misremembering the binding between color and location would also result in a reduced fraction of errors for outward trials. Intuitively, in trials where the color and locations memories are swapped, the perceived displacement of the probe would be large (the distance between items plus the actual displacement) and therefore the response would be correct with higher probability. Thus we carried out another experiment to contrast this misbinding hypothesis with the memory attraction hypothesis supported by our computational model.

To check for evidence of swap errors in our experimental context, we collected behavioral data in a variant of the original paradigm (Fig. 5A and materials and methods). In this task, nine participants had to report the remembered locations by controlling a cursor. We quantified behavioral performance with the standard deviation of the error-to-target distribution, which was 3.6 ± 0.6° of visual angle across subjects (range: 2–7.5°). If we excluded trials for which the error to target exceeded 45° along the circle, the error-to-target standard deviation was 2.8 ± 0.4° of visual angle (range: 1.5–5.8°).

First, we checked that the results shown in Fig. 3 were also verified in the modified experimental paradigm. Indeed, we found that there was a significant difference between the reported errors for the counterclockwise and clockwise trial types (Fig. 5B, P < 0.0001). Similar as in Fig. 3, these data were consistent with attraction of the two memories. We were able to measure the specific fraction of a perfect merge verified in the data. We did this by normalizing the mean error in each trials to the distance between close stimuli. The subjects who showed a significant effect (5 of 9) presented 26 ± 8% (39 ± 6%) of the attraction expected for a total merge of the memories in clockwise (counterclockwise) trials.

We then fitted behavioral reports with statistical models that included Gaussian-like distributions around the target memory items (materials and methods), using a custom expectation maximization algorithm based on Bays et al. (2009). For all tested models, the dispersion parameter σ estimated from trials with close probed items (σ = 7.63 ± 0.88° along the circle; n = 9) did not differ significantly from that estimated from trials with far probed items (paired t-test, P > 0.05; n = 9), suggesting that differences in precision between isolated and clustered memory items (Fig. 3C) were not due to different memory resolutions in these two situations. Instead, we tested the hypothesis that these differences occurred as a result of memory biases caused by neighboring memories, and we contrasted three different models (materials and methods): an attraction model, in which responses to the target stimulus experienced a mean bias toward the neighboring memory; a swap model, in which responses to target stimuli were unbiased but in some trials responses clustered around the neighboring nontarget item; and an attraction + swap model, which combined the two situations: a fraction of swap responses and a mean bias toward neighboring memories (Fig. 5C). Note that for the swap model we only considered swaps between close-by items. We compared the estimated maximum likelihoods of each model using differences in the AIC (materials and methods). We calculated this difference between all the models and the best model. The best model (that with the lowest AIC) was the attraction model for all but one participant, for whom the attraction + swap model had the lowest AIC (ΔAIC for the swap model was 11.7, i.e., a relative likelihood < 0.0001). We excluded this subject to calculate the average information loss of the swap and attraction + swap models relative to the attraction model for the other participants. The swap model was the worst of the three statistical models tested (Fig. 5D). Adding up AICs for these eight participants, the relative likelihood of the swap model compared with the attraction model was <10⁻⁴. These results led us to discard an explanation based on swap errors alone for the memory attraction that we demonstrated in Fig. 3.

Testing Repulsion Biases

Our model also predicts repulsion for intermediate distances between close-by items (Fig. 1B). This is a result of the limited divergence of inhibitory connections in the network (medium-range inhibitory connectivity, see materials and methods). We could test this prediction in our second experiment. As shown in Fig. 6, the interaction between two nearby memories transitioned from attraction to repulsion as the interitem distance grew, matching qualitatively our network simulations (Fig. 1B). We computed the memory bias from the psychometric curve fit for each subject (materials and methods) and plotted it against distance between items (Fig. 6A). Across subjects, the attractive memory bias of the psychometric curve decreased significantly (1-tailed paired t-test, P = 0.02; n = 9) from very close memories (3.0–3.5° of visual angle, memory bias 95% confidence interval [0 0.7]°, permutation test P = 0.05) to slightly more distant ones (4.2° of visual angle), at which point the memory bias became marginally negative (memory bias 95% confidence interval [−1.2 0.1]°, permutation test P = 0.07). In addition, we tested significant memory biases within subjects (materials and methods), and we found that the number of subjects with a significant repulsive (attractive) memory bias increased (decreased) with distance between items (Fig. 6B; multinomial regression model P = 0.035, materials and methods), indicating a consistent but individually specific dominance of repulsion for intermediate distances.

DISCUSSION

In the present study we investigated the neural circuit mechanisms of vsWM limitations by formulating predictions from a specific neural circuit hypothesis and by testing them in new behavioral experiments. Specifically, we confirmed model-predicted attractive and repulsive biases in the recollection of items located nearby in space, and we found that the model-predicted reduction in vsWM precision caused by the presence of nearby memorized items could explain the previously reported decrease of vsWM precision with load (Bays and Husain 2008). Taken together, our results support the encoding of vsWM in sustained activity of topographically organized neural circuits.

Item Similarity, Interference, and WM

With this work we contribute to two partially overlapping debates on the behavioral aspects of visual WM. One of these debates revolves around the impact of similarity and interference between items, between items and distractors, and between items and landmarks on WM performance. Several studies have demonstrated such effects in vsWM in the presence of landmarks (Werner and Diedrichsen 2002), WM with distractors (Herwig et al. 2010; Kerzel 2002; Macoveanu et al. 2007; Van der Stigchel et al. 2007), memory of sequential items (Papadimitriou et al. 2015), vsWM with memory manipulation (Oberauer and Kliegl 2006), WM of colors (Brady and Alvarez 2011; Elmore et al. 2011; Johnson et al. 2009; Lin and Luck 2009), WM of spatial frequency (Huang and Sekuler 2010; Mazyar et al. 2012; van den Berg et al. 2012; Viswanathan et al. 2010), WM of sizes (Brady and Alvarez 2011), and WM of orientation (Johnson et al. 2009; van den Berg et al. 2012). However, these studies found discrepant results concerning the impact of item similarity and interference. To our knowledge we are the first to demonstrate a similarity effect for WM of simultaneously memorized spatial locations: the attraction effect of neighboring items. We have provided evidence of a detrimental effect of similarity interference on performance, but we identified one specific condition under which the similarity effect results in vsWM performance enhancement: when the test is presented away from the nearby memorized item (Fig. 3C). This is consistent with an attraction of the representations of memorized nearby locations. The analogy between the attraction of memories and the previously reported attraction between a memory and a distractor (Herwig et al. 2010; Macoveanu et al. 2007) and between a memory and an irrelevant previous memory (Papadimitriou et al. 2015) suggests that distractors compete for a representation in the same memory circuits as actual memories, similar to the hypothesis of current neural models of vsWM (Cano-Colino et al. 2013; Compte et al. 2000; Macoveanu et al. 2007).

Conceptually, the very existence of similarity effects has led some authors (Elmore et al. 2011; van den Berg et al. 2012) to interpret them as support for a resources model of WM (Ma et al. 2014; Wilken and Ma 2004), which in its most basic formulation states that WM can be seen as a resource shared between the memory representations of the different items. Indeed, similarity effects are not accommodated naturally in the alternative model, the slots model of WM, which states that one memorizes each item independently until a maximal number of items is reached (Luck and Vogel 1997, 2013). As some authors have noted, however, similarity or interference effects would not pose any problem for the slots model if they primarily occurred in the encoding phase, not the mnemonic phase of the task (Johnson et al. 2009; Lin and Luck 2009). In our experiments, similarity effects are not present when there is no delay period and the task is otherwise identical. This suggests that spatial interference of memorized locations occurs during the maintenance of information in WM and not during the encoding of information. An alternative explanation for the results in Fig. 3, C and F, is that the participants remembered in some trials the colors of two nearby items swapped (Bays et al. 2009; Ma et al. 2014; Pertzov et al. 2012). To have an idea about how prevalent this type of error was in our experimental setup, we ran an additional experiment. We found clear evidence that swap errors alone cannot explain the prediction of attraction biases, and so we conclude that attraction of memory traces is a more plausible explanation for our results. Note, however, that the amount of swap errors is probably closely related to the specifics of the task and previous studies that found substantial evidence for swap errors did not use vsWM but tasks based on WM of color (Bays et al. 2009) or orientation (Pertzov et al. 2012).

WM Precision with Load

A second debate concerns the relation between precision of vsWM and number of items to memorize (WM load) and its implications for the nature of WM. Some authors found a decrease of precision with load (Bays et al. 2009; Bays and Husain 2008), supporting the resources model (Wilken and Ma 2004) of WM, while others found a saturation of precision with load (Zhang and Luck 2008), supporting models of the family of the slots models (Luck and Vogel 1997; Zhang and Luck 2008). Crucially, in these slots models information about further items cannot enter WM after reaching a maximum number of memorized items. Much ongoing research on WM limitations has focused on resolving the dichotomy between these two alternatives, providing new experimental evidence and leading to further development of algorithmic models, including hybrid models with characteristics from the slots and resources models (Alvarez and Cavanagh 2004; Anderson et al. 2011; Bays et al. 2009; Bays and Husain 2008; Buschman et al. 2011; Elmore et al. 2011; Luck and Vogel 2013; Ma et al. 2014; van den Berg et al. 2012; Xu and Chun 2006; Zhang and Luck 2008). A parallel line of research is focusing on the circuit mechanisms of vsWM in biologically detailed network models (Bays 2014; Compte et al. 2000; Edin et al. 2009; Macoveanu et al. 2007; Wei et al. 2012) that are typically hard to classify into any of these abstract model categories. We took one such biologically detailed model and found that the interference between items causes, on average, loss of memory precision (see also Wei et al. 2012). As the number of items in a constrained area increases, the probability of having interference between memories increases and hence a loss of precision with load is observed. The model thus predicts that the decrease of vsWM precision with load depends largely on the relative location of the items. Our experimental results were consistent with a distance-dependent relation between precision and load, showing both a reduction of precision with load (Fig. 4E) and a lack thereof (Fig. 4D) on the same behavioral data, depending on a selection of trials based on interitem distance. This suggests that interitem distance could be a factor explaining the conflicting results in the literature (Bays and Husain 2008; Zhang and Luck 2008). Furthermore, our experiments showed that the relationship between spatial memory precision and load emerged through the delay. This suggests that explanations based on the processes of memory encoding and decoding (Bays 2014) need to incorporate also the role of memory maintenance mechanisms.

WM Model

The network model was used with the same parameters as in Edin et al. (2009), without further tuning. We did not seek a quantitative match between the angles or times used for the behavioral experiments and model simulations. Such a match can be sought by changing parameters of the model; for example, increasing the size of the network would make the values of angular distances and times in the model approach those of the experiments, at the cost of slower simulations. Such procedure would make model testing impractical without providing any significant conceptual advantage. Hence, we searched for qualitative robust predictions to test experimentally. Consistent with this, Wei and coauthors (Wei et al. 2012) working in parallel in a similar model derived predictions qualitatively in agreement with ours but based on different activity patterns. Indeed, their model differs from ours fundamentally in that it features a normalization regime in which the same number of active neurons is split among the number of items encoded, with the overall population activity invariant with load (see also Bays 2014). This is not the regime of operation of our network, which shows graded rate responses and mean firing rates increasing with load (Edin et al. 2009). Another difference between the models is that our model, but not the model of Wei et al. (2012), predicts repulsion between memory traces. Our experimental results (Fig. 6) show evidence for repulsion, hence supporting our model. Further exploration of the regimes where the two models operate should provide new discriminating predictions to test against experimental data in the future. Johnson and coauthors (Johnson et al. 2009) also proposed a firing rate model explaining color similarity effects based on a specific decoder mechanism, in contrast with our model, which allocates the mechanism in the dynamics of the circuit during the maintenance phase. Our experimental results for vsWM show that the similarity effects appear with delay and therefore are not originated during the encoding or decoding phases of the task. This is consistent with interference during the active maintenance of memory. We note, however, that different mechanisms might be behind the effects described for color (Johnson et al. 2009) or orientation (Bays 2014) WM tasks. Finally, our model did not simulate all components of the tasks: Our tasks demanded the binding of two different features (color and position), while the model was only simulating the storage of position. This is partly because of the lack of a consensual model for feature binding in WM, but also because the behavioral effects that we are reporting proved not to depend crucially on such binding. Indeed, we demonstrate in our last experiment that the attraction effect is independent of swap errors. This result justifies interpreting our data with a simplified model representing only location information. However, a complete understanding of this task will require explicitly simulating the binding component.

Our results advance our understanding of vsWM in terms of its neuronal circuit underpinnings by providing evidence for a critical assumption of an explicit computational model of vsWM, namely, that vsWM is supported by a network of neurons organized according to a continuous topography in terms of internal connectivity and external inputs received. This topographic connectivity enables the model to sustain a continuous attractor mechanism, in which memories of neighboring items interfere (Amari 1977). Recently, direct experimental evidence from neural activity in the prefrontal cortex of monkeys performing a single-item spatial WM task has been obtained in favor of this continuous attractor mechanism (Wimmer et al. 2014). Here the consistency of our experimental results with the model predictions in the case of multi-item WM lends further support to the continuous attractor as the basis of vsWM. Furthermore, the model explains parsimoniously behavioral effects that cannot be consistently integrated within the prevalent algorithmic models for vsWM. This underscores the potential of using a circuit-based framework to interpret experimental results on the mechanisms of vsWM.

GRANTS

This work was supported by the Ministry of Economy and Competitiveness of Spain, the European Regional Development Fund (Ref: BFU2009-09537, BFU2012-34838), and the Karolinska Institutet Strategic Neuroscience Program. R. Almeida was supported by the Generalitat de Catalunya (Beatriu de Pinós program, 2007BP-B100135). The work was carried out at the Esther Koplowitz Centre, Barcelona.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: R.A. and A.C. conception and design of research; R.A. and J.B. performed experiments; R.A. and J.B. analyzed data; R.A., J.B., and A.C. interpreted results of experiments; R.A. and J.B. prepared figures; R.A. and A.C. drafted manuscript; R.A., J.B., and A.C. edited and revised manuscript; R.A. and A.C. approved final version of manuscript.