Toward a unifying framework for evolutionary processes

Abstract

The theory of population genetics and evolutionary computation have been evolving separately for nearly 30 years. Many results have been independently obtained in both fields and many others are unique to its respective field. We aim to bridge this gap by developing a unifying framework for evolutionary processes that allows both evolutionary algorithms and population genetics models to be cast in the same formal framework. The framework we present here decomposes the evolutionary process into its several components in order to facilitate the identification of similarities between different models. In particular, we propose a classification of evolutionary operators based on the defining properties of the different components. We cast several commonly used operators from both fields into this common framework. Using this, we map different evolutionary and genetic algorithms to different evolutionary regimes and identify candidates with the most potential for the translation of results between the fields. This provides a unified description of evolutionary processes and represents a stepping stone towards new tools and results to both fields.

Highlights

• •A unifying framework for evolutionary processes.
• •
  Formalizing the defining properties of the different kinds of processes:

  • ○
    Variation operators (mutation and recombination).
  • ○
    Selection operators.
• •Formalizing several common examples of these operators in terms of our framework.
• •Proving that these common operators respect the properties that we define for their class.
• •Casting several classical models and algorithms from both fields into our framework.

1. Introduction

Evolutionary computation and population genetics share a common object of study, the evolutionary process. Population genetics tries to understand the evolution of natural populations while evolutionary computation focuses on designing and understanding artificial evolutionary processes used for solving optimization problems. Both fields have developed independently, with very little interaction between them.

Population genetics (PG) studies how evolution is shaped by basic forces such as mutation, selection, recombination, migration among sub-populations, and stochasticity; it forms the core of the modern understanding of evolution (the so-called “modern synthesis”). PG has a long tradition of mathematical modelling, starting in the 1920s with the pioneering work of Fisher, Wright, Haldane and others, and is now a highly sophisticated field in which mathematical analysis plays a central role. Early work focussed on simple deterministic models with small numbers of loci, aiming at understanding how the change in genotype frequencies in a population was affected by basic evolutionary forces. It has since branched out to investigate topics such as the evolution of sexual reproduction, the role of environmental fluctuations in driving genetic change, and how populations evolve to become independent species. Almost all current PG models are restricted to the simplest fitness landscapes. Since natural fitness landscapes are likely to be far more complicated, indeed too complicated to ever be measured completely, there is a need for a theory that describes the speed of adaptation over a broad range of landscapes in terms of just a few key features.

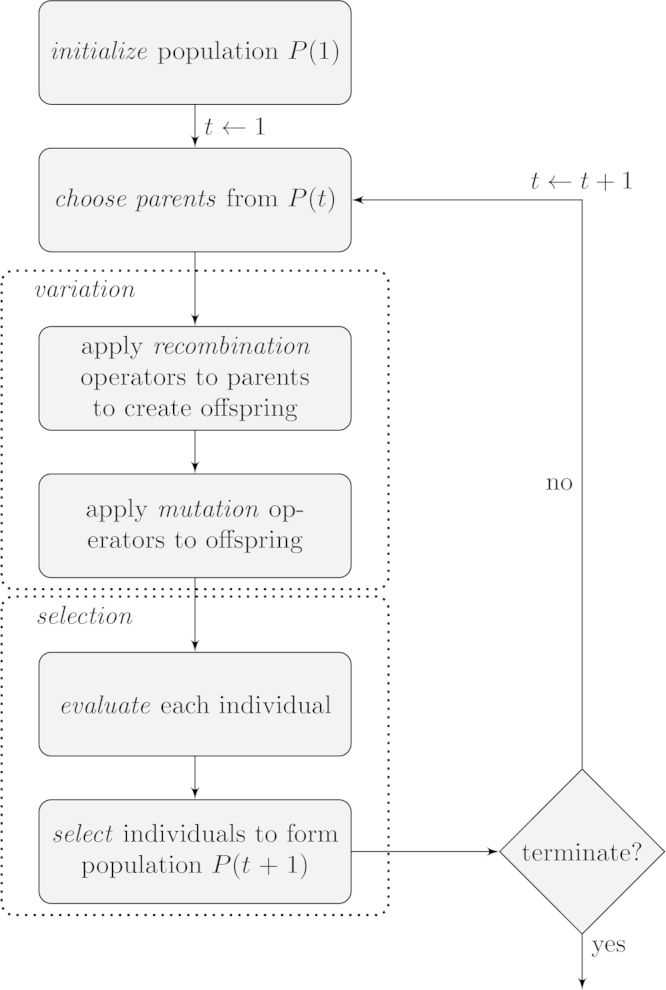
In evolutionary computation (EC), the evolutionary algorithm is the basic object of study. An evolutionary algorithm is a computational process that employs operators inspired by Darwinian principles to search a large state space. The basic scheme of an evolutionary algorithm is depicted in Fig. 1. However, specific concrete evolutionary algorithms differ in the details of each step, for example how elements are selected for reproduction or survival, or which variation operators are used. Evolutionary algorithms typically deal with finite populations and consider classes of fitness functions, in contrast with PG that mostly deals with specific instances. Moreover, these classes can be of arbitrary complexity, such as in the case of combinatorial optimization, again in contrast with PG, where mostly the simplest landscapes are considered.

Fig. 1.

A basic description of an evolutionary algorithm.

As can be seen, the questions and approaches both fields take are very different. However, the underlying processes share striking similarities. The basic processes of variation and selection, as proposed by Darwin, seem to be required, though these can appear in many different forms. Is there something general that could be said about evolutionary processes? Can we compare different evolutionary processes in a common framework, so that we can identify similarities that may not be obvious? What are the general features of an evolutionary process? What are the required properties of operations such as mutation or recombination? In fact, what is an evolutionary process?

In order to tackle these questions, we propose a general framework that is able to describe a wide range of evolutionary processes. The purpose of such a framework is to enable comparisons between different evolutionary models. We require this framework to be modular, so that different components of the evolutionary process can be isolated and independently analysed. In nature, this separation between the different processes does not necessarily exist. However, even when the different processes become entangled with each other, if the dynamics are slow enough, as is typical in natural systems, their relative order in the life-cycle becomes largely irrelevant. This will allow us to identify evolutionary regimes and evolutionary algorithms that are similar, allowing translation of results between the two fields. Furthermore, comparing related but different models and algorithms will allow us to disentangle the relative role of different processes or choices of process for the speed of adaptation.

A general framework for evolutionary models that is able to integrate models from both EC and PG in a way suitable for comparison should display the following properties:

• •The framework should be able to represent the vast majority of different evolutionary processes in a common mathematical framework.
• •The framework should be modular with respect to the different mechanistic processes of evolution (mutation, selection, etc.) and describe evolutionary processes as compositions of these processes.
• •It should be able to describe both finite and infinite populations and make it easy to relate infinite population models to their stochastic counterparts.

In this report we propose such a framework and we show that by instantiating several evolutionary processes within this framework we can find unsuspected similarities between different evolutionary algorithms and evolutionary regimes.

There have been several attempts at creating a general framework to describe different models in both PG and EC (Altenberg, 1995; Affenzeller, 2005), although none that created a general framework to describe different models in both. In the following section we review some of these other attempts at general models of evolution.

2. Related work

2.1. Population genetics models

In population genetics the dynamics of evolution are typically described in terms of the dynamics of allele or genotype frequencies. In a certain sense, this type of framework is a general model of evolution, albeit not a very useful one, because of its generality. It is akin to saying that the theory of differential equations is a general model of dynamics. However, there have been a few attempts at formalizing this dynamical process into more structured forms, suitable for comparison between different models.

Lewontin (1964) first introduced a general model of evolution for deterministic systems that is cast in terms of frequencies of genotypes. In this model, a basic recursion is defined that describes a canonical evolutionary system:

$$p(t+\mathrm{\Delta }t)=\sum _{y,z\in \mathcal{G}}T(x\leftarrow y,z)\frac{w(y,z)}{{\overline{w}}^2}p\left(y\right)p\left(z\right),$$

where p(x) represents the genotype frequency over the search space $\mathcal{S}$, w(x) represents the fitness of genotype x and $T(x\leftarrow z,y)$ is the so-called “genetic operator” that represents the probability (or rate) of generating genotype x from parents y and z due to the combined action of genetic operators (mutation, recombination, etc.). If reproduction is asexual and only selection is acting on the population, this operator will have a simple form, while more complex transmission will yield less simple forms. This model has been used to obtain a number of results for particular instances of the T operator (Slatkin, 1970; Cavalli-Sforza and Feldman, 1976). In order to unify several models of genes controlling transmission processes, Altenberg (1984) utilized and gave the first analysis of general transmission operators, which has since then be extended and analysed in much broader contexts (Altenberg and Feldman, 1987; Altenberg, 2010, 2012).

In the same spirit as the previous model, Barton and Turelli (1991) and Kirkpatrick et al. (2002) proposed a model that structures the different components of the evolutionary process. While the general form of Lewontin׳s model introduced by Altenberg (1984) leaves the transmission in general form so that it can represent any model of reproduction, here the focus is on allele frequencies and their associations between different loci. In the deterministic case, this model amounts to a change of coordinates that facilitates algebraic manipulation. When the population is at “linkage equilibrium”, or close to it, the model takes an especially simple form. This framework uses the notion of “context” in order to model many different situations, from structured populations (where the context is the physical location) to epistasis (where the context is the genetic background) and tracks associations between different sets of genes. This model makes it very easy to deal with multi-locus systems, from an algebraic point of view, and it has been used to address several questions, for example regarding the role of epistasis in different demographic conditions (Turelli and Barton, 2006; Barton and Turelli, 2004).

Both previous examples of a general framework focus on the dynamics of genotype or allele frequencies and are appropriate for analysis of different models. However, both frameworks are very tailored for biological systems, where selection assumes a particular form. For this reason, even though some modifications could be implemented, we believe that they lack some of the flexibility required to compare the structure of models in EC and PG.

Another type of general framework is exemplified by the approach that quantitative genetics takes: a purely phenotypic description of the evolution of some continuous trait (Falconer and Mackay, 1996). In this approach, a population is characterized by its genetic variance and its contribution to fitness. Typically, a decomposition of this genetic variance is used that partitions it into components that can contribute to the advance of the population with different relative strengths. This approach is only useful when (at least some) genetic recombination is assumed. Different processes (such as mutation) can be included in this type of framework by calculating their contribution to the genetic variance of the population. The fundamental relation in this framework is the so-called breeder׳s equation: $R=\beta V_A$, where R is the one generation increase of the mean of a given trait, β is the selection gradient, and V_A is the additive genetic variance of the population. More generally, one can write recursions for all moments of the distribution of phenotypes in the population. Different selection schemes can be cast into this framework, which has been of considerable value in animal breeding. In particular, results concerning the ultimate increase in a trait given a certain initial standing variation in a population, or optimal selection strategies were obtained under this framework. One drawback of this approach is that the recursions do not close, since the change in one of the moments depends on the next highest order moment. The downside of this framework is that it absolutely ignores the dynamics of the underlying genes and their relationships, and models all processes as effects on the dynamics of the genetic variance (or other statistical descriptors) of the population. This makes this framework unable to tackle questions about the optimality of different processes or about dynamics of genes or importance of genetic architecture. However, this approach is related to the previous one, by Barton and Turelli: if one rewrites the recursions in terms of allele frequencies one gets a form very close to the one these authors obtained.

An even more general framework of evolution comes in the form of the Price equation (Price, 1970, 1972). This equation assumes a population of replicating entities and considers the mean increase in some arbitrary property of these entities, which can be a trait, or fitness itself. If we assume that each individual in the population has a relative number of offspring $w_i=n_i/{\sum }_j{n}_j$, then the change of the mean of the trait z in one generation will be $\overline{w}\mathrm{\Delta }z=\mathrm{Cov}(w_i,z_i)+E\left[w_i\mathrm{\Delta }{z}_i\right]$. This approach is very general and related to the approach taken by quantitative genetics. Because the nature of this trait is not specified and the replicating entities are also abstract, this type of approach has been used to derive results in social evolution, and has influenced many other fields. The generality and simplicity of the Price equation make it very useful in comparing different mechanistic models and reduce them to their most fundamental characteristics.

Other general approaches to evolution have also been attempted. For example, genetic algebras (Schafer, 1949) were a field of active research some decades ago, but progress has slowed down considerably in later years. This approach identifies regularities in genetic inheritance rules with operations in mathematical algebras and describes the evolution of these populations. Genetic algebras are highly mathematical; their focus is in describing the consequences of different inheritance rules for the evolution of populations and seem less appropriate to describe other genetic operations such as mutation.

2.2. Evolutionary computation

Evolutionary algorithms (EAs) represent a category of algorithms which mimic artificial evolution of candidate solutions in order to solve or to produce approximate solutions to design and optimisation problems. There exist countless EA variants, often characterised by different principles inspired by nature or related to different problem domains. This made the attempts to unify models of EAs often scattered, or limited to some specific branch of computer science.

De Jong (2006) characterises a Darwinian evolutionary system by a set of core components: one or more populations of individuals competing for limited resources; the notion of dynamically evolving populations due to birth and death of individuals; a concept of fitness which reflects the ability of an individual to survive and reproduce; and a concept of variational inheritance: offspring resemble their parents but are not identical. Further, De Jong models the evolutionary algorithms by three general patterns: a population of constant size m is evolved over time, the current population is used as a source of parents to produce n offspring, and the expanded population is reduced from m+ n to m individuals. The specifications of an EA are the parameters m and n, the method for selecting the parents, the survival selection to reduce the population after reproduction to the original size, and how the reproductive process works.

Primarily inspired by the Simple Genetic Algorithm (SGA), Vose (1999a) has summarised many heuristic searches into a single framework, the so-called Random Heuristic Search. In this framework, a heuristic search can be seen as a collection/population of initial search points P₀ from the set of all possible search points $\mathcal{G}$ where $\left|\mathcal{G}\right|=2^n$, together with some transition rule τ to produce a new population from a given one. The search is then described by the series of transformation $P_0\stackrel{\tau }{\to }{P}_1\stackrel{\tau }{\to }{P}_2\stackrel{\tau }{\to }\cdots$ . The analyses of such a model require the characterisation or localisation of a given population, e.g. the current population, in the space of all possible populations. This is done with population vectors: a population vector of P is a real vector of length n and each component of the vector corresponds to the frequency of a specific element of $\mathcal{G}$ in P. Thus the set of all possible populations is the simplex $\Lambda =\{\langle p_1,\dots ,p_n\rangle \mid p_1+\cdots +p_n=1\}$. This is similar to the typical descriptions of populations used in PG, and detailed in the previous section. The advantage of this representation is that it is not necessary to specify the population size, e.g. it is easy to make assumptions about large or infinite populations. Several theoretical results, such as convergence rates, were deduced based on the properties of the admissible transition rules for large populations (see Vose, 1999a for a summary).

From a geometrical perspective, Moraglio (2007) has proposed a unifying framework to look at evolutionary algorithms. The framework requires a geometric structure to be identified on the space of solutions or the genotype space. Such a structure can be discovered by finding a metric distance measure between solutions, e.g. satisfying the symmetry and the triangle inequality. Based on the metric distance, several geometric objects, such as segments, balls or convex objects, can be defined. Then evolutionary operators can be categorised into geometric and non-geometric ones with respect to the distance measure. For example, a geometric recombination operator of two parent solutions should guarantee that the offspring will lie on the segment defined by the parents. From that the population can be represented by a certain “shape”, e.g., the convex hull enveloping the individuals, and the algorithm evolves by modifying this shape. Several theoretical results, such as the runtime, can be deduced from the geometric properties of the operators and the search space (see Moraglio, 2011). Many evolutionary operators are geometric under an appropriate metric distance measure, while for others it is unknown if such a distance measure exists. In addition, the global characteristic, e.g. non-zero probability of moving the population to any region of the search space in one step, of many variation operators is sometimes uncovered by geometric arguments (Moraglio and Sudholt, 2012). In related work, Droste and Wiesmann (2000) proposed a set of design guidelines for evolutionary algorithms. These included a set of desirable properties to be met by the recombination and mutation operators, as well as the genotype–phenotype mapping. Some of these properties are similar to those described in Section 4 of this paper.

Rabani et al. (1998) and Rabinovich et al. (1992) suggested modelling genetic algorithms by quadratic dynamical systems, a stochastic formalism which generalises Markov chains, much in the same way as Lewontin (1964), Slatkin (1970), and Altenberg (1984) in PG. Although powerful, this formalism has seen limited adoption, partly because starting from certain distributions, sampling from a quadratic dynamical system at any fixed time belongs to the class of PSPACE-complete problems (Arora et al., 1994), which are considered intractable.

As a branch of computer science, evolutionary computation is also concerned with computational complexity which attempts to characterise the inherent difficulty of computational problems when solved within a given model of computation, such as the Turing Machine model. Black box models have been developed in EC to capture the essential limitations of evolutionary algorithms and other search processes. In black box models, an adversary picks a function $f:{\{0,1\}}^n\to \mathbb{R}$ from a class of functions $\mathcal{F}$, which is known to the algorithm. The chosen function f is unknown to the algorithm, but the algorithm can query the function value f(x) for any bitstring $x\in {\{0,1\}}^n$. The goal of the algorithm is to identify a bitstring $x^{⁎}\in {\{0,1\}}^n$ that maximises f. The unrestricted black-box model (Droste et al., 2006) imposes no further restrictions on the algorithm. In the ranking-based black-box model, the algorithm can only query for the relative order of function values of search points (Teytaud and Gelly, 2006; Doerr and Winzen, 2011). In the memory-restricted black-box model (Droste et al., 2006; Doerr and Winzen, 2012), the algorithm has limited memory. The unbiased black-box model (Lehre and Witt, 2012) puts restrictions on how new search points can be generated. This model defined unbiased variation operators of any arity, but only unary variation operators (such as mutation operators) were analysed initially. Later, higher arity operators (such as crossover) were also analysed (Doerr et al., 2011), as well as more general search spaces (Rowe and Vose, 2011). This approach is appropriate to estimate the fundamental limits of an evolutionary process in a given class of functions. However, it seems unnatural to use it to decompose an evolutionary process into its fundamental sub-processes.

Reusability and easy implementation are often concerns of the users of evolutionary algorithms, both practitioners and researchers. Many efforts have been made to address this issue from the perspective of software engineering. In fact, many evolutionary operators have the same type of input and output. In addition, they can handle the elements of the input at a very abstract level and can be unified. From the user perspective the implementation of an evolutionary algorithm on a specific problem is boiled down mostly to the selection of solution representation and the definition of the evaluation procedure. Many software libraries for evolutionary algorithms are based on this principle, some examples are ECJ (Luke), GALib (Wall) or ParadisEO (Cahon et al., 2004, INRIA). Generally speaking, some implicit unified models exist in those frameworks. Our framework is in parts inspired by FrEAK, the Free Evolutionary Algorithm Kit (Briest et al., 2004), a free toolkit for the creation, simulation, and analysis of evolutionary algorithms within a graphical interface. Evolutionary algorithms in FrEAK are represented by operator graphs: acyclic flow graphs leading individuals through various nodes. The nodes represent evolutionary operators like mutation, recombination, and selection. They process the incoming individuals and propagate the result of an operation through their outgoing edges. Every generation, the current population is led through the algorithm graph from a start node towards a finish node where the new population is received. This modular approach allows the representation of a wide variety of evolutionary processes that differ in the composition and sequence of operators applied.

3. A unifying framework for evolutionary processes

In a general sense, any evolutionary process (natural or artificial) can be seen as a population undergoing changes over time based on some set of transformations. Formally, given a finite set $\mathcal{G}$, called the genotype space or genospace, an evolving finite population is a sequence

$$\left(P\left(1\right),P\left(2\right),\dots ,P\left(t\right),\dots \right),$$

where each $P\left(t\right)\in {\mathcal{G}}^k$, meaning that each P(t) contains $k$ elements (individuals) of $\mathcal{G}$. Formally, P (t) is a sequence, a mathematical object that generalizes the notion of set by allowing multiple copies of the same element,and in which the ordering of the elements matter. Our framework is designed to describe and classify the particular operations for transforming P(t) into $P(t+1)$ in any evolutionary process. Specifically, we are interested in characterizing the random mapping¹ $\psi :{\mathcal{G}}^k\to {\mathcal{G}}^k$ such that

$$P(t+1)=\psi \left(P\right(t\left)\right).$$

Our approach decomposes $\psi$ into a collection of modular operators that each has a distinct and elementary role in the evolutionary process. Typically, these operators act on sequences of $\mathcal{G}$. These sequences are typically constructed from the elements of P(t), from the output of operators, and from the concatenation operator. Given two finite sequences $x\in {\mathcal{G}}^{\ell }$ and $y\in {\mathcal{G}}^m$, we denote the concatenation of x and y as $x\cup y$, which is an element of ${\mathcal{G}}^{\ell +m}$. Given two operators $G_1:{\mathcal{G}}^{\ell }\to {\mathcal{G}}^n$ and $G_2:{\mathcal{G}}^m\to {\mathcal{G}}^{\ell }$ that act on sequences of $\mathcal{G}$, we denote the composition of G₁ and G₂ as the operator $(G_1○G_2):{\mathcal{G}}^m\to {\mathcal{G}}^n≔x\mapsto G_1\left(G_2\right(x\left)\right)$.

Sequences describe finite populations and operators typically perform stochastic operations on the elements of these sequences (the individuals in the population). The outcome of the action of these stochastic operators can also be described by a probability distribution of potential outcomes, which can be used to induce a different level of description of the evolutionary process. This suggests that an evolutionary process can be defined as a trajectory through a space of distributions S (the space of all genotype frequency distributions, represented by the $\left|G\right|-1$ dimensional simplex). Formally, we can view these operators acting in this distribution space

$$\left(D\left(1\right),D\left(2\right),\dots ,D\left(t\right),\dots \right).$$

Each D(t) is an element of a set of distributions over populations. Analogously, we might have some transformation

$$D(t+1)=\varphi \left(D\right(t\left)\right),$$

where $\varphi$ can be decomposed into modular operators that are homologous to the operators in $\psi$ (Fig. 2). The distribution at time t+1 might even depend somehow on the state of the finite population at time t. In some algorithms and models, the finite population of size $k$ at time t+1 can be constructed by sampling $k$ elements from the distribution at time t+1. We denote this sampling operator as ${\beta }_k$. Given any distribution $D\in S$ over the set of genotypes, we can obtain a concrete population of size $k$ by applying the sampling operator ${\beta }_k:S\to {\mathcal{G}}^k$ defined as

$${\beta }_k\left(D\right)≔{(X_i)}_{i\in \left[k\right]}\mathrm{where}{X}_1,\dots ,X_k~D.$$

where ~ denotes that all the X_k are independently and identically distributed as the distribution D. An operator $G:{\mathcal{G}}^k\to \mathcal{G}$ acting on genotypes, can be “lifted” to a mapping $\widehat{G}:S\to S$ between distributions as follows. Given any distribution $D\in S$, we define $\widehat{G}\left(D\right)$ to be the distribution where

$$\mathrm{Pr}(Z=z\mid Z~\widehat{G}(D\left)\right)≔\mathrm{Pr}\left(G\right(X_1,\dots ,X_k)=z\mid X_1,\dots ,X_k~D).$$

Fig. 2.

The evolution process represented as a sequence $\left\{D\right(t):t\in \mathbb{N}\}$ of distributions and a sequence $\left\{P\right(t):t\in \mathbb{N}\}$ of vectors in ${\mathcal{G}}^k$ (concrete populations) that depend on each other via various mappings. Each mapping is constructed by a composition of evolutionary operators that we characterize and classify in this work.

To make this concrete, consider an operator that acts on bitstrings and flips each bit with probability p. When acting on a definite bitstring, say ${\overline{g}}_1=\left(0,1\right)$, this operator will create bitstrings ${\overline{g}}_0=\left(0,0\right)$, ${\overline{g}}_2=\left(1,0\right)$, and ${\overline{g}}_3=\left(1,1\right)$ with probabilities ${\psi }_{1|0}=(1-p)p$, ${\psi }_{1|2}=p^2$, and ${\psi }_{1|3}=p(1-p)$. In this example $D\left(t\right)=\left(0,1,0,0\right)$, where the positions refer to the probabilities of g₀, g₁, g₂ and g₃, and, under the action of this operator, $D(t+1)=\left((1-p)p,{(1-p)}^2,p^2,(1-p)p\right)$. The probabilities that the operator produces any genotype, when applied to any genotype represents the “lifting” of this operator. Any finite population can be described as a frequency distribution of genotypes and the action of this operator on a population can be described by convolving this frequency distribution with the “lifted” operator on each of the individual genotypes. This produces a probability distribution on the genotype produced by the operator, given that we are choosing the individual it acts on uniformly from the population. This distribution can then be used to produce a new population by sampling from it.

“Lifted operators” can also be seen as the “infinite population size” version of the stochastic operator, since when applied to a frequency distribution, they produce a frequency distribution of the expectation (a statistic) of this operator. This is done by the map $\alpha :{\mathcal{G}}^k\to S$ (Fig. 2). Sampling operations are the only ones that explicitly project from the distribution space into the populations space. Some types of operators explicitly involve some kind of sampling operation (e.g. selection operators, discussed below), but can always be written as a combination of a “lifted”/deterministic operator and a sampling operation.

Some models operate only at the level of populations, others only at the level of distributions and others shift between the levels. For a complete picture, we model the evolutionary process at both levels by two sequences, one in the space of populations, and one in the space of distributions. Our framework then characterizes and classifies the components that comprise the various transformations between these two sequences, and their roles in defining the evolutionary process. This is described in Fig. 2.

3.1. The nature of evolving entities

In each iteration of an evolutionary process, which is called a generation, the operators that comprise $\psi$, $\varphi$, ${\beta }_k$, and $\alpha$ work together to act on the current population to generate a new one. Each operator acts directly on the genotype space, but some operators also depend on information that lies in a broader phenotype space. Each individual of a population is mapped into this phenotype space, and this transformation is called the genotype–phenotype mapping in population genetics. In evolutionary computation, the transformation corresponds to the decoding process from genome to solution, e.g. in an indirect encoding scheme. Another transformation will act on this set of phenotypes and assign to each individual of the population a “reproductive value”, which can be seen as a probability of survival or inclusion into the next generation. For evolutionary algorithms, the phenotype-fitness mapping is broken down into evaluation of the objective function and various ways to select individuals for the next generation and the next reproduction based on the obtained objective values. Finally, a population that was funnelled through this process is transformed by variation operators, producing a new population.

The two mapping processes are depicted in Fig. 3. The genotype and phenotype spaces are sets $\mathcal{G}$ and $\mathcal{P}$ respectively. The genotype–phenotype mapping is a function $\phi$ from $\mathcal{G}$ to $\mathcal{P}$. An individual g is an element of $\mathcal{G}$ that has phenotype $\phi \left(g\right)$, which in turn as objective value $f\left(\phi \right(g\left)\right)$. A population P is a sequence of elements of $\mathcal{G}$, e.g. $P\in {\mathcal{G}}^k$ for a population of size $k$.

Fig. 3.

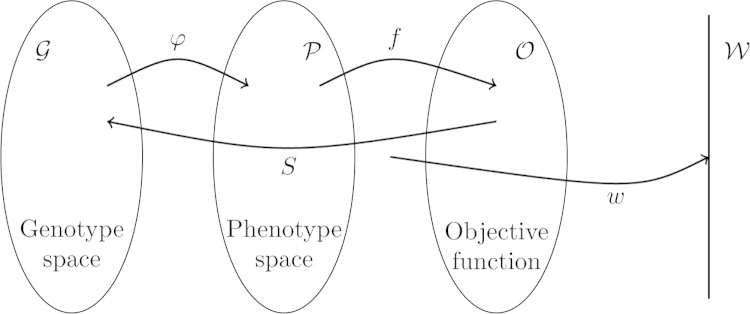
A basic sequence of operations leading to a selectable population. A population distributed over the genotype space $\left(\mathcal{G}\right)$ is assigned phenotype values $\left(\mathcal{P}\right)$ via the genotype–phenotype mapping $\phi$, which are then interpreted by f into objective function values $\left(\mathcal{O}\right)$. Variation operators generate new variation at the genotypic level and selection operators act at the level of the objective function, generating a new population in $\mathcal{G}$. The $\mathcal{W}$ line represents the probability for this individual to be present in the next generation, which is a consequence of the selection operators used. This is typically called “fitness” in PG and is related to the reproductive rate in EC.

The dual representation of individuals as pairs of genotypes and phenotypes immediately suggests the existence of two kinds of operators: operators that act primarily on genotypes and operators that act primarily on phenotypes. Those are the basic ingredients in Darwin׳s theory of natural evolution: variation and selection. As such, it is natural to make the distinction between these two kinds of operators and to identify them with operations that act on these two spaces. We can then see evolution as a series of applications of these two kinds of operators. Because evolutionary algorithms are very diverse in their mode of operation, the relative order and frequency with which any of these operators act on the population are largely arbitrary. Hence, various evolutionary processes can be conceived by specifying different orders, e.g. in which variation operators act first and selection last, or even schemes in which different kinds of selection or variation operators act at different stages of the process and populations are built from the union of the result of the operation of different operators. This will be detailed when we instantiate a particular evolutionary process in our framework in Section 5.

At the same time, this dual nature of evolutionary objects (genotype and phenotype) immediately allows one to deduce some properties of the $\mathcal{G}$ and $\mathcal{P}$ spaces. Even though both $\mathcal{G}$ and $\mathcal{P}$ may have natural metrics the relevant metric distance for evolution is dependent on both the way genotypes change (mutation) and the mapping function between the two spaces $\phi$. How close two genotypes are depends on the mutation operator (Altenberg, 1995), on how likely or difficult it is to turn one into the other, whereas how close two phenotypes are depends on how close the closest genotypes that produce that pair of phenotypes are from each other. From this we see that even though we started by defining both genotype and phenotype spaces as sets, in reality, in the context of an evolutionary process, they can be imbued with more structure. Typically, the cardinality of $\mathcal{G}$ is larger than of $\mathcal{P}\left(\right|\mathcal{G}|\ge |\mathcal{P}\left|\right)$. This is because the genotype–phenotype mapping is typically redundant, meaning that many genotypes map to the same phenotype. This can lead to some phenotypes having a bigger pool of genotypes that map to them and, consequently, even if the change at the genotypic level is isotropic, the change at the phenotypic level is not necessarily so. This is similar to the notion of phenotypic accessibility that Stadler et al. have proposed (Stadler et al., 2001).

In the following section, we define the evolutionary operators and formalise their properties. The following symbols will be used for these purposes.

Symbol	Definition	Examples
$\Sigma$	Set of alleles	$\{0,1\}$, $\{A,T,G,C\}$
$\mathcal{G}$	Space of genotypes	${\Sigma }^n$ (strings of length $n$ over the alphabet $\Sigma$)
$\mathcal{P}$	Space of phenotypes	Genetic traits
S	Space of all distributions of genotype frequencies
P(t)	A finite collection of genotypes at time t	{(0,0), (0,1), (0,0)}
D(t)	A probability distribution describing the probability of sampling any genotype
$\phi :\mathcal{G}\to \mathcal{P}$	Genotype–phenotype mapping	Transformation from genes to proteins then traits
$\mathrm{V}:{\mathcal{G}}^k\to {\mathcal{G}}^{\ell }$	Variation operator	Mutation $\left(\mathrm{M}\right)$, recombination $\left(\mathrm{R}\right)$
$\mathrm{S}:{\mathcal{G}}^k\to {\mathcal{G}}^{\ell }$	Selection operator	Uniform, proportional selection
$\psi$	Mapping between populations at each time step, composition of variation and selection operators	$\psi =\mathrm{V}○\mathrm{S}$, $P(t+1)=\psi \left(P\right(t\left)\right)$
$\varphi$	Mapping between abstract distributions at each time step, composition of lifted variation and selection operators	$\varphi =\widehat{\mathrm{V}}○\widehat{\mathrm{S}}$, $D(t+1)=\varphi \left(D\right(t\left)\right)$
$\alpha$	Mapping from populations to distributions
${\beta }_k$	Distribution sampling operator	$P(t+1)={\beta }_k\left(D\right(t+1\left)\right)$
$w$	The probability of a genotype to be present in the next generation. Fitness (sensu PG) or reproductive rate (sensu EC)

4. Evolutionary operators

In order to be able to compare and contrast different evolutionary algorithms and models (processes) we need to break down these processes into their different components. We typically define operators as acting on finite populations. Given a current population P(t), the population in the next generation becomes $P(t+1)=\psi \left(P\right(t\left)\right)$. As pointed out above, the distinction between variation at the genotypic and the phenotypic levels makes it natural to associate different operators that operate at these different levels, variation and selection operators, respectively.

4.1. Selection operators

Selection operators can be used to choose individuals for either reproduction, the so-called parent selection, or for survival, e.g. deciding which individuals will be kept in the next generation. As a consequence, they model competitiveness in different types of populations. Nevertheless, the selection operators are defined in the same way: they have access to the phenotypic information (or the mappings $\phi$) and transform one population to another, i.e.,

$${\mathrm{S}}_{\phi }:{\mathcal{G}}^k\to {\mathcal{G}}^{\ell }.$$

For simplification, we also omit $\phi$ from the notation. Selection operators do not introduce variation (in the sense of new genotypes), hence their defining property is that every element in the output population should be the exact copy of an element from the input population. Formally,

$$\forall g\in \mathcal{G}\mathrm{if}g\in \mathrm{S}\left(P\right)\mathrm{then}g\in P.$$ (S1)

Selection operators guide the search by taking advantage of local information in the fitness function $w$. To describe this process, the mapping $\phi$ first associates to each genotype g a set of $\tau$ measurable phenotypic traits, denoted by $\left({\phi }_1\right(g),\dots ,{\phi }_{\tau }(g\left)\right)\in {\mathfrak{R}}^{\tau }$. To each of these sets of traits the objective function associates a value, representing the adaptiveness of the combination of the traits through interactions with the environment. The selection operators will then sample individuals to be represented in the next generation based on the value of the objective function. This process effectively assigns each individual a probability that it will be represented in the next generation or a reproduction rate. This is typically what is meant in PG as “fitness” $\left(w\right)$. It is common in both fields to collapse some of these steps into one, effectively assuming the identity operator for one or more of the transformations we just described. In population genetics, $w$ could be arbitrarily chosen, depending on the objective of the study. In evolutionary computation, the phenotypic traits $\left({\phi }_1\right(g),\dots ,{\phi }_{\tau }(g\left)\right)$ are typically collapsed to the objective function, which is multiple for $\tau >1$ or single for $\tau =1$, and $w$ is rather a property deduced from the selection mechanism. However, it should be noted that even implicitly most models still define a phenotype which is distinct from the objective function. For example, in EC, it is common practice to analyze the performance of EAs on functions of unitation (functions that take as argument the number of 1 s in the bitstring). In this case, it is natural to call the number of 1 s the phenotype and the function of unitation the objective function. Very similar models of phenotype - objective function pairs exist in biology.

It should be noted that the distinction we make here between variation and selection operators, and the different properties we will require of them, resolve some philosophical questions regarding the concept of “fitness”. In PG, fitness is typically defined as the “the expected number of offspring of an individual”, while in EC fitness it is the value of the objective function in question. Even though related, the subtly different meanings of this concept in the two communities still lead to much confusion. Because the expected number of offspring of a given genotype can change due to factors that have nothing to do with selection, the concept is hard to operationalize in the real world. In fact, in theoretical population genetics fitness is often defined as a function of some underlying genotype and, in this case, it has exactly the same meaning as in EC, which has lead to confusion even within the PG community. In our framework, fitness, sensu PG, can be obtained directly from the selection operators and consists of a derived property from the selection operator used (and the functions it takes as parameters). In EC, this sense of fitness has been called the reproduction rate (Table 1).

Table 1.

A list of concepts in both fields and their translation between the fields.

PG	EC	Meaning
Neutrality	Uniform selection	All individuals in the target population are equally likely to be selected into the next generation. This is equivalent to no selection or what is called random drift in PG
–	Drift	The change in expectation of some quantity over the stochastic process. It is typically the expected advance of the algorithm, conditional on the current state
Genetic drift	Genetic drift	It is typically meant to refer to the stochasticity associated with sampling from finite populations
Unlinked genes	Uniform crossover	A recombination pattern in which the probability of inheriting the gene copy from any of the parents is 1/2 and does not depend on its position in the genome
Selection coefficient	Reproduction rate	The relative growth advantage of an allele or genotype over the mean of the population. It is formally defined as $s=\frac{W_i-\overline{W}}{\overline{W}}$. It is related to the “reproduction rate” concept in EC. In our framework, this is a quantity derived from the particular selection scheme imposed to the population. As can be seen from the formal definition, it depends on the current composition of the population
Overlapping generation models	Elitist algorithms	Models in which the population at the next time step (iteration) is selected from the combined pool of parents and offspring. In PG this is termed iteroparity. These are termed elitist because when used in conjunctions with cut selection (+-selection) this guarantees that the best individual is always kept
Non-overlapping (or discrete) generation models	Generational algorithms	Models in which the population at the next time step (iteration) is selected solely from the offspring (which may be exact copies of the parents) of the parents. In PG this is termed semelparity.

The following operators are commonly used in evolutionary algorithms (assuming maximization problems) and by their definition satisfying (S1).

Uniform selection: Under this selection operator, denoted by ${\mathrm{S}}_{\mathrm{Unif}}$, each individual of the output population has an equal probability of being a copy of each individual from the input population. Formally,

$${\mathrm{S}}_{\mathrm{Unif}}\left(\right(g_1,\dots ,g_k\left)\right)=(g_1^{\prime },\dots ,g_{\ell }^{\prime })\mathrm{s}.\mathrm{t}.\mathrm{Pr}\left(g_i^{\prime }=g_j\right)=1/k\mathrm{for}\mathrm{all}i\in [\ell ],j\in \left[k\right].$$

There are two ways to implement this selection operator. The standard way, denoted by ${\mathrm{S}}_{\mathrm{Unif}}$, is independent uniform sampling $g_i^{\prime }~\mathrm{Unif}\left(\right(g_1,\dots ,g_k\left)\right)$ with replacement. Another way, which is denoted by ${\mathrm{S}}_{\mathrm{Unif}}^{⁎}$, is to do the sampling without replacement. In this variant, the outcomes of the sampling are no longer independent but exchangeable, hence they preserve the required property on the equal probability $1/k$.

Proportional selection: This selection operator is defined similar to uniform selection, except that instead of having an equal probability for each individual, the probability of choosing a particular individual is proportional to the value of an objective function f on that individual. Formally,

$${\mathrm{S}}_{\mathrm{Prop}\left(f\right)}\left(\right(g_1,\dots ,g_k\left)\right)=(g_1^{\prime },\dots ,g_{\ell }^{\prime })\mathrm{s}.\mathrm{t}.\mathrm{Pr}\left(g_i^{\prime }=g_j\right)=\frac{f\left(g_i\right)}{{\sum }_{j=1}^{k}f\left(g_j\right)}\mathrm{for}\mathrm{all}i\in [\ell ],j\in \left[k\right].$$

Note that in PG, f is replaced by the fitness function $w$, which gave the original name for the selection mechanism. In implementations, $g_i^{\prime }$ is independently sampled from a custom distribution defined by the probabilities $f\left(g_i\right)/{\sum }_{j=1}^{k}f\left(g_j\right)$.

Tournament selection: This selection operator, denoted by ${\mathrm{S}}_{\mathrm{Tour}(f,m)}$, performs a number of experiments, called tournaments, with respect to some objective function f. In those tournaments, an individual with the highest value of f is selected from a randomly chosen subset of P of size $m$. Formally, ${\mathrm{S}}_{\mathrm{Tour}(f,m)}:{\mathcal{G}}^k\to {\mathcal{G}}^{\ell }$ is defined as

$${\mathrm{S}}_{\mathrm{Tour}(f,m)}\left(\right(g_1,\dots ,g_k\left)\right)=(g_1^{\prime },\dots ,g_{\ell }^{\prime })\mathrm{s}.\mathrm{t}.g_i^{\prime }=\underset{f\left(x\right)}{\arg \max }\{x\in P_i\}\mathrm{for}\mathrm{all}i\in [\ell ]\mathrm{where},P_i={\mathrm{S}}_{\mathrm{Unif}\left(m\right)}\left(\right(g_1,\dots ,g_k\left)\right).$$

Here ${\mathrm{S}}_{\mathrm{Unif}\left(m\right)}\left(\right(g_1,\dots ,g_k\left)\right)$ is the uniform selection described above with the size of the output population explicitly given as m. For $m\le k$, the use of ${\mathrm{S}}_{\mathrm{Unif}\left(m\right)}^{⁎}\left(\right(g_1,\dots ,g_k\left)\right)$ instead implies the variant ${\mathrm{S}}_{\mathrm{Tour}(f,m)}^{⁎}$ of the selection.

Truncation selection: Under this selection operator, denoted by ${\mathrm{S}}_{\mathrm{Trunc}(f,m,n)}$, each output individual is uniformly selected from a fixed fraction, for example 10%, of the fittest individuals defined by a measure f of the input population. Formally, an ordering of a population is defined as

$${\mathrm{S}}_{\mathrm{Sort}\left(f\right)}\left(\right(g_1,\dots ,g_k\left)\right)=(g_{\mathrm{r}\left(1\right)},\dots ,g_{\mathrm{r}\left(k\right)})\mathrm{s}.\mathrm{t}.f\left(g_{\mathrm{r}\left(1\right)}\right)\ge \cdots \ge f\left(g_{\mathrm{r}\left(k\right)}\right).$$

The ordering is entirely defined by the bijection $\mathrm{r}:\left[k\right]\to \left[k\right]$ so that $\mathrm{r}\left(i\right)$ is the individual at rank i in the population. Truncation selection of $n$ individuals among the fittest $m$ individuals in the population P is defined as

$${\mathrm{S}}_{\mathrm{Trunc}(f,m,n)}\left(P\right)=({\mathrm{S}}_{\mathrm{Unif}\left(n\right)}○{\mathrm{S}}_{\mathrm{Trim}(f,m)})\left(P\right)\mathrm{where}{\mathrm{S}}_{\mathrm{Trim}(f,m)}\left(\right(g_1,\dots ,g_k\left)\right)=(g_{\mathrm{r}\left(1\right)},\dots ,g_{\mathrm{r}(\ell )})\mathrm{s}.\mathrm{t}.f\left(g_{\mathrm{r}(\ell )}\right)\ge f\left(g_{\mathrm{r}\left(m\right)}\right)\mathrm{and}f\left(g_{\mathrm{r}(\ell +1)}\right)<f\left(g_{\mathrm{r}\left(m\right)}\right).$$

Cut selection: This selection operator, denoted by ${\mathrm{S}}_{\mathrm{Cut}(f,m)}$, is closely related to the truncation selection above. However, it is more deterministic because it simply keeps the best $m$ individuals with respect to f of the input population of size $k\ge m$, whereas ${\mathrm{S}}_{\mathrm{Trunc}(f,m,n)}$ samples uniformly with replacement from this set:

$${\mathrm{S}}_{\mathrm{Cut}(f,m)}\left(\right(g_1,\dots ,g_k\left)\right)=(g_{\mathrm{r}\left(1\right)},\dots ,g_{\mathrm{r}\left(m\right)}).$$

Moreover, the output population size is exactly $m$, the parameter of the selection. In the case that there are many input individuals with the same value $f\left(g_{\mathrm{r}\left(m\right)}\right)$, we additionally require a tie-breaking rule. Unless specified otherwise, it is understood that ties are broken uniformly at random.

Replace selection: It is also useful to define a class of selection operators that act on populations of size 2, and make use of the fact that populations are defined as sequences, as opposed to simply sets. This type of selection uses the difference in objective function value between the two genotypes, filtered through a function $h:\mathcal{O}\to \left[0,1\right]$, to select which of the two will be present in the next generation. We define $S_{\mathrm{Rep},h}$ as

$$S_{\mathrm{Rep},\mathrm{h}}\left(\right(g_1,g_2\left)\right)=\{\begin{array}{cc}{g}_2\hfill & \mathrm{with}\mathrm{probability}h\left(\Delta \right)\hfill \\ g_1\hfill & \mathrm{with}\mathrm{probability}1-h\left(\Delta \right)\hfill \end{array}$$

where $\Delta =f\left(\phi \right(g_2\left)\right)-f\left(\phi \right(g_1\left)\right)$. Note that the previous operators ${\mathrm{S}}_{\mathrm{Trim}(f,m)}$, ${\mathrm{S}}_{\mathrm{Trunc}(f,m,n)}$, ${\mathrm{S}}_{\mathrm{Cut}(f,m)}$, ${\mathrm{S}}_{\mathrm{Prop}\left(f\right)}$ and ${\mathrm{S}}_{\mathrm{Unif}}$ could be cast in terms of replacement operators when applied to populations of size two to produce populations of one individual, given appropriate choices of h functions.

Note that the operators ${\mathrm{S}}_{\mathrm{Sort}\left(f\right)}$, ${\mathrm{S}}_{\mathrm{Trim}(f,m)}$ and ${\mathrm{S}}_{\mathrm{Unif}}$ satisfy (S1) and so does ${\mathrm{S}}_{\mathrm{Trunc}(f,m,n)}$. In evolutionary computation, the particular case of ${\mathrm{S}}_{\mathrm{Trunc}(f,\mu ,\lambda )}:{\mathcal{G}}^{\mu }\to {\mathcal{G}}^{\lambda }$ is referred to as the $(\mu ,\lambda )$-selection mechanism.

4.2. Variation operators

Variation operators create the variability on which selection operators can act. Two classes of variation operators can be distinguished: mutation operators and recombination operators. The major distinction between the two classes of operators is the level of variation they generate. Mutation is typically applied to a single genotype and generates new variation by introducing new variants at the allelic level. On the other hand, recombination is typically applied to a set of genotypes, often two genotypes in the biological systems we know of, and generates variation by constructing new genotypes from the ones that currently exist in the population. Hence recombination can be seen as shuffling the genetic materials within the population without changing the allele frequencies. In the following, we identify the defining features of these two types of operators and also some properties that provide relevant distinctions between operators of the same type.

We say a variation operator $\mathrm{V}$ is uniformity-preserving when the following holds

$$\mathrm{if}P~\mathrm{Unif}\left({\mathcal{G}}^{\left|P\right|}\right),P^{\prime }=\mathrm{V}\left(P\right)\mathrm{then}{P}^{\prime }~\mathrm{Unif}\left({\mathcal{G}}^{\left|P^{\prime }\right|}\right).$$ (V1)

Intuitively, this property simply states that if the population is distributed uniformly through the space of all genotypes, then the variation operator will not change its distribution, i.e. the (mutated or recombined) population will also be uniformly distributed in genotype space. Uniformity-preserving operators do not have an inherent bias towards particular regions of the genospace. This is a desired feature in evolutionary algorithms, when no specific knowledge on the problem is available (Droste and Wiesmann, 2000). For an example of a mutation operator that is not uniformity-preserving, we refer to Jansen and Sudholt (2010); the asymmetric mutation operator presented therein flips zeros and ones with different probabilities and drives evolution towards bitstrings with either very few zeros or very few ones.

Lemma 1 in Appendix A states a sufficient, but not necessary condition for a variation operator $\mathrm{V}:{\mathcal{G}}^k\to \mathcal{G}$ to satisfy (V1). Note that for unary variation operators, i.e. for operators that act on individual genotypes (such as mutation; k=1 in Lemma 1), the conditions of Lemma 1 imply that the variation operator must be symmetric, i.e. the probability of generating genotype x by the application of the variation operator on genotype y is the same as the probability of generating y from x (formally, for all $x,y\in \mathcal{G}$, it holds that $\mathrm{Pr}\left(X=y\mid X~\mathrm{V}\left(x\right)\right)=\mathrm{Pr}\left(X=x\mid X~\mathrm{V}\left(y\right)\right)$.

4.2.1. Mutation operators

Mutations are the raw material on which selection can act. In biological populations, variation is created by mutation and is typically assumed to be random with respect to selection, meaning that the variation generated is isotropic in genotype space.

$$\mathrm{M}:{\mathcal{G}}^k\to {\mathcal{G}}^k.$$

Mutation can be regarded as an operator for both populations and individuals, such that mutation is applied to each individual in the population: $\mathrm{M}\left(\right(g_1,\dots ,g_s\left)\right)=\left(\mathrm{M}\right(g_1),\dots ,\mathrm{M}(g_s\left)\right)$. Mutation typically acts independently on each individual in the population. Formally:

$$\forall P=(g_1,\dots ,g_k)\in {\mathcal{G}}^k,\forall P^{\prime }=(g_1^{\prime },\dots ,g_k^{\prime })\in {\mathcal{G}}^k,\mathrm{Pr}\left(\mathrm{M}\left(P\right)=P^{\prime }\right)=\prod _{i=1}^k\mathrm{Pr}\left(\mathrm{M}\left(g_i\right)=g_i^{\prime }\right).$$ (M1)

Mutation can be seen as the basic search operator. From this perspective it is natural to require that mutation operators, acting on the level of individuals, are able to generate the whole search space $\mathcal{G}$. In other words, mutation is an ergodic operator of $\mathcal{G}$ (meaning that its orbits are aperiodic and irreducible). We formalize this by

$$\forall x,y\in \mathcal{G},\exists t\ge 0,\mathrm{Pr}\left(Y=y\mid Y~{\mathrm{M}}^t\left(x\right)\right)>0,$$ (M2)

where ${\mathrm{M}}^t$ denotes the operator formed by composing $\mathrm{M}$ with itself t times. We hold (M2) to be the defining characteristic of mutation operators.

To illustrate variation operators and their properties, we now discuss common mutation operators.

Uniform mutation: Let $\mathcal{G}={\Sigma }_1\times {\Sigma }_2\times \cdots \times {\Sigma }_n$ where each ${\Sigma }_i$ is a finite set of at least two elements. For $p\in [0,1]$, uniform mutation is a random operator ${\mathrm{M}}_p:\mathcal{G}\to \mathcal{G}$ defined as follows. For any string $x\in \mathcal{G}$, the result of applying the operator to x is another string ${\mathrm{M}}_p\left(x\right)=(Y_1,\dots ,Y_n)$ where each Y_i is an independent random variable defined for all $y_i\in {\Sigma }_i$ by

$$\mathrm{Pr}\left(Y_i=y_i\right)=\{\begin{array}{cc}1-p\hfill & \mathrm{if}{y}_i=x_i\mathrm{and}\hfill \\ {\displaystyle \frac{p}{\left|{\Sigma }_i\right|-1}}\hfill & \mathrm{otherwise}.\hfill \end{array}$$

In many applications in evolutionary computation, uniform mutation is performed on bitstrings, that is ${\Sigma }_i=\{0,1\}$ for all $i\in \{1,\dots ,n\}$. In this case, when $p=1/n$, we refer to the operator as standard mutation, and denote it ${\mathrm{M}}_{1/n}$. It should be noted that this operator satisfies properties (V1) and (M1). Moreover, as long as $0<p<1$, it also satisfies (M2) (see Lemma 2 in Appendix A).

Single-point mutation: Let $\mathcal{G}={\Sigma }_1\times {\Sigma }_2\times \cdots \times {\Sigma }_n$ where each ${\Sigma }_i$ is a finite set of at least two elements. Single-point mutation is a random operator ${\mathrm{M}}_{\mathrm{sp}}:\mathcal{G}\to \mathcal{G}$ that acts as follows. For any string $x\in \mathcal{G}$, the result of applying the operator to x is another string ${\mathrm{M}}_{\mathrm{sp}}\left(x\right)=(Y_{1,k},Y_{2,k},\dots ,Y_{n,k})$ where $k~\mathrm{Unif}(1,n)$ and each $Y_{i,k}$ is a dependent random variable defined for all $y_i\in {\Sigma }_i$ with

$$\mathrm{Pr}\left(Y_{i,k}=y_i\right)=\{\begin{array}{cc}1\hfill & \mathrm{if}i\ne k,y_i=x_i\mathrm{and}\hfill \\ {\displaystyle \frac{1}{\left|{\Sigma }_i\right|-1}}\hfill & \mathrm{if}i=k,y_i\in {\Sigma }_i⧹\left\{x_i\right\}\mathrm{and}\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}$$

Single-point mutation satisfies properties (V1), (M1), and (M2) (Appendix A, Lemma 3).

4.2.2. Recombination operators

The role of recombination is to generate variation at the genotypic level, by shuffling information contained in the existing genotypes. In order to define recombination we require that the elements of $\mathcal{G}$ are ordered Cartesian products of sets: $g\in {\Sigma }_1\times {\Sigma }_2\times \cdots \times {\Sigma }_n$, where ${\Sigma }_i$ is the set of available symbols at position i, e.g. we do not require ${\Sigma }_i={\Sigma }_j$ for $i\ne j$.

Let $[·]$ denote the Iverson bracket, which denotes a 1 if the condition inside the bracket is true and 0 otherwise. We define the allele frequency of allele $a\in {\Sigma }_i$ in population P at position i as

$$p_P(a,i)=\frac{1}{\left|P\right|}\sum _{g\in P}[a\wedge g_i=a].$$

Given these definitions, we define recombination operators as

$$\mathrm{R}:{\mathcal{G}}^k\to {\mathcal{G}}^{\ell },$$

where $k,\ell \in \mathbb{N}$. Here, $\mathrm{R}$ is a random operator that acts on a parent population of size $k$ to produce an offspring population of size $\ell$.

We require that a proper recombination operator $\mathrm{R}\left(P\right)$ should, in expectation, preserve allele frequencies from the population of parents. Formally, we require that

$$\forall i\in \left[n\right],\forall a\in {\Sigma }_i:\mathbf{E}\left[p_{\mathrm{R}\left(P\right)}(a,i)\right]=p_P(a,i).$$ (R1)

Similar to mutation operators, we can describe recombination acting on both the population level and the individual level. At the individual level, we define a recombination operator as a random m-ary operator $\mathrm{R}:{\mathcal{G}}^m\to {\mathcal{G}}^k$, where $k\in \{1,2\}$, that produces one or two offspring given $m>1$ parents. The recombination operator on individuals can then be lifted to the population level by concatenation and composition with selection, that is, given a population P of size $k$,

$$\mathrm{R}\left(P\right)={((\mathrm{R}○\mathrm{S}\left)\right(P))}_{i=1\dots \ell }$$

where $\mathrm{S}:{\mathcal{G}}^k\to {\mathcal{G}}^m$ is a selection operator. Because the role of $\mathrm{S}$ in this case is to select parents for $\mathrm{R}$, we refer to the operation as parent selection.

If parent selection preserves uniform frequencies in expectation, for example selecting m parents uniformly at random from P(t), then if property (R1) holds for an operator $\mathrm{R}$, the allele frequencies in the offspring are preserved in expectation after parent selection and recombination (Appendix A, Lemma 4). If a recombination operator produces the two recombinant offspring, then it preserves allele frequencies exactly, not just in expectation. Moreover, if recombination is performed a finite number of times at the individual level to build up an intermediate population by concatenation, as long as the above properties hold, then the expected allele frequencies in the intermediate population are equal to the allele frequencies in the original population (Appendix A, Lemma 5).

For commonly defined recombination operators, the result of $\mathrm{R}\left(P\right)$ will be in the convex hull of P. However, our restriction on recombination operators excludes some recombination operators, such as geometric crossover on Manhattan spaces. In this example, genotypes are points in continuous space and recombination generates new individuals in the square convex hull (due to the Manhattan metric) between those two points. This does not fulfil our restriction for recombination, since it would not preserve the allele frequencies for the parent genotypes, and instead it constitutes a hybrid operator between recombination and mutation. A proper recombination operator would generate only the genotypes at the corners of the hypercube defined by the parent genotypes (Fig. 4).

Fig. 4.

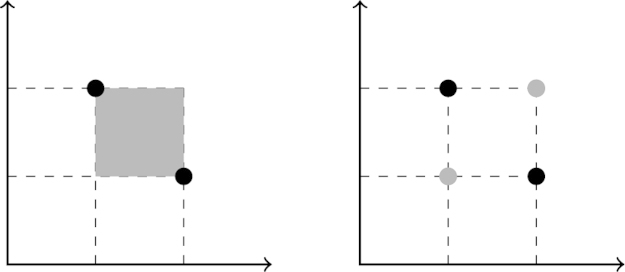
Improper and proper geometric crossovers. In this example, $\mathcal{G}$ is defined as $\mathcal{G}=\mathbb{R}\times \mathbb{R}$. For two parental genotypes $g_1=(x_1,y_1)$ and $g_2=(x_2,y_2)$ crossover could defined either as the convex hull (under some metric d) of the two genotypes: $\mathrm{R}(g_1,g_2)={\mathrm{Conv}}_d(g_1,g_2)$ or as the union of the parental points and their position wise permutations: $\mathrm{R}(g_1,r_2)=\{g_1,g_2,(x_2,y_1),(x_1,y_2\left)\right\}$. Black circles represent parental genotypes and grey areas offspring distribution. Left: geometric crossover in Manhattan space as usually defined. Right: a geometric crossover that respects the allele frequency restriction.

Abstract frameworks for generalizing crossover have been proposed before Moraglio (2011). Our approach differs by not focussing on “natural” metrics of the genotype space, but instead focussing on the result of the application of recombination on elements of this space. We require the genotype space to be an ordered Cartesian product of sets (of alleles), and define recombination as an operation that does not change the frequencies of these symbols on a population. It is in a sense more general than previous approaches, since it does not rely on external information about this space, such as the metric of the space, which may not be relevant for evolutionary processes (this fact has been previously articulated by Jones (1995) and Altenberg (1995)). In fact, our definition does not rely on the genotype being a metric space at all, even though one can always define a metric for Cartesian products of sets (the Hamming distance). However, this definition still respects the notion that the products of recombination are within the convex hull of the parental genotypes, for appropriately defined metrics. Indeed, if property (R1) holds for a recombination operator, then the resulting offspring lie in the convex hull of the parent population almost surely (Appendix A, Lemma 6).

Common recombination operators: We now instantiate common recombination operators and show that they satisfy properties of both variation and recombination operators.

One-point crossover: ${\mathrm{R}}_{1\mathrm{-}\mathrm{point}}:\mathcal{G}\times \mathcal{G}\to \mathcal{G}$. This operator acts on pairs $x,y$ of genotypes selected from the current population. A crossover point $m\in [n-1]$ is selected uniformly at random, and two new individuals $z^{\prime }$ and $z^{″}$ are produced, then one individual, z is uniformly selected at random, called offspring (children) where

$$z_i^{\prime }=\{\begin{array}{cc}{x}_i\hfill & \mathrm{if}i\le m,\hfill \\ y_i\hfill & \mathrm{otherwise};\hfill \end{array}{z}_i^{″}=\{\begin{array}{cc}{y}_i\hfill & \mathrm{if}i\le m,\hfill \\ x_i\hfill & \mathrm{otherwise};\hfill \end{array}$$

$\mathit{k}$-point crossover: ${\mathrm{R}}_{k\mathrm{-}\mathrm{point}}:\mathcal{G}\times \mathcal{G}\to \mathcal{G}$. This operator is a generalization of one-point crossover: for a parameter $1\le k\le n-1$, k crossover points are selected uniformly at random without replacement from $[n-1]$. Let $m_1,\dots ,m_k$ be a sorted list of these points and $m_0=0,m_{k+1}=n$. Two new individuals $z^{\prime }$ and $z^{″}$ are produced as follows, then one individual z is uniformly selected at random, called offspring (children). For all i such that $m_j\le i\le m_{j+1}$

$$z_i^{\prime }=\{\begin{array}{cc}{x}_i\hfill & \mathrm{if}j\mathrm{mod}2=0,\hfill \\ y_i\hfill & \mathrm{otherwise};\hfill \end{array}{z}_i^{″}=\{\begin{array}{cc}{y}_i\hfill & \mathrm{if}j\mathrm{mod}2=0,\hfill \\ x_i\hfill & \mathrm{otherwise};\hfill \end{array}$$

Note that k-point crossover with k=1 yields one-point crossover. Moreover, k-point crossover is a proper recombination operator in the sense that it preserves allele frequencies (Appendix A, Lemma 7).

Uniform crossover: ${\mathrm{R}}_{\mathrm{Unif}}:\mathcal{G}\times \mathcal{G}\to \mathcal{G}≔(g,g^{\prime })\mapsto h$ is defined as follows. The allele at h_i is inherited from g_i with probability 1/2, otherwise it is inherited from $g_i^{\prime }$ for all $i\in \left[n\right]$. This operator also preserves allele frequencies and hence satisfies (R1) (Appendix A, Lemma 7).

All crossover operators introduced here are uniformity-preserving and satisfy (V1) (Appendix A, Lemma 8).

4.2.3. Unbiased variation operators

The unbiased black-box model introduced by Lehre and Witt (2012), defines a general class of variation operators over the genospace $\mathcal{G}={\{0,1\}}^n$ (see also the extension in Rowe and Vose (2011) for other search spaces). Many variation operators on bitstrings, such as bitwise mutation and uniform crossover, are unbiased variation operators. For any integer k, a k-ary unbiased variation operator is any random operator $\mathrm{V}:{\mathcal{G}}^k\to \mathcal{G}$ that for all $y,z,x_1,\dots ,x_k\in \mathcal{G}$ and any permutation $\sigma :\left[n\right]\to \left[n\right]$ satisfies

$$\mathrm{Pr}(X=y\mid X~\mathrm{V}(x_1,\dots ,x_k\left)\right)=\mathrm{Pr}(Y=y\oplus z\mid Y~\mathrm{V}(x_1\oplus z,\dots ,x_k\oplus z\left)\right),\mathrm{Pr}(X=y\mid X~\mathrm{V}(x_1,\dots ,x_k\left)\right)=\mathrm{Pr}(Y=\sigma (y)\mid Y~\mathrm{V}({\sigma }_b\left(x_1\right),\dots ,{\sigma }_b\left(x_k\right)\left)\right),$$

where σ_b is the permutation over $\mathcal{G}$ defined for all $y\in \mathcal{G}$ by ${\sigma }_b(y_1{y}_2\cdots y_n)≔y_{\sigma \left(1\right)}{y}_{\sigma \left(2\right)}\dots y_{\sigma \left(n\right)}$ and ⊕ means bitwise XOR between sequences. In the special case of unary variation (k=1), the unbiased conditions imply that a genotype is mutated with equal probability into any other genotype at a given distance. This has been described as a desirable property of mutation operators (Droste and Wiesmann, 2000). Note that by Lemma 1 with $\sigma \left(u\right)=x_1\oplus y\oplus u$, any k-ary unbiased variation operator satisfies (V1).

5. Instantiation of evolutionary models

We now show how common evolutionary models and algorithms can be instantiated in our framework, and which of these fulfil common properties of our framework. We organize the following section based on the size of population they maintain (or more specifically on the amount of variability they maintain during the evolutionary process), since this seems to be the main factor that differentiates between results in both fields.

In PG it has been found that the interplay between the influx of new mutation and the time they take to go to fixation (which is related to the strength of selection acting on the population) plays an important part in determining the variability present in the evolving population and hence, its evolutionary dynamics.

In EC these restrictions typically do not apply, since many schemes can be implemented that enforce either reduced or increased diversity in the population, which effectively decouple diversity in the population from mutation rate or population size.

The field of evolutionary computation contains a large variety of evolutionary algorithms for optimizing a single objective function, as well as variants for multiple objectives. In this paper, we focus on single-objective evolutionary algorithms, and defer the discussion of multi-objective variants to future work. We also include the so-called estimation-of-distribution algorithms (Larrañaga and Lozano, 2002), a relatively new approach in EC that adopts rather the distribution/sampling point of view than population/applying-operators one.

A common notation for evolutionary algorithms is the $\left(\mu \stackrel{+}{,}\lambda \right)$-notation (see Beyer and Schwefel, 2002), originally developed to classify evolutionary strategies, a type of evolutionary algorithm for continuous search spaces. In any generation t, a $\left(\mu \stackrel{+}{,}\lambda \right)$ EA selects the best μ individuals from the population P(t). These individuals are called the parents. The algorithm then generates λ offspring individuals from the parents. The notation distinguishes between comma-selection and plus-selection, which represent alternative ways to construct the population from which the new generation is sampled from. In a $(\mu ,\lambda )$ EA, the selection operator is applied only to the λ offspring individuals. Such models are also called generational models or non-elitist models (see Table 1). In a $(\mu +\lambda )$ EA, the next generation is selected from the combined pool of both the μ parents and the λ offspring individuals. This strategy – often referred to as elitism – ensures that the best individuals never die (see Table 1).

In each generation of a (μ+λ) EA, λ parents are being selected uniformly at random (Beyer and Schwefel, 2002). New offspring are being created by applying a mutation operator to these parents. Finally, cut selection chooses the best μ individuals among the $\mu +\lambda$ individuals, with ties being broken in favour of keeping offspring. This sequence of individuals replaces the current population.

$$P(t+1)={\mathrm{S}}_{\mathrm{Cut}(f,\mu )}\left(P\left(t\right)\cup {\mathrm{M}}_{1/n}○{\mathrm{S}}_{\mathrm{Unif}\left(\lambda \right)}\left(P\right(t\left)\right)\right).$$

A further distinction is made by whether recombination operators are being used or not. If the algorithm does not use any kind of recombination operator, it is called a mutation-only EA, which many times is shortened to simply EA (even though the consensus is that all search heuristics inspired by natural evolution are EAs). If recombination is in use, it is considered a Genetic Algorithm (GA).

The (μ+λ) EA extends to recombination as follows. We call the result a (μ+λ) GA, Genetic Algorithm, as this term emphasizes the use of recombination in contrast to the term Evolutionary Algorithm. Recombination is typically applied to the set of selected parents. There is an additional parameter called crossover probability p_c, which determines the likelihood of two parents actually being recombined. Formally, recombination creates λ pairs of parents, and for each pair it is decided independently whether crossover is being performed or not. With probability p_c both parents are crossed and one offspring is being returned for this pair. Otherwise, one of the two parents is returned uniformly at random. It is easy to see that (R1) still holds for crossover probabilities $p_c<1$ if it holds for p_c=1. The outcome of the recombination operator is then mutated and fed into a cut selection operator as for the (μ+λ) EA.

The crossover operator may be k-point crossover or uniform crossover; we denote it by ${\mathrm{R}}^{p_c}$ here to include the crossover probability.

$$P(t+1)={\mathrm{S}}_{\mathrm{Cut}(f,\mu )}\left(P\left(t\right)\cup ({\mathrm{M}}_{1/n}○{\mathrm{R}}^{p_c}○{\mathrm{S}}_{\mathrm{Unif}\left(\lambda \right)})\left(P\right(t\left)\right)\right).$$

Note that the (μ+λ) EA emerges as a special case when p_c=0 as then no recombination is performed.

Several choices of μ and λ are of particular interest: the (1+1) EA is arguably the simplest EA and among the best studied ones. The (μ+1) EA was introduced for its mathematical simplicity and is a modification of the Steady State EA (Syswerda and Rawlins, 1991). In the same way, a (μ+1) GA is also often called a Steady-State algorithm. In the following we will mention some of these special cases as we compare them to specific evolutionary regimes from PG.

5.1. Models of monomorphic populations

The simplest type of evolutionary model is when only one genotype is present in the population at any given time. This is true in PG only under certain assumptions on the influx of new mutations. However, this can be enforced by an evolutionary algorithm for parameter ranges (for example on the mutation rate) that can be outside this range.

SSWM regime: The Strong Selection Weak Mutation model applies when the population size, mutation rate and selection strength are such that the time between occurrence of new mutations $(t_{\mathrm{mut}}\approx 1/N\mu )$ is long compared to the time of fixation of a new mutation $(t_{\mathrm{fix}}\approx \log (\mathit{Ns})/s)$ (Gillespie, 1983) (notice another difficulty in translation between the two fields: here N is the population size, and μ is the mutation rate, while in the EC community, μ is the parent population size. For easier accessibility for both communities, we use the typical notation for each community). In this situation, the population is monomorphic (i.e. only one genotype present in the population) most of the time, and evolution occurs in “jumps” between different genotypes (when a new mutation fixes in the population). The relevant dynamics can then be characterized by this “jumping” process. This model is obtained as an approximation to a limit of many other models, such as the Wright–Fisher model. Moreover, this jumping process is also the approach to dynamics employed by adaptive dynamics (Dieckmann, 1997) and its connection to population genetics has been explained by Matessi and Schneider (2009) and Schneider (2007).

This model can be instantiated in many different genotype spaces. Here, for illustrative purposes, we use ${\mathcal{G}}^k$ as genotype space. In this case, the relevant mutation operator is, for example, ${\mathrm{M}}_{\mu }$. Recombination does not apply to this model since the population is always monomorphic (only one genotype in the population at all times). The typical selection operator is proportional selection, with some function w, typically some form of probability of fixation. Because in this model the population size is one, this function will tend to choose preferentially individuals of higher values of the objective function (selection coefficient – Table 1).

Evolution then proceeds by the successive application of these operators:

$$P(t+1)={\mathrm{S}}_{\mathrm{Prop}(w,1)}\left(P\left(t\right)\cup \mathrm{M}\left(P\right(t\left)\right)\right).$$

(1+1) EA: The (1+1) Evolutionary Algorithm is arguably the simplest possible evolutionary algorithm and has been a very popular choice for theoretical research on the performance of evolutionary algorithms. It represents a “bare-bones” evolutionary algorithm with a population of size 1. Because of this, no recombination is used. The (1+1) EA mutates its current individual, and then survival selection picks the best of the offspring and the parent genotypes. Ties in this cut selection are broken towards favouring the offspring. The default mutation operator is bitwise mutation with mutation rate $1/n$. It is formalized by

$$P(t+1)={\mathrm{S}}_{\mathrm{Cut}(f,1)}\left(P\left(t\right)\cup {\mathrm{M}}_{1/n}\left(P\right(t\left)\right)\right).$$

Simulated annealing: Although not usually considered an evolutionary algorithm, simulated annealing also maintains a population of one individual, which is mutated. Then, one individual is chosen to constitute the next generation with a probability that depends on their relative value of the objective function. Simulated annealing makes use of replacement selection explicitly. The model is described by

$$P(t+1)=S_{\mathrm{Rep},h}\left(P\left(t\right)\cup \mathrm{M}\left(P\right(t\left)\right)\right)$$

with h defined as

$$h\left(\Delta \right)=\{\begin{array}{cc}1\hfill & \mathrm{if}\Delta >0\hfill \\ e^{{\gamma }_t\Delta }\hfill & \mathrm{otherwise}\hfill \end{array}$$

where ${\gamma }_t\in \mathfrak{R}$ is a parameter controlling the degree to which deleterious mutations are accepted. Typically, γ_t is a function of time and represents the cooling schedule of the algorithm, making it harder to accept worse solutions as time goes on.

At first glance, the (1+1) EA and the SSWM regime seem to share some similarities, as they both evolve just one genotype. It is reassuring that these similarities are captured in our framework. There is an obvious structural similarity between the two models, with the only difference being that the (1+1) EA uses cut selection ${\mathrm{S}}_{\mathrm{Cut}(,)}$ while the SSWM model uses ${\mathrm{S}}_{\mathrm{Prop}\left(\right)}$ as selection operator. The consequence of this difference is that in the SSWM regime some mutations may not fix even if they are beneficial. This, of course depends on the choice of the probability of fixation used in the ${\mathrm{S}}_{\mathrm{Prop}\left(\right)}$, which, in some circumstances could be justified to be close to cut selection (choosing the best among the current genotype and its mutated version).

SSWM can be regarded in some sense as a slower version of the (1+1) EA, as in the former some beneficial mutations may be rejected. On the other hand, in the SSWM regime the average “jump” will be larger than in the (1+1) EA. A more important difference is that SSWM may accept detrimental steps, depending on the form of probability of fixation used, whereas the (1+1) EA will not. The behaviour of SSWM in that respect resembles that of simulated annealing (Kirkpatrick et al., 1983). However, depending on the choice of the probability of fixation in SSWM, SSWM and (1+1) EA may follow similar trajectories and show similar dynamics.

It is interesting that both SSWM and (1+1) EA can also be cast in terms of replacement selection operators. For SSWM, one would choose h as the probability of fixation of a new genotype, given its objective function value, and for (1+1) EA one would choose $h\left(\Delta \right)$ to be 1 for $\Delta \ge 0$ and 0 otherwise.

Because there is a substantial body of work in all three models, we expect a translation of results to prove very fruitful for both fields. Furthermore, the consequences of the (small) difference in selection operators will also be analyzed.

5.2. Models of polymorphic populations with “slow” dynamics

Moran model: In contrast with the SSWM model, the Moran model maintains a polymorphic population but updates only one individual at each step (Moran, 1958). Each step updates exactly one individual, which is chosen with a certain probability to displace another (uniformly chosen) individual in a constant size (N) population. Typically this process includes only selection but it can include other forces as well, such as mutation. In this model, a full generation of the whole population corresponds roughly to N updates. This process can be described by

$$P(t+1)=\left(P\left(t\right)⧹{\mathrm{S}}_{\mathrm{Unif}\left(1\right)}\left(P\right(t\left)\right)\right)\cup ({\mathrm{M}}_{\mu }○{\mathrm{S}}_{\mathrm{Prop}(w,1)})\left(P\right(t\left)\right).$$

Alternatively, one could alleviate the restriction that the new individual necessarily displaces another individual and allow for it to be selected to die. This leads to the following representation:

$$P(t+1)={\mathrm{S}}_{\mathrm{Unif}\left(N\right)}\left(P\left(t\right)\cup ({\mathrm{M}}_{\mu }○{\mathrm{S}}_{\mathrm{Prop}(w,1)})\left(P\right(t)\right).$$

Steady state EA: As mentioned above, the Steady State EA is a special case of the (μ+λ) EA, for a choice of λ=1, and specifying cut selection as the selection operator. In each generation a single offspring is produced and included in the population. As in the case of the Moran model, this slow change means that Steady-State EAs such as (μ+1) EAs are generally more amenable for a theoretical analysis than (μ+λ) EAs.

$$P(t+1)={\mathrm{S}}_{\mathrm{Cut}(f,\mu )}\left(P\left(t\right)\cup ({\mathrm{M}}_{1/n}○{\mathrm{S}}_{\mathrm{Unif}\left(1\right)})\left(P\right(t\left)\right)\right).$$

Both the Moran model and Steady-State EAs/GAs keep a population of individuals but update only one individual per iteration. This strategy has proven to be popular in both fields for its mathematical convenience: updating just one individual makes models change slowly and hence facilitates a theoretical analysis, while still retaining most characteristics of evolutionary processes. By casting these two models in our framework, we realize that the main difference between them is the time of the life cycle at which selection acts. In the Moran model, selection acts when selecting one individual to update, while in the steady state EA, selection acts on the combined set of the mutated individual and the rest of the population. The implications of this discrepancy will be interesting to pursue. Major results obtained using the Moran model include the probability of fixation of a genotype, especially when the population is distributed over a graph (Nowak, 2006).

5.3. Models of finite polymorphic populations

Wright–Fisher model: The Wright–Fisher model (WF) for two alleles is a stochastic model that tracks the number of copies of particular alleles in a population of N individuals. It may or may not include mutation and/or selection (if none of these are included, it just reflects the neutral Wright–Fisher model, its original formulation). Genotypes in this model are just $\mathcal{G}=\{0,1\}$ and phenotypes can be defined to be $0\to 1$ and $1\to 1+s$. Selection is fitness proportional $\left({\mathrm{S}}_{\mathrm{Prop}(w,N)}\right)$ and mutation is bitwise $\left({\mathrm{M}}_{\mu }\right)$. One important characteristic of this model is that both mutation and selection are taken as deterministic, and that the only source of stochasticity comes from the sampling of the genotypes into the next generation. For the case illustrated here, this would mean that the number of copies of genotype 1 would be distributed as $n(t+1)~\mathrm{Bin}\left(p\right(t+1),N)$, where $p(t+1)=(1-\mu )\left(\right(1+s)/(1+\mathit{sp}\left)\right)p\left(t\right)+\mu 1/(1+\mathit{sp})(1-p(t\left)\right)$. In our framework, the Wright–Fisher model is seen as manipulating a distribution according to some (deterministic) operators and then employing our sampling operator $\left({\beta }_N\right)$ to sample a population of N individuals from this distribution. The resulting population is mapped back to a distribution via our $\alpha$ operator and the process repeats. We formalize this as

$$D(t+1)=({\widehat{\mathrm{M}}}_{\mu }○{\widehat{\mathrm{S}}}_{\mathrm{Prop}\left(w\right)}○\alpha )\left(P\right(t\left)\right),P(t+1)={\beta }_N\left(D\right(t+1\left)\right).$$

Population selection variation algorithm: The Population Selection Variation Algorithm (PSVA) introduced in Lehre (2011) covers all generational evolutionary algorithms that are limited to unary variation operators and independent selection of individuals (see Corus et al., 2014 for a recent generalisation to higher arity operators). In the framework described in this paper, it evolves a population $P\in {\mathcal{G}}^k$ of k individuals. The next population $P(t+1)$ is generated by applying a mutation operator $\mathrm{M}:\mathcal{G}\to \mathcal{G}$ to k individuals, which are sampled independently from the current population P(t) by any selection mechanism ${\mathrm{S}}_k:{\mathcal{G}}^k\to {\mathcal{G}}^k$. Formally, the next population is generated by

$$P(t+1)=(\mathrm{M}○{\mathrm{S}}_k)\left(P\right(t\left)\right).$$

The $(\mu ,\lambda )$ EA is the special case of this algorithm where ${\mathrm{S}}_k={\mathrm{S}}_{\mathrm{Trunc}(f,\mu ,\lambda )}$.

Simple Genetic Algorithm (SGA): The Simple Genetic Algorithm (SGA) (Goldberg, 1989) is a well-known algorithm that has been studied extensively by Vose (1999b).

The Simple Genetic Algorithm evolves a population of size k and is defined as follows. The initial population $P\left(1\right)$ is generated by selecting k elements of $\mathcal{G}$ uniformly at random. Recall that ${\mathrm{M}}_{1/n}$ denotes standard mutation, ${\mathrm{R}}_{\mathrm{Unif}}$ denotes uniform crossover and ${\mathrm{S}}_{\mathrm{Prop}\left(f\right)}$ denotes proportional selection.

$$P(t+1)=({\mathrm{M}}_{1/n}○{\mathrm{R}}_{\mathrm{Unif}}○{\mathrm{S}}_{\mathrm{Prop}\left(f\right)})\left(P\right(t\left)\right).$$

As can be seen from the above, these models share the same structure, with the difference being that the Wright–Fisher model uses a deterministic operator followed by a sampling procedure, while the Population Selection Variation Algorithm uses exclusively population level operators, as opposed to operators that act on distributions. This shows that the PSVA may be seem as a fully stochastic version of the Wright–Fisher model. These (small) differences will be interesting to explore in future work, especially regarding the effect of the potentially added stochasticity in the PSVA compared to the WF model. The SGA is also very similar in structure to the Wright–Fisher model when the latter is cast for multiple loci and recombination. In this case, the Wright–Fisher model is written as

$$D(t+1)=({\widehat{\mathrm{M}}}_{\mu }○{\widehat{\mathrm{R}}}_{\mathrm{Unif}}○{\widehat{\mathrm{S}}}_{\mathrm{Prop}\left(w\right)}○\alpha )\left(P\right(t\left)\right),P(t+1)={\beta }_N\left(D\right(t+1\left)\right).$$

Again, we see that the Wright–Fisher model is a more deterministic version of its EC counterpart, as it condenses all the stochasticity in the sampling procedure to recreate the next generation, while the SGA operates solely using finite operators.

5.4. Models operating at the level of allele frequencies

Linkage equilibrium models: One common way to describe the evolution of natural populations is to assume that they are always in linkage equilibrium and describe the population solely based on their allele frequency dynamics. These are typically fully deterministic models, typically described by differential or difference equations for these allele frequencies, assuming 2 alleles per locus and that mean fitness $\overline{w}$ can be written as a function of allele frequencies p_i:

$$\mathrm{\Delta }{p}_i=\frac{p_i(1-p_i)}{2}\frac{\partial \log \overline{w}}{\partial p_i}.$$

Because these models are deterministic, they act solely at the level of distributions, without ever instantiating a particular population. In our framework, these models can be described using either genotypes $\mathcal{G}={\left\{0,1\right\}}^n$ or at the level of allele frequencies, using $\mathcal{G}={\mathfrak{R}}^n$. In the first case,

$$D(t+1)=({\widehat{\mathrm{S}}}_{\mathrm{Prop}\left(w\right)}○{\widehat{\mathrm{R}}}_{\mathrm{Unif}})\left(D\right(t\left)\right).$$

When we take the allele perspective (the more common case), each allele is assigned a fitness (marginal fitness of an allele), defined as its mean fitness across all other loci. In this case, the model reduces to

$$D(t+1)={\widehat{\mathrm{S}}}_{\mathrm{Prop}\left(w_{\mathrm{marg}}\right)}\left(D\right(t\left)\right),$$

with the function w defined as the marginal fitness of each allele: $w_i={\sum }_{g\in \mathcal{G}}W\left(g\right)\prod P\left(g_i\right)$, where g_i denotes the allele at position i in genotype g, $P\left(g_i\right)$ the frequency of the allele g_i and W(g) the fitness of genotype g.

Stochastic versions of these models are also trivially expressed simply by sampling from D(t), as in the Wright–Fisher model:

$$D(t+1)=({\widehat{\mathrm{S}}}_{\mathrm{Prop}\left(w_{\mathrm{marg}}\right)}○\alpha )\left(P\right(t\left)\right),P(t+1)={\beta }_k\left(D\right(t+1\left)\right).$$

Univariate marginal distribution algorithm: In an Estimation Distribution Algorithm (EDA), the algorithm tries to determine the distribution of the solution features, e.g. probability of having a 1-bit at a particular position, at the optimum. Some EDAs can be regarded abstractions of evolutionary processes: instead of generating new solutions through variation and then selecting from these, EDAs use a more direct approach to refine the underlying probability distribution. The perspective of updating a probability distribution is similar to the Wright–Fisher model.

The Univariate Marginal Distribution Algorithm (UMDA) (Mühlenbein and Paaß, 1996) is the simplest EDA, as it assumes that all features are independent. The algorithm is described at the distribution level,

$$D(t+1)=(\alpha ○{\mathrm{S}}_{\ell }○{\beta }_k)(D(t\left)\right).$$

In this process, D(t) are the univariate distributions from a vector of frequencies, e.g. if $(X_1,\dots ,X_n)~D\left(t\right)$ and the component of the vector of frequencies at position $i\in \left[n\right]$ for allele $a\in {\Sigma }_i$ is ${\pi }_{a,i}$, then $\mathrm{Pr}\left(X_i=a\right)={\pi }_{a,i}$. The other operators are ${\beta }_k$ is the sampling operator resulting in a population of size $k$; ${\mathrm{S}}_{\ell }$ can be any non-uniform selection operator that outputs a population of size $\ell$; $\alpha$ computes a new vector of frequencies from the selected population for each allele at each string position, specifically, it sets ${\pi }_{a,i}≔p_{P\left(t\right)}(a,i)$, then builds up a new univariate distribution from that vector.

In addition, UMDA can also be described at the population level by looking at the intermediate populations generated by ${\beta }_k\left(D\right(t+1\left)\right)$. In fact, the use of univariate distributions and the frequency counting implies a population-wise uniform crossover over the selected population, e.g. the population could be seen as a matrix where rows are the individuals, and to generate a new solution x, the value of x_i is picked from column i and from a randomly selected row.

$$P(t+1)={\beta }_k\left(D\right(t+1\left)\right)\mathrm{equivalently},\mathrm{P}(\mathrm{t}+1)={\mathrm{R}}_k\left({\mathrm{S}}_{\ell }\right(\mathrm{P}\left(\mathrm{t}\right)\left)\right).$$

As can be seen, the previous two models share a striking similarity. The same connection was recently pointed out by Chastain et al. (2014) and previously by Mühlenbein and Paaß (1996). Taking the genotype frequency perspective, the linkage equilibrium models can be written as

$$D(t+1)=({\widehat{\mathrm{S}}}_{\mathrm{Prop}\left(w\right)}○{\widehat{\mathrm{R}}}_{\mathrm{Unif}})\left(D\right(t\left)\right),$$

while EDAs such as the UMDA can be written in genotype space at the population level as

$$P(t+1)=({\mathrm{R}}_k○{\mathrm{S}}_{\ell })\left(P\right(t)).$$

Here, ${\mathrm{R}}_k$ can be seen as uniform recombination on the entire population, as is typical for the UMDA, what is called a panmictic population in PG. As can be seen here, deterministic linkage equilibrium models from PG can be seen as the deterministic limit of the UMDA. This hints at opportunities to translate results between the two models.

Compact Genetic Algorithm (cGA): The compact Genetic Algorithm (Harik et al., 1999) (cGA) is also an EDA, which makes the same assumptions as UMDA and uses the same type of distributions. The main difference to UMDA is that the UMDA updates allele frequencies proportionally to their relative success in the population, while the cGA makes use of a finite population just as an intermediate step to determine which alleles should increase or decrease in frequency, and updates these by a fixed amount, typically chosen to be 1/n.

For $\mathcal{G}={\{0,1\}}^n$, the vector of frequencies at time t can be represented by $\left(p_1\right(t),\dots ,p_n(t\left)\right)$ where p_i is the probability of having a 1 at position i. At initialization, $D\left(1\right)$ is the univariate distribution from vector $(1/2,\dots ,1/2)$, and two individuals are constructed from this distribution. Using the tournament selection operator, we select the individual out of this pair with the highest fitness and update the allele frequencies in the population according to the winner. Formally, let $P\left(t\right)={\beta }_2\left(D\right(t\left)\right)$. We call the individual $u={\mathrm{S}}_{\mathrm{Tour}(f,2)}\left(P\right(t\left)\right)$ the winner, and the remaining individual $\left\{v\right\}=P\left(t\right)⧹\left\{u\right\}$ the loser. Allele frequencies are then updated according to the following equation.

$$p_i(t+1)=p_i\left(t\right)+(u_i-v_i)\frac{1}{n}.$$

This means that the alleles in the winning genotype are increased in frequency by an arbitrary amount ($1/n$, where n is the genotype length), while the losing ones are decreased in frequency by the same amount. The one-step description of the algorithm is simply:

$$P\left(t\right)={\beta }_2\left(D\right(t\left)\right),P(t+1)={\mathrm{S}}_{\mathrm{Tour}(f,2)}\left(P\right(t\left)\right)\cup \left(P\left(t\right)⧹{\mathrm{S}}_{\mathrm{Tour}(f,2)}\left(P\right(t\left)\right)\right)D(t+1)={\mathrm{S}}_{P_{t+1}}\left(D\right(t\left)\right),$$

where ${\mathrm{S}}_{P(t+1)}\left(D\right(t\left)\right)$ is this special selection operator.

The cGA has no counterpart in PG, due to this special selection operator. However, it seems that in expectation this model should not be much different from linkage equilibrium models. The consequences of the added stochasticity from such an extreme sampling will be interesting to explore, and we expect that many results could be useful for finite versions of linkage equilibrium models.

5.5. Other models

The previous sections detail classical models in theoretical population genetics and in the theory of evolutionary computation. However, both fields are vast and comprised of many different formalisms and models. As such, it is not clear how of this diversity can be represented by our framework. To this effect, we conducted a survey of the recent literature in both fields and analysed the models presented there, where applicable, for the ability of the present framework to represent them (Supplementary Information).

The results are encouraging: most of the models in PG can be easily represented in the current framework. This is expected since most models in PG are a version of the classical models presented above. One special comment goes for models involving migration. The current framework possesses the ability to represent these models, even though we did not detail here the structure of the migration operators: these operators are a subset of selection operators, and indeed it is easy to see that they respect property S1 (the population generated by the operator is a subset of the original population). Sub-populations are easily represented by sequences, and indeed this is one of the reasons why populations are represented by this mathematical object. However, for the sake of brevity we decided against presenting this extension here.

In Evolutionary Computation virtually all of the models used in the theory of EC are representable. However, in EC at large, we found that a substantial fraction is not. This is mainly due to the existence of many highly problem-specific algorithms. These are also unlikely to be of interest for biologists, since they typically involve heuristics that incorporate a lot of problem-specific knowledge. As such, these are also of little interest for a possible translation of tools and results between the fields.

6. Conclusions

The two complementary research fields – Population Genetics and Evolutionary Computation – study natural and artificial evolutionary processes, but have developed independently. The two fields therefore use substantially different terminology and mathematical models, preventing a comparison and translation of results.

Here, we introduce a unifying, mathematical framework for evolutionary processes and accompanying terminology, covering both classical evolutionary regimes in PG and typical evolutionary algorithms in EC. The generality of the framework is demonstrated by instantiating classical evolutionary models from population genetics, including the SSWM model, the Wright–Fisher Model, and the Moran Model, as well as classical evolutionary algorithms, such as (1+1) EA, (μ+λ) EA, (μ,λ) EA, the Simple Genetic Algorithm, (μ,λ) GAs, and simple estimation-of-distribution algorithms (EDAs) such as the UMDA.

The framework sets the stage for transfer of results between the two disciplines. In particular, the framework provides a common mathematical language within which to contrast and compare models, methods, and results. Surprisingly, by describing the most common models and algorithms in population genetics and evolutionary computation, it has become clear that they share striking similarities. Most of the algorithms and models satisfy five mathematical properties (V1), (M2), (M1), (R1), and (S1). This suggests that the framework may not only be useful as a mathematical language, but could be useful for deriving general theoretical results, valid both for artificial and natural evolution.

Furthermore, by formalizing the properties expected from the different kinds of operators, we were able to show that certain operators used in the literature do not respect the defining properties for their type. In particular, we identified that geometric crossovers defined in certain spaces do not respect the restrictions we impose on recombination operators. This has implications for claims about the effect of crossover on the runtime of algorithms using these operators, one of the central topics in the EC literature.

It should be noted that some models in both fields may require extensions to this framework in order to be able to be cast into it. A case in point is spatially structured populations, both in PG as in EC (for example, as in the case of distributed algorithms). We have not shown how these models can be cast into this framework since this would be out of the scope of this manuscript. It suffices to say that these are a subtype of selection operators.

It should also be noted that some fields of Evolutionary Computation were left out from our treatment of evolutionary processes, the main one being Genetic Programming but also other algorithms working on continuous or permutation spaces (Supplementary Information). This was intentionally done in order to strike a balance between mathematical simplicity and inclusiveness of our framework. This does not mean that, in principle, genetic programming could not be cast into a generalized version of our model. Instead, it means that we would have to make concessions about the finiteness of the set of alleles at each locus, which would increase the mathematical complexity of the description we present here.

It is interesting that some models seem to have no equivalent in the opposite field. This should not be surprising: EC is typically concerned with efficiency of the algorithms and is free to do things that are impossible in natural populations. For example, keeping always the best individual found so far, seems unrealistic in nature, given the stochastic nature of populations. However it is striking that, given this freedom, most models do not stray much from the typical scheme in PG. One could expect that certain selection schemes could be devised that make use of the whole lineage of an individual to construct the next generation (which in fact is used in artificial selection for animal breeding), but these types of selection seem to be relatively rare in the EC literature.

Appendix A. Lemmas and proofs

Lemma 1

Let $\mathcal{G}$ be a finite set, and $\mathrm{V}:{\mathcal{G}}^k\to \mathcal{G}$ is a random operator such that for all $y,x_1,\dots ,x_k\in \mathcal{G}$, there exists a permutation σ over $\mathcal{G}$ such that

• (1)$\sigma \left(x_1\right)=y$ and $\sigma \left(y\right)=x_1$
• (2)$\mathrm{Pr}(X=y\mid X~\mathrm{V}(x_1,\dots ,x_k\left)\right)=\mathrm{Pr}(Y=\sigma (y)\mid Y~\mathrm{V}(\sigma \left(x_1\right),\dots ,\sigma \left(x_k\right)\left)\right)$

then $\mathrm{V}$ satisfies (V1).

Proof

To simplify the notation, define

$$p\left(y\right)≔\mathrm{Pr}(Y=y\mid Y~\mathrm{V}(x_1,\dots ,x_k),x_1,\dots ,x_k~\mathrm{Unif}(\mathcal{G}\left)\right)p(y\mid x_1,\dots ,x_k)≔\mathrm{Pr}(Y=y\mid Y~\mathrm{V}(x_1,\dots ,x_k\left)\right)q\left(y\right)≔\mathrm{Pr}(Y=y\mid Y~\mathrm{Unif}(\mathcal{G}\left)\right)=|\mathcal{G}{|}^{-1}.$$

Given any $y\in \mathcal{G}$, we have

$$p\left(y\right)=\sum _{x_1,\dots ,x_k\in \mathcal{G}}q\left(x_1\right)q\left(x_2\right)\dots q\left(x_k\right)p(y\mid x_1,x_2,\dots ,x_k)=\left|\mathcal{G}{|}^{-k}\sum _{x_1\in \mathcal{G}}\sum _{x_2,\dots ,x_k\in \mathcal{G}}p\right(x_1\mid y,\sigma \left(x_2\right),\dots ,\sigma \left(x_k\right))=|\mathcal{G}{|}^{-k}\sum _{x_1\in \mathcal{G}}\sum _{z_2,\dots ,z_k\in \mathcal{G}}p(x_1\mid y,z_2,\dots ,z_k)=\left|\mathcal{G}{|}^{-k}\sum _{z_2,\dots ,z_k\in \mathcal{G}}\sum _{x_1\in \mathcal{G}}p\right(x_1\mid y,z_2,\dots ,z_k)=|\mathcal{G}{|}^{-k}\sum _{x_2,\dots ,x_k\in \mathcal{G}}1=|\mathcal{G}{|}^{-1}.\square$$

Lemma 2

Uniform mutation satisfies properties (V1) and (M1). Moreover, if $0<p<1$, it also satisfies (M2).

Proof

Property (M1) follows by the definition. For any pair of strings $x,y\in \mathcal{G}$, define $H=\{i\mid x_i\ne y_i\}$ ($\left|H\right|$ is the Hamming distance between x and y). Let $Y={\mathrm{M}}_p\left(x\right)$ and $X={\mathrm{M}}_p\left(y\right)$, for property (V1) to hold, from Lemma 1, it suffices to prove that the mutation operator is symmetric, e.g. $\mathrm{Pr}\left(Y=y\right)=\mathrm{Pr}\left(X=x\right)$. By the definition of ${\mathrm{M}}_p$,

$$\mathrm{Pr}\left(Y=y\right)=\prod _{i=1}^n\mathrm{Pr}\left(Y_i=y_i\right)={(1-p)}^{n-\left|H\right|}\left(\frac{p^{\left|H\right|}}{{\prod }_{i\in H}\left(\right|{\Sigma }_i|-1)}\right)=\prod _{i=1}^n\mathrm{Pr}\left(X_i=x_i\right)=\mathrm{Pr}\left(X=x\right)$$

Finally, as long as $0<p<1$, Eq. (Appendix A) is strictly positive and we also have property (M2) in that case.     □

Lemma 3

Single-point mutation satisfies properties (V1), (M1), and (M2).

Proof

Property (M1) holds by the definition of single point mutation. For property (V1), from Lemma 1, it suffices to prove that the mutation operator is symmetric. For any $x,y\in \mathcal{G}$, define $H=\{i\mid x_i\ne y_i\}$. Let $Y={\mathrm{M}}_{\mathrm{sp}}\left(x\right)$ and $X={\mathrm{M}}_{\mathrm{sp}}\left(y\right)$, then it is clear that $\mathrm{Pr}\left(Y=y\mid \left|H\right|>1\right)=\mathrm{Pr}\left(X=x\mid \left|H\right|>1\right)=0$. Otherwise, let h be the single element of H when $\left|H\right|=1$, then

$$\mathrm{Pr}\left(Y=y\mid \left|H\right|=1\right)=(1/n)\left(\frac{1}{\left|{\Sigma }_h\right|-1}\right)=\mathrm{Pr}\left(X=x\mid \left|H\right|=1\right)$$

So overall, $\mathrm{Pr}\left(Y=y\right)=\mathrm{Pr}\left(X=x\right)$.

Let us consider the process ${\{Z_i\}}_{i\in \mathbb{N}}$ where $Z_1={\mathrm{M}}_{\mathrm{sp}}\left(x\right)$, and $Z_{i+1}={\mathrm{M}}_{\mathrm{sp}}\left(Z_i\right)$, then to prove property (M2), it suffices to show that $\mathrm{Pr}\left(Z_{\left|H\right|}=y\right)>0$, e.g. the property holds with $t=\left|H\right|$. The set H implies that there exists a path which is a set of strings $(x_1,\dots ,x_{\left|H\right|}=y)$, for which the Hamming distances satisfy $H(x_i,x_{i+1})=1$ for all i and $H(x,x_1)=1$. In fact, each element of x_i of the path corresponds to the correction of a position $h\left(x_i\right)\in H$, so

$$\mathrm{Pr}\left(Z_{\left|H\right|}=y\right)\ge \mathrm{Pr}\left(Z_1=x_1\right)\mathrm{Pr}\left(Z_{\left|H\right|}=y\mid Z_1=x_1\right)=(1/n)\left(\frac{1}{\left|{\Sigma }_{h\left(x_1\right)}\right|-1}\right)\mathrm{Pr}\left(Z_{\left|H\right|}=y\mid Z_1=x_1\right)\ge {(1/n)}^2\left(\frac{1}{\left(\right|{\Sigma }_{h\left(x_1\right)}|-1)\left(\right|{\Sigma }_{h\left(x_2\right)}|-1)}\right)\mathrm{Pr}\left(Z_{\left|H\right|}=y\mid Z_1=x_1,Z_2=x_2\right)\ge \cdots \ge {(1/n)}^{\left|H\right|}\left(\frac{1}{\prod _{i\in H}\left(\right|{\Sigma }_i|-1)}\right)>0\square$$

Lemma 4

Suppose $P\left(t\right)\in {\mathcal{G}}^k$ and $\mathrm{R}:{\mathcal{G}}^m\to {\mathcal{G}}^{\ell }$ is a recombination operator for which property (R1) holds. Let $\mathrm{S}:{\mathcal{G}}^k\to {\mathcal{G}}^m$ be any parent selection operator such that for all $i\in \left[n\right]$ and all $a\in {\Sigma }_i$, $\mathbf{E}\left[p_{P^{\prime }}(a,i)\mid P^{\prime }~\mathrm{S}\left(P\right(t\left)\right)\right]=p_P(a,i)$. Then

$$\mathbf{E}\left[\mathbf{E}\left[p_{P^{″}}(a,i)\mid P^{″}~\mathrm{R}\left(P^{\prime }\right)\right]\mid P^{\prime }~\mathrm{S}\left(P\right(t\left)\right)\right]=p_{P\left(t\right)}(a,i).$$

Proof

By property (R1),

$$\mathbf{E}\left[\mathbf{E}\left[p_{P^{″}}(a,i)\mid P^{″}~\mathrm{R}\left(P^{\prime }\right)\right]\mid P^{\prime }~\mathrm{S}\left(P\right(t\left)\right)\right]=\mathbf{E}\left[p_{P^{\prime }}(a,i)\mid P^{\prime }~\mathrm{S}\left(P\right(t\left)\right)\right]=p_{P\left(t\right)}(a,i).$$

The final equality holds by our requirement for $\mathrm{S}$.□

Lemma 5

Let $\mathrm{R}$ and $\mathrm{S}$ be a recombination and a parent selection operator, respectively, for which

$$\mathbf{E}\left[p_{P^{\prime }}(a,i)\mid P^{\prime }~(\mathrm{R}○\mathrm{S})\left(P\right(t\left)\right)\right]=p_{P\left(t\right)}(a,i).$$

Then for any finite concatenation of $\ell$ applications of $\mathrm{R}○\mathrm{S}$ to P(t),

$$\mathbf{E}\left[p_{P^{″}}(a,i)|P^{″}~\bigcup _{i=1}^{\ell }(\mathrm{R}○\mathrm{S}\left)\right(P\left(t\right))\right]=p_{P\left(t\right)}(a.i).$$

Proof

It suffices to show that

$$\mathbf{E}\left[p_{A\cup B}(a,i)\mid A~(\mathrm{R}○\mathrm{S})\left(P\right(t\left)\right)\mathrm{and}B~(\mathrm{R}○\mathrm{S})\left(P\right(t\left)\right)\right]=p_{P\left(t\right)}(a.i).$$

Let $A~(\mathrm{R}○\mathrm{S})\left(P\right(t\left)\right)$ and $B~(\mathrm{R}○)\mathrm{S}\left(P\right(t\left)\right)$. Then

$$p_{A\cup B}(a,i)=\frac{1}{\left|A\right|+\left|B\right|}\left(\left|A\right|p_A(a,i)+\left|B\right|p_B(a,i)\right),$$

and by linearity of expectation,

$$\mathbf{E}\left[p_{A\cup B}(a,i)\mid A~(\mathrm{R}○\mathrm{S})\left(P\right(t\left)\right)\mathrm{and}B~(\mathrm{R}○\mathrm{S})\left(P\right(t\left)\right)\right]=\frac{1}{\left|A\right|+\left|B\right|}\left(\left|A\right|\mathbf{E}\left[p_A(a,i)\mid A(~\mathrm{R}○\mathrm{S})\left(P\right(t\left)\right)\right]+\left|B\right|\mathbf{E}\left[p_B(a,i)\mid B~(\mathrm{R}○\mathrm{S})\left(P\right(t\left)\right)\right]\right)=\frac{1}{\left|A\right|+\left|B\right|}\left(\left|A\right|p_{P\left(t\right)}(a,i)+\left|B\right|p_{P\left(t\right)}(a,i)\right)=p_{P\left(t\right)}(a,i).\square$$

Lemma 6

Let $\mathrm{Conv}\left(P\right)$ denote the convex hull of a set P of genotypes with respect to the Hamming metric.

$$\left(\mathrm{R}1\right)\Rightarrow \mathrm{Pr}\left(\mathrm{Conv}\left(Y\right)\subseteq \mathrm{Conv}\left(P\right)\mid Y~\mathrm{R}\left(P\right)\right)=1.$$

Proof

By the definition of the convex hull, $z\in \mathrm{Conv}\left(P\right)$ if and only if for all $i\in \left[n\right]$, there exists an $x\in P$ with x_i=z_i. Suppose that $\mathrm{Pr}\left(\mathrm{Conv}\left(Y\right)\supset \mathrm{Conv}\left(P\right)\mid Y~\mathrm{R}\left(P\right)\right)\ne 0$. Then there exists some $z\notin \mathrm{Conv}\left(P\right)$ such that $\mathrm{Pr}\left(z\in Y\mid Y~\mathrm{R}\left(P\right)\right)>0$. Moreover, since $z\notin \mathrm{Conv}\left(P\right)$ there exists an $i\in \left[n\right]$ such that for all $x\in P$, $x_i\ne z_i$.

In this case the frequency of allele z_i at locus i in all elements of P is $p_P(z_i,i)=0$, but since z is contained in the result of $\mathrm{R}\left(P\right)$ with nonzero probability, $\mathbf{E}\left[p_{\mathrm{R}\left(P\right)}(z_i,i)\right]\ne 0$. The claim follows by contraposition.    □

Lemma 7

Both k-point and uniform crossover satisfy property (R1).

Proof

Let $x,y\in {\Sigma }_1\times \cdots \times {\Sigma }_n$ and $z^{\prime }$ and $z^{″}$ be the two intermediate offspring produced by k-point crossover. Recall that the offspring is selected uniformly at random from $\{z^{\prime },z^{″}\}$. Hence, for all $i\in \left[n\right]$ and all $a\in {\Sigma }_i$,

$$\mathbf{E}\left[p_{{\mathrm{R}}_{k\mathrm{-}\mathrm{point}}(x,y)}(a,i)\right]=\frac{1}{2}[z_i^{\prime }=a]+\frac{1}{2}[z_i^{″}=a]=p_{\{x,y\}}(a,i),$$

since $\left(\right[z_i^{\prime }=a]+[z_i^{″}=a\left]\right)=\left(\right[x_i=a]+[y_i=a\left]\right)$. Similarly, for uniform crossover,

$$\mathbf{E}\left[p_{{\mathrm{R}}_{\mathrm{Unif}}(x,y)}(a,i)\right]=\frac{1}{2}[a\in {\Sigma }_i\wedge x_i=a]+\frac{1}{2}[a\in {\Sigma }_i\wedge y_i=a]=p_{\{x,y\}}(a,i).$$

It follows that in both cases the allele frequencies are preserved, and thus property (R1) is satisfied.□

Lemma 8

Both k-point crossover and uniform crossover satisfy property (V1).

Proof

Let $x,y~\mathrm{Unif}\left(\mathcal{G}\right)$ be the two parents and z be the generated offspring from a crossover of x and y. Fix an allele i and note that z_i is taken from x_i or y_i with equal probability. This is obvious for uniform crossover; for k-point crossover it follows from the fact that one of two potential offspring is returned uniformly at random. Hence, for any $a\in {\Sigma }_i$ we have

$$\mathrm{Pr}(z_i=a)=\frac{1}{2}·\mathrm{Pr}(x_i=a)+\frac{1}{2}·\mathrm{Pr}(y_i=a)=\frac{1}{\left|{\Sigma }_i\right|}.$$

Furthermore, as both $x_1,\dots ,x_n$ and $y_1,\dots ,y_n$ are sequences of mutually independent random variables, any sequence $z_1,\dots ,z_n$ with $z_i\in \{x_i,y_i\}$ also represents mutually independent random variables. Hence $z\in \mathrm{Unif}\left(\mathcal{G}\right)$.    □