Abstract.
Holographic interferometric methods typically require the use of three sensitivity vectors in order to obtain three-dimensional (3-D) information. Methods based on multiple directions of illumination have limited applications when studying biological tissues that have temporally varying responses such as the tympanic membrane (TM). Therefore, to measure 3-D displacements in such applications, the measurements along all the sensitivity vectors have to be done simultaneously. We propose a multiple-illumination directions approach to measure 3-D displacements from a single-shot hologram that contains displacement information from three sensitivity vectors. The hologram of an object of interest is simultaneously recorded with three incoherently superimposed pairs of reference and object beams. The incident off-axis angles of the reference beams are adjusted such that the frequency components of the multiplexed hologram are completely separate. Because of the differences in the directions and wavelengths of the reference beams, the positions of each reconstructed image corresponding to each sensitivity vector are different. We implemented a registration algorithm to accurately translate individual components of the hologram into a single global coordinate system to calculate 3-D displacements. The results include magnitudes and phases of 3-D sound-induced motions of a human cadaveric TM at several excitation frequencies showing modal and traveling wave motions on its surface.
Keywords: three-dimensional displacement measurements, digital holography, image registration, multiplexed holography, tympanic membrane
1. Introduction
The eardrum, or tympanic membrane (TM), transforms acoustic energy in the ear canal (at its lateral side) into mechanical motions of the ossicles (at its medial side: the middle ear). The acousto-mechanical-transformer behavior of the TM is determined by its shape, thickness, boundary conditions, and mechanical properties. For a better understanding of hearing mechanisms, full-field-of-view techniques are required to quantify shape and nanometer-scale sound-induced displacement of the TM in three-dimensions (3-D).1–4 Common 3-D displacement measurement techniques require repeating the measurement at least along three sensitivity directions, which rely on the assumption of reproducibility (i.e., the observed specimen behaves similarly when stimulated and measured several times). Reproducibility is not applicable in cases where the measured phenomena are of temporally varying nature, which is the case of biological tissues such as the TM. Therefore, ideally, 3-D motions of such membranes should be quantified simultaneously.
For in vivo measurements,5 reproducibility is affected by a number of factors including changes in static pressure preloading or slight changes in shape due to respiration, motion of the subject, and the subject’s pulse. For measurements in cadaveric specimens, although the reproducibility is typically better than in live subjects, the response of the TM over time can also be affected, e.g., by the drying of the tissue. The motivations to measure the 3-D motion of the TM in response to sound in vivo potentially include the use of the results for a more accurate diagnostic of TM and middle ear pathologies or to evaluate middle ear surgeries.
In this paper, the development of a single-frame multiplexed lensless holographic system is described in order to minimize the measurement times to address the time-varying nature of the TM. In this method, the hologram is simultaneously illuminated with three incoherently superimposed pairs of reference and object beams, such that the images corresponding to each illumination direction are reconstructed at a different position on the image plane because of the slightly different spatial carrier frequency introduced by the incident off-axis angles of the reference beams.6,7 Due to the differences in the position of the reference beams and the wavelength of each pair of beams, the reconstruction distance and magnification of each numerically reconstructed hologram corresponding to each sensitivity vector are different. We, therefore, developed and implemented a registration algorithm to accurately translate individual views into a single global coordinate system. The registration method uses phase-only correlation (POC)8 and a swept cut-off filtering to improve robustness. Three images obtained from three sensitivity vectors in a reconstructed multiplexed hologram are registered and, consequently, 3-D displacement components are extracted. To validate the method, the 3-D motion of a synthetic (time-invariant) membrane is measured with the presented method and with a method involving sequential measurements from multiple illumination angles. Once the accuracy of the measuring system is verified, the sound-induced 3-D motions of human cadaveric TM samples are measured at different tonal frequencies and the results are presented.
2. Methods
2.1. Off-Axis Digital Holography
In holography, the recorded intensity at the CCD (hologram) plane, , is given by
| (1) |
where and are the complex amplitudes of the reference and object waves, respectively, and are the coordinates of the pixels in the CCD (hologram) plane, and * stands for the complex conjugate. In an off-axis digital holographic configuration9–12 similar to the one shown in Fig. 1(a), the CCD sensor is illuminated with a plane reference wave, , at an angle , and an object wave, , so that the resulting interference has a fringe pattern with equidistant spacing of13,14
| (2) |
where is the period of the fringe pattern, is the laser wavelength, and is the off-axis angle. Therefore, the spatial frequency of the interferogram, i.e., reciprocal of the , can be written as
| (3) |
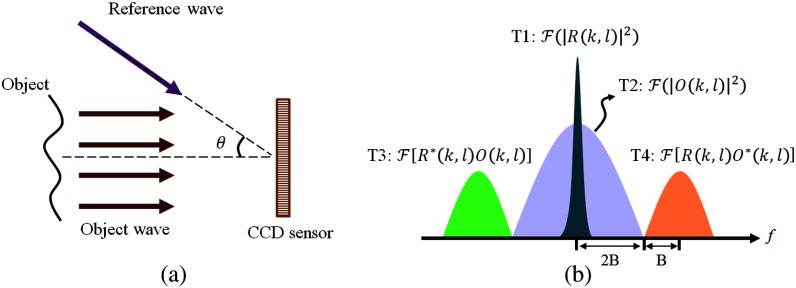
Fig. 1.
Principles of the off-axis holographic configuration: (a) spatial carrier frequency is induced by the off-axis angle of the reference wave with respect to the system’s optical axis; and (b) four terms in the spectrum of the hologram that consists of two autocorrelation terms T1 and T2 and two cross-correlation terms T3 and T4. The bandwidths of the cross-correlation terms are half the bandwidth of autocorrelation terms.
The four terms of Eq. (1) are superimposed in the hologram (spatial) domain. However, if the hologram is recorded in an off-axis geometry, these terms can be separated by taking the Fourier transform, , of the intensity to obtain
| (4) |
The spectrum of such an off-axis hologram is schematically shown in Fig. 1(b). The central parts of the hologram spectrum, , lack the phase information and contain only intensity values and are called the zero-order diffraction (ZOD) terms. The other two terms, symmetrically located from the origin, encode both intensity and phase and are called the twin images.
Based on the Wiener–Khinchin theorem, the Fourier transforms (FTs) of the squared fields and , termed T1 and T2 in Fig. 1(b), are equal to the autocorrelation of the FT of wave fields and in the Fourier domain, respectively, and the FT of the term is the cross-correlation of the FT of and [and similarly for the term]. It should be noted that the correlation integral, similar to the convolution integral, represents the scanning of one function by another. The range of variables over which the integral is nonzero is given by the sum of the widths of the scanning and scanned signals. In the case of autocorelation, the maximum extent is twice the width of the function being autocorrelated.15 Therefore, considering an ideal plane reference wave providing a single spatial frequency, the bandwidths of cross-correlation terms and are half of the bandwidth of the autocorrelation term . As shown in Fig. 1(b), assuming that the object wave field has a bandwidth of B, the bandwidth of each of the cross-correlation terms, T3 and T4, corresponds to the bandwidth of the object’s wavefront and is equal to B, and the bandwidth of the autocorrelation term T2, , is 2B.
To ensure that the information recorded by the off-axis holography is resolvable and useful, two requirements should be satisfied. First, the cross-correlation terms (conjugated data) should be completely separate from the autocorrelation (ZOD) terms; this requirement can be satisfied using a minimum off-axis angle of the reference wave. Second, the CCD sensor should be able to resolve the interference pattern, which can be obtained by limiting the off-axis angle to be less than the Nyquist sampling limit, which requires at least two pixels per fringe period.
2.1.1. Minimum off-axis angle
In order to separate useful data that contain phase information (conjugated data) from the autocorrelation terms, which only include intensity values (ZOD terms), a minimum off-axis angle should be considered for the reference wave. To determine this minimum angle, it is sufficient to determine the minimum carrier frequency for which the autocorrelation and cross-correlation terms are completely separated from each other. As shown in Fig. 1(b), the minimum carrier frequency that produces separated terms occurs when , resulting in a highest spatial frequency of at least 4B and a total spatial bandwidth of 8B. Therefore, the optimum bandwidth of the hologram in the case of the Fresnel approximation is adjusted to be 8B.
It was demonstrated that for the case of Fresnel approximation in the scalar diffraction theory, the total bandwidth of the hologram is equal to the sum of the bandwidths of the convolution kernel (quadratic phase-factor) and the bandwidth of the FT of the object field.16,17 The spatial bandwidth of the convolution kernel can be determined by taking a partial derivative of the convolution kernel with respect to the two directions and can be calculated with and , where is the number of pixels in the hologram plane, and are the pixel sizes in the and directions, and is the reconstruction distance. On the other hand, it can be geometrically shown that the maximum bandwidth of the object can be calculated from and , where and are the dimensions of the object in the horizontal and vertical directions.18,19 Assuming and , the summation of these two bandwidths defines the total bandwidth of the hologram field and can be written as
| (5) |
Therefore, the minimum spatial frequency of 3B can be calculated with
| (6) |
hence, the minimum off-axis angle of the reference wave can be obtained by combining Eqs. (3) and (6) and can be written as
| (7) |
Therefore, a minimum angle of should be considered to avoid any overlapping of the twin images and ZOD terms. However, in order for the CCD sensor to be able to resolve the interference patterns, one needs to limit the maximum off-axis angle.
2.1.2. Maximum off-axis angle
The achievable resolution for holographic reconstruction is dictated mainly by the spatial carrier frequency of the reference wave (which influences the fringe spacing) and the sampling resolution of the CCD. Based on the Nyquist theorem, the maximum spatial frequency of the interferogram that the CCD can resolve is
| (8) |
where is the pixel size of the camera. Combining Eqs. (3) and (8) and considering the small angles for , the maximum angle can be obtained using
| (9) |
Therefore, considering the points mentioned in Sec. 2.1 and, in particular, Eqs. (7) and (9), for a CCD sensor with of size of , an object size of 1 cm, and an object-to-CCD distance of 10 cm, the allowable off-axis angle should be within the range of . These results are considered in the design of our experimental setup.
2.2. Off-Axis Multiplexed Lensless Digital Holography
For 3-D displacement measurements using off-axis multiplexed holography, three incoherently superimposed pairs of object and reference beams are simultaneously recorded with the CCD sensor. As shown schematically in Fig. 2(a), the object of interest is illuminated concurrently with three object beams from different directions to provide three sensitivity vectors that are required for 3-D displacement measurements.14 The reference beams provide slightly different spatial carrier frequencies on the CCD to enable single-frame phase extraction.20 The total intensity recorded on the CCD detector, , due to incoherent superposition of three pairs of reference-object beams is6,7
| (10) |
where and are the coordinates of the pixels in the CCD (hologram) plane, and are the ’th reference and object waves, respectively, with , 2, 3. Similar to single sensitivity vector off-axis holography, described in Eqs. (1) and (4), Eq. (10) can be expanded to
| (11) |
where and . The two-dimensional (2-D) FT of Eq. (11) is
| (12) |
where the uppercase notation denotes the FT components. The terms and describe the spatial frequency distribution of the twin images components that are mathematically expressed as complex conjugates of one another, each containing the required phase information. As shown in Fig. 2(b), these terms are shifted in the Fourier domain due to the off-axis angles of the reference waves and can be separated from one another by an appropriate calculation and the setting of carrier frequencies and , as described in Sec. 2.1.
Fig. 2.
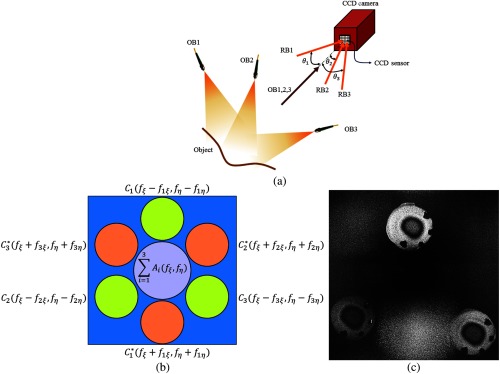
Multiplexed off-axis holography: (a) schematic of the recording procedure by simultaneous illumination with three pairs of reference and object beams; (b) spectrum of the recorded multiplexed off-axis hologram consisting of three incoherently superimposed interference patterns; and (c) representative numerically reconstructed double-exposure multiplexed hologram that is used for 3-D displacement measurements. The object of interest is a 1-cm diameter latex membrane, acoustically excited by a tone of 1.5 kHz. Sound-induced concentric fringe patterns and four painted marks used to test registration algorithms are visible on each of the reconstructed images.
Our techniques are based on single-frame lensless digital holography21–23 in which reconstructions of the multiplexed holograms are obtained by the Fresnel–Kirchhoff integral that is efficiently computed with the 2-D FFT as
| (13) |
where is the complex reconstructed hologram at coordinates and in the reconstruction plane, is the complex amplitude of the plane reference wave that is considered to be one in the numerical reconstruction, and is the 2-D chirp function defined with
| (14) |
where and are the pixels sizes of the CCD sensor, is the laser wavelength, and is the reconstruction distance. Additionally, the DC component can be mathematically removed from the multiplexed hologram by recognizing that the DC component in the Fourier domain is due to the low-frequency spatial variation in the hologram, and it can thus be isolated by applying a high-pass filter.10,11 Therefore, the optical phase of the reconstructed hologram is obtained with
| (15) |
where and denote the imaginary and real parts of the complex number . Thus, in one single frame of the camera, optical phase information corresponding to all three sensitivity vectors exists. With the use of double-exposure techniques, i.e., subtracting optical phases of two reconstructed holograms corresponding to deformed and reference states of the object, the 3-D motion components of the objects can be obtained with the method of multiple sensitivity vectors in holographic interferometry.24 Considering the fact that the fringe-locus function ,25 i.e., the unwrapped optical phase difference between the two states, is the scalar product of the sensitivity vector, , with the object’s displacement vector, , the 3-D displacements components are obtained by
| (16) |
However, in the case of off-axis multiplexed holography, the differences in the position of each reference beam and wavelength of each pair of beams cause the position, reconstruction distance, and magnification of each image corresponding to each sensitivity vector to differ. The translation between the images could be computed analytically if the exact relative orientation and position of the reference beams were known. However, such an approach would require additional hardware, and small errors in the measurement of the orientation could lead to large errors in the estimate of the translation. It is thus more efficient to register the resulting images in a postprocessing step. Therefore, for quantification of the 3-D displacement, an image registration algorithm is required to position each image into a common global coordinate system.
2.3. Registration of Multiplexed Holograms
In order to place the images in a common coordinate system, prior to applying Eq. (16), a registration algorithm based on POC has been developed and implemented.8,26,27 This algorithm accounts for pure translation of the reconstructed images and is an intensity-invariant approach to compensate for slight differences in the overall brightness and intensity of the images.
Considering two translated images and , with relative separations of and in the horizontal and vertical axes, respectively, their corresponding FT images, and , are related to each other through the shift theorem with
| (17) |
where and are the number of pixels in the image, and and are the coordinates in the frequency domain. Therefore, the normalized cross-power spectrum of and is
| (18) |
where * defines the corresponding complex conjugated functions. By applying the inverse 2-D FFT to Eq. (18), the POC function, is calculated with
| (19) |
with being the Kronecker delta function having a single peak, whose location defines the translation between the two images8 and can be computed with
| (20) |
The phase correlation, [Eqs. (19) and (20)] was calculated from a series of subsets of with regularly decreasing high-frequency limit (equivalent to spatial filtering with regularly decreasing low-pass cut-off frequencies). The translation between two images is obtained by considering the most frequent peak of the POC functions resulting from the calculation series.
2.4. Multiplexed Holographic System
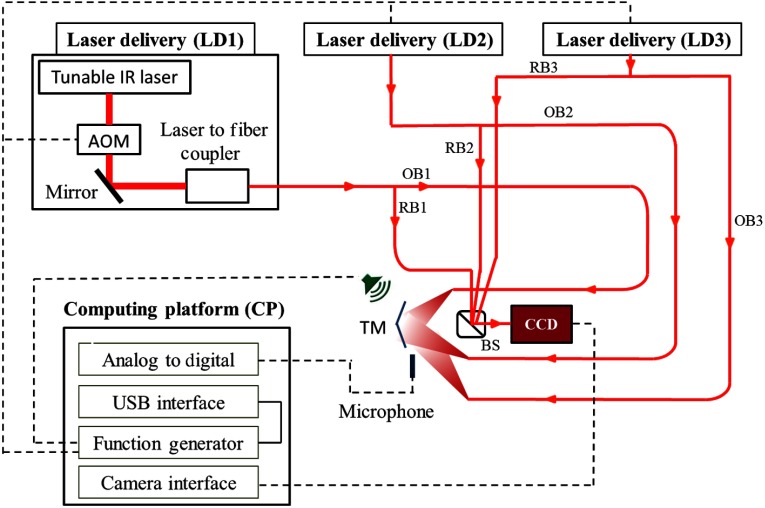
In our experimental system, incoherent superposition of the beams is implemented by using three different near-infrared external cavity tunable laser sources with wavelengths centered at 779.8, 780.2, and 780.6 nm. As shown in Fig. 3, the acousto-optic modulators (AOMs) contained in each laser delivery subsystem (LD1 to LD3) are used to switch the laser on/off to enable stroboscopic measurement capabilities.2,21,28 A dual-channel function generator is used with one of the channels sets to acoustically stimulate the TM sample with a calibrated speaker, while the second channel is set to pulse mode to simultaneously drive all three AOMs. The duty cycle of the pulse signal sent to the AOMs is typically set to 2% to 5% of the period of the tonal stimulus; however, the multiplexed holographic system (MHS) temporal resolution, i.e., the system’s maximum detection bandwidth, is determined by the 200-kHz limit of the AOMs used to strobe the phasic illumination. As shown in Fig. 3, each laser is coupled into single-mode polarization maintaining fibers and then split into reference and object beams. The reference beams illuminate the CCD in an off-axis configuration by a beam splitter and the object beams concomitantly illuminate the sample from three different directions to define the sensitivity vectors for 3-D displacement measurements. In Fig. 3, the optoelectronic components are shown for only one of the laser delivery subsystems; however, all three laser delivery subsystems contain similar components.
Fig. 3.
Experimental system for simultaneous 3-D displacement measurements with multiplexed holography. The solid lines denote the beam paths and the dashed lines the connections between components. AOM is the acousto-optic modulator; RB and OB are the reference and object beams, respectively; BS is the beam splitter; and TM is the tympanic membrane sample. Each of the three laser delivery subsystems contains similar components.
The computing platform performs multiple tasks that include synchronizing the stroboscopic illumination of the lasers with different stimulus phases, acquiring multiplexed holograms with a 5 MPix CCD camera having a pixel size of , and reconstructing the holograms in real time. A live 2-D FFT is used to ensure that the components of the frequency spectrum of the hologram do not overlap with each other.29
3. Validation of Measuring Capabilities
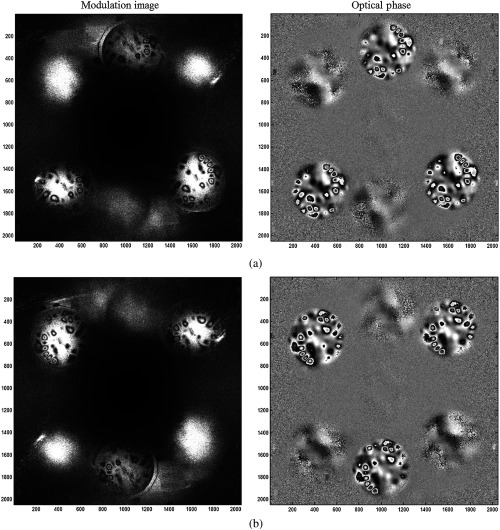
In order to validate the measuring capabilities of the MHS, the results of an artificial membrane obtained with our MHS are compared with the ones obtained with a documented repetitive holographic interferometric method.23 The artificial sample is a thin semispherical membrane mounted on a mechanical shaker that can operate over a wide range of frequencies up to 150 kHz. The results of the vibration of this sample at 25-kHz frequency are shown in Fig. 4. Modulation and wrapped optical phase images of both twin components are shown to illustrate how the three pairs of complex conjugated reconstructed holograms are distributed.
Fig. 4.
Stroboscopic measurements of a vibrating thin semispherical membrane clamped around its perimeter: (a) and (b) are the modulation and wrapped optical phase of the real and conjugated reconstructed multiplexed holograms. The excitation frequency is 25 kHz and the membrane is concomitantly illuminated from three different directions to define the sensitivity vectors for 3-D measurements, which in this case correspond to the difference in the motion of the membrane between two stimuli phases of 0 deg and 90 deg. The images for each of the three sensitivity vectors and their corresponding conjugates (fuzzy images) are symmetrically arranged around the center of each figure panel.
To determine the 3-D deformations of the membrane, the POC image registration algorithm described in Sec. 2.3 is used to place the wrapped optical phases in a common coordinate system prior to unwrapping and applying Eq. (16). Figures 5(a)–5(c) show the registered wrapped and corresponding unwrapped optical phases of the artificial sample along three sensitivity vectors to that are used to quantify 3-D displacements of the membrane. Unwrapping of the optical phases might add a constant phase value (DC) to the unwrapped data, therefore, as shown in Fig. 5(c), a seed point at an area with no deformation is selected and the value of this point is considered as the DC, so that all the pixels’ values in this image are subtracted from this DC. This step is repeated for all three unwrapped phases so that the data are all normalized before quantification of 3-D motion.
Fig. 5.
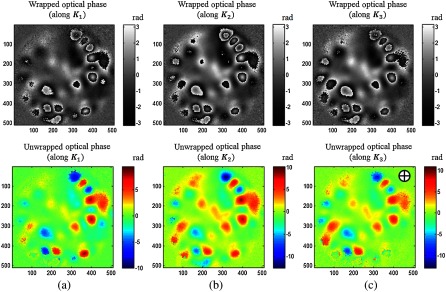
Registered optical phases corresponding to sound-induced displacement of an artificial membrane: (a)–(c) wrapped and unwrapped optical phases corresponding to sensitivity vectors to , respectively. “+” in the unwrapped optical phase along denotes the location of the seed point to identify the DC of the unwrapped data. The color and grayscale coded wrapped and unwrapped phases are in radians.
The registered, unwrapped, normalized phases are used to quantify 3-D deformation. To test and verify the validity of the measurements obtained with MHS, the results are compared with results obtained with a documented repetitive holographic interferometric method.23 The results obtained with both methods are shown in Fig. 6. On visual inspection, the results of both methods are almost indistinguishable from each other. A point-by-point correlation measure indicates a Pearson correlation coefficient of 97%, 96%, and 99% along the -, -, and -axes, respectively. It should be noted that since the resolution of the results obtained from the two methods is different (in the MHS the image resolution is while in the regular repetitive method the resolution is ), the images with higher resolution are first downsampled and then the correlations are evaluated.
Fig. 6.
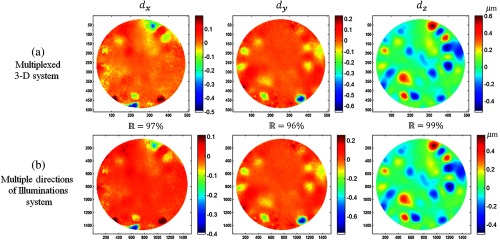
Validation of the results of three-dimensional (3-D) displacement measurements versus a documented method:23 (a) displacement components along , , and obtained using MHS; and (b) displacement components along , , and obtained with the method of repetitive holographic interferometry. is the Pearson correlation coefficient between the results obtained with the two methods.
4. Representative Measurements of Three-Dimensional Motions of Human Tympanic Membrane
The cadaveric human TM of a female, 46-year-old donor was prepared by removing the bony portion of the ear canal in a lightly fixed temporal bone. The middle-ear space of the sample was widely opened, which enabled assessment of the normality of the TM and ossicles. The temporal bone was immersed in Thiel embalming solution for several weeks before the experiments to stop decay and eliminate potential pathogens.30 Due to semitransparency of the mammalian TMs, the sample was coated with a thin layer of zinc oxide to increase the laser light reflection, as shown in Fig. 7(a). The effect of coating on shape and deformation patterns has been studied by several researchers and found to be negligible.31,32 The temporal bone was held with an adjustable clamp and mounted on a post in front of the holographic system. Figure 7(b) schematically shows the simultaneous recording of a multiplexed hologram of the cadaveric human TM. As shown in this figure, the -axis is along the superior-inferior direction and the -axis is along posterior-anterior direction, while the -axis is perpendicular to the tympanic ring plane and along the lateral side of the TM. Figure 7(c) shows a representative example of wrapped optical phase of sound-induced motion of the TM acquired with a double-exposure multiplexed hologram of the TM surface. The three fringe patterns show the similarities and differences in their spatial arrangement and their optical phase magnitudes.
Fig. 7.
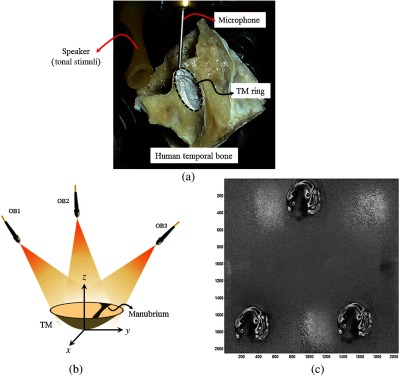
Simultaneous recording of a multiplexed hologram of a cadaveric human TM in order to acquire 3-D sound-induced displacements: (a) the human temporal bone including the TM under investigations with the location of speaker and microphone; (b) schematic of the recording of the multiplexed hologram illustrating simultaneous illumination of the three light sources on the TM samples from different sensitivity vectors; and (c) acoustically induced wrapped optical phase corresponding to the stroboscopic measurement of a human TM motion at a stimulus frequency of 6.884 kHz. The optical phases correspond to the difference in the motion of the TM at two acoustic phases of 0 deg and 90 deg. Bright blurry regions facing each of them on the opposite of the image’s center are the corresponding complex conjugates.
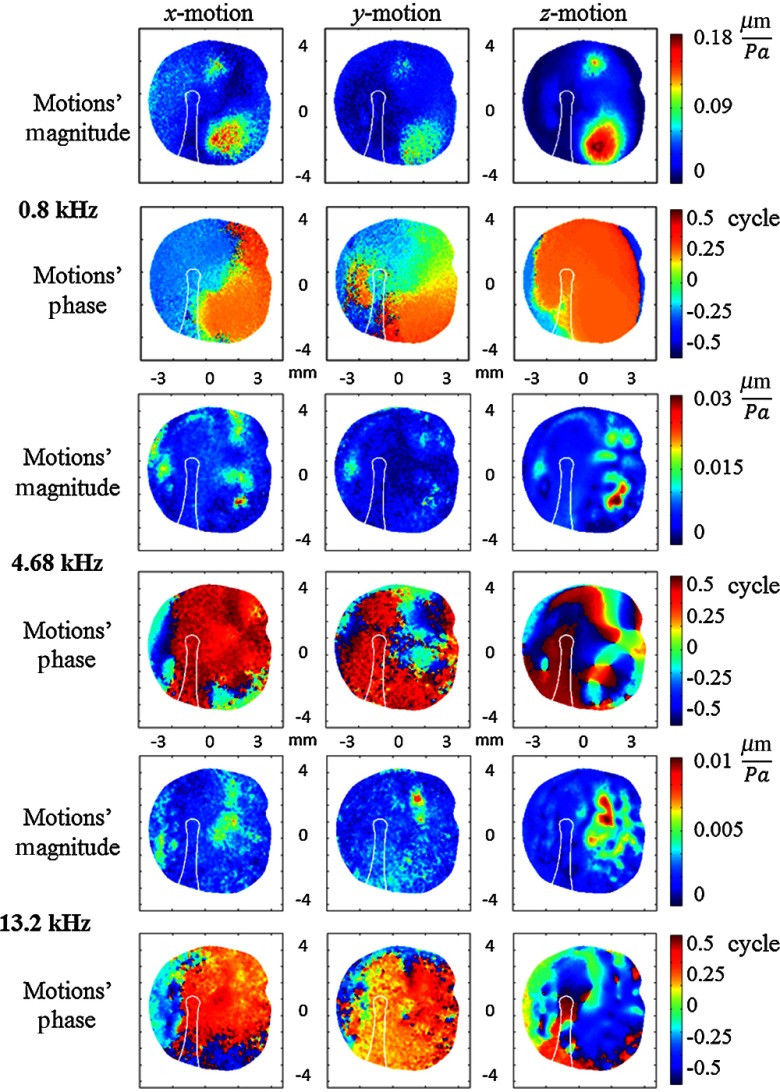
Prior to stroboscopic measurements, the time-averaged response of the TM at different tonal stimuli was monitored32 and the excitation frequencies were chosen at the maximum motion of the TM. At each stroboscopic phase, sound-induced motions of the TM along three orthogonal axes , , and are calculated from the unwrapped optical phases, as described in Sec. 2.2. Then, FFT algorithms are used to reconstruct magnitudes and phases of motions along all three axes2 and the results are shown in Fig. 8. The displacement patterns are simpler at lower frequencies, and as the excitation frequency increases, the complexity of the displacement maps also increases. At 0.8 kHz, one or two regions of large displacement are visible with a relatively homogenous phase along all three axes. As excitation frequency increases nodal lines appear, characterized by lines of minimum magnitude corresponding to separations between regions where the phase is different by 0.5 cycles, suggesting that the number of areas on the surface of the TM that are moving out-of-phase also increases. Such a phenomenon can be clearly seen in TM’s motion patterns obtained with excitation frequencies of 4.68 and 13.2 kHz, as shown in Fig. 8. An interesting observation is that in low excitation frequencies, the magnitude of motion along the -axis is slightly greater than along the -axis. Since the manubrium is located along the -axis of the measuring system [Fig. 7(b)], a possible interpretation is that the TM, in response to sound, deforms more in the direction parallel to the manubrium than in the direction perpendicular to it.
Fig. 8.
Magnitudes and phases of 3-D sound-induced displacements of the human TM excited at three different frequencies obtained with FFT-reconstruction algorithm along three orthogonal axes , , and . The displacements are normalized based on the sound pressure level obtained from the microphone. The outline of the manubrium is shown in white in all the figures.
The presence of delay in the sound transfer of the middle ear triggered the idea of the existence of traveling waves on the surface of the TM and it was suggested by several researchers.33,34 Although our data show that the majority of the TM motions are modal, there are indications of a combination of modal and traveling wave like motions on the surface of the TM. Figure 9 shows the sound-induced motions of the TM excited with a tone of 6.884 kHz at several instances of the full-cycle vibration obtained from stroboscopic illumination at different phases of the excitation signal. Two arrows shown in Fig. 9 illustrate the main traveling waves’ paths. As shown in this figure, the motion of the first traveling wave is initiated from the posterior-inferior quadrant and travels in a semicircular way toward the posterior-superior quadrants. The second one circulates in the posterior-inferior quadrant. Considering the excitation frequency and the travel distance, a wave speed of can be calculated.
Fig. 9.
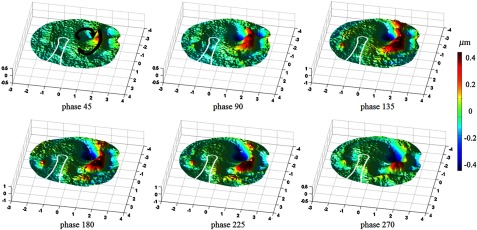
Responses of the human TM excited with a tone of 6.884 kHz at different acoustic phases suggesting the presence of a combination of modal and traveling wave patterns. Black arrows shown in the pattern of phase 45 deg indicate the main paths of the traveling waves.
5. Discussion
In this paper, we have shown the results of simultaneous 3-D vibrometry of the human eardrum using MHS. The results show great similarities with state-of-the-art multiple sensitivity vectors holographic methods, while the recording time is drastically reduced (decrease in the acquisition time by a factor of 3 in the case of a single frame and a factor of 12 in the case of four phase-stepping techniques). The developed method has promising applications in the experimental measurement of the motion of biological membranes such as the TM. Simultaneous 3-D motion measurement is a crucial step toward holographic measurements of live biological specimens.
5.1. Choice of the Registration Technique
The success of the registration depends on the similarities in spatial patterns. In theory, if the motion of the measured object is very different along the multiple sensitivity vectors, the registration might be less accurate. However, since the sensitivity vectors are not orthogonal, the motions along all sensitivity vectors are correlated. Moreover, the pattern made by nodes (regions with no membrane motion) is likely to be similar along several vectors since the displacement is equally zero along the multiple directions. The choice of an FFT-based method over a moving correlation method is motivated by its lower computational load. Also, the FFT needs to be calculated only once for spatial filtering and registration. An alternative to use a posteriori registration would be the analytic computation of the translation between the reconstructed images. In this case, a very accurate measure of the position and orientation of all elements of the optical system would be required. Such an approach would not only be cumbersome, but small errors could lead to large errors in the translation calculation. For these reasons, the developed method is preferred.
5.2. Dynamics of Human Tympanic Membranes
Our previous studies have shown that the sound-induced motions of the mammalian TMs follow several patterns (simple, complex, ordered) at different stimulus frequency ranges.21,32 It was shown that at low excitation frequencies (up to 1 kHz), most of the points () on the surface of the TM are moving in-phase and the surface displacements are well described by low-order modal motions without any nodal points.2,35 As the excitation frequency increases, the displacement patterns can be described with a combination of higher-order modal displacements (with multiple nodes) and traveling waves. The 3-D results shown in this paper show similar types of dynamics along all three axes, which are in the plane of the tympanic ring (along the - and -axes) and normal to such a plane (along the -axis). The motion pattern is simple at 0.8 kHz (top 2 rows of Fig. 8), complex at 4.68 kHz (middle 2 rows of Fig. 8), and ordered at 13.2 kHz (bottom 2 rows of Fig. 8) stimuli.
6. Conclusions
Due to the time-varying nature of biological tissues like the TM, a unique method for 3-D displacement measurements based on multiplexed holography is developed that allows for simultaneous holographic measurements along multiple sensitivity vectors. The developed methodology is a critical step toward in vivo measurements of 3-D TM motions. In our approach, the hologram of an object of interest is recorded with three simultaneous incoherently superimposed pairs of reference and object beams, such that the modulation image corresponding to each illumination direction is reconstructed at a different position of the image. An image registration algorithm based on the shift theorem of the FT is implemented to register the images. The displacement measurements are in good agreement (greater than 96%) with other documented methods, while simultaneous acquisition of all three measurements reduces the effects of temporal variations of the specimens. The time needed for a given 3-D displacement measurement is decreased at least threefold. We demonstrate that the present method is a valid alternative to repetitive holographic methods and offers promising perspectives toward faster accurate displacement measurements of biological specimens.
Acknowledgments
This work was supported by the National Institute on Deafness and other Communication Disorders (NIDCD), Massachusetts Eye and Ear Infirmary (MEEI), the Swiss National Science Foundation (SNSF), and the Mechanical Engineering Department at Worcester Polytechnic Institute. We also acknowledge the support of all the members of the CHSLT labs at WPI and Eaton-Peabody labs at MEEI, in particular Ellery Harrington and Jeffrey Tao Cheng.
Biographies
Morteza Khaleghi is a PhD candidate in mechanical engineering at Worcester Polytechnic Institute, Worcester, Massachusetts. His research interests include biomedical imaging and developments of optical and nondestructive metrology systems.
Jérémie Guignard received his MSc degree from the Swiss Federal Institute of Technology (EPFL), in 2009 and completed his PhD at the University of Bern, Switzerland, in 2013. He subsequently received a fellowship from the Swiss National Science Foundation (SNSF) to work on eardrum holography at the Massachusetts Eye and Ear Infirmary. His research interests include middle-ear physiology and prosthetics and biomedical image processing.
Cosme Furlong is an associate professor of mechanical engineering, working in mechanics, optical metrology, nanoengineering, science, and technology.
John J. Rosowski is a professor of otology and laryngology, and also of health sciences and technology, working in acoustics and mechanics of the external, middle, and inner ear, with an interest in comparative middle and external ear structure and function.
References
- 1.Decraemer W. F., Khanna S. M., Funnell W. R. J., “A method for determining three-dimensional vibration in the ear,” Hear. Res. 77, 19–37 (1994). 10.1016/0378-5955(94)90250-X [DOI] [PubMed] [Google Scholar]
- 2.Rosowski J. J., et al. , “Measurements of three-dimensional shape and sound-induced motion of the chinchilla tympanic membrane,” Hear. Res. 301, 44–52 (2013). 10.1016/j.heares.2012.11.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Motallebzadeh H., Charlebois M., Funnell W. R. J., “A non-linear viscoelastic model for the tympanic membrane,” J. Acoust. Soc. Am. 134(6), 4427–4434 (2013). 10.1121/1.4828831 [DOI] [PubMed] [Google Scholar]
- 4.De Greef D., et al. , “Viscoelastic properties of the human tympanic membrane studied with stroboscopic holography and finite element modeling,” Hear. Res. 312, 69–80 (2014). 10.1016/j.heares.2014.03.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Løkberg O. J., Hagmoen K., Gundersen T., “Vibration measurement of the human tympanic membrane-in vivo,” Acta Oto-Laryngol. 89(1–2), 37–42 (1980). 10.3109/00016488009127106 [DOI] [PubMed] [Google Scholar]
- 6.Schedin S., et al. , “Simultaneous three-dimensional dynamic deformation measurements with pulsed digital holography,” Appl. Opt. 38(34), 7056–7062 (1999). 10.1364/AO.38.007056 [DOI] [PubMed] [Google Scholar]
- 7.Picart P., Moisson E., Mounier D., “Twin-sensitivity measurement by spatial multiplexing of digitally recorded holograms,” Appl. Opt. 42(11), 1947–1957 (2003). 10.1364/AO.42.001947 [DOI] [PubMed] [Google Scholar]
- 8.Takita K., et al. , “High-accuracy subpixel image registration based on phase-only correlation,” IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 86(8), 1925–1934 (2003). [Google Scholar]
- 9.Leith E. N., Upatnieks J., “Reconstructed wavefronts and communication theory,” J. Opt. Soc. Am. 52(10), 1123–1128 (1962). 10.1364/JOSA.52.001123 [DOI] [Google Scholar]
- 10.Cuche E., Marquet P., Depeursinge C., “Spatial filtering for zero-order and twin-image elimination in digital off-axis holography,” Appl. Opt. 39(23), 4070–4075 (2000). 10.1364/AO.39.004070 [DOI] [PubMed] [Google Scholar]
- 11.Pavillon N., et al. , “Suppression of the zero-order term in off-axis digital holography through nonlinear filtering,” Appl. Opt. 48(34), H186–H195 (2009). 10.1364/AO.48.00H186 [DOI] [PubMed] [Google Scholar]
- 12.De Nicola S., et al. , “Infrared holography for wavefront reconstruction and interferometric metrology,” in Advanced Holography—Metrology and Imaging, pp. 157–180, Intech, Florence, Italy: (2011). [Google Scholar]
- 13.Kreis T. M., Adams M., Jüptner W. P. O., “Methods of digital holography: a comparison,” Proc. SPIE 3098, 224 (1997). 10.1117/12.281164 [DOI] [Google Scholar]
- 14.Schnars U., et al. , Digital Holography and Wavefront Sensing, Springer, Berlin, Heidelberg: (2015). [Google Scholar]
- 15.Collier R. J., Burckhardt C. B., Lin L. H., Optical Holography, Academic Press, New York: (1971). [Google Scholar]
- 16.Goodman J., Eds., Introduction to Fourier Optics, 2nd ed., McGraw-Hill Series in Electrical and Computer Engineering, McGraw-Hill, New York: (1968). [Google Scholar]
- 17.Picart P., et al. , “Spatial bandwidth extended reconstruction for digital color Fresnel holograms,” Opt. Express 17(11), 9145–9156 (2009). 10.1364/OE.17.009145 [DOI] [PubMed] [Google Scholar]
- 18.Gori F., “Fresnel transform and sampling theorem,” Opt. Commun. 39(5), 293–297 (1981). 10.1016/0030-4018(81)90094-8 [DOI] [Google Scholar]
- 19.Stern A., Javidi B., “Improved-resolution digital holography using the generalized sampling theorem for locally band-limited fields,” J. Opt. Soc. Am. A 23(5), 1227–1235 (2006). 10.1364/JOSAA.23.001227 [DOI] [PubMed] [Google Scholar]
- 20.Takeda M., Ina H., Kobayashi S., “Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry,” J. Opt. Soc. Am. 72, 156–160 (1982). 10.1364/JOSA.72.000156 [DOI] [Google Scholar]
- 21.Hernández-Montes M., et al. , “Optoelectronic holographic otoscope for measurement of nano-displacements in tympanic membranes,” J. Biomed. Opt. 14(3), 034023 (2009). 10.1117/1.3153898 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Flores‐Moreno J. M., et al. , “Holographic otoscope for nanodisplacement measurements of surfaces under dynamic excitation,” Scanning 33(5), 342–352 (2011). 10.1002/sca.v33.5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Khaleghi M., et al. , “Three-dimensional vibrometry of the human eardrum with stroboscopic lensless digital holography,” J. Biomed Opt. 20(5), 051028 (2015). 10.1117/1.JBO.20.5.051028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Vest C. M., Holographic Interferometry, John Wiley and Sons, Inc., New York: (1979). [Google Scholar]
- 25.Pryputniewicz R., Stetson K. A., “Holographic strain analysis: extension of fringe-vector method to include perspective,” Appl. Opt. 15(3), 725–728 (1976). 10.1364/AO.15.000725 [DOI] [PubMed] [Google Scholar]
- 26.Foroosh H., Zerubia J. B., Berthod M., “Extension of phase correlation to subpixel registration,” IEEE Trans. Image Process. 11(3), 188–200 (2002). 10.1109/83.988953 [DOI] [PubMed] [Google Scholar]
- 27.Guignard J., “POCShift,” http://www.mathworks.com/matlabcentral/fileexchange/46978-pocshift-m (20 February 2014).
- 28.Leval J., et al. , “Full-field vibrometry with digital Fresnel holography,” Appl. Opt. 44(27), 5763–5772 (2005). 10.1364/AO.44.005763 [DOI] [PubMed] [Google Scholar]
- 29.Harrington E., et al. , “Development of an optoelectronic holographic platform for otolaryngology applications,” Proc. SPIE 7791, 77910J (2010). 10.1117/12.862130 [DOI] [Google Scholar]
- 30.Guignard J., et al. , “Bone conduction in Thiel-embalmed cadaver heads,” Hear. Res. 306, 115–122 (2013). 10.1016/j.heares.2013.10.002 [DOI] [PubMed] [Google Scholar]
- 31.Dirckx J. J. J., Decraemer W. F., “Coating techniques in optical interferometric metrology,” Appl. Opt. 36(13), 2776–2782 (1997). 10.1364/AO.36.002776 [DOI] [PubMed] [Google Scholar]
- 32.Rosowski J. J., et al. , “Computer-assisted time-averaged holograms of the motion of the surface of the mammalian tympanic membrane with sound stimuli of 0.4–25 kHz,” Hear Res. 253(1), 83–96 (2009). 10.1016/j.heares.2009.03.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Olson E. S., “Observing middle and inner ear mechanics with novel intracochlear pressure sensors,” J. Acoust. Soc. Am. 103(6), 3445–3463 (1998). 10.1121/1.423083 [DOI] [PubMed] [Google Scholar]
- 34.Puria S., Allen J. B., “Measurements and model of the cat middle ear: evidence of tympanic membrane acoustic delay,” J. Acoust. Soc. Am. 104(6), 3463–3481 (1998). 10.1121/1.423930 [DOI] [PubMed] [Google Scholar]
- 35.Cheng J. T., “Wave motion on the surface of the human tympanic membrane: holographic measurement and modeling analysis,” J. Acoust. Soc. Am. 133(2), 918–937 (2013). 10.1121/1.4773263 [DOI] [PMC free article] [PubMed] [Google Scholar]