A Model for Shaping Membrane Sheets by Protein Scaffolds

Abstract

Membranes of peripheral endoplasmic reticulum form intricate morphologies consisting of tubules and sheets as basic elements. The physical mechanism of endoplasmic-reticulum shaping has been suggested to originate from the elastic behavior of the sheet edges formed by linear arrays of oligomeric protein scaffolds. The heart of this mechanism, lying in the relationships between the structure of the protein scaffolds and the effective intrinsic shapes and elastic properties of the sheets’ edges, has remained hypothetical. Here we provide a detailed computational analysis of these issues. By minimizing the elastic energy of membrane bending, we determine the effects of a rowlike array of semicircular arclike membrane scaffolds on generation of a membrane fold, which shapes the entire membrane surface into a flat double-membrane sheet. We show, quantitatively, that the sheet’s edge line tends to adopt a positive or negative curvature depending on the scaffold’s geometrical parameters. We compute the effective elastic properties of the sheet edge and analyze the dependence of the equilibrium distance between the scaffolds along the edge line on the scaffold geometry.

Introduction

The endoplasmic reticulum (ER) is a central cellular organelle responsible for synthesis of proteins, lipids, and other compounds crucial for cell life (1). From a physical point of view, the ER of a mammalian cell is a complex membrane system consisting of a nearly spherical double membrane of the nuclear envelope and a highly branched membrane network of the peripheral ER, connected to the nuclear envelope’s outer membrane (2,3). The peripheral ER spanning the entire intracellular volume is characterized by unique shapes and complex morphologies (4,5). One can think of two basic types of structural units that compose the peripheral ER—lipid tubules and flat sheets. The tubule diameters and the sheet thicknesses are close to 50 nm for mammalian and 30 nm for yeast cells, while the tubule lengths and sheet widths are in the micrometer range (2,3). The tubules and sheets are connected into elaborate networks by three-way tubular junctions (3,6,7), and helicoidal connections between sheets (7–9). Finally, the ER networks are dynamic: undergoing persistent remodeling through membrane fusion, mediated by atlastins (10,11), and membrane fission. Understanding the molecular mechanisms responsible for shaping and remodeling of intracellular membranes, in general, and ER membranes, in particular, became one of the hot topics of structural cell biology (see, for review, Shibata et al. (2)) and computational membrane biophysics (12–15).

Lipid bilayers constituting the bases of cell membranes tend to be nearly flat and resist bending (16,17). Therefore, the key event in ER shaping is the generation of the large curvatures of the ER tubules and sheet edges. A series of relatively recent experimental studies revealed a set of proteins that are necessary and sufficient for formation of ER tubules (18), and appear to be responsible for generation of the sheet edges (19). The related computational studies demonstrated that the major types of ER morphologies observed to date can be understood in terms of a simple mechanism based on elastic behavior of the sheet edges formed by the specialized proteins (7,8,19,20). However, the physical origin of the sheet-edge elastic properties and their relationship to the specific structural properties of the curvature-generating proteins remained to be elaborated. The goal of this work is to fill this gap in the understanding of the ER membrane shaping.

The proteins that proved to be crucial for ER membrane shaping belong to the reticulon and DP1/Yop1 families (18,20). For the sake of brevity, we will refer to all these proteins as reticulons. How exactly reticulons generate curvature of membrane tubules and sheet edges is unknown, but they have the structural prerequisites for two mechanisms of membrane bending: by shallow insertion of hydrophobic hairpins into the membrane matrix (2,18), which is a powerful mode of local curvature production (21,22); and by assembly into rigid arclike oligomers on the membrane surface that scaffold the membrane into a curved shape (2). Reticulons have been found on the surfaces of ER tubules (18) and edges of ER sheets (7,19), but were absent from the sheet surfaces (18). While reticulons appear to represent the core proteins driving the curvature generation of ER membranes, there are, apparently, more protein types involved in this process and modulating the reticulon action. An example is lunapark (6,23), a protein recently suggested to participate in bending ER membranes within three-way junctions of the tubules (7,24).

The phenomenological mechanism predicting generation of the whole plethora of ER morphologies (7,8,19,20) is based on the following postulates:

First, specialized ER proteins, such as (but not only) the reticulons, sculpt the ER sheet edges. Specifically, the model assumed that arc-shaped protein scaffolds, separated from each other by spaces of a few tens of nanometers, form a stripelike array on the membrane surface. This array molds the membrane underneath into a nearly half-cylindrical fold. The fold connects two parallel membranes, which are flat, do not contain any edge-generating proteins, and form the upper and lower sheet surfaces. The distance between these membranes is set by the fold cross-sectional diameter and corresponds to the 50-nm thickness of a mammalian ER sheet. In mathematical modeling, the upper and lower flat membranes were described by a single sheet plane, while the axis of the half-cylindrical edge represented the edge line of the sheet plane. The feasibility of the fold formation was indirectly supported by computations of tubular membrane shapes formed as a result of membrane constriction by ringlike scaffolds sparsely dispersed across the tubular surface (20,25). Yet the ability of arclike scaffolds to form a nearly half-cylindrical surface of the edge connecting the upper and lower sheet membranes remained hypothetical. In particular, the detailed structure of the membrane fold and the specific geometrical features of the arclike protein scaffolds required to guarantee that the upper and lower sheet surfaces are indeed parallel and flat, have to be understood.

Second, the energetically preferable shape of the edge formed by a stripelike array of protein scaffolds can be characterized by a certain edge-line curvature referred to as the edge-line spontaneous curvature, C_e^s. This edge-line spontaneous curvature can be positive, C_e^s > 0, or negative, C_e^s < 0, corresponding, respectively, to the edge’s tendency to bulge away or indent the sheet plane. The value and the sign of the spontaneous curvature, C_e^s, were conjectured to stem from the type of the edge-forming proteins. The physical mechanism behind the hypothetical ability of different proteins to induce the edge-line spontaneous curvatures, C_e^s, of different signs and absolute values remained to be understood.

Third, bending of the sheet edge resulting in deviation of the edge line from its spontaneous curvature, C_e^s, requires energy. The resistance of the edge to such bending has been quantified by the edge-line bending modulus, κ_B, which sets the energy scale of ER deformations and morphological changes. The previously used value of κ_B was obtained through a rough estimation neglecting the presence of the protein scaffolds and assuming a simplified shape of the edge membrane (19). Rigorous quantitative determination of κ_B and its relationship to the geometrical properties of the edge-forming protein scaffolds remained to be performed.

Fourth, it has been assumed that the distance, L, between the edge-forming protein scaffolds remains constant and equal to a few tens of nanometers for all morphological transformations of the system (7,20). This implies that the effective elastic modulus, κ_S, describing the system resistance to variations of the interscaffold distance, L, and referred to below as the edge-line stretching modulus, is sufficiently large compared to the edge-line bending modulus, κ_B, normalized to the proper units. The constancy of L and the large values of the stretching modulus, κ_S, can result from nonstretchable proteinic links between the scaffolds. While such links cannot be generally excluded and may exist between scaffolds formed by lunapark and/or other yet undiscovered edge-generating proteins, structural data argue against direct proteinic connections between reticulons. Another possibility is that the interscaffold distance, L, and the relatively large value of the stretching modulus, κ_S, are established by the sufficiently strong scaffold-scaffold interactions mediated by membrane deformations (26).

The goal of this study is to perform an explicit computational analysis of membrane shapes formed by linear stripelike arrays of arclike protein scaffolds, then characterize, quantitatively, the elastic and structural properties of the resulting sheet edges and relate them to the geometrical characteristics of the scaffolds. The results will provide a molecular-scale background for the previous phenomenological model of ER morphology generation.

We model a single oligomeric protein scaffold as a strongly elongated and infinitely rigid surface patch, which is curved along its long and short axes. Based on minimization of the energy of membrane bending induced by a stripelike scaffold array, we show that the whole system can acquire the expected shape of a sheet with uniform thickness in the case where the scaffold’s long axis has a certain form depending on the scaffold’s curvature along its short axis. We further demonstrate, quantitatively, that the edge line can, indeed, have a tendency to bulge out or indent the sheet plane, i.e., to be characterized by a positive or negative spontaneous curvature, depending on the curvature of the scaffold’s short axis. The latter scaffold parameter determines also the equilibrium spacing between the scaffolds along the edge line. We compute the effective bending and stretching rigidities of the edge line as functions of the scaffold’s geometrical parameters. Finally, we analyze the edge-line spontaneous curvature for the case where the scaffolds are connected by nonstretchable links establishing a constant interscaffold distance.

Materials and Methods

System description

We consider a one-row stripelike array of protein scaffolds embedded into the membrane. Because for some edge-forming proteins the scaffolds may be connected by nonstretchable proteinic links, we will analyze the cases of both existence and absence of such links.

Scaffold shape

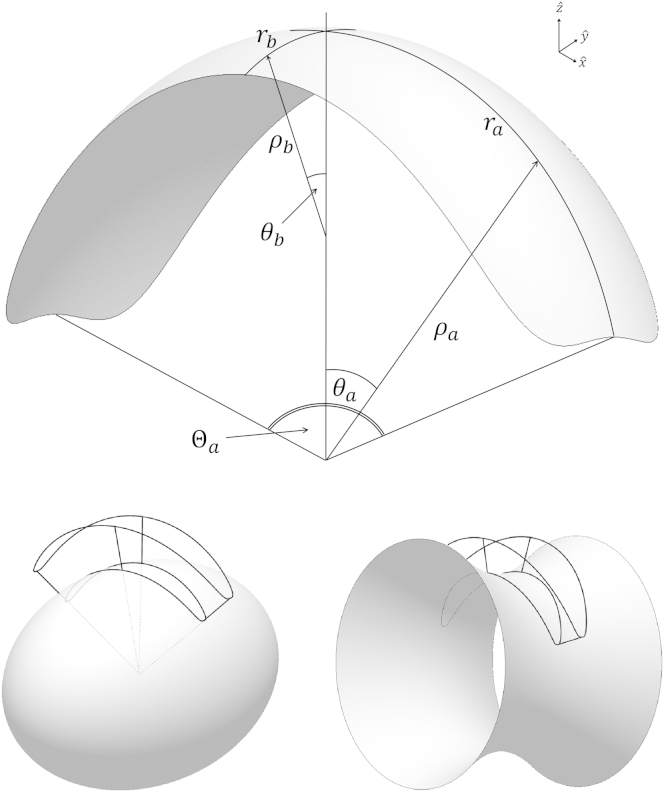
Protein scaffolds are assumed to be formed by short oligomers of specialized proteins such as reticulons (27). Because no exact structural data is available concerning these arclike scaffolds, a scaffold shape is modeled as an elongated surface patch, whose geometry is characterized by the lengths and the curvatures of its long and short axes. For computational convenience, we model the scaffold shape as a surface element, which results from cutting an ellipsoidal (or hyperboloidal) surface by a cone with a hyperelliptical cross section (Fig. 1). Variations of the parameters of the ellipsoidal surface and the cutting cone enable analysis of the model predictions for different scaffold structures.

Figure 1.

Shape of a single scaffold. The scaffold is characterized by the principal radii of curvature, ρ_a and ρ_b, in its central point, and by the arc lengths 2r_a and 2r_b of the scaffold cross sections in the principal directions (top). The concave (ρ_b > 0) and saddlelike (ρ_b < 0) scaffold shapes are obtained by cutting, respectively, an ellipsoid (bottom left) and a hyperboloid (bottom right) surface with a hyperelliptical cone (given by Eq. 2).

The equation for the ellipsoidal (hyperboloid) surface in Cartesian coordinates is

$${\left(\frac{x}{{\rho }_a}\right)}^2+\text{sign}\left({\rho }_b\right){\left(\frac{y}{{\rho }_b}\right)}^2+{\left(\frac{z}{{\rho }_a}\right)}^2=1,$$ (1)

while the hyperelliptical cone is determined by

$${\left(\frac{{\theta }_a{\rho }_a}{r_a}\right)}^4+{\left(\frac{{\theta }_b{\rho }_b}{r_b}\right)}^4=1.$$ (2)

Here, θ_a = (x/ρ_a) and θ_b = (y/ρ_b), which are the cone-head angles along the principal axes of the surface (Eq. 1) (Fig. 1). The parameters, ρ_a and ρ_b, determine the curvatures of the scaffold surface in its central point along the x axis, c_a = 1/ρ_a, and the y axis, c_b = 1/ρ_b. Positive values of ρ_a > 0 and ρ_b > 0 correspond to ellipsoidal shapes of the scaffolds with two positive principal curvatures, whereas a positive ρ_a > 0 but negative ρ_b < 0 describe hyperboloidal saddlelike shapes, whose principal curvatures have opposite signs (Fig. 1).

The parameters 2r_a and 2r_b determine the arc lengths of the scaffold’s cross sections along the x and y axes, respectively (Fig. 1). We will assume the scaffolds to be elongated in the x direction so that r_a > r_b.

In the following, we will refer to x and y directions as, respectively, the longitudinal and transverse ones. Accordingly, c_a and c_b will be referred to as the scaffold longitudinal and transverse curvatures, while 2r_a and 2r_b will be called the scaffold longitudinal and transverse dimensions.

The angles Θ_a = 2r_a/ρ_a and Θ_b = 2r_b/ρ_b are the total longitudinal and transverse arc angles, respectively (Fig. 1).

Each scaffold is attached to the membrane such that the membrane surface is continuously connected to that of the scaffold, meaning that at every point along the scaffold-membrane border the normal vector of the membrane surface coincides with that of the scaffold surface.

To simplify the computations and avoid introducing into the model additional unknown parameters, we assumed the scaffolds to be infinitely rigid with respect to bending compared to membrane. In the case where the bending rigidity of the scaffolds is comparable to that of the membrane, the scaffold curvatures, c_a and c_b, depend on the interscaffold distance, L. The smaller the distance, L, the closer c_a and c_b are expected to be to their intrinsic values determined by the scaffold structure, whereas for increasing L the absolute values of the curvatures c_a and c_b must decrease. This effect was accounted for, computationally, in the case of membrane tubulation by ringlike scaffolds (20). Relaxing the assumption of the infinite scaffold rigidity in this work would change the quantitative but not qualitative predictions of the model.

Membrane shaping by a scaffold array. Previous analysis of the membrane-mediated interaction of two strongly elongated scaffolds, r_a ≫ r_b, has shown that for relevant values of the transverse curvature, c_b, the scaffolds mutually orient such that their long axes tend to be parallel to each other and perpendicular to the line connecting their centers (26). In addition, the scaffolds exhibit a long-range attraction and short-range repulsion resulting in an equilibrium distance between them, which is comparable to the scaffold dimension (26). While the membrane-mediated forces between multiple scaffolds are not pairwise (28), their qualitative features should be similar to those of the two-scaffold interactions. Therefore, we assume that, even if there are no direct proteinic connections between the scaffolds, multiple scaffolds self-arrange in a one-row array. The scaffolds orient such that their long axes are parallel to each other and perpendicular to the row line connecting the scaffold centers (Fig. 2). This assumption is supported by the numerical results on arrangement of BAR scaffolds on membrane surfaces (29).

Figure 2.

Computed membrane shapes generated by periodic stripelike arrays of rigid scaffolds. (A) Sheet with negative curvature of the edge line, C_e < 0 (top) and its elementary section (bottom). (B) Sheet with positive curvature of the edge line, C_e > 0 (top) and its elementary section (bottom). (C) Side view of a typical sheet section. Each section has mirror up-down symmetry; (dashed line) symmetry plane. To see this figure in color, go online.

As we show below, such a scaffold array bends the membrane underneath into a fold connecting two nearly flat membranes, forming a sheetlike structure. The membrane fold underneath the scaffold array serves as a sheet edge so that the line connecting, smoothly, the scaffold centers and passing, therefore, along the mid of the fold will be referred to as the edge line. The membranes connected by the fold will be referred to as the upper and lower membranes.

We consider the scaffold array to be sufficiently long or closed into a circle so that the effects of the array ends can be neglected. In most of the calculations, we assume an even distribution of the scaffolds along the edge line characterized by a distance between the scaffold centers, L, referred to below as the interscaffold spacing. In this case, the membrane shape is periodic with a repeating unit associated with one scaffold, which will be referred to as a section (Fig. 2). The length of the edge-line segment belonging to the section is the interscaffold spacing, L. The curvature of the edge line averaged over the section will be referred to as the edge-line curvature, C_e.

Our task is reduced to determination of the membrane shape within one section, which includes finding the membrane local shape at every point of the edge as well as of the upper and lower membranes. This will enable determination of the equilibrium values of the edge-line curvature, C_e, and interscaffold spacing, L.

Boundary conditions for the membrane shape. We consider the overall membrane shape within one section to possess a mirror up-down symmetry with respect to the plane lying between the upper and lower membranes and containing the edge line (Fig. 2 C).

From left and right, the section is limited by two planes, which are perpendicular to the edge line and are directed mirror-symmetrically with respect to the section midline (Fig. 2, A and B, bottom panels). These planes intersect at a distance R₀ from the edge line with a certain angle, θ (Fig. 2 A). The angle θ can be positive (Fig. 2 B) or negative (Fig. 2 A) depending on whether the edge line bulges from, θ > 0, or indents, θ < 0, the upper and lower membranes. The interscaffold spacing, L, is related to the distance, R₀, and the absolute value of the angle, |θ|, by L = R₀|θ|. The absolute value of the average edge-line curvature is |C_e| = 1/R₀, while its sign is determined by that of the angle, sign(C_e) = sign(θ).

The membrane shape and curvature must be continuous at the borders between the adjacent sections. This requirement sets a boundary condition of perpendicularity of the membrane surface to the left and right limiting planes.

We require the upper and lower membranes to be mutually parallel far from the edge, which prevents an unlimited increase of the spacing between them. We put the distal border at a distance from the edge line equal to 0.9 R₀ for the cases of positively curved, C_e > 0 (θ > 0) (Fig. 2 B), and 100ρ_a for negatively curved or straight edge line, C_e ≤ 0 (θ ≤ 0) (Fig. 2 A).

Membrane energy

Our goal is to determine, computationally, the membrane shape corresponding to the mechanical equilibrium of the system by minimizing the elastic energy of the membrane bending induced through the membrane attachment to the curved scaffolds. We use the Helfrich model for the bending energy per unit area of the membrane, f_B, according to which (30,31)

$$f_B=\frac{1}{2}{\kappa }_m{J}^2,$$ (3)

where κ_m is the membrane-bending modulus (30) taken to have a value κ_m = 20 k_BT (where k_BT is the product of the Boltzmann constant and the absolute temperature) (32,33), and J is the total curvature of the membrane surface (30,31). In Eq. 3, we assumed vanishing values of the membrane spontaneous curvature and lateral tension (30). Moreover, we took into account that, according to Gauss-Bonnet theorem, the energy of Gaussian curvature (30,31) is constant and does not affect the membrane shape because the membrane does not undergo any topological remodeling and the direction of the normal to the membrane surface at the scaffold boundaries is fixed.

The total elastic energy of the membrane is obtained by integration of Eq. 3 over the membrane area A except for the segments occupied by the scaffolds,

$$F_{el}=\int f_{B}dA.$$ (4)

The energy minimization will be performed with respect to the local membrane shape at each point. In addition, we will assume that the membrane is, effectively, connected to a lipid reservoir of zero lateral tension, which means that there are no restrictions on the total membrane area within the section, which can change according to the need of the energy minimization. Because of this, the interscaffold spacing, L, and the edge-line curvature, C_e, will be considered as independent free parameters, whose values have to be found from the energy minimization.

The main part of the work is devoted to computation of the system conformation in the case where the scaffold’s position is fixed in the middle of the section (l_φ = 0). In the Supporting Material, we provide an estimation of the effects of fluctuations of the scaffold’s position within the section.

Computational analysis

Computations of the membrane shapes satisfying all boundary conditions and minimizing the bending energy have been performed using the program SURFACE EVOLVER (34).

Energy landscape

We find the elastic energy as a function of the interscaffold distance, L, and the edge-line curvature, C_e, for the scaffold positioning at the center of the edge section, which is the energetically favorable position (see the Supporting Material). This provides the elastic energy landscape, F_el(L,C_e), for the uniform spacing between the scaffolds.

The convergence of the optimization conditions, the error estimations, and the accuracy criteria of the calculations have been described in our previous study of a two-scaffold system (26).

The energy landscape, F_el(L,C_e), enables quantitative characterization of all the effective structural and elastic features of the edge line.

Spontaneous edge-line curvature and interscaffold distance

Finding the absolute minimum of the elastic energy, F_el(L,C_e), we determine the corresponding optimal values of spacing, L^s, and edge-line curvature, C_e^s. These values describing the state of mechanical equilibrium of the system will be referred to as the spontaneous interscaffold spacing, L^s, and the spontaneous edge-line curvature, C_e^s. In addition, our computations for L = L^s and C_e = C_e^s establish the detailed equilibrium shape of the whole system including the upper and lower membranes corresponding to the energy minimum.

Both the spontaneous distance, L^s, and curvature, C_e^s, can be attained by the system in case there are no proteinic links between scaffolds. In case such links exist and establish a certain constant interscaffold distance, L_l, we find the optimal edge-line curvature under this constraint, C_e^o(L_l). To this end we determine the point of the minimal energy in the cross section of the energy landscape, F_el(L,C_e), by the plane L = L_l.

Edge-line elastic moduli

Based on the energy landscape, F_el(L,C), we compute the effective bending and stretching elastic moduli of the edge line that is valid for deformations close to the mechanical equilibrium state and denoted by κ_B and κ_S, respectively. These moduli describe the case of no interscaffold links.

To compute the edge-line bending modulus, κ_B, we find for each value of the edge-line curvature, C_e, in the vicinity of the spontaneous curvature, C_e^s, the energetically most favorable spacing, L(C_e). We then expand the energy F_el(L(C_e),C_e) around the optimal curvature C_e^s up to the lowest nonvanishing order in the deviation, C_e − C_e^s. Because C_e^s corresponds to the energy minimum, we obtain

$$F_{el}=\frac{1}{2}\cdot L^s\cdot {\kappa }_B\cdot {\left(C_e-C_e^s\right)}^2,$$ (5)

where the effective bending modulus, κ_B, is defined as the second derivative of the energy,

$${\kappa }_B=\frac{1}{L^s}\frac{d^2}{d{C}_e^2}{F}_{el}\left(L\left(C_e\right),C_e\right),$$ (6)

computed at the point of the energy minimum C_e = C_e^s.

If the protein scaffolds are not connected by rigid links, the edge line adopts a finite stretching modulus, κ_S. To determine this edge-line stretching modulus, κ_S, we compute for each value of the interscaffold spacing, L, in the vicinity of the spontaneous spacing, L^s, the energetically most favorable edge-line curvature, C_el(L). We then expand the resulting energy, F_el(L,C_e(L)), with respect to the relative deviation of the interscaffold spacing from its spontaneous value λ = (L – L^s)/L^s, up to the second order in this parameter, and present the result as

$$F_{el}=\frac{1}{2}\cdot L^s\cdot {\kappa }_S\cdot {\lambda }^2=\frac{1}{2}\cdot L^s\cdot {\kappa }_S\cdot {\left(\frac{L-L^s}{L^s}\right)}^2,$$ (7)

where the effective stretching modulus of the edge line is defined as the second derivative of the energy with respect to λ,

$${\kappa }_S=\frac{1}{L^s}\frac{d^2}{d{\lambda }^2}{F}_{el}\left(L,C_e\left(L\right)\right),$$ (8)

calculated at the point of the energy minimum, L = L^s.

Because the ER is thought to interact with microtubules (35,36), the scaffolds might be exposed to external forces such as those developed by molecular motors. For such cases, it is useful to derive the interscaffold force, f_el(L), mediated by the edge membrane’s elastic energy. Equilibrium between f_el(L) and the external forces sets, in these cases, the preferred interscaffold distance and the stretching modulus, κ_S. To compute f_el(L), we find for each interscaffold distance L the energetically most favorable edge-line curvature C_el(L). Derivative of F_el(L,C_e(L)) with respect to the spacing, L, gives the required interaction force,

$$f_{el}\left(L\right)=\frac{d}{dL}{F}_{el}\left(L,C_e\left(L\right)\right).$$ (9)

Results

Initially, we consider scaffolds (Fig. 1) having shapes of half-circular arcs, meaning that the arc angle of the longitudinal axis is Θ_a = 180°. The longitudinal curvature of the scaffold is taken as $c_a=1/{\rho }_a\cong 1/25\text{nm}$, so that the arc diameter, 2ρ_a, corresponds to the typical 50-nm diameter of ER tubules (2) formed by reticulons (18). The parameter determining the scaffold longitudinal dimension will be taken as $r_a={\Theta }_a{\rho }_a/2\cong 40\text{nm}$ (Fig. 1). The transverse width of a scaffold depends on the specific protein but, typically, constitutes several nanometers (20). Here we use a specific width of 5 nm corresponding to r_b = 2.5 nm. The structural difference between the scaffolds will be accounted for by a single parameter, the transverse curvature, c_b = 1/ρ_b. We will refer to scaffolds with positive, c_b > 0, vanishing, c_b = 0, and negative, c_b < 0 values as ellipsoidal, cylindrical, and saddlelike scaffolds, respectively.

We determine the membrane shape and the corresponding geometrical characteristics of the membrane edge in dependence upon the transverse curvature of the scaffold, c_b.

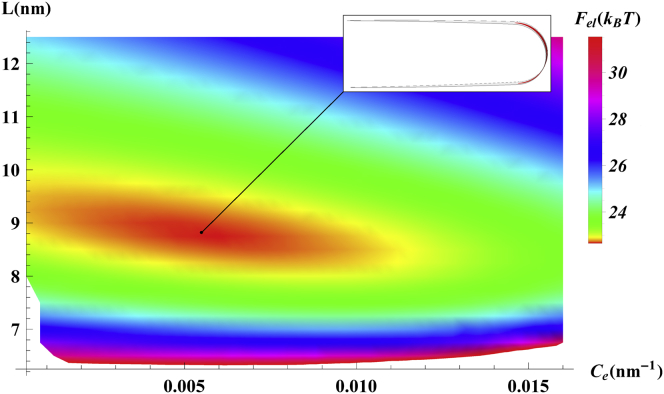
A typical elastic energy landscape F_el(L,C_e) is presented in Fig. 3 for an ellipsoidal scaffold with equal longitudinal and transverse curvatures, c_b = c_a = 1/25 nm. In this specific case, the energy exhibits a clear minimum at the spontaneous interscaffold spacing, L^s = 8.8 nm, and the spontaneous edge-line curvature, C_e^s = 0.0056 nm⁻¹, which describe the equilibrium state of the system.

Figure 3.

Elastic energy F_el(L,C_e) of a membrane section as a function of the interscaffold spacing, L, and the edge-line curvature, C_e, calculated for isotropically curved scaffold, c_b = c_a = 1/25 nm. The membrane bending modulus is κ_m = 20 k_BT. The energy minimum, representing the optimal spacing and edge-line spontaneous curvature, is achieved for L^s = 8.8 nm and C_e^s = 0.0056 nm⁻¹. (Inset) Side view of the membrane section shape corresponding to the energy minimum. To see this figure in color, go online.

Sheet shape

The typical equilibrium membrane shape computed for scaffolds with c_b = c_a = 1/25 nm, with no proteinic links, is presented in Fig. 3 (inset). The edge of the computed shape is nearly semicylindrical, while the upper and lower membrane surfaces are, practically, flat and separated by a distance, D, that appears uniform. To quantify the homogeneity of the sheet thickness, D, we define its distal, D_dist, and proximal, D_prox, values. The former, D_dist, is defined as an average of D along the system boundary distal with respect to the edge. The value of D_prox is defined as the thickness averaged along the effective border between the edge and the flat membranes, and is ∼D_prox = 50 nm. We characterize the uniformity of the sheet thickness by the ratio between its distal and proximal values, D_dist/D_prox. This ratio is plotted in Fig. 4 as a function of the transverse scaffold curvature, c_b, for c_a = 1/25 nm.

Figure 4.

Uniformity of the sheet thickness, given by D_dist/D_prox, as a function of the scaffold’s transverse curvature c_b. For a broad range of scaffold curvatures, the sheet remains practically flat, and only for relatively large c_b does the sheet thickness becomes noticeably inhomogeneous. The results are shown for Θ_a = 180°. The D_dist/D_prox dependence on Θ_a is presented in Fig. 5. The values of C_e^s and L^s used in the computations were taken according to the results presented in Fig. 6.

In the considered case of perfect semicircular arclike scaffolds, Θ_a = 180°, the ratio D_dist/D_prox remains close to 1 for a broad range of c_b; meaning that the saddlelike, cylindrical, and moderately ellipsoidal scaffolds form sheets with a practically homogeneous thickness. The behavior of D_dist/D_prox at very small values of c_b appears to be sensitive to the specific hyperelliptical shape of the scaffold boundary, which results in a slightly nonmonotonous character of this function at c_b = 0. At the same time, for large c_b, the distal value of the sheet thickness, D_dist, significantly exceeds the proximal one, D_prox, meaning that the upper and lower membranes are considerably nonparallel. As shown below, this situation corresponds to relatively large interscaffold equilibrium distances, L^s.

To explore how sensitive the sheet-thickness homogeneity is, with respect to the shape of the long scaffold axis, we have computed the dependence of D_dist/D_prox on the scaffold arc angle, Θ_a (Fig. 5).

Figure 5.

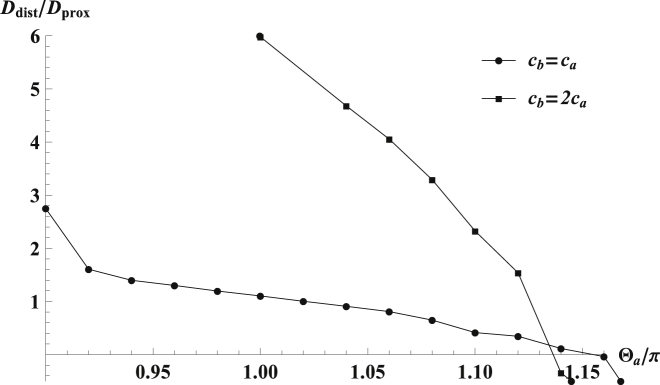
Uniformity of the sheet thickness, given by the ratio D_dist/D_prox, as a function of the normalized scaffold’s arc angle, Θ_a/π, for two sample scaffolds. Small deviations of the arc angle Θ_a from Θ_a^∗ lead to large nonuniformity in sheet thickness. The results are shown for the scaffold transverse curvature c_b = 1/25 nm. The D_dist/D_prox dependence on c_b is presented in Fig. 4. The values of C_e^s and L^s used in the computations were taken according to the results presented in Fig. 6.

We find that for scaffolds with c_b = c_a, a homogeneous sheet thickness, D_dist/D_prox = 1, is attained for nearly semicircular scaffold shape with arc angle of Θ_a^∗ ≈ 1.02π ≈ 180°. For strongly ellipsoidal scaffolds, c_b = 2c_a, maintaining a uniform thickness requires a considerable deviation of the scaffold long axis from a semicircle corresponding to the arc angle of Θ_a^∗ ≈ 1.14π ≈ 205°. A qualitative explanation for this result is based on an interplay between the effects of the scaffolds themselves and those of the membrane gaps between the scaffolds. The scaffolds with Θ_a^∗ > π favor tilting of the upper and lower membranes toward each other, which leads to a decreasing sheet thickness. In contrast, the membrane gaps between the scaffolds tend to unbend, hence favoring a splay of the sheets surfaces, which leads to an increasing sheet thickness.

As shown below, large values of c_b correspond to large equilibrium interscaffold distances (Fig. 6) and, hence, to a relatively strong effect of the membrane gaps between the scaffolds. To keep the sheet surfaces parallel on average, the latter has to be counteracted by the effect of scaffold arc angles Θ_a^∗ exceeding 180°. In both cases, scaffolds with arc angles that fall below Θ_a^∗ result in a rapid expansion of the sheet thickness, leading to sheets that dilate away from the edge. Scaffolds with arc angles that exceed Θ_a^∗ form sheets with a thickness that decreases away from the edge, up to a contact between the upper and lower membranes. This sensitivity of the sheet thickness homogeneity to variations in the scaffold arc angle Θ_a with respect to Θ_a^∗ is most pronounced in the case of highly ellipsoidal scaffolds, c_b = 2c_a (see Fig. 5).

Figure 6.

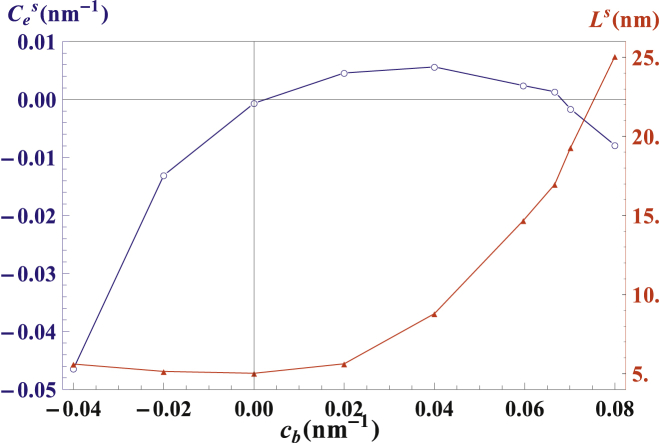
Equilibrium interscaffold distance, L^s (red), and edge-line curvature, C_e^s (blue), as functions of the scaffold transverse curvature, c_b. For zero or negative c_b, the scaffolds are nearly closely packed and the edge-line curvature is approximately equal to the transverse curvature of the scaffold, while at larger c_b values the interscaffold distance, L^s, increases and the edge-line curvature, C_e^s, is a nonmonotonic function of c_b. To see this figure in color, go online.

Edge-line spontaneous curvature

We first analyzed the case of unlinked scaffolds. The dependences of the edge-line spontaneous curvature, C_e^s, and the spontaneous interscaffold spacing, L^s, on the transverse scaffold curvature, c_b, are presented in Fig. 6.

For cylindrical scaffolds, c_b = 0, the equilibrium interscaffold spacing equals the scaffold transverse dimension L^s = 2r_b = 5 nm, which means that the scaffolds tend to be closely packed, side by side, along the edge line. The close packing is nearly retained also for the saddlelike scaffolds in the calculated range of c_b < 0. For ellipsoidal scaffolds, c_b > 0, the interscaffold spacing, L^s, increases with growing c_b. For feasibly large values of the scaffold transverse curvature, c_b, the equilibrium spaces between ellipsoidal scaffolds are of the order of the scaffold longitudinal dimension, 2r_a, so that the equilibrium area coverage of the sheet edge by ellipsoidal scaffolds becomes relatively small.

The dependence of the edge-line spontaneous curvature, C_e^s, on c_b is presented in Fig. 6. For saddlelike, c_b < 0, and cylindrical, c_b = 0, scaffolds, the edge-line spontaneous curvature, C_e^s, is negative and vanishing, respectively. In these cases, the C_e^s value is directly determined by the scaffold transverse curvature, C_e^s = c_b. This is a consequence of the scaffold close packing along the edge line for these values of c_b (Fig. 6). Hence, the edge formed by saddlelike scaffolds adopts a saddlelike shape, characterized by a negative edge-line curvature. For positive transverse curvatures of the scaffolds, c_b > 0, the dependence of the edge-line curvature, C_e^s, on c_b is nonmonotonic (Fig. 6). This nonmonotonicity is a result of interplay between two opposing factors. The first is the positive transverse curvature of the scaffolds themselves, c_b > 0, providing a positive contribution to the spontaneous curvature of the edge line, C_e^s. The second is the edge-line curvature favored by the membrane regions between the scaffolds. These regions tend to adopt saddlelike shapes (8) where the effect of the positive curvature in the direction perpendicular to the edge line is compensated by the spontaneously acquired negative curvature in the edge-line direction, so that the magnitude of the membrane mean curvature remains as small as possible. As a result, the edge-line spontaneous curvature, C_e^s(c_b), increases with c_b as long as the interscaffold gaps remain relatively small. Once the equilibrium spacing, L^s(c_b), exceeds a particular value, the effect of the interscaffold regions takes over so that C_e^s starts decreasing, vanishes for a certain value of the transverse scaffold curvature c_b^∗, and subsequently becomes negative.

Summarizing: for saddlelike, c_b < 0, or strongly ellipsoidal, c_b > c_b^∗, scaffolds, the spontaneous curvature of the edge line is predicted to be negative, C_e^s < 0. For the scaffold transverse curvature varying in the interval 0 < c_b < c_b^∗, the edge-line spontaneous curvature is predicted to be positive C_e^s > 0.

We further analyzed the case of scaffolds connected by nonstretchable links of different length, L_l, by computing the optimal edge-line curvature, C_e^o, for different values of this length. According to the results presented in Fig. 7, the interscaffold links change quantitatively, but not qualitatively, the dependence of the preferred edge-line curvature on the scaffold transverse curvature, C_e^o(c_b).

Figure 7.

Edge-line spontaneous curvature, C_e^o, as a function of the scaffold transverse curvature, c_b, for different lengths, L_l, of nonstretchable links between scaffolds. The nonmonotonic dependence C_e^o(c_b) is apparent for the tested distances. Edge-line curvature for unlinked scaffolds, C_e^s (solid black), is shown for comparison with Fig. 6. To see this figure in color, go online.

The function C_e^o(c_b) remains nonmonotonous with a region of positive C_e^o for intermediate values of c_b. At the same time, for negative or moderately positive values of c_b, establishment of a constant interscaffold spacing, L_l, is predicted to result in more negative values of the edge-line curvature, C_e^o, as compared to those formed by unconstrained scaffolds, C_e^o < C_e^S. The reason for this prediction is that for relatively small c_b values the length of the links exceeds the spontaneous interscaffold spacing, L^l > L^s, and the resulting extra membrane space between the scaffolds leads to more negative values of the edge-line curvature, C_e^o. For larger c_b values, the relationship between L_l and L^s reverses, turning to L^l < L^s, and that the predicted optimal edge-line curvature becomes larger than the spontaneous one, C_e^o > C_e^S.

Elastic moduli of the edge line

The effective bending rigidity of the edge line, κ_B (Eq. 6), is presented in Fig. 8 as a function of the scaffold transverse curvature, c_b.

Figure 8.

Effective bending rigidity of the edge line, κ_B, as a function of the scaffold’s transverse curvature, c_b, according to Eq. 6. The bending rigidity diverges for close packing of the scaffolds and decreases with increasing interscaffold distance. The membrane bending modulus is κ_m = 20 k_BT.

The bending rigidity, κ_B, adopts large values for small c_b, and diverges if c_b vanishes. The reason for this is a decrease of the length of the relatively soft interscaffold membrane gaps (Fig. 6), which leads to a growing effective contribution to κ_B of the infinitely rigid scaffolds. For the larger values of c_b, corresponding to large interscaffold spacings (Fig. 6), the edge’s bending rigidity, κ_B, is mainly determined by the long membrane regions between the scaffolds and adopts a value of several hundreds of k_BT⋅nm, in accord with the previous estimations for edges formed only by lipid bilayers (7,8).

The computed values of the edge-line stretching modulus, κ_S, and their comparison with the edge-line bending modulus, κ_B, are presented in Fig. 9. In the most relevant range of the transverse scaffold curvature, c_b, the stretching modulus exceeds considerably that of bending (Fig. 9 b), hence supporting the assumptions of the previous modeling.

Figure 9.

Edge-line stretching modulus, κ_S, as a function of the scaffold’s transverse curvature, c_b, according to Eq. 8. (A) The stretching modulus reaches a maximum for vanishing interscaffold distance. (B) Comparison between the edge-line stretching κ_S and bending κ_B moduli. The membrane bending modulus is κ_m = 20 k_BT.

The effective membrane-mediated force between scaffolds, f_el (Eq. 9), is presented in Fig. 10 for the case of c_b = c_a = 1/25 nm. For a characteristic 5-nm deviation of the interscaffold spacing, L, from its equilibrium value, L^s, the force attains values of ∼f_el = 1.5 pN. Development of such forces is feasible for molecular motors and polymerizing actin filaments (see, e.g., Mogilner (37)). Hence, the spacing, L, and the related curvature of the edge line, C_e, can be regulated by intracellular force-generating machines.

Figure 10.

Elastic-membrane-mediated force between scaffolds as a function of the interscaffold spacing, according to Eq. 9. Results are shown for isotropically curved scaffolds, c_b = c_a = 1/25 nm. The membrane bending modulus is κ_m = 20 k_BT.

Discussion

Stripelike arrays of arclike protein scaffolds have been suggested to underlie formation of sheets, tubules, and complex morphologies of ER membranes by oligomers of reticulons and DP1/Yop1 family proteins (19,20), with a possible participation of additional membrane-shaping proteins (7,24). This simple model for ER membrane shaping was based on a few critical assumptions.

First, it was proposed that an edgelike membrane fold generated by the protein oligomers is sufficient to guarantee that the upper and lower membranes connected to the edge are flat and parallel to each other, so that the thickness of the resulting sheet is homogeneous.

Second, it was assumed that the preferred (spontaneous) curvature of the sheet’s edge line, C_e^s, is dependent on the specific structure of the curvature-generating protein oligomers and, for different proteins, adopts either positive or negative values, which correspond, respectively, to the edge’s tendency to bulge away from or indent the sheet plane. The negative edge-line spontaneous curvature, C_e^s < 0, was predicted to support formation of intertubule three-way junctions in ER networks and helicoidal connections between sheets within stacks (7), whereas the vanishing spontaneous curvature, C_e^s = 0, was expected to favor generation of tubules and external edges of larger sheets (7).

Third, the sheet edge’s area coverage by the major curvature generating proteins of reticulon and DP1/Yop1 families, was supposed to be relatively low rather than dense (20).

Here we modeled, computationally, the detailed structure of membrane edges generated by a linear array of arclike protein scaffolds in order to relate the geometrical and elastic characteristics of the membrane edges to the effective structural features of the edge-generating proteins.

Conclusions

Our computations substantiated all the assumptions of the previous modeling and, to our knowledge, led to three important new conclusions.

First, in order to generate sheets with a uniform thickness, the angle spanned by the protein scaffold arc must have a certain value, Θ_a^∗, depending on the transverse curvature of the scaffolds, c_b. In case the longitudinal and transverse curvatures of the scaffolds are equal, c_a = c_b, this angle has to be close to 180°, i.e., the long axis of the scaffold has to be half-circular. Even small deviations from Θ_a^∗ result in a strong splay of the upper and lower sheet membranes, so that the sheet thickness varies significantly with the distance from the edge. Protein scaffold arcs with angles below Θ_a^∗ result in rapid dilation of the sheets away from the edge, while arcs that exceed Θ_a^∗, result in sheets with diminishing thickness, leading to contact of the upper and lower membranes close to the sheet edges. In both cases, these effects may be mitigated by proteins that bridge the upper and lower membranes, such as Clipm63 (19), serving to fix the nonuniformity of the intermembrane gap and create a homogeneous sheet thickness.

Second, as may be expected, the spontaneous curvature of the edge line, C_e^s, is determined by the transverse scaffold curvature, c_b. Indeed, according to our computations, in the case the scaffolds are not connected by protein links; for saddlelike, c_b < 0, or cylindrical, c_b = 0, scaffolds, the edge-line curvature is almost equal to scaffold transverse curvature, C_e^s ≈ c_b. At the same time, our analysis resulted in a striking prediction concerning the effect of elliptical scaffolds, c_b > 0. For such scaffolds, the edge-line spontaneous curvature, C_e^s, is predicted to change nonmonotonously with c_b. For relatively small positive values of the scaffold transverse curvature, c_b, the edge-line curvature is positive, C_e^s > 0; whereas, for c_b larger than a certain threshold value, c_b^∗ ≈ 1.7c_a, the edge-line curvature becomes negative, C_e^s < 0.

Third, the saddlelike, c_b < 0, and cylindrical, c_b = 0, unlinked scaffolds are predicted to pack densely along the edge, while elliptical scaffolds, c_b > 0, arrange at relatively large distances from each other, leaving substantial regions of uncovered membrane between them.

It has to be noted that a positive transverse scaffold curvature, c_b > 0, can result not only from the shape of the scaffold per se, but, effectively, also from protein domains, such as amphipathic α-helices (38) or short hydrophobic loops (39), which are attached to the scaffold and get shallowly inserted into the membrane matrix. The relevance of the latter mechanism for the ER shaping protein Yop1 was recently demonstrated experimentally (40). Elliptical scaffolds without membrane inserting domains might have a relatively small positive transverse curvature, c_b, and generate an edge line with positive spontaneous curvature, C_e^s > 0; whereas the addition of hydrophobic hairpins (18) or amphipathic N-terminal helices may result in substantially larger c_b. According to our predictions, this can promote edge lines with a negative spontaneous curvature, C_e^s < 0, and the related ER morphologies (7).

Finally, we analyzed the edge line’s effective elastic moduli. In the case of elliptical scaffolds, we have found that the edge line resists stretching and compression to a much greater degree than it resists bending. This, therefore, implies that the edge length is primarily determined by the concentration of scaffolding proteins in the system, providing a quantitative validation of our previous assumption (7).

While our computational model substantiate the previously assumed dependence of the edge line’s elastic properties on the geometry of the underlying protein scaffolds, two fundamental questions regarding the system’s self-organization remain open: what the pathway of the scaffold arrangement arcs into stripelike arrays would be, and what factors limit the polymerization of monomeric proteins into relatively short arc-shaped scaffolds. One of possible answers to the former question has been suggested in Guven et al. (9). The latter question, most especially, may have significant implications on the results presented here, because the geometric dimensions and the elastic properties of each scaffold arc must be directly related to the number of protein monomers in it, and to their mode of interaction. Indeed, the relationship between the elastic energy of the membrane-protein system and the binding energy between protein monomers may affect the equilibrium size of the oligomers. Such interdependence may, for example, fix the oligomer arc angle at the value optimal for maintaining homogeneity of the sheet thickness predicted in this study.

To conclude, it has to be emphasized that this analysis is limited by several assumptions, whose relaxation, which is a matter of the future work, may result in prediction of new effects. We assumed a circular overall geometry of the edge line, which suggests a mirror symmetric shape of the elementary section of the structure (Fig. 2). The stability of the sheet configuration with respect to deviations from the circular shapes of the edge line, which appears plausible based on the previous analysis of membrane-mediated interaction between two scaffolds (26), can be verified by more sophisticated computational methods. At the distal boundary of the section we applied a boundary condition of the sheet flatness, but, importantly, did not put any limit on the sheet thickness. Hence, the homogeneity of the sheet thickness all the way from the edge up to the distal boundary and, hence, the overall flatness of the sheet is, according to our model, mainly due to the effects of the protein scaffolds and is largely independent of this boundary condition. At the same time, a biological background for the distal boundary condition is the presence in realistic ER sheets of protein complexes, such as Climp63, which are supposed to bridge the upper and lower sheet membranes and, hence, stabilize the flatness of ER sheets beginning from some distances from the sheet edges (19). While the sheet formation and homogeneity is independent of Climp63 bridges (19) inclusion of the bridge effects into the future models will extend our understanding of the detailed morphology of ER sheets.

Author Contributions

Y.S. performed the research, analyzed data, and worked on the article; T.S. analyzed data and worked on the article; and M.M.K. designed the research, analyzed data, and wrote the article.

Editor: Tobias Baumgart.