Abstract
Primary cilia are ubiquitous mammalian cellular substructures implicated in an ever-increasing number of regulatory pathways. The well-established ciliary hypothesis states that physical bending of the cilium (for example, due to fluid flow) initiates signaling cascades, yet the mechanical properties of the cilium remain incompletely measured, resulting in confusion regarding the biological significance of flow-induced ciliary mechanotransduction. In this work we measure the mechanical properties of a primary cilium by using an optical trap to induce resonant oscillation of the structure. Our data indicate 1) the primary cilium is not a simple cantilevered beam; 2) the base of the cilium may be modeled as a nonlinear rotatory spring, with the linear spring constant k of the cilium base calculated to be (4.6 ± 0.62) × 10−12 N/rad and nonlinear spring constant α to be (−1 ± 0.34) × 10−10 N/rad2; and 3) the ciliary base may be an essential regulator of mechanotransduction signaling. Our method is also particularly suited to measure mechanical properties of nodal cilia, stereocilia, and motile cilia—anatomically similar structures with very different physiological functions.
Introduction
The primary cilium is a microtubule bundle that extends from the mother centrosome into the extracellular space and is hypothesized to be a mechanotransducing structure (1–4). A decade of experimental results has demonstrated that bending the primary cilium is correlated with initiation of a variety of signaling cascades (1,2,5–26). Measurements of the essential mechanical properties of this mechanical sensor are surprisingly few, and have relied on static deformations induced either by steady fluid flow (9,16,27), by glass pipette (7), or by optical trapping of a bead attached to the cilium tip (3). Experiments that infer the mechanical properties through relaxation methods have been performed on microtubules and cilia (3,28) as well. It must be emphasized that while models of the mechanical properties of motile cilia and flagella are plentiful (for example, see the literature (29–42)), they are not relevant here due to the significant physiological and structural differences between motile and nonmotile cilia. Nodal cilia (43) are structurally identical to a primary cilium, but again, while the mechanical properties of nodal cilia have been inferred from models of induced flow (43–45), they have not yet been directly measured.
In contrast to the previous methods, we have directly excited a resonant oscillation of a primary cilium with a single beam three-dimensional optical tweezer (46,47). Measuring dynamic responses of the cilium provides information that cannot be measured using static methods such as, for example, recording mechanical properties of the cilium base. In addition, use of dynamics rather than statics potentially obviates the need for detailed shape fitting, which requires either side-on views of the cilium (48) or insertion of fluorescent transmembrane proteins (16). We will demonstrate that a single dynamic measurement provides a wealth of reliable information about not only the mechanical properties of the primary cilium, but of the cilium-fluid interaction as well. The method described here provides results equivalent to multiple independent experiments, and our method could be applied to the study of motile cilia (49), nodal cilia, and more complex structures such as hair-cell stereocilia (50). Our experimental approach compares favorably with similar experiments performed using magnetic tweezers on motile cilia (49). One advantage of optical trapping over magnetic tweezers is the noncontact generation of force; magnetic tweezers require a paramagnetic bead to be affixed to the cilia, significantly altering the fluid flow in the neighborhood of the cilium.
Materials and Methods
Cell culture
Experiments were carried out with a mouse cell line derived (51) from the cortical collecting duct (mCCD 1296 (d)) of a heterozygous offspring of the Immortomouse (Charles River Laboratories, Wilmington, MA). The Immortomouse carries as transgene a temperature-sensitive SV40 large T antigen under the control of an interferon-γ response element. Cells were maintained on collagen-coated Millicell-CM inserts (inner diameter 30 mm, permeable support area 7 cm2; Millipore, Billerica, MA) to promote a polarized epithelial phenotype. Cells were grown to confluence at 33°C, 5% CO2 and then maintained at 39°C, 5% CO2 to enhance differentiation. The growth medium consisted of the following (final concentrations): Dulbecco’s Modified Eagle’s Medium w/o glucose and Ham’s F12 at a 1:1 ratio, 5 mM glucose, 5 μg/mL transferrin, 1 nM T3 (triiodothyronine), 5 μg/mL insulin, 10 ng/mL EGF (epithelial growth factor), 4 μg/mL dexamethasone, 15 mM HEPES (4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid), 0.06% NaHCO3, 2 mM L-glutamine, 10 ng/mL interferon-γ, 50 μM ascorbic acid 2-phosphate, 20 nM selenium, and 5% FBS (fetal bovine serum). For differentiation, FBS, EGF, insulin, and interferon-γ were omitted from the apical medium and insulin, EGF, and interferon-γ from the basal medium.
Optical tweezers
The source for the single-beam three-dimensional trap was a Crystalaser IRCL-0.5W-1064 (Reno, NV), a diode-pumped Nd:YAG continuous-wave single mode laser providing 0.5-W optical power from a 10-W electrical power supply. The optical tweezer breadboard layout was constructed using optomechanical mounts ( Qioptiq, Munich, Germany; Excelitas Technologies, Fremont, CA). Achromatic doublets were used for the beam expansion. The first lens has a 10-mm focal length, while the second has a 200-mm focal length. Both lenses were anti-reflection-coated for 1064 nm. The focal lengths were chosen simply for convenience: the distance between the entrance port of the microscope and the objective lens is 140 mm, and the laser beam was expanded a factor of ∼6× to fill the aperture. The objective lens used was a 63× NA 0.9 U-V-I HCX long-working-distance Plan Apochromat dipping objective (Leica Microsystems, Buffalo Grove, IL) with a 2.2-mm working distance. The tweezer couples into the microscope through an existing lateral port. A side-looking dichroic mirror (Chroma Technology, Bellows Falls, VT) mounted within the fluorescence turret provides the ability to perform normal microscope viewing while the tweezers are operating. The fixed-position optical trap has a beam waist of 0.3 μm and Rayleigh length of 0.4 μm.
Objects held within the trap diffract the trapping beam. The spatial dynamics of the diffracted beam were recorded using a quadrant photodiode (QPD) and the data analyzed as per Glaser et al. (52). Briefly, the QPD outputs the centroid location of the diffracted trapping beam, digitally sampled at 10 kS/s. The data was then analyzed to calculate the force applied by the trap to the trapped object. The relationship between the centroid position and the location of the trapped object is known, allowing calculation of the cilium tip position.
Applying the trap to a primary cilium proceeded as follows. First, the trap location was precisely determined by trapping a small piece of floating cell debris. Turning the trapping laser off and using bright-field illumination, a cilium was moved to the center of the trap and focus-adjusted to align the trapping plane to the cilium tip. The cilium was then laterally displaced slightly from the trap axis and recorded using the XY translation stage digital readout. The optical trap was turned on and QPD data acquired for several seconds. The trap was then turned off, another cilium moved into position, and the procedure repeated.
Microscopy
Imaging and manipulations of terminally differentiated epithelial monolayers were carried out using a DM 6000 upright microscope (Leica Microsystems) equipped with a heated and CO2-controlled incubation chamber (Solent Scientific, Segensworth, UK). The microscope stage (Cat. No. H30XY2; Prior Scientific, Rockland, MA) was accurate to ±0.04 μm. Bright-field image acquisition and optical trap monitoring were performed by a Flea digital video-rate camera (Point Grey, Richmond, British Columbia, Canada).
Cilium length measurement
After the trapping experiments, cells were fixed and stained for high-resolution imaging. Image stacks (0.1 μm z-step size) were obtained via the software MICRO-MANAGER (https://www.micro-manager.org/) (53) using a 100× 1.46 NA immersion lens (Leica Microsystems) and cilium lengths measured directly from the image stack. For the measurements reported here, the cilium length was measured to be L = 2.1 ± 0.05 μm. It is important to note that we use the immunostained axoneme length as a proxy for the cilium length; the actual cilium length could be slightly different.
Immunocytochemistry
Fixation and immunocytochemistry were performed using standard techniques. The cells were fixed in 4% paraformaldehyde for 10 min. After rinsing, the monolayers were permeabilized for 10 min with a solution of 0.1% Triton-X and 0.5% saponin in a blocking buffer containing 5% donkey serum, 5% sheep serum, 1% BSA (bovine serum albumin), and 5% FBS (fetal bovine serum). The monolayers were then stained with a monoclonal mouse antibody against acetylated α-tubulin (Invitrogen, Carlsbad, CA) and a polyclonal goat antibody against Polycystin-1 (Abcam, Cambridge, UK) followed by an anti-mouse antibody labeled with AlexaFluor 488 (Invitrogen) and an anti-goat antibody labeled with AlexaFluor 594 (Invitrogen). The stained filter was cut out of the culture insert and transferred to a microscope slide, monolayer side up. The filter was mounted in a VectaShield (Vector Labs, Burlingame, CA) with DAPI. A No. 1.5 coverslip was placed on top of the monolayer, then sealed with nail polish and stored at 4°C for later imaging.
Culture media viscosity and density measurement
The dynamic viscosity of apical media was measured with a Cannon-Fenske Routine Viscometer (Induchem Lab Glass, Roselle, NJ) with the apparatus and media equilibrated to 37°C. The density of the media was measured with a pycnometer (Thermo Fisher Scientific, Waltham, MA).
Results
An en face view of stained cells with primary cilia indicated is shown in Fig. 1. Most of the cells are ciliated, and the cilia are oriented vertically, appearing as a diffraction-limited point. The length of cilia were measured to be L = 2.1 ± 0.05 μm. The viscosity of fluid was measured to be η = 0.637 ± 0.012 cP, the density measured to be ρ = 1.00 ± 0.01 g/cm3. The density of the cilium is estimated to be 1.11 g/cm3 (10) and the cilium diameter a = 0.2 μm.
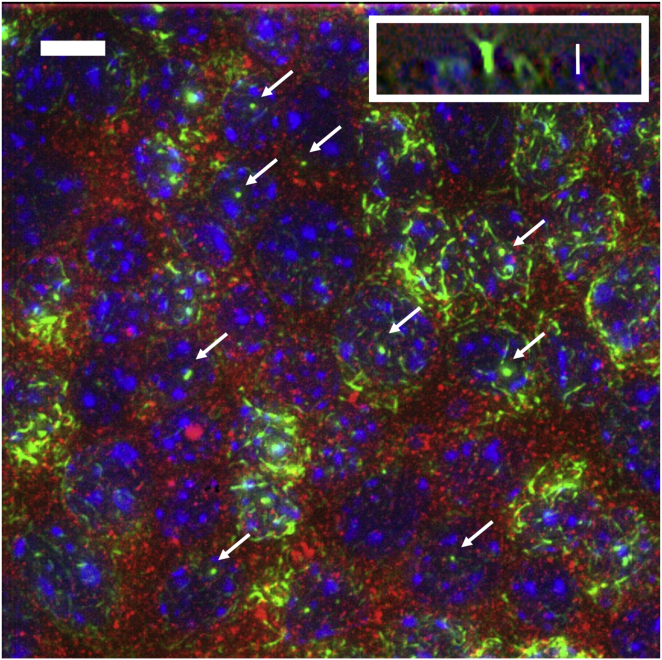
Figure 1.
En face view of fixed and stained epithelial monolayer. (Green) Acetylated α-tubulin, identifying the primary cilia. (Red) Polycystin-1. (Blue) DAPI (nuclear DNA). (Arrows) Several of the primary cilia. (Inset) An x-z slice showing the orientation of the primary cilium with respect to the cell layer. Scale bars = 2 μm. To see this figure in color, go online.
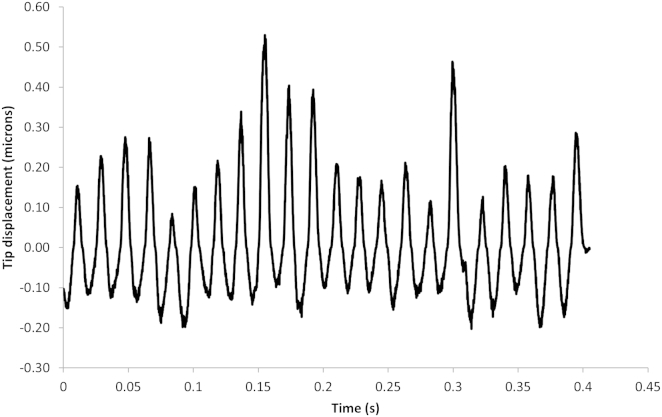
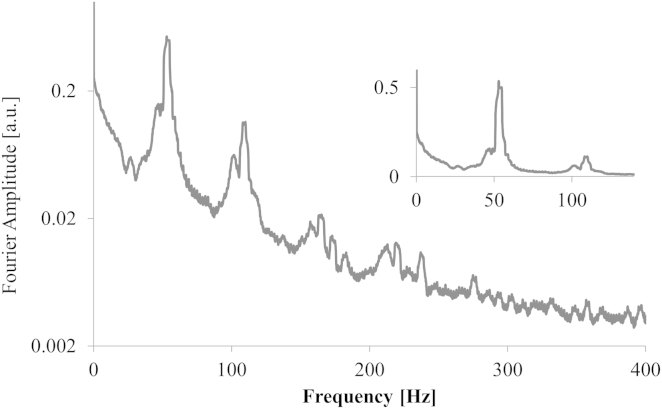
The direct QPD output from a trapped cilium is shown in Fig. 2, showing the time-varying position of the cilium tip. This result was unexpected, because the cilium tip was not held steady within the trap as for trapped microspheres. The Fourier transform of the QPD output results in Fig. 3, clearly showing a resonant oscillation frequency and multiple harmonics.
Figure 2.
QPD output data. A subset of the full dataset is shown here, scaled in time (10 kS/s) and centroid displacement (volts/meter). Each individual datapoint corresponds to the centroid location of the diffracted trapping beam and is, after scaling, a trace of the actual position of the trapped object (the cilium tip) within the trapping plane in time.
Figure 3.
Discrete Fourier transform of the (full) dataset shown in Fig. 2. The spectrum (log plot) shows the resonant frequency as well as the first, second, and third harmonics. (Inset, linear plot) Detailed graph of the fundamental and first harmonic.
We directly obtain the following: oscillation amplitude = 0.22 ± 0.047 μm and resonant oscillation frequency f = 57 Hz = ω/2π. The Reynolds number (Re) associated with this motion is = 5.6 × 10−6, indicating viscous effects dominate. We performed this measurement on (N = 6) cilia and obtained the oscillation amplitude and resonant frequency for each. Taken as a whole, the average resonant frequency is f = 55.9 ± 1.4 Hz.
Analysis
Our analysis begins with the simple and most widely used mechanical model for a primary cilium, a cantilevered beam. After demonstrating that this model gives incorrect predictions, we include both hydrodynamic effects (viscous drag) and a driving force (optical trap). After demonstrating that this extended model also does not accurately predict the resonance frequency, we introduce a nonlinear rotatory spring located at the cilium base to reconcile our model with our measured results.
Classical cantilever beam
The most basic model for a primary cilium, the classical cantilever, neglects hydrodynamic interactions and models a cilium as a homogeneous flexible cylindrical beam that is anchored at the basal end and is free to move at the distal end. Because primary cilia, unlike motile cilia, do not actively generate internal forces, we can model the primary cilium in terms of a passive beam: there is no generation of forces and/or moments within the cilium. Because the slenderness (length/diameter) of the cilium is large, we may neglect both rotatory inertia and transverse shear and approximately describe the cilium shape in terms of a one-dimensional object, the so-called neutral axis (54). Under the conditions described above, the time-dependent shape Y(s,t) of the neutral axis of a cilium is given by the linearized Euler-Bernoulli law for pure bending,
| (1) |
where w is the (externally applied) distributed force per length, μ is the mass/unit length of the cilium, E is the Young’s modulus of the cilium, I is the area moment of inertia (for a cylinder of radius a, I = πa4/4), and EI is referred to as the flexural rigidity, having units of Force × area. Careful measurements by several groups (6,16,17,27,55) have measured the flexural rigidity EI for primary cilia and while there is incomplete agreement, reported values typically vary within the range 1 × 10−23 < EI < 2 × 10−23 Nm2. Thus, we set EI = 1.5 × 10−23 Nm2 here. Note that a mechanical model of a cilium accounting for microstructure simply replaces the single-valued homogeneous EI with a spatially varying E and modified I; the homogeneous EI used in this model (and others) can therefore be considered an effective flexural rigidity. EI functions as a spring constant when describing the deformation of the cilium.
The natural (w = 0) resonant frequencies of a cantilever of length L can be determined analytically by first separating Y(s,t) = S(s)T(t), resulting in the solutions
| (2) |
| (3) |
where the oscillation frequency ω is related to α by . Solving for eigenvalues (ω) and mode shapes (C1, C2, etc.) requires application of boundary conditions to S(s). Determining the coefficients A1 and A2 requires specification of initial conditions (say at t = 0), but because the detailed solution of T(t) is not needed here, we do not determine them.
The boundary conditions for a cantilevered beam are as follows:
-
1)
the fixed end cannot move, ;
-
2)
the fixed end cannot deflect, ;
-
3)
at the free end (s = L), the bending moment vanishes, ; and
-
4)
at the free end, the shear force vanishes, .
The eigenvalues are most easily found by solving the eigenvalue equation , where the vector and the matrix A is provided from the four boundary conditions, giving the well-known result . For the cilia studied here, this model returns a resonant frequency of 83.6 kHz, clearly at variance with our measurement (57 Hz).
Viscous effects (hydrodynamic interaction)
There are at least two approaches to incorporate hydrodynamics into the Euler-Bernoulli law. One treats the viscous force as a distributed load wdrag, while a second approach (56) treats the interaction as a virtual mass due to the displaced fluid. Treating the hydrodynamic interaction as a distributed load appears straightforward; we could potentially use the result obtained by Resnick and Hopfer (10) for the viscous force exerted onto a moving cylinder (motion perpendicular to the cylinder axis),
| (4) |
where U is the (local) relative velocity between cilium and fluid, and γ is Euler’s constant (0.577…). Treating the cilium tip as a half-sphere, boundary condition 4 becomes, at the free end, the shear force from viscosity: .
Because the velocity U is time-dependent and a function of position along the neutral axis, this approach is not suited for dynamics. However, if the relative velocity is time-independent (steady fluid flow past a cilium, discussed below) and the cilium deflection is not too large, the equilibrium deflection can be easily computed, and we do so below.
Consequently, for dynamics we used the alternate model that treats the cantilever-fluid interaction in terms of a virtual mass due to the displaced fluid (56). This model provides an implicit function for the resonant frequency of a cantilever within a viscous fluid,
| (5) |
where Γ(ω) is the hydrodynamic function for a cylinder:
| (6) |
The functions and are modified Bessel functions of the third kind, and the approximation valid in the limit . Numerical solution of Eq. 5 predicts a resonant frequency of 269 Hz for the cilia used in this study. While this is an improvement in accuracy, there is still considerable disagreement with measurement.
Optical trap: end-loaded cantilever
Optical traps apply a force proportional to the gradient of the intensity. A detailed model of the force applied by an optical trap to a cilium is beyond the scope of this report and is being prepared separately. Our QPD data analysis returns the time-averaged value of the applied force, which must then scaled depending on the space- and time-dependence of the applied force to calculate, for example, the maximum applied force W. Because the cilium tip oscillates through the fixed trap location, the applied force can be separated into , simplifying the analysis. Compared to the cilium length, the Rayleigh length of the trap allows us to treat the applied force as localized to the cilium tip: . is a function of distance between trapped object and trap center and scales as , where ω0 is the beam waist.
Boundary condition 4 is now:
-
4)
at the free end, the shear force from the trap, .
Although inclusion of this end load complicates boundary condition 4, our analysis may be simplified by first considering the static limit, corresponding to the maximum cilium deflection, maximum applied force W, and no viscous drag because the cilium is momentarily stationary. The maximum displacement of a cantilevered beam is , where w is the cantilever’s weight per unit length (w = μg). For our system, this model predicts , again in disagreement with our measurements.
To summarize the above findings, we provide Table 1.
Table 1.
Summary of experimental measurements and initial model predictions
| Measured resonant frequency | 55.9 ± 1.4 Hz |
| Predicted resonance, classical cantilever | 83.6 kHz |
| Predicted resonance, cantilever in a viscous medium | 269 Hz |
| Measured oscillation amplitude | 0.22 ± 0.047 μm |
| Predicted amplitude | 0.43 μm |
Improved model for cilium base
We have now demonstrated that none of our results can be explained by modeling the cilium as a cantilevered beam. Given this persistent discrepancy between the above predictions and our measured data, following the example of Young et al. (16), we now incorporate an improved mechanical model for the cilium base: a nonlinear rotational spring. We model the cilium base as a nonlinear rotational spring with linear spring constant and nonlinear coefficient , while leaving the cilium itself as a uniform homogeneous beam as before. We do not treat the individual base components (basal body, transition fibers, ciliary necklace, cilium membrane, etc.) as separate lumped parameters because those additional degrees of freedom (masses, spring constants, etc.) have not yet been constrained by experiment and thus could result in an ill-posed model. Boundary conditions 2 and 4 are now given by:
2. The fixed end has a bending moment due to the spring, ; and
4. The free end is subject to a shear load, .
Boundary condition 2 is nonlinear and boundary condition 4 is inhomogeneous, while the static shape can be computed through direct integration:
| (7) |
The eigenvalue method fails due to the inhomogeneous boundary condition. Consequently, the spring constants were numerically computed using the Rayleigh method (57). The time-averaged potential energy P and kinetic energy T of the beam are set equal to each other:
| (8) |
Solving this results in two resonance frequencies (and two additional unphysical negative frequencies):
| (9a) |
| (9b) |
| (9c) |
As before, is scaled to using Eq. 5. We now have analytic expressions for and that depend on the two (unknown) spring constants k and α to compare with measurements ω and . Constraining the spring constants k and α to be real and requiring k > 0 selects the unique physically relevant solution. Specifically, we find that k = 4.6 × 10−12 ± 0.62 10−12 N/rad and α = −1 × 10−10 ± 0.34 × 10−10 N/rad2 produces agreement with our measurements. If we model the base of the cilium as a nonlinear spring, then under conditions of periodic forcing the primary cilium is a Duffing oscillator (58), and because α < 0, the primary cilium is a softening spring. Our results have significant biological relevance (discussed below).
Model results
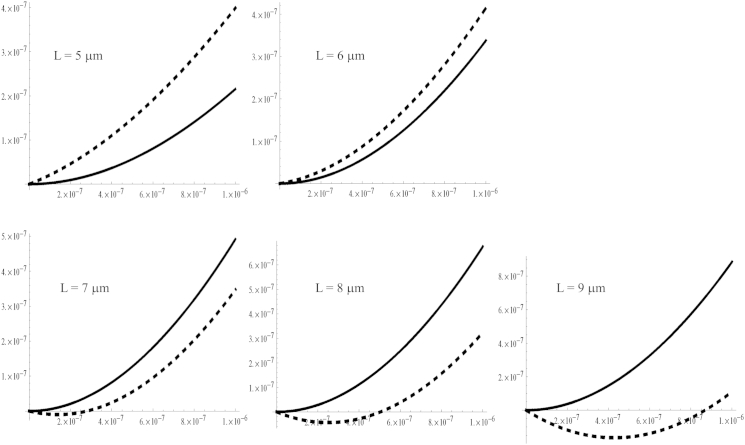
Equilibrium profiles of deformed cilia of various lengths are shown in Figs. 4 and 5, using fluid flow conditions typical in a mouse tubule (Poiseuille flow, tubule radius 10 μm, volume flow rate 5 nL/min, and ). The deformed profile was calculated by solving the time-independent form of Eq. 1, using the viscous drag loading in Eq. 4. Fig. 4 shows equilibrium profiles for cilia modeled as simple cantilevers and for comparison, equilibrium profiles of cilia using our proposed model. Both the cilium profile and slope are different between the two models.
Figure 4.
Graph of the neutral axis of cilia ranging in length from 6 to 8 μm exposed to physiologically relevant steady tubule flow (R = 10 μm, Q = 5 nL/min). (Left) Cilia modeled as a cantilever; (right) results of our proposed model incorporating a nonlinear rotatory spring at the base. The most striking result is that as the cilium length increases past a certain threshold (∼7 μm here), the rotatory spring at the cilium base causes a change in sign in the slope of the cilium at the base.
Figure 5.
Plots of the basal region of the primary cilium without (solid line) and with (dashed line) a rotatory spring, detailing the effect of the rotatory spring. Cilium length indicated for each plot; fluid flow velocity is the same as in Fig. 4.
Fig. 5 presents more detailed plots comparing the equilibrium deformation of a primary cilium. We show only the basal region of the cilium, emphasizing the significant effect caused by the rotatory spring. For cilia that are <7 μm long, the modified model predicts a somewhat larger cilium deformation as compared to the classical cantilever. However, for cilia longer than 7 μm, our proposed model shows a dramatic difference as compared to the classical cantilever: the slope of the cilium at the base changes sign. We conclude that our proposed model lends support to the idea that physical structures located at the base of the cilium (basal body, transition fibers, ciliary necklace, etc.) may have essential roles in regulating the mechanosensation mechanism.
Biological relevance of a cilium modeled as a Duffing oscillator
It is worthwhile to briefly review the rationale behind this measurement and analysis. First, the cilium length of most mammalian cells is autoregulated (MDCK cells, as a contrary example, are not), and while the mechanism has been clearly identified (regulation of intraflagellar transport rates shown in, for example, Pedersen et al. (59)), the origin of the set point is not known. Second, recent results (60) demonstrated that chemically stimulating cilia-localized dopamine receptors under no-flow conditions caused an increase in cilioplasmic calcium that was not accompanied by an increase in cytosolic calcium. That is, calcium did not diffuse from the cilioplasm into the cytoplasm when the cilium was stimulated chemically. Both of these phenomena (length setpoint, diffusion barrier) could be explained by our finding that the base of the cilium acts as a softening spring.
Duffing oscillators exhibit a physical property that may have relevance here: hysteresis. As a cilium grows, the resonant frequency scales as L−2 while the driving frequency (the pulse) remains essentially constant. For a softening spring (α < 0) like the primary cilium, when the resonant frequency decreases beyond a threshold, the oscillation amplitude discontinuously jumps, shown schematically in Fig. 6. In Fig. 6, the reference length for a cilium (L0 = 6.7 μm) was determined by setting the driving frequency to the mouse heartrate (10 Hz) and solving Eq. 8.
Figure 6.
Schematic of cilium oscillation amplitude as a function of cilium length. Hysteresis occurs as the cilium length exceeds a threshold value; the oscillation amplitude discontinuously drops.
As the cilium is lengthening, the cilium oscillates with amplitude sufficient such that the bending energy at the base is large enough to allow calcium to diffuse into the cytoplasm: the mechanotransduction pathway is constitutively activated. When the cilium reaches a certain threshold length, the oscillation amplitude spontaneously decreases to a very low value, decreasing the available energy below the threshold needed to allow calcium to diffuse, switching off the mechanotransduction pathway. This sudden loss of signal would then be used by the cell to stop growing the cilium.
Extensions of model to nodal and motile cilia
It is instructive to compare our model calculations with measurements of the ciliary beat frequency (CBF). An example measurement of motile cilia (49) reports L = 7 μm, EI = 6 × 10−22 Nm2, and CBF = 10 Hz. Using these reported values for L and EI in our model results in a resonant frequency of 12 Hz, perhaps indicating that the CBF is near the resonant frequency. Similarly, using reported values for nodal cilia (43) (a = 0.3 μm, L = 5 μm, EI = 1.5 × 10−23 Nm2), our model predicts a resonant oscillation at 5.7 Hz, rather than the reported 10 Hz, potentially indicating the role of motor proteins in the basal body as force generators.
Conclusion
Our primary finding of interest is definitive evidence showing the primary cilium cannot be plausibly modeled as a simple cantilever, and we provide measurements of the mechanical properties of the cilium base. Bending the primary cilium is associated with a variety of downstream biological responses, including opening transmembrane ion channels, regulation of transepithelial salt and water transport, and regulation of pro-growth, pro-inflammatory gene transcription programs. However, the essential biological relevance of ciliary flow sensing remains uncertain due in part to a lack of causal mechanisms linking ciliary bending to initiation of signaling cascades. Our measurements demonstrate that the ciliary base could be the link.
We have, for the first time to our knowledge, characterized the mechanical properties of a primary cilium through resonant excitation excited by an optical trap. A single dynamic measurement is sufficient to constrain multiple model properties and provides fresh insight into the mechanosensation mechanism. Our findings highlight a possible role of the basal body (or more generally, the base of the cilium) as a site of mechanotransduction regulation. We believe our method could be successfully applied to other ciliated cell types, for example MDCK cells, endothelial cells, and hair cells.
Author Contributions
A.R. designed and performed the research, analyzed the data, and wrote the article.
Acknowledgments
This research was supported by National Institutes of Health award No. DK092716.
Editor: Charles Wolgemuth.
References
- 1.Veland I.R., Awan A., Christensen S.T. Primary cilia and signaling pathways in mammalian development, health and disease. Nephron, Physiol. 2009;111:39–53. doi: 10.1159/000208212. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Werner M.E., Mitchell B.J. Planar cell polarity: microtubules make the connection with cilia. Curr. Biol. 2012;22:R1001–R1004. doi: 10.1016/j.cub.2012.10.030. [DOI] [PubMed] [Google Scholar]
- 3.Battle C. Georg-August-Universität Göttingen; Göttingen, Germany: 2013. Mechanics & Dynamics of the Primary Cilium. [Google Scholar]
- 4.Nguyen A.M., Jacobs C.R. Emerging role of primary cilia as mechanosensors in osteocytes. Bone. 2013;54:196–204. doi: 10.1016/j.bone.2012.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Praetorius H.A., Spring K.R. Bending the MDCK cell primary cilium increases intracellular calcium. J. Membr. Biol. 2001;184:71–79. doi: 10.1007/s00232-001-0075-4. [DOI] [PubMed] [Google Scholar]
- 6.Liu W., Xu S., Satlin L.M. Effect of flow and stretch on the [Ca2+]i response of principal and intercalated cells in cortical collecting duct. Am. J. Physiol. Renal Physiol. 2003;285:F998–F1012. doi: 10.1152/ajprenal.00067.2003. [DOI] [PubMed] [Google Scholar]
- 7.Praetorius H.A., Frokiaer J., Spring K.R. Bending the primary cilium opens Ca2+-sensitive intermediate-conductance K+ channels in MDCK cells. J. Membr. Biol. 2003;191:193–200. doi: 10.1007/s00232-002-1055-z. [DOI] [PubMed] [Google Scholar]
- 8.Praetorius H.A., Spring K.R. The renal cell primary cilium functions as a flow sensor. Curr. Opin. Nephrol. Hypertens. 2003;12:517–520. doi: 10.1097/00041552-200309000-00006. [DOI] [PubMed] [Google Scholar]
- 9.Liu W., Murcia N.S., Satlin L.M. Mechanoregulation of intracellular Ca2+ concentration is attenuated in collecting duct of monocilium-impaired OrpK mice. Am. J. Physiol. Renal Physiol. 2005;289:F978–F988. doi: 10.1152/ajprenal.00260.2004. [DOI] [PubMed] [Google Scholar]
- 10.Resnick A., Hopfer U. Force-response considerations in ciliary mechanosensation. Biophys. J. 2007;93:1380–1390. doi: 10.1529/biophysj.107.105007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Weimbs T. Polycystic kidney disease and renal injury repair: common pathways, fluid flow, and the function of polycystin-1. Am. J. Physiol. Renal Physiol. 2007;293:F1423–F1432. doi: 10.1152/ajprenal.00275.2007. [DOI] [PubMed] [Google Scholar]
- 12.Nauli S.M., Kawanabe Y., Zhou J. Endothelial cilia are fluid shear sensors that regulate calcium signaling and nitric oxide production through polycystin-1. Circulation. 2008;117:1161–1171. doi: 10.1161/CIRCULATIONAHA.107.710111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Resnick A., Hopfer U. Mechanical stimulation of primary cilia. Front. Biosci. 2008;13:1665–1680. doi: 10.2741/2790. [DOI] [PubMed] [Google Scholar]
- 14.Resnick A. Chronic fluid flow is an environmental modifier of renal epithelial function. PLoS ONE. 2011;6:e27058. doi: 10.1371/journal.pone.0027058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Shi Z.D., Tarbell J.M. Fluid flow mechanotransduction in vascular smooth muscle cells and fibroblasts. Ann. Biomed. Eng. 2011;39:1608–1619. doi: 10.1007/s10439-011-0309-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Young Y.N., Downs M., Jacobs C.R. Dynamics of the primary cilium in shear flow. Biophys. J. 2012;103:629–639. doi: 10.1016/j.bpj.2012.07.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Downs M.E., Nguyen A.M., Jacobs C.R. An experimental and computational analysis of primary cilia deflection under fluid flow. Comput. Methods Biomech. Biomed. Engin. 2014;17:2–10. doi: 10.1080/10255842.2011.653784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Nauli S.M., Alenghat F.J., Zhou J. Polycystins 1 and 2 mediate mechanosensation in the primary cilium of kidney cells. Nat. Genet. 2003;33:129–137. doi: 10.1038/ng1076. [DOI] [PubMed] [Google Scholar]
- 19.Watnick T., Germino G. From cilia to cyst. Nat. Genet. 2003;34:355–356. doi: 10.1038/ng0803-355. [DOI] [PubMed] [Google Scholar]
- 20.Nauli S.M., Zhou J. Polycystins and mechanosensation in renal and nodal cilia. BioEssays. 2004;26:844–856. doi: 10.1002/bies.20069. [DOI] [PubMed] [Google Scholar]
- 21.Pazour G.J. Intraflagellar transport and cilia-dependent renal disease: the ciliary hypothesis of polycystic kidney disease. J. Am. Soc. Nephrol. 2004;15:2528–2536. doi: 10.1097/01.ASN.0000141055.57643.E0. [DOI] [PubMed] [Google Scholar]
- 22.Higginbotham H., Eom T.Y., Anton E.S. Arl13b in primary cilia regulates the migration and placement of interneurons in the developing cerebral cortex. Dev. Cell. 2012;23:925–938. doi: 10.1016/j.devcel.2012.09.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yuan S., Li J., Sun Z. Target-of-rapamycin complex 1 (Torc1) signaling modulates cilia size and function through protein synthesis regulation. Proc. Natl. Acad. Sci. USA. 2012;109:2021–2026. doi: 10.1073/pnas.1112834109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Weimbs T., Olsan E.E., Talbot J.J. Regulation of STATs by polycystin-1 and their role in polycystic kidney disease. JAK-STAT. 2013;2:e23650. doi: 10.4161/jkst.23650. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wong S.Y., Seol A.D., Reiter J.F. Primary cilia can both mediate and suppress Hedgehog pathway-dependent tumorigenesis. Nat. Med. 2009;15:1055–1061. doi: 10.1038/nm.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Boehlke C., Kotsis F., Kuehn E.W. Primary cilia regulate mTORC1 activity and cell size through Lkb1. Nat. Cell Biol. 2010;12:1115–1122. doi: 10.1038/ncb2117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Schwartz E.A., Leonard M.L., Bowser S.S. Analysis and modeling of the primary cilium bending response to fluid shear. Am. J. Physiol. 1997;272:F132–F138. doi: 10.1152/ajprenal.1997.272.1.F132. [DOI] [PubMed] [Google Scholar]
- 28.Felgner H., Frank R., Schliwa M. Flexural rigidity of microtubules measured with the use of optical tweezers. J. Cell Sci. 1996;109:509–516. doi: 10.1242/jcs.109.2.509. [DOI] [PubMed] [Google Scholar]
- 29.Rikmenspoel R. Elastic properties of the sea urchin sperm flagellum. Biophys. J. 1966;6:471–479. doi: 10.1016/S0006-3495(66)86670-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Satir P. Studies on cilia. 3. Further studies on the cilium tip and a “sliding filament” model of ciliary motility. J. Cell Biol. 1968;39:77–94. doi: 10.1083/jcb.39.1.77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Brokaw C.J. Bend propagation by a sliding filament model for flagella. J. Exp. Biol. 1971;55:289–304. doi: 10.1242/jeb.55.2.289. [DOI] [PubMed] [Google Scholar]
- 32.Rikmenspoel R. Contractile mechanisms in flagella. Biophys. J. 1971;11:446–463. doi: 10.1016/S0006-3495(71)86227-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Baba S.A. Flexural rigidity and elastic constant of cilia. J. Exp. Biol. 1972;56:459–467. doi: 10.1242/jeb.56.2.459. [DOI] [PubMed] [Google Scholar]
- 34.Brokaw C.J. Flagellar movement: a sliding filament model. Science. 1972;178:455–462. doi: 10.1126/science.178.4060.455. [DOI] [PubMed] [Google Scholar]
- 35.Rikmenspoel R., Rudd W.G. The contractile mechanism in cilia. Biophys. J. 1973;13:955–993. doi: 10.1016/S0006-3495(73)86037-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Rikmenspoel R. The equation of motion for sperm flagella. Biophys. J. 1978;23:177–206. doi: 10.1016/S0006-3495(78)85442-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Hines M., Blum J.J. Three-dimensional mechanics of eukaryotic flagella. Biophys. J. 1983;41:67–79. doi: 10.1016/S0006-3495(83)84406-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Brokaw C.J. Computer simulation of flagellar movement. IX. Oscillation and symmetry breaking in a model for short flagella and nodal cilia. Cell Motil. Cytoskeleton. 2005;60:35–47. doi: 10.1002/cm.20046. [DOI] [PubMed] [Google Scholar]
- 39.Gadelha C., Wickstead B., Gull K. Flagellar and ciliary beating in trypanosome motility. Cell Motil. Cytoskeleton. 2007;64:629–643. doi: 10.1002/cm.20210. [DOI] [PubMed] [Google Scholar]
- 40.Hilfinger A., Chattopadhyay A.K., Jülicher F. Nonlinear dynamics of cilia and flagella. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009;79:051918. doi: 10.1103/PhysRevE.79.051918. [DOI] [PubMed] [Google Scholar]
- 41.Dillon R.H., Fauci L.J., Yang X. Fluid dynamic models of flagellar and ciliary beating. Ann. N. Y. Acad. Sci. 2007;1101:494–505. doi: 10.1196/annals.1389.016. [DOI] [PubMed] [Google Scholar]
- 42.Dillon R.H., Fauci L.J. An integrative model of internal axoneme mechanics and external fluid dynamics in ciliary beating. J. Theor. Biol. 2000;207:415–430. doi: 10.1006/jtbi.2000.2182. [DOI] [PubMed] [Google Scholar]
- 43.Buceta J., Ibañes M., Izpisúa-Belmonte J.C. Nodal cilia dynamics and the specification of the left/right axis in early vertebrate embryo development. Biophys. J. 2005;89:2199–2209. doi: 10.1529/biophysj.105.063743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Chen D., Norris D., Ventikos Y. The active and passive ciliary motion in the embryo node: a computational fluid dynamics model. J. Biomech. 2009;42:210–216. doi: 10.1016/j.jbiomech.2008.10.040. [DOI] [PubMed] [Google Scholar]
- 45.Cartwright J.H., Piro O., Tuval I. Fluid-dynamical basis of the embryonic development of left-right asymmetry in vertebrates. Proc. Natl. Acad. Sci. USA. 2004;101:7234–7239. doi: 10.1073/pnas.0402001101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Ashkin A., Dziedzic J.M., Chu S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986;11:288. doi: 10.1364/ol.11.000288. [DOI] [PubMed] [Google Scholar]
- 47.Resnick A. Design and construction of a space-borne optical tweezer apparatus. Rev. Sci. Instrum. 2001;72:4059–4065. [Google Scholar]
- 48.Roth K.E., Rieder C.L., Bowser S.S. Flexible-substratum technique for viewing cells from the side: some in vivo properties of primary (9+0) cilia in cultured kidney epithelia. J. Cell Sci. 1988;89:457–466. doi: 10.1242/jcs.89.4.457. [DOI] [PubMed] [Google Scholar]
- 49.Hill D.B., Swaminathan V., Superfine R. Force generation and dynamics of individual cilia under external loading. Biophys. J. 2010;98:57–66. doi: 10.1016/j.bpj.2009.09.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kitajiri S., Sakamoto T., Friedman T.B. Actin-bundling protein TRIOBP forms resilient rootlets of hair cell stereocilia essential for hearing. Cell. 2010;141:786–798. doi: 10.1016/j.cell.2010.03.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kolb R.J., Woost P.G., Hopfer U. Membrane trafficking of angiotensin receptor type-1 and mechanochemical signal transduction in proximal tubule cells. Hypertension. 2004;44:352–359. doi: 10.1161/01.HYP.0000136645.90116.1a. [DOI] [PubMed] [Google Scholar]
- 52.Glaser J., Hoeprich D., Resnick A. Near real-time measurement of forces applied by an optical trap to a rigid cylindrical object. Opt. Eng. 2014;53:074110. [Google Scholar]
- 53.Edelstein A., Amodaj N., Stuurman N. Computer control of microscopes using μMANAGER. Curr. Protoc. Mol. Biol. 2010;Chapter 14 doi: 10.1002/0471142727.mb1420s92. Unit14.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Huang T.C. University of Wisconsin-Madison; Madison, WI: 1964. Eigenvalues and Modifying Quotients of Vibration of Beams. [Google Scholar]
- 55.Han Y.F., Ganatos P., Weinbaum S. Transmission of steady and oscillatory fluid shear stress across epithelial and endothelial surface structures. Phys. Fluids. 2005;17:031508. [Google Scholar]
- 56.Sader J.E. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 1998;84:64–76. [Google Scholar]
- 57.Kelly S.G. McGraw-Hill; Boston, MA: 2000. Fundamentals of Mechanical Vibrations. [Google Scholar]
- 58.Guckenheimer J., Holmes P. Springer; New York: 1997. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. [Google Scholar]
- 59.Pedersen L.B., Geimer S., Rosenbaum J.L. Dissecting the molecular mechanisms of intraflagellar transport in Chlamydomonas. Curr. Biol. 2006;16:450–459. doi: 10.1016/j.cub.2006.02.020. [DOI] [PubMed] [Google Scholar]
- 60.Jin X., Mohieldin A.M., Nauli S.M. Cilioplasm is a cellular compartment for calcium signaling in response to mechanical and chemical stimuli. Cell. Mol. Life Sci. 2014;71:2165–2178. doi: 10.1007/s00018-013-1483-1. [DOI] [PMC free article] [PubMed] [Google Scholar]