A Powerful Pathway-Based Adaptive Test for Genetic Association with Common or Rare Variants

Abstract

In spite of the success of genome-wide association studies (GWASs), only a small proportion of heritability for each complex trait has been explained by identified genetic variants, mainly SNPs. Likely reasons include genetic heterogeneity (i.e., multiple causal genetic variants) and small effect sizes of causal variants, for which pathway analysis has been proposed as a promising alternative to the standard single-SNP-based analysis. A pathway contains a set of functionally related genes, each of which includes multiple SNPs. Here we propose a pathway-based test that is adaptive at both the gene and SNP levels, thus maintaining high power across a wide range of situations with varying numbers of the genes and SNPs associated with a trait. The proposed method is applicable to both common variants and rare variants and can incorporate biological knowledge on SNPs and genes to boost statistical power. We use extensively simulated data and a WTCCC GWAS dataset to compare our proposal with several existing pathway-based and SNP-set-based tests, demonstrating its promising performance and its potential use in practice.

Introduction

Genome-wide association studies (GWASs) have been successful in identifying many genetic variants, mainly SNPs, associated with complex and common disease (see, for example, the online Catalog of Published Genome-Wide Association Studies). However, only a small proportion of the estimated heritability for most human complex traits can be explained by the identified genetic variants. One possible reason is that, due to small effect sizes and genetic heterogeneity (i.e., multiple causal variants), the standard single-SNP-based analysis might not have enough power to identify many causal variants. Although many human genetic diseases are caused by variants in multiple genes, it has been increasingly recognized that, because genomic variants of these genes lead to the same or similar phenotypes, these genes are likely to be functionally related, and such functional relatedness can be exploited to identify novel genes containing variants related to disease. One way to organize functionally related genes is through biological pathways, such as annotated in the Kyoto Encyclopedia of Genes and Genomes (KEGG) database.¹ Association analysis of multiple genes with related functions is here generically called pathway analysis (or gene set analysis), which might improve power over testing on single SNPs or single genes one by one. One convincing source of evidence is from tumor sequencing studies, e.g., The Cancer Genome Atlas (TCGA).² Although a few genes (e.g., TP53 [MIM: 191170]) harbor many mutations related to cancer, most harbor few mutations in a tumor-dependent way. For example, a tumor might contain mutations in PTEN (MIM: 601728), not in NF1 (MIM: 613113), whereas another tumor contains mutations in NF1, not in PTEN. Individually, each of the genes in a related pathway has only a low mutation frequency, but collectively, they have a much higher mutation frequency. Hence, for a disease (e.g., cancer) involving a few pathways, a pathway analysis by aggregating information across multiple genes in a relevant pathway will boost statistical power, and thus is preferred. For example, among the 316 ovarian cancer (MIM: 167000) tumors studied by TCGA, 45% of them had genomic alterations (somatic mutations and DNA copy-number changes) in the PI3K/RAS signaling pathway. This pathway contains seven genes—PTEN, PIK3CA (MIM: 171834), AKT1 (MIM: 164730), AKT2 (MIM: 164731), NF1, KRAS (MIM: 190070), and BRAF (MIM: 164757)—each with only low to moderate genomic alterations in 7%, 18%, 3%, 6%, 12%, 11%, and 0.5% of the tumors, respectively; hence, it should be more powerful to detect genomic alterations at the pathway level than at the individual gene level.

The importance of pathway analysis and many existing approaches have been reviewed by several authors.^3–5 Many pathway-based analysis methods for GWAS data are evolved from those for gene expression data;^6,7 however, higher-dimensional data are involved in the former with up to hundreds to thousands of SNPs, compared to only tens to hundreds of genes in the latter. On the other hand, because it is known that not all the SNPs in any gene or any pathway are related to a disease, statistically it is most important and challenging to adaptively aggregate information over multiple unknown causal SNPs while minimizing the effects of non-causal SNPs. Existing approaches have some limitations. For example, a popular approach⁸ used the minimum p value of the multiple SNPs in a gene to summarize association information for the gene, which is not efficient if there are multiple weakly associated SNPs inside the gene. Two other methods, GATES-Simes⁹ and HYST,¹⁰ combine gene-level p values based on GATES,¹¹ a gene-based test using an extended Simes procedure to correct multiple testing while calculating the p value quickly and possibly based on SNP summary statistics (instead of individual-level SNP and phenotype data); GATES-Simes uses an extended Simes procedure to extract the most significant gene-level p value for a pathway, whereas HYST uses Fisher’s method to combine multiple genes’ p values. Hence, as to be confirmed later, GATES-Simes behaves like the minimum p value method, losing power if there are multiple SNPs and/or multiple genes with only weak association strengths; in contrast, HYST, as Fisher’s method, is expected to be low powered if an increasing number of the genes in a pathway are not associated with the trait. A very recent approach¹² uses a variance-component test to aggregate information across multiple SNPs non-adaptively, which will lose power in the presence of many non-associated genes. The fundamental problem is the non-adaptive nature of these methods at both the SNP and gene levels. Our proposal is based on a highly adaptive test called adaptive sum of powered score (aSPU) test originally proposed for analysis of rare variants (RVs).¹³ The main idea of the aSPU test is that, because we do not know which and how many SNPs in the given set are associated with a trait, we first construct a class of tests over-weighting a sequence of increasingly smaller sets of the top-ranked (i.e., most statistically significant) SNPs, then select the test with the most significant result (with a proper adjustment for multiple testing). For relatively small sets of RVs, the aSPU test often outperforms other tests.¹³ Here we extend the aSPU test to pathway analysis of either common variants (CVs) or RVs. One change we made is that, because the analysis unit of a pathway analysis is a gene but genes can contain quite different numbers of SNPs, we need to modify the aSPU test to treat each gene equally a priori. More importantly, the proposed test is adaptive with respect to both genes and SNPs, which is critical because we do not know a priori how many genes in a pathway are associated and how many SNPs in an associated gene are associated with the given trait. We will compare our proposal with two aforementioned pathway-analysis methods, GATES-Simes and HYST, and two other popular ones, one based on penalized regression (called GRASS) and the other as a representative two-step approach based on SNP screening then combining as implemented in the software PLINK (called simply Plink in the sequel),^14,15 largely because the latter two methods have been widely applied to GWASs in practice.^16–18

Material and Methods

Data and Notation

We consider the most popular case-control study design as adopted in GWASs, though the methods can be extended to other study designs, e.g., with a quantitative or survival trait. Suppose that for subject i = 1,…,n, Y_i = 0 or 1 is a binary trait, e.g., an indicator of disease, and X_i = (X_i1,…, X_ik)′ is the vector of the genotype scores for k SNPs, possibly drawn from multiple genes in a pathway. We use additive coding for each SNP; that is, X_ij is the number of the copies of an allele at SNP j for subject i. It is possible to include other covariates, but for simplicity we ignore them. We consider a logistic regression model:

$$\text{Logit}\left[Pr\left(Y_i=1\right)\right]={\beta }_0+\sum _{j=1}^k{X}_{ij}{\beta }_j.$$ (Equation 1)

We’d like to test the null hypothesis H₀ : β = (β₁,…, β_k)′ = 0; that is, there is no association between any SNPs and the trait under H₀. The score vector U = (U₁,…, U_k)′ for β and its covariance matrix are

$$U=\sum _i{X}_i\left(Y_i-\overline{Y}\right),V=Cov\left(U\right)=\overline{Y}\left(1-\overline{Y}\right)\sum _i\left(X_i-\overline{X}\right){\left(X_i-\overline{X}\right)}^{\prime },$$

where $\overline{Y}$ and $\overline{X}$ are the sample means of Y_is and X_is, respectively. The classic score test statistic is T_Score = U′V⁻¹U, which, however, in the current context with a large k, relative to the sample size n, might be low powered, as its asymptotically equivalent Wald test and likelihood ratio test. As shown theoretically,¹⁹ as the dimension k increases, the power of the score test might diminish, tending to the type I error rate α. The most popular univariate single SNP-based test, call UminP here, is $T_{UminP}={\text{max}}_{j=1}^k{U}_j^2/V_{jj}$ with V_jj = Var(U_j), which might also be low powered if we have many small $\left|{\beta }_j\right|\ne 0$. Two alternatives, called the Sum and SSU tests, are

$$T_{Sum}=1^{\prime }U/\sqrt{1^{\prime }V1}=\sum _{j=1}^k{U}_j/\sqrt{1^{\prime }V1},T_{SSU}=U^{\prime }U=\sum _{j=1}^k{U}_j^2.$$

The Sum test is powerful when all or most $\left|{\beta }_j\right|\ne 0$ with the same sign, but not otherwise. As shown by Pan,²⁰ the SSU test can be regarded as a variance-component test^21,22 and is closely related to an empirical Bayes test for high-dimensional data²³ and a nonparametric MANOVA test.²⁴ In particular, variance-component tests, including kernel machine regression (KMR), have been advocated for SNP set analysis and empirically shown to be powerful in many cases.^21,22,25 Nevertheless, as shown in Pan et al.,^13,26 because a variance-component test is not adaptive, in the presence of many non-associated SNPs as anticipated in the current context of pathway analysis, it might lose power. Accordingly, a more powerful and adaptive test was proposed as reviewed next.

Review: The Data-Adaptive aSPU Test

Pan et al.¹³ proposed a class of sum of powered score (SPU) tests in a different context for analysis of RVs:

$$T_{\text{SPU}}=T_{SPU\left(\gamma \right)}\left(U\right)=\sum _{j=1}^k{U}_j^{\gamma }.$$ (Equation 2)

The SPU tests cover the Sum and SSU tests as two special cases with a corresponding γ = 1 and γ = 2, respectively. Importantly, as γ → ∞ (and as an even integer), then the SPU test would approach the UminP test if the variances of the score components are a constant (or if their varying variances are ignored, which might be advantageous in certain cases); the reason is simple:

$${\Vert U\Vert }_{\gamma }={\left(\sum _{j=1}^k{\left|U_j\right|}^{\gamma }\right)}^{1/\gamma }\to {\Vert U\Vert }_{\infty }=\stackrel{k}{\underset{j=1}{\text{max}}}\left|U_j\right|,\text{as}\gamma \to \mathrm{\infty }.$$

Without covariates, we propose using permutations to obtain p values. More generally, to adjust for covariates, the parametric bootstrap (or, alternatively, permuting residuals) can be used for inference. Specifically, we will first fit a null model under H₀, then simulate a new set of traits Y^(b)s from the fitted null model for b = 1,…,B; we calculate the test statistic $T_{SPU}^{\left(b\right)}$ based on each set of simulated Y^(b); finally, we calculate the p value as $\left[{\sum }_{b=1}^{B}I\left(\left|T_{SPU}^{\left(b\right)}\right|\ge \left|T_{SPU}\right|\right)+1\right]/\left(B+1\right)$. We used B = 500 in our simulations for a nominal significance level at 5%.

There is no uniformly most powerful test in multilocus association testing; on the other hand, it has been found empirically that the Sum, SSU, and UminP tests performed well under different situations. For a given dataset, to adaptively choose the value of γ for the SPU tests, Pan et al.¹³ propose an adaptive SPU (aSPU) test that simply combines the results of multiple SPU tests: suppose that we have some candidate values of γ in Γ, e.g., Γ = {1, 2, 3, …, 8} as used in our later experiments, and suppose that the p value of the SPU(γ) test is p_γ, then the aSPU test simply takes the minimum p value:

$$T_{\text{aSPU}}=\underset{\gamma \in \text{Γ}}{\text{min}}{p}_{\gamma }.$$

Of course, T_aSPU is no longer a genuine p value; we recourse to the parametric bootstrap to estimate its p value. As before, first, we simulate B independent copies Y^(b) from the null distribution of Y and obtain the null score vectors U^(b) for b = 1,2,…,B. We then calculate the corresponding SPU test statistics $T_{SPU\left(\gamma \right)}^{\left(b\right)}$ and their p values $p_{\gamma }^{\left(b\right)}=\left[{\sum }_{b_1\ne b}I\left(T_{SPU\left(\gamma \right)}^{\left(b_1\right)}\ge T_{SPU\left(\gamma \right)}^{\left(b\right)}\right)+1\right]/B$. Thus, we have $T_{aSPU}^{\left(b\right)}={\text{min}}_{\gamma \in \text{Γ}}{p}_{\gamma }^{\left(b\right)}$, and the final p value of the aSPU test $P_{aSPU}=\left[{\sum }_{b=1}^{B}I\left(T_{aSPU}^{\left(b\right)}\le T_{aSPU}\right)+1\right]/\left(B+1\right)$.

A Data-Adaptive Pathway-Based Test: aSPUpath

Given a pathway S with |S| genes, we partition the score vector according to the genes as $U={\left(U_{1.}^{\prime },\dots ,U_{\left|S\right|.}^{\prime }\right)}^{\prime }$ with the score subvector for gene g (with k_g SNPs) as $U_{g.}={\left(U_{g1},U_{g2},\dots ,U_{g{k}_g}\right)}^{\prime }$ based on the logistic regression model (or other generalized linear models or proportional hazards model). The gene-specific SPU statistic and the pathway-based SPU statistic are, respectively,

$$\text{SPU}\left(\gamma ,w_g;g\right)={\Vert U_{g.}\Vert }_{\gamma }={\left(\sum _{j=1}^{k_g}{\left(w_{gj}{U}_{gj}\right)}^{\gamma }/k_g\right)}^{1/\gamma },$$ (Equation 3)

$$\text{PathSPU}\left(\gamma ,{\gamma }_G,w,w_G;S\right)=\sum _{g\in S}{\left(w_{G,g}\text{SPU}\left(\gamma ,w_g;g\right)\right)}^{{\gamma }_G},$$ (Equation 4)

where two scalars γ > 0 and γ_G > 0, gene-specific weights for SNPs $w={\left(w_1^{\prime },\mathrm{..},w_{\left|S\right|}^{\prime }\right)}^{\prime }$ and $w_g={\left(w_{g1},\dots ,w_{g{k}_g}\right)}^{\prime }$, and gene-specific weights for genes $w_G={\left(w_{G,1},\dots ,w_{G,\left|S\right|}\right)}^{\prime }$ are pre-specified. w_g is used to incorporate prior information on SNPs, e.g., to up-weight SNPs associated with gene expression, whereas w_G can be based on gene functional annotations or gene expression data to represent prior likelihoods of their being functional (and associated with the trait); without prior knowledge or data, or for simplicity, we can simply use w_g = 1 and w_G = 1, which are to be used by default unless specified otherwise in this paper. Note that SPU (γ, w_g; g) is standardized by the gene-specific number of SNPs, k_g, so that large genes will not dominate a pathway analysis (since the genes in a pathway are the analysis units and are thus treated equally a priori if no weighting is desired). The intuition behind using γ_G is like that for γ: in general, a larger γ_G (or γ) is more effective if there are fewer associated genes (or SNPs) with larger effects in a pathway (or in a gene), but not otherwise. Two extreme examples are the following: (1) γ_G = 1 (or γ = 1), treating all genes (or SNPs) equally, which is most powerful if all the genes (or SNPs) are associated with the trait with similar effect sizes and in the same direction (i.e., all positive or all negative); (2) γ_G = ∞ (or γ = ∞), using only the most significant gene (or SNP) as the evidence against the null hypothesis, which is most powerful if there are only one or few genes (or SNPs) associated with the trait with a large effect size. Between the two extremes, other values of γ_G (or γ) might be more powerful. For example, if only a subset of the genes (or SNPs) are associated with different effect sizes and different directions, using γ_G = 2 (or γ = 2) might be more powerful, as variance-component tests (e.g., KMR); on the other hand, if the proportion of the associated genes (or SNPs) decreases, a larger value, say γ_G = 4 (or γ = 4), might lead to a more powerful test; often γ_G = 8 or 16 (or γ = 8 or 16) gives the results similar to using γ_G = ∞ (or γ = ∞). We also note that, if the association directions of (most) associated genes (or SNPs) are in the same direction, using an odd integer of γ_G (or γ) might be more powerful; otherwise, using an even integer is more promising. These points have been empirically verified for RV analysis¹³ and polygenic testing in GWASs.²⁶ In practice, because an optimal value of γ_G (or γ) is unknown, depending on the unknown genetic association patterns, one has to conduct a grid search over a wide range of possible values for γ_G (or γ), but searching over too many will introduce extra variability and thus lead to power loss. Based on our experience coupled with the goal of a pathway-based analysis, to take advantage of possibly multiple associated genes (and SNPs), we suggest trying ${\gamma }_G\in \left\{\mathrm{1,2,4,8}\right\}$ (and $\gamma \in \left\{\mathrm{1,2,3},\dots ,8\right\}$) as shown in the results below, though this needs to be further studied.

For any given (γ,γ_G), as for SPU(γ), we recourse to resampling to calculate its p value $P_{\text{PathSPU}\left(\gamma ,{\gamma }_G,w,w_G;S\right)}$. Its power depends on the choice of (γ,γ_G). A pathway-based aSPU test is defined as

$$\text{aSPUpath}\left(S\right)=\underset{\gamma ,{\gamma }_G}{\text{min}}{P}_{\text{PathSPU}\left(\gamma ,{\gamma }_G,w,w_G;S\right)},$$ (Equation 5)

aiming to select from multiple PathSPU tests the most powerful one. Similar to that for the aSPU test, we propose using a single layer of the permutation or parametric bootstrap to calculate the p values.

For the possible situation where multiple genes in a pathway might contain quite different proportions of causal SNPs, we might use a more general pathway-based test with a gene-specific γ_g for each gene g. Denote $\mathit{\gamma }={\left({\gamma }_1,\dots ,{\gamma }_{\left|S\right|}\right)}^{\prime }$, we can modify the tests as

$$\text{PathSPU}2\left(\mathit{\gamma },{\gamma }_G,w,w_G;S\right)=\sum _{g\in S}{\left(w_{G,g}\text{SPU}\left({\gamma }_g,w_g;g\right)\right)}^{{\gamma }_G},$$ (Equation 6)

$$\text{aSPUpath}2\left(S\right)=\underset{\mathit{\gamma },{\gamma }_G}{\text{min}}{P}_{\text{PathSPU}2\left(\mathit{\gamma },{\gamma }_G,w,w_G;S\right)}.$$ (Equation 7)

The corresponding aSPUpath2 test is computationally more demanding in searching for suitable values of more parameters in γ and γ_G, which will also introduce more variability to the results and thus might lead to loss of power. This needs to be studied further.

Other Modifications

We also considered single-gene-based approaches and those based on dimension reduction. Because they did not outperform the proposed aSPUpath, we will present just a summary that might be interesting.

As a representative of single gene-based approaches, we considered applying SPU and aSPU tests to each gene in a pathway, then using the minimum gene-level p value as a final test statistic for the pathway. It is easy to see that the pathway-based SPU(∞) (after ignoring the inverse weighting by the number of SNPs and the possible use of weights) and single gene-based SPU(∞) are almost the same; hence, our proposed aSPUpath test is more adaptive and thus expected to be more flexible and powerful.

For dimension reduction, as in GRASS, for each gene we replaced its individual SNP genotype scores by their top few principal components (PCs) that accounted for at least 95% of total variation, and then we applied the pathway-based aSPU test to these PCs. Perhaps due to the adaptivity of the original aSPUpath test and possible loss of information by PCs, we did not find improvement by the use of PCs in our simulations. However, given that PC-based tests^27,28 are viable competitors to variance-component tests as discussed in Schaid et al.,¹² we had an interesting, perhaps surprising, observation: applying the SPU(2) (i.e., SSU) test (that is equivalent to a variance-component test) to the original genotypes or the PCs gave almost the same result; an explanation is offered below.

Suppose that X is the n × k matrix of the original genotype scores. We apply a singular value decomposition: $X{X}^{\text{'}}=V{\text{Λ}}^2{V}^{\text{'}}$, where we assume that the eigen values have been put in descending order as the diagonal elements of ${\text{Λ}}^2$. The first L PCs are the columns of $P_L=V_L{\text{Λ}}_L$, where V_L is an n × L matrix containing the first L columns of V and ${\text{Λ}}_L$ is an L × L diagonal matrix containing the first L eigen values. Now we can compare the two SSU statistics when applied to X and P_L, respectively:

$$\begin{array}{c}SSU\left(X\right)=U{\left(X\right)}^{\prime }U\left(X\right)={\left(Y-\overline{Y}\right)}^{\prime }X{X}^{\prime }{\left(Y-\overline{Y}\right)}^{\prime }={\left(Y-\overline{Y}\right)}^{\prime }V{\text{ΛΛ}}^{\prime }{V}^{\prime }{\left(Y-\overline{Y}\right)}^{\prime }\\ \approx {\left(Y-\overline{Y}\right)}^{\prime }{V}_L{\text{Λ}}_L{\text{Λ}}_L^{\prime }{V}_L^{\prime }{\left(Y-\overline{Y}\right)}^{\prime }=SSU\left(P_L\right).\end{array}$$

But for other γ ≠ 2, we would expect that, in general, SPU(γ) would give different results when applied to the original genotype scores X and its top PCs P_L, respectively.

Simulation Set-ups

We conducted extensive simulation studies to evaluate and compare the performance of the aSPUpath test with several alternative methods. Our general set-ups were similar to those (set-ups A–D) in Chen et al.¹⁴ except that we simulated SNPs, not PCs (called eigenSNPs therein) of SNPs, to mimic real data. Specifically, set-up A was the null case with no causal SNP, while the other three set-ups contained causal SNPs in 1, 5, and 10 genes, respectively. We considered one pathway containing 20 genes, each of which might contain 1–20 SNPs, or 3–100 SNPs; there was at most one causal SNP inside each gene. To cover possible situations with more than one causal SNP inside a gene, we added set-ups B′–D′, in which we randomly selected 1–3 causal SNPs in a gene. Furthermore, to mimic real pathways as in KEGG, we also considered cases E and F with 40 and 80 genes, respectively, in a pathway while all other aspects were similar to set-up D′. The SNPs inside each gene might or might not be correlated whereas the SNPs from different genes were always independent, and the causal SNPs might or might not be included in the data.

The simulated genotypes were generated as in Wang and Elston.²⁹ First, we generated a latent vector Z = (Z₁,…,Z_k)′ from a multivariate Normal distribution with a first-order auto-regressive (AR1) covariance structure: $Corr\left(Z_i,Z_j\right)={\rho }^{|i-j|}$ between any latent components i and j; ρ = 0 and ρ > 0 randomly chosen from a uniform distribution U(0, 0.8) were used to generate (neighboring) SNPs in linkage equilibrium and in linkage disequilibrium (LD), respectively. The number of SNPs inside each gene, k_g, was randomly chosen between 1 and 20, or between 3 and 100. Second, the latent vector was dichotomized to yield a haplotype with MAFs each randomly selected uniformly between 0.05 and 0.4 for CVs or between 0.001 and 0.01 for RVs. Third, we combined two independent haplotypes and obtained genotype data: X_i = (X_i1,…,X_ik)′ for subject i. Fourth, for a non null case, the first SNP inside the first k₁ = 1 or 5 or 10 genes, corresponding to set-ups B–D, was chosen to be causal with β_j = logOR ≠ 0, and all other β_j = 0; we also tried set-ups B′–D′, E, and F with 1–3 randomly chosen causal SNPs. For the null case, all β_j = 0. Fifth, the disease status Y_i of subject i was generated from the logistic regression model (Equation 1). We used β₀ = −log(0.05 / 0.95) for a 5% background disease probability; that is, $Pr\left(Y_i=1|X_i=0\right)=0.05$. Sixth, as in a case-control study, we sampled n/2 = 500 cases and n/2 = 500 controls in each dataset.

Throughout the simulations, we fixed the test significance level at α = 0.05. We used the R package SNPath implementing GRASS and Plink;¹⁴ we implemented other methods in R package aSPU. Because the program for Plink was quite slow, we ran only 100 independent replicates for Plink, but 1,000 replicates for others in each set-up.

Results

Simulation Results for CVs

For comparison, we included the SSU (i.e., SPU(2)) and UminP tests; the former is equivalent to a global pathway-based test of Goeman et al.⁶ as shown in Pan,³⁰ and the latter is the most popular single SNP-based test in GWASs. The UminP test often performed similarly to SPU(∞) (data not shown).

Type I Error

As shown in Table 1, it appears that each test could control its type I error rate satisfactorily around or within 0.05.

Table 1.

Empirical Type I Error Rates of the Tests for CVs

Set-up	aSPUpath	GRASS	Plink	aSPU	SSU	UminP	GATES-Simes	HYST
200 indep SNPs	.055	.057	.02	.053	.046	.057	.047	.022
1,000 indep SNPs	.048	.067	.03	.050	.052	.040	.040	.028
200 corr SNPs	.054	.064	.05	.048	.040	.062	.050	.042

Comparison of the aSPUpath Test with Other Tests

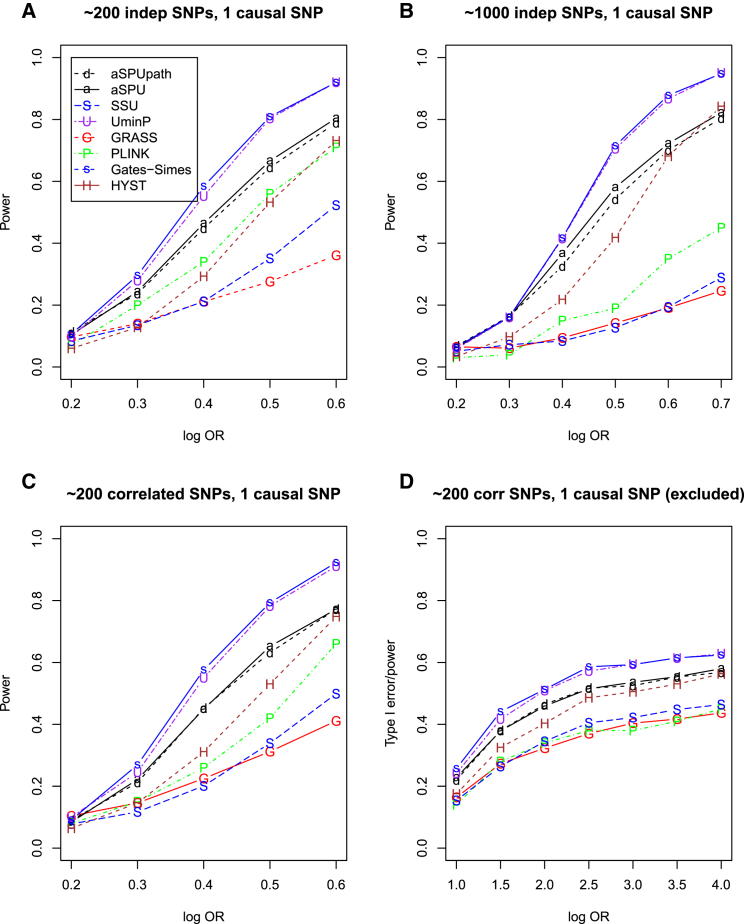
We first consider set-up B, an extreme scenario that is least favorable to pathway or SNP set analysis: because there was only one causal SNP, single SNP-based analysis as implemented in the UminP test was expected to be most powerful, which was confirmed as shown in Figure 1; GATES-Simes also achieved the highest power as UminP. Nevertheless, the aSPU and aSPUpath tests performed similarly and were the next most powerful. As shown in Figure 1A with about 200 independent SNPs, besides UminP/GATES-Simes and aSPU/aSPUpath, Plink was most powerful, closely followed by HYST, then by SSU, and finally GRASS. Figure 1B shows that, with about 1,000 independent SNPs, the aSPU and aSPUpath tests showed even a more striking advantage over the other pathway- or SNP set-based tests except GATES-Simes, suggesting the former two’s (and the latter four’s) robustness (and lack of robustness) to an increasing number of SNPs. In particular, the performance of SSU deteriorated with its power close to that of GRASS. Figure 1C shows that, with about 200 correlated SNPs (with the causal SNP included), the power trend was similar to that with 200 independent SNPs, though GRASS performed better than Plink and SSU with smaller ORs. As shown in Figure 1D, with about 200 correlated SNPs with the causal SNP excluded, again we found GATES-Simes and UminP, closely followed by the aSPU and aSPUpath tests, then by HYST, to be the top performers, while the other three tests were similarly low powered.

Figure 1.

Empirical Power for Simulation Set-up B with a Pathway of 20 Genes

One gene included one causal SNP.

(A and C) Each gene contained 1–20 independent (A) or correlated (C) SNPs.

(B) Each gene contained 3–100 independent SNPs.

(D) Each gene contained 1–20 correlated SNPs and the causal SNP was excluded in analysis.

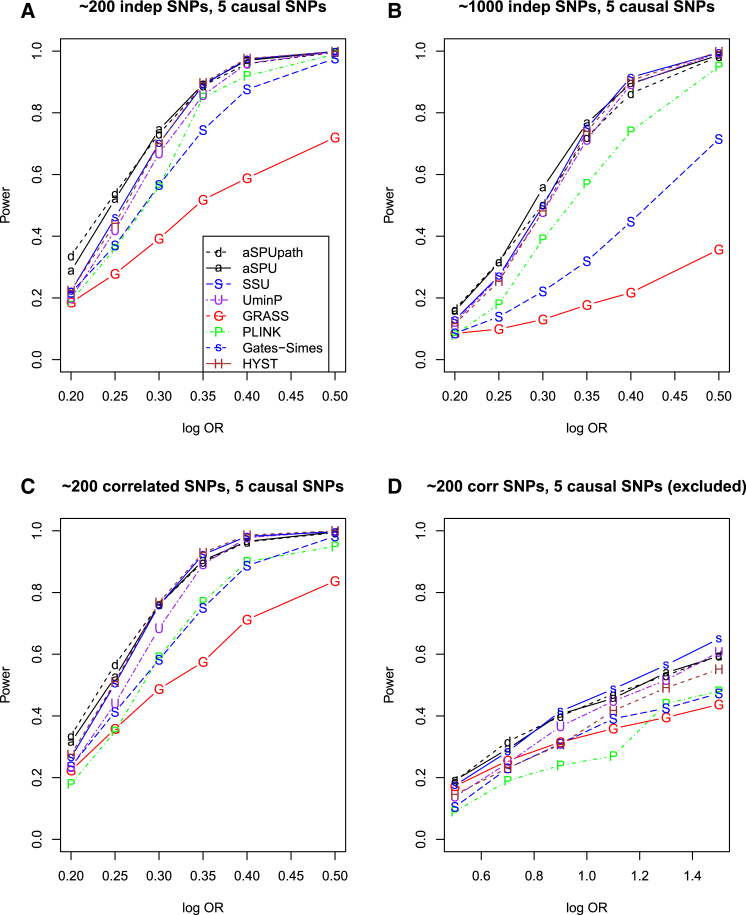
In set-up C with five causal SNPs (Figure 2), again the aSPU and aSPUpath tests performed similarly and now they had an edge over the UminP test, especially for smaller ORs, since the latter uses only the single SNP with the strongest signal while ignoring the signals from other four causal SNPs. HYST also performed well, especially for large ORs, and the power of GATES-Simes was close to or slightly higher than that of the UminP test. However, differing from set-up B, we notice that the SSU test and Plink performed similarly, shown in Figures 2A and 2C, and one was more powerful than the other in Figures 2B and 2D, respectively. Figure 2D showed that, with the five causal SNPs excluded, GRASS could perform well when the causal effect size was small (and the power was low).

Figure 2.

Empirical Power for Simulation Set-up C with a Pathway of 20 Genes

Five genes each included one causal SNP.

(A and C) Each gene contained 1–20 independent (A) or correlated (C) SNPs.

(B) Each gene contained 3–100 independent SNPs.

(D) Each gene contained 1–20 correlated SNPs and the causal SNP was excluded in analysis.

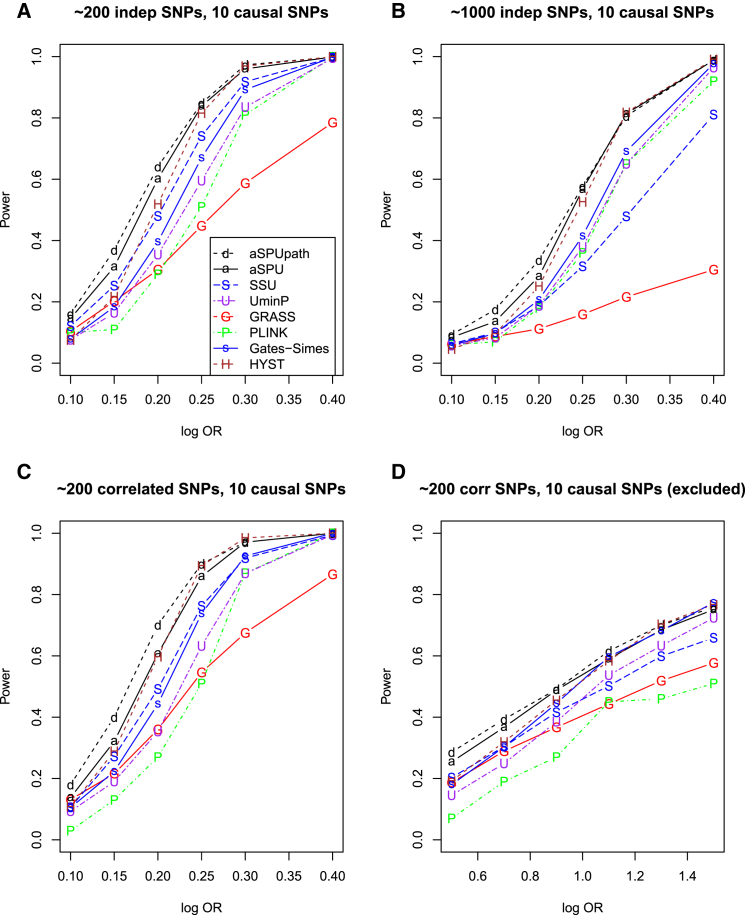
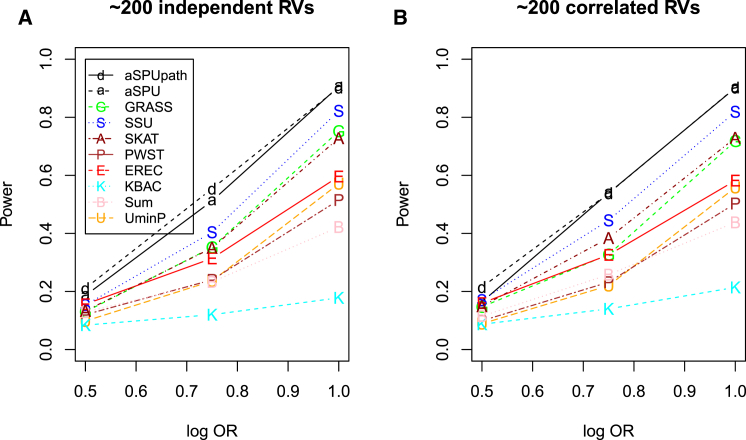
Now consider a case favoring pathway or SNP set analysis in set-up D with ten causal SNPs (Figure 3). The aSPUpath test was the sole winner, having an edge over the aSPU test; in particular, the two tests could be much more powerful than the UminP test and GATES-Simes, although HYST performed well for large effect sizes. As shown in Figures 3A and 3C, even the SSU test was much more powerful than the UminP test, confirming the advantage of combining information across multiple causal SNPs. On the other hand, in Figure 3B with about 1,000 SNPs, GATES-Simes, UminP, and Plink were tied (after aSPUpath, aSPU, and HYST) as the next tier of the most powerful, followed by SSU, then by GRASS; the low power of SSU test was due to its non-robustness to a large number of non-associated SNPs: it did not down-weight enough the larger number of non-associated SNPs; in contrast, the two adaptive tests, aSPU and aSPUpath, did not suffer much from the presence of a large number of non-associated SNPs. GRASS could beat Plink when the causal effect size was small with (Figures 3A and 3C) or without (Figure 3D) the presence of the causal SNPs.

Figure 3.

Empirical Power for Simulation Set-up D with a Pathway of 20 Genes

Ten genes each included one to three causal SNPs.

(A and C) Each gene contained 1–20 independent (A) or correlated (C) SNPs.

(B) Each gene contained 3–100 independent SNPs.

(D) Each gene contained 1–20 correlated SNPs and the causal SNP was excluded in analysis.

In all the above three situations, each gene contained either no or only one causal SNP, which might be too restrictive. To cover possible situations with more than one causal SNP inside a gene, we considered set-ups B′–D′, in which we randomly selected 1–3 causal SNPs in 1, 5, and 10 genes, respectively (while other genes contained no causal SNPs). The main results remained the same as before except the following as shown in Figure 4 for set-up D′. First, there was a larger power advantage of the aSPUpath over the aSPU test for a larger number of SNPs (Figure 4B). Second, there was improved performance of GRASS: for example, for small effect sizes, GRASS was consistently more powerful than Plink, though it was still outperformed by aSPUpath. It is clear that GATES-Simes behaved like, albeit a little more powerful than, the UminP test, and HYST was more powerful than the other two but less powerful than aSPUpath.

Figure 4.

Empirical Power for Simulation Set-up D′ with a Pathway Containing 20 Genes

Ten genes each included one to three causal SNPs.

(A and C) Each gene contained 1–20 independent (A) or correlated (C) SNPs.

(B) Each gene contained 3–100 independent SNPs.

(D) Each gene contained 1–20 correlated SNPs and the causal SNP was excluded in analysis.

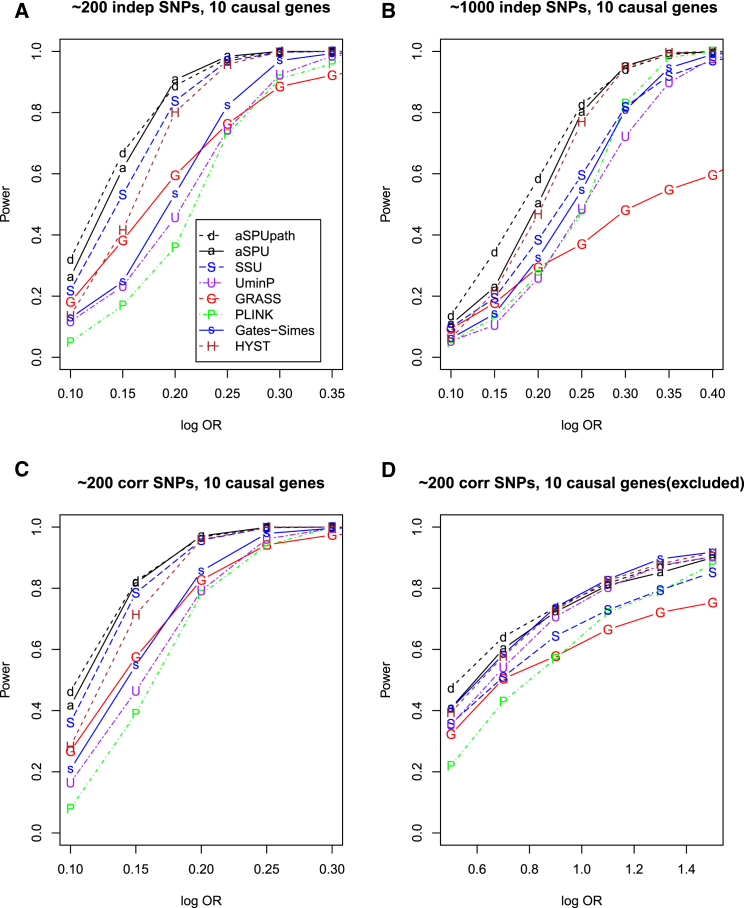
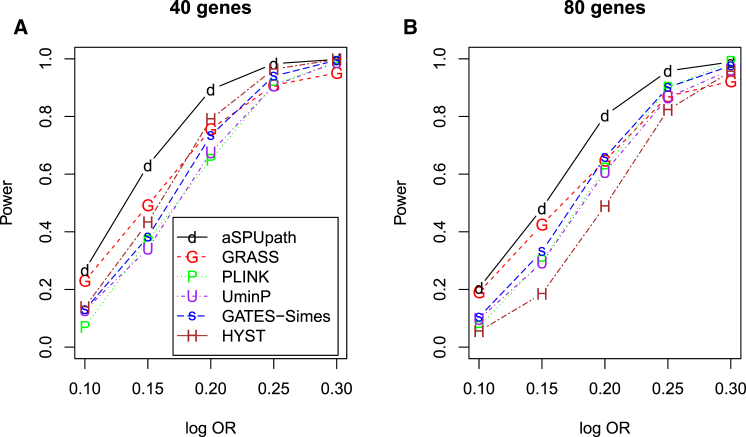
To mimic KEGG pathways, most of which contain more than 20 genes (e.g., Table 4), we considered two set-ups similar to set-up D′ but with 40 or 80 genes in each pathway and each gene with 1–20 correlated SNPs. As shown in Figure 5, aSPUpath remained the most powerful in most situations, especially with relatively small ORs as in typical GWASs for complex traits, under which GRASS performed second best. Again, GATES-Simes performed similarly as the UminP test, and HYST lost power as the number of the non-associated genes in the pathway increased.

Table 4.

Results of the WTCCC CD GWAS Data Application: KEGG Pathways with p Values < 0.00001 by Any of aSPUpath, GRASS, GATES-Simes, and HYST

KEGG ID	Pathway Names	No. of Genes	No. of SNPs	p Values
aSPUpath	GRASS	GATES-Simes	HYST
hsa04630	Jak-STAT signaling pathway∗	145	1,410	<0.00001	<0.00001	<0.00001	<0.00001
hsa04060	cytokine-cytokine receptor interaction∗	247	2,506	<0.00001	<0.00001	<0.00001	.00001
hsa04660	T cell receptor signaling pathway∗	105	1,373	<0.00001	<0.00001	.00081	.00021
hsa04310	Wnt signaling pathway	143	2,087	<0.00001	<0.00001	.00089	.00238
hsa05310	asthma	27	271	<0.00001	<0.00001	.00071	.00002
hsa05330	allograft rejection	34	466	<0.00001	<0.00001	.00089	<0.00001
hsa05414	dilated cardiomyopathy (DCM)	89	2,605	<0.00001	<0.00001	.00382	.02188
hsa05416	viral myocarditis	67	1,263	<0.00001	<0.00001	.00148	<0.00001
hsa04972	pancreatic secretion	93	2,187	<0.00001	.00003	.00072	.00211
hsa04621	NOD-like receptor signaling pathway∗	57	502	<0.00001	.00542	<0.00001	.01012
hsa04062	chemokine signaling pathway∗	174	2,714	<0.00001	.00061	.00131	.00119
hsa04810	regulation of actin cytoskeleton	201	3,347	<0.00001	.00108	.00156	.00962
hsa05131	shigellosis	60	784	<0.00001	.00434	<0.00001	.00159
hsa00230	purine metabolism	154	2,810	.00759	<0.00001	.05376	.02156
hsa04144	endocytosis	180	2,575	.00190	<0.00001	.00139	.01397
hsa04145	phagosome	136	1,469	.00101	<0.00001	.00314	.00272
hsa04270	vascular smooth muscle contraction	113	2,887	.00025	<0.00001	.00086	.00566
hsa04350	TGF-beta signaling pathway	82	831	.00080	<0.00001	.00060	.01381
hsa04514	cell adhesion molecules (CAMs)	122	3,312	.00120	<0.00001	.00311	.00043
hsa04612	antigen processing and presentation	63	543	.00129	<0.00001	.00146	.00016
hsa04650	natural killer cell mediated cytotoxicity	124	1,464	.00199	<0.00001	.02586	.00336
hsa04672	intestinal immune network for IgA production	45	393	.00073	<0.00001	.00105	.00009
hsa04940	type I diabetes mellitus	39	714	.00031	<0.00001	.00102	<0.00001
hsa05332	graft-versus-host disease	33	440	.00036	<0.00001	.00086	.00001
hsa04622	RIG-I-like receptor signaling pathway	65	474	.00004	.0318	<0.00001	.30502

Asterisks (^∗) indicate positive control pathways.

Figure 5.

Empirical Power for Simulation Set-ups E and F with a Pathway Containing 40 and 80 Genes, Respectively

Ten genes each included 1–3 causal SNPs, and each gene contained 1–20 correlated SNPs. Set-up E with a pathway of 40 genes (A) and set-up F with a pathway of 80 genes (B) are shown.

In summary, we found that the aSPUpath and aSPU tests were much more powerful than pathway-based GRASS, HYST, and Plink, and the SSU test for SNP set analysis, across all the simulation set-ups considered. In the presence of multiple causal SNPs or of multiple genes containing causal SNPs, as anticipated for pathway analysis, they also outperformed the single SNP-based UminP test, which often operated like GATES-Simes; between the two adaptive tests, the aSPUpath test had an edge over the aSPU test in some situations, especially for a larger number of non-associated SNPs and for casual SNPs with small effect sizes.

Comparison of the aSPUpath Test with Its Other Variants

For set-up B with only one causal SNP, the single-gene-based aSPU and pathway-based aSPU tests had almost identical power and were much more powerful than the PC-based aSPU test. The reason was the following. First, because there was only one single causal SNP, a single-gene-based approach would not lose power as compared to a pathway-based approach aiming to combine information across multiple genes; at the same time, a pathway-based approach in general would not gain either under this situation. Second, note that the aSPU test could realize effective SNP selection by adaptively choosing the tuning parameter γ to down-weight non-associated SNPs; however, each PC is a linear combination of all the SNPs, a mixture of both associated and non-associated SNPs, hindering the ability of the PC-based aSPU test to select SNPs effectively.

For set-up C with five causal SNPs, the pathway-based aSPU test was more powerful than the gene-based aSPU test, and the PC-based aSPU test was still the least powerful.

For set-up D with ten causal SNPs, the pathway-based aSPU test was by far the most powerful. For 200 SNPs, the PC-based aSPU test was more powerful than the single-gene-based aSPU; however, with about 1,000 SNPs, the single-gene-based aSPU was more powerful than the PC-based aSPU, presumably due to the fact that each PC contained too many non-associated SNPs, diluting the association effects.

As in GRASS, we also tried to first construct gene-specific SPU test statistics before combining them across a pathway but did not find it working better than the simple aSPUpath test discussed here.

In summary, we found that overall our proposed aSPUpath test performed better than the single-gene-based aSPU and PC-based aSPU tests.

Incorporating Prior Knowledge by Weighting

As discussed earlier, our proposed method can incorporate biological knowledge or prior data on the likelihood of SNPs and genes being functional through weighting them differentially. We did a preliminary study to explore the use of informative weighting in set-up D with ten genes, each containing one causal SNP and with a total of about 200 correlated SNPs. We applied our proposed test with w_g = 1, but with w_G = 1 or w_G ≠ 1 to assess the effects of some correctly specified and some mis-specified gene weights (while the effects of SNP weighting could be explored similarly). We generated w_G,g ∼ U (0.2, 0.6), a uniform distribution between 0.2 and 0.6, for genes containing no causal SNPs, but for other genes (containing causal SNPs) w_G,g ∼ U (0.2 + δ, 0.6 + δ) for several values of δ ≥ 0. Increasing values of δ reflected increasing informativeness of the weights, while δ = 0 represented completely random and non-informative weighting. Note that, with the overlapping weights for the genes containing causal SNPs and for those without any causal SNP, although the weights might be informative, strictly speaking they were mis-specified. As shown in Table 2, it is clear that our proposed aSPUpath test was most powerful; its weighted version was robust to mis-specified and completely random weights (with δ = 0) with only small power loss, while gaining higher power with more informative weights.

Table 2.

Empirical Type I Error logOR = 0 and Power at logOR ≠ 0 of Various Tests for about 200 Correlated SNPs in a 20-Gene Pathway for Set-up D

logOR	aSPUpath						GRASS	Plink	aSPU	SSU	UminP	GATES-Simes	HYST
wG= 1	δ = 0	δ = .1	δ = .2	δ = .3	δ = .4
0	.054	.052	.051	.050	.048	.044	.064	.05	.048	.040	.062	.050	.042
0.15	.400	.397	.430	.468	.489	.517	.216	.13	.321	.272	.190	.223	.289
0.2	.701	.656	.713	.747	.769	.791	.360	.27	.607	.492	.353	.443	.597
0.25	.900	.873	.907	.926	.931	.936	.546	.51	.859	.763	.632	.738	.894

Simulation Results for RVs

With the increasing availability of sequencing data, it has become more important and urgent to develop and apply pathway-based analysis of RVs; there have been few such studies. For this purpose, we did a simulation study to assess the performance and show the potential of our proposed test for pathway analysis of RVs. To save space, we present results only for a simulation set-up similar to set-up D: a pathway contained 20 genes, 0 or 10 of which each contained one causal RV among 1–20 RVs for the null or non null cases, respectively. The MAFs for the RVs were randomly drawn between 0.1% and 1% for the control samples. We considered both independent and correlated RVs within each gene.

For comparison, we also included several existing popular or competitive tests. In particular, we included the Sum (i.e., SPU(1)) as a representative burden test, the SSU (i.e., SPU(2)) test that was shown by Basu and Pan³¹ to be competitive and closely related to several other association tests such as C-alpha test³² and kernel machine regression or SKAT,³³ and three adaptive tests that appeared recently, a kernel-based adaptive clustering (KBAC) test,³⁴ a p value weighted sum test (PWSU),³⁵ and an estimated regression coefficient (EREC) test.³⁶

As shown in Table 3, all the methods seem to have type I error rates around the nominal level of 0.05.

Table 3.

Empirical Type I Error Rates of the Tests for RVs

Set-up	aSPUpath	GRASS	aSPU	Sum	SSU	UminP	SKAT	KBAC	PWST	EREC
200 indep SNPs	.059	.058	.060	.048	.051	.068	.050	.054	.053	.048
200 corr SNPs	.058	.065	.047	.051	.060	.045	.058	.048	.054	.052

As shown in Figure 6, the relative performance of the various tests did not strongly depend on whether there were within-gene correlations among the RVs. Clearly, the aSPUpath test was the most powerful, closely followed by the usual aSPU test, then followed by the SSU test, then GRASS, SKAT, and EREC tests. Although the SSU and SKAT are closely related, because SKAT over-weights rare variants with smaller MAFs, which was not a correct assumption in our simulations, here the SSU test was more powerful than SKAT. It is worth noting that here GRASS was much more powerful than Plink, perhaps due to the latter’s ineffective screening on each individual RV, which contained only a quite limited association information content with a low MAF.

Figure 6.

Empirical Power for RVs in Simulation Set-up D2 with a Pathway Containing 20 Genes

Ten genes each included one causal RV. Each gene contained 1–20 independent (A) or correlated (B) RVs.

The PWST and the single RV-based UminP test performed similarly. The KBAC had lowest power. Note that here all the causal RVs had an equal association strength (and direction), which was supposed to be ideal for the Sum test (or other burden tests); however, due to the presence of many non-associated RVs, the Sum test and several other adaptive tests did not perform well due to their non- or not-so-good selection or down-weighting of the many non-associated RVs, as discussed in Pan et al.¹³

Example

We applied the proposed aSPUpath test, as well as the GRASS test, to the Wellcome Trust Case Control Consortium (WTCCC) GWAS data for Crohn disease (CD [MIM: 266600]).³⁷ CD, a type of inflammatory bowel disease, is also considered an autoimmune disease with a strong genetic component.³ The WTCCC GWAS dataset contains 2,000 CD-affected case subjects and 3,000 control subjects with a total of 500,568 SNPs. Following the WTCCC’s quality control (QC) recommendations, we removed subjects and SNPs that did not pass the QC criteria, resulting in 469,612 SNPs in 1,748 case subjects and 2,938 control subjects. We further restricted the pathway analysis to SNPs with MAF of at least 1%. We retrieved a total of 214 human biological pathways from the KEGG database.¹ Because a too-small pathway can give results not too different from a gene-based analysis, whereas the annotated function of a large pathway is likely to be non-specific, many authors restricted their analyses to pathways of certain sizes. For example, Chen et al.¹⁴ and Wang et al.³ considered pathways with at least 10 genes, whereas Gui et al.⁹ included only pathways containing between 10 and 300 genes. Following the previous authors, to facilitate interpretation of the results, we excluded too-small (<10 genes) and too-big (>500 genes) pathways, which resulted in 197 pathways. We obtained the genomic coordinates of SNPs and genes according to human reference genome hg19 and assigned a SNP to a gene if it is located within 20,000 base pairs (20 kb) upstream or downstream of the gene to include SNPs in regulatory regions. A total of 64,557 SNPs were mapped to the 197 pathways including 4,572 unique genes. The median number of genes in a pathway was 47 with the first and third quartiles being 27 and 76, and the median number of SNPs in a gene was 8 with the first and third quartiles being 4 and 17, respectively. We employed a stage-wise permutation strategy for both aSPUpath and GRASS tests: we first performed 5,000 permutations for all pathways and then increased to 100,000 permutations for those pathways with p values < 0.01 in the first stage. We set the significance threshold at 0.00025 to control the family-wise error rate (FWER) at 0.05 based on the Bonferroni correction for 197 pathways.

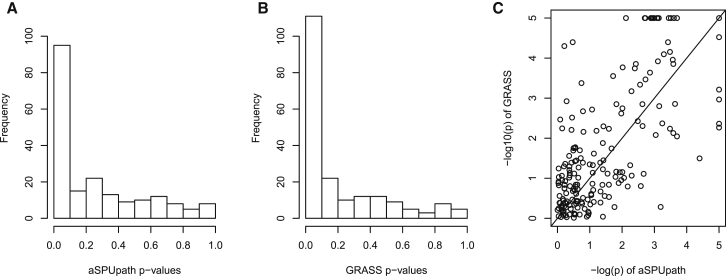
Figure 7 shows the histograms of the p values across the 197 KEGG pathways by the new method and GRASS; their distributions were similar, though GRASS gave a larger number of more significant p values. Overall, the two methods gave similar and complementary results: although many common pathways were identified to be significant by both methods, each also detected some unique pathways. For example, at the significance threshold of 0.00025, aSPUpath and GRASS identified 18 and 35 significant pathways, respectively, among which 11 were common. The Spearman’s rank correlation coefficient between the p values of the two methods was 0.65.

Figure 7.

Distributions of the p Values from aSPUpath and GRASS and Their Comparison in the Log₁₀ Scale for the WTCCC CD Data

Shown are aSPUpath (A) and GRASS (B) and comparison (C).

Table 4 shows 24 KEGG pathways with p values less than 0.00001 by either method, i.e., none of the permuted test statistics exceeded the observed one based on 100,000 permutations. Interestingly, five pathways that have been confirmed to be associated with susceptibility to CD by meta-analysis and replication studies^3,38,39 are all among the 24 pathways. Three of them had p values less than 0.00001 by both methods. Of note, the JAK-STAT signaling pathway (hsa04630) has been identified in quite a few previous pathway analyses.^9,10,40 This pathway has 145 genes, including IL23R (MIM: 607562) with a cluster of genome-wide significant SNPs in the WTCCC GWAS of CD, and nine additional genes, for example, JAK2 (MIM: 147796) and STAT3 (MIM: 102582), which were found to be associated with CD in a large-scale meta-analysis.³⁸ Therefore, it is relatively easy to be identified by several pathway analysis methods.^3,9 On the other hand, two positive control pathways, namely, NOD-like receptor signaling pathway (hsa04621) and Chemokine signaling pathway (hsa04062), had p values < 0.00001 only by aSPUpath, but were not significant by GRASS (p values > 0.00025). It is noteworthy that SNPs in NOD2 (MIM: 605956) in the NOD-like receptor signaling pathway were the first to be identified to be associated with CD and confer the highest risk for CD development among all CD-susceptibility SNPs discovered thus far.^39,41 The NOD-like receptor signaling pathway includes not only NOD2, but also several other CD-associated genes, including TNF (MIM: 191160), CCL2 (MIM: 158105), and CCL7 (MIM: 158106), making it one of the most-well-understood pathways underlying CD susceptibility.⁴² The data application here demonstrates that our proposed aSPUpath test is a competitive and complementary approach to the GRASS test.

For comparison, we also ran GATES-Simes and HYST, yielding 5 and 4 pathways with p values < 0.00001, respectively, all but one of which had a p value < 0.00001 by either aSPUpath or GRASS. The only exception was pathway hsa04622 “RIG-I-like receptor signaling;” the four methods, aSPUpath, GRASS, GATES-Simes, and HYST, gave p values of 0.00004, 0.0318, <0.00001, and 0.3050, respectively.

Discussion

We have proposed a powerful adaptive test for pathway analysis of genetic SNP data as arising in GWASs.^3,4,43 Because any pathway analysis involves multiple genes, each containing multiple SNPs, it is desirable to apply a test that can maintain high power with a large number of non-associated SNPs (or genes) and multiple only weakly associated SNPs (or genes), an ideal case for our proposed test. On the other hand, because the genes in a pathway can contain different numbers of SNPs, to avoid undue influence from a large (or small) gene, we modify the tests to take account of varying gene lengths. Our proposed test introduces two parameters (γ and γ_G) to achieve the objective. For example, if there are only few genes, each containing many associated SNPs (e.g., due to LD), a large value of γ and a small value of γ_G would yield a more powerful test; because the truth is unknown, we use data to adaptively estimate their optimal values. The adaptivity of the proposed test at the gene level and/or at the SNP level is missing from many existing tests for pathway or SNP set analysis, such as the SSU and SKAT tests. As supported by our numerical examples, the proposed test can gain power in many situations and serve as a tool complementary to existing methods like GRASS.

Our proposed test is general and applicable to CVs or RVs. It can be modified, e.g., via suitable weighting on SNPs, for analysis of both CVs and RVs, as shown for the SSU test in Basu and Pan.³¹ In addition, we can also introduce some weights at the gene and SNP levels to incorporate biological knowledge on which genes or SNPs are more likely to be causal. We have focused on testing on a single pathway; an alternative is to take account of possible overlapping or hierarchical structures of some pathways as discussed in Schaid et al.¹² These topics warrant future investigation.

Finally, we note that our proposed approach is in the category of “self-contained tests,” not “competitive tests,” because the null hypothesis to be tested here fits the former better than the latter: we are interested in detecting any pathways with any SNPs associated with a trait, not in detecting ones that are over-enriched with associated SNPs. Furthermore, as argued by Goeman and Buhlmann,⁴⁴ the same test on the former is necessarily more powerful than on the latter. Following Zhou et al.,⁴⁵ we can extend our aSPUpath to competitive testing. Our goal also differs from that of Newton et al.,⁴⁶ which goes beyond only identifying significant pathways, but also aims to uncover the common theme shared among the identified significant pathways.

Published: June 25, 2015

Web Resources

The URLs for data presented herein are as follows:

• aSPU, http://cran.r-project.org/web/packages/aSPU/index.html

• GWAS Catalog, http://www.genome.gov/gwastudies/

• OMIM, http://www.omim.org/

• SNPath, https://www.fredhutch.org/en/labs/profiles/hsu-li.html

• WTCCC, http://www.wtccc.org.uk