Inferring Diffusion Dynamics from FCS in Heterogeneous Nuclear Environments

Abstract

Fluorescence correlation spectroscopy (FCS) is a noninvasive technique that probes the diffusion dynamics of proteins down to single-molecule sensitivity in living cells. Critical mechanistic insight is often drawn from FCS experiments by fitting the resulting time-intensity correlation function, G(t), to known diffusion models. When simple models fail, the complex diffusion dynamics of proteins within heterogeneous cellular environments can be fit to anomalous diffusion models with adjustable anomalous exponents. Here, we take a different approach. We use the maximum entropy method to show—first using synthetic data—that a model for proteins diffusing while stochastically binding/unbinding to various affinity sites in living cells gives rise to a G(t) that could otherwise be equally well fit using anomalous diffusion models. We explain the mechanistic insight derived from our method. In particular, using real FCS data, we describe how the effects of cell crowding and binding to affinity sites manifest themselves in the behavior of G(t). Our focus is on the diffusive behavior of an engineered protein in 1) the heterochromatin region of the cell’s nucleus as well as 2) in the cell’s cytoplasm and 3) in solution. The protein consists of the basic region-leucine zipper (BZip) domain of the CCAAT/enhancer-binding protein (C/EBP) fused to fluorescent proteins.

Introduction

Building dynamical models applicable to crowded and complex environments is essential in describing protein dynamics inside living cells. Despite the wealth of data, our ability to extract meaningful mechanistic insight from experiments in living cells is limited by our theoretical modeling tools (1). Thus, terms suggesting deviations from simple model behavior such as anomalous transport and heterogeneous dynamics often arise in biophysics (2,3).

Anomalous diffusion (4) is a process often used to describe dynamics in complex environments (5,6). It has been used to describe the dynamics of telomeres inside mammalian cell nuclei (7) and bacterial chromosomal loci (8), the diffusion of mRNA molecules inside the bacterial cytoplasm (9), and the diffusion of viruses inside infected cells (10).

In normal diffusion, the mean square displacement (MSD) of the observed particle, 〈r²(t)〉 increases linearly with time t according to 〈r²(t)〉 = qDt, where q is a constant dependent on dimensionality and taking values 2, 4, or 6 for one-dimensional, two-dimensional, and three-dimensional diffusion, respectively, and D is the diffusion coefficient. By contrast, in anomalous diffusion the particle MSD does not increase linearly with time but instead exhibits a power-law behavior 〈r²〉 ∝ t^α, where α is called the anomalous diffusion exponent and depends on the precise diffusion mechanism in the system of interest (11).

In practice, anomalous diffusion is attributed to a number of factors including molecular crowding (12), active transport (13), binding (14), or combinations of the above (15). In theory, anomalous diffusion can be derived from generalized Langevin equations (8), fractional Brownian motion (FBM) (16),percolation (17), diffusion in fractals (18), diffusion in a heterogeneous landscape (19,20), or using power law jump size or waiting time distributions in continuous time random walk (CTRW) models (21).

Although anomalous diffusion arises in all these models, there are substantial differences in the dynamics the models describe. For example, in CTRWs particle jump size distributions and waiting time distributions between jumps can give rise to anomalous MSDs.

Here, our focus is on fluorescence correlation spectroscopy (FCS)—a powerful noninvasive technique with single molecule capability (22)—often used to describe in vivo protein diffusion (12,23–26).

The output of FCS experiments is fluorescence intensities of labeled proteins as they traverse an illuminated confocal volume (27). In simple FCS, the diffusion coefficient, D, is typically extracted by fitting fluorescence intensity time autocorrelation curves, G(t) (28)

$$G\left(t\right)=\frac{1}{n}{\left(1+\frac{t}{{\tau }_D}\right)}^{-1}{\left(1+\frac{1}{Q^2}\frac{t}{{\tau }_D}\right)}^{-1/2},$$ (1)

where n is the number of particles in the population and Q = z₀/w where z₀ and w are constants characterizing the confocal volume’s asymmetry. The diffusion time, τ_D, across the confocal volume of width w is related to the diffusion constant, D, using this expression: τ_D = w²/4D. For simplicity of illustration only, we ignore triplet corrections in Eq. 1 (29).

When single-component diffusion models fail, G(t) can instead be expressed using 1) a two-component normal diffusion model (30), or, more generally, 2) a multicomponent normal diffusion model (31–34)

$$G\left(t\right)=\frac{1}{n}\sum _{{\tau }_D}p\left({\tau }_D\right){\left(1+\frac{1}{Q^2}\frac{t}{{\tau }_D}\right)}^{-3/2},$$ (2)

or, even, 3) an anomalous diffusion model (2,30,35)

$$G\left(t\right)=\frac{1}{n}{\left[1+\frac{2\delta r^2\left(t\right)}{3w^2}\right]}^{-1}{\left[1+\frac{2\delta r^2\left(t\right)}{3z_o^2}\right]}^{-1/2}=\frac{1}{n}{\left(1+{\left(\frac{t}{{\tilde{\tau }}_D}\right)}^{\alpha }\right)}^{-1}{\left(1+\frac{1}{{\tilde{Q}}^2}{\left(\frac{t}{{\tilde{\tau }}_D}\right)}^{\alpha }\right)}^{-1/2}.$$ (3)

In going from the first to the second equality an anomalous mean square displacement, δr²(t) ∝ t^α, is assumed (2) and a new diffusion time, ${\tilde{\tau }}_D$, and confocal volume asymmetry parameter, $\tilde{Q}$, were introduced. It is worth noting that in Eq. 2 each term of the sum corresponds to the contribution from one set of particles with diffusion time τ_D through the confocal volume. Though the particles may be identical, their diffusion time depends on their interactions in the confocal volume; in this way they are naturally divided into different sets (see Fig. 1).Rather than fit the data using Eq. 3, we instead use the maximum entropy method to extract a multicomponent diffusion model from data that could otherwise be fit equally well by adjusting an anomalous exponent, α. Using synthetic data first, we show how molecular-level insight can be drawn from the form of our multicomponent diffusion model. For instance, we will show that our multicomponent diffusion model can arise from stochastic binding/unbinding of proteins to different affinity sites and that, under some circumstances that we will discuss, distributions over diffusion coefficients can yield distributions over affinity strengths.

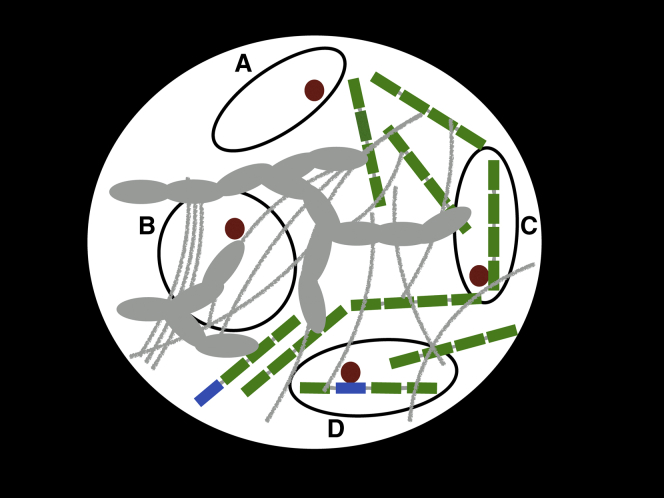
Figure 1.

A schematic illustrating how small protein probes (such as BZip) tagged with fluorescent particles may interact with different areas of the nucleus. White: laser-illuminated confocal volume inside the nuclear ROI. Black ovals: Different local environment areas. Proteins (red) diffuse across the heterogeneous illuminated area of the nucleus. In area (A) the protein diffuses essentially freely as the area is largely clear. In area (B) the protein is diffusing through a crowded area without specifically interacting with the molecules there (gray) except via Brownian collisions. In area (C) the protein is diffusing while binding nonspecifically to an area of DNA where it has no specific targets (green rectangles), and in area (D) the protein has encountered one of its targets, i.e., a high-affinity DNA site (blue rectangle) to which it binds long enough to slow its diffusion. To see this figure in color, go online.

Next, we will turn our attention to real FCS data on the diffusion of the basic region-leucine zipper (BZip) domain. Specifically, we will consider the truncated BZip domain of the transcription factor CCAAT/enhancer binding protein α (C/EBPα) whose diffusion in the nucleus as measured by FCS can be fit to an apparent anomalous diffusion model (Eq. 3) (36).

Molecular modeling (37) and single molecule techniques (38,39) suggest that the multiple interactions of transcription factors (TFs) with nuclear elements—such as specific and nonspecific DNA interactions, protein interactions, and molecular crowding—can give rise to complex diffusive behavior.

Our treatment of the FCS data will reveal that fundamental processes such as a combination of free particle diffusion, crowded diffusion, and stochastic binding/unbinding events give rise to a complex G(t) observed without resorting to an anomalous diffusion model. Our findings will be consistent with knowledge of the fact that BZip interacts with specific elements in target gene promoters, as well as similar consensus DNA elements that are found in α-satellite DNA repeat sequences located in regions of centromeric heterochromatin (36,40). In analyzing real data, we will also consider specific fluorophore properties, such as flickering, which we can quantify in our analysis.

However, we emphasize that because our starting point is the multicomponent normal diffusion model (Eq. 2), we make the assumption from the onset that each diffusion component is normal. That is, for each component the mean square displacement (if individual proteins could be tracked and their mean squared displacement recorded) would be proportional to time. We cannot therefore preclude, for example, the possibility that a CTRW model with a power law waiting time distribution (that could describe, say, anomalous escape kinetics of a tightly bound protein) could not be a better description of the microscopic dynamics. Likewise, we cannot preclude other, more sophisticated anomalous diffusion models, either.

Moreover, FCS data does not provide single protein trajectories. Thus, trapping time distributions are not directly observable from FCS. By assuming a multicomponent normal diffusion model, our parsimonious approach implicitly treats the unobserved waiting times as exponential and, from this starting point, provides insight into what processes may be responsible for the complex diffusion dynamics we observe.

We will end by discussing the possible clinical implications of the insights gathered from our approach.

Materials and Methods

We begin by considering an FCS confocal volume populated by M stationary binding sites with N diffusing particles and assume that particles, P, reversibly bind to sites, S, according to P + S ↔ PS. We define a forward, or association rate, k₊; a backward, or dissociation rate, k₋; an affinity, K = k₊/k₋; and an affinity distribution, p(K). By assumption, when unbound, all particles in the confocal volume diffuse with the same diffusion coefficient, D₀.

If we consider a situation like the one presented in Fig. 1, where the proteins are confined to small regions for the duration of the experiment and taking the nonergodic limit meaning the proteins do not interact with each other while diffusing (41)), the MSD of proteins in one region, say region A, will then be

$$\langle r_A^2\rangle =\frac{1}{n}\sum _{i=1}^n{\left(r_i\left(\tau \right)-r_i\left(0\right)\right)}^2\propto D_A\tau ,$$ (4)

where n is the number of proteins in the region and D_A is the average diffusion coefficient in the region. This diffusion is a priori assumed to be normal. If we now assume the binding sites in the region are in equilibrium with the proteins, we have [P][S]/[PS] = K⁻¹. K does not depend on the diffusion coefficient in the region if the region is well mixed (42). The probability p_f that a protein is free to diffuse with the normal diffusion coefficient D₀, will then be p_f = [P]/([P] + [PS]) and therefore $\langle r_A^2\rangle \propto D_A\tau =p_f{D}_0$. Therefore, the effective diffusion coefficient, D_A, is related to the bound and unbound fraction of particles as follows:

$$D_A=D_0\frac{\left[P\right]}{\left[P\right]+\left[PS\right]}+D_b\frac{\left[PS\right]}{\left[P\right]+\left[PS\right]}=D_0\frac{1}{1+K\left[S\right]},$$ (5)

where, in going from the first to the second equality, we have assumed that the bound diffusion coefficient is zero. We also assumed that particles do not interact. In fact—as we will discuss shortly—because binding sites will be present in excess, particles will not be assumed to interact by competing for sites either. In this way each region exhibits a different diffusion coefficient that depends on the specific protein-binding site interactions in the region. If there are sets of regions where the interactions are similar but not quite the same, a probability distribution p(D) of normal diffusion coefficients will arise.

When dealing with particles that can bind to sites of differing affinities, we must consider whether: 1) particles interact (either directly or by competing for affinity sites); 2) whether, over the timescale of an experiment, each particle explores all types of affinity sites multiple times (the ergodic limit); 3) or whether, over the timescale of an experiment, particles remain mostly confined to regions with few affinity sites (the nonergodic limit).

In case 2, for independent particles, the net diffusion coefficient for all particles $p\left(D^{\prime }\right)$, tends to a sharp Gaussian by the central limit theorem. In this case, it is not possible to individually extract different affinity constants from $p\left(D^{\prime }\right)$. Rather,

$$D^{\prime }=D_0\frac{\left[P\right]}{\left[P\right]+\left[P{S}_1\right]+\left[P{S}_2\right]+\cdots }=D_0\frac{1}{1+K_1\left[S_1\right]+K_2\left[S_2\right]+\cdots },$$ (6)

where K_i is the affinity for the ith site present at concentration [S_i]. However, if the affinity for one of two sites is known, then the affinity of the other can be determined. Thus, direct insight may be obtained by mutating one known affinity site.

For case 3, for independent particles, each protein has a unique diffusion coefficient (given by Eq. 5), which is related to the affinity of the site to which it is binding/unbinding. This is the nonergodic limit where, in principle, the number of binding sites is determinable from a distribution of diffusion coefficients. In this limit, p(K) is related to $p\left(D^{\prime }\right)$.

We note that later, in our data analysis, we will find multiple $p\left(D^{\prime }\right)$ s (one for each experiment which covers, for instance, different regions of euchromatin in the cell’s heterogeneous nucleus). By averaging over the individual $p\left(D^{\prime }\right)$ s, we will be configurationally averaging over affinity site distances. Thus, information on affinity site distances will be lost.

Case 3 is the one that is most relevant to our analysis focused on the BZip domain of a transcription factor (C/EBPα) in regions of euchromatin based on the following observations.

• 1)In general, within the confocal volume we expect to have a few hundreds of thousands of binding sites (43–46). Furthermore, we anticipate these binding sites are not, for the most part, selective of BZip because areas rich in binding sites selective of BZip attract large numbers of BZip proteins and we take data in regions of the nucleus that visually appear to have the lowest concentrations of BZip. Incidentally, these are likely regions comprised mostly or entirely of euchromatin. This expectation is confirmed because when the confocal volume is positioned in these regions for FCS collection, there is no discernible immobile fraction (because no bleach out occurs during data collection) (47). Thus, there is a far larger number of nonspecific trapping sites in the confocal volume than there are diffusing particles; [S] ≈ 0.1 mM. By contrast, we assume [P] = 1 nM for the particle concentration (this is roughly the concentration of red fluorescent protein (RFP)-tagged BZip proteins in the experimental data we use). Given the size of our confocal volumes (∼2 μm), this translates to only a few (1–10) RFP-tagged BZips. In practice, experimental conditions determine [P]. Thus, the number of low affinity binding sites far exceeds the number of BZip and, because there are only a few RFP-tagged BZips in the confocal volume, we expect cooperation or competition for the high affinity sites by BZips to be negligible.
• 2)TFs have very specific targets on the genome to which they bind with high affinity, and tend to bind to the rest of the DNA with very low affinities (38,48).

We end with two additional observations on possible alternatives to our multicomponent diffusion model.

First, percolative diffusion (i.e., trapping of the diffusing molecules in the chromatin or other networks) may not be responsible for the G(t) that is well fit by an anomalous model that we will observe in the cell’s nucleus. This is because the size of diffusing particles is small relative to any large structures in the region of interest (ROI). This ensures that particles do not become enmeshed in filaments or structures, which could lead to percolative diffusion (17). For our BZip data, we have RFP tags of size ∼5 nm which, even with the addition of the BZip domain, is much less than the limit (around 60 nm) at which we expect percolative diffusion (17,49).Furthermore, because we have avoided taking data in areas of heterochromatin, we do not expect our probes to often encounter dense network formations that could trap them into percolative diffusion.

Second, it has been suggested that heterochromatin is closely packed in a fractal-like structure (18), and that particles diffusing through it would be forced to explore self-similar structures leading to anomalous diffusion where FBM models have been used (50). However, we explore regions specifically far away from heterochromatin where this should not be an issue. Furthermore, particles that exhibit FBM are typically at least an order of magnitude larger (50,51) than our small probes, which are of a size for which such effects are not expected to occur (52). In general, although the possibility that a small fraction of our probes will undergo percolate diffusion or FBM cannot be excluded, the small size of our probes combined with our averaging over many different ROIs, which are all chosen specifically far away from heterochromatin ensure that in the aggregate the contribution from FBM and percolate diffusion is negligible even if present.

Numerical methods and analysis of synthetic data

In principle, the p(τ_D) appearing in our multicomponent normal diffusion model, Eq. 2, can be extracted from the data—the FCS curve we call $\overline{G}\left(t\right)$—by minimizing a χ² residual between the data and the theoretical G^th(t) as follows:

$${\chi }^2=\sum _t{\left[G^{th}\left(t\right)-\overline{G}\left(t\right)\right]}^2,$$ (7)

where

$$G^{th}\left(t\right)=\sum _{{\tau }_D}p\left({\tau }_D\right){\left(1+\frac{t}{{\tau }_D}\right)}^{-1}{\left(1+\frac{1}{Q^2}\frac{t}{{\tau }_D}\right)}^{-1/2}.$$ (8)

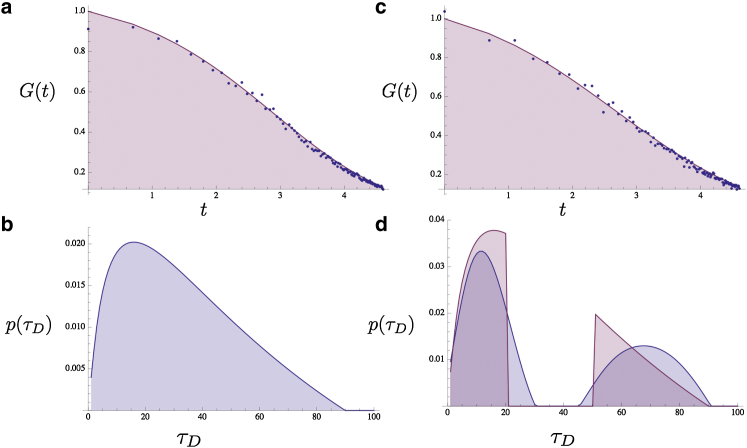
In practice, for noisy $\overline{G}\left(t\right)$, this extraction must be regularized to avoid numerical error propagation. Sengupta and co-workers (31) used entropy, $-\sum _{{\tau }_D}p\left({\tau }_D\right)\text{log}\left(p\left({\tau }_D\right)/q\left({\tau }_D\right)\right)$, as a regularizing function along with standard χ² minimization to obtain p(τ_D) where q(τ_D) is a prior on p(τ_D). However, for our results (benchmarked in Figs. 2 and 3) we use the prior, q(τ_D) obtained from a first round of Tikhonov regularization (53). Our code is implemented on Mathematica and is available (on http://www.statphysbio.physics.iupui.edu/ or by contacting the corresponding author). Once the p(τ_D) has been acquired, a simple change of variable transformation according to D = w²/4τ_D yields p(D) and, through Eq. 5, p(K). Fig. 2 is synthetic data we generated by taking Eq. 3 and plotting it using α = 0.9 with 5% white noise (blue dots, Fig. 2 a). In other words, this synthetic data coincides with the G(t) generated by an anomalous diffusion model. If this were real data, we could either fit it using an adjustable anomalous exponent or we could extract a p(τ_D).

Figure 2.

Protein binding sites of different affinities can give rise to apparent anomalous diffusion. A theoretical G(t) (containing 150 points) was created from an anomalous diffusion model, Eq. 3, with α = 0.9, to which 5% white noise was added (a, blue dots, logarithmic in time). In (b), a p(τ_D) is extracted from this G(t) and, as a check, we used it to reproduce the G(t) (a: solid curve). Part of p(τ_D) is then excised, which yields a new, to our knowledge, p(τ_D) (d: pink curve). A G(t) is created from this theoretical distribution with 8% white noise (c: blue dots, logarithmic in time). A p(τ_D) is then extracted from this (d, blue curve) and the G(t) is reconstructed from this p(τ_D) as a check (c, solid curve). Time is in arbitrary units. To see this figure in color, go online.

Figure 3.

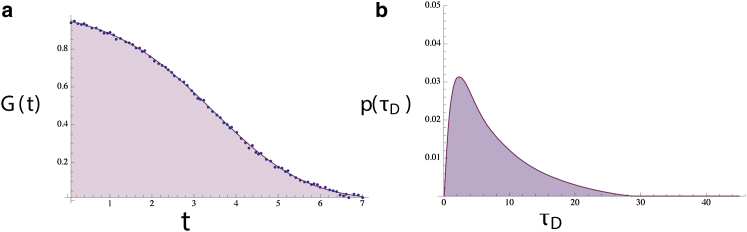
G(t) s may arise from unusual p(τ_D) distributions that cannot easily be fit using anomalous diffusion models. A skewed-normal distribution (b) plus 6% added noise was used to generate a 100 point G(t) (a, blue dots, equidistant in time). The p(τ_D) was then extracted (b) and used to reconstruct the noiseless G(t) (a, solid curve). The original and extracted p(τ_D) are indistinguishable, although agreement of our reconstructed G(t) with the original noisy G(t) is excellent at this noise level. To see this figure in color, go online.

The p(τ_D) we extracted from this curve is given in Fig. 2 b. As a sanity check, we use the p(τ_D) to recreate the original data (solid line, Fig. 2 a).

Here is the type of insight we could gather from our p(τ_D) that would not otherwise be attainable had we simply fit G(t) to an anomalous diffusion model with an adjustable anomalous exponent: Suppose a specific binding site were removed either by mutating/removing a particular DNA binding site or a cooperative binding partner without which successful binding is improbable. In this case, we would expect the theoretical p(τ_D) to show a gap for some τ_D values (pink curve, Fig. 2 d). We show a theoretical p(τ_D) with an exaggerated excision for illustrative purposes.

However, in experiments, we would measure the G(t) coinciding with this theoretical p(τ_D) (i.e., not the p(τ_D) directly). This G(t) (with some added noise) is shown in blue dots, Fig. 2 c. At this point our goal would be to ask: how can a mutation, say, alter the p(τ_D)? To answer this question, we would take this G(t) (blue dots, Fig. 2 c) and extract a p(τ_D) (blue curve, Fig. 2 d). What would then be clear is that this extracted p(τ_D) shows a clear excision from which we would be able to infer the binding site’s affinity. Alternatively, in the case of a mutated or removed binding partner, we could confirm the role the binding partner played in binding to a specific affinity site.

Indeed, this exercise highlights that a great deal of microscopic information (such as binding site affinities and binding partners) can in principle be inferred from curves that could have been equally well fit using anomalous diffusion models. Of course, we can repeat this exercise for any anomalous exponent (other examples can be found in the Supporting Material).

If the dynamics were actually anomalous (i.e., if their mean square displacement obtained by tracking individual hypothetical trajectories was not proportional to time) our analysis would then draw incorrect inferences about affinities from our p(τ_D). However, a change in affinity because of the loss of a binding site, for instance, would suggest that p(τ_D) could be used to estimate affinities.

Furthermore, it is conceivable that G(t) may be sufficiently complicated that it may not be well fit using an anomalous diffusion model and that distributions of anomalous exponents (or increasingly complex forms for waiting time and jump size distributions in CTRWs) would be required to fit the data. We do not have this problem because we do not assume a functional form for p(τ_D) (i.e., our treatment is nonparametric). Thus, we can treat, in principle, arbitrarily complex G(t) s. As an example, we used a skewed Gaussian p(τ_D) (see Fig. 3 b) to create a theoretical G(t) to which we added 6% white noise (blue dots, Fig. 3 a). We then extracted the p(τ_D) from the noisy synthetic data. At this noise level, the extracted p(τ_D) overlaps completely with the theoretical p(τ_D) in Fig. 3 b. As a sanity check, we used this extracted p(τ_D) to reconstruct the expected G(t) (solid line, Fig. 3 a).

Having benchmarked the method on synthetic data, we now turn to real FCS data.

Survey of the experimental methods

Standard recombinant DNA methods were used to generate the plasmids encoding the RFPs mCherry (54) or mRuby (55) that were linked to the sequence encoding the BZip domain of the rat C/EBP α (starting at the methionine at position 237 of the full length C/EBP protein). The cell line used was mouse pituitary GHFT1 cells maintained in monolayer culture. 400 μl of the cell suspension was transferred to each 0.2 cm gap electroporation cuvette containing 1 μg of the plasmid DNA, the content were gently mixed, and pulsed with 200 V at a capacitance of 1200 microfarads in pulses of 10 ms duration. Recovered cells were then diluted in a phenol red-free tissue culture medium containing serum plated on a Nunc Lab-Tek chambered coverglass and transferred to an incubator for imaging the following day. FCS measurements were made using the ISS Alba FastFLIM system (ISS, Champagne, IL) coupled to an Olympus IX71 microscope and a stage-top environmental control system. Emission events were collected at 2 kHz. For further details see (36,56).

Results and Discussion

As an experimental test for our model, we considered a BZip domain of the C/EBPα tagged with either the RFP mCherry or mRuby2. We subsequently used FCS to characterize the diffusion of the proteins in solution and in living mouse cells. Within the cell, we looked at diffusion of the labeled proteins in the cytosol and within the nucleus in regions away from heterochromatin (Fig. 4), which is easily visualized in cells of mouse origin (57).

Figure 4.

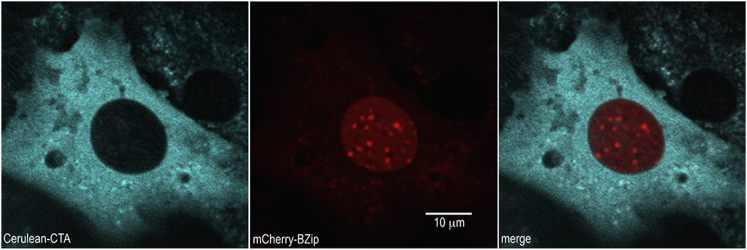
We used FCS to investigate ROIs at various cell locations, both in the cytosol and in the nucleus but far from areas of heterochromatin. In this instance, Cerulean-CTA FP was used to image the cytosol and mCherry RFP was used to tag BZip protein domains; the tagged BZips were observed diffusing in the nucleus via FCS. Because BZip preferentially attaches to heterochromatin, we were able to choose ROIs far from heterochromatin by avoiding RFP congregation areas (bright red spots). To see this figure in color, go online.

The selection of the ROI (solution, cytosol, nucleus away from heterochromatin) limited the expected types of protein interactions and simplified our analysis.

A nucleus has an approximate volume of ∼528 μm³ and the volume of the DNA cylinder is 3.14 μm³ (43,44). The DNA cylinder of the mouse genome contains ∼2.6 × 10⁹ bases, of which ∼75% are in euchromatin (46), so the concentration of bases in euchromatin is ∼3.7 million bases/μm³. Therefore, for a BZip domain length of ∼70 bases (45) and a confocal volume of ∼2 μm³, we expect to have a few hundreds of thousands of binding sites within the confocal volume.

We determine the relative size of the high-affinity site populations by measuring the immobile fraction during bleach out experiments. Because there is a low immobile fraction in the regions observed, there are few high-affinity binding sites in those ROIs (36,47). The concentration of RFP-tagged BZips is 1 nM, which within the range of confocal volumes used in these experiments (36), translates to BZip numbers on the order of 1–10, given the size of the confocal volume (∼2 μm³ in the experiments). We therefore expect cooperation or competition between the BZips to play a negligible role.

As we will discuss, proteins in solution will allow us to identify the peak in p(D) due to free diffusion (and flickering as well) from which we will deduce the contribution to p(D) for proteins diffusing in the cytosol due to molecular crowding.

Finally, we will show that although diffusion in the nucleus can be fit using an anomalous diffusion model and appears the most complicated, the features of its p(D) can be quantitatively interpreted. For instance, the BZip proteins homo- or heterodimerize by forming parallel coiled coils (leucine zipper), and bind to specific DNA elements using a region rich in basic amino acids (58). These proteins also undergo relatively unhindered diffusion in the nucleus in regions away from heterochromatin. We will determine from the p(D) those features from diffusion in crowded environments (now readily identifiable due to our analysis of the diffusion in the cytosol) and features arising from nonspecific DNA binding. We will then associate features from the p(D) s with affinities, Ks, and physical mechanisms that could give rise to those specific interactions.

In solution: free diffusion and protein flickering contribute to p(D)

The raw data we analyzed was first used to characterize the behavior of our RFPs (56). The FCS curves that were acquired for this purpose consisted of 50–100 data points depending on experimental settings and arise from millions of RFPs diffusing in and out of the confocal volume in concentrations of the order of 1 nM per data set. In these FCS experiments, both flickering (59) as well as other known photophysical contributions contribute to the G(t).

Flickering is a fast, reversible photoswitching event that arises from instabilities in the core RFP chromophore (60). A particle flickering faster than the free diffusion time ${\tau }_{D_0}$ would appear in the G(t) as a fast-moving (high diffusion coefficient) component, whereas a particle flickering slower than ${\tau }_{D_0}$ would simply appear as an additional component in p(D) with a lower diffusion coefficient. Because each flickering particle registers as multiple high-D particles, high-D particles appear more numerous, and so p(D) shows substantial probability density at higher values of D when flickering is present. In fact, in our analysis, flickering will appear as a plateau in the p(D) at high values of D. The plateau arises because fast flickering can be interpreted as diffusion times across the confocal volume, which become vanishingly small such that its corresponding diffusion coefficient is infinitely fast.

To determine whether this is correct and ensure that our method does not produce such a plateau when no flickering is present, we ran a control by acquiring FCS data for Alexa568, which is well behaved in FCS studies (56,61). The extracted diffusion coefficient distribution of Alexa568 showed no plateau (see Fig. 5 a), and a peak at ∼360 μm²/s. As the experimental confocal volume was originally calibrated by setting the diffusion coefficient for Alexa568 to 363 μm²/s (56), our recovery of this value was expected and it validates our approach. We also performed simulations of mCherry and mRuby2 diffusing while flickering, which reproduced the plateau (Fig. 5 b). Finally, we used the Spearman rank coefficient ρ as a simple measure of the quality of the data sets we worked with; because G(t) curves ought to be perfectly monotonic in the absence of noise, we limited ourselves to analyzing data sets with ρ ≤ −0.9.

Figure 5.

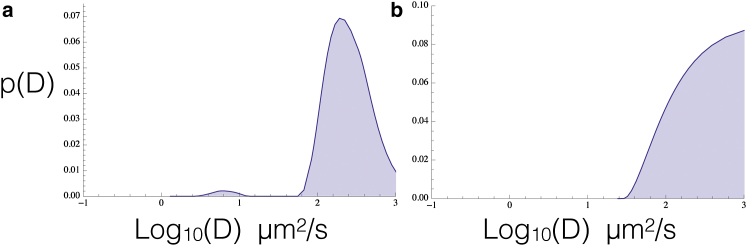
FP flickering gives rise to the plateaus we see for larger D values. We used FCS data acquired for freely diffusing Alexa568, which is well behaved, as a control for our experimental data to determine if it would show a superdiffusive plateau in our analysis: results were negative (a). We then performed a similar analysis for mCherry and mRuby2 freely diffusing while flickering and extracted the resulting p(D) from G(τ) using our method: a superdiffusive plateau was reproduced; we show here the data for mRuby2 (b) 56. We conclude that the superdiffusive plateaus in the p(D) s extracted from our data sets are consistent with flickering of the FP. Furthermore, we conclude the remaining features at lower D values in p(D) that may arise from binding of TFs to DNA are well separated from the flickering plateau if it arises in the data. The small peak at low values of D for Alexa568 (a) is due to FP aggregation. To see this figure in color, go online.

In the cytosol: we extract (label-dependent) molecular crowding effects on protein diffusion

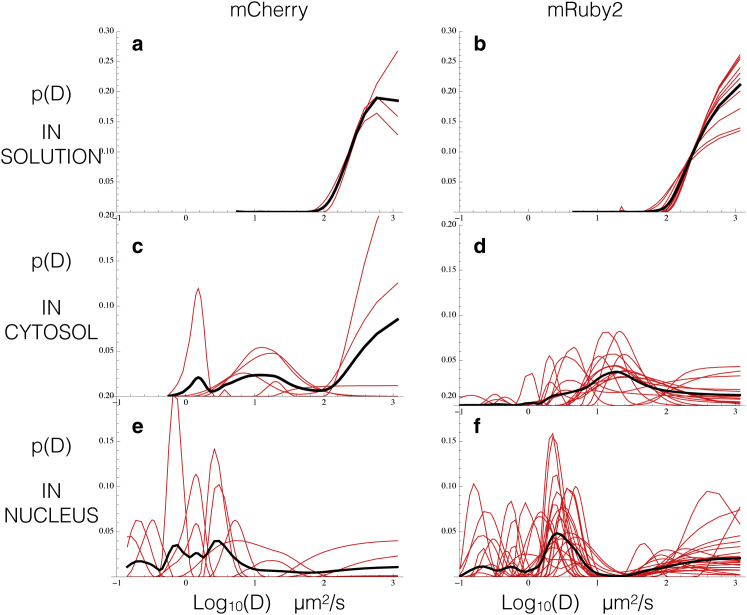
We first describe results of our method employed on an ensemble of different FCS data sets that can be found in Fig. 6 (left for mCherry, right for mRuby2). Here, we used purified mCherry and mRuby2 FPs to compare the analysis of their diffusion characteristics in three different environments: 1) in solution (Fig. 6, a and b) and tagging BZip domains expressed in living cells both 2) in the cytosol (Fig.6, c and d) and 3) in the nucleus away from areas of heterochromatin (Fig. 6, e and f).

Figure 6.

We extract probability distributions of diffusion coefficients from FCS curves. To extract p(D) s, we used FCS data acquired for mCherry and mRuby2 diffusing freely in solution (a and b), and for BZip protein domains tagged with mCherry and mRuby2 diffusing, whereas in the cytosol (c and d) and in the nucleus but far from regions of heterochromatin (e and f) 56. The p(D) s for the freely diffusing FPs in solution exhibit superdiffusive plateaus due to flickering and triplet corrections, with the actual free diffusion coefficient appearing as a lower bound. In the cytosolic and nuclear data, these plateaus are still present for the FP-tagged BZips but they are accompanied by rich landscapes that capture the many different interactions between the FP-tagged BZips and their environment detailed in the main body. Red curves represent the p(D) s extracted from individual data sets; Black curves are the average of all underlying red curves. The total number of data sets averaged is per plot: (a) 3, (b) 9, (c) 5, (d) 16, (e) 7, and (f) 21. In cases where only a few data sets were available the average occasionally exhibits features that are only found in one data set; we consider such features to be most likely artifacts of heterogeneity between different ROIs in the cytosol or nucleus and ignore them in our analysis. In cases where more data sets are averaged such single data set features are naturally muted. We note that, predictably, in solution the p(D) s are far less noisy as compared to the heterogeneous environment of a living cell. To see this figure in color, go online.

In all cases, a plateau appears at the right side of the p(D) distribution corresponding to the apparent superdiffusive component that we now know is the result blinking/flickering.

The lower bound of the superdiffusive plateau coincides with expected free diffusion for mCherry or mRuby2 (D ≈ 120 μm²/s). To obtain this D, we used the Einstein-Stokes relation D = k_BT/6πηr in water at 300 K and a molecular size of 2 nm (62), which is the radius of gyration of the RFPs if we think of them as tumbling spheres. In addition, FP-tagged BZip proteins are expected to be somewhat slower, because the BZip domain represents a 122 AA (13 kDa) tail, and therefore 120 μm²/s can be considered an upper bound. This value for the free diffusion coefficient D₀ for mCherry and mRuby2—which has also been experimentally determined to be ∼100 μm²/s (56)—is therefore a natural lower bound for the flickering plateau, and indeed it appears as such in our analysis (see Fig. 6, a and b). Furthermore, the value of p(D) at D₀ is low but nonzero, again as expected.

In the cytosol, we believe mCherry-BZip has few interactions. This is because C/EBPα—the parent protein of the BZip domain used here—has not been demonstrated to have any interactions with cytosolic proteins other than during its degradation (63). The question of whether mCherry has interactions in the cytosol has not, to our knowledge, been directly investigated, however it does not exhibit behavior indicative of such interactions during experiments (56).

In the absence of known interaction, the p(D)’s peak obtained for mCherry-BZip and mRuby2-BZip in the cytosol (Fig. 6, c and d), which is roughly centered at 20–40 μm²/s—which is smaller than that expected for free diffusion—is therefore attributed to the slower diffusion arising from cytoplasmic crowding. Furthermore, the peak of our extracted p(D) is in the range of diffusion coefficient values determined by FCS and fluorescence recovery after photobleaching (FRAP) experiments (56,64,65)

In addition to the peak centered at 20–40 μm²/s (the crowding peak), the p(D) for mCherry in the cytosol shown in Fig.6 c shows a component of free diffusion and a third very slow diffusion component. This third component, however, only shows up strongly in a single data set and could be a result of a particular feature of the cytosol in the ROI from which the data set originates. By contrast, the p(D) curves for mRuby2 in the cytosol also show a similar peak at 20–40 μm²/s but no substantial slower component as was the case for mCherry, strengthening the view that this particular feature is an experimental outlier. The overlap of the 20–40 μm²/s peak and free diffusion peak for mRuby2 may be caused by interactions between mRuby2 and cytosolic proteins or organelles. In fact, previous analyses of FCS data suggested that mRuby2 expressed in living cells displays a reduced diffusion that is tentatively attributed to possible interactions of the chromophore with other cytosolic molecules or structures (56).

In the nucleus: the diffusion of BZip (whose G(t) is well fit by anomalous diffusion) is attributed to DNA site binding

The crowding peak is much less prominent in the nucleus where other interactions dominate, as we now describe.

In the nucleus, DNA-binding domains–such as those of the BZip proteins–are expected to engage in at least four different types of binding interactions: 1) direct binding with high affinity to specific DNA elements (58); 2) binding to nonspecific DNA elements with lower affinity; 3) interactions with other proteins involved in chromatin binding (36); 4) association with proteins that form subnuclear domains such as nucleoli, speckles, or promyelocytic leukemia bodies (66) or oligomeric complexes with other proteins (67).

These interactions are captured by the traces shown in Fig. 6, e and f. In particular, these traces exhibit a number of peaks in the p(D) in the nucleus, with three common types of interactions identified for both the mCherry-BZip and the mRuby2-BZip fusion proteins. There is a very slow interaction centered around 0.2 μm²/s, another centered at 0.8 μm²/s, and a third interaction centered around 5 μm²/s. These likely identify different types of nuclear interactions, one or more of which may be related to interactions with other proteins involved in chromatin binding (interaction 3), as a typical residence of TFs in chromatin has been shown to be about 2 s (66). In addition, the BZip domain is known to interact with the heterochromatin protein 1 alpha (HP1α), which binds directly to histones and interacts with both histone- and DNA-methyltransferases (interaction 3) (36,67). Histones are very stable and slow diffusing (66), and protein complexes containing histones would be expected to exhibit extremely long binding times, i.e., small diffusion coefficients.

Furthermore, based on the timescales involved, at least one of the captured interactions might be related to associations with subnuclear domains (interaction 4), which can be on longer timescales than chromatin binding (66). However, the intermediate interaction identified might be another type of interaction with chromatin. Using FRAP, two different interactions for the parent protein C/EBPα were identified—by fitting the FRAP results to a double exponential decay curve—but both interaction times were attributed to chromatin binding (68).

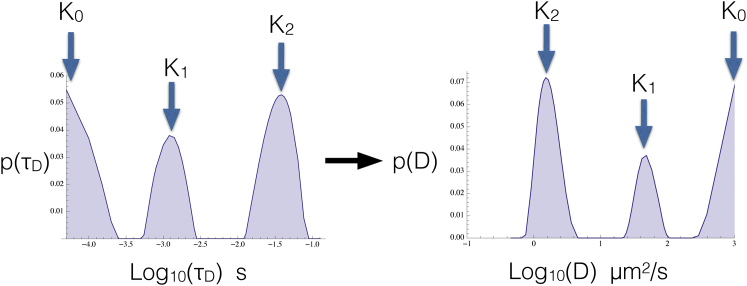
Results for a single data set of real FCS data for mRuby2-tagged BZip diffusing in the nucleus away from regions of heterochromatin are shown in Fig. 7. This single trace contains three peaks (K₀,K₁,K₂) found in both the p(τ_D) and the p(D), which correspond to diffusion coefficients of about 1000, 80, and 2 μm²/s, respectively. Each of the three peaks arises from a different physical mechanism, namely blinking/flickering and free diffusion (K₀), molecular crowding of freely diffusing mRuby2-tagged BZips (K₁) and finally mRuby2-tagged BZips (K₂) engaged in one of the types of binding discussed previously.

Figure 7.

Affinity constants for key interactions can be determined from data collected in the cell’s nucleus. Here a p(τ_D)—extracted from a data set acquired from mRuby2-tagged BZip domain diffusing in the nucleus far from areas of heterochomatin (56)—is transformed into the corresponding p(D). The data set presented here is atypical. It was the nuclear data set that exhibited the smallest χ² of all experimental data sets we examined. Now—using the accepted free diffusion coefficient for mRuby2 of ∼100 μm²/s (56) and Eq. 5—we find that 1) the peak corresponding to K₀ is most consistent with a superdiffusive component appearing as an artifact of flickering/blinking in our data, bounded below by the expected free diffusion coefficient for mRuby2 as seen in FCS of mRuby2 in solution; 2) the peak corresponding to K₁ ≈ 5 nM⁻¹ can be attributed to molecular crowding interactions; and 3) the peak corresponding to K₂ ≈ 500 nM⁻¹ represents one of the types of binding discussed in the text. (In deriving the values for K we assumed, for simplicity only, [S] = 0.1 mM). To see this figure in color, go online.

Unlike the curves in (homogeneous) solution, the curves in the cytosol and especially in the cell’s nucleus differ somewhat from one another. We emphasize that this data is in vivo and that, despite this fact, qualitative differences on diffusion of BZip are clearly detected by our method between the solution, the cytosol, and the nucleus. Furthermore, because there are a number of interactions possible in the nucleus, a very large number of ROIs may be required to yield a smoother p(D).

Conclusions

Diffusion in the complex heterogeneous environment of the cell often shows strong deviations from normal diffusion (2,7,8,17,18,69). Here, we have focused on FCS and demonstrate that processes described by time autocorrelation, G(t), which are generally fit using anomalous models that could also be interpreted as multicomponent diffusion processes. Our method provides insight into flickering phenomena, crowding interactions, and may also reveal binding site affinities in some regimes.

Measurements of binding site affinities and even binding site affinity distributions in the cell’s nucleus are of current interest (39,69–73). A number of single-molecule localization and tracking methods (such as TIRF, EPI, SPIM, FSM, smFRET) (74)) exist to measure affinities (39,71). Although powerful, these methods can be problematic because of the difficulty in distinguishing transitions in the noisy dynamics of the diffusing particle (69,70), and can suffer from bias, arising for example from over detection of slow versus fast moving particles (69).

Here, we argue that FCS—a widespread technique poised to provide dynamical insight into in vivo systems—complements single-molecule localization and tracking methods and may provide an independent assessment of binding affinities. FCS’s potential to help quantify nuclear ligand-dependent interactions has previously been explored (75); in that study, MaxEnt, diffusion time distribution analysis, and standard fitting techniques were used to determine the existence of multiple diffusing species and interactions in the nucleus.

Here, we used a combination of MaxEnt and Tikhonov regularization to infer models from FCS data collected from the complex environment of live cells. We have shown that the diffusion time and diffusion coefficient distributions, p(τ_D) and p(D), respectively, for BZip protein interactions in the nucleus yield information on diffusion times, diffusion coefficients, and, ultimately, binding affinities of the proteins to nuclear structures. Our results can be used to create a detailed quantitative map of the types and strength of specific binding interactions that provide data from a sufficient number of different regions inside the living cell.

BZip proteins—evolutionarily conserved from plants to humans—play critical roles in both physiological and pathophysiological processes, from the control of reproduction to cancer progression. In fact, over 50 human BZip proteins participate in a wide range of important biological processes, making these proteins attractive clinical targets for selective inhibition (76). For example, specific dominant-negative heterodimer partners for the BZip proteins, called AZip, were designed to specifically inhibit BZip DNA binding in equimolar competition (77). The expression of AZip proteins in cells and in transgenic animals demonstrated that the selective inhibition of BZip DNA binding had significant physiological effects, from the prevention of skin papilloma formation (78) to the reduction in adipose tissue (79).

In addition, small molecules that inhibit BZip DNA binding have been identified, providing important structural information for the design of drugs targeting this important transcription factor family (80). Our method has the potential to reveal how BZips binding potency and specificity changes with the addition of these novel drugs. In other words, if a particular value of K—otherwise prominent—should disappear from p(K) obtained from treated cells, we would collect valuable insight into the types of interactions these drugs have disrupted.

Of course, the technique we presented here is not specific to BZip; rather, our method should be applicable to other proteins—and even cellular structure—monitored by FCS.

Author Contributions

K.T. and S.P. wrote the theory and software. A.S. and R.D. performed the experiments. K.T. and A.S. analyzed the data. R.D. and S.P. oversaw research. K.T., A.S., R.D., and S.P. wrote the article. S.P. designed the research.

Editor: Jennifer Ross.