Mapping the Dynamics Landscape of Conformational Transitions in Enzyme: The Adenylate Kinase Case

Abstract

Conformational transition describes the essential dynamics and mechanism of enzymes in pursuing their various functions. The fundamental and practical challenge to researchers is to quantitatively describe the roles of large-scale dynamic transitions for regulating the catalytic processes. In this study, we tackled this challenge by exploring the pathways and free energy landscape of conformational changes in adenylate kinase (AdK), a key ubiquitous enzyme for cellular energy homeostasis. Using explicit long-timescale (up to microseconds) molecular dynamics and bias-exchange metadynamics simulations, we determined at the atomistic level the intermediate conformational states and mapped the transition pathways of AdK in the presence and absence of ligands. There is clearly chronological operation of the functional domains of AdK. Specifically in the ligand-free AdK, there is no significant energy barrier in the free energy landscape separating the open and closed states. Instead there are multiple intermediate conformational states, which facilitate the rapid transitions of AdK. In the ligand-bound AdK, the closed conformation is energetically most favored with a large energy barrier to open it up, and the conformational population prefers to shift to the closed form coupled with transitions. The results suggest a perspective for a hybrid of conformational selection and induced fit operations of ligand binding to AdK. These observations, depicted in the most comprehensive and quantitative way to date, to our knowledge, emphasize the underlying intrinsic dynamics of AdK and reveal the sophisticated conformational transitions of AdK in fulfilling its enzymatic functions. The developed methodology can also apply to other proteins and biomolecular systems.

Introduction

Conformational transitions are essential for the function of enzymes (1,2). It is important to understand the relationship between the dynamics of enzyme in conformational transitions and the biological activities (3). For a wide range of enzyme functions, determining the conformational transition pathways and mapping the energy landscape can lead to the design and control of biological processes at the molecular level (4,5). However, this is truly challenging as protein conformational transitions generally span a wide range of timescales and size-scales, and different modes of motion may exhibit complex correlations with various functions. Furthermore, to establish a rational relationship requires multiscale high-resolution dynamics details. A quantitative depiction of the energy landscape and the conformational dynamics at large (∼ microsecond timescale or more) is desirable (6,7).

An ideal system for pursuing the dynamics-function rationale is adenylate kinase (AdK) protein, a ubiquitous cellular energy homeostasis enzyme, for catalyzing the phosphoryl transfer between two adenosine diphosphate (ADP) molecules and adenosine triphosphate (ATP) and adenosine monophosphate (AMP), i.e., ${\text{Mg}}^{2+}·\text{ATP}+\text{AMP}\leftrightarrow {\text{Mg}}^{2+}·\text{ADP}+\text{ADP}$ (8,9). Structurally AdK consists of two binding sites and three major domains: a CORE domain, an ATP-binding domain (LID), and an AMP-binding domain (NMP), as shown in Fig. 1. AdK can transit between an open conformational state (likely the unbound state) and a closed conformational state (likely with substrates/inhibitors) (8,9). An early experiment (10) showed that the equilibrium state of AdK favors the closed conformation, even in the unbound apo state. However, a solution-state NMR experiment (11) showed that binding of ATP induces a dynamic equilibrium of the open and the closed conformations, and the ATP binding motif populates with almost equal populations. Supposedly, for the transition from the open to the closed states, most of the conformational transitions occur at the LID and NMP domains (with the CORE domain being relatively rigid). Henzler-Wildman et al. (2) further showed that the large-scale domain motions in ligand-free AdK are not random, but preferentially follow the pathways capable of proficient chemistry. These experiments show that the enzyme-substrate interactions follow a mechanism different to the conventional induced-fit theories. They suggest a conformational selection/population shift mechanism, where the ligand binding shifts the equilibrium of enzyme’s conformational ensembles that preexist regardless of ligands (12–14). However, there remain debates about the transition pathways and the conformational selection/population-shift mechanism in AdK (15–21). Consequently a quantitative and molecular understanding of conformational transitions and the energetics of AdK is highly valuable.

Figure 1.

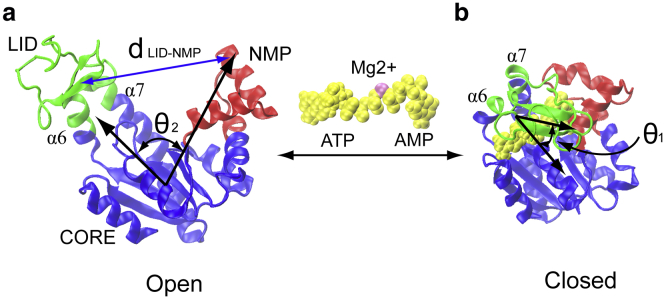
Conformational transitions in AdK: (a) the open state (e.g., PDB code: 4AKE); and (b) the closed state with ligands (e.g., PDB code: 1AKE). The enzyme consists of three well-defined domains: the rigid CORE (blue, residues 1–29, 60–121, and 160–214); nucleotide triphosphate binding domain LID (green, residues 122–159); and nucleotide monophosphate binding domain NMP (red, residues 30–59). The alpha helices α6 and α7 correspond to residues 112 to 122 and residues 160 to 189, respectively. The ligands Mg²⁺•ATP/AMP are represented by yellow van der Waals (VDW) spheres. The angle LID-CORE ${\theta }_1$ is formed by the centers of mass of the backbone of residues of LID (a.a. 123–155 (LID), hinge (a.a. 161–165), and CORE (a.a. 1–8, 79–85, 104–110, and 190–198), whereas the angle NMP-CORE ${\theta }_2$ is formed by the centers of mass of the backbone of residues of NMP (a.a. 50–59), CORE (a.a. 1–8, 79–85, 104–110, and 190–198), and hinge (a.a. 161–165). The variable $d_{LN}$ is used to monitor the distance by the centers of mass between domains LID and NMP, respectively. To see this figure in color, go online.

A number of theoretical efforts, such as all-atom molecular dynamics (MD) simulations, were done to capture the conformational transitions of AdK with local motions (21–24). However, as demonstrated in experimental works (2), the conformational transitions of AdK are in multitimescale ranging from nanosecond to microsecond and millisecond, which challenges the accessible timescale of all-atom simulations. To overcome the timescale limit and reach the large length scale dynamics of AdK, some coarse-grained models were developed (17–20,25–31) to determine dynamic correlations and transition pathways, and to estimate the free energy changes. Nonetheless, the coarse-grained models lack the atomic details of the interactions, yet the interaction parameters were fitted by all-atom simulations or experimental results. There is still uncertainty and disagreement on the competitive transition orders of the LID and NMP domains and the allostery mechanism in AdK (17,21,22,25–27,29,32,33).

In recent years, to achieve long time simulations using an all-atom description, the accelerating MD simulation methods, such as temperature-enhanced essential dynamics replica exchange (TEE-REX) algorithm (32), have been developed to explore the conformational space of AdK. However, these TEE-REX simulations lack the quantitative description of conformational transitions of AdK. Recently, the umbrella sampling and distance replica exchange methods were applied to calculate the free energy landscape of AdK along its conformational pathways in a one-dimensional reaction coordinate (16,24,34,35). Nonetheless, using a one-dimensional reaction coordinate is insufficient to identify the conformational transitions and pathways of AdK (which typically acts via coupled motion of multidomains). More recently, there have been studies on mapping two-dimensional free energy landscapes of AdK’s conformational transition (17,19,27). These two-dimensional free energy landscapes were obtained based on the structure-based coarse-grained model, which lack atomic details of the interactions. Thus to more accurately understand the conformational transitions of AdK, the use of multidimensional free energy landscape with all-atom description is needed.

In this study we aimed to comprehensively understand AdK’s operation dynamics and conformational transition mechanism by long timescale (i.e., ∼ micro seconds) explicit MD (LT-MD) and bias-exchange metadynamics (BE-META) simulations. BE-META is capable of exhaust sampling of conformational changes and calculating the corresponding free energy landscapes along multidimensional coordinates (36–42). We determined the conformational transitions of apo and ligand-bound AdKs from the BE-META simulations. Most significantly we quantitatively mapped the free energy landscape of AdK to inclusive transition pathways, which can lead to the design and control of biological processes of AdK at the molecular level. We hope this work helps to advance the knowledge on how conformational transitions affect an enzyme’s biological process and functionality.

Materials and Methods

We performed long timescale (up to ∼ micro seconds) explicit MD and BE-META dynamics simulations of AdK starting from a large variation of states. Table S3 in the Supporting Material summarizes the system MD setups and dynamics and transitions we have observed.

Long-time explicit MD simulations

In LT-MD simulations the starting conformations of AdK were taken from the crystal structures of mesophilic Escherichia coli (E. coli) deposited in the Protein Data Bank (PDB), i.e., an open state without ligand was adopted from PDB 4AKE (8), and a closed state without ligands was from PDB 1AKE (9) (with the ligand AP₅A removed). For the simulations with ligand, an open state was chosen from PDB 4AKE, in which the ligands ATP and Mg²⁺•AMP were docked to PDB 4AKE; and a closed state was from PDB 1AKE, in which the ligands ATP and Mg²⁺•AMP were used instead of AP₅A. Table S3 details the various AdK states we constructed for the MD simulations.

All LT-MD simulations were performed on the GROMACS program (43,44) using the AMBER force field of ffamber03 (45) (with the explicit force field parameters of ATP and AMP by Carlson et al. (46)). The AdK systems were set up following similar procedure of our previous studies (47–49). The protonation states of AdK residues were set normally according to a pH 7 environment, e.g., the aspartic residues adopted deprotonation state and the histidine residues were protonated only at its N-3 position. The system was solvated in an approximate 80 × 80 × 80 Å³ TIP3P (50) water box, with ∼15,000 water molecules. Appropriate magnesium ions were added to neutralize the system. Each simulation system contained ∼50,000 atoms. The particle mesh Ewald (PME) method (51) was used to calculate the long-range electrostatic interactions. The systems were minimized first using a steepest descent algorithm of 10,000 steps. Then the system was gradually heated to 300 K in 200 ps while positional restraints were used and the restraint force constants were gradually decreased from 2.39 to 0 kcal/(mol·Å²). All production simulations were fully unrestrained at 300 K with Nose-Hoover (52) thermostat, with a relaxation time of 0.5 ps and a pressure of 1 bar using the Parrinello-Rahman approach (53,54). The LINCS algorithm (55) was applied to constrain the bonds with H-atoms. The time step of the production simulations was 2.0 fs. The cutoff of the nonbonded interactions was set to 10 Å. The nonbonded pairs were updated in every 10 steps. Visualization of protein structures was performed using the Visual Molecular Dynamics (VMD) program (56).

The conformational transitions of AdK were monitored by four variables: 1) the root-mean-square deviation (RMSD) of the Cα atoms with reference to the open and closed conformation, 2) the angle of LID-CORE ${\theta }_1$, 3) the angle of NMP-CORE ${\theta }_2$, and 4) the distance between LID and NMP $d_{LN}$, respectively. The two angles ${\theta }_1$ and ${\theta }_2$ directly defined the changing state of LID and NMP domain, i.e., in crystal structures, ${\theta }_1^O\approx {95}^{\circ }$ for LID open (PDB 4AKE) and ${\theta }_1^C\approx {68}^{\circ }$ for LID closed (PDB 1AKE), ${\theta }_2^O\approx {61}^{\circ }$ for NMP open (PDB 4AKE) and ${\theta }_2^C\approx {28}^{\circ }$ for NMP closed (PDB 1AKE) (see Fig. 1). The variable $d_{LN}$ was used to monitor the distance between the center of mass of LID and NMP, e.g., $d_{LN}^O\approx 38\AA$ in PDB 4AKE and $d_{LN}^C\approx 20\AA$ in PDB 1AKE, respectively. Table S3 summarizes the distinctive conformational transitions and pathways observed in the LT-MD simulations.

Bias-exchange metadynamics simulations

The BE-META algorithm (36–42) was recently used to accelerate the simulation of rare events and reconstruct the free energy landscape in ligand-receptor binding system (38) and protein folding (36,37). The BE-META technique accelerates rare events by simultaneously biasing several selected reaction coordinates, i.e., the collective variables (CVs). More details of the BE-META algorithm can be found in Text S1 in the Supporting Material and in the works by Laio et al. (36–41). Some of previous studies have chosen various CVs, such as the order parameters in RMSD (10,19,27), the distance between domains (19,35), or the fraction of contacts between different domains (17,34). In this study, we chose CVs of angle LID-CORE ${\theta }_1$, angle NMP-CORE ${\theta }_2$ and the distance between LID and NMP $d_{LN}$, because they are widely used by experimental and structural investigation (which define the open, semi-open–semi-closed, and closed conformations of AdK, see Fig. 1). The parameters implemented in the BE-META simulations were as follows: Gaussian height 0.05 kcal/mol, Gaussian widths 0.01 radian for ${\theta }_1$ and ${\theta }_2$, and 0.1 Å for $d_{LN}$, deposition of a Gaussian every 1 ps, and swaps of bias attempted every 2 ps. To reduce the computational cost and maintain the reasonable conformation of AdK, walls were placed on CVs to restrict them in a reasonable zone: ${58}^{\circ }\le {\theta }_1\le {100}^{\circ }$, ${20}^{\circ }\le {\theta }_2\le {70}^{\circ }$, and $15\AA \le d_{LN}\le 45\AA$.

BE-META simulations were performed biasing each of the three CVs on a different replica (plus one replica without any bias) for 200 ns per replica, thus a total of 800 ns timescale per BE-META simulation were conducted in this study, as described in Table S4. It should be noted that the BE-META simulations of free AdK used both the open and closed initial structures, i.e., two replicas started from the open structure (PDB 4AKE) and two started from the closed ones (PDB 1AKE). The different initial structures help sample the open and closed states. Simulations were first equilibrated in NPT ensemble at 300K and 1 bar. After 1 ns of equilibration, the barostat was removed and the BE-META simulation was started. The atomic coordinates were saved every 5 ps and the energy was saved every 0.05 ps. The BE-META simulations were performed in GROMACS (43,44) plus PLUMED package (57), and the results were analyzed using METAGUI (58) developed by Laio and co-workers (36–41) with the VMD program (56).

Results

Conformational transitions and pathways in the ligand-free AdK

We directly observed in LT-MD simulations the large conformational transitions of ligand-free AdK through distinctive pathways, as summarized in Table S3 and illustrated in Figs. 2 and S1–S6.

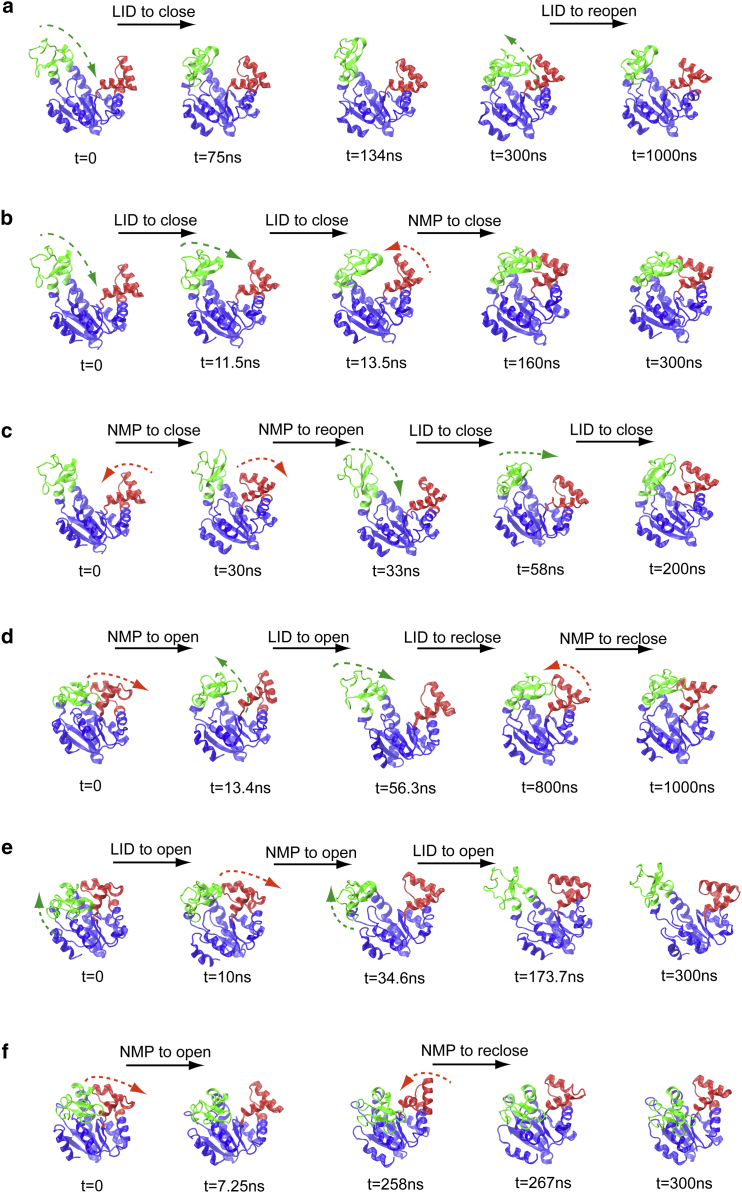
Figure 2.

Conformational transitions of AdK (without ligands) observed in LT-MD simulations. (a) Simulation O₁ starting from the open state, corresponding to the transition: LID open ↔ LID closed. (b) Simulation O₂ starting from the open state, corresponding to the transition: 1st step, LID open → LID closed; 2nd step, NMP open → NMP semi-open. (c) Simulation O₃ starting from the open state, corresponding to the transition: 1st step, NMP open ↔ NMP semi-open; 2nd step, LID open → LID closed. (d) Simulation C₁ starting from the closed state, corresponding to the transition: 1st step, NMP closed ↔ NMP semi-open → NMP open; 2nd step, LID closed ↔ LID open. (e) Simulation C₂ starting from the closed state, corresponding to the transition: 1st step, LID closed → LID open; 2nd step, NMP closed → NMP open. (f) Simulation C₃ starting from the closed state, corresponding to the transition: NMP closed → NMP semi-open → NMP open → NMP semi-open. More details can be found in Text S2, Table S3, and Figs. S1–S6. To see this figure in color, go online.

Simulations starting from the unbound open states show that AdK prefers to shift its conformation from the open to closed state via the following pathways: LID closed first and then NMP moved toward the closed state (see Table S3 and Fig. 2, a–c). This pathway is similar to that observed in the TEE-REX MD study (32). Typical trajectories show that the LID domain can be closed from the open state at ∼10 ns timescale and reopens on a ∼100 ns timescale (see Figs. 2 a and S1). Interestingly, from the simulations we observed some intermediate states, where the LID domain is not only close to the CORE domain, but also has contact with the NMP domain while NMP is open (i.e., ${\theta }_1\approx {60}^{\circ }\sim {70}^{\circ }$, ${\theta }_2\approx {35}^{\circ }\sim {60}^{\circ }$, and $d_{LN}\approx 16\AA \sim 30\AA$; e.g., the snapshots at 300 ns in Fig. 2 a, 160 ns in Fig. 2 b, and 200 ns in Fig. 2 c; also see Figs. S1–S3). These intermediate states deviated from the open crystal structure (e.g., PDB 4AKE) and the closed crystal structure (e.g., PDB 1AKE). Hereafter we referred these intermediate states as the semi-open–semi-closed structures. The intermediate states suggested that the motions of NMP domain can be facilitated by the contact with the LID domain, i.e., the NMP domain moves from the open toward the closed state after the contact established. We showed that the NMP domain can adopt a semi-open state at the timescale of ∼100 ns, i.e., with the angle NMP-CORE in the range of ${35}^{\circ }\le {\theta }_2\le {45}^{\circ }$ (see t = 160 ns in Figs. 2 b and S2; the angle is a bit larger than the crystal closed structure ${\theta }_2^C\approx {28}^{\circ }$). However, given no ligands, no simulation starting from open conformation achieved the crystal closed structure even at the 1,000 ns timescale. This observation is consistent with the NMR experiments (2) showing that the fully closed conformation from the open state occurs on the microsecond-to-millisecond timescale.

Previous unbiased all-atom MD simulations (22,24) showed that AdK stabilizes at the open conformation in ∼100 ns timescale when using the CHARMM force field (59,60). In contrast, AdK can transit to the LID closed state in 25∼80 ns, a semi-open–semi-close state (23,32), using the OPLS-AA force field (61,62). To compare the results of previous studies, we performed two more LT-MD simulations up to 500 ns timescale starting from the open state using CHARMM (59,60) and OPLS-AA (61,62) force field. As shown in Figs. S11 and S12, AdK is stabilized at the open state in the 500 ns timescale with the CHARMM27 force field (which is consistent with previous studies (22,24) with the same force field). In contrast, using the OPLS-AA force field, AdK reached the LID closed states within ∼100 ns timescale (as shown by t = 169, 250, and 355 ns in Fig. S12), which is similar to the findings in this study and previous ones (23,32). In general, the research community accepts that there is subtle discrepancy when using different force fields (63,64). For example, it was found that Amber force field favors α-helical structures, OPLS-AA overpredicts β-sheet structures, and CHARMM predicts a more stiff transition between the helix and sheet structures (63). This may explain our results that AdK transits from an open to a semi-open–semi-closed state below 100 ns timescale. Our results and conclusions are consistent and coherent under the Amber force field ff03. The comparison of the different force fields, however, is beyond this study.

For the simulations starting from the unbound closed state, we observed two distinct pathways toward the open conformation in independent LT-MD simulations: (I) first, NMP fluctuated between the closed state and the semi-open state (i.e., ${35}^{\circ }\le {\theta }_2\le {45}^{\circ }$); after the opening of NMP domain, the LID domain then opens gradually (see Table S3 and Figs. 2 d and S4); (II) second, LID opens from the closed state rapidly, the NMP domain can stay in the closed state for a couple of nanoseconds before opening (see Table S3 and Figs. 2 e and S5). Similar to the simulations starting from the open state, the NMP domain can move toward the semi-open state at the timescale ∼100 ns after the closure of LID (see Fig. S4 at t = 800 ns and Fig. S6 at t = 258 ns in Supporting Material). Fig. 2 f showed the result that only the NMP domain transits between the closed ↔ semi-open ↔ open conformations, while the LID domain remains in the closed state.

Ligands binding impacts on conformational transitions of AdK

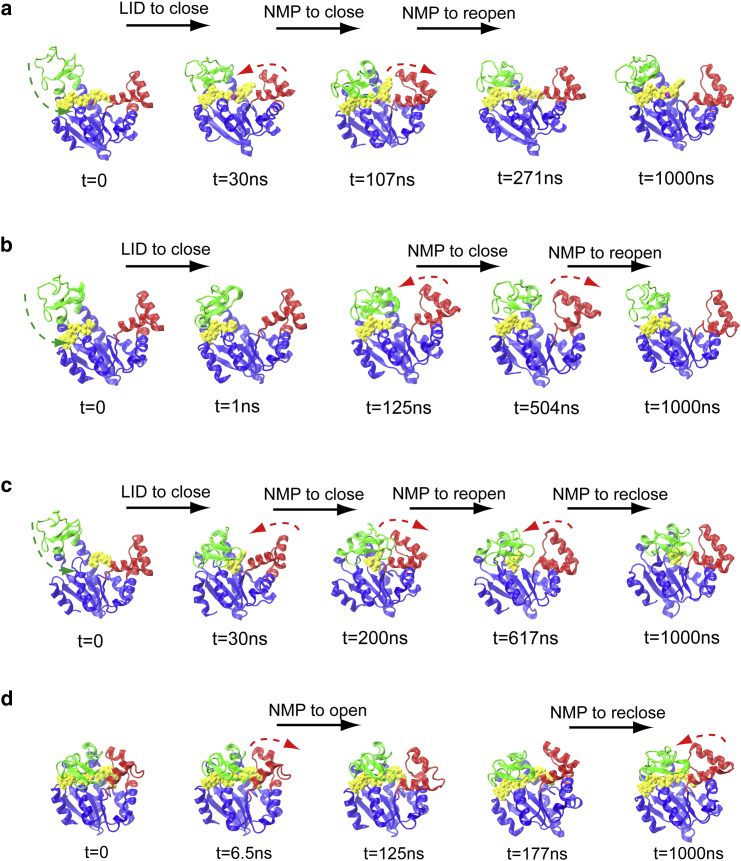
To check the conformational dynamics of AdK when binding with ligands, we docked various ligands into AdK at different states. As found by Ådén et al. (65), ATP initiates interactions with the contact surface of CORE when it starts binding. In our simulation, the ligands started docking to the CORE surface around the binding site at the early stage of simulation runs. The simulations starting from the open state bound with ATP and AMP show that the LID domain closes rapidly (while the NMP domain can close to its intermediate state, i.e., ${\theta }_2\approx {45}^{\circ }$) much faster than the ligand-free state, with the timescale ∼50∼100 ns as shown in Figs. 3 a and S7. However, even extending the simulation up to 1,000 ns, AdK did not transit to the fully closed conformation (such as PDB 1AKE) (see Figs. 3 a and S7). The simulations starting from the open state docked with ATP alone showed identical motions (see Figs. 3 b and S8). The simulations with AMP alone led to a more compact structure: the LID domain fully closes and the NMP domain closes to the semi-open state (see Figs. 3 c and S9).

Figure 3.

Conformational transitions of AdK (with ligands) observed in LT-MD simulations. (a) Starting from the open state with both ATP and AMP, simulation O-ATP-AMP. (b) Starting from the open state with only ATP, simulation O-ATP. (c) Starting from the open state with only AMP, simulation O-AMP. (d) Starting from the closed state with both ATP and AMP, simulation C-ATP-AMP. More details can be found in Text S2, Table S3, and Figs. S7–S10. To see this figure in color, go online.

When starting from the closed state with both ATP and Mg²⁺•AMP, the structure is likely stabilized as in the crystal closed conformation (with the angle ${\theta }_1$ and ${\theta }_2$ around $\sim {65}^{\circ }$ and $\sim {30}^{\circ }$, respectively (see Figs. 3 d and S10). Interestingly, after∼125 ns running, the NMP domain presented a significant motion as the NMP-CORE angle ${\theta }_2$ increased from $\sim {30}^{\circ }$ to $\sim {45}^{\circ }$ in a few nanoseconds. The above observation suggests that the LID domain is much more dynamic affinitive than NMP, and the NMP domain motion is the rate-limiting step for enzyme catalysis.

Mapping the transitions and pathways of AdK from LT-MD simulations

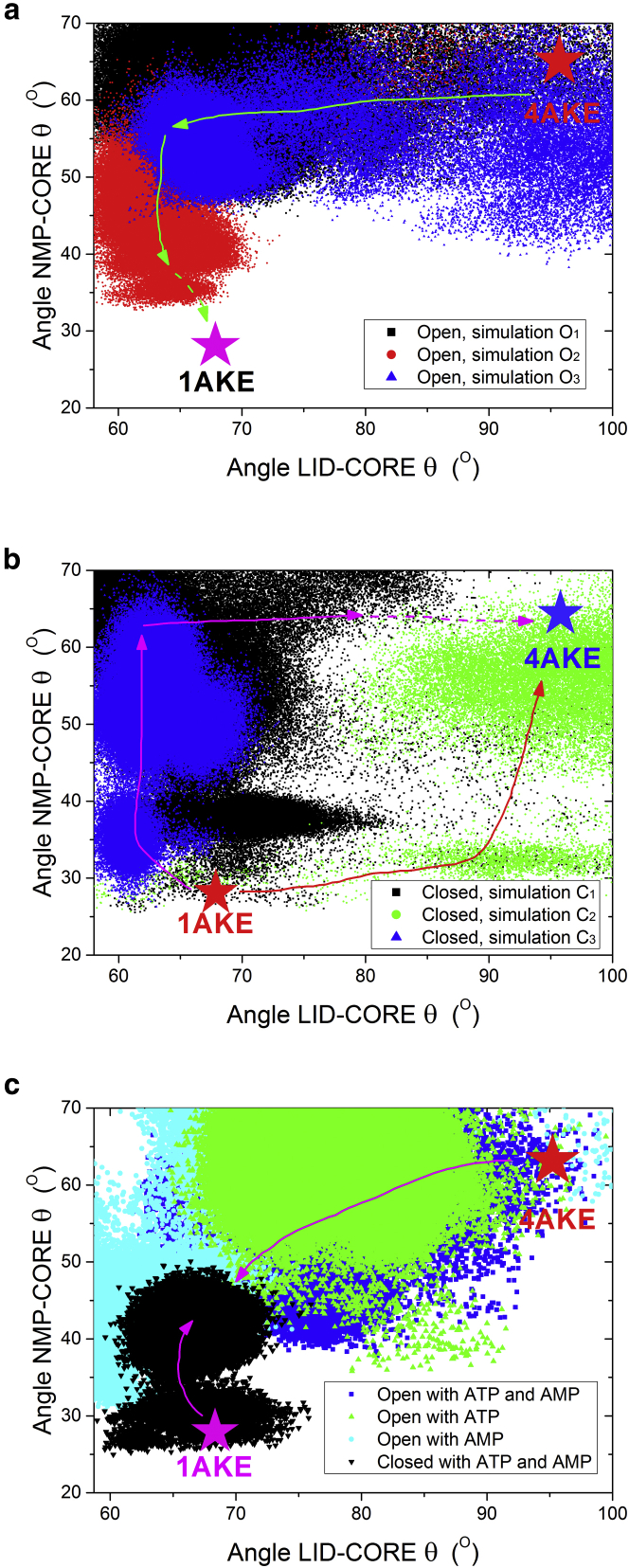
Fig. 4 shows the correlations between angles ${\theta }_1$ and ${\theta }_2$ during the simulated trajectories, which can quantify the conformational transitions in AdK. LT-MD simulations starting from the open state without ligands, see Fig. 4 a, show a significant transition in the angle of LID-CORE, ${\theta }_1$. Angle ${\theta }_1$ changes from $\sim {95}^{\circ }$ to$\sim {60}^{\circ }$, corresponding to the open and the closed state of LID domain, respectively. In contrast, the angle of NMP-CORE, ${\theta }_2$, varies from $\sim {65}^{\circ }$ to $\sim {35}^{\circ }$, corresponding to the open and semi-open state of the NMP domain, respectively (after the LID domain is closed). Fig. 4 a shows that the conformation transits as the LID domain closes first and NMP closes afterward. It should be noted that conventional MD simulation suffers insufficient sampling in current timescale, in which intermediate states and conformational transition pathways may miss out. When more independent MD simulations are performed, the complete pathways may be explored (see Fig. S13). For example, AdK also has the probability to follow another pathway that NMP closes first and then LID closes afterward.

Figure 4.

The distribution of angles LID-CORE ${\theta }_1$ and NMP-CORE ${\theta }_2$ from LT-MD simulations. (a) Starting from the open state without ligand, corresponding to simulations O₁, O₂, and O₃. The green line indicates the transition pathway that LID closed first and then NMP to close. (b) Starting from the closed state without ligand, corresponding to simulations C₁, C₂, and C₃. The red and pink lines indicate two distinctive transition pathways, one is that NMP open first and then LID to open (pink line), and the other one (red line) is in the opposite direction. (c) Starting from the open or the closed state with ligands, corresponding to simulations O-ATP-AMP, O-ATP, O-AMP, and C-ATP-AMP. The crystal structures of PDB 4AKE and PDB 1AKE are marked. The arrows illustrate the conformational transition and pathways as observed in the LT-MD simulations. (Simulation names can be found in Table S3.) To see this figure in color, go online.

Fig. 4 b shows the simulations starting from the closed state without ligands have two distinctive conformational transition pathways. The first pathway, indicated by trajectory C₁ and C₃ in Fig. 4 b (corresponding to the snapshots of Fig. 2, d and f, respectively, shows that the NMP domain transits from the closed state to semi-open and to open state, while the LID domain stays in a closed state $\left({\theta }_1\approx {60}^{\circ }\right)$. The second pathway, as shown in simulation C₂ in Fig. 4 b (corresponding to the snapshots of Fig. 2 e), is that LID may open first before NMP opens up. More independent MD simulations starting from the closed state confirmed the existence of these two transition pathways, as shown in Fig. S14.

Significantly, the simulations with bound ligands show different correlations between angles ${\theta }_1$ and ${\theta }_2$, as shown in Fig. 4 c. From trajectories starting from the closed state (bound with ATP and AMP), a distinct semi-open state of the NMP domain occurs (as indicated by the black dots in Fig. 4 c). It shows that AdK now prefers to stay in the close state, yet trajectories starting from the open (bound with ligands) could hardly reach the full close state at the 1,000 ns timescale.

Metadynamics exploration of the free energy landscapes of AdK

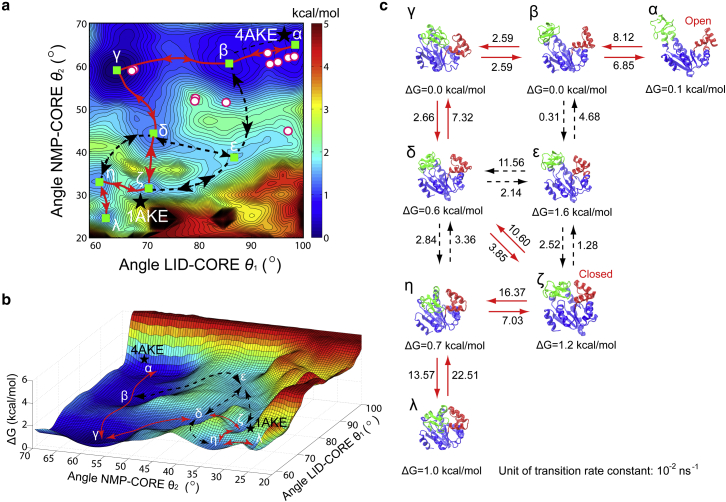
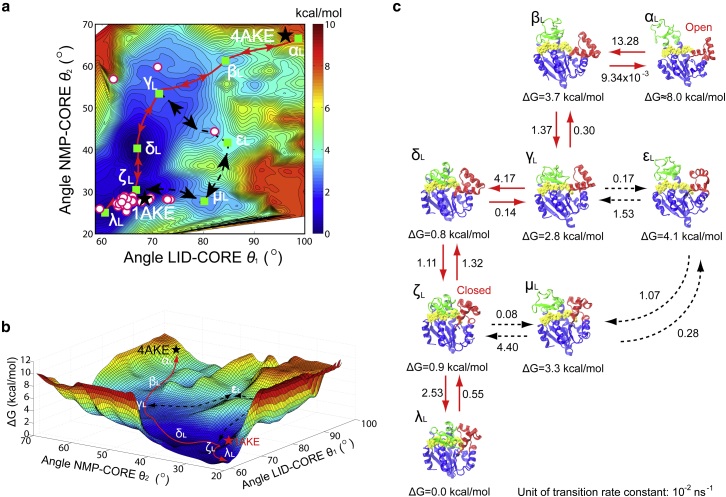
Our comprehensive LT-MD simulations show that AdK can undergo dynamic equilibrium between the open and the semi-open–semi-closed states (i.e., the LID in closed form and NMP in open or semi-open form) without the presence of ligands, whereas the introduction of ligands shifts the populations of the open and closed forms and to transit AdK into a closed state. According to the LT-MD simulations, AdK follows complex transition pathways and its conformational transitions navigate on a rugged free energy landscapes. However, regular MD simulations suffer from insufficient sampling that some of the conformations are trapped in local energy wells. The LT-MD simulations may miss crucial states and transition pathways. For example, even in our multitrajectory LT-MD simulations up to 1,000 ns timescale, AdK cannot reach the fully closed conformation state from the open state. Hence, mapping these multidimensional landscapes according to specific reaction coordinates is critically important for a molecular and quantitative insight of dynamics and the conformational transition pathways (6). We mapped the energy landscape by BE-META simulations of the AdK system (details as described in Materials and Methods and Tables S3 and S4). The states identified by BE-META simulations along the transition pathways were characterized by three CVs (angle LID-CORE ${\theta }_1$, angle NMP-CORE ${\theta }_2$, and the distance between LID and NMP $d_{LN}$, respectively), as shown in Figs. 5 and 6. Figs. S15 and S16 show that the BE-META simulations converge well while the bias potentials $-V_G^i\left(S,t\right)$ are converged to the free energy with corresponding CVs (36). The error on the free energies in metadynamics, estimated according to Marinelli et al. (36), is less than 0.5 kcal/mol. Thus the free energy errors estimated here are ∼0.5 kcal/mol.

Figure 5.

BE-META simulations of AdK without ligands. (a) A multiwell relative free energy landscape against the CVs of angles LID-CORE ${\theta }_1$ and NMP-CORE ${\theta }_2$. The state with the minimum free energy was set as the reference state, i.e., the $\gamma$ state. The contour map represents the free energy, with the scale bar in kcal/mol units. The states $\alpha$ and $\zeta$ correspond to the crystal structures of the open and closed states, respectively.$\beta$, $\gamma$, $\delta$, and $\epsilon$ indicate the intermediate states corresponding to the semi-open–semi-closed conformations, whereas the states $\eta$ and $\lambda$ are more near the closed conformations. The red line indicates the most favorable path. The dashed black lines are possible alternative pathways. The green squares represent the intermediate states. The circular symbols represent the conformational states of AdK crystal structures without ligands (see Table S1). (b) A three-dimensional plot of free energy landscapes of the conformational transitions of AdK without ligands. (c) Representative conformational transition pathways derived from the free energy landscape. The relative free energy of each state, in kcal/mol (1.0 kcal/mol equal to 1.7 k_BT with temperature 300 K), is labeled below the corresponding structures. The number above the arrows are in 10⁻² ns⁻¹ units, representing the transition rate constants between states as calculated by the Kramers’ transition state theory (see Text S3 in the Supporting Material) (88), with the diffusion coefficient $D\approx 4.47\times {10}^{-3}ra{d}^2/ns$ determined from the LT-MD simulations (89,90). To see this figure in color, go online.

Figure 6.

BE-META simulations AdK with ligands. (a) A multiwell relative free energy landscape with two CVs: angles LID-CORE ${\theta }_1$ and NMP-CORE ${\theta }_2$. The state with the minimum free energy was set as the reference state, i.e., the ${\lambda }_L$ state. The contour map represents the free energy, with the scale bar in kcal/mol units. The states ${\alpha }_L$ and ${\zeta }_L$ correspond to the crystal open and closed conformation, respectively. The states ${\beta }_L$, ${\gamma }_L$, ${\delta }_L$, ${\epsilon }_L$ and ${\mu }_L$ are the intermediate ones corresponding to the semi-open–semi-closed conformations, whereas the state ${\lambda }_L$ is a more compact closed conformation. The red lines indicated the minimum free energy paths. The dashed black lines are the possible alternative pathways. The green squares represent the intermediate states. The circular symbols represent the conformational states of AdK crystal structures with ligands (see Table S2). (b) A three-dimensional plot of free energy landscapes of the conformational transitions of AdK with ligands. (c) Representative conformational transition pathways derived from the free energy landscape. The relative free energy of each state, in kcal/mol (1.0 kcal/mol equal to 1.7 k_BT with temperature 300 K), is labeled below the corresponding structure. The number above the arrows are in 10⁻² ns⁻¹ units, representing the transition rate constants between the states as calculated by the Kramers’ transition state theory (see Text S3 in the Supporting Material) (88), with the diffusion coefficient $D\approx 5.13\times {10}^{-4}ra{d}^2/ns$ determined from the LT-MD simulations (89,90). To see this figure in color, go online.

Metadynamics of the ligand-free AdK

Fig. 5 shows the relative free energy landscape for conformational transitions of the unbound AdK, against two reaction coordinates of angles ${\theta }_1$ and ${\theta }_2$. The red line in Fig. 5 indicates the most possible pathway determined by the Metropolis Monte Carlo simulations (with the two end points set to the open and closed state, respectively). When starting from the open state (e.g., PDB 4AKE), see Fig. 5 a, the energy maps indicates that the LID domain should close through the pathway along $\alpha \leftrightarrow \beta \leftrightarrow \gamma$ (reversible in 1,000 ns timescale of LT-MD simulations), as falling in the energy valley (states $\alpha$, $\beta$, and $\gamma$ are nearly at the same free energy level). We have seen in the BE-META and LT-MD simulations that the conformation is sometimes trapped in intermediate states, where the LID domain closes and is in contact with the NMP domain while the NMP domain stays in the open and/or semi-open state (e.g., the $\gamma$ and $\delta$ configurations, respectively; see also the snapshots at 300 ns in Fig. 2 a, 160 ns in Fig. 2 b, and 200 ns in Fig. 2 c and Figs. S1–S6). After closure of the LID domain, the NMP domain can start closing through the pathway $\gamma \to \delta \to \zeta$. This transition pathway needs to climb over a few energy barriers, as shown in Fig. 5. This pathway is consistent with TEE-REX (32) and the structure-based coarse-grained model studies (19,30,31). In comparison with previous works (19,30,31), our current study has more quantitative results with atomistic details. Here we have determined not only the conformational transition pathways, but also the quantitative multidimensional free energy landscape and the critical intermediate states. There is another pathway observed in LT-MD simulations, i.e., NMP closes first and LID closes afterward when starting from open state (see the pathway $\alpha \to \beta \to \epsilon \to \zeta$, illustrated by the dashed line in Fig. 5).

According to Hammes (66), we calculate the proportion of the two pathways starting from open to closed state, i.e., LID closes first and then NMP closes afterward $\left(\alpha \to \beta \to \gamma \to \delta \to \xi \right)$ and the pathway in which NMP closes first and then LID closes afterward $\left(\alpha \to \beta \to \epsilon \to \xi \right)$

$$\frac{P_{\alpha \to \beta \to \gamma \to \delta \to \xi }}{P_{\alpha \to \beta \to \epsilon \to \xi }}=\frac{F_{\alpha \to \beta \to \gamma \to \delta \to \xi }}{F_{\alpha \to \beta \to \epsilon \to \xi }}\approx \frac{5.7}{1},$$ (1)

where $F_{\alpha \to \beta \to \gamma \to \delta \to \xi }$ and $F_{\alpha \to \beta \to \epsilon \to \xi }$ are the flux of the conformational transition through the pathway $\alpha \to \beta \to \gamma \to \delta \to \xi$ and $\alpha \to \beta \to \epsilon \to \xi$, respectively (see Text S4 in the Supporting Material). This shows that the transition of AdK mainly follows the pathway in which LID closes first and then NMP closes afterward, which is consistent with Esteban-Martin et al.’s experimental work (67). It also explains our observation in LT-MD simulations that AdK mainly follows this pathway (see Figs. 4, S13, and S14).

The crystal structures show the conformational transition pathway found by BE-META is consistent with the experiments (see the circular symbols in Fig. 5 a), that most of the crystal structures of AdK without ligands prefer to the open conformation (i.e., ${\theta }_1\approx {95}^{\circ }$ and ${\theta }_2\approx {60}^{\circ }$). Specially, there are two crystal structures (i.e., PDB 1AK2 and PDB 2AK2) that stay near the $\gamma$ state, which confirms the end point of the conformational transition pathway of $\alpha \leftrightarrow \beta \leftrightarrow \gamma$.

Metadynamics of the ligand-bound AdK

The simulations with ligands show significantly different free energy landscape (Fig. 6). The red solid line in Fig. 6 indicates the most-favored transition pathway. There is a clear gorge in the free energy landscape of ${\alpha }_L\to {\beta }_L\to {\gamma }_L\to {\delta }_L\to {\zeta }_L$, corresponding to the conformational transition from the open state to the closed state of AdK. Interestingly, the free energy in the ${\delta }_L$ state (i.e., the semi-open state of NMP) is a bit lower than that in the ${\zeta }_L$ state (i.e., the closed state). Our simulations show the free energy difference between the open and closed state with ligands is about $\Delta G_{O\to C}\approx 8.0kcal/mol$ (equal to 13.5 k_BT, corresponding to transition from ${\alpha }_L$ to ${\zeta }_L$), which is consistent with previous calculations by Brooks et al. (16). Various points on the transition pathway found by BE-META are consistent with the known crystal structures (see the circular symbols in Fig. 6 a). Most of the crystal structures of AdK with ligands stay in the closed state (i.e., ${\theta }_1\approx {65}^{\circ }$ and ${\theta }_2\approx {28}^{\circ }$). As shown in Fig. 6 a, the region around ${\theta }_1\approx {90}^{\circ }$ and ${\theta }_2\approx {30}^{\circ }$ is energetically strongly unfavorable. This suggests that AdK is unlikely to transit NMP to close first while binding with ligands (also see Fig. 4 c). There are two crystal structures found near the ${\gamma }_L$ state and one near the ${\epsilon }_L$ state, which meets the transition pathways found in this study, see Fig. 6 a.

Discussion

Rate-limiting step and domain-transition order in AdK

We show that the coordinated conformational transitions over large timescale are intrinsic property of AdK. Compared with previous MD studies at ∼100 ns timescale (22–24), our ∼1,000 ns LT-MD results have revealed reversible large-scale conformational transitions (i.e., the switch between the open to the semi-open–semi-closed states) of AdK at the 100 ns ∼800 ns timescale. LT-MD simulation results indicate that the unbound AdK undergoes rapid dynamic equilibrium between the open and semi-open–semi-closed states, which agree with experimental (10,11) and previous MD studies (22–24). It was proposed that local unfolding and folding, i.e., the cracking, lowers the activation energy barrier for conformational transition of AdK (19,29–31). Cui and co-workers (33) argued that in AdK’s transitions the cracking from primary pathways is not necessary. But, as they admitted, local unfolding over short timescale may not reflect the cracking of large conformational transitions. In our LT-MD simulations, we can clearly identify three cracking regions related to the large conformational transitions, i.e., residues 60 to 63, 110 to 120, and 160 to 175, where the secondary structures switched in 10 to 100 ns timescale (see Fig. S17). The three cracking regions found in this study are consistent with previous coarse-grained models (19,29–31). Olsson and Wolf-Watz’s experiment suggested that the unfolding and refolding of helixes α6 and α7 (see Fig. 1) is correlated to the closure of the LID domain (68). The cracking regions identified in our study, i.e., residues 110 to 120 and 160 to 175, are exactly the helixes α6 and α7 (see Fig. S17), respectively. Our study also showed that the cracking of helixes α6 and α7 is strongly correlated to the closure of LID domain, which is consistent well with Olsson and Wolf-Watz’s experiment (68). This study provides for the first time, to our knowledge, the atomic pictures of the cracking motion and its impacts on the large conformational transition of AdK.

AdK can intrinsically undergo an open to semi-open–semi-closed cycle of conformational changes on the timescale of ∼100 ns, but it did not reach a fully closed state at the timescale of a microsecond (when starting from an open structure). Our LT-MD results confirm that the LID domain is much more flexible and affinitive than the NMP domain. Given that, for enzyme, a tight mechanochemical coupling between conformational transitions and chemistry is essential; the motion of NMP domain is the rate-limiting step for AdK’s activity.

We have observed that, from the open to the closed state, AdK (in both unbound and ligand-bound states) follows the primary pathway: LID closes first and then in a coordinative fashion NMP closes afterward (see Fig. 5). This observation is consistent with Esteban-Martin et al.’s work (67) in the case of the unbound state. To experimentally verify this order of domain closure, one may do site mutations at helixes α6 and α7 to restrict their cracking motion. It might be observed that the probability of closure of NMP domain decreases because of the restricted opening of LID. In another way, one can design experiments that only allow ATP to bind with LID so that the probability of closure of the NMP domain can be increased because the ATP-induced closure of LID facilitates the closing of NMP.

Ligand-binding can induce a population-shift mechanism

Our LT-MD simulations showed that AdK can transform (at a timescale of ∼100 ns) from the open to the semi-open–semi-closed state reversibly even without ligands; this agrees well with the experiment results (2,10,11) that the transition between the open and the closed states of AdK undergo dynamic equilibrium in the absence of ligands. The simulations with ligands showed a more compact structure because of the interactions with ligands. This is consistent with the experiments (2,10,11) that the presence of ligands shifts the populations of the open/closed states and changes the transition rates.

We observed that the open state of AdK can quickly reach a few semi-open–semi-closed states (see in Fig. 5 a the open circles around states $\gamma$ and $\delta$, such as PDB 1AK2 and PDB 2AK2). Fig. 5 indicates that AdK conformation favors the open state without ligands, as observed from many crystal structures (8,9). Single-molecular FRET experiment by Henzler-Wildman et al. (2) also showed that the open state is a major population in the absence of ligand. However, another FRET experiment by Hanson et al. (10) suggested that the equilibrated conformation of AdK favors the closed state in the absence of ligands. We understand that, the two FRET experiments have different labeling positions, i.e., in the FRET experiment by Henzler-Wildman et al. (2), the dyes were tagged to residues Lys145 and Ile52 (which are located at the LID and NMP domains, respectively), whereas in the experiment by Hanson et al. (10), the dyes were tagged to residues Ala127 and Ala194 (which are located at the LID and CORE domains, respectively). Therefore, Henzler-Wildman et al.’s experiment (2), measuring the motion of LID and NMP domains, showed the open state (corresponding to $\alpha$ or $\beta$ states) was more favorable; but the experiments by Hanson et al.’s (10), measuring the motion of LID domain alone, showed the close state (corresponding to $\gamma$ state) was more favorable.

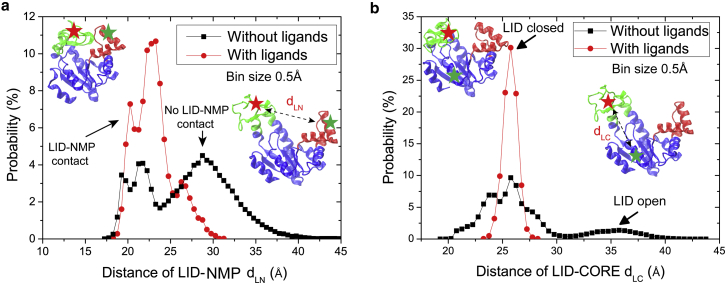
Fig. 7 shows the distribution of the distance d_LN and d_LC, which are corresponding to the distance between the dyes in FRET experiment by Henzler-Wildman et al. (2) and Hanson et al. (10), respectively. Provided with no ligand, the LID-NMP d_LN distribution significantly showed two major states, i.e., with and without LID-NMP contact. This result is consistent with the finding of Henzler-Wildman et al.’s FRET experiment (2). That is, both of the two states sampled to significant fractions even in the absence of any ligand, in which the fraction of closed-like state is smaller than that of open-like state. While binding with ligands, the enzyme is confined to the closed state with a more compact structure. However, when the dyes label changed to the LID and CORE domains (i.e., in Hanson et al.’s FRET experiment (10)), the LID-CORE d_LC with a bias-weighted preference for LID was closed to the CORE domain (see Fig. 7 b). Obviously, the AdK in these states could still be in the open form because of the opening of the NMP domain. Once bound with ligands, d_LC is confined to the closed state with a more compact structure. The above results demonstrate the population shift mechanism. It also solves the puzzle raised by the different results in the above two single-molecular FRET experiments (2,10), which is caused by the different labeling position. Our simulation results show that in the intermediate states (e.g., states $\beta$, $\gamma$, and $\delta$ in Fig. 5) LID closes to contact with NMP/CORE and causes the decreasing of the distance d_LN and d_LC. Consequently, the closed state indicated by FRET experiment is likely a semi-open–semi-closed conformation, but not the fully closed state of the AdK’s LID and NMP domains. As argued by Potoyan et al. (34), the conformation state of AdK near the open state may still retain many LID-NMP contacts, suggesting that the free energy basin of the closed state is larger than expected. Our BE-META dynamics results show that AdK has this type of free energy landscape, e.g., in Fig. 5 a, the γ and δ states correspond to the intermediate states that the LID domain has contacts with NMP while NMP is open or semi-open. Now we prove that there is a discrepancy in the relative populations of the open and closed state of the unbound AdK, as observed in FRET experiments (2,10) as well as predicted by other simulations (34).

Figure 7.

The distribution of distance (a) d_LN between the LID and NMP domains and (b) d_LC between the LID and CORE domains based on LT-MD simulations. The insets illustrate the corresponding conformations. The stars illustrate the labeling positions in single-molecule FRET experiments. The bin size of the distance is 0.5 Å. To see this figure in color, go online.

Intermediate states critical for the conformational transitions

Recently, Esteban-Martin et al. (67) exploited the shape information encoded in residual dipolar couplings via steric alignment by NMR. They found experimental evidence that there is a closed-like state in the absence of substrate with high probability along the opening/closing pathway of AdK. From the LT-MD simulations, we observed a few intermediate conformational states: the LID domain is closing to the CORE domain and has contact with the NMP domain, while NMP is in open/semi-open states (such as the snapshots at 300 ns in Fig. 2 a, 160 ns in Fig. 2 b, and 200 ns in Fig. 2 c; see also Figs. S1–S3). These intermediate states are also exclusively identified in the BE-META simulations, e.g., the γ and δ states in landscape of Fig. 5 and the ${\gamma }_L$ and ${\delta }_L$ states in Fig. 6 (also see Fig. S18). These intermediate conformations suggest the existence of the closed-like state along the transition pathway, as identified by Esteban-Martin et al. (67), and by the crystal structures of PDB 1AK2 and PDB 2AK2 around γ state (see Fig. 5 a and Table S1), and PDB 1DVR and PDB 2C9Y around ${\gamma }_L$ state (see Fig. 6 a and Table S2).

Dynamically these intermediate states are the key steps of motion of the NMP domain, i.e., the NMP domain moves from the open toward the closed state after forming the contact with the LID domain. We conclude that transiting through the key intermediate states is critical for AdK’s operating mechanism. These intermediates tell us not only the domains’ transition order, but also the stepwise paths how NMP motion is rate-limiting and how two binding sites cooperate with each other.

Multiwell free energy landscape allows conformational selection and induced fit operations coupling the conformational transitions

A few previous studies (16,24,34,35) have constructed one-dimensional free energy landscape of AdK’s dynamic changes. However, the one-dimensional reaction coordinate is insufficient to capture the conformational changes of AdK, where multidomain motions and two binding site activation are coupled. For example, as shown in the insets of Fig. S18, a one-dimensional free energy landscape against the distance of LID-NMP d_LN does indicate the double-well pattern and shifted population upon ligand binding (collectively averaging all possible states regardless the collective variables of θ₁, and θ₂). But once we construct the multidimensional free energy landscape by simultaneously searching and mapping the dynamic angles θ₁, and θ₂ and distance between LID, CORE, and NMP (i.e., the distance d_LN is well related to the single-molecular FRET experiment (10)), the three-dimensional free-energy landscapes showed more complex but complete conformational transition pathways (see Fig. S18), in comparison with the one- and two-dimensional landscapes (i.e., Figs. 5 and 6).

Our simulation of AdK without ligands indicates that the open $\leftrightarrow$ closed free energy difference is only a few kcal/mol (in the range of 1∼2 k_BT, which agrees with previous estimations (16,24,34,35)). Most significantly, the free energy landscape found from our study is in a good quantitative agreement with the single-molecular FRET and NMR spin relaxation experiments (which reported fast collective domain motions that take place on a nanosecond timescale). A relatively rare event of attaining catalytically competent closed conformation (e.g., consistent with x-ray structure for the closed state) on a microsecond timescale is also captured (2,69). From the biological perspective, the relatively small free energy difference between conformations can facilitate fine control of transitions by environmental perturbations and signaling (34). The low-barrier free energy landscape of ligand-free AdK suggests that the transitions between the open and the closed states of AdK can undergo dynamic equilibrium even without the induction of ligand, as known from some experiments (10,11). Even in the intermediate states in which LID-NMP form contacts that last for a long timescale, the typical conformations are still structurally similar to the open state. These suggest a transition state for domain opening (see Fig. S1) or domain closing (see Fig. S2) may occur.

Furthermore, the free energy landscape shows us that open-like conformations are heavily populated and transit to the closed states in the presence of ligands (see Figs. 5, 6, and 7, strongly indicating that the conformational population shifted by the interaction with ligands). There is no clear minimum toward the ligand-bound open state (see the ${\alpha }_L$ state in Fig. 6 a), indicating that the ligand does not bind effectively to a fully open conformation of AdK, but somewhere later along the pathway. This mechanism was also predicted by Arora and Brooks (16). It was suggested that the multiwell free energy landscape of free enzyme supports a conformational selection/population shift operation (70). However, it was proposed that enzymes with LID-gated active sites should operate by an induced fit mechanism instead of conformational selection (70). Although AdK has a multiwell energy landscape and the closed conformation preexists, the fully closed state of AdK cannot capture the ligands because the closure of LID/NMP prevents ligands from binding to their active sites. Hammes et al. (66) proposed that both of the conformational selection and induced fit operations may occur, depending on the ligand and protein concentrations. As shown in Fig. 5, there are a few of intermediate states that the LID/NMP domains are in semi-open–semi-closed conformations (such as the $\beta$, $\gamma$, $\delta$, and $\epsilon$ states in Fig. 5). The semi-open–semi-closed intermediate states do not rule out the binding of ligands with these states. Once the ligand binds to these accessible intermediate states, it should change the shape of the free energy landscape of AdK toward the fully closed conformations. Consequently, mechanism of ligand binding to AdK could involve both conformational selection and induced fit operations. When the ligand is in low concentration, the conformational selection will dominate, because the binding of ligand is in low stochastic frequency compared with the conformational transition of protein. In contrast, the mechanism will switch to be dominated by induced fit at high ligand concentration (66). Accordingly, our findings suggest a plausible perspective for a hybrid of conformational selection and induced fit operations of ligand binding to AdK. This mechanism was once suggested by Ådén et al. (65) for the binding of ATP to AdK. It was also found in other systems, e.g., the dihydrofolate reductase and flavodoxin (66).

Conclusions

We applied extensive long timescale explicit MD and BE-META simulations to explore the pathways and free energy landscape of dynamic changes in AdK. We have comprehensively determined at atomistic level the transition pathways and intermediate states of AdK in the presence and absence of ligands; most significantly, we quantitatively mapped the free energy landscape of AdK to its dynamic transitions. In AdK, there is chronological operation of the functional domains. Specifically the free energy landscape reveals that in the ligand-free state, we identified the low-energy barriers to intermediate conformational states that facilitate the transitions of AdK by environmental perturbations and signaling. Once bound with a ligand, the conformational population of AdK prefers to shift to the closed form. These observations help to establish insightful pictures of intrinsic dynamics of AdK, and rationalize the complex conformational transitions of AdK in regulating its enzymatic functions. We have suggested a perspective for a hybrid of conformational selection and induced fit operations of ligand binding to AdK. This methodology can also extend to apply on other enzymes and biomolecular systems.

For understanding the regulation in protein functions, researchers have been bypassing the static structures interpretation and focusing more on dynamics, flexibility, and fluctuations (14). We show in this article AdK functionalities are accomplished via, to our knowledge, novel dynamics (e.g., a hybrid of conformational selection and induced fit operations). This suggests that a dynamics-based strategy to investigate the design of proteins and ligands systems is critically important. It is increasingly accepted that conformational couplings are intrinsic properties for all proteins in action (71). A rational design of ligands targeting the population shift, conformational transitions, fluctuations, and flexibility of protein (17,72) shall be core practice for development of enzymes and other biomolecular systems.

Author Contributions

D.C.L., M.S.L., and B.H.J. conceived and designed the research; D.C.L. and M.S.L. performed the experiments; D.C.L., M.S.L., and B.H.J. analyzed the data; and D.C.L., M.S.L., and B.H.J. wrote the article.

Editor: Gerhard Hummer

Supporting Citations

References (73–87) appear in the Supporting Material.