Behavior of the Gibbs Sampler When Conditional Distributions Are Potentially Incompatible

Abstract

The Gibbs sampler has been used extensively in the statistics literature. It relies on iteratively sampling from a set of compatible conditional distributions and the sampler is known to converge to a unique invariant joint distribution. However, the Gibbs sampler behaves rather differently when the conditional distributions are not compatible. Such applications have seen increasing use in areas such as multiple imputation. In this paper, we demonstrate that what a Gibbs sampler converges to is a function of the order of the sampling scheme. Besides providing the mathematical background of this behavior, we also explain how that happens through a thorough analysis of the examples.

1. INTRDUCTION

The Gibbs sampler is, if not singularly, one of the most prominent Markov chain Monte Carlo (MCMC)-based methods. Partly because of its conceptual simplicity and elegance in implementation, the Gibbs sampler has been increasingly used across a very broad range of subject areas including bioinformatics and spatial analysis. While its root dates back to earlier work (e.g., [1]), the popularity of the Gibbs sampling is commonly credited to Geman and Geman [2], in which the algorithm was used as a tool for image processing. Its use in statistics, especially Bayesian analysis, has since grown very rapidly [3–5]. For a quick introduction of the algorithm, see Casella and George [6].

One of the recent developments of the Gibbs sampler is in its application to potentially incompatible conditional-specified distributions (PICSD) [7, 8]. When statistical models involve high-dimensional data, it is often easier to specify conditional distributions instead of the entire joint distributions. However, the approach of specifying a conditional distribution has the risk of not forming a compatible joint model. Consider a system of d discrete random variables X = {X₁, X₂, ⋯, X_d}, whose fully conditional model is specified by F = {f₁, f₂, ⋯, f_d}, where $f_k\equiv f_{x_k|x_k^c}=f(x_k|x_1,\cdots ,x_{k-1},x_{k+1},\cdots ,x_d)$. If the conditional models are individually specified, then there may not exist a joint distribution that will give rise to the specified set of conditional distributions. In such a case, we call F incompatible.

The study of PICSD is closely related to the Gibbs sampler because the latter relies on iteratively drawing samples from F to form a Markov chain. Under mild conditions, the Markov chain converges to the desired joint distribution, if F is compatible. However, if F is not compatible, then the Gibbs sampler could exhibit erratic behavior [9].

In this paper, our goal is to demonstrate the behavior of the Gibbs sampler (or the pseudo Gibbs sampler as it is not a true Gibbs sampler in the traditional sense of presumed compatible conditional distributions) for PICSD. By using several simple examples, we show mathematically that what a Gibbs sampler converges to is a function of the order of the sampling scheme in the Gibbs sampler. Furthermore, we show that if we follow a random order in sampling conditional distributions at each iteration—i.e., using a random-scan Gibbs sampler [10]—then the Gibbs sampling will lead to a mixture of the joint distributions formed by each combination of fixed-order (or more formally, fixed-scan) when d = 2 but the result is not true when d > 2. This result is a refinement of a conjecture put forward in Liu [11].

Two recent developments in the statistical and machine-learning literature underscore the importance of the current work. The first is in the application of the Gibbs sampler to a dependency network, which is a type of generalized graphical model specified by conditional probability distributions [7]. One approach to learning a dependency network is to first specify individual conditional models and then apply a (pseudo) Gibbs sampler to estimate the joint model. Heckerman et al. [7] acknowledged the possibility of incompatible conditional models but argued that when the sample size is large, the degree of incompatibility will not be substantial and the Gibbs sampler is still applicable. Yet another example is the use of the fully conditional specification for multiple imputation of missing data [12, 13]. The method, which is also called multiple imputation by chained equations (MICE), makes use of a Gibbs sampler or other MCMC-based methods that operate on a set of conditionally specified models. For each variable with a missing value, an imputed value is created under an individual conditional-regression model. This kind of procedure was viewed as combining the best features of many currently available multiple imputation approaches [14]. Due to its flexibility over compatible multivariate-imputation models [15] and ability to handle different variable types (continuous, binary, and categorical) the MICE has gained acceptance for its practical treatment of missing data, especially in high-dimensional data sets [16]. Popular as it is, the MICE has the limitation of potentially encountering incompatible conditional-regression models and it has been shown that an incompatible imputation model can lead to biased estimates from imputed data [17]. So far, very little theory has been developed in supporting the use of MICE [18]. A better understanding of the theoretical properties of applying the Gibbs sampler to PICSD could lead to important refinements of these imputation methods in practice.

The article is organized as follows: First, we provide basic background to the Gibbs chain and Gibbs sampler and define the scan order of a Gibbs sampler. In Section 3, we offer several analytic results concerning the stationary distributions of the Gibbs sampler under different scan patterns and a counter-example to a surmise about the Gibbs sampler under a random order of scan pattern. Section 4 describes two simple examples to numerically demonstrate the convergence behavior of a Gibbs sampler as a function of scan order, both by applying matrix algebra to the transition kernel as well as using MCMC-based computation. Finally in Section 5 we provide a brief discussion.

2. GIBBS CHAIN AND GIBBS SAMPLER

Continuing the notation in the previous section, let a = (a₁, a₂, ⋯, a_d) denote a permutation of {1, 2, ⋯, d}, x = {x₁, x₂, ⋯, x_d} denote a realization of X with x_k ∈ {1, 2, ⋯, C_k}, where C_k is the number of categories of the k^th variable. Thus, x_a ≡ (x_a1, x_a2, ⋯, x_ad) is a realization of X defined in the order of a. We also denote ${\mathit{x}}_{a_k}^c=(x_{a_1},\cdots ,x_{a_{k-1}},x_{a_{k+1}},\cdots ,x_{a_d})$, the relative complement of x_ak with respect to x_a.

For a specified F, the associated fixed (systemic)-scan Gibbs chain governed by a scan pattern a can be implemented as follows:

1. Pick an arbitrary starting vector ${\mathit{x}}_{\mathit{a}}^{(0)}=(x_{a_1}^{(0)},x_{a_2}^{(0)},\cdots ,x_{a_d}^{(0)})$.

2. On the t^th cycle, successively draw from the full conditional distributions according to scan pattern a = (a₁, a₂, ⋯, a_d) as follows:

   $$X_{a_1}^{(td+1)}~f_{a_1}\left(x_{a_1}\right|{({\mathit{x}}_{a_1}^{(td)})}^c)$$

   $$\begin{array}{c}\hfill X_{a_2}^{(td+2)}~f_{a_2}\left(x_{a_2}\right|{({\mathit{x}}_{a_2}^{(td+1)})}^c)\hfill \\ \hfill ⋮\hfill \\ \hfill X_{a_{d-1}}^{(td+d-1)}~f_{a_{d-1}}\left(x_{a_{d-1}}\right|{({\mathit{x}}_{a_{d-1}}^{(td+d-2)})}^c)\hfill \end{array}$$

   $$X_{a_d}^{((t+1)d)}~f_{a_d}\left(x_{a_d}\right|{({\mathit{x}}_{a_d}^{((t+1)d-1)})}^c)$$

The series ${\mathit{x}}_{\mathit{a}}^{(0)},{\mathit{x}}_{\mathit{a}}^{(1)},{\mathit{x}}_{\mathit{a}}^{(2)},\cdots ,{\mathit{x}}_{\mathit{a}}^{(s)}$, ⋯ obtained by a single draw (iteration) is called a realization of Gibbs chain defined by F with scan pattern a; and the series ${\mathit{x}}_{\mathit{a}}^{(0)},{\mathit{x}}_{\mathit{a}}^{(d)},{\mathit{x}}_{\mathit{a}}^{(2d)},\cdots ,{\mathit{x}}_{\mathit{a}}^{(td)}$, ⋯ obtained by a single cycle is a realization of the associated Gibbs sampler. For example, let = {X₁, X₂, X₃, X₄}, a = (2, 4, 1, 3), and given initial value ${\mathit{x}}_{\mathit{a}}^{(0)}=(x_2^{(0)},x_4^{(0)},x_1^{(0)},x_3^{(0)})$, the Gibbs chain in cycle 1 performs the following draws and produces the corresponding states:

$$X_2^{(1)}~f_2\left(x_2\right|X_4=x_4^{(0)},X_1=x_1^{(0)},X_3=x_3^{(0)}),{\mathit{x}}_{\mathit{a}}^{(1)}=(x_2^{(1)},x_4^{(0)},x_1^{(0)},x_3^{(0)});$$

$$X_4^{(2)}~f_4\left(x_4\right|X_2=x_2^{(1)},X_1=x_1^{(0)},X_3=x_3^{(0)}),{\mathit{x}}_{\mathit{a}}^{(2)}=(x_2^{(1)},x_4^{(2)},x_1^{(0)},x_3^{(0)});$$

$$X_1^{(3)}~f_1\left(x_1\right|X_2=x_2^{(1)},X_4=x_4^{(2)},X_3=x_3^{(0)}),{\mathit{x}}_{\mathit{a}}^{(3)}=(x_2^{(1)},x_4^{(2)},x_1^{(3)},x_3^{(0)});\text{and}$$

$$X_3^{(4)}~f_3\left(x_3\right|X_2=x_2^{(1)},X_4=x_4^{(2)},X_1=x_1^{(3)}),{\mathit{x}}_{\mathit{a}}^{(3)}=(x_2^{(1)},x_4^{(2)},x_1^{(3)},x_3^{(4)}).$$

In this example, the series ${\mathit{x}}_{\mathit{a}}^{(0)},{\mathit{x}}_{\mathit{a}}^{(4)},{\mathit{x}}_{\mathit{a}}^{(8)}(=(x_2^{(5)},x_4^{(6)},x_1^{(7)},x_3^{(8)}\left)\right)$, ⋯, is the realization of Gibbs sampler defined by F with scan pattern a.

We can also express a Gibbs sampler of random scan order as a Gibbs chain. Let r = {r₁, r₂, ⋯, r_d} be the set of selection probabilities, where r_k > 0 is the probability of visiting a conditional f_k, and ${\sum }_{k=1}^d{r}_k=1$. The random-scan Gibbs sampler can be stated as follows [19]:

1. Pick an arbitrary starting vector ${\mathit{x}}^{(0)}=(x_1^{(0)},x_2^{(0)},\cdots ,x_d^{(0)})$.

2. At the s^th iteration, s = 1, 2, ⋯,

   1. Randomly choose k ∈ {1,2, ⋯, d} with probability r_k;
   2. $X_k^{(s)}~f_k\left(x_k\right|{({\mathit{x}}_k^{(s-1)})}^c)$

3. Repeat step 2 until a convergence criterion is reached.

Example 1

Consider the following bivariate 2 × 2 joint distribution π and for (X₁, X₂) defined on the domain {1, 2}, with its corresponding conditional distributions f₁ (x₁|x₂) and f₂ (x₂|x₁) [20, page 242]:

$$\pi =\frac{1}{10}\left[\begin{array}{cc}\hfill 1\hfill & \hfill 2\hfill \\ \hfill 3\hfill & \hfill 4\hfill \end{array}\right],\text{and}{f}_1=\frac{1}{12}\left[\begin{array}{cc}\hfill 3\hfill & \hfill 4\hfill \\ \hfill 9\hfill & \hfill 8\hfill \end{array}\right],f_2=\frac{1}{21}\left[\begin{array}{cc}\hfill 7\hfill & \hfill 14\hfill \\ \hfill 9\hfill & \hfill 12\hfill \end{array}\right].$$

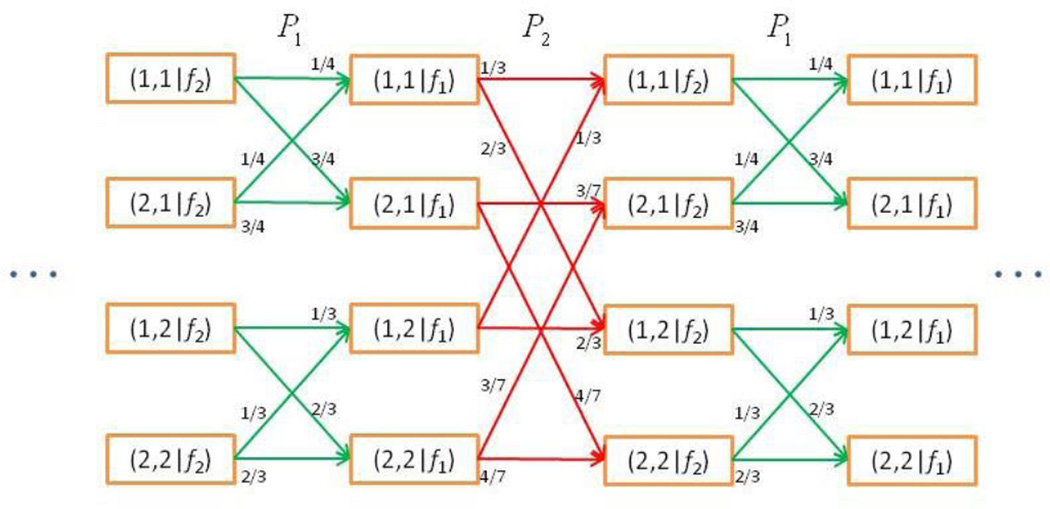
There are 4 possible states, (1, 1), (1, 2), (2, 1), and (2, 2) for the Gibbs chain. The transition from one state to another is governed by the conditional matrices f₁ and f₂ as shown in Figure 1. As a shorthand, we denote an entry in the matrix as f₁ (·,·); e.g. f₁ (1,2) = 1/3. In order to keep track of the scan order, we denote the state in the Gibbs chain as (x^(s)|f_k), if the current state x^(s) at iteration s is the result of drawing from the conditional f_k. To fix ideas, we use a fixed-scan Gibbs sampler with a = (1,2) and the conditional distributions {f₁, f₂}. In such case, the realization of this Gibbs sampler is the collection of states {(x^(2t)|f₂)|t = 1,2, ⋯}.

Figure 1.

Transition probabilities of the Gibbs chain in Example 1.

The local transition probability P_ak [21, page 71] for two successive states of Gibbs chain, (x^(s−1)|f_ak−1) and (x^(s)|f_ak), can be defined by

$$P_{a_k}({\mathit{x}}^{(s-1)},{\mathit{x}}^{(s)})=\{\begin{array}{cc}\hfill f_{a_k}\left({\mathit{x}}^{(s)}\right),\hfill & \hfill \text{if}{({\mathit{x}}_{a_k}^{(s)})}^c={({\mathit{x}}_{a_k}^{(s-1)})}^c;\hfill \\ \hfill 0,\hfill & \hfill \text{otherwise}.\hfill \end{array}$$

For example, as shown in Figure 1, the local transition probability from (x^(2t) = (1,1)|f₂) to (x^(2t+1) = (1,1)|f₁) is f₁ (1,1) = 1/4, and (x^(2t) = (1,1)|f₂) to (x^(2t+1) = (1,2)|f₁) is 0.

By arranging the state in lexicographical order such that the first index changes the fastest and the last index the slowest (as shown in Figure 1), a transition probability matrix T_ak can be constructed according to local transition probability P_ak. In Example 1, the transition probability matrices T₁ and T₂ that correspond respectively to matrices P₁, and P₂:

$$T_1=\frac{1}{12}\left[\begin{array}{cccc}\hfill 3\hfill & \hfill 9\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 3\hfill & \hfill 9\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 4\hfill & \hfill 8\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 4\hfill & \hfill 8\hfill \end{array}\right]\text{and}{T}_2=\frac{1}{21}\left[\begin{array}{cccc}\hfill 7\hfill & \hfill 0\hfill & \hfill 14\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 9\hfill & \hfill 0\hfill & \hfill 12\hfill \\ \hfill 7\hfill & \hfill 0\hfill & \hfill 14\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 9\hfill & \hfill 0\hfill & \hfill 12\hfill \end{array}\right].$$

The matrices T₁ and T₂ have two pairs of identical rows and are idempotent but not irreducible.

As the above example illustrates, the local transition probability matrices defined by the given conditional distributions are in general not identical. Thus a Gibbs chain implemented using either fixed or random scan order is not homogeneous. However, if one defines a surrogate transition probability matrix T_a ≡ T_a1T_a2T_a3 ⋯ T_ad, then a homogeneous chain with transition matrix T_a can be formed for the scan pattern a = (a₁, a₂, ⋯, a_d) [21]. In other words, for a collection of full conditional distributions F and a scan pattern a the fixed-scan Gibbs sampler is a homogeneous Markov chain with transition matrix T_a. Analogously, a random-scan Gibbs sampler with selection probability r = (r₁, r₂, ⋯, r_d) can be also transferred to a homogeneous Markov chain by defining $T_{\mathit{r}}\equiv {\sum }_{k=1}^d{r}_k{T}_k$ as the surrogate transition probability matrix [21]. Their corresponding stationary distributions π_a and π_r can be directly computed (under a mild condition) respectively by evaluating $\underset{m\to \infty }{\text{lim}}{(T_{\mathit{a}})}^m={\mathbf{1}}_{\mathbf{C}}{\pi }_{\mathit{a}}^T$ and $\underset{m\to \infty }{\text{lim}}{(T_{\mathit{r}})}^m={\mathbf{1}}_{\mathbf{C}}{\pi }_{\mathit{r}}^T$, where $\mathbf{C}={\prod }_{k=1}^d{C}_k$, and 1_C is a C-dimensional vector of 1’s [22].

3. SOME ANALYTIC RESULTS

In this section, we offer several general results regarding the behaviors of the fixed-scan and the random-scan Gibbs sampler for discrete variables in which the transition matrices are finite. For these results, it is not necessary to assume compatibility, unless stated otherwise. Besides providing theoretical underpinning to the previous illustrative examples, the results here allow a closer look at the mechanisms through which incompatibility impacts the behaviors of the different Gibbs sampling schemes. Note that these results are special cases that can be derived from more general theories for Markov chains, but for our purpose, focusing on the special case of discrete variables and scan patterns makes it easier to examine the dynamics of convergence. General results regarding convergence of Markov chains can be found elsewhere [5, 24]. All of the proofs of the following results are included in the Appendix.

Theorem 1

If F is positive (f_k > 0, ∀ k) then the Gibbs sampler, either fixed-scan with a scan pattern a or random scan with selection probability r > 0, converges to a unique stationary distribution π_a and π_r respectively.

Note that Theorem 1 does not require F to be compatible. The result assures that when F is positive—a stronger condition than F being non-negative—any scan pattern can have one and only one stationary distribution. Furthermore, the transition for any fixed-scan pattern is governed by the following theorem:

Theorem 2

If F is positive then for each state set, (x₁, x₂, ⋯, x_d|f_ak), k = 1, ⋯, d, of the Gibbs chain with scan pattern a = (a₁, a₂, ⋯, a_d) has exactly one stationary distribution π_ak. In particular, ${\pi }_{a_1}^T={\pi }_{a_d}^T{T}_{a_1}$ and ${\pi }_{a_k}^T={\pi }_{a_{k-1}}^T{T}_{a_k}$, k = 2, ⋯, d, and π_ad = π_a.

A direct consequence of Theorem 2 is that for any fixed-scan pattern, one of the specified conditional distributions in F can always be derived from its stationary distribution. This is summarized in the following corollary:

Corollary 1

If F is positive then the stationary distribution π_a of the Gibbs sampler has f_ad as one of its conditional distributions for the scan pattern a = (a₁, a₂, ⋯, a_d), i.e., π_a (x_ad|x_a1, x_a2, ⋯, x_ad−1) = f_ad.

When F is compatible, all scan patterns converge to the same joint distribution. The following theorem provides a formal statement.

Theorem 3

Given F is positive. F is compatible if and only if there exists a unique joint distribution π with either π_a = π, ∀ a or π_r = π, ∀ r. Furthermore, π is the joint distribution characterized by F.

An interesting observation about the random scan is that it forms a mixture of the fixed-scan patterns only for d = 2. We state the Corollary for the case d = 2 and give a counter-example for d = 3.

Corollary 2

If F > 0 and d = 2 then π_r, r = (r, 1 − r), is formed by the convex combination of π_{a2 = (2,1)} and π_{a1 = (1,2)}; i.e., for all r ∈ [0, 1], π_r = (1 − r) π_a1 + rπ_a2.

A three-dimensional counter example to Corollary 2 for the case d = 3 is presented in Table 1. In this example, F = {f₁, f₂, ⋯, f₃} is positive but not compatible. There are a total of six scan patterns and for each scan pattern, the solution to which the individual Gibbs sampler converges (using matrix multiplication) is shown as a row in Table 1. Convergence is defined here as all cell-wise differences between estimates from two consecutive iterations to be less than 0.5 × 10⁻⁴. The average of all six fixed-scan Gibbs sampler $\overline{\pi }=\frac{1}{6}{\sum }_{i=1}^6{\pi }_{{\mathit{a}}_i}$ is provided, as well as a reference. In order to solve for a non-negative linear combination (mixture) of the fixed-scan distributions,

$${\pi }_{{\mathit{r}}_0}={\sum }_{i=1}^6{c}_i{\pi }_{{\mathit{a}}_i}$$ (1)

where ${\mathit{r}}_0=(\frac{1}{3},\frac{1}{3},\frac{1}{3})$, we treated equation (1) as a system of linear equations and solved for c = (c_i), i = 1, ⋯, 6. As it turned out, our result indicated that there was no solution that satisfied c > 0. This observation led us to believe that the surmise [11] that the stationary distribution for a random-scan Gibbs sampler is a mixture of the stationary distributions for all systematic scan Gibbs samplers is not true in general. It only holds for d = 2.

Table 1.

A three-dimensional counter example for Corollary 2.

	(1,1,1)	(2,1,1)	(1,2,1)	(2,2,1)	(1,1,2)	(2,1,2)	(1,2,2)	(2,2,2)
f1	0.1	0.9	0.2	0.8	0.3	0.7	0.4	0.6
f2	0.5	0.6	0.5	0.4	0.7	0.8	0.3	0.2
f3	0.9	0.1	0.1	0.9	0.1	0.9	0.9	0.1
πa1 = (2,3,1)	0.0199	0.1795	0.0411	0.1646	0.1484	0.3462	0.0401	0.0602
πa2 = (3,1,2)	0.0305	0.2064	0.0305	0.1376	0.1319	0.3251	0.0565	0.0813
πa3 = (1,2,3)	0.1462	0.0532	0.0087	0.1970	0.0162	0.4784	0.0784	0.0219
πa4 = (3,2,1)	0.0228	0.2050	0.0355	0.1421	0.1399	0.3263	0.0513	0.0770
πa5 = (1,3,2)	0.0775	0.1502	0.0775	0.1002	0.0661	0.4001	0.0283	0.1000
πa6 = (2,1,3)	0.1464	0.0531	0.0087	0.1972	0.0163	0.4782	0.0782	0.0219
π̄	0.0739	0.1412	0.0337	0.1565	0.0865	0.3924	0.0555	0.0604
${\pi }_{{\mathit{r}}_0=(\frac{1}{3},\frac{1}{3},\frac{1}{3})}$	0.0728	0.1406	0.0331	0.1532	0.0873	0.3944	0.0575	0.0613

4. NUMERICL EXAMPLES

We illustrate the mathematical results using two numerical examples. In Example 1, the transition matrices for fixed- and random-scans are respectively T_a1 = T₁T₂ for a₁ = (1,2) and T_a2 = T₂T₁ for a₂ = (2,1) and T_r = (T₁ + T₂)/2. Table 2 directly compares the joint distributions obtained from the following computations: (i) direct MCMC Gibbs sampler for the only two possible fixed-scan patterns a₁ = (1,2) and a₂ = (2,1); (ii) direct MCMC Gibbs sampler for random-scan patterns with the following selection probabilities: ${\mathit{r}}_0=\frac{1}{2}(1,1)$; ${\mathit{r}}_1=\frac{1}{3}(1,2)$, and ${\mathit{r}}_2=\frac{1}{3}(2,1)$, and (iii) matrix multiplication using (T_a)^m and (T_r)^m with power m. To achieve numerical convergence, we used the first 5,000 cycles as burn-in and the subsequent 1,000,000 cycles for sampling for both (i) and (ii). And the smallest m ∈ {2^k|k = 0,1,2,⋯} such that all cell-wise differences between estimates from two consecutive iterations to be less than 0.5 × 10⁻⁴ is adopted for (iii).

Table 2.

Joint distributiuons produced by various Gibbs samplers for Example 1.

	(1,1)	(2,1)	(1,2)	(2,2)
π	0.1	0.3	0.2	0.4
a1 = (1,2)	0.1002	0.3002	0.2000	0.3997
a1 = (1,2)	0.0998	0.3004	0.1999	0.4000
${\mathit{r}}_0=\frac{1}{2}(1,1)$	0.1007	0.2998	0.2000	0.3995
πa1(m = 4)	0.1000	0.3000	0.2000	0.4000
πa2(m = 4)	0.1000	0.3000	0.2000	0.4000
πr0(m = 32)	0.1000	0.3000	0.2000	0.4000
πr1(m = 32)	0.1000	0.3000	0.2000	0.4000
πr2(m = 32)	0.1000	0.3000	0.2000	0.4000

As expected, both the fixed-scan, regardless of scan order, and the random-scan Gibbs samplers numerically converge to the same joint distribution. Table 2 also demonstrates that direct matrix multiplication of the transition probabilities produces rapid convergence even for a small m and different values of r. However, we also observed that if r was heavily imbalanced, it took many more iterations to achieve numerical convergence (not shown). For example, if $\mathit{r}=(\frac{1}{10},\frac{9}{10})$, it took m > 120 to achieve the same numerical convergence (up to 4 decimal places).

Example 2

(Incompatible conditional distributions). Consider a pair of 2 × 2 conditional distributions f₁ (x₁|x₂) and f₂ (x₂|x₁) defined on the domain {1, 2} as follows [20, page 242]:

$$f_1=\frac{1}{12}\left[\begin{array}{cc}\hfill 3\hfill & \hfill 4\hfill \\ \hfill 9\hfill & \hfill 8\hfill \end{array}\right]\text{and}{f}_2=\frac{1}{30}\left[\begin{array}{cc}\hfill 10\hfill & \hfill 20\hfill \\ \hfill 3\hfill & \hfill 27\hfill \end{array}\right].$$

These two conditional distributions are not compatible. Table 3 shows the results for the joint distributions derived from the simulated Gibbs samplers and matrix-multiplication of Example 2 for conditions that are identical to those presented in Table 2. Several observations can be made here: (1) The Gibbs samplers that use the fixed-scan pattern a₁ and a₂ respectively converge to two distinct joint distributions; (2) Each individual fixed-scan Gibbs sampler converges to the corresponding solution computed from the matrix-multiplication method; (3) The random-scan Gibbs sampler converges to the mixture distribution of the individual fixed-scan distributions—i.e., π_r = (1 − r) π_a1 + rπ_a2; and (4) Regardless F is compatible or not, a random-scan Gibbs sampler always needs much larger m (using matrix-multiplication) to achieve numerical convergence than a fixed-scan Gibbs sampler does. Such phenomena should result from the idempotent property of the transition probability matrices, and it also implies slower convergence of random-scan Gibbs sampler should be expected in a MCMC simulation.

Table 3.

Joint distributiuons produced by various Gibbs samplers for Example 2.

	(1,1)	(2,1)	(1,2)	(2,1)
a1 = (1,2)	0.1062	0.0680	0.2128	0.6130
a1 = (1,2)	0.0435	0.1314	0.2753	0.5498
${\mathit{r}}_0=\frac{1}{2}(1,1)$	0.0748	0.0990	0.2447	0.5815
πa1(m = 4)	0.1063	0.0681	0.2125	0.6131
πa2(m = 4)	0.0436	0.1308	0.2752	0.5504
πr0(m = 32)	0.0749	0.0995	0.2439	0.5817
πr1(m = 32)	0.0854	0.0890	0.2334	0.5922
πr2(m = 32)	0.0645	0.1099	0.2543	0.5713

5. DISUSSION

In this paper, we show that for a given scan pattern, a homogeneous Markov chain is formed by the Gibbs sampling procedure and under mild conditions, the Gibbs sampler converges to a unique stationary distribution. Unlike compatible distributions, different scan patterns lead to different stationary distributions for PICSD. The random-scan Gibbs sampler generally converges to “something in between” but the exact weighted equation only holds for simple cases – i.e., when the dimension is two.

Our findings have several implications for the practical application of the Gibbs sampler, especially when they operate on PICSD. For example, the MICE often relies on a single fixed-scan pattern. This implies that the imputed missing values could change beyond expected statistical bounds when a seemingly innocuous change in the order of the variable is being made. Although in this paper we have not studied the issue of which fixed-scan pattern produces the “best” joint distribution, some recent work has been done in that direction. For example, Chen, Ip, and Wang [8] proposed using an ensemble approach to derive an optimal joint density. The authors also showed that the random-scan procedure generally produces promising joint distributions. It is possible that in some cases the gain from using multiple Gibbs chains, as in the case of random-scan, is marginal. As argued by Heckerman et al. [7], the single-chain fixed-scan (pseudo) Gibbs sampler asymptotically works well when the extent to which the specified conditional distributions are incompatible is minimal. This may be true for models that are applied to one single data set with a large sample size. However, the extent of incompatibility could be much higher when multiple data sets are used and when multiple sets of conditional models are specified. While it is likely that even in more complex applications a brute-force implementation of the (pseudo) Gibbs sampler will still provide some kinds of solutions, the qualities and behaviors of such “solutions” will need to be rigorously evaluated.

APPENDIX: PROOFS OF ANALYTIC RESULTS

Proof of Theorem 1

We need a lemma to prove Theorem 1 about irreducibility (ability to reach all interesting points of the state-space) and aperiodicity (returning to a given state-space at irregular times).

Lemma 1

If F is positive then T_a and T_r are irreducible and aperiodic w.r.t. any given a and r > 0.

Proof

Let ${\mathit{x}}^{\mathbf{1}}=(x_1^1,x_2^1,x_3^1,\cdots ,x_d^1)$ d and ${\mathit{x}}^{\mathbf{2}}=(x_1^2,x_2^2,x_3^2,\cdots ,x_d^2)$ be two states for the chain induced by T_a or T_r, and define (T)_ij as the (ij)^th element in the matrix T. Without loss of generality, we also let a = (1,2, ⋯, d) and $\mathit{r}=\frac{\mathbf{1}}{\mathit{d}}(1,1,\cdots ,1)$, T_a = T₁T₂T₃ ⋯ T_d and $T_{\mathit{r}}=\frac{1}{d}(T_1+T_2+T_3+\cdots +T_d)$.

To prove that T_a and T_r are aperiodic, we must have (T_a)_ii > 0 and (T_a)_ii > 0, ∀ i. By the definition of local transition probability, we have (T_k)_ii > 0, ∀ k, if F is positive. Consequently, ${(T_{\mathit{a}})}_{ii}\ge {\prod }_{k=1}^d{(T_k)}_{ii}>0$ and ${(T_{\mathit{r}})}_{ii}=\frac{1}{d}{\sum }_{k=1}^d{(T_k)}_{ii}>0,\forall i$.

To prove that T_a and T_r are irreducible is equivalent to prove that x¹ and x² commute, i.e., to show the transition probability P (x¹ → x²) > 0 and P (x² → x¹) > 0. Given the scan pattern a we have

$$P({\mathit{x}}^{\mathbf{1}}\to {\mathit{x}}^{\mathbf{2}})=f_1(x_1^2,x_2^1,\cdots ,x_d^1)f_2(x_1^2,x_2^2,x_3^1\cdots ,x_d^1)\cdots f_d(x_1^2,x_2^2,x_3^2,\cdots ,x_d^2)>0$$

And

$$P({\mathit{x}}^{\mathbf{2}}\to {\mathit{x}}^{\mathbf{1}})=f_1(x_1^1,x_2^2,\cdots ,x_d^2)f_2(x_1^1,x_2^1,x_3^2\cdots ,x_d^2)\cdots f_d(x_1^1,x_2^1,x_3^1,\cdots ,x_d^1)>0$$

Similarly, for the random-scan case we have

$$P({\mathit{x}}^{\mathbf{1}}\to {\mathit{x}}^{\mathbf{2}})\ge {(\frac{1}{d})}^d[f_1(x_1^2,x_2^1,\cdots ,x_d^1)f_2(x_1^2,x_2^2,x_3^1\cdots ,x_d^1)\cdots f_d(x_1^2,x_2^2,x_3^2,\cdots ,x_d^2)]>0$$

and

$$P({\mathit{x}}^{\mathbf{2}}\to {\mathit{x}}^{\mathbf{1}})\ge {(\frac{1}{d})}^d[f_1(x_1^1,x_2^2,\cdots ,x_d^2)f_2(x_1^1,x_2^1,x_3^2\cdots ,x_d^2)\cdots f_d(x_1^1,x_2^1,x_3^1,\cdots ,x_d^1)]>0.$$

It is well known that if a Markov chain is irreducible and aperiodic, then it converges to a unique stationary distribution [24]. Consequently, we have the uniqueness and existence theorem (Theorem 1) for the Gibbs sampler.

Proof of Theorem 2

We need a lemma to prove Theorem 2.

Lemma 2

If F is positive then the stationary distribution π_a of the Gibbs sampler has f_ad as one of its conditional distribution for the scan pattern a = (a₁, a₂, ⋯, a_d), i.e., π_a(x_ad|x_a1, x_a2, ⋯, x_ad−1) = f_ad.

Proof

Since $X_{a_d}^{(td)}~f_{a_d}\left(x_{a_d}\right|{({\mathit{x}}_{a_d}^{(td-1)})}^c)$, t = 1,2,3, ⋯, it follows π_a ∝ f_ad (x_ad|x_a1, x_a2, ⋯, x_ad−1). Consequently, π_a (x_ad|(x_ad)^c) = f_ad(x_ad|(x_ad)^c).

Theorem 2 easily follows from Lemma 2.

Proof of Theorem 3

“If” part. Since F is positive and compatible, there exists a positive joint distribution π > 0 characterized by F. Under the positivity assumption of π, it is well known that the Gibbs sampler governed by F determines π [25].

“Only if” part. Let a = (a₁, a₂, ⋯, a_d) be a scan pattern with a_d = i, i = 1, ⋯, d. Assuming that there exists a π such that π_a = π, ∀ a. From Theorem 1 and Lemma 2, it follows that π_a (x_ad|(x_ad)^c) = f_ad(x_ad|(x_ad)^c), ∀ a. Thus, π (x_i|(x_i)^c) = π_ai(x_i|(x_i)^c) = f_i (x_i|(x_i)^c), ∀ i. Hence F is compatible and π is the joint distribution of F.

Assuming that there exists a π such that π_r = π, ∀ r. We only need to prove that π_a = π, ∀ a. From Theorem 1, we have π_aT_a = π_a. By the definition of random-scan Gibbs sampler, we have π_rT_k = π_r = π, ∀ k, ∀ r. It follows that

$$\pi =\pi T_{a_d}=(\pi T_{a_{d-1}})T_{a_d}=\cdots =\pi (T_{a_1}{T}_{a_2}\cdots T_{a_{d-1}}{T}_{a_d})=\pi T_{\mathit{a}}.$$

Form Theorem 1, π is uniquely determined by T_a. As a result, π_r = π = π_a, ∀ r, ∀ a.

Proof of Corollary 1

The proof follows directly from Theorem 2 and 3.

Proof of Corollary 2

Since F is positive, π_a1, π_a2 and π are stationary distributions uniquely determined by a₁, a₂ and r, respectively. Therefore,

$$[r{\pi }_{{\mathit{a}}_2}^T+(1-r){\pi }_{{\mathit{a}}_1}^T][r{T}_1+(1-r)T_2]=r^2{\pi }_{{\mathit{a}}_2}^T{T}_1+r(1-r){\pi }_{{\mathit{a}}_1}^T{T}_1+r(1-r){\pi }_{{\mathit{a}}_2}^T{T}_2+{(1-r)}^2{\pi }_{{\mathit{a}}_1}^T{T}_2=r^2{\pi }_{{\mathit{a}}_2}^T+r(1-r){\pi }_{{\mathit{a}}_2}^T+r(1-r){\pi }_{{\mathit{a}}_1}^T+{(1-r)}^2{\pi }_{{\mathit{a}}_1}^T=r{\pi }_{{\mathit{a}}_2}^T+(1-r){\pi }_{{\mathit{a}}_1}^T$$

Because T_r = rT₁ + (1 − r) T₂ is the transition kernel for the random-scan Gibbs chain with selection probability r, we have the uniquely determined π_r which equals rπ_a2 + (1 − r) π_a1.■