Correcting for Sample Contamination in Genotype Calling of DNA Sequence Data

Abstract

DNA sample contamination is a frequent problem in DNA sequencing studies and can result in genotyping errors and reduced power for association testing. We recently described methods to identify within-species DNA sample contamination based on sequencing read data, showed that our methods can reliably detect and estimate contamination levels as low as 1%, and suggested strategies to identify and remove contaminated samples from sequencing studies. Here we propose methods to model contamination during genotype calling as an alternative to removal of contaminated samples from further analyses. We compare our contamination-adjusted calls to calls that ignore contamination and to calls based on uncontaminated data. We demonstrate that, for moderate contamination levels (5%–20%), contamination-adjusted calls eliminate 48%–77% of the genotyping errors. For lower levels of contamination, our contamination correction methods produce genotypes nearly as accurate as those based on uncontaminated data. Our contamination correction methods are useful generally, but are particularly helpful for sample contamination levels from 2% to 20%.

Introduction

Advances in next-generation sequencing have resulted in higher sequencing throughput and lower sequencing costs, enabling a wide range of large-scale genomic studies. Although the quality of sequence data is generally improving, methods and protocols are imperfect and errors inevitably occur. One such error is DNA sample contamination, in which DNA from two or more individuals is accidentally mixed.

DNA sample contamination is a common occurrence in large-scale sequencing studies and can arise at many steps of the experiment: during sample collection; any time a sample is placed into or taken out of storage; during shipping, particularly if plates are not properly sealed or kept frozen; and during the many steps of preparing DNA sequencing libraries. For example, if barcoded samples are amplified in pools, template switching might occur if amplification conditions result in templates that are only partially extended at the end of each round, resulting in DNA from one sample being paired with the barcode of another. Even if samples are sequenced without contamination on a particular run, a sample might be included in multiple runs and merged afterward. If samples are improperly labeled or there are errors in the processing pipeline, reads from multiple samples might be combined in error.

Screening for sample contamination is becoming a standard quality-control step for DNA sequencing projects, and the patterns of contamination identified vary greatly. In the 1000 Genomes Project, DNA samples were screened for contamination¹ by our method.² Out of 1,166 sequenced samples, 39 had an estimated contamination level >3% and were dropped from analysis. In a psychiatric genetics study, we detected 64 DNA samples each with estimated contamination >25%. These samples were traced back to two 96-well plates in which contamination probably occurred during shipping. In a type 2 diabetes exome sequencing study (unpublished data), ∼20% of a set of DNA samples had estimated contamination rates from 10%–15%. Here, the apparent cause was a change in the library preparation protocol to allow processing of two samples at a time. Even in the most challenging contamination scenarios we have encountered, a subset of DNA samples show no evidence of contamination, so that most studies include a mixture of contaminated and uncontaminated DNA samples.

If left uncorrected, contamination results in systematic genotype misclassification with a bias in favor of heterozygotes. This bias arises because when a mixture of two DNA samples is sequenced, the presence of the contaminating sample DNA makes it more likely that reads supporting different alleles at the same site will be present. The impact of contamination typically increases with the contamination level and decreases with sequencing depth.

Here we propose likelihood-based methods that improve genotyping accuracy by explicitly modeling DNA sample contamination during genotype calling. We apply these methods to in silico contaminated samples based on low-pass and high-depth sequence data from the 1000 Genomes Project and to actual contaminated samples from a type 2 diabetes exome sequencing project. We demonstrate that over a wide range of contamination levels and sequencing depths, modeling contamination can dramatically increase concordance between genotype calls and the true underlying genotypes, resulting in larger effective sample sizes for downstream genetic association studies than is possible by either ignoring contamination or dropping contaminated samples from the analysis.

Material and Methods

Outline

First, we introduce notation and assumptions and review our methods to detect DNA sample contamination.² Second, we describe our model for calling genotypes from sequence read data and propose a generalization of that model to account for DNA sample contamination. Third, we extend our model and method to provide even better results when the source of contamination is known and the corresponding sample is also sequenced. Finally, we describe a series of experiments and datasets used to evaluate the performance of our proposed methods.

Detecting and Estimating DNA Sample Contamination

Consider the case where one DNA sample is contaminated by another.² Let $g_i^{\left(1\right)}$ and $g_i^{\left(2\right)}$ be the genotypes for the intended and contaminating samples, respectively, at variant site i (1 ≤ i ≤ M). Let b_ij be the observed base at position i for read j (1 ≤ j ≤ R_i) and e_ij be a latent variable indicating whether a base calling error occurred (e_ij = 1) or did not (e_ij = 0). Finally, let α be the proportion of reads from the contaminating sample and π be the proportion of samples that are contaminated. We assume that sites are independent, that reads at each site are independent, and that sequencing errors are equally likely to result in any of the three incorrect bases.

To model the probability of observing a particular base, we employ the mixture model

$$P\left(b_{ij}|g_i^{\left(1\right)},g_i^{\left(2\right)};\alpha \right)=\left(1-\alpha \right)P\left(b_{ij}|g_i^{\left(1\right)}\right)+\alpha P\left(b_{ij}|g_i^{\left(2\right)}\right)$$ (Equation 1)

where

$$P\left(b_{ij}|g_i\right)=P\left(b_{ij}|g_i,e_{ij}=1\right)P\left(e_{ij}=1\right)+P\left(b_{ij}|g_i,e_{ij}=0\right)P\left(e_{ij}=0\right).$$

We present the read probabilities allowing for error $P\left(b_{ij}|g_i,e_{ij}\right)$ in Table 1. We estimate the probability of a read error as $P\left(e_{ij}=1\right)={10}^{-Q_{ij}/10}$ and P(e_ij = 0) = 1 − P(e_ij = 1), where Q_ij is the phred-scaled base quality score for the sequence data.³ To estimate the genotype probability P(g_i), we use allele frequencies from the population from which the sample was drawn and assume Hardy-Weinberg equilibrium. Allele frequencies can be estimated from a closely related reference population (for example, HapMap or 1000 Genomes), from array-based genotypes from the same population, or even from the proportion of reads that carry each allele across all sequenced samples.

Table 1.

Conditional Probability $P\left(b_{ij}|g_i,e_{ij}\right)$ of Base b_ij Given Genotype g_i and Error Event e_ij

True Genotype	Base Read Error Indicator	P(bij= A)	P(bij= B)	P(bij= E)
gi = AA	eij = 0	1	0	0
	eij = 1	0	1/3	2/3
gi = AB	eij = 0	1/2	1/2	0
	eij = 1	1/6	1/6	2/3
gi = BB	eij = 0	0	1	0
	eij = 1	1/3	0	2/3

Assumes a biallellic site with alleles A and B; E represents any base other than A or B. e_ij = 1 corresponds to a sequencing error; or 0 corresponds to a correct base call.

Taking expectations over the unknown genotypes and assuming that all reads and loci are independent, we write the likelihood for contamination level α in a sample as

$$L\left(\alpha \right)=P\left(B|\alpha \right)=\prod _{i=1}^M{\sum }_{g_i^{\left(1\right)}}{\sum }_{g_i^{\left(2\right)}}\left\{P\left(g_i^{\left(1\right)}\right)P\left(g_i^{\left(2\right)}\right)\prod _{j=1}^{R_i}\left[\left(1-\alpha \right)P\left(b_{ij}|g_i^{\left(1\right)}\right)+\alpha P\left(b_{ij}|g_i^{\left(2\right)}\right)\right]\right\}.$$

For each sample, we first maximize L(α) by using a grid search in the interval 0.0 ≤ α ≤ 0.5 and then apply Brent’s⁴ algorithm to obtain the maximum likelihood estimate of α. By using information across a large number of variants M, we determine whether the observed reads are better explained by a single sample or a combination of two samples with mixing proportion α. Even if not all markers are independent, there is little impact on the estimation of α.

Genotype Likelihoods for Contaminated Sequence Data: Source Unknown

Having estimated the contamination level α for sample k, we explicitly model contamination during genotype calling by using the estimated sample-specific contamination rate ${\hat{\alpha }}_k$. Treating the genotypes of the intended and contaminating genotypes as the unknowns, we calculate the likelihood for the combination of genotypes via the probability defined in Equation 1 as

$$L\left(g_i^{\left(1\right)},g_i^{\left(2\right)}|B_i;{\hat{\alpha }}_k\right)=P\left(B_i|g_i^{\left(1\right)},g_i^{\left(2\right)};{\hat{\alpha }}_k\right)=\prod _{j=1}^{R_i}\left[\left(1-{\hat{\alpha }}_k\right)P\left(b_{ij}|g_i^{\left(1\right)}\right)+{\hat{\alpha }}_{k}P\left(b_{ij}|g_i^{\left(2\right)}\right)\right],$$

where $B_i=\left\{b_{ij}|j=1\dots R_i\right\}$ is the set of bases overlapping position i in the sequence reads that cover the variant site. Usually, we do not know the genotype of the contaminating sample, and so we sum over this unknown variable to obtain the genotype likelihood

$$L\left(g_i^{\left(1\right)}|B_i;{\hat{\alpha }}_k\right)=P\left(B_i|g_i^{\left(1\right)};{\hat{\alpha }}_k\right)={\sum }_{g_i^{\left(2\right)}}\left[P\left(g_i^{\left(2\right)}\right)P\left(B_i|g_i^{\left(1\right)},g_i^{\left(2\right)};{\hat{\alpha }}_k\right)\right].$$

In contrast to the analysis in which we identified contaminated samples and estimated contamination level (α) for each sample k by using a list of known variant sites and allele frequencies, during genotype calling we examine every site. This step requires allele frequencies at each site, which we estimate via the EM algorithm⁵ to maximize the above likelihood. Thus, we estimate the allele frequency as:

$${\hat{f}}_i=\arg {\max }_{f_i}\prod _{k=1}^n\left[{\sum }_{g_{ik}}P\left(g_{ik}|f_i\right)P\left(B_{ik}|g_{ik};{\hat{\alpha }}_k\right)\right],$$

where g_ik is the true genotype for individual k (1 ≤ k ≤ n) at site i. Given the allele frequency estimate ${\hat{f}}_i$, we estimate the genotype probabilities assuming Hardy-Weinberg equilibrium.

Finally, to call a genotype for an individual at locus i, we select the value of $g_i^{\left(1\right)}$ with the highest likelihood. We calculate the corresponding genotype dosage (D_i ranging from 0 to 2) for bi-allelic sites by taking a weighted average of the number of alternative alleles for each of the possible genotypes $g_i^{\left(1\right)}$

$$D_i=\frac{P\left(g_i^{\left(1\right)}=\text{A}\text{R}|B_i;\hat{\alpha },{\hat{f}}_i\right)+2\cdot P\left(g_i^{\left(1\right)}=\text{A}\text{A}|B_i;\hat{\alpha },{\hat{f}}_i\right)}{P\left(g_i^{\left(1\right)}=\text{R}\text{R}|B_i;\hat{\alpha },{\hat{f}}_i\right)+P\left(g_i^{\left(1\right)}=\text{A}\text{R}|B_i;\hat{\alpha },{\hat{f}}_i\right)+P\left(g_i^{\left(1\right)}=\text{A}\text{A}|B_i;\hat{\alpha },{\hat{f}}_i\right)},$$ (Equation 2)

where R and A are the reference and alternate alleles and

$$P\left(g_i^{\left(1\right)}|B_i;\hat{\alpha },{\hat{f}}_i\right)\propto P\left(B_i|g_i^{\left(1\right)};\hat{\alpha }\right)P\left(g_i^{\left(1\right)};{\hat{f}}_i\right).$$

Genotype Likelihoods for Contaminated Sequence Data: Source Known

If the identity of the contaminating sample is known, as in the type 2 diabetes example described in the Introduction, we can use that information to improve genotype calls. In that case, we examine all available data from the paired DNA samples and call their genotypes simultaneously by considering all potential 3 × 3 = 9 genotype pairs $\left(g_i^{\left(1\right)},g_i^{\left(2\right)}\right)$. Let $B_i^{\left(1\right)}=\left\{b_{ij}^{\left(1\right)}|j=1\dots R_i^{\left(1\right)}\right\}$ and $B_i^{\left(2\right)}=\left\{b_{ij}^{\left(2\right)}|j=1\dots R_i^{\left(2\right)}\right\}$ be the observed bases for reads labeled as originating from samples 1 and 2, respectively, and let ${\hat{\alpha }}^{\left(1\right)}$ and ${\hat{\alpha }}^{\left(2\right)}$ be the estimated contamination levels for those two samples. We then write the joint likelihood for the paired samples as

$$L\left(g_i^{\left(1\right)},g_i^{\left(2\right)}|B_i^{\left(1\right)}{B}_i^{\left(2\right)};{\hat{\alpha }}^{\left(1\right)},{\hat{\alpha }}^{\left(2\right)}\right)=\prod _{j=1}^{R_i^{\left(1\right)}}\left[\left(1-{\hat{\alpha }}^{\left(1\right)}\right)P\left(b_{ij}^{\left(1\right)}|g_i^{\left(1\right)}\right)+{\hat{\alpha }}^{\left(1\right)}P\left(b_{ij}^{\left(1\right)}|g_i^{\left(2\right)}\right)\right]\times \prod _{j=1}^{R_i^{\left(2\right)}}\left[{\hat{\alpha }}^{\left(2\right)}P\left(b_{ij}^{\left(2\right)}|g_i^{\left(1\right)}\right)+\left(1-{\hat{\alpha }}^{\left(2\right)}\right)P\left(b_{ij}^{\left(2\right)}\text{|}{g}_i^{\left(2\right)}\right)\right].$$

This likelihood can also be calculated for different possible contaminating samples and compared to find the most likely source of contamination (assuming both samples were sequenced). When inconvenient to work with the joint likelihood (such as when calculating per-individual dosages), we calculate per-sample genotype likelihoods by marginalizing over the partner genotype.

$$L\left(g_i^{\left(1\right)}|B_i^{\left(1\right)}{B}_i^{\left(2\right)};{\hat{\alpha }}^{\left(1\right)},{\hat{\alpha }}^{\left(2\right)}\right)={\sum }_{g_i^{\left(2\right)}}\left[P\left(g_i^{\left(2\right)}\right)P\left(B_i^{\left(1\right)}{B}_i^{\left(2\right)}|g_i^{\left(1\right)},g_i^{\left(2\right)};{\hat{\alpha }}^{\left(1\right)},{\hat{\alpha }}^{\left(2\right)}\right)\right].$$

We also calculate these individual likelihoods prior to genotype refinement for low-pass sequence data (see below).

LD Refinement for Low-Pass Sequence Data

Genotype refinement using linkage disequilibrium (LD) on low-pass sequence data leverages information about surrounding markers to help infer haplotypes and improve genotype accuracy.^6,7 After adjustment for contamination, we use Beagle⁶ on our genotype likelihoods for low-pass (4×–6×) whole genome data to refine and improve genotype calls. Such an adjustment is less important for exome sequence data because of insufficient flanking markers to infer haplotypes accurately.

Experimental Data

To construct in silico contaminated samples to test our methods, we chose 198 European 1000 Genomes Phase 1 samples¹ with (1) low-pass (4×–6×) genome sequence data, (2) high-depth (50×–150×) whole exome sequence data, (3) Illumina HumanOmni2.5 and HumanExome chip data, and (4) estimated contamination levels $\hat{\alpha }$ < 0.5% for chip and sequence data. We chose two samples at a time (without replacement) and combined sequence reads to achieve synthetic contamination levels (α) from 2% to 30%. We paired samples with similar depths so as to approximately preserve total read counts and varied the proportion of contaminated samples (π) in each simulation from 0% to 100%.

We also analyzed 1,503 samples from a type 2 diabetes exome sequencing project (average sequencing depth ∼100×), 1,009 of which (67%) were estimated to have contamination level $\hat{\alpha }$ > 5%. In this study, we learned after sequencing was completed that changes to sequencing library preparation protocols that were designed to improve efficiency and reduce cost resulted in contamination due to template switching during PCR amplification of pairs of barcoded samples. In this case, we could reconstruct the identity of the contaminating sample by checking experimental records to identify samples that were amplified together.

Evaluation

For both examples, we compared sequence-based best-guess genotypes and genotype dosages to available array-based genotypes to estimate genotype concordance and squared Pearson’s correlation r² between true genotypes and estimated genotype dosages. The genotypes for the in silico contaminated low-pass samples were LD refined and then compared to all 41,847 Illumina HumanOmni2.5 genotype array chromosome 20 SNPs. Genotypes for in silico contaminated high-depth samples were compared to all 33,884 SNPs from the Illumina HumanExome array that were variable within the 198 samples from the 1000 Genomes Project. Genotypes for the type 2 diabetes example were compared to all 3,881 SNPs from the Affymetrix 6.0 array that overlapped the targeted sequence regions and were variable within the sequenced samples.

Results

In Silico Contaminated Data: Contaminating Sample Unknown

When we did not model contamination, increasing DNA contamination levels (α) resulted in decreasing concordance between sequence and array genotypes. For low-pass whole genome sequence data, as α increased from 2% to 30%, total genotype concordance decreased from 98.1% to 83.8%, compared to an average concordance of 98.9% for uncontaminated samples (Figure 1A; Table S1). For high-depth exome sequence data, total concordance decreased from 99.6% to 92.9% over the same contamination range compared to 99.8% for uncontaminated samples (Figure 1B; Table S1). Similarly, r² values for genotype dosages decreased from >0.96 to <0.75 as α increased from 2% to 30% (Figures 1C and 1D). Genotyping errors resulted in an increase in heterozygous calls roughly equal to α for the high-depth data and α/2 for the low-pass data (Figure S1). The impact of contamination was greater for common variants than for rare ones (Table S1), corresponding to the greater probability of a contamination resulting in a false heterozygote.

Figure 1.

Effects of Contamination Adjustment on Constructed Contaminated DNA Samples: Genotype Concordance and r²

Each point represents overall genotype concordance or dosage r² for contaminated samples when the proportion of contaminated samples (π) is 50%. Genotype concordance (A and B) and dosage (r²) (C and D) for low-pass data (A and C) and high-depth exome data (B and D) is shown.

Applying our method to these contaminated samples markedly increased genotype concordance and genotype dosage (r²). Estimated sample contamination levels $\left({\hat{\alpha }}_k\right)$ closely matched intended α values (Table S2). By accurately modeling contamination, we reduced the difference in genotype concordance rates between the contaminated and uncontaminated samples by up to 60%–80% for the high-depth exomes and up to 50%–80% for the LD-refined low-pass genomes (Figures 1A and 1B) for contamination levels 5%–20%. We observed a similar pattern for r² (Figures 1C and 1D). For the low-pass data, these improvements were seen only after LD refinement (Figure S2).

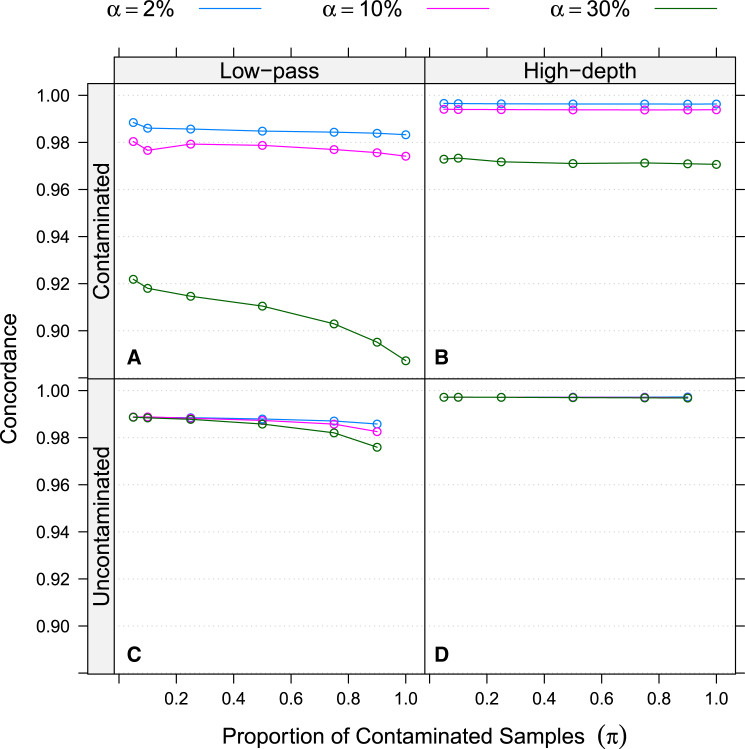
Joint calling uncontaminated samples with contaminated samples had little effect on the genotypes for the uncontaminated samples. For low-pass data, when the proportion of contaminated samples (π) was 50% and contamination levels (α) were ≤30%, the largest observed reduction in genotype concordance for uncontaminated samples was 0.4%; average reductions were ∼0.2%. Results changed only slightly as we varied the proportion of contaminated samples (π) from 5% to 90% (Figure 2). For high-depth data, the effect using our contamination-aware likelihoods when calling genotypes for uncontaminated samples was negligible for all π and α (Table S3).

Figure 2.

Effects of Increasing Proportion of Contaminated Samples on Genotype Concordance for Various Levels of Contamination

Notation: π, proportion of contaminated samples; α, level of contamination. Genotype concordance of contaminated (A and B) and uncontaminated (C and D) samples for low-pass data (A and C) and high-depth exome data (B and D) is shown.

In Silico Contaminated Data: Contaminating Sample Known

When the source of the contaminating DNA sample was known and sequence data for both samples were available, modeling this information explicitly further improved concordance with array genotypes. For low-pass data, adding the pair information reduced the difference in concordance by an additional ∼25% as α increased from 2% to 20% (Figure 1A). However, at α = 30%, concordance was actually slightly lower. This reduction in concordance appears only after LD adjustment on the data; it might be the result of a loss of information from marginalizing our pairwise genotype likelihoods as required for analysis with Beagle. Improvements to r² ranged from 0.1% to 1.3% for α = 2% to 20%. For high-depth data, we did not see a meaningful difference in concordance or r² when using the known pair information (Figure 1B).

In Silico Contaminated Data: Association Information

Ultimately we wish to use the sequence-based genotypes to test for disease or trait association. In association analysis, we can choose one of three strategies: (1) ignore contamination, (2) exclude highly contaminated samples from analysis, or (3) adjust for contamination. To estimate the relative efficiencies of these three strategies, we note that effective sample size scales linearly with nr², the product of sample size and the squared correlation between the true genotype and the sequence-based genotype dosages.⁸ Because even contaminated samples provide information about the true underlying genotype (r² > 0), including contaminated samples could provide association information even when contamination is ignored. The reduction in sample size due to contamination is at least 80% smaller when applying our correction compared to dropping contaminated samples (Table 2). In our evaluations, we maximized effective sample size when adjusting for contamination and using all samples, whether contaminated or not. For example, when all samples are contaminated at α = 10%, association information for the low-pass data is reduced by 10.6% if we ignore contamination and 4.0% if we correct for contamination (compared to 8.0% and 2.5%, respectively, for high-depth data). In this example, where all samples are contaminated, it would have been impractical to exclude contaminated samples from association analyses.

Table 2.

Effective Sample Size for Association Test

Method	Percent of Samples Contaminated
5%	10%	25%	50%	75%	90%	100%
	Low-Pass
Adjusted	194	194	193	192	191	190	190
Ignored	193	193	190	186	182	179	177
Dropped	184	174	144	96	47	18	0
	High-Depth
Adjusted	195	195	195	194	194	193	193
Ignored	195	194	192	189	186	184	182
Dropped	186	176	146	98	48	18	0

Shown here are the effective sample size estimates when α = 10% and total sample size is 198 under three scenarios: all samples included and adjusted with our method (“adjusted”), all samples included but contamination ignored (“ignored”), and contaminated samples $\left(\hat{\alpha }>0.01\right)$ removed from analysis (“dropped”).

In Silico Contaminated Data: Impact of Over- or Underestimating Contamination

To evaluate whether misspecified values of α could result in decreased genotype quality, we ran simulations in which we scaled the contamination estimate $\hat{\alpha }$ by 0.5, 0.75, 1.5, and 2 for samples in which the true α = 5%, 10%, or 15%. Overestimating $\hat{\alpha }$ had little impact on total concordance and r² whereas underestimating contamination more negatively affected both statistics (Figure S3). For the low-depth data, overestimating $\hat{\alpha }$ by 1.5× actually resulted in better concordance then using the “true” $\hat{\alpha }$; this effect was observed only after LD refinement. The difference in concordance when reducing α by half was at least 40% greater than difference from doubling α for the low-pass samples; there was very little difference for the high-depth samples. The negative impact of inflated $\hat{\alpha }$ estimates for samples that were not contaminated was very modest compared to the benefits of modeling contamination for the remaining samples.

Type 2 Diabetes Data

Convinced of the value of adjusting for contamination, we next applied our method to data from the type 2 diabetes exome sequencing project. In these data, $\hat{\pi }$ = 67% of samples were contaminated and we knew the likely contaminating sample. When we applied our correction methods, concordance with array genotypes dramatically improved: the average per-sample concordance increased from 94.5% to 99.4% (a 9-fold reduction in discordance), further increasing to 99.6% (a 14-fold reduction in discordance) when we both modeled contamination and used knowledge of its source. Similar patterns were observed for non-reference concordance and r² (Table 3).

Table 3.

GWAS Concordance for Type 2 Diabetes Exome Sequencing Data

$\hat{a}$	No. Samples	Ignored	Adjusted	Paired
Total Concordance
0%–1%	202	0.998	0.998	0.998
1%–5%	293	0.996	0.998	0.998
5%–10%	218	0.958	0.997	0.998
10%–15%	591	0.920	0.993	0.996
15%–20%	169	0.878	0.984	0.992
>20%	30	0.841	0.950	0.971
Total	1,503	0.945	0.993	0.996
Non-reference Concordance
0%–1%	202	0.996	0.997	0.997
1%–5%	293	0.992	0.995	0.995
5%–10%	218	0.908	0.993	0.994
10%–15%	591	0.833	0.985	0.991
15%–20%	169	0.760	0.964	0.983
>20%	30	0.702	0.890	0.936
Total	1,503	0.882	0.985	0.991
r2
0%–1%	202	0.997	0.998	0.998
1%–5%	293	0.994	0.996	0.996
5%–10%	218	0.929	0.995	0.996
10%–15%	591	0.863	0.990	0.994
15%–20%	169	0.791	0.977	0.989
>20%	30	0.725	0.930	0.946
Total	1,503	0.905	0.990	0.994

Mean per-sample genotype accuracy with the GWAS data when we ignore contamination, adjust without regard for the source of contamination, and adjust using known contamination source.

Discussion

We have shown that genotyping accuracy for contaminated samples can be dramatically improved by modeling contamination using a mixture model. For example, in the type 2 diabetes exome sequencing example, our method reduced genotype discordance by 14-fold (4.2% to 0.3%) for α = 5%–10% contaminated samples. Consistent with our previous study, we observed that even low levels of contamination (e.g., α = 2%–5%) can result in increases in genotype discordance of >2-fold. Our correction method nearly eliminates the impact of low levels of DNA contamination (α = 2%–5%) and reduces by >80% genotype discordance incurred by moderate level of DNA contamination (α = 5%–15%) in the type 2 diabetes exome sequencing examples. We expect our method to be particularly useful when a large fraction of sequenced samples are contaminated at small to moderate levels (α = 2%–15%).

We demonstrated (Figure S3) that genotype calling methods that model contamination perform best when the contamination level α is well estimated and that underestimating α is more detrimental than overestimating it. Situations that can lead to deflated contamination estimates are (1) the use of misspecified allele frequency estimates (incorrect population as well as systematic overestimates or underestimates; data not shown), (2) contamination from related individuals,² and (3) limited sequencing library complexity, which results in decreased heterozygosity. If one or more of these situations are suspected, modestly inflating (e.g., 2%–5%) the estimated contamination level $\hat{\alpha }$ when correcting for contamination can improve overall genotype accuracy.

As long as contamination affects case and control samples similarly, we do not expect contamination adjustments to increase the rate of false positive findings in downstream association studies. For single-variant associations, results depend on accurate estimations of allele frequency differences in case and control subjects. As long as contamination patterns do not differ drastically in the case and control subjects and there are no issues of population stratification, we can accurately estimate allele frequencies after correction (Figure S4). For rare-variant association, contaminated samples can appear to carry high numbers of rare heterozygous variants when analyzed with standard protocols. Our proposed correction will decrease the number of false positive heterozygotes (Figure S5), so false positive associations will be less likely.

Although we have focused on sequencing genomic DNA, in principle our methods can be used for other sequencing studies as well. For example, we have used our methods to identify contamination in RNA-seq experiments. Using our existing method and restricting analyses to expressed exons in protein-coding genes, we detected that 11 of 249 RNA-seq samples were contaminated by >2%. Detection and estimation of contamination in these experiments might be made more robust by accounting for allele-specific expression (ASE), where gene transcription varies based on allele; we are exploring this possibility.

We described the methods in this paper specifically in the context of biallelic SNPs. Extension to multiallelic SNPs is straightforward, requiring only that we sum over a larger number of possible genotypes. Genotyping of other variant types, such as indels and structural variants, is also affected by contamination. We expect that the same principles, focused on modeling the observed data as a mixture of two samples, can be usefully applied to these more complex situations.

We observed that the LD-aware genotype refinement algorithm improves genotype accuracy for low-pass sequence data. However, accuracy was still substantially lower than for uncontaminated data when the contamination level α was high. This might be due in part to the fact that our LD-aware genotype refinement algorithm is not aware of the possibility of contamination. With increasing interest in whole genome sequencing studies, accounting for the contamination in the genotype refinement step has the potential to further improve genotyping and phasing accuracy.

Our contamination modeling methods are implemented in the program cleanCall (source code is available online). cleanCall requires sequencing data in samtools⁸ pileup format. Extracting pileups only for variant sites allows cleanCall to read data quickly compared to scanning large BAM files. The total runtime for cleanCall is comparable to other simple likelihood-based genotype callers; modest additional time is spent estimating allele frequencies via the EM algorithm, but the average number of iterations at a given site is minimal (2–5) and does not significantly affect overall performance.

We developed methods to correct for DNA contamination in variant calling by extending our likelihood-based framework to detect and estimate contamination. Our correction methods improve genotype calling accuracy and association power compared to ignoring contamination or discarding contaminated samples. Even if the contamination level is low ($\hat{\alpha }$ < 5%), we observe considerable improvement in genotype accuracy with our correction methods. Our methods are effective both for high-depth and low-pass data, and given the ubiquity of DNA sample contamination, we expect our methods to be of real benefit to a large number of DNA sequencing studies.

Published: July 30, 2015

Web Resources

The URLs for data presented herein are as follows:

• 1000 Genomes, http://browser.1000genomes.org

• cleanCall, https://github.com/hyunminkang/cleanCall