Leveraging Functional-Annotation Data in Trans-ethnic Fine-Mapping Studies

Abstract

Localization of causal variants underlying known risk loci is one of the main research challenges following genome-wide association studies. Risk loci are typically dissected through fine-mapping experiments in trans-ethnic cohorts for leveraging the variability in the local genetic structure across populations. More recent works have shown that genomic functional annotations (i.e., localization of tissue-specific regulatory marks) can be integrated for increasing fine-mapping performance within single-population studies. Here, we introduce methods that integrate the strength of association between genotype and phenotype, the variability in the genetic backgrounds across populations, and the genomic map of tissue-specific functional elements to increase trans-ethnic fine-mapping accuracy. Through extensive simulations and empirical data, we have demonstrated that our approach increases fine-mapping resolution over existing methods. We analyzed empirical data from a large-scale trans-ethnic rheumatoid arthritis (RA) study and showed that the functional genetic architecture of RA is consistent across European and Asian ancestries. In these data, we used our proposed methods to reduce the average size of the 90% credible set from 29 variants per locus for standard non-integrative approaches to 22 variants.

Introduction

Genome-wide associations studies (GWASs) have reproducibly identified thousands of risk loci associated with complex traits and diseases.^1–7 Unfortunately, the index variants reported in these studies are typically not biologically causal but rather correlated with the underlying causal variant through linkage disequilibrium (LD).⁸ Fine-mapping experiments identify causal variants responsible for the GWAS signal first by gathering dense genetic information, either through targeted sequencing or dense imputation, and second by statistically prioritizing variants that can subsequently be validated in functional studies.^3,6,9,10

Divergent population histories due to various demographic forces such as bottlenecks and expansions have produced unique genomic landscapes across ethnicities.^11,12 Such differences in LD patterns and variant frequencies across populations can increase the power of statistical fine mapping if they are properly modeled.^3,13–18 Intuitively, if a locus contains a causal variant, the neighborhood of LD partners linked to this variant will be distinct in different populations. Thus, aggregating the strength of association across multiple populations might accentuate the signal from the true causal variant(s) while dampening the noise from correlated variants.

A common approach to combining information across multiple studies is through inverse-variance fixed-effects meta-analysis,¹⁹ which assumes that effect sizes of causal variants are similar across studies or populations. This assumption can be relaxed by a random-effects strategy, although it has been observed that this usually results in a decrease in statistical power.²⁰ A recent, and more robust, Bayesian meta-analysis framework¹⁵ was proposed to reason over trans-ethnic studies with potential allelic heterogeneity. Both the fixed-effects meta-analysis statistics and the Bayes factors supplied by the latter approach can be readily converted into posterior probabilities of association (PPAs) for the construction of fine-mapping credible sets.^3,21 However, these credible sets are commonly built under the assumption that a locus harbors at most a single causal variant,^3,22–24 which might be invalidated at many risk loci,^17,25,26 leading to miscalibrated credible sets.^27,28 Although conceptually it might be possible to create credible sets on the basis of independent signals identified through conditional analysis, this strategy suffers from necessitating an ad hoc re-definition of the fine-mapping region. Furthermore, multiple causal variants in LD can create at neighboring sites synthetic associations that are potentially stronger than the association at the true causal variants. The iterative conditioning strategy would necessarily select these synthetic SNPs first, thereby dissipating the signal from the true causal variants.²⁷

In addition to the strength of association between genotype and phenotype, an orthogonal source of information lies within a variant’s functional genomic context. Projects such as ENCODE²⁹ and ROADMAP³⁰ have provided a rich atlas of functional information, and numerous groups have reproducibly demonstrated that disease-associated variants are systematically enriched within chromatin marks that delineate active regulatory regions in phenotypically relevant cell types.^31–35 Whereas functional genomic data are often used as a post hoc validation of association findings,^4,10,36 a number of principled approaches have been proposed to jointly integrate functional and association data.^28,35,37,38 In addition to increasing the accuracy of fine mapping, these integrative approaches also provide insights into the genetic architecture of the trait by identifying relevant tissue-specific functional marks without making any prior assumptions. However, to the best of our knowledge, functional integrative approaches have not been extended to trans-ethnic fine mapping, and a rigorous assessment of trans-ethnic fine mapping in the presence of multiple causal variants is currently lacking. Although in principle the single-population frameworks that allow for multiple causal variants^27,28 can operate directly on trans-ethnic meta-analysis statistics, they require ad hoc averaging of trans-ethnic LD and do not properly account for heterogeneity by ancestry at causal variants.

In this work, we propose a statistical framework that integrates three sources of information to triangulate causal variants in fine-mapping studies: (1) the strength of association between genotype and phenotype, (2) differential genomic background across ethnic groups, and (3) tissue-specific functional genomic annotations (Figure 1). Different allele frequencies (or sample sizes) across populations induce differential standardized effect sizes at all the variants in a region, even in the presence of no allelic effect-size heterogeneity by ancestry. We model this induced heterogeneity across populations through a multivariate normal (MVN) framework wherein the sets of population-specific association statistics are realizations from population-specific MVN distributions. Similar to the case of a single population,^27,28 this allows us to consider multiple causal variants at any risk locus. We integrate functional genomic data by using Empirical Bayes,²⁸ which provides a means of selecting functional annotations most relevant to the trait of interest. Most importantly, our proposed approach requires only the summary association data for each population, thereby avoiding the many restrictions that can accompany analysis of individual-level genotype data.

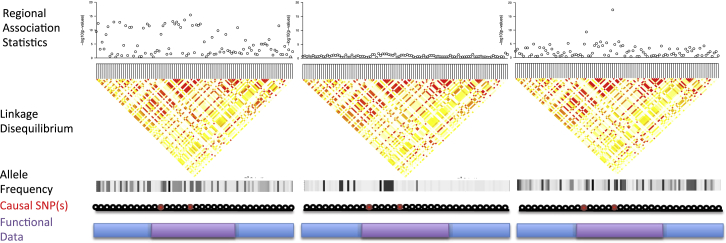
Figure 1.

Example of a Fine-Mapping Locus in Three Different Populations

In population 1 (left), the causal variants are present, but strong regional LD makes it difficult to distinguish them from tagging SNPs. In population 2 (middle), the causal variants both have a very low frequency and/or are monomorphic, resulting in no observable association between the SNPs and the trait. In population 3 (right), the causal variants are common and have few tagging SNPs. Our framework jointly models population-specific LD structure and integrates functional genomic data to prioritize causal variants.

Through extensive simulations, we show that our trans-ethnic framework significantly improves fine-mapping resolution over conventional meta-analysis strategies and demonstrate that considering multiple causal variants in multi-ethnic cohorts yields large gains in fine-mapping efficiency. We showcase our framework by reanalyzing empirical summary data from a large trans-ethnic rheumatoid arthritis (RA [OMIM: 180300]) GWAS.⁴ We first demonstrate that the functional architecture of RA is consistent across ethnicities and that there is a strong preponderance of immune-related functional classes that are enriched with causal variants. We then fine map the RA GWAS loci by using functional data and show that our method greatly outperforms current state-of-the art methodologies and uncovers a number of plausible functional variants.

Material and Methods

Multi-population Fine-Mapping Framework

Without loss of generality (given that similar results can be derived for case-control traits), let y be a quantitative phenotype such that $y_i=g_i\beta +{\mathit{ϵ}}_i$, where ${\mathit{ϵ}}_i\sim \mathcal{N}\left(0,{\sigma }_e^2\right)$, and $g_i$ denotes a multi-SNP genotype containing {0,1,2} counts of the reference allele at M SNPs for an individual i. The β vector represents allelic effects where the j^th entry will be non-zero only if SNP j is causal. Given genotype (G_p) and phenotype (Y_p) data over N_p individuals from population p, a standard approach to measuring association strength at SNP j is through the Wald statistic

$$z_p^j=\frac{{\hat{\beta }}_p^j}{\text{SE}\left(\widehat{{\beta }_p^j}\right)}=\frac{\text{Cov}\left(G_p^j,Y_p\right)\sqrt{N_p}}{\text{Var}\left(G_p^j\right){\sigma }_e^2},$$

which asymptotically follows a normal distribution:

$$\mathcal{N}\left(\frac{{\beta }_p^j\sqrt{\text{Var}\left(G_p^j\right)}}{{\sigma }_e}\sqrt{N_p},1\right).$$

We denote the non-centrality parameter (NCP) of the normal distribution as

$${\lambda }_p^j=\frac{{\beta }_p^j\sqrt{\text{Var}\left(G_p^j\right)}}{{\sigma }_e}\sqrt{N_p}.$$

Under the null hypothesis that SNP j is not causal (or does not tag a causal variant; see below), ${\beta }_p^j=0$ and thus ${\lambda }_p^j=0$. If the SNP is causal, then ${\beta }_p^j\ne 0$, yielding a non-zero ${\lambda }_p^j$, and governs the power of detecting this variant in an association study (i.e., rejecting the null at some confidence level). Importantly, even when the allelic effects at the causal variants are similar across populations (i.e., ${\beta }_p^j={\beta }_{p^{\prime }}^j$), different allele frequencies and sample sizes induce population-specific NCPs, yielding larger NCPs at more common SNPs and/or larger studies. This leads to the well-known result that causal variants are more readily detectable in populations in which they are present more frequently.

Pervasive LD at fine-scale resolutions induces correlations between tag SNPs and causal SNPs, thus creating an indirect association between tag SNPs and traits.¹³ More specifically, the LD-induced NCP at a SNP j $\left({\text{Λ}}_p^j\right)$ can be approximated as a linear combination of NCPs at the causal SNPs with LD-adjusted weights^13,27,28,39 as

$${\text{Λ}}_p^j=\sum _c{r}_p^{j,c}{\lambda }_p^c,$$ (Equation 1)

where the sum is taken across all causal SNPs c, and $r_p^{j,c}$ is the Pearson correlation coefficient between SNPs j and c in population p. We expand Equation 1 to include all SNPs in the locus by incorporating indicator variable $C_p^k$, which is set to 1 if SNP k is causal in population p and 0 otherwise:

$${\text{Λ}}_p^j=\sum _{k=1}^M{r}_p^{j,k}{\lambda }_p^k{C}_p^k.$$ (Equation 2)

In vector notation,

$${\text{Λ}}_p={\text{Σ}}_p\left({\lambda }_p\circ C_p\right),$$ (Equation 3)

where ${\text{Σ}}_p$ is the LD matrix of Pearson correlations among the M SNPs, C_p is a binary vector indicating which SNPs are causal, and $\circ$ denotes the element-wise multiplication between two vectors. We can now write the probability of the data (i.e., the observed standardized effect sizes, Z scores) given the causal variants (C_p) in population p under a MVN assumption:

$$Z_p|{\lambda }_p,C_p\sim \mathcal{N}\left({\text{Λ}}_p,{\text{Σ}}_p\right).$$ (Equation 4)

This allows us to define the total likelihood of the data by marginalizing across all sets of causal SNPs ($\mathcal{C}$) as

$$L\left(Z_1,Z_2,\cdots ,Z_P;{\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_P\right)=\prod _p\sum _{C_p\in \mathcal{C}}P\left(Z_p|{\lambda }_p,C_p\right)P\left(C_p\right),$$ (Equation 5)

which we simplify under the assumption that the causal vector set is identical across populations:

$$L\left(Z_1,Z_2,\cdots ,Z_P;{\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_P\right)=\sum _{C\in \mathcal{C}}\prod _{p}P\left(Z_p|{\lambda }_p,C\right)P\left(C\right).$$ (Equation 6)

Here, $P\left(Z_p|{\lambda }_p,C_p\right)$ is defined as the probability density function of the MVN (see Equation 4), and $P\left(C\right)$ is the probability of a given causal set. Note that Equation 6 assumes that the causal set is identical across populations but allows for different effect sizes at causal SNPs across populations.

Integration of Functional-Annotation Data

We assume that each variant can potentially have several phenotypically relevant genomic functional annotations (e.g., transcription factor binding site), which can be encoded as binary variable $A_{jk}$ for variant j and annotation k or as a continuous value (e.g., a probabilistic membership of variants in different functional classes). We integrate the functional information through the probability of the causal set C as follows,

$$P\left(C;\gamma \right)=\prod _j{\left(\frac{1}{1+\text{exp}\left(-{\gamma }^T{A}_j\right)}\right)}^{C_j}{\left(\frac{1}{1+\text{exp}\left({\gamma }^T{A}_j\right)}\right)}^{1-C_j},$$ (Equation 7)

where γ is a vector containing the prior log-odds ratio of causality for every functional annotation. We extend the likelihood to incorporate functional data as

$$L\left(Z_1,Z_2,\cdots ,Z_P;{\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_P,\gamma \right)=\sum _{C\in \mathcal{C}}\prod _{p}P\left(Z_p|{\lambda }_p,C\right)P\left(C;\gamma \right),$$ (Equation 8)

which we can further simplify by assuming that data at different loci are independent:

$$L\left(Z_1,Z_2,\cdots ,Z_P;{\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_P,\gamma \right)=\prod _l\sum _{C_l\in {\mathcal{C}}_l}\prod _{p}P\left(Z_{l,p}|{\lambda }_{p,l},C_l\right)P\left(C_l;\gamma \right).$$ (Equation 9)

Finally, to obtain posterior probabilities that each SNP is causal, we use Bayes theorem to compute the joint posterior for each causal set,

$$P\left(C_l|Z_{l,1},Z_{l,2},\cdots ,Z_{l,P};{\lambda }_{l,1},{\lambda }_{l,2},\cdots ,{\lambda }_{l,P},\gamma \right)=\frac{{\prod }_{p}P\left(Z_{l,p}|{\lambda }_{p,l},C_l\right)P\left(C_l;\gamma \right)}{{\sum }_{C_l\in {\mathcal{C}}_l}{\prod }_{p}P\left(Z_{l,p}|{\lambda }_{p,l},C_l\right)P\left(C_l;\gamma \right)},$$ (Equation 10)

and subsequently marginalize across all $C_l=\left(C_{1l},C_{2l},\dots ,C_{N_l}\right)$ such that $C_{jl}=1$:

$$P\left(C_{jl}|Z_1,Z_2,\cdots ,Z_P;{\lambda }_{l,1},{\lambda }_{l,2},\cdots ,{\lambda }_{l,P},\gamma \right)=\sum _{C_l\in {\mathcal{C}}_l:C_{jl}=1}P\left(C_l|Z_1,Z_2,\cdots ,Z_P;{\lambda }_{l,1},{\lambda }_{l,2},\cdots ,{\lambda }_{l,P},\gamma \right).$$ (Equation 11)

Model Fitting

Because of the finite nature of either the sample or the reference panel, the LD matrix in practice could be ill conditioned. We apply a Tikhonov Regularization⁴⁰ to all LD matrices to ensure their invertibility and as a result preserve the non-degeneracy and numerical stability of the MVN approximation. Furthermore, because we ensure that all $\text{Σ}$ are positive definite, there exists a Cholesky decomposition for each LD matrix and its corresponding inverse. Let $L_p=\text{Chol}{\left({\text{Σ}}_p\right)}^{-1}$; it follows that $\widetilde{Z_p}=L_p{Z}_p\sim \mathcal{N}\left(L_p{\text{Λ}}_p,I\right)$. In practice, we operate in the transformed-Z-score space $\left(\widetilde{Z_p}\right)$ because it improves numerical stability and reduces computational burden by removing a large, repetitive matrix multiplication when computing the MVN density.

We fit the parameters of the model to the data across all loci by using a variant of the expectation maximization over the functional annotations (γ) and approximate the NCPs by using a simple function of the observed Z scores (see Appendix A). We note that because enumerating over all possible causal sets is combinatorially intractable, we typically restrict the number of causal variants per locus to two or three in practice.

Simulation Data

We benchmarked our proposed framework by using simulations starting from real genotype data. Using the NHGRI catalog of GWAS variants on chromosome 1,¹ we centered 25-kb windows on the lead SNP and used HAPGEN2⁴¹ and 1000 Genomes¹² to simulate individuals from the Asian (n = 286), African (n = 246), and European (n = 379) ancestries. SNPs that were polymorphic with a minor allele frequency ≥ 0.01 in at least one population were retained for analysis. For each simulation, we randomly chose 50 loci and simulated causal variants by drawing causal status according to the logistic prior model described above. Unless otherwise noted, we used the annotations (coding, UTR, promoter, DNase hypersensitivity site [DHS], intronic, and intergenic) and functional enrichments (13.8×, 8.4×, 2.8×, 5.1×, and 0.1×) observed in Gusev et al.³⁵ for simulations below. We simulated phenotypes under a linear model such that for individual i of population p, their phenotype Y was drawn as $Y_{i,p}={\sum }_{j=1}^{N_c}{\beta }_j\cdot g_{j,i,p}+{\mathit{ϵ}}_{i,p}$, where N_c is the total number of causal variants, ${\beta }_j$ is the effect size of the j^th causal SNP, $g_{j,i,p}$ is the number of copies of the risk allele j for individual i of population p. Following recent works, we simulated similar heritability across populations.⁴² The population-specific error term, ${\mathit{ϵ}}_{i,p}$, was drawn according to a $\mathcal{N}\left(0,{\sigma }_{e,p}^2\right)$, where ${\sigma }_{e,p}^2=({\sigma }_{g,p}^2-h_g^2\text{∗}{\sigma }_{g,p}^2)/h_g^2$, ${\sigma }_{g,p}^2={\beta }^{\prime }\text{Cov}\left(X_p\right)\beta$, and $\text{Cov}\left(X_p\right)$ is the population-specific covariance of the genotypes (LD). The effect size, ${\beta }_j$, was set to be inversely proportional to the average SD of the population allele frequencies; this is roughly equivalent to assuming that each causal SNP explains an equal proportion of the phenotypic variance.⁴³

Existing Methods

We compared our proposed methods with other well-established probabilistic methods for fine mapping. First, we investigated MANTRA, a Bayesian trans-ethnic meta-analysis technique proposed by Morris.¹⁵ We obtained the software implementation from the author and ran it with the default settings; we provided the fixation index (F_ST) between the three populations as determined in Nelis et al.⁴⁴ as the prior for the Bayesian partition model. The output of MANTRA is a Bayes factor, which we subsequently converted to

$${\text{PPA}}_i=\frac{B{F}_i}{{\sum }_{k}B{F}_k}$$

as previously recommended.^3,22,45 Similarly, we calculated posterior probabilities that SNPs are causal strictly on the basis of the inverse-variance fixed-effects¹⁹ meta-analysis by using the PAINTOR (Probabilistic Annotation Integrator)²⁸ and CAVIARBF⁴⁶ frameworks. We note that the CAVIARBF and PAINTOR models require LD as input, which we calculated as the average of the population-specific LD weighted by the sample size of each population. We assessed accuracy by rank ordering SNPs across all fine-mapping loci according to the output of each method and then determined the proportion of identified causal variants as more SNPs were selected. We typically report the median number of SNPs one would need to validate in order to resolve 90% of the causal variants as our main metric of accuracy.

RA Multi-ethnic Fine-Mapping Dataset

We downloaded summary statistics from a large trans-ethnic RA GWAS consisting of over 100,000 individuals (∼68,000 of European ancestry and ∼36,000 of Asian ancestry).⁴ We used the reported genome-wide-significant loci, excluding human leukocyte antigen regions, and centered 100-kb windows around the top SNP, yielding a total of 89 fine-mapping loci. For each of these regions, we estimated LD by using the European and Asian individuals from 1000 Genomes.¹² We integrated 482 publicly available functional annotations comprising 406 DHSs spanning numerous cell types and tissues,^31,47 the seven genomic segmentations of the eight primary ENCODE cell lines,⁴⁸ Fantom5 enhancer and transcription start site regions,⁴⁹ immune cell enhancers,¹⁰ genic elements derived from GenCode,⁵⁰ and overall methylation and acetylation marks from ENCODE.²⁹ The construction of a phenotypically specific fine-mapping model requires two phases. First, we ran the model marginally on each annotation and subsequently rank ordered all the annotations according to likelihood-ratio statistics.^28,37 Second, we selected the top annotations that were minimally correlated with one another (usually no more than five) to enter a final model to estimate posterior probabilities that variants are causal.

Results

Joint Modeling of Association Statistics across Populations Increases Fine-Mapping Performance

We used simulations to investigate the benefit of jointly modeling population-specific association statistics versus standard meta-analysis approaches. We simulated fine-mapping datasets over 10,000 individuals equally divided among European, Asian, and African ancestries with total heritability of $h_g^2=0.25$ across 50 loci with genetic architecture similar to that in Gusev et al.³⁵ The loci were simulated such that in expectation, each locus harbored a single causal variant with allelic effects shared across populations (see Material and Methods). This yielded an average of 15 loci with a single causal variant and 13 loci with multiple causal variants per simulation. In general, we find that trans-ethnic fine-mapping strategies that assume a single causal variant are less optimal than those that allow for multiple causal variants (Table 1). For example, MANTRA meta-analysis requires 1.9 and 96.8 SNPs per locus in order to identify 50% and 90% of the causal variants, respectively, whereas methods that allow multiple causal variants but do not incorporate functional data require 1.2 and 7.0 SNPs per locus to identify 50% and 90% of the causal variants, respectively.⁴⁶ Existing integrative fine-mapping methods that leverage functional data²⁸ applied to fixed-effects meta-analysis statistics achieve accuracy of 1.0 and 5.6 SNPs per locus to find 50% and 90% of the causal variants, respectively. In contrast, our proposed framework resolves causal variants with the greatest efficiency (Figure 2) in that it requires only 0.9 and 5.2 SNPs per locus to find 50% and 90% of the causal variants, respectively (paired t test, p < 0.001). Overall, this can be attributed to the fact that our approach models population-specific LD patterns while allowing for multiple causal variants in the presence of functional information.

Table 1.

Our Trans-ethnic Integrative Framework Is Superior to Conventional Meta-analysis Strategies and Current State-of-the-Art Methodologies

Heterogeneity Level	Identified Proportion of Causal Variants	Single Causal Variant per Locus		Multiple Causal Variants per Locus
Fixed-Effects Meta-analysis	MANTRA15	Fixed-Effects CAVIARBF46	Fixed-Effects PAINTOR28a	Trans-ethnic PAINTORa
None	0.50	1.9	2.0	1.2	1.0	0.9
0.75	29.8	30.3	2.9	2.1	1.9
0.90	96.8	96.8	7.0	5.6	5.2
Weak	0.50	1.9	2.0	1.1	0.9	0.9
0.75	62.3	62.7	2.9	2.0	1.8
0.90	118.1	118.6	6.8	4.9	4.1
Strong	0.50	29.0	11.1	12.6	9.6	2.3
0.75	105.0	92.7	68.6	58.4	19.7
0.90	143.9	139.8	134.4	121.3	56.5

We simulated 1,000 multi-ethnic fine-mapping datasets under various levels of allelic heterogeneity across populations. For the first two levels of heterogeneity (“none” and “weak”), we invoked the standard infinitesimal assumption on allelic effects either globally or at the population level by setting effect sizes $\left({\beta }_{c,p}\right)$ at the causal SNPs inversely proportional to either the mean allele-frequency SD or the population-specific allele-frequency SD. To simulate strong heterogeneity across ancestries, we drew effect sizes from a standard normal distribution for each population independently and added enough Gaussian noise to maintain $h_g^2=0.25$. Displayed here is the median number of SNPs selected per locus for identifying a specified proportion of the causal variants.

^aMethods that also integrate functional data.

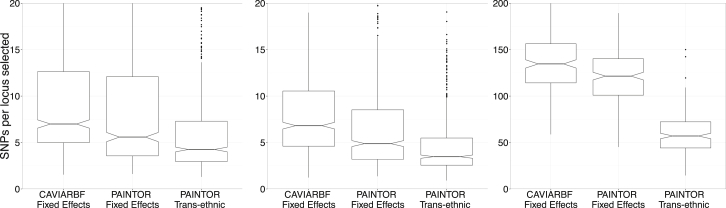
Figure 2.

Trans-ethnic PAINTOR Is Most Efficient in Identifying Causal Variants

The distributions of the number of SNPs required for follow-up identification of 90% of the causal variants across 1,000 simulations are displayed as boxplots. The different panels represent increasing levels of effect-size heterogeneity by ancestry: none (left), weak (middle), and strong (right). The widths of the notches in each boxplot roughly correspond to 95% confidence intervals for the median number of SNPs required for resolving 90% of the causal variants. For the sake of clarity, we have cut the y axis to emphasize the significant difference in performance across all three methods.

Recent studies have shown that GWAS findings generally replicate across populations,^42,51 thus suggesting sharing of underlying causal variants. However, it is generally unknown whether these variants contribute to disease risk uniformly across populations. We sought to assess the performance of fine mapping in the situation where the causal variants have either weak or strong heterogeneity by ancestry. In addition to fine mapping datasets in which causal effects were similar across populations (no heterogeneity), we simulated allelic effects inversely proportional to the population-specific allele-frequency SD (weak heterogeneity) and normally distributed allelic effects for each ancestry independently (strong heterogeneity). We found that our framework significantly outperformed the fixed-effects meta-analysis followed by probability estimation by existing methods. For example, in the case of weak heterogeneity, our approach required 4.1 as opposed to 4.9 SNPs per locus (19.5% improvement); in addition, in the presence of strong heterogeneity, our approach dramatically outperformed existing meta-analysis strategies by reducing the number of SNPs required for identifying 90% of the causal variants from 121.3 to 56.5 (214% improvement) (Table 1; Figure 2). The increase in performance is likely due to the fact that our framework makes no assumptions pertaining to the population-specific allelic effects at causal SNPs, given that we allow the empirically observed Z scores in each population to dictate the effect size. This allows for arbitrary levels of heterogeneity in the effect size by population, whereas fixed-effects meta-analysis assumes similar effect sizes across populations.

Performance of Trans-ethnic Fine Mapping

The benefit of trans-ethnic fine mapping has been thoroughly documented both in simulations and in empirical data.^3,13,15 However, previous works have assumed a single causal variant at a risk locus, and this assumption is often invalidated in practice. Here, we sought to assess trans-ethnic fine mapping in the presence of multiple causal variants at a risk locus while integrating functional-annotation data. Consistent with previous works,¹³ we found that for the same sample size, multi-ethnic cohorts attained superior accuracy over single-population studies. However, allowing for multiple causal variants enabled trans-ethnic fine mapping to perform even better than single-population fine mapping. We observed a near 3- to 4-fold increase in the median resolution for methods that model multiple causal variants but only a 1.4- to 1.6-fold gain for methods that assume a single causal (see Table 2). We attribute this to the much smaller number of sets of causal variants (as a proportion of the total possible sets) that are compatible with the observed association statistics. Diversity in LD patterns across populations additionally penalizes sets of variants that do not contain the true causal variants because they are unlikely to explain the observed data. Consequently, multi-ethnic cohorts not only will have proportionally more LD patterns than single-population cohorts (therefore placing larger penalties on incorrect causal sets) but can also borrow power from populations where the causal variants are present more frequently.

Table 2.

Modeling Multiple Causal Variants in Multi-ethnic Cohorts Yields Larger Relative Gains in Fine-Mapping Efficiency

Ethnic Group	Single Causal Variant		Multiple Causal Variants
−	+	−	+
Asians	136.9	134.4	89.3	36.2
Europeans	135.0	130.9	82.9	33.5
Africans	104.0	95.0	34.4	14.7
Trans-ethnic	72.6	58.4	8.5	4.9
Relative	1.4	1.6	4.0	3.0

We simulated fine-mapping datasets with various ethnic compositions and allelic effects shared across populations. Displayed here are four fine-mapping strategies that consider either single or multiple causal variants at each risk locus and either have (+) or do not have (−) access to functional data across different ethnic study designs. The bottom row represents the relative gain in the median 90% causal-variant resolution of trans-ethnic cohorts over the next best-performing group.

Genetic-Trait Architecture Affects Fine-Mapping Performance

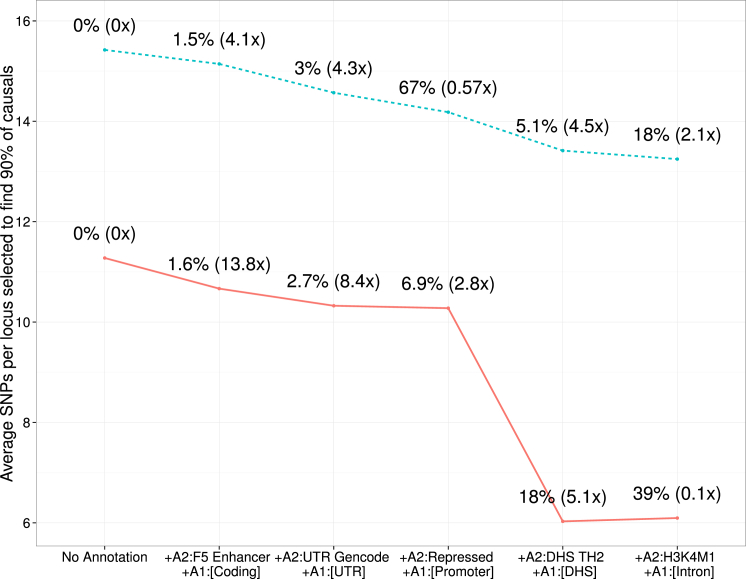
Functional information was demonstrated to improve fine-mapping resolution in a single population,^10,28,37,38 and we investigated the potential gains in a trans-ethnic setting. We simulated two disease architectures by using five functional annotations where causal variants either localize predominantly within a single broad functional class, as observed by Gusev et al.³⁵ (A1), or have a smaller, more diffuse localization within functionally specific cell types²⁸ (A2). For each class of disease architectures, we fit six trans-ethnic integrative models such that each successive model incorporated an additional functional annotation into a joint framework. Not surprisingly, when the true genetic architecture of a trait at fine-mapping regions has a strong enrichment of causal variants within a common functional class (i.e., DHSs³⁵), these functional annotations will be most informative for the purposes of fine mapping (see Figure 3). On the other hand, more diffuse localization of causal variants requires multiple annotations for maximizing the utility of functional data. For example, for genetic architecture A1, the addition of the DHS annotation yielded a 70% increase in fine-mapping resolution, whereas genetic architecture A2 required all five annotations to improve resolution by 18% (see Figure 3).

Figure 3.

The Underlying Functional Architecture of a Trait Affects Fine-Mapping Performance

We simulated two classes of disease architectures: A1 (solid line) and A2 (dashed line). Architecture A1 was based on the functional enrichment observed in Gusev et al.³⁵ and had a strong enrichment within a single DHS class. Architecture A2 was simulated with a more diffuse enrichment in various cell types and classes and was based on what we empirically observed in the RA dataset. Displayed on top of each point is the percentage of SNPs falling within that annotation and its corresponding enrichment.

Integrative Fine Mapping in a Multi-ethnic RA Dataset

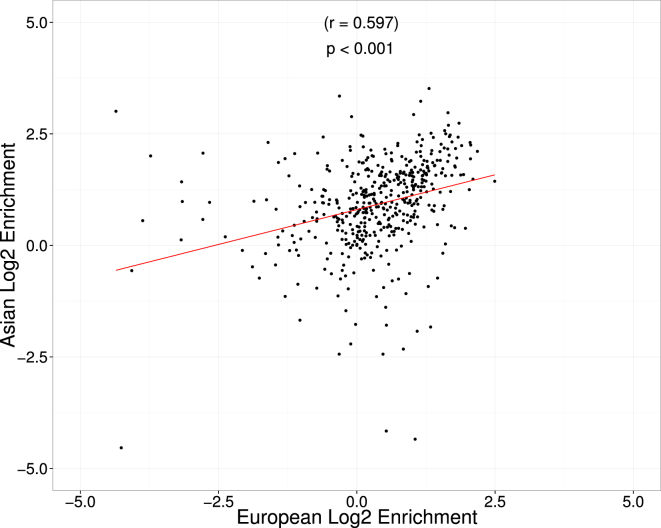
We investigated whether similar results from simulations can be attained in empirical data from a trans-ethnic RA GWAS over more than 100,000 individuals⁴ (see Material and Methods). Because the functional genetic architecture of RA across different populations is unknown, we first quantified whether the enrichment of causal variants in various functional annotations is consistent across ancestries. Reassuringly, we saw a strong correspondence in functional enrichment at the fine-mapping loci across all 482 functional categories we investigated (r = 0.597; Figure 4). This provides evidence supporting the assumption that a single functional prior can be applied across populations uniformly in trans-ethnic fine mapping.

Figure 4.

Functional Enrichment Is Consistent across Europeans and Asians

We compared the enrichment across 482 functional annotations at 89 RA-associated loci in Europeans (n ≈ 68,000) and Asians (n ≈ 36,000) separately. Each point represents the estimated enrichment of an annotation in both European and Asian populations.

Next, we estimated trans-ethnic enrichment for each of the 482 annotations independently to allow the model to discern the most functionally relevant cell types and classes. The enrichment likelihood ratios supplied by this procedure provide a natural way to prioritize functional annotations to move forward with fine mapping.²⁸ We consistently found a strong and significant enrichment of causal variants within activity regulatory regions of immune-related cell types (see Figure 5), which is largely in line with RA etiology (rank permutation p < 0.001). The final trans-ethnic integrative model included annotations of DHS regions specific to three cell types (skin keratinocytes, T helper 2 cells, and B lymphocytes), immune enhancer regions described in Farh et al.,¹⁰ and GENCODE-defined exon regions. We found that simply applying existing multi-causal frameworks^27,28 on the trans-ethnic meta-analysis statistics yielded wider 90% credible sets (it required approximately 28.5 SNPs per locus as opposed to 24.0 SNPs per locus for our proposed framework), thus demonstrating the benefit of modeling population-level LD. Furthermore, the integration of functional data additionally reduced the size of the credible set to 21.7 SNPs per locus (see Table 3), showing that leveraging functional annotations refines trans-ethnic fine-mapping signal.

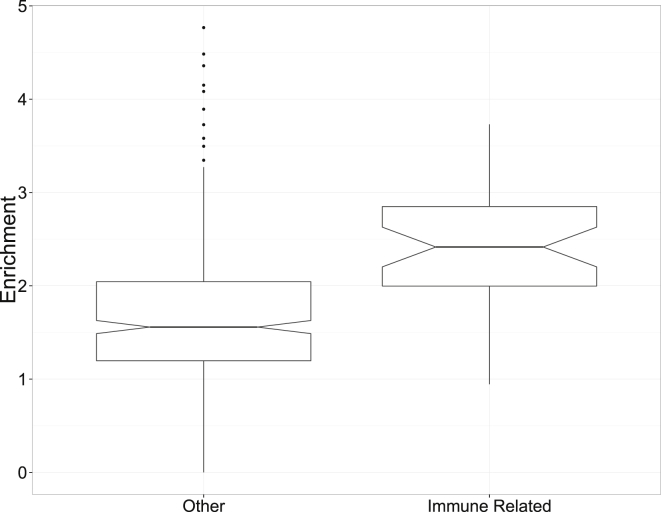
Figure 5.

Trans-ethnic Functional Enrichment at RA GWAS Loci Indicates Immune-Related Regulatory Architecture

Here, we compare the enrichment of casual variants within 42 DHSs of immune-related cell types (B cells, T cells, natural killer cells, keratinocytes, monocytes, and thymic cells) and the enrichment of causal variants in 354 DHS annotations of other cell types. The widths of the notches in each boxplot roughly correspond to 95% confidence intervals for the median enrichment.

Table 3.

Integrative Approaches that Model Population-Level LD Yield the Smallest Credible Sets in Empirical Data

Association Statistics	Average No. of SNPs
Without Annotations	With Annotations
Asians	35.2	31.9
Europeans	32.0	28.7
Fixed-effects meta-analysis	28.5	25.0
Trans-ethnic	24.0	21.7

Displayed here is the average number of SNPs per locus in the 90% credible sets for single and multi-population fine mapping of RA-associated loci. To compute credible sets, we first ordered the SNPs across all 89 loci and then took the total number of ordered SNPs that consumed 90% of the total posterior probability mass. Consistent with simulation findings, integrating multiple populations with functional data improved fine-mapping resolution.

Next, we explored the plausible causality of the SNPs that attained a high posterior probability under our framework (Table 4). For example, rs968567, which lies within the promoter region of FADS2 (OMIM: 606149) and was functionally validated to disrupt transcription factor binding and subsequent gene expression,⁵² achieved a trans-ethnic posterior probability of 0.29. However, this variant fell within all five functional annotations that our framework deemed important for this trait and, upon appropriate re-weighting, achieved a posterior probability of 0.84. Alternatively, trans-ethnic association can be extremely beneficial on its own. For example, rs12693993, a variant within the coding region of CD28 (OMIM: 186760), a gene implicated for its importance in T cell development and proliferation and cytokine production, achieved a posterior probability for causality of 0.34 and 0.02 in Europeans and Asians, respectively. However, upon integration of trans-ethnic association with functional data, it achieved a posterior probability for causality of 0.85. The identification of these two SNPs, among others, serves as an important illustration of the benefit of our proposed methodologies.

Table 4.

Integrating Trans-ethnic Association Strength with Functional Data Promotes a Number of SNPs to Attain a High Posterior Probability for Causality

rsID	Chromosomal Position	European Association (Z Score)	Asian Association (Z Score)	Posterior Probability without Annotations	Posterior Probability with Annotations	Functional Annotations
rs2476601	chr1: 114,377,568	−26.04	NA	1.00	1.00	coding exons, skin keratinocyte DHSs
rs7731626	chr5: 55,444,683	−9.84	NA	1.00	1.00	GM12865 DHSs, Th2 DHSs, immune enhancers
NA	chr1: 2,523,878	−5.22	−4.18	1.00	1.00	immune enhancers
rs1893592	chr21: 43,855,067	−5.73	−4.01	1.00	1.00	coding exons, immune enhancers
NA	chr19: 10,771,941	−6.13	NA	1.00	1.00	immune enhancers
rs72767222	chr5: 55,440,788	5.11	NA	0.99	0.99	skin keratinocyte DHSs, immune enhancers
rs12715125	chr3: 27,763,427	5.58	NA	0.95	0.99	coding exons, GM12865 DHSs, Th2 DHSs, skin keratinocyte DHSs, immune enhancers
rs71508903	chr10: 63,779,871	7.26	5.88	0.76	0.93	GM12865 DHSs, skin keratinocyte DHSs, immune enhancers
rs12693993	chr2: 204,595,597	−2.74	−1.76	0.68	0.88	Th2 DHSs, skin keratinocyte DHS, immune enhancers
rs968567	chr11: 61,595,564	−4.95	NA	0.29	0.85	coding exons, GM12865 DHSs, Th2 DHSs, skin keratinocyte DHSs, immune enhancers
rs909685	chr22: 39,747,671	6.29	4.62	0.65	0.84	Th2 DHSs, skin keratinocyte DHSs, immune enhancers
rs657075	chr5: 131,430,118	2.54	4.46	0.73	0.82	skin keratinocyte DHSs, immune enhancers

We applied our framework across all 89 GWAS RA loci with relevant functional data. Displayed in this table are SNPs achieving a trans-ethnic posterior probability of greater than 0.8. Abbreviations are as follows: NA, not applicable; Th2, T helper 2 cell.

Discussion

In this work, we introduced a fine-mapping framework that bridges several sources of evidence to prioritize functional SNPs and demonstrated its efficacy in real and simulated datasets. As fine-mapping data become increasingly multi-ethnic^3,4 and functional data become larger and more refined,³⁰ we believe that our proposed methodology will have increasing relevance. By operating exclusively on summary data, our approach reduces the need to share individual data, which often prohibits large-scale analyses. In addition, a key advantage of our proposed methodology is that it provides an unbiased perspective on which functional genomic data are most relevant to the trait within an Empirical Bayes framework. Rather than relying on careful and manual selection of functional elements when conducting fine mapping,^10,36 we allow the data to dictate the functional relevance of a particular annotation. As the catalog of functional data expands to encompass more diverse cell types and genomic signatures, a principled strategy to parsing these annotations is paramount.

We note that although our model does not assume a priori that there exists allelic heterogeneity by ancestry,¹⁵ by construction, it is capable of handling trans-ethnic heterogeneity whether it is due to a true difference in the per-allelic effects or simply a result of genetic drift that yielded distinct allele frequencies at the causal SNPs. We have found that as the level of heterogeneity across populations increases, our framework increasingly outperforms competing strategies. Although extreme heterogeneity might be unlikely, gene-environment interactions in complex traits can manifest themselves as distinct allelic effects across populations.⁵³

We conclude with several limitations of our proposed framework. The efficacy of our proposed method is intimately connected to the underlying functional architecture of the trait being examined. In the scenario where the correct functional annotation is unavailable or the distribution of casual variants is more or less uniform across the functional-annotation categories, our method will most likely underperform fine-mapping strategies that either do not estimate parameters for functional enrichment^27,46 or pre-specify the correct enrichment parameters from other external analyses.³⁵ However, there is mounting evidence that suggests that casual variants for most complex traits co-localize with epigenetic marks^10,31,35,37 that are now available for the vast majority of human cell types.⁵⁴ Finally, additional improvements in performance could be made through a Bayesian treatment of non-centrality parameters within our framework,⁴⁶ which we leave as a potential direction for future work.

Published: July 16, 2015

Appendix A: Optimization Procedure

We optimize the parameters of our model by using expectation maximization. First, we take expectations of the complete data log-likelihood with respect to the posterior distribution of causal sets and simplify to obtain a function, Q, that is readily optimized via standard techniques. Let $Z_{l,\ast }$ represent all P vectors of association statistics $\left(Z_{l,1},Z_{l,2},\cdots ,Z_{l,P}\right)$ at locus l, and let ${\lambda }_{l,\ast }$ be the corresponding vectors of non-centrality parameters,

$$\begin{array}{c}Q\left(\gamma ,\lambda |{\gamma }^{\left(t\right)},\lambda \right)=\sum _l\sum _{C_l}P\left(C_l|Z_{l,\ast }{\lambda }_{l,\ast },{\gamma }^{\left(t\right)}\right)\text{ln}P\left(Z_{l,\ast };{\lambda }_{l,\ast },{\gamma }^{\left(t\right)}\right)\\ =\sum _l\sum _{C_l}P\left(C_l|Z_{l,\ast }{\lambda }_{l,\ast },{\gamma }^{\left(t\right)}\right)\left(\text{ln}P\left(C_l;{\gamma }^{\left(t\right)}\right)+\sum _p\text{ln}P\left(Z_{l,p}|C_l,{\lambda }_{l,p}\right)\right)\\ =\sum _l\sum _{C_l}P\left(C_l|Z_{l,\ast }{\lambda }_{l,\ast },{\gamma }^{\left(t\right)}\right)\text{ln}P\left(C_l;{\gamma }^{\left(t\right)}\right)+\sum _l\sum _{C_l}P\left(C_l|Z_{l,\ast },{\gamma }^{\left(t\right)},{\lambda }_{l,\ast }\right)\sum _p\text{ln}P\left(Z_{l,p}|C_l,{\lambda }_{l,p}\right)\\ =Q\left(\gamma |{\gamma }^{\left(t\right)}\right)+Q\left({\lambda }_p|{\lambda }_p\right),\end{array}$$

thereby decoupling the prior from the likelihood. We simplify $Q\left(\gamma |{\gamma }^{\left(t\right)}\right)$ to obtain

$$\begin{array}{l}Q\left(\gamma |{\gamma }^{\left(t\right)},\lambda \right)=\sum _l\sum _j\sum _{c_{jl}\in \mathrm{0,1}}P\left(c_{jl}|Z_{l,\ast };{\gamma }^{\left(t\right)},{\lambda }_{l,\ast }\right)\text{ln}P\left(c_{jl};{\gamma }^{\left(t\right)}\right)\\ =-\sum _l\sum _{j}P\left(c_{jl}=1|Z_{l,\ast };{\gamma }^{\left(t\right)},{\lambda }_{l,\ast }\right)\text{ln}\left(1+\text{exp}\left(-{\gamma }^T{A}_{jl}\right)\right)\\ -\sum _l\sum _{j}P\left(c_{jl}=0|Z_{l,\ast };{\gamma }^{\left(t\right)},{\lambda }_{l,\ast }\right)\text{ln}\left(1+\text{exp}\left({\gamma }^T{A}_{jl}\right)\right),\end{array}$$

which is a concave function whose gradient is simply

$$\begin{array}{l}\frac{\partial Q\left(\gamma |{\gamma }^{\left(t\right)},\lambda \right)}{\partial \gamma }=\sum _j\sum _{l}P\left(c_{jl}=1|Z_{l,\ast };{\gamma }^{\left(t\right)},{\lambda }_{l,\ast }\right)\frac{1}{1+\text{exp}\left(-{\gamma }^T{A}_{jl}\right)}{A}_{jl}\\ -\sum _j\sum _{l}P\left(c_{jl}=0|Z_{l,\ast };{\gamma }^{\left(t\right)},{\lambda }_{l,\ast }\right)\frac{1}{1+\text{exp}\left({\gamma }^T{A}_{jl}\right)}{A}_{jl}.\end{array}$$

To avoid potential numerical instability resulting from inverting a Hessian matrix, as would be required for standard Newton-Raphson, we optimize this function Q by using a limited-memory Broyden-Fletcher-Goldfarb-Shanno algorithm implemented in the NLopt library. Finally, as previously mentioned, the non-centrality parameter for SNP j at locus l from population p, ${\lambda }_{p,l}^j$, is set simply as

$$f\left(Z_{p,l}^j\right)=\{\begin{array}{cc}\text{arg}\text{min}\left(-3.7,Z_{p,l}^j\right)& \text{if}{Z}_{p,l}^j<0\\ \text{arg}\text{max}\left(3.7,Z_{p,l}^j\right)& \text{if}{Z}_{p,l}^j>0\\ 0& \text{if}{Z}_{p,l}^j=0\left(\text{SNP}j\text{is monomorphic in population}p\right),\end{array}$$

a strategy that was previously demonstrated to work well in practice.²⁸ This iterative algorithm is repeated until the change in the log-likelihood is less than 0.01.

Web Resources

The URLs for data presented herein are as follows:

• 1000 Genomes, http://www.1000genomes.org/data

• DHS maps 1, http://www.uwencode.org/proj/Science_Maurano_Humbert_et_al/

• DHS maps 2, http://hgdownload.cse.ucsc.edu/goldenPath/hg19/encodeDCC/wgEncodeAwgDnaseUniform/

• ENCODE Genome Segmentation, http://hgdownload.cse.ucsc.edu/goldenPath/hg19/encodeDCC/wgEncodeAwgSegmentation/

• Ensembl, http://www.ensembl.org/index.html

• FANTOM 5, http://fantom.gsc.riken.jp/5/data/

• Finemapping Data Portal, http://www.broadinstitute.org/pubs/finemapping/?q=data-portal

• OMIM, http://www.omim.org

• PAINTOR, http://bogdan.bioinformatics.ucla.edu/software/paintor/

• RA GWAS summary statistics, http://plaza.umin.ac.jp/∼yokada/datasource/software.htm