A Novel Methodology for the Simulation of Athletic Tasks on Cadaveric Knee Joints with Respect to In Vivo Kinematics

Abstract

Six degree of freedom (6-DOF) robotic manipulators have simulated clinical tests and gait on cadaveric knees to examine knee biomechanics. However, these activities do not necessarily emulate the kinematics and kinetics that lead to anterior cruciate ligament (ACL) rupture. The purpose of this study was to determine the techniques needed to derive reproducible, in vitro simulations from in vivo skin-marker kinematics recorded during simulated athletic tasks. Input of raw, in vivo, skin-marker-derived motion capture kinematics consistently resulted in specimen failure. The protocol described in this study developed an in-depth methodology to adapt in vivo kinematic recordings into 6-DOF knee motion simulations for drop vertical jumps and sidestep cutting. Our simulation method repeatably produced kinetics consistent with vertical ground reaction patterns while preserving specimen integrity. Athletic task simulation represents an advancement that allows investigators to examine ACL-intact and graft biomechanics during motions that generate greater kinetics, and the athletic tasks are more representative of documented cases of ligament rupture. Establishment of baseline functional mechanics within the knee joint during athletic tasks will serve to advance the prevention, repair and rehabilitation of ACL injuries.

Introduction

Six-degree-of-freedom (DOF) robotic manipulators have been used to simulate knee joint motions on cadaveric specimens for two decades.¹⁶ These prior investigations have gleaned important biomechanical information on the function of the anterior cruciate ligament (ACL) and the relative performance of various reconstructions (ACLR) during simulated clinical motions, such as the Lachman's and pivot shift tests and walking gait cycles.^{6,11,21,23,36} These clinical tests were created to assess normal ACL and ACLR integrity, but do not assess how the native ACL or ACLR functions during activities of daily living (ADLs) including athletic activities. While gait is a physiologic activity, it does not provide insight into the potential injury mechanics or how ACLRs will perform in return to sport. ACL injuries are most commonly associated with tasks that involve rapid deceleration and/or change in direction, and these same activities will provide a significant challenge to the ACLR.⁵ Therefore, to better understand the biomechanical precursors to ACL injury and assess the performance of ACLR grafts in athletic settings it would be valuable to simulate jump landing and sidestep cutting tasks on cadaveric specimens using six DOF robotic manipulators.

In order to execute joint simulations, robotic manipulators require kinematic positional or kinetic force data inputs to define the 6-DOF of motion. Unfortunately, 3D kinematics collected in vivo from skin-marker-based motion capture are known to incorporate multiple sources of error.^3,4,29,32,33 It has been documented that, relative to the gold-standard of biplanar-videoradiography-based motion capture, skin-based markers overestimate the range of motion (ROM) that occurs in the three rotational degrees of freedom of the knee during athletic tasks.²⁹ In respect to the translational DOFs, the standard errors associated with data collection can exceed the ROMs that actually occur within the knee joint.³ Such large errors make translational kinematics unreliable and, unless bone-pin markers or videoradiography were used during capture, they often go unreported for this reason. In relation to cadaveric simulations, the noted errors can lead to impingement of the bony structures and/or excessive distraction within the joint. When large enough, these disassociations of the joint can result in structural damage. In order to avoid the confounding errors described, the majority of robotic simulations of motion on cadaveric knee joints up to this point has been confined to clinical exams such as the Lachman's and pivot-shift tests.² While valuable clinical tools, these exams limit the knee to controlled uni-and bi-axially motion without respect to in vivo kinematics, which is not conducive to the physiologic joint loading that occurs during sport. Specifically, current robotic simulation models are limited to clinical exams or gait,² neither of which are readily associated with mechanisms of ACL injury. An in vitro robotic simulation of in vivo athletic tasks that involve the rapid deceleration motion associated with non-contact ACL rupture would offer investigators a novel mechanism to directly assess intra-articular knee mechanics during movements that are actually linked to injury risk.^5,22,27,31 Such a simulation would allow investigators to examine ACLs and ACL reconstruction grafts in a more physiologically-relevant loading environment. Data from simulations of this nature could likely lead to improvements in ACL injury prevention and repair. Therefore, in order to create such physiologically-representative in vitro simulation from in vivo motion data, investigators must account for the aforementioned sources of error.

The purpose of this report is to define techniques used with a 6-DOF robotic manipulator to create reproducible, physiologically-representative, in vitro simulations derived from in vivo skin-marker-based kinematics recorded during athletic tasks. It was hypothesized that the novel methodology presented would produce reliably reproducible cadaveric simulations intra-specimen as well as between-specimens that would not cause joint damage when applied across a multitude of specimens.

Methods

Specimen preparation

Lower extremity cadaveric specimens were defined from the femoral head to the distal end of the tibia and were obtained from an anatomical donations program (Anatomical Gifts Registry, Hanover, MD). Specimen criteria were defined as no previous history of knee trauma, knee surgery, bone cancer, or ankle or shin implants. The limbs were kept frozen at -20° C until the day before testing, then removed from the freezer and allowed to thaw overnight. Specimens were dissected down to the joint capsule, leaving the collateral and cruciate ligaments and menisci intact. Anatomical landmarks at the center of the femoral head, femoral condylar notch, femoral lateral collateral ligament origin, femoral medial collateral ligament origin, medial tibial spine, tibial lateral collateral ligament insertion, tibial medial collateral ligament insertion, and distal tibial articular surface were used to locate the joint coordinate system of the knee according to Grood-Suntay system.¹⁷ The joint coordinate system was used to define the placement of mechanical fixtures on the tibia and femur of each specimen as has been previously reported in the literature.^6,20,21,30 Briefly, on the femur, a cylinder was placed over the long axis of the bone approximately 10 cm proximal to the joint line.⁶ On the tibia, a rod defining the medial/lateral axis was drilled through two points just distal of the LCL and MCL insertion sites and in line with the tibial spines. A pipe defining the longitudinal axis was then secured over the distal end of the bone and oriented perpendicular to the rod and parallel to the long axis of the bone. In order to fit this pipe around the distal geometry of the tibia, the bone was cut transversely 15 cm inferior to the joint line and the fibula was cut inferior to the insertion site of the lateral collateral ligament. The transverse cut through the tibia also allowed for the robot end effector to be affixed as closely as possible to the knee joint center without disrupting any of the tibial attachment sites for the remaining, intact joint structures. After being positioned, both the femoral and tibial fixtures were filled with bone cement that was further secured in place with Steinmann pins drilled through the bones after being positioned. The tibial fixture was attached to a 6-axis load cell (Theta Model Industrial Automation Load Cell, ATI Industrial Automation, Apex, NC) mounted on the end effector of a 6-DOF robotic manipulator (KR210; KUKA Robotics Corp., Clinton Township, MI). A digital coordinate measuring machine (FARO Gauge; FARO Technologies, Lake Mary, FL) was used to determine the tibial coordinate system within the robot coordinate axes and define the knee joint center.^6,17 The femur was then secured to a rigid base and the robotic manipulator moved the tibia with respect to the static femur, Figure 1. 6-DOF kinematic inputs were then used to drive the robotic simulations.

Figure 1.

Depicts frontal and sagittal plane views of a lower-extremity, cadaveric specimen affixed to the 6-DOF robotic manipulator and prepared for the simulation of athletic tasks at the knee joint.

3-dimensional (3D) optical motion capture

Kinematic data were collected on a male (age = 24; height = 175 cm; mass = 68.8 Kg) and female subject (age = 25; height = 170 cm; mass = 64.4 Kg) who were matched for age, height, mass, and athletic activity. These subjects were devoid of prior knee injuries and participated in athletics at the time of data collection. Informed consent was obtained from each subject prior to data collection and testing procedures were approved by the Cincinnati Children's Hospital IRB.

Thirty-seven (37) skin-based, retroreflective markers were instrumented at anatomical landmarks on each subject in a modified Helen Hayes marker set.¹⁵ Motion was sampled at 240 Hz with a 10-camera motion analysis system (Eagle cameras, Motion Analysis Corporation, Santa Rosa, CA). Ground reaction force (GRF) data was simultaneously sampled at 1200 Hz with dual, in-ground, multi-axis force platforms (AMTI, BP600900, Watertown, MA) such that each platform corresponded with a single leg.¹⁵

Participants performed three trials each of a drop vertical jump (DVJ) and sidestep cutting task as previously described.^13,14 3D kinematics data were processed through Visual3D (version 4.0, C-Motion, Inc., Germantown, MD) with custom MATLAB code (version 2012b, The Mathworks, Inc., Natick, MA) using an established biomechanical model.¹⁵ Marker trajectories were filtered through a fourth-order, low-pass, digital filter with a cutoff frequency of 6 Hz, while GRF data were filtered at a cutoff frequency of 100 Hz for calculation of lower extremity joint kinematics and kinetics within the Visual3D model. Kinematic and kinetic data was time normalized to 101 points starting with initial ground contact and ending when the minimum center of gravity was achieved. This period represents the landing phase of an athletic task where injury is most likely to occur.^1,27 Kinematic curves for all three trials were averaged into an ensemble subject mean for each motion performed. 3D kinematics have demonstrated high intra-session waveform reliability in previous literature, with interclass correlation coefficients and coefficients of multiple correlation (CMC) values above 0.600 in most all DOFs.¹⁵ As such each of the three in vivo trials recorded from each subject were averaged into a set of subject mean kinematics for each motion task performed.

Rotational kinematic input

Scale factors were developed to restrict the overestimation of in vivo ROMs recorded for each rotational DOF. These scale factors were determined via comparison of 3D motion data that was concomitantly collected with biplanar videoradiography and skin-markers throughout the stance phase of sidestep cutting tasks.²⁹ Based on the literature, the biplane videoradiographic range of motion was 47.0% of the skin-marker range in internal/external rotation, 85.0% in flexion/extension, and 78.7% in abduction/adduction. The athletic tasks to be simulated via the 6-DOF robotic manipulator were of a similar level of rigor as those performed in the literature. Therefore, to reduce rotational overestimation from in vivo recordings, the listed scale factors were individually applied to each rotational DOF. These scaled rotational curves were then used as input to control the robotic manipulator. A representative set of input kinematics from the male DVJ are displayed in Figure 2, while kinematic input from the remaining three athletic tasks are available in the supplemental attachment to this manuscript (Figure S1, Figure S4, Figure S7).

Figure 2.

Rotational knee joint kinematics recorded in vivo (solid line) with the adjusted input for the robotic manipulator (dashed line). All 3 rotational degrees of freedom from a male subject DVJ are represented. Time series was normalized to percent of landing phase.

Translational kinematic input

Early iterations of this model attempted to directly utilize in vivo recorded kinematic translations derived from skin-based markers as input constraints to drive simulations. However, the need for adjustments became apparent when these recorded translations consistently caused specimens to fail via oblique femoral fracture. Kinematic errors propagated from skin-artifacts were too great for the simulation model to sustain as the tibia was being driven through the femur rather than around the articulating surface of the knee. To reduce the influence of skin-artifact errors on outcome measures, a single set of translational input was established for each motion task and utilized as input for all simulated conditions of that task. Translational input for the compression/distraction DOF were selected from in vivo recordings and were based on curve shape. For each athletic task, the male and female kinematics recorded in vivo were examined and the compression/distraction curve that best emulated the trajectory of the vertical ground reaction force curve was selected to represent this DOF. The anterior/posterior motion that corresponded with the selected compression/distraction curve was also used. Prior to this investigation, the previously specified digital coordinate measuring machine was used to collect pilot data on the translational ROMs experienced by the tibia when cadaveric knees were passively flexed from 0-90°. In order to do this, the coordinate measuring machine was used to track the position of the tibial origin in 5° increments as it was hand-flexed about the femur while maintaining constant contact between both compartments of the tibial plateau and the articular surface of their respective femoral condyles. The purpose of this pilot testing was to establish functionally realistic ranges of translational motion in the knee throughout a flexion. The ROM of the origin of the tibial axis with respect to the origin of the femoral axis was 7-8 mm in the anterior/posterior DOF, which compares favorably to the 8-10 mm ROM previously reported during a videoradiographic investigation of sidestep cutting.²⁹ In order to articulate around, rather than through, the bony geometry of the knee, the translations recorded in vivo were adjusted to match to this ROM. It was previously been demonstrated in the literature that the anterior/posterior ROM at the knee during passive flexion and during a dynamic task are comparable.⁹ This made the anterior/posterior DOF ideal to initiate translational adjustments. Compression/distraction input was then scaled to exhibit 0.6 times the ROM of the anterior/posterior curve. This factor was established relative to the ROM relationships observed in the pilot data. Medial/lateral translations recorded in vivo consistently exhibited unrealistically large ROMs in excess of 1 cm. During passive flexion, the mean medial/lateral ROM was under 2 mm. Previous literature has demonstrated that small perturbations in the medial/lateral DOF during robotic knee simulations have a negligible effect on joint forces and torques.²⁰ Therefore, rather than input data degraded by skin artifact error, the medial/lateral DOF did not change from the initial limb alignment, Figure 3.

Figure 3.

Translational knee joint kinematics recorded in vivo (solid line) with the adjusted input for the robotic manipulator (dashed line). All 3 rotational degrees of freedom from a male subject DVJ are represented. Time series was normalized to percent of landing phase.

Initial position

The limb was initially oriented to the rotations specified by the scaled in vivo kinematics at the time of initial contact. Initial translational orientation was defined by articulating the specimen to a position that satisfied the conditions of near zero joint forces and torques, articular cartilage contact in both the medial and lateral compartments on the tibial plateau, and minimal distance between the origins of the tibial and femoral coordinate axes. During in vivo testing, initial contact represented the time point when 10 N of force registered on the force platform. Therefore, the net external forces propagated to the knee joint should initially be negligible, which supports a zero force orientation. While this process determined a good preliminary position for the specimen, muscle pre-activation makes it unlikely that the joint is actually unloaded at initial contact. However, when the joint was compressed relative to the force normalization parameters described below, forces were incorporated at initial contact that may represent muscle pre-activation.

Force normalization

In vitro joint forces and torques were measured with a 6-DOF force sensor mounted on the end effector of the robotic manipulator that was aligned with the vertical anatomical axis of the tibia for each specimen as was previously noted. The force sensor was calibrated up to 2500 N axial force and 120 N*m torque. This method has been readily applied during previous robotic simulation protocols.^6,21,30 Previous in vivo investigations have demonstrated that subjects generate between 2.0-2.5 times bodyweight of vertical ground reaction force per leg when landing from a drop DVJ with an initial height of 31 cm.¹ As approximately 90% of a person's mass is supported above the knee,^10,25,37 axial joint compression was applied through the tibia while the joint was oriented in the initial contact position. As previously described, the vertical axis of the force sensor was aligned with the mechanical axis of the tibia; therefore, axial joint compression acting on the knee was measured directly through the tibia. This axial compression was incrementally increased until peak compressive forces recorded within each knee during simulation were between 2.0-2.5 times bodyweight, relative to each specimen's weight. Thus, the parameter of peak axial joint compression was defined with respect to previously recorded in vivo reaction force values from a large population cohort.¹ Once set, initial axial force was maintained throughout all simulations related to a single task. Between tasks, the axial compressive force would be removed and re-identified during preconditioning cycles. Initial axial joint compression for sidestep cutting simulations were established in a similar manner.

Simulation Duration

Simulations of the DVJ and sidestep cut were restricted to the landing phase of their respective motions. Landing phase has been previously defined in the literature and consists of the period between initial contact with the force platforms and minimum height of the center of mass.¹ For the present subjects, landing phase spanned 0.25 sec for the male and 0.23 sec for the female. These values correspond well with previous literature that indicates landing phase duration is approximately 0.25 sec during a DVJ.¹ The landing phase was isolated for simulation as this stage represents the timeframe where the ACL is most likely to experience injury and should be exposed to the most significant loading from ground reaction forces. Video analysis of ACL injuries supports this timeframe as footstrike was noted to immediately precede leg collapse in all observed noncontact injuries.²⁷

Reliability

Once established, the presented methodology was applied to 19 limbs from 12 unique donors (age = 47.9 ± 7.0 years; total body weight = 832 ± 190 N, height = 172.9 ± 12.0 cm). Three additional specimen were excluded due to specimen failure or non-functional ACLs. Specimens were preconditioned for 10 cycles, then simulated through an additional 10 cycles where force/torque values were recorded by the force sensor. One cycle consisted of simulating the input kinematics for a given task from the point of initial contact through the point where minimum center of gravity was achieved in vivo and then retracting that kinematic path back to the starting position. The period from initial contact through minimum center of gravity is known as landing phase and is used in biomechanical analysis as it represents the period where ACL injuries are most likely to occur.¹ Only data from the first half of each cycle, where the specimen was moving forward through the input kinematic pathway, were considered for analysis. A mean of the 8^th and 9^th cycle from each 10-cycle test were used for statistical analysis to eliminate cycle effects. All data was time normalized to percentage of landing phase. Waveform reliability for the entire landing phase was calculated between specimens using CMC.^18,26 CMC was developed, and has been used, to assess the reliability of joint kinetic and kinematic data collected via in vivo motion capture during dynamic tasks.^15,26 Clinically, CMCs of <0.4 are considered poor, 0.4-0.75 are considered fair-to-good, and >0.75 are considered excellent.¹² Calculations were performed with custom code in MATLAB.

Results

The use of the raw skin-marker-based, in vivo motion capture kinematics as position-control input for robotic simulations of athletic tasks at the knee joint resulted in consistent specimen failure (Figure 4). Femoral fracture (Figure 4b) was the most common form of failure with raw kinematics as the femur could not support the large shear forces generated from improper tibial alignment during deep flexion.

Figure 4.

Failures that resulted after raw in vivo kinematics were used as input to drive the robotic simulations. Tibia fracture from excessive joint compression (A), femoral fracture from excessive anterior translation (B), and lateral joint dislocation from overestimated rotations (C).

Following the described methodology, a robotic manipulator simulated 6-DOF knee motion corresponding to DVJs and sidestep cutting with no damage to the specimen (Video 1). Reliability and functionality outcomes were consistently excellent across all four simulated motion tasks. As such the results from male DVJ task were randomly selected for representation due to publication space restrictions. Corresponding data for the simulated female DVJ, male sidestep cut, and female sidestep cut are available in the supplement to this manuscript (Figures S1-S9). Joint kinetics recorded by the force sensor across multiple motion cycles of the male DVJ indicated that the athletic task articulations were consistently reproducible throughout the simulation (Figure 5). This was also true of the additional motion tasks simulated (Supplemental Figure S2, Figure S5, Figure S8). The specimen depicted in Figure 5 had a mass of 848 N and exhibited a maximal compressive force of 1726 N (2.03 * body weight) during simulation, which was within our design parameters. Peak internal joint torques attained at this level of loading were physiologically sustainable as mean peak torques exhibited by the specimen across all simulated cycles were 52.37 ± 2.13 N*m in knee extension, 25.80 ± 1.38 N*m in knee adduction, and 6.84 ± 0.30 N*m in knee external rotation. Between-subject CMC reliability for all 3 translational DOFs and all 3 rotational DOFs was excellent with all values exceeding 0.930 in the male DVJ and 0.860 overall (Table 1; Figure 6). Between-subject CMC reliability for the female DVJ, male sidestep cut, and female sidestep cut simulations visually depicted in the supplemental attachment to this manuscript (Figure S3, Figure S6, Figure S9).

Figure 5.

Unfiltered internal knee torques and translational forces during each cycle of a 10-cycle male DVJ simulation on a single specimen. After viscoelastic effects have been compensated, the forces and torques produced at the knee were highly reliable between cycles.

Table 1.

CMC values for each DOF across all specimens for each of the simulated motion tasks.

	Male DVJ	Female DVJ	Male Cut	Female Cut
Anterior/Posterior	0.957	0.987	0.975	0.867
Medilal/Lateral	0.990	0.990	0.988	0.989
Compression/Distraction	0.964	0.965	0.968	0.950
Internal/External	0.934	0.935	0.951	0.888
Flexion/Extension	0.963	0.991	0.986	0.916
Abduction/Adduction	0.982	0.967	0.987	0.989

Figure 6.

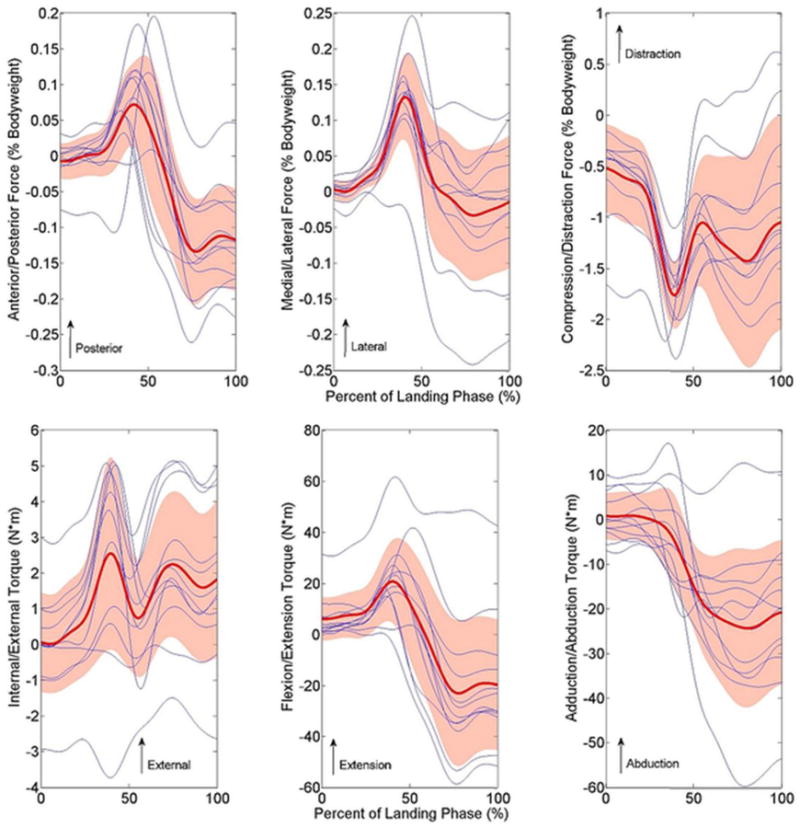
Knee joint loading for all 12 unique donors throughout the DVJ simulation that was derived from the male model. Blue lines represent individual subjects, while the red line and shaded area represent the population mean and standard deviation, respectively. Waveforms were highly repeatable between specimens as CMC values exceeded 0.900 in all DOFs.

Discussion

The techniques defined in this investigation allowed a 6-DOF robotic manipulator to successfully simulate physiologically-representative motions from skin-marker-based recorded in vivo athletic tasks, which supported the hypothesis. Development of a methodology to simulate physiologic, in vivo athletic tasks offers investigators several advantages over current methods. Current robotic simulations are limited to clinical tests that do not represent physiologic motion or low intensity gait cycles, neither of which represent tasks related to ACL injury. The simulation of athletic tasks represents an advancement that will allow investigators to examine ligament biomechanics over a broader range of activities, with the potential to examine biomechanics during activities that are associated with non-contact ACL injuries.^5,31 Additionally, a variety of kinematic adjustments can be incorporated into the proposed methodology to simulated the biomechanical effects of ACL injury risk factors, such as exaggerated knee valgus,²² on intra-articular knee loading. Also, as with previous methods, the current technique can be combined with ACLRs to evaluate the performance of graft type and surgical strategies during athletic tasks.^11,24,36 As one of the objectives of ACLR is to return athletes to sport, biomechanical data on graft performance in simulated athletic environments could prove instrumental for improving the tissue engineering, surgical, and rehabilitation design parameters.

Functional tissue engineering has demonstrated that ACLR graft constructs do not need to replicate the maximal mechanical properties of the intact-ACL. Rather, grafts only need to function at and provide a safety factor for physiologically relevant levels of mechanical loading that are seen during activates of daily living.⁷ However, there exists a disparity between graft failure mechanics and those of activities of daily living.² Similarly, there is also likely a disparity between ADLs and athletic tasks. Grafts that perform well during robotic simulations of clinical tasks and ADLs may not function as effectively during athletic tasks. Therefore, it is important to understand ACL and ACLR biomechanics during athletic tasks, as return to sport is often a driving factor behind patients choosing ACL reconstruction.³⁴ The novel methodology presented in this report could be used in future studies to examine ACLR graft performance relative to the native ligament during clinically-relevant, athletic tasks on the same specimens. This would mimic the scientific design that has been applied to robotic simulations of clinical tests.² Mechanical data that is gleaned from such investigations will likely provide a critical bridge to understanding the required design criteria for efficacious surgical technique and graft improvements.

In addition to ACL and ACLR mechanics, the methods developed in this investigation could be further applied to evaluate additional structures within the knee. Such applications could include investigations of the alterations in knee mechanics that occur after meniscus injury, menisectomy, total or partial joint reconstruction, microfracture surgery, and any other form of intra-articular surgical repair. Enhanced understanding of how injuries and current surgical interventions effect mechanical change relative to the native knee is essential for investigators to make efficacious improvements that will result in superior knee-quality-of-life outcomes following repair. Also, understanding mechanical changes following injury and repair may lead to better explanations of osteoarthritis onset in the knee and advance the methods that are currently used to combat this condition.

The direct input of 6-DOF skin-marker-based in vivo kinematics to the robotic manipulator did not produce physiologic simulations of knee motion. The published literature documents that skin-marker based in vivo motion capture suffers from skin artifact errors due to the skin moving in relation to bone orientation.^3,4,29,32,33 When skin-marker kinematics were simulated using robotic, these errors produced large joint dislocations, femoral fractures, and tibial fractures. (Figure 4) The implementation of scale factors to reduce the ROM recorded in rotational DOFs reduced the disarticulation in both the medial and lateral compartments of the tibiofemoral joint. Similarly, the adjustment of translational inputs with respect to passive flexion constraints prevented further fractures of the tibia and femur. Prior to this modification, translational inputs were failing to articulate around the bony geometry of the joint and causing the bones to drive through one another to the point of fracture.

Though physiologic translations would change for every unique motion simulation, the unification of translational input in the current methodology removes the impact of translational errors on our results. Perturbations in the medial/lateral DOF have minimal impact on the resulting biomechanics during robotic simulation of knee joints, but anterior/posterior and compression/distraction perturbations do influence joint forces and torques.²⁰ Therefore, the unreliable and inconsistent errors associated with skin-marker-based motion capture would make it difficult to discern the root of mechanical differences in robotically controlled simulations. Instead, a universal set of physiologically-derived translations applied across multiple simulations of the same task will allow the present methodology to more accurately represent biomechanical differences related to rotational kinematic differences recorded between subjects during athletic tasks. Understanding the mechanical influence of rotational kinematics is important to ACL biomechanics as increased abduction and decreased flexion during landing have been associated with injury risk.²²

The biomechanical properties of cadaveric tissues are known to degrade with age.^8,19,28,35 In previous robotic studies that simulate lower intensity tasks such as clinical Lachman's test or gait cycles, specimen age has not affected the ability to perform reliable simulations.^11,21,36 However, the current procedures simulate athletic tasks with higher levels of intensity up to 2.5 times body weight. Specimens from elderly donors have often proven unable to sustain such high force magnitudes; and therefore, it is important to limit the specimen population during these simulations to younger and physically active donors.

Tibiofemoral joint geometry varies between specimens. Therefore, specimen specific normalization of input kinematics may be necessary to account for the unique anatomy of each specimen. Currently, the peak magnitudes of data that has been collected in limited pilot simulations do not support the consistent need for specimen specific normalization; however, the timing variation observed in peak posterior force between specimens may be a byproduct of variable specimen geometry. Peak posterior force was achieved between 35-54% of landing phase for the 12 unique donors tested (Figure 6). While the same kinematics were input to each specimen, between-specimen differences in condylar arc radius, condylar protrusion height, or tibial compartment surface area could alter the relative timing of peak posterior load. Accordingly, this theory will be revisited once a greater database is established. Another limitation faced by this study is that in vivo intra-articular joint mechanics cannot yet be directly quantified. As such, it was assumed that matching the magnitude of in vitro compressive joint loads that of in vivo recorded ground reaction forces combined with in vivo recorded kinematics, while not exact, would be representative of physiologic conditions in all loading DOFs.

Conclusion

The current methodological report presents a critical step in bridging the gap between laboratory observations and in vivo performance. Through the establishment of baseline functional mechanics within the knee joint during athletic tasks the methodology presented will serve to advance the prevention, repair, and rehabilitation of ACL injuries. Moving forward this methodology will allow researchers to identify mechanical differences between ACL-intact, ACL-deficient, and ACL-reconstructed specimens during physiologically-relevant athletic tasks where ACL function is critical to joint stability. Comparatively, current methods of simulation present limited clinical relevance to athletic settings. As athletes commonly experience osteoarthritis following ACL injury, the assessment of biomechanical differences between intact and reconstructed knees for athletic tasks may lead to surgical adjustments that compensate for deficiencies and improve the long term joint quality of life following ACLR.

Supplementary Material

10439_2015_1285_MOESM1_ESM

Video 1: Simulation of the kinematics recorded for the male subject performing the DVJ task.

Figure S1: Knee joint kinematics recorded in vivo (solid line) with the adjusted input for the robotic manipulator (dashed line). All 3 rotational degrees of freedom (top) and 3 translational degrees of freedom (bottom) from a female subject DVJ are represented. Time series was normalized to percent of landing phase.

Figure S2: Unfiltered internal knee torques and translational forces during each cycle of a 10-cycle female DVJ simulation on a single specimen. After viscoelastic effects have been compensated, the forces and torques produced at the knee were highly reliable between cycles.

Figure S3: Knee joint loading for all 12 unique donors throughout the DVJ simulation that was derived from the female model. Blue lines represent individual subjects, while the red line and shaded area represent the population mean and standard deviation, respectively. Waveforms were highly repeatable between specimens as CMC values exceeded 0.930 in all DOFs.

Figure S4: Knee joint kinematics recorded in vivo (solid line) with the adjusted input for the robotic manipulator (dashed line). All 3 rotational degrees of freedom (top) and 3 translational degrees of freedom (bottom) from a male subject sidestep cut are represented. Time series was normalized to percent of landing phase.

Figure S5: Unfiltered internal knee torques and translational forces during each cycle of a 10-cycle male sidestep cut simulation on a single specimen. After viscoelastic effects have been compensated, the forces and torques produced at the knee were highly reliable between cycles.

Figure S6: Knee joint loading for all 12 unique donors throughout the sidestep cut simulation that was derived from the male model. Blue lines represent individual subjects, while the red line and shaded area represent the population mean and standard deviation, respectively. Waveforms were highly repeatable between specimens as CMC values exceeded 0.950 in all DOFs.

Figure S7: Knee joint kinematics recorded in vivo (solid line) with the adjusted input for the robotic manipulator (dashed line). All 3 rotational degrees of freedom (top) and 3 translational degrees of freedom (bottom) from a female subject sidestep cut are represented. Time series was normalized to percent of landing phase.

Figure S8: Unfiltered internal knee torques and translational forces during each cycle of a 10-cycle female sidestep cut simulation on a single specimen. After viscoelastic effects have been compensated, the forces and torques produced at the knee were highly reliable between cycles.

Figure S9: Knee joint loading for all 12 unique donors throughout the sidestep cut simulation that was derived from the female model. Blue lines represent individual subjects, while the red line and shaded area represent the population mean and standard deviation, respectively. Waveforms were highly repeatable between specimens as CMC values exceeded 0.860 in all DOFs.