Patient-specific airway wall remodeling in chronic lung disease

Abstract

Chronic lung disease affects more than a quarter of the adult population; yet, the mechanics of the airways are poorly understood. The pathophysiology of chronic lung disease is commonly characterized by mucosal growth and smooth muscle contraction of the airways, which initiate an inward folding of the mucosal layer and progressive airflow obstruction. Since the degree of obstruction is closely correlated with the number of folds, mucosal folding has been extensively studied in idealized circular cross sections. However, airflow obstruction has never been studied in real airway geometries; the behavior of imperfect, non-cylindrical, continuously branching airways remains unknown. Here we model the effects of chronic lung disease using the nonlinear field theories of mechanics supplemented by the theory of finite growth. We perform finite element analysis of patient-specific Y-branch segments created from magnetic resonance images. We demonstrate that the mucosal folding pattern is insensitive to the specific airway geometry, but that it critically depends on the mucosal and submucosal stiffness, thickness, and loading mechanism. Our results suggests that patient-specific airway models with inherent geometric imperfections are more sensitive to obstruction than idealized circular models. Our models help to explain the pathophysiology of airway obstruction in chronic lung disease and hold promise to improve the diagnostics and treatment of asthma, bronchitis, chronic obstructive pulmonary disease, and respiratory failure.

1 Introduction

Airway remodeling is a common manifestation of chronic lung disease, which affects millions of people worldwide. Diseases such as asthma and chronic obstructive pulmonary disease are characterized by a spectrum of abnormalities that include airway narrowing, bronchial hyper-responsiveness and easily collapsable airways which, in turn, result in airflow obstruction, increased work of breathing, and breathlessness [14, 29]. Asthma affects 20 million adults and nine million children; its annual cost is 56 billion dollars [3, 9, 41, 55]. Chronic obstructive pulmonary disease, which includes chronic bronchitis and emphysema, leads to 120,000 deaths per year; it is directly associated with health care costs of 11.7 billion dollars [72]. The impact and health concerns of these diseases motivate studies to explore and understand the underlying mechanisms of airway obstruction and, ultimately, to identify risk factors for the individual patient [56].

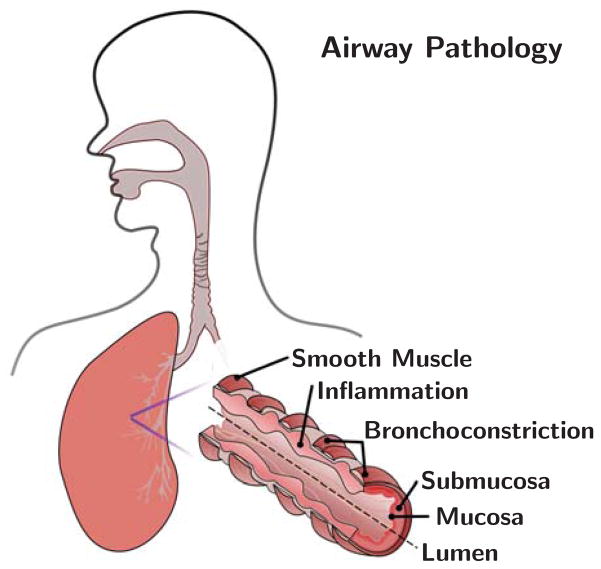
Figure 1 illustrates the two mechanisms of airway remodeling: constriction and inflammation as shown in [12,48]. Airway constriction is caused by the thickening and contraction of the smooth muscle surrounding the airway wall; inner airway wall lining inflammation is triggered by the influx of cells [30, 38]. Mechanically, these two manifestations of airway obstruction can be classified as pressure and growth.

Fig. 1.

Anatomy of the airway illustrating the mechanisms of airway obstruction. The primary components of the airway, the smooth muscle, submucosa, and mucosa, are shown. Bronchoconstriction is caused by chronic muscle thickening around the submucosa and mucosa layers; smooth muscle thickening and hyper-responsiveness cause spastic contraction and lumen occlusion. Inflammation triggers chronic mucosal growth and airway obstruction.

Figure 2 depicts a histological view of the airways: diseased airways are wrinkled and folded inwards due to the force applied from the smooth muscle to the outer layer and the airway wall is engorged due to inflammation. In modeling the effects of pressure and growth, previous studies have focused on the critical failure conditions that cause folds to occur [24, 70]. Analytical models of the airway as a two-dimensional circular ring indicate that a few large folds greatly obstruct the lumen whereas numerous small folds leave the lumen open [16, 43].

Fig. 2.

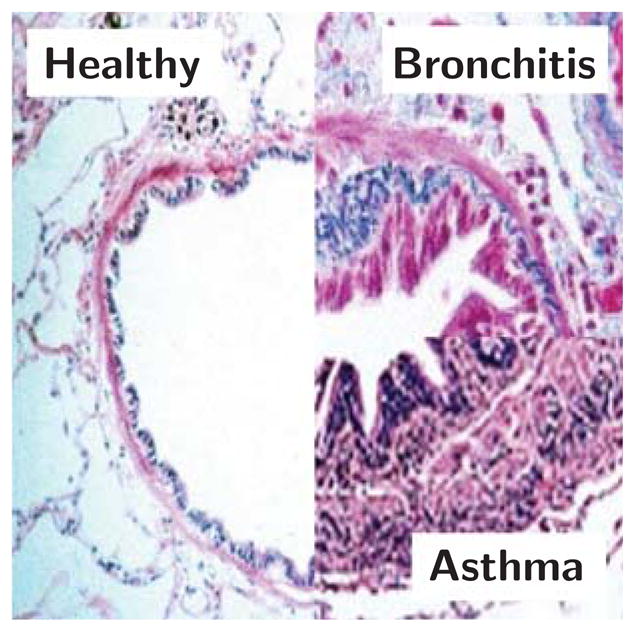
Histology of healthy and diseased airways of bronchitis and asthma. Smooth muscle thickening creates an increased pressure on the external airway wall. Inflammation of the mucosal lining is mechanically classified as growth on the internal airway wall. Both mechanisms obstruct the lumen and lead to difficulty in breathing; adapted from [14, 29].

Several studies investigated the critical pressure or critical growth at the onset of folding [33, 36, 44, 45, 52, 53, 71]. These studies identify three non-dimensional parameters to be key in folding pattern formation of tubular structures: the normalized thickness of the inner mucosal layer, the normalized thickness of the outer submucosal layer, and the stiffness ratio between mucosa and submucosa [44, 71]. These parameters describe the distinguishing layers of the epithelium, basement membrane, and subepithelial collageneous layer that form the mucosa, and the loose connective tissue composed of elastin and collagen which form the thicker submucosa [5]. The distinct composition of these two layers motivates mechanical models with a soft outer and a stiff inner layer [19,61]. These models reveal correlations between the non-dimensional parameters and the emerging folding pattern for idealized, cylindrical geometries [46,53,71]: for example, the number of folds is highly sensitive to variations in the mucosal thickness [52,53]. These findings agree with the clinical observation that smaller airways, with a larger thickness-to-radius ratio, are most often the site of occlusion [42, 67].

While obstruction in response to airway remodeling is now well understood for regular, uniform geometries [20,40], obstruction in imperfect, branching three-dimensional airways has not been studied to date. The fluid mechanics of the lung have been extensively studied using both idealized and patient-specific models [32,59]. However, existing solid mechanics studies which focus on three-dimensional biological geometries are few [54,63], mainly analytical [7,17], fail to predict emerging surface morphologies beyond the onset of folding [60,73], and typically neglect the characteristic branching of the lung [8, 27, 38]. Here we address these limitations by extending airway remodeling mechanics to realistic patient-specific airway branch models created from magnetic resonance images.

2 Materials and Methods

To simulate airway obstruction in response to constriction and inflammation, we apply pressure and growth using a continuum mechanics approach. We create a patient-specific model of the pulmonary tree from magnetic resonance images. Then we discretize the model and employ a finite element analysis, for which we implement growth as a user-defined material subroutine.

2.1 Continuum Model

To model airway remodeling, we adopt the kinematics of finite growth [21,28]. The mapping from a point X in the healthy configuration 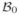to corresponding point x in the diseased configuration 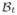at any given time t is denoted by the mapping x = φ(X, t). Infinitesimal line elements dX from the healthy configuration to infinitesimal line elements dx = F · dX in the diseased configuration are mapped using the material gradient F = ∇_Xφ. The multiplicative decomposition of the deformation gradient F is split into an elastic part F^e and a growth part F^g [2,62],

$$\mathit{F}={\nabla }_{\mathit{X}}\mathit{\phi }={\mathit{F}}^{\mathrm{e}}·{\mathit{F}}^{\mathrm{g}}.$$ (1)

The Jacobian J = det (F) defines the change in airway volume via dv = J dV, where the infinitesimal volume elements dV are the healthy configuration and the infinitesimal volume elements dv are in the diseased configuration. We multiplicatively decompose the total volume change J into a reversible elastic volume change J^e and an irreversible growth volume change J^g,

$$J=det(\mathit{F})=det({\mathit{F}}^{\mathrm{e}})det({\mathit{F}}^{\mathrm{g}})=J^{\mathrm{e}}{J}^{\mathrm{g}}.$$ (2)

The airway wall is assumed to grow isotropically and we introduce its growth tensor F^g as the scaled identity tensor I, 

$${\mathit{F}}^{\mathrm{g}}={\vartheta }^{1/3}\mathit{I},$$ (3)

where ϑ = J^g is the scalar-valued growth multiplier that characterizes the growth-induced increase in volume [20]. In chronic lung disease, growth is driven non-mechanically, by chemical or biochemical stimuli [51]. We propose a linear growth model in time, ϑ̇ = G_ϑ, which we can integrating explicitly to obtain the following expression for the growth multiplier,

$$\vartheta =1+G_{\vartheta }t.$$ (4)

Here ϑ = 1 signifies no growth, G_ϑ > 0 is the growth rate, and t is the time. By inverting the growth tensor, F^g−1 = I/ϑ^1/3, an explicit formulation for the elastic tensor may be obtained as

$${\mathit{F}}^{\mathrm{e}}=\mathit{F}/{\vartheta }^{1/3}.$$ (5)

Therefore, the elastic Jacobian is 

$$J^{\mathrm{e}}=J/\vartheta ,$$ (6)

and the elastic left Cauchy-Green deformation tensor is 

$${\mathit{b}}^{\mathrm{e}}=\mathit{F}·{\mathit{F}}^{\mathrm{t}}/{\vartheta }^{2/3},$$ (7)

related to the growth-scaled total deformation gradient F, total Jacobian J, and total left Cauchy-Green deformation tensor b = F · F^t. For simplicity, we model the airway wall as isotropic, hyperelastic Neo-Hookean material and assume that its Helmholtz free energy function consists of an isochoric and a volumetric part,

$$\psi =\frac{1}{2}\mu [{\overline{I}}_1^{\mathrm{e}}-3]+\frac{1}{2}\kappa {[J^{\mathrm{e}}-1]}^2.$$ (8)

It depends on two invariants, the first deviatoric invariant ${\overline{I}}_1^{\mathrm{e}}={\overline{\mathit{b}}}^{\mathrm{e}}:\mathit{I}={\overline{I}}_1$ and the Jacobian J^e = J/ϑ, where b̄^e = F̄^e · F̄^{e t} = (J^e)^−2/3 b^e = J^−2/3 b = b̄ is the nothing but the deviatoric left Cauchy-Green deformation tensor and I is the second order identity tensor. The shear modulus μ characterizes the stiffness of the quasi-incompressible material [31, 65] and the penalty parameter κ enforces the incompressibility constraint, J^e = 1. Since our study focuses on the kinematics of airway wall remodeling, the particular choice of the constitutive equation in equation (8) plays a rather minor role. To model the onset of folding, when stresses are low, a Neo-Hookean model seems to be a reasonable first approach. To quantify stress distributions in highly folded airway structures, constitutive models designed specifically for soft biological tissues including the Holzapfel model [31] or the Arruda-Boyce model [39] are certainly a more appropriate choice.

2.2 Computational Model

We implement the finite growth model as a user defined subroutine UHYPER into the non-linear finite element program Abaqus/Standard version 6.13 [1], where we calculate the free energy 

$$\mathrm{U}=\psi =\frac{1}{2}\mu [{\overline{I}}_1-3]+\frac{1}{2}\kappa {\left[\frac{J}{\vartheta }-1\right]}^2,$$ (9)

and its non-vanishing first and second derivatives with respect to the invariants Ī₁ and J,

$$\begin{array}{l}\text{UI}1(1)=\frac{\partial \psi }{\partial {\overline{I}}_1}=\frac{1}{2}\mu \\ \text{UI}1(3)=\frac{\partial \psi }{\partial J}=\kappa \left[\frac{I}{{\vartheta }^2}-\frac{1}{\vartheta }\right]\\ \text{UI}2(3)=\frac{{\partial }^2\psi }{\partial J^2}=\frac{\kappa }{{\vartheta }^2}.\end{array}$$ (10)

Because of the volumetric nature of growth, only the penalty term, $\frac{1}{2}\kappa [J/\vartheta -1]$, and its derivatives depend on the growth multiplier ϑ [20]. We introduce this growth multiplier as an internal variable, which we store locally on the integration point level in the array STATEV. Since the user subroutine UHYPER does not provide information about the current time step t, we define a uniform temperature field TEMP, which we increase gradually from zero to one, 0 ≤ TEMP ≤ 1, and reinterpret the current temperature as the current time step t = TEMP to update the internal variable using equation (4),

$$\text{STATEV}(1)=\vartheta =1+[{\vartheta }^{max}-1]t.$$ (11)

Since the folding pattern does not depend on the absolute value of the stiffness parameters, but rather on the stiffness ratio between mucosa and submucosa μ_m/μ_s [38], we choose the shear modulus and the penalty parameter in equation (8) to μ = 5MPa and κ =5000MPa. In the linear regime, these values would correspond to a Young’s modulus of E = 15MPa and a Poisson’s ratio of ν = 0.4995, to characterize the quasi-incompressible nature or airway wall tissue. We restrict maximum growth to ϑ^max= 1.15, which introduces a growth rate of G_ϑ = ϑ^max −1 = 0.15. To maintain convergence of the global Newton Raphson iteration scheme, especially at the onset of folding, we adopt an automatic time step size adjustment. We model airway wall remodeling through growth of the inner layer [44] and pressure on the outer layer [71]. While these phenomena occur simultaneously in chronic lung disease [53], here we study both scenarios individually to compare our results with the existing literature. In the following, we explore growth of the inner layer and pressure on the outer layer of selected patient-specific segments of the pulmonary tree.

2.3 Pulmonary Tree and Airway Segment Models

To create a patient-specific model of the human pulmonary tree, we utilize magnetic resonance images of a healthy human lung. Images were taken at full lung capacity; the subject was asked to inhale at full breath and hold the breath during the scan. Healthy airways, especially the larger ones analyzed here, do not deform markedly during breathing: large airways are held open by semiflexible, fibrous connective tissue; smaller airways are tethered open by the parenchyma [47]. We analyze the transverse plane images with a slice thickness of 1.25mm using the medical image viewer OsiriX. To select spline points around the airways, we define regions of interest and highlight all visible airways per slice using the pixel contrast between the black regions of the inner air as a threshold. We export these regions of interest into the pre-processing meshing software Altair HyperWorks Hyper-Mesh where we stack and connect the segments to create the three-dimensional patient-specific branching airway tree. We filter and refine the preliminary mesh to create a smooth surface model of the inner airway wall [74].

Figure 3 illustrates five representative Y-branches within the pulmonary tree. To create volume meshes from the initial surface representation, we offset the geometry outward to generate the mucosal and submucosal layers with dimensions according to Table 1 [64]. For each geometric parameter set, we create a new Y-branch model. Specifically, we use the largest radial cross section to calculate the t_m and t_s offsets from the non-dimensional t_m/R and t_s/R parameterization. The resulting models replicate the clinically observed airway physiology: the airway wall thickness increases from proximal to distal airways [38, 70].

Fig. 3.

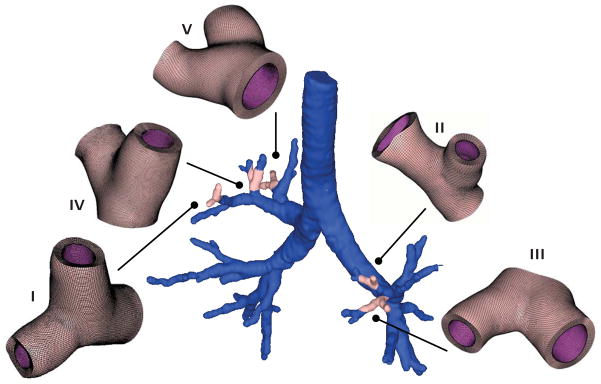
Patient-specific airway model and representative Y-branch models created from magnetic resonance image segmentation. We select regions of interest in each transverse plane image and segment the airway boundaries with splines. We then stack the images to create a three-dimensional surface model of the inner airway wall. From the surface model, we create volume models of five representative Y-branches, which we mesh with more than 300,000 hexahedral elements and 1,000,000 degrees of freedom.

Table 1.

Stiffness and geometric parameters for sensitivity analysis. We fix two parameters to the baseline values shown in bold and vary the third within the given range.

μm/μs	10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 200, 300, 400, 500
tm/R	0.010, 0.025, 0.050, 0.075, 0.100, 0.125, 0.150, 0.175, 0.200
ts/R	0.05, 0.10, 0.15, 0.20, 0.25, 0.30, 0.35, 0.40, 0.45, 0.50, 0.55, 0.60

Figure 4 shows a representative Y-branch model and its characteristic geometric parameters, the radius R and the mucosal and submucosal thicknesses t_m and t_s. We mesh each Y-branch using 8-noded linear hybrid hexahedral C3D8H elements. While linear elements are known to perform poorly in bending-dominated problems, our preliminary sensitivity analyses confirmed that linear and quadratic elements generally produced identical folding patterns, since bending effects at the onset of folding are relatively low. All Y-branches are larger than 3.0mm in diameter and all elements are smaller than 0.1mm in length. We use four element layers across the mucosa and ten element layers across the submucosa. The size of the Y-branches varies between 3.24mm and 5.15mm using a discretization of more than 300,000 elements and 1,000,000 degrees of freedom.

Fig. 4.

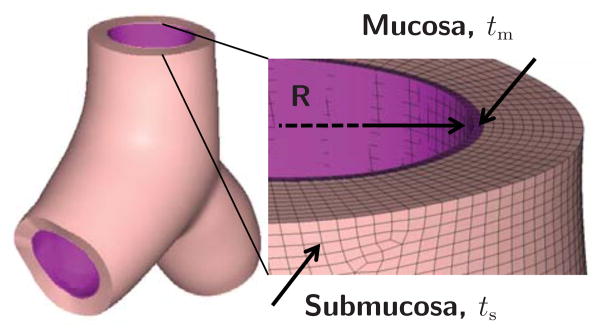
Representative Y-branch model created from magnetic resonance image segmentation. We segment the inner airway wall to generate a surface model, which we project outward to create a volume model parameterized in terms of the radius R and the mucosal and submucosal thickness offsets t_m and t_s. We mesh the volume model using linear hybrid hexahedral elements with four and ten elements across the mucosal and submucosal layers.

The choice of appropriate boundary conditions for patient-specific simulations remains challenging. While boundary conditions are relatively straightforward for idealized two-dimensional circular cross sections, fixing irregular three-dimensional geometries in space and yet allowing them to deform physiologically is a nontrivial task. Here, we select boundary conditions that allow us to compare our results with the existing literature: For the simulation of inner wall growth, we apply homogeneous Dirichlet boundary conditions at the outer wall [44] and Robin boundary conditions at the three open ends using quasi-fixed springs of 1MPa [23], and gradually increase growth to its maximum value of ϑ^max= 1.15. For the simulation of outer wall pressure, we apply Robin boundary conditions at the outer wall, again using quasi-fixed springs of 1MPa in each Cartesian direction [64] and homogeneous Neumann boundary conditions at the three open ends [36], and gradually increase the pressure to a maximum value of p^max = 7.5MPa, to maintain physiological parenchymal to smooth muscle force generation ratio of no more than eight [26,66,71]. In agreement with opening angle experiments on human airways, which displayed rarely any opening at all [50], we model the initial airway as residual stress free.

Table 1 summarizes the dimensionless parameters used in the sensitivity analysis. To explore the effects of airway stiffening and thickening during asthma and chronic obstructive pulmonary diseases [4, 13, 34, 49], we systematically vary the stiffness and geometry of our representative Y-branches. The baseline stiffness and geometry ratios are μ_m/μ_s = 50, t_m/R = 0.05, and t_s/R = 0.5. We fix two parameters to their baseline values and vary the third parameter within a wide range suggested in the literature [44, 71]. This wide range is valuable to indicate general trends; however, stiffness ratios beyond μ_m/μ_s = 50 represent purely academic values and seem to be non-physiological. While the stiffness sensitivity analysis only requires minor modifications of the input file, the geometric sensitivity analysis requires the creation of an entirely new Y-branch model for each parameter set.

We perform stiffness sensitivity analyses for all five airway segments in Figure 3 and stiffness and geometry sensitivity analyses for the representative airway segment I in Figure 5, for which we create 20 independent models, with the same underlying mesh for consistency, according to Table 1.

Fig. 5.

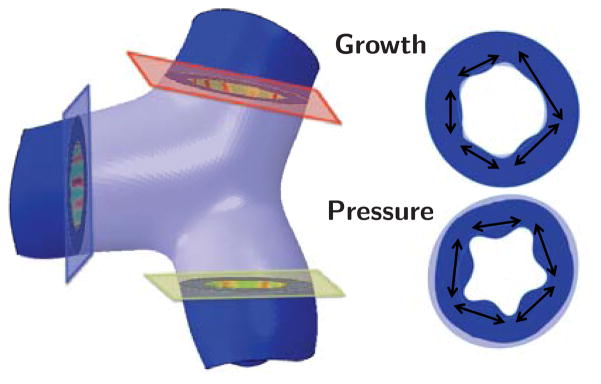
Secant distance used as surrogate quantification of airway obstruction along with fold number. In contrast to regular cylindrical geometries with a constant wavelength, the distance between two neighboring folds differs in irregular patient-specific geometries. Here, we use the average secant distance and the associated fold number to quantify the potential for airway obstruction. Red, green, and blue planes correspond to locations where the secant distance and fold number are measured in Y-branch I.

2.4 Quantification of Airway Obstruction

To characterize the potential for airway obstruction, we select the secant distance between two folds as a surrogate for lumen closure. Previous studies have used the wavelength and the number of folds to quantify the potential for airway obstruction in regular geometries [10, 33, 43]. In irregular, patient-specific geometries, the distance between two neighboring folds varies. Accordingly, instead of the wavelength, we use the secant distance and the associated fold number to quantify the potential for airway obstruction. For each Y-branch, we measure the secant distance in three representative cross sections at the tubular ends and report the mean and standard deviation. Figure 5 illustrates the three cross sections of a representative Y-branch and the secant distances for the two scenarios of inner wall growth and outer wall pressure.

3 Results

All simulations ran smoothly and robustly, all elements remained regularly shaped, even in the branching region. We did not encounter element distortion or serious convergence issues throughout the entire simulation.

3.1 Parameter Sensitivity of Representative Airway Segment

Figure 6 illustrates the parameter sensitivity of a representative airway segment, Y-branch I in Figure 3, subjected to growth and pressure loading. To highlight the folded surface morphology, we have color coded the valley regions in red and the ridges in blue using the von Mises stress. Growth triggers combined circular and longitudinal folding, which can be seen in transverse and longitudinal cuts; pressure loading triggers pronounced circular folding, extending along the tubular axis. For both cases, the simulation predicts different folding morphologies for varying stiffness ratios μ_m/μ_s and varying geometric ratios t_m/R and t_s/R: for smaller ratios, the emerging folds are densely packed and the folds appear numerous; for increasing ratios, the folds increase in size and decrease in number, and the spaces between the folds widen.

Fig. 6.

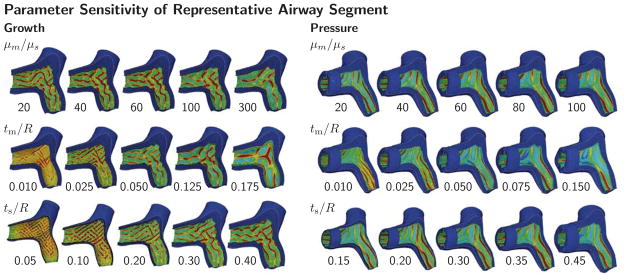
Parameter sensitivity of representative airway segment. Growth and pressure loading initiate folding patterns for varying stiffness ratio μ_m/μ_s and varying geometric ratios t_m/R and t_s/R. As stiffness and geometric ratios increase, the spacing between neighboring folds increases for both growth and pressure loading. Growth triggers combined circular and longitudinal folding; pressure triggers pronounced circular folding. The color code visualizes the folding pattern through the von Mises stress; stresses are highest in the red valley regions and lowest in the blue ridges.

3.2 Stiffness Sensitivity of Five Airway Segments

The stiffness sensitivity of five airway segments, Y-branches I through V in Figure 3, subjected to growth and pressure loading are shown in Figure 7. Red regions of high von Mises stress indicate valleys and blue regions of low von Mises stress indicate ridges. Regardless of the overall airway shape and geometry, as stiffness ratio increases, the spacing between neighboring folds increases for both growth and pressure loading. In all five airway segments, growth results in combined circular and longitudinal folding and pressure leads to pronounced circular folding. The growth-induced folds seem to emerge throughout the entire inner wall, independent of the branch junction. The pressure-induced folds emerge along the long axis without interfering with the branch junction.

Fig. 7.

Stiffness sensitivity of five airway segments. Growth and pressure loading initiate folding patterns for varying stiffness ratios μ_m/μ_s. As the stiffness ratio increases, the spacing between neighboring folds increases for both growth and pressure loading. Growth causes combined circular and longitudinal folding; pressure leads to pronounced circular folding. These trends are similar in all five airway segments. The color code visualizes the folding pattern through the von Mises stress; stresses are highest in the red valley regions and lowest in the blue ridges.

3.3 Quantification of Airway Obstruction in Representative Airway Segment

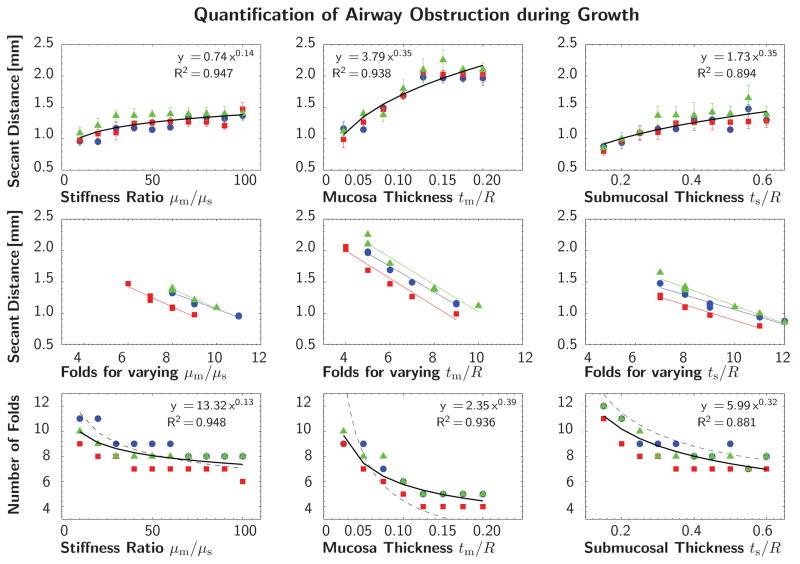
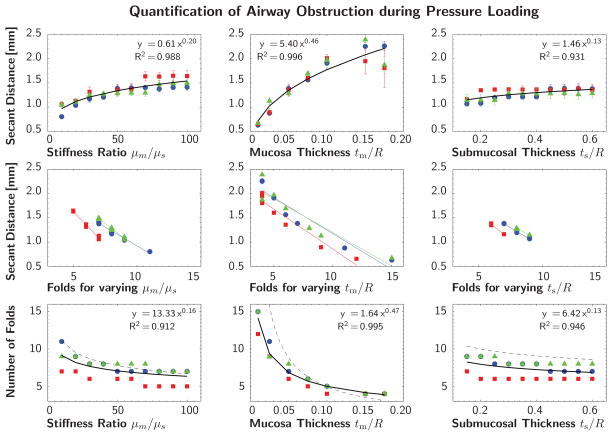
Figures 8 and 9 quantify the potential of airway obstruction for both scenarios, growth and pressure loading. The three columns indicate the sensitivity with respect to the stiffness ratio μ_m/μ_s and the geometric ratios t_m/R and t_s/R. The red, green, and blue colors correspond to the planar cross sections of Y-branch I in Figure 5. The black curve represents the power relation regression fit of averaged secant distances and fold numbers for all three cross sections. The dashed trend lines in the bottom row indicate agreement with the solution of the idealized circular cross section for growth [44] and pressure loading [71].

Fig. 8.

Quantification of airway obstruction during growth of representative airway segment. Secant distances and number of folds for varying stiffness ratio μ_m/μ_s and varying geometric ratios t_m/R and t_s/R. The red, green, and blue colors correspond to the planar cross sections of Y-branch I in Figure 5. The black curve represents the power relation regression fit of averaged secant distances and fold numbers for all three cross sections. The dashed trend lines in the bottom row indicate agreement with the solution of the idealized circular cross section [44].

Fig. 9.

Quantification of airway obstruction during pressure loading of representative airway segment. Secant distances and number of folds for varying stiffness ratio μ_m/μ_s and varying geometric ratios t_m/R and t_s/R. The red, green, and blue colors correspond to the planar cross sections of Y-branch I in Figure 5. The black curve represents the power relation regression fit of averaged secant distances and fold numbers for all three cross sections. The dashed trend lines in the bottom row indicate agreement with the solution of the idealized circular cross section [71].

This quantitative analysis confirms the trends observed during the parameter sensitivity study in Section 3.1: The secant distance increases with increasing stiffness ratio, mucosal thickness, and submucosal thickness, top row. The secant distance is inversely proportional to the number of folds, middle row. This implies and results confirm that the number of folds decreases with increasing stiffness and thickness, bottom row. These trends are similar during growth in Figure 8, and pressure loading in Figure 9. The bottom rows of Figures 8 and 9 represent the most common illustration of airway obstruction in prior works: a decreasing number of folds for increasing stiffness ratios, μ_m/μ_s, and increasing geometric ratios, t_m/R and t_s/R [33, 44, 52, 53, 71].

The three parameters μ_m/μ_s, t_m/R, and t_s/R, each have different impact on airway obstruction. During both growth and pressure loading, the mucosal thickness t_m/R causes the most drastic change in pattern formation within the analyzed parameter range. An increase in mucosal thickness is thus a critical contributor to airway obstruction. During growth, the submucosal thickness seems to be the second most important parameter, followed by the stiffness ratio. During pressure loading, the stiffness ratio appears to be the second most important parameter, followed by the submucosal thickness.

3.4 Quantification of Airway Obstruction in Five Airway Segments

Figure 10 quantifies the potential of airway obstruction for varying stiffness ratios μ_m/μ_s for both scenarios, growth and pressure loading in different airway segments. The red, green, blue, yellow, and magenta colors correspond to the five Y-branches in Figure 3. This quantitative analysis confirms the trend observed during the parameter sensitivity study in Section 3.2: The number of folds decreases with increasing stiffness ratio for both growth and pressure loading. Yet, some airway segments remain insensitive to changes in the small stiffness ratio regime; for instance, during growth, for stiffness ratio variations between 10 and 100, segment II folds with ten to nine folds, while segment V folds with eleven to eight folds. However, for all five airway segments, the number of folds decreases by either four or five with increasing stiffness ratio during both growth and pressure loading.

Fig. 10.

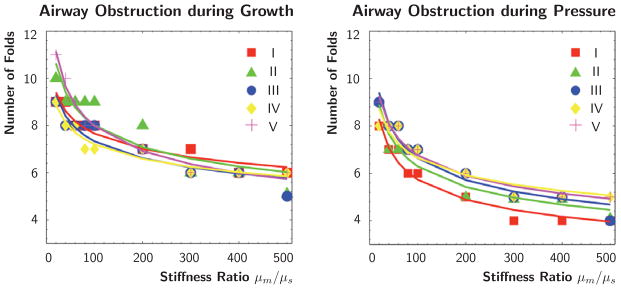
Quantification of airway obstruction during growth and pressure loading of five airway segments. Number of folds for varying stiffness ratio μ_m/μ_s. The red, green, blue, yellow, and magenta colors correspond to the five Y-branches in Figure 3. For all five airway segments, the number of folds decreases with increasing stiffness ratio during both growth and pressure loading.

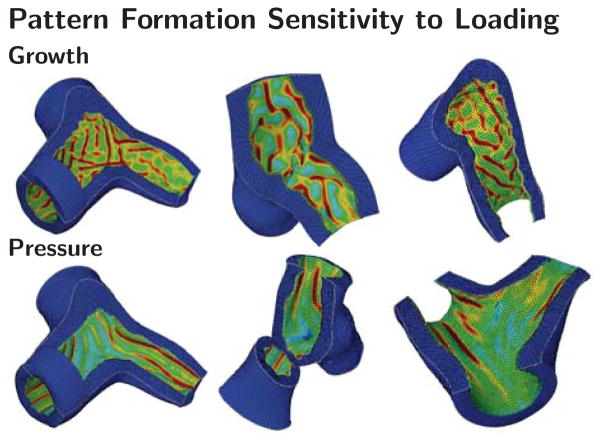
3.5 Pattern Formation Sensitivity to Loading

Figure 11 illustrates the pattern formation sensitivity to loading type in representative airway segments. Irrespective of Y-branch geometry, growth seems to trigger combined circular and longitudinal folding patterns while pressure loading triggers pronounced circular folding. During growth, emerging folds seem to interfere and interact with other folds, particularly in the region of the junction. During pressure loading, folds emerge circumferentially, they seem relatively consistent in width and direction, they expand in parallel along the airway’s long axis, and bypass each other in the region of the junction. Drastically increasing the stiffness or thickness ratios during growth seems to have similar effects as pressure and favor circumferential folding as indicated in the rightmost columns of the growth simulations in Figures 6 and 7.

Fig. 11.

Pattern formation sensitivity to loading. Growth triggers combined circular and longitudinal folding; pressure triggers pronounced circular folding. These trends are specific to the three-dimensional simulations of airway obstruction and independent of Y-branch shape. The color code visualizes the folding pattern through the von Mises stress; stresses are highest in the red valley regions and lowest in the blue ridges.

4 Discussion

The objective of this manuscript was to explore the mechanisms of airway wall remodeling in realistic patient-specific geometries. Using representative Y-branch segments of the pulmonary tree, we have shown that three non-dimensional parameters critically impact airway obstruction: the mucosal-to-submucosal stiffness ratio and the mucosal and submucosal thickness. Airway obstruction is a result of an inward folding of the inner mucosal layer, a phenomenon, which is more pronounced for low fold numbers. Our simulations indicate that an increase in any of the three parameters decreases the fold number and increases the risk for lumen occlusion. We show that lumen occlusion has a mechanical origin in either inner wall growth or outer wall pressure.

Our study is the first to demonstrate these phenomena in realistic patient-specific airway wall segments. Our results in Figures 6 and 7 agree conceptually with previous studies on idealized circular geometries: larger stiffness ratios and thickness values decrease the number of folds and increase the risk for airway obstruction [53,71]. We show that variations in stiffness and thickness impact airway obstruction to a different degree: The mucosal thickness is the most critical parameter for both growth and pressure loading, which is in agreement with previous two-dimensional studies [33, 38, 44, 45, 53, 71]. Figures 8 and 9 indicate that the submucosal thickness is the second-most important parameter for growth [44], whereas the stiffness ratio is the second-most important parameter for pressure loading [71]. Our solution displays an excellent agreement with the dashed trend lines of idealized circular cross sections for growth [44] and pressure loading [71]; small deviations arise because of different parameterizations, and, inherently, because of the three-dimensional irregular nature of our patient-specific model. Our findings also agree with analytical estimates for compression-induced instabilities in rectangular bi-layered systems, which suggest that the wave number is inversely proportional to the mucosal thickness, but only inversely proportional to the third root of the stiffness ratio [10,11]. For circular or elliptical bi-layered systems, these estimates require additional correction terms, which suggest that folding is more likely to occur in flat rather than curved geometries; however, the overall trends remain the same [20, 25]. Despite the regional variation introduced by patient-specific modeling, our sensitivity analysis agrees well with previous work and suggests that regular, circular models provide a reasonable estimate to assess the risk of airway obstruction [15, 37, 53]. Yet, regional heterogeneities can drastically affect the degree of bronchoconstriction [22], and patient-specific airway modeling seems critical to fully understand the interplay between airway structure and function [68].

The fold number has long been established as the metric of airway collapse: fewer folds have the ability to progress further inwards and block the lumen entirely [43]. Dissection of porcine airways revealed fold numbers on the order of 30 for healthy, non-occluded, larger airway segments [45]. Anatomical optical coherence tomography, a non-invasive, in vivo imaging technique recorded similar fold numbers of the order of 30 for living porcine airways with a radius of 3mm and an inner wall thickness 0.2mm, values that were also confirmed using tissue histology [57]. Using the same method in vitro, the authors demonstrated that the bronchial tree expresses intrinsic serial heterogeneity [58]: airway narrowing increases from proximal to distal, a trend that we have previously predicted using our model on regular geometries [20]; but airway narrowing remains unaffected by structural variations at branching sites, a trend that agrees with our present findings.

Our fold numbers agree well with previous studies on regular, idealized circular cross sections. For growth, our fold numbers for variations in stiffness, mucosal thickness, and submucosal thickness display a nice agreement with the trends reported for idealized geometries [44] as indicated through the dashed lines in Figure 8. For pressure, our fold numbers also agree nicely with the trends reported for idealized geometries [71] as indicated through the dashed lines in Figure 9. The tendency for patient-specific airways to record fewer folds may explain greater risk of obstruction in realistic geometries. This highlights the importance of nonuniform, patient-specific geometries in airway obstruction.

In comparison to regular, idealized circular cross sections, our irregular, realistic patient models are highly sensitive to geometric imperfections: circular cross sections require artificial perturbations to trigger the onset of folding [20], and these perturbations often override the natural folding pattern [60]; patient-specific models possess inherent geometric irregularities, and folding occurs naturally without numerical artifacts. This implies that the critical values for the onset of folding in realistic patient geometries may be significantly lower than in perfect geometries, further suggesting that idealized models underestimate the risk of airway obstruction.

In comparison to idealized models, our physiological models are sensitive to the choice of boundary conditions: we found that Robin boundary conditions agree with the clinical conditions in asthma and chronic bronchitis. Robin boundary conditions closely mimic the physiology of the parenchyma in tethering open the airway and allow us to model severe smooth muscle hyper-reactivity and airway collapse modes [69, 71]. While homogeneous Dirichlet boundary conditions are often chosen as a matter of pure convenience, and we have selected them here to compare our results to existing studies in the literature [44], it is now increasingly recognized that fixed boundaries fail to reproduce the physiology of biological systems in an in vivo setting [6]. This agrees well with a recent study on growth of tubular organ systems, which has shown that free boundaries are essential to reproduce the physiological environment of the gastrointestinal tract [18]. Now that we have compared our simulations against previous studies [44, 52, 53, 71], in follow-up simulations, we will use Robin boundary conditions throughout and study the effect of simultaneous growth and pressure loading.

Patient-specific airway modeling reveals mechanisms which are invisible to idealized circular simulations. Our folding patterns in Figures 6 and 7 are truly unique to three-dimensional Y-branch analysis. Prior two-dimensional works have neglected the folding patterns along the airway axis and focused on occlusion in circular cross sections [44,52,60,71]. When viewed through a two-dimensional lens, the folding mechanisms during growth and pressure loading are virtually indistinguishable [71]. Our three-dimensional analysis demonstrates that the real folding patterns during growth and pressure loading are quite distinct: growth creates both circular and longitudinal folds, while pressure generates exclusively circular folds. As Figures 6, 7, and 11 indicate, these observations are consistent across all Y-branch segments. This insensitivity to branching is in agreement with imaging studies of the porcine bronchial tree, which found that airway narrowing was unaffected by branching [58]. Our parameter studies also suggest that increasing the thickness drives the complex growth-induced folding morphology towards the simplistic pressure-induced pattern of purely circular folding. This almost regular pattern of a few plain folds is believed to be most vulnerable to lumen occlusion and agrees most favorably with histological observations [29, 35]. This suggests that a chronic increase in thickness or pressure – rather than growth – is the major mechanism of airway obstruction.

5 Conclusion

Chronic lung disease affects one fourth of the adult population, but the true origin of airway obstruction remains poorly understood. Previous studies have addressed airway narrowing using two-dimensional mechanical models of idealized circular cross sections. Here we expand these models to realistic three-dimensional geometries created from magnetic resonance images and show that previous models underestimate the risk of airway obstruction. While patient-specific modeling of the lung has gained increasing interest in the fluid mechanics community, the solid mechanics of the pulmonary system are understudied and insufficiently characterized. Our model is the first to computationally explore airway mechanics in realistic patient-specific geometries, before and beyond the onset of airway occlusion. Our realistic three-dimensional simulations reveal mechanisms, which are invisible to previous two-dimensional analyses: while airway obstruction is relatively insensitive to the underlying geometry itself, it is truly sensitive to the loading mechanism, growth or pressure loading. The comparison of our predicted folding patterns with the pathophysiology of chronic airway wall remodeling suggests that airway obstruction is caused by airway wall thickening and increased smooth muscle contraction rather than by an increase in mucosal volume. Taken together, our simulations indicate that patient-specific features cannot be ignored when modeling chronic lung disease – they lead to earlier folding, fewer folds, and greater lumen occlusion not characterized by previous studies. The extension of pulmonary solid mechanics to patient-specific modeling moves the field closer towards clinical applications and holds promise to improve the diagnostics and treatment of asthma, chronic obstructive pulmonary disease, and respiratory failure.