Simulating current-voltage relationships for a narrow ion channel using the weighted ensemble method

Abstract

Ion channels are responsible for a myriad of fundamental biological processes via their role in controlling the flow of ions through water-filled membrane-spanning pores in response to environmental cues. Molecular simulation has played an important role in elucidating the mechanism of ion conduction, but connecting atomistically detailed structural models of the protein to electrophysiological measurements remains a broad challenge due to the computational cost of reaching the necessary time scales. Here, we introduce an enhanced sampling method for simulating the conduction properties of narrow ion channels using the weighted ensemble (WE) sampling approach. We demonstrate the application of this method to calculate the current-voltage relationship as well as the non-equilibrium ion distribution at steady-state of a simple model ion channel. By direct comparisons with long brute force simulations, we show that the WE simulations rigorously reproduce the correct long-timescale kinetics of the system and are capable of determining these quantities using significantly less aggregate simulation time under conditions where permeation events are rare.

1 Introduction

Ion channels are required for many basic processes in human physiology such as cell signaling, cell excitability, and intracellular homeostasis. One reason for their role in such diverse areas is that they have evolved to be precisely controlled by a wide array of environmental cues such as temperature, voltage, ion concentrations, lipid composition, and membrane tension. However, the primary result of all of these input signals is to open or close the channel, thus controlling ion flow across membranes. To this end, the intrinsic properties of individual, open channels – their selectivity, absolute conductance values, current-voltage (I–V) characteristics – determine their biological function. The invention of the voltage clamp in the 1940s and patch clamp in the 1970s made it possible to record ion channel I–V curves, and these techniques have remained the primary tools for determining channel biophysical properties.¹ Unfortunately, electrophysiology does not provide a direct mapping between conductance of the channel and the precise molecular conformations giving rise to the observed dynamics. Since 1998, crystallographic structures of channels have revealed the architecture of channels in exquisite detail², complementing functional studies of these proteins. These structures, however, are often in unknown states, and they do not reveal the dynamics of the channel or how ions move through them. It can therefore be difficult to make a direct connection between these high-resolution, but static, structures and electrophysiological and functional data.

Molecular dynamics (MD) simulations have the potential to bridge these experimental regimes by providing a dynamic picture of the permeation process with unmatched temporal and spatial resolution. In principle, MD is capable of accounting for most of the important biophysical processes underlying ion transport, including ion diffusion into the channel, changes in ion hydration upon transfer from the bulk solvent into the proteinaceous environment, and detailed interactions between the ion and coordinating residues lining the permeation pathway. The I–V relationship and conductance of a channel can be calculated from an MD simulation in which a constant electric field^3,4 or asymmetric ionic concentration^5,6 are imposed giving rise to the non-equilibrium flow of ions through the channel. Counting the number of permeation events per unit time crossing the channel provides a direct measure of the current arising under a particular set of conditions. Such simulations are crucial for validating the fidelity of the computational models (by reproducing experimentally measurable electrophysiological properties of a channel) and for then connecting motions on the atomic scale to macroscopic observables. The current can also be calculated by integrating the instantaneous net charge displacement in the system^7,8, but this method does not necessarily inform the complete permeation mechanism, which requires observing continuous ion crossing events.

In practice, though, it remains a computationally difficult task to simulate ion transport through many channels. Long trajectories are required to collect enough ion crossing events to accurately calculate the current, and these calculation must be repeated at multiple transmembrane voltages to build an I–V curve. Curves have been successfully computed from all-atom MD simulations for large pores with large conductance values above 100–200 pA.^5,8–12 However, few studies have attempted to determine the I–V relationship of low conductance channels.^13–16 Of these, the majority were carried out using special-purpose hardware¹⁷ and all except Ref. 16 were performed predominantly in a high voltage regime, well above typical physiological values of the membrane potential. Such high voltages increase the number of observed permeation events, but the extreme electric fields may induce transport mechanisms different from those that occur under more modest fields, and the large values make it difficult to compare with experimental currents recorded at lower voltages.

To avoid these shortcomings, many studies have adopted alternative strategies for characterizing the permeation process. Fully or partially continuum treatments of the channel and solvent, coupled with either Poisson-Nernst-Planck (PNP) models or Brownian dynamics have provided a direct way of probing channel conductance at reduced computational cost^18–24, albeit at reduced chemical accuracy. Conversely, MD can be used to efficiently probe the energetics of the process in atomistic detail, using sophisticated free energy methods.^25–35 These latter approaches can then be combined with electro-diffusion theory to estimate the conductance of a channel.^{27,30,35–38} However, application of electro-diffusion theory requires additional assumptions that are not always met by the original MD simulations.^38,39 There remains, therefore, a need for more efficient approaches that are capable of determining the conductance and other dynamic properties of the permeation process directly from the simulation data.

Here, we present a method based on the weighted ensemble (WE) path sampling strategy⁴⁰ to calculate the non-equilibrium current of ions through a channel in the presence of a constant electric field, as well as the resulting steady-state distribution of ions in the membrane-spanning pore. WE sampling is a general and rigorous enhanced sampling procedure for probing systems at equilibrium and in non-equilibrium steady-state.^41–43 It belongs to a larger class of rare-event sampling methods capable of directly extracting kinetic quantities from trajectory data including Milestoning⁴⁴, Transition interface sampling (TIS)⁴⁵ and Forward flux sampling (FFS).⁴⁶ Of these techniques, we are not aware of any that have been applied to calculate the conduction properties of an ion channel. Perhaps most similarly, Milestoning has been used to look at the kinetics of small molecules slowly permeating through a lipid membrane.^47,48 That said, WE is a particularly attractive sampling strategy as it generates an ensemble of continuous trajectories, can be used with any stochastic simulation method without modifying the source code of the MD software, is easily parallelizable, and does not introduce any external bias to the molecular motions, instead letting simulated trajectories follow their natural dynamics. Additionally, WE sampling is not hampered by the presence of metastable intermediate states and has been shown to rigorously reproduce the results of conventional brute force dynamics, often using significantly less computational resources.^42,43,49,50

We test our new method by performing WE sampling of a simple model ion channel over a range of applied voltages and at different ionic concentrations. The simulations allow us to establish unbiased estimates of both the anionic and cationic currents at various membrane potentials, as well the steady-state distributions of ions within the channel. The small system size permits a direct comparison with a series of long brute force simulations, making it possible to both validate the accuracy of the WE approach and quantify the method’s efficiency. Despite its simplicity, the model channel still captures key characteristics of biological ion channels such as realistic current values and cation selectivity. This work provides evidence for the efficacy of WE sampling in determining channel I–V characteristics, and provides a foundation for fully generalizing the approach to more realistic and complex biological channels.

2 Theory and Computational Methods

2.1 Weighted Ensemble sampling

Weighted Ensemble sampling is a general and rigorous multi-replica method for simulating equilibrium and non-equilibrium processes.^{40,41,43,49,50} In a WE simulation, a collection of copies of the system (replicas) evolve simultaneously in time and are subject to a resampling protocol governed by a partition of configuration space (bins) and weights assigned to the replicas. The simulation begins with multiple replicas of the system and each is assigned a weight such that the sum of all weights is one. These replicas are then simulated independently for a time interval, τ, following their natural dynamics. Each replica is then assigned to a bin based on its conformation at the end of the time interval. The bins are defined by discretizing a set of progress coordinates into non-overlapping regions. The choice of progress coordinates is completely arbitrary, and they can be the full configurational space of the system or a drastically reduced subset of collective coordinates. After assignment, the number of replicas within each bin is adjusted by either enriching or terminating replicas to a predefined target level, M. When an occupied bin contains fewer than M replicas, one or more of the replicas within the bin are selected via a statistical procedure and are replicated so that there are M total replicas. The newly generated copies inherit equal shares of their parent’s weight. If a bin contains more than M replicas, excess replicas are culled and the their weights are assigned to a subset of the remaining replicas in that bin. Every τ time units, this procedure is repeated until the total weight within each bin and the flux of weight between bins becomes stationary. Importantly, the WE algorithm resamples the ensemble of trajectories by adjusting the weight of observed configurations and therefore the frequency of observed dynamical processes, while correctly compensating for these changes in weight so that there is no statistical bias.^40,41 Our current implementation follows the replica resampling scheme outlined by Huber and Kim⁴⁰ using the WESTPA software package described in Section 2.7, differing only in that a steady-state is obtained via the flow of ions across the periodic boundary, rather than by reintroducing probability reaching a target state back into the initial state.

2.2 Calculating the ionic current

2.2.1 Direct calculation

The non-equilibrium steady-state flow of ions across the membrane gives rise to a current, which can be measured directly from simulation. If enough permeation events occur, the current carried by species k can be estimated from a long, conventional simulation as

$$I_k=\underset{T\to \infty }{lim}\frac{1}{T}{q}_k(N_{k,\text{out}}-N_{k,\text{in}}),$$ (1)

where q_k is the charge on ion species k, N_k,out and N_k,in are the number of observed permeation events from the inside to the outside and from the outside to the inside compartments, respectively, and T is the total simulation time. In practice, the simulation box is divided into three regions (inner bulk, channel and outer bulk), using two planes oriented parallel to the membrane, positioned at the interfaces between the channel and the bulk solution. Permeation events are then strictly defined as the sequential movement of an ion from one bulk phase to the other through the channel.

In the context of a conventional, brute force simulation, every trajectory carries equal weight in defining the flux in Eq. 1, whereas in a WE simulation, each trajectory is assigned the weight of the associated replica in the ensemble. Therefore, it is necessary to re-write Eq. 1 in terms of the average flux into each bulk region. For a WE simulation, these averages are estimated from the flux of weight carried by each replica crossing the boundary between regions after the weights in the bins have relaxed from their initial, possibly non-steady-state, distribution. If we denote the inner bulk, outer bulk and channel regions as 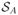, 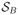and 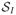, respectively, then the current carried by species k can be expressed as

$$I_k=q_k({\overline{\mathrm{\Phi }}}_{k,B\mid {\mathcal{S}}_I,{\mathcal{S}}_A}-{\overline{\mathrm{\Phi }}}_{k,A\mid {\mathcal{S}}_I,{\mathcal{S}}_B}),$$ (2)

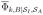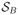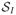where is the average flux of trajectories into from , which last visited 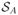more recently than 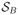. Formally, I_k is the average reactive flux into 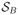, with a similar definition for 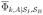. While for conventional, brute force simulations we gather statistics from all of the ions of species k in the system, we use the fact that ions of a particular species are indistinguishable to simplify and reduce the computational cost of determining the current in the WE simulations. For indistinguishable ions, the total current arising from the population of ionic species k is $n_k{I}_k^{(0)}$, where n_k is the number of ions of species k in the simulation box, and $I_k^{(0)}$ is the single-ion current of an arbitrary ion in the population. Here, we assume that ions permeate independently, and we track the progress of a single ion, which reduces the overall computational cost of the calculation due to the reduced dimension of the progress coordinate. In the Discussion and Conclusion, we discuss potential limitations associated with only tracking a single ion.

2.2.2 Non-Markovian matrix analysis

The estimate of the current in Eqs. 1 and 2 is derived from observing the direct permeation of ions through the channel. We can also calculate the current through the channel using a non-Markovian matrix formalism, as previously described in Ref. 43. This formalism reweights the probability contained within each bin using kinetic information about the transitions between bins to obtain steady-state estimates of distributions and fluxes.

The rates between bins are estimated as

$$k_{i,j}^{\mu ,\nu }=\frac{\langle w_{i,j}^{\mu ,\nu }\rangle }{\langle w_i^{\mu }\rangle }$$ (3)

where $w_{i,j}^{\mu ,\nu }$ is the flux of weight from bin i to j during an iteration, labeled with initial and final states μ and ν, respectively, $w_i^{\mu }$ is the weight of the total population in bin i with label μ, and brackets denote time averages over WE iterations. The state labels are introduced explicitly to track the history of a given replica, and this history dependence is why the method is termed “non-Markovian”. For a system with periodic boundary conditions, the reactive ion flux is given by passage events that permeate the channel rather than those that simply cross the periodic boundary in z. Thus, labels μ and ν refer to pairs of states indicating the current and previous region a trajectory has visited, respectively. For example, a fruitful permeation event into 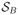has μ = { 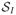, 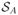} and ν = { 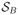, 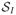}, while an example of a non-reactive event has μ = { 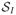, 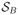} and ν= { , }.

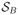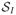Given the labeled non-Markovian transition matrix $K=\left\{k_{i,j}^{\mu ,\nu }\right\}$ calculated from Eq. 3, the steady-state populations of the labeled bins, π, are determined by solving

$$K^T\pi =\pi .$$ (4)

The steady-state population together with the labeled transition matrix give the steady-state flux of weight in both directions through the channel. The reactive flux into 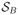is then expressed as

$${\mathrm{\Phi }}_{B\mid \{{\mathcal{S}}_I,{\mathcal{S}}_A\}}^{ss}=\sum _i\sum _j{k}_{i,j}^{\mu ,\nu }{\pi }_i^{\mu }:\mu \to \{{\mathcal{S}}_I,{\mathcal{S}}_A\}.\nu \to \{{\mathcal{S}}_B,{\mathcal{S}}_I\},$$ (5)

The reactive flux into 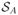is similarly obtained using the same values of K and π, and these quantitates can then be used to calculate the current as in Eq. 2. It should be noted that the bins used in the construction of the transition matrix do not have to correspond to the bins used in the WE simulation. Additionally, the state definitions and corresponding labels can be assigned as part of the post-production analysis of the WE data.⁴³ We find, however, that in practice defining the states and using them to construct history-dependent bins that are employed to perform resampling during the WE simulation can dramatically increase the efficiency of the non-Markovian matrix analysis. The use of such pre-defined states and history-dependent bins was previously suggested by Darve and Ryu⁵¹, and we independently developed a similar strategy⁵⁰ based on a variant of the non-equilibrium umbrella sampling method.⁵² History-dependent binning in the current context separates the extremely low-probability population of replicas moving through the channel against the membrane potential from higher weight replicas moving with the field. In the absence of history-dependent bins, these replicas are rapidly merged during resampling and only rarely, if at all, do they make the full transition across the entire length of the simulation box. These rare transitions are required to estimate all of the necessary elements of K such that a solution to Eq. 4 can be obtained. The loss of these rare pathways through the channel is more pronounced at high voltages, and we found here, and in other systems, that history-dependent bins improve the performance of WE sampling when the forward and backward rates between key states differ significantly.

Finally, this analysis is carried out “offline” on completed simulation data (post-production), as opposed to previous WE reweighting protocols that were either applied once after some initial sampling period^42,53 or on-the-fly during a running WE simulation.⁵⁰ While the non-Markovian matrix analysis could, in principle, be used to carry out on-the-fly reweighting, the adjusted bin probabilities are not propagated forward in a running simulation.

2.3 Calculation of ion distributions and effiective steady-state energy profiles

Steady-state probability distributions were calculated by binning the z-positions of each ionic species independently. For the brute force simulations, all ions of a particular species in the simulation were assigned to bins. In the WE simulations, only the tagged ion’s position was used to generate the one-dimensional distribution, while all ions were considered for the two-dimensional distribution. A bin width of 0.2 Å was used for both brute force and WE simulations. An effective steady-state energy profile was then calculated from the density in each bin i, P_i(z), as −k_BT ln(P_i(z)). For the WE simulations, the density was calculated by averaging the trajectory weights within the same set of bins as the brute force simulations. We excluded contributions to the average from iterations early in the simulation, which were part of the pre-steady-state transient. Extra care must be taken to rigorously match the ion free energies with reference values in bulk solution, because the ions in solution are unbounded in the xy plane.^28,29 Here, we are only concerned with comparisons between WE and brute force, so we do not apply these corrections, which would influence both methods identically.

2.4 Model system

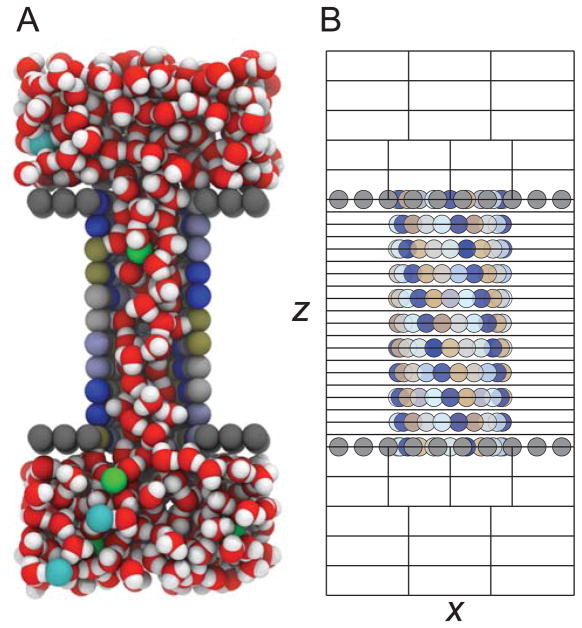
As a test of the Weighted Ensemble’s ability to calculate the conductance properties of a narrow membrane-spanning channel, we used a model system developed by Crozier et al. consisting of a rigid cylindrical pore with polar walls spanning two rigid uncharged slabs embedded in an electrolyte bath of explicit solvent and ions^7,54 (Figure 1A). Each model membrane leaflet was composed of neutral Lennard-Jones (LJ) spheres placed on a square lattice with side length 2.5Å, positioned at z =15 and 40 Å. A section of 4×4 LJ spheres at the center of each leaflet was removed to accommodate a central channel composed of a stack of eleven rings spaced 2.5 Å apart stretching from the bottom leaflet to the top. Each ring is identical with 20 atoms and a diameter of 10.625 Å measured from the pore axis. The atoms in each ring are charged with a repeating set of partial charges carrying [−0.5, +0.5, −0.35, +0.35] fundamental charge units, and each ring is rotated 9° about the z-axis relative to the adjacent rings.

Figure 1.

A model ion channel. (A) A cut-away view of the solvated model channel showing the solvated pore. The particles comprising the hydrophobic sheets mimicking the membrane are shown as gray spheres, whereas the charged atoms of the intervening pore are blue, gold, gray and light blue and carry charges of −0.5 e, +0.5 e, −0.35 e, and +0.35 e, respectively. Mobile Na⁺ (green) and Cl⁻ (cyan) ions are shown in the bath of SPC/E water molecules. (B) For the WE simulations, the simulation box in (A) is discretized into bins, shown here for the x and z dimensions. A cartoon of the membrane and pore atoms are overlaid to highlight the fine discretization through the pore and the coarser binning in the bulk regions. The bin spacing in the y dimension (not shown in this projection), is identical to binning in x.

Both channel and membrane particles were assigned the same LJ parameters (σ = 2.5 Å, and ε/k_B = 60 K) and van der Waals’ interactions with mobile particles were calculated using the Lorentz-Berthelot (LB) combining rules. Membrane and channel atoms were fixed and forces on these atoms ignored. The mobile electrolyte solution consisted of varying concentrations of Na⁺ and Cl⁻ ions in a bath of extended simple point charge (SPC/E) water molecules.⁵⁵ Water-water, water-ion and ion-ion LJ interaction parameters were derived from Ref. 56 as in Ref. 7 rather than calculated from the LB rules. The simulation box was 25 × 25 × 55 ų with periodic boundary conditions imposed in all three dimensions. While mobile species filled the channel, the spacing of the atoms comprising the model membrane and channel prevent entry between the leaflets of the membrane, creating a low-dielectric environment mimicking a biological bilayer.

Systems were prepared at two different ion concentrations. The low concentration system contained a single Na⁺/Cl⁻ pair with 614 water molecules, while the high concentration system contained 8 Na⁺ ions and 8 Cl⁻ ions with 600 water molecules, corresponding to the 1 M nominal ion concentration used in Ref. 7. From the approximate density of SPC/E water and considering only the solvent accessible region of the simulation box, the calculated ion concentrations were 90 mM and 740 mM for the low and high concentration systems, respectively. Initially, the pore and membrane were solvated using Packmol⁵⁷ and then the Gromacs genion tool⁵⁸ was used to randomly replace water molecules with ions for the low-salt and high-salt systems.

2.5 Simulation details

Both brute force and WE simulations were performed using Gromacs 4.6.3^58,59 with identical parameters. Dynamics were propagated in the NVT ensemble using the stochastic velocity rescaling thermostat⁶⁰ with a coupling constant of 0.1 ps to maintain an average temperature of 298.15 K. Both van der Waals and short-range electrostatic interactions were truncated at 10 Å; long-range electrostatics were calculated using the smooth particle-mesh Ewald (PME) method.⁶¹ Bond lengths within each SPC/E water were constrained using the SETTLE algorithm⁶², permitting a time step of 2 fs.

We established a membrane potential, V, by applying a constant force, F_i = q_iE, in the z direction to every mobile particle, i, in the system carrying a charge q_i. The applied electric field was given by E = V/L_z, where L_z is the extent of the simulation box along the z-axis. In response to the linear potential, the charged mobile species in solution reorganize and the sum of the applied and reaction potentials result in the desired potential drop across the system focused over the length of the membrane.^3,4,7,54

2.6 Brute force dynamics propagation

Brute force simulations were initiated for each ion concentration and applied voltage with multiple independent replicates per condition. The initial velocities for each replica were assigned according to a Maxwell distribution at the target temperature using a unique random seed. The simulations were extended to a length sufficient to observe permeation events for both the Na⁺ and Cl⁻ ions along the direction of the field (Table S1). The directional bias induced by the applied field is sufficiently strong that we only observe retrograde permeation events (ions fully permeating against the electric field) for the smallest field strength of 0.2 V. Solvent and ion coordinates were recorded either every 2 or 20 ps. For comparison with the WE simulations, all brute force trajectories were down sampled to 20 ps between snapshots.

2.7 Weighted Ensemble dynamics propagation

Weighted ensemble simulations were carried out using the open-source Weighted Ensemble Simulation Toolkit (WESTPA), which implements the WE algorithm and manages the parallel propagation of replicas as well as data storage and analysis.⁶³ Trajectory segments were propagated using simulation parameters identical to those used in the brute force calculations. The cartesian coordinates of a single Na⁺ or Cl⁻ ion define a set of three spatial progress coordinates. The simulation box was then partitioned into bins using a rectangular grid (Figure 1B). In the channel, bins were spaced at regular 1.25 Å intervals along the z-axis and extended to the edge of the simulation cell in the xy-plane. In the bulk regions immediately adjacent to the channel (9–15 Å and 40–46 Å), bins were spaced at an interval of 3 Å in the z direction and 6.25×6.25 Å in the xy-plane. The remainder of the bulk region was discretized using bins with dimensions 12.5×12.5×3.0 Å. Additionally, we employed a fourth, history-dependent progress coordinate that identified the last region visited by the tagged ion prior to the current region. This progress coordinate takes on discrete values from the set { 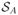, , 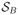, 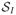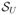}, where 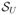denotes having an unknown or undetermined previously visited state. The current region is uniquely determined by a replica’s instantaneous z position.

The majority of the WE simulations were initiated from a set of conformations taken from snapshots sampled at a 100 ps interval from the final 5 ns of eight brute force simulations at the same set of conditions (ion concentration and applied voltage). For two of the simulations, described in Sec. 3.3, we instead initiated WE simulations from the final conformations of another WE run at a different voltage. The voltage was adjusted instantaneously before restarting, and the complete history of those replicas was retained in terms of identifying the previously visited state, but this history was not used in subsequent analysis.

Conformations taken from the brute force simulations were used to generate an initial set of replicas as follows. For the low-salt system (1:1 Na⁺:Cl⁻), the 400 conformations were assigned to bins and a single WE split-merge iteration was performed to obtain the target number of replicas per occupied bin (see below). For the high-salt system (8:8 Na⁺:Cl⁻), we took advantage of the fact that ions of the same species are indistinguishable to increase the initial coverage of the ion-accessible volume. Specifically, from each of the 400 conformations, 7 additional snapshots were created by permuting the atom indices of the tracked ion species. That is, each of the 7 had identical coordinates to the snapshot from which they were generated and only differed in which of the 8 ions was marked as the single tracked ion. Like the low-salt system, the 3200 total conformations were assigned to bins and were resampled to obtain the target number of replicas per occupied bin. Under both ionic conditions, approximately 10–15 % of the total bins in the system were initially occupied.

All initial replicas generated from brute force data were marked as having an unknown previous region ( 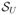) and therefore do not contribute to the permeation statistics until they have transitioned into another region such that they then have a well-defined previous state. Bins corresponding to the unknown previous region label initially begin with 3 replicas per bin for the first 10 WE iterations, and then this target value is reduced to 2 between iterations 10 and 20 and then to 1 replica per bin for iterations ≥ 20. This ensures that the computational resources dedicated to replicas of unknown previous state are limited. All other bins have a target replica count of 10, and the simulations at full bin occupancy have ~192 populated bins. Weighted ensemble resampling was performed at an interval τ =20 ps, and all simulations reported here were 700τ in length.

2.8 Error estimation for conductance measurements

Ion crossing events observed in the brute force simulations appear to be well-described as a Poisson process with exponentially distributed waiting times between consecutive permeation events (Supporting Fig. S1). We therefore used a Bayesian approach developed for single-exponential kinetics to calculate the confidence interval for the currents calculated from the brute force sampling.⁶⁴ Using a uniform prior distribution on the rates, the normalized posterior density of the rate of permeation in one direction through the channel given the data is

$$P(k\mid T,n)=\frac{T^{n+1}}{n!}{k}^{n}exp[-kT],$$ (6)

for n≥0 and T > 0, where k is the ion permeation rate, n is the number of observed permeation events, and T is the total simulation time taken to observe those events. Equation 6 is a two-parameter gamma distribution in k. The value of k that maximizes this distribution is n/T, which is the same maximum likelihood estimate of k that appears in Eq. 1.

Uncertainties in the currents measured from the observed probability flux across the channel in the WE simulation (Eq. 2) were determined using the Bayesian bootstrap method.⁶⁵ The Bayesian bootstrap resamples the original observations, a_i (i = 1…n), by selecting n observations from the original set with replacement. Each observation is selected with probability w_i, where w_i is a random variable drawn from a uniform distribution. For each synthetic data set generated by the bootstrapping procedure, a new set of selection probabilities are generated. Uncertainties in the currents calculated from the non-Markovian matrix analysis were calculated by generating an ensemble of transition matrices {K₁, K₂…K_N} by resampling the fluxes contributing to Eq. 3 using the same bootstrapping protocol. All fluxes from a given iteration of the WE procedure were considered to be a single observation and were selected together during resampling.

In the WE simulations, the probability fluxes used in calculating the current (Eq. 2) arise from the movement of replicas across the channel, which may have a partially shared history. Therefore, the fluxes measured in each iteration are not statistically independent resulting in a time series of correlated samples. The use of correlated samples would underestimate the true uncertainty in the calculated average, so instead we divide the time series into non-overlapping independent blocks and the mean of each block forms a new set of uncorrelated observations. The block length is chosen from a statistical inefficiency analysis⁶⁶ combined with an automatic steady-state detection procedure using the timeseries module included in pymbar.⁶⁷ Briefly, for a time series of total length τN_τ, where τ is the length of a single WE iteration, and N_τ is the total number of iterations, we determine the statistical inefficiency, g, over the interval [τN₀, τN_τ], discarding iterations [1, N₀). From g, we calculate the effective number of uncorrelated samples in the interval, N_eff = τ (N_τ − N₀)/g. Starting from N₀ = N_τ − 1, and moving backward in time to iteration N₀ = 1, N_eff increases until we begin to include observations from the pre-steady-state transient. When those samples are included, the correlation time increases and N_eff consequently decreases sharply. The block length is then τ(N_τ − N₀)/N_eff for the value of N₀ that maximizes N_eff.

3 Results

To validate the accuracy and assess the efficiency of the Weighted Ensemble approach in determining ion channel conduction properties, we carried out a systematic comparison between a set of WE simulations and brute force simulations of the model system in Sec. 2.4 at various ionic conditions and voltages.

3.1 Steady-state ion distributions within the channel

The distributions of ions within and around a channel at steady-state help to identify key interactions between the permeating ions and the channel and reveal the structure of the energetic landscape over which the ions traverse. The effective steady-state energy profiles, calculated from the non-equilibrium steady-state ion densities as described in Sec. 2.3, are shown in Fig. 2 for the brute force and WE simulations at 0.55 V. The profiles show excellent agreement between the WE simulations and the long brute force simulations for both ionic species at each concentration, and this strong correspondence is observed over the full range of applied voltages (Supporting Fig. S2). Differences in the barrier heights experienced by the Na⁺ and Cl⁻ ions at both high and low concentrations suggest that the channel is selective for cations. Although the channel has mirror symmetry along the z axis about z = 0, the applied electric field breaks the symmetry of the effective steady-state profiles. In low salt, where the simulation box contains only a single Na⁺/Cl⁻ pair, the Na⁺ ion has a weak preference to accumulate near the lower membrane face, while the Cl⁻ ion accumulates at the upper membrane plane. These features of the profile are absent in the high concentration system, possibly due to intra-species repulsion in the bulk solvent phase. Inside the channel, the ion distributions are patterned by the charge structure of the 11 rings comprising the channel. Peaks in the Na⁺ profile roughly correspond to local minima in the Cl⁻ profile, and these features likely arise from the strong ordering of water within the channel as suggested by earlier studies of this model channel.⁷

Figure 2.

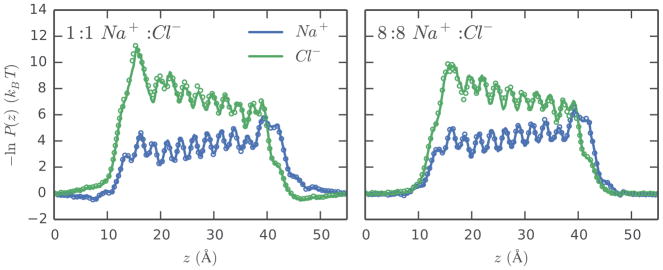
Effective steady-state energy profiles for Na⁺ and Cl⁻ as a function of ion position at 0.55 V calculated from the projection of the steady-state ion distribution along the z axis of the simulation box. Profiles calculated from the brute force simulations are shown as solid lines for the low (left) and high (right) concentration systems. The profiles for the corresponding WE simulations are calculated from the final 400 iterations and are shown as open circles.

The energy profiles from the WE simulations are computed from the single tracked ion whose sampling is enhanced by the binning procedure. It is assumed that the non-tracked ions also sample their correct steady-state distributions. To explicitly test this assumption, we calculated the joint probability of finding a pair of Na⁺ ions at positions z₁ and z₂, P (z₁, z₂), for the high concentration system at 0.55 V. The resulting two-dimensional effective steady-state energy profiles are shown in Fig. 3 for both simulation methods. The surface for the WE simulation is slightly noisier than the brute force surface as the WE distribution was calculated with ~12× fewer snapshots due to a lower sampling frequency (20 ps vs 2 ps). Like the one-dimensional profiles shown in Fig. 2, the WE and brute force results show a close correspondence. The absolute energy difference between the two approaches is < 1.2 k_BT over all configurations involving a single ion in the pore. Double occupancy is rare (P (2Na⁺) < 1.5×10⁻⁵), and we excluded them from the profiles due to poor convergence for both methods.

Figure 3.

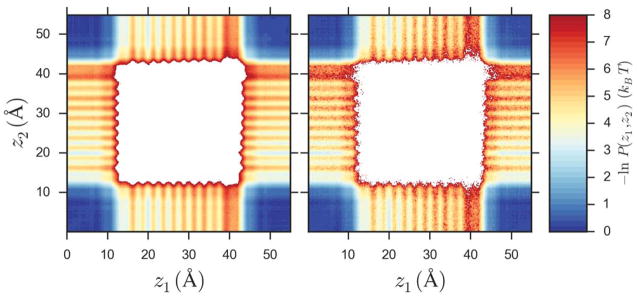
Effective steady-state energy profiles for the pairwise steady-state distribution of Na⁺ at 0.55 V for the high concentration system along the z axis of the simulation box. The probability of finding a pair of Na⁺ ions at positions z₁ and z₂, P (z₁, z₂), is calculated over all 8 cations in the box using either all of the brute force data (left panel) or the final 400 iterations of the WE simulation (right panel).

3.2 The current-voltage relationship of a model ion channel

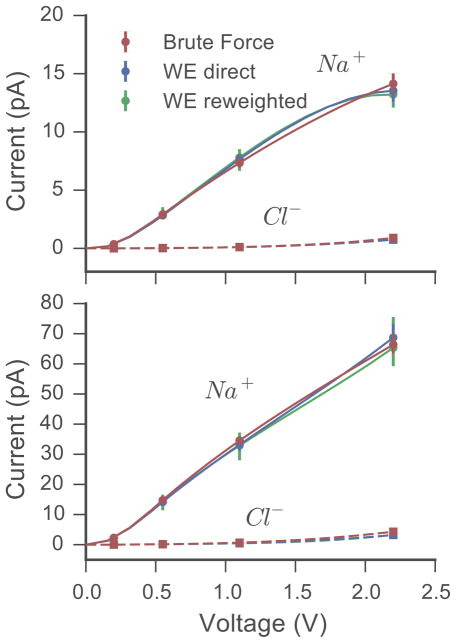
The current-voltage (I–V) relationship of the model channel at both high and low ion concentrations is shown in Fig. 4. Across the complete range of applied voltages investigated here, current measured from the brute force simulations (Eq. 1) and both the direct flux (Eq. 2) and non-Markovian matrix reweighting (Eq. 5) analyses of the WE data agree within statistical uncertainty. For reference, 1 pA is equivalent to 6.25 permeation events per microsecond. The transport properties of the system, while likely affected by finite-size effects stemming from the limited extent of the periodic cell⁴, are consistent between both the brute force and WE simulations.

Figure 4.

I–V relationship of the model ion channel. At each applied voltage, the current carried by the Na⁺ and Cl⁻ is shown for the brute force trajectories as well as the corresponding WE simulations. The latter are analyzed using both the direct and reweighting procedures. Simulations carried out using the low concentration system are shown in the upper panel and simulations using the high concentration system are shown in the lower panel. Error bars indicate the 95% confidence interval. The solid lines (Na⁺) and dashed lines (Cl⁻) are spline fits to the data and carry no theoretical meaning.

Currents arising from the flow of Na⁺ and Cl⁻ are plotted separately, revealing that the channel is strongly cation selective, in agreement with the one-dimensional ion distribution profiles shown in Fig. 2 and Supporting Fig. S2. The currents from each ion species increase with applied voltage and concentration as expected, with no apparent saturation across the simulated conditions. Crozier and co-workers noted a sigmoidal I–V curve with saturating current above 1.1 V for their simulations with a ratio of 4:4 (Na⁺:Cl⁻).⁷ Their data set, however, consisted of ten 10 ns trajectories at each voltage/concentration condition, and the error in the measured current made interpreting the I–V characteristic difficult. Here, in both high and low salt, the Na⁺ currents behave linearly above 0.1 V, but switch to a much more shallow conductance at low applied voltages. Meanwhile, the Cl⁻ current also displays a similar non-linear I–V response, although the current is super-linear over the full voltage range examined.

While rare, as a result of stochastic fluctuations, chemical events can proceed in an energetically unfavorable direction. Here, ions can move against the applied voltage through the channel. In the brute force simulations, we never see this happen at high voltages, and at low voltages (0.2 V), we observed one such rare event for Na⁺ at high ion concentrations, and a second event at low concentrations. Conversely, for the WE simulations, since we separate the populations of ions flowing through the channel in each direction by using a history-dependent binning scheme, we can estimate this retrograde current across all applied voltages. For example, the current carried by the Cl⁻ in the high concentration system at 2.2 V against the field is 2.8×10⁻⁶ pA with a (1.6, 4.4)×10⁻⁶ pA 95% confidence interval, or about 20 permeation events per second. While this component of the current contributes little to the overall shape of the I–V curve for this system, and it may not play a significant role for in biological phenomena, rare events on the millisecond to second timescale can be very important biologically in related processes such as ion flow through small conductance channels or channel activation. The ability of the method to capture such rare events highlights the power of WE to directly probe permeation-related phenomena across a broad temporal spectrum inaccessible by traditional simulation.

3.3 Convergence characteristics and efficiency of the Weighted Ensemble approach

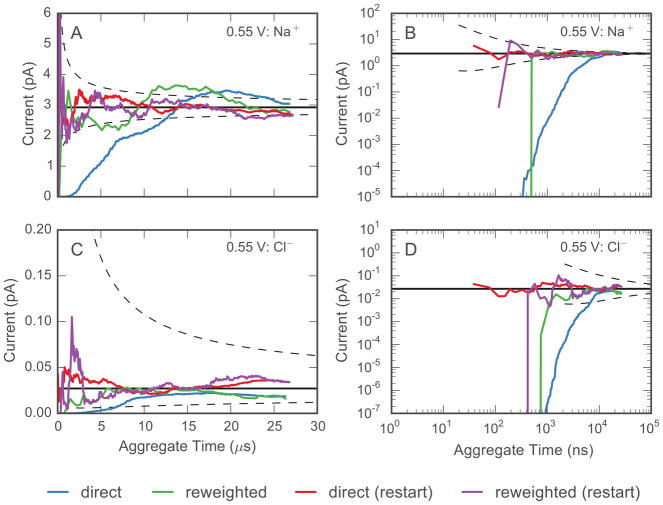
We analyzed the convergence behavior of the WE approach by examining the estimated current through the channel as a function of aggregate simulation time for all simulated replicas. This analysis was carried out for both ion species with a single ion pair in the simulation volume at 0.55 V. In both cases, the initial distribution of replicas is far from steady-state, and the currents obtained from the direct flux of replicas through the channel displays a slow rising transient before reaching steady state (Fig. 5A,B). We also analyzed the same simulation data using the non-Markovian matrix analysis formalism presented in Sec. 2.2.2, which reweights the distribution of probabilities within the ensemble of replicas using information about the local flux between bins. The non-Markovian matrix method only requires that (1) the replicas explore the regions of bin space relevant to describing the transition process, and (2) that the probability distribution within each bin has relaxed such that the inter-bin rates, $k_{i,j}^{\mu ,\nu }$ (Eq. 3), are accurate, even if the absolute magnitude of the flux, $w_{i,j}^{\mu ,\nu }$, has not reached steady-state. The direct method, conversely, requires that the system’s full probability distribution has reached steady-state.⁴³ As such, the currents obtained using the reweighting method converge to the steady-state current significantly faster than the direct flux method. The difference in the performance of the two approaches is particularly evident in Fig. 5B and D, which are log-log plots of the data in panels A and C, respectively.

Figure 5.

Convergence of the current estimates from WE simulations. For the simulations carried out at 0.55 V, the estimates of the current as a function of aggregate simulation time are shown for the Na⁺ current (A and B) and the Cl⁻ current (C and D). Panels B and D show the same data as in A and C, respectively, but are plotted on a log-log scale to highlight the estimated currents early in the simulations. The solid black line is the current estimated from brute force trajectories, with dashed lines corresponding to the evolution of the 95% confidence interval calculated using Eq. 6 assuming n = k_ref T, where k_ref is the estimate from all of the available brute force simulation data. The direct and reweighted curves for each ion type are calculated from a single simulation discarding the first 50% of the WE iterations up until a given time point. The restart simulations (direct - red and reweighted - purple) are initiated from a converged WE simulation with an applied voltage of 0.6 V.

The time to convergence for a WE simulation is related to the time required for the replicas to first fill all important bins in the system and then relax to their true steady-state distribution. Thus, if an initial distribution of replicas could be established that was very close to steady-state, then the replica weights would rapidly relax to the true steady-state value and significantly increase the efficiency of the WE method. Unfortunately, for any non-trivial molecular system, it is extremely hard, if not impossible, to posit a priori a good estimate for the steady-state distribution. The converged distribution from a previous WE simulation run at slightly perturbed conditions, however, could serve as an excellent starting point. For example, when constructing a complete I–V curve for a channel, the distribution obtained from a converged WE simulation at one voltage should provide a better estimate of the steady-state distribution of the channel at a different voltage than a naïve set of initial replicas taken from a short brute force trajectory. A small change in voltage will perturb the steady-state distribution, but if the change is sufficiently small, the weights should rapidly relax to the new steady-state.

To test this hypothesis, we ran additional WE simulations of the low concentration model at 0.6 V, and then used the final distribution of replicas and their corresponding weights, to initiate a new simulation at 0.55 V. At 0.6 V, the steady-state currents after 700 iterations of WE resampling were approximately 3.6 pA and 0.05 pA for Na⁺ and Cl⁻, respectively, requiring a small but measurable relaxation when switching the applied transmembrane potential to 0.55 V. These new simulations were analyzed using the same convergence protocols already discussed, and panels B and D in Fig. 5 confirm that they converge much more rapidly than our original simulations. While we stepped the membrane potential by 50 mV, experimentally, I–V curves are typically constructed at 5 or 10 mV increments. A smaller perturbation would likely result in a shorter relaxation time.

To quantitatively estimate the efficiency of WE compared to brute force, we calculated the error in the current for a given simulation using either the direct or non-Markovian matrix reweighting protocol as

$$\text{error}(t)=\mid logI(t)-log{I}_{\text{ref}}\mid ,$$ (7)

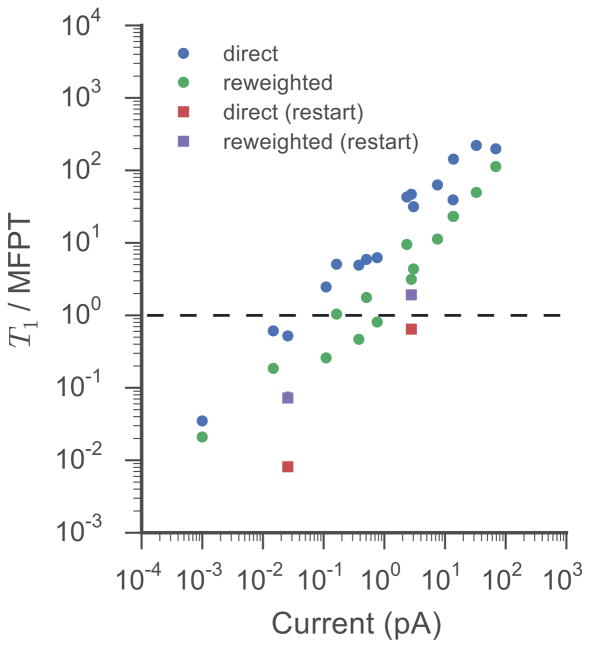
where I_ref is the target current and I(t) is the computed current after accumulating a total aggregate time of t from the start of the simulation. Target currents were calculated as the mean of the direct and reweighed currents using all available WE sampling. The performance of the WE simulations over all applied voltages, ion types and ion concentrations is shown in Fig. 6 by plotting T₁/MFPT as a function of the target current, where T₁ is the aggregate simulation time required to reach and maintain an error ≤1 and MFPT is the mean first passage time for ion movement through the channel. The MFPT is calculated as the inverse of the reactive flux or rate of ion permeation through the channel. Measuring the error on a logarithmic scale, T₁ is the total simulation time required to obtain an order-of-magnitude estimate of the current. For a conventional brute force simulation, T₁/MFPT is approximately equal to 1 at all conditions.

Figure 6.

Efficiency of the WE method as a function of observed current. Efficiency is defined as the ratio of the total aggregate simulation time required to reach and maintain an error ≤1, T₁, to the MFPT of the system at a particular current. The error is defined in Eq. 7. Points represent all of the WE simulations for both Na⁺ and Cl⁻ at the two ion concentrations. The dashed line at T₁/MFPT = 1 corresponds to the ratio expected from a conventional brute force simulations over the same range of currents.

The WE simulations become more efficient under conditions that produce small currents (Figure 6). As noted for the subset of simulations shown in Fig. 5, when initiated far from steady-state, the direct flux method of calculating the current is less efficient than the non-Markovian reweighting analysis across all observed currents. At the lowest currents measured, the standard WE simulations are 30–50 times more efficient than brute force simulations using the metric employed here. Low concentration Cl⁻ simulations restarted from previously converged WE distributions at closely related voltages (red squares in Figure 6) increase the efficiency of the method by a factor of 64 compared to blindly started WE simulations and a factor of 120 compared to brute force. Interestingly, the restarting method converges more quickly if matrix reweighting is not used (red versus purple squares). This is due to the finite time required to collect sufficient bin-to-bin transition statistics, which appears to occur on a longer timescale than the relaxation of the direct flux through the channel when starting near steady-state.

On a log-log scale, standard WE and WE restart simulations both linearly increase in efficiency as the current decreases, with similar slopes, but different intercepts. A similar relationship was observed for WE simulations of Brownian motion on a two-dimensional energy surface when looking at the efficiency of calculating transition rates between metastable states as a function of temperature.⁵⁰ These results add further empirical evidence that WE sampling is capable of exhibiting super-linear scaling in terms of estimating observables and thus significantly decreasing the computational cost of such calculations when compared to conventional brute force simulation. This analysis also highlights that the WE approach can be non-optimal for processes where the MFPT is short compared to the relaxation time of the distribution of replicas and their weights. The non-optimal character of WE for this system and choice of binning scheme is exhibited here for currents greater than 5 pA (Figure 6). It should be noted that we employed the same binning for all WE simulations in this study and did not attempt to tune either the bins or the resampling time in order to optimize the efficiency under different conditions. As WE is equivalent to brute force sampling if a single bin encompassing the entire simulation cell is chosen along with a large resampling time, we expect that it should be possible for WE to at least match the efficiency of a brute force simulation by appropriately adjusting these parameters.

4 Discussion and Conclusions

We have introduced a method based on the Weighted Ensemble sampling approach to determine the current-voltage dependence of an ion channel from atomistically detailed molecular dynamics simulations. Using a simplified model of a channel, we demonstrate that the method is capable of rigorously reproducing the conductance properties, as well as distributions of ions within the channel, determined from long brute force simulations over a range of applied voltages and ion concentrations. For conditions where permeation events through the channel are rare, a direct comparison between the WE simulations and equivalent brute force calculations reveals that WE was significantly more efficient. Importantly, the WE approach does not impose any assumptions about the nature of the permeation process, as quantities such as the current of ions through the channel and their steady-state distributions are calculated directly from the replicas following their natural dynamics.

We have also demonstrated that our method provides an efficient protocol for scanning through a range of applied voltages and calculating the resulting current at each value. Once a WE simulation reaches convergence at one voltage, the current at a neighboring value can be obtained at a fraction of the computational cost, assuming that the voltage change represents a small perturbation to the steady-state distribution of ions in the system. This feature of our WE based approach makes the technique particularly well-suited for simulating the I–V dependence of a channel, permitting direct comparisons with experiment. Conversely, an I–V curve calculated using brute force simulations would require observing a sufficient number of permeation events at each voltage independently; collecting statistics at one voltage would not hasten convergence of a simulation at another. Additionally, this procedure of bootstrapping one WE simulation from another under different conditions is general and could be applied not only to perturbations in voltage, but also to changes in ionic concentration, point mutations or reparameterizations of the force field.

Unlike the simple model channel examined here, many biological channels contain multiple ions binding sites within their selectivity filter, and these sites are often occupied simultaneously. Multiple occupancy can lead to complex interactions between the ions resulting in multi-ion conduction mechanisms, such as “knock on”, where ions entering the selectivity filter cause bound ions to be displaced in a coordinated manner through electrostatic repulsion. Under these conditions, the single ion binning scheme used here may prove inefficient since it would not explicitly account for potentially slow, orthogonal degrees of freedom related to the movement of other ions. Formally, deploying the same binning strategy would yield the correct results given sufficient sampling since results derived from converged WE sampling are independent of bin space⁴¹, but binning has a strong influence on the rate of convergence. Extending the methodologies described here to multi-ion channels will require the development and validation of alternative binning strategies that properly account for the higher state space and aid in sampling these states. While these additional complications may pose certain methodological challenges that need to be addressed to make the method fully general, we believe they should not be prohibitively difficult to implement.

The current binning scheme also neglects changes in conductance resulting from slow conformational changes within the channel. These effects are absent in the present calculations since the channel is rigid, but conformational changes likely play an important role in biological channels.⁶⁸ For example, recent simulations of the bacterial K⁺ channel KcsA have shown that the slow release of water molecules from behind the selectivity filter is coupled to subtle structural rearrangements that dramatically impact the conduction properties of the channel.⁶⁹ Since these structural rearrangements in the protein are unlikely to occur during a given simulation if not explicitly accounted for in the progress coordinate, it would be possible to carry out a series of independent WE simulations to examine conduction properties of each ion channel state separately. Conversely, simulations of the Na⁺ channel Na_V Ab suggest that side chains lining the pore display conformational flexibility that is intimately linked to the permeation process with isomerization timescales similar to that of the ion movement.^70,71 If the motions are fast enough, it is possible that they will not impede convergence of our method even if these changes are not explicitly tracked. However, it is difficult to know a priori when orthogonal degrees of freedom have been sufficiently sampled. That said, the problem of hidden barriers, unaccounted for in the sampling enhancement strategy, is of course not unique to WE sampling, but rather it is a general challenge and source of systematic error in many molecular simulations.^72,73

As we shown in Sec. 3.3, the efficiency of the WE method increases with decreasing current. While WE is significantly more efficient than brute force simulation at low currents, the method is not optimal for channels or conditions eliciting large currents. As such, for large pore and/or high conductance channels, a rare-event sampling approach like the WE method is unnecessary and likely inefficient as I–V curves can be readily constructed from brute force calculations.^5,8–12

For channels with narrow pores, directly observing the permeation process with brute force MD remains a challenge as their conductance values are incongruous with current molecular dynamics simulation timescales, except under conditions of unphysiological membrane potential bias, high ionic concentration or using special purpose hardware. The difficulty of simulating these systems is exacerbated by deficiencies in current fixed-charge molecular force fields, including lack of polarizability and overestimation of membrane dipolar potentials thought to contribute to significantly smaller simulated permeation rates compared to actually experimental rates.¹⁴ These shortcomings were evident in earlier studies of gramicidin A using potential of mean force-based approaches, where corrections were applied resulting in conductances in closer agreement with experiment.^28,29,74 For such small currents, our proposed method is an excellent candidate for efficiently simulating channel conductance; however, a recent study of several K⁺ channels suggested that near-experimental conduction speeds could be simulated using current force fields if the ions in the selectivity filter are in direct contact with one another.¹⁶ If this is true and current force fields provide high transfer rates through narrow K⁺ channels, our WE method will be less useful for studying K⁺ permeation through this class of channels. However, the method could still be used to quantitatively address the contribution of particular conduction pathways toward the total flux, as we did previously for conformational transitions in a transport protein⁵³ or using a flux analysis based on transition path theory.⁷⁵

Nonetheless, even with future gains in computational hardware, the intrinsically small conductance values of a large number of biologically important channels will likely necessitate the use of enhanced sampling approaches like the one developed here. For example, SK (small conductance Ca²⁺ activated K⁺) channels possess a relatively small unitary conductance of ~10 pS⁷⁶, while the Ca²⁺ release-activated Ca²⁺ (CRAC) channels have a Ca²⁺ conductance three orders-of-magnitude lower (~10 fS) and a small Na⁺ conductance of ~0.2 pS.⁷⁷ Furthermore, understanding processes like the movement of non-selective ions through a selective channel, low conduction regimes in the presence of blockers, the effect of conductance mutations, and determining the conduction of a channel of known structure but undetermined state, all likely involve permeation timescales that lay outside of the capabilities of conventional simulation methods. In each of these cases, WE sampling could potentially enable simulators to access the required timescales, lending structure-based insight into these and other processes.

This proof-of-principle study lays the foundation for future development of Weighted Ensemble sampling to investigate permeation of ions through biological channels of known structure. The method allows us to directly calculate I–V curves for the channel, thus allowing for a direct comparison between simulation results and experimental electrophysiological data. Additionally, our general approach could be readily extended to other biologically important processes such as small molecule permeation across protein channels and membranes as well as determining the transport properties of synthetic nanopores.