Modeling the Effect of Dendritic Input Location on MEG and EEG Source Dipoles

Abstract

The cerebral sources of magneto- and electroencephalography (MEG, EEG) signals can be represented by current dipoles. We used computational modeling of realistically-shaped passive-membrane dendritic trees of pyramidal cells from the human cerebral cortex to examine how the spatial distribution of the synaptic inputs affects the current dipole. The magnitude of the total dipole moment vector was found to be proportional to the vertical location of the synaptic input. The dipole moment had opposite directions for inputs above and below a reversal point located near the soma. Inclusion of shunting type inhibition either suppressed or enhanced the current dipole, depending on whether the excitatory and inhibitory synapses were on the same or opposite side of the reversal point. Relating the properties of the macroscopic current dipoles to dendritic current distributions can help to provide means for interpreting MEG and EEG data in terms of synaptic connection patterns within cortical areas.

1. Introduction

In electro- and magnetoencephalography (EEG, MEG) electrical activity in the brain is studied non-invasively by recording scalp potentials and extracranial magnetic fields, respectively (see, e.g., [63]). The sources of the EEG and MEG signals can be described as current dipoles, representing contributions from regional activity within the cerebral cortex [15,64]. The relationship between the macroscopic current dipole and the underlying neural events is important for the interpretation of MEG and EEG data [19,38,49].

Biophysically based compartmental models have been used extensively to examine how the properties of the dendritic tree affects the somatic potential and thereby the firing patterns of individual cells [30,32,42,53,54,60,61,65,70]. Computational modeling can also provide valuable insights for understanding the neural origins of MEG and EEG [28,29,45–47] and other noninvasive recordings of brain activity [9,12,13,27,35,41]. When modeling the neural currents generating the MEG and EEG signals, it is essential to take into account the orientation of the dendritic branch elements in 3D space, which is usually not required for modeling the somatic potential.

Spatially asymmetric currents, known as open source configurations [39], are necessary to generate the far-field signal measured by MEG and EEG. The main structural asymmetry in the pyramidal cell models is along the trunk of the apical dendrite, oriented approximately perpendicular to the cortical surface. Previously, Murakami and Okada [46] demonstrated the importance of the dendrites in the generation of the current dipole by computing the dipole resulting from somatic stimulation of realistically shaped cortical cells. The current dipole also strongly depends on the spatial distribution of synaptic inputs within the dendrites [6]. Using reduced-complexity computational models for cortical neurons in a network, Jones and colleagues found a reversal of the dipole direction in response to stimulation of basal vs. distal apical dendrites, with the dynamics closely matching experimental somatosensory MEG data [28,29]. In a computational model with realistic dendritic geometry of a layer-5 pyramidal cell from the cat visual cortex, Linden et al. [34] found that for low-frequency (1 Hz) inputs the magnitude of the current dipole moment was approximately proportional to the distance from the soma. The objective of the present study was to determine whether a linear relationship between the dendritic input location and the macroscopically observable dipole moment can be found also in models of pyramidal cells from the human cerebral cortex.

2. Methods

2.1 Pyramidal Cell Models

Biophysically motivated computational models for human cortical pyramidal cells were constructed using the NEURON software [11,23] (http://www.neuron.yale.edu). Dendritic geometries of the cells were obtained from the NeuroMorpho database (http://neuromorpho.org); axons were omitted. In total, 86 different cells were examined: Group I: 36 layer-5 pyramidal cells from human anterior cingulate cortex (ACC) [69]; Group II: 36 layer-3 magnopyramidal neurons from human inferior frontal gurys (IFG, Brodmann area 45) [22]; Group III: 14 layer-3 pyramidal cells from human infant superior frontal gyrus [67].

Passive membrane properties were assumed [24,59]. The specific membrane capacitance was chosen to be C_m = 1 µF/cm², the specific membrane resistance R_m = 5000 Ωcm², the equilibrium potential V_rest = −75 mV, and the specific intracellular (axial) resistivity R_a = 80 Ωcm [62]. The value for R_m, was close to the value found for distal dendrites in a non-uniform model [62], but somewhat lower than what is commonly used in modeling studies (10⁴ – 10⁵ Ωcm²).

The coordinate system was chosen such that the positive z-axis was aligned with the trunk of the apical dendrite in the proximal-distal direction, and thus expected to be approximately perpendicular to the cortical surface for most pyramidal cells. The origin was at the soma and the xy-plane was normal to the z-axis.

2.2 Synaptic input

Synaptic inputs were modeled as changes in the transmembrane conductivity g_syn [57], and were implemented using the NEURON software’s point process mechanism. The synaptic transmembrane current was

$$I_{\text{syn}}(t)=g_{\text{syn}}(t)[V_{\text{syn}}(t)-E_{\text{syn}}],$$ (1)

where E_syn is the reversal potential for the synapse, V_syn(t) is the transmembrane potential, and t is time. For excitatory synapses we used E_syn = 0, and for shunt-type inhibitory synapses E_syn = V_rest. The time course of the excitatory synaptic activation was assumed to have the form of the alpha function:

$$g_{\text{syn}}(t)=g_{\text{max}}[(t-t_0)/{\tau }_{\text{syn}}]\exp [1-(t-t_0)/{\tau }_{\text{syn}}]\text{for}t\ge t_0,$$ (2)

with the onset time t₀, time constant τ, and the amplitude scaling factor g_max; g_syn(t) = 0 for t ≤ t₀. The maximum conductivity occurred at time t₀ + τ. For excitatory synapses, we used t₀ = 0 ms, τ_syn = 0.7 ms, and g_max = 1 nS, approximating the time course of AMPA type receptor mediated conductances [21]. When included, the shunting type inhibitory synapses were assumed to be continuously active with g_syn(t) = g_max = 10 nS.

The locations of the synapses were chosen to match the node points within each dendritic segment, as determined by the d_lambda rule function in the NEURON software [11]. Synapses were placed throughout the model cells, with an average (± s.d.) distance between neighboring synapses being 11±4 µm (Group I), 16±5 µm (Group II), and 13±5 µm (Group III). Synapses were activated either individually or in groups involving all synapses within 100 µm in their z-coordinate (“z-bands”).

2.3 Current Dipole Moment

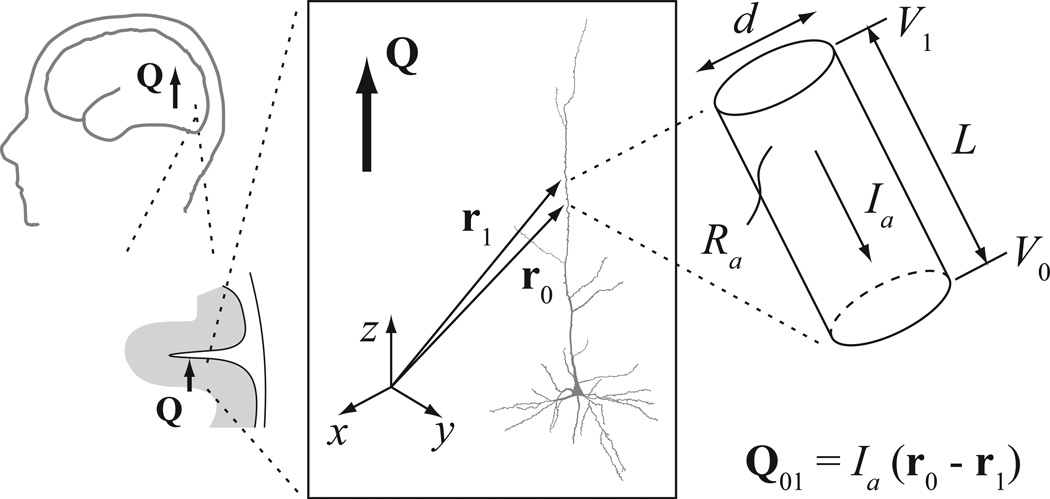
Dendritic segments were assumed to be cylindrical (Fig. 1). Within a segment, the axial current vector is I_a = I_a e_a, where e_a = (r₀ – r₁) / L is a unit vector in the axial direction, r₀ and r₁ are the corresponding position vectors for the proximal and distal ends of the segment, and L = ‖ r₀ – r₁ ‖ is the length of the cylinder. The magnitude of the axial current is, according to Ohm’s law, I_a = (V₁ – V₀) / R = (V₁ – V₀) π d² / (4 R_a L), where V₀ and V₁ are the membrane voltages at the two ends of the segment, R = R_a L / π (d / 2)² is the total resistance of that segment, R_a is the specific intracellular resistivity, and d is the diameter of the cylinder.

Figure 1.

Modeling the current dipole resulting from dendritic currents in a pyramidal cell. The total macroscopic current dipole Q (symbolized by the thick arrow) was computed as the sum of the dipole moment vectors calculated for cylindrical segments. L denotes the length and d the diameter of a single segment. The proximal and distal ends of the segment relative to the soma are labeled as “0” and “1”, respectively. The position vectors of the end points are r₀ = (x₀, y₀, z₀) and r₁ = (x₁, y₁, z₁), and the transmembrane potentials are V₀ and V₁. R_a is the axial resistance of the intracellular fluid. The current dipole moment vector for this segment is Q₀₁ = I_a (r₀ – r₁), cf. Eq. (3). The coordinate system was chosen such that the positive z-axis is aligned with the trunk of the apical dendrite, pointing upward; the xy-plane is normal to the z-axis. The positive direction of the axial current I_a is by convention towards the soma; thus, a positive I_a in the trunk of the apical dendrite results in a negative z-component Q_z of the current dipole

The current dipole moment vector Q for a dendritic cylinder was obtained by multiplying the intracellular axial current vector by the length of that segment [48,68]:

$$\mathbf{Q}={\mathbf{I}}_{\mathrm{a}}L=[(V_1-V_0)\mathrm{\pi }{d}^2/(4R_{\mathrm{a}})]{\mathbf{e}}_{\mathrm{a}}.$$ (3)

The NEURON software computed V₁ and V₀ for all segments of a model cell by solving the cable equation [23]. For each cell, the total current dipole was obtained as the vector sum of the dipole moments for all compartments [47]. We examined the dipole moment component Q_z approximately perpendicular to the cortical surface; for symmetry reasons, the lateral dipole moment components are expected to cancel out in a large population of cells [39]. We were particularly interested in the sign of Q_z, which indicates whether the direction of the current dipole is towards or away from the white matter below the cortex.

The simulation time window was from 5 ms before to 35 ms after the onset of the excitatory input. The magnitudes of the response time courses were quantified by the time integrals (area under the curve), denoted by V_s^A and Q_z^A. For the latency, we used the centroid point [1]. A linear regression model was determined for the dependence of Q_z^A on the z-location of the synaptic input:

$${Q_z}^A(Z)=k_Q(Z-Z_0)+\epsilon (Z),$$ (4)

where z₀ indicates the input location where the direction (sign) of the current dipole vector reverses and ε(z) is the residual error.

The transient excitatory synaptic conductivity change was always unidirectional (alpha function, Eq. 2), and we did not directly address the frequency dependence of the response (cf. [34,51]). However, we examined the presence of sign reversals in the response time course of Q_z was identified with the help of a bidirectionality index

$$\beta =1-|\int Q_z(t)dt|/\int |Q_z(t)|dt.$$ (5)

If the response Q_z(t) for a given input has the same sign for all time points t, then β = 0 (unidirectional); for equal amount of positive and negative values, β = 1 (maximally bidirectional).

3. Results

3.1 Current dipole in response to excitatory input at different dendritic locations

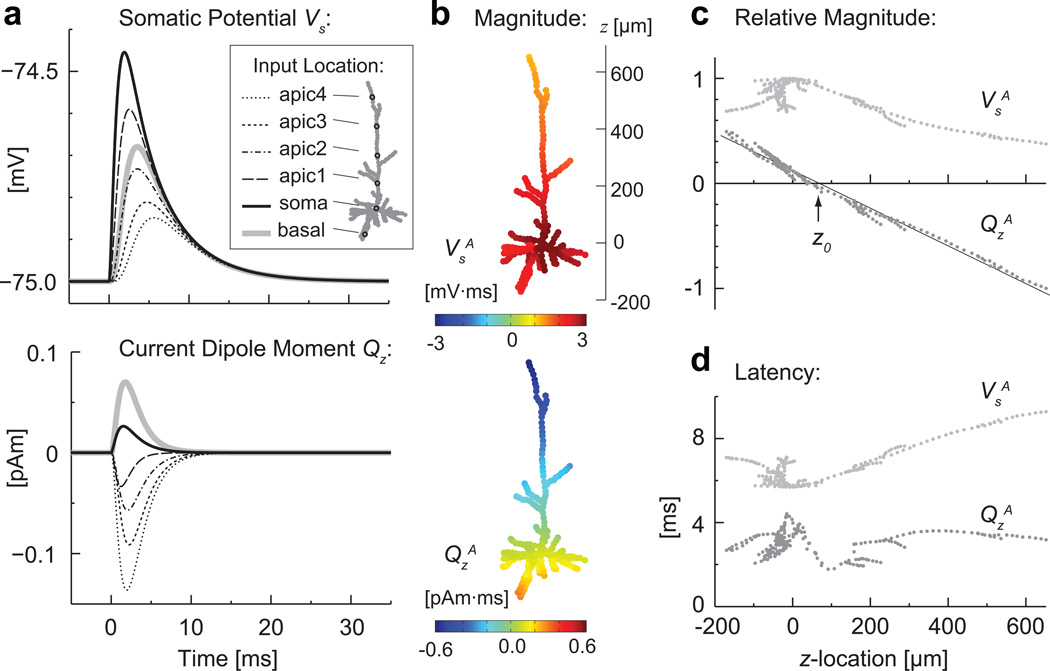
Fig. 2a shows simulated time courses of the somatic potential V_s and the vertical component Q_z of the total current dipole moment in response to a single excitatory synaptic input at six different locations of a pyramidal cell model. The spatial distribution of the synaptic inputs influenced several types of qualitative dissociations between V_s and Q_z in terms of the magnitude, direction, and timing of the transient responses. The responses in V_s were largest for inputs at or near the soma, and the direction was always the same, i.e., depolarization for excitatory inputs. In contrast, the response in Q_z was largest with the most distal apical input. Furthermore, Q_z reversed its direction, being negative (dipole pointing downward, toward the white matter) for the apical input locations and positive for the soma and basal locations. The response magnitudes V_s^A and Q_z^A for individual synapses throughout the cell further illustrate the characteristic dependence on the input location (Fig. 2b). When plotted as a function of the z-coordinate of the synaptic input location, the data revealed that the sign of Q_z^A reversed at a small positive z-value near the soma (Fig. 2c). For this cell, a linear fit for Q_z^A gave z₀ = 67 µm above the soma for the reversal point and k_Q = −1.1 fAm·ms/µm for the slope, with the coefficient of determination r2 = 0.988. The latency of the response was shorter for Q_z^A than for V_s^A for all input locations (Fig. 2d), consistent with the time courses of Q_z being more closely related to the time course of the local membrane potential and the post-synaptic currents near the site of the input than to those at the soma.

Fig. 2.

The computed somatic potential (V_s) and the total current dipole moment in the z-direction (Q_z) in response to synaptic inputs at different locations of a pyramidal cell model. a) Time courses of V_s (top) and Q_z (bottom). The excitatory input occurred at time “0 ms” at one of the six locations indicated in the inset. b) Response magnitudes V_s^A and Q_s^A (area under curve) for all individual synaptic input locations for the same cell. The scale on the right indicates the vertical (z-) location relative to the soma. c) Normalized values of V_s^A and Q_s^A as a function of the z-coordinate of the synaptic input location. V_s^A was largest when the input was at soma; Q_s^A showed near linear dependence on the z-location of the input. The reversal point for the sign of Q_s^A, as determined by a linear fit, was z₀ = 67 µm. d) The centroid point latency of V_s^A and Q_s^A. The latency of V_s^A was longer than the latency of Q_s^A for all input locations. The dendritic morphology of this cell model was from [69], labeled “04a_pyramidal4aACC” in the NeuroMorpho database

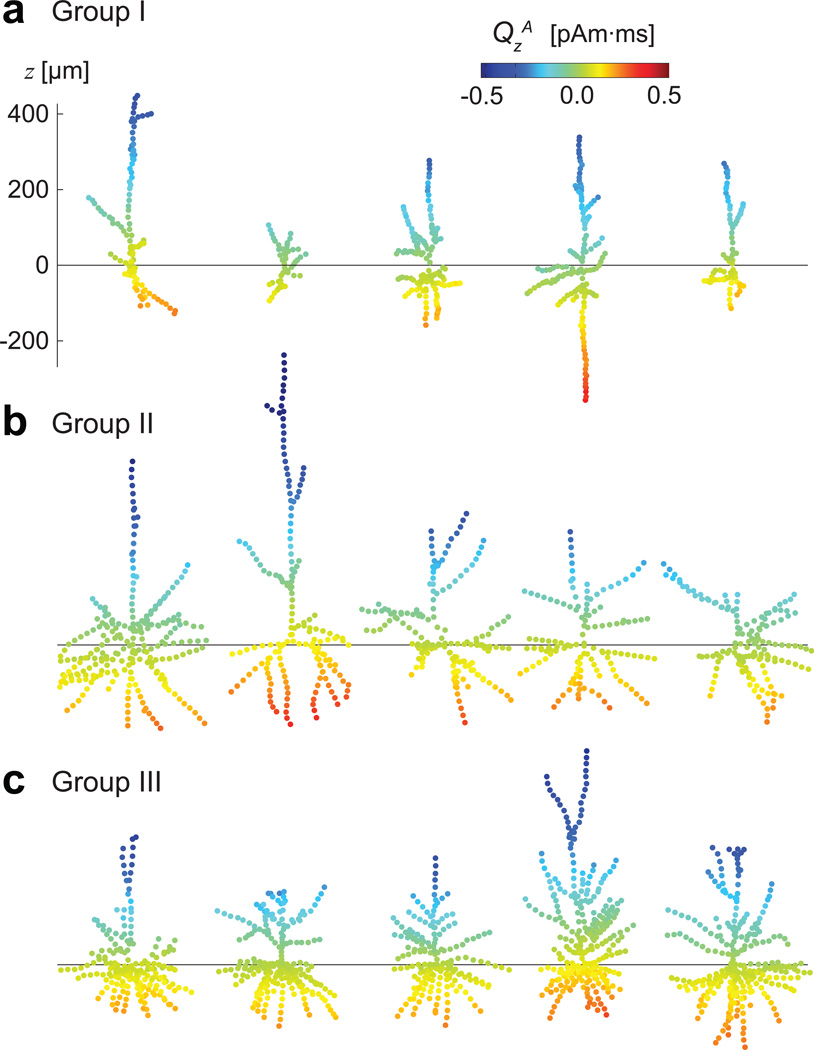
The response magnitudes V_s^A and Q_s^A as a function of the synapse location are illustrated in Fig. 3 for several individual cells from each group. The sign of Q_s^A reversed consistently near the soma in all these models.

Fig. 3.

Response magnitudes V_s^A and Q_s^A for cells from the three groups: a) Group I, b) Group II, c) Group III. Five examples of cell geometries from each group were chosen to illustrate the structural variability among the cells. The horizontal lines indicate the location of the soma (z = 0) for each cell. The dependence of Q_s^A on the vertical location of the synaptic input shows a consistent pattern despite the varying dendritic architectures

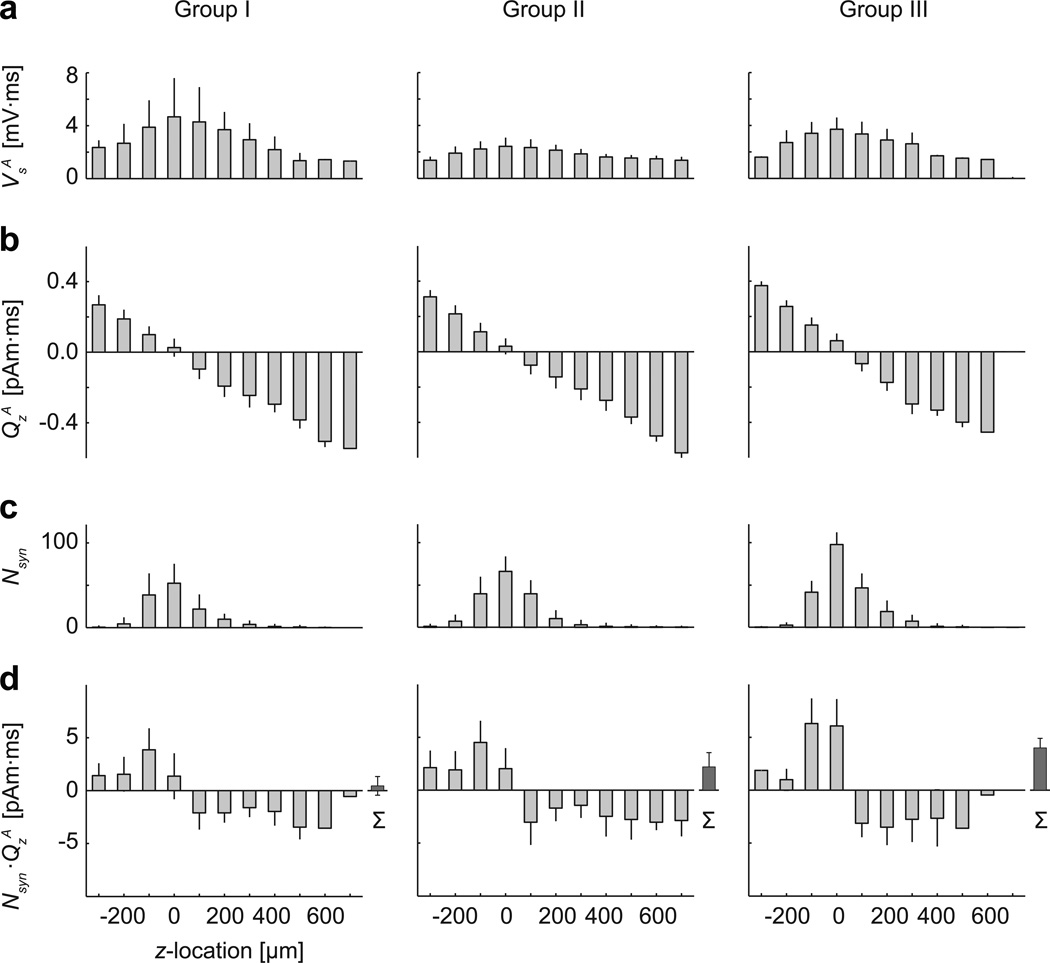
Averaged data from the three groups of human cortical cell models are depicted in Fig. 4. The change in the somatic potential was always positive and largest for inputs proximal to the soma (Fig. 4a), whereas the magnitude of the dipole moment Q_s^A was proportional to the z-location of the synapse (Fig. 4b). Linear regression for Q_s^A gave the mean (± s.d.) values of z₀ = 13±30 µm, k_Q = −1.2±0.2 fAm/µm, r² = 0.954±0.026 (Group I); z₀ = 26±41 µm, k_Q = −1.1±0.06 fAm/µm, r² = 0.987±0.012 (Group II); and z₀ = 40±24 µm, kQ = −1.3±0.08 fAm/µm, r² = 0.983±0.023 (Group III). The dendritic segments were not equally distributed across the z-bands: most of the segments (and thus also the simulated input locations) were close to the soma (Fig 4c). The sum of the current dipole magnitudes to all individual synaptic inputs within z-bands showed a step-function like dependence on the input location (Fig. 4d).The smaller number of inputs in the most distal z-bands appeared to counteract the effect of the larger dipole moments for individual inputs at these locations. For all three groups of cell models, the mean values of the centroid latency for Q_s^A were systematically shorter than those for V_s^A, and showed only weak dependence on the input location, similar to the single cell results in Fig. 2d.

Fig. 4.

Response magnitudes of the somatic potential V_s^A and the current dipole moment Q_s^A as a function of the vertical location of the synaptic input, averaged over multiple cell models. Group I: 36 layer-5 pyramidal cells from human anterior cingulate cortex [69]; Group II: 36 layer-3 magnopyramidal neurons from human inferior frontal gurys [22]; Group III: 14 layer-3 pyramidal cells from human infant superior frontal gyrus [67]. Mean and standard deviation of a) V_s^A, b) Q_s^A, c) the number of simulated synapses N_syn within 100-µm wide bands of the z-coordinate, and d) the total dipole moment Q_s^A weighted by N_syn. In (d), the rightmost bar (Σ) indicates the net dipole moment for the sum of responses to all input locations. For each individual cell model, the soma was at z = 0. The current dipole moment Q_s^A for individual synapses (b) showed approximately linear dependence on z for all three model groups. However, when the number of synapses was taken into account (d), the weighted dipole moment was more uniform across the z-bands

For all three groups of cell models bidirectional responses were relatively rare and associated with low overall response amplitude. The mean percentage (± s.d.) of input locations for which the bidirectionality index β > 0.1 was 9.7±7.1% (Group I), 4.0±3.6% (Group II), and 5.6±4.8% (Group III).The ratio of the largest value of the time integral of the absolute dipole moment magnitude (∫ | Q_z(t)| dt) among input locations for which β > 0.1 vs. that among all input locations was 12±9% (Group I), 4±3% (Group II), and 10±6% (Group III).

3.2 Combination of excitatory and inhibitory inputs

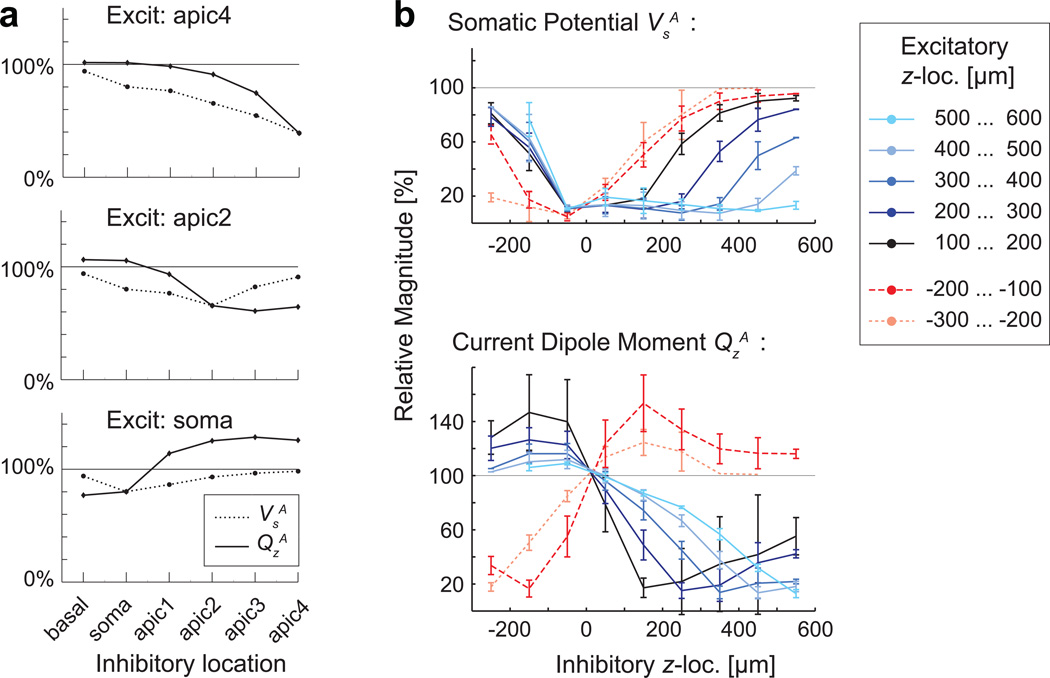
The effect of simultaneous excitatory and inhibitory synapses is illustrated in Fig. 5. When a shunting type inhibitory synapse was located anywhere between the excitatory input and the soma, V_s^A was suppressed. The suppression of Q_s^A depended more strongly than that of V_s^A on the distance between the inhibitory and excitatory synapses (e.g., the case of “Excit: apic4”, for inhibitory at apic2” and “apic3” in Fig. 5a). When the inhibitory synapse was more distal than the excitatory one, there was relatively little suppression in V_s^A but a strong suppression in Q_s^A (“Excit: apic2”, for inhibitory at “apic3” and “apic4”). The combination of excitatory input at the soma or the basal dendrites and inhibitory input at apical locations resulted in an enhancement rather than suppression in Q_s^A (“Excit: soma”, inhibitory at “apic1- 4”).

Fig. 5.

Response magnitudes V_s^A and Q_s^A for combined excitatory and inhibitory inputs. a) Relative magnitudes, compared with the excitatory-only case (=100%), for pairs of individual synapses in the single cell model shown in Fig. 2. Each panel corresponds to one location of excitatory input (apic4, apic2, or soma) with a shunting-type inhibitory synapse at one of six locations (basal, soma, apic1–4). V_s^A and Q_s^A showed different dependence on the relative location of the excitatory and inhibitory synapses. b) Average normalized magnitude of V_s^A and Q_s^A for the combinations of excitatory and inhibitory inputs within 100-µm bands of z-location in the 36 cell models of Group I (100% = excitatory only). Again, prominent differences between V_s^A and Q_s^A dependent on the relative location of excitatory and inhibitory inputs were seen. For example, the inclusion of inhibitory inputs always suppressed V_s^A, particularly when the inhibitory synapses were near the reversal point, which was typically close to the soma. In contrast, the inhibitory inputs could either suppress or enhance Q_s^A. Enhancement of Q_s^A was seen when excitatory and inhibitory synapses were on the opposite sides of the soma

Fig. 5b depicts average values of the relative change in V_s^A and Q_s^A for the 36 cell models of Group I, when excitatory and inhibitory inputs were presented simultaneously within bands of the z-coordinate. Inhibitory synapses at or near the soma strongly suppressed V_s^A. In contrast, Q_s^A was suppressed more when the inhibitory synapses were located on the distal rather than proximal side (with respect to the reversal point z₀, which typically was close to the soma) of the excitatory synapses. When the excitatory and inhibitory synapses were on the opposite sides of the reversal point z₀, Q_s^A was enhanced. This result can be understood in terms of the effective strength of the shunting-type inhibition being dependent on the local transmembrane potential, which is typically much larger on the distal than on the proximal side of an excitatory synapse [54], thereby enhancing the effect of distal inhibitory inputs on Q_s^A.

4. Discussion

The dependence of the total current dipole moment on the location of the synaptic input was examined in computational models of 86 human pyramidal cells from three different regions of the cerebral cortex. The vertical component of the dipole moment was found to be proportional to the vertical location of the synapse within the dendritic tree. The dipole moment had opposite directions for inputs above and below a reversal point close to the soma, inward (pointing toward white matter) for excitatory inputs for distal apical input locations and outward for basal locations. The results are consistent with previous modeling studies based on a cat visual cortex pyramidal cell [34] as well as on a simplified dendritic geometry [6].

The dependence of the dipole moment on the input location was similar for the three groups of cells studied, in spite of the differences among the cells in the length and branching structure of the dendrites. The current dipole results from an asymmetric flow of post-synaptic axial currents. The likely contributors to the axial currents being larger towards the soma than away from it are the asymmetric distribution of dendritic diameters, viz., larger diameters proximal to the soma provide a lower resistance for the axial current, and the sealed ends of the dendritic branches. All the cell models studied here shared these general features. Furthermore, the reversal point for the current dipole was not sensitive to the specific model parameters: using the model with six input locations depicted in Fig. 2a as a test case, we varied the values of the axial conductance, membrane resistance, membrane capacitance, and an overall scaling factor for the segment diameters by 25 to 400%, but in no case did a change in any of these parameters result in a reversal of the dipole moment direction.

The systematic dependence of the current dipole magnitude and direction between the spatial location of synaptic inputs and may allow experimentally observed MEG and EEG source dipoles to provide information about the distribution of synaptic input patterns across cortical layers. Since hierarchical organization between cortical areas is associated with specific laminar patterns of anatomical connections [7,18,56], it is conceivable that feedforward and feedback type inputs into a cortical area can result in different directions for the MEG and EEG source dipoles [25,29]. MEG and EEG are sensitive to the orientation of the source currents, and both the physical orientation and the physiological direction of the current dipole can in many cases be determined reliably [2,3]. In particular, excitatory inputs to the apical tuft of pyramidal cells in the superficial cortical layers result in surface negative EEG [14,66], corresponding to current dipole direction towards the white matter. Multi-contact intracranial recordings can provide data about the expected dipole direction in terms of laminar input patterns and neural excitation [8,20,40,44,52,58]. For the interpretation of the macroscopic current dipole in terms of the input type, however, it will be important to relate the laminar locations of the synaptic inputs to their locations within the dendritic tree of the individual neurons [50].

The dipole direction is affected not only by the spatial distribution of the synaptic inputs, but also by their excitatory vs. inhibitory nature [5,37]. For example, changing the synaptic reversal potential from excitatory to inhibitory would reverse the sign of both V_s and Q_z. However, when excitatory and inhibitory synapses were combined, the response properties of V_s and Q_z showed notable differences. Shunting type inhibition is known to prominently reduce V_s when placed between the excitatory inputs and the soma [31]. The magnitude of Q_z, however, was either suppressed or enhanced, depending on whether the excitatory and inhibitory inputs were on the same or on the opposite side of the location where the dipole moment to a single synapse was minimal (the reversal point z₀). Thus, the interpretation of the current dipole magnitude and direction in the presence of inhibitory inputs is challenging because of the combined effect of the type and the spatial distribution of the inputs.

In general, cancellation effects at various spatial scales can diminish the magnitude of far-field signals such as the MEG and EEG. For example, cancellation of MEG and EEG signals may occur due to cortical folding when there are source currents in opposing sulcal walls [4,26]. Substantial cancellation also takes place locally, both within individual cells as well as in cell populations. In individual cells, as examined here, contributions from axial currents of opposite directions will partially cancel in the computation of the current dipole moment. An example of complete cancellation of this type is the vanishing of the dipole moment when the synaptic input is at the reversal point. For local cell populations, cancellation in the total current dipole will occur when the dipoles for individual cells have opposite directions, for example if sets of excitatory inputs simultaneously connect to the basal dendrites of one subpopulation and to the apical dendrites of another.

For sinusoidal inputs, the total current dipole moment is suppressed because of phase delays among the axial currents within the dendritic tree [34]. Computational modeling studies of the local field potential (LFP) have demonstrated how the current dipole representing the source of far-field LFP (and also of MEG and scalp EEG) has temporal low-pass filtering characteristics due to the dendritic tree [33,34,51]. In the present study, the response waveforms for Q_z to transient unidirectional excitatory inputs were mostly unidirectional, except for inputs located near the reversal point z₀. Suppression of the current dipole moment for biphasic responses to repeated inputs can occur, for example, if a late reversed-sign part of the response coincides with the early part of the response to a subsequent input. For the cell models studied here, however, when the responses were bidirectional, the overall magnitude of the dipole moment was found to be small, and therefore, expected to contribute only little to the observability of macroscopic current dipoles.

Restricting to the passive cell membrane model allowed us to simplify the exploration of the effects of the spatial distribution of synaptic inputs within the dendrites. However, active membrane properties are of major importance to dendritic function [36,43], and are likely to have important contributions to LFP as well as MEG and EEG [46,55]. Evidence for the importance of complex dendritic processing is accumulating, with dendritic segments being considered as computational units [10]. Furthermore, the dynamics within populations of neurons contributing to the net current dipole is of essential importance [16,17,29]. It would be of interest in future work to apply computational biophysical modeling to examine the effects of spatial distribution of synaptic inputs within subsets of dendritic branches associated with specific computational functions, combined with active membrane models and networks of neurons, to further illuminate the neural origins of MEG and EEG.

5. Conclusions

The compartmental biophysical models of human pyramidal cells suggested a linear relationship between the vertical location of the synaptic input and the corresponding current dipole moment. This relation may help to provide means to interpret MEG and EEG source estimates in terms of specific synaptic connection patterns within cortical areas.