Observation of sound-induced corneal vibrational modes by optical coherence tomography

Abstract

The mechanical stability of the cornea is critical for maintaining its normal shape and refractive function. Here, we report an observation of the mechanical resonance modes of the cornea excited by sound waves and detected by using phase-sensitive optical coherence tomography. The cornea in bovine eye globes exhibited three resonance modes in a frequency range of 50-400 Hz. The vibration amplitude of the fundamental mode at 80-120 Hz was ~8 µm at a sound pressure level of 100 dB (2 Pa). Vibrography allows the visualization of the radially symmetric profiles of the resonance modes. A dynamic finite-element analysis supports our observation.

1. Introduction

The microstructure of the cornea provides mechanical integrity necessary to maintain normal corneal shape against intraocular pressure (IOP). Alterations in the biomechanical properties, such as a decrease of stiffness, can lead to abnormal corneal shape and refractive errors. Keratoconus explants have shown disrupted collagen orientation [1] and decreased mechanical modulus [2]. Similar findings have been observed in corneas that developed ectasia after refractive surgery [3]. The ability to characterize the mechanical as well as structural integrity of the cornea can be useful for diagnosis of keratoconus. Corneal biomechanical characterization may also improve identification of candidates at high risk of post-LASIK ectasia. In addition, it may allow biomechanical assessment of the effects of corneal collagen cross-linking treatment that is aimed at increasing stiffness of the corneal tissue [4].

There have been considerable efforts to develop noninvasive, sensitive methods to characterize corneal biomechanics in vivo. The most widely used approach employs air-puffs to induce a burst of pressure on the cornea and analyzes corneal deformation and recovery (Fig. 1(b)). The Ocular Response Analyser is an instrument based on this principle and has been approved for in vivo measurement of properties, so-called corneal hysteresis, which is associated with viscous damping of tissue deformation [5]. Corneal hysteresis has shown to be reduced in ectatic disease, but its sensitivity and specificity have been insufficient to differentiate normal eyes from low-grade keratoconus [6]. Air-puff can be combined with Scheimpflug camera [7] or optical coherence tomography (OCT) [8] for image-based analysis and estimates of corneal viscoelastic parameters [9]. Other emerging techniques for measuring elastic modulus with spatial resolution include supersonic shear imaging [10], optical coherence elastography [11–16], and Brillouin microscopy [17].

Fig. 1.

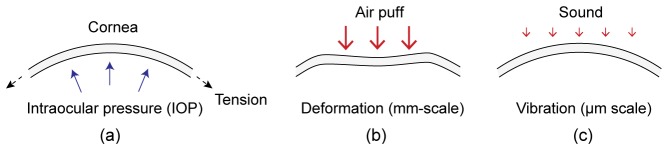
Methods for analyzing the mechanical stability of the cornea. (a) A simple model of the cornea under in-plane membrane tension and IOP. (b) Conventional air-puff method. (c) The proposed method based on sound-induced vibrations.

Here we present a novel technique using sound-driven corneal vibration. This is based on our observation of the acoustic resonance modes of the cornea in the frequency range of 50-400 Hz. The magnitude of corneal deformation is in the order of µm or less, compared to typical mm-scale deformation by an air puff (Fig. 1). The technique uses a sound source, a loudspeaker, and phase-sensitive OCT [18] to measure the natural frequencies of mechanical resonance in the cornea and its spatial profiles.

2. Experimental methods

Bovine eye globes with different weights (10-18.5 g) and ages (not specified) were acquired from a local distributor within less than 2-4 hours postmortem, and experiments were performed within 8 hours after delivery. The eyeball was placed on a rigid holder and fixed with a tape (Fig. 2(a)). Proper fixation was needed to avoid bulk motion of the eyeball by sound stimuli. Care was given to minimize the vibration of the mount and especially to avoid mechanical resonance in the frequency span of interest. The IOP level of the eyeball was controlled by using a syringe and water column for all measurements. In all the experiments, the IOP was set at 6 mm Hg, which is the typical IOP level of eye globes ex vivo as delivered, but lower than the typical in vivo range of 10-20 mmHg. Eyeballs were grouped into four age groups depending on their weights.

Fig. 2.

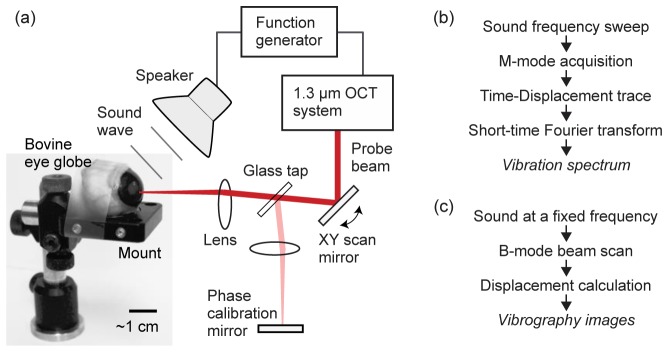
(a) Schematic of the experimental setup. The sound wave emitted from a loudspeaker is directed toward the eyeball, and the motion of the cornea is captured and recorded by the OCT system. A needle syringe connected to a water column (not shown in this picture) is placed into the globe, by which the IOP was set to 6 mmHg. (b) Signal processing sequence for the measurement of vibration spectrum at a fixed spatial location in the cornea. (c) Signal processing sequence to generate vibrography images at a specific sound frequency.

A home-built phase-sensitive OCT system [19] was used, which employed a polygon-scanner swept laser in the spectral range from 1.22 to 1.34 µm with a typical sweep rate of 48 kHz and an optical power of 15 mW on the sample. The reflectivity sensitivity of the OCT system was 105 dB. The axial and lateral resolutions were about 10 and 20 µm, respectively. The sound source was a high-fidelity loudspeaker (Pioneer TS-A878), which was controlled by an arbitrary waveform function generator (Tektronix, AFG3021C). The optical interference data were acquired at 100 MHz by a digitizer (Signatech).

For the measurement of resonance frequencies, the optical beam was fixed at a specific location in the cornea, and the output frequency of the function generator was linearly swept from 50 Hz to 400 Hz over duration of 20 s at a constant voltage (+/− 1 V), during which 960,000 A-line profiles were continuously acquired. From the M-mode images, the phase over time at each depth point within the cornea was determined. The phase-time trace was divided into segments, each consisting of typically 1,000 A-lines acquired over 21 ms. From Fourier analysis of each segment, the amplitude of vibration at the sound frequency corresponding to the segment was determined (Fig. 2(b)). From the frequency-amplitude curve, the mechanical resonance modes were identified, and their natural frequencies were determined. During the frequency sweep at constant voltage, small variation in sound pressure level (SPL) occurs as a function of frequency, due to the frequency-dependent impedance of the loudspeaker. This SPL variation was compensated by measuring the speaker output as a function of frequency, and by dividing all amplitude-frequency traces by this calibration data.

The spatial profile of corneal vibration was determined by using the principle of vibrography previously described [19,20]. Briefly, at a constant sound frequency the optical beam was scanned along a line (~10 mm) or over an area. At each lateral location, a series of A-lines were recorded during one or two full cycles of the sound wave. Once all the lateral locations were scanned, the A-lines that were taken at the same phase of the acoustic signal were grouped together to create a cross-sectional “snapshot” image corresponding to the motion phase (Fig. 2(c)).

3. Results and discussion

The frequency response curve of a sample measured at the center of the cornea revealed three distinctive peaks at 86 Hz, 200 Hz, and 310 Hz, respectively (Fig. 3(a)). The amplitude of the first peak was ~8 µm at 100 dB SPL (2 Pa). The vibration amplitude was proportional to the sound pressure over a range of 80 to 120 dB SPL. Variations in the speaker orientation left the resonance frequencies unchanged, but the relative amplitude of the different vibration modes varied, which we attribute to a change in the coupling efficiency between the incoming sound wave and the vibration modes. The variance in repeated frequency sweeps was less than ± 2%. The vibrational amplitude of the eyeball mount was less than the noise level of ~30 nm except for a resonance peak of ~100 nm at 260 Hz (Fig. 3(a)). The amplitude of the three resonance modes of the cornea decreased roughly with the inverse square of the sound frequency. This is expected because the sound pressure is proportional to the second-order derivative of displacement over time: i.e. acceleration. Our calculation of this parameter showed the approximately equal vibrational “stress” of the three modes (Fig. 3(b)).

Fig. 3.

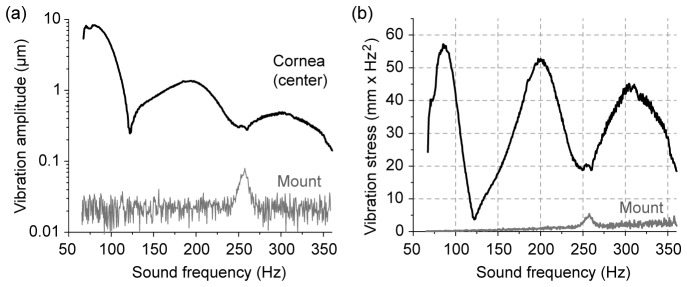
Frequency-domain response. (a) The amplitude of sound-induced vibration measured at the center of the cornea in a bovine eye globe ex vivo, in comparison with the vibration of the sample mount. (b) The induced stress calculated from the amplitude spectra. There are three distinct resonance peaks at 86, 200, and 310 Hz, respectively, which correspond to the first three symmetric modes, [0,1], [0,2], and [0,3] modes. The SPL was 100 dB.

We found a significant correlation between the weight (age) and resonance frequencies. The heavier and larger the eyeball was, the higher, in general, were the resonance frequencies (Fig. 4(a)). This trend is interesting because the resonance frequencies of a circular membrane decrease with an increasing diameter. Our observation suggests that other parameters, such as precise shapes including thickness and age-dependent stiffness of the corneal tissue, might play important roles. The resonance frequencies of each eyeball had well-defined relationship: the ratio of the [0,2] mode frequency to the [0,1] mode frequency was ~2 to 2.4, whereas the ratio of the [0,3] to [0,1] modes was ~3.4 (Fig. 4(b)).

Fig. 4.

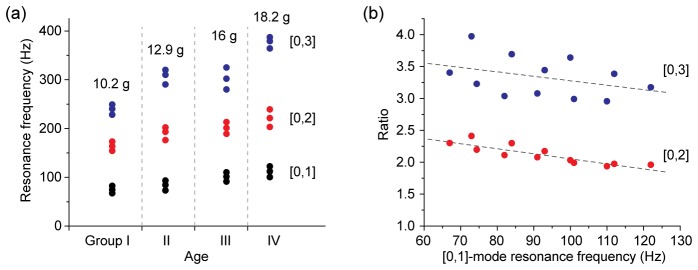
Resonance frequencies of 12 bovine eyeballs ex vivo. (a) Frequency response curves of four sample groups divided by their weights and ages (unspecified). Each group consists of three eyeballs with similar weights (the mean value is given). For each eyeball, the resonance frequencies of three modes—[0,1], [0,2] and [0,3]—are plotted. (b) The ratio of the resonance frequencies of the [0,2] or [0,3] mode to the fundamental [0,1] mode. Dotted lines, linear fit.

The spatial profiles of the resonance modes at 86, 200, and 310 Hz were reconstructed by the principle of vibrography (Fig. 5(a)). Cross-sectional images through the midline through the center of the cornea confirmed that the first [0,1] mode at 86 Hz is the fundamental resonance, and the [0,2] mode and [0,3] mode are the second and third radial modes. Uniform vibration across the full thickness of the cornea was observed. The higher-order modes at 200 and 310 Hz exhibit nodes with zero amplitude. 3-D vibrography images indicated the approximate radial symmetry of the three modes (Fig. 5(b)).

Fig. 5.

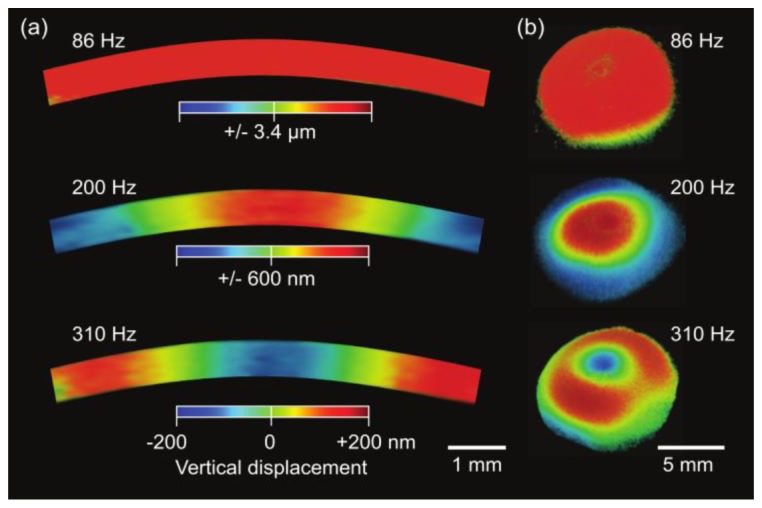
Experimentally measured vibration modes of the bovine cornea. The timing of the snapshot images corresponds to a zero phase when the potential energy of vibration is the maximum. (a) Cross-sectional OCT vibrography images for sound frequencies at 86 Hz, 200 Hz, and 310 Hz. (b) 3-D rendered vibrography images. Color scale represents anterior-posterior (vertical, upward normal to the corneal surface) displacement.

To gain an insight into the experimental data, we considered a uniform thin circular plate with radius a. The natural vibrational modes are identified by two integers m and n denoting the numbers of amplitude peaks of a mode in the circumferential (m) and radial (n) coordinates. The resonance frequency f_m,n of the mode [m, n] is given by:

$$f_{m,n}=\frac{{\lambda }_{m,n}}{2\pi a}{V}_{m,n}.$$ (1)

Here λ_m,n is given by boundary conditions, and V_m,n is the speed of mechanical wave guided along the plane at the frequency f_m,n. The speed depends on in-plane tension and Young’s modulus, as well as geometrical factors such as the size, curvature and thickness [21]. The measured resonance peaks seem to fit well with the circular membrane theory [22], in which λ_m,n denotes the n-th root of Bessel function of the first kind of order m: J_m(λ_m,n) = 0, and the frequency ratio of the [0,2] and [0,1] modes is f_0,2 / f_0,1 = 2.30 and the ratio of the [0,3] and [0,1] frequencies is f_0,3 / f_0,1 = 3.60 (compare with Fig. 4(b)). Curve fitting of the radial profile at 310 Hz (Fig. 5(a)) yields a = 5.8 mm and V_0,3 = 0.73f_0,3a ≈1.3 m/s. For f_0,1 = 86 Hz and a = 5.8 mm, we obtained V_0,1 = 2.61f_0,1a ≈1.3 m/s. This acoustic velocity is on the same order of magnitude as 1.1-1.3 m/s for rabbit corneas measured by exciting propagating Lamb waves with weak air-puff [23] and 1.7 m/s measured by supersonic shear wave imaging for porcine eyes [24].

To validate our observation, we performed a finite element (FE) numerical simulation [25]. For simplicity of computation, an axis-symmetric eye model was used, and only on-axis excitation was applied (Fig. 6(a)). The cross-section of a quarter of the eye was defined by 3,564 elements and 5,007 nodes. A linear viscoelastic material model was applied to the eye model. A Poisson's ratio of ν = 0.499 and a mass density of 1.16 g/cm³ were used for all ocular tissues. The crystalline lens was neglected, for simplicity. The Young’s elastic moduli of the cornea and sclera were assumed to be 37 kPa and 79 kPa, respectively, which best fit the experimental data. These values are close to previously published experimental data obtained with magnetic resonance elastography [26]. The viscoelastic properties of the cornea were described by two-parameter Prony series with a coefficient (P₁) of 0.45 and a relaxation time of 2 ms. The aqueous and vitreous humors were modeled as incompressible fluid with density of 1 g/cm³ and viscosity of 0.9 g/s/m. The geometric dimensions were chosen to represent an average sized bovine eye (cornea thickness of 730 µm, cornea diameter of 26 mm, eye globe diameter of 35 mm). The modal analysis was performed to retrieve the resonance frequencies and modal shapes for the cornea under different conditions using proprietary software (ANSYS APDL 14.0-Academic; ANSYS, Inc., Canonsburg, PA). Radial symmetry was assumed so that only symmetric vibrational modes were considered.

Fig. 6.

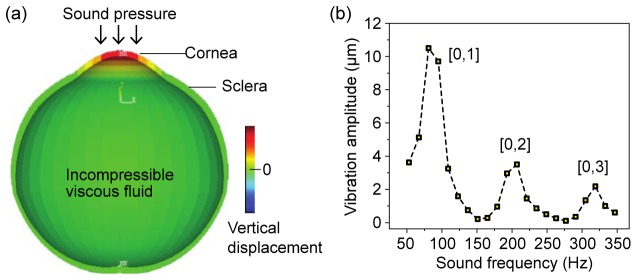
(a) A schematic of the eye model used in numerical finite-element analysis. Vibration excited by sound pressure is primarily localized in the cornea. Vibration of the aqueous humor (fluid) is also seen. (b) Simulation reproduces three resonance peaks in good agreement with the experiments results.

With the reasonable simulation parameters, the FE model reproduced corneal vibration in agreement with the experimental results. It correctly predicted the presence of three resonance modes in the frequency range of 50-350 Hz (Fig. 6(b)). The simulation produced mode patterns in the cornea (Fig. 7), which agree with the experimental results. These numerical results confirmed that the experimentally observed [0,1], [0,2], and [0,3] modes indeed originate from corneal vibration and represent the first three radially symmetric modes.

Fig. 7.

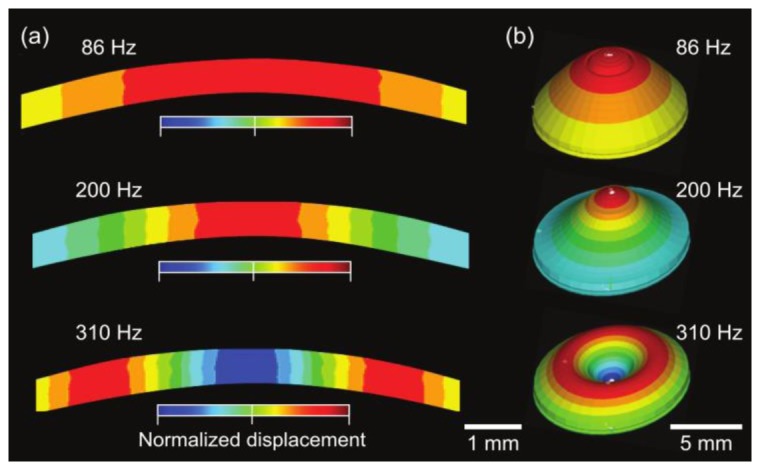
Simulated vibration modes. (a) Cross-sectional vibration profile for sound frequencies at 86, 200, and 310 Hz, respectively. (b) 3-D rendered vibration modes with exaggerated deformation. The color scale represents normalized anterior-posterior (vertical) displacement.

4. Conclusions

We have reported the presence of well-defined vibrational modes of the cornea, for the first time to our knowledge, using low-power sound waves in a frequency range of 50 to 400 Hz. The amplitudes and frequencies of the modes and their specific spatial distributions in the cornea are thought to provide rich information about the cornea. Further research is necessary to understand how different corneal parameters manifest themselves in vibrational resonance. Besides corneal parameters such as stiffness and geometrical parameters, corneal vibration is thought to be sensitive to IOP because it may affect in-plane tension. Further work is needed to investigate the effect of aqueous humor and IOP. Ultimately, using numerical methods it may be possible to extract the various biomechanical parameters from corneal vibration. The measurement of sound-induced corneal vibration can be readily implementable in ophthalmic OCT and may lead to a novel diagnostic technique based on the biomechanical characterizations of the cornea.