Abstract
A novel method (Sophia) is presented to track oxygen saturation changes in a controlled environment using an RGB camera placed approximately 1.5 m away from the subject. The method is evaluated on five healthy volunteers (Fitzpatrick skin phenotypes II, III, and IV) whose oxygen saturations were varied between 80% and 100% in a purpose-built chamber over 40 minutes each. The method carefully selects regions of interest (ROI) in the camera image by calculating signal-to-noise ratios for each ROI. This allows it to track changes in oxygen saturation accurately with respect to a conventional pulse oximeter (median coefficient of determination, 0.85).
OCIS codes: (170.1460) Blood gas monitoring, (170.0170) Medical optics and biotechnology, (170.0110) Imaging systems, (170.1470) Blood or tissue constituent monitoring, (280.0280) Remote sensing and sensors, (170.3660) Light propagation in tissues
1. Introduction
Peripheral blood oxygen saturation (SpO2) is a measure of the relative concentration of oxygenated haemoglobin molecules in the arterial blood with respect to the total amount of haemoglobin. SpO2 is widely used in clinical practice, for example in the assessment of acutely ill patients, monitoring during anaesthesia, and in the follow-up of patients with chronic lung disease [1, 2].
The invasive technique of blood gas analysis remains the clinical gold standard for the assessment of arterial blood oxygenation and is still widely used in many clinical contexts [1,3], however it was only with the development of the current standard for SpO2 measurement in the early 1980s [4] that SpO2 could be measured both continuously and non-invasively. This new technique, known as pulse oximetry, was a revolution for in-hospital monitoring [5].
Pulse oximetry is based on the technique of photoplethysmography, and takes advantage of the fact that oxyhaemoglobin (HbO2) and reduced haemoglobin (Hb) absorb light differently at different wavelengths; that arterial blood is mostly pulsatile in nature; and that an optical window exists in the far visible and short-wave infrared for water which allows radiation in this wavelength range to probe the vasculature of the dermis [6]. These three factors underpin pulse oximetry, in which tissue is illuminated with red and infrared light and the reflected or the transmitted light intensity is measured.
Achieving the full potential of conventional pulse oximetry, that is, the ability to determine both heart rate and oxygen saturation, has been the goal of non-contact imaging PPG (iPPG) methods since their inception [7]. In fact, although contact SpO2 methods present many advantages over invasive alternatives, SpO2 probes still need to be worn – generally on fingers or clipped to earlobes – leading to poor compliance and risks associated with infection and skin irritation [8]. Despite this, recent work in the field of non-contact imaging using cameras has concentrated mostly on methods for the determination of heart rate, with little or no effort dedicated to deriving oxygen saturation [9–12].
The tracking of oxygen saturation with RGB cameras (visible light cameras with three channels: red, green and blue respectively) presents a number of additional problems compared to standard pulse oximetry. The near-monochromatic light sources with known intensity common to all pulse oximeters are replaced by broadband light-sources with unknown intensity; sensors that are specific to the red and infrared wavelengths of interest and that are sampled at very high frame rates (> 60 Hz) are replaced with broad-spectrum RGB sensors that have been developed to emulate the human eye and usually sample at low frame rates (∼ 30 Hz). Furthermore, the relatively controlled and limited tissue volume over which the measurement occurs for standard PPG - optically isolated and with a degree of robustness to motion - is replaced with a region of skin that is subject to movement and other artefacts such as surface reflections and shadowing. Finally, the use of visible wavelengths means a more superficial vasculature is probed than with the longer wavelengths of red or infrared.
Several groups have attempted different approaches to the non-contact measurement of SpO2 with cameras. In [13] a Monte Carlo simulation of light transport was employed in an attempt to convert the RGB signals obtained into a relative concentration of oxygen saturation, whereas [7] sought to control the light-source and [14] attempted to control the sensor response by introducing narrow band-pass filters. Our own preliminary results showed that oxygen saturation changes could be followed for periods with little or no motion using two of the RGB channels (red and blue) or by simply using the baseline changes of the colour of the skin from one of the RGB channels [15, 16], and the same channels were later used by [17].
Nonetheless, the majority of the existing work in this field suffers from the significant limitation that it has not examined a pathophysiologically/clinically relevant SpO2 range. The results cannot therefore be securely extrapolated to clinical practice, and over-fitting is a risk. [13] does not have any reference SpO2; [7] used in vitro blood samples; and [14] did not present any desaturations occurring below 95%. Finally, in our previous work ([16]) that showed the relationship between the derived oxygen saturation and the reference oxygen saturation over an extended period of time (20 minutes) and for a clinically significant desaturation, the relationship was found to vary over time. With regards to the methods used to choose the regions of interest in order to obtain the colour signals that are employed in the estimation of the SpO2, previous work in this field is either dependent on the use of fixed regions of interest ([13–16]) or on a colour-based segmentation of the skin [17].
The present work introduces a novel method for Skin-Oxygen Photoplethysmographic Image Analysis (Sophia), which allows oxygen saturation changes to be tracked accurately over time. Sophia uses broad-band lighting and an RGB camera, and is tested on subjects whose arterial oxygen saturation was varied over a clinically significant range (80–100%) with both fast and slow desaturations. The novelty of the method lies in the selection of the regions of interest, the use of signal averaging to improve on the analysis of the amplitude of the signal, and the methods for deriving the variables used in the algorithm.
Although an absolute measure of oxygen saturation is not claimed (this will depend on factors such as the lighting and the skin colour of the subject), the method is shown to be able to track changes in oxygen saturation changes with accuracy comparable to that of a conventional pulse oximeter, when the algorithms are applied retrospectively to the test data.
2. Method
2.1. Theory
Ignoring all specular reflectance components (we will see this is sufficient later on), light with a spectral distribution given by L(λ), incident on a surface with a reflectance function given by s(λ), and reaching a sensor c with a response given by the function rc(λ), will yield a sensor response that may be expressed as follows:
| (1) |
where the wavelength dependence is given by λ, the time-dependence is given by t, and the position-dependence is given by the position vector . For incident light that is spectrally time-invariant, we may expand L(λ) to:
| (2) |
where l(, t) is the intensity of the incident light and L̂(λ) is the spectral distribution of the light normalised with respect to the total energy. We may also assume that the sensor response is constant in time, such that
| (3) |
The reflectance function s(λ, , t) will be dependent on the absorbance properties of the surface on which the light is incident. These will include the influence of the chromophores in which we are interested, namely oxygenated and deoxygenated haemoglobin, melanin, and other absorbers and scatterers. In the case of skin perfused by blood, we may divide s(λ, , t) into its two main components, the contribution of non-blood tissue-light interactions m(λ, ), assumed to be time-invariant, and the function describing the contribution of blood-light interactions b(λ, , t).
| (4) |
The pulsatility of the blood due to the change in the perfusion of the skin tissue imaged may be modelled further, such that:
| (5) |
where v(, t) describes the static, non-pulsatile (DC) blood present in the tissue at all times, Δv(, t) the pulsatile (AC) component, and bDC(λ, t) and bAC(λ, t) are the functions describing the reflectance of the static and pulsatile components respectively. Note that these are also time-variant as they will depend on the oxygen saturation in each type of blood.
We may finally write the sensor response as:
| (6) |
By normalising the AC component with respect to the DC component, we find that the dependence on light intensity is eliminated:
| (7) |
However, the ratio of R̂c(t) is still dependent on the volumes of the static (v) and pulsatile (Δv) blood. This dependence is eliminated by taking the ratio of two AC components, as v and Δv are not dependent on wavelength.
| (8) |
The remaining function, the ratio of ratios, now only depends on the properties of the blood reflectance functions, and will therefore be a function of SpO2.This is the same ratio of ratios as that used in the original theoretical treatment for pulse oximetry [3]. Equation 8, however, has been rederived from first principles for the more general context of colour channels using a number of simplifying assumptions. Under the conditions of the model described, and further assuming that the properties of the skin we image do not vary spatially in such that
| (9) |
the ratio of ratios S(t) should at this point be locally invariant and uniquely dependent on the oxygen saturation. However, as mentioned in Section 1, the effects of specular reflections have been ignored. This is particularly important because, as has been shown in [18], the AC component will not only be due to colour changes as a result of the in- and out-flow of blood in tissue, but also as a result of changes in colour due to movement. In the following section, we will discuss how we can minimise the influence of locations i where specular reflections and movement have a large effect, thereby reducing the conditions to those in which the model’s assumptions are valid.
2.2. Implementation
The model introduced above predicts in Equation 8 that, for areas in which the skin is uniform in tissue composition, the ratio of ratios will be independent of the choice of region of interest (ROI) and light intensity. This is of considerable importance as it means that any or all of a set of candidate regions of interest may be used to derive the value of oxygen saturation at any point in time. If any region of interest may be used, then an average of the regions of interest may be taken instead, as previous research has shown that averaging over a large number of physiologically relevant pixels will improve the definition of the resulting PPG signal [15]. This may be understood as the reduction of the sensor noise amplitude by a factor equal to the square root of the number of pixels used in the averaging process. Furthermore, the resulting metric, the ratio of ratios, is robust against changing geometries, movement and illumination artifacts, as it is invariant to these in time. As a result of Equation 8, provided that conditions such as the spectral distribution of the light-source and the melanin concentration of the skin do not vary, neither temporally nor spatially, the measurements will be consistent with one another for different imaging geometries. Hence the resulting metric is therefore robust to changes in the position of the observed subject.
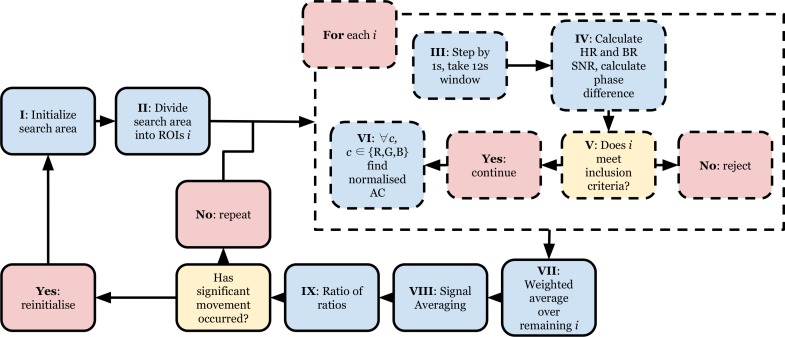
These conclusions are taken into account in Sophia (shown schematically in Fig. 1), which is based on the heart rate maps introduced in [15] and further explored in [19]. During the intialisation phase (Step I), the skin region of interest is identified. This may be achieved either by applying specific prior knowledge about the scene (for example by using face-detection if a face is known to be in the image), or by simply doing a search using a very large region of interest for the position at which the value of the signal-to-noise ratio (SNR) function for heart rate (SNRHR) is maximised, where the SNR function is defined as follows:
| (10) |
for an integral over frequencies f from f = a to f = b, containing a detrended and appropriately filtered timeseries x(t), consisting of successive samples from one of the R, G,B colour channels averaged over the ROI, its Fourier transform ℱ{x(t)}, and a double-step function 𝒱(f) defined by the convolution:
| (11) |
centred on the fundamental frequency of interest f̂ and its second harmonic f̂ = f̂HR for heart rate), with δ as the dirac delta function and Π as the rect function of half-width fh.
Fig. 1.
Schematic illustration of Sophia. Steps that are the same for all ROIs i are drawn in dashed lines. HR = Heart Rate; BR = Breathing Rate; SNR = Signal-to-Noise-Ratio.
For the purpose of initialization, x(t) is taken as the green signal from the RGB camera over a period of 12-seconds, and the double-step function for the heart rate SNR is constructed with fHR = 1.4 Hz and fh = 0.7 Hz so as to cover the entire span of the expected physiological heart rate range.
Once a search area has been defined in which all the skin to be imaged has been included, the area is divided into N contiguous n × n pixel regions of interest i (n=40) and the algorithm is intiated (Step II). Crude estimates for the heart rate, f̂HR, and the breathing rate, f̂BR, are first found from the analysis of 12-second windows which are slid 1 second at a time (Step III). The heart rate estimate is found by taking the average of all the signals resulting from the per-frame spatial average of the green channel in each of the N regions of interest, then detrending and high-pass filtering this average prior to finding the peak of the Fourier Transform. The breathing rate estimate is found by taking the average of the power spectral density (PSD) of the detrended blue signal across all N regions of interest and then searching for a peak in the expected physiological range (between 0.1 and 0.7 Hz, corresponding to 6 to 42 breaths per minute). While the green channel usually has a high heart rate SNR as a result of its poor absorption by melanin but high absorption by blood, the blue channel is used to determine the breathing rate for the opposite reason. This is done under the assumption that the three channels are equally likely to be affected by changes in reflectance and in the imaged scene as a result of motion, but this gives rise to a higher SNR in the blue channel for respiratory rate estimation, as it is the channel least affected by heart rate information.
The pulsatile, cardiac-synchronous signals which are caused by colour changes due to the in-and outflow of blood will have a relative phase shift between them that is uniquely determined by the maximum pulse transit time within the area of skin observed. From values previously reported in the literature [20], this phase shift is expected to be much smaller than radians, and the signals can therefore be said to be more in phase with each other than in antiphase. The breathing rate signals are instead caused by changes in colour due to movement, and can be either in overall phase or in antiphase. As a result of this, a temporal average over all the signals together would minimise the breathing rate signal.
The spatial averages across the 12-second windows are calculated for each of the RGB channels of the N regions of interest i to compute three 1-D signals. The heart rate SNR function is applied to each of the N red windows, selecting the frequency limits a and b to be a = 0.7 Hz and b = 2.4 Hz and with fb taken to be the quantisation limit of the Fast Fourier Transform (FFT) applied. The choice of the use of the red channel for the calculation of the heart rate SNR function is dictated by the fact that it is then this channel that is used (in conjunction with the blue channel) to derive oxygen saturation and it is therefore crucial to obtain ROIs that are relevant to this channel in particular. The breathing rate SNR function is instead applied to each of the N blue windows, with a = 0.1 Hz and b = 0.7 Hz and the half-width of the breathing rate rect function fb once more the quantisation limit of the FFT (Step IV).
The results of the heart rate and breathing rate SNR functions serve to create a logical inclusion function Li that determines whether the region of interest will be used in further calculations for that window or will be rejected (Step V). For a timeseries whose pulsatility is due to a true skin colour change, we would expect a high value for the heart rate SNR, but a low value for the breathing rate SNR. This is because breathing rate is mostly associated with movement, and any region of interest that has a high breathing rate SNR will therefore have some component (whether a physical feature or a specular reflection) that is moving and thus does not fit the initial assumptions of the model described by equations 6 to 8.
A further binary condition Pi is imposed: the cardiac-synchronous AC component of the green channel of the region interest has to be in phase with the green heart rate signal derived for the whole search area, such that:
| (12) |
where is the phase of the heart rate frequency estimate for the green signal of the region of interest i, and ϕG(f̂HR) is the phase of the heart rate frequency estimate for the green signal averaged over the entire area. A phase difference of is chosen here to differentiate between cases for which phase estimates can be said to be in phase but for the addition of a phase shift caused by a delay introduced by the pulse transit time and cases for which the two phase estimates are exactly in antiphase. The latter will only occur as a result of the cardiac-synchronous signal in the ROI being the result of movement induced pulsations. The green channel is chosen as it has been shown [11] that this channel has the highest SNR for heart rate and will thus lead to a more accurate comparison of phase estimates.
The overall logical inclusion function Li is then given by the heart rate, breathing rate, and phase components – , , respectively – such that
| (13) |
with and determined by the initial conditions of the video recording (these thresholds will depend on skin colour, light intensity, light spectrum and distance from the camera). The use of the inclusion function removes from the estimation of oxygen saturation those regions of interest for which changes in AC amplitude are caused by specular reflections, including only those regions of interest for which the changes in normalised AC amplitude (ratio of ratios) are caused by colour change.
In Step VI, the normalised AC amplitude is determined for each colour channel as per Equation 7 in all M regions of interest that meet the condition Li = 1. As the method depends on multiple regions to reduce the measurement error, a minimum number of regions M ≥ 3 is required at each iteration or the time window is rejected. The DC component is taken as the time-average of the 12-second window for each colour channel and each region of interest individually, and the AC component is taken to be the residual of the original timeseries after the DC component has been subtracted. A weighted average of all the M normalised amplitudes of the AC component for the heart rate timeseries is then taken for each of the colour channels, in which the region of interest weightings ωi are a function of the heart rate SNR (Step VII), such that:
| (14) |
The weighting favours regions of interest that have a high heart rate signal-to-noise ratio as these are more likely to conform to the theoretical model described by Equation 6. Note that the averaging takes place prior to the ratio of ratios being computed, so as to minimise the effect of noise in both the numerator and denominator of Equation 8.
Finally, a self-referential signal-averaging procedure is applied to the averaged waveforms (Step VIII). This is done by taking the green averaged waveform, high-pass filtering it and finding the positions of the peaks in the waveform. The green channel is again chosen for its high SNR. All samples around the peaks are then averaged together to obtain a single representative waveform for the entire 12-second period for each channel. The amplitude of the waveform is taken as the normalised amplitude for that channel and the ratio of ratios is calculated as the ratio of the blue amplitude to the red amplitude (Step IX). Steps II to IX are then repeated until the subject moves outside the search area, at which point the algorithm is halted until there is a period of no movement and reinitialisation is possible.
2.3. Further vital signs
Although the method presented here has been devised to obtain an estimate for oxygen saturation, the need for an accurate calculation of the heart rate is inherent in the model used and the assumptions made, and heart rate may be estimated in conjunction with the oxygen saturation estimate. It can be derived by applying established signal processing techniques (detrending, band-pass filtering, Principal Component Analysis) to the waveform obtained in Step VII. The peak of the resulting PSD then corresponds to the HR. The interested reader is referred to [12, 15] for more detailed discussions on the methods for heart rate estimation.
Breathing rate is also estimated as part of the algorithm described, but due to the short length of the windows considered (12 seconds), the low frame rate, and the use of the Fast Fourier Transform (FFT), the results are heavily quantised. Since an accurate measure of breathing rate is not necessary for the algorithm, breathing rate estimation is outside the scope of this paper.
2.4. Dataset
The algorithm was tested using the video recordings of five volunteers who had undergone a controlled study in a hypoxic environment. The recordings were made with a 3-CCD (JAI AT-200CL) RGB camera placed about 1.5 m from the subject, shooting at 16 frames per second. The skin phenotype of the volunteers was determined through the use of the Fitzpatrick scale standard [21]. The distribution of Fitzpatrick skin types may be seen in Table 1. The study was conducted in the University of Oxford Department of Physiology, Anatomy and Genetics, using a purpose-built chamber within which the inspired concentrations of nitrogen, oxygen and carbon dioxide could be carefully controlled [22]. Participants were first recorded for seven minutes breathing air. The ambient oxygen concentration was then reduced by introducing nitrogen into the chamber until the SpO2 settled at 95%. The process was repeated every seven minutes to a nadir SpO2 of 80%. This process was entirely under manual control and was performed by a critical-care physician who constantly monitored physiological variables to permit careful titration of FiO2 to achieve the desired SpO2. Heart rate, end-tidal O2, end-tidal CO2, respiratory rate and respiratory pattern were continuously monitored and the live video-feed was also available to guide safe induction of hypoxaemia. That values below 80% were occasionally obtained reflects the fact that, at this degree of hypoxaemia, even very small changes in a subject’s ventilatory pattern can result in further falls in SpO2 in spite of FiO2 remaining unchanged. When SpO2 fell below 80%, oxygen was immediately introduced into the chamber; if this did not bring about a rapid correction then oxygen was delivered by nasal cannula to re-saturate the participant. Throughout the procedure, the SpO2 levels of the participants were measured using a clinical-grade ear pulse oximeter (Datex-Ohmeda 3900 with Tru-Trak) and their heart rate was monitored using a 3-lead ECG in order to ensure their safety. This monitoring equipment was separate to that used to record the reference vital signs, detailed below.
Table 1.
Skin colour type (Fitzpatrick scale I through to VI), and proportion of data used per subject. Both the algorithm (Sophia) and post-processing techniques applied to the results reject data that are detected as noise or outliers.
| Subject | Fitzpatrick Type | Total Recording Time (mins) | Accepted Time (mins) | Rejected Time (mins) | Proportion of Total Used (%) |
|---|---|---|---|---|---|
|
| |||||
| 1 | II | 41.7 | 36.3 | 5.4 | 87.1 |
| 2 | IV | 44.7 | 41.2 | 3.5 | 92.2 |
| 3 | III | 44.7 | 30.3 | 14.4 | 67.7 |
| 4 | III | 42.9 | 42 | 0.9 | 97.9 |
| 5 | III | 34.1 | 29.1 | 5.0 | 85.4 |
All windows were covered so as to minimise the amount of stray incident lighting from any source other than that in the chamber itself. The interior of the chamber was lined with sheets of Tyvek 1443R to ensure a maximal and equal reflection of all wavelengths from the source. This created an environment of diffuse and spectrally uniform lighting. Throughout the study, the volunteers were illuminated with two 576-LED Mosaic 30cm lighting panels (Limelite Ltd). The lights were directed at reflecting panels (also lined with Tyvek 1443R) to ensure the light was spread evenly accross the subject’s face.
Reference data for the study were acquired using two BlackShadow (Stowood Scientific Instruments, Oxford, UK) devices, with a pulse oximeter probe positioned on the index fingers of each hand, a three-lead ECG, and abdominal and thoracic elastic belts that measure respiratory rate via inductance plethysmography. The pulse oximeter used by the BlackShadow was a MS2040 oximeter (Masimo Inc) with an averaging time of 2–4 seconds and a reported accuracy of ±2% in stationary adults in the SpO2 range between 70% and 100%.
3. Results
3.1. Post-processing
In order to obtain accurate estimates for the vital sign values and prior to linear regression, a simple but robust univariate outlier detection method [23] was applied retrospectively to the camera heart rate timeseries and the normalised channel amplitude timeseries, to reject anomalies. Outliers were taken to be those that had absolute values that were more than three times the median absolute deviation (MAD) away from the median of the distribution. The proportion of data rejected as a result of these procedures and the algorithm’s own logical inclusion index is shown in Table 1. As two reference signals were available for heart rate and oxygen saturation from the two pulse oximeters used (RefL and RefR), the mean of the two (Refμ) was employed as a comparative reference. All data presented in the Figures and Tables will be made available at [24].
3.2. Oxygen saturation
Two representative quantities are used to determine the efficacy of the method: the coefficient of determination (r2) between the log ratio of ratios and the reference oxygen saturation, and the mean absolute error (MAE) between the fitted results and the reference oxygen saturation. A log-linear fit was found of the type:
| (15) |
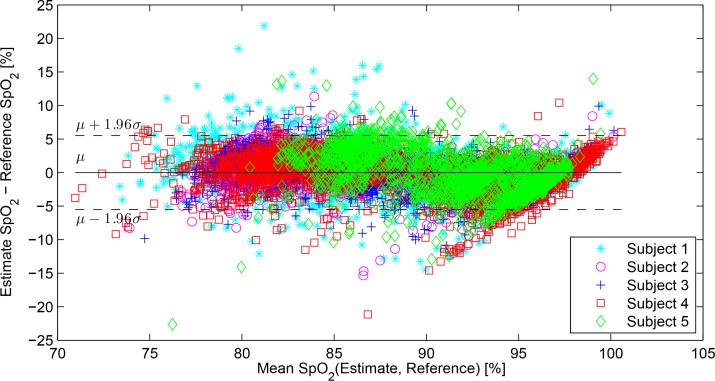
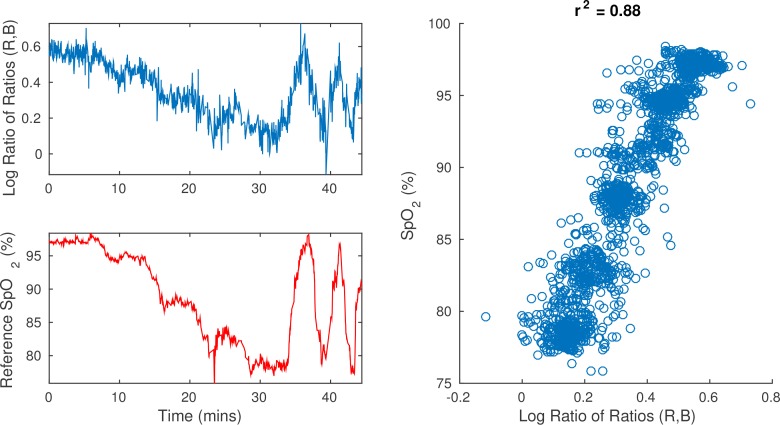
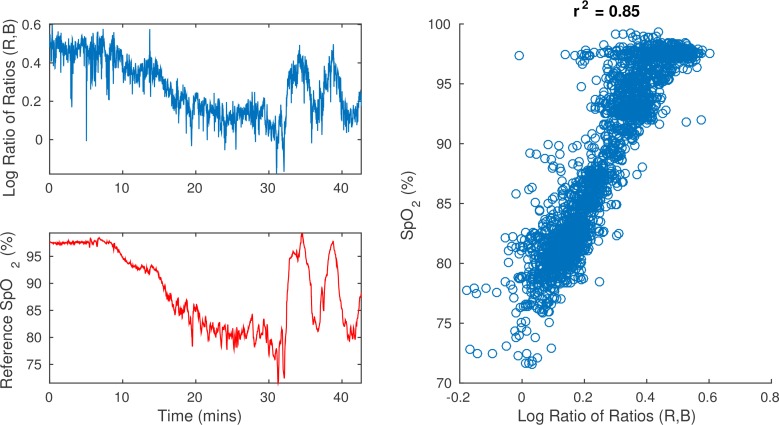
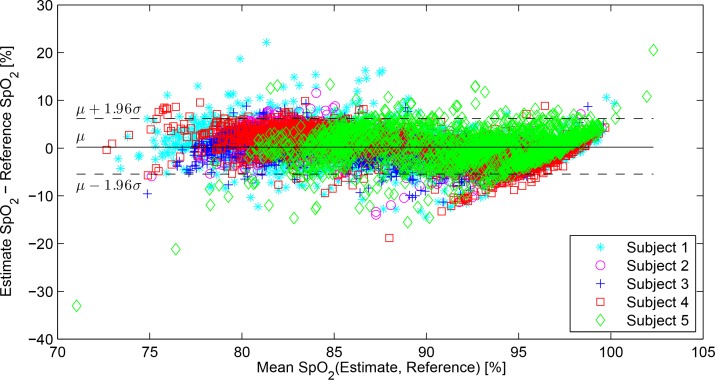
where S is the ratio of ratios from Equation 8 – normalised blue amplitude divided by normalised red amplitude. The parameters c and β were found via least squares regression analysis, and E is the camera estimate of peripheral oxygen saturation. The use of the logarithm arises because the normalised amplitude of the red channel will be smallest (and thus most sensitive to noise) when the oxygen saturation is high, magnifying the noise greatly. The application of the logarithm simply attenuates this effect by reducing the impact of variation when the oxygen saturation is high. The results are reported in Table 2, alongside the mean absolute error between the two reference pulse oximeters, reported for comparison, and the mean and standard deviation of the reference oxygen saturation, giving an indication of the spread of the oxygen saturation throughout the session. The mean error (ME) between the reference SpO2 from the pulse oximeters is also reported to verify that there is no bias between the two oximeters. The accuracy and biases present in the data that has been linearly regressed onto the reference oxygen saturation are shown graphically through a Bland-Altman plot in Fig. 2. Two representative examples of the camera and reference data are shown in Fig. 3 and 4, in which both the timeseries and the correlation between the reference oxygen saturation and the derived estimate for oxygen saturation are shown for Subject 3 and Subject 4 respectively.
Table 2.
Oxygen saturation results for the non-contact (Camera) estimates versus the mean of the two reference pulse oximeters (Refμ), reported as the gradient between the two, the coefficient of determination, and the mean absolute error (MAE) and the mean error (ME). The MAE and ME between the right reference pulse oximeter (RefR) and the left reference pulse oximeter (RefL) are also reported, as is the spread of the mean reference data in the form of mean and standard deviation (μ ± σ).
| Subject | Gradient β | Coefficient of Regression (r2) | Camera-Refμ MAE (%) | RefR−RefL MAE (%) | RefR−RefL ME (%) | Refμ μ ± σ (%) |
|---|---|---|---|---|---|---|
| 1 | 38.7 | 0.81 | 2.37 | 1.36 | −0.58 | 89.4 ± 7.2 |
| 2 | 43.2 | 0.89 | 1.63 | 0.42 | 0.36 | 89.0 ± 6.7 |
| 3 | 40.8 | 0.88 | 1.85 | 1.17 | −0.88 | 89.4 ± 7.0 |
| 4 | 44.8 | 0.85 | 2.06 | 0.73 | −0.67 | 88.7 ± 7.2 |
| 5 | 29.7 | 0.60 | 2.53 | 0.74 | −0.50 | 91.3 ± 5.0 |
Fig. 2.
Bland-Altman plot of all results for oxygen saturation. The estimated oxygen saturations (obtained by fitting a linear model to the data) are compared with the mean reference oxygen saturation. The red line and green lines either side of it show μ±1.96σ = 0.00 ± 5.51.
Fig. 3.
Oxygen saturation results for Subject 3. Top-left: results with the camera using the method described. Bottom-left: reference oxygen saturation from the pulse oximeter. Right Scatter plot showing the relationship between the logarithm of the ratio of ratios using the red and blue channels of the camera and the oxygen saturation from the pulse oximeter.
Fig. 4.
Oxygen saturation results for Subject 4. Top-left: results with the camera using the method described. Bottom-left: reference oxygen saturation from the pulse oximeter. Right Scatter plot showing the relationship between the logarithm of the ratio of ratios using the red and blue channels of the camera and the oxygen saturation from the pulse oximeter.
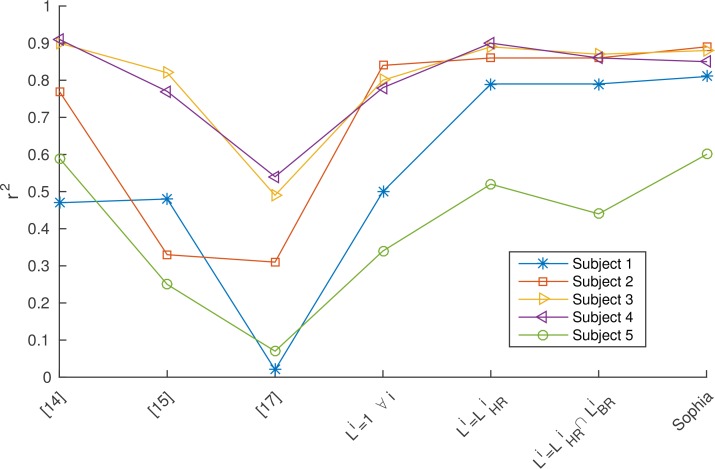
In order to have a baseline against which to compare the method in an effective manner, other ROI selection methods were taken from the literature and applied to all subjects. A comparison was made with the few available methods that are applicable: [14], which uses a fixed region of interest covering the face below the eyes of the volunteers; [15], which uses a fixed region of interest placed on the cheek of the subject; and [17], which proposes segmenting the skin of a face after face-detection using a cut-off in YCbCr colour space and using the skin mask as the ROI. Of these methods, it should be noted that [14] was used within a two-camera architecture that employed narrow-band filters, and both [15] and [14] appear to have used manually selected, fixed regions of interest. These two methods were therefore applied as fixed regions of interest to the data, which was possible since it was recorded for subjects who were asked to remain as still as possible, whereas the ROI-extraction method taken from [17] was updated every frame as it was understood to be dynamic. Once the raw red and blue signals were acquired by taking the average of the pixel intensities for these two colour channles in the respective ROIs, the same signal processing steps that had been used in Sophia were applied to the methods, and the resulting oxygen saturation estimates were compared to the reference mean oxygen saturation in order to obtain the coefficient of determination.
These results for the different ROI selection methods are shown in Fig. 5. Plotted alongside them are the estimates resulting from the subsequent application of the inclusion criteria – no thresholds, HR threshold, HR and BR threshold, and all thresholds – taken from Equation 13. These are shown to give an understanding of the effect of each criterion on the final accuracy.
Fig. 5.
A comparison of different ROI selection methods and of the effect of the inclusion criteria on the ROI selection in Sophia, carried out on all subjects considered. From left to right: the method introduced by [14], using a fixed region manually set onto the lower part of the face; the method introduced by [15], using a fixed region placed on the cheek of the subject; the method introduced by [17], using the entirety of the skin as segmented by a segmentation in YCbCr space; Sophia with none of the thresholds introduced in Equation 13; Sophia using only the heart rate SNR threshold; Sophia using the heart rate and the breathing SNR rate thresholds; Sophia using all thresholds as described in this paper. The line between the points does not indicate any continuity between reported measures: it has been added to aid the reader.
The potential for the relationship between colour and oxygenation to be generalised for different subjects viewed in near-identical experimental conditions was explored through the use of an iterative, leave-one-out technique. For each subject, the log-linear fit was estimated by taking the gradient β as the average of the gradients of all other subjects. The value of the intercept c was determined in each case by relating the median value of the log ratio of ratios over the first minute of data (in which the oxygen saturation is expected to remain constant) to the assumed value of oxygen saturation in healthy adults (97%). The MAE and ME between the transformed estimates and the average reference oxygen saturation are reported in Table 3, and the data for all subjects is shown in Fig. 6.
Table 3.
Oxygen saturation results through leave-one-out. For each subject, the mean of the gradients of the lines of best fit to the data from all other subjects is used as the gradient β of the linear relationship between the data and the oxygen saturation. The intercept c is instead found by using the first minute of data from the subject. The results indicate that the method can not only be used to track oxygen saturation changes, but effectively measure it based on a training data across similar skin colours and under ideal conditions.
| Subject 1 | Subject 2 | Subject 3 | Subject 4 | Subject 5 | |
|---|---|---|---|---|---|
| Gradient | 39.6 | 38.5 | 39.1 | 38.1 | 41.9 |
| MAE (%) | 2.37 | 1.76 | 1.95 | 2.34 | 2.71 |
| ME (%) | 0.20 | 0.27 | −0.56 | 0.47 | 0.45 |
Fig. 6.
Bland-Altman plot of all results for oxygen saturation. The estimated oxygen saturations (obtained by fitting a linear model via the leave-one-out procedure to the data for each subject) are compared to the mean reference oxygen saturation. The red line and green lines either side of it show μ ± 1.96σ = 0.19 ± 5.81.
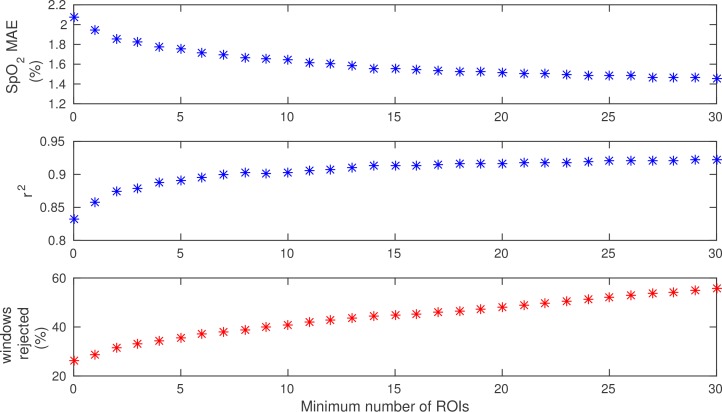
Finally, the influence of the number of regions of interest on the results is shown in Fig. 7, in which the mean absolute error between the best fit and the mean reference Refμ, the coefficient of determination, and percentage of windows rejected are each plotted against a changing threshold for the minimum number of ROIs that need to be present for a window to be accepted.
Fig. 7.
Effect of varying the minimum number of regions of interest on the results for Subject 3. Top: mean absolute error between the reference and camera oxygen saturations for varying the minimum number of ROIs in each window. Middle: effect of varying the minimum number of ROIs on the coefficient of determination. Bottom: percentage of windows rejected as a result of varying the minimum number of ROIs.
4. Discussion
The results presented are shown for non-contact estimates based on the log of the ratio of the normalised AC blue signal to normalised red AC signal. Previous evidence [15], has shown that the DC intensity of the red channel is the most affected by oxygen saturation and is positively correlated with it. Application of this knowledge to Equation 8, leads to the red channel appearing in the denominator so as to ensure that this relationship is reflected in the model. The linear form of the relationship, chosen as it explains the data sufficiently without needing to resort to further polynomial fits, also closely matches that found between the ratio of ratios in classical pulse oximetry and the arterial oxygen saturation, which had been found to be linearly [25] or quadratically [26] related to oxygen saturation. Nonetheless, this may only be taken to be an approximation, in the same way as current pulse oximetry technology uses lookup tables to account for the fact that the theoretical model underpinning it neglects the effect of multiple scattering.
The results presented in this paper show that, with a careful, dynamic selection of the ROIs and with a log-linear relationship fitted to the data, the error margin for non-contact estimation when compared to measures of SpO2 with conventional pulse oximetry is comparable to the standard manufacturing claim for pulse oximeters of 2–3% over the range of 70–100% oxygen saturation [27]. Even more interestingly, this error margin is maintained when a set gradient is fitted to the data and the intercept is evaluated for the first minute of data (Table 3), as this indicates that a common relationship may be found for subjects who have similar skin colours (Fitzpatrick Types II–IV). The purpose of the leave-one-out strategy was to demonstrate that the method proposed is not limited to individual correlations but may also be used to infer a general relationship between colour changes and oxygen saturation changes under very strict conditions (quasi-identical lighting, identical camera and recording parameters, healthy subjects with similar skin tones). Under these conditions, the method proposed could be used to measure oxygen saturation, rather than simply tracking oxygen saturation changes. It is possible that such a relationship could be found only due to the very large range of oxygen saturations that are sampled in the course of the experiments – around 20% – enabling a relationship to be found even in high noise conditions.
The analysis was carried out with respect to a pulse oximeter rather than blood-gas analysis as would be standard practice when analysing the accuracy of standard pulse oximeters. This of itself entails some errors as the assessment of the accuracy of the new method is linked to the accuracy of the pulse oximeters, which have a reported accuracy of ±2% in adults during no motion. The fact that the difference between the two pulse oximeters (reported in Table 2) was minimal however indicates that the reference values were at the very least consistent with one another. Another difference in the estimation of oxygen saturation using the camera data and pulse oximeter is the averaging time. The Masimo pulse oximeters employed a variable averaging time of 2–4 seconds, whereas, due to the lower SNR, the camera needs a longer averaging window (12 seconds) which is then employed in the signal averaging process. This difference in window-length will not have a great effect during slow changes in saturation but may hide the effect of faster changes, especially if compounded by further smoothing techniques. Nonetheless, the visual results shown in Fig. 3 and 4 would seem to indicate that for the protocol investigated (fast desaturations and resaturations with changes occurring in <1 minute), the window-lengths employed were sensitive to fast saturation changes and followed the reference closely, capturing, for example, the fast desaturations just before the 20th minute and just after the 30th minute in Fig. 4. In turn, a faster rate of frame acquisition and a higher imaging resolution, to levels which are now easily within range of commercially available cameras, will reduce the need for longer windows and bring the averaging time to that expected of a pulse oximeter.
Figure 5 indicates that the ROI selection method employed in Sophia consistently matches or outperforms other approaches that have previously been attempted. Importantly, Sophia maximises the accuracy for all estimates, whereas the other methods tended to give more variable values. This should not come as a surprise, as the selection of regions of interest was not a particular concern of previous works on oxygen saturation estimation with cameras: these mainly tended to concentrate on demonstrating that such an estimation was possible in the first place. As a result, the majority of the methods relied on carefully chosen fixed regions of interest [14–16], that were manually placed and poorly defined. These types of methods work very well when subjects remain very still, a condition that was both met by their original protocol and by our study. Indeed, this may be seen for Subjects 3 and 4, two subjects who moved very little (as measured by simple frame differencing). However Subject 1 moved a lot more throughout the study, and this is reflected in the low value of correlation when using fixed regions of interest. It is also interesting to note that the ROI given by [15] actually uses a subset of the pixels that are used in [14], and that the estimates are almost always less accurate than those of the larger set. This again would indicate that averaging over larger regions of interest, particularly when there is no movement and the breathing rate movement is eliminated by the signal averaging step, leads to a reduction in noise. Subject 5 also yields very poor results across all methods; however this is not so much due to motion as to the fact that the session was terminated after a single desaturation-resaturation cycle, and hence a more restricted range of SpO2 values was explored for this subject.
Although the fixed region methods provide an excellent baseline – the optimal result in cases for which there is no movement – any effort towards their automation would have to rely on the tracking of particular features. On the other hand, [17] explicitly used a method that is non-static and that is furthermore not overly reliant on face detection as it also uses a skin segmentation step. This ROI selection method can therefore be used in scenarios in which facial-feature based methods might fail as a result of having to track features that are either hard to identify or simply not there, such as in [16]. Unfortunately, probably due to the instability of the colour-based masking (which identified pixels from background regions neighbouring the face as skin), [17] actually produced the most noisy results and consistently under-performed with respect to all other ROI-selection methods. The results obtained for Subjects 3 and 4 are in line with the coefficient of determination reported in the original paper (r2 > 0.50); however the method is strongly under-performing in all other subjects.
When comparing the effects of subsequent ROI-selection steps within Sophia in Fig. 5, the most noticeable change in the resulting correlation with the reference values occurs immediately as a result of the application of a weighted average (as may be seen in Subjects 3–4), after which the introduction of the thresholds does not overly affect the results. Only in the cases for which the initial weighted average gives poor results does the thresholding contribute significantly to the final result (Subjects 1 and 5). Furthermore, in Subject 5 we see that the introduction of the breathing rate SNR threshold decreases the correlation coefficient (from0.52 to 0.44), and it is only with the addition of the final phase condition that the accuracy of the estimate increases again. This phenomenon may to some extent be explained by the fact that the addition of subsequent criteria will reduce the number of regions of interest that are averaged, increasing the noise if the regions of interest do not have data of a high enough quality. This explanation is to some extent validated by the curves showing the effect of changing the minimum number of regions of interest used for the calculation of the oxygen saturation estimate in Subject 3 (Fig. 7). These show that if results that are obtained by combining fewer than 5 regions of interest are allowed, they have a strongly negative effect on the resulting accuracy. This in turn means that averaging over fewer regions, however well chosen, will lead to an increase in noise. A balance therefore needs to be found between the inclusion criteria imposed and the quality of the signal obtained. The results indicate that this may be done by eschewing fixed SNR thresholds and instead using a dynamic approach for the thresholds, such as by sensitivity analysis.
A number of factors have however been controlled for in this study as described in Section 2, the effects of which need to be explored in greater depth. The method appears to be relatively robust to changes in the imaging geometry, something that is underlined by the fact that the error remains low even when the β and c values are taken to be the averge values for the other subjects – the “training” dataset– but the effect of movement has not been investigated systematically and only considered in passing. Furthermore, three additional factors are likely to have a further influence on the relationship between oxygen saturation and the log ratio of ratios: the camera employed, the lighting used and the concentration of melanin in the skin. The log-linear relationship found in Section 3 may change with these three parameters, and might affect the gradient and/or the degree of linearity. In [28], the use of the wideband blue sensor in the calculation of oxygen saturation is also questioned with relation to the fact that it has a lower sensitivity than the infrared wavelengths employed in standard optical oxygen sensing. This reinforces the need and use of dynamic algorithms for ROI selection such as Sophia that increase the quality of the signal in order to increase the sensitivity of the blue channel for the estimation of oxygen saturation with cameras, something that is also clearly shown by the influence of the minimum number of ROIs on the final accuracy of the estimate in Fig. 7, as averaging over multiple ROIs will lead to a clearer signal. In turn, this indicates that a strategy such as that chosen in [15] or [16], in which a single region of interest is chosen (whether manually or automatically), will fare worse than a system based on averaging over multiple regions of interest such as that proposed in Sophia. Finally, a fourth factor not controlled for in our studies is perfusion. The subjects’ skin perfusion is likely to have varied, partly as a result of the oxygenation changes themselves, and partly because of temperature variations.
In addition to this, the technique proposed still suffers from the large amount of noise present in the signal. As may be observed in Table 1, in each case a highly varying number of windows (2.1–41.5%) is rejected by the algorithm and by the post-processing procedure, although the variability in the reference SpO2 explored still covers the 80–100% oxygen saturation range examined (Table 2). Conversely, this means that the technique employed is largely successful in rejecting low-quality data caused by subject motion: even when sitting still in front of the camera, subjects do make small movements from time to time over the course of more than half an hour. The normalisation technique applied to each ROI (Step VI in Fig. 1) is effective in discounting local variations in light intensity due to shadows. All of these factors lead to an accurate assessment of oxygen saturation changes using camera-based techniques. Furthermore, Fig. 7 suggests that the number of regions of interest available when taking a measurement may be used as a measure of uncertainty for each measure. These uncertainty estimates may then be incorporated into a Kalman-filter framework to allow the optimal calculation of multiple estimates of oxygen saturation. A number of lossy post-processing techniques such as median filtering may further be employed to ensure a cleaner signal and reduce the amount of noise present in the final estimate, as had been done in previous publications [14].
Finally, it should be noted that the cameras may be imaging different vessel types to the pulse oximeters on the fingers, as visible light penetrates less than infrared light. Therefore it is perhaps more accurate to talk of skin-oxygen saturation (StO2) rather than the pulse oximetry (SpO2) estimate of arterial saturation (SaO2), as the vasculature imaged is more likely to be composed of capillaries and smaller vessels such as arterioles rather than any large arterial vessel [29]. Although [30] has shown that StO2 and SaO2 are correlated over limited ranges, no extensive study has been carried out on humans to date. That the cameras may be measuring mixed arterial and venous oxygen saturation is further supported by the shapes of the Bland Altman plots (Fig. 2 and 6), which have a characteristic bias only in the upper range of the oxygen saturation. This may perhaps be explained by the fact that, because of the nature of the haemoglobin oxygen-dissociation curve, while the arterial oxygen saturation will change very little in this range for quite large variations in oxygen partial pressure, venous oxygen saturation will vary more considerably.
5. Conclusion
A novel algorithm to determine changes in oxygen saturation in visible light, both relatively and absolutely, for predefined lighting and RGB camera conditions has been described. The method uses an automated ROI-selection process that may be extended to scenes not limited by the presence of facial features. The results obtained conclusively indicate that it is possible to use an RGB camera to determine changes in oxygen saturation and to do so with an accuracy that is comparable to that of commercial pulse oximeters. The development of a non-contact method of determining oxygen saturation paves the way for a global measurement of oxygen saturation and perfusion across the body rather than being limited to the peripheries as with pulse oximetry. It has been suggested [31], that this would allow important additional information about the peripheral circulation to be made available to clinicians.
Further work is necessary to understand the effect of external factors on the relationship between the channel ratios and the oxygen saturation. These factors include external factors such as changing light conditions and camera spectral responses, as well as physiological factors such as melanin concentration and skin. A more refined model of the light-tissue interactions than the simplistic one considered in this paper may be helpful in these investigations, and the incorporation of uncertainty into the measurements (that is readily available through the number of regions of interest and the variations in power of the heart-rate signal in each region of interest) may be used to ensure a less noisy signal. Finally, improved camera technology (higher bit resolution and sampling frequency) will lead to improvements in estimating oxygen saturation with a non-contact method.
Acknowledgments
Alessandro Guazzi, João Jorge, and Jonathan Daly were supported by the RCUK Digital Economy Programme grant number EP/G036861/1 (Oxford Centre for Doctoral Training in Healthcare Innovation). Mauricio Villarroel was supported by the Biomedical Research Centre under the Biomedical Information & Technology Theme DFRWAO00. Matthew Frise was supported by a British Heart Foundation Clinical Research Training Fellowship grant number: FS/14/48/30828. The study gained approval from University Ethics (CUREC number: MSD-IDREC-C3-2014-003). We would like to thank all the volunteers who agreed to take part in the study and Dr. Tasos Papastylianou for the lengthy discussions on the subject.
References and links
- 1.O’Driscoll B.R., Howard L. S., Davison A.G., “BTS guideline for emergency oxygen use in adult patients,” Thorax 63(6 Suppl.), S1–S68 (2008) [DOI] [PubMed] [Google Scholar]
- 2.Kent B. D., Mitchell P. D., McNicholas W. T., “Hypoxemia in patients with COPD: cause, effects, and disease progression,” Int. J. Chron. Obstruct. Pulmon. Dis. 6, 199–208 (2011) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Webster J. G., Design of Pulse Oximeters (CRC Press, 1997) 10.1887/0750304677 [DOI] [Google Scholar]
- 4.Severinghaus J. W., “Discovery of pulse oximetry,” Anesth. Analg. 105(6), S1–S4 (2007) 10.1213/01.ane.0000269514.31660.09 [DOI] [PubMed] [Google Scholar]
- 5.Hanning C. D., Alexander-Williams J. M., “Pulse Oximetry: A Practical Review,” Brit. Med. J. 311(7001), 367–370 (1995) 10.1136/bmj.311.7001.367 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Palmer K. F., Williams D., “Optical properties of water in the near infrared,” J. Opt. Soc. Am. 64(8), 1107–1110 (1974) 10.1364/JOSA.64.001107 [DOI] [Google Scholar]
- 7.Wieringa F. P., Mastik F., van der Steen A. F., “Contactless multiple wavelength photoplethysmographic imaging: a first step twoard SpO2 camera technology,” Ann. Biomed. Eng. 33(8), 1034–1041 (2005) 10.1007/s10439-005-5763-2 [DOI] [PubMed] [Google Scholar]
- 8.Wilkins M. C., “Residual bacterial contamination on reusable pulse oximetry sensors,” Respir. Care 38(11), 1155–1160 (1993) [PubMed] [Google Scholar]
- 9.de Haan G., van Leest A., “Improved motion robustness of remote-PPG by using the blood volume pulse signature,” Physiol. Meas. 35(9), 1913–1926 (2014) 10.1088/0967-3334/35/9/1913 [DOI] [PubMed] [Google Scholar]
- 10.Bousefsaf F., Maaoui C., Pruski A., “Continuous wavelet filtering on webcam photoplethysmographic signals to remotely assess the instantaneous heart rate,” Biomed. Signal Proces. 8(6), 568–574 (2013) 10.1016/j.bspc.2013.05.010 [DOI] [Google Scholar]
- 11.Verkruysse W., Svaasand L. O., Nelson J. S., “Remote photoplethysmographic imaging using ambient light,” Opt. Express 16(26), 21434–21445 (2008) 10.1364/OE.16.021434 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Poh M. Z., McDuff D. J., Picard R. W., “Non-contact, automated cardiac pulse measurements using video imaging and blind source separation,” Opt. Express 18(10), 10762–10774 (2010) 10.1364/OE.18.010762 [DOI] [PubMed] [Google Scholar]
- 13.Nishidate I., Sasaoka K., Yuasa T., Niizeki J., Maeda T., Aizu Y., “Visualising of skin chromophore concentrations by use of RGB images,” Opt. Lett. 33(19), 2263–2265 (2008) 10.1364/OL.33.002263 [DOI] [PubMed] [Google Scholar]
- 14.Kong L., Zhao Y., Dong Y., Jian Y., Jin X., Li B., Feng Y., Liu M., Liu X., Wu H., “Non-contact detection of oxygen saturation based on visible light imaging device using ambient light,” Opt. Express 21(15), 1764–1771 (2013) 10.1364/OE.21.017464 [DOI] [PubMed] [Google Scholar]
- 15.Tarassenko L., Villarroel M., Guazzi A., Jorge J., Clifton D. A., Pugh C., “Non-contact video-based vital sign monitoring using ambient light and auto-regressive models,” Physiol. Meas. 35(5), 805–831 (2014) 10.1088/0967-3334/35/5/807 [DOI] [PubMed] [Google Scholar]
- 16.Villarroel M., Guazzi A., Jorge J., Davis S., Watkinson P., Green G., Shenvi A., McCormick K., Tarassenko L., “Continuous non-contact vital sign monitoring in the neonatal intensive care unit,” Healthc. Technol. Lett. 1(3), 87–91 (2014) 10.1049/htl.2014.0077 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bal U., “Non-contact estimation of heart rate and oxygen saturation using ambient light,” Biomed. Opt. Express 6(10), 86–97 (2015) 10.1364/BOE.6.000086 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Balakrishnan G., Durand F., Guttag J., “Detecting pulse from head motions in video,” in Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (IEEE, 2013), pp. 3430–3437 [Google Scholar]
- 19.Kumar M., Veeraraghavan A., Sabharwal A., “DistancePPG: robust non-contact vital signs monitoring using a camera,” Biomed. Opt. Express 6(5) 1488–1565 (2015) 10.1364/BOE.6.001565 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kaur B., Tarbox E., Cissel M., Moses S., Luthra M., Vaidya M., Tran N., Ikonomidou V. N., “Remotely detected differential pulse transit time as a stress indicator,” Proc. SPIE 9496, 949604 (2015) 10.1117/12.2177886 [DOI] [Google Scholar]
- 21.Fitzpatrick T. B., “Soleil et peau,” J. de Medecine Esthetique 2, 33–34 (1975) [Google Scholar]
- 22.Howard L. S., Barson R. A., Howse N. P., McGill T. R., McIntyre M. E., O’Connor D. F., Robbins. P. A., “Chamber for controlling end-tidal gas tensions over sustained periods in humans,” J. Appl. Physiol. 78(3), 1088–1091 (1985) [DOI] [PubMed] [Google Scholar]
- 23.Pearson R. K., “Outliers in process modeling and identification,” IEEE Trans. Control Syst. Technol. 10(1), 55–63 (2002) 10.1109/87.974338 [DOI] [Google Scholar]
- 24.Guazzi A. R., “Sophia Dataset,” (2015), http://dx.doi.org/10.5072/bodleian:xp68kh800.
- 25.Mendelson Y., Kent J. C, “Variations in optical absorption spectra of adult and fetal haemoglobins and its effect on pulse oximetry,” IEEE Trans. Biomed. Eng. 36(8), 844–848 (1989) 10.1109/10.30810 [DOI] [PubMed] [Google Scholar]
- 26.Fine I., Weinreb A., “Multiple scattering effect in transmission pulse oximetry,” Med. Biol. Eng. Comput. 33(5), 709–712 (1995) 10.1007/BF02510791 [DOI] [PubMed] [Google Scholar]
- 27.Milner Q. J., Matthews G. R., “An assessment of the accuracy of pulse oximeters,” Anaesthesia 67(4), 396–401 (2012) 10.1111/j.1365-2044.2011.07021.x [DOI] [PubMed] [Google Scholar]
- 28.Karlen W., Lim J., Ansermino J. M., Dumont G., Scheffer C., “Design challenges for camera oximetry on a mobile phone,” in Proceedings of IEEE Engineering in Medicine and Biology Society Annual Conference (IEEE, 2012), pp. 2448–2451 [DOI] [PubMed] [Google Scholar]
- 29.Zonios G., Bykowski J., Kollias N., “Skin melanin, hemoglobin, and light scattering roperties can be quantitatively assessed in vivo using diffuse reflectance spectroscopy,” J. Invest. Dermatol. 117(6), 1452–1457 (2001) 10.1046/j.0022-202x.2001.01577.x [DOI] [PubMed] [Google Scholar]
- 30.Benaron A. D., Parachikov I. H., Friedland S., Soetniko R., Brock-Utne J., van der Starre P. J. A., Nexhat C., Terris M. K., Fincher E. F., Hsu C. P., Clark F. L., Cheong W., Duckworth J. L., Stevenson D. K., “Continuous, noninvasive and localised microvascular tissue oximetry using visible light spectroscopy,” Anaesthesiology 100(6), 1469–1475 (2004) 10.1097/00000542-200406000-00019 [DOI] [PubMed] [Google Scholar]
- 31.Allen J., “Photoplethysmography and its application in clinical physiological measurement,” Physiol. Meas. 28(3), R1 (2007) 10.1088/0967-3334/28/3/R01 [DOI] [PubMed] [Google Scholar]