Abstract
Microscale quantification of cilia-driven fluid flow is an emerging area in medical physiology, including pulmonary and central nervous system physiology. Cilia-driven fluid flow is most completely described by a three-dimensional, three-component (3D3C) vector field. Here, we generate 3D3C velocimetry measurements by synthesizing higher dimensional data from lower dimensional measurements obtained using two separate optical coherence tomography (OCT)-based approaches: digital particle image velocimetry (DPIV) and dynamic light scattering (DLS)-OCT. Building on previous work, we first demonstrate directional DLS-OCT for 1D2C velocimetry measurements in the sub-1 mm/s regime (sub-2.5 inch/minute regime) of cilia-driven fluid flow in Xenopus epithelium, an important animal model of the ciliated respiratory tract. We then extend our analysis toward 3D3C measurements in Xenopus using both DLS-OCT and DPIV. We demonstrate the use of DPIV-based approaches towards flow imaging of Xenopus cerebrospinal fluid and mouse trachea, two other important ciliary systems. Both of these flows typically fall in the sub-100 μm/s regime (sub-0.25 inch/minute regime). Lastly, we develop a framework for optimizing the signal-to-noise ratio of 3D3C flow velocity measurements synthesized from 2D2C measures in non-orthogonal planes. In all, 3D3C OCT-based velocimetry has the potential to comprehensively characterize the flow performance of biological ciliated surfaces.
OCIS codes: (110.4500) Optical coherence tomography; (120.7250) Velocimetry; (170.3340) Laser Doppler velocimetry; (170.6480) Spectroscopy, speckle
1. Introduction
Cilia driven-fluid flow is an important physiological process in numerous organ systems. Ciliary flow is responsible for clearance of mucus from the respiratory tract, movement of cerebrospinal fluid (CSF) in the ventricles of the brain, determination of left-right patterning in the embryonic node, and movement of ova in the Fallopian tubes [1]. Because ciliary flow results from the shearing action of many cilia along a complex geometrical surface, ciliary flow lacks certain symmetries, such as unidirectionality and axisymmetry [2–4]. While these symmetries can simplify the quantification and analysis of other types of flow, such as Poiseuille flow in arteries, they are typically not applicable in the context of cilia-driven fluid flow. As such, the most complete description of the flow generated by cilia is a three-dimensional, three-component (3D3C) vector field v(r). v(r) describes the velocity field v(r) = (vx(r), vy(r), vz(r)) at every point in space r = (x, y, z). That is, for a steady-state flow field described in three spatial dimensions, the fluid motion at each location in three-dimensional space is described by a three-component vector.
A number of optical techniques have shown utility in imaging microfluidic ciliary flow [1]. These techniques include brightfield, epifluorescence, confocal fluorescent microscopy, and optical coherence tomography (OCT). In particular, OCT has shown great promise for visualizing and quantifying ciliary physiology due to its combination of intrinsic contrast from scattering, relatively high resolution (∼1–10 μm), and inherent parallelization of axial scanning without mechanical movement of samples [4–6].
Additionally, within OCT, multiple velocimetry techniques have been implemented using OCT-based data, including Doppler [7], particle tracking velocimetry [4], digital particle image velocimetry (DPIV) [5, 8], and dynamic light scattering (DLS)-based approaches [9]. Traditional Doppler velocimetry is perhaps the most common type of flow measurement in OCT but inherently only recovers a single component of velocity (axial or vz). We previously demonstrated the implementation of particle tracking to quantify ciliary flow [4] as well as investigate ciliary physiology and pathophysiology [10]. Particle tracking, however, requires sparse seeding of particles, a condition that typically leads to relatively sparse measurements of the velocity flow field. More recent work has demonstrated measurements of total speed from the OCT signal in addition to the Doppler signal [9]. In particular, these newer techniques employ either the autocorrelation or cross-correlation of the OCT signal, and in some cases can be extended to generate directional velocity measurements. In this manuscript, we will focus on an autocorrelation-based technique we previously demonstrated, directional DLS-OCT [11], as well as a related cross-correlation based technique, DPIV.
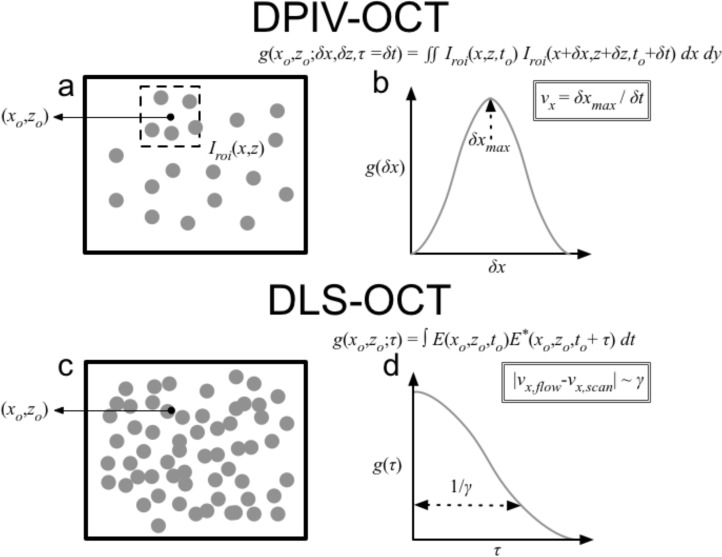
DPIV refers to an image processing method in which regions of an image are tracked from frame to frame in order to estimate velocity (Fig. 1(a,b)) [12]. In DPIV, images are divided into smaller regions of interest (ROIs), and ROIs of adjacent image frames are cross-correlated against one another. By calculating a correlation function g(x0, z0; δx, δz, τ) between regions from frame to frame and estimating the spatial location that maximizes the cross correlation (Fig. 1(b)), features can in effect be tracked in order to estimate a displacement, and thus a velocity.
Fig. 1.
In this study, we use two distinct correlation-based approaches to directional OCT velocimetry: DPIV (a,b) and DLS (c,d). (a) In DPIV, two frames of intensity information I(x0, z0), acquired with an interframe time of δt, are compared against each. Each image is segmented into smaller regions of interest (ROI) Iroi(x, y), centered around the point (x0, y0), and cross-correlation is calculated in the spatial domain (δx, δz). The process is then repeated for multiple ROIs. (b) The corresponding correlation function g(x0, z0; δx, δz, τ) for each region exhibits a peak where δx = vxδt and δz = vzδt. Estimation of this peak location yields the velocity estimate for (vx, vz) (c) In DLS-OCT, the temporal signal at a single point (x0, z0) is correlated with itself, except now the complex field signal E(x0, z0, t), instead of the intensity, is used, and the correlation is calculated in the time domain. Additionally, scatterers are seeded significantly more densely such that speckle formation occurs. (d) The correlation function g(x0, y0; τ) exhibits a peak at τ = 0, but the rate of decorrelation (γ), i.e. the inverse of the width of the Gaussian, is proportional to the difference in velocity of the scanner and fluid flow. By modulating the scan speed , we can minimize the decorrelation rate γ and estimate as the minimum of that curve. The process is then repeated at multiple spatial locations (x0, z0).
If performed on two-dimensional imaging data, DPIV yields 2D2C velocity data. In principle, DPIV can also be performed on serial volumetric data to yield 3D3C velocity estimates [13,14]. However, if serial volume acquisition is not sufficiently fast, ensembles of particles may decorrelate due to non-translational motion including diffusion, shearing, and rotation. These non-translational motions then lead to a degradation of signal-to-noise ratio (SNR) [15]. Additionally, many imaging acquisition protocols and image processing algorithms are already available and optimized for two-dimensional data [16], and we wished to leverage these preexisting algorithms.
In order to circumvent the needs for repeated volume measurements, multiple measurements of lower dimensional quantities can be combined to synthesize higher dimensional data. In the simplest example, multiple one-component velocity measurements made at different angles can be combined into a single two- or three-component measurement [17]. Stereoscopic PIV, for example, uses two cameras angled with respect to one another to compute 2D3C data from 2D2C data [18]. Stereoscopic PIV as implemented with a brightfield microscope is not truly cross-sectional, however, as velocity measurements may arise from the movement of defocused particles. In contrast, OCT offers truly cross-sectional data, and thus the ability to localize velocimetry measurements in three-dimensional space. As such, OCT offers the possibility of generating 3D3C data from cross-sectional 2D2C data. We describe this process in further detail in the methods section.
An alternative approach to feature tracking methods such as DPIV is to quantify the decorrelation rate of a time varying signal to estimate speed [9,11,19,20]. In dynamic light scattering-based OCT (DLS-OCT), the temporal decorrelation of a light-scattering signal is fit to a model autocorrelation function in order to recover the axial velocity and total speed of the underlying fluid (Fig. 1 (c,d)). DLS is typically implemented in highly scattering media. In this highly scattering regime, each focal volume is occupied on average by multiple particles such that pixel intensities are random quantities governed by speckle statistics, and the decorrelation of these speckle patterns gives an estimate of total flow speed (Fig. 1(d)).
We previously showed that by imparting a variable scan bias to our measurements, we could extend DLS-OCT to yield directional velocimetry measurements [11], a technique we term directional DLS-OCT. In our previous demonstration, the velocity component data was only two-component, and the measurements were only made along a single axial line (1D). However, by (a) scanning along an additional orthogonal plane to get 3C measurements, and (b) repeating these measurements at multiple spatial locations to get 3D measurements, 3D3C data can in principle be synthesized from lower dimensional measurements.
Here, we demonstrate two OCT-based, correlation-based methods of generating 3D3C vector flow fields without serial volume acquisition. First, we utilize existing DPIV implementations in order to measure 2D2C data, and we extend the measurements to synthesize 3D3C data using multiple 2D2C planes at two different angles. In the process, we investigate the signal-to-noise ratio (SNR) properties of this process to optimize those two angles. Secondly, building on our previous work in DLS-OCT, we show 1D2C DLS-OCT measurements in vivo in the Xenopus laevis model of epithelial ciliary flow. We then extend these measurements by implementing an orthogonal scan plane (yielding 3C measurements) at multiple spatial locations (yielding 3D measurements) in order to generate 3D3C data. We validate DPIV-OCT and DLS-OCT in a calibrated flow phantom and then demonstrate both techniques to quantify Xenopus epithelial flow. Finally, we show the possibility of measuring 3D3C flow in two additional ciliated systems using DPIV. We measure CSF flow in Xenopus tropicalis using endogenous particulate matter in the ventricles of the developing brain, and we measure ex vivo ciliary flow in mouse trachea using exogenous particle tracers.
2. Methods
2.1. OCT Data acquisition and processing
All OCT measurements were made using a spectral domain OCT system (Thorlabs Telesto) with 1325 nm center wavelength. Images were acquired at a 28 kHz linerate with an estimated sensitivity of 96 dB. The optical power incident on the sample was measured at 1 mW.
2.2. Animal measurements
All Xenopus and mouse procedures were reviewed and approved by Yale’s Institutional Animal Care and Use Committee, which is Association for Assessment and Accreditation of Laboratory Animal Care-accredited. For epithelial flow measurements, Nieuwkoop-Faber (NF) [21] Stage 32 Xenopus laevis tadpoles were immobilized with benzocaine and imaged in a 6 mm diameter, 1 mm deep cylindrical well [22] as previously described [10]. Polystyrene microspheres (Bangs Labs, density 1.05 g/cm3) of various sizes were used as a contrast agent. For DPIV measurements, 5 μm microspheres were diluted 1:100 in 1/9× Modified Ringer’s (MR) solution. For DLS-OCT measurements, 500 nm microspheres were diluted 1:100 in 1/9× MR with 0.1% Tween added to prevent bead aggregation. Additionally, for DLS tadpole epithelial measurements, a liquid immersion adapter was used to minimize common path signal due to reflection off the fluid surface. For CSF measurements, stage 46 Xenopus tropicalis embryos were immobilized with benzocaine, but no exogenous scattering agents were added.
For tracheal flow measurements, the trachea from a one-month old mouse pup was prepared as in [23]. The pup was euthanized using intraperitoneal urethane. The trachea was removed by making two cross-sectional cuts: a cranial cut near the larynx, and a caudal cut above the level of the carina. The lumen of the excised trachea was then flushed with phosphate buffered saline (PBS) and filled with 5 μm microspheres diluted 1:100 in PBS. Temperature was maintained at 36–38° C using a heat-controlled stage.
2.3. 2D2C DPIV
DPIV processing of log-scale intensity image data was performed using PIVlab [16]. Contrast limited adaptive histogram equalization was employed as an image preprocessing method for CSF flow images. Window sizes ranged between 32–128 pixels, and were chosen such that each window had ∼5 particles on average. A two-pass algorithm was employed to use half the original window size on a second-pass attempt at peak identification.
DPIV can lead to false matches especially in areas of low back-scattered intensity. Specifically, in our CSF and mouse trachea flow measurements, particles were significantly sparser than in epithelial flow measurements. Because we typically correlated over 20 frames and thus had n = 19 measurements at each spatial location, we were also able to calculate a standard deviation σ and mean μ of our velocity measurements at every spatial location. Thus, for the CSF and tracheal measurements, velocity measurements were discarded at locations where the standard deviation was greater than 100 μm/s and 20 μm/s, respectively.
2.4. Synthesis of 3D3C data from 2D2C DPIV
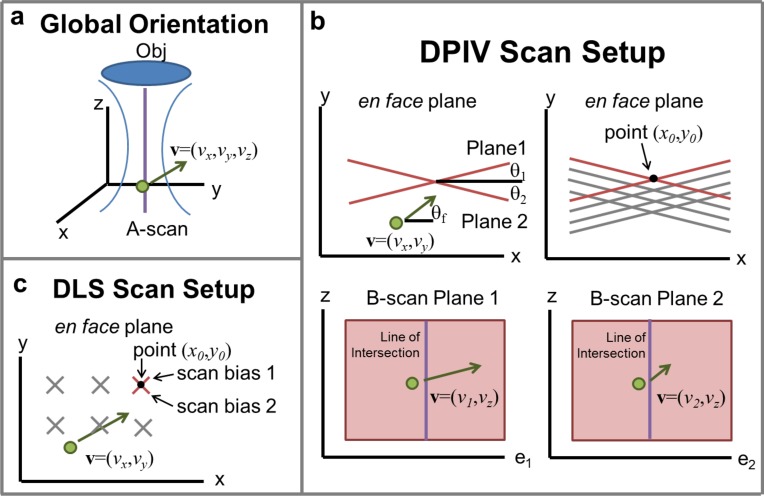
After generating 2D2C data using DPIV, we synthesized 3D3C data using the following method. An OCT B-scan is in a plane that is located in a global xyz coordinate system (Fig. 2(a)). The angular orientation of any given image plane in that global volume can be described by the angle θ that the image plane forms with the global xz-plane (Fig. 2(b), top left). In principle, one could measure DPIV data in two orthogonal planes that correspond to the global xz- and yz-planes (θ1 = 0° and θ2 = 90°, respectively). In this framework, the global vx component corresponds to the transverse velocity component (the component orthogonal to the optical axis) measured at θ1 = 0°. Likewise, the global vy component corresponds to the transverse velocity component measured at θ2 = 90°. Lastly, the global vz component is the average of the axial components measured at each θ. In practice, however, DPIV becomes less reliable when there is a significant out of plane flow in a given image plane (see Appendix for details on SNR tradeoff) [15]. Thus, we chose to measure flow in two non-orthogonal planes that were still primarily directed along the expected direction of flow θf.
Fig. 2.
Scan setup for DPIV and DLS-OCT. (a) Three-dimensional coordinate system, with optical axis defined along z, and en-face plane defined as xy-plane. A particle with velocity v = (vx, vy, vz) can be decomposed into three components based on this Cartesian system. (b) DPIV scan setup, showing (top left) two non-orthogonal plane measurements. The angle of each scan plane, θ1 and θ2, as well as the angle of flow in the en face plane θf, are all defined with respect to the global x-axis. The velocity as measured by DPIV in each plane is the vector component of the velocity v on the unit vector tangent to the plane, either e1 or e2 (bottom left / right). The vector projections of velocity in these two planes are denoted as v1 and v2. From v1 and v2, vx and vy can be calculated along the line of intersection at these planes. Acquiring multiple scan plans (top right) allows for calculation of v at multiple points (x0, y0), to reconstruct an entire 3D volume. (c) DLS-OCT scan protocol showing series of scan bias acquisitions. Each line measurement along z-axis at location (x0, y0) in the en face plane consists of a set of scans along axes oriented around ±45°. Much like the DPIV measurements, the directional DLS-OCT protocol yields two velocity measurements v1 and v2. vx and vy can then be recovered along a single axial line using Eqs. (3) and (4). These scans are then repeated at various (x0, y0) points.
In order to generate 3C data from two non-orthogonal measurements (Fig. 2(b), top left), we first define each plane with respect to the global x-axis as θ1 and θ2. We define the unit vector associated with these axes as e1 and e2. When we generate a DPIV measurement in plane 1, we estimate an axial (vz) and lateral (v1) velocity (Fig. 2(b), bottom). Similarly, in plane 2 we generate an axial (vz) and lateral (v2) measurement. The key step is to note that the lateral flow measurements v1 and v2 in each plane are just the projections of the global velocity vector (vx, vy) onto the image plane axes e1 and e2. More explicitly:
| (1) |
| (2) |
Solving for vx and vy yields:
| (3) |
| (4) |
Equations (3) and (4) are valid for the points that two planes intersect. For two imaging planes, there is only one (x0, y0) line of data intersection (Fig. 2(b), bottom). In order to increase the number of intersecting sampling points, we acquired parallel imaging planes with an offset in the xy-plane, typically approximately 10 for each angle, leading to a grid of 100× A-scan depths (Fig. 2(b), top right). As described above, the global vz estimate was calculated by averaging the measurements of the local vz measurement from each plane.
2.5. Directional DLS velocimetry
The methodology for recovering the lateral flow velocity by directional DLS-OCT is described in depth in [11]. Given the time-varying complex-valued interferometric signal E(x0, y0, t) at a single spatial location (x0, y0) (Figs. 1(c) and 2(c)), we can compute the autocorrelation g(x0, y0; τ), where τ is the correlation time lag. The decorrelation rate γ of the signal can be estimated by fitting the autocorrelation to the function |g(τ)| = exp[−(γτ)2]. γ is a measure of the total decorrelation time of the signal, which is proportional to the speed of particles flowing through a focal volume. By additionally imparting a scan bias either in the direction of or opposite flow, we increase or decrease the effective decorrelation rate γ as measured by our system (Fig. 1(d)). By measuring γ over a range of scan velocities, we recover a curve that follows the form: . We can then fit this decay-rate scan bias curve to solve for the parameter B. The B parameter corresponds to the scan bias speed that best matches the flow rate along the scan axis, and thus is equal to vx. A typical set of scan biases was, for example, ± 0.24, 0.42, 0.56, 0.84, 1.05, and 1.4 mm/s, with 5 repeats at each scan bias.
The effect of the directional DLS-OCT procedure is to give us the projection of the lateral velocity along the plane of our scan bias. By scanning along the perpendicular axis with the same scheme, we can additionally estimate the perpendicular velocity component vy. Similar to DPIV, we can in principle set up our two scan axes to coincide with the global x and y axes. Also similar to DPIV, however, SNR considerations [24], combined with prior knowledge that flow is primarily directed along the global x-axis, led us to rotate our scan axes by 45° (Fig. 2(c), red X). We measure v1 and v2 and similarly reconstruct the global vx and vy measurements using Eqs. (3) and (4).
In each of our measurements, we can estimate the Doppler signal simultaneously, giving an estimate of vz. Overall, then, each set of scans yields v = (vx, vy, vz) along an A-scan. Repeating this procedure at multiple locations (Fig. 2(c), gray X’s) then yields a 3D3C velocity field estimate.
2.6. Three-dimensional volume rendering
In order to optimally display and visualize three-dimensional data, we used two subroutines downloaded from the MATLAB Central File Exchange. The first subroutine was a 3D Canny edge-detection algorithm to perform volumetric image segmentation [25]. Edge detection was performed after simple intensity-based thresholding and allowed us to identify the structural features of the tadpole, ventricle, and tracheal morphology. The second subroutine enabled vector field visualization using a 3D quiver plot [26].
3. Results
3.1. Validation of 3D3C OCT velocimetry using calibrated flow phantoms
We validated 3D3C DPIV-OCT and DLS-OCT by measuring velocity fields in a flow phantom. Using a syringe pump running at a bulk rate of 100 μL/min, we pumped a bead solution through a 0.5 mm (z-direction) × 5 mm (y-direction) rectangular cross-section capillary tube (Fig. 3(a)). A rectangular tube was chosen to avoid any refraction artifacts due to scanning laterally (y-direction) over the curved surface of a cylindrical tube. Because the phantom cross-section has a large aspect ratio, flow was expected to approximate Poiseuille flow between two planes, characterized by flow directed along the x-direction (vx) with a parabolic profile varying along the z-axis. We predicted a maximum speed of approximately 0.9 mm/s. The tube was additionally tilted to impart a small z-velocity component.
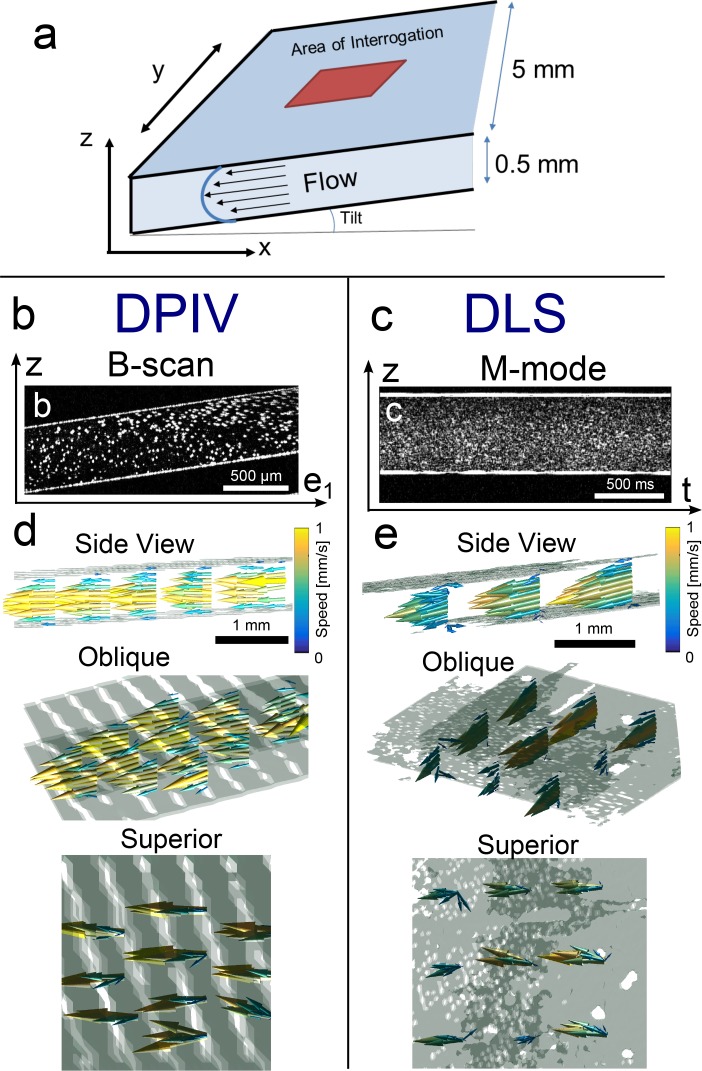
Fig. 3.
Flow phantom demonstration of 3D3C velocimetry using DPIV and DLS-OCT. (a) Global orientation of planar flow phantom, which is very wide in the y-dimension as compared with z-dimension, yielding a planar Poiseuille flow in region of interrogation far from the lateral walls. (b,c) Log-scale intensity images representing raw data acquisition in flow phantom channel. (b) DPIV single frame of 5 μm polystyrene microspheres in a flow phantom, in a single plane, where e1 emphasizes that the plane is oblique to the x-axis. (c) DLS-OCT single M-mode image of densely seeded 500 nm polystyrene microspheres in the same flow phantom, at single scan bias. (d,e; Visualization 1 (464KB, MP4) , Visualization 2 (461.5KB, MP4) ) 3D3C flow phantom reconstruction using (d) DPIV and (e) DLS-OCT, from a side, oblique, and superior view. Both methods show expected Poiseuille-like flow in between two parallel plates. Flow is consistent with the geometric orientation of the flow phantom, and flow speed peaks near the expected 0.9 mm/s.
For DPIV measurements, we acquired a series of 20 B-scans (representative B-scan shown in Fig. 3(b)) at 11 different planes. Each B-scan was 3 mm in length, with 1024 A-scans. The entire acquisition was 450,000 A-scans taken over 16 s. Particles were seeded sparsely enough such that the average number of particles per focal volume was much less than 1. Log-intensity images were cross-correlated in order to yield 2D2C images as described in Section 2.3 and reconstructed into 3D3C measurements as described in Section 2.4. For our DPIV protocol, we had to choose angles θ1 and θ2 for our scan plane acquisition. Based on the considerations of our SNR analysis in the Appendix, we chose our imaging planes to be ±15° oblique to the direction of flow along the x-axis.
For DLS-OCT, particle density seeding was increased such that there were multiple particles per focal volume. A representative M-mode image in Fig. 3(c) shows the intensity trace over time, although we used the complex signal for correlation calculations. For our scan protocol, we scanned at 6 different scan biases from 0.23–2.0 mm/s, with 5 repeats each in a 3x3 grid of xy points, leading to a total of 2,556,000 A-scans over 90 s of acquisition. Note that although both measurements employ correlation analysis, DLS-OCT data was correlated along the temporal axis, while DPIV data was correlated in the spatial domain at a single, fixed time delay corresponding to one inter-frame period (Fig. 1).
As shown in Fig. 3(d) and Visualization 1 (464KB, MP4) , the 3D3C reconstruction using DPIV yielded the expected flow profile oriented in the direction of the length of the capillary tube. From the side, oblique, and superior views of the flow field, one can see that the flow resembles planar Poiseuille flow, with the geometric tilt of the tube also apparent. Flow speeds reach approximately 1 mm/s, in good agreement with the expected 0.9 mm/s peak flow. In Fig. 3(e) and Visualization 2 (461.5KB, MP4) is a 3D3C reconstruction using DLS-OCT with similar views. The recovered velocity field again shows a parabolic flow profile resembling planar Poiseuille flow with a peak of approximately 1 mm/s.
The possible sources of error in this validation measurement include an element of pulsatility (i.e. non-stationarity) in flow due to motor stepping or capacitance in the tube system, small imperfections in the geometry of the rectangular tube leading to non-idealized Poiseuille flow, and a small settling velocity of the beads along the z-axis (estimated <10 μm/s).
3.2. Demonstration of directional DLS-OCT in vivo
Because we previously used our directional DLS-OCT protocol to measure flow only in a calibrated phantom profile, we first wanted to confirm that we could extend the measurements towards in vivo flow using our basic 1D2C protocol before moving towards 3D3C acquisition. As such, we tested our methodology by making measurements of vx and vz on epithelial ciliary flow in Xenopus laevis tadpoles.
Measurements were made by allowing the epithelial cilia in Xenopus to drive fluid flow of a physiological solution seeded with polystyrene microspheres (Fig. 4, right). After initial testing, we had to make two changes to our experimental setup in comparison to our original phantom measurements. First, it was qualitatively noted that 100 nm beads, which we had used in our previous studies, seemed to abrogate ciliary flow. In contrast, 500 nm beads did not appear to diminish flow. As such, we selected a 500 nm bead solution, with 0.1% Tween added to prevent bead aggregation. Secondly, it was noted that common path reflections caused a non-overlapping ghost image to appear. We reasoned that the ghost image would also be erroneously incorporated in our autocorrelation computations. Thus, we used a liquid immersion focal spacer with a tilted air-glass interface in order to avoid a direct reflection (Thorlabs Focal Spacer SD-OCT probe) and to eliminate the ghost image.
Fig. 4.
In vivo demonstration of directional DLS-OCT protocol in X. laevis epithelial ciliary flow. (right) B-scan of single embryo showing head to tail flow of a bead solution along the ciliated surface of an embryo, with scanning EM micrograph of ciliary patch on surface of animal (inset). The B-scan plane corresponds to the coronal section in Fig. 5. The red bar indicates location of depth-scan where velocimetry data is acquired, where width of bar represents the lateral spatial extent of scanning. (left) Velocimetry profile of vx, as determined by directional DLS-OCT, and vz, as determined by Doppler, along the depth scan highlighted in red. The colored lines indicate the location of the glass-liquid interface (blue) and the embryo surface (green). Flow is zero at the glass-liquid interface, increases to >500 μm/s near the embryo surface, and diminished back to zero at the body of the embryo itself. Axes labels: L-Left, R-right, Cr-cranial, Ca-caudal
After making these two changes to our experimental protocol, we then measured epithelial ciliary flow. Figure 4 shows a B-scan of the embryo corresponding to a coronal cross-section of the embryo (see Fig. 5(a) for global orientation). Here, our scan protocol consisted of 5 scan biases between 0.35 – 1.4 mm/s, with 5 repeats each. We acquired a total of 230,000 A-scans over 8.2 s. Our reconstructed flow profile along a single line highlighted in red in Fig. 4, is shown on the left. The flow exhibited multiple characteristics consistent with previous measurements of epithelial flow. Flow was directed from head to tail, reaching a peak speed of ∼500 μm/s. Flow was primarily transverse (vx) in nature, with axial flow (vz) approximately an order of magnitude lower. Moreover, the measured flow speed was minimal near the glass-liquid interface (Fig. 4, blue line), consistent with a no slip boundary from the focal spacer. As we measured deeper into the fluid, the flow speed increased to a maximum near the surface of the embryo, dropping back to zero in the body of the animal itself (Fig. 4, green line).
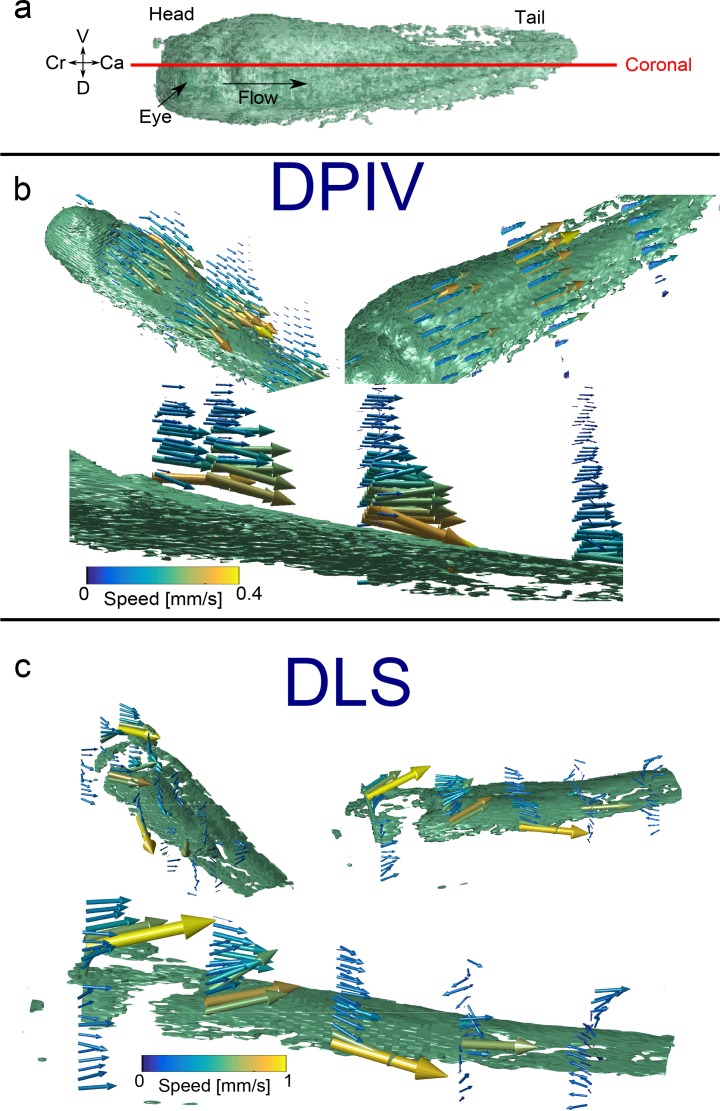
Fig. 5.
Measurement of 3D3C epithelial cilia-driven fluid in X. laevis. (a) Global oriention of embryo, showing rendering of surface (green) and flow directed primarily along the head-tail axis. Red line shows orientation of coronal planes. (b, Visualization 3 (1.3MB, MP4) ) Tadpole rendering with 3D quiver plot showing 3D3C velocimetry data, as reconstructed using DPIV from several perspectives. (c, Visualization 4 (1,009KB, MP4) ) Similar rendering, now with velocity field estimated using directional DLS-OCT. A portion of the embryo surface on the head is missing due to difficulties in automated segmentation. Note the difference in scale bar between the (b) and (c). Axes labels: L-left, R-right, Cr-cranial, Ca-caudal, D-dorsal, V-ventral
We found that when using our procedure to obtain velocimetry measurements, in a certain subset of animals, the resulting flow was unphysical in that it did not conform to the qualitative criteria above, such as head-to-tail flow, and maximal speed near the surface. Indeed, DLSOCT techniques have previously been described to fail in vivo when the model correlation function does not properly fit the data [9]. Additionally, the technique suffers from high error measurement when decorrelation due to diffusivity approaches decorrelation due to advective flow [24]. In our case, we found that measurements failed subjectively in 4/9 animals.
3.3. Measurement of epithelial cilia-driven fluid flow
We next measured the 3D3C flow field produced by the epithelium of Xenopus laeivs tadpoles using both DPIV and directional DLS-OCT. For our DPIV protocol, we again had to choose angles θ1 and θ2 for our scan plane acquisition. As previously noted, flow is primarily head-to-tail in nature. Thus, we chose our angles θ1 and θ2 to be ±15° with respect to the cranial-caudal axis of the animal (Fig. 5(a)). For each angle we acquired 11 planes, with 20 repeats per plane. Each B-scan was 6 mm in length, with 1024 A-scans per B-scan, for a total of 450,560 A-scans taken over 16 s. For DLS-OCT, we performed 1D3C measurements over a 3x5 grid along the length of the animal. At each point, we acquired 6 scan biases from 0.24–1.4 mm/s, with 5 repeats each, for a total of 1,692,000 A-scans taken over 60 s.
Figure 5(b) and Visualization 3 (1.3MB, MP4) show the results of our DPIV velocimetry measurements. The 3D3C vector field again shows many of the same qualitative features we previously measured in Xenopus epithelial flow. Flow near the surface is primarily directed head to tail. Flow is nearly zero far from the surface of the embryo and reaches a maximum near the surface, consistent with shear-driven fluid flow. Peak flow speeds reach ∼500 μm/s.
Figure 5(c) and Visualization 4 (1,009KB, MP4) show the results of DLS-OCT 3D3C velocimetry. Once again, the epithelial flow exhibits qualitatively similar behavior, with flow primarily directed head to tail and with highest magnitude near the surface of the embryo. Maximal flow speeds in this particular embryo reach nearly 1 mm/s. Of note, as we observed when acquiring 1D2C DLSOCT measurements, certain data sets resulting from our DLS-OCT protocol did not exhibit the expected features of flow.
3.4. Measurement of CSF flow
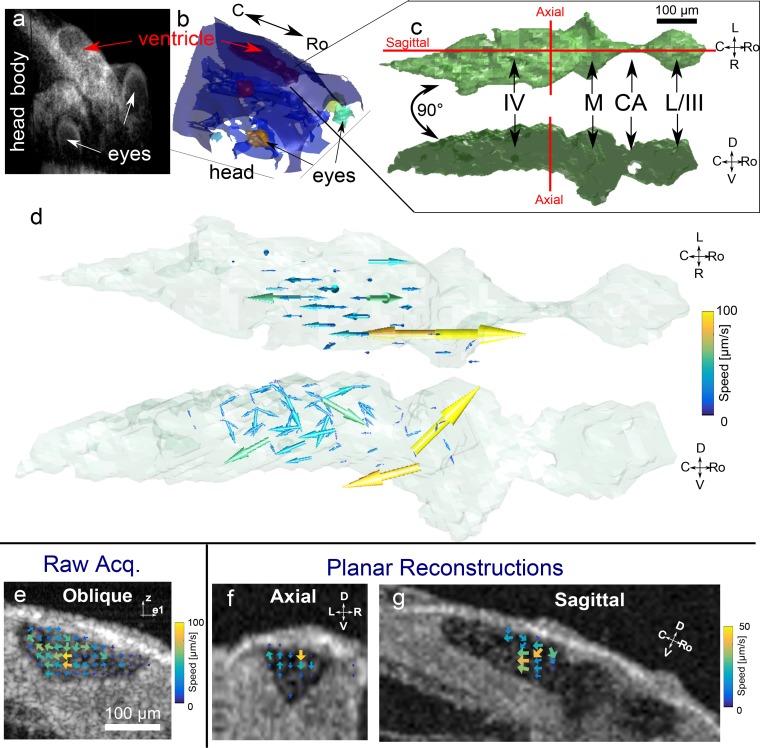
We next measured cerebrospinal fluid (CSF) flow in NF Stage 46 Xenopus tropicalis tadpoles using DPIV. During development, cerebrospinal fluid circulates through the ventricular system of the brain. OCT-based volumetric measurements (Fig. 6(a)) provide an intensity-based contrast that can be used to delineate the boundaries of these ventricles within the embryo (Fig. 6(b)) based on morphological appearance [27]. As previously described in NF Stage 47–49 X. laevis embryos, CSF circulates amongst the various chambers of the ventricles (Fig. 6(c)), from the fourth ventricle and midbrain ventricle, through the cerebral aqueduct, to the third and lateral ventricles [28]. While previous studies of CSF flow were all performed by injecting exogenous contrast agents [29, 30], we observed that endogenous particulate matter provided a native scattering contrast agent in OCT that can be used to perform DPIV (Fig. 6(e) and Visualization 5 (770.9KB, MP4) ).
Fig. 6.
Measurement of cilia-driven cerebrospinal fluid flow in X. tropicalis ventricle using DPIV. (a) 3D intensity-based rendering of the head region of X. tropicalis, with (b) ventricular space segmented out, and highlighted in red. (c) Rendering of segmented ventricular space as viewed from above (top) and from the side (bottom), showing location of individual ventricles as well as orientation of sagittal and axial planes. IV-fourth ventricle. M-Midbrain ventricle. CA-cerebral aqueduct. L-lateral ventricles. III-third ventricle. (d, Visualization 6 (329.6KB, MP4) ) 3D3C vector flow field in ventricular system. (e, Visualization 5 (770.9KB, MP4) ) Example of raw acquisition of single cross-sectional movie showing endogenous cellular material circulating in ventricle (with e1 emphasizing that plane is oblique to rostrocaudal axis by 15°). The resulting DPIV 2D2C quantification shows recirculation. (f,g) Axial and sagittal planar reconstructions of velocity data from 3D3C data. Note the different scale bar in (f,g), referring to the magnitude of only the projected velocity component onto each given plane. Axes labels: L-left, R-right, Ro-rostral, C-caudal, D-dorsal, V-ventral
Using this native contrast, we quantified 3D3C CSF flow in the ventricular system of Stage 46 tadpoles. Noting that flow was primarily oriented along the rostral-caudal axis, we used two non-orthogonal planes oriented at ±15° from the rostral-caudal axis. We acquired 13 planes with 20 repeats each. Each B-scan was 1.2 mm in length and contained 1024 A-scans, for a total of 532,480 A-scans acquired over 20 s.
From the video and subsequent DPIV processing of a single oblique cross-section (Fig. 6(e) and Visualization 5 (770.9KB, MP4) ), one can see that there is recirculatory flow in the ventricles. Our 3D3C reconstruction is shown in Fig. 6(d) and Visualization 6 (329.6KB, MP4) . As previously described [28], flow was directed primarily along the length of the ventricular system, exhibiting a complex recirculatory pattern. In order to better visualize the recirculation, we computationally reconstructed the native axial and sagittal planes of the embryo from our 3D3C data set. The axial cross section shows non-zero vorticity in its plane of motion. Overall, speeds were significantly slower here than epithelial ciliary flow, approximately ∼20–80 μm/s. Notably, due to a sparsity in sampling flow in the third and lateral ventricles, we were unable to reconstruct flow in those chambers.
3.5. Measurement of tracheal cilia-driven fluid flow in ex vivo mouse trachea
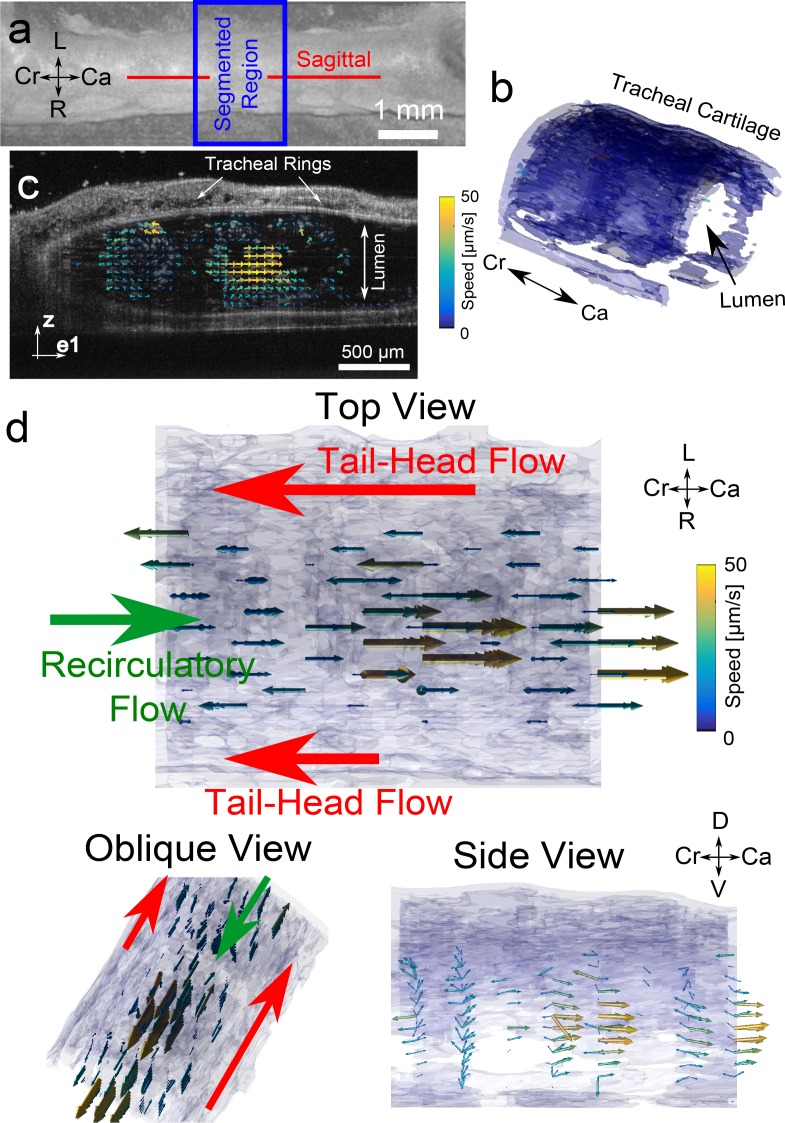
Using our DPIV protocol, we estimated the 3D3C flow field generated by the ciliated epithelium in an ex vivo trachea from an adolescent mouse. In adolescent mice, the tracheal wall is sufficiently thin to enable cross-sectional flow imaging of the lumen through the wall itself (Fig. 7(a,b)). As described in [23], the flow in the excised trachea can be quantified by the imaging the movement of beads in a physiological solution filling the lumen of the trachea (Fig. 7(c) and Visualization 7 (2.3MB, MP4) ). Because flow is primarily oriented along the length of the trachea, in a caudal-cranial (tail-head) orientation, we imaged in non-orthogonal planes at ±15° to the cranial-caudal axis. We acquired 13 planes with 20 repeats each. Each B-scan was 6 mm in length and contained 2048 A-scans for a total of 1,064,960 A-scans acquired over 50 s.
Fig. 7.
Quantification of cilia-driven tracheal fluid flow in adolescent mouse using DPIV. (a) 3D intensity-based rendering of trachea, with sagittal plane orientation shown (b) Segmented region of trachea within blue box of (a) showing spatial location where fluid flow was quantified. (c, Visualization 7 (2.3MB, MP4) ) Raw acquisition of 5 μm polystyrene microspheres being driven by ciliary fluid flow, and subsequent 2D2C flow field quantification with DPIV. The acqusition is oblique to the sagittal plane by 15° (d, Visualization 8 (1.1MB, MP4) ) 3D3C flow field rendering from top view (consistent with view in (a)), oblique superior view, and side view. Large arrows denoting the location and direction of primary tail-head flow as well as recirculatory head-tail flow. Axes labels: L-left, R-right, Cr-cranial, Ca-caudal, D-dorsal, V-ventral
As can be seen in Visualization 7 (2.3MB, MP4) , flow very near to the edges is tail-to-head in nature, but recirculation occurs in the middle of the trachea. We have previously observed that recirculation occurs due to geometric effects. As the ciliated surface moves fluid from head to tail, if the outlet of the trachea is unobstructed, flow remains uniderctional. The presence of an air-fluid meniscus at the cranial aspect of the trachea, however, may effectively block outflow, thus causing fluid to recirculate back down the center of the trachea. As a result, the portions of the flow may appear to be in the opposite (head-to-tail) direction. We typically minimize recirculation in the context of diagnostic tests by ensuring the trachea remains patent. In the context of general flow imaging, however, it may be advantageous to be able to quantify such recirculatory patterns.
The 3D3C reconstruction is shown in Fig. 7(d) and Visualization 8 (1.1MB, MP4) . From the top view, the 3D3C reconstruction again shows flow in a tail-to-head direction near the ciliated surface, and recirculatory in the center of the trachea. Consistent with previous reports, [23], the average flow speed is ∼20 μm/s, with maximum speeds reaching ∼50 μm/s. The primary tail-to-head flow pattern is not as evident on the side view. This lack of easily visualizable head-to-tail flow is possibly due to the fact that head-to-tail flow is localized to a relatively small region near the tracheal surface, as reported previously [23]. DPIV effectively performs spatially averaging when the images are subdivided into smaller regions of interest. Thus the technique may not be as ammenable to highly spatially-localized flow patterns.
4. Discussion
4.1. OCT-based approaches are useful for quantifying 3D3C flow in ciliated systems
Measurement of cilia-driven fluid flow is important for studying multiple organ systems. Cilia are important for clearance of mucus in the bronchi, circulation of fluid in the ventricles of the brain, establishment of the right-left axis in the embryonic node, and for movement of ova in the Fallopian tubes. Each of these ciliated organ systems has a unique geometry, ranging from tubular (bronchi, Fallopian tubes) to ellipsoid (node) to irregularly shaped (ventricles). Because the direction of flow cannot be inferred from the shape of the enclosing structure, full characterization of cilia-driven fluid flow requires 3D3C velocity estimation.
Here we showed that two OCT-based techniques, DPIV-OCT and DLS-OCT, are capable of quantifying 3D3C flow. Both techniques performed well on a pressure-driven flow phantom, correctly obtaining the direction of flow, and yielding a parabolic profile consistent with planar Poiseuille flow. Additionally, we found that both techniques are capable of measuring biological cilia-driven fluid flow in the Xenopus animal model system. Consistent with previous results from particle tracking velocimetry, we found that flow was primarily directed in a head-tail direction, with highest speeds of 500–1000 μm/s near the epithelial surface and decreasing farther from it.
We also showed that DPIV can be used to quantitatively characterize CSF flow patterns in the brain. Cilia-dependent CSF flow has been characterized previously, and several genes are known to disrupt proper development of flow in the ventricles due to their effects on cilia [30–32]. In particular, Xenopus provides an important animal model system for studying CSF flow because the ventricles can be imaged without dissection of the brain [27], and many tools exist that allow rapid and facile genetic manipulation [33]. Our results are in line with previously described flow patterns in the ventricular system of Xenopus embryos showing recirculatory flow directed primarily along the rostral-caudal axis [28]. Previous imaging studies of Xenopus CSF, however required injection of exogenous contrast agents, typically visualized with epifluorescence or brightfield microscopy. In contrast, endogenous particulate matter in the CSF is sufficient to perform OCT-based DPIV and quantify fluid flow. We are currently uncertain of the nature of the scattering material in the developing embryo brain, although 600 nm extracellular membrane particles have been reported in rat embryonic ventricular fluid [34]. The material was present in approximately 50% of the embryos we imaged at NF Stage 46. Further investigation may determine the exact nature of this light-scattering material.
We lastly showed that the use DPIV to quantify the 3D3C flow field in mouse trachea. In the trachea, the airway surface liquid (ASL), which consists of the mucus layer and the periciliary layer, is known to be cleared in a tail-to-head fashion [35]. Because of the typically thin layer size (7 μm periciliary layer and 8–80 μm mucus layer) [1], imaging the ASL directly can be challenging. μOCT, a variant of OCT with higher spatial resolution, has recently been used to quantify ciliary dynamics and tracheal mucus velocity in swine trachea [36]. In other studies, however, the mucus layer is either chemically lysed or washed away prior to quantifying ciliary flow dynamics [37, 38], and we previously used a similar protocol [23]. Here, we showed that DPIV-OCT can be used to quantify the vectorial flow field in mouse trachea. Although in typical experiments we ensure that the trachea is patent and flow is unidirectional, here we were able to observe the primary tail-head flow direction of flow in addition to more complex recirculatory flow patterns arising secondary to outflow blockage. Overall, we believe that this type of assay will be useful for quantifying the effects of physical, chemical, and genetic changes to tracheal ciliary flow. Such studies may include the deleterious effects of hyperoxia in a neonatal setting as well as the ability of pharmacological agents to improve ciliary function [23].
4.2. Comparison of DPIV versus DLS-OCT
Based on the underlying physics of signal formation, DPIV and DLS-OCT are both suited for different imaging regimes. DPIV is better suited for slower, less densely scattering fluids, and DLS-OCT for faster, more densely scattering fluids. DPIV relies on image cross-correlation, which in turn is dependent on the same pattern being identified in subsequent frames. In DPIV, pattern decorrelation diminishes SNR (see Appendix for additional details). As a result, fast flows can cause patterns to move through the plane of motion, leading to a decrease in SNR. Additionally, for implementation of DPIV in a coherent imaging modality such as OCT, it is helpful, though not strictly necessary, to use a scattering solution with less than one particle per focal volume on average. In more densely scattering regimes, decorrelation can occur more rapidly due to speckle formation [40], imposing a requirement for higher imaging speed.
In contrast, the decorrelation time of speckle patterns, a limiting factor in DPIV, is actually utilized in DLS-OCT to provide an estimate of speed. DLS-OCT is typically restricted to regimes where there are many particles per focal volume. Additionally, DLS-OCT requires many independent speckle decorrelation events, and thus is optimal at faster flow speeds that lead to more rapid decorrelation. In this sense, the two techniques are optimized for different flow regimes, but DPIV is capable of operating in a wider range of scattering conditions. For these reasons, although both techniques were suitable for relatively fast (∼500 μm/s) epithelial ciliary flow, DPIV was better suited for the sparsely scattering CSF, and the slower tracheal flow speeds.
Both techniques as implemented here have an implicit assumption of temporal stationarity. In both of our techniques, we reconstructed a 3D3C fluid flow field from lower dimensional data. Because the underlying data is not acquired simultaneously, the ability to reconstruct the fluid flow field requires that the fluid is undergoing steady state flow. That is, although the individual ensembles of particles may change, the vectorial flow field must be invariant in time, with dv/dt = 0. In the case of cilia-driven flow, this stationarity condition is typically met [4].
Both techniques also make use of the spatiotemporal correlation function g(x0, z0; δx, δz, τ). In the case of DPIV, the spatial correlation function at a fixed time lag δt is calculated, while in DLS-OCT, the temporal correlation function is calculated at a fixed δx = δz = 0 (i.e. autocorrelation). In both cases, in order to empirically calculate the correlation function, statistical averaging over some domain needs to be performed. In the case of DPIV, averages are calculated over spatial data (i.e. local regional binning), while in DLS-OCT, averages are calculated over temporal data. As a result, DPIV implicitly assumes local spatial stationarity, while DLSOCT assumes local temporal stationarity.
One consideration regarding the assumption of stationarity is whether the addition of tracer particles affects either the stationarity of flow or the flow field itself. Specifically, we observed that 100 nm beads appeared to affect ciliary flow. Beads have the potential to affect the flow pattern either by interacting with the ciliated surface or by changing the rheological properties of the surrounding fluid. As to the second point, our beads occupied less than 0.1% of the volume, leading to an estimated <0.25% change in viscosity [39]. Regarding the overall effect of particles, we qualitatively observed that the flow pattern was unchanged upon addition of beads of any size ≥500 nm over a period of ∼1–2 min. This observation guided us to use 500 nm beads for our DLS-OCT acquisitions, and 5 μm beads for our DPIV acquisitions. As such, we believe that the addition of tracer particles in our experiments was unlikely to affect the actual flow field or the assumption of stationarity.
Additionally, although both techniques are acquired by the same OCT system with equivalent spatial resolution and sampling, because DPIV uses spatial averaging, with typical window sizes of 32–128, the final spatial resolution of velocity measurements is lower. Analogously, because DLS-OCT uses temporal averaging, the temporal resolution of the technique is somewhat lower than DPIV. In practice, DLS-OCT requires longer data acquisitions to reliably make velocity estimates, approximately 400,000 data points at a single location or 2 seconds of signal integration per scan bias. Thus, we found it impractical to acquire data at more than 15 or so (x0, y0) points given our current data processing framework. Because of this overall constraint, our final reconstructed 3D3C data was significantly coarser in spatial sampling than DPIV.
Lastly, as mentioned previously, in a certain subset of data sets acquired using DLS-OCT, the expected dynamics of the autocorrelation function do not appear to be well-modeled using the traditional DLS-OCT autocorrelation function. This phenomenon has been previously reported [9]. As a result, in large subset of data sets, we observe non-physical vectorial field reconstructions, including predictions of no flow where flow is clearly visible from OCT video acquisition. Possible reasons may include violations of temporal stationarity (i.e. the flow field changes over time), a non-Gaussian focus, scanner noise, and propagation of noise (i.e. shot noise) of the original signal.
A summary of some of the comparisons between DPIV-OCT and DLS-OCT is included in Table 1:
Table 1.
Comparison of DPIV and Scanning DLS-OCT. A comparison of the benefits and limitations of each technique is shown. Sample values as demonstrated in our experiments are given, although these values do not necessarily reflect the theoretical limits of the techniques. ROI = region of intersest. SNR = signal-to-noise ratio. CSF = cerebrospinal fluid.
| DPIV | Scanning DLS-OCT | |
|---|---|---|
| Scattering Regime | Optimized for sparsely scattering media (<1 particle / focal volume), but possible to be used in speckled regime | Optimized for densely scattering media (≫1 particle / focal volume) |
| Speed of Flow | Slow (<100 μm/s) or faster flow possible, but SNR decreased by fast out-of-plane flow (Trachea 20–50 μm/s, CSF 20–100 μm/s, Epithelium 100–1000 μm/s) | Optimized for faster flows (Epithelium 100–1000 μm/s) |
| Assumption of Stationarity | Spatial stationarity in xz plane over ROI (CSF 20×20 μm2, Trachea 50×50 μm2, Epithelium 120×120 μm2), temporal stationarity over the aquisition of two separate velocity measurements at a single location (15 – 50 s acquisition time) | Temporal stationarity for duration of scanning at a single point (6 –10 s) or entire sample (60 – 90 s), spatial stationarity over lateral extent of scan (30 – 50 μm) |
| Temporal Resolution | Dictated by interframe time for 2D2C ∼50 ms, or by duration of total acquisition in 3D3C (15 – 50 s) | Dictated by temporal duration of scan for 1D3C (6 – 10 s), or entire acquisition time for 3D3C (60 – 90 s) |
| Spatial Resolution | Axial and lateral spatial resolution dictated by ROI in processing (20×20 μm2 − 120×120 μm2) | Axial spatial resolution equivalent to imaging system (∼7 μm), lateral resolution limited by extent of lateral scanning (30–50 μm) |
5. Conclusion
We demonstrated that complex three-dimensional, three-component (3D3C) microfluidic cilia-driven fluid flow can be quantified using OCT-based, correlation-based velocimetry methods. We showed that both DLS-OCT and DPIV-based approaches yield reasonable estimates in a flow phantom. Additionally, both techniques can characterize the flow field of epithelial-driven ciliary flow in Xenopus, although DLS-based methods seem to have a high rate of artifact. DPIV can additionally take advantage of endogenous scattering material to quantify fluid flow in the ventricles of the brain, and can also be used for slower tracheal ciliary flow. Overall, we believe that OCT-based approaches have great promise for elucidating important ciliary physiology.
Acknowledgments
We would like to thank Andrew Robson, Emily Mis, Sarah Kubek, and Engin Deniz for their help with Xenopus work. This work was supported by a March of Dimes Basil O’Connor Starter Scholar Research Award and NIH1R01HL118419-01. BKH was additionally supported by NIH MSTP TG T32GM07205. MKK was supported by NIH1R21HL120783 and 1R01HD081379. VB was supported by NIHR01HL085103.
6. Appendix
6.1. SNR Optimization in DPIV
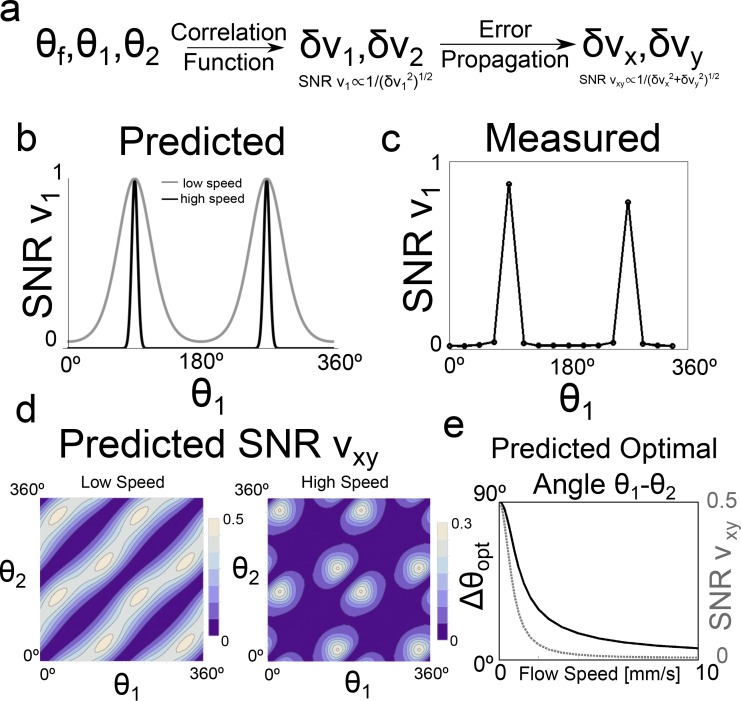
Prior to implementing our DPIV protocol, we investigated the signal-to-noise ratio (SNR) properties of our method to optimize acquisition. SNR in DPIV typically depends on many factors including shot noise of the original acquired images, diffusive motion, and the number of independent measurements averaged [15]. In the context of this work, we focused specifically on the effects of measurement angles θ1 and θ2 relative to the flow direction θf (Fig. 2(b)). As described in Eqs. (3) and (4), two measurements v1 and v2 are required to reconstruct two orthogonal flow components vx and vy. The SNR of this reconstruction in turn depends on (1) the SNR of each of the two independent measurements v1 and v2, and (2) the degree of linear independence of the two measurements. As outlined in Fig. 8(a), we will show how both of these quantities depend on the measurement angles, first by calculating the dependence of the error of v1 and v2 on measurement angle, and then by propagating that error through equations (3) and (4).
Fig. 8.
Optimization of signal-to-noise ratio (SNR) in DPIV measurements with respect to measurement angle. (a) Overall flow of SNR predictions. Two components of velocity vx and vy are synthesized from two non-orthogonal measurements v1 and v2. The error of the final measurements δvx and δvy, and thus the SNR, depend on error propagation from v1 and v2, as well as on the initial error δv1 and δv2. δv1 and δv2 in turn depend on multiple factors, including the flow angle θf relative to the angles of measurement, θ1 and θ2. (b) Predicted SNR of v1 (and equivalently v2) as a function of angle of measurement θ1, based on relative height of main correlation peak. θf here set to be 90°, and maximum SNR defined to be unity. (gray) low speed flow, (black) high speed flow. (c) Measured SNR of v1 as a function of measurement angle θ1 where θf set at 90°. (d) Predicted SNR of final measurement vxy, defined as , as a function of measurement angles θ1 and θ2. (left) low speed, (right) high speed. (e) Predicted optimal relative angle of measurement θ1 − θ2 (black), and subsequent optimal SNRvxy (gray hatched) as a function of flow speed.
In DPIV, two adjacent frames are used to calculated the spatiotemporal cross-correlation function g(x0, y0; δx, δz, τ = δt) at a variety of spatial lags δx and δz for a fixed temporal lag δt, equal to the interframe time (Fig. 1(a)). The location of the peak of this function gives the displacement (Δx, Δz) between the two frames, which is then used to calculate the velocity. It has been previously described that the SNR of velocity measurements in DPIV is proportional to the height of this correlation peak relative to the height of the second highest peak [15]. At low particle concentrations (<1 particle per focal volume on average), OCT-based correlation methods reduce to that of incoherent image formation [41]. Additionally, from image correlation spectroscopy, it is known that the spatiotemporal correlation function of an incoherent image takes the form [42]:
| (5) |
where wxy and wz are the beam waist of the Gaussian focus in the xy-plane and z-axis, respectively; D is the diffusivity of the sample; N is the number of particles per focal volume; and v = (vx, vy, vz) is the flow velocity of the sample. Equation (5) gives the height of the correlation peak. The physical interpretation of Eq. (5) is as follows. There is perfect correlation when an image is compared to itself with zero temporal and spatial lag, i.e. g(δx = 0, δz = 0, δt = 0) = 1 because we are multiplying the signal with a duplicate of itself. A maximum in correlation is found between two adjacent frames (δt ≠ 0) when δx = vxδt and δz = vzδt, as these terms correspond to in-plane translation. In this case, however, the correlation may no longer be unity because of particle diffusion and out-of-plane (vy) motion. In other words, diffusion and out-of-plane motion cause image patterns to be lost instead of translated purely in-plane, thus leading to a decrease in the magnitude of the correlation.
We know that the SNR is proportional to the height of this correlation (assuming that the noise floor is constant) but also depends on other factors including signal intensity. We introduce a pre-factor α to encapsulate other non-angle dependent factors. Additionally, we neglect the diffusive contribution and in the exponentials, noting that based on the diffusivity of 5 μm beads and an interframe time of 80 ms, this term is 0.999, or approximately 1. Lastly, based on the angle of flow θf, the angle of the plane of imaging θi (i = 1, 2), and the total speed , we define vy = vsin(θi − θf). These definitions leave us with an expression for SNR:
| (6) |
Equation (6) now relates how SNR in 2D2C DPIV depends on the relative flow angle. Plotted in Fig. 8(b) is Eq. (6) for two values of flow as a function of scan angle, with the flow angle arbitrarily set to be 90°. The SNR has a peak both where θ1 = θf and θ1 = θf + 180°. These two cases occur when flow has only in-plane components. Equation (6) reaches a minimum where the imaging plane is 90° (perpendicular) to flow. The degree to which SNR is decreases from out-of-plane flow depends on the quantity vδt/wxy, or the magnitude of out-of-plane motion.
To confirm these predictions, we performed DPIV on our parabolic flow phantom and varied the angle of the imaging plane with respect to the flow angle, defined to be 90°. We calculated an empirical SNR as follows. We recorded 20 frames, leading to n = 19 independent measurements of vx at each location. SNR was calculated at a point by point basis in the channel as μvx/σvx, where μvx and σvx were the mean and standard deviation, respectively, of the 19 measurements at a single location. The SNR was averaged over all points in the channel to come up with a single 〈SNR〉. Shown in Fig. 8(c) is the SNR(θ) curve, which shows the same qualitative behavior as predicted by Eq. (6), reaching a peak near 0° where flow is nearly coincident with the imaging plane, and dropping sharply, and increasing again at 180°. Notably, the SNR points on Fig. 8(c) have been scaled to reach a maximum of unity in order to better compare with Fig. 8(b).
Once we know the SNR of each individual measurement, the next step is to predict how that error due to our measurements of v1 and v2, which we denote as δv1 and δv2, propagates to our estimation of vx and vy. We denote the errors of our global velocity measurements as δvx and δvy. Assuming relatively small error, this step can be predicted based on standard error propagation formulas:
| (7) |
| (8) |
Applying Eq. (6) to Eqs. (7) and (8), we derive the formula:
| (9) |
| (10) |
where θ1 and θ2 are the angles of the imaging planes. The dependence of δv1 and δv2 on flow angle and plane angle has been highlighted by writing them as a function of θf and θi. Importantly, the error in each of these terms diverges when θ1 = θ2. This large increase in error is a statement of the fact that in order to measure two orthogonal velocity components, two linearly independent measurements must be made. Measurements that are linearly independent but non-orthogonal will give a unique answer, but the degree of error propagation depends on how orthogonal the two angles are.
In order to optimize our acquisition, we optimize not δvx or δvy alone, but rather the sum of the two. Shown in Fig. 8(d) are contour plots of the relative SNR vxy, defined as as a function θ1, θ2 for low and high speed, with θf now set to be 0°. SNR is very low when θ1 = θ2 or θ1 = θ2 + 180° due to the linear dependence of the two measurements. For low flow speeds, maximal SNR occurs near θ1 = ±45°, θ2 = −θ1. (θi and θi + 180° are equivalent, because the imaging plane is coincident with flow, and thus there are 8 total equivalent solutions that maximize SNR.) At higher flow speeds, because SNR of v1 and v2 drops significantly when θ1 and θ2 are not coincident with θf, it becomes more advantageous to align each independent plane closer with the direction of flow, even if the two planes are no longer orthogonal. In the case of high flow, then, SNR is still maximized when θ1 = −θ2, but now at some angle that is less than 45°.
The maximum at each of these contour plots can be calculated numerically, and the location of the maxima can be plotted as a function of flow speed. Figure 8(e) shows these results. As the magnitude of speed approaches zero, the optimal imaging angle approaches ±45°, while when magnitude of speed is high, the optimal imaging angle moves closer towards being coincident with the direction of flow.
The interpretation of Fig. 8(e) is as follows. At low flow speeds, the absolute error δv1 and δv2 are relatively low, so these two measurements should be orthogonal in order to minimize error propagation from v1 and v2 to vx and vy. As such, the planes are placed optimally at ±45° oblique to the direction of flow. Even at these slow speeds, however, the SNR is less than unity because both imaging planes cannot be placed coincident with flow simultaneously. As the flow speed is increased the absolute value of δv1 and δv2 begins to increase. As that error increases, the gains from having two orthogonal measurements starts to be outweighed by the fact that the absolute error in v1 and v2 can be reduced by bringing both planes closer to coincident with the angle of flow. In the most extreme scenario, when flow is very fast, both planes must be nearly coincident to it to get any reasonable value of v1 and v2. As v1 and v2 begin to become more collinear, however, small errors propagate more strongly. Thus, at higher flow speeds, even though we optimize SNR by bringing the two imaging planes coincident with flow, the total SNR of the process is still much worse than when we can make completely orthogonal measurements in the low flow speed regime.
References and links
- 1.Huang B. K., Choma M. A., “Microscale imaging of cilia-driven fluid flow,” Cell Mol. Life Sci. 72, 1095–113 (2015). 10.1007/s00018-014-1784-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Smith D. J., Gaffney E. A., Blake J. R., “Modelling mucociliary clearance,” Respiratory Physiol. Neurobiol. 163, 178–188 (2008). 10.1016/j.resp.2008.03.006 [DOI] [PubMed] [Google Scholar]
- 3.Supatto W., Fraser S. E., Vermot J., “An all-optical approach for probing microscopic flows in living embryos,” Biophys. J. 95, L29–L31 (2008). 10.1529/biophysj.108.137786 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jonas S., Bhattacharya D., Khokha M. K., Choma M. A., “Microfluidic characterization of cilia-driven fluid flow using optical coherence tomography-based particle tracking velocimetry,” Biomed. Opt. Express 2, 2022–2034 (2011). 10.1364/BOE.2.002022 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Oldenburg A. L., Chhetri R. K., Hill D. B., Button B., “Monitoring airway mucus flow and ciliary activity with optical coherence tomography,” Biomed. Opt. Express 3, 1978–1992 (2012). 10.1364/BOE.3.001978 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Liu L., Chu K. K., Houser G. H., Diephuis B. J., Li Y., Wilsterman E. J., Shastry S., Dierksen G., Birket S. E., Mazur M., Byan-Parker S., Grizzle W. E., Sorscher E. J., Rowe S. M., Tearney G. J., “Method for quantitative study of airway functional microanatomy using micro-optical coherence tomography,” PLoS One 8, e54473 (2013). 10.1371/journal.pone.0054473 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Izatt J. A., Kulkami M. D., Yazdanfar S., Barton J. K., Welch A. J., “In vivo bidirectional color doppler flow imaging of picoliter blood volumes using optical coherence tomograghy,” Opt. Lett. 22, 1439–1441 (1997). 10.1364/OL.22.001439 [DOI] [PubMed] [Google Scholar]
- 8.Chen C.-Y., Menon P. G., Kowalski W., Pekkan K., “Time-resolved OCT-μ PIV: a new microscopic PIV technique for noninvasive depth-resolved pulsatile flow profile acquisition,” Experiments in Fluids 54, 1–9 (2013). [Google Scholar]
- 9.Lee J., Wu W., Jiang J. Y., Zhu B., Boas D. A., “Dynamic light scattering optical coherence tomography,” Opt. Express 20, 22262–22277 (2012). 10.1364/OE.20.022262 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Huang B. K., Gamm U. A., Jonas S., Khokha M. K., Choma M. A., “Quantitative optical coherence tomography imaging of intermediate flow defect phenotypes in ciliary physiology and pathophysiology,” J. Biomed. Opt. 20, 30502 (2015). 10.1117/1.JBO.20.3.030502 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Huang B. K., Choma M. A., “Resolving directional ambiguity in dynamic light scattering-based transverse motion velocimetry in optical coherence tomography,” Opt. Lett. 39, 521–524 (2014). 10.1364/OL.39.000521 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Willert C. E., Gharib M., “Digital particle image velocimetry,” Experiments in Fluids 10, 181–193 (1991). 10.1007/BF00190388 [DOI] [Google Scholar]
- 13.Brücker C., “Digital-particle-image-velocimetry (DPIV) in a scanning light-sheet: 3D starting flow around a short cylinder,” Experiments in Fluids 19, 255–263 (1995). 10.1007/BF00196474 [DOI] [Google Scholar]
- 14.Klein S. A., Moran J. L., Frakes D. H., Posner J. D., “Three-dimensional three-component particle velocimetry for microscale flows using volumetric scanning,” Meas. Sci. Technol. 23, 085304 (2012). 10.1088/0957-0233/23/8/085304 [DOI] [Google Scholar]
- 15.Keane R. D., Adrian R. J., “Theory of cross-correlation analysis of PIV images,” Appl. Sci. Res. 49, 191–215 (1992). 10.1007/BF00384623 [DOI] [Google Scholar]
- 16.Thielicke W., Stamhuis E. J., “PIVLab–Towards User-friendly, Affordable and Accurate Digital Particle Image Velocimetry in MATLAB,” 2, 5334 (2014). [Google Scholar]
- 17.Trasischker W., Werkmeister R. M., Zotter S., Baumann B., Torzicky T., Pircher M., Hitzenberger C. K., “In vitro and in vivo three-dimensional velocity vector measurement by three-beam spectral-domain Doppler optical coherence tomography,” J. Biomed. Opt. 18, 116010 (2013). 10.1117/1.JBO.18.11.116010 [DOI] [PubMed] [Google Scholar]
- 18.Prasad A. K., Adrian R. J., “Stereoscopic particle image velocimetry applied to liquid flows,” Experiments in Fluids 15, 49–60 (1993). 10.1007/BF00195595 [DOI] [Google Scholar]
- 19.Srinivasan V. J., Sakadzic S., Gorczynska I., Ruvinskaya S., Wu W., Fujimoto J. G., Boas D. A., “Quantitative cerebral blood flow with optical coherence tomography,” Opt Express 18, 2477–2494 (2010). 10.1364/OE.18.002477 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Weiss N., van Leeuwen T. G., Kalkman. J., “Localized measurement of longitudinal and transverse flow velocities in colloidal suspensions using optical coherence tomography,” Phys. Rev. E 88, 042312 2013 10.1103/PhysRevE.88.042312 [DOI] [PubMed] [Google Scholar]
- 21.Normal table of Xenopus laevis (Daudin) : a systematical and chronological survey of the development from the fertilized egg till the end of metamorphosis (Garland Pub., New York, 1994). [Google Scholar]
- 22.Jonas S., Zhou E., Deniz E., Huang B., Chandrasekera K., Bhattacharya D., Wu Y., Fan R., Deserno T. M., Khokha M. K., Choma M. A., “A novel approach to quantifying ciliary physiology: microfluidic mixing driven by a ciliated biological surface,” Lab on a Chip 13, 4160–4163 (2013). 10.1039/c3lc50571e [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gamm U. A., Huang B. K., Syed M., Zhang X., Bhandari V., Choma M. A., “Quantifying hyperoxia-mediated damage to mammalian respiratory cilia-driven fluid flow using particle tracking velocimetry-optical coherence tomography,” J. Biomed. Opt. in press (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Weiss N., van Leeuwen T. G., Kalkman J., “Simultaneous and localized measurement of diffusion and flow using optical coherence tomography,” Opt. Express 23, 3448–3459 (2015). 10.1364/OE.23.003448 [DOI] [PubMed] [Google Scholar]
- 25.Naeter W., “3D differential Canny Edge Detector,” (MATLAB Central File Exchange 2014). http://www.mathworks.com/matlabcentral/fileexchange/46260-3d-differential-canny-edge-detector, adapted from W. Naeter and O. Scherze, “Quantitative photoacoustic tomography with piecewise constant material parameters,” SIAM J. Imaging Sci. 3 1755–1774(2014). [Google Scholar]
- 26.Arseneau S., “3D Quiver with volumized arrows,” (MATLAB Central File Exchange 2006), http://www.mathworks.com/matlabcentral/fileexchange/12285-3d-quiver-with-volumized-arrows/content/quiver3D_pub/quiver3D.m.
- 27.Boppart S. A., Brezinski M. E., Bouma B. E., Tearney G. J., Fujimoto J. G., “Investigation of developing embryonic morphology using optical coherence tomography,” Dev. Biol. 177, 54–63 (1996). 10.1006/dbio.1996.0144 [DOI] [PubMed] [Google Scholar]
- 28.Mogi K., Adachi T., Izumi S., Toyoizumi R., “Visualisation of cerebrospinal fluid flow patterns in albino Xenopus larvae in vivo,” Fluids Barriers CNS 9, 9 (2012). 10.1186/2045-8118-9-9 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Miskevich F., “Imaging fluid flow and cilia beating pattern in xenopus brain ventricles,” J. Neurosci. Meth. 189, 1–4 (2010). 10.1016/j.jneumeth.2010.02.015 [DOI] [PubMed] [Google Scholar]
- 30.Hagenlocher C., Walentek P., C M. L., Thumberger T., Feistel K., “Ciliogenesis and cerebrospinal fluid flow in the developing Xenopus brain are regulated by foxj1,” Cilia 2, 12 (2013). 10.1186/2046-2530-2-12 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wodarczyk C., Rowe I., Chiaravalli M., Pema M., Qian F., Boletta A., “A novel mouse model reveals that polycystin-1 deficiency in ependyma and choroid plexus results in dysfunctional cilia and hydrocephalus,” Plos One 4, 7137 (2009). 10.1371/journal.pone.0007137 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Guirao B., Meunier A., Mortaud S., Aguilar A., Corsi J. M., Strehl L., Hirota Y., Desoeuvre A., Boutin C., Han Y. G., Mirzadeh Z., Cremer H., Montcouquiol M., Sawamoto K., Spassky N., “Coupling between hydrodynamic forces and planar cell polarity orients mammalian motile cilia,” Nat. Cell Biol. 12, 341–350 (2010). 10.1038/ncb2040 [DOI] [PubMed] [Google Scholar]
- 33.Khokha M. K., Chung C., Bustamante E. L., Gaw L. W., Trott K. A., Yeh J., Lim N., Lin J. C., Taverner N., Amaya E., Papalopulu N., Smith J. C., Zorn A. M., Harland R. M., Grammer T. C., “Techniques and probes for the study of xenopus tropicalis development,” Dev. Dyn. 225, 499–510 (2002). 10.1002/dvdy.10184 [DOI] [PubMed] [Google Scholar]
- 34.Marzesco A. M., Janich P., Wilsch-Brauninger M., Dubreuil V., Langenfeld K., Corbeil D., Huttner W. B., “Release of extracellular membrane particles carrying the stem cell marker prominin-1 (CD133) from neural progenitors and other epithelial cells,” J. Cell Sci. 118, 2849–2858 (2005). 10.1242/jcs.02439 [DOI] [PubMed] [Google Scholar]
- 35.Wanner A., Salathe M., O’Riordan T. G., “Mucociliary clearance in the airways,” Am. J. Respir. Crit. Care Med. 154, 1868–1902 (1996). 10.1164/ajrccm.154.6.8970383 [DOI] [PubMed] [Google Scholar]
- 36.Liu L., Shastry S., Byan-Parker S., Houser G., Chu K., Birket S. E., Fernandez C. M., Gardecki J. A., Grizzle W., Wilsterman E. J., Sorscher E. J., Rowe S. M., Tearney G. J., “An autoregulatory mechanism governing mucociliary transport is sensitive to mucus load,” Am. J. Respir. Cell. Mol. Biol. 51, 485–493 (2014). 10.1165/rcmb.2013-0499MA [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Matsui H., Randell S. H., Peretti S. W., Davis C. W., Boucher R. C., “Coordinated clearance of periciliary liquid and mucus from airway surfaces,” J. Clin. Invest. 102, 1125–1131 (1998). 10.1172/JCI2687 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hoegger M. J., Fischer A. J., McMenimen J. D., Ostedgaard L. S., Tucker A. J., Awadalla M. A., Moninger T. O., Michalski A. S., Hoffman E. A., Zabner J., Stoltz D. A., Welsh M. J., “Cystic fibrosis. impaired mucus detachment disrupts mucociliary transport in a piglet model of cystic fibrosis,” Science 345, 818–822 (2014). 10.1126/science.1255825 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Chhabra. R. P., “Fluid particles in non-Newtonian media”, in Bubbles, Drops, and Particles in Non-Newtonian Fluids (CRC Taylor & Francis, Boca Raton, FL: ) (2007), p. 771 . [Google Scholar]
- 40.Adrian R. J., “Particle-imaging techniques for experimental fluid-mechanics,” Ann. Rev. Fluid Mechanics 23, 261–304 (1991). 10.1146/annurev.fl.23.010191.001401 [DOI] [Google Scholar]
- 41.Broillet S., Sato A., Geissbuehler S., Pache C., Bouwens A., Lasser T., Leutenegger M., “Optical coherence correlation spectroscopy (OCCS),” Opt. Express 22, 782–802 (2014). 10.1364/OE.22.000782 [DOI] [PubMed] [Google Scholar]
- 42.Hebert B., Costantino S., Wiseman P. W., “Spatiotemporal image correlation spectroscopy (STICS) theory, verification, and application to protein velocity mapping in living CHO cells,” Biophys. J. 88, 3601–3614 (2005). 10.1529/biophysj.104.054874 [DOI] [PMC free article] [PubMed] [Google Scholar]