Abstract
Traditional Chinese herbal medications (TCHMs) are comprised of a multitude of compounds and the identification of their active composition is an important area of research. Chromatography provides a visual representation of a TCHM sample's composition by outputting a curve characterized by spikes corresponding to compounds in the sample. Across different experimental conditions, the location of the spikes can be shifted, preventing direct comparison of curves and forcing compound identification to be possible only within each experiment. In this article we propose a sparse semiparametric nonlinear modeling framework for the establishment of a standardized chromatographic fingerprint. Data-driven basis expansion is used to model the common shape of the curves while a parametric time warping function registers across individual curves. Penalized weighted least squares with the adaptive lasso penalty provides a unified criterion for registration, model selection, and estimation. Furthermore, the adaptive lasso estimators possess attractive sampling properties. A back-fitting algorithm is proposed for estimation. Performance is assessed through simulation and we apply the model to chromatographic data of rhubarb collected from different experimental conditions and establish a standardized fingerprint as a first step in TCHM research.
Keywords: Adaptive lasso, Chromatography, Curve registration, Herbal medicine, Variable selection
1 Introduction
Traditional Chinese Herbal Medicines (TCHMs) have been used for thousands of years for the treatment and prevention of a wide range of medical ailments and diseases (Duke, 2002). TCHMs are comprised of substances extracted from the roots, stems, or leaves of plants and herbs by boiling (Liang et al., 2004). The structure of TCHMs is complex and their therapeutic effects are due to a combination of multiple compounds. Furthermore, the preparation process is difficult to replicate exactly, inhibiting proper quality control. Thus efficacy research, classification, and the development of standardized medications is problematic and has been the focus of much research in recent years.
The first step in TCHM research is identifying compounds in an herbal medicine. Chromatography is a standard technique used in the exploration of biological sample composition and has become a key tool in herbal medication research. A chromatographic experiment outputs a curve displaying an intensity measurement over experiment time characterized by a number of sharp, narrow spikes, where each spike corresponds to a compound in the sample. The location in time of a spike, called retention time, can be used to identify the compound. For instance, a sample of a known compound can be analyzed under the identical experimental condition and if its retention time is the same as one of the spikes in the study chromatogram, this is evidence that the particular spike corresponds to the known compound.
Therefore the chromatographic curve, termed chromatogram, provides a visual representation of the composition of a study sample. As the combination of compounds is unique to a TCHM, its chromatogram serves as a fingerprint of the medicine. The main difficulty in fingerprinting is that, due to variations in experimental conditions, spikes are often shifted in time across experiments. The incomparability of spikes across experiments prevents the establishment of an overall standardized fingerprint. In addition, due to the shifting of retention times, any known samples used to identify compounds must be analyzed under every experimental condition, which can become cost-prohibitive. Hence retention time warping poses a large obstacle in the practical application of chromatographic experiments in TCHM research.
Recent statistical methods proposed to address the time warping seek to align spikes across experiments. Alignment is performed through parametric models of the warping function or dynamic time warping of the chromatograms (Kassidas et al., 1998; van Nederkassel et al., 2006). Generally, alignment is performed as a pre-processing step and the mean curve is obtained separately on the aligned curves. The disadvantages of such two-step approaches have been noted previously (Morris et al., 2008). Two-step methods do not take the variability in the alignment step into account which leads to downward attenuation of subsequent parameter estimates and optimizing different objective functions for each step does not guarantee overall convergence. In addition, these methods usually focus on a few large spikes and the smaller spikes are ignored. Curve registration offers a framework to model chromatograms and warping functions jointly (Ramsay and Li, 1998). By assuming time has been warped by some unknown monotonic function and estimating the warping function jointly with the standardized fingerprint, estimation and alignment of chromatograms are accomplished in a unified fashion.
In regards to modeling the fingerprint shape, wavelets are a particular family of functions that have become popular due to their ability to estimate curves with local features, such as sharp spikes. This ability has prompted their use in modeling mass spectrometry (MS) data which is similar in nature to chromatographic data (Randolph and Yasui, 2006; Morris et al., 2008). In particular, Morris et al. (2008) considered proteomic MS data and applied the discrete wavelet transform (DWT) to the curves and fit a linear functional mixed effects model to the transformed data. Their methodology can accommodate functional effects and can be used in nested designs. However, their methods are restrictive in that the DWT is a linear transformation and their model is linear in the mixed effects. In our setting, the warping function parameters enter into the model nonlinearly, thus we cannot employ the DWT. Instead wavelet basis expansion can be utilized to supply a finite-dimensional representation of the curves that can accommodate nonlinear parameters.
A salient feature of chromatograms is that only a small fraction of each curve is true signal. While the curves are comprised of thousands of data points, there are relatively few narrow spikes along with long, flat regions. This sparse structure suggests that their basis representation is also sparse, in that most of the basis functions correspond to the flat regions of the curves and the true values of their coefficients are zero. It is imperative, then, to identify the subset of nonzero coefficients and include only their corresponding basis functions in the model. In other words, model selection should be performed on the basis functions. Imposing an ℓ1 penalty on the basis functions shrinks irrelevant coefficients to 0, in essense dropping them from the model while retaining and estimating the important variables. Thus model selection is performed on the basis functions as well as nonparametric estimation, as the dimension of the basis parameter vector is chosen by the data.
The semiparametric nonlinear regression models of Wang and Ke (2009) is a large class of flexible models that can accommodate nonlinear parameters, such as warping function parameters. However, Wang and Ke (2009) use smoothing splines to estimate the mean function. They induce smoothness in the functional estimate via an ℓ2 penalty, which does not perform model selection as all variables are included in the model. Furthermore, the estimation algorithms used for ℓ2-penalized methods differ from those for ℓ1-penalized methods.
In this article we propose a sparse semiparametric nonlinear model for the registration of chromatograms and establishment of a standardized chromatographic fingerprint. We assume the chromatograms arise from a common spiky function and employ basis expansion by the Battle-Lemarié spline wavelets to model this function. We assume each curve has been distorted by a smooth, monotonic, nonlinear warping function, and model the warping functions by monotonic parametric smooth functions. We impose the Adaptive Least Absolute Shrinkage and Selection Operator (Adaptive Lasso) penalty on the coefficients of the wavelet basis functions. Penalized weighted least squares provides a unified criterion to simultaneously select wavelet basis parameters and estimate the standardized fingerprint and warping functions, guaranteeing a unique solution and enabling us to study sampling properties of the estimates (Fan and Li, 2001; Zou, 2006). We propose a computationally efficient back-fitting algorithm for the estimation of model parameters which is equivalent to a blockwise coordinate descent algorithm and utilizes existing algorithms.
Estimating the warping functions enables recovery of information across experiments in establishing a standardized fingerprint. By averaging across samples, the consistent spikes will be preserved even if their amplitudes are small, and the inconsistent spikes will be averaged out even if their amplitudes are large. This is key as the large spikes do not necessarily represent the active set of compounds. As the number of curves grows larger, a consistent estimate of the standardized fingerprint is obtained. The search for active compounds can then be focused on the common compounds reflected in the standardized fingerprint. Furthermore, if the time scale of a particular experiment is used as the reference scale to which all experiments are warped, any known compounds used to identify compounds in the study chromatograms need be analyzed under only the reference condition as opposed to every condition. Thus comparisons of retention times of a large number of known compounds to those in the study chromatograms is much more financially possible than the current practice.
The use of the adaptive lasso results in root-n consistency, asymptotic normality and variable selection consistency of the model estimates, known as the oracle property (Donoho and Johnstone, 1994). Statistical inference can be made on the curves and warping functions and the variance estimates reflect the variability in their joint estimation.
We construct chromatographic experiments to demonstrate the application of our procedure. We obtain chromatograms of samples of the herbal medicine, rhubarb, through High Performance Liquid Chromatography (HPLC) under a set of uniquely calibrated experimental settings, chosen to induce time retention warping across settings. More details about rhubarb, HPLC, and the design of our experiments are given in Section 2. We further assess our procedure via simulation.
The remainder of the article is organized as follows: We discuss rhubarb, HPLC, and the design of our experiments in Section 2. In Section 3 we present the sparse semiparametric nonlinear model. In Section 4 we discuss estimation and properties of the estimates. Application of the model to fingerprint data and simulations are presented in Sections 5 and 6, respectively. We conclude with discussion in Section 7.
2 Data
Rhubarb is a medicinal plant that has been used since at least 250 A.D. for the treatment and prevention of number of medical conditions including cancer, constipation, fever, and inflammations (Peigen et al., 1984; Duke, 2002). The rhizomes and roots of the plant are typically used for its medical applications. The structure of rhubarb is quite complex, with more than one hundred compounds identified across six species of the plant, and its medicinal properties are still not fully understood (Ye et al., 2007). As rhubarb is one of the more popular and widely-used TCHMs, there is much interest in the exploration of the medicine. Before identification and quantification of the active compounds in rhubarb is possible, its chemical composition must be determined.
High Performance Liquid Chromatography (HPLC) is a particular technique for separating compounds of a biological sample. HPLC dissolves a sample into a liquid solution of two solvents, called the mobile phase. The relative composition of the two solvents is varied at a controlled rate over time, where the levels and timings together are termed the gradient program. The sample and mobile phase are pumped through a column containing sorbent materials, called the stationary phase. As the sample passes through the column, the compounds separate from each other. Due to the unique properties of the individual compounds and the mobile and stationary phases, the compounds travel through the column at different rates and leave the column at different times (Snyder and Kirkland, 1979). A detector, such as an Ultraviolet (UV) detector, records two measurements: the time a compound leaves the column, or retention time, and an intensity measurement.
UV detectors measure UV absorbance, which is a function of concentration and molar absorptivity of each compound. The amplitude of the resulting spike in the chromatogram increases with compound concentration and molar absorptivity (Meyer, 2010). Thus spike amplitude is not indicative of the importance of the corresponding compound in the medicine's therapeutic effects, but instead provides information regarding a combination of the amount of the compound in the sample and its structural properties.
The retention time of a compound is a function of various conditions such as column length, temperature, and stationary and mobile phase volumes. As a compound's particular behavior in the column is due to its unique structure, and under identical conditions remains unchanged, its retention time provides an indicator to its identity (Meyer, 2010). If after a large number of known compounds are analyzed and a retention time match has not been found for every compound in the study sample, then mass spectrometry (MS) can be used to elucidate the ionic structure of any remaining unknown compounds. MS ionizes a compound through some mechanism, such as electrospray ionization, and then measures ion abundance and the mass to charge ratio of the ions. Plotting ion abundance over mass to charge ratio provides an ion chromatogram of the compound and can be used to identify it.
Between HPLC experiments, a number of experimental factors can vary, altering retention times of compounds. For example, unique calibrations of different HPLC equipment can result in slight differences in column temperature, gradient program, and the rate of flow of the mobile phase. These differences lead to variation in the separation and velocity of compounds which alters retention time and thus, spike timings, across experiments. In this article we wish to emulate this phenomenon.
We consider the setting in which we have samples of rhubarb with identical compositions. The samples are analyzed using HPLC under eight experimental conditions set to induce changes in retention times of sample compounds. Under the same experimental conditions, the resulting chromatograms are identical apart from measurement error. Across experiments, the differing conditions induce nonlinear shifting of spikes.
For each of the eight experimental conditions, we analyze three samples of rhubarb via HPLC. The conditions are constructed by varying the gradient program and flow rate as described in Table 1. Each sample is run using the ACQUITY BEH C18 column held at 30 degrees Celsius. The wavelength of the UV detector is set at 260 nm. The mobile phase is comprised of 0.1% phosphoric acid aqueous solution and acetonitrile. The observed total retention times ranged from 14.0021 to 16.0025 minutes. The observed vectors for conditions 1–8 were of respective lengths {19200, 18000, 18000, 18000, 18000, 18000, 18000, 16800}. Figure 1 displays the chromatograms for the 24 samples. To illustrate the ability to identify compounds across different conditions using the fingerprint of a set of known compounds under one single condition, we also analyzed a mixture of seven compounds known to be in rhubarb under condition 1 (Ye et al., 2007) and the resulting chromatogram is displayed in Figure 1. The 7 known compounds are (1) gallic acid, (2) catechin, (3) aloe-emodin, (4)
Table 1.
Gradient program and flow rate for the eight experiments. Shown are the proportion of 0.1% phosphoric acid aqueous solution (A) and acetonitrile (B) in the mobile phase and the timings of the changing of relative proportions along with the flow rate of the mobile phase. The italicized values indicate the altered parameters in comparison to those in condition 1.
| 1 | 2 | 3 | 4 | |||||
|---|---|---|---|---|---|---|---|---|
| Time (min) | A | B | A | B | A | B | A | B |
| 0 | 82 | 18 | 83 | 17 | 83 | 17 | 83 | 17 |
| 2 | 72 | 28 | 72 | 28 | 72 | 28 | 72 | 28 |
| 6.8 | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 |
| 9.6 | 41 | 59 | 41 | 59 | 41 | 59 | 41 | 59 |
| 13 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 |
| 15 | 82 | 18 | 83 | 17 | 83 | 17 | 83 | 17 |
| Flow rate (mL/min) | 0.21 | 0.21 | 0.18 | 0.20 | ||||
|
| ||||||||
| 5 | 6 | 7 | 8a | |||||
| Time (min) | A | B | A | B | A | B | A | B |
|
| ||||||||
| 0 | 83 | 17 | 83 | 17 | 85 | 15 | 85 | 15 |
| 2 | 72 | 28 | 72 | 28 | 72 | 28 | 72 | 28 |
| 6.8 | 55 | 45 | 60 | 40 | 50 | 50 | 50 | 50 |
| 9.6 | 41 | 59 | 41 | 59 | 41 | 59 | 41 | 59 |
| 13 | 0 | 100 | 0 | 100 | 0 | 100 | 0 | 100 |
| 15 | 83 | 17 | 83 | 17 | 85 | 15 | 85 | 15 |
| Flow rate (mL/min) | 0.21 | 0.21 | 0.21 | 0.21 | ||||
Time at which last two concentration changes occur at 12 and 14 minutes, respectively rhein, (5) emodin, (6) chrysophanol, and (7) physcion.
Figure 1.
Top portion of each panel: chromatograms for one of the eight experimental conditions. The three samples within each condition are displayed with an arbitrary vertical shift. The set of known compounds are denoted as: (1) gallic acid, (2) catechin, (3) aloe-emodin, (4) rhein, (5) emodin, (6) chrysophanol, and (7) physcion. Bottom portion of each panel: the chromatogram from known compound sample under Condition 1 transformed to the time in the given condition using the corresponding estimated warping function.
3 Model
Let yijk be observation k from chromatogram j in experimental condition i at time point tijk, where we assume without loss of generality that tijk ∈ [0,1], i = 1, 2, …, n, j = 1, 2, …, m, k = 1,2, …, Li. Our model is
| (1) |
where f is an unknown spiky function, τijk is the warped time relating to tijk via some smooth monotonic function g, indexed by unknown condition-level parameter vector bi, and eij = (eij1, …,eijLi)T is the vector of measurment errors for chromatogram j with mean 0 and covariance matrix σ2Vi(θ), where θ is a vector of unknown parameters and σ2 is an unknown scale parameter. Vi depends on i through its dimension. In this article we assume equal number of experiments per condition and each experiment within a condition are observed on the same time vector, however these assumptions can be relaxed.
The common shape function f is expanded into the Battle-Lemarié spline wavelet basis, that is , where xs(τijk) is the sth spline wavelet basis function evaluated at τijk and βs is the corresponding unknown basis function parameter. In wavelet bases, the xs estimate oscillations in the observed signal at particular dyadic scales and integer translates for different s. Battle-Lemarié spline wavelets possess a number of attractive properties such as orthogonality, regularity, vanishing moments, symmetry, and a closed-form expression (Daubechies, 1992; Unser, 1997).
Some common examples of parametric models for the warping functions include: a linear combination of polynomial function . By setting bq = 0 for q > 1 we get the location and scale functions as in shape-invariant and self-modeling regression models (Lawton et al., 1972). A more flexible example is a linear combination of B-splines: g(tijk,bi) = Bq,r(tijk)bi, where Bq,r(tijk) is the 1 × Q design matrix of B-spline basis functions of order q and knot sequence r evaluated at tijk (Brumback and Lindstrom, 2004). We focus on estimation using B-splines with a uniform knot sequence in the current article.
The time warping functions are constrained to be monotonic so that no time point in the original scale is mapped to more than one time point in the warped scale. B-splines are a convenient choice of basis as imposing monotonicity in the warping functions can be accomplished by imposing monotonicity in the B-spline coefficients (Schumaker, 2007, chap. 4.9). Numerically, we can either invoke inequality constraints for each i or reparametrize the sequential increments of the coefficients by an exponential transformation resulting in a sequence of increasing B-spline coefficients. That is, for condition i, letting bil be the lth parameter for condition i, we set
where δij ∈ (−∞,∞), j = 2,…,Q. As with most wavelet bases, a boundary constraint must also be placed on the wavelet basis, such as periodicity or symmetry. As such, a further constraint must be placed on the B-spline coefficients to maintain identifiability of the warped time vector. For example, assuming periodic wavelets, we can constrain bi1 to be in [ −0.5, 0.5] to ensure identifiability. This can be accomplished by letting bi1 = exp(δi1)/(1+exp(δi1))−0.5 where δi1 ∈ (−∞, ∞). While there is a monotonic constraint among the B-spline coefficients, we do not need to consider explicit constraints in estimating δi1, …, δiQ.
To set a particular experimental condition as the reference time scale, we set the warping function parameters of one condition to correspond to the 45 degree line, which denotes no warping. For example, for cubic B-splines with k uniform knots, the coefficients for the reference condition are equal to {0, 1/(3k − 3), …, 3z/(3k− 3), …, (3k − 4)/(3k − 3), 1}, for z = 1,… k − 2. Without loss of generality, we select condition 1 as the reference condition.
Thus (1) can be expressed as:
| (2) |
As we wish to restrict the number of parameters to be less than the number of data points per curve, p should be less than min(Li) − Q(n − 1). Thus the total number of parameters to be estimated is less than min(Li).
4 Estimation
Let yij = (yij1, …, yijni)T, tij = (tij1, …, tijni)T, and . The penalized weighted least squares criterion is:
| (3) |
where wˆj are data-driven weights, and λ is a tuning parameter for the Adaptive Lasso penalty which controls the amount of shrinkage. We use where is the unpenalized, nonlinear weighted least squares estimator of βj as it is a root-n consistent estimator of βˆj (Jennrich, 1969).
Letting , computation can be greatly simplified by setting λ* = σ2λ, and noting that for fixed b = bˆ and θ = θˆ, solving (3) for β simplifies to a penalized least squares problem with the Adaptive Lasso penalty:
| (4) |
where and where is the sth row of . Minimizing (4) can be accomplished using standard algorithms for (ℓ)1-penalized regression (Zou, 2006). For fixed β = βˆ and θ = θˆ, using the reparameterization of bi described in the previous section, solving (3) for b is equivalent to solving the following unpenalized nonlinear least squares problem for δ = (δ21, …, δ2Q, …, δn1, …, δnQ)T:
| (5) |
Similarly, for fixed β= βˆ and b = bˆ, solving (3) for θ is also an unpenalized nonlinear least squares problem:
| (6) |
Hence we propose the following iterative back-fitting algorithm to estimate β, b, and θ: At iteration k:
Fix the b and θ at their estimates from iteration (k − 1), denoted b(k−1) and θ(k−1). Solve (4) for β, obtaining βˆ(k−1).
Fix β at βˆ(k−1) from step 1 and θ at θ(k−1). Solve (5) for δ, obtaining δˆ(k−1) and bˆ(k−1).
Fix β at βˆ(k−1) and b at bˆ(k−1) from steps 1 and 2, respectively. Solve (6) for θ, obtaining θ(k−1).
Iterate steps 1–3 until convergence. At convergence, estimate σ2 via
| (7) |
The algorithm as a whole minimizes the unified criterion, (3), and by using line searches to solve (4), (5), and (6), is equivalent to a blockwise coordinate descent algorithm (Tseng, 2001).
Convergence of the back-fitting algorithm depends on good initial estimates. Specifically, the algorithm requires good initial estimates of the warping function parameters. One method for obtaining initial estimates is to set λ = 0 and solve (3). In this situation, (3) is an unpenalized nonlinear least squares problem. As standard nonlinear least squares procedures are iterative, initial estimates of the warping function parameters are necessary for this step, as well. These can be obtained by first estimating the warping functions via dynamic time warping (Kassidas et al., 1998; Giorgino, 2009) and then modeling the estimated warping functions using monotonic B-splines.
It is important to note that since the bi are updated at each iteration, the wavelet basis design matrix also changes at each iteration. The adaptive weights, | βˆNLS|−1, are calculated at the initial estimation step using the unpenalized estimates and are kept constant throughout the estimation procedure.
The estimates obtained from (3) depend on the particular value of the tuning parameter, λ, as the proposed back-fitting algorithm is for a fixed λ. Numerous techniques to choose the optimal value of λ exist with varying degrees of properties. In penalized least squares problems with the smoothly clipped absolute deviation (Fan and Li, 2001) chosen as the penalty, it has been shown that BIC consistently chooses the correct model (Wang et al., 2007). This results follows when using the Adaptive Lasso. We use the BIC to choose the optimal value of λ.
Our proposed method does not require normality. In practice, when applying our procedure to chromatographic data, we have found that the tails of the distribution of the residuals are fatter than those of normally distributed residuals. The robustness of the Lasso to fat-tailed errors has been studied previously. Finite sample performance is affected by fat tails, however Fan et al. (2013) showed that Lasso estimates retain sign consistency if the signal is large enough. Bunea and Gupta (2010) and Sang and Sun (2012) consider Lasso and SCAD estimates under correlated data, including auto-regressive errors, and show that their asymptotic properties are still valid. As chromatograms exhibit a large signal-to-noise ratio and contain thousands of data points, heavy-tailed errors should not pose a problem in practice.
The model estimates possess attractive sampling properties. As in Zou (2006), we assume, without loss of generality, that there is a p0 < p such that |βk| > 0 for k ≤ p0 and βk = 0 for p0< k ≤ p. Thus the true active set of β,
 , is {1,2,…p0}. Let
, is {1,2,…p0}. Let
 n = {j : βˆj≠ 0} be the estimated active set of β, where βˆj is the estimate of βj from the adaptive lasso criterion.
n = {j : βˆj≠ 0} be the estimated active set of β, where βˆj is the estimate of βj from the adaptive lasso criterion.
Theorem 1
Let ψ = (θT,bT, βT)T and . Under the regularity conditions described in Fan and Li (2001); Zhang and Lu (2007); Bunea and Gupta (2010), the estimates obtained by minimizing (3) satisfy the following:
limn→∞P(
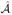 n =
n =
 ) = 1.
) = 1..
where
The proof of Theorem 1 follows very closely to the corresponding proofs in Fan and Li (2001); Zhang and Lu (2007); Bunea and Gupta (2010), so it is omitted. Theorem 1 shows that the adaptive lasso estimators obtained from (3) are variable selection consistent, root-n consistent, and asymptotically normal. Thus, the estimators possess the oracle property (Donoho and Johnstone, 1994). The root-n consistency is achieved due in part to the parametric rate of the estimates of the warping function parameter coefficients. The asymptotic normality of the estimates enables the construction of asymptotic confidence intervals for the estimated fingerprint and warping functions which reflect the combined variability in estimating β, b, and θ jointly. For example, by taking a Taylor expansion of f about the true value of ψ, we estimate the approximate asymptotic variance for the estimated fingerprint as σˆ2s(ψˆ)C−1s(ψˆ)T, where s(ψˆ) = ∂f (ψˆ)/∂ψ.
5 Application to Data Example
We applied (2) to the rhubarb chromatographic dataset described in Section 2. For computational efficiency, we subsampled the data such that the data vectors for the eight conditions were of respective lengths {2743, 2572, 2572, 2572, 2572, 2572, 2572, 2400}. The observed time vectors were mapped to [0, 1] by setting the maximum observed time, 16.0025 min., to 1.
Spline wavelets can be evaluated at any arbitrary time point, however the computation involves nested summations of many terms, so for computational speed, we computed the design matrix at arbitrary time points using the following procedure: a reference design matrix is evaluated on a grid of 217 time points in [0, 1]. Design points are computed via a table-look-up and for time values not in the reference design matrix, interpolation between adjacent points is used. We chose the finest wavelet scale to be 10, resulting in 2048 basis functions where the 2i, 2i + 1, …, (2i+1 − 1)th functions correspond to the wavelet basis functions at scale i. The finest level wavelet scale is chosen based on the data so that the resolution is fine enough to capture the narrowest spikes. We assume periodic boundary conditions for convenience.
To model the warping functions, we used monotonic cubic B-splines with 14 uniform knots. From our simulation presented in the subsequent section, uniform knots appear to work well for a moderate amount of warping. We assume a first-order auto-regressive correlation structure, thus θ is a scalar, denoted θ, and represents the correlation between points one unit of time apart.
The algorithm was written in MATLAB and run on an Intel Xeon CPU E7-4860. For each value of λ, the algorithm converged in less than five outer iterations, and finished, on average, in 10 minutes. The adaptive lasso parameter λ, found using BIC and a golden search algorithm, was 0.489. The estimated variance of the measurement error was 1.24 × 10−3 and the estimate for θ was 0.698.
The population averaged estimate of the standardized chromatographic fingerprint along with pointwise 95% confidence intervals are displayed in Figure 2. The time scale corresponds to the real time scale under condition 1. The population-averaged curve captures the shape of the individual chromatograms quite well, resulted from a good alignment across conditions. As the known compounds were analyzed under condition 1, spike locations between the reference chromatogram and the estimated fingerprint can be compared. The seven spikes that correspond to the known compounds are labeled in Figure 2.
Figure 2.
Population averaged fingerprint (solid) from the estimates along with 95% confidence bands (dashed). Identified compounds are denoted: (1) gallic acid, (2) catechin, (3) aloe-emodin, (4) rhein, (5) emodin, (6) chrysophanol, and (7) physcion.
To identify the seven known compounds in other conditions, we use the inverse estimated warping functions to warp the reference chromatogram in condition 1 to the time scale of each other condition. The estimated reference chromatograms are displayed in Figure 1 along with the raw data. By comparing with the estimated reference chromatograms, the seven known compounds are identified in each condition. These also show that we are able to estimate each warping function accurately.
The final estimate of the fingerprint shape contained 427 nonzero wavelet coefficients, while the remaining 1621 were shrunk to 0. This highlights the sparse nature of the fingerprint shape as a little more than 79% of the wavelet basis functions are irrelevant. The confidence intervals for the fingerprint can be used to determine whether a spike is artificial or real based on whether the corresponding confidence interval contains 0 or not. For example, the amplitude of the spike corresponding to catechin is small however the confidence interval at the peak of the spike is [0.014, 0.044], suggesting it is present in rhubarb, which coincides with previous research (Ye et al., 2007).
The groups of tightly-packed spikes located between 4 and 6 minutes in the fingerprint can either correspond to single compounds or multiple compounds which were not well separated in the HPLC column. If we wished to identify the compounds in this region of the fingerprint, parameters of the experiment would have to be adjusted so that these particular compounds are better separated and travel through the column at more distinct velocities. This would result in more spacing among spikes in this region of the chromatograms.
Figure 3 displays the estimated warping function for each of the eight conditions. Confidence intervals were computed for the warping functions however due to the low variance of the B-spline coefficients (Var(bi) ∼ O(10−4)), the bands are visually indistinguishable from the estimated warping functions. The low order of variance is due to the large effective sample size.
Figure 3.
The estimated warping functions (solid) along with the 45 degree line denoting no warping for each condition (dashed).
The estimated warping functions represent the distortion in retention time of conditions 2–8 in comparison to condition 1. The relative proportions of phosphoric acid and acetonitrile differs by only 1% at time 0 between conditions 1 and 2, and this difference caused little to no warping, as evidenced by the estimated warping function of condition 2. Conversely, a 3% change, as in condition 7, results in substantial warping after minute 4. The estimated warping functions for conditions 3 and 4 in comparison to those for conditions 5–8 suggest that flow rate does not have quite as large of an impact on retention time as the composition of the mobile phase.
6 Simulation
A vast number of mathematical functions have been proposed to simulate chromatographic data (Di Marco and Bombi, 2001). One such example is the Laplace distribution function. We simulated the true fingerprint shape by overlaying a fixed number of spikes, where each spike was generated via f(t) = a exp(− |t − c|/b)/(2b) where a controls the amplitude of the spike, c the location of the maximum of the spike, and b is a scale parameter, affecting the width and tails of the spike. We used twelve spikes with locations randomly chosen from [0.1, 0.9]. The amplitudes of the eight spikes were generated from a N(20, 25) distribution and the scale parameters were sampled with replacement from the set {0.45, 0.50, …, 0.75}.
To simulate time warping similar to those seen in the rhubarb data, the time warping functions were generated by the following logistic function, g(t) = [1 + exp(-14t + 7))]−1. The point-wise mean between g(t) and the 45 degree line, denoting no warping, can be iteratively calculated to generate warping functions with similar shape, but less and less degrees of warping. If we let z be the number of iterated averages between the function and the 45 degree line, then the warping function deviates less from the 45 degree line as z increases and converges to the 45 degree line as z → ∞. The inverse logistic function was used to generate one warping function with a mirrored shape to the rest. For notational brevity, a negative value of z corresponds to iterated averaging the 45 degree line with the inverse logistic function z times.
A set of four warping functions were generated using z = {∞, 4, 3, -3}, representing four different experimental conditions, and the warping functions were estimated using three, four, and five uniform knots. For each condition we generated 4 fingerprints sampled on 1000 equispaced time points in [0,1]. We added t-distributed noise, with 9 degrees of freedom, to each curve. The t-distribution was used as it has longer tails than the normal distribution. Figure 4 displays an example of a noisy fingerprint from each condition.
Figure 4.
Simulated warped fingerprints with 12 peaks and additive t-distributed noise. The fingerprint was generated using the Laplace distribution function and the warping functions were generated by logistic and inverse-logistic functions.
For comparison, we also fit a two-step model where the first step used dynamic time warping to align the curves and the second applied a wavelet thresholding to the aligned curves and averaged across the curves to obtain the population averaged fingerprint. The dynamic time warping step was accomplished using the ‘dtw’ package in R (Giorgino, 2009) and the wavelet thresholding was performed using the ‘wavethresh’ package in R (Nason, 2008). We simulated 100 datasets and performed the four methods on each set.
The proposed model was fit using 29 = 512 cubic Battle-Lemarié spline wavelet basis functions to model the shape and cubic B-splines to model the warping function. For each value of λ, our algorithm converged in less than five outer iterations and finished, on average, in 40 seconds. We also used 512 cubic Battle-Lemarié spline wavelets for the two-step method and the Bayesian approach of Abramovich et al. (1998) was used to select λ.
To assess the fits, boxplots of the mean squared error (MSE) between the true and estimated fingerprints were used, which are displayed in Figure 5. First, the proposed 4-and 5-knot models performed the best. The 3-knot model performed the worst of the four methods. This is due to the fact that three knots does not provide enough flexibility in capturing the shape of the warping functions. The boxplots suggest that by estimating the warping function using B-splines with at least four uniform knots, the degree of the warping does not appear to affect the MSE in any substantial way. The two-step approach does not perform as well as the proposed 4- and 5-knot models, though it outperforms the 3-knot model.
Figure 5.
Boxplots of the mean square error of the estimated fingerprints for the proposed procedure using 3-, 4-, and 5-knots and the two-step procedure using dynamic time warping and wavelet thresholding.
Figure 6 displays the mean of the estimated warping functions across all 100 simulations for the proposed 4-knot model overlaid on the true warping functions. The proposed model with four knots estimates the true warping functions well except at the ends of the tails, where there is slight deviation. Though we only consider uniform knots and there are numerous other possible parametric models for the warping function, our simulation shows that a large amount of flexibility is not required for quality performance of the modeling procedure.
Figure 6.
True (solid) and mean of 100 estimated warping functions (dashed) using 4 uniform knots.
7 Discussion
We have proposed a sparse semiparametric nonlinear model for the registration of chromatographic data and establishment of a standardized fingerprint. The common shape of the chromatograms is modeled via data-driven basis expansion. Curve registration is accomplished by parametric modeling of the time warping functions. As chromatograms are sparsely-structured curves, we impose the adaptive lasso penalty on the common shape basis function parameters to induce sparsity in the estimated fingerprint. A unified penalized weighted least squares criterion is minimized to simultaneously register chromatograms, perform model selection on the fingerprint shape, and estimate the model parameters. From the penalized criterion naturally arises a back-fitting algorithm which is equivalent to a blockwise coordinate descent algorithm. The unified criterion results in a unique solution and allows the study of asymptotic properties, as opposed to two-step methods which can guarantee neither. Our resulting estimators possess the oracle property.
We applied our model to a chromatographic dataset of the TCHM, rhubarb. Our model was effective in establishing a standardized fingerprint of rhubarb based on chromatograms arising from different experimental conditions. A sample of known compounds was analyzed under a single condition to identify compounds in the fingerprint. We demonstrated that known compounds need only be analyzed under a single condition, substantially decreasing both time and cost of chromatographic experiments.
We use BIC to select the tuning parameter λ however other tuning parameter selection techniques such as AIC, GCV, and Stein's unbiased risk exist, and in our simulations, performed similarly. We have focused the discussion on modeling the common shape using a linear combination of wavelet basis function and the warping functions using monotonic B-splines, however the proposed model can be easily extended to include multiple population average curves or in the situation that the observations relate to the population-average curves through some known nonlinear function.
Acknowledgments
Michael R. Wierzbicki's research is supported by a grant from the National Institutes of Health (No. 5T32MH065218). Professor Li-Bing Guo and Qing-tao Du's research is supported by a grant from National Science Foundation of China (No. 81073045). Professor Wensheng Guo's effort is partially supported by R01 GM104470. The last author is the corresponding author. The authors thank the editor, associate editor, and referees for their helpful comments which greatly improved the article.
References
- Abramovich F, Sapatinas T, Silverman BW. Wavelet thresholding via a Bayesian approach. Journal of the Royal Statistical Society: Series B. 1998;60(4):725–749. [Google Scholar]
- Brumback LC, Lindstrom MJ. Self modeling with flexible, random time transformations. Biometrics. 2004;60(2):461–70. doi: 10.1111/j.0006-341X.2004.00191.x. [DOI] [PubMed] [Google Scholar]
- Bunea F, Gupta S. Technical Report, Dept of Statistics. Florida State University; 2010. A study of the asymptotic properties of Lasso for correlated data. [Google Scholar]
- Daubechies I. Ten Lectures on Wavelets. Society for Industrial and Applied Mathematics; 1992. [Google Scholar]
- Di Marco VB, Bombi GG. Mathematical functions for the representation of chromatographic peaks. Journal of chromatography A. 2001;931(1-2):1–30. doi: 10.1016/s0021-9673(01)01136-0. [DOI] [PubMed] [Google Scholar]
- Donoho D, Johnstone I. Ideal spatial adaptation by wavelet shrinkage. Biometrika. 1994;81(3):425–455. [Google Scholar]
- Duke J. Handbook of Medicinal Herbs. 2nd CRC Press; 2002. [Google Scholar]
- Fan J, Fan Y, Barut E. Adaptive Robust Variable Selection. arXiv preprint arXiv. 2013;1205:4795. doi: 10.1214/13-AOS1191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan J, Li R. Variable Selection via Nonconcave Penalized Likelihood and its Oracle Properties. Journal of the American Statistical Association. 2001;96(456):1348–1360. [Google Scholar]
- Giorgino T. Computing and visualizing dynamic time warping alignments in R: The dtw package. Journal of Statistical Software. 2009;31(7) [Google Scholar]
- Jennrich R. Asymptotic properties of non-linear least squares estimators. The Annals of Mathematical Statistics. 1969;40(2):633–643. [Google Scholar]
- Kassidas A, MacGregor JF, Taylor Pa. Synchronization of batch trajectories using dynamic time warping. AIChE Journal. 1998;44(4):864–875. [Google Scholar]
- Lawton W, Sylvestre E, Maggio M. Self modeling nonlinear regression. Technometrics. 1972;14(3):513–532. [Google Scholar]
- Liang YZ, Xie P, Chan K. Quality control of herbal medicines. Journal of chromatography B. 2004;812(1-2):53–70. doi: 10.1016/j.jchromb.2004.08.041. [DOI] [PubMed] [Google Scholar]
- Meyer VR. Practical High-Performance Liquid Chromatography. 5th John Wiley & Sons, Inc; 2010. [Google Scholar]
- Morris JS, Brown PJ, Herrick RC, Baggerly Ka, Coombes KR. Bayesian analysis of mass spectrometry proteomic data using wavelet-based functional mixed models. Biometrics. 2008;64(2):479–89. doi: 10.1111/j.1541-0420.2007.00895.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nason G. Wavelet Methods in Statistics with R. Springer; 2008. [Google Scholar]
- Peigen X, Liyi H, Liwei W. Ethnopharmacologic study of Chinese rhubarb. Journal of Ethnopharmacology. 1984;10(3):275–93. doi: 10.1016/0378-8741(84)90016-3. [DOI] [PubMed] [Google Scholar]
- Ramsay JO, Li X. Curve registration. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 1998;60(2):351–363. [Google Scholar]
- Randolph TW, Yasui Y. Multiscale Processing of Mass Spectrometry Data. Biometrics. 2006;62(2):589–597. doi: 10.1111/j.1541-0420.2005.00504.x. [DOI] [PubMed] [Google Scholar]
- Sang H, Sun Y. Simultaneous sparse model selection and coefficient estimation for heavy-tailed autoregressive processes. arXiv Pre-print. 2012:1–23. arXiv:1112.2682v2. [Google Scholar]
- Schumaker L. Spline Functions: Basic Theory. 3rd Cambridge University Press; 2007. [Google Scholar]
- Snyder L, Kirkland J. Introduction to Modern Liquid Chromatography. 2nd John Wiley & Sons, Inc; 1979. [Google Scholar]
- Tseng P. Convergence of a block coordinate descent method for nondifferentiable minimization. Journal of optimization theory and applications. 2001;109(3):475–494. [Google Scholar]
- Unser M. Ten good reasons for using spline wavelets. Proceedings of SPIE. 1997;3169:422–431. [Google Scholar]
- van Nederkassel A, Daszykowski M, Eilers P, Heyden YV. A comparison of three algorithms for chromatograms alignment. Journal of Chromatography A. 2006;1118(2):199–210. doi: 10.1016/j.chroma.2006.03.114. [DOI] [PubMed] [Google Scholar]
- Wang H, Li R, Tsai CL. Tuning parameter selectors for the smoothly clipped absolute deviation method. Biometrika. 2007;94(3):553–568. doi: 10.1093/biomet/asm053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Ke C. Smoothing Spline Semiparametric Nonlinear Regression Models. Journal of Computational and Graphical Statistics. 2009:1–27. [Google Scholar]
- Ye M, Han J, Chen H, Zheng J, Guo D. Analysis of phenolic compounds in rhubarbs using liquid chromatography coupled with electrospray ionization mass spectrometry. Journal of the American Society for Mass Spectrometry. 2007;18(1):82–91. doi: 10.1016/j.jasms.2006.08.009. [DOI] [PubMed] [Google Scholar]
- Zhang HH, Lu W. Adaptive Lasso for Cox's proportional hazards model. Biometrika. 2007;94(3):691–703. [Google Scholar]
- Zou H. The Adaptive Lasso and Its Oracle Properties. Journal of the American Statistical Association. 2006;101(476):1418–1429. [Google Scholar]