Bayesian Function-on-Function Regression for Multilevel Functional Data

Summary

Medical and public health research increasingly involves the collection of complex and high dimensional data. In particular, functional data—where the unit of observation is a curve or set of curves that are finely sampled over a grid—is frequently obtained. Moreover, researchers often sample multiple curves per person resulting in repeated functional measures. A common question is how to analyze the relationship between two functional variables. We propose a general function-on-function regression model for repeatedly sampled functional data on a fine grid, presenting a simple model as well as a more extensive mixed model framework, and introducing various functional Bayesian inferential procedures that account for multiple testing. We examine these models via simulation and a data analysis with data from a study that used event-related potentials to examine how the brain processes various types of images.

1. Introduction

Medical and public health research increasingly involves the collection of complex and high dimensional data. In particular, functional data—where the unit of observation is a curve or set of curves that are finely sampled over a grid—is frequently obtained (Ramsay and Silverman, 2005). Moreover, researchers often sample multiple curves per subject which yields repeated functional measures. A common question is how to analyze the relationship between two functional variables. While the field of functional data analysis (FDA) has progressed considerably in recent years, gaps remain in the literature with regards to function-on-function regression where both the predictor and outcome are functional.

Regression in FDA can be classified into three broad sub-classes: scalar-on-function, function-on-scalar, and function-on-function. Morris (2015) contains a thorough review on existing work on functional regression. Scalar-on-function regression, on which a large literature exists, involves a scalar outcome and fucntional predictor, with functional regression coefficients. See for instance Ramsay and Dalzell (1991), Cardot, Ferraty, and Sarda (1999), Reiss and Ogden (2007), Malloy et al. (2010), Goldsmith et al. (2011), McLean et al. (2012), Gertheiss, Maity, and Staicu (2013), and references therein. Function-on-scalar regression, also heavily investigated in the literature, involves regressing a functional predictor on to a set of scalar covariates, each of which has a functional regression coefficient. See for instance Brumback and Rice (1998), Morris and Carroll (2006), Reiss, Huang, and Mennes (2010), Staicu et al. (2011), Chen and Müller (2012), Goldsmith, Greven, and Crainiceanu (2013), and references therein.

In contrast, the literature addressing function-on-function regression, with functional outcome, functional predictor, and a coefficient surface, is rather sparse. Ramsay and Silverman (2005) do devote chapters to concurrent function-on-function regression and fully functional linear models for functional responses which assume iid residual errors, have no random effect functions, and no modeling of within-function correlation in the errors. Additionally, they focus on point estimation, not inference, and the authors further emphasize that Bayesian methods that model the variability in basis function selection would be welcome. Beyond that, much of the literature is dedicated to the historical functional linear model (HFLM), as described by Malfait and Ramsay (2003) and further examined by Harezlak et al. (2007) and Kim, Şentürk, and Li (2011). The primary assumption in an HFLM is that the association between curves is uni-directional. Function-on-function regression allowing for bi-directional associations—that is, with unconstrained regression coefficient surfaces—is explored by Yao, Müller, and Wang (2005), Müller and Yao (2008), and Wang (2014). Also, there are some recent technical reports on the topic from one research group, Ivanescu et al. (2012), Scheipl and Greven (2012), Scheipl, Staicu, and Greven (2014), that discuss a penalized spline approach, identifiability issues, and function-on-function regression in Functional Additive Mixed Models, respectively. Inferential procedures, if addressed, rely on 95% point-wise confidence intervals (PWCI) to determine significance without adjusting for multiple comparisons. These use penalized splines, which may not be the best basis choice in various settings, including the spiky functions in this paper. Much existing work also assumes iid residual curve-to-curve deviations, which is not realistic for most functional data settings.

To illustrate the function-on-function regression problem, we examine data from a smoking cessation trial conducted at the University of Texas M. D. Anderson Cancer Center (Cinciripini et al., 2013). Event Related Potentials (ERPs) were obtained at baseline during the presentation of a series of images depicting neutral, positive, negative, and cigarette-related contents. ERPs were collected using a 129 channel Geodesic Sensor Net. Finely sampled curves were produced over the course of 900 ms (100 ms prior to picture presentation and 800 ms after). Electrical potentials every 4ms were collected from 129 electrodes distributed on the surface of the scalp resulting in 225 measurements for each electrode. While many analyses are of interest for these data, in this paper we focus on characterizing the time-varying relationship between ERP outputs from specific electrode pairs.

In this paper, we propose a general Bayesian function-on-function regression modeling framework that can accommodate this type of multilevel functional data which we fit using a Monte-Carlo Markov Chain (MCMC) procedure. The model is flexible enough to incorporate a variety of basis expansions including such common approaches as principal components, splines, and wavelet-based functional representations. Our approach not only allows for correlation between functions through random effect functions, but also allows heteroscedasticity and within-function correlation in the residual error functions, unlike existing methods assuming iid errors. While the approach can be applied generally for any number of functional predictors and arbitrary interactions with other discrete and continuous predictors, we present specific model formulations for both a single functional predictor of interest as well an interaction of a discrete factor with a functional predictor resulting in separate function-on-function regressions for each factor.

We propose three approaches for inference that account for multiplicity. First we extend the Bayesian False Discovery Rate (BFDR) procedure for functional regression implemented by Morris et al. (2008) to the function-on-function setting. Second, from joint credible bands as in Ruppert, Wand, and Carroll (2003), we generate two novel summaries: (1) Simultaneous Band Scores (SimBaS), a functional measure that summarizes for each position in the regression surface the smallest α for which the 100(1 − α)% joint credible bands exclude zero, and (2) Global Bayesian P-Values (GBPV), which can be interpreted as a type of Bayesian p-value corresponding to a global functional null hypothesis of no relationship. These summaries are of general interest and can be used in other functional regression settings. To our knowledge global inference procedures within function-on-function regression have not previously been considered in the literature.

Section 2 develops a simple version of our proposed function-on-function mixed model, presents a more general model, and describes our basis function modeling strategy. Section 3 details the BFDR, SimBaS, and GBPV inference procedures. In Section 4 we present the results of a simulation assessing model fit and the BFDR, SimBaS, and GBPV procedures. Section 5 presents the results obtained by applying the proposed methods to the ERP data, and Section 6 contains further discussion.

2. Function-on-Function Regression Model for Multi-Level Functional Data

Here we introduce the function-on-function model we will use to regress one function y(t), t ∈ 𝒯 on another x(υ), υ ∈ ν. First we consider a simple case with a single functional predictor and repeated measures of {y(t), x(υ)} pairs for each subject, and then in Section 2.3 we describe more complex models that can be handled by our approach.

Individual subjects are denoted as i = 1, …, n. Let c = 1, …, C_i index repeated pairs of curves observed on subject i. Then for subject i, curve set c, we observe x_ic(υ) and y_ic(t), {y_ic(t), x_ic(υ) : t ∈ 𝒯, υ ∈ ν},

$$y_{ic}(t)=\alpha (t)+{\int }_{\upsilon \in \nu }{x}_{ic}(\upsilon )\beta (\upsilon ,t)d\upsilon +U_i(t)+E_{ic}(t).$$ (1)

We assume observation-specific and subject-specific Gaussian process errors E_ic(t) ~ 𝒢𝒫 (0, Σ_E) and U_i(t) ~ 𝒢𝒫 (0, Σ_U). The integration over the entire support of υ allows an unconstrained exposure-response relationship, i.e. we do not assume the timing of an effect of x on y occurs in one direction or the other. That relationship is characterized by the surface β(υ, t).

In this paper, our focus is on functional data sampled on a common fine grid. Here, we consider a discretized version of Model (1). Let y_ic(·) be finely sampled on a grid t = [t₁ ⋯ t_T] of length T. Similarly, x_ic(·) is observed on a grid v = [υ₁ ⋯ υ_V] of length V. We can then define the row vectors y_ic = [y_ic(t₁) ⋯ y_ic(t_T)] and x_ic = [x_ic(υ₁) ⋯ x_ic(υ_V)] and express Model 1 in the discrete form

$${\mathbf{y}}_{ic}={\mathbf{x}}_{ic}\mathit{\beta }{\mathrm{\Delta }}_{{\upsilon }_j}+{\mathbf{u}}_i+{\mathbf{e}}_{ic},$$ (2)

where y_ic, u_i, and e_ic are 1 × T, x_ic is 1 × V, and β is the V × T matrix of coefficients and Δ_υj = υ_j − υ_j−1. If we sample on an equally spaced grid, then Δ_υj is a constant equal to the distance between measurement occurrences. Also note that e_ic ~ 𝒩(0, Σ_E) and u_i ~ 𝒩(0, Σ_U). In practice, we center and scale both y_ic(t) and x_ic(υ) and thus, without loss of generality, α(t) in Model (1) is zero and not needed in Model (2). If one of the two functions is not centered, than α(t) can be incorporated into β with a corresponding column of ones added to the design matrix.

Now let N be the total number of observed response curves. Stacking the row vectors by subject, Y and X represent the N × T and N × V matrices of observed curves. Further, Z is the N × n random effects design matrix. Our discretized model for all subjects is then

$$\mathbf{Y}=\mathbf{X}\mathit{\beta }+\mathbf{Z}\mathbf{U}+\mathbf{E},$$ (3)

where β is as defined in Model (2), U is the n × T matrix of subject specific random effect functions on the grid, and E is the N × T matrix of model errors, interpretable as residual curve-to-curve deviations. Assuming an equally spaced grid, we omit Δ_υj from Model (3).

As is typical in functional regression (Morris, 2015), we will represent y(t) and x(υ) using basis representations prior to model fitting. The basis transform modeling approach we use allows us fast calculations while inducing regularization in the coefficient surface β(υ, t) through basis-space prior distributions, and can be used with various choices of lossless or near-lossless basis choices, including wavelets, splines, PCs, and Fourier series. We will begin by describing the modeling approach in terms of general basis functions, and then we will present the rest of the modeling details using specific basis functions chosen for our simulation and data analysis, with the Web Appendix A mentioning some adaptations for other bases.

2.1 General Basis Transform Modeling Approach

Here we describe our general basis function transform approach for fitting the function-on-function regression models, which involves projecting both the functional responses and predictors into a chosen basis space, fitting the model in the basis space, and then transforming the results back to the original function space for interpretation and inference.

Let $y_{ic}(t)={\sum }_{j=1}^{T^{*}}{y}_{icj}^{*}{\xi }_j(t)+r_{ic}^{\xi }(t)$ and $x_{ic}(\upsilon )={\sum }_{j=1}^{V^{*}}{x}_{icj}^{*}{\varphi }_j(\upsilon )+r_{ic}^{\varphi }(\upsilon )$ be some chosen truncated basis expansions for the functional responses and predictors, respectively, and suppose this expansion results in a lossless (

$$r_{ic}^{\xi }(t)=0$$

and

$$r_{ic}^{\varphi }(\upsilon )=0$$

∀ i, c, and observed t), or virtually lossless (

$$r_{ic}^{\xi }(t)<\epsilon$$

and

$$r_{ic}^{\varphi }(\upsilon )<\epsilon$$

for some small ε) transform so the r(·) can effectively be ignored. Potential choices with these properties include wavelets, Fourier bases, splines (given sufficient knots), PCs, or independent components. Let Ξ be a matrix of size T* × T containing the basis functions on discrete grid t with element (j, t) given by ξ_j(t), and likewise let Φ be a V* × V matrix containing the basis functions for x(υ) on the grid v. Considering the discretely sampled functions in matrix form, we can write the basis expansion as Y = Y*Ξ and X = X*Φ, with Y* and X* being N × T* and N × V* matrices, respectively, containing the basis coefficients for the observed functions. Here we assume that Φ and Ξ are of full row rank, possibly but not necessarily orthogonal, so rank(Φ) = V*, rank(Ξ) = T* and ΦΦ′ and ΞΞ′ are invertible matrices of size V* × V* and T* × T*.

Replacing each functional quantity in Model (3) with its basis expansion, we have

$${\mathbf{Y}}^{*}\mathbf{\Xi }={\mathbf{X}}^{*}\mathbf{\Phi }\mathbf{\Phi }\prime {\mathit{\beta }}^{*}\mathbf{\Xi }+\mathbf{Z}{\mathbf{U}}^{*}\mathbf{\Xi }+{\mathbf{E}}^{*}\mathbf{\Xi },$$ (4)

where β* is V* × T*, U* is n × T*, and E* is N × T*, representing quantities of Model (3) in the transformed basis space. When Φ is orthogonal so that ΦΦ′ = I_V*, if we multiply each side of (4) by Ξ⁻ = Ξ′(ΞΞ′)⁻¹, then we arrive at the basis space model

$${\mathbf{Y}}^{*}={\mathbf{X}}^{*}{\mathit{\beta }}^{*}+\mathbf{Z}{\mathbf{U}}^{*}+{\mathbf{E}}^{*}.$$ (5)

When Φ is not orthogonal, we instead replace β* in Model (5) with β^† = ΦΦ′β*. Thus, we can fit this basis space model after first transforming the functional responses and predictors to their respective basis spaces, Y* = YΞ⁻ and X* = XΦ⁻, with Φ⁻ = Φ′(ΦΦ′)⁻¹, and then after fitting the model, transform back to the original function space to obtain estimates and inference for β = Φ′β*Ξ when Φ is orthogonal, β = Φ⁻β^†Ξ otherwise. Note that for some choices of basis functions, fast transform algorithms can be used in lieu of matrix multiplication to compute the basis functions or transform back to the original space, e.g., discrete wavelet transform (DWT) for wavelets, discrete Fourier transform (DFT) for Fourier bases, and fast algorithms for computing independent components (Hyvarinen et al., 2001).

We take a Bayesian approach to fit Model (5), using an Markov Chain Monte Carlo (MCMC) procedure to sample from the posterior distributions using appropriate prior distributions for each model parameter. Different choices of basis functions corresponds to different choices of Ξ and Φ. For example, for wavelets Ξ and Φ are inverse discrete wavelet transform (IDWT) matrices, for principal components they are the eigenvectors, possibly rescaled by the eigenvalues, for Fourier series they are the Inverse Discrete Fourier Transform (IDFT) matrices, and for splines they can be constructed based on B-splines or orthogonalized B-spline design matrices. Note that the same basis transform does not need to be used for both y(t) and x(υ). In this paper, we use wavelet bases to represent the functional form of y(t), and for x(υ), we use a composite strategy involving wavelets followed by principal components or wavelet Principal Components (wPC), which is similar to strategies used by Johnstone and Lu (2009) and Røislien and Winje (2012).

2.2 Model Formulation

Here, we present our modeling details using wavelets for y(t) and wPC for x(υ). First, we transform the functions to the wavelet space by applying the O(T) DWT to each row of Y and X, which can be represented as

$${\mathbf{y}}_{ic}\stackrel{\mathrm{D}\mathrm{W}\mathrm{T}}{\to }{\mathbf{y}}_{ic}^{*}=\left\{y_{ic,jk}^{*}\right\}$$

and

$${\mathbf{x}}_{ic}\stackrel{\mathrm{D}\mathrm{W}\mathrm{T}}{\to }{\mathbf{x}}_{ic}^{*}=\left\{x_{ic,s\ell }^{*}\right\}$$

. Wavelets are multi-resolution bases that are double-indexed by scale and location. The scales are j = 1, …, J^y and s = 1, …, S^x and locations

$$k=1,\dots ,K_j^y$$

and

$$\ell =1,\dots ,L_s^x$$

for Y and X, respectively. The dimension of

$${\mathbf{y}}_{ic}^{*}$$

is 1 × T* where

$$T^{*}={\sum }_{j=1}^{J^y}{k}_j^y$$

. Similarly,

$${\mathbf{x}}_{ic}^{*}$$

has dimensions 1 × V* where

$$V^{*}={\sum }_{s=1}^{S^x}{\ell }_s^x$$

. After performing a DWT on each row of X, we then compute the wavelet-space PC scores by applying a singular value decomposition to obtain the matrix of right singular vectors. All coefficients can be kept for a lossless transform or a large number kept for a near-lossless transform.

Both transformations can be represented in matrix form. Thus performing the DWT on Y is equivalent to taking Ξ to be the matrix of wavelet basis functions evaluated on the T grid. And performing wPC on X is equivalent to letting Φ be the composite transform consisting of the product of the matrix of wavelet basis functions and the reduced matrix of right singular values. Web Appendix A has further discussion on the details of wPC.

Thus, after transforming the data, recall our basis space model (5) is given by Y* = X*β* + ZU* + E*. Consistent with previous work (Morris and Carroll (2006), Morris et al. (2008), Zhu, Brown, and Morris (2011), among others), we assume independence in the wavelet space. That is, for the subject specific version of Model (5), ${\mathbf{y}}_{ic}^{*}={\mathbf{x}}_{ic}^{*}{\mathit{\beta }}^{*}+{\mathbf{u}}_i^{*}+{\mathbf{e}}_{ic}^{*}$, we assume ${\mathbf{e}}_{ic}^{*}~𝒩(0,{\mathbf{\Sigma }}_e^{*})$ where ${\mathbf{\Sigma }}_e^{*}$ is a diagonal matrix with elements varying by j, k, ${\mathbf{\Sigma }}_e^{*}=\text{diag}\left\{{\sigma }_{e(j,k)}^2\right\}$, and equivalently ${\mathbf{u}}_i^{*}~𝒩(0,{\mathbf{\Sigma }}_u^{*})$ where ${\mathbf{\Sigma }}_u^{*}=\text{diag}\left\{{\sigma }_{u(j,k)}^2\right\}$. The induced within-function covariances in the data space are given by ${\mathbf{\Sigma }}_e=\mathbf{\Xi }\prime {\mathbf{\Sigma }}_e^{*}\mathbf{\Xi }$ and ${\mathbf{\Sigma }}_u=\mathbf{\Xi }\prime {\mathbf{\Sigma }}_u^{*}\mathbf{\Xi }$, which with wavelets accommodates a broad class of covariances allowing heteroscedasticity and differing degrees of autocorrelation, and thus different degrees of borrowing of strength, in different regions of the function (Morris and Carroll, 2006).

The basis space independence assumption allows us to split Model (5) into a series of T* separate models for each basis coefficient in the y-space, double-indexed by (j, k), giving ${\mathbf{y}}_{(j,k)}^{*}={\mathbf{X}}^{*}{\beta }_{(j,k)}^{*}+\mathbf{Z}{\mathbf{u}}_{(j,k)}^{*}+{\mathbf{e}}_{(j,k)}^{*}$, where ${\mathbf{y}}_{(j,k)}^{*}$ and ${\mathbf{e}}_{(j,k)}^{*}$ are N × 1, ${\beta }_{(j,k)}^{*}$ is V* × 1, and ${\mathbf{u}}_{(j,k)}^{*}$ is n × 1. X* and Z are as previously defined. This separability allows computational scalability to extremely large T, as calculations are linear in T*, sparse near-lossless basis functions frequently yield T* ≪ T, and when cluster computing resources are available, allows parallel computing across (j, k). For prior specification, we assume vague proper priors on the variance components and a spike-and-slab prior similar to that found in Morris and Carroll (2006), Malloy et al. (2010), and others. Note that the spike-and-slab prior for selecting among PCs has been used in other PC regression contexts (Joliffe, 1982; Aston et al., 2010; Yang et al., 2013). Posterior samples are generated for β* and projected back into the data-space using β = Φ⁻β*Ξ. These posterior samples are used to perform Bayesian inference on β, as detailed in Section 3. The MCMC algorithm used for estimation can be found in the Web Appendix. Code for running the above model is also available online (http://odin.mdacc.tmc.edu/~jmorris/FonF.zip). DWTs and wPC were performed using the MATLAB functions wavedec and princomp which are available in the wavelet and statistics toolboxes (MATLAB, 2013a).

2.3 More Complex Function-on-Function Mixed Models

Model (1) is a special case of a general function-on-function mixed model that incorporates arbitrary scalar covariates {𝒳_a, a = 1, …, p_s}, functional covariates {X_a(υ_a), a = 1, …, p_f}, scalar-by-function interactions, and multiple levels of random effect covariates { $Z_l^h$, h = 1, …, H; l = 1, …, L_h}. In principle, our approach can also accommodate function-by-function interactions, but we omit that here. The general model can be written

$$y_i(t)=\sum _{a=1}^{p_s}{𝒳}_{ia}{B}_a(t)+\sum _{a=1}^{p_f}{\int }_{{\upsilon }_a\in {\nu }_a}{X}_{ia}({\upsilon }_a){\mathit{\beta }}_a({\upsilon }_a,t)d{\upsilon }_a+\sum _{a_s=1}^{p_{s_I}}\sum _{a_f=1}^{p_{f_I}}{\int }_{{\upsilon }_{a_f}\in {\nu }_{a_f}}{𝒳}_{i{a}_s}{X}_{i{a}_f}({\upsilon }_{a_f}){\mathit{\beta }}_{a_s{a}_f}({\upsilon }_{a_f},t)d{\upsilon }_{a_f}+\sum _{h=1}^H\sum _{l=1}^{L_h}{Z}_{il}^h{U}_l^h(t)+E_i(t),$$ (6)

where B_a(t) are functional coefficients for scalar predictors, β_a(υ_a, t) are function-on-function coefficient surfaces for functional predictors, β_asaf (υ_af, t) coefficient surfaces for the interaction of scalar covariate a_s and functional predictor a_f, and the random effects $U_l^h(t)~𝒢𝒫(0,{\mathbf{\Sigma }}_U^h)$. The multiple levels of random effects allow the model to handle various types of multi-level models needed to accommodate many complex designs commonly encountered in practice. Our code is capable of fitting this general model.

For the ERP data considered in Section 5, we include a discrete factor image type both as a main effect as well as effect modifier for the functional predictor, which allows different functional intercepts and function-on-function regression surfaces for each image type. See Model (9) in Section 5 for specification. Inference can then be performed on any number of desired statistics resulting from the model.

2.4 Model Assessment

To assess our models we examine a functional R² as well as the proportion of total variance contributed by the random effects. For the functional R² measures, we propose the use of an average functional R² which Harezlak et al. (2007) implemented. Given the predicted values ŷ_ic(t), we formulate R² as

$$R_{\mathit{\text{ave}}}^2=\frac{1}{T}{\int }_0^T{R}^2(t)dt\text{where}{R}^2(t)=1-\frac{{\sum }_{c=0}^C{\sum }_{i=1}^n{(y_{ic}(t)-{ŷ}_{ic}(t))}^2}{{\sum }_{c=0}^C{\sum }_{i=1}^n{(y_{ic}(t))}^2}.$$

Since we sample on a grid, the integral above can be approximated as $R_{\mathit{\text{ave}}}^2\approx \frac{1}{T}{\sum }_0^T{R}^2(t)\mathrm{\Delta }(t)$ where Δ(t) is the distance in time between measurements. For assessing the contribution of the random effects we use the ratio tr(Σ_U)/tr(Σ_U + Σ_E) where tr denotes the trace.

3. Posterior Functional Inference

Previous work in the function-on-function setting has focused solely on estimation or inference based on the construction of point-wise confidence intervals over the surface considering intervals that don’t contain zero as significant (Scheipl, Staicu, and Greven, 2014). However, such an approach does not account for the inherent multiple testing problem from testing multiple locations within the coefficient surface. When applied to Bayesian credible intervals, we refer to this as the point-wise credible interval (PWCI) procedure. This unadjusted approach may lead to coefficients spuriously designated as significant. Thus we propose two posterior functional inference procedures aimed at identifying significant regions of a surface while controlling overall α, either using false discovery rate or experiment wise error rate, plus a Bayesian global test for testing whether the regression surface is identically zero.

First, we extend to the function-on-function setting previous Bayesian False Discovery Rate (BFDR) approaches that were originally proposed by Müller, Parmigiani, and Rice (2006), and then extended to functional regression by Morris et al. (2008) and Malloy et al. (2010). The BFDR is reliant upon the selection of δ-fold intensity change. Ideally this value is biologically motivated, however such a value may not necessarily exist or may be difficult to determine. Therefore, we also consider joint credible bands similar to those considered by Ruppert, Wand, and Carroll (2003) and invert them to construct what we call Simultaneous Band Scores (SimBaS) that are based on experiment wise error rate.

Suppose we have M MCMC samples. Let β^(m)(υ, t) be one posterior sample of the estimated surface for sample m, m = 1, …, M. Then for a specific υ, υ = 1, …, V, and t, t = 1, …, T, with δ a pre-determined intensity change of practical interest, consider

$$P_{BFDR}(\upsilon ,t)=\mathit{\text{Pr}}\{|\beta (\upsilon ,t)|\le \delta |y\}\approx \frac{1}{M}\sum _{m=1}^{M}1\{|{\beta }^{(m)}(\upsilon ,t)|\le \delta \}.$$

Note that standardized predictors should be used so δ has a consistent scale across β(υ, t). To correct for the discrete nature of the MCMC we replace any P_BFDR(υ, t) = 0 with the quantity (2M)⁻¹. As discussed by Morris et al. (2008), this quantity can be interpreted as a local FDR for a true discovery defined by an effect size of at least δ in magnitude.

For a pre-specified global FDR-bound α, we select the set of points (locations) satisfying ψ = {(υ, t) : P_BFDR(υ, t) ≤ ν_α}. To obtain ν_α, we sort {P_BFDR(υ, t), υ = 1, …, V, t = 1, …, T} in ascending order across all sets of locations. This gives us the set {P_(r), r = 1, …, R}, where R = VT or the ordered set of probabilities calculated above. We then define $\lambda =\text{max}[r^{*}:\frac{1}{r^{*}}{\sum }_{r=1}^{r^{*}}{P}_{(r)}\le \alpha ]$. The cutoff for selecting significant coefficients is then ν_α = P_(λ).

Alternatively, in the spirit of Ruppert, Wand, and Carroll (2003), consider constructing joint credible bands. A 100(1 − α)% credible band of β(υ, t) must satisfy

$$\mathit{\text{Pr}}\{L(\upsilon ,t)\le \beta (\upsilon ,t)\le U(\upsilon ,t)\forall \upsilon \in \nu ,t\in 𝒯\}\ge 1-\alpha ,$$ (7)

where L(υ, t) and U(υ, t) are the lower and upper bounds respectively. It follows from Ruppert, Wand, and Carroll (2003) that an interval satisfying (7) is

$$I_{\alpha }(\upsilon ,t)=\hat{\beta }(\upsilon ,t)\pm q_{(1-\alpha )}\left[\widehat{\mathrm{S}\mathrm{t}.\text{Dev}}\right\{\hat{\beta }(\upsilon ,t)\left\}\right],$$

where β̂ (υ, t) and $\widehat{\mathrm{S}\mathrm{t}.\text{Dev}}\{\hat{\beta }(\upsilon ,t)\}$ are the mean and standard deviation for a given (υ, t) taken over all M MCMC samples, adjusted for autocorrelation as described in Web Appendix G. The variable q_(1−α) is the (1 − α) quantile taken over M of the quantity

$$Z^{(m)}=\underset{\upsilon \in \nu ,t\in 𝒯}{\text{max}}\left|\frac{{\beta }^{(m)}(\upsilon ,t)-\hat{\beta }(\upsilon ,t)}{\widehat{\mathrm{S}\mathrm{t}.\text{Dev}}\{\hat{\beta }(\upsilon ,t)\}}\right|.$$

These joint bands control for multiple testing in a strong experiment-wise fashion while also not requiring a pre-specified δ-fold intensity change as in the BFDR.

Now consider inverting these joint bands, constructing I_α(υ, t) for multiple levels of α and determining for each (υ, t) the minimum α at which each interval excludes zero, denoted P_SimBaS(υ, t) = min {α : 0 ∉ I_α(υ, t)}, which can be directly computed by

$$P_{\mathit{\text{Sim}}BaS}(\upsilon ,t)=\frac{1}{M}\sum _{m=1}^M\left\{\right|\frac{\hat{\beta }(\upsilon ,t)}{\widehat{\mathrm{S}\mathrm{t}.\text{Dev}}\{\hat{\beta }(\upsilon ,t)\}}|\le Z^{(m)}\}.$$ (8)

We call these probabilities Simultaneous Band Scores or SimBaS. Similar to the BFDR and PWCI, we can select a specific α and identify (υ, t) for which P_SimBaS(υ, t) < α as significant, which is equivalent to checking if the joint credible intervals cover zero at a specific α-level. We can also compute global Bayesian p-values (GBPV), P_GBPV = min_υ,t{P_SimBaS(υ, t)}, a measure for testing the global null hypothesis that β (υ, t) = 0 ∀ υ ∈ ν, t ∈ 𝒯, when desired.

The BFDR, SimBaS, and GBPV can be computed for individual surfaces β(υ, t) or any transformation or contrast defined across surfaces. For example, in the two surface setting, interest focuses on applying the procedure to both β_g(υ, t), g = 0, 1, as well as the difference surface, D(υ, t) = β₁(υ, t) − β₀(υ, t). This allows us to detect differences between surfaces corresponding to two different experimental conditions or groups and determine where those differences occur.

4. Simulation

We generate data in two phases. First, we draw x_ic, u_i, and e_ic. Second, we generate y_ic using y_ic = x_icβ + u_i + e_ic, where β is one of four true surfaces of association. To generate predictor curves, random effects, and model errors, we use Gaussian Processes with auto-regressive 1 [AR(1)] covariance structures. Estimates for parameters of the covariance of x_ic come from estimating autoregressive parameters from the output of one electrode from our ERP data. We assign pairs of curves to each subject to induce repeated measures and consider three different sample sizes: n = 25, 50, and 100. Repeated measures brings the total number of observations up to N = 50, 100, and 200 respectively. We select parameters for the covariances of u_i and e_ic as ${\sigma }_u^2=0.05$ and ρ_u = 0.75 and ${\sigma }_e^2=0.1$ and ρ_e = 0.5 respectively. Additionally, the maximum value of any location on the true surface does not exceed 0.13. Prior to constructing y_ic, we center and scale x_ic across i, c across all curves so that the variance at each time point is 1.

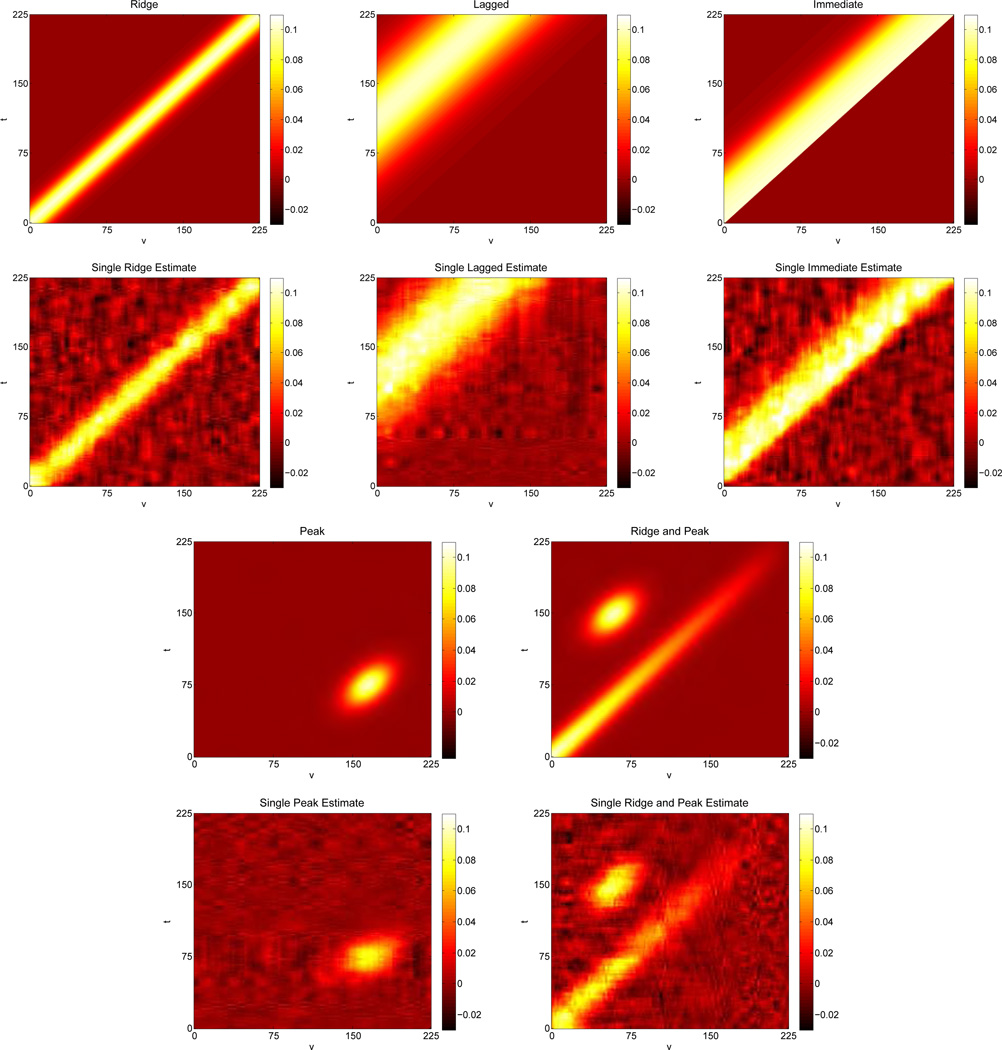
We select true surfaces to mimic biologically plausible time varying associations. The first and third rows of Figure 1 contains the heat maps of each surface. Each surface represents a different type of association, equations for which can be found in Web Appendix C. The ridge surface represents a relationship where the strongest association between x(υ) and y(t) occurs along the line υ = t. In other words, changes in y(t) are associated with concurrent changes in x(υ). The lagged surface suggests a relationship where changes in x(υ) at a given time are associated with later changes in y(t), but the strongest effect is delayed. The relationship between x(υ) and y(t) in the immediate surface is similar to that in the lagged, however the strongest effect occurs immediately before dying off. The peak scenario demonstrates a setting where changes in y(t) at a given time are associated with later changes in x(υ) and the association is characterized by a single peak. Finally, we consider one slightly more complicated scenario which involves a ridge effect that attenuates as both t and υ increase along with a single peak above the attenuated ridge.

Figure 1.

Heat maps of the true surfaces for simulation study are above heat maps of a single estimated surfaces for each simulated scenario based on a sample size of n = 25 with two measure per subject, C_i = 2 ∀ i, for a total of N = 50 observations. Each surface has near average rMSE and is based on a total of 2000 MCMC chains with the first 1000 discarded.

For each surface, we generate 200 simulated data sets and draw 2000 posterior samples, discarding 1000 of them. We use Daubechies wavelets with four vanishing moments and three levels of decomposition. In preliminary simulations, zero-padding reduced edge effects better than symmetric-half point padding. Thus we implement zero-padding for all models. Motivated by the ERP data structure, we set the total number of time points in both time domains to be 225. For the wPC decomposition, we keep components accounting for 99.0% of the variability in X*. A single posterior estimate with near average rMSE for each surface can be found in Figure 1. Results from all three sample sizes were similar, thus we only present simulations for n = 25, N = 50 here. Results for n = 100, N = 200 can be found in the Web Appendix. For each dataset we also calculate root Mean Square Error (rMSE).

We also examine the performance of the BFDR, SimBaS, and GBPV procedures in simulation using a global α of 0.05. For the BFDR, we use a δ-intensity change of 0.05 which is roughly half the max signal from each surface. For comparison, we also generate unadjusted PWCIs. To evaluate the three procedures, we calculate false discovery rate, sensitivity, experiment-wise error rate (EWER), and type I error. Define false discovery rate, FDR_ε, as the number of selected locations (υ, t) with true value ≤ ε divided by the total number of selected locations. Next define the sensitivity, SEN_ϒ, as the number of selected locations (υ, t) with true magnitude > ϒ divided by the total number of locations with true magnitude > ϒ. EWER_ε is calculated as the proportion of simulated datasets with at least one falsely discovered location, i.e. a selected location with true value ≤ ε. Type I error is calculated using a null simulation with true surface β(υ, t) = 0 ∀ υ ∈ ν, t ∈ 𝒯 and determining the proportion of simulated datasets with at least one location identified as significant.

Figure 1 allows for direct comparison of each estimated surface to the truth. For all surfaces, we see the model performed quite well, effectively reconstructing all the true surfaces. Estimation improves as sample size increases. Not surprisingly, rMSE decreases as sample size increases though even the smallest sample size produced small rMSEs. Heat maps containing the averaged set of identified coefficients for the BFDR and the average SimBa scores across datasets can be found in the Web Appendix. Both procedures correctly identified regions of elevated association in all four surfaces.

Table 1 displays both the average false discovery rate, FDR_ε, and the average sensitivity, SEN_ϒ, for each scenario using ε = 0.01, 0.05 and ϒ = 0.05, 0.075. For each procedure, we use α = 0.05 to select the set of selected locations. We can see that the BFDR and SimBaS procedures performs similarly well by both measures, though BFDR does better for a higher ε and ϒ. While the PWCI has very good sensitivity, it comes at the cost of an inated false discovery rate. EWER_ε is calculated using ε = 0.01. Additionally, SimBaS controls experiment-wise type I error quite well at 0.05. While BFDR has a slightly low type I error of 0.04, PWCI has a very high value of 0.645. To assess P_GBPV we determine the percent of datasets under each scenario with P_GBPV < 0.05 which was all datasets in each scenario.

Table 1.

FDR, sensitivity, experiment-wise error rate (EWER), and type I error values by inference procedure. The BFDR use a δ intensity change of 0.05. To determine assessment values for SimBaS, a cutoff of α = 0.05 was used. Likewise, the PWCI used 95% point-wise credible intervals to determine significant locations.

Measure	Surface	BFDR	SimBaS	PWCI
FDR0.01	Lagged	0.06%	0.08%	5.80%
	Peak	0.48%	0.75%	22.9%
	Ridge	0.12%	0.19%	20.5%
	Immediate	2.25%	2.80%	20.9%
	Ridge + Peak	0.20%	0.35%	17.4%
FDR0.05	Lagged	5.74%	13.9%	44.7%
	Peak	4.01%	20.4%	73.5%
	Ridge	9.75%	15.6%	53.3%
	Immediate	5.74%	7.58%	38.1%
	Ridge + Peak	5.45%	22.7%	73.4%
SEN0.05	Lagged	98.1%	96.2%	99.9%
	Peak	64.9%	73.4%	99.9%
	Ridge	96.8%	93.4%	99.9%
	Immediate	97.9%	93.8%	99.9%
	Ridge + Peak	63.6%	76.3%	99.9%
SEN0.075	Lagged	99.9%	99.3%	100%
	Peak	94.4%	88.2%	99.9%
	Ridge	99.8%	97.6%	99.9%
	Immediate	99.9%	96.2%	99.9%
	Ridge + Peak	95.7%	93.3%	99.9%
EWER0.01	Lagged	7.00%	16.5%	100%
	Peak	4.50%	10.5%	100%
	Ridge	9.50%	49.0%	100%
	Immediate	100%	100%	100%
	Ridge + Peak	6.00%	29.0%	100%
Type I Error	Null	4.00%	5.00%	64.5%

These simulation results suggest our method performs well both in estimation and in inference. Even at the smallest sample size we considered, the model effectively reproduces the true surface. Both the BFDR and SimBaS capture the regions of strongest association without spuriously selecting too many non-significant coefficients. They also control well for type I error. Further, BFDR and SimBaS outperform the PWCI while maintaining reasonable sensitivity. Increasing sample size improves these facets of the model. Our method using wavelets and wPCs better captured the local features of these simulations than the spline-based methods of Scheipl, Staicu, and Greven (2014), as shown in Web Appendix F.

5. Application

5.1 Description of ERP Data Set

To illustrate the performance of our proposed methods, we analyzed data from the Department of Behavioral Sciences at the University of Texas M. D. Anderson Cancer Center. As part of a smoking cessation trial, researchers obtained Event Related Potentials (ERPs) at baseline for subjects viewing a series of images of different types, including neutral, emotional (positive and negative), and cigarette-related.

EEG was continuously recorded during image presentation and collected using a 129-channel Geodesic Sensor Net and amplified with AC-coupled high-input impedance (200 MΩ) amplifier (Geodesic EEG System 250; Electrical Geodesics, Inc., Eugene, OR) referenced to the Cz electrode. The time series were preprocessed as described in Versace et al. (2010a), with 0.1Hz high pass and 100Hz low pass filters, blink-corrected using spatial filtering, transformed to average reference, segmented into 900ms segments from 100ms before each image shown to 800ms after, obvious artifacts removed, and ERPs obtained by averaging across images for each image type per subject/electrode. After this processing, for each subject, we are left with functions of length 225 for each image type for all 129 electrodes.

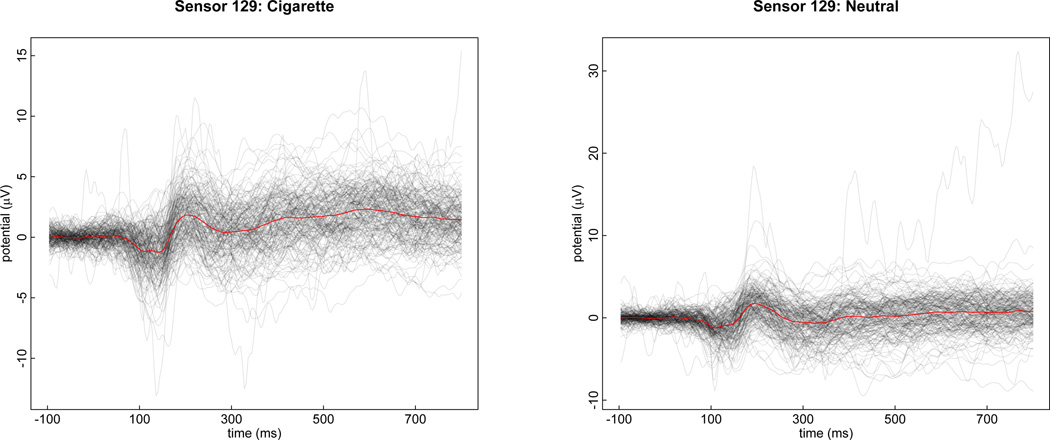
Example curves recorded from 180 participants at electrode Cz (#129, in the middle of the crown of the head) during presentation of cigarette-related and neutral images can be seen in Figure 2 with the average over curves included in red. Curves under the other image-types are similar in appearance. The irregularity and localized spikiness of the raw curves motivates our use of wavelets and wPC in our modeling approach (Figure 2).

Figure 2.

On the left, raw profile curves are plotted in gray with the mean in red from electrode 129 under the cigarette image condition. On the right, are raw curves and the mean from electrode 129 under the neutral image condition.

While many analyses are of interest for these data, in this paper we aim to characterize the time-varying relationship between ERP output from pairs of electrodes, focusing on two pairs in particular. The first pair is 55 and 129. Electrode 129, as previously mentioned, is positioned at the top of the head and electrode 55 is located directly behind it. We expect these two adjacent electrodes to be positively associated along the diagonal, t = υ, axis. The second pair is 75 and 11. Electrode 75 is an occipital electrode located at the back of the head while electrode 11 is at the front. Output from these two electrodes is expected to exhibit a negative correlation and thus we anticipate a negative association along the diagonal axis. For each pair of electrodes, we jointly model the association between the electrodes under both the neutral and cigarette image conditions resulting in a multilevel data structure. Thus, for each model, subjects have four curves resulting from measurements from two electrodes while viewing two different image types. We would like to assess the inter-electrode relationships, determine whether these relationships vary over the time the image is shown, and differ by image type. Note that our goal in this analysis is not a broad-scale analysis of all pairwise associations, for which other approaches may be more suitable (e.g. Montagna et al. (2012)), but rather perform function-on-function regression analyses of pre-specified pairs.

5.2 Analysis

We fit two models to the data. In general, the model is given by

$$y_{icg}(t)=1(g=0)[{\alpha }_0(t)+{\int }_{\upsilon \in \nu }{x}_{ic0}(\upsilon ){\beta }_0(\upsilon ,t)d\upsilon ]+1(g=1)[{\alpha }_1(t)+{\int }_{\upsilon \in \nu }{x}_{ic1}(\upsilon ){\beta }_1(\upsilon ,t)d\upsilon ]+U_i(t)+E_{ic}(t),$$ (9)

where g denotes group membership, 0 for neutral, 1 for cigarette. For the first model we used Electrode 129 as the outcome function and Electrode 55 as the predictor function. For the second we used Electrode 11 as the outcome and Electrode 75 as the predictor. In both models, inference was drawn on both image-specific surfaces, β₀ and β₁, as well as the difference surface D(υ, t) = β₁(υ, t) − β₀(υ, t). As in the simulation study, we used Daubechies wavelets with four vanishing moments, three levels of decomposition, and zero-padding. Prior to decomposition, we standardized both outcome and predictor functions by time. After DWT, the dimensions of the transformed functional outcomes from Electrodes 129 and 11 were both 360 × 245. After wPC and preserving 99% of the total variability in the signals, the dimensions of the transformed functional predictors were 360 × 72 for Electrode 55 and 360 × 62 for Electrode 75. We obtained 1000 posterior samples from the MCMC after a burn-in 1000.

MCMC convergence was assessed using Geweke’s Convergence Diagnostic (Geweke, 1992) and evaluation of first order auto-correlation coefficients for each coefficient on the surface. Both diagnostics suggest chain convergence. Details of the diagnostics along with histograms of Metropolis-Hastings acceptance rates can be found in the Web Appendix. For the model regressing Electrode 129 on to 55, the 95% interval of acceptance rates across all variance components was (0.431, 0.777) with a mean of 0.588. Acceptance rates for the model regressing Electrode 11 on to 75 were similar with 95% interval (0.405, 0.787) and mean 0.56.

We considered inference for both models using all three procedures. For the BFDR procedure, we selected a global α of 0.05 when implementing it on the difference surfaces. We choose a somewhat strict intensity change of δ = 0.05 to focus on large differences between the surfaces. Choice of δ will potentially affect results, thus additional choices of δ can be found in the Web Appendix. We also implemented BFDR on the image-specific surfaces in both models. There the α-level was reduced to 0.025 for each surface, however the intensity change, δ, remained at 0.05 so to only select relatively large associations. For comparability, the same intensity change was used for both models. For the PWCI, we also used α = 0.05.

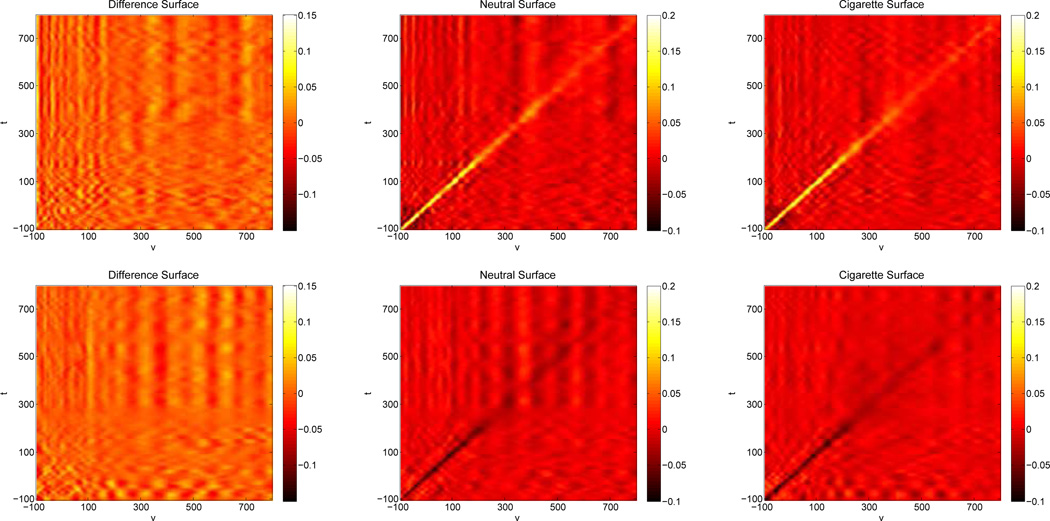
Figure 3 contains posterior means of all three surfaces for both models. Examination of the posterior estimates of the difference surfaces found in the first column of Figure 3 suggest little to no systematic difference between image type in both models. When we look at the image-specific surfaces in the model using electrodes 129 and 55 (top row, second and third column, Figure 3), we see an elevated ridge of association along the t = υ diagonal, which is the relationship we anticipated between these two adjacent electrodes. Note that this relationship is strongest in the first 300 ms in the ERP or 200 ms post picture presentation (image presentation occurred at t = υ = 0), corresponding to the initial response to viewing the image. Transitioning to the image-specific surfaces of the model using electrodes 11 and 75 (bottom row, second and third column, Figure 3), we see a valley of negative association along the t = υ diagonal that also begins to die out around 200 ms to 300 ms past presentation. Once again, this is consistent with the expected relationship between these two electrodes.

Figure 3.

The top row contains surface estimates for the association between electrodes 129 and 55. Posterior surfaces comparing electrodes 11 to 75 are in the second row. The estimated posterior surface of the difference between cigarette and neutral is found in the first column. Group specific surface estimates are in the second and third columns, Neutral and Cigarette respectively. ERP output from electrode 129 is the response and the output from electrode 55 is the predictor for the first model and electrode 75 is the predictor of electrode 11 in the second model.

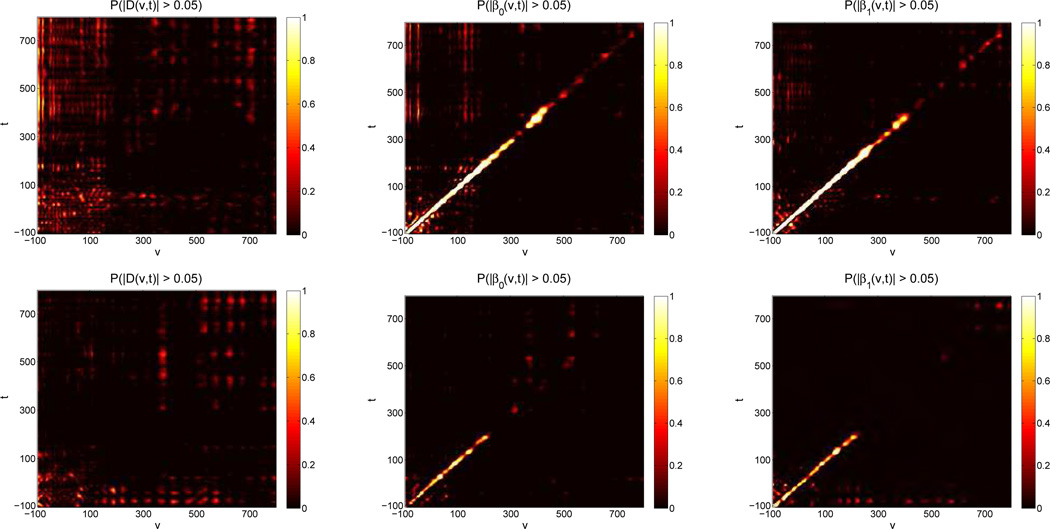
Figure 4 contains results from the BFDR procedure on the difference surface for both models. Each heat map plots the posterior probabilities P_BFDR. We see that for both models, most locations have a low probability of being greater than δ. In fact, plotting ψ, we see no regions identified as significant (see the Web Appendix), suggesting there is little evidence that the correlation across the two electrodes differs across image types. The second and third columns of Figure 4 show the application of the BFDR to the image-specific surfaces in each model, and again the heat maps plot the posterior probabilities P_BFDR. We see that the probabilities along the ridge are quite large suggesting that ridge of positive association is significant up until almost 300 ms past image presentation. However the negative association along the ridge we saw in the second model has lower probabilities along the ridge at the δ = 0.05 cut-off. The regions identified as significant by the procedure as well as additional choices of δ are presented in heat maps in Web Appendix.

Figure 4.

Heat maps containing the posterior probabilities from the BFDR procedure using a δ intensity change of 0.05. Locations (υ, t) in white have a high probability of being greater than δ and thus likely to be included in ψ, the set of locations identified as significant. Black locations (υ, t) have a low probability of being greater than δ and are thus less likely to be identified as significant. The top row contains results from the model using electrodes 129 and 55 while the second row contains results from the model using electrodes 75 and 11.

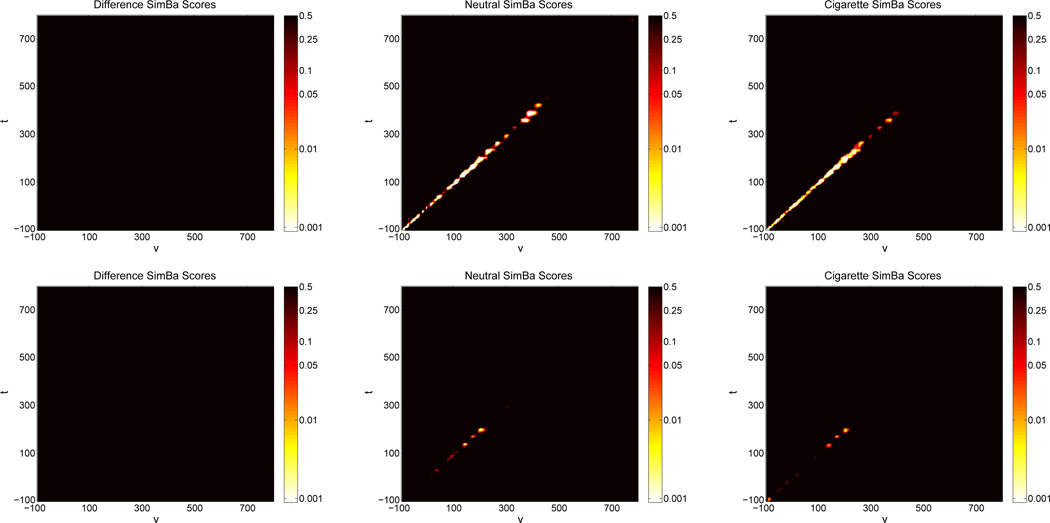
For the SimBaS procedure, we plot heat maps of the logged SimBa Scores in Figure 5. We see that for both difference surfaces, the SimBa scores are all relatively large (at least 0.5 or more), and the global Bayesian p-value for both is $P_{GBPV}^D=0.5$, suggesting there is not enough evidence to conclude differences in the coefficient surfaces between image types. The second and third columns of Figure 5 show the SimBaS procedure applied to the image-specific surfaces. These heat maps are also plotted on the log-scale so to distinguish variations in small SimBa scores. For both models, we see evidence of a non-zero coefficient surface for each image type (

$$P_{GBPV}^0=P_{GBPV}^1=0.001$$

for the model using Electrodes 129 and 55,

$$P_{GBPV}^0=0.001$$

and

$$P_{GBPV}^1=0.005$$

for the model using Electrodes 11 and 75). Additionally, the SimBaS procedure detects the ridge of positive association in first model but only finds some of the negative associations in second.

Figure 5.

Heat maps containing the SimBa scores for each surface of both models. The top row contains results from the model using electrodes 129 and 55 while the second row contains results from the model using electrodes 75 and 11. Scores are plotted on the log-scale with the color axis on the exponential scale. White regions represent coefficients with low SimBa scores, black regions represent coefficients with high SimBa scores.

Heat maps of significant locations using PWCI can be found in the Web Appendix. Not surprisingly, the PWCI is more sensitive to minor variations in the surface where there appears to be no systematic association. While both BFDR and SimBaS found no significant locations in the difference surfaces, the PWCI discovers a number of regions and also finds a number of significant locations in the image-specific surfaces that are off the t = υ axis while suggesting the association lingers longer. Given the results in the simulation studies, we interpret these results cautiously, as they may likely be spurious, and feel more confident in the multiplicity-adjusted inference from the BFDR and SimBaS procedures.

We calculated functional R² as described in Section 2.4. The model regressing Electrode 129 on to 55 had $R_{\mathit{\text{ave}}}^2=0.698$ while the model regressing Electrode 11 on to 75 had $R_{\mathit{\text{ave}}}^2=0.455$. We also examined the proportion of the variance attributable to the random effects. For the model regressing Electrode 129 on to 55, the random effects contributed to 35.6% to the total variability and residuals 64.4%, while for Electrode 11 regressed on 75 random effects contributed to 43.5% to the total variability and residuals 56.5%.

6. Discussion

Functional data analysis is an expanding field requiring more work to fill in gaps in the literature and build upon the general knowledge of the field. Previous work on function-on-function regression is limited. Here we present a general approach to function-on-function regression modeling which benefits from several attributes. First, our approach can use any basis function for y(t) and x(υ) allowing us to handle functions of various types, including those with spiky and smooth features, can be used with functions on higher dimensional domains like images, and allows us to parsimoniously model correlated residuals rather than assuming iid errors. Second, we get fully Bayesian inferences on all model quantities including point-wise credible intervals, posterior probabilities interpretable as Bayesian FDRs, joint credible intervals, and SimBaS that provide global and experiment-wise inferential quantities. Third, our inference procedures correctly identify regions of elevated association without falsely identifying too many non-significant coefficients. Fourth, our method resides within the functional mixed model (FMM) framework as put-forth by Morris and Carroll (2006) that handles correlation between functions and random effects through random effect function distribution, and thus accounting for the various sources of variability in multi-level models. Using the mixed model representation of penalized splines, this also allows the relaxation of the linearity assumption between Y (t) and X(υ), although details are beyond the scope of this paper. Finally, the FMM framework also allows any combination of continuous and discrete scalar predictors, functional predictors, and their interactions, allowing function-on-function regression to be done in a much broader modeling context.

We demonstrated by simulation that our model performs well for realistic sample sizes and forms of functional association with fits improving as sample size increases. Simulations also show the BFDR and SimBaS procedures have better false discovery and type I error rates than the PWCI with comparable sensitivity. Our approaches for global inference and multiple-testing adjustment for Bayesian inference using BFDR, SimBaS, and GBPV are of general interest and can be used in other functional regression settings.

Our application displays the ability of the model to estimate the forms of the relationship of ERP output between different electrodes on the scalp. With the neighboring electrodes, a positive association was expected and seen along the diagonal axis t = υ while a negative association was expected and seen between electrodes on opposite sides of the scalp. Further, both our inference procedures were able to detect these associations as significant, even the one based on experiment wise error rate.

In summary, the function-on-function mixed model with basis-space modeling comprises a flexible approach to the function-on-function regression setting. The method performed well in both simulation and application. Further studies are needed to explore the model’s performance in more complex settings, including non-functional components beyond a factor variable, incorporating multiple functional predictors, and various types of random effect correlation structures. Additionally, further examination of data reduction techniques could improve the modeling prowess of the method.